Abstract
This paper presents a stochastic method to estimate the multijoint mechanical impedance of the human arm suitable for use in a clinical setting, e.g., with persons with stroke undergoing robotic rehabilitation for a paralyzed arm. In this context, special circumstances such as hypertonicity and tissue atrophy due to disuse of the hemiplegic limb must be considered. A low-impedance robot was used to bring the upper limb of a stroke patient to a test location, generate force perturbations, and measure the resulting motion. Methods were developed to compensate for input signal coupling at low frequencies apparently due to human–machine interaction dynamics. Data was analyzed by spectral procedures that make no assumption about model structure. The method was validated by measuring simple mechanical hardware and results from a patient's hemiplegic arm are presented.
Keywords: Biomechanics, endpoint stiffness, stochastic estimation, stroke rehabilitation
I. Introduction
ABNORMAL muscle tone—a muscle's resistance to passive elongation or stretch—is one of the common and debilitating sequelae of neurological injury such as stroke. However, persons with stroke who had robotic therapy using a performance-based, progressive protocol experienced a marked reduction of abnormal tone [1], [2] which prompted us to investigate better ways to measure it. Hypertonia, an increase in resistance that occurs when a lesion is present in the upper motor neurons, may increase with movement and suddenly decrease (“clasp-knife spasticity”) or it may remain constant throughout the range-of-motion (“lead-pipe rigidity”); spasticity implies disease of the direct corticospinal tracts, whereas rigidity may suggest a lesion of the basal ganglia [3]. Clinicians are trained to judge muscle tone subjectively with, for example, the Modified Ashworth Scale (MAS). The MAS is an ordinal scale ([0, 1, 1+, 2, 3, 4] or [0, 1, 2, 3, 4, 5]) that describes the amount of resistance to passive motion [4]. MAS clinical evaluations are conducted by moving a limb about a joint at different speeds, and by noting the muscular response throughout the range of motion of the limb (i.e., both speed and position dependent). Although the MAS has been shown to be a reliable clinical scale [5], an objective measure would provide valuable insight about the effect of stroke on a hemiplegic limb and may better characterize the effect of rehabilitation therapy.
The physical quantity corresponding to clinical assessment of muscle tone is mechanical impedance1 Z(s), which characterizes the dynamic relation between motion and force, and may be considered a dynamic generalization of stiffness K (i.e., the static relation between displacement and force) [6]. The physical quantity relating applied forces to motion, termed mechanical admittance Y(s), is the inverse of impedance and may be considered a dynamic generalization of compliance C (i.e., the static relation between force and displacement). Hence, “dynamic stiffness” (K(s) = sZ(s)) and “dynamic compliance” (C(s) = Y(s)/s) are other common terms for related physical quantities but in this paper we use the term impedance generically to refer to all of the above. Robots such as MIT-MANUS [7] or InMotion2 (Interactive Motion Technologies, Inc., Cambridge MA) are able to deliver forces to a patient's limb and measure the position, velocity, and interaction forces between the robot and that limb. Therefore, these robots are well suited to objectively quantify at least one aspect of muscle tone.
Past reasons for measuring arm impedance range from understanding basic physiological properties of muscle [8] to testing different hypotheses concerning the maintenance of posture or the control of movement [9], [10]. Behavioral studies have also investigated how impedance properties vary with motor learning [11]. An initial attempt to measure human arm stiffness measured the restoring forces evoked when a series of displacement perturbations were applied in eight different directions in a horizontal plane while the subjects held the hand at the perturbation location [8]. The force and displacement vectors were then used to characterize stiffness. Since Mussa–Ivaldi et al. [8] were interested in measuring biomechanical properties subserving arm posture, the measurement procedure was designed to increase the duration of the subject reaction time in order to reduce the occurrence of voluntary movement.
Later studies were extended to include the estimation of dynamic parameters commonly used to quantify arm impedance, such as inertia and viscous damping. For example, Dolan et al. [12] applied several rapidly rising, underdamped position perturbations. By assuming a linear model structure, they were able to estimate the arm's inertial, damping, and stiffness properties using the force and displacement time histories in a Cartesian reference frame. Again, the experimental procedure attempted to limit voluntary responses to the applied perturbations. Tsuji et al. [13] conducted a similar experiment to estimate impedance properties and also transformed the property matrices from Cartesian coordinates at the hand to joint coordinates at the shoulder and elbow. In a later experiment by Gomi and Kawato [10], static stiffness was estimated by applying trapezoidal positional perturbations in eight randomly ordered directions. In addition, dynamic inertia, viscosity, and stiffness parameters were estimated during movement by applying a small, randomized force perturbation. As with previous experiments, the subjects were given instructions not to intervene voluntarily during perturbations.
The method described by Perreault et al. [14] used small stochastic force perturbations to estimate the impedance transfer function matrix and subsystem impulse response functions in the presence of output measurement noise and input coupling (via linear and nonlinear numerical simulations). Unlike the previous methods, a model structure was not assumed, although the system was assumed to behave linearly for small perturbations. System properties were estimated by using a previously developed multiple-input, single-output (MISO) system identification technique [15] applied to each output simultaneously, resulting in a multiple-input, multiple-output (MIMO) methodology. The unpredictable magnitude and direction of stochastic perturbations make it difficult for subjects to generate forces equal in magnitude and opposite in direction, hence minimize the likelihood of voluntary reactions [14], though compensatory actions such as muscle cocontraction or relaxation may still occur. However, random perturbations are also desirable as they obviate the need for separate measurements in different directions and provide a frequency-rich input to the subject in a relatively short time frame, rendering them more attractive for use with patients. This research group later modified their method and applied stochastic position perturbations instead of force perturbations [16]. However, given the extreme vulnerability of patients’ joints, we believe it would be unwise to apply position perturbations that might impose excessive forces on the limbs.
Impedance measurement in persons with stroke is complicated by their special circumstances, which may include hypertonicity, profound muscle weakness due to central denervation, tissue atrophy due to disuse of the hemiplegic limb, and concomitant vulnerability of the musculoskeletal system to externally applied forces [3]. For example, the shoulder joint is especially vulnerable in patients with upper-limb paresis, and joint pain and shoulder-hand syndrome are common side-effects of conventional physiotherapy. Nevertheless, because of the clinical importance of muscle tone, we have developed a new method to estimate limb impedance during stroke rehabilitation treatment.
In this paper, we present a methodology to estimate impedance that is tailored for clinical use. In addition to the application of force perturbations, a simple proportional-derivative (PD) controller is used to gently bring the patient's arm to a test location and limit large-scale deviations from that location. Although unimpaired subjects are able to relax their arm at a given location, the hemiplegic arms of patients often exhibit hypertonicity, causing their arms to substantially drift in the workspace. Two methods to reduce the impact of the human-machine interaction on the impedance estimate are introduced—an experimental method that modifies the commanded perturbation and an analytical method that improves the numerical conditioning of the estimate. The stochastic estimation method is validated using a mechanical spring array and results from a patient are presented.
II. Spectral Estimation of Human Arm Impedance
A. Apparatus
MIT-MANUS, a robot designed for clinical neurological applications, is configured for safe, stable, and compliant operation in close physical contact with humans [7], [17]. It was designed to have low intrinsic endpoint impedance (i.e., to be back-drivable), with low and nearly isotropic inertia (1 ± 0.33 kg; maximum anisotropy 2:1) and friction (0.84 ± 0.28 N; maximum anisotropy 2:1); its actuators are capable of producing a predetermined range of forces (0−45 N) and impedances (0−2000 N/m)2 [7], [17]. The angular displacements of the motors were measured by 16-bit resolvers3 and a forward kinematic transformation was used to define the Cartesian coordinates of the robot workspace, i.e., (x, y). Velocities were approximated by computing backward differences of the displacement values and then filtering the differences with a first-order Butterworth filter (cut-off frequency of 20 Hz). An ATI Gamma force transducer (ATI Industrial Automation, Inc., Apex, NC) was mounted to the end-effector to measure the interaction forces and torques between the robot and subject. Perturbation commands were generated at a sampling rate of 500 Hz by filtering a set of uniformly distributed random numbers with an eighth-order Butterworth filter that had a cutoff frequency of 15 Hz (selected to exceed the natural frequency of the human arm, ∼2 to 3 Hz). Tests with the end-effector of MIT-MANUS bolted to ground verified that it had sufficient bandwidth to deliver the desired force perturbations. The seed of the random number generator was varied to find a pair of signals with low coherence.
During the impedance measurement, patients were seated in the same configuration as the robot therapy sessions. Custom-made forearm troughs connected the subject's limb to the robot end-effector; the subject grasped a conical section of the trough while Velcro straps immobilized the wrist by securing the forearm to the trough [17]. Three-point seat-belts were used to minimize movement of the subject's trunk so that the therapy and impedance measurement focused on the subject's shoulder and elbow joints/muscles [17]. Trials lasted for 50 s (25 000 data points) allowing a number of sequential epochs of data to be averaged to reduce random error while allowing an acceptable spectral resolution. Patients were instructed to “simply relax and allow the robot to shake your arm” during the trials (six 50 s trials separated by 30 s of rest). The following section describes how a spectral estimate of impedance was computed using the force and displacement measurements.
B. Direct Estimate Using Stochastic Force Perturbations
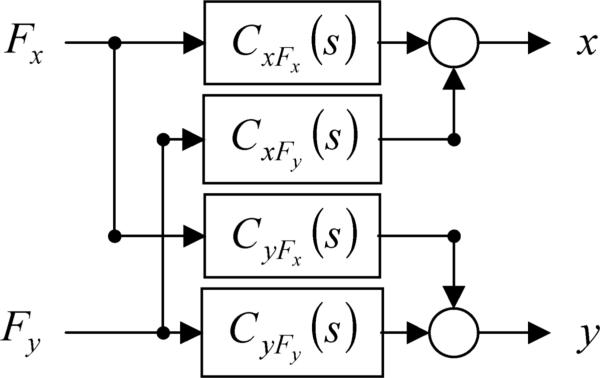
Although assuming a linear structure with second-order dynamics in each degree-of-freedom is appealing from intuitive and pedagogical standpoints (e.g., Dolan et al. [12], Tsuji et al. [13]), it is difficult to justify for the biological system being studied as it would neglect the higher-order dynamics of neuromuscular excitation, reflex action, and excitation-contraction coupling [6]. Frequency-domain MISO and MIMO system-identification algorithms assume the system behaves linearly for small perturbations, but otherwise do not assume any explicit structure. Fig. 1 displays a block diagram of the structure used to represent a linear impedance transfer function matrix, i.e.,
| (1) |
To simplify notation, the dependence of (1) on frequency f (or Laplace variable s) is implied. Spectral analysis of general MISO and MIMO systems is described in detail in Bendat and Piersol [15]. The spectral equations used to estimate impedance are defined in Palazzolo [18].
Fig. 1.
Block diagram of linear MIMO impedance structure: CxFx (s) and CxFy (s) are the transfer functions from the interaction forces, Fx and Fy, to the displacement x: CxFx (s) and CxFy (s) are the transfer functions from the interaction forces to the displacement the displacement y.
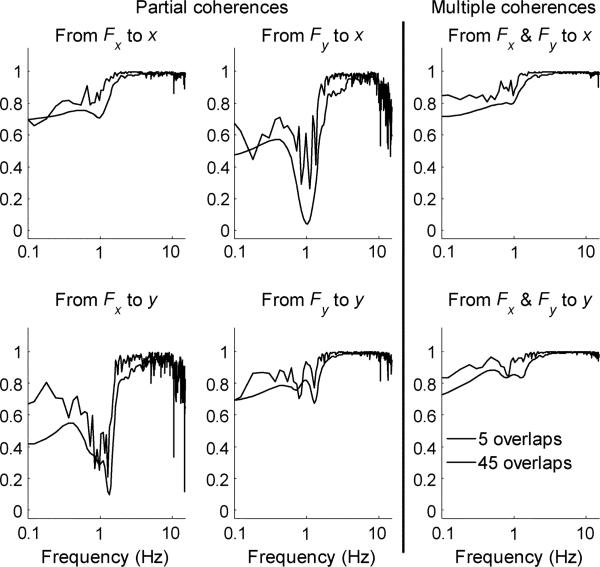
Partial and multiple coherence functions were used to assess the performance of the stochastic method [15]. Partial coherence measures the linear dependency of one input on a particular output and is equivalent to ordinary coherence after the effect of the other input has been removed. For example, the partial coherence from Fx to x after the effect of Fy has been removed is denoted as . Four partial coherence functions for the impedance spectral estimate (, , , and ) are defined in Palazzolo [18].
Multiple coherence functions measure how well a given output can be predicted from both of the inputs. They can also determine over what frequency range a linear model can accurately describe the system dynamics. Low multiple coherence values indicate insufficient input power, system nonlinearities, noise, and/or contributions from unmeasured inputs [14], [15]. The multiple coherence functions for the impedance spectral estimate ( and ) are defined in Palazzolo [18]. Although the analytical foundation of spectral estimation is well established, preliminary trials revealed that it would require modification to be applied to patients, as described next.
C. Compensating for Hypertonicity of Persons With Stroke
A pilot study4 conducted with three persons with stroke at The Burke Medical Research Institute, White Plains, NY revealed one difficulty that usually does not arise with unimpaired subjects, namely, their inability to relax at a given position. The hemiplegic arms of patients exhibiting flexor hypertonicity may curl towards the fetal position because their flexors contract more than their extensors. Therefore, although a patient's arm was brought to a desired position in the workspace and patients were instructed to “simply relax and allow the robot to shake your arm,” the limb often drifted from that position.
Eighteen trials (three patients, six trials each) were conducted in which a clinician manually moved the patient's arm to the desired test location, released it, and initiated the robot trial. The robot controller applied perturbations, but did not attempt to prevent drift. On average, patients drifted 7.8 cm (standard deviation 2.9 cm, minimum 4.4 cm, maximum 12.3 cm) during the test. Since arm impedance parameters vary significantly throughout the workspace this could result in significant nonlinearity or a nonstationary process, either or both of which would invalidate assumptions underlying the stochastic methods to be used. To prevent this, a simple PD controller was added to the robot control
| (2) |
where FC is the vector of commanded forces at the robot manipulandum, FΔ is the vector of commanded force perturbations, d = [x, y]T is the vector of measured Cartesian coordinates in the robot workspace, ddes is the desired test location, v is the first time derivative of d, kp is the controller proportional gain, and kd is the derivative gain.
The robot delivered the desired force perturbations in an open-loop manner (i.e., without feedback of the measured interaction forces). This avoided the difficult coupled instability problems that accompany the use of force feedback, an important consideration for patient safety. However, the closed-loop PD controller that was used to eliminate patient drift in the robot workspace also affected how much of the commanded perturbation was transmitted to the patient's arm. As the PD controller gains increased, the allowable deviation from ddes, along with the magnitude of the transmitted force, decreased. In addition, although the commanded perturbations were specified to have low coherence, the measured interaction forces exhibited a linear dependency in some frequency ranges, apparently because the interaction between robot and human introduced coupling between the x- and y-axes. Since the commanded perturbations are known and the interaction forces are measured, it is possible to estimate the transfer function matrix from FΔ to F denoted as T in Fig. 2.
Fig. 2.
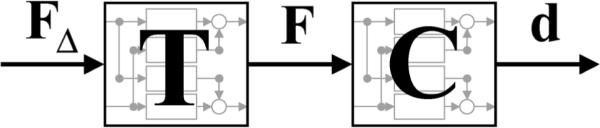
Block diagram of linear MIMO structures using vector and matrix notation: T(s) is the transfer function matrix from the commanded force perturbations, FΔ, to the interaction forces, F; C(s) is the transfer function matrix from the interaction forces to the displacements, d.
To gain a deeper understanding of this transfer function matrix, a state-space model of the human–machine interaction was defined by linearizing a nonlinear model of the robot interacting with a linear model of the human arm through a virtual force transducer [18]. The state space system relating FΔ to F, is defined as
| (3) |
where AT, BT, CT, and DT are the state space matrices of Tmodel(s) = CT(sI8×8 – AT)−1BT + DT, q = [θs, θe, ,,x,y,ẋ,ẏ]T is the state vector of absolute robot joint angles (θs,θe) and Cartesian hand coordinates (x, y) along with their first derivatives. This model suggested an experimental method to compensate for the human–machine interaction, discussed next.
D. Experimental Compensation of Human-Machine Interaction—Modified Perturbation Commands
The dynamics of the human-machine interaction may explain how the interaction forces Fx and Fy could exhibit high coherence even though the commanded perturbations FΔ,x and FΔ,y were specified with low coherence. If the gains of Txx, Txy, and Tyy (elements of T relating FΔ,x and FΔ,y to Fx and FΔ,y to Fy) were approximately equal and significantly larger than the gain of Tyx (element of T relating FΔ,x to Fy), then |Fx(f) = |Txx(f)FΔ,x(f) + Txy(f)FΔ,y(f)| would be linearly related to |Fy(f) ≅ Tyy(f)FΔ,y(f)| since both depend on FΔ,y.
The ideal transfer function matrix from FΔ to F is the identity matrix, i.e., T(f) = I2×2,∀f. To achieve this, a new set of experimental perturbations may be defined by premultiplying the original commanded perturbations by the inverse of Tmodel
| (4) |
When the modified perturbations are commanded, the originally intended set of perturbations will be delivered to the patient
| (5) |
Two drawbacks of this approach are that Tmodel requires an estimated linear model of the human arm and, since Tmodel depends on the operating condition, (4) must be applied at each test location individually. An analytical approach that attempted to improve the numerical conditioning of the spectral calculations by defining the inputs as FΔ instead of F to estimate C(s) is presented next.
E. Analytical Compensation of Human-Machine Interaction—Derived Estimate
An alternative estimate of C(s) can be derived based on the three systems shown in Figs. 2 and 3. Since FΔ, F, and d are known at the same instant in time, we can define the MIMO structures in Figs. 2 and 3 as
| (6) |
| (7) |
| (8) |
The inputs for the spectral estimates in (6) and (8) are the commanded perturbations (which, by design, have low coherence), whereas the inputs for the estimate in (7) are the measured interaction forces (which may have high coherence). By computing the spectral estimates for R and T, a “derived” estimate for C(s) can be defined that only requires low-coherence inputs because d = CF = CTFΔ RFΔ ⇒ CT = R. Specifically, at each frequency f
| (9) |
Furthermore, by assuming the noise output spectrum for the derived estimate is equal to the noise output spectrum of the direct estimate, partial and multiple coherences for Cder(s) can be defined analogously to those defined for C(s) [18].
Fig. 3.
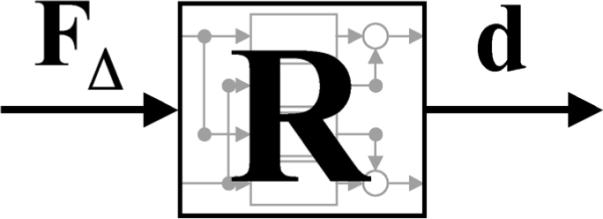
Block diagram of linear MIMO structure using vector and matrix notation: R(s) is the transfer function matrix from the commanded force perturbations, FΔ, to the displacements, d.
III. Experimental Results
A. Validation Via Mechanical Spring Array
Although using stochastic inputs to estimate the frequency response of a system is an established technology [14], [15], tests were conducted on mechanical systems to validate the experimental and analytical procedures [18]. A top view of the apparatus used is shown in Fig. 4. MIT-MANUS was mounted on a patient workstation and the outer fixture of the mechanical assembly was bolted to a bracket clamped to the workstation table. The inner fixture was bolted to the top of a handle used for therapy, which was bolted to the force transducer on the end-effector of the robot. Both the square outer fixture and the square inner fixture have four bolts located at their corners and four bolts at the midpoints of their sides to mount extension springs that generate a stiffness field at the end-effector of the robot. Thus, eight springs could be mounted between bolts on the inner and outer spring array fixtures to generate a variety of stiffness fields. The locations of the spring mounts along the perimeter of the inner and outer fixtures were specified to ensure the springs would always be in tension during testing.
Fig. 4.
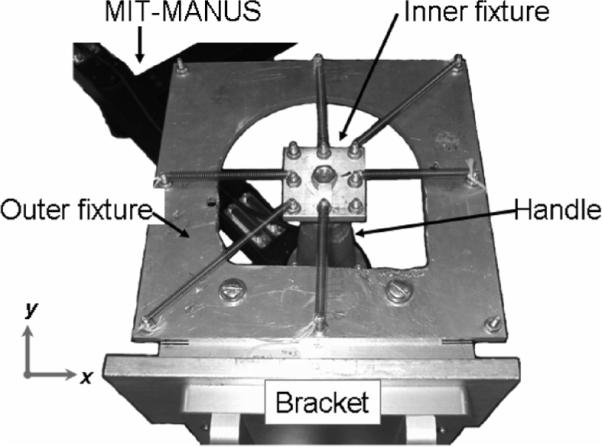
Top view of MIT-MANUS and the mechanical spring array used to validate the impedance spectral estimation method. In this test configuration (sa1), six extension springs are connected between the inner and outer fixtures to generate an elliptical stiffness field whose major and minor axes are different from the x- and y-axes.
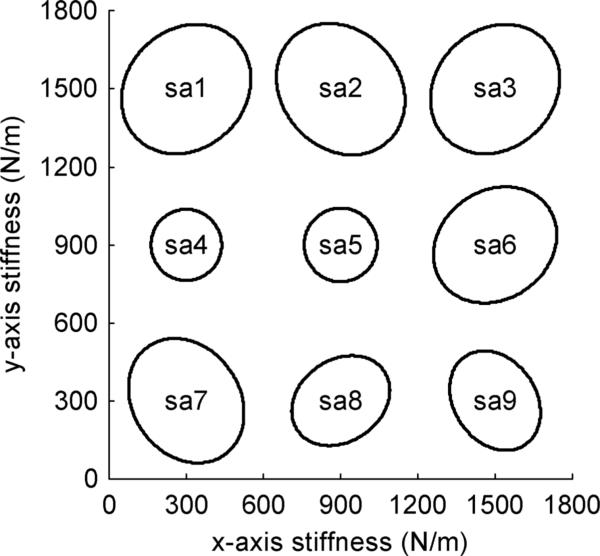
For comparison with the spectral estimates, a linearized model of the test apparatus was developed. The nonlinear restoring forces generated by the spring array were derived and then linearized to obtain an expression for the stiffness matrix K [18]. The magnitude of the linear restoring forces can be visualized by multiplying K by a unit vector that is rotated from 0° to 360°. Fig. 5 depicts stiffness ellipses for the nine test configurations (denoted sa1 to sa9) used during the validation study. Quasi-static calibration trials confirmed the linearized stiffness matrices were within the ±10% manufacturing tolerances of the mechanical spring constants. The mass of the handle and inner fixture was measured on a precision scale to be 0.429 kg. Although mechanical springs are close to ideal energy storage devices, some energy is dissipated during this process, e.g., internal damping present in the springs. Therefore, viscous damping was included in the model. The diagonal elements of the viscous damping matrix were defined such that the damping coefficient ζ was equal to 0.01, whereas the off-diagonal elements were set to zero.
Fig. 5.
Stiffness ellipses for the nine test configurations (sa1 to sa9) that were defined to validate the analytical and experimental procedures in the impedance spectral estimation method.
Six trials of each test configuration were run in succession. Welch's periodogram method was used to estimate the power spectral density and coherence functions needed to calculate Cder(s) [15], [18]. Two sets of parameters were defined to investigate the variation of the estimate with the spectral analysis parameters (the number of data points included in the FFT calculation, NFFT, the length of the Hanning windowing function, NWND, and the number of overlapped samples, NOVL). The first set (NFFT = 8192, NWND = 8192, and NOVL = 4096) resulted in NMNS = 5 overlapping segments of data to be used to calculate the power spectral density and coherence functions, whereas the second set (NFFT = 8192, NWND = 2048, and NOVL = 1536) resulted in NMNS = 45. Although increasing NMNS from 5 to 45 decreases the random error by 70% (e.g., for CxFx(s), exFx = ((1 – γFxx·Fy)/(2(NMNS – 1)γFxx·Fy))1/2, i.e., exFx ∝ 1/(NMNS – 1)1/2), the minimum resolvable frequency of the windowed FFT calculation increases from 0.061 to 0.244 Hz. The mean spectral estimates for six trials of test configuration sa1 are shown in Fig. 6 and the corresponding mean partial and multiple coherence functions are shown in Fig. 7. The expected behavior (based on the linearized model) is depicted by solid gray lines, the spectral estimate with NMNS = 5 by dashed lines, and the spectral estimate with NMNS = 45 by dash–dotted lines.
Fig. 6.
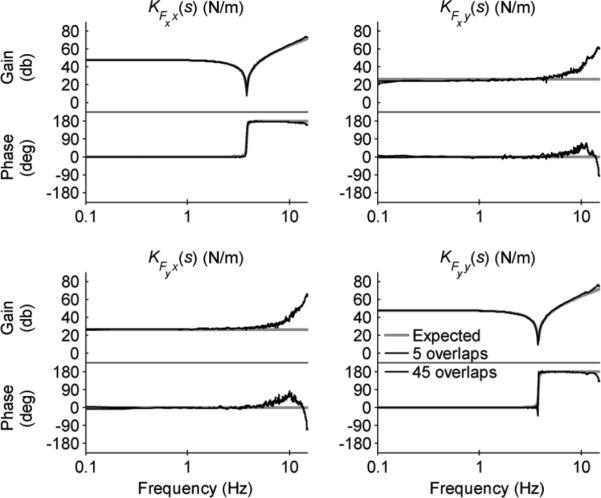
Expected behavior (based on linearized model) and mean spectral estimates for six trials of test configuration sa1. Both sets of spectral analysis parameters result in excellent estimates of the expected impedance frequency response.
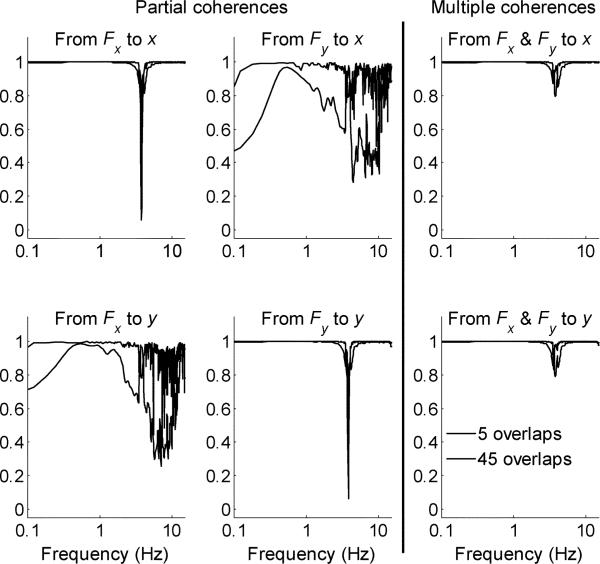
Fig. 7.
Mean partial and multiple coherence functions for six trials of test configuration sa1 that correspond to the spectral estimates shown in Fig. 6. Decreases in the partial and multiple coherences occur near the system resonances. Decreases in the off-diagonal elements of the partial coherence also occur at higher frequencies (inertia is isotropic and the off-diagonal elements are identically equal to zero).
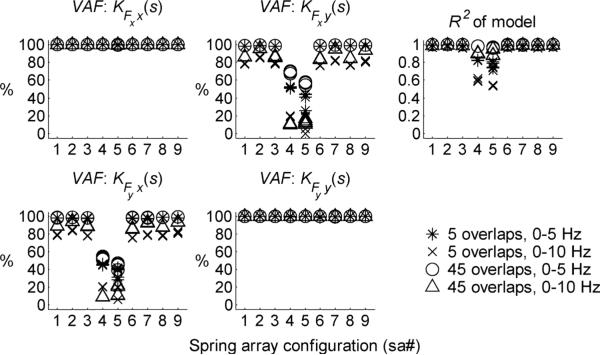
Two different measures (defined in Appendix) were used to evaluate the quality of the impedance estimates. Variance Accounted For (V AF ∈ [0%, 100%]) describes how close each of the estimated frequency responses come to the modeled frequency responses. The correlation coefficient squared (R2 ∈ [0, 1]) is a composite measure of the goodness of fit of all four elements of the transfer function matrix. Results for all six trials at each configuration (sa1 to sa9) with NMNS = 5 and NMNS = 45 over the frequency ranges of 0−5 Hz and 0−10 Hz are shown in Fig. 8. Aside from a small region in the vicinity of the resonant peak (where the phase angle changes rapidly), both measures indicate excellent agreement between measured and estimated behavior, validating the method.
Fig. 8.
Summary of the VAF values for each element of the impedance spectral estimate and the R2 values of the entire estimate for test configurations sa1 to sa9. Off-diagonal elements of VAF for sa4 and sa5 are numerically ill-conditioned because the inertia and stiffness matrices are isotropic (ideally, the off-diagonal elements are identically equal to zero).
B. Sample Results From the Hemiplegic Arm of a Person With Stroke
Similar to Fig. 6, the mean spectral estimates for six trials of a patient's left hemiplegic arm5 are shown in Fig. 9 and the corresponding mean partial and multiple coherence functions are shown in Fig. 10. The data was also fit to a second-order linear model of impedance using the MATLAB function lsqnonlin to determine optimal inertia, damping, and stiffness matrices. The cost function for the nonlinear least-squares problem is defined in Appendix. The resulting impedance (mean of six trials) is depicted by solid gray lines, the spectral estimate with NMNS = 5 by dashed lines, and the spectral estimate with NMNS = 45 by dash-dotted lines. Though the spectral estimates are remarkably similar to the best-fit linear model (especially below 5 Hz), the coherence plots below the resonance frequency are substantially lower than those achieved with the mechanical spring array.
Fig. 9.
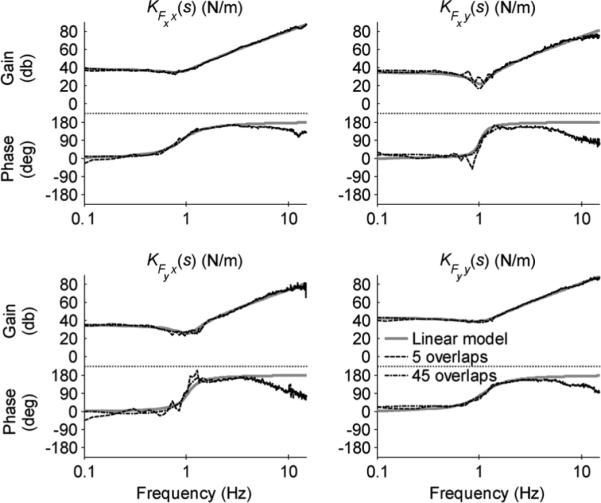
Modeled behavior (based on linear second-order model) and mean spectral estimates for six trials of a patient's hemiplegic left arm. The modeled frequency response elements capture the gain of both estimates throughout the frequency range shown, whereas the phase of both estimates deviates from the model for f > 5 Hz.
Fig. 10.
Mean partial and multiple coherence functions for six trials of a patient's hemiplegic left arm that correspond to the spectral estimates shown in Fig. 9. Decreases in the partial and multiple coherences occur near the system resonances. The partial coherence functions are close to 1 at higher frequencies.
IV. Discussion
Although the primary purpose for MIT-MANUS is to deliver rehabilitation therapy, its ability to deliver forces while measuring the resulting motion may be usable to assess muscle tone objectively. Estimates of impedance can be added to robotic evaluation and treatment sessions, and may complement clinical measures of tone such as the MAS [2], [4], [5]. The work presented here provides a basis for a test that can be used in a clinical setting and has been shown to reliably and accurately identify inertial and stiffness components of impedance.6
A stochastic estimation method was chosen for technical reasons outlined above but another consideration is that the duration of the test (50 s) is short enough that clinicians can measure patients during treatment sessions. It is also long enough to investigate the trade-off between random error and spectral resolution. Patient comfort and tolerance of the procedure is another important consideration. Not only have patients exposed to the measurement procedure tolerated it, they also seem to like the random nature of the test and liken it to a vibrating massage.
Although voluntary reactions to random inputs are unlikely, patients could still exhibit compensatory muscle activations, e.g. tensing up or relaxing. However, a close examination of the data indicated that the three patients in the pilot study did not change their muscle activation levels significantly during the three test runs. To check for stationarity, mean square values of the commanded perturbations and the interaction forces (minus their mean values) were calculated over equal time intervals [15]. The variation of the mean square values between Fy and FΔ,y were similar, but the input coupling along the x-axis caused the variation Fx to be influenced by the variation of both FΔ,x and FΔ,y. However, differences in the variation of Fx between the three tests were small () implying those variations were due to input coupling and not patient compensatory muscle activations. The normalized instantaneous values (e.g., FΔ,x – μ)/σ, where μ and σ are the mean and standard deviation of FΔ,x) of the measured interaction force data were also checked for normality using MATLAB's normplot function. Deviations from a normal distribution were small throughout the probability range 0.05 to 0.95 with the largest deviations below 0.01 and above 0.99. Finally, the force and displacement time histories for the three experimental test runs were similar throughout the test (, where is the average correlation coefficient between signals 1 & 2, 1 & 3, and 2 & 3).
Least-squares fitting of a linear impedance model with second-order dynamics in each degree of freedom showed that the spectral method, which assumed no model structure, resulted in a remarkably similar estimate for the arm's impedance, especially for frequencies below 5 Hz (Fig. 9, f < 5 Hz). However, the coherence plots indicate that this observation must be interpreted with caution. Even putting aside the region close to the system resonant frequency, which yielded low coherence even with the mechanical spring array, for frequencies below 1 Hz the coherence is generally about 0.8 or less. This indicated that, despite appearances, the patient's arm impedance behavior deviated measurably from linearity. Although random data methods do not assume a model structure, they do assume that the system behaves linearly for small perturbations, i.e., that the quantity being measured is a smooth function in the Lipschitz sense. However, nonsmooth nonlinearities abound in biological systems. For example, when active wrist muscles were cyclically stretched and shortened, Gillard et al. [19] showed that hysteresis in angle-torque curves was caused by short-range stiffness effects [20]. Within this range, actin-myosin cross-bridges are thought to remain attached and deform elastically; outside of this range, the cross-bridges detach and the stiffness decreases as the muscle lengthens [21]. Due to the cyclical nature of stochastic perturbations, a similar hysteresis may occur within the hypertonic arm muscles of patients. Further study with a larger patient population is needed to explore this question.
Above 5 Hz, the spectral estimate of impedance phase begins to roll off (Fig. 9, 5 ≤ f ≤ 10 Hz), again indicating a deviation from second-order behavior. However, in this case the coherences remain high, indicating that arm impedance behavior remains close to linear in this frequency range. The fact that the impedance magnitude remains close to that of the linear model while the phase differs suggests the effect of a time delay, possibly due to reflex action. Again, further study with a larger patient population is needed to clarify this matter. Nevertheless, these data indicate the sensitivity of the spectral method and its potential to provide finely resolved measurements of how stroke affects arm impedance.
Although force perturbations with low coherence were commanded, initial tests showed that the resulting interaction forces were linearly dependent, which would compromise the fidelity of the estimate. Inverting a model human-machine interaction () may improve input signal coherence but a problematic aspect of this approach is that Tmodel depends on the operating condition, on the properties of the robot, and, most importantly, on the human arm impedance properties to be estimated. Using parameters representing an average of a wide range of patients and/or unimpaired subjects may be acceptable but, at a minimum, a sensitivity analysis would be required to determine whether this would adversely affect the estimates. Another alternative may be to use a high-impedance robot to deliver position perturbations. In a clinical setting, however, one must take special care so that high forces are not delivered to a patient whose musculo-skeletal system may be substantially more fragile than an unimpaired subject's. Common side-effects of therapy after stroke are joint and tendon pain in the shoulder, wrist, and hand, as well as shoulder-hand syndrome, characterized by burning pain and swelling of the fingers and hand, skin atrophy, and a painful, stiff shoulder. Clinical trials with MIT-MANUS and InMotion2 have resulted in a reduction of these afflictions [1], [17], [22], [23]. This suggests that force perturbations with a low-impedance robot are advantageous, and perhaps required, for this application. The alternative method presented above, based on simultaneously estimating two transfer function matrices (between commanded and applied force, and between commanded force and observed motion), seems more appropriate for clinical work.
Although the present study focused on estimating impedance in the plane, the stochastic method can be easily generalized to any number of inputs and outputs [15]. For example, our research group has also developed a robot for wrist rehabilitation [24], [25] that senses and actuates the wrist in pronation/supination, abduction/adduction, and flexion/extension. Thus, by commanding three stochastic perturbations with low coherence, the impedance of the wrist can be estimated. Furthermore, given a measure of limb segment lengths and initial arm pose, the kinematic equations relating hand motion to joint motion may be formulated. If those equations are invertible (e.g., if the arm motion and the hand motion have the same number of degrees of freedom), it is straightforward to project the measured impedance at the hand to the corresponding impedance of the arm, e.g., about the shoulder and elbow joints, and this may have additional clinical value.
V. Conclusion
An arm impedance test suitable for clinical use was developed by adapting previous methods to the special requirements of this application. Experimental trials are currently underway to determine whether the spectral estimate can discriminate a reduction in tone (correlating to the MAS clinical evaluations) and provide further insight into the process of motor recovery from stroke.
Acknowledgments
This research was supported in part by the National Institutes of Health under Grant R01-HD37397, in part by The Burke Medical Research Institute, and in part by a New York State Score Award.
Biography
 Jerome J. Palazzolo received the B.S. and M.S. degrees in mechanical engineering from Michigan State University, East Lansing, in 1992 and 1994, respectively, and the Ph.D. degree in mechanical engineering from the Massachusetts Institute of Technology (MIT), Cambridge, in 2005.
Jerome J. Palazzolo received the B.S. and M.S. degrees in mechanical engineering from Michigan State University, East Lansing, in 1992 and 1994, respectively, and the Ph.D. degree in mechanical engineering from the Massachusetts Institute of Technology (MIT), Cambridge, in 2005.
After working as a Postdoctoral Associate at the Newman Laboratory for Biomechanics and Human Rehabilitation, Department of Mechanical Engineering, MIT, he began working for the Sentient Corporation, Williston, VT, specializing in model-based prognostics and health management (PHM) of machinery. His research interests are in the areas of dynamic systems modeling, control theory, PHM, adaptive robotic therapy/training, and human–machine interaction
 Mark Ferraro received the B.A. degree from Quinnipiac University, Hamden, CT, in 1996 and the M.S. degree from the International Academy of Orthopedic Medicine, Texas Technical University, Lubbock, in 1998.
Mark Ferraro received the B.A. degree from Quinnipiac University, Hamden, CT, in 1996 and the M.S. degree from the International Academy of Orthopedic Medicine, Texas Technical University, Lubbock, in 1998.
He was a Senior Occupational Therapist at the Burke Rehabilitation Hospital from 1998 to 2000 and joined the research team at the Burke Medical Research Institute in 2000. He was the clinical coordinator for an National Institutes of Health funded study of motor learning in stroke recovery from 1999 to 2004. He has continued his interest in bio-medicine and joined Novartis Pharmaceuticals in 2004.
 Hermano Igo Krebs received the electrician degree from Escola Tecnica Federal de Sao Paulo, Sao Paulo, Brazil, in 1976, the B.S. and M.S. degrees in Naval Engineering (option electrical) from University of Sao Paulo, Sao Paulo, Brazil, in 1980 and 1987, respectively. He received the M.S. degree in ocean engineering from Yokohama National University, Yokohama, Japan, in 1989, and the Ph.D. degree in ocean engineering from the Massachusetts Institute of Technology, Cambridge, in 1997, with the thesis “Robot-Aided Neuro-Rehabilitation and Functional Imaging.”
Hermano Igo Krebs received the electrician degree from Escola Tecnica Federal de Sao Paulo, Sao Paulo, Brazil, in 1976, the B.S. and M.S. degrees in Naval Engineering (option electrical) from University of Sao Paulo, Sao Paulo, Brazil, in 1980 and 1987, respectively. He received the M.S. degree in ocean engineering from Yokohama National University, Yokohama, Japan, in 1989, and the Ph.D. degree in ocean engineering from the Massachusetts Institute of Technology, Cambridge, in 1997, with the thesis “Robot-Aided Neuro-Rehabilitation and Functional Imaging.”
From 1977 to 1978, he taught electrical design at Escola Tecnica Federal de Sao Paulo. From 1978 to 1979, he worked at University of Sao Paulo in a project aiming at the identification of hydrodynamic coefficients during ship maneuvers. From 1980 to 1986, he was a surveyor of ships, offshore platforms, and containercranes at the American Bureau of Shipping—Sao Paulo office. In 1989, he was a visiting researcher at Sumitomo Heavy Industries, Hiratsuka Laboratories, Japan. From 1993 to 1996, he worked at Casper, Phillips & Associates in containercranes and control systems. He joined the Mechanical Engineering Department, MIT, in 1997, where he is a Principal Research Scientist and Lecturer, Newman Laboratory for Biomechanics and Human Rehabilitation. He also holds an affiliate position as an Adjunct Professor at University of Maryland School of Medicine, Department of Neurology and as Adjunct Assistant Research Professor of Neuroscience a Weill Medical College of Cornell University. He is one of the founders of Interactive Motion Technologies, a Cambridge-based startup company commercializing robot technology for rehabilitation. His present goal is to revolutionize the way rehabilitation medicine is practiced today by applying robotics and information technology to assist, enhance, and quantify rehabilitation; particularly neurorehabilitation. This goal translates into research interests in neurorehabilitation, functional imaging, human–machine interactions, robotics, and dynamic systems modeling and control.
Daniel Lynch received the B.S. and M.S. degrees in occupational therapy from the Dominican College, Orangeburg, NY, in 2001, and the M.B.A. degree from Long Island University, Purchase, NY, in 2006.
He was a staff therapist at the Burke Rehabilitation Hospital from 2001 to 2002 and joined the research team at the Burke Medical Research Institute in 2003. He has been the clinical coordinator for a National Institutes of Health funded study of motor learning in stroke recovery since 2004.”
He is the Clinical Coordinator for the study of Rehabilitation Robotics, Division of Neurology, Stroke Recovery Research, Burke Medical Research Institute, White Plains, NY.
Bruce T. Volpe received the B.S. and M.D. degrees from Yale University, New Haven, CT, in 1969 and 1973, respectively. He trained in medicine and neurology at the University of Chicago, Columbia University, and Cornell University.
He is a Professor at the Department of Neurology and Neuroscience, Burke Medical Research Institute, Weill Medical College, Cornell University, White Plains, NY. He is also a Lecturer in the Department of Mechanical Engineering at the Massachusetts Institute of Technology and a member of te Department of Biomedical Engineering at Cornell University. He has a long term interest in brain recovery from stroke. He is also interested in a model of antibody mediated disease.”
 Neville Hogan was born in Dublin, Ireland. He received the Dip. Eng. (with distinction) from Dublin College of Technology, Dublin, Ireland, and the M.S., M.E., and Ph.D. degrees from the Massachusetts Institute of Technology (MIT), Cambridge.
Neville Hogan was born in Dublin, Ireland. He received the Dip. Eng. (with distinction) from Dublin College of Technology, Dublin, Ireland, and the M.S., M.E., and Ph.D. degrees from the Massachusetts Institute of Technology (MIT), Cambridge.
Following industrial experience in engineering design, he joined the Faculty of the School of Engineering, MIT, in 1979 and has served as the Head and Associate Head of the System Dynamics and Control Division, Department of Mechanical Engineering. He is Professor of Mechanical Engineering, Professor of Brain and Cognitive Sciences, and Director of the Newman Laboratory for Biomechanics and Human Rehabilitation, MIT. He is a cofounder of Interactive Motion Technologies, Inc., Cambridge, MA, and a Board Member of Advanced Mechanical Technologies, Inc., Watertown, MA. His research is broad and multidisciplinary, extending from biology to engineering; it has made significant contributions to motor neuroscience, rehabilitation engineering and robotics, but its focus converges on an emerging class of machines designed to cooperate physically with humans. Recent work pioneered the creation of robots sufficiently gentle to provide physiotherapy to frail and elderly patients recovering from neurological injury such as stroke, a novel therapy that has already proven its clinical significance.
Prof. Hogan has received several awards including an Honorary Doctorate from the Delft University of Technology, the Silver Medal of the Royal Academy of Medicine in Ireland, and an Honorary Doctorate from the Dublin Institute of Technology, Dublin, Ireland.
Appendix
Appendix Definition of VAF and R2
In an attempt to weight the inertial and stiffness properties equally, calculations were conducted on the impedance (input velocity, output force) rather than dynamic stiffness (input displacement, output force). Instead of a frequency response that is constant at low frequencies and has a slope of +40 db/decade at high frequencies, the frequency response for impedance has slopes of − 20 and +20 db/decade at low (stiffness-dominated) and high (inertia-dominated) frequencies.
The quadratic cost function was defined in terms of the impedance gain and phase as
| (A.1) |
where zg,w and zp,w are vectors of differences between the estimated [subscript e in (A.2)] and modeled [subscript m in (A.2)] impedance gains (db) and phases (deg) that are weighted [subscript w in (A.1) and (A.2)] by the corresponding partial coherence function (γe) at each frequency data point, i.e.,
| (A.2a) |
| (A.2b) |
Since partial coherence functions indicate whether the relationship between the input and output is linear, weighting by this function will devalue differences between the estimated and expected frequency responses when the partial coherence is close to zero. An additional factor of 10 was used in (A.2a) to weight differences in gain higher than differences in phase (the MATLAB function lsqnonlin uses the vector to to define ψz and to search for the optimum parameter values). The gain and phase of the impedance of the second-order model were used to normalize the value of ψz in order to define VAF and R2. Specifically
| (A.3) |
| (A.4a) |
| (A.4b) |
Next, the VAF matrix and R2 were defined as
| (A.5) |
| (A.6) |
Footnotes
Publisher's Disclaimer: This material is posted here with permission of the IEEE. Such permission of the IEEE does not in any way imply IEEE endorsement of any of this web site's products or services. Internal or personal use of this material is permitted. However, permission to reprint/republish this material for advertising or promotional purposes or for creating new collective works for resale or redistribution must be obtained from the IEEE by writing to pubs-permissions@ieee.org.
In this paper, the term “impedance” is used synonymously with “mechanical impedance” for brevity.
InMotion2 is capable of delivering a far larger range of impedances (0−5000 N/m).
InMotion2 employs 16-bit virtual absolute encoders instead of resolvers.
Although accepted into a robotic study, patients had not yet begun their protocol and had no prior experience with the robot or robotic therapy. The institutional review boards of the Burke Rehabilitation Hospital and the Massachusetts Institute of Technology approved the protocol. Written informed consent was obtained from all patients. Selection criteria: Patients had hemiparesis or hemiplegia of the upper extremity after a single stroke (identified by neuroimaging) that had occurred at least eight months prior to the initial assessment. Sensory or visual field impairment, aphasia, and cognitive impairment were not exclusion criteria, but the patients needed to be able to follow simple instructions.
Male, age 77, left hemiplegia, Total MAS of 12 (nine muscle groups (maximum 45): shoulder internal rotator, elbow flexor/extensor, forearm pronator/supinator, wrist pronator/supinator, digit flexor/extensor).
Although not reported here, trials were also conducted with different masses confirming that the method was able to discriminate impedance at both low frequencies (stiffness) and high frequencies (inertia) [18].
Contributor Information
Jerome J. Palazzolo, Massachusetts Institute of Technology, Department of Mechanical Engineering, Newman Laboratory for Biomechanics and Human Rehabilitation, Cambridge, MA 02139 USA. He is now with the Sentient Corporation, Williston, VT 05495 USA (e-mail: jjpalazz@alum.mit.edu).
Mark Ferraro, The Burke Medical Research Institute, White Plains, NY 10605 USA. He is now with Novartis Corporation, New York, NY 10020 USA..
Hermano Igo Krebs, Massachusetts Institute of Technology, Department of Mechanical Engineering, Newman Laboratory for Biomechanics and Human Rehabilitation, Cambridge, MA 02139 USA, the Weill Medical College of Cornell University, Department of Neurology and Neuroscience, The Burke Medical Research Institute, White Plains, NY 10605 USA, and the University of Maryland School of Medicine, Department of Neurology, Baltimore MD 21201 USA (e-mail: hikrebs@mit.edu)..
Daniel Lynch, The Burke Medical Research Institute, White Plains, NY 10605 USA (e-mail: dlynch@burke.org)..
Bruce T. Volpe, The Burke Medical Research Institute and the Weill Medical College of Cornell University, Department of Neurology and Neuroscience, The Burke Medical Research Institute, White Plains, NY 10605 USA (e-mail: bvolpe@burke.org).
Neville Hogan, Massachusetts Institute of Technology, Department of Mechanical Engineering, Department of Brain and Cognitive Sciences, Cambridge, MA 02139 USA, and Newman Laboratory for Biomechanics and Human Rehabilitation, Cambridge, MA 02139 USA (e-mail: neville@mit.edu)..
References
- 1.Krebs HI, Palazzolo JJ, Dipietro L, Ferraro M, Krol J, Rannekleiv K, Volpe BT, Hogan N. Rehabilitation robotics: Performance-based progressive robot-assisted therapy. Auton. Robot. 2003;15(1):7–20. [Google Scholar]
- 2.Ferraro M, Palazzolo JJ, Krol J, Krebs HI, Hogan N, Volpe BT. Robot-aided sensorimotor arm training improves outcome in patients with chronic stroke. Neurology. 2003;61(11):1604–1607. doi: 10.1212/01.wnl.0000095963.00970.68. [DOI] [PubMed] [Google Scholar]
- 3.Encyclopaedia Britannica, Nervous system disease [Online] Available: http://www.search.eb.com/eb/article?tocId=225715.
- 4.Ashworth B. Preliminary trial of carisoprodol on minimal to moderate spasticity in multiple sclerosis. Practioner. 1964;192:540–542. [PubMed] [Google Scholar]
- 5.Bohannon RW, Smith MB. Interrater reliability of a modified ashworth scale of muscle spasticity. Phys. Ther. 1987;67(2):206–207. doi: 10.1093/ptj/67.2.206. [DOI] [PubMed] [Google Scholar]
- 6.Hogan N. Skeletal muscle impedance in the control of motor actions. J. Mech. Med. Biol. 2002;2(3−4):359–373. [Google Scholar]
- 7.Hogan N, Krebs HI, Sharon A, Charnnarong J. Interactive robotic therapist. 1995 U.S. Patent 5 466 213. [Google Scholar]
- 8.Mussa-Ivaldi FA, Hogan N, Bizzi E. Neural, mechanical, and geometric factors subserving arm posture in humans. J. Neurosci. 1985;5(10):2732–2743. doi: 10.1523/JNEUROSCI.05-10-02732.1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hogan N. The mechanics of multi-joint posture and movement control. Biol. Cybern. 1985;52(5):315–331. doi: 10.1007/BF00355754. [DOI] [PubMed] [Google Scholar]
- 10.Gomi H, Kawato M. Human arm stiffness and equilibrium-point trajectory during multi-joint movement. Biol. Cybern. 1997;76(3):163–171. doi: 10.1007/s004220050329. [DOI] [PubMed] [Google Scholar]
- 11.Burdet E, Osu R, Franklin DW, Milner TE, Kawato M. The central nervous system stabilizes unstable dynamics by learning optimal impedance. Nature. 2001;414(6862):446–449. doi: 10.1038/35106566. [DOI] [PubMed] [Google Scholar]
- 12.Dolan JM, Friedman MB, Nagurka ML. Dynamic and loaded impedance components in the maintenance of human arm posture. IEEE Trans. Syst. Man Cybern. 1993 May/Jun;23(3):698–709. [Google Scholar]
- 13.Tsuji T, Morasso PG, Goto K, Ito K. Human hand impedance characteristics during maintained posture. Biol. Cybern. 1995;72(6):475–485. doi: 10.1007/BF00199890. [DOI] [PubMed] [Google Scholar]
- 14.Perreault EJ, Kirsch RF, Acosta AM. Multiple-input, multiple-output system identification for characterization of limb stiffness dynamics. Biol. Cybern. 1999;80(5):327–337. doi: 10.1007/s004220050529. [DOI] [PubMed] [Google Scholar]
- 15.Bendat JS, Piersol AG. Random Data: Analysis and Measurement Procedures. Wiley; New York: 2000. [Google Scholar]
- 16.Acosta AM, Kirsch RF, Perreault EJ. A robotic manipulator for the characterization of two-dimensional dynamic stiffness using stochastic displacement perturbations. J. Neurosci. Meth. 2000;102(2):177–186. doi: 10.1016/s0165-0270(00)00307-1. [DOI] [PubMed] [Google Scholar]
- 17.Krebs HI, Hogan N, Aisen ML, Volpe BT. Robot-aided neuro-rehabilitation. IEEE Trans. Rehabil. Eng. 1998 Mar.6(1):75–87. doi: 10.1109/86.662623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Palazzolo JJ. Ph.D. thesis. Dept. Mech. Eng., Massachusetts Institute of Technology; Cambridge: 2005. Robotic technology to aid and assess recovery and learning in stroke patients. [Google Scholar]
- 19.Gillard DM, Yakovenko S, Cameron T, Prochazka A. Isometric muscle length-tension curves do not predict angle-torque curves of human wrist in continuous active movements. J. Biomech. 2000;33(11):1341–1348. doi: 10.1016/s0021-9290(00)00127-5. [DOI] [PubMed] [Google Scholar]
- 20.Joyce GC, Rack PM, Westbury DR. The mechanical properties of cat soleus muscle during controlled lengthening and shortening movements. J. Physiol. 1969;204(2):461–474. doi: 10.1113/jphysiol.1969.sp008924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Rack PM, Westbury DR. The short range stiffness of active mammalian muscle and its effect on mechanical properties. J. Physiol. 1974;240(2):331–350. doi: 10.1113/jphysiol.1974.sp010613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Volpe BT, Krebs HI, Hogan N, Edelstein L, Diels C, Aisen M. A novel approach to stroke rehabilitation: Robot-aided sensorimotor stimulation. Neurology. 2000;54(10):1938–1944. doi: 10.1212/wnl.54.10.1938. [DOI] [PubMed] [Google Scholar]
- 23.Fasoli SE, Krebs HI, Stein J, Frontera WR, Hogan N. Effects of robotic therapy on motor impairment and recovery in chronic stroke. Arch Phys Med Rehabil. 2003;84(4):477–482. doi: 10.1053/apmr.2003.50110. [DOI] [PubMed] [Google Scholar]
- 24.Williams DJ, Krebs HI, Hogan N. A robot for wrist rehabilitation. IEEE Proc. 23rd Int. Conf. Eng. Med. Biol. Soc.; Istanbul, Turkey. 2001. pp. 1336–1339. EMBS. [Google Scholar]
- 25.Krebs HI, Celestino J, Williams D, Ferraro M, Volpe BT, Hogan N. A Wrist Extension to MIT-MANUS. In: Bien Z, Stefanov D, editors. Advances in Rehabilitation Robotics: Human-friendly Technologies on Movement Assistance and Restoration for People With Disabilities. Springer-Verlag; New York: 2004. [Google Scholar]