Trypsin-Ligand Binding Free Energies from Explicit and Implicit Solvent Simulations with Polarizable Potential

Abstract

We have calculated the binding free energies of a series of benzamidine-like inhibitors to trypsin with a polarizable force field using both explicit and implicit solvent approaches. Free energy perturbation has been performed for the ligands in bulk water and in protein complex with molecular dynamics simulations. The calculated binding free energies are well within the accuracy of experimental measurement and the direction of change is predicted correctly in call cases. We analyzed the molecular dipole moments of the ligands in gas, water and protein environments. Neither binding affinity nor ligand solvation free energy in bulk water shows much dependence on the molecular dipole moments of the ligands. Substitution of the aromatic or the charged group in the ligand results in considerable change in the solvation energy in bulk water and protein whereas the binding affinity varies insignificantly due to cancellation. The effect of chemical modification on ligand charge distribution is mostly local. Replacing benzene with diazine has minimal impact on the atomic multipoles at the amidinium group. We have also utilized an implicit solvent based end-state approach to evaluate the binding free energies of these inhibitors. In this approach, the polarizable multipole model combined with Poisson-Boltzmann/surface area (PMPB/SA) provides the electrostatic interaction energy and the polar solvation free energy. Overall the relative binding free energies obtained from the PMPB/SA model are in good agreement with the experimental data.

Introduction

Molecular recognition plays a key role in many biomolecular processes such as enzyme catalysis, intracellular signaling and protein conformational switching. The modern drug discovery process begins with an identification of small molecules that interact with specific targets such as receptors, enzymes, hormones, ion channels and other macromolecules with high affinities. Physical-based molecular modeling has been sought after as the potential technique to accelerate and facilitate the drug discovery process. From rapid empirical docking to sophisticated quantum mechanical (QM) ab initio theory, from explicit-water molecular dynamics simulations to implicit solvent continuum approaches, a range of computational methods have been utilized to determine the binding affinity of small molecules to macromolecular targets.^1–5 Although great progress has been made in various fronts, including the rigorous treatment of long-range electrostatic interactions^6,7 and the sophisticated sampling algorithms for free energy calculations,⁸ there remain challenges in using molecular modeling to make reliable predictions of ligand binding affinities. Two immediate obstacles are limited sampling of protein-ligand-water interaction and accuracy of the potential energy function describing the atomic interactions.

The current generation of empirical force fields available for biological systems^{9– 11} is based on the classical molecular mechanics (MM) framework and employs a fixed-charge representation of electrostatics. While the fixed-charge model is computationally efficient and effective for various applications, it lacks the ability to represent non-isotropic charge distributions at the atomic level and does not respond to the change in local environment.^12,13 In recent years, increased effort has been devoted toward developing polarizable electrostatic models based on classical induced dipoles,^14–19 fluctuating charges,^20–22 and Drude oscillators.^23–25 Recently polarizable potentials have been utilized to study ion solvation,^26,27 liquid thermodynamics,^18,19,21,28 the infrared spectra of the polypeptide,²⁹ pKa shift of ionizable residues,³⁰ and the protein-ligand recognition.^31,32

Previously we have utilized a polarizable atomic multipole-based potential to calculate the absolute binding free energy of benzamidine to trypsin.³¹ We concluded that the electronic polarization renders very different effect in protein and water environments and should be taken into account explicitly for accurate free energy evaluation. Unlike the absolute binding free energy, relative binding free energy is more likely to be predicted accurately due to systematic error cancellation. There have been extensive studies of relative binding affinity using an array of explicit and continuum based methods.^2,5 Several have reported good agreements with experiment.^33–35 However, consistent prediction of relative binding affinity from molecular simulations is not yet robust or fully validated due to the relative computational expense compared to docking like approaches.⁵ Further work on a wide range of molecular systems is needed to gain a firm understanding of the capability of molecular modeling to rank ligand affinity in silico.

Trypsin/Benzamidine has been a prototypical system for evaluating modeling techniques. A good number of ligands that inhibit trypsin and other serine proteases have been investigated via computer simulations. Free energy perturbation (FEP)³⁶ and thermodynamic integration (TI)^37,38 with explicit solvent simulations, QM³⁹ and MM-based implicit solvent⁴⁰ and other approximated approaches⁴¹ have all been attempted. Several of the studies have focused on a series of ligands of similar physicochemical properties, e.g. benzamidine derivatives with various p-substituted alkane groups. Essex and Jorgensen have suggested that, although more hydrogen bonds are found in more tightly bound ligand, the bulk solvation effect dominates the binding affinity, i.e. more polar ligands would be weaker inhibitors due to better solvation in bulk water.³⁶ The underestimation of binding affinity for benzamidine has been attributed to a deficiency in the partial charges used. The opinion of bulk-solvation domination has been echoed by others.⁴² According to Grater et al.,³⁹ the van der Waals energy is the major energy term that favors binding to trypsin. A recent study shows that the relative binding affinity results obtained with a polarizable force field are much more correlated with experimental data than a non-polarizable force field, suggesting the inadequacy of the latter for charged systems.³² In this work we present a study of a series of ligands with different aromatic and charged groups using a polarizable potential for the entire system of protein, ligand and water. We report binding free energies from both explicit solvent molecular dynamics simulations and a polarizable Poisson-Boltzmann continuum method.⁴³ Aside from free energy calculations, we have also examined the charge distribution in the ligands and the protein-ligand-water interactions in atomic detail.

Methods

Ligands of trypsin

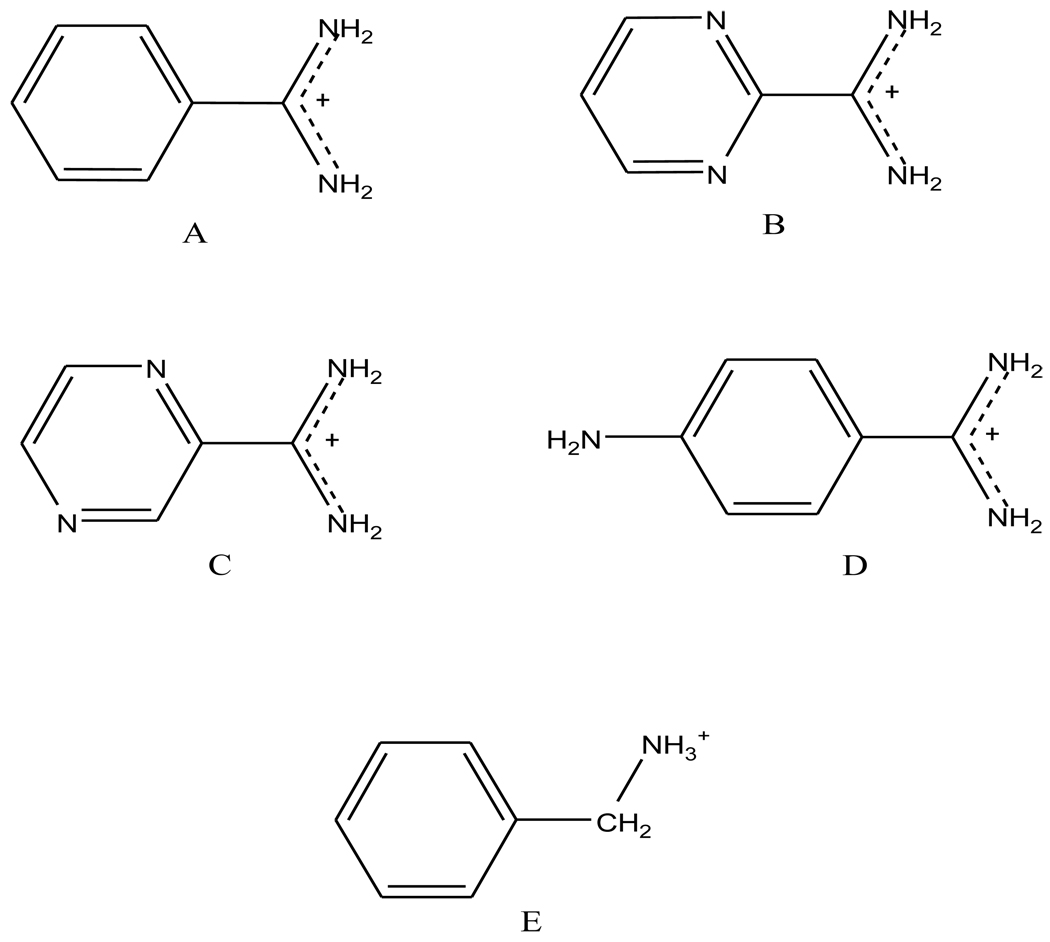
The signature aspartic acid residue located at the binding site of trypsin provides strong electrostatic interactions with counter-charged ligands. All five ligands we have investigated in this work contain a positively charged functional group (Figure 1). Benzamidine (ligand A), consists of a hydrophobic phenyl ring and a positively charged amidinium group that forms a salt bridge with the aspartic acid. The second and third ligands are similar to benzamidine except that the phenyl ring is replaced by a 1,3-dizine (or pyrimidine) and 1,4-diazine (or pyrazine), respectively. Ligand D, 4-amino-benzamidine, contains a NH₂ substitution group at the 4 position of the phenyl ring. In ligand E, a protonated amine replaces the amidinium group.

Figure 1.

Chemical structures of trypsin ligands studied: A. benzamidine; B. 1,3-diazamidine; C. 1,4-diazamidine; D. 4-amino-benzamidine; E. Benzylamine.

Force field and parameterization

Molecular mechanics simulations were performed using a polarizable force field for the entire system, including ligand, water and trypsin. The electrostatic interaction is represented by permanent atomic charges, dipoles and quadrupoles, plus a polarization effect via atomic induced dipoles. The model has been introduced previously for water,¹⁸ ions^26,27 and dipeptides.⁴⁴ The force field was recently applied to compute the absolute binding free energy of benzamidine to trypsin.³¹ The parameters for water and protein are available with the TINKER molecular modeling package.⁴⁵ Parameterization for the new ligands in this work is described as follows.

The structure of each ligand was optimized quantum mechanically at the level of HF/6-31G* using Gaussian 03.⁴⁶ A single point energy calculation was performed subsequently at the MP2/6-311++G(2d,2p) level to compute the molecular dipole moment and the density matrix. The electrostatic parameters, including monopole, dipole and quadrupole moments, were derived from the density matrix using GDMA v2.2.⁴⁷ The hydrogen atomic radius parameter was set to 0.31. The van der Waals (vdW), bond, angle, and atomic polarizability parameters of the ligands were transferred from the AMOEBA potential (amoebapro.prm) available in TINKER. The relevant parameters of the amidinium group were taken from the guanidinium group of arginine. The equilibrium bond and angle values were adjusted to match the geometry obtained from force field and QM optimizations. For ligand A, B, and C, the only rotatable dihedral angle is the one that links the aromatic ring and the amidinium group. We adopted a generic torsional energy term, E_tor = 2.70*(1-cos2(φ) kcal/mol, for all three ligands. The same torsional parameters were applied to the bond between the 4-amino group and the phenyl ring in ligand D. The bonds between the phenyl ring and the amine group of ligand E are single bonds in nature, and the torsional contribution is insignificant to the overall rotational energy barrier (E_tor = 0.064*(1-cos2φ)+0.605*(l-cos3φ) kcal/mol). The molecular dipole moment vector was computed for each ligand in gas-phase using the standard orientation from QM optimization. To calculate the ligand dipole moments in bulk water and solvated complex, the averaged atomic induced-dipole moments were collected from the molecular dynamics simulations. The permanent and induced multipoles were then applied to the same QM geometry to compute the ligand dipole moments. All the structure files and ligand parameters used in this work are included in the supplemental data.

Free energy perturbation

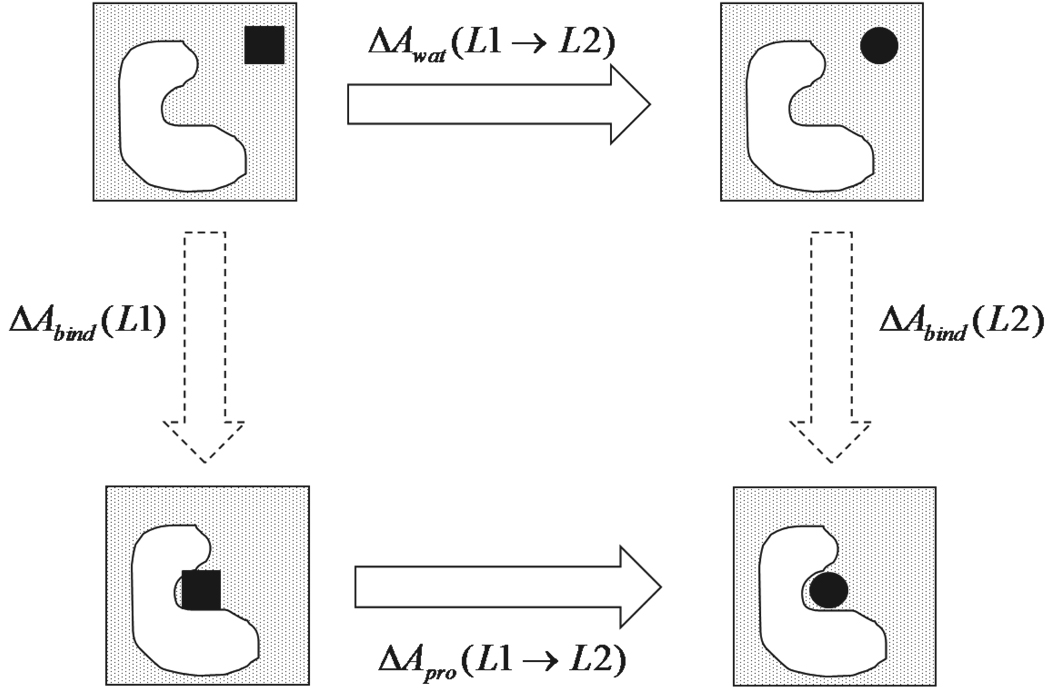
Free energy perturbation (FEP)⁴⁸ was utilized to compute the free energy change between two states. Relative binding free energy was calculated for ligands B through E by perturbing each into benzamidine in both neat water and the protein complex (Figure 2). The relative binding free energy between two ligands was computed as:

$$\mathrm{\Delta }\mathrm{\Delta }{A}_{\mathit{\text{bind}}}(L1\to L2)=\mathrm{\Delta }{A}_{\mathit{\text{pro}}}(L1\to L2)-\mathrm{\Delta }{A}_{\mathit{\text{wat}}}(L1\to L2)$$

Each path of perturbation consisted of ~12 intermediate states, by linearly interpolating the ligand electrostatic and vdW parameters between the two end states.

Figure 2.

Thermodynamic cycle of relative binding free energy calculation in explicit water MD simulations.

The free energies between two neighboring states were calculated using the Bennett Acceptance Ratio estimator.⁴⁹

$$\mathrm{\Delta }A=\frac{1}{\beta }\text{ln}\frac{{\langle 1/(1+\text{exp}\left[\beta (U_0-U_1+C)\right])\rangle }_1}{{\langle 1/\left(1+\text{exp}\left[\beta (U_1-U_0-C)\right]\right)\rangle }_0}+C$$

$$C=\mathrm{\Delta }A$$

The statistical error in the free energy change between two steps was computed from Eq. 10 in ref. (49). The total statistical error in the solvation free energy in bulk water or complex is computed as the sum of the errors from individual perturbation steps. When atoms were being annihilated, the electrostatic interaction between the relevant atoms and environment were turned off before the vdW interactions to avoid numerical instability. Internal valence terms, including bond, angle and torsion, were also changed along the path. In the annihilation of vdW interactions, the soft-core approach was used to turn off the interactions between the dummy atoms and all other atoms in the system:⁵⁰

$$U_{ij}={\lambda }^5{\epsilon }_{ij}\frac{{1.07}^7}{\left[0.7{(1-\lambda )}^2+{(\rho +0.07)}^7\right]}\left(\frac{1.12}{0.7{(1-\lambda )}^2+{\rho }^7+0.12}-2\right)$$

Explicit solvent molecular dynamics simulations

At each perturbation step, molecular dynamics simulations of ligand in bulk water and protein were performed, respectively. The initial systems were prepared using TINKER. The benzamidine-trypsin crystal structure (1BTY)⁵¹ was used as a starting structure to generate new structures for the other ligands. The ligands D and E were placed into trypsin by superimposing the phenyl ring onto that of benzamidine. Based on the crystal structure, HIS40 and HIS91 are deprotonated at εN while HIS57 is deprotonated at εN. The protein-ligand complex was placed in a periodic octahedral water box. For ligands A, B and C, we continued to use our previous system of 2222 water molecules (the containing cubic box is 51Å on each side).³¹ For ligands D and E, we adopted a bigger octahedron box with 4515 water molecules and 58 Å on each side. An internal water molecule is present in the crystal structure, hydrogen-bonded to the amidinium group of benzamidine (Figure 4a). In our system construction, the trypsin-ligand complexes were soaked into a water box and internal water molecules were added into the binding site where space allowed, without utilizing the information on crystal water. TINKER placed one or two water molecules near the Aspl89-amidinium/amine site as shown in Figure 4b through Figure 4e.

Figure 4.

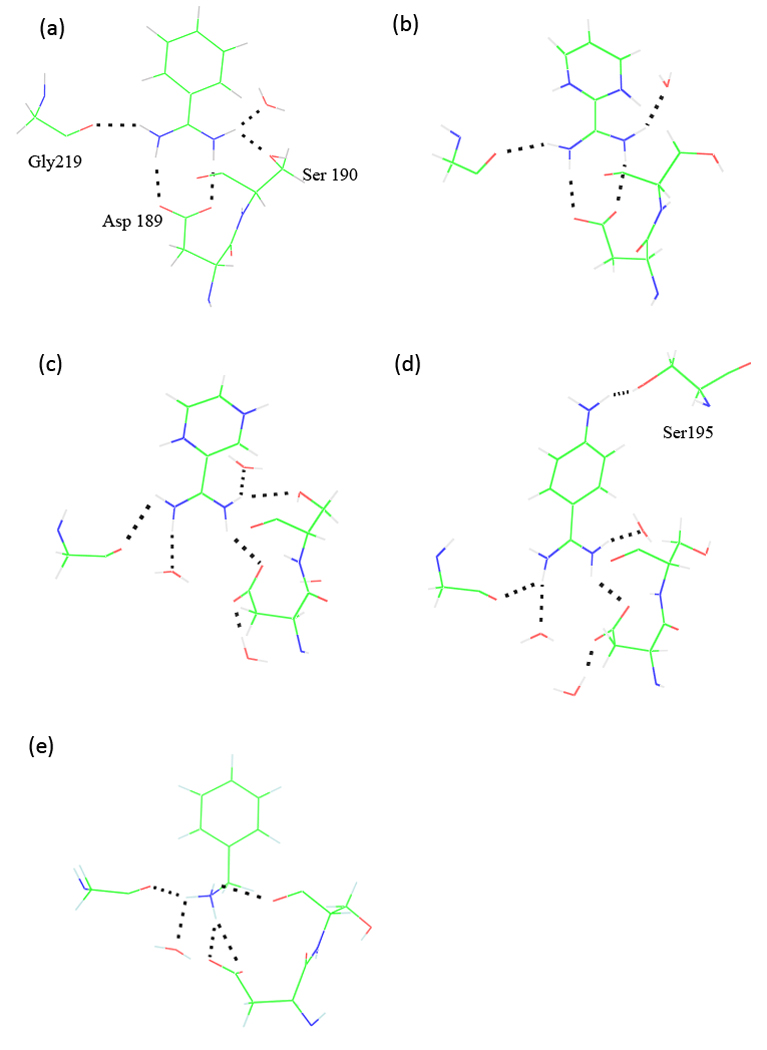
Intermolecular hydrogen bonding structure between ligand and trypsin at the binding site, (a) Crystal structure of trypsin in complex with ligand A (PDBID 1BTY). (b) to (e) are representative snapshots from explicit-water molecular dynamics simulations of trypsin with ligand B to E, respectively.

All production MD simulations were performed along the perturbation pathways described above using PMEMD in AMBER v9.⁵² We were able to achieve more than 200 ps per day with an 8-core 2.8 GHz Xeon computer for the 58 Å system, a speedup of ~4x over a single core. A 100 ps NPT dynamics simulation was first performed to equilibrate the system. The resulting configuration was then subject to the NVT simulations with the density fixed at the NPT-average. The same procedure was applied to prepare the ligand-water systems which were also octahedron boxes containing about 400 water molecules. NVT dynamics simulations of 1 to 2 ns were performed on the trypsin-ligand systems at each perturbation step as required for statistical convergence, whereas 0.5 ns simulations were conducted for all ligand-water systems. A 1 fs time step was used. Atomic coordinates of the simulation system were saved every 500 fs. The temperature was maintained at 298 K using the Berendsen thermostat.⁵³ The vdW cutoff was set to 9 Å, with a long-tail correction included. Particle Mesh Ewald (PME) was used to treat the electrostatic interactions, with a real-space cutoff of 7.0 Å. To speed up the simulation, the induced dipoles were iterated until the root-mean-square change was below 0.05 D per atom. In the post-MD free energy analysis with the Bennett acceptance ratio⁴⁹ (discussed below), we used a tighter convergence criterion, 10⁻⁵ D per atom.

Implicit solvent calculation

In an alternative end-state approach, the polarizable multipole was combined with Poisson-Boltzmann (PMPB)⁴³ method and surface area (SA) approximation of nonpolar solvation free energy to calculate the absolute and relative binding free energies. For each ligand, 80 snapshots were taken from the last 200 ps of the explicit solvent MD simulation trajectories. All water molecules were removed. The free energy was calculated as an average over values obtained from the snapshots using the following equations:

$$\begin{array}{c}\hfill \mathrm{\Delta }{A}_{\mathit{\text{bind}}}=\mathrm{\Delta }{A}_{\mathit{\text{gas}}}+\mathrm{\Delta }{A}_{\mathit{\text{solv}}}^{PL}-\mathrm{\Delta }{A}_{\mathit{\text{solv}}}^P-\mathrm{\Delta }{A}_{\mathit{\text{solv}}}^L=\mathrm{\Delta }{U}_{\mathit{\text{gas}}}-T\mathrm{\Delta }S+\mathrm{\Delta }{A}_{\mathit{\text{solv}}}^{pL}-\mathrm{\Delta }{A}_{\mathit{\text{solv}}}^p-\mathrm{\Delta }{A}_{\mathit{\text{solv}}}^L\hfill \\ \hfill \mathrm{\Delta }{U}_{\mathit{\text{gas}}}\cong \mathrm{\Delta }{E}_{\mathit{\text{gas}}}=\mathrm{\Delta }{E}_{\mathit{\text{elec}}}+\mathrm{\Delta }{E}_{\mathit{\text{vdw}}}\hfill \end{array}$$

where ΔE_gas is the gas phase potential energy change upon ligand and protein binding, and $\mathrm{\Delta }{A}_{\mathit{\text{solv}}}^P,\mathrm{\Delta }{A}_{\mathit{\text{solv}}}^L\text{and}\mathrm{\Delta }{A}_{\mathit{\text{solv}}}^{PL}$ are the solvation free energies of protein, ligand, and complex,, respectively. Each solvation free energy is further decomposed into polar and nonpolar parts:

$$\mathrm{\Delta }{A}_{\mathit{\text{solv}}}=\mathrm{\Delta }{A}_{\mathit{\text{polar}}}+\mathrm{\Delta }{A}_{\mathit{\text{nonpolar}}.}$$

The polarizable multipole-based Poisson-Boltzmann method was used to calculate the polar solvation free energy. The PMPB calculations were performed at 298 K with a dielectric constant of 78.54 for water solution and 1.0 for the protein interior. The probe molecular radius was set to 1.4 Å. Multiple-charge Debye-Hückel Dirichlet boundary conditions were used to solve the equation with a spline window of 0.3 Å and grid spacing of 0.38 Å. The scaling factor for Bondi radius was set to 1.16. In addition, the nonpolar contribution (A_nonpolar) to the solvation free energy was estimated from the solvent-accessible surface area approximation⁵⁴ implemented in TINKER.

The gas phase entropy changes (TΔS) upon binding were estimated by subtracting the entropies of the ligand-free protein (TS^P) and the ligand (TS^L) from that of the complex (TS^PL). For every molecule, the translational, rotational and vibrational entropies were calculated using the equations:^55,56

$$\begin{array}{c}\hfill T{S}_{\mathit{\text{trans}}}=k_{B}T\left[\frac{5}{2}+\frac{3}{2}\text{ln}\left(\frac{2\pi m{k}_{B}T}{h^2}\right)-\text{ln}(\rho )\right]\hfill \\ \hfill T{S}_{\mathit{\text{rot}}}=k_{B}T\left[\frac{3}{2}+\frac{1}{2}\text{ln}(\pi I_A{I}_B{I}_C)+\frac{3}{2}\text{ln}\left(\frac{8{\pi }^2{k}_{B}T}{h^2}\right)-\text{ln}(\sigma )\right]\hfill \\ \hfill T{S}_{\mathit{\text{vib}}}={\displaystyle \sum _{i=1}^{3N-6}\left[\frac{h{\nu }_i}{e^{h{v}_i/k_{B}T}-1}-k_{B}T\text{ln}\left(1-e^{-h{v}_i/k_{B}T}\right)\right]}\hfill \end{array}$$

Here m is the mass, ρ is the number density, I_A, I_B and I_C are the three principal moments of inertia, σ is the symmetry factor (2 for ligand A, B, and D; 1 for ligand C and E), h is Planck’s constant and ν_i is the frequency of the ith normal mode from the normal-mode analysis (NMA).

Performing normal modes analysis is extremely time-consuming especially for large molecular systems. First, an energy minimization is required for each snapshot. Secondly, it is computationally expensive to obtain the Hessian matrix for the proteins. It is therefore impractical to estimate the entropy contribution for many structures. An alternative is to ignore the protein atoms at a certain distance away from the ligand and thus to reduce the degrees of freedom in the calculation. However, both approaches suffer from a large fluctuation in the estimated entropy from one snapshot to another. A recent study suggested that the uncertainty can be reduced by dividing the complex into active and inactive (or buffer) regions.⁵⁷ Following this protocol, we adopted an active region consisting of all atoms within 8 Å from the ligand while all the other atoms outside this region were kept fixed during the minimization of the active region. The Hessian matrix calculation was restricted to the active region only. This approach was applied to both the complex and the free protein. The PMPB/SA and normal mode calculations were performed using the TINKER package.⁴⁵

Results and Discussion

Relative binding free energy

We have performed a series of molecular dynamics simulations to perturb the ligand from benzamidine to another in both bulk water and in the solvated complex. The polarizable potential is applied to the entire system in all simulations. From these simulations, we were able to compute the relative binding free energy for each ligand (Figure 2), as well as the absolute binding free energy based on the previously calculated value for benzamidine.³¹ The results are summarized in both Table 1 and Table 3. The experimental binding free energies are based on inhibition constants determined by spectrophotometry or isothermal titration calorimetry under various assay conditions. The existence of multiple experimental values for the same ligand indicates that the experimental uncertainty is almost 1 kcal/mol in energy or one order of magnitude in binding affinity. The relative affinity from the same source should be more reliable although for ligand D we find two sets of values that differ by 0.3 kcal/mol (Table 3).

Table 1.

Relative and absolute binding free energies from the explicit solvent FEP simulations. All relative values were computed with respect to benzamidine (ligand A). Statistical errors are given in the parenthesis.

	A	B	C	D	E
ΔAwat	0	−25.51(0.5)	−10.55(0.5)	−1.46(0.5)	−20.93(0.7)
ΔApro	0	−23.76(0.4)	−8.74(0.3)	−1.74(0.4)	−19.60(0.6)
ΔΔAbind	0	1.75	1.81	−0.28	1.33
ΔAbind	−6.3	−4.6	−4.5	−6.6	−5.0
Experiment	−6.3,1 −6.4,2 −7.33	−4.71	−4.81	−7.0,2 −7.24	−3.8,5 −4.76
Other computation	−6.41	−7.01	−6.51	−6.14	−4.25, −2.46

¹Ref³⁹. Calculation using PB/S A combined with QM/MM.

²Ref⁴².

³Ref⁶⁶.

⁴Ref⁶⁷. Calculation using PB/SA.

⁵Ref³⁷. Non-Boltzmann thermodynamic integration (NBTI) MD simulations.

⁶Ref⁵⁹. Linear interaction energy (LIE).

Table 3.

Relative binding energies to benzamidine (Ligand A) from explicit and implicit solvent calculations (kcal/mol). See Table 1 for references for the experimental values. The experimental data from the same source were used for ligands B, C and D. For ligand E, we used the more recent data.⁵⁹

	A→B	A→C	A→D	A→E
Experimental	1.6	1.5	−0.6/−0.9	1.6
Explicit FEP (this work)	1.8	1.8	−0.3	1.3
MM-PMPB (this work)	1.9	5.5	−1.2	1.6
QM/MM-PB/SA1	−0.6	−0.1	NA	NA
QM/MM-PB/SA2	0.6	0.6	NA	NA
PB/SA3	1.9	NA	0.70	NA

¹Table 1 in Ref 39. Flexible trypsin.

²Table 2 in Ref39. Rigid trypsin.

³Table 1 in Ref67.

The calculated absolute and relative binding free energies are in excellent agreement with experimental measurements. We are satisfied that in all cases the sign of the binding affinity change has been predicted correctly. All relative solvation free energies are negative, indicating that ligands B through E are all better solvated than benzamidine (ligand A) in bulk as well as in trypsin binding site. The free energy changes in both environments are fairly significant for B, C and E, on the order of −10 to −20 kcal/mol, when the phenyl ring is replaced by a diazine or the charged amidinium by an amine. However, the change in bulk water is mostly compensated by that in the complex, leading to a net decrease in the binding free energy of ~1.5 kcal/mol. Thus, ligands B, C, and E are predicted to be somewhat less potent inhibitors than benzamidine, in agreement with experiment. As for ligand D with an extra NH₂ substituent on the phenyl ring (Figure 1), the free energy changes in water and in the protein complex are relatively small: −1.46 and −1.74 kcal/mol, respectively. As a result, the binding affinity of ligand D increased slightly over that of benzamidine. However, the calculated magnitude of change is less significant than the experimental value.

From our previous analysis,³¹ we concluded that van der Waals interaction is the main cause for the decrease in the binding affinity from ligand A (benzamidine) to ligand B (1,3-diazamidine). Similarly, we found that for ligand C (1,4-diazamidine), the vdW interaction remains the dominant factor in the relative binding affinity. By contrast, the electrostatics amounts to more than 60% of the change in the binding free energy for both ligands D (4-amino-benzamidine) and E (benzylamine). The separation of electrostatics and vdW contribution is somewhat artificial depending on the choice of the specific perturbation path. Nonetheless, the results suggest that the net change from benzamidine to ligand B or C, where two aromatic CH groups are replaced by two N atoms, is mostly a size effect as the electrostatic contribution to ΔA_sol compensate between the water and the protein environments.

Molecular dipole moments of the ligands

Electrostatic interactions are important factors to the trypsin-ligand recognition as the presence of the charged group is crucial.⁴² While the aromatic benzene is commonly considered as a “hydrophobic” group, the accurate account for hydrophobicity also depends on the details of electrostatic interaction with water and other surrounding atoms. In a previous study, we evaluated the effect of polarization in binding by switching off dipole induction between the benzamidine and its environment. We concluded that polarization actually worked to offset the permanent electrostatic attraction between benzamidine and trypsin. Here we have calculated the dipole moment of each ligand in gas phase, bulk water, and protein complex, to characterize the ligand charge distributions (Table 4). The molecular dipole moments computed from polarizable atomic multipoles, which have been derived from QM ab initio calculation, in principle reproduce the ab initio dipole moments exactly. The discrepancy between the gas phase dipole moments from QM and from force field calculations seen in Table 4 is due to the averaging of atomic multipoles over symmetric atoms, such as the hydrogen atoms in amine and amidinium groups. The averaging is for the sake of simplicity, but is also necessary as we are unable to distinguish these atoms individually in our simulations. Electronic polarization in bulk water and in protein complex leads to an increase in the molecular dipole of up to 10%, with the protein environment consistently showing a greater effect than the bulk water environment. Ligand B (1,3-dizamidine) is the least affected by induction. Note that the polarization effect on the ligand is only a small fraction of that in the whole system; the protein is significantly polarized by the ligand as we have discussed previously.³¹

Table 4.

Molecular dipole moments (Debye) in gas, in bulk water and protein-ligand complex from quantum mechanics ab initio calculations (QM) at MP2/6-311++G(2d,2p) and molecular dynamics simulations using the polarizable force field.

		Total	DX	DY	DZ
A	Gas phase(QM)	6.00	−6.00	0.00	0.00
	Gas phase	6.21	−6.21	0.00	0.00
	Water	6.67	−6.67	0.00	0.00
	Protein	6.88	−6.88	0.00	0.00
B	Gas phase(QM)	3.75	−3.75	0.00	0.00
	Gas phase	3.73	−3.73	0.00	0.00
	Water	3.83	−3.83	0.00	0.00
	Protein	3.98	−3.98	0.03	0.00
C	Gas phase(QM)	6.24	−6.23	0.00	0.00
	Gas phase	6.61	−6.60	0.39	0.00
	Water	7.11	−7.10	0.34	0.00
	Protein	7.17	−7.16	0.43	0.00
D	Gas phase(QM)	4.21	4.21	0.00	0.00
	Gas phase	4.37	4.37	0.00	0.00
	Water	4.79	4.79	0.00	0.00
	Protein	5.08	5.08	0.00	0.00
E	Gas phase(QM)	8.93	8.66	0.00	2.19
	Gas phase	9.50	9.15	0.00	2.57
	Water	10.28	9.93	0.02	2.66
	protein	10.80	10.49	−0.15	2.59

When a series of similar ligands are considered, it has been suggested that there is a correlation between the molecular polarity and the binding affinity - the more polar ligand is better solvated in water and therefore has lower affinity to trypsin.^36,42 In our calculation, there is, however, no evident correlation between the molecular dipole and binding affinity. It is interesting that ligands B and C, with 1,3-diazine and 1,4-diazine in place of benzene, respectively, have dramatically different molecular dipole moments as well as solvation energies in bulk water (Table 5) while the binding free energies are essentially identical. According to the solvation free energies calculated from FEP, ligand B, with the smallest molecular dipole moment, is best solvated in bulk water (or in protein complex) of all the ligands (Table 5). Therefore the molecular dipole moment is inadequate to differentiate the electrostatic details among the ligands.

Table 5.

Ligand solvation free energies in bulk water from QM ab initio methods with continuum solvation, MM-PMPB/SA and explicit solvent FEP simulations using the polarizable force field. ΔA_sol is the total ligand solvation free energies (kcal/mol) in bulk water including the polar (ΔA_sol,polar) and the non-polar components.

	$\mathrm{\Delta }{A}_{\mathit{\text{sol}}}^{MP2}$ 1	$\mathrm{\Delta }{A}_{\mathit{\text{sol}},\mathit{\text{polar}}}^{MP2}$ 1	$\mathrm{\Delta }{A}_{\mathit{\text{sol}}}^{DFT}$ 2	$\mathrm{\Delta }{A}_{\mathit{\text{sol}},\mathit{\text{polar}}}^{DFT}$ 2	$\mathrm{\Delta }{A}_{\mathit{\text{sol}}}^{PMPB}$ 3	$\mathrm{\Delta }{A}_{\mathit{\text{sol}},\mathit{\text{polar}}}^{PMPB}$ 3	$\mathrm{\Delta }{A}_{\mathit{\text{sol}}}^{FEP}$
A	−59.3	−64.6	−57.9	−59.1	−54.2	−56.8	−45.8
B	−55.8	−60.8	−57.1	−57.6	−55.6	−58.1	−71.7
C	−62.6	−67.6	−62.1	−62.6	−58.3	−60.9	−56.4
D	−58.6	−64.1	−56.0	−57.1	−53.4	−56.2	−47.1
E	−69.7	−75.4	−64.1	−65.1	−57.6	−60.1	−66.8

¹From MP2/6-31+G* with PCM implicit solvent model.

²From B3LYP/6-31G* with PCM model.

³MM-PMPB/SA approach.

In changing ligand A to B, the phenyl ring is mutated into a pyrimidine (Figure 1). The two N atoms introduced in the ring in place of the two CH groups perturbed the charge distribution significantly (as evident by the 50% decrease in the dipole moment). Nonetheless, as seen from the atomic multipole parameters for both ligands (see the supplemental data), the perturbation is fairly “local”, restricted to the N atoms themselves and the carbon atoms immediately bonded to N. The atomic charges, dipoles and quadrupoles of the amidinium group are essentially invariant between the two ligands. In changing ligand A to C, on the other hand, due to the broken symmetry in the pyrazine (or 1,4-diazine), the effect of the two N atoms cancels out and leaves the molecular dipole moment similar to that of benzamidine. In ligand D, the 4-amino substitution group donates pi-electrons to the aromatic ring which reduces the molecular dipole moment relative to benzamidine. The amine group of ligand E (benzyl amine) causes a significant dipole moment (D_Z) out of the plane of the phenyl ring.

Structural analysis from explicit solvent simulations

Among the five ligands investigated, there is only an X-ray crystal structure available for benzamidine-trypsin (1BTY).⁵¹ In the crystal structure, the surrounding residues and water molecules form specific interactions with the amidinium group of the benzamidine (Figure 4a). The negatively charged Asp 189 residue forms a salt bridge with the positively charged amidinium group by double hydrogen bonding with the two nitrogen atoms. At the same time, Gly219 carbonyl O is hydrogen-bonded to one nitrogen atom of the amidinium group while on the other side both Serl90 O and a water molecule form a bifurcated hydrogen bond with the other nitrogen atom. The thermodynamics of binding of p-substituted benzamidines to trypsin was investigated experimentally by Talhout et al.^42,58 It was suggested that both the hydrogen-bonding amidinium group and the hydrophobic phenyl ring of the benzamidine contributed to trypsin binding, with the former enthalpically favorable and the latter entropically favorable.

There is one internal water molecule in the proximity of the salt bridge between the benzamidine amidinium group and the Asp 189 according to the crystal structure. The internal water is likely to be critical in stabilizing the binding complex. However, detailed information on internal water molecules is not always available for the inhibitors of interest, as with the ligands B through E in this study. Therefore in our models, the internal water molecules have been added into the binding site, after inhibitor is in place, based on the space availability. On average, there are more water molecules added into the complex more than observed in the trypsin-benzamidine crystal structure. During the simulation, one water molecule quickly moved to the location where the crystal water interacts with the amidinium together with Serl90 (Figure 4 a through d), except for benzyl amine as discussed below. This water molecule formed a stable hydrogen bond with one NH₂ group of the amidinium in ligands A through D (Figure 5a).

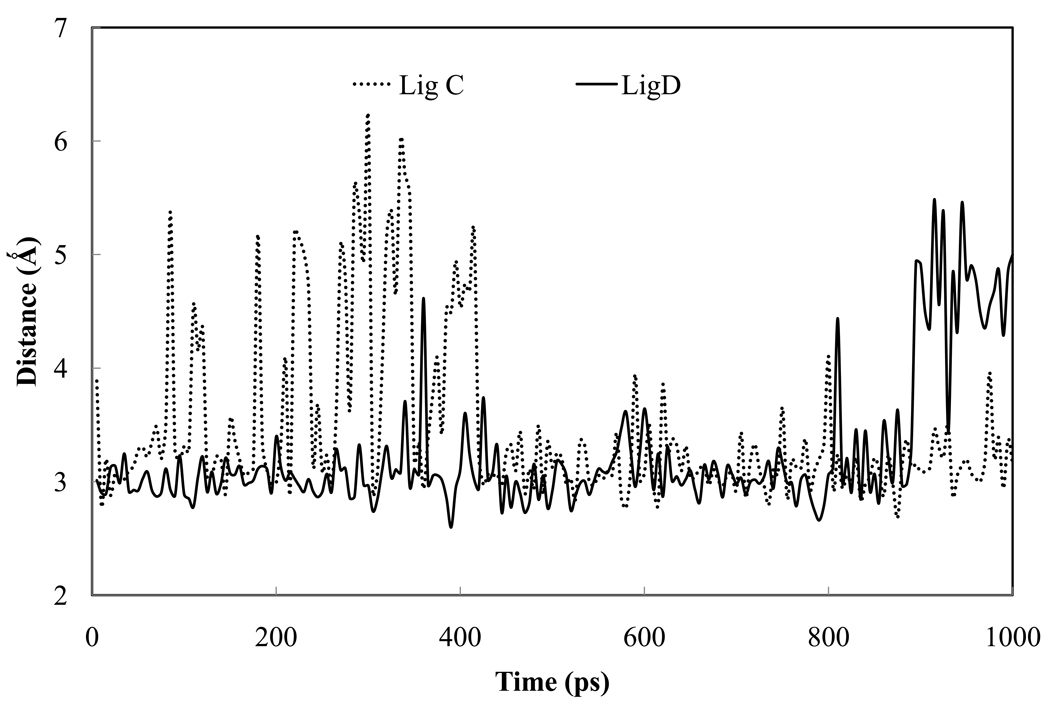
Figure 5.

Evolution of the hydrogen bond distances between the ligand and the surroundings: (a) water hydrogen bonding to amidinium N2 from simulations of ligand C and D. A similar water molecule is present in the crystal structure of trypsin-benzamidine; (b) ligand B hydrogen bonding to the Asp 189 residue in the binding pocket.

The double hydrogen bonding between Asp 189 and amidinium was present in trypsin-ligand B complex throughout the entire simulation (Figure 4b and Figure 5b). In the case of ligand C or D, only one hydrogen bond between Aspl89 (0δ1) and the ligand (N2) was observed. The other initial hydrogen bond between Asp (0δ2) and ligand (Nl) was eventually replaced by a water molecule which was introduced into the pocket during system construction (Figure 4c and d). The Asp 0δ2 that became free, however, bonded to another internal water molecule introduced during the soaking. Neither of the two water molecules is present in the crystal structure of trypsin-benzamidine (1BTY).

The hydrogen bond between Gly219 and the ligands is well conserved in all the simulations and the average bond distance (2.94 Å) is in good agreement with that in crystal structure (2.89 Å). By contrast, great variability was observed in the hydrogen bonding between Serl90 and the ligands. The hydrogen bond between the ligand and the Serl90 Oγ, which is present in crystal structure, was only observed in the simulations of trypsin-ligand A and trypsin-ligand C. For ligands B and D, the interaction seems rather weak and the Serl90 side chain essentially drifted away from the ligand.

Among all the ligands investigated, ligand D (4-amino-benzamdine) has the strongest binding affinity according to both experiment and our calculation. To evaluate the role of the amino group in binding, we have examined the possible interactions between the amino group and trypsin and indentified a stable hydrogen bond between the Serl95 hydroxyl and the amino group (Figure 4d). Ser 195 together with Asp 102 and His 57 constitute the catalytic triad that attacks the peptide bond. The interaction between Ser 195 and ligand D likely enhances the binding of 4-amino-benzamidine to trypsin. However the gain in binding affinity associated with the extra hydrogen bond in trypsin seems to be mostly offset by the increase in solvation free energy in bulk water (Table 1).

In ligand E, as the charged amine replaces the amidinium group, the capacity for hydrogen bonding decreases, which may have been the cause for the weaker binding affinity when comparing to the other ligands. There were a handful of hydrogen bond acceptors competing for the limited hydrogen bond donors on the amine group, including Gly219 O, Ser 190 O, Asp 189 0δ1 and 0δ2, and a water molecule (Figure 4e). It is worth noting that the amine nitrogen of ligand E deviated from the symmetry axis of benzamidine and leaned towards Gly219 for the entire simulation, consistent with previous observations from computer simulation.⁵⁹

Implicit solvent MM-PMPB/SA free energy analysis

We have utilized an end-state method based on PMPB/SA to evaluate the binding affinities of the five ligands. The molecular mechanics-based Poisson-Boltzmann surface area (MM-PB/SA) approach has been widely used to investigate protein-ligand and protein-protein interactions due to its computational efficiency.^1,60,62 In this approach, Poisson-Boltzmann continuum is applied to evaluate solvation thermodynamics of a solute of fixed atomic charges, extract from MD simulations of the complex. In a recent work, Schnieders et al. extended the PB framework to systems with polarizable point multipoles.⁴³ A self-consistent reaction field protocol was used to couple the polarizable solute and PB continuum. This PMPB continuum method has been compared with explicit solvent simulations in the simulation for several small proteins.⁴³ The solvent effects on the protein electrostatic moments produced by the two methods are in good agreement. Using the electrostatic solvation energy from PMPB, we also attempted to estimate the absolute and relative binding free energies to trypsin. We refer to this method as MM-PMPB/SA to reflect the use of polarizable multipoles for solute.

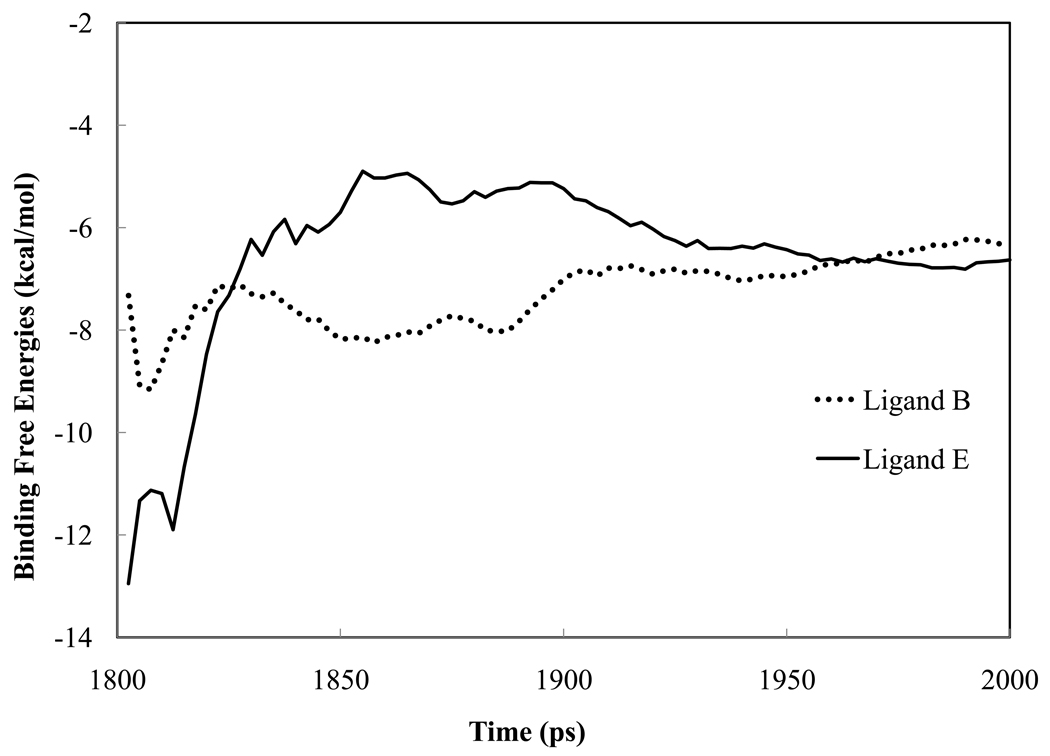
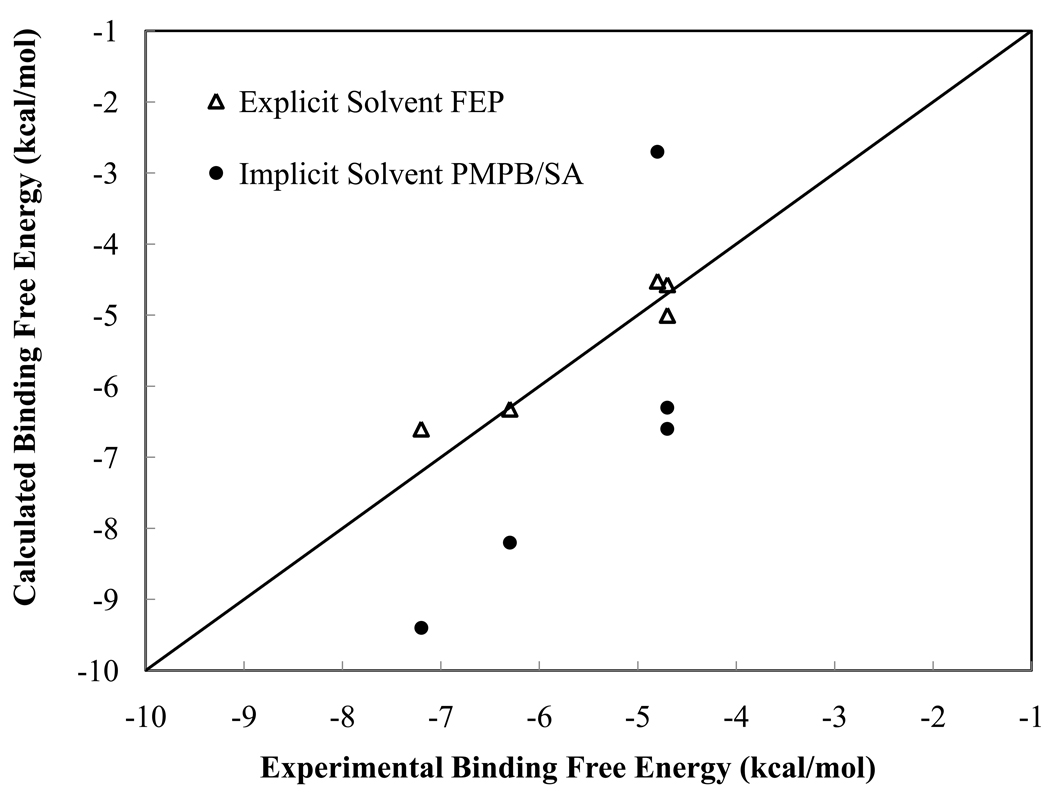
A total of 80 snapshots from explicit solvent MD simulations have been used for each ligand. Figure 7 shows the running average of the absolute binding free energies of ligands B and E as a function of time (snapshot number). The gas phase binding energies, solvation energies and entropy contributions for each ligand, together with the estimated standard errors, are listed in Table 2 and plotted in Figure 3. The root-mean-square deviation of the calculated absolute binding free energies from experimental data is 1.9 kcal/mol. Except for ligand C, there seems to be a systematic overestimation in the absolute binding energy for all ligands. Given that the PMPB/SA model has not been extensively parameterized, the results are quite encouraging. It is evident that the sum of gas phase binding energies and polar solvation energies dominates the order of the binding affinities among the five ligands. In fact, the addition of other energy terms, nonpolar solvation energy and entropy, does not affect the ranking. The sum of gas phase energy and electrostatic solvation energy (Δ E_gas + Δ A_polar) sampled from MD snapshots also displayed substantial fluctuation, with a standard deviation of ~5 kcal/mol, which raises a question about the feasibility of using a single crystal structure to evaluate binding affinity.

Figure 7.

The running average of absolute binding free energies of ligand B and E from MM-PMPB/SA. A total of 80 snapshots were extracted at a 2.5 ps interval from the last 200 ps of the explicit water simulation trajectory.

Table 2.

The calculated binding free energies from Poisson-Boltzmann continuum (MM-PMPB/SA) and the individual energy decomposition for each ligand binding to trypsin (kcal/mol). The number in parentheses represent the standard error of the mean calculated by $\mathit{\text{stderr}}=\mathit{\text{stdev}}/\sqrt{N}.$

	A	B	C	D	E
ΔEgas1 + ΔApolar	−19.3(0.3)	−16.0(0.4)	−13.5(0.4)	−20.6(0.5)	−17.9(0.5)
ΔEvdw	−15.0(0.3)	−14.0(0.3)	−13.0(0.3)	−15.4(0.3)	−10.9(0.3)
ΔEelec	74.7(0.6)	72.4(0.6)	79.1(0.5)	18.4(1.0)	64.4(0.7)
ΔApolar	−78.9(0.4)	−74.4(0.6)	−79.5(0.4)	−23.6(0.7)	−71.4(0.4)
ΔAnonpolar	−3.2(0.0)	−3.1(0.0)	−3.1(0.0)	−3.3(0.0)	−3.0(0.0)
−TASvib	−4.2(0.1)	−5.6(0.1)	−5.0(0.1)	−4.3(0.1)	−4.3(0.1)
−TΔStrans+not	18.5(0.0)	18.4(0.0)	18.9(0.0)	18.8(0.0)	18.6(0.0)
ΔA bind2	−8.2(0.4)	−6.3(0.5)	−2.7(0.5)	−9.4(0.6)	−6.6(0.6)
ΔAexpt3	−6.3, −6.4, −7.3	−4.7	−4.8	−7.0,−7.2	−3.8, −4.7

¹ΔE_gas = ΔE_intemal + ΔE_vdw + ΔE_elec

²ΔG_binding = ΔE_gas + ΔG_polar + ΔG_nonpolar − TΔS_vib − TΔS_trans+rot

³All the references are the same as in Table 1.

Figure 3.

Comparison between experimental and the calculated binding free energies from explicit and implicit solvent calculations (kcal/mol).

While the nonpolar solvation energy is negative (favorable for binding) for all five ligands, the magnitude varies rather insignificantly. This is probably an artifact of the oversimplified surface area term we adopted for the nonpolar solvation energy evaluation. The translational and rotational entropy loss and vibrational entropy gain were observed upon binding. The protein atoms further than 8 Å away from the ligands were frozen in the calculation of vibration entropies. Overall, entropy contributes significantly (unfavorably) to the binding. Nonetheless, according to the harmonic oscillator approximation, the entropy contribution is almost invariant across the five ligands. For the purpose of ranking ligand affinity, it seems that we can ignore the entropy and compute the gas phase binding energy and polar solvation energy alone. However, this may not always be true especially for ligands with significant differences in chemical structure and size.

Among the dominant term of Δ E_gas + ΔA_polar, both the vdW and electrostatic interactions are important. The gas phase electrostatic binding energy is anti-correlated with the polar solvation term ΔA_polar (Table 2). However, the sum of the two (Δ E_elec + Δ A_polar) varies significantly among the five ligands: −4.2, −2.0, −0.4, −5.2 and −7.0 kcal/mol, which has almost as good correlation with the experimental data as the calculated ΔA_bind, except for ligand E. For ligand E, the gas phase vdW binding energy is the determining factor for its lower binding affinity than ligand A. We notice that ligand C has the largest error in the absolute binding free energies. It is also interesting that our calculations overestimate the absolute binding free energies (more favorable) of ligand A through D whereas underestimated that of ligand C (Figure 3). It seems that the electrostatic (ΔE_elec + ΔA_polar) component contributes to the most of the discrepancy; however, recall the same electrostatic parameters give a reasonable binding free energy for ligand C when used in explicit water simulations. Due to the various approximations involved in the implicit solvent approach, it is difficult to track down the actual source of this error.

Table 3 compares the relative binding free energies calculated from MM-PMPB/SA with those from experiment and explicit-water FEP simulations. Although the PMPB based continuum approach is not as accurate as the explicit water FEP for absolute binding free energy prediction, it correctly predicts the direction of free energy change upon ligand mutation in all cases, as with explicit water simulations. In a previously reported QM/M-based study, it was necessary to assume a rigid trypsin in order to correctly predict the direction of the binding free energy change between ligands B, C and A.³⁹ From Figure 3 and Table 3, it is evident that the calculated relative free energy is well correlated with the experimental data, with the exception of ligand C (1,4-diazamidine). Given the computational efficiency and effectiveness, the PMPB-based end-state approach should be of practical use for screening and optimize small molecules against macromolecular targets.

The ligand solvation free energies in bulk water are given in Table 5. The magnitude of ligand solvation energy from MM-PMPB/SA is in general comparable to that given by QM/MM coupled with the polarizable continuum model (PCM).⁶³ However, the ligand solvation free energies from explicit solvent FEP simulation show much greater variation from one ligand to another than those from both QM and PMPB based continuum approaches. Continuum methods are expected to have limitations when specific water molecules are involved in critical interactions with solutes.¹ It has also been suggested the treatment of internal water molecules in the binding site is important for binding free energy calculation using PB.⁴⁰ In addition, the PMPB model has not been extensively tested or parameterized on small molecules with net charges. Even with the sophisticated electrostatic model in the PMPB method, we face the similar problems that traditional MM-PB/SA has yet to overcome, namely the treatment of nonpolar solvation and entropy.^64,65 On the hand, due to the elimination of intermediate MD perturbation steps, the PMPB method is at least ten times more efficient than the explicit solvent FEP simulation. Further gain will be achieved if the molecular dynamics trajectories can be reliably obtained also using the implicit solvent model.^l

Conclusion

We have computed the binding free energies of five positively-charged benzamidine analogs to trypsin using an empirical force field based on polarizable atomic multipole electrostatics. Molecular dynamics simulations were performed to perturb the ligands into (or from) benzamidine in both bulk water and in protein-ligand complex. The calculated relative binding free energies, both in sign and magnitude, are in excellent agreement with experimental measurements, with accuracy comparable to that found in experiment. Replacing the phenyl ring with another aromatic structure or amidinium with amine causes significant changes in solvation free energy in bulk water and in the complex, which however leads to a small net change in the overall binding free energy due to cancellation. The 4-amino substitution at the phenyl affects the solvation and binding free energy insignificantly according to our simulations. The molecular dipole moments of the ligands have been characterized in gas phase, in bulk water and in protein-ligand complex. For the ligands studied, molecular dipole moments show no correlation with either the solvation free energy in bulk water or the trypsin binding free energy. The charge redistribution resulting from the chemical change from benzamidine to the other ligands is fairly local − replacing benzene with diazine has no effect on the atomic multipoles at the charged amidinium group. Detailed structure analysis revealed that a few trypsin residues such as Asp 189, gly219 and Serl90, and internal water molecules participate in and compete for hydrogen-bonding with the ligands. The dynamic fluctuation observed for these interactions during the simulations manifests the challenges for sampling in free energy simulations.

The outcome of our first attempt to utilize a polarizable multipole based Poisson-Boltzmann continuum approach is very encouraging, especially given the better computational efficiency than that of the explicit solvent FEP simulations. The absolute binding free energies estimated from MM-PMPB/SA exhibit a RMS error of 1.9 kcal/mol, most of which is systematic and may be corrected by further refinement of the model. The relative binding free energies are in excellent agreement, again both in sign and magnitude, with the results obtained from explicit water simulations and experiment, with one exception. The solvation free energy calculated by implicit solvent models is not as sensitive to the chemical structure as that from explicit solvent simulations. As with the traditional MM-PB/SA approach, the treatment of nonpolar solvation energy and entropy remains questionable. Although further validation and refinement are needed, our results indicate that the polarizable multipole potential combined with Poisson Boltzmann method is potentially a useful tool in ranking small molecule binding affinities for applications such as drug discovery and molecular design.

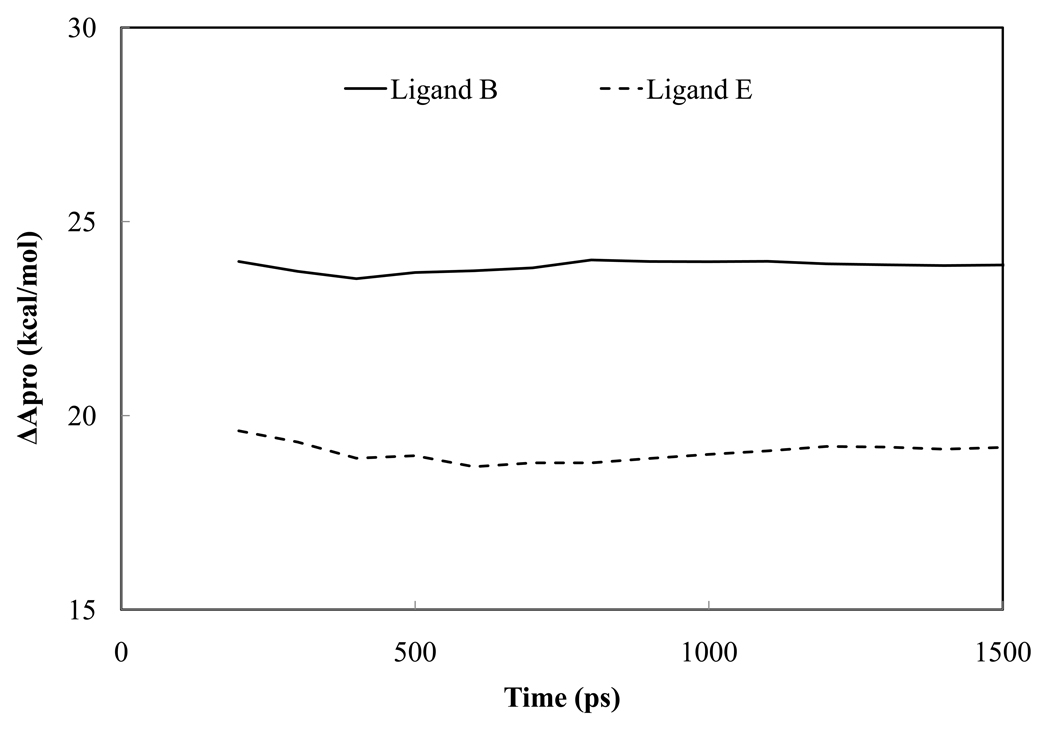
Figure 6.

The running average of relative free energy changes in trypsin-ligand complex from explicit water MD simulations of ligand B and E. In both cases, the ligand is being perturbed into benzamidine.