Abstract
Vessel leakiness is a hallmark of inflammation and cancer. In inflammation, plasma extravasation and leukocyte adhesion occur in a coordinated manner to enable the immune response, but also to maintain tissue perfusion. In tumors, similar mechanisms operate, but they are not well regulated. Therefore, blood perfusion in tumors is non-uniform, and delivery of blood-borne therapeutics is difficult. In order to analyze the interplay among plasma leakage, blood viscosity, and vessel geometry, we developed a mathematical model that explicitly includes blood cells, vessel branching, and focal leakage. The results show that local hemoconcentration due to plasma leakage can greatly increase the flow resistance in individual vascular segments, diverting flow to other regions. Similarly, leukocyte rolling can increase flow resistance by partially blocking flow. Vessel dilation can counter these effects, and likely occurs in inflammation to maintain blood flow. These results suggest that potential strategies for improving perfusion through tumor networks include (i) eliminating non-uniform plasma leakage, (ii) inhibiting leukocyte interactions, and (iii) preventing RBC aggregation in sluggish vessels. Normalization of tumor vessels by anti-angiogenic therapy may improve tumor perfusion via the first two mechanisms.
Keywords: Blood rheology, Vessel leak, Apparent viscosity, Lattice Boltzmann
INTRODUCTION
At sites of inflammation, endothelial adhesion molecules are upregulated, vascular permeability increases1,22,27,36 and venules dilate.37 Leukocytes roll on the endothelium, adhere, and transmigrate into the interstitial matrix, which has been modified by extravasated plasma proteins. All of these events can affect blood perfusion through the network. For example, local flow resistance may increase because the rolling and adherent leukocytes reduce the effective vessel cross section29,41 and because plasma leakage results in hemoconcentration, which increases blood viscosity.28,39 On the other hand, vessel dilation can reduce flow resistance through individual segments. All of these events are carefully regulated by cytokines and growth factors expressed by stromal and inflammatory cells.
Interestingly, many of these same cytokines and growth factors are present in solid tumors: some are produced by hypoxic cancer cells to recruit new blood vessels, while others are secreted by infiltrating immune or stromal cells12 attempting to heal the chronic, growing “wound.”6,11 But these processes are poorly regulated in tumors—both spatially and temporally—and the “inflammation” does not “resolve” as in normal physiology. Thus, blood vessels in tumors are hyperpermeable,11,17,49 with some vessels allowing extravasation of plasma and liposomes as large as 2 μm.5,31 These vessels also have non-uniform diameters and their expression of adhesion molecules is highly variable.20 This results in heterogeneous blood perfusion throughout the tumor network, rendering drug delivery inefficient.17
Previous studies have shown that hemodilution can result in higher RBC flux in the tumor, although overall tumor oxygenation does not improve.23 These studies raised the question as to how hemoconcentration might affect the uniformity of perfusion within a network. It is evident that in order to deliver drugs uniformly to tumor tissue, we need to know how blood rheology, the abnormal network topology and the non-uniform vessel leakiness combine to hinder overall perfusion. Our goal is to develop an analytical framework for studying blood flow that includes all these important features.
Predicting the flow of a particulate solution through such a network of permeable vessels is complex. The flow rate through each vessel segment is determined by the pressure drop and the flow resistance. The resistance to flow, in turn, depends on blood viscosity, which is a complicated function of shear rate, vessel diameter, and blood composition (e.g., hematocrit, aggregation-inducing proteins). In narrow tubes the RBCs migrate to the tube axis, creating a cell free plasma layer along the wall and a cell-rich central core, resulting in the Fahraeus effect, which dictates that the tube hematocrit is lower than the discharge hematocrit, and the Fahraeus–Lindqvist effect, which states that the apparent viscosity decreases with decreasing microvessel diameter.13,16 Because of the cell-free plasma layer at the wall, there is an uneven distribution of cell and plasma flow into the two daughter vessels at branch points. In addition, some of the chaotic nature of blood flow—i.e., the dynamic redistribution of flow velocities within the network16—is due to changes in flow resistances as single blood cells enter and leave individual vessel segments.
Previous studies have analyzed changes in flow velocity in a single, compliant, leaky vessel embedded in a fluid phase at uniform pressure: Netti et al. found that the coupling between the vascular and transvascular fluid transport may have an effect on tumor blood flow and its distribution.32 Baish et al. extended this work, modeling the fluid flow through a grid of leaky vessels embedded in an isotropic porous medium.2 These studies conclude that a buildup of interstitial fluid pressure (IFP) due to vessel leakiness can eliminate the pressure gradients that drive fluid flow through vessels in the center of the mesh. This mechanism could contribute to the inefficient perfusion observed at the center of solid tumors. We recently examined how anti-angiogenic therapy might influence perfusion of tumors with high IFP and showed that decreases in vessel hydraulic conductivity can decrease flux of interstitial fluid, growth factors, and cells from the tumor margin to the surrounding tissue, potentially slowing angiogenesis, lymphangiogenesis, and metastasis.21
In all these studies, blood was assumed to be a Newtonian solution with constant hematocrit. Milosevic et al.30 modified the single-capillary model of Netti et al. by computing the IFP outside the capillary within an idealized tumor using a global mass balance. They included ad hoc empirical relationships to predict the changes in blood viscosity due to local variations in hematocrit and capillary diameter (Fahraeus–Linqvist effect); they also accounted for hemoconcentration and hemodilution due to plasma flow across the semi-permeable capillary wall. The authors concluded that elevated IFP leads to vascular constriction and reduced tumor blood flow, but it is unclear whether elevated IFP can compress vessels or how the dynamic packing of RBCs within leaky vessels might influence microvascular flow.
Because of these complexities, it is necessary to explicitly account for individual blood cells and plasma in order to simulate the dynamic changes in flow resistance and hematocrit due to plasma loss and vessel branching. We previously reported a mathematical model using a lattice-Boltzmann approach (Fig. 1) to characterize the interactions and estimate the forces involved as individual RBCs and WBCs interact in capillaries29 and in postcapillary expansions.40 This model is also ideally suited for analyzing the rheological properties of concentrated cell suspensions, and is able to reproduce the Fahraeus and Fahraeus–Lindqvist effects by explicitly accounting for the particulate nature of blood41; in other studies, we have found that RBC aggregation has dramatic effects on flow resistance and leukocyte margination.42
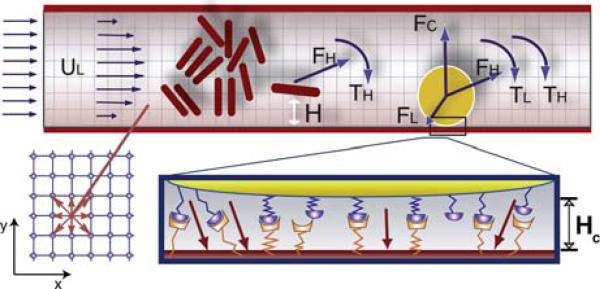
FIGURE 1.
Model geometry and parameters. At top is an illustration of how the blood suspension is modeled. Red blood cells are represented as 2D capsules and the white blood cells are 2D disks (yellow). The leukocyte interacts with the wall through stochastic receptor–ligand interactions (illustrated at bottom right) and a non-specific repulsive force (FC). The leukocyte can interact with the surface when it gets closer than HC. The forces and torques of individual bonds are summed to get the total ligand force (FL) and torque (TL); these are then combined with the hydrodynamic force (FH) and the torque (TH) to calculate the total force on the leukocyte. Fluid particle velocities of a 2D lattice Boltzmann model with nine velocities are illustrated at bottom left.
The advantage of this approach is that blood is explicitly modeled as a suspension of blood cells in a Newtonian fluid and the bulk rheological properties emerge naturally without the need for ad hoc constitutive rules or empirical equations for viscosity and hematocrit variations. In the present study, we use this model to predict blood flow distributions, hematocrit changes, and flow resistance variations resulting from the loss of plasma across leaky vessel walls. This represents a first step toward achieving a fundamental understanding of the complex fluid dynamics of blood in a vessel network with non-uniform plasma leakage.
METHODS
Fluid and Cell Dynamics
We use a lattice Boltzmann method (LBM) to calculate the unsteady flow field and the forces acting on suspended particles. The details of this approach have been described previously.29,40,41 Lattice Boltzmann method is a relatively new numerical scheme for simulating complex flow and transport phenomena.9,34 The LBM uses a mesoscopic equation (the discrete Boltzmann equation) to determine macroscopic fluid dynamics instead of solving the macroscopic, continuum, Navier–Stokes equation, upon which traditional computational fluid dynamics methods are based. Due to its local nature, only the neighboring nodes need to be considered to update the equilibrium distribution at each time step, so the method can be easily parallelized and scaled-up. Lattice Boltzmann method has been successfully applied to various physical problems where direct solution of the Navier–Stokes equations is not practical, including multiphase flows, magneto-hydrodynamics, reaction-diffusion systems, flow through porous media, and solid particle suspensions.10
The ease with which the LBM handles moving boundaries makes it a powerful tool to analyze fluid suspensions of cells at high concentration. Figure 1 illustrates how a LBM is used to calculate the unsteady flow field and the forces acting on the cells in the present work. The red cells are represented by two-dimensional (2D) capsules (rectangles with superimposed half-circles at the ends) and white cells are modeled as a disk with adhesion molecules distributed around the circumference.
Receptor–Ligand Model for Leukocyte Rolling
Similar to our previous work, we implement cell rolling and adhesion by including stochastic binding and detachment of spring-like adhesion molecules on the cell surface29,40,41 (see Fig. 1).
The LBM is very effcient: for the cases with no leakage (Panel a in Fig. 2) the simulation takes about 0.045 s per time step on a Pentium IV 3.6 GH computer and about 20 h for the entire simulation. For the cases with leakage (Panel b in Fig. 2), the simulation time is about 20% longer due to the larger number of cells.
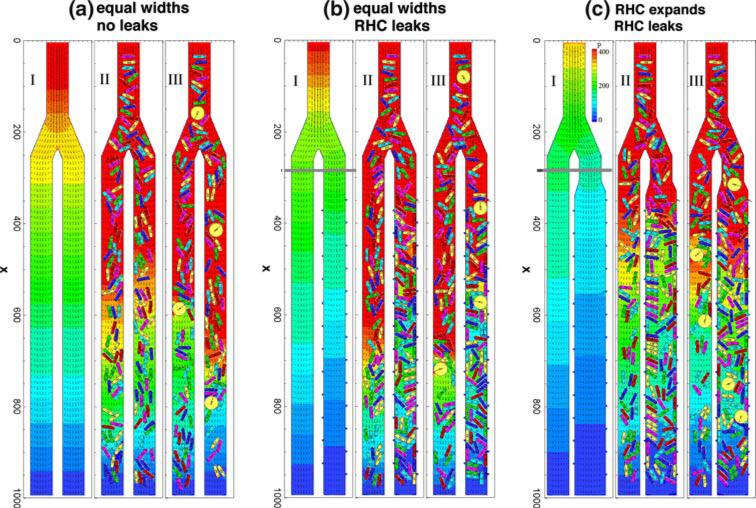
FIG. 2.
Representative snapshots of flow during the simulations. The columns represent (a) equal width, non-leaky daughter branches; (b) equal width branches, but the right-hand channel (RHC) leaks; (c) the RHC is 50% wider, and has the same leaks as case b. In each case, Subpanel I is the steady flow of plasma only (without any cells). Subpanel II shows the developed flow of RBCs for feeding hematocrit 0.35 at the inlet. Subpanel III shows the flow with both RBCs and WBCs included. Lattice size: 1000 × 150; one grid point is equal to 0.3 μm. Total time of 0.9 s is normalized to 1, corresponding to 3 × 106 time-steps. The pressure coefficient (P = 2(p – pex)/ρU2, where pex is pressure at the exit) field is represented by the color gradient and the velocity field is represented by small arrows.
Calculation of Relative Resistances
If we know the pressure drop Δp and flow rate Q in a conduit, we may determine the flow resistance R by Δp = RQ, where Q = AU, U is the mean velocity and A is the cross section. In order to compare different flow conditions, it is useful to introduce a relative resistance (resistance ratio) Rr = R/R* = Q*Δp/QΔp*, where Q* and Δp* are the flow rate and pressure drop of a reference case. The relative resistance is reduced to R/R* = Δp/Δp* if the flow rate is constant and to R/R* = U*/U if the pressure drop and cross section are constant.
The inlet flow rate and the exit pressure pex are maintained constant for all simulations, so the overall relative resistance shown in Fig. 4c is determined by R/RaI = P0/P0–aI where P0 is the pressure coefficient at the inlet (P = 2(p–pex)/ρU02, where U0 is the mean flow velocity at the inlet, and P0–aI is the corresponding value for plasma flow).
FIGURE 4.
Summary of hematocrit (Panel a), overall resistance (Panel b) relative to that of plasma flow in a non-leaky vessel (simulation a-I in Fig. 2), and resistance ratio of right branch to left branch (Panel c). Groups a, b, and c represent the Cases a, b, and c shown in Fig. 2. I, II, and III indicate the simulations I, II, and III in Fig. 2. L and R denote the left and right branch, respectively. The values for II and III are the temporal averages over dimensionless time interval from 2/3 to 1.
In cases with a leaky channel, since the pressures at the exits of the two branches are the same, the pressure drop for each daughter channel measured from the point of bifurcation is also the same. We may then calculate a flow resistance ratio of the left leaky branch to the right non-leaky branch as R2/R1 = U1/U2, where U1 and U2 are the flow velocities in the left segment and right segment measured upstream of the apertures, at the horizontal gray line in Fig. 2, Panels b-I and c-I. In order to evaluate the plasma loss through the apertures, we calculate the leaking velocity Ulk = (U2A2 – U3A3)/A2, where A2 and A3 are the cross section at the entrance and exit of the leaky branch, respectively.
RESULTS
We examined three different scenarios, notated Case a, b, and c (see Fig. 2). Case a has impermeable vessel walls in all segments, and the two daughter branches are 15 μm in diameter, the same as the parent branch. In Case b, plasma is allowed to flow through 25 apertures of 0.9 μm placed on the walls of the right-hand-side daughter vessel. In Case c, we retain the leaks in the right-hand channel, but also expand this channel to simulate vessel dilation in inflammation.
Note that the mechanisms involved here are qualitatively scalable to multi-vessel networks, so each daughter branch can be thought of as an idealized sub-network within a tumor or normal tissue. Thus, assuming that the only changes in a diverging/converging network are the diameter and permeability of the venule(s) of one branch, the results should be consistent. In this context, the input branch represents an arteriole, which splits into two capillary sub-networks (not explicitly modeled) drained by the two venules. What we are interested in—especially in the context of tumors—is the change in sub-network flow caused by diameter or permeability perturbations in downstream vessels. Also, note that the outlet pressures of the two “venules” are the same, so, in essence, they connect to the same downstream vessel.
Each case includes three simulations: (I) with plasma only, (II) plasma + RBCs, and (III) plasma + RBCs + WBCs. The feeding hematocrits in II and III are 0.35. For all simulations, the mean entrance velocity was kept constant U0 = 1 mm/s. A constant and equivalent pressure was maintained at the exits of the two daughter branches for all simulations.
Case a: Non-Leaky Vessels with Equivalent Widths
Panel a-I in Fig. 2 shows the steady-state flow of plasma through equal diameter, non-leaky vessels, which will be taken as the reference state to calculate the overall relative resistance of all the other simulations. Panel a-II shows the developed flow of RBCs with an inlet hematocrit of 0.35, and Panel a-III shows the flow with WBCs included. As the cells fill the system, the resistance increases, velocities decrease, and the pressure at the inlet has to increase to maintain a constant flow rate. This is evident from the changes in pressure distributions in the cases I, II, and III. For RBCs only, the relative resistance across the whole system is 1.81; i.e., the flow resistance is 1.81 times that of Case a-I with only plasma. The WBCs in Case a-III, which are round and larger than RBCs, roll on the vessel wall through stochastic binding interactions, leading to an increase in the relative resistance to 2.24. Figure 4 summarizes the channel hematocrits and resistances.
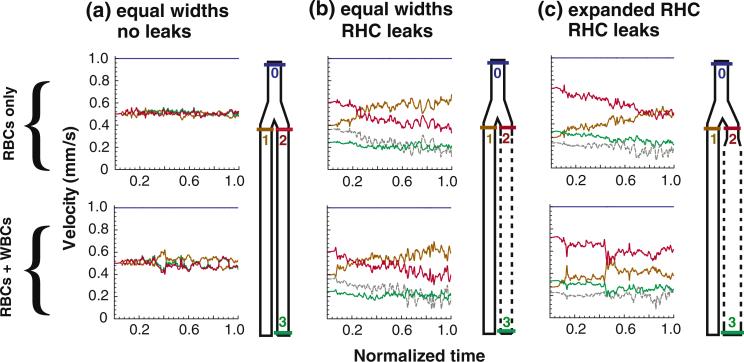
In both cases with cells (II and III), the initial condition consisted of the flow-pressure distribution shown for plasma only (Fig. 2a-I). As cells enter the system, the evolution of velocities in each branch is shown in Fig. 3a. The velocities are measured at the locations marked by the color-coded bars in the illustrations. Comparing the case with RBCs with that of RBCs plus WBCs (top vs. bottom row) reveals that WBCs induce relatively large fluctuations in velocity. The tube hematocrits of developed RBC flow and RBC plus WBC flow are 0.32−0.33 (see Fig. 4a), significantly lower than the feeding hematocrit (0.35) due to the Fahraeus effect.
FIGURE 3.
Velocity evolution in each segment. For the simulations with cells, the initial condition is the flow-pressure distribution for plasma only (i.e., panel I from Fig. 2). Here we show the changes in velocity that occur as RBCs (top row) or RBCs and WBCs (bottom row) enter the system. Velocities have been averaged across the channel width, and the inlet hematocrit is 0.35. The geometries of Cases a, b, and c are illustrated to the right of corresponding velocity plots; the colored lines in these diagrams correspond to the locations of the velocities in the plots (i.e., blue is at the inlet, orange is at the entrance to the left-hand branch, etc.). In (b) and (c), the leaking velocity is depicted by the gray line. The initial steady-state velocity distribution is disturbed as cells fill the system; in (b) and (c), plasma leakage causes dramatic drifts in the velocity distributions.
Note that in these simulations with equivalent, non-leaky daughter branches, the cells introduce fluctuations in velocity, but the velocities in the two branches are symmetric—i.e., when the flow in one branch slows down, it speeds up by the same amount in the other (red versus orange line).
Case b: Equivalent Channel Widths, but the Right-Hand Channel Leaks
In these simulations, we introduce 25 apertures, each 0.9 μm in length, in the walls of the right-hand channel. The left-hand segment remains impermeable. The aperture specification is based on structural and functional data from a number of our studies which have measured pore sizes, hydraulic conductivity, and effective permeability.3,7,8,15,25,31,48 For example, Hashizume et al.14 found, using electron microscopy, that pore sizes in MCaIV tumors lie in the range 0−5 μm with median 1.7 μm. Functional studies support this: in the same tumor, we found that 1 μm liposomes extravasate quite easily, but 5 μm liposomes do not.15 Therefore, to be on the conservative side, we chose to use 0.9 μm pores, spaced at about the width of an endothelial cell. A constant pressure pex is imposed at the apertures; pex is the same as the pressure at the exit of the daughter vessels.
With plasma only, the leaks decrease the flow resistance in the right channel (Fig. 2, panel b-I), and the entrance velocities of the two branches are no longer equal: U1 = 0.4 mm/s on the left and U2 = 0.6 mm/s on the right, yielding a resistance ratio 0.65 (Fig. 4b). That is, the resistance of the leaky branch is 0.65 times that of the non-leaky branch. The overall relative resistance is 0.85 based on the case with plasma flow and no leaks (compare with Panel a-I), indicating that the leaks reduce overall plasma flow resistance, as expected (Fig. 4c).
However, the introduction of RBCs (Fig. 2, Panel b-II) reverses this situation. As shown in Fig. 3b, the addition of RBCs causes a decrease in the velocity U2 from 0.6 to 0.41 (red line in Panel b, top) and a corresponding increase in U1 from 0.4 to 0.59 (orange line). In order to eliminate the fluctuations due to the stochastic nature of the flow, presented values are the average over the last third of the total simulation time of 3 × 106 time-steps (from 2 × 106 to 3 × 106 time-steps). Thus, the resistance ratio at the end of the simulation is 1.45, indicating that the resistance in the leaky branch is higher than that of the non-leaky branch (Fig. 4c). This is due to the increase in the channel hematocrit (to 0.51; Fig. 4a), which in turn increases flow resistance and decreases velocity in the right-hand channel, diverting flow into the left-hand channel. In addition, as RBCs near the wall partially block the apertures, the leaking velocity decreases (gray dashed line in panel b, top). The hemoconcentration due to the leaks in the right-hand channel also increases the resistance compared to the case with RBCs and no leaks (Fig. 4c).
When WBCs are added to the system (Fig. 2, Panel b-III; Fig. 3, Panel b, bottom), the results are similar, but there is an increase in resistance compared to the case with RBCs only (Fig 4c).
Case c: Expanded, Leaky Right-Hand Channel
In this case the leaky branch has been expanded by 50% from 15 to 22.5 μm to simulate vessel dilation during inflammation.37 The results show that this decreases the flow resistance and compensates for the increase in resistance caused by plasma leakage (Fig. 4b). For plasma flow the resistance ratio is 0.38, much lower than the Case b, indicating that the plasma flows more easily into the right-hand channel (entrance velocity U2 = 0.72 mm/s) than the left-hand channel (entrance velocity U1 = 0.28 mm/s). The overall relative resistance is 0.68, again much lower than Case b with the smaller width right-hand channel (Fig. 4c).
The evolution of velocities with RBCs and RBCs + WBCs is shown in Fig. 3c. As RBCs flow in (Panel c, top), the velocity U2 decreases from 0.72 to 0.504 and U1 increases from 0.28 to 0.496, resulting in a resistance ratio of 0.98 (Fig. 4b); this means that the resistances of the leaky and non-leaky branches are approximately equal. The resistance increase caused by the leakage is negated by the expansion, and the flow distributes evenly between the two branches, even though the tube hematocrits are not equal (0.291 at left and 0.482 at right; Fig. 4a).
The rolling WBCs again increase the overall relative resistance (Fig. 4b). However, the effect of the WBCs on the flow resistance depends strongly on the vessel size. As we showed previously,41 because the slowly rolling WBCs occupy a larger portion of a small vessel than a larger vessel, the WBC affects the flow more strongly in the small vessel. The velocity U2 decreases from 0.72 to 0.59 and U1 increases from 0.28 to 0.41, giving a resistance ratio 0.69 which is lower than for RBC flow only (Fig. 4b). Thus, the WBCs add less resistance to the larger right-hand branch than the left-hand branch.
DISCUSSION
Figure 4 summarizes the hematocrits, overall flow resistances, and resistance ratios of leaky branch to non-leaky branch. The simulation is able to reproduce many of the known anomalies of blood flow. For example, the hematocrit in the non-leaky branches is between 0.29 and 0.33, significantly lower than the feeding hematocrit 0.35. This is a demonstration of the Fahraeus effect, which states that vessel hematocrit is lower due to the formation of a lubrication layer of plasma near the walls. On the other hand, the hematocrit in the leaky branch is 0.47−0.52—much higher than the feeding hematocrit. Previous experimental studies by Lipowsky et al. showed that venules have higher hematocrit compared to arterioles26; our results show that this could, indeed, be influenced by plasma leakage from the venules.
Also important is the observation that RBCs increase flow resistance, and rolling WBCs increase the resistance even further (see Fig. 4c). Plasma leakage reduces the overall resistance for plasma flow (Fig. 4c, white bars), but increases the resistance for RBC flow (gray bars) and RBC plus WBC flow (black bars) due to the increased hematocrit and the loss of the lubricating plasma-rich layer near the vessel wall.
Interestingly, expansion of the leaky branch decreases the overall flow resistance for all cases (Fig. 4c, compare b and c). But since WBCs generate much more resistance in small vessels than in large vessels, the expansion is more effective in compensating resistance for flow with WBCs than for flow without WBCs. In Fig. 4b, Case b, the RHC has higher resistance (black bar is larger than the gray bar), but in Case c, with the RHC expanded, the RHC has less resistance (black bar is smaller than the gray bar). Accordingly, venule dilation during inflammation would counter the effects of plasma extravasation and WBC–endothelium interactions, which tend to increase flow resistance. Moreover, at constant flow rate, vessel dilation results in a lower shear rate, which promotes WBC rolling and adhesion. Thus, delivery of both RBCs and WBCs to the vessel is ensured, while, at the same time, WBCs can roll and arrest on the endothelium. This kind of diameter regulation has not been observed in tumor networks, but is common in inflammation.
Also interesting was the unexpected decrease in plasma extravasation during hemoconcentration. As the RBCs packed into the leaky vessel, apertures were blocked, and the transvascular flux decreased. This effect would not be obtainable with a continuum model of blood. It is possible that this is an additional mechanism for achieving hemostasis and limiting plasma leakage in inflamed or damaged tissue. In vivo, this effect may be even more dramatic than in our simulations with rigid RBCs, which might not conform and plug the holes as easily as deformable cells. On the other hand, gaps between 3D cells and the intervening glycocalyx may maintain pathways for plasma percolation, reducing this effect.
These concepts are directly relevant to the hemodynamics in tumor vessels. The fact that tumor blood flow is chaotic and non-uniform has generally been ascribed to poor network topology,24 vessel collapse due to solid stress build-up,33,35 and high IFP, which eliminates the pressure gradients driving flow at the center of the tumor.2,21,32 Our results support the hypothesis that hemoconcentration can reduce blood flow globally.4,16,26,38 But they also show that when plasma leakage is heterogeneous, hematocrit and flow resistance will increase in some segments of the network, diverting it to others. In vessel segments with mild hemoconcentration, the flux of plasma across the vessel wall is higher upstream compared to downstream; this means that any drug carried in the plasma will have difficulty reaching distal regions of the vessel. Extending this argument, in extreme cases of leakage, the RBC solution may become dense enough to stop flow completely and block pathways for plasma flow, preventing local, convective delivery. This would occur in regions where the transvascular pressure gradient driving the flow is maintained, such as near the tumor periphery. In regions where IFP approaches that of the microvascular pressure (such as in the center of many tumors2,21,32), transvascular plasma flux and hemoconcentration would be minimal. Also, it is important to note that the changes in blood flow that we simulate here take place in less than a second. Within this time period, the IFP should not change much, especially at the tumor margin where there are many draining lymphatic vessels. It is likely that at longer time scales a buildup of IFP will cause a leveling-off of the hematocrit and reperfusion of the leaky branch. This would be relevant, since intermittent stagnation and reperfusion are frequently observed in tumors.
Interestingly, our model also predicts that these effects are easily reversible: if the apertures in the vessel wall are sealed, normal flow quickly recovers with re-establishment of the plasma-rich layer, decreased hematocrit and increased flow rate (not shown). This is relevant to clinical and preclinical studies using anti-angiogenic agents. An emerging goal for tumor physiology research is to find ways to “normalize” tumor vasculature to more effectively deliver chemotherapeutics or radiation-sensitizing oxygen to tumor tissue.18,19 This concept emerged from observations of tumors treated with anti-angiogenic therapies (such as VEGF-blocking antibodies and tyrosine kinase inhibitors) that transform tumor blood vessels so they become more normal.43-47 Structurally, vessel diameters become smaller and more uniform, vessel walls become mature with pericyte investment, and immature, redundant vessels are pruned. Functionally, vessels become less permeable and perfusion is more uniform. Based on our simulations and our previous studies,23 it is likely that the decrease in vessel permeability reduces hematocrit throughout the network, which leads to reperfusion of previously sluggish or stagnant vessels.
This suggests that additional interventions that decrease hematocrit (such as systemic hemodilution) could help impose uniform perfusion. This would be most effective, however, when combined with treatments that decrease plasma leakage. Along these same lines, blood viscosity—and therefore flow resistance—is extremely sensitive to the ability of RBCs to aggregate. Since aggregation is greatly enhanced in low shear environments, it is likely that the RBCs in vessels with slow flow are aggregated, further increasing resistance. Therefore, agents that interfere with RBC aggregation might also be used to normalize blood flow in tumors. Finally, patchy expression of adhesion molecules in tumors could cause non-homogenous WBC rolling and adhesion in tumors. In immature, angiogenic vessels with no mechanism for vasodialation, the resistance could increase significantly due to the WBC interactions, contributing to flow heterogeneity. Therefore, another potential approach to improving perfusion would involve blocking WBC–endothelial interactions.
In summary, we have shown that blood flow in networks with non-uniform vascular leakage is greatly affected by hemoconcentration and WBC rolling, and can be balanced by vessel dilation. We propose that some of the same mechanisms occur in inflammation and tumors (i.e., dynamic changes in vessel permeability, WBC rolling), although they function abnormally in tumors, and that reducing focal leakage and alleviating RBC accumulation and aggregation in tumors could help improve perfusion of tumor vasculature.
ACKNOWLEDGMENTS
We thank Drs. T. Padera, C. Migliorini, Y.H. Qian, H.D. Chen, M. Dupin, A. Mulivor, and C.K. Aidun for helpful discussions. This work was supported by NIH Grant R01 HL64240 (LLM) and P01 CA080124 (RKJ, LLM).
ABBREVIATIONS
- RBC
Red blood cell, erythrocyte
- WBC
White blood cell, leukocyte
REFERENCES
- 1.Baffert F, Le T, Thurston G, McDonald DM. Angiopoietin-1 decreases plasma leakage by reducing number and size of endothelial gaps in venules. Am. J. Physiol. Heart Circ. Physiol. 2006;290:H107–H118. doi: 10.1152/ajpheart.00542.2005. [DOI] [PubMed] [Google Scholar]
- 2.Baish JW, Netti PA, Jain RK. Transmural coupling of fluid flow in microcirculatory network and interstitium in tumors. Microvasc. Res. 1997;53:128–141. doi: 10.1006/mvre.1996.2005. [DOI] [PubMed] [Google Scholar]
- 3.Baxter LT, Jain RK. Vascular permeability and interstitial diffusion in superfused tissues: a two-dimensional model. Microvasc. Res. 1988;36:108–115. doi: 10.1016/0026-2862(88)90043-x. [DOI] [PubMed] [Google Scholar]
- 4.Bishop JJ, Popel AS, Intaglietta M, Johnson PC. Effects of erythrocyte aggregation and venous network geometry on red blood cell axial migration. Am. J. Physiol. Heart Circ. Physiol. 2001;281:H939–H950. doi: 10.1152/ajpheart.2001.281.2.H939. [DOI] [PubMed] [Google Scholar]
- 5.Campbell RB, Fukumura D, Brown EB, Mazzola LM, Izumi Y, Jain RK, Torchilin VP, Munn LL. Cationic charge determines the distribution of liposomes between the vascular and extravascular compartments of tumors. Cancer Res. 2002;62:6831–6836. [PubMed] [Google Scholar]
- 6.Carmeliet P, Jain RK. Angiogenesis in cancer and other diseases. Nature. 2000;407:249–257. doi: 10.1038/35025220. [DOI] [PubMed] [Google Scholar]
- 7.Chang YS, Munn LL, Hillsley MV, Dull RO, Yuan J, Lakshminarayanan S, Gardner TW, Jain RK, Tarbell JM. Effect of vascular endothelial growth factor on cultured endothelial cell monolayer transport properties. Microvasc. Res. 2000;59:265–277. doi: 10.1006/mvre.1999.2225. [DOI] [PubMed] [Google Scholar]
- 8.Chang YS, Tomaso ED, McDonald DM, Jones RC, Jain RK, Munn LL. Mosaic blood vessels in tumors: frequency of cancer cells in contact with flowing blood. PNAS. 2000;97:14608–14613. doi: 10.1073/pnas.97.26.14608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chen H, Chen S, Matthaeus WH. Lattice Boltzmann model for simulating flows with multiple phases and components. Phys. Rev. A. 1992;45:5339–5342. doi: 10.1103/physreve.47.1815. [DOI] [PubMed] [Google Scholar]
- 10.Chen S, Doolen GD. Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998;30:329–364. [Google Scholar]
- 11.Dvorak HF. Vascular permeability factor/vascular endothelial growth factor: a critical cytokine in tumor angiogenesis and a potential target for diagnosis and therapy. J. Clin. Oncol. 2002;20:4368–4380. doi: 10.1200/JCO.2002.10.088. [DOI] [PubMed] [Google Scholar]
- 12.Fukumura D, Xavier R, Sugiura T, Chen Y, Parks E, Lu N, Selig M, Nielsen G, Taksir T, Jain R, Seed B. Tumor induction of VEGF promoter activity in stromal cells. Cell. 1998;94:715–725. doi: 10.1016/s0092-8674(00)81731-6. [DOI] [PubMed] [Google Scholar]
- 13.Goldsmith HL, Cokelet GR, Gaehtgens P. Robin Fahraeus: evolution of his concepts in cardiovascular physiology. Am. J. Physiol. 1989;257:H1005–H1015. doi: 10.1152/ajpheart.1989.257.3.H1005. [DOI] [PubMed] [Google Scholar]
- 14.Hashizume H, Baluk P, Morikawa S, McLean JW, Thurston G, Roberge S, Jain RK, McDonald DM. Openings between defective endothelial cells explain tumor vessel leakiness. Am. J. Pathol. 2000;156:1363–1380. doi: 10.1016/S0002-9440(10)65006-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hobbs SK, Monsky WL, Yuan F, Roberts WG, Griffith L, Torchilin VP, Jain RK. Regulation of transport pathways in tumor vessels: role of tumor type and microenvironment. PNAS. 1998;95:4607–4612. doi: 10.1073/pnas.95.8.4607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Jain RK. Determinants of tumor blood flow: a review. Cancer Res. 1988;48:2641–2658. [PubMed] [Google Scholar]
- 17.Jain RK. The next frontier of molecular medicine: delivery of therapeutics. Nat. Med. 1998;4:655–657. doi: 10.1038/nm0698-655. [DOI] [PubMed] [Google Scholar]
- 18.Jain RK. Normalizing tumor vasculature with anti-angiogenic therapy: a new paradigm for combination therapy. Nat. Med. 2001;7:987–989. doi: 10.1038/nm0901-987. [DOI] [PubMed] [Google Scholar]
- 19.Jain RK. Normalization of tumor vasculature: an emerging concept in antiangiogenic therapy. Science. 2005;307:58–62. doi: 10.1126/science.1104819. [DOI] [PubMed] [Google Scholar]
- 20.Jain RK, Koenig GC, Dellian M, Fukumura D, Munn LL, Melder RJ. Leukocyte-endothelial adhesion and angiogenesis in tumors. Cancer Metastasis Rev. 1996;15:195–204. doi: 10.1007/BF00437472. [DOI] [PubMed] [Google Scholar]
- 21.Jain RK, Tong R, Munn LL. Effect of vascular normalization by anti-angiogenic therapy on interstitial hypertension, peri-tumor edema and lymphatic metastasis: insights from a mathematical model. Cancer Res. 2007;67:2729–2735. doi: 10.1158/0008-5472.CAN-06-4102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Joris I, Cuenoud HF, Doern GV, Underwood JM, Majno G. Capillary leakage in inflammation. A study by vascular labeling. Am. J. Pathol. 1990;137:1353–1363. [PMC free article] [PubMed] [Google Scholar]
- 23.Lee I, Demhartner TJ, Boucher Y, Jain RK, Intaglietta M. Effect of hemodilution and resuscitation on tumor interstitial fluid pressure, blood flow, and oxygenation. Microvasc. Res. 1994;48:1–12. doi: 10.1006/mvre.1994.1034. [DOI] [PubMed] [Google Scholar]
- 24.Less JR, Posner MC, Skalak T, Wolmark N, Jain RK. Geometric resistance to blood flow and vascular network architecture in human colorectal carcinoma. Microcirculation. 1997;4:25–33. doi: 10.3109/10739689709148315. [DOI] [PubMed] [Google Scholar]
- 25.Lichtenbeld HC, Ferarra N, Jain RK, Munn LL. Effect of local anti-VEGF antibody treatment on tumor microvessel permeability. Microvasc. Res. 1999;57:357–362. doi: 10.1006/mvre.1998.2140. [DOI] [PubMed] [Google Scholar]
- 26.Lipowsky HH, Usami S, Chien S. In vivo measurements of “apparent viscosity” and microvessel hematocrit in the mesentery of the cat. Microvasc. Res. 1980;19:297–319. doi: 10.1016/0026-2862(80)90050-3. [DOI] [PubMed] [Google Scholar]
- 27.Lu B, Figini M, Emanueli C, Geppetti P, Grady EF, Gerard NP, Ansell J, Payan DG, Gerard C, Bunnett N. The control of microvascular permeability and blood pressure by neutral endopeptidase. Nat Med. 1997;3:904–907. doi: 10.1038/nm0897-904. [DOI] [PubMed] [Google Scholar]
- 28.Mchedlishvili G, Varazashvili M, Gobejishvili L. Local RBC aggregation disturbing blood fluidity and causing stasis in microvessels. Clin. Hemorheol. Microcirc. 2002;26:99–106. [PubMed] [Google Scholar]
- 29.Migliorini C, Qian Y, Chen H, Brown E, Jain R, Munn L. Red blood cells augment leukocyte rolling in a virtual blood vessel. Biophys. J. 2002;83:1834–1841. doi: 10.1016/S0006-3495(02)73948-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Milosevic MF, Fyles AW, Hill RP. The relationship between elevated interstitial fluid pressure and blood flow in tumors: a bioengineering analysis. Int. J. Radiat. Oncol. Biol. Phys. 1999;43:1111–1123. doi: 10.1016/s0360-3016(98)00512-4. [DOI] [PubMed] [Google Scholar]
- 31.Morikawa S, Baluk P, Kaidoh T, Haskell A, Jain RK, McDonald DM. Abnormalities in pericytes on blood vessels and endothelial sprouts in tumors. Am. J. Pathol. 2002;160:985–1000. doi: 10.1016/S0002-9440(10)64920-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Netti PA, Roberge S, Boucher Y, Baxter LT, Jain RK. Effect of transvascular fluid exchange on arteriovenous pressure relationship: implication for temporal and spatial heterogeneities in tumor blood flow. Microvasc. Res. 1996;52:27–46. doi: 10.1006/mvre.1996.0041. [DOI] [PubMed] [Google Scholar]
- 33.Padera TP, Stoll BR, Tooredman JB, Capen D, di Tomaso E, Jain RK. Pathology: cancer cells compress intratumour vessels. Nature. 2004;427:695. doi: 10.1038/427695a. [DOI] [PubMed] [Google Scholar]
- 34.Qian YH, d'Humieres D, Lallemand P. Lattice BGK models for Navier–Stokes equations. Europhys. Lett. 1992;17:479–483. [Google Scholar]
- 35.Roose T, Netti PA, Munn LL, Boucher Y, Jain RK. Solid stress generated by spheroid growth estimated using a linear poroelasticity model small star, filled. Microvasc. Res. 2003;66:204–212. doi: 10.1016/s0026-2862(03)00057-8. [DOI] [PubMed] [Google Scholar]
- 36.Sarelius IH, Kuebel JM, Wang J, Huxley VH. Macromolecule permeability of in situ and excised rodent skeletal muscle arterioles and venules. Am. J. Physiol. Heart Circ. Physiol. 2006;290:H474–H480. doi: 10.1152/ajpheart.00655.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Secomb TW, Konerding MA, West CA, Su M, Young AJ, Mentzer SJ. Microangiectasias: structural regulators of lymphocyte transmigration. Proc. Natl. Acad. Sci. U.S.A. 2003;100:7231–7234. doi: 10.1073/pnas.1232173100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Sevick EM, Jain RK. Viscous resistance to blood flow in solid tumors: effect of hematocrit on intratumor blood viscosity. Cancer Res. 1989;49:3513–3519. [PubMed] [Google Scholar]
- 39.Sevick EM, Jain RK. Effect of red blood cell rigidity on tumor blood flow: increase in viscous resistance during hyperglycemia. Cancer Res. 1991;51:2727–2730. [PubMed] [Google Scholar]
- 40.Sun CH, Migliorini C, Munn LL. Red blood cells initiate leukocyte rolling in postcapillary expansions: a lattice Boltzmann analysis. Biophys. J. 2003;85:208–222. doi: 10.1016/S0006-3495(03)74467-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Sun CH, Munn LL. Particulate nature of blood determines macroscopic rheology: a 2-D lattice Boltzmann analysis. Biophys. J. 2005;88:1635–1645. doi: 10.1529/biophysj.104.051151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Sun CH, Munn LL. Influence of erythrocyte aggregation on leukocyte margination in postcapillary expansions: a lattice-Boltzmann analysis. Physica A. 2006;362:191–196. [Google Scholar]
- 43.Tong RT, Boucher Y, Kozin SV, Winkler F, Hicklin DJ, Jain RK. Vascular normalization by vascular endothelial growth factor receptor 2 blockade induces a pressure gradient across the vasculature and improves drug penetration in tumors. Cancer Res. 2004;64:3731–3736. doi: 10.1158/0008-5472.CAN-04-0074. [DOI] [PubMed] [Google Scholar]
- 44.Willett CG, Boucher Y, di Tomaso E, Duda DG, Munn LL, Tong RT, Chung DC, Sahani DV, Kalva SP, Kozin SV, Mino M, Cohen KS, Scadden DT, Hartford AC, Fischman AJ, Clark JW, Ryan DP, Zhu AX, Blaszkowsky LS, Chen HX, Shellito PC, Lauwers GY, Jain RK. Direct evidence that the VEGF-specific antibody bevacizumab has antivascular effects in human rectal cancer. Nat. Med. 10:145–147. doi: 10.1038/nm988. [erratum appears in Nat. Med. 2004 Jun;10(6):649]
- 45.Willett CG, Boucher Y, Duda DG, di Tomaso E, Munn LL, Tong RT, Kozin SV, Petit L, Jain RK, Chung DC, Sahani DV, Kalva SP, Cohen KS, Scadden DT, Fischman AJ, Clark JW, Ryan DP, Zhu AX, Blaszkowsky LS, Shellito PC, Mino-Kenudson M, Lauwers GY. Surrogate markers for antiangiogenic therapy and dose-limiting toxicities for bevacizumab with radiation and chemotherapy: continued experience of a phase I trial in rectal cancer patients. J. Clin. Oncol. 2005;23:8136–8139. doi: 10.1200/JCO.2005.02.5635. [DOI] [PubMed] [Google Scholar]
- 46.Winkler F, Kozin SV, Tong RT, Chae SS, Booth MF, Garkavtsev I, Xu L, Hicklin DJ, Fukumura D, di Tomaso E, Munn LL, Jain RK. Kinetics of vascular normalization by VEGFR2 blockade governs brain tumor response to radiation: role of oxygenation, angiopoietin-1, and matrix metalloproteinases. Cancer Cell. 2004;6:553–563. doi: 10.1016/j.ccr.2004.10.011. [DOI] [PubMed] [Google Scholar]
- 47.Yuan F, Chen Y, Dellian M, Safabakhsh N, Ferrara N, Jain RK. Time-dependent vascular regression and permeability changes in established human tumor xeno-grafts induced by an anti-vascular endothelial growth factor/vascular permeability factor antibody. PNAS. 1996;93:14765–14770. doi: 10.1073/pnas.93.25.14765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Yuan F, Dellian M, Fukumura D, Leunig M, Berk DA, Torchilin VP, Jain RK. Vascular permeability in a human tumor xenograft: molecular size dependence and cutoff size. Cancer Res. 1995;55:3752–3756. [PubMed] [Google Scholar]
- 49.Yuan F, Leunig M, Berk DA, Jain RK. Micro-vascular permeability of albumin, vascular surface area, and vascular volume measured in human adenocarcinoma LS174T using dorsal chamber in SCID mice. Microvasc. Res. 1993;45:269–289. doi: 10.1006/mvre.1993.1024. [DOI] [PubMed] [Google Scholar]