Modelling spatially correlated survival data for individuals with multiple cancers

Abstract

Epidemiologists and biostatisticians investigating spatial variation in diseases are often interested in estimating spatial effects in survival data, where patients are monitored until their time to failure (for example, death, relapse). Spatial variation in survival patterns often reveals underlying lurking factors, which, in turn, assist public health professionals in their decision-making process to identify regions requiring attention. The Surveillance Epidemiology and End Results (SEER) database of the National Cancer Institute provides a fairly sophisticated platform for exploring novel approaches in modelling cancer survival, particularly with models accounting for spatial clustering and variation. Modelling survival data for patients with multiple cancers poses unique challenges in itself and in capturing the spatial associations of the different cancers. This paper develops the Bayesian hierarchical survival models for capturing spatial patterns within the framework of proportional hazard. Spatial variation is introduced in the form of county-cancer level frailties. The baseline hazard function is modelled semiparametrically using mixtures of beta distributions. We illustrate with data from the SEER database, perform model checking and comparison among competing models, and discuss implementation issues.

1 Introduction

Researchers in different fields have illustrated that accounting for spatial correlation could provide insights that would have been overlooked otherwise, while failure to account for spatial association could potentially lead to spurious and sometimes misleading results (see, for example, Biggeri et al., 2000; Lichstein et al., 2002; Ramsay et al., 2003; Turechek and Madden, 2002). Spatial variation in survival patterns often reveals underlying lurking factors, which, in turn, assist public health professionals in their decision making process to identify regions requiring attention. In epidemiology and biostatistics, modelling spatial variation and associations in survival data have recently emerged as an area of active research. Several studies have been conducted to model survival data accounting for spatial clustering and variation. Li and Ryan (2002) and Banerjee et al. (2003) addressed this problem under a proportional hazards framework from classical and Bayesian perspectives, respectively, while Banerjee and Dey (2005) modelled spatially correlated survival data under a semiparametric proportional odds structure.

The Surveillance Epidemiology and End Results (SEER) database of the National Cancer Institute records ‘primary cancer’ types based on the primary node for each patient, following up the first primary with subsequent cancers. In addition, each patient’s county of residence is also available. Consequently, survival models for multiple cancers are sought for practical reasons, such as to assess survival from multiple primary cancers simultaneously and to adjust the survival rates from a specific primary cancer in the presence of other primary cancers (see, for example, Heinävaara, 2003 and Sankila and Hakulinen, 1998). Recently, Carlin and Banerjee (2003) implemented spatial survival models, where each patient developed possibly several cancers (up to five different types), incorporating spatial frailties to accommodate spatial associations. For modelling the spatial associations, they employed a Multivariate Conditionally Auto-Regressive (MCAR) model, which is, in fact, a multi-layered Markov Random field (MRF) (see, for example, Mardia, 1988 and Gelfand and Vounatsou, 2002). Each type of cancer has its own spatial distribution over an underlying map, but are also spatially correlated amongst themselves, so that the cancer effects nested within space have a joint distribution that follows a multi-layered MRF or, more specifically, an MCAR distribution. They based their modelling upon the first primary cancer, incorporating the effects of subsequent cancers (if any) on that individual as binary regressors indicating presence or absence, but ignored the time-to-event information available for any subsequent primary cancers.

This paper outlines in Section 2 a proposal to treat the multivariate responses (for each individual) in survival data within a modelling framework that would permit the study of the spatial effects of the cancers while still retaining their multivariate spatial structure, thereby extending the work of Carlin and Banerjee (2003) to multivariate responses. At the outset, it is worth mentioning that this richness incurs additional complexity in the proposed models. If mapping disease rates was the sole objective, then splitting the data and performing separate analysis might suffice. However, with broader objectives that involve assessing model fits, estimating correlations between cancers and inferring on variance components are required, a flexible joint modelling framework, such as the one we propose, is desirable. Section 3 discusses aspects of the numerical implementation of the model. In Section 4, we illustrate the performance of our models with a colorectal cancer data set from the SEER database, while Section 5 concludes the paper with a summary and some possible areas of extension.

2 Multiple responses

The SEER database, available from the National Cancer Institute along with a statistical software SEER-STAT, lists cases of multiple cancers by cancer types diagnosed. Together with medicare data, one can extract an individual patient’s complete medical history, say, starting from his visits to the health clinics (from a time when he might have been perfectly healthy) and information about his interim (uneventful) visits between the diagnoses of cancers. Recognizing the potential information that is available, for now, let us consider a relatively simple version of the SEER data involving survival times and covariates for patients and cancers. Along with survival information, patient specific and patient-cancer combination specific covariates are also available. Patient specific information available in the registry includes gender, race, marital status, and their county of residence (provided the state belongs to the SEER registry). Patient-cancer specific information relates to age at diagnosis, the stage of the cancer (local, distant or regional), the type of treatment that each patient underwent for the different stages of the cancer and so on.

As an example, consider a patient, say with ID 1234, who first contracted colorectal cancer (the first primary cancer) in March 1991, subsequently developed cancers of the stomach and pancreas and eventually died in May 1994. Extracting the first ‘row’ for this patient with survival time for colorectal and regressors indicating the presence or absence of stomach, pancreas and perhaps a selection of other cancers, leads to models that ignore the sequence of the cancers and their time of onset (Carlin and Banerjee, 2003). More generally, other cancer-specific covariates used (for example, the stage of the cancer) were with reference to the first primary cancer (colorectal) only, with no time information on the subsequent cancers. We present the prognosis of a particular patient in Table 1, incorporating information about the disease progression. In particular, suppose patient 1234 was diagnosed with colorectal cancer in March 1991, developed stomach cancer in August 1992, pancreatic cancer in February 1994, and eventually succumbed to his illness in May 1994. We can extract information about this patient from the SEER database by cancer type, where each entry corresponding to the patient would list the date of the diagnosis, the type of diagnosis, the date of his end point (death or dropout), his status at end point (Dead or Alive) and his survival time (or censorship time) in months. Note that his status is labelled as ‘Dead’ for all his entries, as it corresponds to his status at the end point.

Table 1.

A sample database entry of a single patient with several cancers

Patient ID	Date of diagnosis	Cancer type	Date of end-point	Status	Survival time (months)
1234	March 1991	Colorectal	May 1994	Dead	38
1234	August 1992	Stomach	May 1994	Dead	21
1234	February 1994	Pancreas	May 1994	Dead	3

Along with the above information, we also know the patient’s county of residence. Assume there are I counties and in the ith county we observe n_i patients. Thus, the total number of patients in our study is $N={\sum }_{i=1}^I{n}_i$ and we uniquely identify every individual through the ordered pair (i, j), as the jth individual (j = 1, 2, …, n_i) from the ith county. Suppose each of these patients have been diagnosed with at least one of K possible cancer types. Our database provides us with the time from diagnosis to death for each type of cancer that the respective individual is suffering from. Let t_ijk denote this time, which we will refer to as the survival time for the (i, j)th individual from his diagnosis with the kth type of cancer. Since not all patients develop all the K types of cancer, we list the possible cancers as {1, 2, …, K}, and form the subset C_(i,j) ⊆ {1, 2, …, K} as the indices of the cancers developed by the (i, j)th patient. Thus, if patient 1234 is the 10th individual from the 8th county and if colorectal, stomach and pancreas are cancer types 1, 3 and 5, in {1, 2, …, K} then C_(8,10) = {1, 3, 5}. Indeed, when referring to t_ijk, k ∈ C_(i,j). Clearly, these survival times will be correlated for similar county-patient-cancer combinations. We capture these correlations by introducing appropriate frailties.

Let u_(i,j) denote the frailty for the (i, j)th patient (these may be looked upon as patient effects nested within counties), υ_k be the frailty for the kth cancer type and let φ_ik be the frailty for the kth cancer type nested within the ith county. Consider a proportional hazards model incorporating main effects for patients and cancers and nested effects for cancers within counties, which we write down as

$$h(t_{\mathit{ijk}})=h_0(t_{\mathit{ijk}})exp\left({\mathbf{x}}_{\mathit{ijk}}^T\mathit{\beta }+u_{(i,j)}+v_k+{\phi }_{ik}\right)$$ (2.1)

for i = 1, 2, …, I, j = 1, 2, …, n_i and k = 1, 2, …, K. Here, x_ijk denotes the patient-cancer specific covariates (includes covariates like age at diagnosis of primary cancer, stage of the individual cancers, indicator as to whether the cancer is the first primary cancer or not, etc.) and β is the corresponding vector of regression coefficients. Also, h₀(t) denotes a baseline hazard function, which is modelled semiparametrically as a mixture of beta functions (see, e.g., Gelfand and Mallick, 1995 and Ibrahim et al., 2001) as cancer-specific (in which case we write h_0k(t)) or county-specific (in which case we write h_0i(t)). In principle, we can also include subject-cancer interaction terms of the form w_(ij)k in (2.1), which may reveal cancer-specific variation in patient frailties. However, in practice, reliably estimating these higher order interaction terms becomes difficult, especially with data, such as ours, in which many subjects yield less than three observations. Since we already had space-cancer interaction terms in equation (2.1) (the φ_ik’s), adding the w_(ij)k’s vastly exacerbates the identifiability problems. Hence, we do not pursue this approach further.

Using the above notation and letting δ_(i,j) be a death indicator (status at endpoint) for the (i, j)th patient, we obtain the likelihood, L (β,η,{u_(i,j)},{υ_k}, {φ_ik}; {t_ijk}, x_ijk), as

$$\prod _{i=1}^I\prod _{j=1}^{n_i}\prod _{k\in C_{(i,j)}}[S(t_{\mathit{ijk}}\mid {\mathbf{x}}_{\mathit{ijk}},\mathit{\beta },\mathit{\eta })]{\left[h_0(t_{\mathit{ijk}};\mathit{\eta })exp\left({\mathbf{x}}_{\mathit{ijk}}^T\mathit{\beta }+u_{(i,j)}+v_k+{\phi }_{ik}\right)\right]}^{{\delta }_{ij}},$$ (2.2)

where S(t_ijk|x_ijk, β, η) is the survival function evaluated at t_ijk conditional on the parameters and observed covariates. Turning to the priors and hyper-priors, we would like to assume the patient frailties to be independent and normally distributed (zero-centered) with county-specific variances, that is, $u_{(i,j)}\stackrel{\mathit{indep}}{\sim }N(0,{\sigma }_i^2)$. Collecting the K cancers into a vector v, we assume v = (υ₁, …, υ_K)^T ~ N(0, Λ), where Λ is a K × K (unknown) covariance matrix. Turning to the spatial effects, we assign an MCAR (α, Λ) distribution (Carlin and Banerjee, 2003; Gelfand and Vounatsou, 2002) for {φ_ik}. More precisely, we form the vector $\mathrm{\Phi }={({\mathit{\phi }}_1^T,\dots {\mathit{\phi }}_I^T)}^T$, where φ_i = (φ_i1, …, φ_iK)^T is the collection of the spatial frailties for the K cancers within the ith county. Then, by {φ_ik} ~ MCAR (α, Λ), we mean

$$\mathrm{\Phi }={({\phi }_1^T,\dots {\phi }_I^T)}^T\sim N(0,{\mathrm{\sum }}_W(\alpha )\otimes \mathrm{\Lambda }),$$

where Σ_W (α) = (Diag (m_i) − αW)⁻¹, m_i, is the number of neighbours of county i and W is the adjacency matrix of the graph representing our region. Note that only α is random in Σ_W (α). It is easy to see (Carlin and Banerjee, 2003) that as long as α ∈ (0, 1), we have a proper MCAR distribution. Note that, in the above setup, we are using the same Λ to model the MCAR and the cancer main effects. Thus, we are modelling the dispersion matrix of the space-cancer interactions, Φ, as a Kronecker product of ‘spatial dispersion’ and ‘cancer dispersion’. This usage of Kronecker products for modelling interactions has been suggested earlier in non-spatial contexts by Clayton (1995). Of course, we may generalize further and set a new matrix ϒ, in MCAR (α, ϒ). Also, we may generalize the MCAR (α, Λ) to MCAR ((α₁, …, α_K), Λ), enriching our model by allowing different spatial smoothness parameters for each type of cancer (Carlin and Banerjee, 2003; Gelfand and Vounatsou, 2002). Yet another modification considers v_i ~ N (0, Λ_i) (not identically distributed), whereupon each county has its own cancer-covariance pattern. Alternatively, one may consider MCAR (α, Λ) to MCAR (α, (Λ₁, …, Λ_I)), where we retain a common smoothness parameter for the different cancers (even put α = 1) but allow different covariance functions for different counties.

However, the above generalizations of the MCAR (α, Λ) will often require substantial information on multiple cancer patients. Unfortunately, such information is rare in practice. For instance, in the SEER database, less than 1% of the patients have moderately large monitoring times with more than two different types of cancers. This scarcity renders many of the more general models unidentifiable. Therefore, we restrict our subsequent attention to the MCAR(α, Λ) specification and compare a spatially independent model with basically the same structure. This is accomplished by replacing the Σ_W (α) with a diagonal matrix which does not account for the spatial structure of the region, whence the collection of independent frailties for the K cancers within the ith county, denoted by Φ, has a N (0, τ²_{I ×I} ⊗ Λ) distribution where τ² is a scale parameter, which could have an inverted-Gamma prior or fixed for computational convenience.

In the next stage, we assign independent inverted-Gamma, I G (a_i, b_i), priors to the ${\sigma }_i^2$’s and an inverted-Wishart hyper-prior, I W (r₀, Λ₀), for the cancer covariance matrix Λ, where a_i’s, b_i’s, r₀ and Λ₀ are specified hyper-parameters. Flat or vague Gaussian priors are assumed for the regression coefficient vector β and a beta (say, Beta (9.5, 0.5) or a U (0, 1)) prior is assigned for the spatial smoothness parameter α. In the Gelfand and Mallick (1995) setup for modelling the baseline hazard function, h₀ (t) (or h_0i (t) or h_0k (t)—as the case may be), the weights in the mixture of beta functions, say η, are assumed random and having a Dirichlet(θ) distribution. θ may be taken as θ1, where θ is a fixed scalar hyperparameter. For county-specific and cancer-specific hazards we will have η_i’s and η_k’s respectively.

3 Numerical implementation

3.1 MCAR model: MCAR (α, Λ)

The model fitting exercise amounts to designing an appropriate Gibbs sampler for the above hierarchical model. For convenience, we first deal with the MCAR (α, Λ) case and introduce the following notations. Let us collect all the subjects in the ith county into a n_i × 1 vector, u_i, and then concatenate them to form the N × 1 (where $N={\sum }_{i=1}^I{n}_i$) vector $\mathbf{u}=({\mathbf{u}}_1^T,\dots ,{\mathbf{u}}_I^T)$. Letting v, φ_i’s, δ_(i,j) and C_(i,j) be as in Section 2, assume β ~ N(0, 10⁵_p×p) (an improper flat prior f (β) ∝ 1 is also legitimate), ${\sigma }_i^2\sim IG(a_i,b_i)$ independently, ${\mathbf{u}}_i\sim N(0,{\sigma }_i^2{\mathbb{I}}_{n_i\times n_i})$, v ~ N(0, Λ), Φ ~ MCAR (α, Λ) and η ~ Dirichlet(θ1).

The elements of β have full conditional distributions that are log-concave (with either flat or vague Gaussian priors) and can be updated using the Adaptive Rejection Sampling (ARS) algorithm (Gilks and Wild, 1992) or a Metropolis step. The same is true for the patient frailties {u_(i,j)}, the cancer frailties {υ_k} and the spatial frailties {φ_ik}. The full conditional distribution for the mixture weights, η, in the baseline hazard function, is

$$[\mathit{\eta }\mid \{t_{\mathit{ijk}}\}]\propto f(\mathit{\eta })\times \prod _{i=1}^I\prod _{j=1}^{n_i}\prod _{k\in C_{(i,j)}}[S(t_{\mathit{ijk}}\mid {\mathbf{x}}_{\mathit{ijk}},\beta ,\eta )]{[h_0(t_{\mathit{ijk}};\mathit{\eta })]}^{{\delta }_{ij}},$$

which needs to be updated using a Metropolis step. The full conditional for each of the ${\sigma }_i^2$ are conjugate inverted-Gamma distributions,

$$\left[{\sigma }_i^2\mid \mathbf{u},a_i,b_i\right]\sim IG\left(a_i+\frac{I}{2},b_i+\frac{1}{2}{\mathbf{u}}_i^T{\mathbf{u}}_i\right),\text{for}i=1,2,\dots ,I.$$

These are, therefore, updated with direct draws from their respective kernels. Also, Λ has a conjugate inverted-Wishart distribution, which follows from the following Lemma proved in the Appendix.

Lemma

Let A and B be I × I and K × K matrices and let x be any vector of length I K. Then, there exists a K × K matrix C and an I × I matrix D such that

$${\mathbf{x}}^T(A\otimes B)\mathbf{x}=tr(CB)=tr(DA).$$

Proof

See Appendix (item 1).

Now consider the computation of the transition kernel for Λ. We see that,

$$[\mathrm{\Lambda }\mid \mathbf{v},\mathrm{\Phi },r_0,{\mathrm{\Lambda }}_0]\propto \frac{1}{\mid \mathrm{\Lambda }{\mid }^{(r_0+K+I+1)/2}}exp\left(-\frac{1}{2}tr\left\{\left({\mathrm{\Lambda }}_0^{-1}+\mathbf{v}{\mathbf{v}}^T+C\right){\mathrm{\Lambda }}^{-1}\right\}\right),$$

where C is the matrix whose existence is guaranteed by the Lemma above. In fact, as we will see in the Appendix, $C={\sum }_{i=1}^I{\sum }_{i^{\prime }=1}^I{\left({\mathrm{\sum }}_W^{-1}(\alpha )\right)}_{i{i}^{\prime }}{\phi }_{i^{\prime }}{\phi }_i^T$. Thus, we have the transition kernel as

$$[\mathrm{\Lambda }\mid \mathbf{v},\mathrm{\Phi },\alpha ,r_0,{\mathrm{\Lambda }}_0]\sim IW\left(r_0+I,{\left({\mathrm{\Lambda }}_0^{-1}+\mathbf{v}{\mathbf{v}}^T+\sum _{i=1}^I\sum _{i^{\prime }=1}^I{\left({\mathrm{\sum }}_W^{-1}(\alpha )\right)}_{i{i}^{\prime }}{\mathit{\phi }}_{i^{\prime }}{\mathit{\phi }}_i^T\right)}^{-1}\right).$$

Note that in case we prefer different ‘cancer parameters’, Λ and ϒ for v and Φ, we can update them from their full conditionals as

$$IW\left(r_0+I,{\left({\mathrm{\Lambda }}_0^{-1}+\mathbf{v}{\mathbf{v}}^T\right)}^{-1}\right)$$

and

$$IW\left(r_{\mathrm{\Upsilon }}+I,{\left({\mathrm{\Upsilon }}_0^{-1}+\sum _{i=1}^I\sum _{i^{\prime }=1}^I{\left({\mathrm{\sum }}_w^{-1}(\alpha )\right)}_{i{i}^{\prime }}{\mathit{\phi }}_{i^{\prime }}{\mathit{\phi }}_i^T\right)}^{-1}\right),$$

where ϒ is assigned an inverted-Wishart prior I W (r_ϒ, ϒ₀).

Finally, the spatial smoothness parameter, α, is updated using a slice sampler (e.g., Agarwal and Gelfand, 2005; Banerjee et al., 2004). For the kernel of α, we note that [α|Φ, Λ] ∝ f (α) × f (Φ| α, Λ), where $f(\mathrm{\Phi }\mid \alpha ,\mathrm{\Lambda })=1/\mid {\mathrm{\sum }}_W(\alpha ){\mid }^{K/2}exp\left(-\frac{1}{2}{\mathrm{\Phi }}^T\left({\mathrm{\sum }}_W^{-1}(\alpha )\otimes {\mathrm{\Lambda }}^{-1}\right)\mathrm{\Phi }\right)$. A slice sampler for the kernel of α draws, within the current state of the Gibbs sampler, U ~ [U|α, Φ, Λ] ≡ Unif (0, f (Φ| α, Λ)) followed by, α ~ [α|Φ, Λ, U] ∝ f (α) × 1_{{(α,U):f (Φ| α, Λ)≥U}}, amounting to a rejection sampling from the prior of α. Letting Ω be the generic collection of parameters apart from α, the stationary distribution of the Markov chain is left invariant by the above scheme, since [α|Φ, Λ, U] and [Ω| α, {t_ijk}, {x_ijk}] (remember that none of the kernels in Ω depend upon U) together determine [α, Ω|U, {t_ijk}, {x_ijk }], which together with [U|α, Φ, Λ] determines the joint distribution, [α, Ω, U|{t_ijk}, {x_ijk}].

3.2 Spatial independence model

The essential difference between the implementation of the MCAR (α, Λ) model and the spatial independence model is in the posterior distribution of the cancer covariance matrix Λ. In this setting, the transition kernel is given by

$$[\mathrm{\Lambda }\mid \mathbf{v},\mathrm{\Phi },r_0,{\mathrm{\Lambda }}_0]\sim IW\left(r_0+I,{\left({\mathrm{\Lambda }}_0^{-1}+\mathbf{v}{\mathbf{v}}^T+\frac{1}{{\tau }^2}\sum _{i=1}^I\sum _{i^{\prime }=1}^I{\mathit{\phi }}_{i^{\prime }}{\mathit{\phi }}_i^T\right)}^{-1}\right).$$

The rest of the model parameters are updated in exactly the same manner as in the MCAR (α, Λ) model with the exception of α, which disappears from the spatial independence model.

4 Illustration

To illustrate the proposed methodology, we obtained data from the 1973–2001 SEER Public Use Incidence Database on patients from the state of Iowa diagnosed with colorectal cancer. Colorectal cancer is the fourth most commonly occurring cancer in both men and women in the United States, behind only skin, lung and prostate or breast cancers. This, and the fact that colorectal cancer involves two gastrointestinal related organs, serve as motivations for using this cancer type to illustrate the methodology. The diagnosis was further classified into the two cancer types (colon and rectum) with survival times recorded in months from diagnosis up to study termination (censored) or death (failure). The 1083 patients in the data represent 96 of the 99 counties in Iowa. Age (in years) at diagnosis for each type of cancer are included as categorical covariates, with categories: <55, ≤ 55–65, ≤ 65–75 and > 75. The stage of each type of cancer are included with categories in situ or unstaged, local, regional, or distant. The total number of primary cancers, dichotomized as 0 (nprimes ≤ 2) and 1 (nprimes > 2), and gender are other covariates believed to impact on the hazard. An indicator variable, colon first, is used to capture the effect of the order of occurrence. In the dataset, 28% of the patients’ survival times were censored, 44% of patients were females, 69% had at most two primary cancers, 47% had colon cancer before rectal cancer, majority of cases (78% for colon and 75% for rectal cancer) were in the local or regional stage, and most of the cases were diagnosed when patients were 65 years or older (76% for colon and 74% for rectal cancer).

We then fitted the MCAR (α, Λ) and the spatial independence models to the data. Under each of the above two models we looked at two submodels: with or without the patient frailties {u_(i,j)}. The submodels were designed to verify if patient specific variation contribute significantly to the model fit. Henceforth, we adopt the naming convention in Table 2. An appropriate Gibbs sampler was set up to obtain samples from the posterior distribution. Metropolis-Hastings algorithms with normal candidates were used to update the posterior distributions of the regression parameters and the frailties. For models with the patient specific frailties {u_(i,j)}, the variances { ${\sigma }_i^2$} were updated using direct draws from the inverted-Gamma full conditional distributions. The cancer variance-covariance matrix Λ was updated using direct draws from the appropriate inverted-Wishart distribution. For models with patient-specific frailties, the hyperparameters for the prior distribution of the county-specific variance parameters, ${\sigma }_i^2$, were fixed at a_i = b_i = 1.0. The scale parameter was fixed at 1.0 for the spatially independent models. We also set r₀ = K and Λ₀ = _k×k for all models.

Table 2.

Model labels and descriptions

Model	Model description
Model I	Full MCAR (α, Λ)
Model II	MCAR (α, Λ) Without Patient Frailties {u(i,j)}
Model III	Full Spatial Independence Model
Model IV	Spatial Independence Model Without Patient Frailties {u(i,j)}

Turning to the mixture of beta distributions for the baseline hazard function, we model h₀ (t_ijk) as

$$\begin{array}{l}{h}_0(t;\mathit{\eta })=\frac{\partial }{\partial t}{H}_0(t;\mathit{\eta })=\frac{b_0{\sum }_{l=1}^q{\eta }_l\mathit{Beta}\left(r_l,s_l,{\stackrel{\sim }{J}}_0(t)\right)}{a_0(1-J_0(t;\eta ))}\left(\frac{\partial }{\partial t}{\stackrel{\sim }{J}}_0(t;\mathit{\eta })\right)\text{where},\\ H_0(t;\mathit{\eta })=\frac{b_0{J}_0(t;\mathit{\eta })}{a_0(1-J_0(t;\eta ))}\\ J_0(t;\mathit{\eta })=\sum _{l=1}^q{\eta }_{l}IB\left(r_l,s_l,{\stackrel{\sim }{J}}_0(t)\right)\\ {\stackrel{\sim }{J}}_0(t)=\frac{a_0{\stackrel{\sim }{H}}_0(t)}{a_0{\stackrel{\sim }{H}}_0(t)+b_0}\\ {\stackrel{\sim }{H}}_0(t)=t,\text{i}.\text{e}.,t\sim \mathit{Exp}(1)\text{at}\text{baseline}.\end{array}$$

The parameters a₀ and b₀ were chosen so that the transformed baseline cumulative hazard function J̃₀(t) would cover as much of the interval [0, 1] as reasonably possible. The parameters of the mixing distributions were chosen so that the means are equally spaced along the interval [0, 1]. Gelfand and Mallick (1995) have shown that fixing the above parameters as well as the parameter of the prior distribution for the mixing weights η is essentially a computational and not a modelling concern. Further, even though there could conceptually be infinitely many mixands, a small number would usually suffice. In this exercise, we fixed a₀ = 1, b₀ = 1, the number of mixing distributions q = 5, and the parameter of the Dirichlet prior for the mixing weights θ = 1. It is also possible to use a different baseline distribution of survival times, such as a Weibull distribution, although we have not attempted this case.

For each of these models, two parallel MCMC chains were run for 20 000 iterations each. The BOA program (Smith, 2005) was used to diagnose convergence by monitoring Geweke’s lone chain convergence diagnostics, autocorrelations and cross-correlations, as well as mixing between the chains. For each of these models and each of the two chains, the first 10 000 were deemed sufficient for burnin, so the remaining 20 000 samples (10 000 × 2) samples were retained for post-burnin analysis.

The results obtained after fitting the four models indicate the covariates considered have significant contributions (Table 3). It can be observed from the table that the parameter estimates are consistent across the different models, which should give some support to the modelling framework. There is evidence suggesting that the relative risk of dying is significantly lower in women than in men, as illustrated by the negative coefficients for gender. This finding is consistent with the estimated mortality rates presented in the SEER cancer statistics review (Ries et al., 2005). Further, the number of primary cancers has a significant negative coefficient, which means a lowering of hazard rate as more primary cancers are observed. It is worth mentioning that this variable is post-hoc in the sense that one does not know how many primaries the patient will develop in the beginning. Also, it is possible that this variable is collinear with some of the random effects (see e.g., Kelderman, 1984, for a similar phenomenon but in a very different context). However, this effect might be explained by the fact that patients who survive longer have greater chances of developing more cancers, as indicated by the shorter median survival time (57 versus 94 months) from diagnosis of the first cancer between patients having at most two primary cancers compared to those having more.

Table 3.

Regression parameter estimates and 95% highest posterior density (HPD) intervals under various models

Parameter	Model I	Model II	Model III	Model IV
Patient-level
Gender = Female†	−3.60 (−3.61, −3.60)	−3.60 (−3.61, −3.60)	−3.60 (−3.61, −3.60)	−3.60 (−3.61, −3.60)
Number of primaries†	−3.04 (−3.05, −3.04)	−3.04 (−3.05, −3.04)	−3.04 (−3.05, −3.04)	−3.04 (−3.05, −3.04)
Colon first‡	3.96 (3.94, 3.97)	3.96 (3.95, 3.97)	3.96 (3.95, 3.97)	3.96 (3.94, 3.97)
Colon cancer
Frailty, ν1	−2.40 (−2.90, −1.98)	−2.46 (−2.92, −2.01)	−1.70 (−1.86, −1.56)	−1.80 (−2.05, −1.57)
Stage
In situ or Unstaged§	—	—	—	—
Local	−0.25 (−0.33, −0.18)	−0.25 (−0.33, −0.18)	−0.25 (−0.33, −0.18)	−0.25 (−0.32, −0.18)
Regional	0.03 (−0.05, 0.10)	0.03 (−0.04, 0.10)	0.03 (−0.05, 0.10)	0.03 (−0.04, 0.11)
Distant	1.12 (1.02, 1.21)	1.12 (1.02, 1.21)	1.12 (1.02, 1.21)	1.12 (1.02, 1.20)
Age
– < 55§	—	—	—	—
55 ≤ – < 65	0.47 (0.36, 0.58)	0.47 (0.36, 0.58)	0.47 (0.36, 0.57)	0.47 (0.35, 0.57)
65 ≤ – < 75	0.74 (0.64, 0.84)	0.74 (0.64, 0.84)	0.74 (0.64, 0.84)	0.74 (0.64, 0.84)
75 ≤ –	1.16 (1.07, 1.27)	1.16 (1.06, 1.26)	1.16 (1.06, 1.26)	1.16 (1.06, 1.26)
Rectal cancer
Frailty, ν2	−2.17 (−2.63, −1.72)	−2.25 (−2.73, −1.80)	−1.88 (−2.07, −1.69)	−2.07 (−2.37, −1.75)
Stage
In situ or Unstaged§	—	—	—	—
Local	−0.40 (−0.81, 0.02)	−0.40 (−0.81, 0.04)	−0.40 (−0.80, 0.02)	−0.40 (−0.82, 0.02)
Regional	0.07 (−0.36, 0.49)	0.07 (−0.35, 0.47)	0.07 (−0.35, 0.49)	0.07 (−0.35, 0.48)
Distant	1.44 (1.16, 1.72)	1.44 (1.16, 1.72)	1.44 (1.16, 1.71)	1.44 (1.17, 1.73)
Age at diagnosis
– < 55§	—	—	—	—
55 ≤ – < 65	0.36 (0.05, 0.66)	0.35 (0.05, 0.65)	0.36 (0.05, 0.66)	0.35 (0.04, 0.64)
65 ≤ – < 75	0.76 (0.36, 1.17)	0.76 (0.35, 1.16)	0.76 (0.36, 1.18)	0.76 (0.36, 1.17)
75 ≤ –	1.28 (0.86, 1.70)	1.28 (0.87, 1.71)	1.28 (0.87, 1.72)	1.28 (0.86, 1.70)

^†,‡Notes: Precision is 1 × 10⁻¹ and 1 × 10⁻², respectively.

^§Reference categories.

The coefficient for the order of occurrence of the two cancers suggests that a slightly elevated risk is expected if colon cancer is diagnosed first. The coefficients for cancer stages indicate that the risk of dying increases when the cancer is diagnosed at later stages. The lower (negative) coefficient for local relative to in situ or unstaged could be due to the conservative approach of pooling done in the reference category. The coefficients for categories of age at diagnosis indicates increased risk as the patient gets diagnosed at an older age. The effects of the covariates on the two cancers considered are in the same direction albeit with slightly different magnitudes. The cancer frailties indicate that the risk of failure from rectal cancer is slightly higher than from colon cancer under the MCAR (α, Λ) models but the direction is reversed under the spatially independent models. This result, better presented in Figure 1, may be indicative of the effect of the spatial structure used.

Figure 1.

Distribution of cancer-specific frailties (Y-axis) under the different models. Y-axis range is from −4.0 to −1.0. Positive frailties indicate higher relative risks while negative values indicate the opposite

The other model parameters are presented in Table 4. The data appeared to have limited information to update the distribution of the spatial smoothness parameter. The estimated weights for the mixture of beta distributions indicate that most of the influence in approximating the baseline hazard function comes from the Beta (5, 1) distribution. It could also be noted that the estimates of the cancer variance-covariance matrix are larger in magnitude in the spatial models compared to the non-spatial models. However, the opposite could be said for the estimated a priori correlation between the two cancers. Nonetheless, the estimated correlation coefficient, ρ, indicates that the hazard rates between the two cancers are positively correlated. This potentially very useful correlation parameter would not be available, or at least directly interpretable, if the cancers were modelled independently. We also observe that the (non-spatial) correlation among diseases drops from around 45% to less than 36% when a spatial dependent model is fitted. A possible explanation is that the unmeasured spatially structured confounding accounts for part of the correlation between the two cancer survival.

Table 4.

Parameter estimates and 95% HPD intervals under various models

Parameter	Model I	Model II	Model III	Model IV
α	0.95 (0.81, 1.00)	0.95 (0.81, 1.00)	—	—
η1	0.90 (0.88, 0.92)	0.90 (0.88, 0.92)	0.90 (0.88, 0.92)	0.90 (0.88, 0.92)
η2	0.03 (0.01, 0.04)	0.03 (0.01, 0.04)	0.02 (0.01, 0.04)	0.02 (0.01, 0.04)
η3	0.02 (0.01, 0.04)	0.03 (0.01, 0.04)	0.03 (0.01, 0.04)	0.03 (0.01, 0.04)
η4	0.03 (0.01, 0.04)	0.03 (0.01, 0.04)	0.02 (0.01, 0.04)	0.02 (0.01, 0.04)
η5	0.03 (0.01, 0.04)	0.03 (0.01, 0.04)	0.03 (0.01, 0.04)	0.02 (0.01, 0.04)
Λ11†	1.29 (0.59, 2.11)	1.30 (0.59, 2.12)	0.41 (0.20, 0.65)	0.41 (0.19, 0.65)
Λ22†	0.54 (0.20, 0.91)	0.57 (0.23, 0.96)	0.27 (0.13, 0.42)	0.29 (0.13, 0.46)
Λ12†	1.78 (0.90, 2.74)	1.84 (0.95, 2.83)	0.87 (0.48, 1.30)	0.98 (0.54, 1.47)
ρ	0.36 (0.20, 0.53)	0.37 (0.21, 0.54)	0.45 (0.31, 0.60)	0.46 (0.31, 0.62)

^†Note: Precision is 1 × 10⁻³.

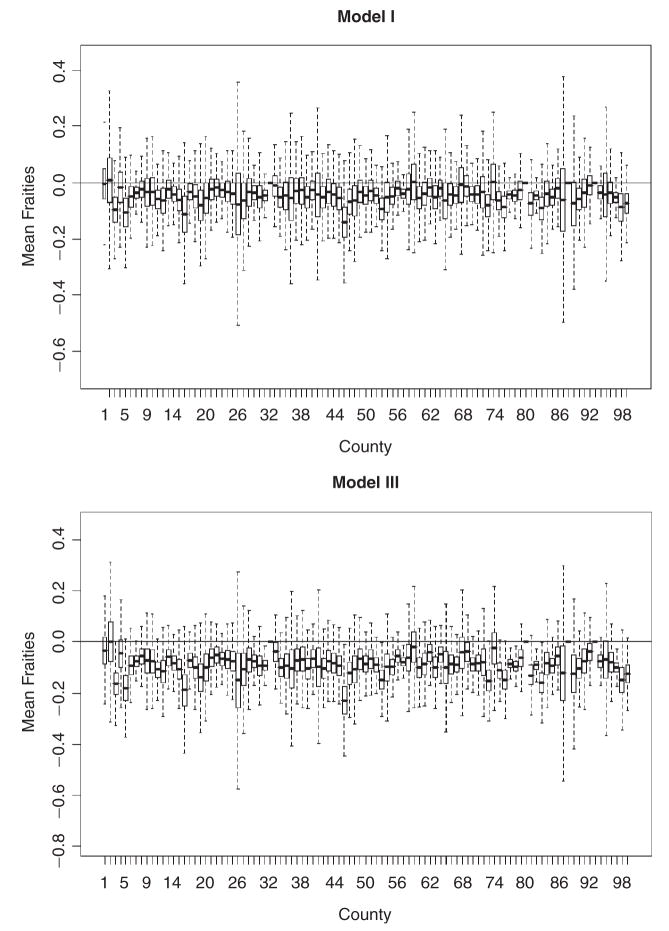
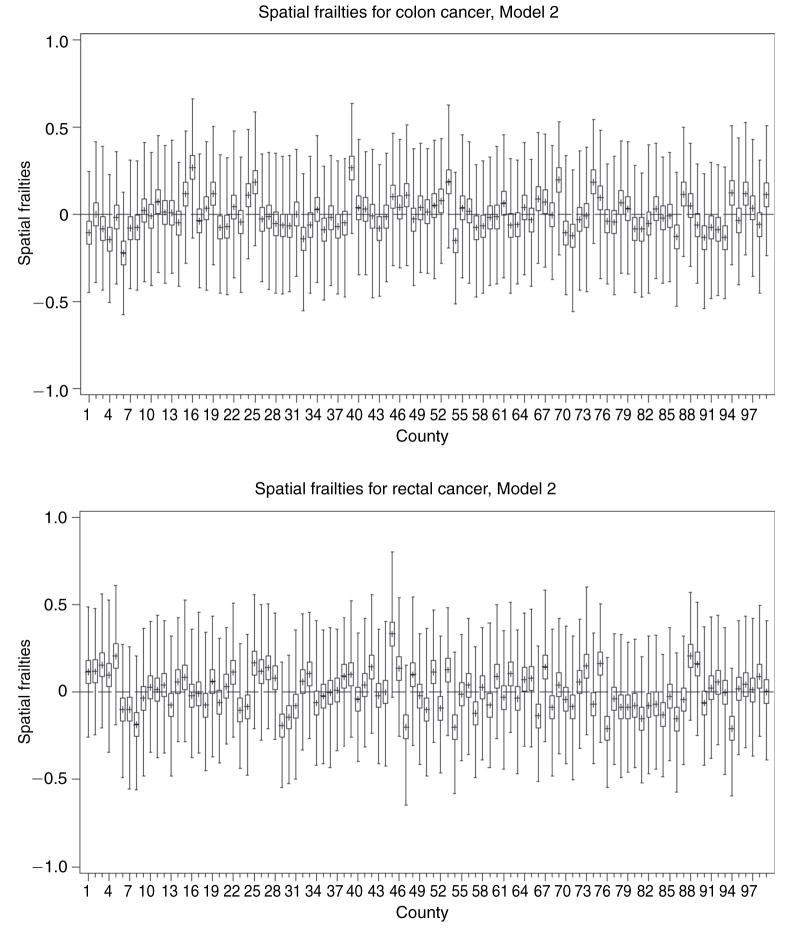
For models with patient-specific frailties (Models I and III), the county-level average of the patient frailties are summarized in boxplots presented in Figure 2. It is worth mentioning that the variation in the patient-specific frailties across the different counties does not appear to be considerable under both, Models I and III. In relation to the cancer frailties, the patient frailties have much smaller magnitudes, suggesting that patient characteristics do not drive the variability observed in the data. The spatial frailties are summarized using boxplots (Figure 3) and choropleth maps (Figure 4). Figure 3 indicates that some counties have slightly higher risks than others. The estimated frailties are also very similar across the four models under each cancer type. Figure 4 shows some degree of clustering, with lower risk counties concentrated around urban areas. The spatial priors do help in evincing the spatial story, which otherwise would have been hard to glean given the considerable imbalance in terms of the number of observed cases across the counties, which potentially dilutes the spatial information. The choropleth maps also reveal that the unmeasured spatially structured confounding we mentioned earlier is represented by two distinct spatial patterns, which might be suggestive of a shared clustering component for the two diseases (see Held et al., 2005; Held and Best, 2001). Correlation between the two cancers is interesting in inferring about common or not common factors (for example, dietary habits) that might have contributed to the disease state. It is an added value of multivariate modelling, especially because inappropriate adjustment for spatially structured confounding could lead to inaccurate results.

Figure 2.

Distribution of average patient-specific frailties (Y-axes) from different counties (X-axes) in Iowa under Model I and Model III. Y-axes reference lines at Y = 0. Positive frailties indicate higher relative risks while negative values indicate the opposite

Figure 3.

Distribution of spatial frailties (Y-axes) for colon and rectal cancers from different counties (X-axes) in Iowa under the different models. Y-axes range is from −1.0 to 1.0 with reference lines at Y = 0. Positive frailties indicate higher relative risks while negative values indicate the opposite. The plots for the other models show very similar patterns

Figure 4.

Spatial frailties for colon and rectal cancers in Iowa under the different models. Color change from white to black indicates an increase from negative to positive spatial frailties. Cutoff values are one standard deviation units from the mean of each cancer type in each model. Locations of urban areas are also indicated to potentially account for clustering

The conditional predictive ordinate (CPO) and the average log-marginal pseudo-likelihood (ALMPL) were used for model checking and comparison. Since we have nested models (patients within counties and cancers within patients and counties), different forms of the CPO statistic may be derived depending on the level of hierarchy being considered. Here, we figured the most intuitive of the CPO definitions is at the patient-county level, which, following Gelfand and Dey (1994) and Chen et al. (2000), is given as

$$CP{O}_{ij}=f\left(D_{ij}\mid {\mathbf{x}}_{ij},{\mathbf{D}}^{(-ij)}\right)={\left(\int \frac{1}{f(D_{ij}\mid {\mathbf{x}}_{ij},\mathbf{\Theta })}\pi (\mathbf{\Theta }\mid \mathbf{D})\partial \mathbf{\Theta }\right)}^{-1}$$ (4.1)

where D_ij = (i, j)th observation, D is the complete data, and Θ is the collection of parameters. It is apparent from the above definition that modifications have to be made to reflect the presence of various random effects in the models, particularly the patient-specific frailties {u_(i,j)}. For models involving the patient-specific frailties (Models I and III) we need to integrate out u_(i,j) to get the distribution of D_ij given the parameters. The CPO expressions for the four models in Table 2 are given in the Appendix (item 2). For each model, the ALMPL was calculated as

$$\mathit{ALMPL}=\frac{1}{N}{\sum }_{ij}log\mathit{CP}{O}_{ij}.$$

Larger values of ALMPL indicate better model fit. See Chen et al. (2000) for more details.

The Deviance Information Criterion (DIC) proposed by Spiegelhalter et al. (2002) was also used for model comparison. The DIC for a particular model with data y and parameters Ω and likelihood f (y|Ω) is given by

$$\mathit{DIC}=-4E_{\mathbf{\Omega }}\left[logf(\mathit{y}\mid \mathbf{\Omega })\mid \mathit{y}\right]+2logf\left(\mathbf{y}\mid \stackrel{\sim }{\mathbf{\Omega }}\right),$$ (4.2)

where the first term is the posterior mean of the log-likelihood evaluated at different realizations of Ω and the second term is the log-likelihood evaluated at the posterior mean (median or mode) of Ω, denoted by Ω̃. However, Celeux et al. (2006) noted that for models with random effects denoted by Z, such as in this setting, the DIC presented above is not as naturally defined. They proposed different types of modifications, one of which is the modified DIC defined as follows:

$$\mathit{DIC}=-4E_{\mathbf{\Omega },\mathit{Z}}\left[logf(\mathit{y},\mathit{Z}\mid \mathbf{\Omega })\mid \mathit{y}\right]+2E_{\mathit{Z}}\left[logp(\mathit{y},\mathit{Z}\mid E_{\mathbf{\Omega }}[\mathbf{\Omega }\mid \mathit{y},\mathit{Z}])\right],$$ (4.3)

which, in principle, essentially integrates out the random effects. According to this criterion, models with smaller DIC are considered relatively better. A related measure of model complexity, the p_D, is given by

$$p_D=\mathit{DIC}+2E_{\mathbf{\Omega },\mathit{Z}}\left[logf(\mathit{y},\mathit{Z}\mid \mathbf{\Omega })\mid \mathit{y}\right],$$ (4.4)

with smaller values pointing to models with lesser complexity. As in the case of the CPO calculations, the expectations were evaluated using Monte Carlo integration.

Table 5 presents the ALMPL, the DIC difference from Model I (reference), and p_D values while the plots (Figure 5) in the appendix present the differences in the {log(CP O_ij)} for each model pair. It appears from the table that the MCAR (α, Λ) models (I and II) performed better (larger ALMPL and smaller DIC) than the spatially independent ones. However, between the two MCAR (α, Λ) models, the ALMPL values are very close but still support the model with patient frailties (Model I) while the DIC and p_D values support the model without patient frailties (Model II). The plots in Figure 5 also indicate better fit for Model I over the other models. However, the head-to-head comparison of Models I and II in the plots indicates only slight preference on Model I. Considering the added complexity of fitting patient-specific frailties in Model I over Model II, we recommend the use of of the MCAR (α, Λ) without the patient-specific frailties (Model II) as the final model.

Table 5.

Summaries of the different model comparison statistics

Model	ALMPL	ΔDIC†	pD
Model I	−5.92	—	90.40
Model II	−6.03	−247.81	2.71
Model III	−6.96	5761.58	276.75
Model IV	−8.48	3588.42	149.13

^†Note: DIC difference from Model I (smaller indicates better model).

Figure 5.

Boxplots of the $CP{O}_{ij}^A-log\mathit{CP}{O}_{ij}^B$ for each model pair. Positive values indicate support for model A over model B while negative values indicate the opposite. A value equal to 0 indicates equivalence of the two models. The wider range of values in comparisons involving Model IV indicate the other models perform considerably better

5 Summary and future work

This paper presented a methodology for modelling spatially correlated multivariate cancer survival data, illustrated using colon and rectal cancer data for the state of Iowa obtained from the SEER database. The results suggest that there is a positive correlation between the hazard rates of colon and rectal cancers. This information may not be available or interpretable when modelling the cancers independently. The significance of studying the correlations between two cancers were also presented in Jin et al. (2005) where they studied lung and esophageal cancers under a disease mapping framework. Other mechanisms for handling spatial covariation, such as the shared component approach, presented by Held and Best (2001), applied to disease mapping of oral and esophageal cancers, are also possible. The shared component idea could be incorporated into our modelling framework by introducing an additional frailty term, say θ_i, which would yield a spatial-cancer model specified by ν_k + θ_i + φ_ik. This approach was not implemented but certainly merits future investigations.

There is also some evidence of spatial variation across the different counties but there was minimal evidence of individual patient variability. We also note that there is minimal increase in risk when colon cancer is diagnosed first. There is also some evidence suggesting that females have lower risk of dying than males, which was consistent with registry reports. A decrease in hazard rate as more types of primary cancers are observed is suggested by the negative coefficient, which could be due to the fact that patients who survived longer have more chance of developing more cancers. Prognosis appears to be worse for patients diagnosed at an older age and when the cancer was already in a later stage when diagnosed. The next step along this line is to look at more covariates at the county, patient, and cancer levels to make the model more informative.

The basic modelling framework may be extended in several ways. In this exercise we worked with the proportional hazards assumption, but the method could be used under a different hazard structure if the need arises. Even though the method was illustrated using only two cancer types, it is conceptually easy to extend this to a higher number of cancers types. Our models assumed that there is a common baseline hazard rate for the two cancers. The model could be further enriched by incorporating different baseline hazards for each cancer type (see Section 2 for details). Other semiparametric approaches in modelling the baseline hazard function are certainly available and the reader is referred to Ibrahim et al. (2001) and references therein for more information. As mentioned in Section 2, the MCAR (α, Λ) structure may be generalized in several ways: MCAR (α,ϒ), which allows for different spatial and non-spatial cancer variance-covariance matrices; MCAR ((α₁, …, α_K), Λ), which allows for different spatial smoothness parameters for each type of cancer; and MCAR (α, (Λ₁, …, Λ_I)), which allows for different cancer variance-covariance patterns for each county. The extensions of the MCAR (α, Λ) model were not implemented due to identifiability constraints arising from sparse data. The complexity of the extended models and the mixture of beta distributions for the baseline hazard would require the development of a more stable computing algorithm and a more robust dataset.

Appendix

1. Lemma: Let A and B be I × I and K × K matrices, respectively, and let x be any vector of length I K. Then, there exists a K × K matrix C and an I × I matrix D such that

$${\mathbf{x}}^T(A\otimes B)\mathbf{x}=tr(CB)=tr(DA).$$

Proof

Partition the I K × 1 vector x into I subvectors, each of length K, as $\mathbf{x}={({\mathbf{x}}_1^T,\dots ,{\mathbf{x}}_I^T)}^T$. Then,

$$\begin{array}{l}{\mathbf{x}}^T(A\otimes B)\mathbf{x}=\sum _{i=1}^I\sum _{j=1}^I{(A)}_{ij}{\mathbf{x}}_i^{T}B{\mathbf{x}}_j=\sum _{i=1}^I\sum _{j=1}^I{(A)}_{ij}tr\left({\mathbf{x}}_j{\mathbf{x}}_i^{T}B\right)\\ =tr\left(\sum _{i=1}^I\sum _{j=1}^I{(A)}_{ij}{\mathbf{x}}_j{\mathbf{x}}_i^{T}B\right)=tr(CB),\text{with}C=\sum _{i=1}^I\sum _{j=1}^I{(A)}_{ij}{\mathbf{x}}_j{\mathbf{x}}_i^T.\end{array}$$

Clearly C is K × K, since ${\mathbf{x}}_j{\mathbf{x}}_i^T$’s are.

Next, consider the fact (see Harville, 1999) that there exists a permutation (hence orthogonal) matrix P, such that A ⊗ B = P^T(B ⊗ A)P. Setting y = P x and partitioning, y into K subvectors, each of length I, so that $\mathbf{y}={({\mathbf{y}}_1^T,\dots ,{\mathbf{y}}_K^T)}^T$, we see

$$\begin{array}{l}{\mathbf{x}}^T(A\otimes B)\mathbf{x}={\mathbf{x}}^T{P}^T(B\otimes A)P\mathbf{x}\\ =\sum _{i=1}^K\sum _{j=1}^K{(B)}_{ij}{\mathbf{y}}_i^{T}A{\mathbf{y}}_j=\sum _{i=1}^K\sum _{j=1}^K{(B)}_{ij}tr\left({\mathbf{y}}_j{\mathbf{y}}_i^{T}A\right)\\ =tr\left(\sum _{i=1}^K\sum _{j=1}^K{(B)}_{ij}{\mathbf{y}}_j{\mathbf{y}}_i^{T}A\right)=tr(DA),\text{with}D=\sum _{i=1}^K\sum _{j=1}^K{(B)}_{ij}{\mathbf{y}}_j{\mathbf{y}}_i^T,\end{array}$$

where y = P x. More explicitly in terms of x, y_k = (x_1k, x_2k, …, x_{I k})^T, k = 1, 2, …, K, where x_i = (x_i1, …, x_iK)^T, i = 1, 2, …, I

2. The CPO expression for each of the four models in Table 2 are as follows:

$$\begin{array}{l}CP{O}_{ij}^I={\left(\int \frac{1}{\int f(D_{ij}\mid {\mathbf{x}}_{ij},u_{(i,j)},\mathbf{Z},{\mathbf{\Theta }}_I)f(u_{(i,j)}\mid {\mathbf{\Theta }}_I)\partial u_{(i,j)}}f(\mathbf{Z}\mid \mathbf{D},{\mathbf{\Theta }}_I)\pi ({\mathbf{\Theta }}_I\mid \mathbf{D})\partial \mathbf{Z}\partial {\mathbf{\Theta }}_I\right)}^{-1}\\ CP{O}_{ij}^{II}={\left(\int \frac{1}{f(D_{ij}\mid {\mathbf{x}}_{ij},\mathbf{Z},{\mathbf{\Theta }}_{II})}f(\mathbf{Z}\mid \mathbf{D},{\mathbf{\Theta }}_{II})\pi ({\mathbf{\Theta }}_{II}\mid \mathbf{D})\partial \mathbf{Z}\partial {\mathbf{\Theta }}_{II}\right)}^{-1}\\ CP{O}_{ij}^{\mathit{III}}={\left(\int \frac{1}{\int f(D_{ij}\mid {\mathbf{x}}_{ij},u_{(i,j)},\mathbf{Z},{\mathbf{\Theta }}_{\mathit{III}})f(u_{(i,j)}\mid {\mathbf{\Theta }}_{\mathit{III}})\partial u_{(i,j)}}f(\mathbf{Z}\mid \mathbf{D},{\mathbf{\Theta }}_{\mathit{III}})\pi ({\mathbf{\Theta }}_{\mathit{III}}\mid \mathbf{D})\partial \mathbf{Z}\partial {\mathbf{\Theta }}_{\mathit{III}}\right)}^{-1}\\ CP{O}_{ij}^{IV}={\left(\int \frac{1}{f(D_{ij}\mid {\mathbf{x}}_{ij},\mathbf{Z},{\mathbf{\Theta }}_{IV})}f(\mathbf{Z}\mid \mathbf{D},{\mathbf{\Theta }}_{IV})\pi ({\mathbf{\Theta }}_{IV}\mid \mathbf{D})\partial \mathbf{Z}\partial {\mathbf{\Theta }}_{IV}\right)}^{-1}\end{array}$$

where D_ij = {t_ijk, δ_ij; k ∈ C_(i,j)}, Z = {υ_k, φ_ik; k ∈ C_(i,j)}, ${\mathbf{\Theta }}_I=(\mathit{\beta },\mathit{\eta },\mathbf{\Lambda },\{{\sigma }_i^2\},\alpha )$, Θ_{I I} = (β, η, Λ, α), ${\mathbf{\Theta }}_{\mathit{III}}=(\mathit{\beta },\mathit{\eta },\mathbf{\Lambda },\{{\sigma }_i^2\})$ Θ _{I V} = (β, η, Λ), $f(u_{(i,j)}\mid \mathbf{\Theta })\equiv N(0,{\sigma }_i^2)$, and

$$\begin{array}{l}f(D_{ij}\mid {\mathbf{x}}_{ij},u_{(i,j)},\mathbf{Z},\mathbf{\Theta })\\ ={\prod }_{k\in C_{(i,j)}}[S(t_{\mathit{ijk}}\mid {\mathbf{x}}_{\mathit{ijk}},\beta ,\eta )]{\left[h_0(t_{\mathit{ijk}};\mathit{\eta })exp\left({\mathbf{x}}_{\mathit{ijk}}^T\mathit{\beta }+u_{(i,j)}+v_k+{\phi }_{ik}\right)\right]}^{{\delta }_{ij}}.\end{array}$$

Note that the integrals given above cannot be obtained in closed form and hence they were evaluated using Monte Carlo integration.