Modeling Intra-tumor Protein Expression Heterogeneity in Tissue Microarray Experiments

SUMMARY

Tissue Microarrays (TMAs) measure tumor-specific protein expression via high-density immunohistochemical staining assays. They provide a proteomic platform for validating cancer biomarkers emerging from large-scale DNA microarray studies. Repeated observations within each tumor result in substantial biological and experimental variability. This variability is usually ignored when associating the TMA expression data with patient survival outcome. It generates biased estimates of hazard ratio in proportional hazards models. We propose a Latent Expression Index (LEI) as a surrogate protein expression estimate in a two-stage analysis. Several estimators of LEI are compared: an Empirical Bayes (EB), a Full Bayes (FB), and a Varying Replicate Number (VRN) estimator. In addition, we jointly model survival and TMA expression data via a shared random effects model. Bayesian estimation is carried out using a Markov Chain Monte Carlo (MCMC) method. Simulation studies were conducted to compare the two-stage methods and the joint analysis in estimating the Cox regression coefficient. We show the two-stage methods reduce bias relative to the naive approach, but still lead to under-estimated hazard ratios. The joint model consistently outperforms the two-stage methods in terms of both bias and coverage property in various simulation scenarios. In case studies using prostate cancer TMA data sets, the two stage methods yields a good approximation in one data set while an insufficient one in the other. A general advice is to use the joint model inference whenever results differ between the two-stage methods and the joint analysis.

1. Introduction

DNA microarray technology has enabled expression measurement of thousands of genes simultaneously, providing a platform for rapid screening of genomic biomarkers in cancer. Translating these discovery-type findings into clinical relevance is a more challenging task. Gene expression profiling studies using spotted cDNA arrays or Affymetrix GeneChip arrays often yield a few hundred candidate cancer genes that are associated with a phenotype. Only a small portion of these will be eventually validated for the corresponding expression changes at the protein level. The advent of Tissue Microarray (TMA) technology has provided a proteomic platform for such validation studies to find clinically useful biomarkers. TMA experiments measure tumor-specific protein expression via high-density immunohistochemical staining assays, allowing simultaneous evaluation of hundreds of patient samples in a single experiment [1]. Since their initial development, TMA-based expression studies have quickly become an integral part of cancer biomarker development [2-4].

A typical tissue array slide comprises up to 1000 tiny biopsy tissue elements, which we will refer to as cores, with multiple cores corresponding to repeated sampling from the same tumor. Expression measures on these replicate cores constitute the TMA core-level data. These can display substantial within-subject variability for both biological and experimental reasons. Biologically, for tumors that are highly infiltrative and heterogeneous in nature (e.g., prostate tumors), protein expression pattern can be quite variable. For example, cell proliferation genes often exhibit localized high expression within a tumor, indicating elevated aggressiveness and metastatic potential in the corresponding areas. Replicate sampling from various regions of the tumor is therefore important in capturing the underlying heterogeneity within a tumor. Experimental sources of the variability can come from a combination of probe affinity, measurement imprecision, and further missing data due to insufficient sampling. Without appropriately accounting for these variabilities, the noise-prone measurements tend to attenuate the prognostic value of a potential biomarker in predicting disease outcome. The lack of a model-based approach for TMA core-level expression data to effectively model the intra-tumor variation has motivated us to carry out a full investigation.

A good analogy for understanding TMA data structure is from probe-level data generated by the Affymetrix GeneChip arrays. GeneChip arrays measure gene expression at the mRNA transcripts level. The probe-level data refer to the replicate expression measures on a set of 16-20 small oligonucleotide probe sets derived for a target gene. The biological variation comes primarily from these oligonucleotide probe sequence variants, while experimental variations arise during the process of slide printing, hybridization and optical reading. Li et al. [6] reported that the variation of a specific probe across multiple arrays could be considerably smaller than the variance across probes within a probe set. Modeling Affymetrix probe-level data has generated much attention [6, 7] as the technology has become more mature and widely used.

Similarly in TMA experiments, modeling within-tumor protein expression heterogeneity is an important problem. In these tissue-based experiments, the variation across core samples within a tumor can be substantially larger than the variation observed across subjects. Etzioni et al. [5] used a compositional analysis to model such heterogeneity, and compared the proportion of cells stained at different intensity levels between normal and tumorous tissues. In this study, we focus on the effect of modeling intra-tumor variation in the context of predicting patient survival outcome. In a latent variable modeling framework, we assume that an underlying `true' expression value predicts survival. In real experiments, this `true' expression can not be precisely measured due to sampling variabilities and measurement imprecision. Instead, we observe the core-level expression measurements that are subject to these measurement errors. In a two-stage method, we adapt ideas from measurement error modeling and propose a latent expression index (LEI) to approximate the underlying true value, and focus on its behavior in proportional hazards models. We adapt an empirical Bayes estimator [8] to 1) incorporate important clinical parameters such as Gleason score and pathological stage of the tumor and 2) adjust for the varying number of cores. We further establish a joint model for TMA core-level data and survival outcome via a shared random effect. There is a large literature on joint modeling of longitudinal data and survival [9-16]. These methods have been developed predominantly for modeling survival and CD4 counts in AIDS patients; here their application to Tissue Microarray data in cancer biomarker studies is novel. Using both simulations and two published TMA data sets, we compare the performances of the naive, two-stage LEI, and the joint model approach in obtaining parameter estimates and associated inference.

The article is organized as follows. Section 2 specifies notation and models for the TMA core-level expression data and for the patient survival data. Section 3 introduces LEI and its use in a two-stage method. Section 4 presents the joint modeling approach and the Bayesian estimation framework. Simulation results to compare the performances of these methods are then discussed in Section 5. Case studies using two prostate cancer TMA data sets are presented in Section 6. Further discussion can be found in Section 7.

2. Model specification

Measurement model for the TMA core-level data

Let $X_i^{\ast }$ be the latent expression value for a biomarker in tumor i, i = 1, … , n. Assuming the observed TMA core-level measurement for the jth core in the ith tumor is

$$X_{ij}=X_i^{\ast }+U_{ij},j=1{,}_{\cdots },r_i;i=1{,}_{\cdots },n,$$ (2.1)

where we assume $X_i^{\ast }~N({\mu }_{x\ast },{\sigma }_{x\ast }^2)$. The mean μ_x* is a linear function of clinical covariates: ${\mu }_{x\ast }={\theta }_0+\theta {\mathit{Z}}_i^{\prime }$, where Z_i = (Z_1i, Z_2i, …,Z_pi) constitutes a row vector of p clinical parameters characterizing histologic and pathologic features of the tumor; and θ = (θ₁, … , θ_p) is the associated p-dimensional row vector of effect sizes. In this model, U_ij represents the variation of the r_i core-level expression measurements about the “true” value $X_i^{\ast }$. We assume U_ij is i.i.d. $N(0,{\sigma }_u^2)$ and independent of $X_i^{\ast }$.

Survival model

Let the observed survival time for patient i (i = 1, …, n) be T_i = min(Y_i, C_i), where Y_i is the time from diagnosis to disease recurrence; C_i is the time to censoring which is independent of Y_i, and δ_i = 1{Y_i < C_i} is the censoring indicator. Under the Cox proportional hazards model, the hazard rate for patient i is

$$\lambda \left(t\right)={\lambda }_0\left(t\right)e^{{\beta }^{\ast }{X}_i^{\ast }+{\mathrm{bZ}}_i^{\prime }},$$ (2.2)

where λ₀(t) is the baseline hazard function, β* is the regression coefficient associated with the `true' protein expression, and b = (b₁, … , b_p) is the row vector of coefficients associated with the vector of clinical variables ${\mathit{Z}}_i^{\prime }$. We also consider a parametric Weibull regression model with the following form for the hazard function:

$$\lambda \left(t\right)=\gamma t^{\gamma -1}{e}^{{\beta }_0+{\beta }^{\ast }{X}_i^{\ast }+{\mathrm{bZ}}_i^{\prime }},$$ (2.3)

3. Two-stage plug-in method

Given the rare disease assumption and the assumption that the measurement error U_ij has no predictive value, i.e., $\lambda (t\mid {\mathbf{X}}_i,X_i^{\ast })=\lambda (t\mid X_i^{\ast })$ Prentice (1982) introduced the induced hazard rate function for Cox regression model with covariates measured with error. When normality is assumed for the error distribution, a first-order bias-correction method is to replace $X_i^{\ast }$ with its conditional mean

$$\lambda (t\mid {\mathrm{X}}_i)={\lambda }_0\left(t\right)e^{{\beta }^{\ast }E[X_i^{\ast }\mid {\mathrm{X}}_i,{\mathrm{Z}}_i]+{\mathrm{bZ}}_i^{\prime }}$$ (3.1)

and estimate β* by maximizing the corresponding partial likelihood. Here ${\mathbf{X}}_i=(X_{i1},X_{i2},\cdots ,X_{i{r}_i})$ denotes the vector of observed expression measures for tumor i. Note that the regression calibration model in (3.1) is an approximation to the true model in (2.2) due to the rare disease assumption and the omission of a higher order term implicit in (2.2). Details of such first-order bias-correction methods can be found in [17, 18]. Define the Latent Expression Index (LEI) to be an estimate of the conditional mean, ${\mathrm{LEI}}_i=\widehat{E}[X_i^{\ast }\mid {\mathbf{X}}_i,{\mathbf{Z}}_i]$, for each subject i. A two-stage plug-in method can be described by the following algorithm: 1) Compute LEI_i (i = 1, …, n) as a surrogate expression estimate that adjusts for measurement error; and 2) Apply the Cox or Weibull regression model using LEI_i to obtain an estimate of β* and the associated standard error.

In the next section, we describe methods for computing LEI for tissue microarray data. These include an empirical Bayes estimator conditional on clinical covariates, a full Bayes approach and a Varying Replicate Number (VRN) method as an extension to adjust for the number of cores per tumor.

3.1. Methods for computing LEI

3.1.1. The Empirical Bayes and full Bayes estimator

Express (2.1) as a mixed effects model

$$X_{ij}={\theta }_0+\theta {\mathrm{Z}}_i^{\prime }+v_i+U_{ij},$$ (3.2)

where ${\nu }_i~N(0,{\sigma }_{x\ast }^2)$. To make a connection between (3.2) and (2.1), $X_i^{\ast }$ is the unobserved “true” protein expression level, which can be expressed as $X_i^{\ast }={\theta }_0+\theta {\mathbf{Z}}_i^{\prime }+{\nu }_i$. Subsequently, ν_i, which is normally distributed with mean zero and variance, has the interpretation of a mean centered “true” protein expression level. The empirical Bayes estimator can then be derived as

$$LE{I}_i^{eb}={\widehat{\gamma }}_i{\stackrel{‒}{X}}_i+(1-{\widehat{\gamma }}_i)({\widehat{\theta }}_0+\widehat{\theta }{\mathrm{Z}}_i^{\prime })$$ (3.3)

where ${\widehat{\gamma }}_i\equiv {\widehat{\sigma }}_{x\ast }^2{({\widehat{\sigma }}_{x\ast }^2+{\widehat{\sigma }}_u^2{r}_i^{-1})}^{-1}$ is the attenuation factor [18]. Parameter estimates $\{{\widehat{\theta }}_0,\widehat{\theta },{\widehat{\sigma }}_u^2,{\widehat{\sigma }}_{x\ast }^2\}$ can be obtained by fitting a mixed effects model as described in (3.2), using a restricted maximum likelihood (REML) approach [19, 20].

The empirical Bayes estimator conditions on the set of parameter estimates derived from the data. The uncertainty of these estimates are not accounted for in LEI^eb. For this reason, we also consider a full Bayesian estimator, ${\mathit{LEI}}_i^{fb}$, where standard conjugate hyperprior distributions are adopted: ${\sigma }_u^{-2},{\sigma }_{x\ast }^{-2}~\Gamma (r_0,{\gamma }_0)$. The full Bayes estimator

$$LE{I}_i^{fb}={\tilde{\theta }}_0+\tilde{\theta }{\mathrm{Z}}_i^{\prime }+{\tilde{v}}_i,$$

is then based on the posterior inference from model (3.2) where $\{{\tilde{\theta }}_0,\tilde{\theta },{\tilde{\nu }}_i\}$ are the posterior means given the data.

3.1.2. The Varying Replicate Number (VRN) method

In a typical TMA construction, K_i cores are placed on the array for each tumor i. However, not all of the measurements $\{X_{i1},\cdots ,X_{i{K}_i}\}$ are available. Several reasons contribute to a varying number of replicate measure. These include heterogeneous tissue composition and technical defects such as image corruption. The expression measurement from non-tumorous tissue types or a corrupted image is typically considered unsuitable for an outcome analysis and excluded. Let M_ij = 0, j = 1, … ,K_i indicate that the jth core from the ith tumor is lost due to the aforementioned reasons and M_ij = 1 if it is available. Expression measures are retained for $r_i\equiv {\Sigma }_{j=1}^{K_i}{M}_{ij}$ cores, where r_i varies across tumor samples and possibly depends on covariate Z_i. We consider r_i to follow a Binomial distribution given K_i and P(M_ij = 1) with possible over-dispersion. Assuming independence and homogeneity across j for M_ij, we adopt a logistic mixed effects model:

$$\text{logit}P(M_{ij}=1)={\psi }_{0i}+\psi {\mathrm{Z}}_i^{\prime },$$ (3.4)

where ${\psi }_{0i}~N({\psi }_0,{\sigma }_{\psi }^2)$, Z_i = (Z_1i, Z_2i, …,Z_gi) is the vector of g clinical covariates that can be the same or different from those in (3.2), and ψ = (ψ₁, ψ₂, …, ψ_g) is the associated vector of coefficients. Therefore

$$r_i\sim \text{Binomial}\left(K_i,p_i=\frac{e^{{\psi }_{oi}+\psi {\mathrm{Z}}_i^{\prime }}}{1+e^{{\psi }_{oi}+\psi {\mathrm{Z}}_i^{\prime }}}\right).$$ (3.5)

The expression index under the VRN model is then derived by averaging over all the possible values of (r_i, K_i). In particular,

$$\begin{array}{cc}\hfill LE{I}_i^{vrn}& =E_{(r_i,K_i)}E[X_i^{\ast }\mid {\mathbf{X}}_i,{\mathbf{Z}}_i,r_i,K_i]\hfill \\ \hfill & =\sum _{s=1}^R\sum _{m=0}^s\left\{\frac{{\widehat{\sigma }}_{x^{\ast }}^{2}m}{{\widehat{\sigma }}_{x^{\ast }}^{2}m+{\widehat{\sigma }}_u^2}{\stackrel{‒}{X}}_i+\frac{{\widehat{\sigma }}_u^2}{{\widehat{\sigma }}_{x^{\ast }}^{2}m+{\widehat{\sigma }}_u^2}({\widehat{\theta }}_0+\widehat{\theta }{Z}_i^{\prime })\right\}\times \left(\begin{array}{c}\hfill s\hfill \\ \hfill m\hfill \end{array}\right){\left(\frac{e^{{\widehat{\psi }}_{0i}+\widehat{\psi }{\mathbf{Z}}_i^{\prime }}}{1+e^{{\widehat{\psi }}_{0i}+\widehat{\psi }{\mathbf{Z}}_i^{\prime }}}\right)}^m{\left(\frac{1}{1+e^{{\widehat{\psi }}_{0i}+\widehat{\psi }{\mathbf{Z}}_i^{\prime }}}\right)}^{s-m}\widehat{P}(K_i=s)\hfill \end{array}$$ (3.6)

Here R is taken to be max_i K_i. An additional assumption for the above is that the expression measures do not correlate with r_i or K_i. Parameter estimates $\{{\widehat{\theta }}_0,\widehat{\theta },{\widehat{\sigma }}_u^2,{\widehat{\sigma }}_{x\ast }^2\}$ can be obtained by fitting a mixed effects model as described in (3.2). A logistic mixed effects model in the form of (3.4) was fitted to obtain $\{{\widehat{\psi }}_{0i},\widehat{\psi }\}$. Estimation is via methods described in [21] and [22]. The empirical proportions were used for $\widehat{P}(K_i=s)$.

In a relatively balanced TMA array where the number of replicate measures r_i does not vary much across subjects, ${\widehat{\gamma }}_i\equiv {\widehat{\sigma }}_{x\ast }^2{({\widehat{\sigma }}_{x\ast }^2+{\widehat{\sigma }}_u^2{r}_i^{-1})}^{-1}$ is an approximately constant adjustment factor. The amount of shrinkage in LEI^eb toward the overall mean depends primarily on the ratio of the within- to between-subject variation in that particular data set. In our example, however, r_i is a highly variable quantity. It exerts a larger role in determining how much weight $LE{I}_i^{eb}$ gives to a particular subject's data relative to the estimated population mean. The motivation for LEI^vrn is to provide a replicate number-averaged expression estimate that alleviates the variability induced by r_i in the empirical Bayes estimator.

4. Joint Modeling of survival and TMA core-level data

The two-stage approaches described above are attractive for their simplicity and straightforward interpretation. They require minimal computation and can be easily implemented using existing statistical packages. However, there are major limitations for the two-stage method [23]. First, the two-stage method involves a first order approximation and ignores the second-order term ${\beta }^{{\ast }^2}{\sigma }^2(X_l^{\ast }\mid \mathbf{X})$ in the induced hazard rate function (3.1). As we will illustrate in the simulation study, such approximation works well when β* is close to zero, but otherwise lead to sizeable bias in ${\widehat{\beta }}^{\ast }$. Second, parameter estimates in the second stage do not account for the uncertainty in estimating LEI in the first stage. The associated standard error for ${\widehat{\beta }}^{\ast }$ will be over-optimistic. Given these considerations, it is desirable to make inference based on the joint likelihood of the failure time and TMA expression data. In this article, we adopt a shared random effect model to induce correlation between the TMA data and the survival outcome.

Given the measurement model specified in (3.2) for the TMA data, we write the proportional hazards model for the survival outcome as

$$\lambda \left(t\right)={\lambda }_0\left(t\right)\exp ({\mathbf{bZ}}_i^{\prime }+{\beta }^{\ast }{v}_i).$$ (4.1)

The parameter ν_i constitutes a shared random effect that connects the measurement model (3.2) and the survival outcome model (4.1). The expression data and survival times are then assumed to be independent given ν_i. The joint likelihood of the observed data {T_i, δ_i, X_i and the random effects ν_i is therefore

$$L_{joint}=\prod _{i=1}^{n}f(t_i,{\delta }_i\mid v_i,{\mathbf{z}}_i)\times \prod _{i=1}^{n}f(X_i\mid v_i,{\mathbf{Z}}_i)f\left(v_i\right)=L_{SURV}\times L_{ME},$$ (4.2)

where

$$\begin{array}{cc}\hfill & L_{ME}=\prod _{i=1}^n\left(\prod _{j=1}^{r_i}\frac{1}{\sqrt{2\pi {\sigma }_u^2}}\exp \left\{-\frac{{(x_{ij}-{\theta }_0-\theta {\mathbf{Z}}_i^{\prime }-v_i)}^2}{2{\sigma }_u^2}\right\}\right)\frac{1}{\sqrt{2\pi {\sigma }_{x^{\ast }}^2}}\exp \left\{-\frac{v_i^2}{2{\sigma }_{x^{\ast }}^2}\right\};\hfill \\ \hfill & L_{SURV}=\prod _{i=1}^n\prod _{l=1}^L{\lambda }_l^{dl}\exp (\sum _{i\in D_l}{\mathbf{bZ}}_i^{\prime }+{\beta }^{\ast }{v}_i)\exp (-{\lambda }_t\sum _{i\in R_l}{\Delta }_{il}{e}^{{\mathbf{bZ}}_i^{\prime }+{\beta }^{\ast }{v}_i})\hfill \end{array}$$ (4.3)

We used a piecewise constant hazards model in which the time axis is partitioned into L disjoint intervals, I₁, …, I_L, where I_l = [a_l-1, a_l) with a₀ < t_i and a_L > t_i for all i = 1, …, n. Assume a constant baseline hazard in the lth interval, λ₀(t) = λ_l for t ∈ I_l. R_l is the set at risk at the beginning of interval l; d_l is the number of failures in interval l; and Δ_il = min(t_i, a_l) - a_l-1.

Alternatively, a parametric Weibull model can be assumed for the survival outcome using the following hazard function:

$$\lambda \left(t\right)=\gamma t^{\gamma -1}\exp (b_0+{\mathbf{bZ}}_i^{\prime }+{\beta }^{\ast }{v}_i).$$ (4.4)

When γ = 1, the above reduces to exponential distribution with constant failure rate $\exp (b_0+{\mathbf{bZ}}_i^{\prime }+{\beta }^{\ast }{\nu }_i)$. The survival time component of the joint likelihood in (4.3) is then replaced by

$$L_{SURV}=\prod _{i=1}^n{\left\{\gamma t_i^{\gamma -1}{e}^{\gamma (b_0+{\mathbf{bZ}}_i^{\prime }+{\beta }^{\ast }{v}_i)}\right\}}^{{\delta }_i}\exp (-e^{\gamma (b_0+{\mathbf{bZ}}_i^{\prime }+{\beta }^{\ast }{v}_i)}{t}_i^{\gamma }).$$ (4.5)

In a Bayesian estimation framework, the following prior distributions are specified for the model parameters:

$$\begin{array}{cc}\hfill & ({\beta }^{\ast },{\theta }_0,\theta ,b_0,b)\sim N({\mu }_0,{\sigma }_0^2);\hfill \\ \hfill & ({\sigma }_u^{-2},{\sigma }_{x^{\ast }}^2)\sim \Gamma (r_0,{\gamma }_0);\hfill \\ \hfill & (\gamma ,{\lambda }_l,l=1{,}_{\cdots },L)\sim \Gamma (r_0,{\gamma }_0).\hfill \end{array}$$ (4.6)

The prior choices in (4.6) render proper noninformative prior distributions with the hyperparameters chosen to achieve large variances (wide spread). In particular, ${\mu }_0=0,{\sigma }_0^2=10000,r_0=0.001,{\gamma }_0=0.001$. The values of r₀ and γ₀ are set to be small to impose noninformativeness (although there have been criticisms that the resulting posterior distributions remain highly sensitive to the choice of r₀ and γ₀). We had tested different sets of values for r₀ and γ₀: (0.1, 0.1), (0.01, 0.01), and (0.001, 0.001). When the sample size is moderate to large, the variance estimates, ${\widehat{\sigma }}_u$ and ${\widehat{\sigma }}_{x^{\ast }}$, are well-behaved and not significantly affected by the choice of r₀ and γ₀. Samples from the posterior distribution are obtained using Markov Chain Monte Carlo (MCMC) methods. In the likelihood function of (4.2), the Bayesian estimation procedure treats ν_i as missing data and imputes it at each MCMC iteration via posterior sampling from the conditional distribution of ν_i given the rest of the variables. One then proceeds with the likelihood function in (4.2) as if ν_i were observed.

5. Simulation

5.1. Simulation Setup

The additive measurement error model in (3.2) with one covariate Z_1i is used to simulate the expression measure X_ij, i = 1, …, n, and j = 1, …, r_i. In this model, θ₀ = 0 and θ₁ = 1. Furthermore, ν_i ~ N(0, 1), U_ij ~ N(0, 0.5). The covariate Z_1i is simulated from a N(0, 1) distribution. The total number of cores sampled, K_i, takes values in {1, 2, …, 12} with P(K_i = 6) = 0.4, P(K_i = 1) = … = P(K_i = 5) = 0.1, and P(K_i = 7) = … = P(K_i = 12) = 1/60, mimicking the proportions from the actual tissue array data set used in this study. We simulate the number of repeated measures $r_i\equiv {\sum }_{j=1}^{K_i}{M}_{ij}$ from a Binomial(K_i, p_i), where p_i = 1 - π^1/K_i such that the missing proportion equals π. The survival time T_i is simulated from a proportional hazards model in the form of (2.2) with λ₀(t) ≡ 1 and β* = 1 or 2. An additional covariate Z_1i is further assumed to associate with T_i with the coefficient being one. The censoring time is simulated from an independent exponential distribution that results in a 30% censoring proportion. Results are summarized over 100 such simulated data sets each of a sample size n = 200. In general, we assigned parameter values in the simulation to mimic those for the real data sets.

Computation of LEI^eb, LEI^vrn were carried out using the PROC MIXED and the IML procedure in SAS (SAS Institute, Cary, NC). LEI^fb and the joint models were implemented using OpenBUGS via the R interface BRugs [24,25]. We ran two chains with 1000 burn-in and 1000 updates per chain for the MCMC convergence.

5.2. Simulation Results

The simulation results are summarized in Table I. For β* = 1 in the survival models, the naive approach (using ${\stackrel{‒}{X}}_i$ as a surrogate expression) attenuates the true effect size by around 25%. The coverage probability of a nominal 95% confidence interval of ${\widehat{\beta }}^{\ast }$ is 0.10 at best. The two stage methods (LEI) achieved a considerable bias correction by adjusting for the measurement error in the LEI imputation. The joint modeling approach gives the best estimate ${\widehat{\beta }}^{\ast }=1.03$ and a coverage probability of 95% compared to the truth.

Table I.

Simulation study. Results are summarized over 100 simulated datasets each of n = 200.

		$\widehat{\beta }\ast$	$\widehat{se}(\widehat{\beta }\ast )$	$sd(\widehat{\beta }\ast )$	coverage	$\widehat{\beta }\ast$	$\widehat{se}(\widehat{\beta }\ast )$	$sd(\widehat{\beta }\ast )$	Coverage
		Weibull				Proportional Hazards
β* = 1	X*	1.01	0.08	0.08	0.96	1.01	0.08	0.08	0.97
	Naive	0.75	0.07	0.08	0.070	0.75	0.07	0.08	0.09
	LEIeb	0.93	0.08	0.09	0.85	0.93	0.08	0.09	0.87
	LEIfb	0.93	0.08	0.09	0.85	0.93	0.08	0.09	0.88
	LEIvrn	0.97	0.09	0.10	0.89	0.96	0.09	0.10	0.87
	Joint Model	1.03	0.11	0.11	0.95	1.03	0.11	0.11	0.95
β* = 2	X*	2.05	0.12	0.12	0.95	2.03	0.11	0.10	0.94
	Naive	1.13	0.08	0.10	0	1.18	0.08	0.11	0
	LEIeb	1.51	0.11	0.13	0.03	1.58	0.11	0.13	0.06
	LEIfb	1.48	0.11	0.12	0	1.55	0.110	0.12	0.04
	LEIvrn	1.62	0.11	0.14	0.19	1.70	0.11	0.15	0.30
	Joint Model	2.16	0.27	0.30	0.89	2.07	0.19	0.20	0.93

Next a larger effect size is simulated (β* = 2). The bias in the two-stage approaches due to the first-order approximation is evident. Overall the two-stage methods generate less biased ${\widehat{\beta }}^{\ast }’\mathrm{s}$ compared to the naive estimate. Nevertheless, these are 15-25% smaller than the true β*. The coverages are poor for the two-stage approaches. The joint modeling approach should be advocated in this scenario for inference. Notice that the joint model estimates of β* are slightly bigger than 2, especially under the Weibull distribution. This may be driven by the prior distributions adopted for the parameters under the Bayesian estimation scheme. We have observed that such a difference disappears when the sample size gets larger.

6. Case study in prostate cancer

6.1. Data description

In this study, we consider two prostate tumor tissue microarray data sets. The α-Methylacyl CoA racemase (AMACR) is a peroxisomal and mitochondrial enzyme that plays an important role in fatty acid metabolism. AMACR has been shown to consistently overexpress in prostate tumors [26]. Rubin et al. [4] profiled AMACR protein expression using a TMA constructed on 203 prostate tumors from a surgical cohort who underwent radical prostatectomy at the University of Michigan as a primary therapy for clinically localized prostate cancer diagnosed between 1994 and 1998. They found AMACR is a significant predictor of the Prostate Specific Antigen (PSA) failure in these 203 patients.

The second biomarker evaluated in this study is BM28. BM28 encodes a highly conserved mini-chromosome maintenance protein (MCM) that is involved in the initiation of genome replication. Bismar et al. [27] profiled a total of 41 genes (including BM28) in a TMA-based proteomic study. They identified a 12-gene model showing the expression combination of the twelve genes significantly associates with tumor progression and PSA failure in a set of 79 men following surgery for clinically localized prostate cancer. The expression level of BM28 however did not show significant prognostic value in their analysis. We chose BM28 to evaluate the possibility of its being a false negative biomarker due to measurement error.

For the AMACR data, an average of K_i =5.5 (range: 2 to 12) tissue core specimens were taken from each tumor sample and put on a tissue array for immunohistochemical staining. After initial diagnostic evaluation of each core, an average of 29% (range: 0-86%) of the cores were excluded due to reasons discussed earlier, leading to 5.5% missing subjects. The BM28 data has a similar tissue array design. A quantitative imaging analysis of the staining intensity was obtained using the ACIS II (Chromavision, San Juan Capistrano, CA) system. The intensity level ranges from 0 to 255 chromogen intensity units, and is transformed using the natural logarithm (one unit added to avoid taking logarithm of 0) and normalized to have mean zero and standard deviation one. Disease recurrence is defined as a serum PSA increase >0.2ng/mL after radical prostatectomy. Censored observations are those free of the recurrence at the time of last follow-up.

6.2. Measurement error and regression attenuation in TMA data analysis

Figure 1 illustrates a considerable amount of measurement error in the core-level expression data from the two TMA experiments. In the AMACR data, methods-of-moments estimates of the variance components are ${\widehat{\sigma }}_u^2=0.46$ and ${\widehat{\sigma }}_{x^{\ast }}^2=0.54$. In the BM28 data, the methods-of-moments estimates of the variance components are ${\widehat{\sigma }}_u^2=0.62$ and ${\widehat{\sigma }}_{x^{\ast }}^2=0.21$. The within-subject variation is almost three times the between-subject variation.

Figure 1.

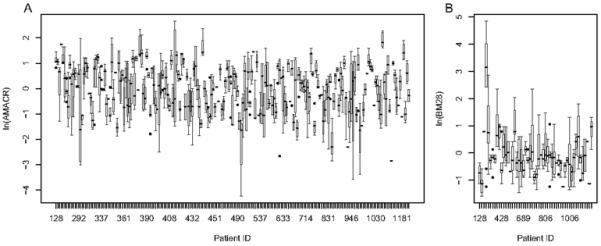
Variance plots to represent the within-subject variation in the TMA core-level expression data. A) The AMACR data. Estimates of the variance components are: ${\widehat{\sigma }}_u^2=0.46$ and ${\widehat{\sigma }}_{x\ast }^2=0.54$. B)

The BM28 data. Estimates of the variance components are: ${\widehat{\sigma }}_u^2=0.62$ and ${\widehat{\sigma }}_{x\ast }^2=0.21$.

In a Cox proportional hazards model context, we did a simple simulation where $X_i^{\ast }~N(0,1)$, β* = 1. A naive estimator ${\stackrel{‒}{X}}_i=r_i^{-1}{\sum }_{j=1}^{r_i}{X}_{ij}$ —the average core-level expression for tumor i— is used as the surrogate expression to replace $X_i^{\ast }$ in (2.2). We simulate situations where measurement error is small $({\sigma }_u^2=0.1)$, moderate $({\sigma }_u^2=0.5)$, and large $({\sigma }_u^2=1)$. Figure 2 shows various degrees of regression attenuation in the estimate of β* as a function of replicate number r_i and the amount of error ${\sigma }_u^2$. When the parameter values are set to resemble the AMACR data, the naive estimate of β* is approximately 30% smaller than the true value. With the current TMA construction protocol specifying three cores per subject due to economic and tissue-preservation reasons, and a great amount of within-subject variability routinely observed in the core-level expression data, Figure 2 effectively conveys the importance of modeling measurement error in TMA data. In the following two sections, we implement the measurement error models to demonstrate how statistical inference differs from the previous results.

Figure 2.

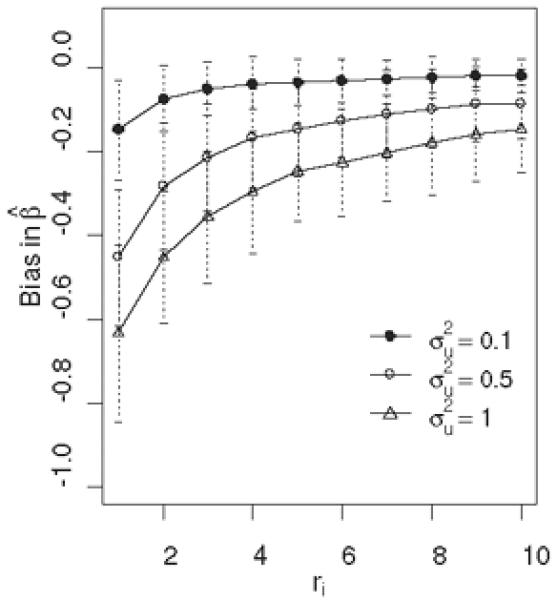
A simulation demonstration of the bias in Cox regression coefficient estimate as a function of the number of repeated measures r_i. The average bias with a 95% CI over 100 simulated datasets of sample size n=200 is plotted.

6.3. AMACR expression and biochemical recurrence in prostate cancer

In prostate cancer, Gleason score, pathologic stage and tumor size are among the most important clinical parameters. We include these as clinical covariates Z_i to adjust in the measurement model (3.2), the replicate number model (3.4), and the survival outcome model (4.1). In the measurement model,${\widehat{\theta }}_{TumorSize}=.32$ with an associated standard error of 0.13, indicating a marginal association of tumor size with AMACR expression level. In the replicate number model,${\widehat{\psi }}_{TumorSize}=.72$ with an associated standard error of 0.16, which is consistent with our expectation that a larger tumor sample provides more abundant number of cores.

Table II lists the estimates and associated standard errors (posterior standard deviation) of β* in the outcome model. The measurement error adjustment has significantly improved upon the naive estimate. The error-adjusted $\widehat{\beta }\ast$ is around 0.75 $\left(\widehat{se}(\widehat{\beta }\ast )=.26\right)$, approximately 31% larger in absolute value than the naive estimate which is 0.57 $\left(\widehat{se}(\widehat{\beta }\ast )=.20\right)$. The amount of attenuation in β* is quite consistent with what we conclude from the simulated datasets in the previous section. In this dataset, the two-stage methods (LEI^eb, LEI^fb, LEI^vrn) perform equally well as the joint modeling approach. The simplicity and computational efficiency of LEI serves as a satisfactory core-level expression index for AMACR. However as mentioned earlier, the two-stage methods are based on a first-order approximation, the accuracy of which is largely driven by the size of β* and the ratio of within- and between-subject variation. As will be shown in the other data example, the two-stage methods will not be always a suitable approach.

Table II.

A case study using prostate cancer TMA datasets.

		$\widehat{\beta }\ast$	$\widehat{se}(\widehat{\beta }\ast )$	$\widehat{\beta }\ast$	$\widehat{se}(\widehat{\beta }\ast )$
		Weibull		Proportional hazards
AMACR(n=203)	Naive	-0.573	0.201	-0.571	0.198
	LEIeb	-0.761	0.266	-0.751	0.266
	LEIfb†	-0.753	0.262	-0.752	0.263
	LEIvrn	-0.735	0.260	-0.737	0.258
	Joint modeling†	-0.742	0.268	-0.745♭	0.268

		$\widehat{\beta }\ast$	$\widehat{se}(\widehat{\beta }\ast )$	$\widehat{\beta }\ast$	$\widehat{se}(\widehat{\beta }\ast )$
		Weibull		Proportional hazards
BM28 (n=52)	Naive	0.828	0.414	0.900	0.399
	LEIeb	1.051	0.519	1.146	0.494
	LEIfb†	1.457	0.564	1.493	0.504
	LEIvrn	1.034	0.552	1.151	0.537
	Joint Modeling†	1.753	0.766	1.592♭	0.600

^†- Estimation is based on MCMC methods, where we sampled 2 chains each with 10000 burn-in and 10000 updates.

^♭We used J = 5 and J = 3 intervals for the piecewise exponential distribution in the AMACR and BM28 dataset respectively.

The estimate of the Weibull shape parameter is $\widehat{\gamma }$ = 0.71, and $\widehat{\gamma }$ = 0.97 from the joint modeling for the AMACR and BM28 dataset respectively.

Kaplan-Meier curves are useful as a graphical representation of the prognostic value of a biomarker. We examined these plots by dividing the subjects into different risk groups based on the values of AMACR expression estimates derived under each method. In Figure 3(a), subjects with AMACR high, median, and low expression groups based on LEI^vrn and the joint model estimates (C and D respectively) are significantly better separated in terms of probability of recurrence-free survival, when compared to that using the naive mean estimates (A).

Figure 3.

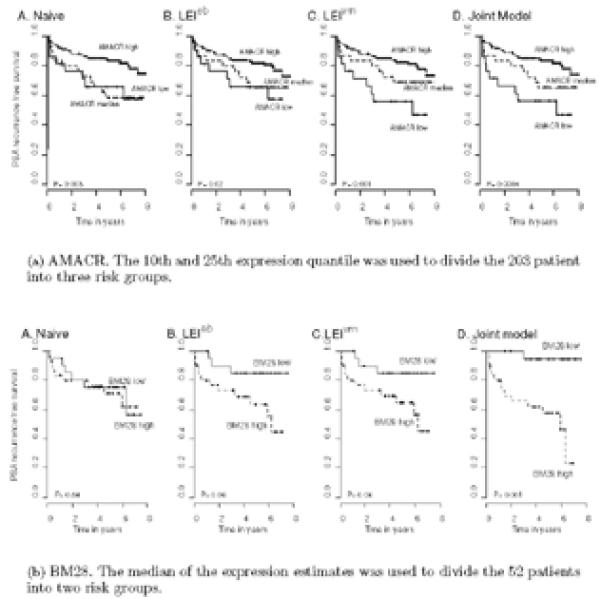
Kaplan-Meier plots of prostate cancer recurrence. Patients are categorized into risk groups based on the protein expression level of (a) AMACR and (b) BM28 profiled using TMAs. The expression estimates are based on the A. Naive B. LEI^eb C. LEI^vrn and D. Joint model.

6.4. BM28 expression and biochemical recurrence in prostate cancer

The measurement model indicates a marginal association of pathologic stage of the tumor with BM28 expression: ${\widehat{\theta }}_{PathStage}=0.59\left(\widehat{se}\left(\theta \right)=0.22\right)$. The replicate number model again suggests a strong dependence on the size of the tumor: ${\widehat{\psi }}_{Tumoresize}=1.12\left(\widehat{se}\left(\psi \right)=0.43\right)$.

In Table II, the differences under various models are more discernable in this datasets. First, the Weibull and piecewise exponential model overall generate slightly different results given a small sample size (n=52). Second, the empirical Bayes estimate differs substantially from the full Bayes LEI estimate. It is likely due to the large uncertainties in the parameter estimates that determine LEI^eb. Finally, the bias introduced by the first-order approximation is prominent here. Both the coefficient β* and the noise ratio in this dataset are much larger in magnitude compared to the AMACR data example. In this case, the two-stage methods alleviate regression attenuation, only to a limited extent. The joint model should be used for parameter estimation and associated inference.

Figure 3(b) plots the Kaplan-Meier curves using different expression estimates. The 5-year PSA recurrence-free survival probability is 0.95 $(\widehat{se}=0.05)$ versus 0.58 $(\widehat{se}=0.10)$ for low and high BM28 expression estimated by the joint model. Adjusting for measurement error in this dataset has made a dramatic change in the conclusion about the prognostic value of BM28, compared to the naive method.

6.5. Improved expression estimates

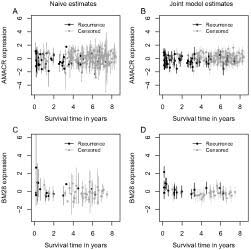
Figure 4 compares the naive and the joint model expression estimates, plotted against the survival time on the x-axis. The mean expression ± two standard deviations is plotted for each individual. Two improvements under the joint model are clear: 1) the noise, represented by the error bars, is greatly reduced via the joint modeling, and 2) the mean expression levels are distributed more tightly around a regression line, accentuating the relationship of the TMA expression data and survival time.

Figure 4.

Comparison of the naive expression estimates (A, C) and the joint model expression estimates (B, D). The top panel depicts the comparison in the AMACR data, the bottom panel depicts the comparison in the BM28 data. The survival times are plotted on the x-axis.

7. Discussion

In TMA data analysis, statistical methods often focus on downstream models in predicting disease outcome assuming ${\stackrel{‒}{X}}_i$ is a suffcient expression summary measure [29, 30]. Relatively little attention has been given to the modeling of within-tumor variation in these TMA experiments. As we have shown in this paper with real data examples, analysis ignoring intra-tumor variation can lead to false negative results, causing a tremendous waste of valuable tissue resource and experimental costs. In this study, we propose and compare a two-stage approach and a joint model to analyze tissue microarray data in a measurement error framework. The two-stage approach computes a Latent Expression Index (LEI) in the first stage and then associate the LEI with patient survival information using a proportional hazards model in the second stage. We further adjust for clinical/pathological covariates Z_i and the number of repeated measures (K_i, r_i) per each tumor to improve the effciency of the expression estimates.

Although the two-stage approach is attractive for its simplicity, interpretability and straightforward computation, practitioners need to be aware of the associated statistical limitations. As we discussed earlier, the regression calibration approach is an approximation of the true model which reduces bias relative to the naive method but still leads to underestimated β*. In addition, the survival information is not used in the first stage to compute LEI, which can cause bias and effciency loss in estimating β* in the second stage. Finally, the uncertainty of estimating the LEI quantity is not assimilated in the second stage, leading to over-optimistic standard error estimates. For a review of this topic, see Tsiatis and Davidian [23]. In simulation studies, we show the two-stage methods reduce bias relative to the naive approach in estimating the Cox regression coefficient, but still lead to under-estimated β*. The joint analysis, however, outperforms the two-stage methods in terms of the bias and coverage property in various simulated scenarios. In case studies, we applied the error methods to prostate TMA data sets where the two-stage approach and the joint analysis generate 1) very similar results in the AMACR data set and 2) disparate results in the BM28 data set. While the first case study demonstrates a scenario where the two-stage approach is a good approximation to the true model, the second suggests one where such approximation is not so accurate (the higher order term can not be ignored when β* is a large value). Inference should be based on the joint analysis whenever results differ.

A final notion is regarding the impact of the technology advancement on TMA data analysis. Recent advances in quantitative assessment of the immunohistochemical staining provide precise, objective, and reproducible protein expression measurements. Compared to the conventional pathologist scoring on an ordinal scale, the Chromavision system used in our data examples enables quantification of the antigen level on a continuous scale, free of the subjectivity associated with pathologist-based visual scoring system. We should point out that the Chromavision system not only quantifies the amount of protein expression, but also provides a more accurate measure of the percentage of tissue that express the protein. A statistical problem of interest is to extend our model to incorporate the percentage information when summarizing the expression profile of a tumor. Another quantitative system, AQUA [28], which stands for Automated Quantitative Analysis, measures fluorescence signals, leading to higher sensitivity to very low antibody concentrations. In addition, it allows the separation of tumor from stromal elements and the sub-cellular localization of signals for a co-localization of the antigens in different cell compartments. As the technology is becoming more and more refined, statistical models underpinning both biological and experimental issues are in great need.