Cofilin Increases the Bending Flexibility of Actin Filaments: Implications for Severing and Cell Mechanics

Abstract

We determined the flexural (bending) rigidities of actin and cofilactin filaments from a cosine correlation function analysis of their thermally driven, two-dimensional fluctuations in shape. The persistence length of actin filaments is 9.8 µm, corresponding to a flexural rigidity of 0.040 pN µm². Cofilin binding lowers the persistence length ∼5-fold to a value of 2.2 µm and the filament flexural rigidity to 0.0091 pN µm². That cofilin-decorated filaments are more flexible than native filaments despite an increased mass indicates that cofilin binding weakens and redistributes stabilizing subunit interactions of filaments. We favor a mechanism in which the increased flexibility of cofilin-decorated filaments results from the linked dissociation of filament-stabilizing ions and reorganization of actin subdomain 2 and as a consequence promotes severing due to a mechanical asymmetry. Knowledge of the effects of cofilin on actin filament bending mechanics, together with our previous analysis of torsional stiffness, provide a quantitative measure of the mechanical changes in actin filaments associated with cofilin binding, and suggest that the overall mechanical and force-producing properties of cells can be modulated by cofilin activity.

Introduction

ADF/cofilin family proteins are actin regulatory proteins that sever actin filaments and in doing so accelerate subunit turnover and assembly dynamics. Cofilin binds cooperatively to actin filaments and severs them^1–3at low binding densities.^4–6 In contrast to the ATP-dependent severing of microtubules by katanin, the energy of cofilin binding alone modulates the mechanical properties of actin filaments so that they destabilize and fragment.

Knowledge of the cofilin-linked changes in actin filament mechanics and structure is essential for formulating predictive models of cofilin-mediated actin filament severing. Structural and biochemical analysis demonstrates that cofilin alters the filament subunit tilt⁷ and increases the filament helical twist,⁸ increases the disorder of actin subdomain 2⁹ and the DNase-binding loop,¹⁰ disrupts the subdomain 1 to 2 interface of adjacent subunits along the long pitch helix,¹¹ and weakens stabilizing lateral contacts.^12,13 Cofilin binding lowers the actin filament torsional stiffness, so cofilin-decorated filaments twist more easily than native filaments.¹⁴ The surface tethering-dependence of severing efficiency suggests that filament flexibility plays a critical role in severing by cofilin,⁶ and implies that changes in the flexibility contribute to cofilin-mediated destabilization and severing. However, the extent, if any, to which filament bending mechanics are affected by cofilin has not been evaluated directly.

In this study, we measured the effect of cofilin on the bending mechanics of actin filaments from analysis of their thermal fluctuations in shape. Our results indicate that a cofilin-decorated actin filament is ∼5-fold more flexible than a bare, native actin filament. These results, together with our previous measurements of torsional stiffness,¹⁴ provide a complete description of the changes in actin filament mechanics associated with cofilin binding and severing, and provide novel insight into the molecular basis of the reported changes in mechanical properties at the leading edge of migrating cells.

Results

We used fluorescence microscopy to visualize Alexa 488-labeled native and cofilin-decorated actin filaments undergoing thermal fluctuations (Fig. 1; Supplementary Data Video 1 and Supplementary Data Video 3). Filament motions were constrained to two dimensions by minimizing the depth of the solution. Uncertainties introduced from out of plane (i.e. three-dimensional) thermal fluctuations are accounted for in the analysis. Stochastic simulations (discussed below) confirm constraint to two dimensions under the experimental conditions.

Fig. 1.

Direct visualization of actin and cofilactin filaments undergoing thermal fluctuations in shape. A sample of the two-dimensional thermal fluctuations in shape of an Alexa 488 fluorescently labeled actin filament recorded sequentially. (a and b), Native actin filaments; c and d, cofilin decorated actin filaments. (b and d), Reconstructions of filament shape given in (a) and (c), respectively. The images in (a) and (c) after a low-pass filter, a binary threshold and skeletonization is colored red, the automatically recognized pixels representing the filament is colored green, and the average Bezier reconstruction of the recognized pixels with three points per pixel is colored blue. Scale bars represent 5 µm.

Both native and cofilin-decorated filaments behave like semi-flexible polymers in solution and undergo thermally driven random fluctuations in shape (Fig. 1 and Fig. 2; Supplementary Data Video 1–Supplementary Data Video 4). Cofilactin filaments (Supplementary Data Video 3), however, fluctuate more rapidly than undecorated, native filaments (Supplementary Data Video 1) and display a weaker tangent angular correlation up to filament lengths of ∼4 µm under identical conditions (Fig. 3). Alexa-labeling does not affect actin polymerization kinetics or energetics at the labeling ratios used in this study,^15,16 and is unlikely to affect subunit interactions and filament mechanics significantly. Therefore, the mechanical properties measured with Alexa-labeled actin filaments are expected to reliably reflect those of native, unlabeled actin filaments.

Fig. 2.

Overlay of filament shape configurations. Digital images of an actin (blue) and a cofilactin filament (red) segment of 2.5 µm length undergoing thermal fluctuations are overlaid. The yellow line represents a rigid filament (i.e. L=2.5 µm ≪L_p). Image processing was done using Matlab software.

Fig. 3.

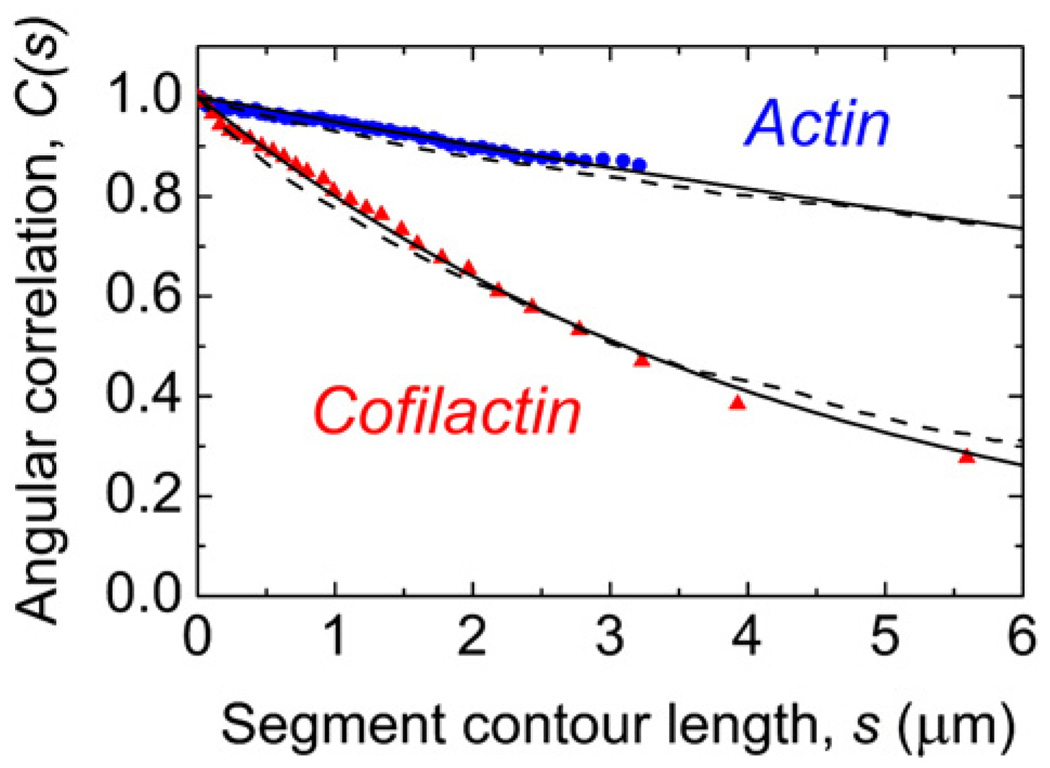
Determination of the filament persistence length. Filament average tangent angle correlation data are represented as squares for native actin filaments and as circles for cofilin-decorated filaments. The data are a pool average of all segment lengths of the reconstructed filament. The number of datum points is the average number of pixels used to represent a filament after autoskeletonization. The continuous lines represent the best fits to the cosine correlation function (Eq. (1)) yielding L_p values of 9.8±0.14 µm for native filaments and 2.2±0.026 µm for cofilin-decorated filaments. The broken lines represent 1000 simulated equilibrium configurations for the corresponding L_p values with the depth constraints imposed from the experimental setup.

The persistence length (L_p) is defined as the characteristic arc length (i.e. contour length of a segment) over which correlation between the corresponding tangent angles (θ(s)) of a fluctuating semi-flexible polymer, such as an actin filament, are lost in three-dimensional space.^17,18 The average cosine correlation function (〈C(s)〉) defines the L_p-dependence of tangent angle (θ) correlation of any segment (arc) length (s) along the contour length (L) of a filament constrained to two-dimensional motion within a plane according to¹⁹:

$$\langle C(s)\rangle =\langle \text{cos}[\theta (s)-\theta (0)]\rangle =e^{\frac{-s}{2L\mathrm{p}}}$$ (1)

The motions of a rigid rod are correlated (i.e. 〈C(s)〉→1), while those of a flexible rod with a length (L≥s in Eq.(1)) that is much longer than its persistence length (s≫L_p) are uncorrelated (i.e. 〈C(s)〉→0). The denominator of the exponential term of Eq.(1) is replaced with L_p when the polymer is free to fluctuate in three dimensions,¹⁷ thereby lowering the angular correlation.

The two-dimensional cosine correlation function (Eq.(1)) was used (Fig. 3) to calculate the actin and cofilactin filament L_p values from digitized filament images (see Materials and Methods). To measure accurately the extent to which cofilin modulates L_p, a continuum mechanical property, we observed actin filaments that were either fully bare or fully decorated with cofilin. Segment lengths (s) with points of origin along the entire length of the filament were used to determine the persistence length values. This procedure minimizes uncertainty from nucleotide-dependent filament “end effects” (i.e. cofilin does not bind the small ATP cap at filament ends).³

Cofilin lowers the persistence length of actin filaments ∼5-fold (Table 1). The persistence length of native actin filaments (without phalloidin) under our experimental conditions is 9.8±0.1 µm (Table1); comparable to a previously reported value of 9.0±0.5 µm measured under slightly different buffer conditions,¹⁹ and the value predicted from molecular dynamics simulations.^20–22 Cofilactin filaments have an L_p of 2.2±0.03 µm (Table 1); comparable to those of intermediate filaments (L_p is 0.3–3 µm for neurofilaments²³ and vimentin^24,25).

Table 1.

Elastic bending and twisting parameters for native actin and cofilactin filaments

Filament	Lp (pN nm)	κ(pN ìm2)	I (nm4)a	E (pN nm−2)a	C (pN ìm2 rad−1)b
Actin	9.8(±0.14)	40(±0.49) × 10−3	120	330	2.30(±1.00) × 10−6
Cofilactin	2.2(±0.026)	9.1(±0.11)×10−3	240	38	0.13(±0.06) × 10−6

Conditions: 20 mM imidazole (pH 6.6), 50 mM KCl, 0.2 mM ATP, 2 mM MgCl₂, 2 mM DTT, 1 mM NaN₃, 25 °C.

^aCalculated by treating the filament as a homogenous isotropic material.

^bThe values of the filament torsional rigidity, C, are taken from Ref. 14.

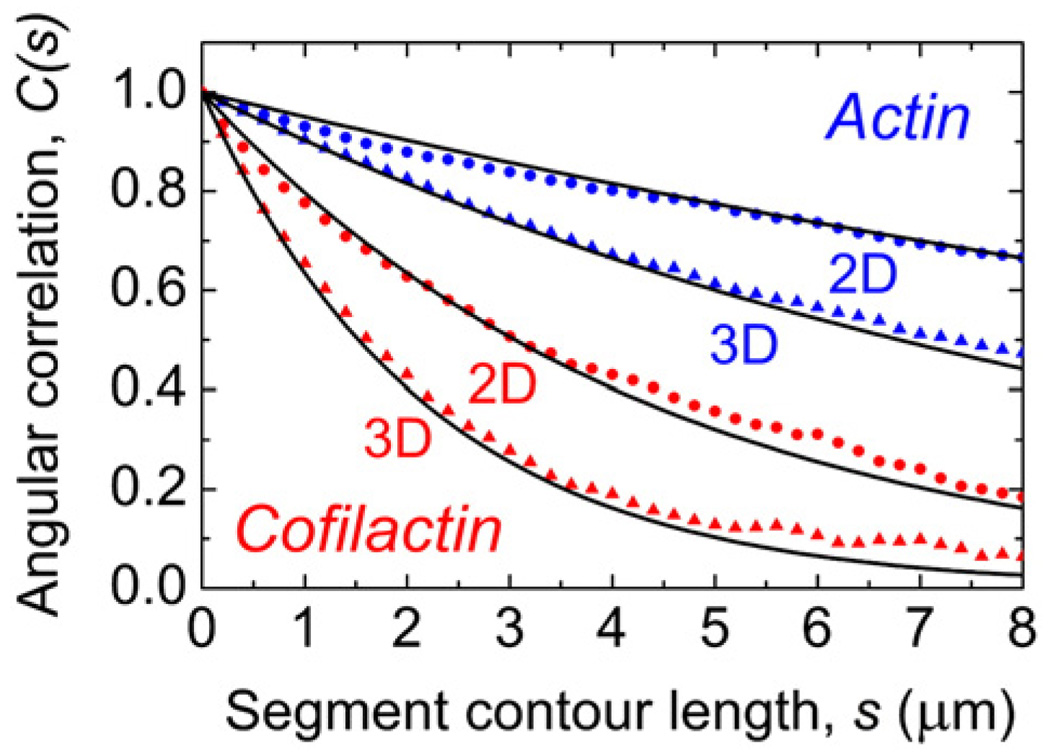
Stochastic simulations of actin and cofilactin filament equilibrium configurations (Fig. 4; Supplementary Data Video 5 and Supplementary Data Video 6) confined to two-dimensional fluctuations account for the experimental data (Fig. 3). The agreement between the observed (Fig. 3) and simulated (Fig. 4) angular correlations confirms that the two-dimensional fluctuation approximation used in the analysis is fulfilled under our experimental conditions.

Fig. 4.

Predicted angular correlation function for filaments free to fluctuate in two and three dimensions. The filament average tangent angle correlation of 1000 simulated equilibrium configurations were obtained with imposed experimental depth constraints for effective two-dimensional motions (circles) and unconstrained three-dimensional motions (triangles). The values of L_p used in the simulations were 9.8 µm for actin (blue) and 2.2 µm for cofilactin (red). The continuous line represents the predicted correlation using Eq. (1).

Quantitative knowledge of the two-dimensional angular correlation allows us to predict the equilibrium configurations of filaments in three dimensions (Fig. 4; Supplementary Data Video 5 and Supplementary Data Video 6). As expected, there is less angular correlation when filaments are free to fluctuate in three dimensions. However, it should be noted that the net effect of cofilin on short filaments (<2 µm) is more pronounced in three dimensions than when constrained to two dimensions. In addition, note that the correlation (i.e. stiffness) of both filament types is high at lengths<0.7 µm (∼ 250 subunits), which may contribute to the inability of cofilin to destabilize or sever filaments of this length.²

The three-dimensional filament flexural rigidity (κ) calculated from the experimental L_p values, Boltzmann’s constant (k_B), and the absolute temperature (T) using Eq.(2):

$$\kappa =L_{\mathrm{p}}{k}_{\mathrm{B}}T$$ (2)

is 0.040 pN µm² for actin filaments and 0.0091 pN µm² for cofilactin filaments (Table 1), indicating that cofilin binding increases the bending flexibility of actin filaments ∼5-fold. The lowest compressive force (i.e. external load, F_c) needed to buckle a filament depends on κ according to:²⁶

$$F_c={\pi }^2\frac{\kappa }{L^2}$$ (3)

Therefore, a cofilactin filament will buckle under a compressive force ∼5-fold smaller than that needed to buckle an actin filament of identical length because of the reduction in κ.

The flexural rigidity (κ) of a semi-flexible polymer can be related to its elastic (Young’s) modulus (E) and geometric moment of inertia (I) when modeled as a homogenous isotropic material by:

$$\kappa =\mathit{EI}$$ (4)

E is the shape-independent measure of material stiffness and I is the shape-dependent, geometric moment of inertia (second moment of area), which is a function of the cross-sectional area and radius of gyration (R_g).²⁷ For a helical polymer that deviates from radial symmetry and possesses roughly an elliptical cross-sectional area,^28,29 I corresponds to the geometric mean of the two principle axes¹⁸ as defined by:

$$I=\frac{\pi r_{\mathrm{a}}^2{r}_{\mathrm{b}}^2}{4}$$ (5)

where r_a and r_b are the major and minor radii, respectively.

There is uncertainty in estimating the Young’s elastic modulus of actin and cofilactin filaments from their flexural rigidities (κ), since they are not isotropic structures.²⁹ Evaluating the contributions of elasticity (E) and geometry (I) to the change in rigidity (κ) of an anisotropic material is complex and requires a detailed geometric model of bending. Without detailed knowledge about the geometries involved at the filament subunit level, we consider a filament to behave as a homogenous material so that the apparent E can be expressed as a simple scalar (Eq.(5)). Although there are limitations in applying such a simplified model, it provides insight and describes well the overall mechanical behavior of actin filaments,^18,30 actin filaments saturated with tropomyosin,²⁶ large-scale actin networks,³¹ and microtubules.¹⁸ In addition, the bending fluctuations analyzed in this study are on length-scales much greater than the filament helical repeat, so anisotropies arising from local, non-cylindrical fluctuations in shape will be averaged.^18,32 We , therefore, consider filaments at lengths and time-scales applicable to the bending fluctuations analyzed in this study to behave as homogeneous, isotropic material.³⁰

An actin filament modeled as a homogenous isotropic elliptical cylinder¹⁸ with a major radius of 4.5 nm²⁸ and mean radius of 3.5 nm²⁹ has a second moment of inertia (I) of 120 nm⁴ calculated using Eq. (6) (Fig. 6). Cofilin binding increases the filament radius ∼20–30%,⁸ and the major radius to 6.7 nm (Fig. 5).¹⁴ Since cofilin increases the mass of the filament ∼40% without increasing the filament length per subunit (rise), the geometric mean radius is ∼4.2 nm (∼20% increase), which corresponds to a value of 240 nm⁴ for I. The experimental flexural rigidity (κ) values (Table 1) and Eq.(5) yield Young’s elastic moduli (E) of 330 pN nm⁻² for native and 38 pN nm⁻² for cofilin-decorated actin filaments.

Fig. 5.

Geometric models of actin and cofilactin filaments. An actin filament (blue) modeled with an elliptical cross-section of a 2.7 nm minor radius, a 4. 5 nm major radius and 37 nm crossover length, and a cofilactin filament (red) modeled with an elliptical cross-section of a 2.7 nm minor radius, a 6.7 nm major radius and 27 nm crossover length. Models are presented with and without overlays of the corresponding reconstructions based on cryoelectron microscopy.⁸ The models were graphed using Grapher software (Apple Computer Inc.).

Changes in the radial mass distribution within the filament could affect the geometric moment (I) and thereby lower the bending rigidity (κ, Eq.(4)) of cofilin-decorated filaments. Actin subdomain 2 makes the highest radius contact in the filament,³³ and disorder of this region significantly affects the filament flexibility.^{14,20–22,33} Cofilin binding leads to the reorganization of subdomain 2,^9–11 and disrupts (longitudinal and lateral) filament subunit contacts.^{11–13,34,35} It is, therefore, likely that the overall reduction in filament stiffness associated with cofilin binding arises from changes in the filament elasticity (E) and geometry (I) achieved by modulating the strength and redistribution of the intra-and intersubunit bonds.

Discussion

Cofilin makes actin filaments more elastic, in marked contrast to the stiffening effects of other filament binding proteins, such as tropomyosin.¹⁹ The stiffness of a tropomyosin-decorated actin filament can be accounted for²⁶ by the increase in filament mass (I); there is little or no effect on the filament Young's elastic modulus (E). Cofilin binding also increases the filament mass (∼40%) and second moment of inertia (Table 1), but differs from tropomyosin in that it dramatically lowers the Young’s filament elastic modulus (Table 1). The reduction in the apparent elastic modulus is sufficiently large (∼10-fold) that decorated filaments bend more readily and rapidly (Fig. 1; Supplementary Data Video 1–Supplementary Data Video 4) and to a greater extent (Fig. 2) than bare filaments, even though they have a greater mass and second moment of inertia.

The elasticity of non-covalent protein polymers such as actin filaments is determined by the strength of the intra-and intersubunit bonds.²⁶ The modulation of filament bending (Fig. 4) and twisting¹⁴ mechanics (Table 1) indicates that cofilin binding disrupts stabilizing contacts between filament subunits and/or enhances their conformational dynamics, both of which have been documented extensively for the cofilin-actin filament interaction.^9–14,35

We favor a mechanism in which the cofilin-linked changes in filament bending and twisting mechanics (Table 1) are mediated largely through the reorganization of actin subdomain 2, since the conformation of this region influences the subunit longitudinal contacts and filament flexibility,³³ and is modulated by cofilin binding.^9–11 Molecular dynamics simulations²² indicate that filament lateral contacts are also dependent on the actin subdomain 2 conformation. Therefore, the weakening of longitudinal and lateral filament contacts with cofilin binding^10–14 could be mediated through interaction with actin subdomain 2.

Cofilin binding to actin is coupled to the dissociation of actin filament-associated ions.³⁶ Ions have long been known to stabilize the polymer form of actin through polysteric linkage (i.e. salt polymerizes actin monomers). It is likely that linked ion dissociation contributes to changes in filament mechanics. Consistent with this interpretation, filaments in low-salt conditions are more flexible than those in high salt (i.e. ion binding makes filaments stiff³³). In addition, hydroxyl radical footprinting reveal that lowering the ionic strength compromises interactions between filament subunits, which increases the conformational flexibility of filaments.³⁷ It is likely that other regulatory actin-binding proteins also dissociate ions from actin without destabilizing filaments. This behavior would arise if the stabilizing ion–actin interactions were replaced with stabilizing protein–actin interactions (e.g. interactions that bridge filament subunits). In the case of cofilin, the stabilizing ion–actin interactions are replaced with net interactions that are non-or de-stabilizing³⁶.

It has been suggested that an asymmetry in filament mechanics, rather than cumulative changes in filament mechanics, generates filament severing⁴ since fully decorated and bare actin filaments are more stable than filaments partially decorated with cofilin.³⁸ Because boundaries between cofilin-bound and unbound actin subunits occur with a higher frequency at low binding densities than at high binding densities, local changes (i.e. boundaries) in the mechanical properties will be more prominent at binding densities where cofilin binds non-contiguously.⁴ The observation that actin filament severing occurs at low cofilin cluster sizes and binding^4–6 but is inhibited at high cofilin-binding densities^5,6 supports this hypothesis and favors a mechanism⁴ in which local changes in filament bending and twisting dynamics introduces an asymmetry in filament mechanics that promotes severing. This behavior arises because stress localizes in regions where changes in the mechanical properties exist, which increases the likelihood of fatigue fractures from thermal fluctuations at these boundaries.³⁹

A mechanical view of the cytoskeleton is critical to understand how it contributes to cell shape, stability and motility.^26,40 Recent studies favor mechanismsin which filaments fully decorated with cofilin exist transiently at the leading edge of cells.⁵ Because a gradient of non-uniformly decorated actin filaments exists at the leading edge of migrating cells,^41,42 a modulated mechanical gradient will also exist. This gradient will modulate the overall stiffness and elasticity of the actin cytoskeleton, such that cofilin activation could contribute to motility by facilitating (lamellipodial) actin bending⁴⁰ in addition to severing.³ Bending flexibility may propagate cooperatively along the filament to subunits without bound cofilin, as do changes in torsional flexibility.¹⁴ Overall softening of the actin network could potentially reduce the net force production or protrusion efficiency of these cellular actin-based structures.⁴³

Materials and Methods

Protein and sample preparation

Rabbit skeletal muscle actin was purified,⁴⁴ labeled with tenfold molar excess Alexa 488 Fluor succinimidyl ester (Molecular Probes, Eugene, OR: cat. # A2000) and gel-filtered over Sephacryl S300 at 4 °C in G buffer (5 mM Tris (pH 7.5), 0.2 mM ATP, 0.2 mM CaCl₂, 0.5 mM DTT, 1 mM NaN₃) as described.¹⁶ Actin concentrations were determined by measuring the absorbance at 290 nm,⁴⁴ and corrected for Alexa 488 labeling.¹⁶ The labeling efficiency was ∼0.8 Alexa 488 fluorophores per actin monomer. Ca²⁺-actin monomers were converted to Mg²⁺-actin monomers with 0.2 mM EGTA and 50 µM MgCl₂ then polymerized with 0.1 vol. 10× polymerization buffer yielding KMI₆₆ buffer (50 mM KCl, 2 mM MgCl₂,2 mM DTT, 0.2 mM ATP, 20 mM imidazole, pH 6.6). Recombinant human non-muscle cofilin-1 was purified as described.^4,14,36

Cofilin-decorated actin filaments (2–10 µM) were made by adding cofilin at a concentration ≥10 times the value needed to reach half maximum saturation of actin.⁴ Equilibrated samples were rapidly diluted five- to ten-fold into KMI_6.6 buffer supplemented with 30 µg mL⁻¹ glucose, 100 µg mL⁻¹ catalase and 10 mM glucose directly on a 70% ethanol-cleaned glass microscope slide. Cofilactin filaments were diluted into buffer with free cofilin at a concentration to ensure the cofilin binding density remained constant and near unity (one cofilin per actin subunit). After dilution, a 6 µL final sample volume was covered with a 22 mm × 22 mm glass coverslip, excess solution was removed and the coverslip was sealed with vacuum grease. The depth of the solution was estimated to be <3 µm by measuring the difference in focus from the two internal glass surfaces.¹⁹ A chamber depth of <3 µm was necessary to prevent the actin filament from rotating axially. Motions out of the focal plane may underestimate the length,¹⁸ but this error (∼0.2% of filament length) from a nonzero depth is smaller than the interval used to calculate 〈C(s)〉 (∼5%) for the minimum length of the filament analyzed and has been confirmed to be adequate through our simulations.

Image processing and analysis

Images of single filaments undergoing thermal fluctuations were acquired using a Nikon Eclipse TE300 microscope equipped with a Coolsnap HQ cooled CCD camera (Roper Scientific, Tucson, AZ) and Metamorph image acquisition software (Molecular Devices, Downington, PA). Digital images were acquired consecutively for 50 frames with exposure times of 50 ms for native actin filaments and 20 ms for cofilactin filaments, rendering the latter to appear dimmer. Digital image stacks were processed using Metamorph software. Individual filaments were cropped to reduce overall background shift and processed with a low-pass 3×3 averaging filter, thresholded for light objects, three-neighbor dilated, all point eroded and autoskeletonized to extract the shape of the filament. This procedure removes artifacts arising from low signal to noise and autoskeletonization without compromising the pixels comprising the filament backbone.

The longest continuous skeleton was detected and reconstructed using an average third-order Bezier spline to minimize measurement error,¹⁹ with functions written using Matlab software (The Mathworks Inc., Natick, MA). The density of guide points used to reconstruct the filament shape was chosen as the minimum that did not change the derived value of the persistence length, L_p.¹⁹ Representations were visually inspected by overlaying the backbone reconstructions above the raw images. Two separate data pools were analyzed independently to validate reproducibility. The actin and cofilactin filament L_p values were calculated from 300 digitized filament images (n ≥ 10 filaments for each data set).

Stochastic simulations

Model-based simulations of equilibrium configurations of filaments undergoing two-and three-dimensional fluctuations in shape were based on the force balance equation:

$$C_d\left(\left(\mathbf{a}\cdot \frac{\partial \mathbf{r}}{\partial t}\right)\mathbf{a}+2\mathbf{a}\times \left(\frac{\partial \mathbf{r}}{\partial t}\times \mathbf{a}\right)\right)=-\kappa \frac{{\partial }^4\mathbf{r}}{\partial s^4}+\mathbf{f}(\Lambda ,\mathbf{r})+\mathbf{\xi }$$ (7)

where boldface variables code for vectors, C_d is the drag coefficient per unit length in a direction parallel with the filament long axis; a is the unit vector tangent to the filament long axis at position s at time t; r(s,t) is a point defining position s along a filament at time t; s is the segment (arc) length (s) along the contour length (L) of a filament; κ is flexural rigidity; f is a force vector used to mimic the presence of walls or to implement inextensibility constraint via tension Λ; ξ is a random force term.

The scalar and vector products in the left-hand side of Eq.(7) implement the drag force, which is proportional to the point velocity vector. However, because it is easier to move in the direction parallel with the local tangent direction (given by vector a) rather than in the orthogonal direction, the velocity parallel with a (given by the term $(\mathbf{a}·\frac{\partial \mathbf{r}}{\partial t})\mathbf{a})$ and orthogonal to a (given by the term $\mathbf{a}\times (\frac{\partial \mathbf{r}}{\partial t}\times \mathbf{a})$) must be considered. The drag coefficient for slender bodies (e.g. an individual filament) moving near a wall (fulfilled under our conditions) is given by:⁴⁵

$$C_{\mathrm{d}}=\frac{2\pi \eta }{\text{ln}\left(\frac{2H}{R_{\mathrm{d}}}\right)}$$ (8)

where η is the solvent viscosity (0.003 Pa·s); H is the distance between the filament and the wall (1.5 µm); R_d is the filament radius (actin, 3.5 nm; cofilactin, 4.2 nm). Each component of the random force has the following properties:

$$\begin{array}{c}\langle {\xi }_i(s,t)\rangle =0\\ \langle {\xi }_i(s,t){\xi }_j(s^{\prime },t^{\prime })\rangle =2k_{\mathrm{B}}T{C}_d{\delta }_{\mathit{ij}}\delta (s-s^{\prime })\delta (t-t^{\prime })\\ i=1,2,3\end{array}$$ (9)

We define new dimensionless variables:

$$\begin{array}{c}h=\frac{L}{N},\\ {\sigma }_0=0<\cdots <{\sigma }_i=\frac{\mathit{ih}}{L}<\cdots <{\sigma }_N=\frac{\mathit{Nh}}{L},\\ {\mathbf{R}}_i(t)=\frac{\mathbf{r}(L{\sigma }_i,t)}{L},i=0,\cdots ,N,\\ {\mathrm{\Lambda }}_i(t)=\frac{\mathrm{\Lambda }(L{\sigma }_i,t)}{{\mathrm{\Lambda }}_0},i=1,\cdots N,\\ {\xi }_i(t)=\left(\sqrt{\frac{2k_{\mathrm{B}}T}{h{L}^2{C}_d}}\right)\xi (L{\sigma }_i,t),i=0,\cdots ,N,\end{array}$$ (10)

so that Eq. (7) becomes:

$$\begin{array}{c}\left({\mathbf{a}}_i\cdot \frac{\partial {\mathbf{R}}_i}{\partial t}\right){\mathbf{a}}_i+2{\mathbf{a}}_i\times \left(\frac{\partial {\mathbf{R}}_i}{\partial t}\times {\mathbf{a}}_i\right)\hfill \\ =-\left(\frac{1}{{\tau }_1{h}^4}\right)\mathrm{D}\mathbf{R}\hfill \\ +\left(\frac{1}{{\tau }_2{h}^2}\right)({\mathrm{\Lambda }}_{i+1}{\mathbf{R}}_{i+1}+{\mathrm{\Lambda }}_i{\mathbf{R}}_{i-1}-({\mathrm{\Lambda }}_{i+1}+{\mathrm{\Lambda }}_i){\mathbf{R}}_i)\hfill \\ -\left(\frac{1}{{\tau }_3}\right)({\mathbf{R}}_i\cdot {\mathbf{e}}_3){\mathbf{e}}_3+{\mathbf{\xi }}_i\hfill \\ ={\mathrm{\Phi }}_i(\mathbf{R},\mathrm{\Lambda },{\mathbf{\xi }}_i)\hfill \end{array}$$ (11)

where L is the filament length; Λ₀ (dimension: force) and τ_1–3 (dimension: time) are given in Table 2; e₃ is the unit vector along the Z direction; R=(R₀,…,R_N)^T; D is a (N+1, N+1) band-diagonal square matrix that approximate the fourth (arc)-length derivative:

$$D=\left(\begin{array}{cccc}\begin{array}{c}\\ 1\\ \end{array}& \begin{array}{c}\ddots \\ -4\\ \end{array}& \begin{array}{c}\\ 6\\ \end{array}& \begin{array}{cc}\begin{array}{c}\\ -4\\ \ddots \end{array}& \begin{array}{c}\\ 1\\ \end{array}\end{array}\end{array}\right)$$

with appropriate modifications of the two first and last rows to accommodate the absence of force or moment at the two filament ends:

$$\left(\frac{{\partial }^2\mathbf{r}}{\partial s^2}\right)(s=0,L)=0,\left(\frac{{\partial }^3\mathbf{r}}{\partial s^3}\right)(s=0,L)=0$$ (12)

Finally, we use:

$${\mathbf{a}}_i=\frac{1}{h}({\mathbf{R}}_i-{\mathbf{R}}_{i-1}),{\mathbf{a}}_0={\mathbf{a}}_1,$$ (13)

to approximate the unit tangent vector.

Table 2.

Parameters used for stochastic simulations

Parameter	Definition	Expression	Numerical value	Units
η	Solvent viscosity		0.003	Pa·s
Rd	Filament radius		Actin:3.5 × 10−9	m
			Cofilactin:4.2 × 10−9	m
H	Observation depth	$\frac{2\pi \eta }{\text{ln}(\frac{2H}{R})}$	1.5 × 10−6	m
Cd	Drag coefficient per unit length (movement parallel with the tangent vector)		Actin: 2.8 × 10−3	Pa·s
			Cofilactin: 2.9 × 10−3	Pa·s
L	Filament length	$\frac{L}{N}$	1×10−5	M
h	Length of one subdivision along the filament		3.33 × 10−7	M
kBT	Thermal energy		4.18 × 10−21	J
κ	Flexural rigidity		Actin: 4×10−26	J·m
			Cofilactin: 9.1 × 10−27	J·m
τ1	Relaxation time associated with filament bending	$(\frac{L^4{C}_d}{\kappa })$	Actin: 680	s
			Cofilactin: 3100	s
Λ0	Force normalization constant	$(\frac{\kappa }{L^2})$	Actin: 4.1 × 10−16	N
			Cofilactin: 9.2 × 10−17	N
τ2	Relaxation time associated with tension	$(\frac{L^2{C}_d}{{\mathrm{\Lambda }}_0})$	Actin: 680	s
			Cofilactin: 3100	s
Spring	Spring stiffness per unit length		1.24 × 10−4	N·m−2
			Actin: 44	s
			Cofilactin: 45	s
τ3	Relaxation time associated with the spring stiffness	$(\frac{C_d}{Spring})$

The algorithm used to simulate filament dynamics runs using three steps. First, the Stochastic Runge-Kutta algorithm⁴⁶ is used to compute the time-dependent increment for the filament position and tension at time t and filament position σ_i:

$$\begin{array}{c}{\mathbf{F}}_1=\mathbf{\Phi }\left({\mathbf{R}}^{(t)},{\mathrm{\Lambda }}^{(t)},0\right)\\ {\mathbf{F}}_2=\mathrm{\Phi }\left({\mathbf{R}}^{(t)}+dt{\mathbf{F}}_1+\sqrt{dt}\mathbf{\xi }(t),{\mathrm{\Lambda }}^{(t)},0\right)\\ \mathbf{\Delta }\mathbf{R}=\frac{dt}{2}({\mathbf{F}}_1+{\mathbf{F}}_2)+\sqrt{dt}{\mathbf{\xi }}^{(t)}\end{array}$$ (14)

The projection on the a(^t)_i at time t is then used to obtain the new filament position at time (t+dt):

$$\begin{array}{c}\left({\mathbf{a}}_i^{(t)}·{\mathbf{R}}_i^{(t+dt)}\right){\mathbf{a}}_i^{(t)}+2{\mathbf{a}}_i^{(t)}\times \left({\mathbf{R}}_i^{(t+dt)}\times {\mathbf{a}}_i^{(t)}\right)\hfill \\ \hfill =\left({\mathbf{a}}_i^{(t)}·{\mathbf{R}}_i^{(t)}\right){\mathbf{a}}_i^{(t)}+2{\mathbf{a}}_i^{(t)}\times \left({\mathbf{R}}_i^{(t)}\times {\mathbf{a}}_i^{(t)}\right)+\mathbf{\Delta }{\mathbf{R}}_i\end{array}$$ (15)

The final procedure is to update the tension along the filament so that the right-hand side of Eq. (15) is orthogonal to the increment ΔR (see Eq. (14)) using:

$$0=\mathbf{\Delta }\mathbf{R}·\mathrm{\Phi }\left({\mathbf{R}}^{(t)},{\mathrm{\Lambda }}^{(t)},{\mathbf{\xi }}^{(t)}\right)+M^{(t)}{\mathrm{\Lambda }}^{(t+\mathit{dt})}$$ (16)

where M(^t) is an (N+1,N) rectangular matrix combining dot product between ΔR and a:

$$M^{(t)}=\left(\begin{array}{cccc}\begin{array}{c}\mathbf{\Delta }{\mathbf{R}}_0·{\mathbf{a}}_1^{(t)}\\ -\mathbf{\Delta }{\mathbf{R}}_1·{\mathbf{a}}_1^{(t)}\end{array}& \begin{array}{c}\\ \mathbf{\Delta }{\mathbf{R}}_1·{\mathbf{a}}_2^{(t)}\end{array}& \begin{array}{c}\\ \end{array}& \begin{array}{c}\\ \end{array}\\ & -\mathbf{\Delta }{\mathbf{R}}_2·{\mathbf{a}}_2^{(t)}& \ddots & \\ & & \ddots & \mathbf{\Delta }{\mathbf{R}}_{N-1}\cdot {\mathbf{a}}_N^{(t)}\\ & & & -\mathbf{\Delta }{\mathbf{R}}_N\cdot {\mathbf{a}}_N^{(t)}\end{array}\right)$$ (17)

Multiplication of Eq.(16) by the transpose of M(^t) yields a (N,N) linear system from which the solution provides the updated tension terms.