Tension Amplification in Molecular Brushes in Solutions and on Substrates

Abstract

Molecular bottle-brushes are highly branched macromolecules with side chains densely grafted to a long polymer backbone. The brush-like architecture allows focusing of the side-chain tension to the backbone and its amplification from the picoNewton to nanoNewton range. The backbone tension depends on the overall molecular conformation and the surrounding environment. Here we study the relation between the tension and conformation of the molecular brushes in solutions, melts, and on substrates. In solutions, we find that the backbone tension in dense brushes with side chains attached to every backbone monomer is on the order of f₀N^3/8 in athermal solvents, f₀N^1/3 in θ-solvents, and f₀ in poor solvents and melts, where N is the degree of polymerization of side chains, f₀≃ k_BT/b is the maximum tension in side chains, b is the Kuhn length, k_B is Boltzmann constant, and T is absolute temperature. Depending on the side chain length and solvent quality, molecular brushes in solutions develop tension on the order of 10–100 picoNewtons, which is sufficient to break hydrogen bonds. Significant amplification of tension occurs upon adsorption of brushes onto a substrate. On a strongly attractive substrate, maximum tension in the brush backbone is ~ f₀N, reaching values on the order of several nanoNewtons which exceed the strength of a typical covalent bond. At low grafting density and high spreading parameter the cross-sectional profile of adsorbed molecular brush is approximately rectangular with thicknes $~b\sqrt{A/S}$, where A is the Hamaker constant and S is the spreading parameter. At a very high spreading parameter (S > A), the brush thickness saturates at monolayer ~ b. At a low spreading parameter, the cross-sectional profile of adsorbed molecular brush has triangular tent-like shape. In the cross-over between these two opposite cases, covering a wide range of parameter space, the adsorbed molecular brush consists of two layers. Side chains in the lower layer gain surface energy due to the direct interaction with the substrate, while the second layer spreads on the top of the first layer. Scaling theory predicts that this second layer has a triangular cross-section with width R ~ N^3/5 and height h ~ N^2/5. Using self-consistent field theory we calculate the cap profile y (x) = h (1 − x²/R²)², where x is the transverse distance from the backbone. The predicted cap shape is in excellent agreement with both computer simulation and experiment.

1 Introduction

The development of the field of polymer brushes has been greatly influenced by the pioneering work of P. G. de Gennes. [1] This work provided basic principles for the fundamental understanding of conformations and structure of polymer brushes. In the present paper, dedicated to the memory of P. G. de Gennes, we apply these principles to describe conformations and bond tension of brush-like macromolecules in various systems, including solutions, melts, and substrates.

Tension in macromolecules is typically induced by applying external forces, e.g. upon mastication and stretching of rubber. Externally applied tension in macromolecules can vary over six orders of magnitude from a very low value of 10fN ≈ k_BT/250nm (where k_B is Boltzmann constant and T is absolute temperature), at which deformation of giant linear chains with a size of 250nm becomes significant, to a very high value of 10nN at which covalent bonds break.

Bond tension can also be induced without externally applied forces through intramolecular interactions, such as Coulomb repulsion in polyelectrolytes or steric repulsion in branched polymers. This self-induced tension is lower, typically ranging from 10fN to 10pN. The upper limit of this range is on the order of k_BT per Kuhn segment corresponding to almost fully stretched polymers. Achieving higher tension (100pN – 10nN) in molecular bonds through intramolecular interactions remains challenging. Tension in this range may have profound implications on the properties of macromolecules as it changes their electronic structure. This in turn directly impacts molecular reactivity, optical properties, and conductivity [2]. Mechanical stress could lower the activation barrier for certain reactions or even, depending on the magnitude of the applied stress, switch them on and off [3].

Whenever a large number of polymer chains is forced to share the same volume of space, the chains get extended. For example, this may occur in densely branched macromolecules, where many linear branches are confined within a small volume due to chemical bonding. We have recently demonstrated that the bond tension in branched macromolecules is non-uniformly distributed between different sections within the same molecule. Further-more, with a proper design of the molecular architecture, this self-generated tension can be focused to a particular strand leading to significant tension amplification. [4] Very high tension can be generated in molecular pom-poms, by focusing lower tension from many individual arms to the pom-pom spacer. The synthesis of well-defined pom-poms with many (~ 100 – 1000) long arms is a laborious process. In the present paper, we consider a different class of branched polymers - molecular brushes with side chains densely grafted to a long flexible backbone, that are synthetically more accessible and thus allow systematic experimental studies. Understanding stress distribution in brush-like macromolecules leads to additional insights into structural integrity and function of branched biological molecules such as aggrecans [5] and mucins [6].

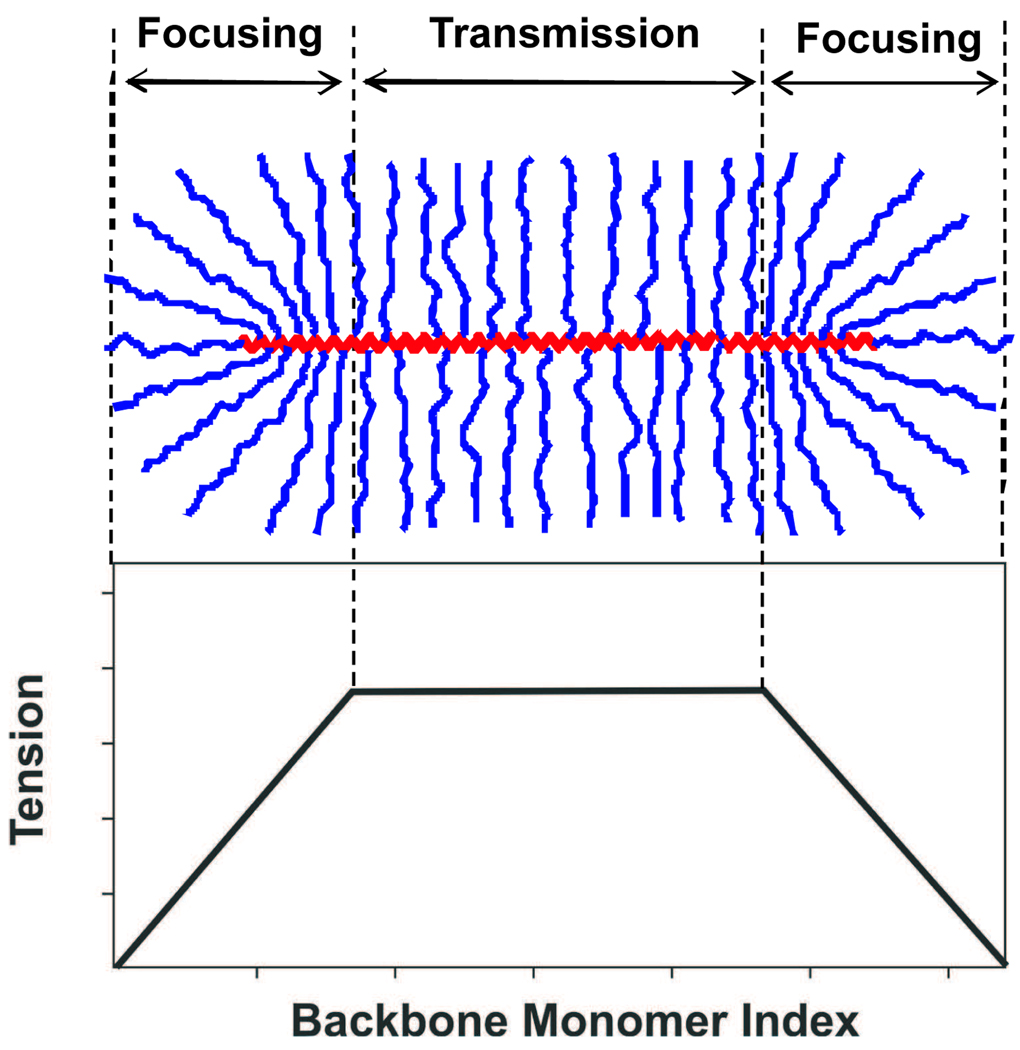
We study two different systems: brushes in dilute solutions and brushes on substrates (Fig. 1). In Section 2, we analyze conformations of molecular brushes in various solvents and the corresponding tension generated in their backbones. The focusing of tension in a molecular brush from its numerous side chains to its backbone occurs at the two ends of the molecule (at the distance from the ends comparable to the width of the molecular brush) and transmitted along the rest of the backbone (see Fig. 2). We observe that backbone tension can be much higher than the maximum tension in densely grafted side chains, f₀ ≃ k_BT/b, i.e. on the order of k_BT per Kuhn segment b. In a theta solvent, tension in the backbone reaches f₀N^1/3, while in an athermal solvent, the maximum backbone tension is higher, f₀N^3/8, where N is the degree of polymerization of side chains.

Figure 1.

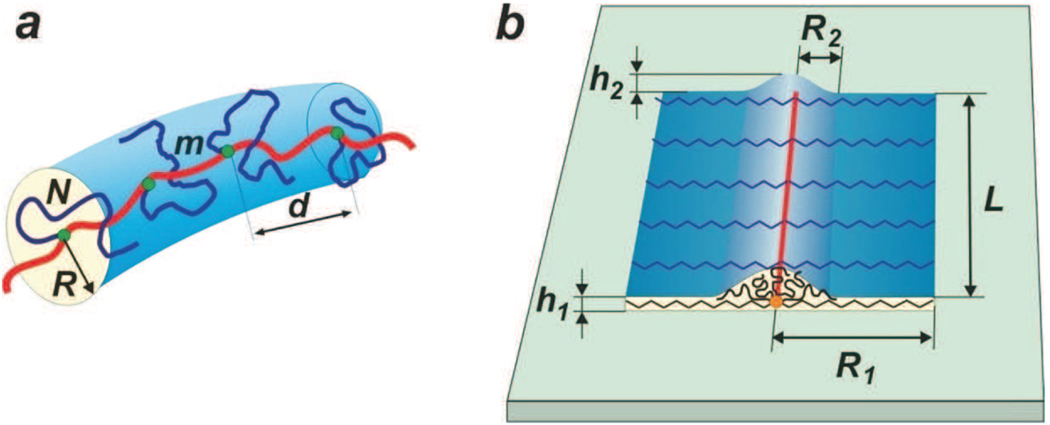
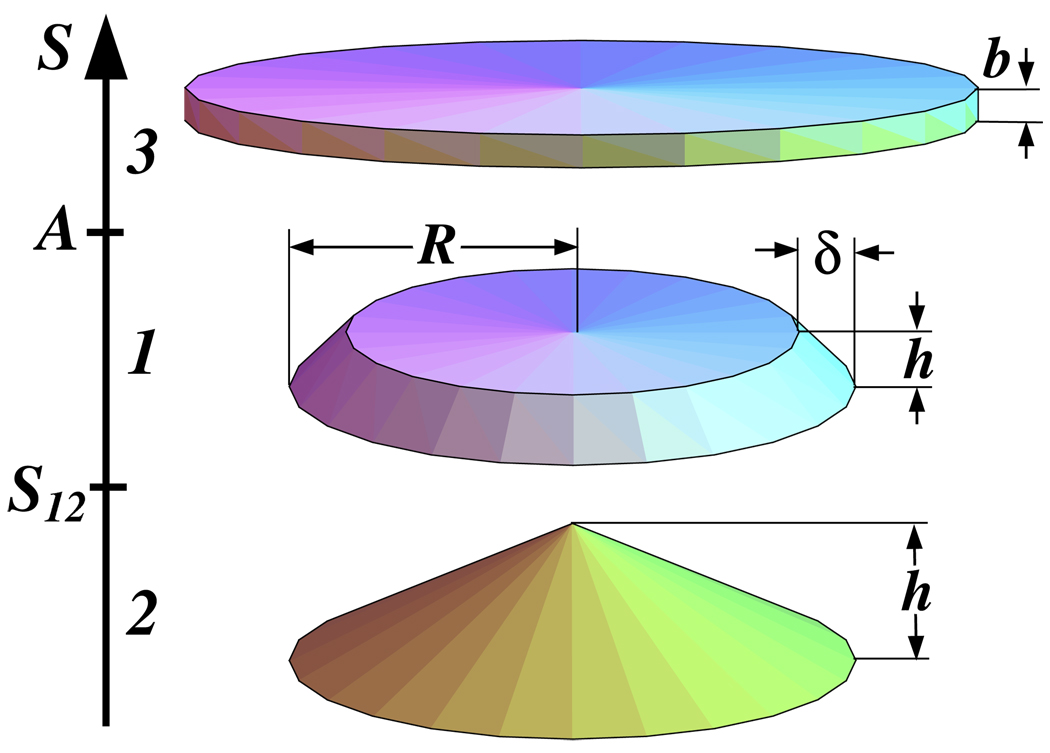
A molecular bottle-brush is a branched macromolecule consisting of a exible backbone and many side chains of size R attached to it. Each side chain contains N monomers and the spacer between neighboring attachment points has average size d and consists of m monomers. Molecular brushes with a high grafting density of the side chains can adopt different conformations, including: (a) a cylindrical worm-like conformation in solutions and (b) a at ribbon with a tent-like cap on strongly attracting substrates. In this paper, one analyzes the following molecular dimensions: radius of the cylinder R, length d of the spacer between neighboring side chains, width R₁ and height h₁ of the first layer (ribbon), and width R₂ and height h₂ of the second layer (cap).

Figure 2.

Theory predicts characteristic variaton of mechanical tension along the backbone of a cylindrical molecular brush. One discriminates three distinct regions of the backbone: (i) two focusing regions at the backbone ends, where amplification of tension occurs, and (ii) one transmission region in the central section of the backbone which acts as a tension transmitter or tension “wire”. In this paper, we analyze bond tension in the transmission region.

Significant amplification of tension occurs upon adsorption onto a substrate. Recently, it has been demonstrated that depending on the branching density and the strength of attraction to the substrate, the adsorption-induced tension can exceed the strength of covalent bonds and lead to the irreversible fracture of brush-like macromolecules [7]. In Section 3, we present a detailed study of the adsorption of molecular brushes from a non-solvent (such as air) onto a solid substrate. We demonstrate that such adsorption may lead to extremely high tension in the backbone of the molecule (on the order of f₀N). We also find that this tension depends on the conformation of adsorbed macromolecules. We consider different adsorption regimes in some of which the cross-sectional profile of molecular brush consists of a strongly adsorbed lower layer and a tent-like cap (see Fig. 1b). Each regime shows different functional dependence of tension on the side chain length, grafting density, and spreading parameter. In Section 4, the shape of adsorbed brushes is calculated using self-consistent field theory (Appendix A) and is found to be in good agreement with the results of computer simulations and molecular imaging experiments.

2 Molecular brush in dilute solution

2.1 Model

In this section, we analyze the conformation of a molecular brush in a dilute solution and relate it to the mechanical tension in the backbone and side chains. We consider molecular brushes with exible and chemically identical backbone and side chains (Fig. 1a). The molecule contains K ≫ 1 side chains each containing N ≫ 1 Kuhn monomers of length b and volume b³. Side chains are tethered to the backbone with grafting density 1/m, where m < N is the number of monomeric units in the spacer between neighboring side chains. The spatial distance between these neighboring attachment points along the backbone is d. The total number of monomers in a molecular brush is thus K (N + m) and the contour length of the molecule is Kd.

The solvent quality is specified by the excluded volume parameter υ = b³τ, where the deviation of absolute temperature T from the θ-temperature is τ = 1 −θ/T for T > θ and τ = T/θ − 1 for T < θ. [8] The free energy per repeating unit, consisting of one side chain and one spacer, is the sum of the elastic free energy of the backbone spacer, F_sp, and the free energy of the side chain F_sc:

$$F_{\mathit{\text{rep}}}(d)=F_{\mathit{\text{sp}}}(d)+F_{\mathit{\text{sc}}}(d)$$ (1)

Minimization of the free energy per repeating unit,∂ F_rep/∂d = 0 gives two properties: the equilibrium end-to-end distance of the spacer d_eq, and the bond tension f_sp in the spacer as

$$f_{\mathit{\text{sp}}}={[\partial F_{\mathit{\text{sp}}}(d)/\partial d]}_{d=d_{\mathit{\text{eq}}}}=-{[\partial F_{\mathit{\text{sc}}}(d)/\partial d]}_{d=d_{\mathit{\text{eq}}}}$$ (2)

This equation is valid at all equilibrium spacer elongations including the strong stretching limit with d_eq ≃ bm. Note that the spacer tension, f_sp, is equivalent to the backbone tension at the location of a given spacer. We keep our discussion at the scaling level and drop numerical coefficients on the order of unity. We are particularly interested in the conditions of strong spacer elongation (d_eq ≃ bm) that correspond to high tension,

$$f_{\mathit{\text{sp}}}\gg f_0=k_{B}T/b,$$ (3)

and can cause significant alterations in the electronic structure of molecular backbone and ultimately rupture of chemical bonds. [2]

To demonstrate the significant difference in tension between macromolecules in solutions and on substrates, we first consider molecular brushes in dilute solutions. Conformations of molecular brushes under various solvent conditions were investigated in previous studies [9, 10]. Below, we review basic results of these studies and calculate tension in molecular brushes in good, Θ, and poor solvents.

2.2 Good and theta solvents

Figure 3 presents the tension in the spacer for different number m of monomers in the spacer and the quality of solvent τ. For very long spacers, m ≳ N, there is no tension in the molecule since both the side chains and spacers are unperturbed coils. A decrease in spacer length m < N leads to the overlap of side chains, and to the increase in backbone tension. According to the scaling model of molecular brushes [9–11], the arrangement of side chains in good and theta solvents is considered as a cylinder of densely packed concentration blobs with the interaction energy k_BT per blob due to binary or ternary monomer-monomer interactions. In all regimes of the diagram, the concentration blob size ξ_c (r) is on the order of average separation between the side chains. At distance r from the backbone the area per side chain is proportional to rd due to the cylindrical symmetry. Therefore, the blob size increases with the distance r from the backbone as

$${\mathrm{\xi }}_c(r)\simeq {(rd)}^{1/2},(\text{good}\text{and}\theta -\text{solvent}).$$ (4)

The side chain tension decreases with the distance from the backbone as

$$f_{\mathit{\text{sc}}}\simeq k_{B}T/{\mathrm{\xi }}_c(r)\simeq k_{B}T{(rd)}^{-1/2},(\text{good}\text{and}\theta -\text{solvent}).$$ (5)

Figure 3.

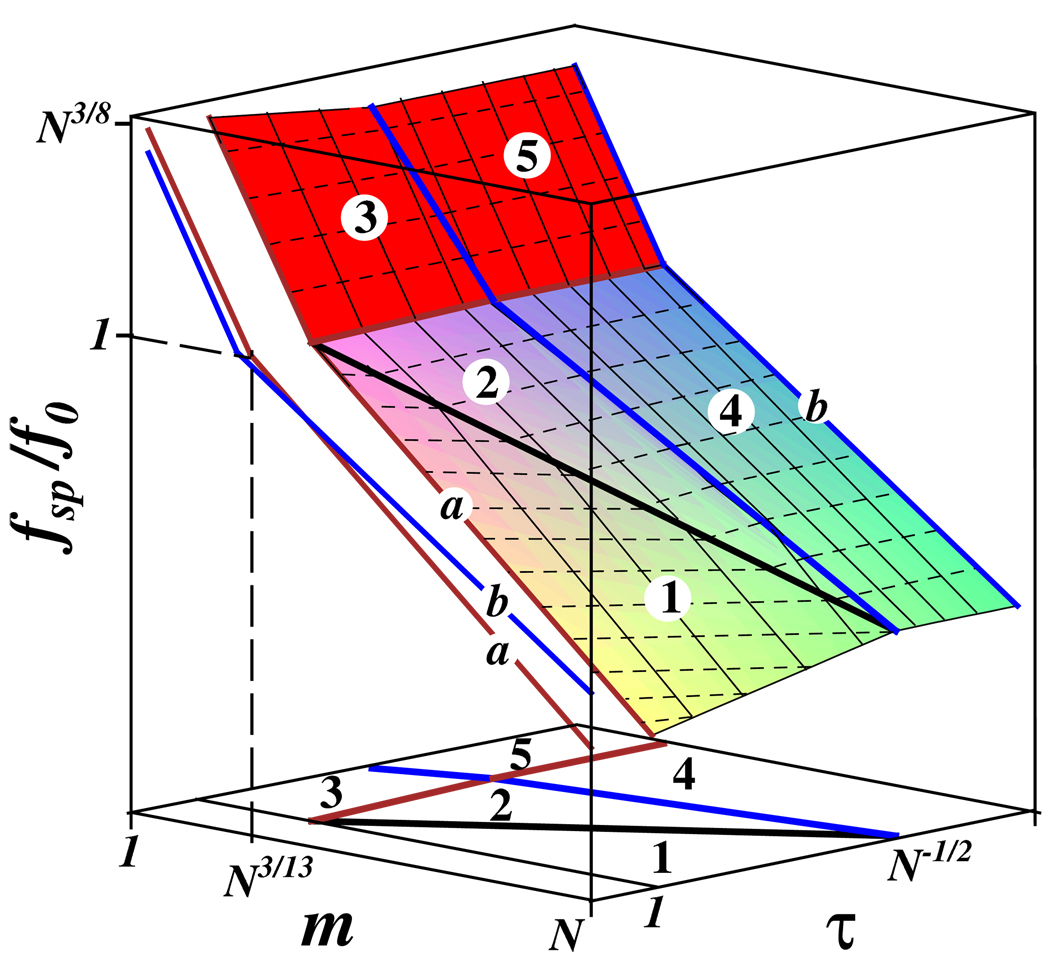
3d logarithmic plot of the tension in the molecular brush spacer in good and theta solvents as the function of the number of Kuhn segments, m, in the spacer and the solvent quality τ > 0. Thin dotted and solid lines correspond to the cross-sections with constant f_sp and τ respectively. Projections on (m,f_sp) plane for two different qualities of solvent τ is shown by lines a and b in 3d plot. Projection on (m,τ) plane presents the diagram of states of the molecular brush. Regimes 1 – 5 of the diagram of states are discussed in the text.

Local crowding of the side chains creates effective local semidilute conditions inside the brush with chain statistics depending on the solvent quality. In the semidilute good solvent regime, the size of the thermal blob

$${\mathrm{\xi }}_{\mathit{\text{th}}}\simeq b{\tau }^{-1}$$ (6)

is smaller than the size of the concentration blob [8, 12]

$${\mathrm{\xi }}_c\simeq b{\tau }^{-1/4}{\varphi }^{-3/4}(r),$$ (7)

where Φ(r) is the local monomer volume fraction at radial distance r from the backbone. Chains are Gaussian on length scales below ξ_th and swollen on intermediate length scales ranging from ξ_th to ξ_c. In order to determine the radial dependence of this volume fraction, we use the condition that concentration blobs are space filling. equating Eq. 4 for the size of concentration blobs and Eq. 7, we find the radial dependence of the volume fraction in the semidilute good solvent regime

$$\varphi (r)\simeq {\tau }^{-1/3}{(rd/b^2)}^{-2/3}.$$ (8)

The radius R of the bottle brush is determined by the condition that the integral of the number density Φ(r)/b³ per spacer is equal to the number of monomers in the side chain,

$$\frac{d}{b^3}{\displaystyle {\int }_0^R\varphi (r)rdr\simeq N,}$$ (9)

leading to the expression

$$R\simeq N^{3/4}{b}^{5/4}{(\tau /d)}^{1/4}.$$ (10)

The number of tension blobs per side chain is given by

$$\frac{d}{b^3}{\displaystyle {\int }_0^R\frac{\varphi (r)}{g(r)}rdr,}$$ (11)

where

$$g(r)\simeq \varphi (r){[\mathrm{\xi }(r)/b]}^3\simeq {\tau }^{-1/3}{(rd/b^2)}^{5/6}$$ (12)

is the number of monomers per concentration blob at the distance r from the backbone. By substituting this expression into integral (11) and multiplying it by k_BT we get the free energy of a side chain [11],

$$F_{\mathit{\text{sc}}}\simeq k_{B}T{\tau }^{1/8}{N}^{3/8}{(b/d)}^{5/8}.$$ (13)

The phase diagram in Fig. 3 depicts different regimes of a brush-like macro-molecule in good and theta solvents. The essential details of these regimes are discussed below.

Regime 1 (swollen brush and swollen spacer)

The stretching free energy of the spacer in a good solvent is proportional to the number of tension blobs in the backbone with the size ξ_sp ≃τ^1/2b^5/2m^3/2/d^3/2 [8,12,13],

$$F_{\mathit{\text{sp}}}\simeq k_{B}T{(d/b)}^{5/2}{m}^{-3/2}{\tau }^{-1/2}.$$ (14)

Minimization of the free energy of the molecular brush corresponds to the balance between the energies of the spacer and side chains, F_sp ≃ F_sc. From this condition we find the equilibrium size of the spacer [9]

$$d_{\mathit{\text{eq}}}\simeq b{\tau }^{1/5}{m}^{12/25}{N}^{3/25}.$$ (15)

The tension in the spacer is higher for shorter spacers with fewer number of monomers m. The higher tension f_sp ≈ k_BT/ξ_sp corresponds to a smaller Pincus blobs of the size [8, 12, 13]

$${\mathrm{\xi }}_{\mathit{\text{sp}}}\simeq b^{5/2}{\tau }^{1/2}{m}^{3/2}{d}_{\mathit{\text{eq}}}^{-3/2}\simeq b{m}^{39/50}{N}^{-9/50}{\tau }^{1/5}.$$ (16)

Note that tension is decreasing with improving solvent quality. This counter-intuitive behavior is due to the change of spacer elasticity from Gaussian to nonlinear regime due to partial swelling of the spacer.

Regime 2 (swollen brush and Gaussian spacer)

The above expressions are valid as long as the Pincus blob of the spacer is larger than the size of the thermal blob, Eq. 6. Otherwise, the elastic energy of the spacer is given by the Gaussian expression

$$F_{\mathit{\text{sp}}}\simeq k_{B}T{d}^2/(b^{2}m),$$ (17)

which is balanced by the free energy of side chains, Eq. 13, at the equilibrium size of the spacer,

$$d_{\mathit{\text{eq}}}\simeq b{m}^{8/21}{N}^{1/7}{\tau }^{1/21}$$ (18)

The cross-over between regimes 1 and 2 occurs for spacers with the number of monomers

$$m_{12}\simeq N^{3/13}{\tau }^{-20/13},$$ (19)

which is shown in the phase plane (m,τ) in Fig. 3 by the thick black line.

Regime 3 (swollen brush and fully stretched spacer)

The Gaussian stretching of the spacer and expression (17) for its free energy is valid as long as the spacer size d (Eq. 18) is much smaller than its contour length bm. Shorter spacers with the number of monomers

$$m<m_{23}\simeq N^{3/13}{\tau }^{1/13}$$ (20)

are almost fully stretched with the tension higher than f₀ = k_BT/b.

In a good solvent, the tension in the spacer of the molecular brush is monotonically increasing with decreasing number of monomers of the spacer:

$$f_{\mathit{\text{sp}}}\simeq f_0{m}^{\mu i}{N}^{\nu i}{\left|\tau \right|}^{t_i},$$ (21)

where the values of exponents μ_i,ν_i and t_i for regimes i = 1,2 and 3 are given in Table 1. Note, that even though for short spacers with m < m₂₃ (in regime 3) the tension is larger than f₀, Eq. 21 is still applicable, because it is determined by the stretching of side chains (see Eq. 2) that are far from full extension.

Table 1.

Exponents μ_i, ν_i, and t_i of the Expression for Spacer Tension f_sp ≃ f₀m^μ_iN^ν_i|τ|^t_i for Molecular Brush in Regime i

i	1	2	3	4	5	6	7	8
μi	−39/50	−13/21	−13/8	−5/8	−5/3	−2/3	−2	−1
νi	9/50	1/7	3/8	1/8	1/3	0	0	0
ti	−1/5	1/21	1/8	0	0	−1/3	−1	−1

In an athermal solvent with the excluded volume parameter τ = 1 the two cross-over spacer lengths coincide, m₁₂ = m₂₃ = N^3/13 (Eq. 19 and Eq. 20), and the intermediate regime 2 disappears. The tension for this case is represented by the line a in Fig. 3, and corresponds to the molecular brush in an athermal solvent. The tension in a fully stretched backbone of a molecular brush with shorter spacers (m < N^3/13) is larger than f₀ (regime 3). The backbone tension reaches its maximum value f₀N^3/8 ≫ f₀ for the monomeric spacer (m = 1).

Regime 4 (theta brush and Gaussian spacer)

At temperatures close to the θ-temperature the size of the thermal blob increases and becomes comparable to the size of the concentration blob at the outer layer of the molecular brush, ξ_c (R) ≃ ξ_th. This condition corresponds to the cross-over between good and θ-solvent regimes of the molecular brush. Substituting Eq. 10 for R in Eq. 4 for ξ_c we find the boundary between regimes 2 and 4:

$$m_{24}\simeq N^{-3}{\tau }^{-8},\tau >0$$ (22)

Chains in regime 4 exhibit Gaussian statistics leading to the size of the concentration blob given by

$${\mathrm{\xi }}_c(r)\simeq b{\varphi }^{-1}(r).$$ (23)

Since such blobs densely fill the molecular brush, the volume fraction Φ(r) can be found by equating Eq. 23 and Eq. 4, and is equal to

$$\varphi (r)\simeq b{(rd)}^{-1/2}$$ (24)

Using calculations similar to the case of a good solvent, one can obtain the free energy of a side chain [11]

$$F_{\mathit{\text{sc}}}\simeq k_{B}T{N}^{1/3}{(b/d)}^{2/3}.$$ (25)

Balancing this side chain free energy with the free energy of the spacer, Eq. 17, we find the equilibrium size of the long spacer

$$d_{\mathit{\text{eq}}}\simeq b{m}^{3/8}{N}^{1/8},$$ (26)

valid for

$$m>m_{45}\simeq N^{1/5}.$$ (27)

The spacer in this regime is Gaussian, and its tension f_sp ≃ k_BTd_eq/ (b²m) can be written in the form of Eq. 21 with exponent t₄ = 0 and exponents μ₄ = −5/8 and ν₄ = 1/8, as listed in Table 1.

Regime 5 (theta brush and fully stretched spacer)

Shorter spacers with m < m₄₅ are fully stretched. The tension increases with decreasing number m of monomers in the spacer, and this is given by Eq. 21 with exponents μ₅ = −5/3, ν₅ = 1/3 and t₅ = 0 (see Table 1). The crossover boundary between good solvent regime 3 and θ-solvent regime 5 for a fully stretched spacer occurs at

$$m_{35}\simeq N^{-1}{\tau }^{-3},\tau >0.$$ (28)

Tension in the backbone of a molecular brush in a θ-solvent is represented by the line b in Fig. 3. The maximum backbone tension (for monomeric spacer m = 1) in a θ-solvent reaches the value f₀N^1/3 ≫ f₀, which is lower than the maximum tension in a good solvent (f₀N^3/8) by the factor N^1/24.

2.3 Poor solvent

It is commonly believed that when macromolecules are collapsed in a poor solvent, the chain dimensions become smaller than or equal to its Gaussian size. We demonstrate that this is not necessary the case for branched macromolecules. Below we describe the situation under which the collapsed molecular brush is strongly stretched without direct application of external forces. To explain the mechanism of chain stretching in poor solvent, consider a droplet of Z chains, each of them consisting of N Kuhn monomers of length b in a solvent with the excluded volume parameter υ < 0. The balance of two-body attraction and three-body repulsion leads to a globule with the volume fraction Φ ≃ |υ|/b³. [8, 12] The size of the corresponding thermal blob is ξ_th ≃ b⁴/|υ| and the number of monomers in this thermal blob is g_th ≃ b⁶/|υ|². The linear size of the droplet, R ≃ (ZN/ |υ|)^1/3, could be either larger or smaller than the Gaussian size of a single chain, R_G ≃ bN^1/2, depending on the number Z of chains in the droplet. In the case of Z < (N/g_th)^1/2 the size of this droplet is smaller than the Gaussian size of the chain and cross-linking of these chains into the star does not significantly modify their conformations. The situation is qualitatively different for larger number of chains, Z > (N/g_th)^1/2. In this case the size of free chains is ideal and each of them overlaps with (N/g_th)^1/2 chains. Formation of a star with Z > (N/g_th)^1/2 arms forces more chains to overlap and, therefore, leads to their stretching.

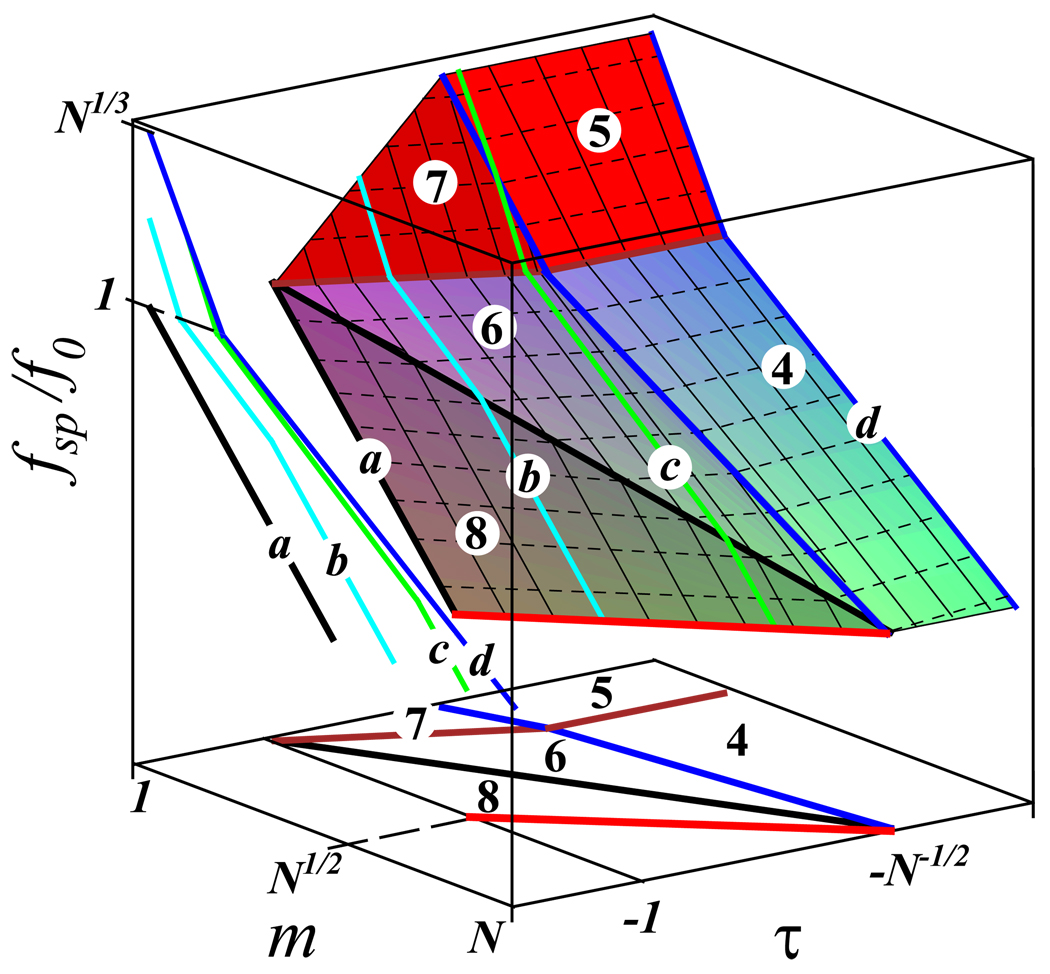
Figure 4 presents the tension in the spacer and the diagram of states for molecular brushes with a different number m of spacer monomers and solvents with various quality below θ temperature (τ < 0). We calculate the tension in the backbone of the molecular brush at conditions corresponding to regimes 4 – 7 of the diagram in this figure, discussed in Refs. [9, 10], as well as for the regime 8, which was not addressed in the literature.

Figure 4.

3d logarithmic plot of the tension in the molecular brush spacer in poor and θ solvents as a function of the number of Kuhn segments, m, in the spacer and the solvent quality τ < 0. The same notations as in Fig. 3. Curves a,b,c,d and their projections on the plane (m,f_sp) present the variation of spacer tension f_sp with m at a different solvent quality τ. Regimes 4 – 8 of the diagram of states (m,τ) are discussed in the text.

Regime 6 (collapsed brush and weakly stretched spacer)

The θ-like behavior of the molecular brush is valid as long as the size of the outer blob ξ ≃ (Rd)^1/2, Eq. 4, is smaller than the size of the thermal blob, b/ |τ|, Eq. 6, where R is the thickness of the molecular brush. The corresponding regimes 4 and 5 of the θ-brush extend in a symmetrical way to the opposite side of the θ-line τ = 0. The boundary of regime 4 on the poor solvent side is obtained from Eq. 22 by replacing τ → −τ:

$$m_{46}\simeq N^{-3}{(-\tau )}^{-8},\tau <0$$ (29)

Arms of the molecular brush are collapsed on the poor solvent side of this boundary (in the regime 6). The polymer volume fraction Φ is determined by the balance of the attractive binary and the repulsive ternary interactions, −k_BTτΦN ≃ k_BTΦ²N, leading to Φ ≃ −τ. [8,12] Conformations of the outer part of the molecular brush in a poor solvent can be represented as the dense packing (melt) of thermal blobs of the size ξ_th, Eq. 6. Although the small inner part of the brush is θ-like, most of its properties are controlled by the outer part with uniform volume fraction Φ ≃ −τ.

The dependence of the polymer brush thickness R on the spacer size d can be found from this volume fraction, Φ ≃ Nb³/ (R²d) ≃ −τ, yielding R² ≃ Nb³/ (−τd). The equilibrium values of the spacer size d_eq and the brush thickness R_eq are determined from the minimum of the free energy per repeating unit, k_BTR²/ (b²N) + k_BTd²/ (b²m) [10]:

$$d_{\mathit{\text{eq}}}\simeq b{m}^{1/3}{(-\tau )}^{-1/3},R_{\mathit{\text{eq}}}\simeq b{N}^{1/2}{m}^{-1/6}{(-\tau )}^{-1/3}.$$ (30)

Since the spacer is Gaussian, the tension in it is f_sp≃ k_BTd_eq/ (b²m), and is given by equation f_sp ≃ f₀m^μ6 (−τ)^t6 (Eq. 21 with i = 6 and ν₆ = 0) with exponents μ₆ = −2/3 and t₆ = −1/3 presented in Table 1. Note that the backbone tension in a poor solvent does not depend on the length of side chains, but only on spacer length and solvent quality.

The case of theta brush, represented by the line d in Fig. 4 for τ < 0, is similar to the line b in Fig. 3 corresponding to θ-brush for τ > 0.

Regime 7 (collapsed brush and fully stretched spacer)

The tension in the spacer f_sp reaches the value f₀ at the boundary between regimes 6 and 7, for the spacer length

$$m_{67}\simeq {(-\tau )}^{-1/2},\tau <0.$$ (31)

The spacer in regime 7 is fully stretched and its tension (Eq. 21) is characterized by the following exponents: μ₇ = −2, t₇ = −1, ν₇ = 0 (Table 1). The crossover for brushes with fully stretched spacers between θ-state (regime 5) and collapsed state (regime 7) can be obtained from Eq. 28 by replacing τ → −τ:

$$m_{57}\simeq N^{-1}{(-\tau )}^{-3},\tau <0.$$ (32)

Regime 8 (collapsed brush and unstretched spacer)

Elastic energy of the spacer decreases with increasing spacer length m, reaching k_BT per spacer at the boundary of the regime 6, where the size of the spacer is equal to the size ξ_th of the thermal blob,

$$m_{68}\simeq {\mathrm{\xi }}_{\mathit{\text{th}}}^2/b^2\simeq {\tau }^{-2},\tau <0.$$ (33)

The θ-like brush conformation in the center of the molecule disappears along this boundary, and the entire molecular brush in this regime can be represented by the uniformly dense packing of thermal blobs.

Along the boundary of regimes 6 and 8, Eq. 33, the thickness R of the brush, Eq. 30, reaches the Gaussian size of side arms, bN^1/2, and retains this value throughout the whole regime 8. Although both the arms and the spacer are almost unstretched in this regime, the entire backbone is still elongated with the stretching energy k_BT distributed over several p > 1 spacers. Thus, the typical conformation of the backbone inside the tension blob of size ξ_t is the random walk of p spacers with mean square end-to-end distance ${\mathrm{\xi }}_t^2\simeq p{b}^{2}m.$ The volume of the molecular brush per contour length ξ_t is ${\mathrm{\xi }}_t{R}_{\mathit{\text{eq}}}^2\simeq {\mathrm{\xi }}_t{b}^{2}N.$ The number of monomers in this volume is equal to the product of the monomer concentration Φ/b³ and the volume of the section of the brush containing p side arms, pN ≃ ξ_tb²N (Φ/b³). This gives the number of arms in a tension blob p ≃ ξ_tb² (Φ/b³), where $P\simeq {\mathrm{\xi }}_t^2/(b^{2}m)$ and Φ ≃ −τ, as derived above. By combining the two equations for p, one obtains the size of the tension blob,

$${\xi }_t\simeq -bm\tau ,\tau <0.$$ (34)

The resulting tension in the backbone, f_sp ≃ k_BT/ξ_t, is given by Eq. 21 with the exponents μ₈ = −1, t₈ = −1, and ν₈ = 0. The tension in the backbone becomes negligible when the size of the tension blob, ξ_t, Eq. 34, reaches the thickness R_eq ≃ bN^1/2 of the brush at the boundary of the regime 8 with the number of monomers in the spacer

$$m_8\simeq N^{1\mathrm{/}2}{(-\tau )}^{-1},\tau <0.$$ (35)

and this boundary is shown by the red lines in Fig. 4. The case of intermediate solvent is represented by two lines b and c in Fig. 4, which pass through regimes 5 – 8. The line a in this figure corresponds to a non-solvent regime (τ = −1) with the tension in the spacer f ≤ f₀. The maximum tension in the non-solvent case f_sp ≈ f₀ is reached for the monomeric spacer m = 1.

Summarizing this section, we conclude that the backbone of molecular brushes experiences tension, f_sp, in solutions, which is determined by the solvent quality, τ, the degrees of polymerization, m, of the spacer, and in good and theta solvents by the degree of polymerization, N, of side chains. High backbone tensions (f_sp > f₀ = k_BT/b) are achieved for relatively short spacers with m < m₄₅ and m < m₆₇ (Eq. 27 and Eq.31). The highest tension f_sp ≃ f₀N^3/8 is developed in densely branched macromolecules (m ≃ 1) in athermal solvent (τ ≃ 1). Decreasing solvent strength (τ < 1) for dense brushes (m ≃ 1) leads to the decrease in the backbone tension (f_sp ≃ f₀N^3/8τ^1/8 in a good solvent, f_sp ≃ f₀N^1/3 in a theta solvent, and f_sp ≃ f₀(−τ)⁻¹ in a poor solvent). Note that loosely grafted brushes (m ≫ 1) in regime 1 exhibit an opposite behavior, i.e. increasing backbone tension with decreasing solvent quality. The maximum tension in a melt (τ ≃ −1) is f_sp ≃ f₀. Although the backbone tension in a solution can be higher than f₀, and even approach the values sufficient to break hydrogen bonds (for the molecular brush with N ≃ 2⁸ and monomeric spacer m ≃ 1 in an athermal solvent, f_sp ≃ f₀N^3/8 ≃ 8f₀ ≃ 30pN), it is still too small to rupture covalent bonds. Below we demonstrate that adsorption of molecular brushes on substrates significantly increases tension in side chains and along the backbone.

3 Macromolecules on a substrate

Here we consider only the case of polymer in a non-solvent environment (τ = −1), which is relevant to a typical experimental system, e.g. polymer chain at solid-air interface. Adsorption of star polymers at solid – good solvent interface was studied by Halperin and Joanny. [14] The strong intramolecular attraction (≃ k_BT per monomer) in a non-solvent environment (e.g., in air) results in dense uniform packing of the monomers in the globular state of a molecule. An attraction to the substrate leads only to the deformation of the macromolecule (changes its shape without perturbing the dense packing of its monomers). The adsorption-induced conformational changes allow increasing the number of monomer-substrate contacts at low entropic costs. The polymer-substrate interaction has both short-term and long-term contributions. The short-range contributions are characterized by two dimensionless parameters - surface tension parameter γ and spreading parameter S, defined as

$$\mathrm{\gamma }={\mathrm{\gamma }}_2{b}^2/(k_{B}T)/$$ (36)

$$S=({\mathrm{\gamma }}_1-{\mathrm{\gamma }}_2-{\mathrm{\gamma }}_{12})b^2/(k_{B}T)$$ (37)

where γ₁, γ₂ and γ₁₂ are respective surface tensions at air-substrate, polymer-air, and polymer-substrate boundaries. Even though the adsorption from non-solvent results in lower tensions compared to adsorption from solution, we show that the tension enhancement due to interaction with the substrate is significant and may lead to a backbone tension on the order of several nanoNewtons. This is sufficient to break covalent bonds as observed experimentally [7].

3.1 An isolated linear polymer on substrate in a nonsolvent

A linear polymer containing N monomers (an isolated chain) spreads on a substrate with S ≥ 0 and adopts a pancake conformation if spreading parameter S is large. This unimolecular pancake has thickness h and radius

$$R\simeq {(N{b}^3/h)}^{1\mathrm{/}2}$$ (38)

where Nb³ is the volume of this polymer in a non-solvent. In general, bottom and top surfaces of the pancake would have different radii, R and R − δ, see Fig. 5. The shape of the pancake can be approximated by the truncated cone with the surface energy consisting of two contributions, the spreading energy

$$F_{\mathit{\text{surface}}}^{\mathit{\text{spread}}}=-k_{B}TS\mathrm{\pi }{R}^2/b^2,$$ (39)

and the excess of the surface energy due to the edge contributions

$$F_{\mathit{\text{surface}}}^{\mathit{\text{edge}}}=k_{B}T\mathrm{\pi }\mathrm{\gamma }(2R-\delta )\left(\sqrt{{\delta }^2+h^2}-\delta \right)/b^2$$ (40)

$$\approx k_{B}T\mathrm{\pi }\mathrm{\gamma }R{h}^2/(\delta b^2),h\ll \delta \ll R.$$ (41)

Figure 5.

The shape of a linear polymer absorbed on a substrate in three regimes: regime 1 at S₁₂ < S < A, regime 2 at 0 < S < S₁₂, and regime 3 at S > A.

The van der Waals energy has the simplest form for the cylindrical shape of the pancake with δ = 0, $F_{\upsilon dW}^{\prime }=k_{B}TA\prime \mathrm{\pi }{R}^2/h^2$, where A′= H/(k_BT) is the effective dimensionless Hamaker constant with traditional dimensional Hamaker constant H. [15] In addition, there is a correlation contribution due to packing of the macromolecule with uniform density into a slit of thickness h, which has the same functional form. [16] The sum of both contributions can be combined into the effective van der Waals part of the free energy

$$F_{\upsilon dW}=k_{B}TA\mathrm{\pi }{R}^2/h^2$$ (42)

Following Refs. [17,18] we assume, that the effective Hamaker constant A and the spreading parameter S are independent variables and are both positive, A > 0 and S > 0. If the shape of the pancake is not a perfect cylinder with δ > 0, the effective van der Waals free energy has an additional contribution

$$F_{\upsilon dW}^{\mathit{\text{edge}}}=C{k}_{B}TA\mathrm{\pi }R\delta /h^2$$ (43)

The coefficient C depends on the shape of the pancake. A more accurate analysis in [17] predicts a parabolic shape of the edge up to monomeric distances from the substrate, which leads to a weak logarithmic dependence of the constant C on the thickness h. Below we discuss the essential details of the different conformational regimes that are depicted in Figure 5.

Regime 1 (rectangular cross-section)

In the case of small deviations from the cylindrical shape, δ ≪ R, the radius of the pancake can be determined from the balance of the spreading energy, Eq. 39, and the van der Waals free energy, Eq. 42. Using the relation between the radius R and the height h, Eq. 38, we obtain the equilibrium height

$$h_{\mathit{\text{eq}}}\simeq b{(A/S)}^{1/2}$$ (44)

and the equilibrium radius

$$R_{\mathit{\text{eq}}}\simeq b{N}^{1/2}{(S/A)}^{1/4}.$$ (45)

of a pancake globule formed by a linear polymer (see Fig. 5). Minimizing the δ-dependent corrections, Eq. 40 and Eq. 43, to the free energy in the case h ≪ δ ≪ R, we find the equilibrium width of the truncated edge of the pancake

$${\delta }_{\mathit{\text{eq}}}\simeq (h_{\mathit{\text{eq}}}^2/b){(\mathrm{\gamma }/A)}^{1/2}\simeq (b/S){(A\mathrm{\gamma })}^{1/2}.$$ (46)

A decrease of the spreading parameter S leads to simultaneous increase in h_eq and δ_eq, and the decrease in R_eq. This change of the shape continues until the molecule transforms from a pancake to a tent-like shape at δ ≃ R. By equating R_eq, Eq. 45, and δ_eq from Eq. 46, we find the value of the spreading parameter at the cross-over,

$$S_{12}\simeq N^{-2/5}{A}^{3/5}{\gamma }^{2/5}.$$ (47)

At this value of the spreading parameter all four terms of the free energy (spreading term, Eq. 39, surface term, Eq. 40, and two parts of the Hamaker free energy, Eq. 42 and Eq. 43) are on the same order of magnitude.

Regime 2 (tent-like cross-section)

For the spreading parameter lower than the cross-over value S₁₂, (Eq. 47), the shape of the molecule remains tent-like, and is determined by the balance of the surface free energy, k_BTγh²/b², which tends to atten the molecule, and the van der Waals term, Eq. 42, which prefers to thicken the molecule. The resulting tent-like shape of the molecule in regime 2, see Fig. 5, is characterized by the height

$$h_{\mathit{\text{eq}}}\simeq b{(AN/\mathrm{\gamma })}^{1/5},S<S_{12}$$ (48)

and by the radius of the base

$$R_{\mathit{\text{eq}}}\simeq b{N}^{2/5}{(\mathrm{\gamma }/A)}^{1/10},S<S_{12}.$$ (49)

The linear in asymmetry h/R decrease of $F_{\mathit{\text{surface}}}^{\mathit{\text{edge}}}$ (Eq. 41) at fixed cross-sectional area hR can be captured at the scaling level by a triangular asymmetric (h_eq/R_eq < 1) cross-section.

Regime 3 (monolayer)

The upper boundary of the regime 1 corresponds to the pancake thickness h₁₃ ≃ b at the value of the spreading parameter (see Eq. 44)

$$S_{13}=A.$$ (50)

At higher values of the spreading parameter, S > S₁₃, the thickness of the pancake saturates at the monomer size, h₃ ≃ b. The lateral size of the pancake in this regime is R₃ ≃ bN^1/2.

3.2 Molecular brush on a substrate in a non-solvent

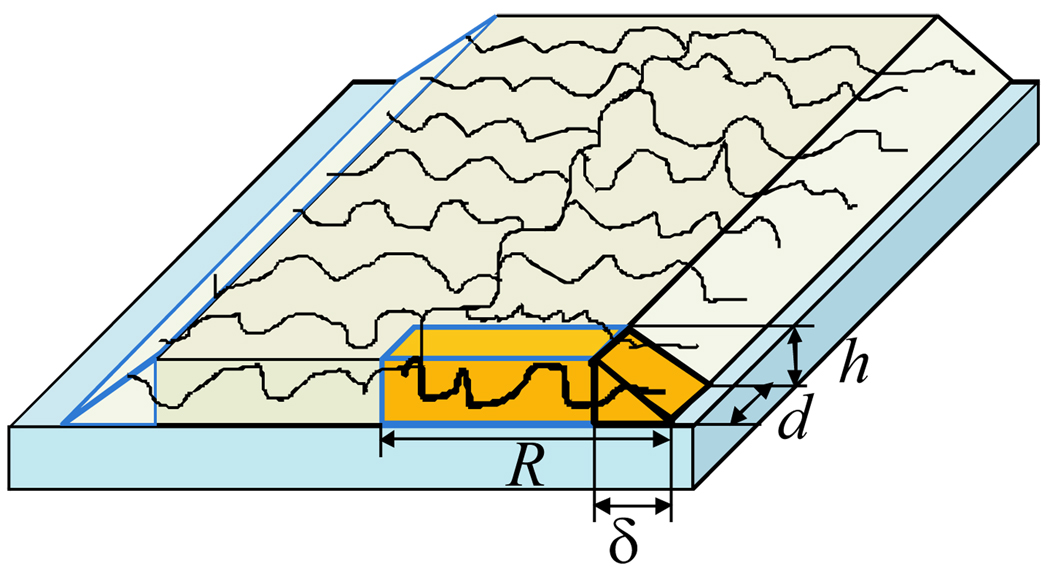
When side chains are tethered to the backbone of the molecular brush with the distance between adjacent grafts d < R_eq, they overlap, and the overall shape of the adsorbed molecular brush transforms from a pancake into a ribbon (Fig. 6). On a strongly adsorbing substrate, the thickness h of the molecule is still governed by the balance of the spreading and the long-range van der Waals interactions (h ≈ h_eq, Eq. 44). Due to dense grafting, side chains stretch in the direction normal to the backbone. The tension of side chains is focused onto the backbone at its ends and transmitted through the middle part of the backbone (see Fig. 2). The molecular backbone also stretches to optimize the overall elastic response of the macromolecule to the deformation.

Figure 6.

Adsorbed molecular brush under non-solvent conditions adopts a ribbon-like confirmation. Volume per side chain with length R, depth d, and height h is marked by darker shading. The width of the edge is δ.

The interplay of spreading, elastic, and van der Waals forces gives rise to a variety of molecular brush conformations with different cross-sections of the molecule. In some cases, brushes may even demonstrare spontaneous curvature of the backbone due to uneven distribution of adsorbed side chains with respect to the backbone [19]. In this paper, we consider only symmetric (50/50) distribution leading to locally straight backbone. To determine optimal conformations of the molecular brush, we consider the free energy F_rep per its repeating unit which includes the backbone spacer and the side chain. F_rep comprises the elastic free energy of the backbone spacer between neighboring attachment points to the side chains, F_sp, and the free energy of a side chain, F_sc, (Eq. 1) consisting of elastic, F_elastic, and interaction, F_interact, contributions:

$$F_{\mathit{\text{rep}}}=F_{\mathit{\text{sp}}}+F_{\mathit{\text{sc}}}=F_{\mathit{\text{sp}}}+F_{\mathit{\text{elastic}}}+F_{\mathit{\text{interact}}}.$$ (51)

The elastic part of the side chain free energy is

$$F_{\mathit{\text{elastic}}}\simeq k_{B}T{R}^2/(b^{2}N)\simeq k_{B}TN{b}^4/(d^2{h}^2),$$ (52)

where the width of the absorbed brush

$$R\simeq N{b}^3/(dh)$$ (53)

is found from the constant monomer number density condition, using d as the distance between side chains and h as its height (Fig. 6). The contributions to the free energy due to interactions with the substrate introduced in Eq. 39 – Eq. 43 above are reformulated for the ribbon-like shape of the adsorbed molecular brush as

$$F_{\mathit{\text{surface}}}^{\mathit{\text{spread}}}\simeq -k_{B}TSRd/b^2,$$ (54)

$$F_{\mathit{\text{surface}}}^{\mathit{\text{edge}}}\simeq k_{B}T\mathrm{\gamma }d{h}^2/(\delta b^2),$$ (55)

$$F_{\upsilon dW}\simeq k_{B}TARd/h^2,$$ (56)

$$F_{\upsilon dW}^{\mathit{\text{edge}}}\simeq k_{B}TAd\delta /h^2,$$ (57)

where δ is the edge width (h ≪ δ ≪ R). The total free energy of a side chain in an adsorbed molecular brush is

$$F_{\mathit{\text{sc}}}=F_{\mathit{\text{elastic}}}+F_{\mathit{\text{interact}}}=F_{\mathit{\text{elastic}}}+F_{\mathit{\text{surface}}}^{\mathit{\text{spread}}}+F_{\mathit{\text{surface}}}^{\mathit{\text{edge}}}+F_{\upsilon dW}+F_{\upsilon dW}^{\mathit{\text{edge}}},$$ (58)

Note that the interaction energy, F_interact, of densely grafted molecular brushes (N ≫ m) with the substrate is dominated by their side chains. Therefore, we include F_interact as a part of the free energy of side chains F_sc (Eq. 58). The average tension in a side chain of a molecular brush adsorbed from a non-solvent is f_sc ≃ k_BTR_eq/ (b²N) (if R_eq ≪ bN), while the backbone spacer tension, f_sp, is given by Eq. 2.

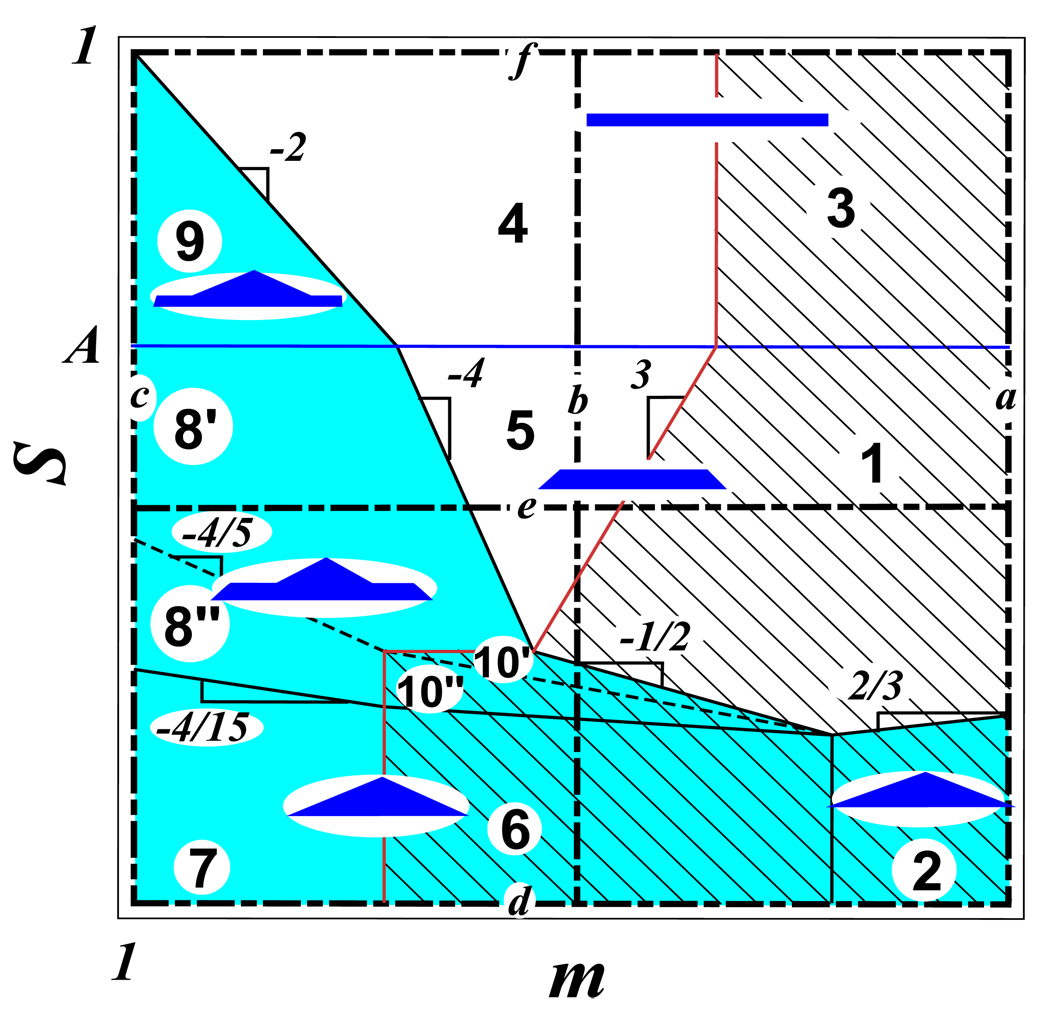
Depending on values of the spreading parameter S and spacer degree of polymerization m, one finds different conformations of the adsorbed molecular brush depicted in the diagram in figure 7.

Figure 7.

Diagram of states of adsorbed molecular brushes with schematically shown cross-sections. Regions with tent-like cap are shaded by a solid color, while regions with weakly stretched spacer, f_sp < f₀, are shaded by inclined parallel lines.

Regime 1 (rectangular cross-section, weakly stretched spacer)

At large values of the spreading parameter S, the molecular brush spreads on a substrate to gain maximum number of polymer-surface contacts. If the distance d between attachment points is relatively large, the entropy loss due to side chain stretching is small compared to the spreading gain, $F_{\mathit{\text{elastic}}}\ll F_{\mathit{\text{surface}}}^{\mathit{\text{spread}}}.$ Here, the equilibrium thickness of the ribbon h_eq, Eq. 44, is dictated by the balance of the same interactions as for a pancake formed by an isolated linear chain (the spreading and the van der Waals parts of the free energy, Eq. 54 and Eq. 56).

Note, that both spreading and van der Waals terms of the free energy depend only on the area Rd of the repeating unit foot-print at the surface, which is reciprocally proportional to the height h of the molecule (see Eq. 53). In order to find the width R and the distance between attachment points d separately, we have to balance the elastic free energies of the side chain F_elastic and of the spacer F_sp that are much smaller than the spreading, and the van der Waals parts of the free energy.

A cross-section of the absorbed molecular brush has the rectangular shape with the width

$$R_{\mathit{\text{eq}}}\simeq N{b}^3/(d_{\mathit{\text{eq}}}{h}_{\mathit{\text{eq}}})\simeq (N{b}^2/d_{\mathit{\text{eq}}}){(S/A)}^{1/2}.$$ (59)

where h_eq is given by Eq. 44. Substituting this expression for the width of the ribbon into the elastic part of the side chain free energy, Eq. 52, and differentiating it with respect to the distance d between neighboring attachment points along the backbone, Eq. 2, we obtain the tension in the spacer

$$f_{\mathit{\text{sp}}}\simeq f_{0}NS{b}^3/(A{d}_{\mathit{\text{eq}}}^3).$$ (60)

The size d_eq of the weakly stretched spacer is obtained using the equation of tension in Gaussian chains

$$k_{B}T{d}_{\mathit{\text{eq}}}/(b^{2}m)\simeq f_{\mathit{\text{sp}}}(\text{weakly}\text{stretched}\text{spacer}).$$ (61)

Thus we find the equilibrium distance between neighboring attachment points (equilibrium size of a spacer)

$$d_{\mathit{\text{eq}}}\simeq b{(mNS/A)}^{1/4}$$ (62)

The tension in the spacer in this regime is obtained by substituting d_eq from Eq. 62 into Eq. 61:

$$f_{\mathit{\text{sp}}}\simeq f_0{m}^{{\mu }_i^f}{N}^{{\mathrm{\nu }}_i^f}{S}^{{\zeta }_i^f}{A}^{{\alpha }_i^f}{\gamma }^{g_i^f}$$ (63)

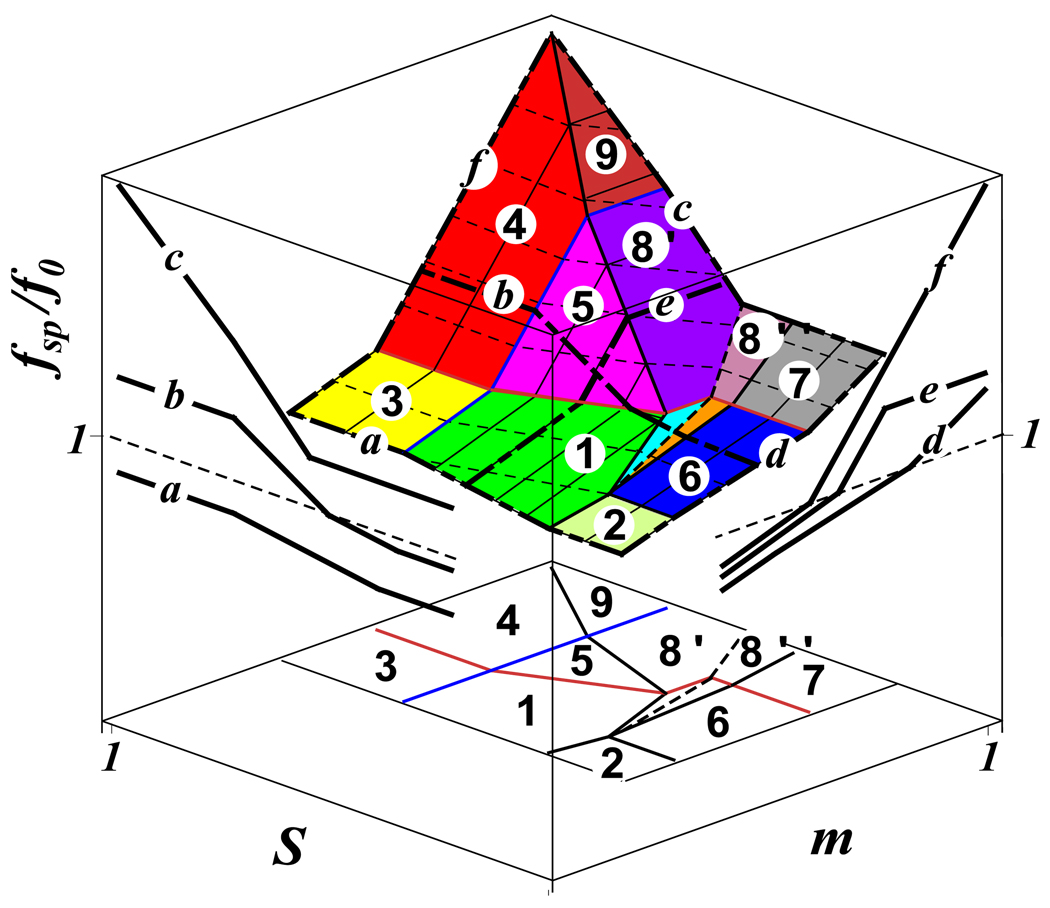
with exponents ${\mu }_1^f=-3/4,{\nu }_1^f=1/4,{\zeta }_1^f=1/4,{\alpha }_1^f=-1/4,g_1^f=0.$ Fig. 8 presents the dependence of backbone tension, f_sc, on spreading parameter S and spacer degree of polymerization m for all predicted regimes with the corresponding exponents listed in Table 2.

Figure 8.

3d logarithmic plot of the tension f_sp in the backbone of an adsorbed brush under non-solvent condition. Left projection on the (S, f_sp) plane presents the variation of the tension f_sp with the spreading parameter S for three different spacer lengths, m_c < m_b < m_a (see vertical lines a − c in the diagram in Fig. 7). Right projection on the (m, f_sp) plane presents the variation of the tension f_sp with the spacer length m for three different spreading parameters S_d < S_e < S_f (see horizontal lines d − f in the diagram in Fig. 7). Projection on the (m,S) plane represents the diagram of states shown in Fig. 7.

Table 2.

Exponents of the Expression for the Backbone Tension $f_{\mathit{\text{sp}}}\simeq f_0{m}^{{\mu }_i^f}{N}^{{\nu }_i^f}{S}^{{\zeta }_i^f}{A}^{{\alpha }_i^f}{\mathrm{\gamma }}^{g_i^f}$for Adsorbed Molecular Brush in Regime i

i	1	2	3	4	5	6	7,8″	8′	9
${\mu }_i^f$	−3/4	−7/10	−3/4	−3	−3	−7/12	−7/5	0	0
${\nu }_i^f$	1/4	1/10	1/4	1	1	1/12	1/5	1	1
${\zeta }_i^f$	1/4	0	0	0	1	0	0	7/4	3/2
${\alpha }_i^f$	−1/4	−1/10	0	0	−1	0	0	−1/4	0
$g_i^f$	0	1/10	0	0	0	1/6	2/5	0	0

Substituting d_eq from Eq. 62 into Eq. 59 we obtain the width of the brush

$$R_{\mathit{\text{eq}}}\approx b{m}^{{\mu }_i^R}{N}^{{\mathrm{\nu }}_i^R}{S}^{{\zeta }_i^R}{A}^{{\alpha }_i^R}{\gamma }^{g_i^R}$$ (64)

with exponents ${\mu }_1^R=-1/4,{\nu }_1^R=3/4,{\zeta }_1^R=1/4,{\alpha }_1^R=-1/4,g_1^R=0$ presented in Table 3 for all regimes i.

Table 3.

Exponents of the Expression for the Width $R_{\mathit{\text{eq}}}\approx b{m}^{{\mu }_i^R}{N}^{{\nu }_i^R}{S}^{{\zeta }_i^R}{A}^{{\alpha }_i^R}{\gamma }^{g_i^R}$ of Adsorbed Molecular Brush in Regime i (1^st and 2^nd refer to lower and upper layers in regimes 8 and 9 with two-layer adsorbed brushes)

i layer	1	2	3	4	5	6	81st	7,82nd,92nd	91st
${\mu }_i^R$	−1/4	−1/5	−1/4	−1	−1	−1/12	0	−1/5	0
${\nu }_i^R$	3/4	3/5	3/4	1	1	7/12	1	3/5	1
${\zeta }_i^R$	1/4	0	0	0	1/2	0	3/4	0	1/2
${\alpha }_i^R$	−1/4	−1/10	0	0	−1/2	0	−1/4	0	0
$g_i^R$	0	1/10	0	0	0	1/6	0	1/5	0

Regime 2 (van der Waals-controlled tent-like cross-section, weakly stretched spacer)

At low values of the spreading parameter S,

$$S<S_{12}\simeq m^{1/5}{N}^{-3/5}{A}^{3/5}{\mathrm{\gamma }}^{2/5},$$ (65)

the spreading part of the free energy, $F_{\mathit{\text{surface}}}^{\mathit{\text{spread}}}$ (Eq. 54), becomes smaller than the edge contribution $F_{\mathit{\text{surface}}}^{\mathit{\text{edge}}}$ (Eq. 55), and the the cross-section becomes tent-like, similar to the case of adsorbed linear chain. [20] The dependencies of the width R and height h of the tent-like cross-section on the distance d between side chains are determined by the balance of the edge contribution to the surface free energy $\mathrm{\Delta }{F}_{\mathit{\text{surface}}}^{\mathit{\text{edge}}}$, Eq. 55, and the edge contribution to the van der Waals energy, Eq. 57 with δ ≃ R. Following the procedure similar to the one described for regime 1, by substituting the expression for the width of the cross-section R into the elastic free energy of a side chain, Eq. 52, and differentiating with respect to distance d we get the dependence of spacer tension on the distance d between neighboring attachment points

$$f_{\mathit{\text{sp}}}\simeq f_0{(\mathrm{\gamma }N/A)}^{1/3}{(b/d)}^{7/3}.$$ (66)

Using Eq. 61 for Gaussian elasticity of the spacer, we obtain the equilibrium distance between attachment points d_eq ≃ b (γN/A)^1/10 m^3/10 and equilibrium width of the cross-section R_eq, given by Eq. 64 with exponents ${\mu }_2^R=-1/5,{\nu }_2^R=3/5,{\zeta }_2^R=0,{\alpha }_2^R=1/10,g_2^R=1/10.$ The height of the brush has similar scaling

$$h_{\mathit{\text{eq}}}\simeq b{m}^{{\mu }_i^h}{N}^{{\nu }_i^h}{S}^{{\zeta }_i^h}{A}^{{\alpha }_i^h}{\mathrm{\gamma }}^{g_i^h}$$ (67)

with exponents ${\mu }_2^h=-1/10,{\nu }_2^h=3/10,{\zeta }_2^h=0,{\alpha }_2^h=1/5,g_2^h=-1/5$ given for all regimes i in Table 4.

Table 4.

Exponents of the Expression for the Height $h_{\mathit{\text{eq}}}\simeq b{m}^{{\mu }_i^h}{N}^{{\nu }_i^h}{S}^{{\zeta }_i^h}{A}^{{\alpha }_i^h}{\mathrm{\gamma }}^{g_i^h}$ of Adsorbed Molecular Brush in Regime i (1^st and 2^nd refer to layers for regimes 8 and 9 with two-layer adsorbed brushes)

i layer	1	2	3,4,91st	5,81st	6	7,82nd,92nd
${\mu }_i^h$	0	−1/10	0	0	−1/3	−4/5
${\nu }_i^h$	0	3/10	0	0	1/3	2/5
${\zeta }_i^h$	−1/2	0	0	−1/2	0	0
${\alpha }_i^h$	1/2	1/5	0	1/2	0	0
$g_i^h$	0	−1/5	0	0	−1/3	−1/5

The asymmetry R/h of the tent decreases with the spacer degree of polymerization m, and increases with the side chain degree of polymerization N,

$$R_{\mathit{\text{eq}}}/h_{\mathit{\text{eq}}}\simeq {(\mathrm{\gamma }N/A)}^{3/10}{m}^{-1/10}.$$ (68)

In this regime the spacer is weakly stretched with the tension given by Eq. 63 with exponents ${\mu }_2^f=-7/10,{\nu }_2^f=1/10,{\zeta }_2^f=0,{\alpha }_2^f=-1/10,g_2^f=1/10$, see Fig. 8 and Table 2.

Regime 3 (monolayer, weakly stretched spacer)

At the highest spreading parameter S > S₁₃ = A, (see Eq. 50), the height of the molecule saturates at the monomer size, h_eq ≈ b. Properties of the absorbed molecular brush are determined by the balance of Gaussian elasticity of the backbone, Eq. 17, and the side chain, F_elastic ≃ kBTNb²/d², see Eq. 52, with distance between neighboring attachment points d ≃ b (Nm)^1/4. Other results are listed in Table 2–Table 4 and plotted in Fig. 8.

Regime 4 (monolayer, strongly stretched spacer)

Tension in the spacer increases with decreasing m, and the spacer becomes fully stretched at tension f_sp ≈ f₀, Eq. 3, at the number of monomers in the spacer

$$m=m_{34}\simeq N^{1/3}\text{for}S>A.$$ (69)

The distance between attachment points for the molecular brush with strongly stretched spacer is

$$d_{\mathit{\text{eq}}}\simeq bm,(\text{strongly stretched spacer})$$ (70)

In this regime the width of the molecule is fixed at the value R ≈ bN/m and the free energy per repeating unit of the brush consists of elastic and spreading contributions

$$F_{\mathit{\text{rep}}}\simeq k_{B}T{b}^{2}N/d^2-k_{B}TSN.$$ (71)

The spreading contribution does not depend on the distance d between attachment points and, therefore, does not contribute to the tension in the spacer, Eq. 2. Corresponding exponents for this regime are given in Table 2, Table 3 and Table 4. Note that none of the properties (Table 2–Table 4) in regimes 3 and 4 (monolayer conformation of the brush) depend on substrate interaction parameters.

Regime 5 (rectangular cross-section, strongly stretched spacer)

As the spreading parameter S decreases below the cross-over value

$$S_{45}\simeq A,$$ (72)

the thickness of the brush h becomes larger than the monomer size b. This regime is analogous to regime 1, with properties of the absorbed molecular brush determined by the balance of the spreading (Eq. 54) and van der Waals (Eq. 56) parts of the free energy. The height of the absorbed molecule in this regime 5, h_eq ≃ b (A/S)^1/2, depends only on the spreading parameter S and the Hamaker constant A, as in regime 1, see Eq. 44. The main difference between regimes 1 and 5 is that in regime 5 the spacer is almost fully stretched d ≃ bm (Eq. 70). The width R of the molecular brush increases with decreasing the number of monomers in the spacer in this regime 5 as

$$R\simeq \frac{bN}{m}\sqrt{\frac{S}{A}.}$$ (73)

The corresponding exponents characterizing spacer tension f_sp, brush width R, and height h_eq are presented in Table 2–Table 4. Note that in order to calculate the tension in the spacer, f_sp, one needs to keep the dependence of the elastic free energy of side chains on the distance d between side chain attachment points (Eq. 52) F_elastic ≃ Nb²S/ (Ad²) and differentiate it with respect to d to obtain the spacer tension f_sp ≃ f₀Nb³S/ (Ad³) before substituting the value of the spacing between attachment points d ≃ bm. The tension in the spacer f_sp ≃ f₀NS/ (Am³) decreases upon increasing the number of monomers m in the spacer, and reaches the cross-over value f₀ at the boundary between regimes 1 and 5:

$$S_{15}\simeq A{m}^3{N}^{-1}.$$ (74)

Regime 6 (stretching controlled tent-like cross-section, weakly stretched spacer)

Decreasing the length of the spacer in the tent-like conformation of the brush in regime 2 leads to the increase of the tension in the arms. The stretching part of the free energy increases and becomes on the order of van der Waals energy at the boundary between regimes 2 and 6 for the spacer length

$$m_{26}\simeq A^{-6/7}{\mathrm{\gamma }}^{-4/7}{N}^{1/7}.$$ (75)

Properties of molecular brushes with shorter spacers (m < m₂₆) are determined by the balance of stretching, F_elastic, Eq. 52, and surface, $F_{\mathit{\text{surface}}}^{\mathit{\text{edge}}}$, (Eq. 55 with δ ≃ R) free energies, resulting in an optimal free energy

$$F_{\mathit{\text{surface}}}^{\mathit{\text{edge}}}\approx F_{\mathit{\text{elastic}}}\simeq k_{B}T{N}^{1/5}{(\mathrm{\gamma }b/d)}^{2/5}$$ (76)

and backbone tension f_sp, brush width R_eq; and height h_eq given in Table 2–Table 4 (see Fig. 8 for the plot of tension f_sp). The aspect ratio of the tent-like cap in this regime increases with the number of monomers in both spacer and side chain,

$$R_{\mathit{\text{eq}}}/h_{\mathit{\text{eq}}}\simeq m^{1/4}{N}^{1/4}{\mathrm{\gamma }}^{1/2}.$$ (77)

Regime 7 (weakly adsorbing substrate, stretching controlled tent-like cross-section, strongly stretched spacer)

Spacers with small numbers of monomers

$$m<m_{67}\simeq {\mathrm{\gamma }}^{2/7}{N}^{1/7}$$ (78)

are fully stretched with spacer sizes d ≈ bm, Eq. 70. Properties of such molecular brushes are determined by the balance of the elastic energy of the side chain F_elastic, Eq. 52, and the surface free energy $F_{\mathit{\text{surface}}}^{\mathit{\text{edge}}}$, Eq. 55 with δ ≃ R, similar to regime 6 (see Table 2–Table 4). The main difference between regimes 6 and 7 is that spacers are fully stretched in regime 7.

The asymmetry R/h of the tent cross-section in this regime is

$$R_{\mathit{\text{eq}}}/h_{\mathit{\text{eq}}}\simeq m^{3/5}{\mathrm{\gamma }}^{2/5}{N}^{1/5}.$$ (79)

The aspect ratio R_eq/h_eq of the tent-like cap in regimes 6, 7, and also in regimes 8 and 9 discussed below, increases with m, while in regime 2 (determined by the balance of van der Waals and surface energies) this aspect ratio decreases with m (Eq. 68).

Note, that the brush properties in tent-like regimes 2, 6 and 7 do not depend on the spreading parameter S because the corresponding spreading free energy $F_{\mathit{\text{surface}}}^{\mathit{\text{spread}}}$, Eq. 54, is smaller than the surface energy $F_{\mathit{\text{surface}}}^{\mathit{\text{edge}}}$, Eq. 55 with δ ≃ R.

Regime 8 (two phases, strongly stretched spacer)

An unexpected prediction of our theory is that the cross-over between the tent-like conformation for small spreading parameter S (regime 7) and the rectangular cross-section for large spreading parameter S (regime 5) occurs over a wide two-phase regime 8. In this regime, the cross-section of the brush consists of two coexisting layers: (i) a lower layer with the rectangular shape of width R₁ and height h₁ and (ii) the tent-like upper layer with width R₂ < R₁ and height h₂ < R₂ (Fig. 1b). Side chains spontaneously partition between these two layers with the ratio of the number of chains in these layers determined by the equality of chemical potentials of side chains in both layers.

Note that the elastic part of the free energy, F_elastic (Eq. 52) in regime 5 is smaller than either spreading (Eq. 54) or van der Waals (Eq. 56) parts of the free energy at large values of the spreading parameter S, but F_elastic increases with decreasing the number of monomers m in the spacer due to increasing elongation of side chains. These three parts of the free energy become comparable at the boundary between regimes 5 and 8:

$$F_{\mathit{\text{elastic}}}\simeq F_{\mathit{\text{surface}}}^{\mathit{\text{spread}}}\simeq F_{\upsilon dW}.$$ (80)

This cross-over takes place for the spreading parameter

$$S_{58}\simeq A^{-1}{m}^{-4}.$$ (81)

Further decreases in the number of spacer monomers m results in a significant decrease of entropy due to the extension of side chains. For spacers with

$$m<m_{58}\simeq {(AS)}^{-1/4},$$ (82)

additional side chains would also like to reach the substrate, but the resulting decrease of the free energy due to the additional contacts with the substrate would be smaller than the free energy increase due to chain extension. To minimize the total free energy, the adsorbed macromolecule changes its conformation through re-partitioning of the side chains. A fraction of side chains are forced to leave the surface and form the second layer on the top of the first layer. Thus, at lower values of the spreading parameter S < S₅₈, Eq. 81, or at shorter spacers (Eq. 82), the second layer (cap) of side chains emerges. The molecules of the second layer are much less stretched, but also do not gain any spreading energy, and their size is determined by the balance of stretching and surface free energies. Side chains remaining in the first layer stay at the marginal conditions of approximate equality of three parts of the free energy, Eq. 80. This condition corresponds to equality of chemical potentials between the two layers.

The effective spreading parameter for this second layer of chains is zero S_cap = 0, because this cap is in contact with the same polymer material, γ₁₂ = 0, γ₁ = γ₂. A cross-section of the molecular brush in regime 8 is an elongated rectangle of length R₁ and height h₁ (first layer) decorated by the tent-like cap of length R₂ and height h₂ (second layer), see Fig. 1b. Properties of the bottom layer (width R₁ and height h₁) can be found from the properties of the adsorbed molecular brush in regime 5 by replacing the number of monomers m in the spacer by the number of monomers m₁ in the section of the backbone between two adjacent side chains belonging to this bottom layer,

$$m_1\simeq {(AS)}^{-1/4},$$ (83)

(see columns 8_1st in Table 3 and Table 4). The width R₂ and height h₂ of the second layer (tent-like cap) in regime 8 have the same scaling behavior as the width R and height h in regime 7, see columns 8_2nd in Table 3 and Table 4. Along the boundary between regimes 7 and 8,

$$S_{78}\simeq m^{-4/15}{N}^{-8/15}{\mathrm{\gamma }}^{4/15}{A}^{1/3},$$ (84)

the width of both layers become comparable, R₂ ≃ R₁, and the overall cross-section of adsorbed macromolecule becomes tent-like.

Note that both top and bottom layers contribute to the tension of the backbone. The bottom layer dominates in Regime 8’, with equilibrium free energy per side chain F_sc(d) ≃ −k_BTdNA^−1/4S^7/4/b. The corresponding tension in the backbone spacer f_sp = −[∂F_sc(d)/∂d]_h=heq is

$$f_{\mathit{\text{sp}}}\simeq f_{0}N{S}^{7/4}/A^{1/4}.$$ (85)

The contributions of both layers to the backbone tension become comparable along the dotted line in regime 8 (Fig. 7)

$$S_8\simeq b^{4/5}{d}^{-4/5}{\mathrm{\gamma }}^{8/35}{A}^{1/7}{N}^{-16/35}$$ (86)

$$\simeq m^{-4/5}{\mathrm{\gamma }}^{8/35}{A}^{1/7}{N}^{-16/35}.$$ (87)

At lower values of the spreading parameter, S < S₈, (regime 8”), the contribution of the upper layer to the backbone tension f_sp dominates, and the backbone tension approaches an independent of S value (similar to regime 7), given by Eq. 63 with exponents, listed in Table 2 in column 8”.

Regimes 8’ and 8” are slightly modified just above regime 6 in Fig. 7 (see the shaded section of regime 8). This section of the diagram is designated as regimes 10’ and 10”, respectively. Here, the spacer is not fully stretched (d < bm), and the tension in the backbone is given by Eq. 61. Above the dotted line

$$S_{10}\simeq A^{1/7}{\mathrm{\gamma }}^{2/21}{N}^{-11/21}{m}^{-1/3}$$ (88)

the tension and all other parameters of the cross-section are the same as in regime 8’ except for the spacer size d which is given here by

$$d_{\mathit{\text{eq}}}\simeq bmN{S}^{7/4}/A^{1/4}.$$ (89)

Below dotted line S₁₀ the parameters of the cross-section are the same as in regime 6.

Regime 9 (strongly adsorbing substrate, densely grafted brush, monolayer with cap, strongly stretched spacer)

This regime is relevant to experiments on adsorption of dense brushes (m ≃ 1) to strongly attractive substrates (S ≃ 1) [7]. At high values of the spreading parameter,

$$S>S_{89}\simeq A,$$ (90)

the thickness of the lower layer saturates at the monomer size h₁ ≃ b. The fraction of side chains in the first layer m/m₁ is controlled by the balance of spreading energy gain −k_BTSR₁d₁/b² (Eq. 54) and the elastic part of the free energy $k_{B}TN{b}^2/d_1^2$ (Eq. 52 with h₁ = b). The width of the first layer is obtained from the condition for the total number of monomers per side chain in the first layer, R₁ ≃ Nb²/d₁ (see Eq. 53 with h₁ ≃ b), where d₁ ≃ bm₁ is the distance between attachment points of side chains in the first layer. The free energy of the first layer per its repeating unit is

$$F_{\mathit{\text{rep}}}^1\simeq k_{B}TN/m_1^2-k_{B}TSN.$$ (91)

(see also Eq. 71 with m replaced by m₁). The equilibrium value of the number of backbone monomers between attachment points of side chains in the first layer

$$m_1\simeq S^{-1/2}$$ (92)

is determined by the condition $F_{\mathit{\text{rep}}}^1\simeq 0.$ This gives the fraction of adsorbed side chains m/m₁ ≃ mS^1/2. Therefore, increasing S leads to the corresponding increase of the number of side chains in the first layer along with its equilibrium width as

$$R_1\simeq bN/m_1\simeq bN{S}^{1/2}.$$ (93)

The dimensions of the second layer have the same dependence on parameters N,γ,m as in regime 8’. The number of chains in the cap decreases with increasing the spreading parameter S and the number of monomers in the spacer m, and the cap disappears at the boundary between regimes 9 and 4,

$$S_{49}\simeq m^{-2}.$$ (94)

The tension in the backbone is dominated by the first layer and is given by

$$f_{\mathit{\text{sp}}}\simeq {(\partial F_{\mathit{\text{rep}}}^1/\partial m_1)}_{m_1=S^{-1/2}}\simeq f_{0}N{S}^{3/2}.$$ (95)

Thus backbone tension in regime 9 is the highest of all regimes for an adsorbed molecular brush in a non-solvent. Note stronger than linear dependence of the backbone tension, f_sp, on the spreading parameter, S. It is due in part to the increase in the number of side chains in the first layer with increasing S (Eq. 92). This increase in the number of side chains results in the increase of the width, R₁, of the first layer with the spreading parameter S (Eq. 93), which leads to additional increase of the force (f_sp ~ R₁S) applied to the backbone. As the spreading parameter increases further, the width of the first layer of an adsorbed molecular brush with very short spacers (m ≃ 1) levels off at the length of almost fully stretched side chains R₁ ≃ bN. This condition corresponds to the upper boundary of our scaling analysis. At higher spreading parameters, we expect tension to grow linearly with both S and N.

Summarizing section 3: we have described three adsorption regimes for a linear chain at a substrate in a non-solvent (Fig. 5): (i) monolayer (regime 3) for high values of the spreading parameter; (ii) regime 2 with tent-like cross-section for a low spreading parameter; and (iii) regime 1 with rectangular cross-section for an intermediate spreading parameter. We found the same three regimes for adsorption of a loose molecular brush with long spacers between attachments of side chains.

(i) At a high spreading parameter (S > A) the conformation of an adsorbed brush is a monolayer with weakly stretched backbone (regime 3) or strongly stretched backbone for relatively shorter spacers (regime 4). Both regimes 3 and 4 are characterized by the monomeric height of the adsorbed molecule h_eq ≃ b and properties independent of interaction parameters S, A, and γ.

(ii) An adsorbed molecular brush has a tent-like cross-section for low values of the spreading parameter (regimes 2, 6, and 7). In regime 2 the dominant parts of the free energy are surface (Eq. 55) and van der Waals (Eq. 57) contributions - similar to the corresponding regime 2 for adsorbed linear chain. In regime 6 with weakly stretched spacer and regime 7 with strongly stretched spacer, the dominant free energy parts are surface (Eq. 55) and stretching (Eq. 52) terms. The properties of the chain in these regimes 6 and 7 do not depend on the spreading parameter S nor on the Hamaker constant A, while in regime 2, all properties depend on A. The difference of the dominant contribution to free energy between regime 2 on one side and regimes 6, 7 (and second layers of regimes 8 and 9) on the other side results in qualitatively different dependence of the “tent” aspect ratio R_eq/h_eq and number of monomers in a spacer m: the aspect ratio R_eq/ h_eq decreases with m in regime 2 and increases with m in all other regimes.

(iii) A rectangular cross-section of adsorbed molecular bottle-brush is found for the intermediate values of spreading parameter with weakly stretched backbone (regime 1) or strongly stretched backbone (regime 5). The thickness of the adsorbed brush in these regimes 1 and 5 is the same as of the adsorbed linear chain in regime 1, $h_{\mathit{\text{eq}}}\simeq b\sqrt{A/S}$, and is determined by the balance of spreading (Eq. 54) and Hamaker (Eq. 56) contributions to the free energy.

(iv) The unexpected result of our calculations is that the cross-over between regimes with tent-like cross-sectional profiles of adsorbed brushes at low values of the spreading parameter and rectangular or monolayer profiles at a high spreading parameter occurs via wide two-layer regimes. The upper layer in these mixed regimes always has a tent-like profile. The lower layer is rectangular with thickness $h_1\simeq b\sqrt{A/S}$ in regime 8 and is a monolayer with thickness h₁ ≃ b in regime 9. The highest backbone tension for all of studied regimes is achieved in regime 9. Even further increase in tension is expected for higher spreading parameters (S > 1).

4 Shape of the adsorbed molecular brush

4.1 Theoretical predictions

Triangular tent-like cross-sectional profile

As discussed in Section 3.2, the triangular profile is the simplest shape that captures a linear in the asymmetry h/R decrease of $F_{\mathit{\text{surface}}}^{\mathit{\text{edge}}}$ at the fixed cross-sectional area hR and minimizes the free energy of the adsorbed brush on the scaling level. This prediction is in contrast to the previous studies of strongly adsorbed brush-like macromolecules [21], where the cap was assumed to be a hemicylinder with the hemicircular cross-section of radius R ≃ (Nb³/d)^1/2. The surface free energy contribution associated with a hemicircular cross-section, F_surface/k_BT ≃ γdR/b² ≃ γ(Nd/b)^1/2 is noticeably larger than the contribution $F_{\mathit{\text{surface}}}^{\mathit{\text{edge}}}/k_{B}T\simeq N^{1/5}{(\mathrm{\gamma }b/d)}^{2/5}$ (Eq. 76) for an asymmetric tent-like configuration. In addition to different molecular weight (N) dependence, the two free energy expressions demonstrate qualitatively different behavior as functions of the distance d between grafting points. For a hemicircular cross-section, F_surface ~ d^1/2 increases with an increase in d, whereas for a triangular cross-section, the surface free energy loss decreases as $F_{\mathit{\text{surface}}}^{\mathit{\text{edge}}}~d^{-2/5.}$ Overall, the hemicircular cross-section leads to a largely overestimated cap free energy that incorrectly predicts the fraction of desorbed side chains and their contribution to both tension and stiffness of adsorbed brush-like macro-molecules.

Shape of the tent from self-consistent field theory

The scaling analysis predicts a tent-like shape of the cap with large aspect ratio R_eq/h_eq ≫ 1. (see e.g. Eq. 68, Eq.77 and Eq.79). Although the tent-like cross-section of the adsorbed molecular brush, presented above, provides correct scaling laws (e.g. Eq. 64 and Eq.67), it is only schematic and does not specify the details of the shape. A more accurate description of the cap shape for regimes 7, 8, and 9 can be obtained using the analytical self-consistent field (SCF) theory developed earlier for strongly stretched dry (solvent-free) brushes [22]. Appendix A presents the derivation of the profile of the molecular cross-section y(x) for S = 0 and long side chains (N ≫ 1)

$$y(x)/h_0={(1-x^2/R_0^2)}^2,$$ (96)

where index “0” is assigned to the parameters of the molecular brush at S = 0. The width R₀ and height h₀ are given by scaling dependences for regime 7 with the numerical coefficients on the order of unity (see Appendix A). The same shape of the cap (second layer) is expected in regimes 8 and 9.

A tent-like configuration of the cap is thermodynamically stable for the molecular brush with any backbone length L = bmK ≫ R in the regimes of the diagram in Fig. 7 above the line S₇₈ (Eq. 84). Here, the macromolecule is envisioned as a ribbon with a rectangular first layer (regime 8) or monolayer (regime 9) and a tent-like cap. The surface free energy losses associated with side edges of the ribbon (first layer) introduces an effective attraction between distal parts of the macromolecule. Therefore, the molecular brush with long backbone will self-organize into a two-dimensional (pancake) globule with the thickness of the first layer $h_{\mathit{\text{eq}}}\simeq b\sqrt{A/S}$ (regime 8) or h_eq ≃ b (regime 9), but still containing almost unperturbed tent-like second layer above the backbone. These pancake globules have been experimentally observed, and the tent-like second layer allows one to study the details of two-dimensional polymer conformations and dynamics using atomic force microscopy (see below). Stability of the tent-like conformation in the absence of the first layer (regimes 2, 6, and 7) depends on the relative value of backbone length L and persistence length l_p controlling the ability of the chain to bend and stick to itself, transferring from a semi-flexible conformation with tent-like cross-section into a pancake globule.

4.2 Experiment and computer simulation

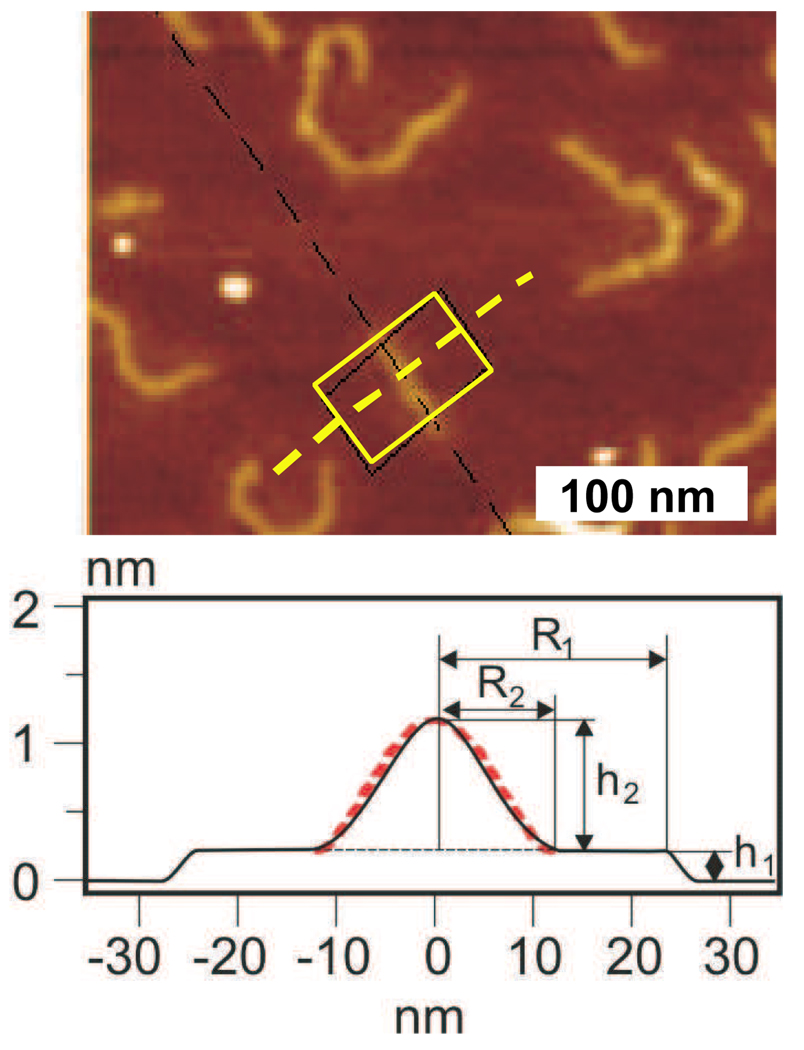
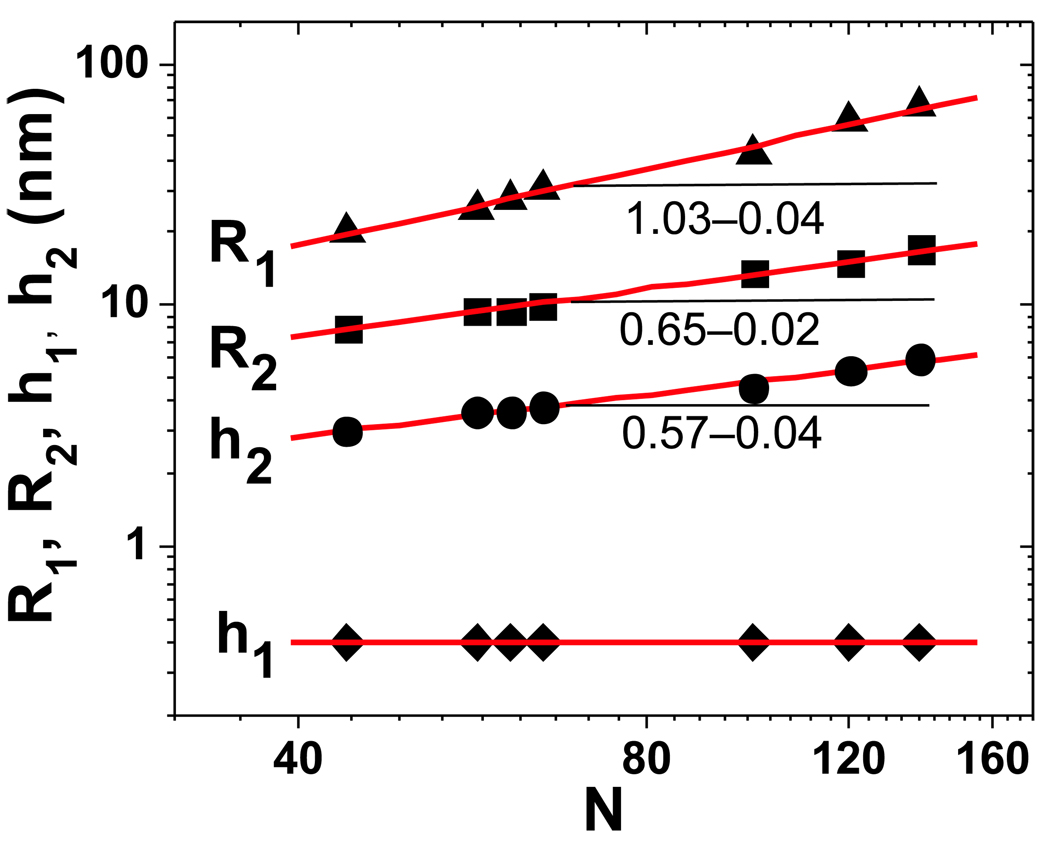
To verify the theoretical prediction of the cap shape, we carried out both molecular imaging and computer simulation studies of adsorbed brushes with different lengths of the side chains. In both cases, the studied systems corresponded to regime 9 with a large spreading parameter of S ~ 1 and a very short backbone spacer of m ~ 1. For molecular imaging experiments, we employed an Atomic Force Microscope (multimode, Nanoscope 3A, Veeco Metrology Group) using soft Si cantilevers with a spring constant of 5 N/m and a resonance frequency of 160 kHz. Figure 9 shows height images of single molecular brushes with poly(n-butyl acrylate) (pBA) side chains measured in tapping mode. The height contrast was sufficient to image both the first layer and the second layer (cap). Figure 9 also shows the cross-sectional profile of the imaged molecules, which allows measurements of the width (R₁) and height (h₁) of the first layer, as well as the width (R₂) and the height (h₂) of the cap. These molecular dimensions were measured for a series of brush-like macromolecules with different degrees of polymerization of the pBA side chains ranging from N = 44 to N = 138. Figure 10 shows log-log plots for the measured molecular dimensions along with the linear fits of the data points that give the following scaling laws: R₁ ~ N^1/03±0/04, h₁ ~ N⁰, R₂ ~ N^0/65±0/04, and h₂ ~ N^0/57±0/02. The best agreement between theory (regime 9) and experiment was found for the dimensions of the first layer, i.e. h₁ and R₁ (Eq. 93), as well as for the width of the cap, R₂, for which the theoretical prediction is R₂ ~ N^3/5 (Table 3). The height of the cap exhibits less good agreement with theory (h₂ ~ N^2/5, see Table 4) due to significant experimental error of AFM measurements in the nanometer range. The physical contact between single molecules and the AFM tip may lead to underestimation of the cap height due to cap deformation and to overestimation of the cap width due to convolution with the tip shape. These effects are particularly significant when studying soft nanometer sized objects, such as polymer molecules. To verify the cap deformation we carried out the AFM measurements under different forces and also used the newly developed soft lithography technique to mold individual molecules. [23] The obtained results indicated that the deformation of the cap was small and did not exceed 20 %. Unlike the cap height, the width of the cap was significantly overestimated by AFM. Since the tip shape on the nanometer scale is largely unknown, we used the generic correction for the tip-induced broadening of the cap $\mathrm{\Delta }{R}_2=2\sqrt{r_{\mathit{\text{tip}}}{h}_2}$, where r_tip = 10nm is the radius of the tip. Figure 10 presents experimental values of R₂ corrected for the tip-induced broadening by subtracting ΔR₂ from the experimental data. Additional contributions to the experimental error may be due to polydispersity of the side chains. Here we expect that longer side chains will preferentially segregate in the first layer, while shorter side chains will stay in the cap. This partitioning will shift the effective molecular weight of side chains in the cap. Despite the described uncertainties, the molecular imaging experiments confirm the strong asymmetry of the cap, i.e. R₂ ≫ h₂ due to spreading and extension of side chains in the second layer on top of the first layer.

Figure 9.

Atomic force microscopy was used to measure height images and cross-sectional profiles of individual molecular brushes (K = 520) with poly(n-butyl acrylate) side chains (N = 61) on mica. The cross-sectional profile was measured along the bold yellow dashed line and averaged for multiple (ca. 50) profiles taken within the rectangular box. The profile clearly depicts both layers of the adsorbed brush macromolecules: (i) the flat first layer of height h1 and width 2R₁ and (ii) the cap on top of the first layer of height h₂ and width 2R₂. Note that the height scale is deliberately exaggerated to visualize the nanometer height of both layers. The profile shows excellent agreement with the cap shape predicted by SCF theory (Eq. 96) and shown as the red dashed line.

Figure 10.

The height (h₁) and width (2R₁) of the first layer and the height (h₂) and width (2R₂) of the cap (second layer on top of the first layer - see Fig. 1b) were measured as a function of the degree of polymerization of the poly(n-butyl acrylate) side chains on mica. The linear fits (red solid lines) of the log-log plots give the following scaling laws: R₁ ~ N^1/03±0/04, R₂ ~ N^0/65±0/02, h₁ ~ N⁰, and h₂ ~ N^0/57±0/04.

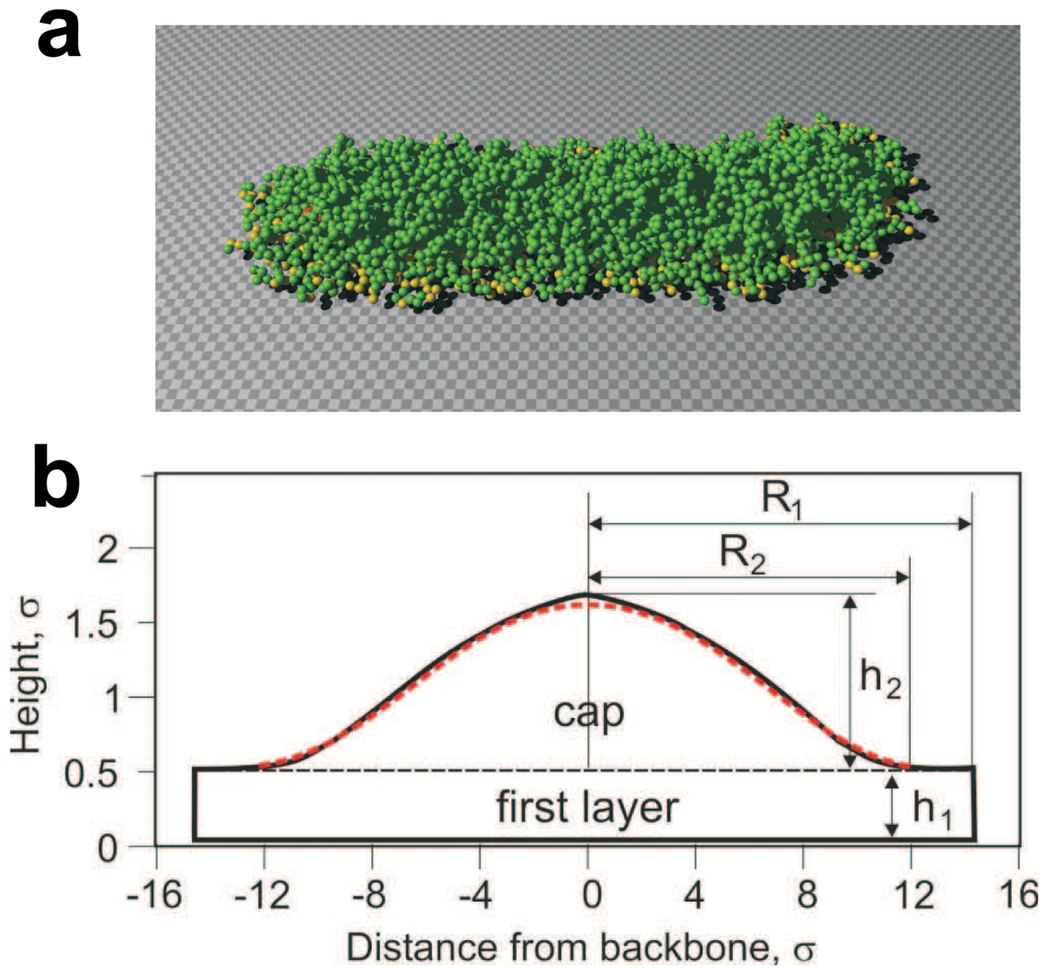
We have carried out molecular dynamics simulations of a brush-like macromolecule on a strongly attractive substrate. In the computer simulations, we have used a truncated and shifted Lennard-Jones potential [24], [8] for monomer-monomer interactions with energy parameter ε = 0.5k_BT, corresponding to poor solvent, and a van der Waals interaction potential between the monomers and the substrate (the 3 − 9 potential) [25] with a variable adsorption strength. For covalent bonds, we investigated two classes of bond potentials: the finitely extensible nonlinear elastic (FENE) potential [24], [8] and an infinitely extensible nonlinear elastic (IENE) potential

$$U_{IENE}(r)=K_2{r}^2[1+{(r/a)}^n]$$ (97)

with the exponent, which affects the steepness of the potential, n = 32, the spring constant K₂ = 8ε/σ², and the bond length parameter a = 1.1σ, where σ is the Lennard-Jones length unit. Figure 11a presents a snap shot of an adsorbed molecular brush with K = 256 side chains each containing N = 16 monomers obtained using an IENE potential. Figure 11b shows a cross-sectional profile of monomer density for an adsorbed brush measured perpendicular to the backbone. The monomer density is time-averaged and averaged over all side chains along the central, i.e. “transmission”, part of the backbone (see Fig. 2). Similar to the AFM experiments (Fig. 9) the profile clearly exhibits the first layer and a tent-like cap. The shape of the cap, obtained by AFM and computer simulations, was compared with the prediction of SCF theory (Eq. 96). The SCF predictions are shown as red dashed lines in cross-sectional profiles in Fig. 9 and Fig. 11 and demonstrate excellent agreement with experiments and simulations. Both techniques (AFM and computer simulation) confirm the strong asymmetry of the cap R₂ ≫ h₂.

Figure 11.

(a) Snap shot of computer simulation of a brush-like macromolecule (K = 256, N = 16) on a attractive substrate. (b) The average cross-sectional profile of the monomer density measured perpendicular to the backbone demonstrates excellent agreement between the computer simulation and SCF theory (red dashed line - see Eq. 96).

5 Discussion and conclusions

The paper describes conformations and bond tension of molecular bottle-brushes in solution, melt and on substrate. In solution, the backbone experiences tension f_sp, which depends on the solvent quality τ, the degree of polymerization of the spacer m, and (in the case of good and θ solvents) the degree of polymerization of the side chains N. The backbone tension becomes significant, i.e. f_sp > f₀ = k_BT/b, for short spacers. The highest tension f_sp = f₀N^3/8 is developed in the maximally dense brushes (m ~ 1) in athermal solvent (τ ~ 1). Lowering the solvent strength leads to the decrease of the backbone tension for densely grafted brushes following different scaling with the solvent quality parameter τ in good (τ > 0) and poor (τ < 0) solvents. In good solvent, tension decreases with decreasing τ as f_sp ≃ f₀N^3/8τ^1/8 reaching f_sp ≃ f₀N^1/3 in theta solvent. In poor solvent backbone tension decreases even further as f_sp ≃ f₀(−τ)⁻¹, reaching f_sp ≃ f₀ in a non-solvent environment (τ ≃ −1), e.g. melt. Note, that the backbone tension in poor solvent does not depend on the length of the side chains. It is interesting that loosely grafted molecular brushes exhibit an opposite behavior in good solvent, i.e. the backbone tension increases with decreasing solvent quality. To summarize, the backbone tension f_sp in a solution can approach the level sufficient to break hydrogen bonds, however, it is too small to rupture a covalent bond. For example, for a molecular brush with N ≃ 10³ Kuhn segments and spacer with m ≃ 1 monomers, the backbone tension ranges from f_sp ≃ f₀ ≃ 4pN in a melt to f_sp ≃ 1000^3/8f₀ ≃ 50pN in an athermal solvent (τ ≃ 1).

Significant amplification of tension occurs upon adsorption onto a substrate even in a non-solvent environment (considered in this paper), which is the most relevant system to experiments at a substrate-air interface. Depending on the spreading parameter S and the spacer length m, this system exhibits many conformational regimes (see Figure 7 and Table 3 and Table 4) with different functional dependences for the backbone tension (see Table 2). Loose brushes on a strongly adsorbing substrate adopt a shape of a monolayer (h ≃ b), which is similar to linear chains. In this regime, the brush molecule optimizes its shape at a constant number of monomeric contacts with the substrate. Therefore, the properties of the brush, such as backbone tension f_sp, width R, and height h depend neither on the substrate-molecule interaction parameters S and A nor on the molecule − non-solvent interaction parameter γ. The key properties for the monolayer conformation can be summarized for weakly stretched backbone (with f_sp < f₀) as

$$f_{\mathit{\text{sp}}}\simeq f_0{(N/m^3)}^{1/4},R\simeq b{(N^3/m)}^{1/4},h\simeq b\text{regime}3$$ (98)

and for strongly stretched backbone (f_sp > f₀) as

$$f_{\mathit{\text{sp}}}\simeq f_{0}N/m^3,R\simeq bN/m,h\simeq b\text{regime}4$$ (99)

At lower values of spreading parameter S < A, a loosely grafted molecular brush adsorbs yielding a thicker layer with rectangular cross-section of thickness h ≃ b (A/S)^1/2 determined by the balance of spreading and van der Waals interactions (similar to an adsorbed linear chain). In adsorption regimes 1 and 5 with rectangular cross-section, the properties of molecular brush are similar to properties in a monolayer regimes 3 and 4, but modified by the ratio of van der Waals and spreading parameters A/S and are still independent of the polymer – non-solvent surface tension, γ. The main properties of an adsorbed molecular brush with a rectangular cross-section and a weakly stretched backbone (f_sp < f₀) are

$$f_{\mathit{\text{sp}}}\simeq f_0{\left(\frac{NS}{m^{3}A}\right)}^{1/4},R\simeq b{\left(\frac{N^{3}S}{mA}\right)}^{1/4},h\simeq b{\left(\frac{A}{S}\right)}^{1/2}\text{regime}1$$ (100)

while for strongly stretched backbone (f_sp > f₀) they are

$$f_{\mathit{\text{sp}}}\simeq f_0\frac{NS}{m^{3}A},R\simeq b\frac{N}{m}{\left(\frac{S}{A}\right)}^{1/2},h\simeq b{\left(\frac{A}{S}\right)}^{1/2}\text{regime}5$$ (101)

At the lowest values of spreading parameter S, the cross-section of an adsorbed molecular brush is tent-like. The properties of loosely grafted brushes on a weakly attracted surface are independent of S and determined by the balance of polymer – non-solvent (e.g. air) surface energy with the surface tension parameter γ and van der Waals interactions with the Hamaker parameter A. Therefore, the properties of an adsorbed brush in the van der Waals − controlled regime (tent-like profile and low backbone tension) depend on the ratio γ/A and can be written as

$$f_{\text{sp}}\simeq f_0{\left(\frac{N\mathrm{\gamma }}{m^{7}A}\right)}^{1/10},R\simeq b{\left(\frac{N^3}{m}\right)}^{1/5}{\left(\frac{\mathrm{\gamma }}{A}\right)}^{1/10},h\simeq b{\left(\frac{N^3}{m}\right)}^{1/10}{\left(\frac{A}{\mathrm{\gamma }}\right)}^{1/5}\text{regime}2$$ (102)

The corresponding properties of molecular brushes with higher grafting density at weakly adsorbing substrates are determined by the balance of polymer- non-solvent surface energy and entropic elasticity of side chains and are independent not only of spreading parameter S, but also of the Hamaker constant A. The molecular cross-section is still tent-like and the main properties for the regime with weakly stretched backbone (f_sp < f₀) are

$$f_{\mathit{\text{sp}}}\simeq f_0{(N{\mathrm{\gamma }}^2/m^7)}^{1/12},R\simeq b{(N^7{\mathrm{\gamma }}^2/m)}^{1/12},h\simeq b{(N/m)}^{1/3}{\mathrm{\gamma }}^{-1/3}\text{regime}6$$ (103)

and for strongly stretched backbone (f_sp > f₀) the tension is

$$f_{\mathit{\text{sp}}}\simeq f_0{(N{\mathrm{\gamma }}^2/m^7)}^{1/5}\text{regime}7\text{and}8”$$ (104)

while the dimension of the tent-like cross-section are

$$R\simeq b{(N^3\mathrm{\gamma }/m)}^{1/5},h\simeq b{(N/m^2)}^{2/5}{\mathrm{\gamma }}^{-1/5}\text{regime}{7,8}^{2\mathit{\text{nd}}},\text{and}{9}^{2\mathit{\text{nd}}}$$ (105)

The cross-over between adsorbed brushes with a tent-like shape at low values of spreading parameter and a rectangular or monolayer cross-section at a higher spreading parameter occurs via unexpectedly wide regimes with a two-layer cross-section. The second layer is formed by those side chains that lose more entropy due to stretching compared to the energy decrease due to extra contacts with the surface in the first layer. The partitioning of side chains between the two layers is determined by the equality of their chemical potentials and the fraction of side chains in the first layer is m/m₁ ≃ m(AS)^−1/4. At intermediate values of spreading parameter, the dimensions of the first layer are determined by the balance of spreading and van der Waals interactions (similar to regimes 1 and 5) and are independent on the length of the spacer m

$$R\simeq bN{(S^3/A)}^{1/4},h\simeq b{(A/S)}^{1/2}\text{first}\text{layer}\text{in}\text{regime}8$$ (106)

The dimensions of the tent-like second layer are the same as in regime 7 (see Eq. 105). The backbone tension is dominated by the side chains in the upper layer for lower values of spreading parameter (regime 8”) and is given by Eq. 104. At higher values of spreading parameter, the tension is controlled by the first layer. The tension depends linearly on the length of the side chains, N, and it is independent on the length of the spacer, m,

$$f_{\mathit{\text{sp}}}\simeq f_{0}N{(S^7/A)}^{1/4}\text{regime}8’$$ (107)

At even higher values of spreading parameter S > A, the first layer becomes a monolayer with dimensions

$$R\simeq bN{S}^{1/4},h\simeq b\text{first}\text{layer}\text{in}\text{regime}9$$ (108)

while the second remains tent-like with size given by Equation 105. The backbone tension in this regime is also linear in the length of side chains

$$f_{\mathit{\text{sp}}}\simeq f_{0}N{S}^{3/2}\text{regime}9$$ (109)

In regimes 9 and 8’, the backbone tension, f_sp, is dominated by the first layer in the segregated molecular brush and is related to the spreading parameter S and the width of the first layer R₁ as f_sp ≃ f₀SR₁/b (see Eq. 106–Eq.109). The fraction of side chains in the first layer in regime 9 is given by m/m₁ ≃ mS^1/2 (Eq. 92). Upon further increase of spreading parameter, side chains become fully stretched, R₁ ≃ bN, and backbone tension reaches f_sp ≃ f₀SN which can approach the level of nanoNewtons sufficient to rupture covalent bonds. For example, for N = 100 Kuhn monomers and the spreading parameter S ≃ 5 (using Eq. 37 at room temperature for γ₁ − γ₂ − γ₁₂ = 20mJ/m² and b² = 1nm²), one obtains f_sp ≃ 2nN. This estimate is consistent with the data in ref. [7], that demonstrate multiple random scissions of C − C bonds in backbones of poly(n-butyl acrylate) molecular brushes with long side chains on various liquid and solid substrates at similar backbone tension. Two projections in Fig. 8 demonstrate scaling dependences of the backbone tension f_sp as the function of m and S, respectively, corresponding to different (horizontal and vertical) cross-sections of the diagram in Fig. 7.

In all regimes, the tent-like shape of the cap is strongly asymmetric (h₂ ≪ R₂), which allows minimization of the surface free energy. The asymmetry was confirmed by both experiments and computer simulations. Depending on the regime, the aspect ratio (asymmetry) R_eq/h_eq of the tent cross-section exhibits different dependences on m, N, γ, and S. For example, in regimes 6 and 7, R_eq/h_eq increases with the number of monomers in spacer (Eq. 77 and Eq. 79), in contrast to regime 2 (Eq. 68).

The above considerations can be generalized to the case of the starlike [26] and dendritic macromolecules. Thus, we observe that special architecture of the molecule may lead to high amplification of the tension in specific chain strands. Structure and properties of branched macromolecules strongly depend on the tension in their bonds. Adsorption-induced tension can exceed the strength of covalent bonds and lead to the irreversible fracture of macromolecules [7]. If molecules are assembled of designed, e.g. DNA [27–29], fragments, then our results hold the key to making architectures that undergo well-defined fragmentation upon adsorption. Even when the bonds are not broken, the self-generated tension (in solution, melt, and on substrate) can alter the electronic structure of monomers and directly impact molecular reactivity, optical properties, and conductivity of macromolecules [3].

Appendix

A Self-consistent field (SCF) model

We use SCF formalism developed for strongly stretched polymer brushes [22] to examine the shape of the cross-section in a dry (solvent-free) molecular brush on a substrate with the spreading parameter S ≤ 0. The case S = 0 applies also to the second layer (cap) of adsorbed molecular brush (regimes 8 and 9 of the diagram in Figure 5).

Consider cross-section profile y(x) of the adsorbed molecular brush. This function represents brush height y(x) at the transverse coordinate position x away from the backbone. Maximum height is y(0) = h and the edges of the brush are defined by x = −R and x = R with y(−R) = y(R) = 0. Since the cross-section of the adsorbed molecular brush is symmetric y(x) = y(−x), we consider only the right half of this cross-section with non-negative argument x ≥ 0. The side chains are extended in the lateral direction (along x-axis). The region of a radius ~ h around the backbone, where the branches emanate in a “star-like” fashion, is small compared to the total area of the cross-section when h ≪ R. Under these conditions, the side chains can be envisioned as “tethered” to the vertical plane (passing through the backbone of the molecular brush, x = 0) with the grafting area s = dh per chain, where d is the distance between branches along the backbone. Side chains are modeled as trajectories x(n) with specified position x of each monomer with the index n, where x is the distance from the backbone (assumed, for simplicity, straight).

Following [22], we introduce the local chain stretching function E(x,x′) = dx/dn, which determines the extension of a side arm at the distance x from the backbone provided that its free end is located at the distance x′ > x. Assuming that free ends of side chains can be found everywhere within the volume of the molecular brush we also introduce the distribution function of the free ends g(x′) normalized as

$${\displaystyle {\int }_0^{R}g(x^{\prime })d{x}^{\prime }}=1.$$ (A.1)

A.1 Free energy functional

For a fixed distance d between attachment points of side chains to the backbone, the free energy F_sc per repeating unit is given by

$$F_{\mathit{\text{sc}}}=F_{\mathit{\text{surface}}}+F_{\mathit{\text{elastic}}},$$ (A.2)

where $F_{\mathit{\text{surface}}}=F_{\mathit{\text{surface}}}^{\mathit{\text{spread}}}+F_{\mathit{\text{surface}}}^{\mathit{\text{edge}}}$, while the van der Waals contribution, F_υdW, is currently omitted. The spreading contribution is specified as

$$\frac{F_{\mathit{\text{surface}}}}{k_{B}T}=\mathrm{\gamma }d{\displaystyle {\int }_0^R(\sqrt{{\dot{y}}^2+1}-1)\mathit{\text{dx}}-SRd,}$$ (A.3)

where y˙ ≡ dy/dx, and we use dimensionless variables y and x, as well as distances R, d and h (measured in units of the monomer size b). The first term in Eq. A.3 is the surface energy of brush - non-solvent (air) with dimensionless surface tension γ (Eq. 36), while the second term is the energy gain due to polymer-surface contact with spreading parameter S defined by Eq. 37. At small curvatures |y˙| ≪ 1 expression (A.3) is simplified as

$$\frac{F_{\mathit{\text{surface}}}}{k_{B}T}\approx \frac{\mathrm{\gamma }d}{2}{\displaystyle {\int }_0^R{\dot{y}}^2\mathit{\text{dx}}-SRd.}$$ (A.4)

The elastic energy of a non-uniformly extended side chain is given by [22]

$$\frac{F_{\mathit{\text{elastic}}}}{k_{B}T}=\frac{3}{2}{\displaystyle {\int }_0^{R}g(x\prime )dx\prime }{\displaystyle {\int }_0^{x\prime }E(x,x\prime )\mathit{\text{dx}},}$$ (A.5)

where E(x,x′) is a function describing local stretching at position x for a chain with free end at location x′. An additional condition of dense packing of the monomers inside the brush, ϕ(x) = 1, can be rewritten as

$$\varphi (x)=1=\frac{1}{y(x)d}{\displaystyle {\int }_0^R\frac{g(x\prime )dx\prime }{E(x,x\prime )}}$$ (A.6)

This equation is similar to that for the planar molten brush except that the effective grafting density [y(x)d]⁻¹ decreases as a function of the distance x from the backbone. Another two constraints on functions E(x,x′) and y(x) insure the conservation of the total number of monomers of the chain with the given position x′ of the end,

$${\displaystyle {\int }_0^{x\prime }{E}^{-1}(x,x\prime )\mathit{\text{dx}}=N}$$ (A.7)

and the conservation of the total number of monomers in the cross-section of the molecular brush,

$${\displaystyle {\int }_0^{R}y(x)\mathit{\text{dx}}=N/d}$$ (A.8)

The total free energy F_sc per repeating unit takes the form

$$\frac{F_{\mathit{\text{sc}}}}{k_{B}T}=\frac{\mathrm{\gamma }d}{2}{\displaystyle {\int }_0^R{\dot{y}}^2\mathit{\text{dx}}+\frac{3}{2}{\displaystyle {\int }_0^{R}g(x\prime )dx\prime }{\displaystyle {\int }_0^{x\prime }E(x,x\prime )\mathit{\text{dx}}-SRd.}}$$ (A.9)

Minimization of F_sc with respect to three unknown functions, y(x), g(x) and E(x,x′), taking into account of additional constraints (A.6), (A.7) and (A.8), determines parameters of the equilibrium structure of the molecular brush at fixed values of S, d and R. Minimization of the elastic free energy (second term in Eq. A.9) by taking into account constraints (A.6) and (A.7) leads to the universal function for the local chain stretching

$$E(x,x\prime )=\frac{\pi }{2N}\sqrt{{(x\prime )}^2-x^2.}$$ (A.10)

The details of this procedure can be found in the original paper [22].

By implementing Eq. A.10 and Eq. A.6 we express the elastic free energy F_elastic in Eq. A.5 as

$$\frac{F_{\mathit{\text{elastic}}}}{k_{B}T}=\frac{3{\mathrm{\pi }}^{2}d}{8N^2}{\displaystyle {\int }_0^R{x}^{2}y(x)\mathit{\text{dx}}}$$ (A.11)

The total free energy F_sc depends on the single unknown function y(x),

$$\begin{array}{cc}\frac{F_{\mathit{\text{sc}}}}{k_{B}Td}\hfill & =\frac{\gamma }{2}{\displaystyle {\int }_0^R{\dot{y}}^2\mathit{\text{dx}}+\frac{3{\mathrm{\pi }}^2}{8N^2}{\displaystyle {\int }_0^R{x}^{2}y(x)\mathit{\text{dx}}-SR}}\hfill \\ & =\gamma {\displaystyle {\int }_0^R\left[\frac{{\dot{y}}^2}{2}+u^2{x}^{2}y(x)\right]}\mathit{\text{dx}}-SR,\hfill \end{array}$$ (A.12)

where the parameter u is determined as

$$u^2=\frac{3{\mathrm{\pi }}^2}{8N^2\mathrm{\gamma }},$$ (A.13)

and the only constraint on y(x) is imposed by Eq. A.8.

Minimization of F_sc with respect to y(x) and taking into account Eq. A.8 is equivalent to unconditional minimization of the functional

$$\frac{F\prime }{k_{B}T\mathrm{\gamma }d}={\displaystyle {\int }_0^R\left[\frac{{\dot{y}}^2}{2}+u^2{x}^{2}y(x)-\lambda y(x)\right]\mathit{\text{dx}}-\frac{SR}{\mathrm{\gamma }},}$$ (A.14)

where λ is the Lagrange multiplier. The function y(x) is determined by the Eulier equation [30] as

$$\frac{d(\dot{y})}{\mathit{\text{dx}}}=u^2{x}^2-\lambda$$ (A.15)

with the boundary conditions y(R) = 0 and y˙ (0) = 0. (The latter condition implies that the contour line is smooth at the top of the cross-section, x = 0). Integration of Eq. A.15 gives

$$y(x)=\frac{u^2{x}^4}{12}-\frac{\mathrm{\lambda }{x}^2}{2}+\frac{\mathrm{\lambda }{R}^2}{2}-\frac{u^2{R}^4}{12}.$$ (A.16)

By applying the conservation condition (A.8) we find the Lagrange multiplier

$$\mathrm{\lambda }=\frac{3N}{d{R}^3}+\frac{u^2{R}^2}{5}.$$ (A.17)

Substituting y(x) in Eq. A.14 and introducing new combinations of parameters,

$$z=\frac{2u^2{R}^{5}d}{45N}\text{and}\alpha =\frac{2}{3}{\left(\frac{45}{2}\right)}^{4/5}\frac{S}{\mathrm{\gamma }}\frac{1}{{(N/d)}^{6/5}{u}^{8/5}}\simeq \frac{S{N}^{2/5}{d}^{6/5}}{{\mathrm{\gamma }}^{1/5}}$$ (A.18)

we express the free energy F_sc as

$$\frac{F_{\mathit{\text{sc}}}}{k_{B}T\mathrm{\gamma }d}=\frac{3}{2}{\left(\frac{2}{45}\right)}^{3/5}{d}^{-7/5}{N}^{7/5}{u}^{6/5}\left[-\frac{3}{7}{z}^{7/5}+3z^{2/5}+\frac{1}{z^{3/5}}-\alpha z^{1/5}\right].$$ (A.19)

Minimization of free energy F with respect to R (which is equivalent to minimizing F with respect to z ~ R⁵, dF/dz = 0) gives

$$3{(1-z)}^2+\alpha z^{4/5}=0.$$ (A.20)

The Lagrange multiplier λ in Eq. A.17 is then expressed as

$$\mathrm{\lambda }=u^2{R}^2\left(\frac{2}{15z}+\frac{1}{5}\right).$$ (A.21)

where z = z(α) is the solution of Eq. A.20. Correspondingly, y(x) in Eq. A.16 is given by

$$y(x)\frac{Rd}{N}=u^2{R}^4\left[1-{\left(\frac{x}{R}\right)}^2\right]\left[\frac{1}{60}+\frac{1}{15z}-\frac{1}{12}{\left(\frac{x}{R}\right)}^2\right],$$ (A.22)

or, equivalently,

$$\frac{y(t)Rd}{N}=\frac{3}{8}(z+4)(1-t^2)\left(1-\frac{5z}{z+4}{t}^2\right),$$ (A.23)

where t = x/R is the reduced distance from the backbone. Eq. A.23 gives

$$y(0)=h=\frac{3N}{8Rd}(z+4),$$ (A.24)

and it can therefore be rewritten as

$$\frac{y(t)}{h}=(1-t^2)\left(1-\frac{5z}{z+4}{t}^2\right),$$ (A.25)

A.2 Distribution function of the free ends g(x′)

The condition (A.6) relates the distribution function of the free ends g(x′) to the profile y(x) of the contour line as

$$y(x)=\frac{2N}{\mathrm{\pi }d}{\displaystyle {\int }_x^l\frac{g(x\prime )dx\prime }{\sqrt{{(x\prime )}^2-x^2}}}$$ (A.26)

By introducing new variables ξ = R² − x², η = R² − (x′)² and the new function υ(η) = g(x′)/2x′, we transform the integral equation (A.26) into the Abel equation,

$${\displaystyle {\int }_0^{\mathrm{\xi }}\frac{\upsilon (\eta )d\eta }{\sqrt{\mathrm{\xi }-\eta }}=\frac{\mathrm{\pi }d}{2N}y\left(\sqrt{R^2-\mathrm{\xi }}\right)\equiv f(\mathrm{\xi })}$$ (A.27)

Its solution

$$\upsilon (\mathrm{\xi })=\frac{1}{\mathrm{\pi }}\left[\frac{f(0)}{\sqrt{\mathrm{\xi }}}+{\displaystyle {\int }_0^{\xi }\frac{\mathit{\text{df}}(\eta )}{d\eta }\frac{d\eta }{\sqrt{\xi -\eta }}}\right]$$ (A.28)

provides the distribution function of the free chain ends,

$$g(x)R=2xR\upsilon (R^2-x^2)=5zt\left[{(1-t^2)}^{3/2}+\frac{3(1-z)}{5z}{(1-t^2)}^{1/2}\right].$$ (A.29)

A.3 Spreading parameter S = 0

When S ~ α = 0, the parameter z = 1, and the transverse size of the molecular cross-section is given by Eq. A.18,

$$R_0={\left(\frac{45N}{2u^{2}d}\right)}^{1/5}={\left(\frac{60}{{\mathrm{\pi }}^2}\right)}^{1/5}{\mathrm{\gamma }}^{1/5}{d}^{-1/5}{N}^{3/5}\simeq 1.435{\mathrm{\gamma }}^{1/5}{d}^{-1/5}{N}^{3/5},$$ (A.30)

whereas the height of the cross-section is determined by Eq. A.24 as

$$h_0=\frac{u^2{R}^4}{12}=\frac{{\mathrm{\pi }}^2}{32}{\left(\frac{60}{{\mathrm{\pi }}^2}\right)}^{4/5}{\mathrm{\gamma }}^{-1/5}{d}^{-4/5}{N}^{2/5}\simeq 1.307{\mathrm{\gamma }}^{-1/5}{d}^{-4/5}{N}^{2/5}.$$ (A.31)

Here, as above, the subscript “0” indicates the cross-section dimensions at S = 0. The corresponding free energy F_sc,0 per side chain is

$$\frac{F_{\mathit{\text{sc}},0}}{k_{B}T}={\left(\frac{{\mathrm{\pi }}^2}{4}\right)}^{3/5}\frac{5^{7/5}{3}^{2/5}}{14}{d}^{-2/5}{\mathrm{\gamma }}^{2/5}{N}^{1/5}\simeq 1.814d^{-2/5}{\mathrm{\gamma }}^{2/5}{N}^{1/5}.$$ (A.32)

The product of the Lagrange multiplier λ₀, γ and N determines chemical potential μ₀ of the side chain,

$${\mu }_0=F_{\mathit{\text{sc}},0}-d\frac{\partial F_{\mathit{\text{sc}},0}}{\partial d}=k_{B}T{\mathrm{\lambda }}_0\mathrm{\gamma }N=k_{B}T\mathrm{\gamma }\frac{u^2{R}_0^{2}N}{3}=\frac{7}{5}{F}_{\mathit{\text{sc}},0}.$$ (A.33)

As expected, Eq. A.30, Eq. A.31 and Eq. A.32 confirm exponents predicted for dimensions of the tent-like cross-section in regimes 2, 6, 7, and for the cap in regimes 8 and 9 in the diagram in Figure 7, and that all numerical coefficients in scaling dependences (A.30) – (A.32) are on the order of unity. (Note that full cross-section is symmetric with the total transverse size 2R₀).

The profile of the molecular brush cross-section y(x) is specified as

$$y(x)/h_0={(1-t^2)}^2,$$ (A.34)

where t = x/R₀ is the reduced distance from the backbone. The corresponding distribution function of the free ends of the side chains for the brush cap (S = 0) at equilibrium is

$$g(x)R_0=5t{(1-t^2)}^{3/2}=5\frac{x}{R_0}{\left(1-\frac{x^2}{R_0^2}\right)}^{3/2}.$$ (A.35)

This distribution has a maximum in the middle of the cross-section, t = x/R₀ = 1/2.

A.4 Spreading parameter S < 0

When S ~ α < 0 the parameter z = (R/R₀)⁵ < 1, and the wetting of the substrate by molecular brush is only partial. When α ≪ −1, the approximate solution of Eq. A.20 is given by

$$z(\alpha )\approx {(-3/\alpha )}^{5/4},$$ (A.36)

leading to asymptotic dependences

$$R=3^{1/2}{2}^{-1/4}{(-\mathrm{\gamma }/S)}^{1/4}{d}^{-1/2}{N}^{1/2}\approx 1.456{(-\mathrm{\gamma }/S)}^{1/4}{d}^{-1/2}{N}^{1/2}$$ (A.37)

and

$$h\approx {(-S/\mathrm{\gamma })}^{-1/4}{d}^{-1/2}{N}^{1/2}.$$ (A.38)

Eq. A.37 and Eq. A.38 are valid when the side chains are still stretched with respect to the Gaussian size, $R>\sqrt{N.}$

The SCF model provides smooth crossover between the two regimes, −1 ≪ α ≤ 0 and α ≪ −1. The profile of the cross-section y(x) and the distribution function of free ends g(x) for arbitrary value of S ≤ 0 are given by Eq. A.25 and Eq. A.29. When z = 1 Eq. A.25 and Eq. A.29 reduce to Eq. A.34 and Eq. A.35, respectively. When z ≪ 1 we find

$$y(x)/h=(3/2)(1-t^2)\text{and}g(x)R=3t{(1-t^2)}^{1/2},$$ (A.39)

with t = x/R. Here, the elastic contribution due to side chains is asymptotically negligible with respect to the surface free energy, but the shape of the molecular brush cross-section is still asymmetric (R/h ≫ 1), indicating partial wetting of the substrate.

The previously omitted van der Waals contribution F_υdW is important only in distal part of the cross-section (close to the contact line, x = R). To estimate where F_υdW affects the shape of the cross-section y(x), we equate the densities of the elastic and the van der Waals free energies, u²x²y(x) ≃ [y(x)]⁻². (For simplicity, A/kBT is assumed here to be on the order of unity). The condition y(x_*) = (ux_*)^−2/3 determines the length x_* beyond which the profile of the contour line y(x) changes significantly. By introducing the relative deviation from the contact line δx_* = R − x_* and using expression (A.34) one finds that when S = 0,δx_*/R₀ ≃ N^−1/15 and y(δx_*)/h₀ ≃ N^−2/15. For long branches N ≫ 1 both δx_*/R₀ and y(δx_*)/h₀ approach zero, thus indicating that in the limit of N → ∞ Eq. A.34 correctly describes the contour line y(x) in the whole interval of 0 ≤ x ≤ R₀. The situation is similar to the case of the planar brush swollen in a solvent. Analytical expression of the SCF model [31] for the polymer density profile in such a brush (when expressed in the reduced dimensionless variables) becomes asymptotically rigorous in the limit N → ∞.

Note that in this limit of large N ≫ 1, when Eq. A.25 is asymptotically rigorous, contact angle Ω = arctan[y˙ (x = R)] obeys the Young’s law,

$$\text{cos}\mathrm{\Omega }=1+S/\mathrm{\gamma }.$$ (A.40)

This is because free ends of side chains are not extended, and the behavior of the molecular brush near solid-liquid-solvent contact line (x = R) is similar to that of the liquid droplet of side chains.