Variable selection in Bayesian smoothing spline ANOVA models: Application to deterministic computer codes

Abstract

With many predictors, choosing an appropriate subset of the covariates is a crucial, and difficult, step in nonparametric regression. We propose a Bayesian nonparametric regression model for curve-fitting and variable selection. We use the smoothing spline ANOVA framework to decompose the regression function into interpretable main effect and interaction functions. Stochastic search variable selection via MCMC sampling is used to search for models that fit the data well. Also, we show that variable selection is highly-sensitive to hyperparameter choice and develop a technique to select hyperparameters that control the long-run false positive rate. The method is used to build an emulator for a complex computer model for two-phase fluid flow.

1 Introduction

Nonparametric regression techniques have become a popular tool for analyzing complex computer model output. For example, we consider a two-phase fluid flow simulation study (Vaughn et al., 2000) carried out by Sandia National Labs as part of the 1996 compliance certification application for the Waste Isolation Pilot Plant (WIPP) in New Mexico. The computer model simulates the waste panel’s condition 10,000 years after the waste panel has been penetrated by a drilling intrusion. The simulation model uses several input variables describing various environmental conditions. The objectives are to predict waste pressure for new sets of environmental conditions and to determine which environmental factors have the largest effect on the response. Since the simulation model is computationally intensive, we would like to develop an emulator, i.e., a statistical model to replicate the output of the complex computer model, to address these objectives.

The nonparametric regression model for response y_i is y_i = μ + f(x_1i,…,x_pi) + ϵ_i, i = 1, …,N, where μ is the intercept, f is the unknown function of covariates x_1i, …,x_pi, and ϵ_i is error. With many predictors, choosing an appropriate subset of the covariates is a crucial, and difficult, step in fitting a nonparametric regression model. Several methods exist for curve fitting and variable selection for multiple nonparametric regression. Multivariate adaptive regression splines (MARS; Friedman, 1991) is a stepwise procedure that selects variables and knots for a spline basis for each curve. However, it is well-known that stepwise selection can be unstable and highly sensitive to small changes in the data, as it is a discrete procedure (Breiman, 1995). Therefore, Lin and Zhang (2006) propose the component selection and smoothing operator (COSSO) in smoothing spline analysis of variance models. The COSSO is a penalization technique to perform variable selection via continuous shrinkage of the norm of each of the functional components.

The Bayesian framework offers several potential advantages for nonparametric regression. For example, missing data and non-Gaussian likelihoods can easily be incorporated in the Bayesian model. Also, prediction is improved via Bayesian model averaging, and posterior model probabilities are natural measures of model uncertainty.

A common approach is to model computer output as a Gaussian process. For example, “blind Kriging” of Joseph et al. (2008) assumes the response is the sum of a mean trend and a Gaussian process and variable selection is performed on the mean trend which is taken to be the sum of second-order polynomials and interactions. However, all potential predictors are included in the Gaussian process covariance and thus blind kriging does not perform any variable selection on the overall model.

In contrast, Linkletter et al. (2006) model the regression function f as a p-dimensional Gaussian process with covariance that depends on the p covariates. They perform variable selection on the overall model using stochastic search variable selection via MCMC sampling (e.g., George and McCulloch, 1993; Chipman, 1996; George and McCulloch, 1997; Mitchell and Beauchamp; 1998) to include/exclude variables from the covariance of the Gaussian process. While this method of variable selection improves prediction for complex computer model output, it is difficult to interpret the relative contribution of each covariate, or groups of covariates, to the p-dimensional fitted surface. Also, the covariance function used results in a model that includes all higher-order functional interactions among the important predictors, that is, their model can not reduce to an additive model where the response surface is the sum of univariate functions. Therefore, the functional relationship between a predictor and the outcome is always dependent on the value of all of the other predictors included in the model. As a result, this model is well-suited for a complicated response surface, however, estimation and prediction can be improved in many cases by assuming a simpler model.

Shively et al. (1999), for instance, propose a model for variable selection in additive non-parametric regression. They take an empirical Bayesian approach and give each main effect function an integrated Brownian motion prior. Wood et al. (2002) extend the work of Shively et al. (1999) to non-additive models. They again assume integrated Brownian motion priors for the main effect functions and model interactions between predictors as two-dimensional surfaces with thin plate spline priors. However, it is difficult to interpret the relative contributions of the main effect and interaction terms because the spans of these terms overlap. To perform model selection, they use data-based priors for the parameters that control the prior variance of the functional components. This allows for a BIC approximation of the posterior probability of each model under consideration. This approach requires computing posterior summaries of all models under consideration, which is infeasible in situations with many predictors, especially when high-order interaction terms are being considered. Gustafson (2000) also includes a two-way interactions but, to ensure identifiability, main effects are not allowed to be in the model simultaneously with interactions and predictors are allowed to interact with at most one other predictor. Complex computer models often have many interaction terms, so this is a significant limitation.

In this paper, we propose a Bayesian model for variable selection and curve fitting for nonparametric multivariate regression. Our model uses the functional analysis of variance framework (Wahba, 1990; Wahba et al., 1995, and Gu, 2002) to decompose the function f into main effects f_j, two-way interactions f_jk, and so on, i.e.,

$$f(x_{1i},\dots ,x_{\mathit{\text{pi}}})={\displaystyle \sum _{j=1}^p{f}_j(x_{\mathit{\text{ji}}})+{\displaystyle \sum _{j<k}{f}_{\mathit{\text{jk}}}(x_{\mathit{\text{ji}}},x_{\mathit{\text{ki}}})+\dots }}.$$ (1)

The functional ANOVA (BSS-ANOVA) is equipped with stochastic constraints that ensure that each of the components are identified so their contribution to the overall fit can be studied independently. Rather than confining the regression functions to the span of a finite set of basis functions as in Bayesian splines, we use a more general Gaussian process prior for each regression function.

We perform variable selection using stochastic search variable selection via MCMC sampling to search for models that fit the data well. The orthogonality of the functional ANOVA framework is particularly important when the objective is variable selection. For example, assume two variables have important main effects but their interaction is not needed. If the interaction is modeled haphazardly so the span of the interaction includes the main effect spaces, it is possible that the inclusion probability could be split between the model with main effects and no interaction and the model with the interaction alone, since both can give the same fit. In this case, inclusion probabilities for the main effects and interaction could be less than 1/2 and we would fail to identify the important terms. Because of the orthogonality, our model only includes interactions that explain features of the data that can not be explained by the main effects alone. Also, due to the additive structure of our regression function, we are able to easily include categorical predictors which is problematic for Gaussian process models (although Qian et al. (2008) suggest a way to incorporate categorical predictors into a GP model). Our model is also computationally-efficient, as we avoid enumerating all possible models and we avoid inverting large matrices at each MCMC iteration. We show that stochastic search variable selection can be sensitive to hyperparameter selection and overcome this problem by specifying hyperparameters that control the long-run false positive rate. Bayesian model averaging is used for prediction, which is shown to improve predictive accuracy.

The paper proceeds as follows. Sections 2 and 3 introduce the model. The MCMC algorithm for stochastic search variable selection is described in Section 4. Section 5 presents a brief simulation study comparing our model with other nonparametric regression procedures. Our Bayesian model compares favorably to MARS, COSSO, and Linkletter et al.’s method in terms of predictive performance and selecting important variables in the model. Section 6 analyzes the WIPP data. Here we illustrate the advantages of the Bayesian approach for quantifying variable uncertainty. Section 7 concludes.

2 A Bayesian smoothing spline ANOVA (BSS-ANOVA) model

2.1 Simple nonparametric regression

For ease of presentation, we introduce the nonparametric model first in the single-predictor case and then extend to the multiple-predictor case in Section 2.2. The simple nonparametric regression model is

$$y_i=\mu +f(x_i)+{ϵ}_i,$$ (2)

where f is an unknown function of a single covariate x_i ∈ [0, 1] and ${ϵ}_i\stackrel{\mathit{\text{iid}}}{~}N(0,{\sigma }^2)$. The regression function f is typically restricted to a particular class of functions. We consider the subset of M^th-order Sobolev space that includes only functions that integrate to zero and have M proper derivatives, i.e., f ∈ ℱ_M where

$${ℱ}_M=\{g|g,\dots ,g^{(M-1)}\text{are absolutely continuous,}{\displaystyle {\int }_0^{1}g(s)ds=0,g^{(M)}}\in L^2[0,1]\}.$$ (3)

To ensure that each draw from f’s prior is a member of this space, we select a Gaussian process prior with cov(f(s), f(t)) = σ²τ²K₁(s,t), where the kernel is defined as,

$$K_1(s,t)={\displaystyle \sum _{m=1}^{M+1}{c}_m{B}_m(s)B_m(t)+\frac{{(-1)}^M}{(2(M+1))!}{B}_{2(M+1)}(|s-t|),}$$

c_m > 0 are known constants, and B_m is the m^th Bernoulli polynomial. Wahba (1990) shows that each draw from this Gaussian process resides in ℱ_M and the posterior mode assuming c_m = ∞ for m ≤ M and c_M+1 = 1 is the (M + 1)^st order smoothing spline. Steinberg and Bursztyn (2004) discuss an additional interpretation of this kernel. They show that for the same choices of c_m that this Gaussian process model is equivalent to a Bayesian trigonometric regression model with diffuse priors for the low-order polynomial trends, a proper Gaussian prior for the (M+1)^st-degree polynomial, and independent Gaussian priors for the trigonometric basis function’s coefficients with variances that depend on the frequencies of the trigonometric functions.

For the remainder of the paper we select M = 1 and set c ≡ c₁ = … = c_M+1. Therefore draws from the prior are continuously differentiable with path properties of integrated Brownian motion. As discussed in Section 3, to perform variable selection we require c < ∞. In this kernel, the term $K_p(s,t)={\mathrm{\Sigma }}_{m=1}^{M+1}{B}_m(s)B_m(t)$ controls the variability of the (M + 1)^st-degree polynomial trend and $K_N(s,t)=\frac{{(-1)}^M}{(2(M+1))!}{B}_{2(M+1)}(|s-t|)$ is the stationary covariance of the deviation from the polynomial trend. In our analyses in Sections 5 and 6, the constant c is set to 100 to give vague, yet proper, priors for the linear and quadratic trends. So our model essentially fits a quadratic response surface regression plus a remainder term which is a zero-mean stationary Gaussian process constrained to be orthogonal to the quadratic trend. We have intentionally overparameterized with τ² and σ² for reasons that will be clear in Section 3.

2.2 Multiple regression

The nonparametric multiple regression model for response y_i is y_i = μ + f(x_1i, …, x_pi) + ϵ_i, where x_1i, …, x_pi ∈ [0, 1] are covariates, f ∈ ℱ is the unknown function, and ${ϵ}_i\stackrel{\mathit{\text{iid}}}{~}N(0,{\sigma }^2)$. To perform variable selection, we use the ANOVA decomposition of the space ℱ into orthogonal subspaces, i.e.,

$$ℱ=\{\underset{j=1}{\overset{p}{{\displaystyle \oplus }}}{ℱ}_j\}\oplus \{\underset{k<l}{\overset{p}{{\displaystyle \oplus }}}({ℱ}_k\otimes {ℱ}_l)\}\oplus \dots$$ (4)

where ⊕ the direct sum, ⊗ is the direct product, and each ℱ_j is given by (3) (See Wahba (1990) or Gu (2002) for more details). Assume that each f_j is a Gaussian process with covariance ${\sigma }^2{\tau }_j^2{K}_1(x_{ji},x_{ji\prime })$ and that each f_kl is a Gaussian process with covariance ${\sigma }^2{\tau }_{kl}^2{K}_2(x_{ki},x_{ki\prime },x_{li},x_{li\prime })$, where

$$\begin{array}{ll}{K}_2(x_{ki},x_{ki\prime },x_{li},x_{li\prime })\hfill & =(K_P(x_{ki},x_{ki\prime })+K_N(x_{ki},x_{ki\prime }))(K_P(x_{li},x_{li\prime })+K_N(x_{li},x_{li\prime }))\hfill \\ \hfill & +(c-1)K_P(x_{ki},x_{ki\prime })K_P(x_{li},x_{li\prime }).\hfill \end{array}$$ (5)

For large c, the final term (c−1) K_P (x_ki, x_ki′) K_P (x_li, x_li′) gives a vague prior to the low-order bivariate polynomial trend. Using this kernel, f_j ∈ ℱ_j and f_kl ∈ ℱ_k ⊗ ℱ_l. This will ensure that each draw from this space will satisfy ${\displaystyle {\int }_0^1{f}_j(s)ds=0,j=1,\dots ,p}$, to identify the intercept. This also identifies the main effects by forcing the interactions to satisfy ${\displaystyle {\int }_0^1{f}_{kl}(s,t)ds=}{\displaystyle {\int }_0^1{f}_{kl}(s,t)dt=}0,k<l=2,\dots ,p$. These constraints allow for a straightforward interpretation of each term’s effect.

Higher order interactions can also be included. However, these terms are difficult to interpret. Therefore, we combine all higher order interactions into a single process. Let the higher-order interaction space be

$${ℱ}_o=ℱ\cap \{\underset{j=1}{\overset{p}{{\displaystyle \oplus }}}{ℱ}_j\oplus \underset{k<l}{\overset{p}{{\displaystyle \oplus }}}({ℱ}_k\otimes {ℱ}_l){\}}^C,$$ (6)

where A^C is the compliment of A. The covariance of the Gaussian process f_o ∈ ℱ_o is

$$\begin{array}{ll}\text{cov}(f_0({\mathbf{x}}_i),f_0({\mathbf{x}}_{i\prime }))\hfill & ={\sigma }^2{\tau }_0^2[{\displaystyle \prod _{j=1}^p(1+K_1(x_{ji},x_{ji\prime }))}\hfill \\ \hfill & -1-{\displaystyle \sum _{j=1}^p{K}_1(x_{ji},x_{ji\prime })-}{\displaystyle \sum _{j<k}^p{K}_2(x_{ji},x_{ji\prime },x_{ki},x_{ki\prime })}].\hfill \end{array}$$ (7)

Defining the covariance this way assures that f₀ will be orthogonal to each main effect and interaction term.

The finite-dimensional model for the vector of observations y = (y₁, …, y_n)′ is

$$\mathbf{y}=\mathit{\mu }+{\displaystyle \sum _{j=1}^p{\mathbf{f}}_j({\mathbf{x}}_j)+{\displaystyle \sum _{k<l}{\mathbf{f}}_{kl}({\mathbf{x}}_k,{\mathbf{x}}_l)+{\mathbf{f}}_0({\mathbf{x}}_1,\dots ,{\mathbf{x}}_p)}}+\epsilon ,$$ (8)

where μ = (μ, …, μ)′ is the intercept, x_j = (x_j1, …, x_jn)′ is a vector of observations for the j^th covariate, f_j(x_j) is the j^th main effect function evaluated at the n observations, f_kl(x_k, x_l) is the vectorized interaction, f₀(x₁, …, x_p) captures higher-order interactions, and ε ~ N (0,σ²I_n). We assume the intercept μ has a flat prior and that σ² ~ InvGamma(a/2, b/2). The priors for the main effect and interaction functions are defined through the kernels in (4) as

$${\mathbf{f}}_j({\mathbf{x}}_j)~N(0,{\sigma }^2{\tau }_j^2{\mathrm{\Sigma }}_j)$$ (9)

$${\mathbf{f}}_{kl}({\mathbf{x}}_k,{\mathbf{x}}_l)~N(0,{\sigma }^2{\tau }_{kl}^2{\mathrm{\Sigma }}_{kl})$$ (10)

$${\mathbf{f}}_0({\mathbf{x}}_1,\dots ,{\mathbf{x}}_p)~N(0,{\sigma }^2{\tau }_0^2{\mathrm{\Sigma }}_0),$$ (11)

where the (i, i′) component of the covariance matrix Σ_j is K₁(x_ji; x_ji′), the (i, i′) component of the covariance matrix Σ_kl is K₂(x_ki, x_ki′, x_li; x_li′), Σ₀ is defined similarly following (7), and τ_j, τ_kl, and τ₀ are unknown with priors given in Section 3. To help specify priors for τ_j, τ_kl, and τ₀, we rescale Σ_j, Σ_kl, and Σ₀ to have trace n. After this standardization, στ_j (στ_kl) can be thought of as the typical prior standard deviation of an element of f_j (f_kl).

2.3 Categorical predictors

Complex models often have categorical variables that represent different states or point to different submodels to be used in the analysis. The BSS-ANOVA framework is also amendable to these unordered categorical predictors. Assume x_i ∈ {1, 2,…,G} is categorical and f(x_i) = θ_xi, where ${\theta }_g\stackrel{\mathit{\text{iid}}}{~}N(0,{\sigma }^2{\tau }^2)$, g = 1, …, G. To identify the intercept we enforce the sum-to-zero constraint ${\displaystyle {\sum }_{g=1}^G{\theta }_g=0}$. This model can also be written in the kernel framework by taking f to be a mean-zero Gaussian process with singular covariance cov(f(s), f(t)) = σ²τ²K₁(s, t), where the kernel is defined as K₁(s, t) = K_N(s, t),

$$K_N(s,t)=\frac{G-1}{G}I(s=t)-\frac{1}{G}I(s\ne t),$$ (12)

and I(·) is the indicator function. Note that with unordered categorical predictors we exclude the low-order polynomial trend, i.e., K_P (s, t) = 0 for all s and t.

Interactions including categorical predictors with the kernel given in (12) are handled no differently than interactions between continuous predictors. For example, assume x₁ ∈ {1, …, G} is categorical and x₂ ∈ [0, 1] is continuous. The kernel-based interaction is equivalent to the model f_1,2(x₁; x₂) = h_x1(x₂) for some h_x1 ∈ ℱ_M that is, the effect of x₂ is different within each level of x₁. An attractive feature of this kernel is that it enforces the restrictions ∫ h_x1(x₂)dx₂ = 0 for all x₁ ∈ {1, …, G} and Σ_g h_g(x₂) = 0 for all x₂ ∈ [0, 1] to separate the interaction from the main effects.

3 Variable selection

It is common in variable selection to represent the subset of covariates included in the model with indicator variables γ_j and γ_jk, where γ_j is one if the main effect for x_j is in the model and zero otherwise, and γ_jk is one if the interaction for x_j and x_k is in the model and zero otherwise. To avoid enumerating all possible models, stochastic search variable selection (e.g., George and McCulloch, 1993; Chipman, 1996; George and McCulloch, 1997; Mitchell and Beauchamp, 1998) assigns priors to the binary indicators and computes model probabilities using MCMC sampling. To perform variable selection in the nonparametric setting, we specify priors for the standard deviations τ_j and τ_kl in terms of indicators γ_j and γ_kl to give priors with positive mass at zero. Given that τ_j (τ_kl) is zero and c is finite, the curve f_j (f_kl) is equal to zero and the term is removed from the model. This approach is slightly different than the original formulation of George and McCulloch (1993), who give small but non-zero variance to negligible variables; in contrast with their approach, setting the variance precisely to zero completely removes variables from the model.

Parameterization, identification, and prior selection for the hypervariances in Bayesian hierarchical models is notoriously problematic and is an area of active research. After a comparative study of several commonly-used priors, Gelman (2006) recommends either a uniform or half-Cauchy prior on the standard deviation. Following this recommendation, we assume ${\tau }_j={\gamma }_j{\eta }_j\text{where}{\gamma }_j\stackrel{\mathit{\text{iid}}}{~}\text{Bern}(0.5)\text{and}{\eta }_j\stackrel{\mathit{\text{iid}}}{~}\text{HC}(\rho )$, where ρ is the median of the half-Cauchy prior. The interaction standard deviations τ_kl are modelled similarly.

Variable selection can be sensitive to the prior standard deviation. To illustrate the effect of the prior standard deviation on model selection, first consider the simpler case of multiple linear regression with orthogonal covariates, i.e., $y_i={\displaystyle {\sum }_{j=1}^p{\gamma }_j{X}_{ij}{\beta }_j+{ϵ}_i}$, where $\mathbf{X}\prime \mathbf{X}=I_n,{\gamma }_j\stackrel{iid}{~}$ Bern (0.5), β ~ N (0, σ²τ²I_n), and ϵ ~ N (0, σ²I_n). Assuming σ₂ ~ InvGamma (a/2, b/2), the marginal posterior log odds of γ_j = 1 are approximately

$$\text{log}\frac{p({\gamma }_j=1|\mathbf{y},\tau )}{p({\gamma }_j=0|\mathbf{y},\tau )}\approx -\frac{1}{2}\text{log}\left(1+{\tau }^2\right)+\frac{t_j^2{\tau }^2}{2\left(1+{\tau }^2\right)},$$ (13)

where $t_j^2={\widehat{\beta }}_j^2/{\widehat{\sigma }}^2,\widehat{\beta }=\mathbf{X}\prime \mathbf{y}$ is the least squares estimate of β and σ̂² = (y′y + b)/(n + a) is σ²’s posterior mode. If τ = 0, the log odds are zero for any value of $t_j^2$; as τ goes to infinity, the log odds decline to negative infinity for any value of $t_j^2$. Therefore, if τ’s prior is chosen haphazardly, the influence of the data can be completely overwhelmed by the prior standard deviation.

Given the subtle relationship between τ and the posterior of γ_j, it is difficult to chose a prior for τ that accurately depicts our prior model uncertainty. To alleviate this issue, we select priors for the standard deviations to give desirable long-run false positive rates. The marginal log odds for the univariate nonparametric model in Section 2.1 (analogous to (13) for linear regression) are approximately

$$\text{log}\frac{p(\gamma =1|\mathbf{y},\tau )}{p(\gamma =0|\mathbf{y},\tau )}\approx -\frac{1}{2}\text{log}|{\tau }^2\mathrm{\Sigma }+I|+\frac{1}{2}\mathbf{y}\prime {({\mathrm{\Sigma }}^{-1}/{\tau }^2+I)}^{-1}\mathbf{y}$$ (14)

Appendix A.1 shows that under the null distribution y ~ N(0,σI),

$$\mathbf{E}\left[\text{log}\left(\frac{p(\gamma =1|\mathbf{y},\tau )}{p(\gamma =1|\mathbf{y},\tau )}\right)\right]\approx -n{\tau }^2,$$ (15)

where the expected value is taken with respect to y. This suggests that τ’s prior should be scaled by $\sqrt{n}$, e.g., we take $\tau ~\text{HC}(\lambda /\sqrt{n})$. This is similar to the unit-information prior of Kass and Wasserman (1995) which uses $\sqrt{n}$-scaling and to the approach of Ishwaran and Rao (2005) who use $\sqrt{n}$-scaling for the Bayesian linear regression model to give desirable frequentist properties. It is important to note that since our prior depends on the sample size n the procedure is not technically fully-Bayesian, however the procedure could easily be modified to be fully-Bayesian by incorporating reliable prior information for τ.

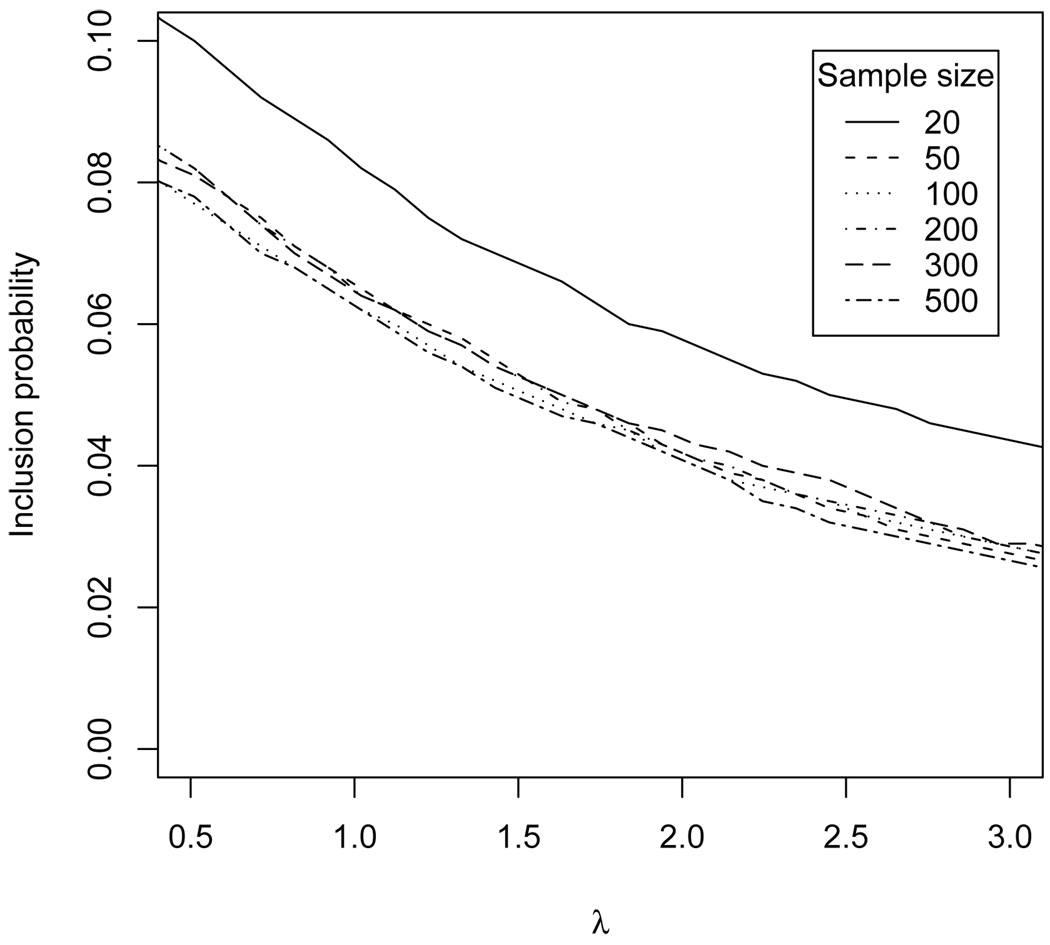
To select λ, we randomly generate 10,000 y for various n assuming y ~ N(0, I_n). For each simulated data set, we compute E(π|y). Since it is common to select a variable if E(π|y) > 0.5 (e.g., Barbieri and Berger, 2004), Figure 1 shows the proportion of the 10,000 data sets that give E(π|y) > 0.5 for each n and λ. After tuning τ’s prior to depend on n, the false positive rate remains stable for n ≥ 50 and is around 0.05 for λ = 2. Although this result applies to the univariate model, we also use half-Cauchy priors with λ = 2 for each standard deviation in the multivariate model. Section 5’s simulation study verifies that this prior controls the false positive rate in the multiple-predictor setting as well, even in the presence of correlated predictors.

Figure 1.

Plot of the probability (with respect to y’s null distribution) that E(π|y, λ) > 0.5 by λ.

4 MCMC algorithm

This section describes the algorithm used to draw MCMC samples from the posterior of the models defined in Sections 2 and 3. Gibbs sampling is used for μ and σ². The full conditionals for these parameters are

$$\mu |\text{rest}~N(\mathbf{1}\prime [\mathbf{y}-\mathbf{f}({\mathbf{x}}_1,\dots ,{\mathbf{x}}_p)]/n,{\sigma }^2/n)$$ (16)

$${\sigma }^2|\text{rest}~\text{InvGamma}([n(p+p(p-1)/2+1)+a]/2,[SSE+SSM+b]/2),$$ (17)

where

$$\mathit{\text{SSE}}=(\mathbf{y}-\mathbf{f}({\mathbf{x}}_1,\dots ,{\mathbf{x}}_p){)}^{\prime }(\mathbf{y}-\mathbf{f}({\mathbf{x}}_1,\dots ,{\mathbf{x}}_p))$$ (18)

$$\mathit{\text{SSM}}={\displaystyle \sum _{j=0}^p{f}_j({\mathbf{x}}_j)\prime }{\mathrm{\Sigma }}_j^{-1}{f}_j({\mathbf{x}}_j)/{\tau }_j^2+{\displaystyle \sum _{k<l}{f}_{kl}({\mathbf{x}}_k,{\mathbf{x}}_l)\prime }{\displaystyle {\sum }_{kl}^{-1}{f}_{kl}}({\mathbf{x}}_k,{\mathbf{x}}_l)/{\tau }_{kl}^2.$$ (19)

In the case of categorical predictors the covariance matrices will be singular, and we use the generalized inverses.

Define all the parameters in the model other than the j^th main effect parameters f_j(x_j) and τ_j as Θ_j. Draws from p(f_j(x_j), τ_j|Θ_j) are made by first integrating over f_j(x_j) and making a draw from p(τ_j|Θ_j) and then sampling f_j(x_j) given τ_j and Θ_j. Integrating over f_j(x_j) gives

$$p({\tau }_j|{\mathrm{\Theta }}_j)\propto \{\begin{array}{ll}\text{exp}\left(-\frac{{\mathbf{z}}_j^{\prime }{\mathbf{z}}_j}{2{\sigma }^2}\right),\hfill & \text{if}{\tau }_j=0;\hfill \\ |{\mathrm{\Delta }}_j{|}^{1/2}\text{exp}\left(-\frac{{\mathbf{z}}_j^{\prime }{\mathrm{\Delta }}_j{\mathbf{z}}_j}{2{\sigma }^2}\right)g({\tau }_j|\lambda ),\hfill & \text{if}{\tau }_j>0\hfill \end{array}$$ (20)

where ${\mathrm{\Delta }}_j=I_n-{\left(I_n+{\displaystyle {\sum }_j^{-1}/}{\tau }_j^2\right)}^{-1}$, z_j = y − f(x₁,…,x_p) + f_j(x_j), and g(τ_j|λ) is the half-Cauchy density function. Samples are drawn from p(τ_j|Θ_j) using adaptive-rejective sampling with candidates taken from the τ_j’s prior. Note that we do not directly sample γ_j or η_j, but rather we directly sample the standard deviation τ_j = γ_jη_j assuming its zero-inflated half-Cauchy prior. Given τ_j, the main effect curve has full conditional

$${\mathbf{f}}_j({\mathbf{x}}_j)|{\tau }_j,{\mathrm{\Theta }}_j~N({\mathrm{\Delta }}_j{\mathbf{z}}_j,{\sigma }^2{\mathrm{\Delta }}_j),$$ (21)

and is updated using Gibbs sampling. This approach is also used to update the interaction curves.

Inverting the n × n matrix $I_n+{\displaystyle {\sum }_j^{-1}/{\tau }_j^2}$ at each MCMC iteration can be cumbersome for large data sets. However, matrix inversion can be avoided by computing the spectral decomposition Σ_j outside of the MCMC algorithm. Let ${\displaystyle {\Sigma }_j={\mathrm{\Gamma }}_j{D}_j{\mathrm{\Gamma }}_j^{\prime }}$, where Γ_j is the n × n orthonormal eigenvector matrix and D_j is the diagonal matrix of eigenvalues d_j1 ≥ … ≥ d_jn. Then f_j(x_j) can updated by drawing ${\mathbf{r}}_j~N\left(0,{\sigma }^2{\left[I_n+{\tau }_j^2{D}_j\right]}^{-1}\right)$ and setting

$${\mathbf{f}}_j=\mathrm{\Gamma }\left[{\left(I_n+{\tau }_j^2{D}_j\right)}^{-1}\mathrm{\Gamma }\prime {\mathbf{z}}_j+{\mathbf{r}}_j\right].$$ (22)

This sampling procedure only requires inversion of the diagonal matrix $I_n+{\tau }_j^2{D}_j$.

In practice retaining all n eigenvector/eigenvalue pairs in the spectral decomposition of Σ_j may be unnecessary. A reduced model replaces ${\displaystyle {\mathrm{\Sigma }}_j={\mathrm{\Gamma }}_j{D}_j{\mathrm{\Gamma }}_j^{\prime }}\text{with}{\mathrm{\Sigma }}_j^{*}={\mathrm{\Gamma }}_j^{*}{D}_j^{*}{\mathrm{\Gamma }}_j^{*}\prime ,\text{where}{\mathrm{\Gamma }}_j^{*}$ is the first K rows of Γ_j and $D_j^{*}$ is the diagonal matrix with diagonal elements d_j1, …, d_jK. Analogous simplifications may be used for the interaction curves.

MCMC sampling is carried out in the freely available software package R (R Development Core Team, 2006). We generate 20,000 samples from the posterior and discard the first 5,000. Convergence is monitored by inspecting trace plots of the deviance and several of the variance parameters. For each MCMC iteration our model is on the order of (number of terms in the model)*K². Therefore as the number of interactions increases computation becomes more time-consuming. For the WIPP data in Section 6 the two-way interaction model runs in a few hours on an ordinary PC.

We compare models using the deviance information criterion (DIC) of Speigelhalter et al. (2002), defined as DIC = D̄ + p_D where D̄ is the posterior mean of the deviance, p_D = D̄ − D̂ is the effective number of parameters, and D̂ is the deviance evaluated at the the posterior mean of the parameters in the likelihood. The model’s fit is measured by D̄, while the model’s complexity is captured by p_D. Models with smaller DIC are preferred.

5 Simulation study

In this section we conduct a simulution study to compare the BSS-ANOVA model described in Section 2 to MARS, the COSSO, and the Gaussian process model of Linkletter et al. (2006). MARS analyses are done in R using the “polymers” function in the “polspline” package. The Gaussian process model of Linkletter assumes that f (x₁,…, x_p) is multivariate normal with mean μ and covariance

$$\text{Cov}(f(x_{1i},\dots ,x_{pi}),f(x_{1i\prime },\dots ,x_{pi\prime }))={\tau }^2{\displaystyle \prod _{j=1}^p{\rho }_j^{4{(x_{ji}-x_{ji\prime })}^2}}.$$ (23)

The correlation parameter ρ_j’s prior is a mixture of a Uniform(0,1) and a point mass at one, with the point mass at one having prior probability 0.25. If ρ_k = 1, x_k does not appear in the covariance and is essentially removed from the model.

5.1 Setting

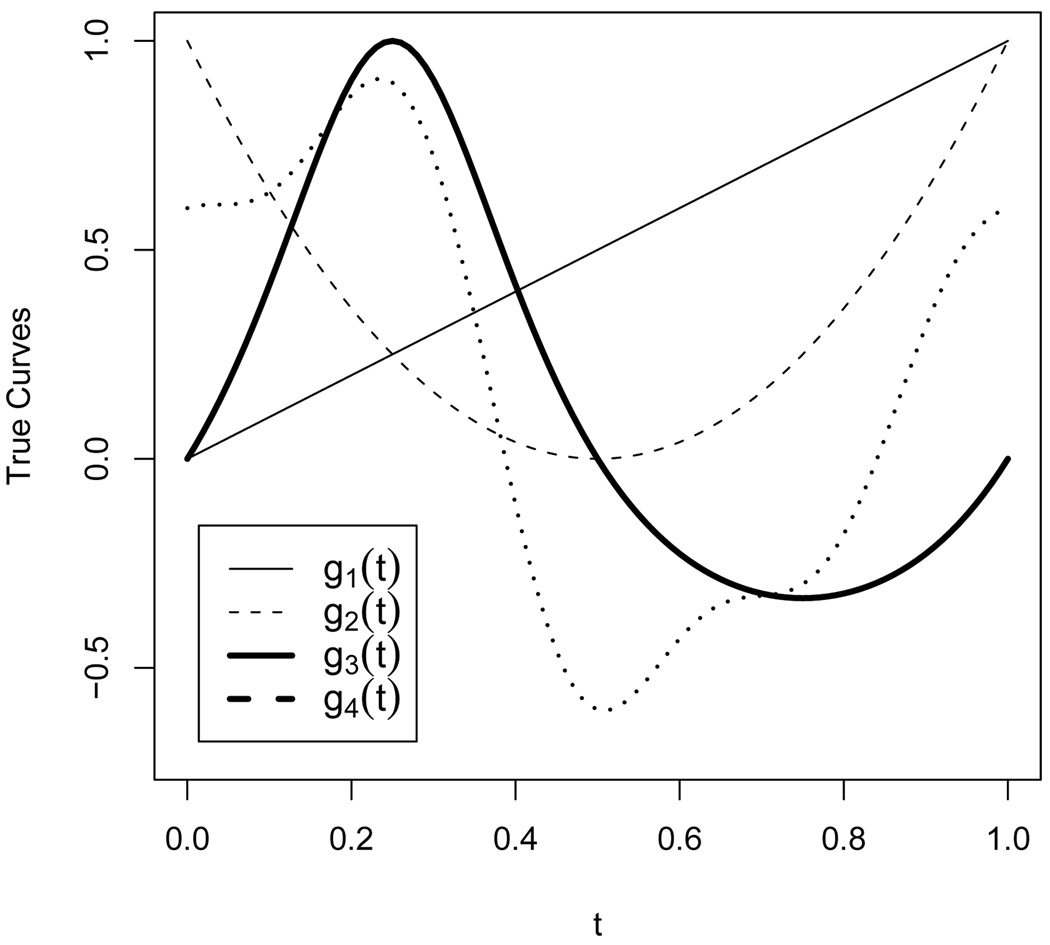
Data are generated assuming the underlying models in Table 1. We use 50 simulated data sets for each simulation scenario. Following Li and Zhang (2006), we specify models using four building block functions (plotted in Figure 2):

• g₁(t) = t

• g₂(t) = (2t − 1)²

• g₃(t) = sin(2πt)/(2 − sin(2πt))

• g₄(t) = 0.1 sin(2πt) + 0.2 cos(2πt) + 0.3 sin²(2πt) + 0.4 cos³(2πt) + 0.5 sin³(2πt).

Table 1.

Simulation study design.

Design	n	p	σ	f (x1, …, xp)
1	100	10	2.28	5g1(x1) + 3g2(x2) + 4g3(x3) + 6g4(x4)
2	100	4	2.28	5g1(x1) + 3g2(x2) + 4g3(x1x2x3)
3	100	6	2.28	5g1(x1) + 3g2(x2) + 4g3(x3) + 6g4(x4) 4g3(x1x2)

Figure 2.

Plots of the true functions used in the simulation study.

The covariates x₁, …, x_p are generated on the interval [0,1] using three covariance structures: independence, compound symmetry (CS), and autoregressive (AR). For the independence case, the covariates are generated as independent Uniform(0,1). To draw covariates with a compound symmetric covariance, we sample w₀, …, w_p as independent Uniform(0,1) variables and define x_j = (w_j + tw_o)/(1 + t), to give $\text{Cov}({\mathbf{x}}_j,{\mathbf{x}}_j^{\prime })=t^2/(1+t^2)$ for any pair (j, j′). The autoregressive covariates are generated by sampling w₁, …, w_p as independent Normal (0,1) variables, and defining x₁ = w₁ and ${\mathbf{x}}_j=\rho {\mathbf{x}}_{j-1}+\sqrt{1-{\rho }^2}{\mathbf{w}}_j\text{for}j>1$. The covariates are trimmed on [−2.5, 2.5] and scaled to [0,1].

The methods are compared in terms of prediction accuracy and variable selection. For each data set and method we compute

$$\mathit{\text{MSE}}=\frac{1}{1000}{\displaystyle \mathrm{\sum }_{j=1}^{1000}{\left(f(z_{1j},\dots ,z_{pj})-\widehat{f}(z_{1j},\dots ,z_{pj})\right)}^2},$$ (24)

where f is the true mean curve, f̂ is the estimated value (the posterior mean, averaged over all models, for Bayesian methods), x_i, i = 1, …, n, are the observed design points, and z_j, j = 1, …, 1000, are unobserved locations drawn independently from the covariate distribution.

We also record the true positive and false positive rates for each model. The true (false) positive rate is computed by recording the proportion of the important (unimportant) variables included for each data set and averaging over all simulated data sets. A variable is deemed to be included in the BSS-ANOVA model if the posterior inclusion probability is greater than 0.5. Linkletter et al. use an added-variable method to select important variables at a given Type I error level. For computational convenience, we assume a covariate is in the model if the posterior median of ρ_k < 0.5. This gives Type I error of approximately 0.05 for the simulation below. We also tune MARS’s generalized cross-validation penalty to give Type I error near 0.05 (gcv = 2.5 for design 1 and gcv = 2 for designs 2 and 3).

Main effects only models are used for design 1 for MARS, COSSO, and the BSS-ANOVA models; all possible two-way interactions are included as candidates for the other designs. The f₀ component is included for all BSS-ANOVA fits.

5.2 Results

For each simulation design, the Bayesian MSE is substantially smaller than the MSE for MARS and COSSO (Table 2a). Although MARS is able is mimic many of the important features of the true curves, its piece-wise linear fit does not match the smooth true curves in Figure 2. As also shown by Lin and Zhang (2006), the COSSO improves on MARS. Although the fitted curves from the COSSO are often similar to the Bayesian model, the Bayesian model achieves smaller MSE through model averaging. It may also be possible to improve the performance of the frequentist methods using non-Bayesian model averaging such as bagging (Brieman, 1996).

Table 2.

Results of the simulation study. PMSE is reported as the mean (standard error) over the simulated datasets for each simulation setting. The true (false) positive rate is computed by recording the proportion of the important (unimportant) variables included for each data set and averaging over all simulated data sets. A variable is deemed to be included in the Bayesian models if the posterior inclusion probability is greater than 0.5.

(a) Prediction mean squared error (PMSE)
Design	Correlation of the predictors	MARS	COSSO	BSS-ANOVA	Linkletter
1	Ind	3.23 (0.28)	2.33 (0.13)	1.67 (0.08)	3.50 (0.12)
1	CS (t=1)	7.60 (0.83)	6.08 (0.40)	4.11 (0.27)	7.39 (0.24)
1	AR (ρ=0.5)	5.86 (0.44)	5.37 (0.33)	3.72 (0.18)	6.38 (0.22)
2	Ind	2.26 (0.08)	1.68 (0.04)	1.63 (0.04)	1.40 (0.05)
3	Ind	5.03 (0.38)	4.79 (0.23)	2.72 (0.09)	4.50 (0.08)

(b) Inclusion percentage for variables not in the true model
Design	Correlation of the predictors	MARS	COSSO	BSS-ANOVA	Linkletter
1	Ind	0.04	0.06	0.03	0.03
1	CS (t=1)	0.04	0.13	0.03	0.08
1	AR (ρ=0.5)	0.03	0.12	0.05	0.06
2	Ind	–	–	–	–
3	Ind	0.04	0.13	0.10	0.11

(c) Inclusion percentage for variables in the true model
Design	Correlation of the predictors	MARS	COSSO	BSS-ANOVA	Linkletter
1	Ind	0.78	0.91	0.91	0.81
1	CS (t=1)	0.74	0.83	0.79	0.80
1	AR (ρ=0.5)	0.75	0.82	0.78	0.80
2	Ind	–	–	–	–
3	Ind	0.67	0.77	0.82	0.89

For each simulation design (inclusion rates are not given for Design 2 because it is does not fall within our BSS-ANOVA model that does not include three-way interactions) the BSS-ANOVA model also maintains the nominal false positive rate; for all simulations 3–10% of the truly uninformative variables are included in the model (Table 2b), supporting the choice of hyperparameters in Section 3. To further support the hyperparameter selection, we also simulated 50 data sets from the null model with p = 10 unimportant predictors and σ = 2.28 (not shown in Table 2). The false selection rate was no more than 7.5% for independent, CS, or AR(1) covariates. Also, despite the potential effects of concurvity (Gu, 1992; Gu, 2004), nonparametric analogue of multicollinearity, the BSS-ANOVA is able to identify truly important predictors at a high rate even with correlated predictors.

The BSS-ANOVA model also outperforms Linkletter’s method for designs 1 and 3. These designs exclude some of the interactions involving the important main effects, and therefore Linletter’s full-interaction model is not appropriate. Linkletter’s method does perform well for design 2 which includes a three-way interaction and no variables not included in the three-way interaction. This illustrates that Linkletter et al.’s method is preferred if the response surface is a complicated function of high-order interactions between all of the significant predictors, whereas the proposed method is likely to perform well if the response surface is the sum of simple univariate and bivariate functions.

6 Analysis of the WIPP data

In this section we analyze the WIPP data described in Section 1. The outcome variable of interest here is cumulative brine flow (m3) into waste repository at 10,000 years for a drilling intrusion at 1000 year that penetrates the repository and an underlying region of pressurized brine; an E1 intrusion in the terminology of Helton et al. (2000). The four main pathways by which brine enters the repository are flow through the anhydrite marker beds, drainage from the disturbed rock zone, flow down the intruding borehole from overlying formations, and brine flow up the borehole from a pressurized brine pocket. There are n = 300 observations and we include p = 11 possible predictors. The predictors involved in the Two-Phase Fluid Flow model describe various environmental conditions and are described briefly in Appendix A.2 and in detail in Vaughn et al. (2000). All of the predictors are continuous except for the pointer variable for microbial degradation of cellulose (WMICDFLG) which has three levels: (1) no microbial degradation of cellulose, (2) microbial degradation of only cellulose, and (3) microbial degradation of cellulose, plastic, and rubber.

We compare the BSS-ANOVA model with two-way interactions with the model of Linkletter et al. (2007). It is difficult to incorporate categorical predictors in Linkletter et al.’s Gaussian process model, but to facilitate the comparison we order the three categories of microbial degradation of cellulose by their within-level mean response and treat the ordered variable as continuous. The inclusion probabilities in Table 3 for the BSS-ANOVA’s main effects are fairly similar to the inclusion probabilities for Linkletter et al.’s model. Five variables have posterior inclusion probabilities equal to 1.00 for both models: anhydrite permeability (ANHPRM), borehole permeability (BHPRM), bulk compressibility of brine pocket (BPCOMP), halite porosity (HALPOR), and microbial degradation of cellulose (WMICDFLG). This set of important variables is consistent with previous analysis of this model using stepwise regression approaches (Helton, 2000 and Storlie, 2007).

Table 3.

Comparison of variable importance for the WIPP data. “Inc. Prob” in the posterior inclusion probability and “L2 norm” is the posterior 95% interval of ${\displaystyle \int {}_0^1{f}_j^2(s)ds}$.

	BSS-ANOVA		Linkletter	BSS-ANOVA best model
	Inc. Prob.	L2 norm	Inc. Prob.	L2 norm
ANHPRM	1.00	(0.43, 1.10)	1.00	(0.41, 0.89)
BHPERM	1.00	(1.59, 3.13)	1.00	(1.81, 2.88)
BPCOMP	1.00	(0.78, 1.67)	1.00	(0.83, 1.45)
BPPRM	0.08	(0.00, 0.03)	0.01	–
HALPOR	1.00	(0.56, 1.67)	1.00	(0.58, 1.09)
HALPRM	0.46	(0.00, 0.10)	0.03	–
SHPRMCLY	0.28	(0.00, 0.07)	0.01	–
SHPRMSAP	0.12	(0.00, 0.03)	0.07	–
SHPRNHAL	0.11	(0.00, 0.04)	0.00	–
SHRBRSAT	0.66	(0.00, 0.14)	0.03	(0.01, 0.13)
WMICDFLG	1.00	(0.66, 1.55)	1.00	(0.80, 1.57)
BPCOMP × WMICDFLG	1.00	(0.41, 0.99)	–	(0.44, 0.92)
BPCOMP × BHPERM	0.93	(0.00, 0.21)	–	(0.04, 0.34)
SHPRMSAP × WMICDFLG	0.85	(0.00, 0.18)	–	(0.02, 0.15)
SHRGSSAT × SHPRNHAL	0.60	(0.00, 0.10)	–	(0.01, 0.12)

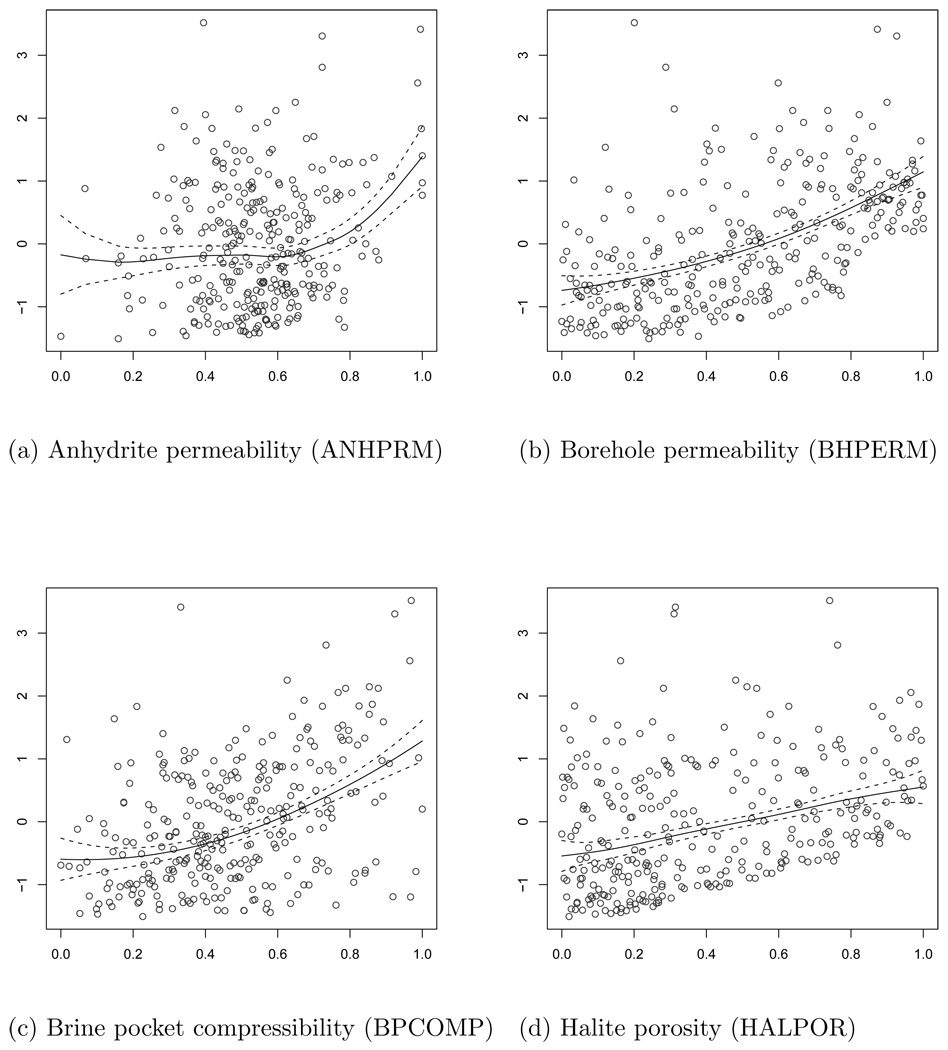
The posterior mean curves from the BSS-ANOVA model for several predictors are plotted in Figure 3. Note that due to the BSS-ANOVA decomposition the estimates of the main effect curves are interpretable on their own. There is no need to numerically integrate over the other predictors as in partial dependence plots (Hastie et al., 2001). The effects for bulk compressibility (BPCOMP) and borehole permeability (BHPERM) are postive. Increasing BPCOMP increases the amount of brine that leaves the brine pocket for each unit drop in pressure, and increasing BHPRM both reduces the pressure in the repository and reduces resistance to flow between the brine pocket and the repository. Both of these result in a larger brine flow into the repository through the borehole. Positive effects are also indicated for ANHPRM and HALPOR. These result from reducing the resistance to flow in the anhydrite and halite, respectively which increases brine flow from the marker beds. Notice also how the effect from ANHPRM is flat for the first half of its range. This is because it needs to exceed a threshold before the permeability is high enough to counteract the pressure in the repository and allow for brine to flow from the marker beds. There is also an overall negative effect when going from levels 1 to 2 to 3 for the microbial degradation flag (WMICDFLG) as seen in Figure 4b. This is because the more microbial gas that is generated, the higher the repository pressure which discourages brine inflow.

Figure 3.

Raw data vs main effect curves (i.e., f_j(x)) for the WIPP data. The solid lines are the medians and the dashed lines are 95% intervals.

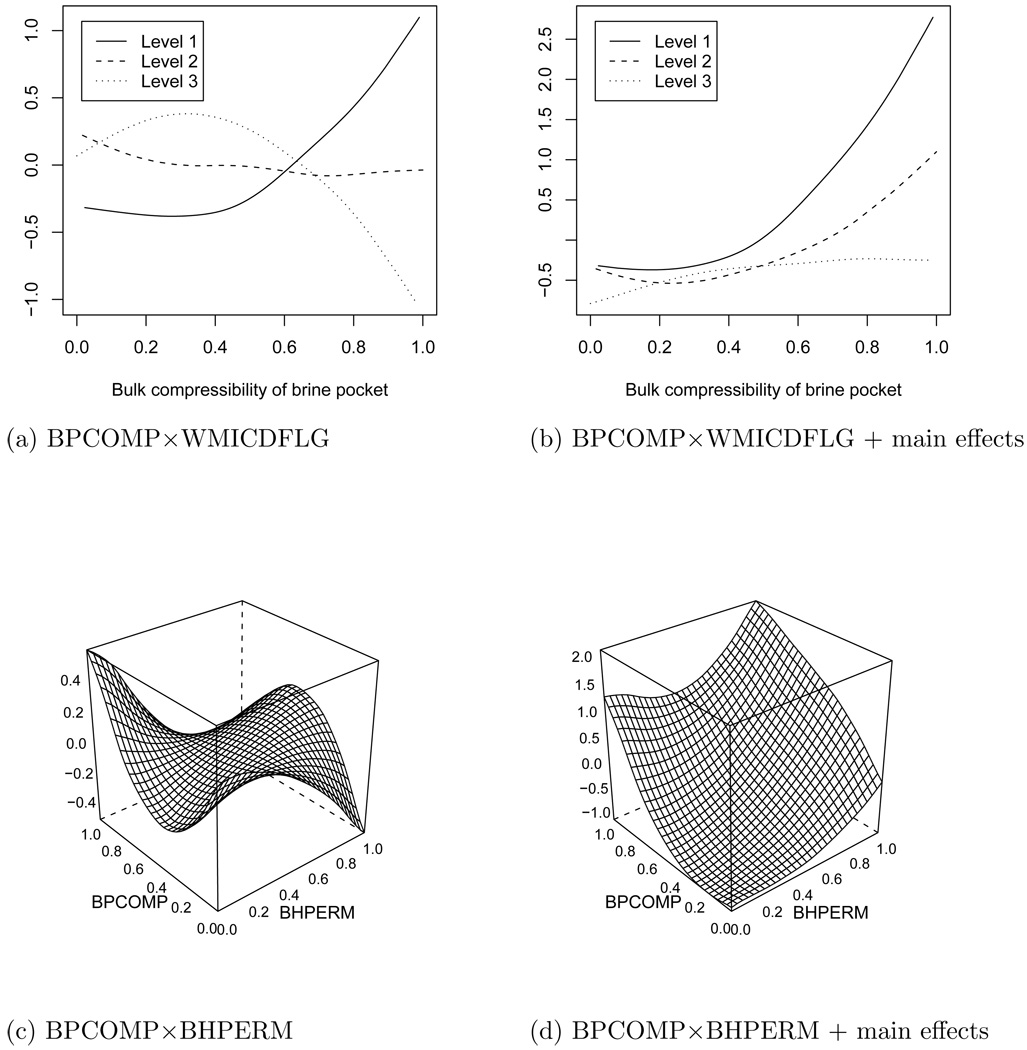
Figure 4.

Interaction plots for compressibility of brine pocket (BPCOMP) × microbial degradation of cellulose (WMICDFLG) and compressibility of brine pocket (BPCOMP) × intrinsic brine pocket permeability (BHPERM). Panels (a) and (c) give the posterior mean of f_jk(x_j, x_k) and Panels (b) and (d) give the posterior means of f_j(x_j) + f_k(x_k) + f_jk(x_j, x_k).

The inclusion probabilities for the remaining variables are less than 0.10 using Linkletter et al.’s model. The BSS-ANOVA model identifies an additional main effect, residual brine saturation in the shaft (SHRBRSAT), with inclusion probability 0.66. This association is somewhat surprising because the shaft seals are quite effective so the flow is unlikely to go down the shaft. This is being looked into further.

The inclusion probability for the BSS-ANOVA’s main effects are as high or higher than the inclusion probabilities for Linkletter et al.’s model for each predictor. This may be due to the fact that when a variable is included in the Gaussian process model all interactions must be included, whereas the additive model can simply add a main effect curve. The posterior mean curves in Figure 3 are fairly smooth, suggesting that low-order polynomial fits are adequate. The priors for these low-order polynomials are vague under the BSS-ANOVA model, so the model is able to essentially reduce to quadratic regression for these predictors. This is a very different fit from Linkletter et al.’s model which for most draws is a full Gaussian process in these five dimensions. For these data DIC prefers the BSS-ANOVA decomposition (DIC = 362; p_D = 68.4) compared to Linkletter et al.’s model (DIC = 375; p_D = 65.3). Note that we do not use DIC for variable selection – this is done using the Bayesian variable selection algorithm described in Section 3 – we use DIC to compare the fits of the non-nested BSS-ANOVA and Gaussian process models, both of which average over several models defined by the binary inclusion indicators.

Of the 55 possible two-way interactions in the BSS-ANOVA, 4 have inclusion probability greater than 0.5 (Table 3). Also, the f₀ term for higher order terms is included only 7% of the time. The interaction with the highest inclusion probability (1.00) is the interaction between bulk compressibility of brine pocket (BPCOMP) and microbial degradation of cellulose (WMICDFLG). Figures 4a and 4b plot the fitted values (posterior mean, averaging over all models) of the interaction effect for this pair of predictors. Figure 4a clearly demonstrates the constraints of the BSS-ANOVA model for interactions. The curve for each level of WMICDFLG integrates to zero and the sum of the three curves equals zero for each value of BPCOMP. Figure 4b is the sum of the interaction and main effect curves. Here we see an increasing trend for BPCOMP for each level of WMICDFLG, however the trend is nearly flat when WMICDFLG equals level 3, which implies microbial degradation of cellulose, plastic, and rubber. This is reasonable because the gas produced by the degradation could cause enough pressure to make brine inflow negligable for this range of BPCOMP. Figures 4c and 4d plot the fitted values for the interaction between compressibility of brine pocket (BPCOMP) and intrinsic brine pocket permeability (BHPERM) which has the second largest inclusion probability (0.93). Notice in the upper right corner that the interaction indicates a decrease in brine inflow from the additive effects. This is very interesting because at large values of BHPERM and BPCOMP so much brine flows down the borehole that the repository saturates and rises to hydrostatic pressure, which reduces brine inflow from the brine pocket. These important interactions have not been studied in the previous analysis of this problem. However, they would easily help to give the scientists an increased understanding and/or confirmation of their model.

We measure variable importance with the posterior 95% interval of f_j and f_kl’s L2-norms, ${\displaystyle {\int }_0^1{f}_j{(s)}^{2}ds}\text{and}{\displaystyle {\int }_0^1{\displaystyle {\int }_0^1{f}_{kl}{(s_1,s_2)}^2}d{s}_{1}d{s}_2}$, respectively. The L2-norms are proportional to the proportion of variation in the model explained by each term. We approximate these integrals by taking the sum at the n = 300 design points. The L2-norm intervals in Table 3 show that of the predictors included with probability 1.00, borehole permeability (BHPRM) generally explains the largest proportion of the variance in the fitted function. Also, even though there are interactions selected with probability greater than 0.5, these terms explain less variation in the fitted surface than the important main effects. This sensitivity analysis accounts for variable selection uncertainty, that is, the L2-norm is computed every MCMC iteration, even iterations that exclude the variable. Another common approach to sensitivity analysis is to first select the important variables and then compute the L2-norms for the important variables using the model including only the selected variables. To illustrate how these approaches differ, we refit the BSS-ANOVA model using only the variables with inclusion probability greater than 0.5. The resulting L2-norms are given in Table 3 (“BSS-ANOVA best model”). The intervals for this model are generally narrower than the intervals from the full model. Therefore, accounting for variable selection uncertainty in sensitivity analysis gives wider, more realistic, posterior intervals.

Section 3 develops a method for selecting the hyperparameter λ which controls the strength of the variances’ priors. Based on these results we recommend using λ = 2. For these data however the posterior inclusion probabilities are robust to the selection of λ. We refit the model with λ ∈ {1, 2, 3}; the posterior mean number of variables in the model (i.e., the posterior mean of ${\displaystyle {\sum }_{j=0}^{p}I({\tau }_j>0)+}{\displaystyle {\sum }_{k<l}I({\tau }_{kl}>0)}$) was 16.4 with λ = 1, 14.8 with λ = 2, and 13.4 with λ = 3. Also, for all three choices of λ the same subset of terms with inclusion probability greater than 0.5 are identified with the sole exception that halite permeability (HALPRM) is included in the model with inclusion probability 0.51 with λ = 1 (compared to 0.46 with λ = 2).

7 Discussion

This paper presents a fully-Bayesian procedure for variable selection and curve-fitting for nonparametric regression. Our model uses the smoothing splines ANOVA decomposition and selects components via stochastic search variable selection. We tune the model to have a desired false positive rate. The simulation study shows that the Bayesian model has advantages over other nonparametric variable selection models in terms of both prediction accuracy and variable selection. The model is used to build an emulator for complex computer model output.

Another challenge in the analysis of complex computer model output is jointly modeling computer model output and actual field data. A common approach is to model both the true response and the bias between field and simulated data with separate Gaussian processes. Our approach could be used in this case to identify important variables for both Gaussian processes, that is, to identify conditions that affect the true process and to identify potentially different variables that predict a discrepancy between simulated and real data. Also, although we applied our method to the deterministic WIPP model, our simulation study suggests that the BSS-ANOVA model is also adept at estimating the mean response for data having random errors.

Appendix

A.1 Approximate expected log odds of π = 1

For the univariate nonparametric model in Section 2.1, integrating over f and σ² gives

$$\frac{p(\gamma =1|\mathbf{y},\tau )}{p(\gamma =0|\mathbf{y},\tau )}=|{\tau }^2\mathrm{\Sigma }+I{|}^{-1/2}{\left(1-\frac{\mathbf{y}\prime {({\mathrm{\Sigma }}^{-1}/{\tau }^2+I)}^{-1}\mathbf{y}}{\mathbf{y}\prime \mathbf{y}+b}\right)}^{-(n+a)/2}.$$ (25)

Assuming the data are standardized so that y′y = n and assuming a = b, for large n we have

$$\text{log}\frac{p(\gamma =1|\mathbf{y},\tau )}{p(\gamma =0|\mathbf{y},\tau )}\approx -\frac{1}{2}\text{log}|{\tau }^2\mathrm{\Sigma }+I|+\frac{1}{2}\mathbf{y}\prime {({\mathrm{\Sigma }}^{-1}/{\tau }^2+I)}^{-1}\mathbf{y}$$ (26)

Taking the expected value with respect to y ~ N (0, I) gives

$$\mathrm{E}\left[\text{log}\frac{p(\gamma =1|\mathbf{y},\tau )}{p(\gamma =0|\mathbf{y},\tau )}\right]=-\frac{1}{2}\text{log}|{\tau }^2\mathrm{\Sigma }+I|+\frac{1}{2}\text{trace}\left[{({\mathrm{\Sigma }}^{-1}/{\tau }^2+I)}^{-1}\right]$$ (27)

$$=-\frac{1}{2}{\displaystyle \sum _{i=1}^n\text{log}}(1+{\tau }^2{d}_i)+\frac{1}{2}{\displaystyle \sum _{i=1}^n\frac{{\tau }^2{d}_i}{1+{\tau }^2{d}_i},}$$ (28)

where d₁, …, d_n are the eigenvalues of Σ. Recalling that Σ is scaled so that trace$(\mathrm{\Sigma })={\displaystyle {\sum }_{i=1}^n{d}_i=n}$, a first-order Taylor series at τ² = 0 gives $\mathrm{E}\left[\text{log}\frac{p(\gamma =1|\mathbf{y},\tau )}{p(\gamma =0|\mathbf{y},\tau )}\right]\approx -n{\tau }^2$.

A.2 Variable Descriptions for Two-Phase Fluid Flow Example

ANHPRM - Logarithm of anhydrite permeability (m²)

BHPRM - Logarithm of borehole permeability (m²)

BPCOMP - Bulk compressibility of brine pocket (Pa⁻¹)

BPPRM - Logarithm of intrinsic brine pocket permeability (m²).

HALPOR - Halite porosity (dimensionless)

HALPRM - Logarithm of halite permeability (m²)

SHPRMSAP - Logarithm of permeability (m2) of asphalt component of shaft seal (m2)

SHPRMCLY - Logarithm of permeability (m2) for clay components of shaft.

SHPRMHAL - Pointer variable (dimensionless) used to select permeability in crushed salt component of shaft seal at different times

SHRBRSAT - Residual brine saturation in shaft (dimensionless)

WMICDFLG - Pointer variable for microbial degradation of cellulose. WMICDFLG = 1, 2, and 3 implies no microbial degradation of cellulose, microbial degradation of only cellulose, microbial degradation of cellulose, plastic, and rubber.