Abstract
Markov chain Monte Carlo (MCMC) techniques revolutionized statistical practice in the 1990s by providing an essential toolkit for making the rigor and flexibility of Bayesian analysis computationally practical. At the same time the increasing prevalence of massive datasets and the expansion of the field of data mining has created the need for statistically sound methods that scale to these large problems. Except for the most trivial examples, current MCMC methods require a complete scan of the dataset for each iteration eliminating their candidacy as feasible data mining techniques.
In this article we present a method for making Bayesian analysis of massive datasets computationally feasible. The algorithm simulates from a posterior distribution that conditions on a smaller, more manageable portion of the dataset. The remainder of the dataset may be incorporated by reweighting the initial draws using importance sampling. Computation of the importance weights requires a single scan of the remaining observations. While importance sampling increases efficiency in data access, it comes at the expense of estimation efficiency. A simple modification, based on the “rejuvenation” step used in particle filters for dynamic systems models, sidesteps the loss of efficiency with only a slight increase in the number of data accesses.
To show proof-of-concept, we demonstrate the method on two examples. The first is a mixture of transition models that has been used to model web traffic and robotics. For this example we show that estimation efficiency is not affected while offering a 99% reduction in data accesses. The second example applies the method to Bayesian logistic regression and yields a 98% reduction in data accesses.
Keywords: Bayesian inference, massive datasets, Markov chain Monte Carlo, importance sampling, particle filter, mixture model
1. Introduction
The data mining community recognizes the central role of rigorous statistical analysis. Statistical concepts such as regularization, latent variables, spurious correlation, and problems involving model search and selection have appeared in widely noted data mining literature (Elder and Pregibon, 1996; Glymour et al., 1997). However, algorithms for mainstream statistical procedures that actually work on massive datasets, have been slow to appear.
Bayesian analysis is a widely accepted paradigm for estimating unknown parameters from data (Andrieu et al., 2003). In applications with small to medium sized datasets, Bayesian methods have found great success in statistical practice. In particular, applied statistical work has seen a surge in the use of Bayesian hierarchical models for modeling multilevel or relational data in a variety of fields including health and education (Carlin and Louis, 2000). Spatial models in agriculture, image analysis, and remote sensing often utilize Bayesian methods and invariably require heavy computation (Besag et al., 1995). Shrinkage methods in kernel regression, closely related to recent developments in support vector machines, admit a convenient Bayesian formulation, producing posterior distributions over a general class of prediction models (see, for example, Figueiredo, 2001). The appeal of the Bayesian approach stems from the transparent inclusion of prior knowledge, a straightforward probabilistic interpretation of parameter estimates, and greater flexibility in model specification.
While Bayesian models and the computational tools behind them have revolutionized the field, they continue to rely on algorithms that perform thousands or even millions of laps through the dataset. Furthermore, standard algorithms often begin with an implicit “load data into memory” step. These characteristics preclude Bayesian analyses of massive datasets.
The Bayesian approach does lend itself naturally to sequential algorithms. The posterior after the ith datapoint becomes the prior for the i + 1 datapoint, and so on. For analyses that adopt conjugate prior distributions, this can provide a simple, scaleable approach for dealing with massive datasets. However, the simple conjugate setup describes only a small fraction of the modern Bayesian armory. In this paper we propose a general algorithm that performs a rigorous Bayesian computation on a small, manageable portion of the dataset and then adapts those calculations with the remaining observations. The adaptation attempts to minimize the number of times the algorithm loads each observation into memory while maintaining inferential accuracy.
There exists a small literature focused on scaling up Bayesian methods to massive datasets. A number of authors have proposed large-scale Bayesian network learning algorithms, although most of this work is not actually Bayesian per se (see, for example, Friedman et al., 1999). Posse (2001) presents an algorithm for large-scale Bayesian mixture modeling. DuMouchel (1999) presents an algorithm for learning a Gamma-Poisson empirical Bayes model from massive frequency tables. The work of Chopin (2002) is closest to ours. He describes a general purpose sequential Monte Carlo algorithm and mentions applications to massive datasets. While his algorithm is similar to ours, his mathematical analysis differs and he considers examples of smaller scale.
2. Techniques for Bayesian computation
Except for the simplest of models and regardless of the style of inference, estimation algorithms almost always require repeated scans of the dataset. We know that for well-behaved likelihoods and priors, the posterior distribution converges to a multivariate normal (DeG-root, 1970; Le Cam and Yang, 1990). For large but finite samples this approximation works rather well on marginal distributions and lower dimensional conditional distributions but does not always provide an accurate approximation to the full joint distribution (Gelman et al., 1995). The normal approximation also assumes that one has the maximum likelihood estimate for the parameter and the observed or expected information matrix. Even normal posterior approximations and maximum likelihood calculations can require heavy computation. Newton-Raphson type algorithms for maximum likelihood estimation require several scans of the dataset, at least one for each iteration. When some observations also have missing data, the algorithms (EM, for example) likely will demand even more scans. For some models, dataset sizes, and applications these approximation methods may work and be preferable to a full Bayesian analysis. This will not always be the case and so the need exists for improved techniques to learn accurately from massive datasets.
Summaries of results from Bayesian data analyses often are in the form of expectations such as the marginal mean, variance, and covariance of the parameters of interest. We compute the expected value of the quantity of interest, h(θ), using
| (1) |
where f(θ|x), is the posterior density of the parameters given the observed data. Computation of these expectations requires calculating integrals that, for all but the simplest examples, are difficult to compute in closed form. Monte Carlo integration methods sample from the posterior, f(θ|x), and appeal to the law of large numbers to estimate the integral,
| (2) |
where the θi compose a sample from f(θ|x).
Sampling schemes are often difficult enough without the burden of large datasets. The additional complexity of massive datasets usually causes each iteration of the Monte Carlo sampler to be slower. When the number of iterations already needs to be large, efficient procedures within each iteration are essential.
2.1. Importance sampling
Importance sampling is a general Monte Carlo method for computing integrals. As previously mentioned, Monte Carlo methods approximate integrals of the form (1). The approximation in (2) depends on the ability to sample from f(θ|x). When a sampling mechanism is not readily available for the “target density,” f(θ|x), but one is available for another “sampling density,” g(θ), we can use importance sampling. Note that for (1) we can write
| (3) |
| (4) |
where θi is a draw from g(θ) and wi = f (θi|x)/g(θi). Since the expected value of wi under g(θ) is 1, we need only compute weights up to a constant of proportionality and then normalize:
| (5) |
Naturally, in order for the sampling distribution to be useful, drawing from g(θ) must be easy. We also want our sampling distribution to be such that the limit converges quickly to the value of the integral. If the tails of g(θ) decay faster than f(θ|x) the weights will be numerically unstable. If the tails of g(θ) decay much more slowly than f(θ|x) we will frequently sample from regions where the weight will be close to zero, wasting computation time. Second to sampling directly from f(θ|x), we would generally like a sampling density slightly fatter than f(θ|x). See chapter 5 of Ripley (1987) for more details.
In section 2.3 we show that when we set the sampling density to be f(θ|x1,…,xn), where n ≪ N so that we condition on a manageable subset of the entire dataset, the importance weights for each sampled θi require only one sequential scan of the remaining observations. Before beginning that discussion, the next section introduces the most popular computational method for Bayesian analysis of complex models.
2.2. Markov chain Monte Carlo
While some statisticians have long argued that Bayesian analysis is appropriate for a wide class of problems, practical estimation methods were not available until Markov chain Monte Carlo (MCMC) techniques became available. Importance sampling is a useful tool, but for complex models crafting a reasonable sampling distribution can be extremely difficult. The collection Gilks et al. (1996) contains a detailed introduction to MCMC along with a variety of interesting examples and applications.
The goal of MCMC is to generate draws from the posterior density f(θ|x). Whereas importance sampling generates independent draws and associated weights, MCMC methods build a Markov chain, generating dependent draws, θ1,…,θM, that have stationary density f (θ|x). It turns out that it is often easy to create such a Markov chain with a few basic strategies. However, there is still a bit of art involved in creating an efficient chain and assessing the chain’s convergence.
Figure 1 shows the Metropolis-Hastings algorithm (Hastings, 1970; Metropolis et al., 1953) the common form for MCMC algorithms. Assume that we have a single draw θ1 from f(θ|x) and a proposal density for a new draw, q(θ|θ1). If we follow step 2 of the MCMC algorithm then the density of θ2 will also be f (θ|x). This is one of the key properties of the algorithm. Iterating this algorithm we will obtain a sequence θ1,…,θM that has f(θ|x) as its stationary density.
Figure 1.
The Metropolis-Hastings algorithm
MCMC methods have two main advantages that make them so useful for Bayesian analysis. First, subject to certain conditions, we can choose a q from which sampling is easy. Special choices for q, which may or may not depend on the data, simplify the algorithm. If q is symmetric, for example a Gaussian centered on θi−1, then the entire proposal distributions cancel out in (6). If we choose a q that proposes values that are very close to θi−1 then it will almost always accept the proposal but the chain will move very slowly and take a long time to converge to the stationary distribution. If q proposes new draws that are far from θi−1 and outside the region with most of the posterior mass, the proposals will almost always be rejected and again the chain will converge slowly. With a little tuning the proposal distribution can usually be adjusted so that proposals are not rejected or accepted too frequently. The second advantage is that there is no need to compute the normalization constant of f(θ|x) since it cancels out in (6).
The Gibbs sampler (Geman and Geman, 1984) is a special case of the Metropolis-Hastings algorithm and is especially popular. If θ is a multidimensional parameter, the Gibbs sampler sequentially updates each of the components of θ from the full conditional distribution of that component given the current values of all the other components and the data. For many models used in common practice, even ones that yield a complex posterior distribution, sampling from the full conditionals is often a relatively simple task, though sometimes involving a lap through the dataset for each draw from each full conditional. Conveniently, the acceptance probability (6) always equals 1 and yet the chains often converge relatively quickly. The example in section 4.1 utilizes a Gibbs sampler and goes into further detail of the example’s full conditionals.
MCMC as specified, however, is computationally infeasible for massive datasets. Except for the most trivial examples, computing the acceptance probability (6) requires a complete scan of the dataset. Although the Gibbs sampler avoids the acceptance probability calculation, precalculations for simulating from the full conditionals of f(θ|x) require a full scan of the dataset, sometimes a full scan for each component! Since MCMC algorithms produce dependent draws from the posterior, M usually has to be very large to reduce the amount of Monte Carlo variation in the posterior estimates. While MCMC makes fully Bayesian analysis practical, it seems dead on arrival for massive dataset applications.
Although this section has not given great detail about MCMC methods, the important ideas for the purpose of this paper are that MCMC methods make Bayesian analysis practical, MCMC often requires an enormous number of laps through the dataset, and, given a θ drawn from f(θ|x) we can use MCMC to draw another value, θ′, from the same density. This last point will be the key to implementing a particle filter solution that allows us to apply MCMC methods to massive datasets. We will use this technique to switch the inner and outer loops in Figure 1. The scan of the dataset will become the outer loop and the scan of the draws from f(θ|x) will become the inner loop.
2.3. Importance sampling for analysis of massive datasets
So far we have two tools for Bayesian data analysis, MCMC and importance sampling. In this section we discuss a particular form of importance sampling that will help perform Bayesian analysis for massive datasets. Later sections will combine this with a particular MCMC algorithm.
Our proposed approach relies on a factorization of the integrand of the right hand side of (3) that is possible when the observations, xi, are independent given the parameters, θ. Such conditional independence is often satisfied even when the observations are marginally dependent like in hierarchical models, models for cluster sampled data, or time series models. In what follows, we assume this conditional independence prevails. Let D1 and D2 form a partition of the dataset so that every observation is in either D1 or D2. As noted for (1) we would like to sample from the posterior conditioned on all of the data, f(θ|D1, D2). Since sampling from f(θ|D1, D2) is difficult due to the size of the data-set, we consider setting g(θ) = f(θ|D1) for use as our sampling density and using importance sampling to adjust the draws. If θi, i = 1,…,M, are draws from f(θ|D1) then we can estimate the posterior expectation (1) as
| (7) |
where the wi’s are the importance sampling weights . Although these weights still involve f(θi|D1, D2), they greatly simplify.
| (8) |
| (9) |
| (10) |
Equation (9) follows from (8) since the observations in the dataset partition D1 are conditionally independent from those in D2 given θ. Conveniently, (10) is just the likelihood of the observations in D2 evaluated at the sampled value of θ. Figure 2 summarizes this result as an algorithm. The algorithm maintains the weights on the log scale for numerical stability.
Figure 2.
Importance sampling for massive datasets
2.4. Efficiency and the effective sample size
So rather than sample from the posterior conditioned on all of the data, D1 and D2, which slows the sampling procedure, we need only to sample from the posterior conditioned on D1. The remaining data, D2, simply adjusts the sampled parameter values by reweighting. The for loops in step 4 of Figure 2 are interchangeable. The trick here is to have the inner loop scan through the draws so that the outer loop only needs to scan D2 once to update the weights. Although the same computations take place, in practice physically scanning a massive dataset is far more expensive than scanning a parameter list. However, massive models as well as massive datasets exist so that in these cases scanning the dataset may be cheaper than scanning the sampled parameter vectors. We will continue to assume that scanning the dataset is the main impediment to the data analysis.
We certainly can sample from f(θ|D1) more efficiently than from f(θ|D1, D2) since simulating from f(θ|D1) will require a scan of a potentially much smaller portion of the dataset. We also assume that, for a given value of θ, the likelihood is readily computable up to a constant, which is almost always the case. When some data are missing, the processing of an observation in D2 will require integrating out the missing information. Since the algorithm handles each observation case by case, computing the observed likelihood as an importance weight will be much more efficient than if it was embedded and repeatedly computed in a Metropolis-Hastings rejection probability computation. Placing observations with missing values in D2 greatly reduces the number of times this integration step needs to occur, easing likelihood computations.
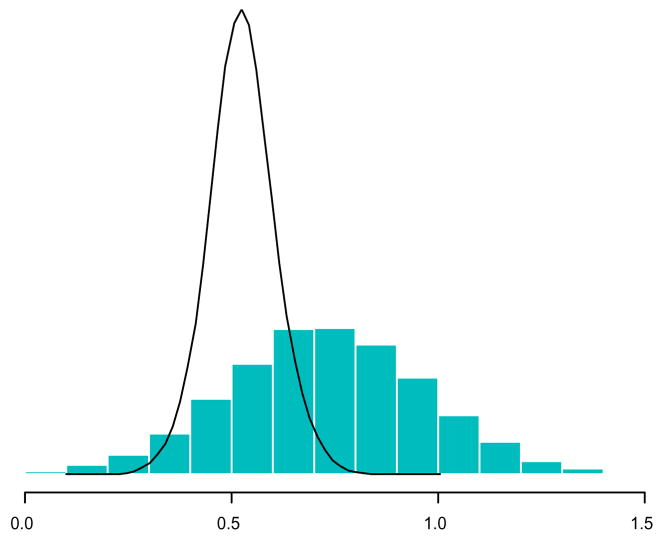
The algorithm shown in Figure 2 does have some drawbacks. While it can substantially reduce the number of times the data need to be accessed, the Monte Carlo variance of the importance sampling estimates grows quickly. Figure 3 demonstrates the problem. The wide histogram represents the sampling density f(θ|D1) that generates the initial posterior draws. However, the target density, f(θ|D1, D2), shown as the density plot, is shifted and narrower. About half of the draws from f(θ|D1) will be wasted. Those that come from the right half will have importance weight near zero. Since all of the terms are positive in the familiar variance relationship
Figure 3.
Comparison of f(θ|D1, D2) and f (θ|D1)
| (11) |
the posterior variance with the additional observations in D2 on average will be smaller than the posterior variance conditioned only on D1. Therefore, although the location of the sampling density should be close to the target density, its spread will most likely be wider than that of the target. As additional observations become available, f(θ|D1, D2) becomes much narrower than f(θ|D1). The result of this narrowing is that the weights of many of the original draws from the sampling density approach 0 and so we have few effective draws from the target density.
The effective sample size (ESS) is the number of observations from a simple random sample needed to obtain an estimate with Monte Carlo variation equal to the Monte Carlo variation obtained with the M weighted draws of θi. Although computing the ESS depends on the quantity we are trying to estimate, the h(θ) in (1), Kong et al. (1994) show that it can be approximated as
| (12) |
Hölder’s inequality implies that ESS is always less than or equal to M. Expressing the ESS in terms of the sample variance of the wi facilitates the study of its properties in Theorem 1. If the θi are dependent from the start, as will be the case for MCMC draws, the effective sample size will further decrease in addition to reductions due to unequal importance weights. When the MCMC algorithm “mixes well” so that the set of θi are not too dependent, this is not too much of a problem.
The following theorem concerning the variance of the important sampling weights can help us gauge the effect of these problems in practice. The theorem assumes that we observe a finite set of multi-variate normal data, xi. As before we will partition the xi’s into two groups, D1 and D2. To get accurate estimates of the mean, μ, we will be concerned about the variance of the importance sampling weights, φ(μ|D1, D2, Σ)/φ(μ|D1, Σ), where φ(·) is the normal density function. The theorem gives the variance of these importance sampling weights averaged over all possible datasets with a flat prior for μ.
THEOREM 1
If, for j = 1,…,N,
xj ~ Nd(μ, Σ) with known covariance Σ,
D1 = {x1,…,xn} and D2 = {xn+1,…,xN}, and
μ~Nd(μ0, Λ0)
then
| (13) |
Proof
The most straightforward proof of the theorem involves simply computing the big multivariate Gaussian integral in (13).
Theorem 1 basically says that in the multivariate normal case with a flat prior the variance of the importance sampling weights is on average (N/n)d − 1. These results may hold approximately in the non-normal case if the posterior distributions and the likelihood are approximately normal. As we should expect, when n = N the variance of the weights is 0. As N increases relative to n the variance increases quickly. This is unfortunate in our case since we would like to use this method for large values of N and high dimensional problems. Looking at this result from the effective sample size point of view we see that
| (14) |
If we draw M times from the sampling distribution when the size of the second partition D2 is equal to the size of the first partition D1, the effective sample size is decreased by a factor of 2d.
Although things are looking grim for this method, recent advances in particle filters sidestep this problem by a simple “rejuvenation” step.
3. Particle filtering for massive datasets
The efficiency of the importance sampling scheme described in the previous section deteriorates when the importance weights accumulate on a small fraction of the initial draws. These θi with the largest weights are those parameter values that have the greatest posterior mass given the data absorbed so far. The remaining draws are simply wasting space.
Sequential Monte Carlo methods (Doucet et al., 2001) aim to adapt estimates of posterior distributions as new data arrive. Particle filtering is the often used term to describe methods that use importance sampling to filter out those “particles,” the θi, that have the least posterior mass after incorporating the additional data. All of the methods struggle with maintaining a large effective Monte Carlo sample size while maintaining computational efficiency.
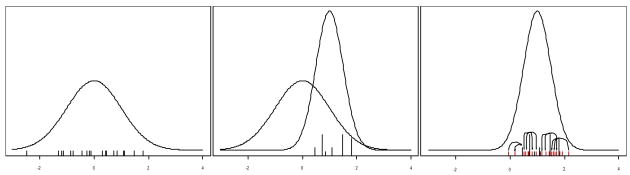
The “resample-move” or “rejuvenation” step developed in (Gilks and Berzuini, 2001) greatly increases the sampling efficiency of particle filters in a clever fashion. We can iterate step 4’s outer loop shown in Figure 2 until the ESS has deteriorated below some tolerance limit, perhaps 10% of M. Assume that this occurs after absorbing the next n1 observations. At that point we have an importance sample from the posterior conditioned on the first n + n1 data points. Then resample M times with replacement from the θi where the probability that θi is selected is proportional to wi. Note that these draws still represent a sample, albeit a dependent sample, from the posterior conditioned on the first n + n1 data points. Several of the θi will be represented multiple times in this new sample. For the most part this refreshed sample will be devoid of those θi not supported by the data.
Recall that the basic idea behind MCMC was that given a draw from f(θ|x1,…, xn+n1) we can generate another observation from the same distribution by a single Metropolis-Hastings step. Additional MCMC steps will increase the ESS, but also increase the number of times the algorithm accesses the first n + n1 observations. Therefore, to rejuvenate the sample, for each of these new θi’s we can perform a single Metropolis-Hastings step “centered around” θi where the acceptance probability is based on all n + n1 data points. Our rejuvenated θi’s now represent a more diverse set of parameter values with an effective sample size closer to M again. Figure 4 graphically walks through the resample-move process step-by-step and Figure 5 shows the new reweighting step to replace step 4 of Figure 2. After rejuvenating the set of θi, we can continue where we left off, on observation n + n1 + 1, absorbing additional observations until either we include the entire dataset or the ESS again has dropped too low and we need to repeat a rejuvenation step. As opposed to standard MCMC, the particle filter implementation also admits an obvious path toward parallelization.
Figure 4.
The resample-move step. 1) generate an initial sample from f(θ|D1). The ticks mark the particles, the sampled θi. 2) Weight based on f (θ|D1, D2) and resample, the length of the vertical lines indicate the number of times resampled. 3) For each θi perform an MCMC step to diversify the sample.
Figure 5.
Particle filtering for massive datasets
4. Examples
In this section we present two examples to offer proof-of-concept. We demonstrate that the particle filter approach greatly reduces the number of data accesses while maintaining accurate parameter estimates. Code for these examples is available from the authors’ web sites.
4.1. Mixtures of transition models
Mixtures of transition models have been used to model users visiting web sites (Cadez et al., 2000; Ridgeway, 1997) and unsupervised training of robots (Ramoni et al., 2002). Cadez et al. (2000) also develop visualization tools (WebCANVAS) for understanding clusters of users and apply their methodology to the msnbc.com web site.
Transition models (Ross, 1993), or finite state Markov chains (although related, in this context these are not to be confused with Markov chain Monte Carlo), are useful for describing discrete time series where an observed series switches between a finite number of states. A particular sequence, for example (A,B,A,A,C,B) might be generated by a first-order transition model where the probability that the sequence moves to a particular state at time t + 1 depends only on the state at time t. Perhaps web users traverse a web site in such a manner. Given a set of sequences we can estimate the underlying probability transition matrix, the matrix that describes the probability of specific state to state transitions. In fact the posterior distribution is computable in closed form with a single pass through the dataset by simply counting the number of times the sequences move from state A to state A, state A to state B, and so on for all pairs of states.
However, a particular set of sequences may not all share a common probability transition matrix. For example, visitors to a web site are heterogeneous and may differ on their likely paths through the web site depending on their profession, their Internet experience, or the information that they seek. The mixture of transition models assumes that the dataset consists of sequences, each generated by one of C transition matrices. However, neither the transition matrices nor the group assignments nor the number from each group are known.
The goal, therefore, is to understand the shape of the posterior distribution of the elements of the C transition matrices and the mixing fraction given a sample of observed users’ paths. Independent samples from this posterior distribution are not easily obtained directly but the full conditionals, on the other hand, are simple enough so that the Gibbs sampler is easy to implement (Ridgeway, 1997). Let C be the number of clusters and S be the number of possible states. The unknown parameters of this model are the C S × S transition matrices, P1,…,PC, the mixing vector α of length C containing the fraction of observations from each cluster, and the N cluster assignments, zj ∈ {1,…,C}. Placing a uniform prior on all parameters, the Gibbs sampler proceeds as follows. First randomly initialize the cluster assignments, zj. Given the cluster assignments, the full conditional of the ith row of the transition matrix Pc is
| (15) |
where ni1c, for example, is the number of times sequences for which zj = c transition from state i to state 1. The mixing vector is updated with a draw from
| (16) |
where Σ I(zj = c) counts the number of observations assigned to cluster c. Lastly we update the cluster assignments conditional on the newly sampled values for the transition matrices. The new cluster assignment for sequence j is drawn from a Multinomial(p1, p2,…,pC) where pc is the probability that transition matrix Pc generated the sequence. With these new cluster assignments we return to (15) and so the Gibbs sampler iterates.
As noted in section 2.2, each iteration of the MCMC algorithm requires a full scan of the dataset, in this case two scans, one for the matrix update and one for the cluster assignment update. To test the improvement available using the particle filtering approach, we generated 25 million sequences of length between 5 and 20 from two 4 × 4 transition matrices (about 1 gigabyte of data). We used the first n = 1000 sequences to obtain the initial sample of M = 1000 draws, step 1 of the algorithm shown in Figure 2. We then sequentially accessed the additional sequences, reweighting the M draws until the ESS dropped below 100. At that point, we resampled and applied the rejuvenation step to the set of draws and continued again until the ESS dropped too low. At any time we only kept 1000 sequences in memory, leaving the remainder of the dataset on disk.
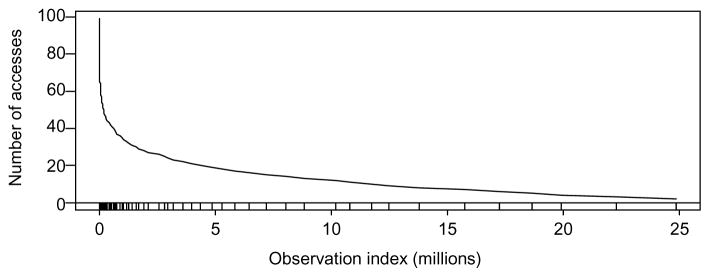
Figure 6 shows the results for the number of times the particle filtering algorithm read each observation off of the disk. Except for the first 1000 observations, which were used to generate the initial sample, the number of times read from disk is the same as the number of times they were accessed in memory as well. The lower curve indicates the number of accesses. The first 1000 observations show the greatest number of accesses (99 for this example). However, the additional observations were accessed infrequently. For example, the algorithm accessed the 10 millionth observation only 12 times and the last observation only twice.
Figure 6.
The frequency of access by observation. The marks along the x-axis refer to occurrences of the rejuvenation step.
For comparison, there would be a horizontal line at 2000 in Figure 6 in order to indicate the number of times the Gibbs sampler, conditioned on the entire dataset, would need to access each observation. Each of the 1000 iterations requires one scan for the cluster assignments and a second scan for the parameter updates (15) and (16). Figure 6 shows a 99.4% reduction in the total number of data accesses from disk when using the particle filter.
The tick marks along the bottom mark the points at which a rejuvenation step took place. Note that they are very frequent at first and decrease as the algorithm absorbs additional observations. The marginal posterior standard deviation approximately decreases like so that the target is shrinking at a slower rate as we add more data. From the ESS approximation in (14) we can estimate the frequency of rejuvenation. As before, let n be the size of the initial sample. Now let Nk be the total number of observations accommodated at the kth rejuvenation step. If we rejuvenate the θi’s when the ESS drops to p×M then the Nk are approximately related according to
| (17) |
Unraveling the recursion implies that
| (18) |
where d is the dimension of the parameter vector from theorem 1. When we let the ESS get very small before rejuvenation, equivalently setting p to be small, the Nk can become large quickly. Naturally, there will be a balance between loss in computing efficiency and estimation efficiency. Fortunately Nk grows exponentially in k so that Nk may grow quickly. This means that with each additional rejuvenation the algorithm can withhold future rejuvenations until many more observations have been accommodated. While Nk grows exponentially with k it grows only linearly with n, the number of observations in D1. This implies that, depending on d, it may be better to spend more computational effort on the rejuvenation steps than the initial posterior sampling effort.
For the mixture example, the effective number of parameters is no more than 25. Each transition matrix is 4 × 4 with the constraint that the rows sum to 1. So each of the two transition matrices has 12 free parameters. With the single mixing fraction parameter the total parameter count is 25. With additional correlation amongst the parameters the effective number of parameters could be less. In fact in our example we found that equation (18) matches the observed frequency of rejuvenation to near perfection when d = 17.
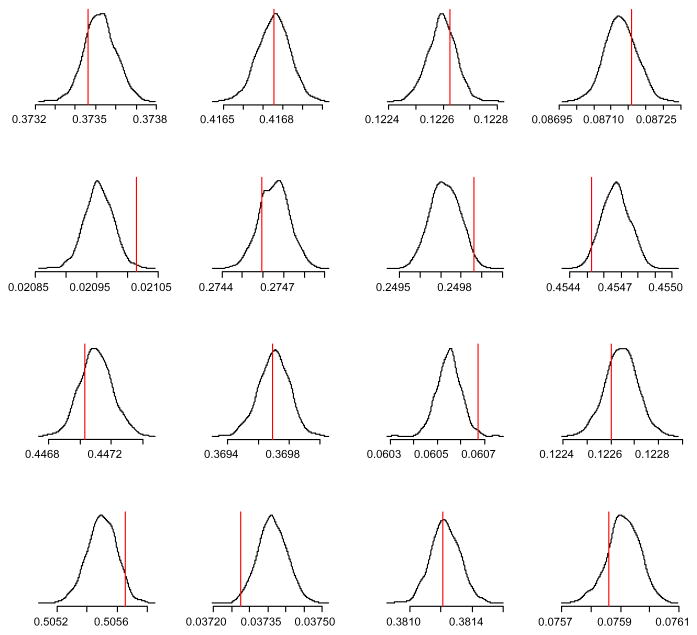
While efficiency as measured with the number of data accesses is important in the analysis of massive datasets, precision of parameter estimates is also important. Figure 7 shows the marginal posterior densities for the 16 transition probabilities from the first cluster’s transition matrix. The smooth density plot is based on the M = 1000 draws using the particle filtering method. The figure also marks the location of the parameter value used to generate the data. All of these values are within the region with most of the posterior mass. While achieving a 99% reduction in the number of data points accessed, the posterior distribution the particle filter produces still captures the true parameter values. On a smaller dataset for which the Gibbs sampler could be run on the full dataset, the two methods produced nearly identical posterior distributions. Note that increasing M does not change the number of data accesses for the particle filter while each additional draw represents yet another scan for the standard implementation. If for some reason one was not confident in the particle filter results, one could generate additional MCMC iterations utilizing the entire dataset initiated from the particle filter draws. If the densities change little then that would be evidence in favor of, but not necessarily proof of, the algorithm’s estimation accuracy.
Figure 7.
The posterior distribution of the transition probabilities for one of the transition matrices. The density is based on the particle filter. The vertical line marks the true value used to simulate the dataset.
4.2. Fully Bayes regression
In this example we show that the particle filtering algorithm may be a pathway for scaling MCMC methods to supervised learning problems. While the actual model fit here is of relatively low dimension, this example offers evidence that particle filtering can offer a substantial reduction in data access requirements for supervised learning tasks.
Inductive supervised learning infers a functional relation y = f(x) from a set of training examples D = {(x1, y1),…,(xn, yn)}. For this example, the inputs are vectors [xi1,…,xid]T in ℜd, y ∈ {−1, 1}, and we refer to f as a classifier. We assume that a vector of parameters, β defines f and we write f(x; β).
The overriding objective is to produce a classifier that makes accurate predictions for future input vectors. Secondary objectives may include estimates of prediction error. Developing an accurate classifier typically requires the learning procedure to control complexity and avoid over-fitting the training data. The Bayesian approach to complexity places a prior distribution on β, typically resulting in estimates that shrink towards zero. Using so-called Laplacian (i.e., double exponential) priors can result in posterior modes for some components of β that are exactly zero. Such “sparse classifiers” can yield excellent predictive performance and are closely related to support vector machines (SVM) (see Girosi, 1998 and Zhang and Oles, 2001), relevance vector machines (RVM) (Tipping, 2001), and to the lasso (Tibshirani, 1995).
Figueiredo (2001) and Figueiredo and Jain (2001) considered classifiers of the form:
They adopted a probit model, ψ (z) = Φ(z), the Gaussian cdf. Here we instead adopt the logistic link function. We set h(x) = [1, x1,…,xd]T, the original input variables. More generally h could invoke a kernel representation (see Ju et al., 2002 for details).
We adopt a hierarchical prior for β. Specifically, for i = 1,…,d
where ϕ is the Gaussian density function. This induces a Laplacian prior on β, . The maximum a posteriori (MAP) estimates under the Laplacian prior equal the lasso estimates. Note that the Laplacian prior needs a choice for the hyperparameter γ.
For fully Bayesian inference, we adopt a Gibbs sampling procedure drawing in turn from the conditional posterior distribution of β given τ and the data, then τ given β and the data. Neither conditional density is available in closed form so we use Metropolis-within-Gibbs steps (see, for example, Gilks et al., 1996). For each component j = 1,…,d of β, the algorithm proposes a candidate uniformly from an interval around of width hβ. Then, the algorithm accepts the proposed move with probability:
otherwise set β(t+1) = β(t). Then for τ, propose a candidate similarly using intervals of width hτ and then accept with probability:
In the analysis reported below hβ = 0.1, hτ = 1, and γ = 5. Further tuning minimally impacted convergence behavior. Note that computation of the acceptance probability for β requires a pass through the dataset.
Here we report a fully Bayesian logistic regression analysis of a customer database comprising 744,963 customer records, 57 Mb when stored in double precision. These data originated in a major telecommunications company. The binary response variable identifies customers who have switched to a competitor. There are seven predictor variables. Five of these are continuous and two are 3-level categorical variables. Thus for logistic regression there are 10 parameters. This dataset is small enough that regular MCMC, while cumbersome, is still feasible.
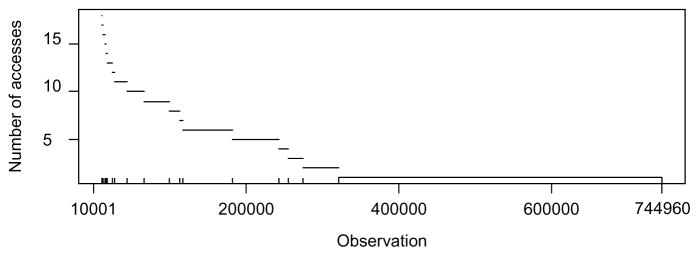
Conditioning on the first 10,000 observations, we generated 25,000 draws using the above described MCMC algorithm, dropping the first 5,000 draws as “burn-in” draws. Figure 8 shows the number of times the algorithm accessed each subsequent observation. We ran the rejuvenation step whenever ESS dropped below 10,000. The algorithm accessed the initial 10,000 observations over 25,000 times in order to get the initial set of parameter values, but scanned the remaining observations very little. More than half of the observations were accessed only once. This represents a 98% reduction in data accessing compared to running the Gibbs sampler on the full dataset.
Figure 8.
Frequency of access by observation for the outpic example. The inward tickmarks on the x-axis indicate rejuvenation steps.
In addition to the particle filter, we also fit the logistic regression model using maximum likelihood and using a full MCMC run on the entire dataset. The following table shows the estimates for β using the posterior mean from the particle filter (P), the posterior mean from MCMC on the full dataset (M), and the maximum likelihood logistic regression model (L).
| P | −0.557 | 0.172 | 0.057 | 0.195 | −0.119 | 0.376 | −0.391 | −0.183 | 0.093 | 0.058 |
| M | −0.574 | 0.155 | 0.056 | 0.220 | −0.087 | 0.360 | −0.358 | −0.204 | 0.080 | 0.078 |
| L | −0.574 | 0.155 | 0.056 | 0.220 | −0.087 | 0.361 | −0.358 | −0.204 | 0.079 | 0.079 |
While conditioning on the full dataset, the MCMC algorithm nearly matches the logistic regression estimates. The particle filter estimates, while in the neighborhood, do not match as closely. After conditioning on the first 10,000 observations, ||βP − βM||2 = 1.4. The last rejuvenation step occurred after absorbing the first 320,500 observations at which point ||βP − βM||2 = 0.0046, remaining at that level of accuracy through the remainder of the algorithm’s run. Therefore, most likely a single MCMC step at the rejuvenation stage might not have been enough to ensure good mixing properties. Even though the posterior means did not match up exactly, the full MCMC estimates were within a region that the particle filter estimated to have high posterior mass. Perhaps, at the expense of a data scan, an additional MCMC step for each of the final particles would provide a more accurate estimate.
5. Discussion
MCMC has established itself as a standard tool for the statistical analysis of complex models. Data mining research, in contrast, rarely features MCMC. Indeed, for data mining applications involving massive datasets, computational barriers essentially preclude routine use of MCMC. MCMC is however an indispensable tool for Bayesian analysis, especially in those applications where the inferential targets are more complex than posterior means or modes. As such we contend that extension of MCMC methods to larger datasets is an important research challenge. We have presented one particular line of attack.
Working with samples from massive datasets represents an alternative strategy for large-scale Bayesian data analysis and may be viable for some applications. In high dimensional applications, however, throwing data away may be too costly.
Likelihood based data squashing (Madigan et al., 2002) is another potential tool for enabling Bayesian analysis of massive datasets. It too uses the factorization of the likelihood (10) to avoid too many scans of the dataset. Likelihood based data squashing constructs a small number of pseudo-data points with appropriate weights so that a weighted analysis of the pseudo-dataset produces similar results as the unweighted analysis of the massive dataset. It is possible that a posterior conditioned on the pseudo-dataset may offer a good importance sampling distribution so that some combination of data-squashing, importance sampling, and particle filtering could provide a coherent solution.
As noted earlier Chopin (2002) has also developed similar particle filtering strategies. One practical development in that work is the use of the current set of particles to adaptively construct a Gaussian proposal distribution for the Metropolis rejuvenation step. In high dimensions naïve applications of such a proposal distribution may be problematic, but clever variants may produce an efficient particle filter.
While clearly the method needs to undergo more empirical work to test its limitations, the derivation and preliminary simulation work shows promise. If we can generally reduce the number of data accesses by 95%, MCMC becomes viable for a large class of models useful in data mining. The sequential nature of the algorithm also allows the analyst to stop when uncertainty in the parameters of interests has dropped below a required tolerance limit. Parallelization of the algorithm is straightforward. Each processor manages a small set of the weighted draws from the posterior and is responsible for updating their weights and computing the refresh step. The last advantage that we discuss here involves convergence of the MCMC sampler. As noted in section 2.2, the key to MCMC begins with assuming that we have an initial draw from f(θ|x). While in practice the analyst usually just starts the chain from some reasonable starting point, the particle filter approach allows us to sample directly from the prior to initialize the algorithm. Sampling from the prior distributions often used in practice is usually simple. Then the particle filter can run its course starting with the first observation. Even though subsequent steps introduce dependence, the algorithm will always generate new draws from the correct distribution without approximation.
Bayesian analysis coupled with Markov chain Monte Carlo methods continues to revitalize many areas of statistical analysis. Some variant of the algorithm we propose here may indeed make this pair viable for massive datasets.
Acknowledgments
Grant NIH/NIDDK 1R01DK/HL61662-01 provided support for Greg Ridgeway’s research. The U.S. National Science Foundation supported David Madigan’s research.
Contributor Information
Greg Ridgeway, RAND, PO Box 2138, Santa Monica, CA 90407-2138, gregr@rand.org.
David Madigan, Department of Statistics, 477 Hill Center, Rutgers University, Piscataway, NJ 08855, madigan@stat.rutgers.edu.
References
- Andrieu C, de Freitas N, Doucet A, Jordan MI. ‘An Introduction to MCMC for Machine Learning’. Machine Learning. 2003;50(12) [Google Scholar]
- Besag J, Green P, Higdon D, Mengersen K. Bayesian computation and stochastic systems (with Discussion) Statistical Science. 1995;10:3–41. [Google Scholar]
- Cadez I, Heckerman D, Meek C, Smyth P, White S. ‘Visualization of navigation patterns on a Web site using model-based clustering’. Microsoft Research; 2000. Technical Report MSR-TR-00-18. [Google Scholar]
- Carlin B, Louis T. Bayes and Empirical Bayes Methods for Data Analysis. 2 Boca Raton, FL: Chapman and Hall; 2000. [Google Scholar]
- Chopin N. A sequential particle filter method for static models. Biometrika. 2002;89(3):539–552. [Google Scholar]
- DeGroot M. Optimal Statistical Decisions. New York: McGraw-Hill; 1970. [Google Scholar]
- Doucet A, de Freitas N, Gordon N. Sequential Monte Carlo Methods in Practice. Springer-Verlag; 2001. [Google Scholar]
- DuMouchel W. Bayesian data mining in large frequency tables, with an application to the FDA spontaneous reporting system (with discussion) The American Statistician. 1999;53(3):177–190. [Google Scholar]
- Elder J, Pregibon D. ‘A Statistical Perspective on Knowledge Discovery in Databases’. In: Fayyad UM, Piatetsky-Shapiro G, Smyth P, Uthurusamy R, editors. Advances in Knowledge Discovery and Data Mining. Chapt 4 AAAI/MIT Press; 1996. [Google Scholar]
- Figueiredo M. ‘Adaptive sparseness using Jeffreys prior’. Neural Information Processing Systems - NIPS 2001 2001 [Google Scholar]
- Figueiredo M, Jain AK. ‘Bayesian Learning of Sparse Classifiers’. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition - CVPR’2001.2001. [Google Scholar]
- Friedman N, Nachman I, Peer D. ‘Learning Bayesian Network Structures from Massive Datasets: The Sparse Candidate Algorithm’. Proceedings of the Fifteenth Conference on Uncertainty in Articial Intelligence (UAI99); 1999. pp. 206–215. [Google Scholar]
- Gelman A, Carlin J, Stern H, Rubin D. Bayesian Data Analysis. New York: Chapman Hall; 1995. [Google Scholar]
- Geman S, Geman D. Stochastic relaxation, Gibbs distributions and the Bayesian restoration of images. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1984;6:721–741. doi: 10.1109/tpami.1984.4767596. [DOI] [PubMed] [Google Scholar]
- Gilks W, Berzuini C. Following a moving target - Monte Carlo inference for dynamic Bayesian models. Journal of the Royal Statistical Society B. 2001;63(1):127–146. [Google Scholar]
- Gilks W, Richardson S, Spiegelhalter DJ, editors. Markov Chain Monte Carlo in Practice. London: Chapman and Hall; 1996. [Google Scholar]
- Girosi F. An Equivalence Between Sparse Approximation And Support Vector Machines. Neural Computation. 1998;10:1455–1480. doi: 10.1162/089976698300017269. [DOI] [PubMed] [Google Scholar]
- Glymour C, Madigan D, Pregibon D, Smyth P. Statistical themes and lessons for data mining. Data Mining and Knowledge Discovery. 1997;1(1):11–28. [Google Scholar]
- Hastings WK. Monte Carlo Sampling Methods Using Markov Chains and Their Applications. Biometrika. 1970;57:97–109. [Google Scholar]
- Ju W-H, Madigan D, Scott S. On Bayesian learning of sparse classifiers. Technical report, Rutgers University; 2002. Available at http://stat.rutgers.edu/~madigan/PAPERS/sparse3.ps. [Google Scholar]
- Kong A, Liu J, Wong W. Sequential imputation and Bayesian missing data problems. Journal of the American Statistical Association. 1994;89:278–288. [Google Scholar]
- Le Cam L, Yang G. Asymptotics in Statistics: Some Basic Concepts. New York: Springer-Verlag; 1990. [Google Scholar]
- Madigan D, Raghavan N, DuMouchel W, Nason M, Posse C, Ridge-way G. Likelihood-based data squashing: A modeling approach to instance construction. Data Mining and Knowledge Discovery. 2002;6(2):173–190. [Google Scholar]
- Metropolis N, Rosenbluth A, Rosenbluth M, Teller A, Teller E. Equations of state calculations by fast computing machine. Journal of Chemical Physics. 1953;21:1087–1091. [Google Scholar]
- Posse C. Hierarchical Model-based Clustering For Large Datasets. Journal of Computational and Graphical Statistics. 2001;10(3):464–486. [Google Scholar]
- Ramoni M, Sebastiani P, Cohen P. Bayesian Clustering by Dynamics. Machine Learning. 2002;47(1):91–121. [Google Scholar]
- Ridgeway G. ‘Finite discrete Markov process clustering’. Microsoft Research; 1997. Technical Report MSR-TR-97-24. [Google Scholar]
- Ripley B. Stochastic Simulation. New York: Wiley; 1987. [Google Scholar]
- Ross SM. Probability Models. 5 San Diego, CA: Academic Press; 1993. [Google Scholar]
- Tibshirani R. Regression selection and shrinkage via the lasso. Journal of the Royal Statistical Society, Series B. 1995;57:267–288. [Google Scholar]
- Tipping ME. Sparse Bayesian Learning and the Relevance Vector Machine. Journal of Machine Learning Research. 2001;1:211–244. [Google Scholar]
- Zhang T, Oles FJ. Text categorization based on regularized linear classification methods. Information Retrieval. 2001;4:5–31. [Google Scholar]