Saccade Trajectories Evoked by Sequential and Colliding Stimulation of the Monkey Superior Colliculus

Abstract

Using microstimulation we employed explicit experimental control of activity in the superior colliculus at two sites within the motor map. We compared saccade metrics and dynamics evoked at each site independently with those caused by sequential presentation and collisions of the two stimulation trains. Essentially, we forced controlled spatio-temporal patterns of activity into the saccade control circuit with various timing relationships from known sites within the collicular motor map, thus revealing the spatio-temporal transformation from superior colliculus to eye movement dynamics under experimentally controlled conditions. We extend prior findings about decreasing time intervals between sequential presentations of stimulations to include mid-flight combinations and dynamic modifications of trajectory. We explore how asynchronous collisions between two movements systematically engage a normalization mechanism of movement metrics, and demonstrate how dynamic patterns of activity across the SC motor map can create mid-flight curvature of movement through the post-collicular dynamics of a displacement controller. The explicit control addresses feasibility for systems control models and provides benchmark data for experimental verification of model mechanisms.

Introduction

Rapid eye movements known as saccades are thought to be generated by a displacement controller in the brainstem which executes movements under dynamic control of trajectory by means of short-latency, “local” feedback mechanisms (Robinson, 1975; Jürgens et al., 1981; Scudder et al., 2002). The Superior Colliculus (SC) includes a network of cell types (Moschovakis, Scudder and Highstein, 1996; Munoz and Wurtz, 1995) that ultimately output a critical component of the controller that appears to generate some form of desired eye displacement by means of a spatio-temporal transformation (Van Gisbergen et al., 1987; Lee et al.,1988) into a so-called brainstem burst generator (Scudder et al., 2002). Sustained activation of this saccadic circuit by microstimulation at the SC transforms a steady-state pattern of activation into a ratchet-like activation of the burst generator (Paul & Gnadt, 2006) with cyclic, periodic movements (Robinson, 1972) much like a central pattern generator, or CPG (Jackson et al., 2001). The displacement signal occurs within a highly organized group of neurons acting as a movement-related vector map of the contraversive world (Robinson, 1972). Briefly, neurons within the map display stereotyped bursts of activity specifying a saccade vector just prior to movement (Schiller and Koerner, 1971; Wurtz and Goldberg, 1971). Individual SC neurons are broadly tuned for direction and amplitude of movement (Sparks et al.,1976; Ottes et al., 1986). Saccades are initiated by a burst of activity from a concentrically-organized population of neurons centered on a specific point in the map, with the highest and earliest bursts in the center (Sparks et al., 1976). This population of bursting neurons with overlapping movement fields guides a saccade at high velocity with great accuracy and precision. While at any given time there are many potential saccade targets, most of the time one target is selected by volitional or reflexive processes and executed at a latency of about 200 ms. This is appropriately adaptive since primates and other species with frontal-eyed, high-acuity central vision can use saccades to direct binocular gaze to only one target at a time. However, in some cases there appears to be competing or dynamically changing selection of desired targets (e.g., Ottes et al., 1984; McPeek and Keller; 2001; Port and Wurtz, 2003). We investigate here in macaque monkeys how the SC and its outputs would transform multiple, competing target representations within its topographic map under experimentally controlled conditions. We employed a specific experimental pattern of activation that extends previous empirical descriptions of the system dynamics of the saccade circuit from a single SC site (Breznen et al., 1996; 1 Gnadt et al, 2001) to explicitly controlled spatial and temporal patterns across the collicular motor map. These patterns of activation are derived from techniques for obtaining characteristic system responses of a control system (Breznen et al., 1996; Gnadt et al., 2001) and can be used to challenge numerical or analytical models in computational studies (e.g., Breznen and Gnadt, 1997; Jackson et al., 2001).

In early behavioral experiments using visual double-stimulation, a number of investigators have described endpoint averaging (Ottes et al., 1984; Findlay, 1982) and curved saccades (Van Gisbergen et al., 1987). In more recent work in macaque monkeys, McPeek and Keller (2001) studied a task situation where two potential targets were presented; either target could be used to guide the eye movement. Their subjects sometimes made two saccades with exceptionally short latency between them. The trajectory of the initial saccade tended to curve toward the goal of the second movement. Arai et al. (2004) later reported that the presence of visual distracters were responsible for the curved trajectories, but were unaffected by the total number of distracters. This was interpreted by McPeek and Keller as evidence for concurrent processing of two movements by the oculomotor system. McPeek (2006) later showed that perisaccadic activity in frontal eye field neurons appeared to reveal persistent distracter-related activity during curved movements. Port and Wurtz (2003) provided evidence for this proposition at the level of the SC when they noted corresponding changes in neuronal activity from multiple recording sites in superior colliculus during rare, but strongly curved voluntary saccades. Quantitative analysis of neurons’ movement fields led them to conclude that the initial timing of the trajectory curvature could be accounted by the neural dynamics, but not the final trajectory or endpoint. A later modeling study by Walton et al. (2005) concluded that a saccade control model that places the SC upstream of the local feedback loop could accurately predict the trajectory curvature and final endpoint due to dynamic properties of the controllers feedback. In further experimental studies by Aizawa and Wurtz (1998) an inhibited “hole” was created by injecting muscimol into the collicular motor map. The inactivation caused voluntary saccades with curved trajectories away from the inhibited location consistent with a suppression of activity from that point in the motor map. Conversely, Watanabe et al (2005) showed that increases in activity of SC neurons by microinjection of the cholinergic agonist nicotine produced saccade end points biased toward the location of the injection. In addition, subthreshold microstimulation in the SC motor map can cause saccades that bend toward the site of stimulation (Keller et al., 2005). This body of work indicates that the level and topography of activity within the SC as a whole dynamically contributes to guiding the trajectory of saccades. In this study we explore specific SC spatio-temporal patterns in experimentally controlled conditions with microstimulation.

Robinson first described the interaction between two experimental stimulation sites within the SC (Robinson, 1972). Based on movement metrics derived from straight-line vectors between starting and ending points, he noted that simultaneous activation of sustained trains of stimulation evoked a single movement with a trajectory reflecting a weighted vector average of the movements evoked at each site individually. The relative contribution of each site to the vector average was scaled according to the relative intensity of the two stimulation currents, including sub-threshold currents for inducing a movement. Because he could reduce the size of movement induced at one site by incrementally recruiting larger stimulus intensities at a second site with a smaller characteristic vector, he concluded that the movement amplitude was determined by the location of the stimulation sites within the motor map, and not the (absolute) intensity of the stimulation. Robinson also described relative and absolute “refractory periods” between two sequential activations, whether at the same stimulation site or between two sites. He claimed there was a relative refractory period between stimulations for inter-stimulus intervals of 75 ms down to 30 ms. Within this range, the second movement became incrementally smaller to half the original size, along with a relative increase in both latency and threshold. Below 30 ms inter-stimulus intervals, he reported complete failure of the second stimulus to induce a movement even at very large stimulation currents. Because these relative refractory interactions were not realized for two stimulation sites with opposite directions of movement (left and right, up and down), he concluded that there must be one independent brainstem circuit for each of the cardinal directions of movement that would remain refractory for several tens of milliseconds. During the “absolute refractory period” below 30 ms, where the second movement would often occur before the first movement completed, movements in opposite directions interacted more linearly where “the first saccade was interrupted in mid-flight and replaced by part or all of the second.”

We revisit these issues here with a more highly controlled exploration of inter-site stimulation dynamics and millisecond resolution of in-flight movement dynamics. Extending our earlier systems response strategy (Breznen et al., 1996; Breznen and Gnadt, 1997; Gnadt et al, 2001; Jackson et al., 2001), we explored interacting patterns of frequency-modulated input patterns at two sites within the SC topographic map. Essentially, this reveals the spatio-temporal system response of the biological circuit, and can be compared to quantitative analyses of candidate models. By use of overlapping sinusoidal-frequency patterns of activation, we effectively invoked forced patterns of smoothly changing activity across the motor map providing experimental tests about how dynamically spreading patterns of activation would be related to on-line control of saccades. It also explores the probable physiological mechanisms of dynamically curved saccades during volitional movements by simulating competing neural activity within the SC under experimental control.

We found reliable, characteristic patterns of end point distribution, movement dynamics and saccade curvature that reveal how two competing commands interact temporally within the saccade control circuit. We explored how the overlapping patterns of activation at progressively shorter time intervals between two sites systematically changed from the simple vector sum of two sequential movements; through systematic interactions for end points between two sequential movements; through characteristically-curved, continuous movements; to a single saccade approximating the straight-path vector average of the two simultaneous movements. Movements caused by the second train of stimulation pulses revealed a truncation of size proportional to the time interval from the initiation of the first (or ongoing) movement. The truncation observed is consistent with earlier data demonstrating a gradual reset of the dynamic feedback acting as a leaky integrator (Kustov and Robinson, 1995; Nichols and Sparks, 1996; Breznen et al. 1996). Because residual activity would remain in the feedback mechanism, triggering a new movement prematurely would have the effect of errantly diminishing dynamic motor error, producing a truncated and abnormally slowed movement.

The curved saccades generated by the competing excitatory drive of our stimulation pulses also match well to those voluntary saccades with curved trajectories produced by distracting targets. When temporally overlapping stimulations invoked a second movement while the first movement was still in flight, we found a reliable pattern of curved trajectories. These data provide a physiologic explanation for the occasionally curved trajectories that can occur in the face of the volitional selection of competing saccade targets and provide benchmark measures for comparison to systems control models for spatio-temporal transformation in the saccade circuit. Similar patterns of activation can now be used to test the responses for quantitative models of the saccadic circuit. Preliminary considerations are consistent with models that implement a displacement controller distal to the SC with a time response on the order of 20–60 ms. The physiologic decoding of the SC topography includes a pan-SC normalization that appears to be implemented distal to the SC. Different computational forms of normalization can now be tested against these empirical data.

Results

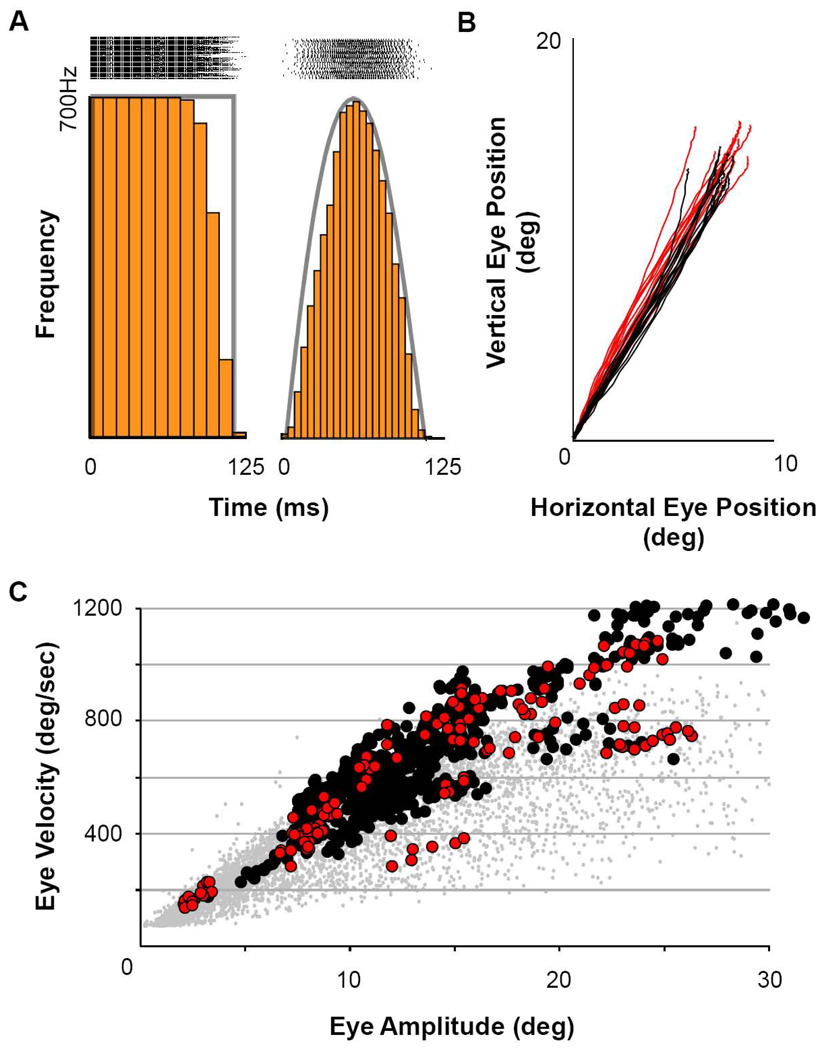
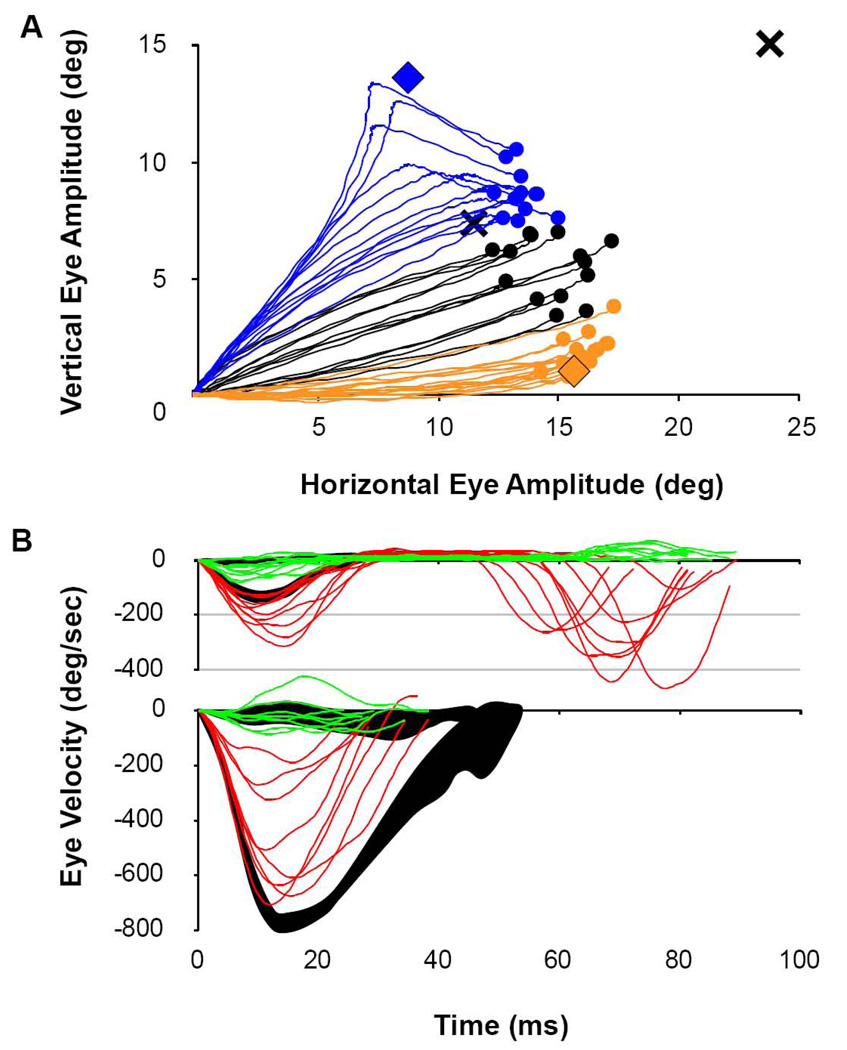
Figure 1 illustrates the patterns of stimulation pulses employed. Pulse patterns were created using a custom LabView program that created step-function or sinusoidal modulation of a rate-modulated pulse generator, which triggered a constant-current, bi-phasic pulse stimulator (A-M Systems). The sinusoidal modulation was imposed onto a baseline rate of 3 Hz, so that the timing of the sinusoidal modulation within the long baseline pulse interval (333ms) created different pulse patterns within each cycle (Figure 1A). The low-rate of baseline pulses created isolated impulse functions to which the saccadic system is refractory (Gnadt et al., 2001). Figure 1A on the left shows the step pattern of pulses that instantaneously stepped to a constant pulse frequency of 700 pulses/sec for approximately 125 ms. Pulse rasters for a sample of 55 trials are shown at the top with the idealized step pattern of instantaneous frequency superimposed (ending of the step was staggered according to the randomized timing within the baseline pulse interval, as described above). This frequency step is the standard pattern of excitation that has been used for over 30 years to reveal the collicular motor map by microstimulation and to produce the “staircase” sequence of saccades to a steady-state, constant-frequency stimulation (Robinson, 1972).

Figure 1. Stimulation Patterns and Saccade Dynamics.

A) Illustration of square and sinusoidal functions used to elicit saccades. Rasters above each waveform are aligned on stimulus start (n=55 trials). B) Saccade trajectories evoked using the stimulus patterns in A (red = square wave, black = sinusoidal). C) Main sequence of eye movements from stimulated sites for both subjects, monkey MA (black filled circles) and monkey SA (red filled circles). For reference, gray filled circles illustrate the main sequence of visually-guided saccades collected across numerous days and under varying conditions in both animals prior to beginning these stimulation experiments.

This step pattern provided comparison for our sinusoidal pattern, shown at the right. The frequency sinusoidal activation was chosen for its utility in deriving the intrinsic dynamics of the SC-to-movement circuitry (Breznen and Gnadt, 1997; Jackson et al., 2002; Gnadt et al., 2001) and not meant to recapitulate the volitional pattern of activation. On the other hand, it is arguably more natural than the step function in applying a supra-threshold, excitatory “burst” of activation to the superior colliculus with a supra-asymptotic number of stimulus pulses (Stanford et al., 1996). Further, we have shown previously (Gnadt et al., 2001) that the post-collicular saccadic circuit receives this output pattern faithfully (see Discussion). For the frequency-modulated sinusoidal pattern of pulses on the right, only the excitatory half-phase of the sinusoid (0–180 deg) defines positive firing rates. The negative phase of the sinusoid is irrelevant and not illustrated. The sinusoidal pattern was adjusted so that the positive going portion of the waveform was usually 100ms in duration with a peak frequency of 700 pulses/sec. Current per pulse was adjusted to >>2X of threshold for each site (usually 50–80 µA). Note that the average pattern of instantaneous frequencies illustrated by the stimulus frequency histogram (5ms bins) approximates the desired sinusoidal function, though the exact pattern of pulses varied between trials. Because the evoked-movement dynamics remained nearly constant (see panel B), this shows that the exact pattern of pulses was not confounded with the average trajectory metrics analyzed below. Figure 1B illustrates a sample of dynamic trajectories in Cartesian coordinates for the characteristic movements from one site for both patterns of stimulation (red = step pattern; black = frequency sinusoid). Consistent with our earlier studies (Gnadt et al, 2001), the end points for the two patterns of stimulation were statistically indistinguishable by two-tailed t-test of the averages of the horizontal and vertical end positions.

Figure 1C shows the main sequence plot of peak eye speed as a function of movement amplitude for samples from all individually stimulated sites included in the following analyses (black = subject MA ; red = subject SA). The stimulation-induced main sequence overlapped substantially with the main sequence of voluntary saccades (gray dots). Especially for the movements smaller than 20 deg., where recruitment of head movements would be minimized (Freedman et al., 1996), the plot demonstrates that the stimulated movements were reasonably physiologically-normal saccades.

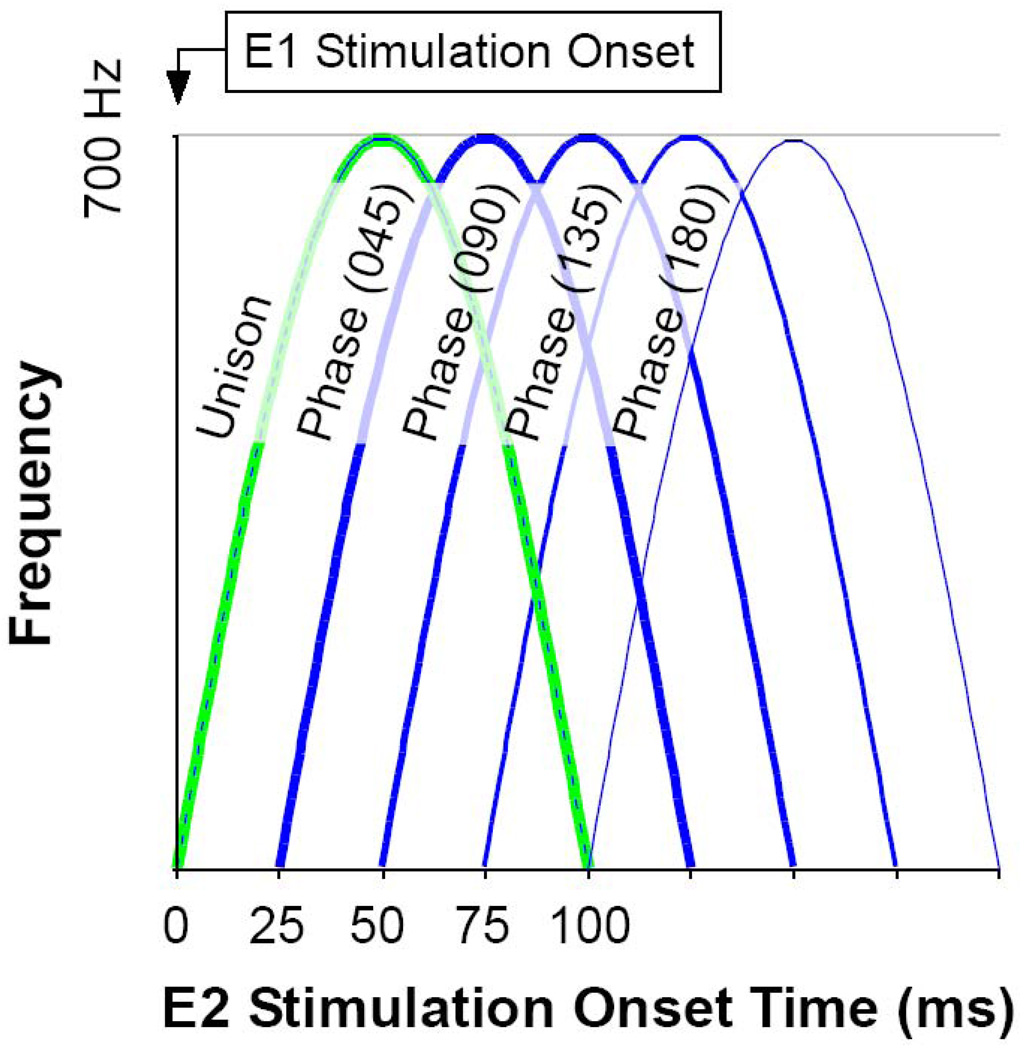
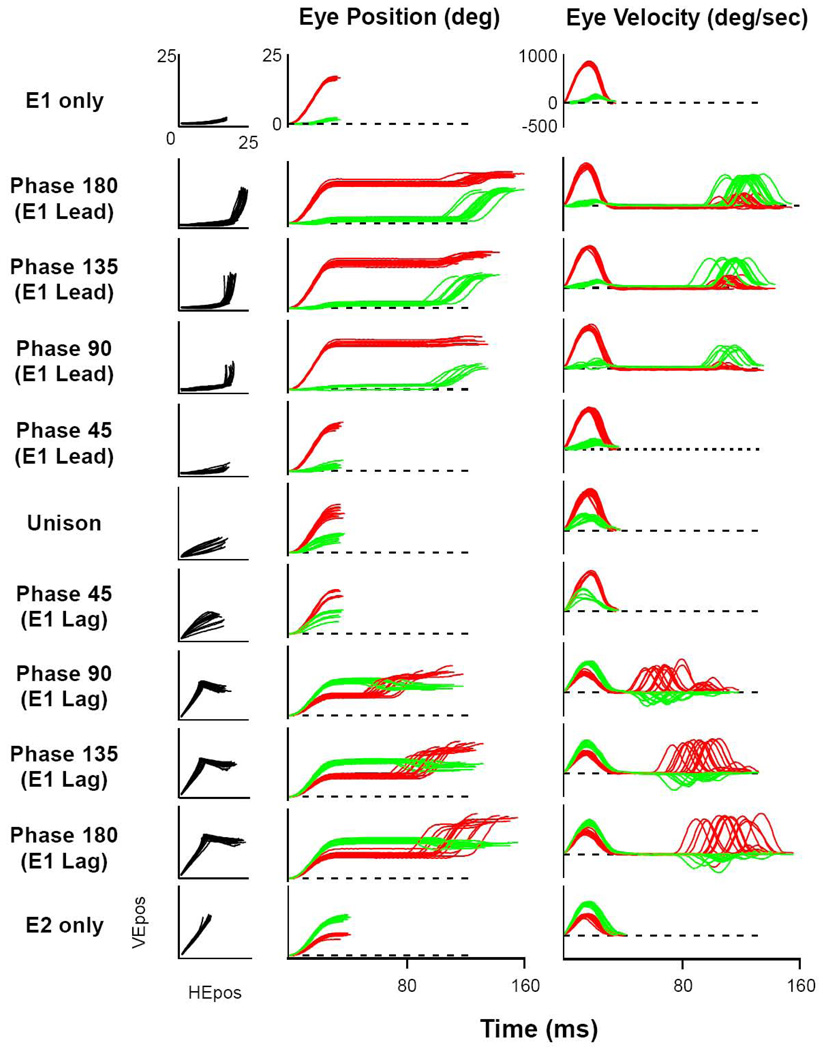
Figure 2 illustrates the most commonly used pattern of shifting phase difference between stimulation sites, where first one site, then the other, would lead by phases of 45 degree increments between 0 (simultaneous) to 180 (sequential with no overlap). Each half-sinusoid was adjusted to a time period of 100ms, which kept the stimulation pattern above the number of pulses to reach asymptotic, physiologic dynamics (average = 42) (Stanford et al., 1996) and below that which would have created multiple movements per cycle (Gnadt et al, 2001). During the few experiments that required shorter duration stimulation trains, the number of pulses was always greater than that required to attain normal saccades. As illustrated, each phase shift of 45 deg produced a 25 ms shift in timing between stimulation sites. Thus, each pair of stimulus sites was tested individually with the step function and the frequency sinusoidal function to obtain the characteristic movement for that site. Then each pair of stimulation sites was stimulated in sequential 45 deg phases (25 ms) between 180 deg out-of-phase (100 ms) with site E1 leading, through unison between E1 and E2 (simultaneous), to 180 deg (100 ms) with E2 leading. This created a family of smoothly overlapping patterns of activation between sites which can be replicated numerically to test details of saccade models. Phase conditions were applied in blocks with order of presentation randomized.

Figure 2. Experimental Design.

A) Diagram of the shifting phases of stimulation pairs used to evoke saccades. This example shows the most commonly used set of time shifts. The timing of the stimulation train E2 is plotted with respect to the stimulation train E1. Beginning with time 0 (Unison), E2 shifted in 25ms increments until the stimulation was sequential (Phase 180). A similar sequence was employed with E2 leading E1. Order of presentation was randomized.

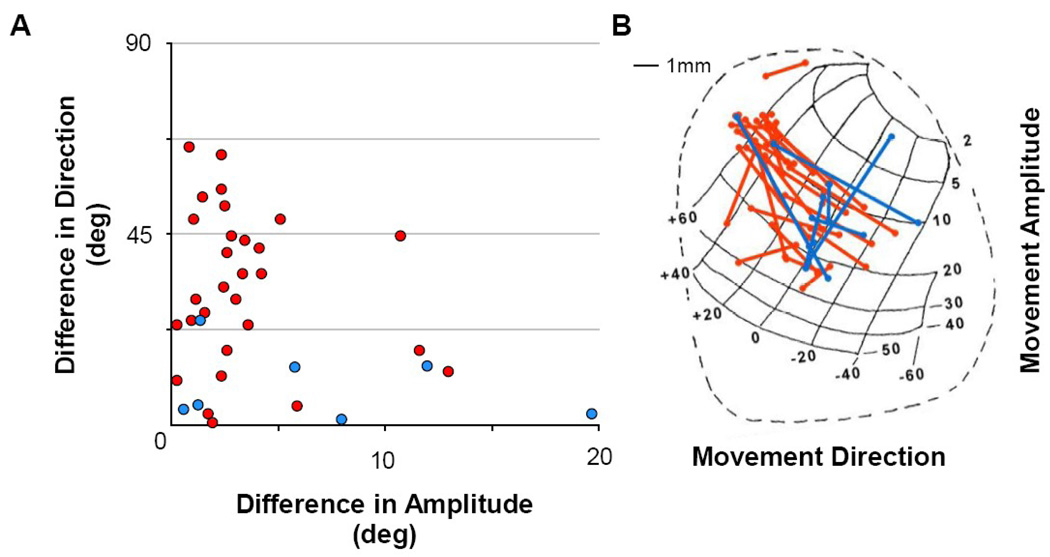
Figure 3A shows the difference in movement directions between paired sites versus the difference in movement amplitudes for all stimulation pairs. The various combinations of values were well sampled. Data points in the lower-right and upper-left portions of the graph constitute paired sites testing iso-direction movements of different amplitudes and iso-amplitude movements of different directions, respectively. Figure 3B plots the pairs of stimulation sites (connected by lines) onto an anatomical representation of the SC motor map as viewed from above (Robinson, 1972). Presentation of results from the left SC (subject MA) has been reflected onto the corresponding, mirror-image right SC.

Figure 3. Metrics of Movements.

A) Difference between movement directions and amplitudes from pairs of individual sites within the SC motor map. Iso-direction and iso-amplitude movements are located at the top left and bottom right of the graph, respectively. B) Illustration of the standard anatomical and topographic map of the Superior Colliculus (from Robinson, 1972). Stimulation occurred in the left SC of monkey MA and from the right SC in monkey SA, but here are overlapped on a single map for ease of viewing. Red and blues traces in both panels represent pairs of stimulation sites in monkey MA and monkey SA, respectively.

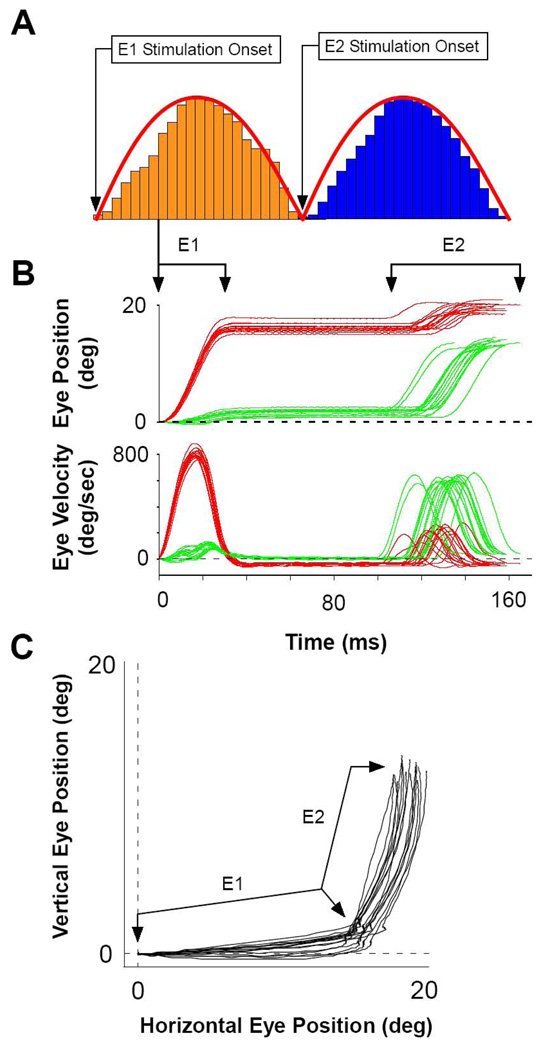
Figure 4 shows one of the 180 phase conditions (100ms time lag) for one pair of stimulation sites with similar amplitudes at nearly right angles. Figure 4 panel A shows the sequence of stimulation patterns at each site (first at electrode E1 in rust followed by electrode E2 in blue) for the 180 deg phase condition. Panel B plots the sequence of the two induced movements as position and velocity as functions of time for 16 pairs of stimulations. Panel C plots the same movements in Cartesian coordinates of horizontal and vertical eye position. As shown in Figure 4C, stimulation at E1 created movements of ∼16 deg at an angle near the horizontal meridian. Stimulation at E2 created movements of ∼14 deg near the vertical meridian. Plots in panel B are time locked to the start of movement E1, showing that saccades evoked by the stimulation train E1 leads those evoked by E2 with a 60–80 ms period of fixation between them. The variability in E2 latency is due to the variability of the individual stimulation patterns to reach threshold for movement interacting with the prior movement. Variability for E1 latency was removed graphically by the alignment procedure for the first movement.

Figure 4. Sequential Stimulations Evoked Sequential Saccades.

A) The typical pattern and timing for sequential presentation of sinusoids. The duration of each sinusoid was adjusted so that the positive half-wave was 100 ms. B) Eye position and velocity of sequential saccades, E1 and E2. Here, E1 first evokes horizontal movements at an average latency of ∼30 ms followed by E2 evoking vertical saccades with latencies between ∼30–50 ms. Traces are aligned on the start of the E1 saccade. C) Cartesian plot of the data presented in B (n = 16 trails).

Figure 5 plots these data from the same two stimulation sites under all 11 phase conditions (from E1 leading, through unison, to E2 leading, by 25 ms increments). The 4 columns from left to right, respectively, illustrate phase condition, Cartesian eye trajectory, eye trajectory as a function of time, and eye velocity as a function of time. Traces begin and end with a 30 deg/sec eye speed threshold for start and end of the appropriate movement(s). The top and bottom rows show individual activations of E1 and E2, respectively. The middle row (unison) plots the data from simultaneous activation. The top half of the figure shows the progression from E1 leading by 100 ms and decreasing by 25 ms increments to unison; whereas the bottom half shows the opposite progression with E2 leading. For this set of data, the second movement combined with the first for a single curved trajectory only for the phase-45 conditions, which is analyzed separately below. For the other conditions the second movements were separated from the end of the first movements by a period of fixation determined by the inter-stimulus timing. Inspection reveals that the direction and amplitude of the second movements were progressively changed by their proximity in time to the preceding movements. It is important to note that throughout this range of phase relationships, the induced movements expressed saccadic dynamics, not a simple linear following of the input functions. The induced movements reveal the transformation of the input functions by the saccadic circuit from controlled activation patterns at the SC and can be used to test the mechanistic assumptions of specific models.

Figure 5. Exemplar Presentation of Complete Data Set for One Pair of Stimulation Sites.

Columns from left to right: phase, Cartesian plot, eye position in time, and eye velocity in time. Top and bottom rows illustrate the effect of stimulation at each site individually. The middle row shows simultaneous stimulation (Unison). Phase 180 (E1 lead) is shown in Figure 4. Phase between stimulation sites progresses down rows with 25 ms increments in delays, with E1 leading in the top half, to E2 leading in the bottom half. The Phase-45 rows demonstrate single, curved movements to closely overlapping stimulation waveforms (25 ms).

Analysis of time-dependent end point distortions

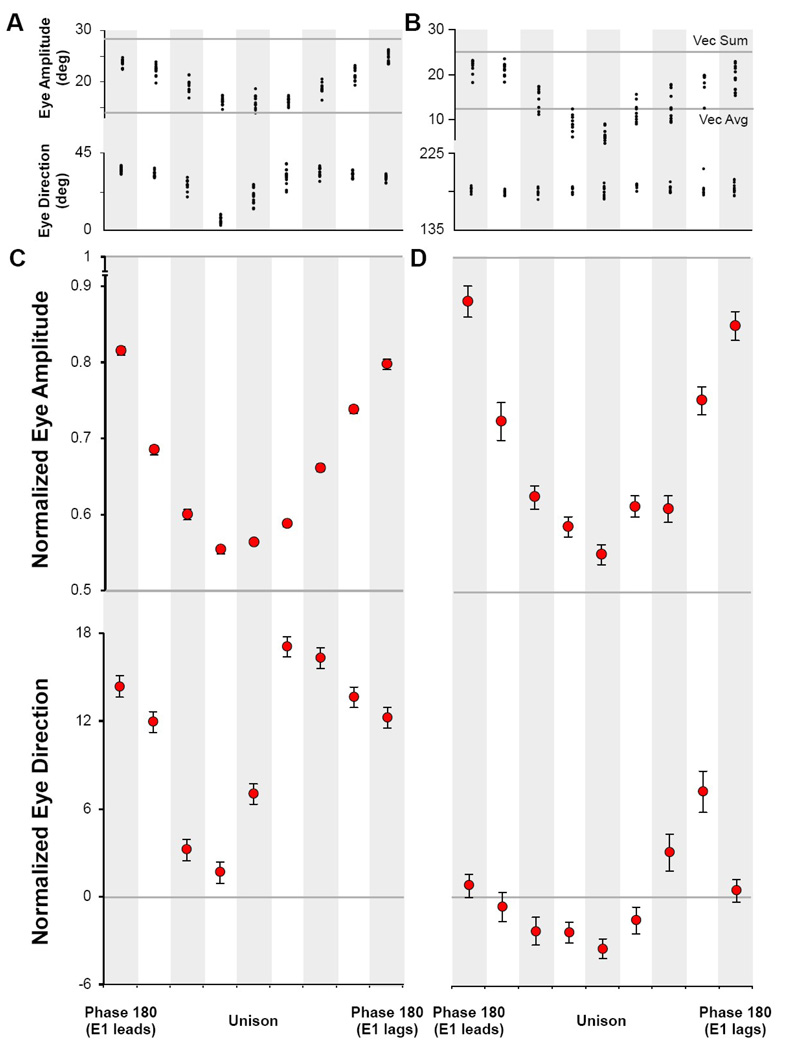
The time-dependent relationship of movement endpoints reveals the interactions of multiple spots of activity within the SC and is analyzed quantitatively in Figure 6. Figure 6A plots the amplitude and direction of the final endpoints (as a vector from the origin) for each phase condition from the same pair of stimulation sites as illustrated in Figure 4 and Figure 5. The scatter of data points at each condition can be compared to lines running across the top and bottom of the graph. These lines are the hypothetical end position values if the combination of individual movements had expressed the simple sum of the two individual stimulations (top line), or the numerical vector average of the movement vectors (bottom line). Note that the unison condition approximates the values for the vector average; whereas, the phase 180 conditions approaches the vector sum. The intermediate phases for each site (E1 leading to the left of center, E2 leading to the right, by 25 ms increments) increase in a symmetric sinusoid toward the vector sum value beyond the 100 ms time period of the phase 180 condition. This symmetry indicates that the endpoint amplitudes are nearly the same regardless of which movement was stimulated first. Data illustrated in Figure 6B were collected in monkey SA and show the same general pattern of movement changes as monkey MA. In both cases, there is a significant effect of inter-stimulus phase on endpoint amplitude (ANOVA: MA F(8,110)=136.540, p<0.001; SA F(8,79)=56.781, p<0.001).

Figure 6. Analysis of Evoked Endpoints as a Function of Phase.

A) Subject MA and B) Subject SA, single experiments from a pair of electrodes during which all phase shifts were collected. Panels illustrate the eye amplitude and eye direction at the top and bottom, respectively, for each paired stimulation. Eye amplitude decreases in size as stimulation trains merge toward unison; eye direction changes with respect to the direction of the first saccade. C) A summary of all experiments in monkey MA and D) for monkey SA. Plots show the normalized mean and standard error for all data collected at each phase. The direction values were organized such that E1 always had the more downward value of the pair.

This symmetry is not seen for the endpoint direction parameter at the bottom of Figure 6A. For this iso-amplitude pair of movements with differing directions, the order of the two stimulations in time makes a substantial difference in the direction of the final endpoint (ANOVA F(8,110)=60.208, p<0.001) - especially for the shorter phase conditions near the unison condition in the middle. On the other hand, Figure 6B illustrates an iso-direction pair of movements from the other subject differing only in movement amplitudes, which would not be expected to show differences for the direction parameter (ANOVA F(8,79)=1.839, NS).

Figure 6C & D summarize a similar analysis for all pairs of stimulation sites by plotting a normalized average and standard error of the endpoint amplitudes and directions at all temporal phases of stimulation in monkey MA and monkey SA, respectively. The amplitude was normalized to values ranging between 0.5, corresponding to the value for vector mean, to 1.0, representing the vector sum using the formula

$$\text{Amplitude}=(\text{X-mean})/(\text{sum-mean})*0.5+0.5$$

for each pair of sites. To compare movements in various directions, the direction parameter was rotated by the magnitude of one of the two vector angles,

$$\text{Direction}=(\text{X-E1}\text{or}\text{E2}),$$

to bring values near zero. Because of some direction bias toward one or the other stimulation vector (discussed further below) the vector angle giving curves with best overlap with zero was used. Since many pairs of movements represented iso-direction angles very close to zero, no scaling was applied to avoid exaggerating small differences in directions of movement.

The ANOVA of mean values for all pairs of sites reveals significant effects of phase on amplitude (ANOVA: MA F(8,3651)=4.081, p<0.001; SA F(8,405)=56.683, p<0.001) and direction (ANOVA: MA F(8,3651)=60.904, p<0.001; SA F(8,405)=9.193, p<0.001). One can see that – like the single examples in panels A and B – the 100 ms time delay between stimuli for the phase 180 conditions creates a pair of movements with an endpoint amplitude slightly less than the sum of their individual values. This residual effect on the second movement becomes increasingly larger at shorter phase relationships near unison. As the sequential stimulations increasingly overlap in time toward unison, the trajectory amplitude parameter approaches, but does equal, the value predicted by simple vector average of the independent stimulations. Thus, the simultaneous activation approximates the vector average, but reliably includes an activation mechanism that tends to overdrive the resulting movement slightly toward a linear summing of simultaneous activations. The plot of average endpoint direction in the lower part of Figure 6C & D also reflects a strong effect of temporal order.

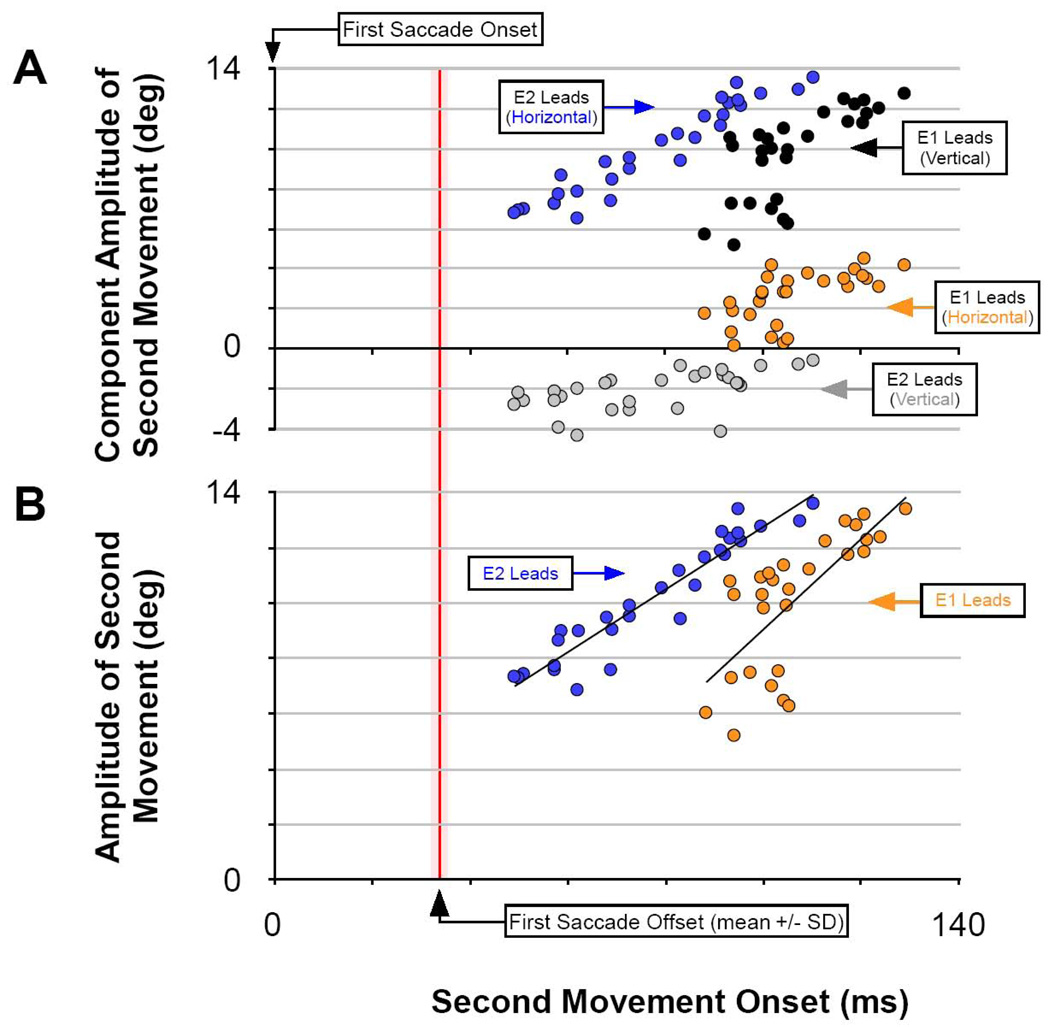
We investigated this residual effect of the first movement on the second in Figure 7 and Figure 8 by plotting the amplitudes of the second movements as a function of time from the start of first movement for each pair of stimulations. For illustration, Figure 7 includes data from the same pair of stimulation sites as shown in Figure 4, Figure 5, and Figure 6A from all trials for which the movements were clearly separated in time. Because the effects of recurrent feedback are purported to accumulate from the start of movement (Jackson et al., 2001), the data are plotted with respect to the beginning of the first movement, which had an average duration of 37 ms. Trials for which the second movement occurred while the first movement was still in flight (phase 45 conditions) are analyzed separately below. Figure 7A plots the horizontal and vertical component amplitudes of the second movements as separate colors. There is a decreasing function of each parameter with decreasing time between movements. So that we can compare movements of all directions and amplitudes from the entire sample of stimulation pairs, we re-plotted the data in panel B using the radial amplitude of the second movement vector. There is clearly a decreasing size of the second movement the closer in time it occurs to the preceding movement. If these decreasing sizes are the result a slow reset of a “neural integrator”, one might expect an exponential relationship for these decreasing values. Kustov and Robinson (1995) and Nichols and Sparks1 (1995) offered a ∼45 ms time constant of “leak”. However, we have concluded that the time constant of the reset is dependent on the ongoing activity within the circuit, which produces a variable time response in the range of 20–60 ms (Jackson et al., 2001). Thus, we fit the curves in Figures 7B with simple linear regressions, without implying any functional significance to its form. With correlation coefficients in the range of 0.52 to 0.90, this function captures a significant amount of the variance in the data.

Figure 7. Analysis of the Amplitude of the Second Saccade.

A) The component amplitude of second saccades evoked in a single experimental series (see Figure 5 Phase 90 through Phase 180 for example). B) The same data as panel A plotted as radial eye amplitude and fit with a least-squared, linear regression. Second saccades decrease in size as their inception nears the end of the first saccade.

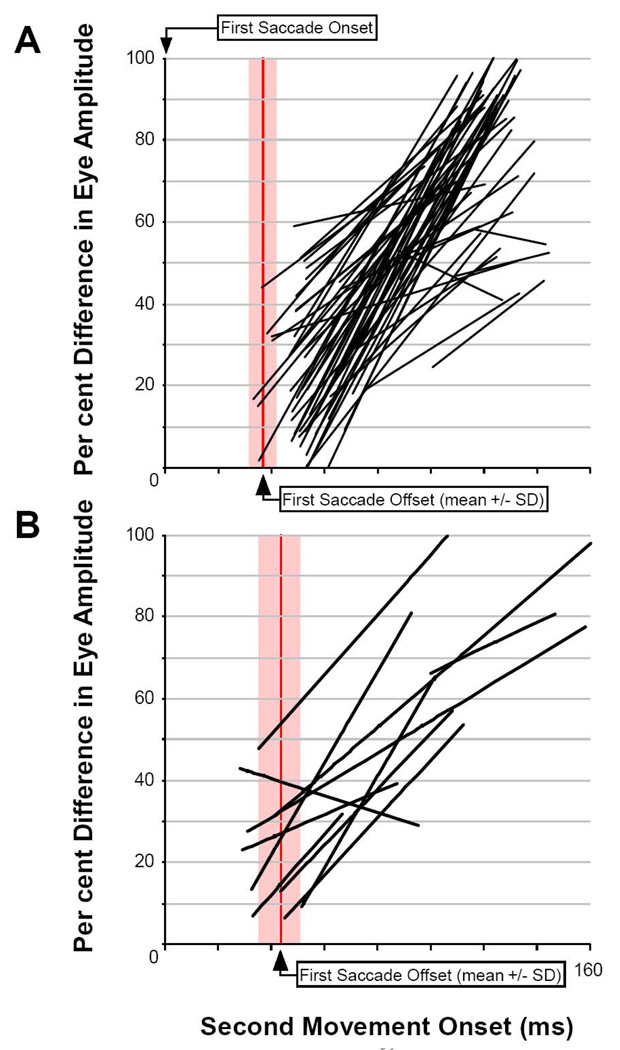
Figure 8. Summary of Regressions of Eye Amplitude for the Second Saccade.

A) Eye amplitude represented as a percent difference from the amplitude of normal saccades evoked by the stimulation train alone relative to all second saccades evoked by the second train of pulses and collected in monkey MA. B) Same as A for monkey SA. Each linear fit represents one half an experiment with either E1 or E2 leading toward the unison condition.

Panels 8A & 8B, respectively, plots similar linear regressions of radial amplitude for each of the stimulation pairs as a function of time from beginning of the first movement for each subject. For comparison among movements of various sizes, movement amplitudes were normalized as a percentage of the size of the characteristic movement at that site. With the exception of only 3 out of 74 regressions, there is clearly a time-dependent, residual effect of the first movement on the size of the second. The linear half-amplitude of that function is approximately 60 ms for 50 percent reduction, which fits well with an exponential constant in the 20–60 ms range.

As we consider the effect of further decreasing the time interval between stimulation sites, we can not apply this simple time-delay analysis on movement amplitude when the second movement begins before the first movement ends. Unlike the prior analysis of repeating, “staircase” movements of Breznen et al. (1996), we are here colliding a subsequent movement from a second stimulation site having different metrics. The time-dependent effect of a slow reset becomes confounded with a dynamic, normalizing effect of the output from 2 sites within the SC motor map. We can no longer assume a stationary and independent report of 2 collicular outputs of desired trajectory. In this condition, the movement endpoints reflect a dynamically changing pattern of topographic output from the SC (simulating dynamic, “colliding waves” of activity rising and falling at a site in one location and then another), interacting with the time course of the displacement controller (“leaky feedback integrator”). Complete analysis of this will require explicit testing of non-linear, spatio-temporal mechanisms for both processes by comparison to dynamic, numerical models, which is beyond the scope of this initial behavioral study.

Instead, we first test the simple hypotheses that the endpoints of these colliding movements are the result of a simple linear sum (independent processes) or simple vector average (center of mass) of 2 movement mechanisms. The endpoints of all but 6 of the 74 phase-45 conditions are reliably different from the value of either mechanism of combining movements (paired t-tests of whether the hypothetical values are included in the horizontal and vertical 95% confidence intervals of the mean landing point). Further, the mean end points for the unison conditions excluded the vector sum premise for all 37 stimulation pairs and excluded the vector average value for 33 of 37 cases (t-tests at 95% confidence interval, as above). These 33 unison cases exceeded the vector average in every case for a mean overshoot of ∼15%, which is a direction bias highly unlikely due to chance (binomial sign-test, p = 0.5³³ <<0.001).

Analysis of Curvature and Tortuosity

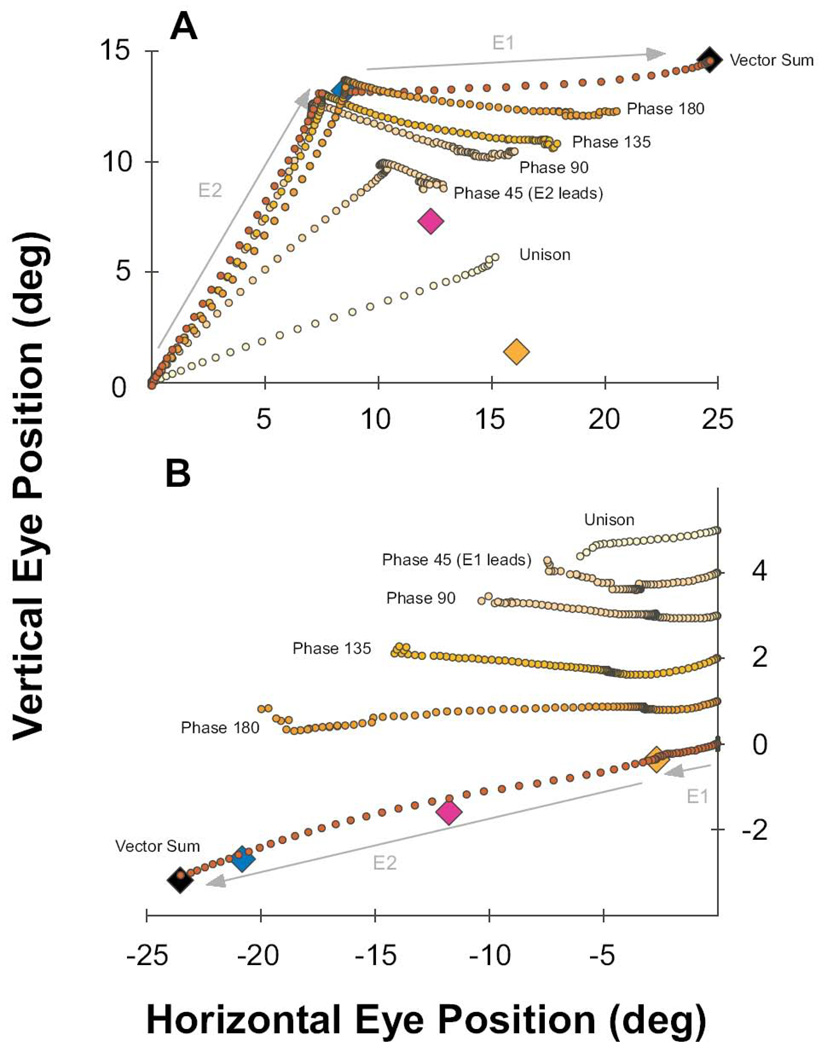
Next, we analyze the curvature of colliding movements caused by sequential activation of two sites for the 25 ms delay of the phase 45 conditions. In Figure 9, we illustrate examples of these interactions at the two extremes of possible spatial interaction: the dynamically curved trajectories of combining iso-amplitude movements of very different direction, and the dynamically accelerating/decelerating effects of combining iso-direction movements of very different amplitudes. To be representative, each example is taken from different subjects. Among the iso-amplitude movements in the upper-left corner of Figure 3A, we selected the movement pair with the largest amplitudes (14.4 and 16.6 degrees). For the iso-direction movements, we selected the sample with the largest discrepancy between amplitudes (19.8 degrees) in the lower-right portion of Figure 3A.

Figure 9. Comparison of Trajectories for Temporally-Colliding Movements.

A) Dynamic curvature of saccades caused by colliding stimulations. Here movements are caused by stimulation sites having similar amplitudes, but differing directions. Saccades are segregated based on which electrode was stimulated first. Orange traces and orange filled circles show the trajectory and endpoints of E1 stimulations leading E2 by 25 ms. Blue traces and blue filled circles show the trajectories for the reverse order of stimulation. Black traces and black filled circles illustrate the unison condition. The X at the far right top corner is the projected end point for a simple linear sum of E1 and E2, individually. The X nearer the end points of the evoked saccades is the value predicted from the formal vector average of E1 and E2. Orange and blue filled diamonds indicate the mean end points of stimulated saccades for E1 and E2, respectively. Note that none of the movements stopped moving prior to their final end position. B) Dynamic eye velocity profiles for movements having similar direction, but different amplitudes. Red traces illustrate the horizontal velocity component while green traces illustrate the vertical velocity component for each saccade. Top traces illustrate single trials of recruiting the smaller movement (2.7 deg) first, followed by a large movement of 22.6 deg. (antidromic, rostral-to-caudal pattern). Individual trials are superimposed onto the 95% confidence interval for the control condition of activating the rostral site alone (black shading). Bottom traces show single trials of recruiting the larger movement first, followed by the small one (orthodromic, caudal-to-rostral pattern), superimposed onto the control condition of activating the caudal site alone (black shading).

Extending beyond the original analysis of Robinson (1972) for movement endpoints, Figure 9A plots a set of trajectories sampled every millisecond for “colliding” movements of similar size, but different direction for the two phase-45 conditions (E1 or E2 leading by 25ms). These trajectories are compared graphically to the vector endpoints for each site independently (filled diamonds), to the trajectories of the unison condition and to the hypothetical end positions predicted by the vector sum and vector averaging premises (Xs). The phase-45 stimulations created continuous movements that started in the direction of the vector for the leading site, and then curved through a movement direction not represented by either stimulation site to an endpoint near the landing point of the unison condition. These highly curved trajectories appear to be following the dynamic, multi-site spatial pattern of activity evoked within the SC, which is particularly obvious for the E2-leading condition. Inspection of the blue traces reveals that early deviations away from the E2 vector to the right leads to moderate curvature of the trajectory through an arc that lands near the vector mean. Later recruitment of the second stimulation peals the in-flight trajectory away from E2 later and with greater curvature to the right, with all endpoints landing near the vector mean regardless of their total curvature. There was a fairly narrow window of timing for mid-flight interactions. Our method of creating stimulus pulse trains (see methods) created random jitter of timing, and we did not exert explicit control for the start of the second stimulus train at specific points in initial movement trajectory. Especially for small movements with brief durations, the difference between getting colliding movements and 2 separate movements with an inter-saccadic delay could be less than 10 ms of timing delay.

To see the dynamic response to iso-direction stimulation sites, we show in Figure 9B the dynamic velocity profiles to a spatial pattern of activity that rises first at a caudal site and then at a rostral location, or visa-versa (movements of 2.7 and 22.5 degrees along the horizontal meridian). Note that these sequential activations effectively create smooth patterns of activation that spread from caudal-to-rostral, or visa-versa, across the SC motor map. Though we made no attempt to match the natural rate of caudal-to-rostral spread of activity across the motor map during single, large movements (Munoz and Wurtz, 1995), this does simulate forced spread of activity across the motor map in “orthodromic” and “antidromic” directions. The eye velocity profiles resulting from slow, small movements spreading to fast, large movements, and the converse, can be seen by comparing individual trials to the 95% confidence envelope of velocity profiles. The top panel of Figure 9B illustrates the horizontal (red) and vertical (green) eye velocity traces superimposed upon the 95% control envelopes (shaded in black) when the small-movement site led by 25 ms. Note that 7 of 9 trials accelerate to peak horizontal velocities higher and later than the control condition, followed by a second movement 20–45 ms later. These second movements are substantially reduced in velocity (and size) from that normally encoded by the second stimulation site (compare to control trace in Figure 9B bottom). Thus, the initial movements are distorted to abnormally fast (and large) due to an averaging process with the “colliding” large movement, followed by an abnormally slow (and small) second movement due to short latency from a residual effect of the first movement. In the bottom panel of Figure 9B, we illustrate the opposite effect when the large-movement site led by 25 ms. In each of the 8 trials, the horizontal eye velocity decelerates abnormally within 15 ms of a normal duration of 42 ms. This truncation of the larger, first movement apparently occurs due to a topographic averaging effect with the metrics of the second stimulation site.

Because of differences in size, direction and duration of movements from the various pairs of stimulation sites, it is not possible to create a composite summary figure of curvature for all 37 pairs of sites. Instead, we selected a sample of stimulation pairs representing the best examples of iso-amplitude and of iso-direction as representative of the two extremes. This sample also includes the most interesting data for analysis of perturbed trajectories when the two movements were collided in time. From Figure 3A, we selected the 7 iso-amplitude cases with differences in direction greater than 45 degrees (upper-left data in Figure 3A), and we selected the 4 iso-direction cases with differences in amplitude greater than 10 degrees (lower-right data in Figure 3A).

To measure dynamic curvature of movement trajectory, we adopted a modification of the arc-chord index of tortuosity (Grisan, Foracchia & Ruggeri, 2008). The arc-chord ratio of a curve is the total length of a curve (L) divided by the linear distance between its ends (C) and would be 1 for a straight line:

$$T=L/C$$

Curvature of these movement trajectories was determined as the limit case of parsing the total movement into incremental pieces of zero-adjusted, arc-chord measure:

$$T=\mathit{(}N-\mathit{1}\mathit{)}/L\cdot {\Sigma }_{i=\mathit{1},N}\mathit{(}{L}_i/C_i-\mathit{1}\mathit{)}$$

The arc-chord ratio at each sequential triplet of samples of the movement positions (3 milliseconds) in Cartesian coordinates (horizontal and vertical eye position) was adjusted to a value of 0 for a straight line (Li/Ci – 1), summed for a total of N samples within the movement, and normalized by total movement length, L. Regardless of movement size or duration, this index of tortuosity equals 0 for a straight line and scales with movement curvature at any time or spatial resolution.

The tortuosity of the control values of single movements to the 22 single sites of stimulation are tabulated in Table I. The value of T among the individual sites ranged from 0.08 to 3.63 with a mean of 0.85 +/− 0.87SD. The control movements illustrated in Figure 1B had an average T = 1.0 +/− 0.3 (MA10 E2). Table I also includes the T values for the 11 cases of stimulation for the two sites in unison, which ranged from 0.09 to 8.14 with a mean of 1.21 +/− 2.37, which was not significantly different than the control movements (t=0.65, df=31, NS). The tortuosity of the unison condition movements illustrated in Figure 9A was 1.9 +/− 1.2. In Table I, ten of the 11 pairs of sites had significantly elevated tortuosity for at least one of the phase-45 conditions (range of values: 0.10 – 81.18), with an overall average of 16.50 +/− 22.72. From the 295 individual phase-45 trials, 44% had values of T greater than 3 standard deviations above the mean of the control values. Thus, we experimentally enriched the incidence of exceptionally curved saccades substantially. When present, the overall curvature of trajectory was always in the “attracting” direction of interaction between sites. The tortuosity of the two cases of phase 45 collisions of stimulation shown in Figure 9A were 54.44 +/− 67.03 and 2.29 +/− 1.21, respectively, for the E2-leading and E1-leading conditions. The E2-leading case was reliably different from the control values of the same pair of single stimulations (t=3.16, df=15 unequal variances, p<0.001), and the difference for E1-leading case was only marginally significant (t=1.35, df=42, p<0.011).

Table I. Tortuosity.

Summary of Tortuosity for the Iso-Direction and Iso-Amplitude examples. For each condition, the difference between pairs in direction (Diff Dir) and amplitude (Diff Amp) of movement is tabulated and averaged (Means). The average values of Tortuosity for each case are shown, along with the overall mean for all single cases (E1 or E2), for the unison cases and for all Phase-45 cases of stimulation.

	Iso-Amplitude Pairs					Phase-45
	Diff Dir	Diff Amp	El	E2	Unison	El→E2	E2→E1
MA22	63	2.2	3.63	1.00	1.87	4.94	16.72
MA28	65	0.7	1.47	1.76	1.36	0.27	3.42
MA29	53	1.3	0.20	1.68	0.13	21.75	8.66
MA27	51	2.4	0.53	0.32	0.09	0.18	0.10
MA10	55	2.2	1.42	0.12	0.15	2.29	54.44
MA23	48	0.9	0.33	0.08	0.16	8.80	0.47
MA13	48	5.0	0.33	0.16	0.16	22.74	7.94
Means:	55	2.1
	Iso-Direction Pairs
SA3	2	19.8	0.43	0.13	0.42	71.08	8.63
MA5	12	13.0	1.98	0.88	8.14	81.18	18.79
SA6	13	12.0	1.31	0.26	0.33	5.39	11.69
MA17	17	11.6	0.51	0.30	0.46	4.09	9.49
Means:	11	14.1
			All single		Unison	All Phase-45
		Means:	0.85		1.21	16.50
		SD:	0.87		0.16	22.72

Figure 10 summarizes the range of inter-site collision effects by plotting examples of the two extremes of possible interactions: Panel A plots the average trajectory at each millisecond for collisions between sites with the largest different directions, and panel B plots average trajectory for collisions between sites of largest different amplitudes.

Figure 10. Progression of Dynamic Eye Trajectory as a Function of Phase Between Stimulation Sites.

Orange and blue diamonds indicate the end point of saccades generated by stimulation of sites E1 and E2 , respectively. Pink and black diamonds, respectively, represent the vector average and vector sum locations. A) Mean trajectories for all phase conditions in which E2 leads E1 for a typical iso-amplitude case (upward movement followed by horizontal). The unison condition produced a straight line trajectory to an end point near the vector average of the E2 and E1 vectors. The phase 45 condition (25 ms delay) is initially dominated by movement toward E2, then curves dynamically through a trajectory not represented by either stimulation site or the unison activation. The movement ends at a point near the vector mean despite persistence of the stimulation at both sites. Overlaid plots of the Phase 90 to Phase 180 movements demonstrate the progression of dynamic trajectories where movement from E2 stimulation completes before the influence of E1 manifests, with greater separation in time between stimulation sites (50, 75, 100, >>100 ms). B) Same as in panel A for a typical iso-direction example with E1 leading E2 (small movement followed by large). Plots are offset vertically for ease of viewing. Similar to the iso-amplitude case in A, the unison condition induced a single, straight movement to an endpoint near the vector average. The phase 45 to 180 conditions shows some stretching of the size of the E1 movements by collision with the E2 stimulation, with progressively complete and fast expression of the large E2 movement at longer phase delays (25 to >>100 ms). For both A and B, some plotting discontinuities occur near the ends of each average plot due to drop out of shorter individual trials in time.

Figure 10A plots as colored diamonds the average endpoints of individual stimulations from E1 and E2, and the hypothetical endpoints for the vector sum and vector average for the iso-amplitude example. Simultaneous co-activation of the sites produced the average movement trajectory (@1 ms resolution) indicated as “Unison”. Differences in stimulation currents relative to recruitment threshold can bias the “average” endpoint toward one or the other vector (Robinson, 1972), which we did not attempt to manipulate. Regardless, this empirical balance was constant for all temporal phases of interactions for each experimental pair of sites. Average trajectories (@ 1 ms) are plotted for the phase 45, 90, 135 and 180 conditions, for which E2 lead E1 by time delays of 25, 50, 75 and 100ms, respectively (n=13 to 20 trials each case). These can be compared to the “vector sum” case which plots superposition of the average trajectory (@ 1 ms) of E2 (alone) followed by E1 (alone), starting from the endpoint of E2. The trajectory for the phase 45 condition is the mean curvature for which the eyes never stopped their tortuous motion. For each of the other phase conditions, the 2 legs of the trajectory were separated by a period of fixation at the E2 endpoint proportional to the increasing time delay to the E1 stimulation. It is striking how the second legs of movement monotonically increase in amplitude and rotate up in proportion to the increasing time delay between the start of the first movement and the second, including the phase 45 condition for which the eyes curved continuously in midflight in a dynamically bending trajectory toward the co-activation of E2 and E1. Along with the extrapolation of the curves in Figure 8 to values shorter than the duration of the first movement, this is consistent with our previous suggestion (Gnadt et al., 2001; Jackson et al., 2001) that the decline of the “leaky feedback integrator” is continuous and includes the time course of the initial movement. Note also that the velocity of these second phases of movement were much slower than normal saccadic dynamics (note the distance between 1 ms points in trajectory).

It is important to understand that both the single curved movements and the double movements end even as the various SC stimulations persist for many tens of milliseconds longer than the movements themselves. According to the consensus assumption that the saccade circuit acts as a displacement controller, the movements reveal the dynamic mechanisms of the displacement controller moving toward a “desired movement” SC activation pattern, not a linear report of the pattern of SC activation. The movements were the brainstem generator’s reactions that dynamically followed the changing displacement commands. Similar to volitional saccades, it appears the movements ultimately stopped according to a recurrent mechanism for comparing when the dynamic trajectory matched the displacement commands experimentally created in the SC motor map. For all but the unison stimulation, which progressed straight toward an approximation of the vector average of the 2 sites, the initial trajectory of each stimulation condition was toward the vector for the leading stimulation site (E2). For the phase-45 condition, after starting toward the vector of the initial stimulation site, a second stage of movement curved through a direction and size not represented in the characteristic vector of either stimulation site. Instead, it moved through a curved path that represented the current trajectory following the dynamically changing displacement command toward the approximation of the vector average of E2 and E1. Like the unison condition, it is notable that this tortuous path to dynamic combination of E2 and E1 approached its vector average, not its sum. For the phase 90, 135, and 180 conditions, as the overlap between stimulation cycles progressively separated to 50, 75, 100 ms (respectively), the time between stimulus cycles began to exceed the duration of the first movement. With progressively longer intervals from the first movement, the second movement expressed a progressively veridical representation of E1.

Analysis of the iso-direction pair of movements in Figure 10B reveals a similar sequence of endpoint and velocity distortions as a function of time from prior movement. At the bottom of panel B, colored diamonds represent the average endpoints of individual stimulations from E1 and E2, and the hypothetical endpoints for the vector sum and vector average for the iso-direction example. Superimposed on those icons is the average trajectory (@1 ms) for a small E1 movement, followed by plot of the E2 large movement from the E1 endpoint. Simultaneous co-activation of the sites produced the near-average movement trajectory indicated as “unison” at the top of the panel. Moving down the series of plots from the top are the movement trajectories (@ 1 ms) of the phase 45, 90, 135 and 180 conditions spanning time delays of 25, 50, 75 and 100 ms for the sequence of small, slow E1 movements followed by large, fast E2 movements. Note that for graphical clarity each average trace is offset vertically on the ordinate according to inter-stimulus timing and the vertical scale is expanded to roughly twice that of the abscissa. The speed and size of the second movements were progressively truncated for progressively shorter time delays between stimulation sites. As for the iso-amplitude data, this is consistent with a normalizing interaction between co-activated sites, followed by a sub-optimal response to the dynamic error of the second stimulation in a time-dependent fashion.

Discussion

These data appear to capture the parametric combination of two dynamic parameters of the SC-to-eye movement spatio-temporal transform in non-human primates: Normalization of total topographic activity of the SC to define a desired movement and a distal displacement controller with time dynamics in the tens of milliseconds. In addition, the results appear to reveal how two competing saccade targets can lead to abnormally curved trajectories and distorted end points under some conditions. The results can be used to test hypotheses about mechanisms for translating patterns of activity within the SC motor map for eye movement control. By describing these dynamic interactions under experimental control for a relatively complete set of spatial and temporal relationships, we provide benchmark data for testing computational models. The interacting, sinusoidal frequency-modulation provides an exploration of spatio-temporal activation that overlaps with -- and extends beyond --that of volitional conditions, while using a set of activation functions with explicit numerical and analytical solutions for quantitative system control models. Models that are found to simulate these findings will gain support for their mechanisms and assumptions; models that fail to recapitulate these results must be modified or rejected.

Summary of Results

Compared to the characteristic movement vectors for each stimulation site alone, the movements resulting from increasing amounts of temporal overlap changed systematically from that with an end point of the vector sum of the two sites to a value approaching a vector average for simultaneous activation. It seems that the overall activity across the SC motor map normalizes the drive recruited around a specific point – or pair of points – in the map (Ottes et al., 1984; Findlay, 1982; Lee et al., 1988). This normalization approximates that of a numerical vector average, with a 15% overshoot under the conditions used in this study. Because our experimental forcing functions by microstimulation are probably overriding most synaptic influences near the electrode tip by direct activation of the excitable axons, this normalization by overall SC activity must be accomplished downstream of the SC (see below for technical considerations of this assumption).

For movements with less than 100ms from prior movements, including those where a second movement collided dynamically with a prior movement, the leading movement always truncated some component of the second movement. The end point of the combined movements landed at a position intermediate between the hypothetical premises of a vector sum versus vector average. If the interaction between the two movements were a simple linear sum of each vector, they would have expressed sequential or curved trajectories that always ended at the value of the sum regardless of the timing between sites. Consistent with earlier studies (e.g., Robinson, 1972; Ottes et al., 1984; Findlay, 1982), we can definitively exclude this possibility. For temporal overlap of less than 25ms between sites, many movements followed single, curved trajectories that were entirely dependent on the temporal order between the two sites. The trajectory always started in the direction of the vector for the first site and subsequently bent along a curved trajectory representing the dynamically changing topographic representation of the SC activation pattern interacting with the dynamic truncation of the second movement by the first. This persistent and time-decreasing influence of one movement on the next is further evidence for a “slow reset” of the brainstem feedback mechanisms for dynamic control of movement metrics (Kustov and Robinson, 1995; Nichols and Sparks, 1996).

Intra-collicular mechanisms

We consider 3 basic mechanisms for translation of activity at two electrode sites within the motor map: 1) winner-take-all for one of the vectors, 2) a sum of individual vectors and 3) an average of individual vectors.

We find no evidence in our data for a winner-take-all mechanism. None of our data pairs exhibited complete cancellation of one site by the other. Though we do point out, this tests for cancellation distal to the SC and does not exclude intra- or pre-SC mechanisms that might shape SC activity under volitional conditions (Munoz and Istvan, 1998; Hikosaka and Wurtz, 1983; Liu and Basso, 2008). Experimental microstimulation would probably overcome any intra-collicular inhibition by direct excitation of SC output axons. These data do not include sites of stimulation in a verifiable rostral “fixation zone” (Munoz and Wurtz, 1992). However, in earlier, preliminary studies (Carasig and Gnadt, 2004) we tested one pair of sites with an electrode in a far rostral position that produced tiny, inconsistent movements less than 0.2 degree and a second site with a 3 degree movement vector. Co-activation at both sites produced a single saccade with an end position slightly less than the vector average. This is more consistent with interpretation of the rostral SC as an extension of SC motor map to tiny saccades (Hafed, Goffart and Krauzlis, 2009) than a functionally separate structure for active fixation (Munoz and Wurtz, 1992). In the earlier pilot data of Carasig and Gnadt (2004), we found vector cancellation only for one pair of sites by stimulating with opposing contraversive vectors of movement from stimulating the SC bilaterally. A similar observation has been made by Robinson (1972).

Since the normal behavior for frontal-eyed, foveated species like primates is to first select a single target for the binocular point of regard, this collision of competing targets within the SC seems to be relatively rare during volitional behavior (e.g., Port and Wurtz, 2003). Furthermore, the normal, obligatory latency of 200 ms or more to generate voluntary saccades can be understood as highly adaptive for a displacement controller with a relatively slow reset. When the movement vectors of each site are invoked at times much longer than 100 ms, the complete trajectory for the combination of movements is their vector sum. If this were not the case, a displacement controller would be useless. Otherwise, the saccadic command for a new displacement of eye position would be dependent on its history of how it got to the current position. A servo-like, end position controller would better operate in this environment, since it would always drive the eye toward a certain orbital position in comparison to its current position. Clearly, the SC and the brainstem saccade generator is not an end position controller. Further proof of this is evident in the fact that movement vectors invoked from stimulation of the SC produces movements of a characteristic vector with relatively minor deviations due to different starting positions (Roucoux et al., 1980; Freedman et al., 1996).

On the other hand, when two points on the SC motor map are activated simultaneously, there is a single saccade with normal dynamics to an endpoint that approximates the vector average of the two sites. This shows that both the dynamics and the metrics of the end point are normalized to near the vector average of the two. Notably, our results found that the unison activation of the two sites produced an overall result that exceeded the exact vector average by about 15%. This stimulation-induced overshoot differs from the undershoot that is typical for averaging behavior of volitional movements (Ottes et al., 1984, McPeek et al., 2000, Arai, McPeek & Keller, 2004), which is probably a methodological variation on a similar normalization mechanism. We interpret this to indicate either that overlapping diameters of stimulation recruitment might overcome the normalization from “shared” distal regions or that a larger fraction of entire map might be recruited than can be normalized by the remaining fraction. As noted above, we speculate that the normalization must take place distal to the SC. We discuss two proposed mechanism of normalization below (Lee et al., 1988; Goossens and Van Opstal, 2006), but further comparison of computational and empirical studies will be necessary to explore possibilities.

Rostral-Caudal Collicular Activation

For iso-direction pairs of stimulation sites with different sizes of movements, we have effectively created intra-saccadic patterns of activity between two sites that first rise caudally and then is smoothly replaced at a rostral location, or visa versa, in the collicular motor map. Especially for the phase-45 conditions such as those in Figure 9 and Figure 10, if the spreading wave theory of intra-collicular activity is what controls the normal saccade dynamics (e.g., Munoz and Wurtz, 1995; Optican, 1995), we might expect reasonably normal, single saccades from the large-to-small spread of activity, or perhaps a movement that would dynamically follow the caudal-to-rostral pattern across the motor map. Further, we should expect that the opposite small-to-large pattern of activity would disrupt normal saccade dynamics severely. Alternatively, the stationary hill hypotheses predicts that the individual movement dynamics will match the activity-weighted vector average (Lee et al., 1988) of the two sites in all cases with smooth changes between vector average to vector sum for increasing times between stimulations. Our results from 5 pairs of iso-direction rostral/caudal points appear to best match the stationary hill hypothesis. While we concede that our timing relationships do not replicate volitional, intra-collicular motor map dynamics, this conclusion using experimental manipulation of rostral/caudal patterns of activity supports the findings of Anderson and Keller (1998) who attempted to measure the spread of activity in neurons scattered across the motor map. These investigators found the posterior to anterior spread of activity to be less well organized than would be required by the spreading wave theory.

Considerations of experimental microstimulation methodology

To avoid complications of interpretation, we specifically delivered and selected our data to avoid contamination by inadvertent voluntary movements. However, interpretation of these stimulus-induced movements is dependent on the assumption that the collicular output faithfully follows the experimental patterns of stimulation to create a reasonably physiologic activation of the saccadic circuit distal to the SC. We do not refute that our stimulations recruit an unnatural pattern of cell types near the stimulation site, or that axons in passing are not excited. It is also true that microstimulation pulses probably recruit a more synchronous volley of action potentials than volitional activation. On the other hand, we have shown that the stimulated movements have properties consistent with reasonably physiologic recruitment of the post-collicular saccadic circuit and have argued against hypotheses that SC stimulation results in non-human primates are due to recruitment of non-saccadic subsystems (Breznen et al.,1996.; 1 Gnadt et al., 2001).

It is clear from neurophysiologic studies that the SC receives some form of feedback during voluntary saccades (e.g., Anderson and Keller 1998; Kaneko, 2000). However, we have pointed out that our experimental stimulations (Breznen et al.,1996; 1 Gnadt et al., 2001) are most compatible with a post-collicular mechanism for controlling saccade amplitude. The direct recruitment of neurons by microstimulation, in theory and in practice (Gnadt et al., 2001), is sufficient to override or blunt synaptically-mediated influences. Thus, we can reasonably expect that “long-loop” feedback influences into the SC are largely superseded by the experimental pattern of microstimulation.

Furthermore, we can be reasonably certain that our stimulation electrodes effectively control the neural activity in the immediate vicinity of the tip (∼1 mm radius at 50 µA, Gamlin, Gnadt & Mays, 1989; Gnadt et al., 2001). We have presumed that natural intra-collicular mechanisms recruit a population of cells beyond the immediate vicinity of the electrode tip, probably on the order of a 3 mm diameter (McIlwain, 1982; Gnadt et al., 2001). Thus, with 2 electrodes we can probably control the activity in a large fraction of the collicular map with overlapping spatial domains of influence. The exact patterns of SC motor map activity have not been verified directly. However, we have shown previously at individual sites (Gnadt et al., 2001) that the sinusoidal, frequency-modulated patterns can create interference patterns of saccade size when collided with the periodic movements of the “staircase” saccades to prolonged, steady activation. Periodic re-triggering of stereotypical saccades would not produce this result. These interference patterns conformed quite accurately to constructive/destructive interference between two independent oscillations on the same circuit downstream of SC, which were absent when either oscillation was presented alone. Instead, these amplitude modulations reflected the moment-to-moment drive from competing inputs at the brainstem burst neurons. One of the inputs was derived from the sinusoidally modulated collicular output; the other came from the recurrent, inhibitory influence of the circuit’s feedback. Depending on the dynamic drive at the burst neurons, the resulting movements were super-normal, sub-normal or equal to the characteristic movement from that site (Jackson et al., 2001). Notably, this is consistent with the suggestion of Goossens and Van Opstal (2006) and Van Opstal and Goossens (2008) that the SC provides a dynamic drive to ongoing movements. An alternative hypothesis that this amplitude modulation might be due to partial inhibition of the OPN has been refuted by studies of the OPN activity during the stimulation-induced “staircase saccades” (Paul and Gnadt, 2006).

On average, the pulse arrival times between stimulation sites in this study were randomly applied in time. The pulse pattern of each stimulation cycle was unique and pseudorandom (see Methods). Furthermore, the synaptic, intra-SC recruitment of neurons beyond the direct cellular activation would have been synchronized to each pulse but scattered in time with various transmission times. This would have created asynchronous volleys of action potentials to the brainstem burst generator between stimulation sites, with each site’s pattern dominated by synchronized volleys of rising instantaneous frequency and some synaptic variation within the volley. We can compare this to the results of Brecht et al. (2004), who stimulated two sites within the SC of cats with 50 Hz trains (20 ms intervals) of triplets at 833 Hz (1.2 ms intervals). This would have injected into the cat’s burst generator a di-modal frequency pattern of interlocked 50 and 833 Hz oscillations. The 50 Hz mode of this pattern would have been sub-threshold for inducing saccades, whereas the 833 Hz triplet would have approached saturation of action potential refractory periods. Interestingly, they found that synchronous application of the stimulations at two sites produced a movement end point at the vector average of the two sites; whereas, asynchronous, interdigitated application of the triplets tended to cause movements expressing the vector sum of the two sites. In this study, we expect our analyses would have most closely resembled the Brecht et al. (2004) asynchronous case, even though individual arrival times at the burst generator on given trials might have had local spatio-temporal interactions on the scale of the synchrony of the Brecht et al. (2004) high frequency triplets. Thus, our data seem to be inconsistent with predictions from the Brecht et al. (2004) study for a vector sum from asynchronous activation of two sites. An alternative interpretation of the Brecht et al. (2004) data may be that both simultaneous and randomly interspersed patterns of spikes from two sites equally engage a normalizing mechanism; whereas, the artificial alternating synchrony between interdigitated volleys creates an additive interaction that overcomes the normalizing mechanisms usually present between two sites of SC activity. Further, it remains undetermined if the effect described by Brecht et al. (2004) might be intra-collicular or post-collicular, since their pattern of stimulation might have produced oscillations at either or both levels.

Comparison to published models

These data lend further support to the hypothesis that there is a recurrent inhibitory mechanism within the saccadic circuit that resets slowly between movements. We demonstrate a consistent monotonic reduction in component size of movements proportional to the time from the start of a prior saccade. The time “constant” of the declining residual influence of one movement on the next appears to be on the order of 20–60 ms, as suggested previously (Kustov and Robinson, 1995; Nichols and Sparks, 1996; Breznen and Gnadt, 1997; Jackson et al., 2001). These data also conform to the assumption that the beginning of this truncation process can precede the end of the first movement (Breznen and Gnadt 1997, Schlag et al., 1998; Jackson et al., 2001).

This stands at odds with some behavioral studies (Goossens and Van Opstal, 1997; Corneil et al., 1999) reporting that closely-spaced, voluntary movements can exhibit metrics that appear to correctly compensate for prior movements. It might be tempting to attribute these contradictions to a methodological flaw in the microstimulation technique, but that seems unlikely. Explicit intervention of collicular activity undoubtedly reveals a time-dependent process in eye movements mediated by a reasonably physiologic activation of the saccadic circuit (see also Gnadt et al., 2001; Paul and Gnadt, 2006). In addition, it appears that these time-overlapping experimental stimulations reasonably mimic the transient expression of multiple, competing targets naturally expressed in the superior colliculus (Port and Wurtz, 2003). Moreover, curved movements induced by multiple loci of activity within the SC can be accounted for in a system with a slow reset (Walton et al., 2005). We can only speculate that, in situations of forced behavioral ambiguity for competing targets, subjects can learn to employ adaptive compensation of volitional command strategy to accommodate these time-dependent properties, or engage a process that bypasses the collicular/brainstem mechanism revealed here (e.g., Schlag et al., 1998). Experimental verification of this would be difficult in human subjects. However, under normal conditions, the obligate response latency of 200 ms or more allows uncomplicated engagement of the SC and the brainstem burst generator as a highly adaptive displacement controller, despite the slow “refractory period” revealed by experimental intervention.

Next, we make comparison to three recent saccade models, selected for their relevance to multiple target considerations and vector expression of the SC-to- movement transduction. Walton et al. (2005) incorporated a traditional control scheme of the SC providing a static displacement command to a brainstem burst generator. Aria and Keller (2005) describe a distributed model with the SC as a direction element within a closed-loop displacement controller. Goossens and Van Opstal (2006) suggested an ensemble-coding model with the SC as a motor command module.

Walton et al. (2005) coupled a vector component decomposition of SC output to a two-dimensional feedback model that used dynamic motor error to complete movements with kinematics matching normal saccades. Collicular output was modeled as a normalized vector average of total SC activity. They challenged the model with simultaneous activation of two sites, followed by premature truncation of activity at one site. The resulting movements progressed first toward an endpoint representing the vector average of the two sites, followed by a curved trajectory that brought the eye position near the target point of the remaining site of activation. Similar to our stimulation profiles, they also delayed the activation of one site by up to 40 ms after the other. This also produced curved trajectories initially progressing toward an intermediate position between desired vectors, followed by curvature toward an end point defined by the later site. The longer the time delay for the second site, the later and stronger the deviation toward the end point defined by the second stimulation. In the data of this study with stimulation delays of 25 ms, we observed similar results (e.g., red traces of Fig.9), except that the initial movement was biased more directly toward the first vector with final curvature toward the vector mean.

In the Walton et al. (2005) configuration, the curvature of trajectory was produced by a displacement controller distal to the SC. By comparison, they found that a direction controller that included the SC within the feedback loop (Port and Wurtz, 2003) did not produce reasonable endpoints of movement. This suggests that the downstream, brainstem mechanism of curvature was reasonable. The discrepancy between predictions of the Walton model and our data for the directions of movement suggest that their mechanism of normalization of the SC output between sites was not accurate. Our empirical data suggest an interaction where the early drive is dominated by the first site’s activity which then dynamically rotates toward expression of a vector average as the two sites are co-activated. Further, their model used a resettable feedback integrator, but did not incorporate an ability to retrigger “staircase” saccades. Nor did these authors test longer delays between movements. Their model also did not investigate mechanisms related to dynamic control of velocity during curved movements.

Another model examining curved trajectories was investigated by Arai and Keller (2005). This model included the alternate assumption that dynamic feedback for controlling movement end is mediated through feedback from the brainstem to the SC. These authors also included dynamic interaction between the SC and a topographic dis-inhibitory influence from the Substantia Nigra pars reticulata. This model controlled both dynamic direction and speed from the total, weighted activity of the SC output. Interactions with a static topographic inhibition from the Substantia Nigra and the dynamically changing feedback from the brainstem served to shape and position the topography of the SC output in patterns that created curved movement trajectories approximating those occasionally seen behaviorally. This model also investigated the nature of intra-collicular balance of inhibition and excitation, but concluded that additional extra-collicular mechanisms must be present to account for sharply curved trajectories.

This model might prove useful in simulating the intra-collicular recruitment of SC output from our microstimulation studies. However, the very nature of inducing saccades by forced patterns of microstimulation at the SC is not compatible with having SC within the “local” dynamic control loop that ends the movement (Breznen et al., 1996; Gnadt et al., 2001; Walton et al., 2005). If there was not an independent mechanism distal to the SC to end movements at some approximation of desired target, then persistent activation of the SC would induce movements without saccadic dynamics that would never stop.

In a model proposed by Goossens and Van Opstal (2006), the SC specifies a straight-displacement trajectory from a dynamic, linear vector summation into a feedback-controlled burst generator. Each action potential from the SC specifies a site-specific “minivector” drive, such that the resulting movement reflects a linear sum of the topographic output of the SC. Importantly, the output of the SC for a given movement is normalized to a constant number of total spikes by an unspecified mechanism distal to the SC. Like the Walton et al. (2005) model, this model elaborates dynamic motor error explicitly as the difference between SC output and current eye position. On the other hand, unlike the Walton et al. (2005) model, the SC of this model dynamically expresses a motor command with no intrinsic normalization. This scheme was shown to account for slowed saccades from sub-optimal activation of SC, but it is not clear how this model would express relatively normal or even slowed dynamics to super-normal drive from multiple sites of activity or from experimental recruitment with different patterns of activation, as used here. This model does not specify how prolonged, experimental recruitment of SC spikes would be able to count up to a set number of spikes, which would be changing dynamically in the cases here, to end the movements with the intermediate metrics such as those in Figure 10. In addition, this model has not been shown to conform to the burst generator re-activation and hypometric staircase movements from prolonged experimental activation (Breznen et al., 1996).

In summary, initial comparison of these data to contemporary models is most consistent with some form of vector decomposition of total topographic output of the SC with a downstream feedback controller that drives movements by minimizing dynamic motor error. This is captured schematically in Figure 11. Spatially encoded output of the SC is summed to provide a dynamic image of overall activity across the SC, including multiple targets -- regardless of whether the multiple targets are due to experimental recruitment (as in this study) or unusual volitional uncertainty involving multiple targets (e.g., McPeek and Keller; 2001; Port and Wurtz, 2003; Ottes et al., 1984). Some mechanism distal to the SC normalizes the topographically encoded activity by a separate representation of total activity. Vector average models such as Lee et al. (1988) and Walton et al. (2005) implement this normalization as a topographically encoded sum of activity normalized by a sum of non-topographic activity; whereas, the sum of mini-vectors model of Goossens and Van Opstal (2006) implements a cancelation according to a sum of total spikes parametrically scaled to saccade size. The normalized activity then drives a brainstem “burst generator” network that acts as a displacement controller to drive the eyes toward a desired target defined by the SC output. Simultaneous with release from chronic inhibition from brainstem omnipause neurons (OPN; not shown, but discussed in Gandhi and Keller,1999), the output of the burst generator (burst neurons, BN) drives a feedforward eye plant circuit that moves the eyes with saccadic dynamics (Cullen and Guitton, 1997). Another, parallel output of the BN latches a reciprocal inhibitory loop through OPN into quiescence (Bergeron and Guitton, 2002; Paul and Gnadt, 2006), while a third parallel output passes through a comparator loop that provides delayed, recurrent inhibition onto the BN (Jurgens et al., 1981). An alternative implementation of this comparator loop posits an additional feedforward, spatial transformation though an SC-to-cerebellum mechanism (Optican, 2005). The dynamics of the comparator loop simulates a leaky integrator with variable time response on the order of tens of milliseconds (Jackson et al., 2001). At a given moment, the direction of movement would be determined by the dynamic topographic output of the SC relative to the current displacement of the eyes. Once the recurrent inhibition overcomes the SC drive, the BN shut down and the inhibitory OPN reactivate to silence the BN (Paul and Gnadt, 2006). Under usual, volitional conditions the output drive from SC is a time-limited burst and new output patterns of activity are not expressed for 100s of milliseconds (Ottes et al., 1986; Sparks et al.,1976). In the face of persistent or rebuilding drive from the SC, as the recurrent inhibition slowly declines, excitatory drive from the SC would trigger a diminished burst of the BN under the residual inhibition of the recurrent feedback (Jackson et al., 2001). This results in a truncated, sub-normal component of movement. Of course, this does not exclude that the SC motor map could also experience dynamic patterns of activity during natural behavior due to intra-SC network dynamics (Arai and Keller, 2005), or changing target selection in antecedent brain areas (McPeek, 2006), or long-loop control influence from areas such as the Substantia Nigra (Hikosaka and Wurtz, 1983; Liu and Basso, 2008) or midbrain reticular formation (Waitzman, 2002). We simply suggest those influences would engage the SC spatio-temporal transform revealed here.

Figure 11. Schematic model of the topographic decoding and displacement controller for multiple sites of activity within the SC.

The topographic gradients of size and direction across the SC motor map are spatially summed (Σ_s) downstream of the SC. At post-SC locations, the summed-vector activity is diminished by a parametric representation of total SC activity by a currently undetermined mechanism (1/ Σ_s, see text). With near instantaneous dynamics (excluding the response time of OPN pause), the sum of any and all output activity across the SC is dynamically conveyed to a two-dimensional controller of conjugate horizontal and vertical eye position. In the temporal domain (Σ_t) of a down-stream brainstem burst generator, with the OPN locked in mutual inhibition to the output burst neurons (BN), the BN reflect the difference between SC output and a delayed, recurrent representation of BN output (efference copy as a variable time-course “leaky” integrator). The output of the BN is sent to the eye plant, moving the eyes with high velocity. Normally, the SC burst output is declining as the building recurrent inhibition overcomes SC drive, thus ending the movement and disinhibiting the OPN. Under conditions of prolonged experimental SC activation, the recurrent inhibition still overcomes the persistent SC drive, ending the movement at a point when the current displacement matches a normalized representation of current topographic SC output. However, as the recurrent inhibition slowly declines, persistent SC drive can trigger another cycle of movement that is component-hypometric due to residual activity from the feedback inhibition. Normally, only one site of activity across the SC map is active at any one time. Due to volitional uncertainty or experimental intervention, two sites of SC activity can lead to “averaged” and/or curving trajectories of movement. This diagram captures those operations that need to be mapped onto quantitative models for testing of these experimental SC spatio-temporal transformations. Various known and postulated feedforward and feedback loops that would be over-ridden by these experimental manipulations are not represented.

The topographic decoding of the SC appears to incorporate the dynamic output of the entire movement map. This may include both SC (e.g., Robinson, 1972; Carasig and Gnadt, 2004), but that was not tested here. For the topographic decoding of the SC motor map, these data appear to be generally compatible with either the vector averaging mechanism (Lee et al.,1988; Walton et al., 2004) or the sum of minivector mechanism (Goossens and Van Opstal, 2006) as long as there exists a post-SC mechanism for normalizing total activity or parametrically cancelling the summation, respectively. However, at present, neither form of the current models appears to accommodate all of the details of these new empirical data. We expect further testing of models against these data will refine and differentiate viable mechanistic assumptions.

Methods

Two adult female macaque monkeys (one M. radiata, subject “MA”; one M. mulatta, subject “SA”) participated in these studies. Each of our instrumented, trained subjects participated in multiple projects over the period of many years. Each was implanted with chronic recording chambers (2.0 cm diameter) stereotacticly aimed at the superior colliculus (SC) of one side (+4.0mm A/P, 15mm lateral of midline with a 15 deg. lateral-to-medial angle), and with scleral search coils (Judge et al, 1980, one subject monocular, one binocular) during aseptic surgical procedures as described in detail elsewhere (Ramcharan et al., 2001). After at least two weeks recovery from surgery, we used the magnetic field induction technique (Robinson, 1963) over a period of weeks to months to train each subject in a variety of eye movement tasks for juice reward (Ramcharan et al., 2003). Subjects worked to satiation each work session or were supplemented up to their usual daily amount. From trans-dural recordings with fine wire electrodes (Microprobe, Inc.) mounted onto the chronic recording chambers with a custom X/Y/Z micropositioner, we advanced the tip of an electrode toward the SC until we identified the characteristic perisaccadic, visual-motor neuron bursts. The left SC of subject MA was approached from the contralateral side by adjusting the electrode manipulator to a total lateral-to-medial angle of 23 degrees, thus crossing midline with an electrode path that tended to slip across the medial-to-lateral coordinates of the contralateral SC motor map. The right SC in subject SA was approached ipsilaterally along a path roughly normal to the SC surface. From a train of microstimulation pulses (0.3ms bi-phasic pulses, 1–100µA at 300Hz for 100–500ms) in head-fixed subjects (Ramcharan et al., 2003), we confirmed localization within the SC and found the deep-layer, low-threshold zone (<15 uA) by observation of characteristic, “staircase” saccades (e.g., Breznen et al. 1996). By reinserting the stimulating electrode at various anterior/posterior and medial/lateral positions we revealed the organized map of movement vectors, as expected. After localizing the SC, we began our two electrode stimulation study. During these dual stimulation experiments, we advanced a pair of electrodes into the SC until stimulation trains from each electrode reliably evoked saccades. Each electrode pair was constructed of 2 low-impedance (300–500 KOhms) tungsten microelectrodes (Microprobe, Inc) insulated with 0.01” polyimide tubing and glued together along the shafts with various configurations of tip spacing. The tips were positioned with up to 1 mm advance of one before the other and/or splayed apart by up to 1 mm before entering the brain. Freedom of movement at unglued electrode tips allowed variability in spacing for different tracts. These configurations allowed us to reach different positions within the same SC using a single microdrive and a 14 gauge guide tube to pierce the dura mater. Post-mortem reconstruction of electrode paths confirmed the general electrode paths across (from contralateral access) and through (from ipsilateral access) the SC.

The stimulation data was collected while the subjects’ performed a fixation task for a continuously-lit LED target located straight-ahead at a distance of 1.2 meters in a dimly lit room. Stimulation was applied randomly during the trials and the subjects received juice reward as long as the eyes were on target within a 2 degree window for at least 1000 ms at randomly applied times. This kept the subjects alert with the eyes near straight-ahead at the time of each stimulation. Stimulations that occurred with the eyes directed away from the target or in close time proximity to voluntary movements were excluded.

During stimulation trials, data was collected continuously on a lab microcomputer (PC running Windows98) by a custom real-time program. These data included horizontal and vertical eye and target position, and the function generator waveform. Each trace was digitized at 1000Hz and saved to a combination of synchronous binary and asynchronous text files. We also sampled one digital channel that held a time stamp of the stimulation pulses of one electrode at a time resolution of 0.01ms. We then analyzed the data off-line using custom-made analysis scripts. Essentially, the scripts allowed a user to define a velocity threshold (30 deg/sec) for defining saccade beginning and end that had to occur within a 100 ms window of time following stimulation onset. If a saccade was found to occur within the time window, a number of metrics about the movement were calculated and written to a text file. Text files were loaded into a spreadsheet program where basic statistics were employed to describe the movements evoked by the stimulations. Statistical comparisons were made using the parametric t-test and ANOVA, and the non-parametric Mann-Whitney U, as appropriate.

All experimental and surgical procedures preformed were approved by the Georgetown University Institutional Animal Care and Use Committee. Animal husbandry and medical care was performed in accordance with AAALAC standards and within federal and institutional guidelines.