Abstract
The patellar tendon moment arm is a critical quantity in that it defines the quadriceps ability to generate a moment on the tibia. Thus, the primary purpose of this study was to establish the first in vivo three-dimensional measures of the patellar tendon moment arm, measured non-invasively and in vivo during dynamic activity in a large normative population (n=34) using a dynamic MRI technique (fast-PC MRI). The magnitude of the moment arm was defined as the shortest distance between the finite helical axis and the patellar tendon line of action. Using these data, the hypothesis that the patellar tendon moment arm is independent of gender was tested. In general, the moment arm increased from 20 mm to 50 mm during knee extension. There were significant differences (P<0.05) in the moment arm between gender, but these differences were eliminated when the moment arm was scaled by the femoral epicondylar width. This study took a large step forward towards the ultimate goal of defining how pathology may alter joint dynamics through alteration in moment arms by establishing the first in vivo normative data base for the patellar tendon moment arm using non-invasive measures during volitional activity in a relatively large population (n=34). The fact that the scaled moment arm was independent of gender may lend insights into impairments that tend to be gender specific, such as patellar maltracking. The next steps will be to quantify the patellar tendon moment arm in populations with specific pathologies.
Introduction
The patellar tendon moment arm (MA) is a critical quantity in that it defines the quadriceps ability to generate a moment on the tibia. Although it has been clearly recognized that accurately quantifying the patellar tendon MA is key for musculoskeletal modeling, its importance in establishing the effects of pathology and clinical interventions has not been explored. Nor has the effect of gender on the patellar tendon MA been fully investigated. Past studies have focused primarily on statically measuring the 2-dimensional perpendicular distance from the patellar tendon to the lateral tibiofemoral point of contact (the TF contact method). These studies (Herzog and Read, 1993; Nisell, 1985) have typically used a small set of cadaver limbs (<10), but in vivo studies have also been performed: one static (Wretenberg et al., 1996) and the other dynamic (Kellis and Baltzopoulos, 1999). Since the primary aim of these studies was to provide experimental data for 2-dimensional static knee joint models, this approach was logical. In particular, by summing moments about the point of contact for a static system, the contact forces do not contribute to the moment equations.
As musculoskeletal models have advanced to 3-dimensional dynamic models, a need for accurate 3-dimensional in vivo measures of the patellar tendon MA acquired during dynamic activities with volitional muscle control has arisen. When using a full 3-dimensional dynamic model, summing moments about a point on the finite helical axis (FHA) typically simplifies the moment equations because the FHA is either fixed or can be considered fixed for a specific instant in time. If moments are summed about the tibiofemoral contact point, then the acceleration of this point would need to be accounted for within the moment equations (Riley and Sturges, 1996). The simplicity of the tendon excursion method (Buford, Jr. et al., 1997) makes this methodology appealing, but the required assumptions (Appendix A) are quite difficult to match experimentally. Two recent studies have proposed methodologies for measuring the 3-dimensional patellar tendon MA. Both use the closest point on the FHA, relative to the patellar tendon line of action, as the reference (the FHA method). One was a cadaver study (Krevolin et al., 2004) and the other was based on cat knees (Boyd and Ronsky, 1998). Care must be taken when applying these equations as they have similar, but unique definitions of patellar tendon MA (Appendix B).
The long-term goal of this work is to explore how pathology (e.g., cerebral palsy, ACL loss and Ehlos Danof syndrome) alter tendonous and ligamentous moment arms and if specific interventions increase or decrease the lever arm of these structures. As part of this overall goal, the primary purpose of this study was to provide the first in vivo 3-dimensional measures of the patellar tendon MA, measured during dynamic activity in a large normative population using the FHA method. Using these data, the hypothesis that the patellar tendon MA is independent of gender was tested.
Methods
Twenty-five healthy subjects [14 female, 11 male; age=26.7 (SD 8.8) years; weight=172.3 (SD 7.5) kg, height=67.5 (SD 12.7 cm)] participated in this IRB approved study and gave informed consent. If time allowed, both knees were imaged resulting in data from 34 knees (9 knee pairs, 18 left, 16 right; 20 female, 14 male). All subjects had no prior history of knee problems or pain and were excluded if they had clinically diagnosed knee pathology, had previous knee joint surgery or had any contraindications to having an MRI scan.
Subjects were placed supine in a 1.5-Tesla MR imager (LX; GE Medical Systems, Milwaukee, WI, USA) and asked to cyclically extend/flex their knee from ~45° flexion to ~0° (full extension) at 35 cycles/min, aided by an auditory metronome. Prior to data collection, subjects practiced the task until they could comfortably repeat the motion. Using a sagittal or sagittal-oblique imaging plane, which was generally perpendicular to the femoral epicondyles and bisected the patella, a full fast-PC MRI data set (anatomic and x,y,z velocity images for 24 time frames) was acquired. The MR scanning protocol details have been provided previously (Rebmann and Sheehan, 2003).
The femoral, tibial, and patellar attitude were individually quantified by integrating velocity data obtained during the fast-PC acquisition (Sheehan et al., 1999). From these data, the angular velocity of the tibia relative to the femur as a unit vector (ω̂) was calculated and defined as the direction of the FHA (Sheehan, 2006). Next, the patellar tendon line of action (F̂), defined by the patellar tendon tibial and patellar insertions, was identified in the full extension anatomic image of the fast-PC sequence (Sheehan and Drace, 2000) and tracked throughout the motion cycle based on the patellar and tibial attitude. The entire movement cycle was used for the integration process, but all further analysis and data presentation was limited to the extension portion of the movement.
The MA was calculated such that the magnitude of the MA multiplied by the magnitude of the patellar tendon force produced the magnitude of the moment created by that force about the point on the FHA that was closest to the patellar tendon line of action (Boyd and Ronsky, 1998). Thus, MA was equal to the perpendicular distance between the F̂ and the FHA:
| (eq1) |
Bolds, “ˆ”, and non-bolded characters denote vectors, unit vectors and magnitudes, respectively.
rOQ = The position vector from any point on the FHA to any point on F̂
This methodology defined a unit vector that was perpendicular to both F̂ and ω̂ (cross product) and then quantified the portion of rOQ that was along that direction (dot product). For comparison, the effective MA (MAeff) was also calculated using the methodology (Appendix B) proposed by Krevolin et al. (2004). The MAeff is defined such that multiplying MAeff and the patellar tendon force produced the moment created by that force about the closest point on the FHA to the F̂, in the direction of the FHA only.
The MA was scaled by multiplying it with the ratio of the average epicondylar width to the epicondylar width of the individual knee. The epicondylar width was defined as the distance between the lateral and medial epicondyles. This scaling process was selected in order to minimize the effect of knee size. Since the FHA is ill-defined as ω approaches zero, data were eliminated when ω was less than 0.3rad/s. Thus, an extension movement was defined for knee angles from “maximum” flexion (begin≈ 40°) and to “full” knee extension (end≈ 0°), meeting the above criterion.
In order to create population averages, all data were interpolated to single degree knee angle increments. Certain subjects achieved greater or less than the full 45° range of motion, thus not all subjects are represented at all knee angles. Data representing 5 or fewer subjects were eliminated. Statistical differences between genders were investigated using a 2-tailed student t-test, assuming unequal variances.
Results
The magnitude of the MA increased from 18 mm (SD: 15.6) to 49 mm (SD 8.4) when the knee angle decreased from maximum flexion to 6° of extension. (Figure 1A). From a knee angle of 6° of extension to full extension there was little change (2.1mm) in the MA. Since the FHA displaces 23 mm posteriorly during extension (Figure 2), most of the increase in the MA can be attributed to the displacement of the FHA. There were significant differences (P<0.05) in the MA, ranging from 4.9 mm to 9.17 mm, between genders (Figure 1A). Yet, these significant differences were eliminated with scaling (Figure 1B). The values for the MA did not match with previous reports based on the tibiofemoral contact method and had lower values than those reported using the tendon excursion method (Figure 3A & 3B).
Figure 1.
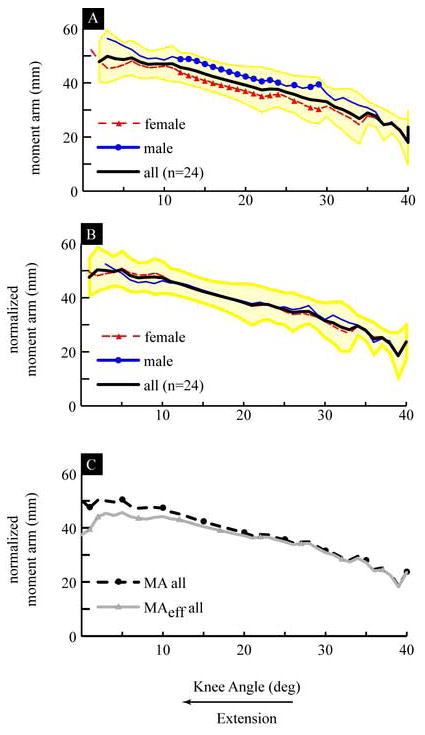
A) Moment Arm: Average for all subjects (thick black line), with ±1 standard deviation shown with a yellow shaded area, average for all male subjects (thin blue line with circles) and average for all female subjects (thin dashed red line with triangles). The sections of the line with symbols indicate the knee angles where there were significant differences between the genders. B) Scaled Moment Arm: with same symbol definitions as in A. The average epicondylar width was equal to 77.3 (SD = 5.9) mm. C) Comparison of the Scaled Moment Arm and the Scaled Effective Moment Arm: The average scaled moment arm (MA) is shown with a dashed black line with black circles and the average scaled effective moment arm (MAeff) is shown with a solid grey line and grey triangles.
Figure 2. Scaled Posterior-Anterior Displacement of the FHA.
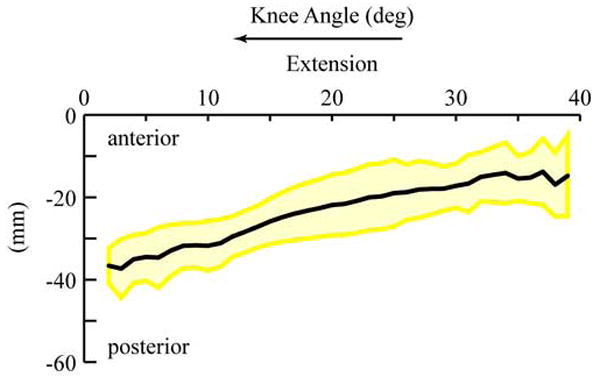
Average for all subjects (thick black line), with ±1 standard deviation shown with a yellow shaded are. The posterior-anterior displacement of the FHA was defined as the posterior-anterior displacement of the sagittal plane point. This point was defined for all time as the point on the FHA that crossed the sagittal plane at the x=0 location, relative to the femoral coordinate system (the deepest point in the sulcus groove is the origin of the femoral system (Seisler and Sheehan FT, 2006)). The scaling used was identical to that used for the MA. Further details on the calculations involved have been published previously (Sheehan, 2006).
Figure 3. Previously Reported Patellar Tendon Moment Arms calculated using.
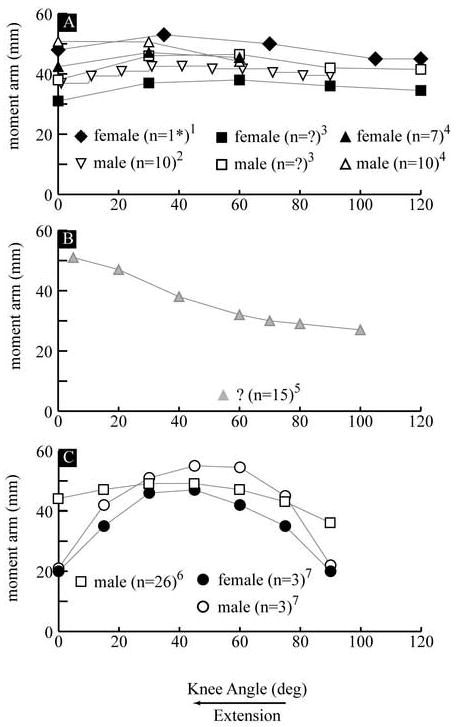
A) the TF contact method 1(Herzog and Read, 1993) –CS, 2(Kellis and Baltzopoulos, 1999) - ID, 3(Nisell, 1985) –CS and 4(Wretenberg et al., 1996) –IS B) 5(Buford, Jr. et al., 1997) - CD and C) the 2-dimensional 6(Smidt, 1973) –IS and the 3-dimensional FHA method 7(Krevolin et al., 2004) -CS. The curves represent the average of each population (male and female) in the study except for the study of Herzog and Read. A single female specimen (there were a total of 2 male and 3 female specimens) with a median value for the moment arm is shown in graph A. If a study used both male and female subjects, the averages for the two populations are shown using the same symbol (e.g., square, triangle or circle), with the female average represented by the black filled symbol and the male average represented by the white filled symbol. Data from female subjects are shown with black symbols, male subjects in white and unknown gender in grey. For studies 3 and 5 (graphs A and B) the number of subjects was not reported. Notation: CS: cadaver and static, ID: in vivo and dynamic, IS: in vivo and static, n: sample size and ?: information was not provided.
The magnitudes of the MA and the MAeff were nearly identical from 39° to 20° of knee extension and had the largest difference at full extension, where the MAeff was 6.5 mm smaller than the MA (Figure 1C). Both the MA and the MAeff increased in extension, but the MA stopped changing value at ~5°, whereas the MAeff held a constant value from ~12° to ~5° of knee extension, after which it decreased in value. The MAeff demonstrated a different slope and value than that previously reported (Figure 3C).
Discussion
This study accomplished the first of its primary goals by providing the first in vivo 3-dimensional database for the patellar tendon MA based on the FHA method, acquired for a large normative population during dynamic knee extension. For the secondary aim, the hypothesis that patellar tendon moment arm is dependent on gender could not be supported when the data was scaled. This demonstrated that knee size, not gender, had the largest influence on MA. The small inter-subject variability (average SD for the scaled MA = 6.0 mm) and the similarity between genders makes these data readily applicable to 3-dimensional dynamic musculoskeletal models.
It is difficult to directly compare the current results to the majority of past studies due to the different methodologies used. The fact that MA disagreed with previous reports based on the tibiofemoral contact method was as expected since this method calculates the distance from F̂ to the tibiofemoral point of contact, not to the FHA, as was done in the current paper. The validity of the past results using the tendon excursion method is questionable since the methodology used required numerous assumptions that were not met (Appendix A). Specifically, this methodology assumes that no work is done in moving the knee through its range of motion and that the displacement of the patellar tendon’s insertion into the tibia is equal to the excursion of the insertion of quadriceps tendon into the muscle belly. Since numerous knee joint structures store energy and neither tendon is rigid, both assumptions were violated. Without further experimental details, it is difficult to assess the magnitude of error caused by violating the assumptions. Yet, if positive work was done an overestimation of the moment arm would be expected.
The past work using the TF contact method demonstrated surprisingly small inter-study differences, which ranged from ~10 to 20 mm. The slight decrease in the MA, using the TF contact method, in terminal extension agrees with the fact that the tibiofemoral contact point moves anteriorly during this part of extension (Buford, Jr. et al., 1997; Pinskerova et al., 2004). Since one of these studies (Kellis and Baltzopoulos, 1999) used a slow extension movement with a simulated maximal extensor load and the others were static without load, it would appear that overall muscle loading did not alter the MA, when calculated using the TF contact method.
The increase in the MA found in this study and the previous study using the tendon excursion method (Buford, Jr. et al., 1997) agrees with the posterior movement of the FHA in terminal extension; ~40° – 0° of knee extension (Blankevoort et al., 1990; Karrholm et al., 1994; Sheehan, 2006).
The disagreement between the MAeff as calculated in the current study and that reported previously (Krevolin et al., 2004) is most likely due to differences in quadriceps loading, which affects the twist angle (defined as the angle between the patellar tendon and the FHA – Appendix B: equation B7). In the current study, the twist angle decreased from 83° in early extension to 60° at full extension, with the sharpest decline occurring from 20° – 0° of knee extension, which mirrored the change in the FHA orientation in the frontal plane (Sheehan, 2006). Thus, the change in twist angle is due mostly to the change in the FHA orientation. Krevolin et al. (2004) reported a twist angle of “less then 60°” from 30° - 0° of extension. Since, the patellar tendon is directed primarily in the superior direction, as the FHA direction shifts from lateral to lateral-inferior, the ability of the patellar tendon to generate a moment in the direction of the FHA diminishes. Thus, the differences between the two studies are most likely due to the fact that the previous study was a cadaver study with the extensor force emulated by a single force applied to the quadriceps tendon. This possibly created excessive tibial external rotation, which would shift the FHA direction inferior, decreasing the twist angle and the MAeff. Since the overall force exerted on the joint can affect both the FHA and the MA, an anterior shift in the FHA during terminal extension in the previous study could also explain some of the sharp decline in MA. This is unlikely since a posterior shift in the FHA throughout extension has been consistently reported (Karrholm et al., 1994; Sheehan, 2006; Woltring, 1994). Therefore, cadaver studies may not provide the realistic data when trying to model volitional exercise using the FHA method, because emulating actual in vivo quadriceps muscle force is difficult.
The current study was delimited to a non-weight bearing partial range of anatomically available extension movement. Fortunately, this range of motion (from 45° of knee flexion to full extension) is one most commonly used in activities of dialing living, such as gait. As open MRI technology improves, experiments looking at the full range of motion will become available. Yet, in the range excluded from this study, the FHA is primarily static (Woltring, 1994), being guided by the circular posterior femoral condyles (Pinskerova et al., 2004). Thus, at higher knee angles, the MA likely continues to decrease with increasing knee angle, due to a posterior displacement of the patellar tendon line of action. In addition, the results from this study are likely relevant to weight bearing activities since Shiavi et al (1987) reported that the stance and swing phase of gait had very similar patterns for the FHA and that the current study required self-selected activation of the quadriceps. The non-invasive nature of this experiment and its high accuracy and precision justifies these potential delimitations.
In conclusion, this study took a large step forward towards the ultimate goal of defining how pathology may alter joint dynamics through alteration in moment arms by establishing a relative large normative data base using non-invasive in vivo measures during volitional activity. The fact that the scaled MA was independent of gender may lend insights into impairments that tend to be gender specific, such as patellar maltracking. The next steps will be to quantify the patellar tendon moment arm in populations with specific pathologies.
Acknowledgments
I would like to thank Mrs. Andrea J Siesler for her help with data collection and compression, Ms. Jeanine Graham and Ms. Kaitlyn Helling for their support in patient data management, Mr. Tom Kepple and Dr. Saryn Goldberg for their editorial comments and Dr. Steven Stanhope for guidance throughout this project. I would also like to thank Susan O’Connell, Bonnie Damaska, and the Diagnostic Radiology Department for their support and research time. This material is based upon work begun under the support of the National Science Foundation (Grant No. 0134205). Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author and do not necessarily reflect the views of the National Science Foundation, the National Institutes of Health or the US Public Health Service.
Appendix A: Tendon Excursion Methodology
In order to estimate the MA using the tendon excursion method, two primary assumptions are made: 1) The patellar tendon force (F) is part of a couple; and 2) The total work done by the forces and moment of this couple equates to zero. Therefore:
| (eq A1) |
dr: The distance traveled by the point of application of F
F’: A force equal and opposite to F
dr’: The distance traveled by the point of application of F’
M: The moment caused by the couple of F and F‘
dθ: The change in joint angle cause by M
If dr is calculated by the excursion of the quadriceps tendon, which has been typically done in past cadaver experiments, then it is assumed that the quadriceps and patellar tendons have zero strain, thus the displacement of the muscle is equal to the displacement of the tibial patellar tendon insertion. By defining the moment to be taken about a point on the FHA and that F’ is applied to a point coincident with the FHA, which is not necessarily on the tibia, but is rigidly attached to the tibia, the following equation is derived:
| (eq A2) |
and equation A1 reduces to:
| (eq A3) |
and M is defined as:
| (eq A4) |
Where MA is defined as in equation 1: The perpendicular distance between F̂ and the FHA.
By knowing that dr acts in the same direction as F and combining equations A3 and A4:
| (eq A5) |
and MA is calculated:
| (eq A6) |
Appendix B: Mathematical Comparisons of MA and MAeff
The MAeff was defined by Krevolin et al (2004) as:
| (eq B1) |
This methodology assumes that:
| (eq B2) |
Meff = The moment produced by F in the direction of the FHA.
F = The magnitude of the force F
Using the basic principles of vector multiplication, the above method can be more readily compared to that presented in equation 1. Rewriting equation B1:
| (eq B4) |
Based on the principle of a vector triple product:
| (eq B5) |
equation B4 becomes:
| (eq B6) |
Comparing equations 1 and B6 demonstrates:
| (eq B7) |
where;
θ = The twist angle (the angle between F̂ and ω̂)
Thus, when F̂ and ω̂ are mutually perpendicular, the MA and the MAeff are identical. As F̂ and ω̂ rotate towards a mutually parallel position, without a change in the direction of the MAeff, the MAeff reduces to zero and MA remains unchanged. A simple example is to set ω̂=z and MA =x. If F̂ =y, then MA=MAeff, but if F̂ =z, then MAeff=0 MA remains unchanged.
Appendix C
Tabulated Average, Scaled and Scaled Effective Moment Arms (mm).
The standard deviation (SD) was similar across the average, scaled and scaled effective moment arms. Thus, the standard deviation is given only for the scaled moment arm.
| Knee Angle | Average MA | Scaled MA | Scaled MAeff | ||||||
|---|---|---|---|---|---|---|---|---|---|
| All | Male | Female | All | Male | Female | All | Male | Female | |
| Degrees | mm | mm | mm | mm | mm | mm | mm | mm | mm |
| Ave | Ave | Ave | Ave (SD) | Ave (SD) | Ave (SD) | Ave | Ave | Ave | |
| 1 | 52.2 | 49.5 (8.1) | 39.8 | ||||||
| 2 | 47.8 | 48.2 | 50.3 (15.6) | 48.2 (6.5) | 44.1 | 41.5 | |||
| 3 | 49.8 | 56.4 | 45.5 | 50.1 (7.0) | 52.4 (8.5) | 48.9 (6.0) | 45.5 | 48.0 | 44.2 |
| 4 | 48.9 | 55.3 | 45.8 | 49.6 (8.1) | 50.6 (6.2) | 49.2 (5.4) | 44.7 | 47.8 | 43.4 |
| 5 | 48.6 | 53.7 | 46.7 | 50.4 (6.7) | 49.1 (5.1) | 50.9 (7.2) | 45.8 | 46.4 | 45.5 |
| 6 | 49.3 | 52.3 | 48.1 | 48.2 (5.5) | 46.6 (7.3) | 49.1 (5.5) | 44.3 | 43.5 | 44.7 |
| 7 | 47.8 | 50.0 | 46.5 | 47.4 (6.2) | 45.6 (6.3) | 48.4 (4.7) | 43.6 | 42.3 | 44.4 |
| 8 | 46.9 | 48.9 | 45.7 | 47.6 (5.4) | 45.9 (6.2) | 48.5 (4.6) | 43.3 | 42.3 | 43.9 |
| 9 | 47.0 | 49.2 | 45.8 | 47.7 (5.3) | 45.2 (5.7) | 48.9 (6.8) | 44.0 | 42.0 | 45.0 |
| 10 | 47.0 | 48.5 | 46.2 | 47.4 (6.6) | 46.3 (6.7) | 48.0 (5.4) | 44.3 | 43.2 | 44.9 |
| 11 | 47.1 | 49.7 | 45.5 | 46.0 (5.9) | 45.4 (5.7) | 46.3 (4.1) | 43.4 | 42.9 | 43.8 |
| 12 | 45.7 | 48.8 | 43.9 | 45.3 (4.7) | 45.6 (6.1) | 45.1 (4.0) | 43.1 | 43.5 | 42.9 |
| 13 | 45.1 | 48.8 | 42.7 | 44.3 (4.8) | 44.8 (5.3) | 44.0 (4.1) | 42.3 | 42.6 | 42.0 |
| 14 | 44.3 | 48.1 | 41.7 | 43.3 (4.6) | 43.8 (4.7) | 43.0 (4.3) | 41.4 | 41.8 | 41.1 |
| 15 | 43.3 | 47.0 | 40.7 | 42.3 (4.4) | 42.7 (4.5) | 42.0 (4.6) | 40.6 | 41.0 | 40.3 |
| 16 | 42.4 | 45.9 | 39.9 | 41.5 (4.5) | 41.9 (4.6) | 41.3 (4.6) | 39.9 | 40.2 | 39.6 |
| 17 | 41.5 | 45.0 | 39.1 | 40.7 (4.9) | 41.0 (5.1) | 40.5 (4.9) | 39.2 | 39.5 | 38.9 |
| 18 | 40.7 | 44.1 | 38.4 | 39.9 (5.3) | 40.2 (5.5) | 39.7 (5.3) | 38.5 | 38.8 | 38.3 |
| 19 | 40.0 | 43.2 | 37.7 | 39.1 (5.9) | 39.4 (6.2) | 38.9 (5.8) | 37.8 | 38.1 | 37.6 |
| 20 | 39.2 | 42.4 | 36.9 | 38.2 (6.8) | 38.6 (7.0) | 37.9 (6.7) | 37.2 | 37.4 | 37.1 |
| 21 | 38.4 | 41.5 | 36.0 | 37.3 (7.5) | 37.8 (7.7) | 36.9 (7.6) | 36.3 | 36.6 | 36.1 |
| 22 | 37.4 | 40.6 | 35.1 | 37.7 (6.4) | 38.3 (6.7) | 37.2 (6.3) | 36.7 | 37.1 | 36.4 |
| 23 | 37.7 | 41.1 | 35.3 | 37.5 (5.7) | 37.5 (7.1) | 37.5 (4.5) | 36.6 | 36.4 | 36.8 |
| 24 | 37.6 | 40.1 | 35.7 | 36.5 (6.0) | 36.3 (8.0) | 36.6 (4.4) | 35.7 | 35.3 | 35.9 |
| 25 | 36.6 | 38.8 | 34.9 | 35.7 (5.9) | 36.6 (7.1) | 35.0 (4.9) | 34.9 | 35.7 | 34.4 |
| 26 | 35.8 | 39.2 | 33.3 | 34.6 (7.1) | 35.6 (8.5) | 33.8 (6.3) | 33.9 | 34.8 | 33.3 |
| 27 | 34.6 | 38.0 | 32.3 | 34.9 (5.5) | 36.0 (6.6) | 34.1 (4.8) | 34.3 | 35.5 | 33.5 |
| 28 | 33.8 | 38.5 | 30.9 | 34.9 (4.8) | 37.1 (4.2) | 33.7 (4.7) | 34.4 | 36.5 | 33.1 |
| 29 | 33.5 | 39.4 | 30.3 | 33.2 (5.1) | 33.9 (5.4) | 32.9 (5.1) | 32.6 | 33.2 | 32.2 |
| 30 | 33.0 | 36.0 | 31.3 | 31.5 (6.5) | 31.9 (6.9) | 31.2 (6.5) | 31.0 | 31.6 | 30.6 |
| 31 | 31.1 | 33.6 | 29.8 | 30.7 (7.6) | 33.5 (5.0) | 29.5 (8.3) | 30.1 | 33.1 | 28.9 |
| 32 | 30.1 | 34.5 | 28.3 | 29.1 (9.1) | 32.0 (5.1) | 28.0 (10.3) | 28.5 | 31.5 | 27.3 |
| 33 | 28.6 | 33.0 | 26.8 | 28.2 (8.1) | 30.7 (4.6) | 26.9 (9.3) | 27.5 | 30.1 | 26.2 |
| 34 | 26.8 | 31.7 | 24.6 | 29.6 (3.7) | 29.9 (3.3) | 29.4 (4.2) | 28.9 | 29.1 | 28.7 |
| 35 | 28.9 | 30.8 | 27.8 | 27.9 (4.0) | 28.3 (1.6) | 27.8 (4.9) | 27.3 | 27.3 | 27.3 |
| 36 | 27.8 | 29.3 | 27.0 | 24.8 (5.9) | 23.5 (6.8) | 25.5 (5.7) | 24.2 | 22.5 | 25.1 |
| 37 | 24.5 | 24.3 | 24.7 | 25.3 (3.0) | 24.9 (1.2) | 25.6 (3.9) | 24.6 | 23.6 | 25.2 |
| 38 | 25.0 | 25.6 | 24.7 | 23.1 (3.9) | 24.0 (0.0) | 22.9 (4.3) | 22.6 | 23.2 | 22.5 |
| 39 | 22.5 | 22.1 | 18.6 (8.3) | 18.6 (8.3) | 18.3 | 18.3 | |||
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Reference List
- Blankevoort L, Huiskes R, de Lange A. Helical axes of passive knee joint motions. J Biomech. 1990;23:1219–1229. doi: 10.1016/0021-9290(90)90379-h. [DOI] [PubMed] [Google Scholar]
- Boyd SK, Ronsky JL. Instantaneous moment arm determination of the cat knee. J Biomech. 1998;31:279–83. doi: 10.1016/s0021-9290(97)00135-8. [DOI] [PubMed] [Google Scholar]
- Buford WL, Jr, Ivey FM, Jr, Malone JD, Patterson RM, Peare GL, Nguyen DK, Stewart AA. Muscle balance at the knee--moment arms for the normal knee and the ACL-minus knee. IEEE Trans Rehabil Eng. 1997;5:367–379. doi: 10.1109/86.650292. [DOI] [PubMed] [Google Scholar]
- Herzog W, Read LJ. Lines of action and moment arms of the major force-carrying structures crossing the human knee joint. J Anat. 1993;182(Pt 2):213–230. [PMC free article] [PubMed] [Google Scholar]
- Karrholm J, Jonsson H, Nilsson KG, Soderqvist I. Kinematics of successful knee prostheses during weight-bearing: three-dimensional movements and positions of screw axes in the Tricon-M and Miller-Galante designs. Knee Surg Sports Traumatol Arthrosc. 1994;2:50–59. doi: 10.1007/BF01552655. [DOI] [PubMed] [Google Scholar]
- Kellis E, Baltzopoulos V. In vivo determination of the patella tendon and hamstrings moment arms in adult males using videofluoroscopy during submaximal knee extension and flexion. Clin Biomech (Bristol Avon) 1999;14:118–124. doi: 10.1016/s0268-0033(98)00055-2. [DOI] [PubMed] [Google Scholar]
- Krevolin JL, Pandy MG, Pearce JC. Moment arm of the patellar tendon in the human knee. J Biomech. 2004;37:785–788. doi: 10.1016/j.jbiomech.2003.09.010. [DOI] [PubMed] [Google Scholar]
- Nisell R. Mechanics of the knee. A study of joint and muscle load with clinical applications. Acta Orthop Scand Suppl. 1985;216:1–42. [PubMed] [Google Scholar]
- Pinskerova V, Johal P, Nakagawa S, Sosna A, Williams A, Gedroyc W, Freeman MA. Does the femur roll-back with flexion? J Bone Joint Surg Br. 2004;86:925–931. doi: 10.1302/0301-620x.86b6.14589. [DOI] [PubMed] [Google Scholar]
- Rebmann AJ, Sheehan FT. Precise 3D skeletal kinematics using fast phase contrast magnetic resonance imaging. J Magn Reson Imaging. 2003;17:206–213. doi: 10.1002/jmri.10253. [DOI] [PubMed] [Google Scholar]
- Riley WF, Sturges LD. Engineering Mechanics: Dynamics. John Wiley & Sons, Inc.; New York: 1996. Chapter 16: Kinetics of Rigid Bodies: Newton’s Laws; p. 249. [Google Scholar]
- Seisler A, Sheehan FT. Correlating three-dimensional patellofemoral and tibiofemoral kinematics: a dynamic, in vivo study. IEEE Transactions on Biomedical Engineering. 2006 doi: 10.1109/TBME.2007.890735. [DOI] [PubMed] [Google Scholar]
- Sheehan FT. The Finite Helical Axis of the Knee Joint (a non-invasive in vivo study using fast-PC MRI) J Biomech. 2006 doi: 10.1016/j.jbiomech.2006.04.006. [DOI] [PubMed] [Google Scholar]
- Sheehan FT, Drace JE. Human patellar tendon strain. A noninvasive, in vivo study. Clin Orthop. 2000:201–207. [PubMed] [Google Scholar]
- Sheehan FT, Zajac FE, Drace JE. In vivo tracking of the human patella using cine phase contrast magnetic resonance imaging. J Biomed Eng. 1999;121:1–7. doi: 10.1115/1.2800868. [DOI] [PubMed] [Google Scholar]
- Shiavi R, Limbird T, Frazer M, Stivers K, Strauss A, Abramovitz J. Helical motion analysis of the knee--I. Methodology for studying kinematics during locomotion. J Biomech. 1987;20:459–469. doi: 10.1016/0021-9290(87)90247-8. [DOI] [PubMed] [Google Scholar]
- Smidt GL. Biomechanical analysis of knee flexion and extension. J Biomech. 1973;6:79–92. doi: 10.1016/0021-9290(73)90040-7. [DOI] [PubMed] [Google Scholar]
- Woltring HJ. 3-D attitude representation of human joints: a standardization proposal. J Biomech. 1994;27:1399–414. doi: 10.1016/0021-9290(94)90191-0. [DOI] [PubMed] [Google Scholar]
- Wretenberg P, Nemeth G, Lamontagne M, Lundin B. Passive knee muscle moment arms measured in vivo with MRI. Clin Biomech (Bristol Avon) 1996;11:439–446. doi: 10.1016/s0268-0033(96)00030-7. [DOI] [PubMed] [Google Scholar]


