Fluid phase structure of EPC and DMPC bilayers

Abstract

X-ray diffraction data taken at high instrumental resolution were obtained for EPC and DMPC under various osmotic pressures, primarily at T = 30°C. The headgroup thickness D_HH was obtained from relative electron density profiles. By using volumetric results and by comparing to gel phase DPPC we obtain areas $A_{\mathrm{EPC}}^F=69.4\pm 1.1{\mathrm{Å}}^2$ and $A_{\mathrm{DMPC}}^F=59.7\pm 0.2{\mathrm{Å}}^2$. The analysis also gives estimates for the areal compressibility K_A. The A^F results lead to other structural results regarding membrane thickness and associated waters. Using the recently determined absolute electrons density profile of DPPC, the A^F results also lead to absolute electron density profiles and absolute continuous transforms |F(q)| for EPC and DMPC. Limited measurements of temperature dependence show directly that fluctuations increase with increasing temperature and that a small decrease in bending modulus K_c accounts for the increased water spacing reported by Simon et al. (1995) Biophys. J. 69, 1473−1483.

1. Introduction

One of the most important issues in membrane biophysics concerns the diversity of lipids that occur in nature. Information that should be useful in addressing this issue includes structural characteristics of the lipid bilayers formed from different kinds of lipids. While it has been quite clear that different lipid bilayers have different thicknesses, the uncertainties in the structural characteristics for any one lipid bilayer in the fully hydrated, biologically relevant fluid F (i.e. L_α) phase have often been larger than the putative differences between different lipid bilayers. Because there are so many different thicknesses that can be defined, hydrocarbon thickness D_C, Luzzati thickness D_B and steric thickness $D_B^{\prime }$ we prefer to focus upon the average area A per lipid at the liquid interface, from which the various thicknesses can then be obtained (Nagle and Wiener, 1988). For example, for DPPC, one of the most studied lipids, literature uncertainties in $A_{DPPC}^F$ range from 56 to 73 Ų (Nagle, 1993). This range is enormous, especially when one considers that the DPPC gel G (i.e. ${\mathrm{L}}_{\beta }^{\prime }$) phase has $A_{\mathrm{DPPC}}^G=47.9{\mathrm{Å}}^2$ (Sun et al., 1994); therefore, the effect of fluidization, namely, A^F – A^G has an uncertainty over 100%! Such uncertainties are unacceptable when trying to set up simulations at fixed area (Feller et al., 1997; Perera et al., 1997) or when trying to evaluate the results of simulations in constant pressure ensembles (Tieleman et al., 1997; Tobias et al., 1997).

It has been a goal in this laboratory to obtain more reliable structure determinations of lipid bilayers. Recently, $A_{\mathrm{DPPC}}^F=62.9\pm 1.3{\mathrm{Å}}^2$ was obtained using X-ray methods (Nagle et al., 1996). It is the purpose of this paper to use similar methods to obtain the bilayer structure of two more lipids, DMPC and EPC.

One of the problems with applying traditional diffraction methods to the F phase is that these systems are not crystals, but liquid crystals, which have only quasi-long-range-order, with fluctuations that degrade the intensity of the higher order diffraction peaks (Zhang et al., 1994). By using high instrumental resolution synchrotron X-rays, we were able to correct for these effects (Zhang et al., 1996). Another key element in our analysis (Nagle et al., 1996) was to determine the difficult F phase structure by making use of measured differences with the structure of the G phase; G phase structure is determined independently because of the extra data from wide angle scattering (Sun et al., 1994). At first, it would seem to be difficult to employ this method for EPC because it has no G phase. However, the method assumes only that the headgroups are the same in both lipids being compared. Therefore, we propose in this paper to use measured differences between F phase EPC and G phase DPPC. We also apply the method to DMPC by comparing F phase DMPC and G phase DPPC. Our results for DMPC agree well with an independent structure determination of DMPC that uses quite different assumptions (Koenig et al., 1997).

Our main structural results for DMPC and EPC are for T = 30°C. Of course, one would also like to know the temperature dependence of the structure. We report in this paper some observations that were inspired by a temperature study of Simon et al. (1995). That study showed that the water spacing $D_W^{\prime }$ increased with increasing T, while the bilayer thickness $D_B^{\prime }$ decreased and a plausible explanation was advanced that connects these two observations. The decrease in $D_B^{\prime }$ would be expected to decrease the bending modulus K_C, which would then increase the fluctuations and the corresponding repulsive fluctuation pressure, which would result in larger water spacing $D_W^{\prime }$. Since our synchrotron data give us information about the fluctuations, we directly show that the fluctuations do indeed increase with T.

2. Experimental procedures

2.1. Sample preparation

DMPC (1,2-dimyristoyl-sn-glycero-3-phosphatidylcholine) and EPC (egg phosphatidylcholine, lot no. 341) were purchased from Avanti Polar Lipids (Alabaster, AL) in the lyophilized form and were used without further purlfication. Thin layer chromatography using chloroform:methanol:7 N NH₄OH (46:18:3, v/v) revealed only a single spot when stained with a molybdenum blue reagent (Dittmer and Lester, 1964). Polyvinylpyrrolidone (PVP) with a molecular weight of 40000 was purchased from Aldrich and dried in a vacuum oven at 70°C overnight. PVP/water solutions from 0 to 60% PVP (w:w) were prepared by mixing PVP with Barnstead deionized nanopure water in 3-ml nalgene vials and allowed to equilibrate overnight at room temperature. PVP solutions were added to lipid at nominal 3:1 (when 40% PVP in water and below) or 5:1 (when 45% PVP in water and above) weight ratio in 0.1-ml nalgene vials. The final PVP concentration in the bulk water phase was different from the initial concentration because some of the water left the polymer phase to hydrate the lipid. This effect was small, amounting to only 0.1−0.2 in the usual log₁₀ P plots. However, all weight ratios were recorded in order to calculate the final concentrations of PVP in water. The samples were kept at room temperature for 24 h with occasional vortexing. Thin walled 1-mm glass X-ray capillaries (Charles Supper) were cleaned by sequentially washing with a chromic acid bath, deionized water, acetone and finally copious amounts of deionized water. After drying with nitrogen, the capillaries were flame-sealed at one end. About 10 mg of lipid dispersion was then loaded into each capillary and these samples were centrifuged for 10 min at 1100 × g in a small, nalgene holder using a glycerol cushion. At PVP concentrations of 12% and above for EPC, and at 25% and above for DMPC, the lipid dispersions centrifuged up instead of down at 5°C. The capillaries were then flame sealed and loaded into cassettes with 12 slots/cassette with the ends of the capillaries embedded in a slab of silicone sealer to insure further against evaporation.

2.2. Specific volume measurements

The absolute specific volumes v_L at 30°C were determined as described by Wiener et al. (1989) and the molecular volume V_L = v_LM_w/N_Avogadro was obtained using the molecular weights M_W = 677.95 for DMPC and 768.5 for EPC (using the fatty acid chain content from Avanti products catalog).

2.3. X-Ray diffraction

Data were taken at the F3 station of the Cornell High Energy Synchrotron Source (CHESS). The cassette was mounted so that the capillaries were positioned horizontally inside a cylindrical aluminum sample chamber with mylar windows for entry and exit of X-rays. The cassettes fit directly into a custom holder which was attached to X-Y-Z motorized translations to move the samples relative to the X-ray beam. Temperature was controlled to within 0.02°C. The CHESS beamline monochromator was used to select X-rays with λ = 1.2147 Å. An in-plane resolution of 0.002° (FWHM) in 2θ was achieved using a silicon analyzer crystal for selecting the scattered radiation (Zhang et al., 1996). The flux at the sample was 4 × 10⁹ photons s⁻¹ in an area of 0.75 mm (vertical) × 1.0 mm (horizontal). For each peak a coarse step scan in 2θ was taken to obtain data well into the tails of the peak, e.g. for the second order reflection centered at 2θ₂ the range for 2θ was 2θ₂ ± 0.1°. At the end of the range for each order h, the signal to background ratio was between 3 and 7 depending on the PVP concentration. A fine step scan (e.g. of total width 0.02° for h = 2) was then taken to obtain more data in the central peak. The backgrounds were nearly constant, with values of 5 and 7 counts for water and 40% PVP solutions, respectively, compared to roughly 10000 counts at the top of the first order peak. Lamellar D-spacing was determined from the second order peak; no slit smear correction was necessary due to small beam size in the out-of-scattering-plane direction. Normal X-ray exposures were 15−30 min and negligible damage occurred for periods of up to an hour as assayed by observing negligible changes in the width and position of the first order peak. Thin layer chromatography performed a month after the experiments generally gave lysolecithin contamination less than 2% which is comparable with the fraction found in unexposed samples.

2.4. Raw data fitting and fluctuation determination

The backgrounds were subtracted from scattering data before fitting all orders simultaneously using the modified Caille theory, essentially following Zhang et al. (1994). This theory has been shown to fit lipid bilayer data (Zhang et al., 1996). The parameters determined by the fitting program are the Caille η₁ fluctuation parameter, the mean domain size L, and the fluctuation corrected (and Lorentz-corrected) ratios of form factors r_h≡|F_h/F₁|. From η₁ the mean square fluctuation in the water spacing between bilayers, ${\sigma }^2\equiv \langle {(D_w^{\prime }-\langle D_W^{\prime }\rangle )}^2\rangle$, is obtained from the result (Petrache et al., 1998)

$${\sigma }^2={\eta }_1{D}^2∕{\pi }^2$$ (1)

Raw data showing fits for DMPC and experimental results for σ are given in a recent paper (Petrache et al., 1998). Results for the form factors are presented in this paper.

2.5. Electron density profiles

Absolute electron density profiles can be expressed as

$${\rho }^{\ast }\left(z\right)-{\rho }_W^{\ast }=\frac{1}{D}F\left(0\right)+\frac{2}{D}{F}_1\sum _{\mathrm{h}=1}^{h_{\text{max}}}{\alpha }_h{r}_h\text{cos}\left(\frac{2\pi hz}{D}\right),$$ (2)

where h_max = 4 for our data. The phase factors α_h = (−, −, +, −) are well established for these lipids (Shipley, 1973; McIntosh and Simon, 1986a). The quantity ${\rho }_{\mathrm{W}}^{\ast }$ is the water electron density at 30°C. The ‘zero-order’ form factor F(0), which represents the total electron contrast between the bilayer and the water solution, is given by Nagle and Wiener (1989)

$$AF\left(0\right)=2(n_{\mathrm{L}}^{\ast }-{\rho }_{\mathrm{W}}^{\ast }{V}_{\mathrm{L}})=2({\rho }_{\mathrm{L}}^{\ast }-{\rho }_{\mathrm{W}}^{\ast })V_{\mathrm{L}},$$ (3)

where A is the area per lipid, $n_{\mathrm{L}}^{\ast }$ is the number of electrons in the lipid molecule, V_L is the lipid volume and ${\rho }_{\mathrm{L}}^{\ast }\equiv n_{\mathrm{L}}^{\ast }∕V_{\mathrm{L}}$ is the average electron density of the lipid molecule. The first order diffraction form factor F₁ is initially undetermined due to approximately 15% uncertainty in the amount of lipid in the X-ray beam, so only the absolute ratio r_h = |F_h/F₁| of form factors can be measured directly. This means that only relative electron density profiles can be routinely obtained. Determining F₁ and the absolute electron density profiles will be accomplished in Section 3.3.

2.6. Headgroup spacing D_HH

The headgroup spacing D_HH is defined as the distance between the two peaks in the electron density profile and is usually supposed to be a good approximation to the phosphatephosphate thickness of the bilayer (Pearson and Pascher, 1979). D_HH is the same, of course, for the relative and the absolute electron density profiles. In practice, at least four orders (h_max = 4) are needed to obtain a reasonably accurate estimate of D_HH. Furthermore, even with four orders, the measured D_HH needs to be corrected due to the limited number of Fourier terms. We follow the procedure introduced by Sun et al. (1996) (see Fig. 1 in that paper) and used by Tristram-Nagle et al. (1998).

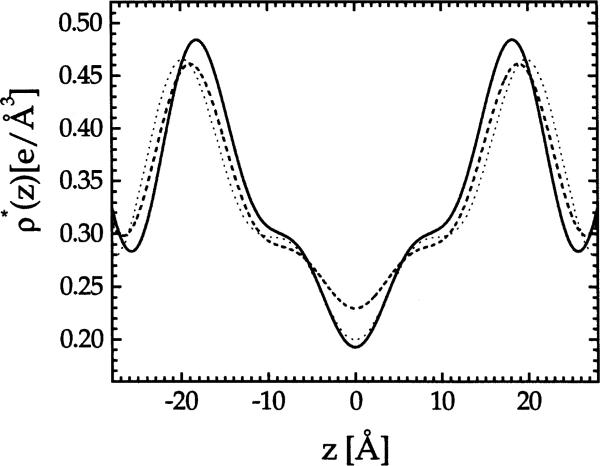
Fig. 1.

Absolute electron density profiles ρ*(z) for DMPC (solid), EPC (dashed) and DPPC (dotted).

3. Results

3.1. Volumetric results and relative electron density profiles

The results of volumetric measurements and some basic information about DMPC and EPC are shown in Table 1. Relative electron density profiles were first obtained for samples under osmotic pressure that have four orders of diffraction. Fig. 1 shows typical absolute electron density profiles; the conversion to absolute electron density, performed in Section 3.2, is not necessary to obtain D_HH. The corrected head group spacing D_HH was then obtained from the electron density profiles, and the value of D_HH is given in Table 2 for EPC at P = 29 atm and for DMPC at P = 27 atm.

Table 1.

Volumetric results (30°C)

	DMPC	EPC
MW (g mol−1)	677.95	768.5
νL (ml g−1)	0.978	0.988
VL (Å3)	1101	1260.6
$n_{\mathrm{L}}^{\ast }\left(\mathrm{e}\right)$	374	424.2
AF(0) (e)	14	8

Table 2.

Structural results (30°C)

	DMPC	DMPC	EPC	EPC
P [atm]	0	27	0	29
D (Å)	62.7	51.5	66.3	53.4
DHH (Å)	34.4a	35.2	35.4a	36.6
A (Å2)	59.7	57.9	69.4	66.3
DB (Å)	36.9	38.0	36.3	38.0
DW (Å)	25.8	13.5	30.0	15.4
nW	25.7	13.0	34.7	17.0
DC (Å)	13.1	13.5	13.6	14.2
D′B (Å)	44.2	45.0	45.2	46.4
D′W (Å)	18.5	6.5	21.1	7.0
nW–n′W	18.4	6.3	24.4	7.7
n′W	7.3	6.7	10.3	9.3

^aCalculated as 2(D_C+D_H1).

3.2. Area per molecule

The area per molecule is obtained following a procedure initiated by McIntosh and Simon (1986b) and employed by Nagle et al. (1996). These studies compared a lipid bilayer in the F phase with the same lipid in the G phase. In this paper we extend this method to compare a lipid bilayer in the F phase with a different lipid in the gel phase, provided only that the headgroup is the same for both lipids. Since this is not an obvious extension, a derivation is now given.

The first basic assumption is that headgroups are fully solvated for both the reference R lipid bilayer and the F phase lipid bilayer under study. (Note that the reference lipid bilayer R could be either G phase or F phase.) Under the condition that the headgroups are chemically identical, the headgroup volume must therefore be the same in R as in F. This means that the difference in lipid volumes is given by the difference in the volumes of the remainder of the molecule

$$V_L^F-V_L^R=A^F{D}_C^F-A^R{D}_C^R,$$ (4)

where D_C is half the thickness of the hydrocarbon region, corresponding to one monolayer. The condition that the headgroups are chemically identical also plays a role in the second basic relation

$$D_C^F-D_C^R=\frac{D_{\mathrm{HH}}^F-D_{\mathrm{HH}}^R}{2}.$$ (5)

This assumes that the major determinant of differences in D_HH is differences in the hydrocarbon region, which is a reasonable approximation even if the headgroup tilt is different because the lever arm for the distance between the phosphate group and the carbonyls is short. Solving Eq. (4) and Eq. (5) for A^F yields

$$A^F=\frac{V_L^F-V_H^R}{D_C^R+\Delta D_{\mathrm{HH}}∕2}$$ (6)

In our study we take DPPC in the gel phase to be our reference lipid with headgroup volume $V_H^R=319{\mathrm{Å}}^3$ determined by Sun et al. (1994). Values of A^F were obtained from Eq. (6) for samples with four orders of diffraction and one of these values is given in Table 1 for both EPC and DMPC for non-zero values of P.

The external osmotic pressure not only pushes the bilayers closer to one another by decreasing D_W, but also removes water by decreasing A (Rand and Parsegian, 1989). Since the lipid volume remains constant with varying P_osm ( White et al., 1987), the bilayer thickness increases with increasing P_osm. The change in area with the applied osmotic pressure is determined by the bilayer compressibility modulus K_A; the defining relation is

$$A-A_0=-A{D}_{W}P∕K_A.$$ (7)

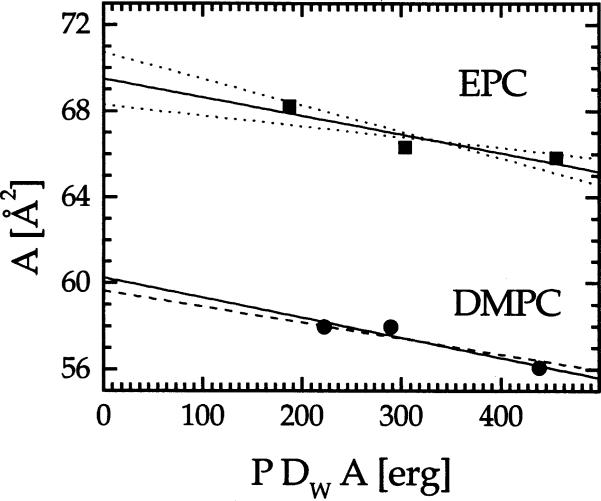
A linear fit to A versus AD_WP gives the fully hydrated area A₀ as the intercept at P = 0, and the slope −1/K_A, from which the compressibility modulus K_A can be obtained. Fig. 2 shows the fitting result with solid line and standard deviations with dotted lines. Our best fit to DMPC data gives A₀ = 60.2 ± 1.0 Å and K_A = 108 ± 35 dyn cm⁻¹. Our result for K_A agrees with Evans and Rawicz (1990) (K_A = 145 ± 10 dyn cm⁻¹) and the more recent measurement of Koenig et al. (1997) (K_A = 136(123 − 152) dyn cm⁻¹), who also report a fully hydrated area A₀ = 59.5 ± 0.2 Ų. Agreement for A₀ with Koenig et al. (1997) becomes even better if we constrain K_A to their value. Then, we obtain A₀ = 59.7 ± 0.2 Ų. For EPC our best fit in Fig. 2 yields A₀ = 69.4 ± 1.2 Ų and K_A = 116 dyn cm⁻¹.

Fig. 2.

Determination of A₀ and K_A. EPC: solid line represents the best fit giving K_A = 116 dyn cm⁻¹ and the dotted lines show one standard deviation corresponding to K_A = 201 dyn cm⁻¹ (smaller slope) and K_A = 81 dyn cm⁻¹ (larger slope). DMPC: dashed line is the best unconstrained fit giving K_A = 108 dyn cm⁻¹ and the solid line shows the fit constrained to K_A = 136 dyn cm⁻¹ from Koenig et al. (1997).

3.3. Other structural quantities

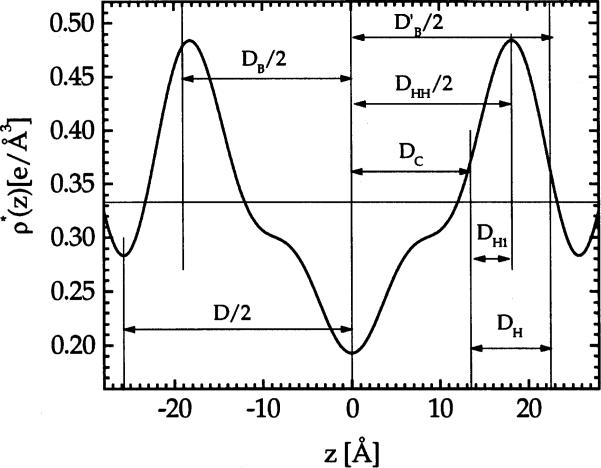
With A determined, we can now calculate many structural parameters of interest. The results are summarized in Table 2. For each lipid we present the results for the fully hydrated sample (P = 0) and for one of the less hydrated samples. The hydrocarbon thickness per monolayer is D_C = (V_L – V_H)/A. The Luzzati bilayer thickness is defined as D_B = V_L/A and the corresponding water thickness is D_W = D – D_B with the number of waters per lipid n_w = AD_W/(2V_w). The steric definition of the bilayer thickness (McIntosh et al., 1987; Nagle and Wiener, 1988) is $D_B^{\prime }\equiv 2(D_C+D_H)$, where we choose D_H = 9 Å, consistent with neutron diffraction results (Buldt et al., 1979), to estimate the PC headgroup thickness. Fig. 3 shows where these various thicknesses fall on the electron density profile. Using $D_B^{\prime }$ we then calculate the interbilayer spacing $D_W^{\prime }\equiv D-D_B^{\prime }$ and the number of water molecules in the headgroup region $n_{\mathrm{w}}^{\prime }\equiv A(D_B^{\prime }-D_B)∕\left(2V_{\mathrm{W}}\right)$.

Fig. 3.

Comparison of various bilayer thicknesses with the 4th order Fourier electron density profile for DMPC at P_osm = 27 atm.

3.4. Absolute electron density profiles

Once the area per molecule is known, the electron density in Eq. (2) can be set on an absolute scale. Starting with Eq. (3), F(0) is determined. In order to calculate F₁ we consider the headgroup peak integral H, above the water level, which is defined as

$$H={\int }_{D_C}^{D∕2}({\rho }^{\ast }\left(z\right)-{\rho }_w^{\ast })dz.$$ (8)

Then, we have

$$AH=n_H^{\ast }-{\rho }_W^{\ast }{V}_H=({\rho }_H^{\ast }-{\rho }_W^{\ast })V_H.$$ (9)

For a PC headgroup, $n_H^{\ast }=164e$ and at T = 30°C Eq. (9) yields A_H = 57.7e. This value of AH should be a constant for all lipids with PC headgroups. This derivation assumes that there is only water, and no hydrocarbon, mixed with the headgroups; although this is undoubtedly not true, the electron density of the methylene region is quite close to ${\rho }_{\mathrm{w}}^{\ast }$, so this is still a good approximation. (A further refinement could be constructed along the lines of the development given by Nagle and Wiener (1989), but this is unwarranted for only four orders of diffraction.) Then, F₁ in Eq. (2) is varied until the headgroup peak in the electron density profile gives a value of H, which together with the already determined A, satisfies Eq. (9). Figs. 1 and 3 show absolute electron density profiles.

3.5. Continuous transform

In the previous section we focused on partially dehydrated samples which, having a lower level of fluctuations, have more diffraction peaks. We now test whether there is any major structural change upon mild dehydration that could invalidate the extrapolation of A in Fig. 2. If there is no structural change at all, then the form factors must all lie on the same continuous transform (Torbet and Wilkins, 1976; McIntosh and Simon, 1986b), defined as

$$F\left(q\right)={\int }_{-D∕2}^{D∕2}[{\rho }^{\ast }\left(z\right)-{\rho }_W^{\ast }]{\mathrm{e}}^{-iqz}dz.$$ (10)

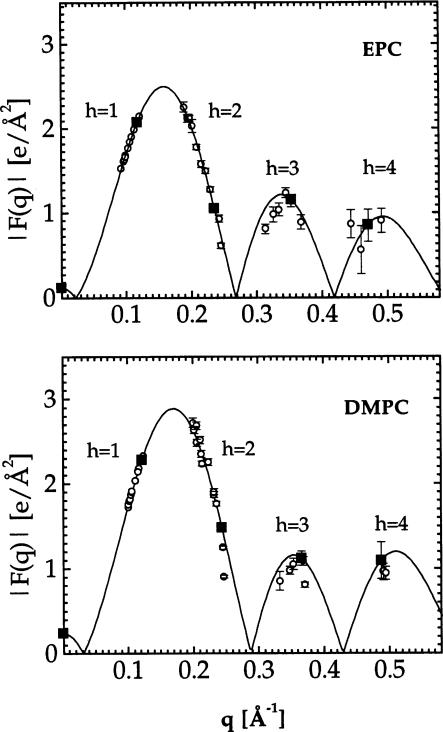
Fig. 4 shows the continuous transforms for EPC and DMPC obtained using the sampling theorem

$$F\left(q\right)=\sum _{h=-h_{\text{max}}}^{h_{\text{max}}}{F}_h\frac{\text{sin}[(q-q_h)D∕2]}{(q-q_h)D∕2},$$ (11)

where q_h = 2πh/D and F_h was obtained for each lipid under one osmotic pressure P′. Due to variations in amount of lipid in the X-ray beam, there were random variations of about 15% in the relative values of F₁ obtained directly from the measured intensity, so F₁ for all other samples was obtained by placement on the F(q) curve. There are then no additional free parameters for the absolute values of the other F_h, which are then shown on Fig. 4. Small systematic deviations of F₂ from the F(q) curve, especially for DMPC, at values of P higher and lower than P′ are consistent with the effect of area compressibility shown in Fig. 2, as we checked by varying the bilayer thickness in model electron density profiles of the 1-Gaussian hybrid type (Wiener et al., 1989). However, the small deviations of the measured F_h from the continuous transform indicates that there are no major structural changes with the range of osmotic pressures P employed.

Fig. 4.

Absolute continuous transforms |F(q)| obtained for EPC at P′ = 29 atm and for DMPC at P′ = 27 atm. The solid symbols represent the form factors used in the reconstruction.

3.6. Temperature behavior

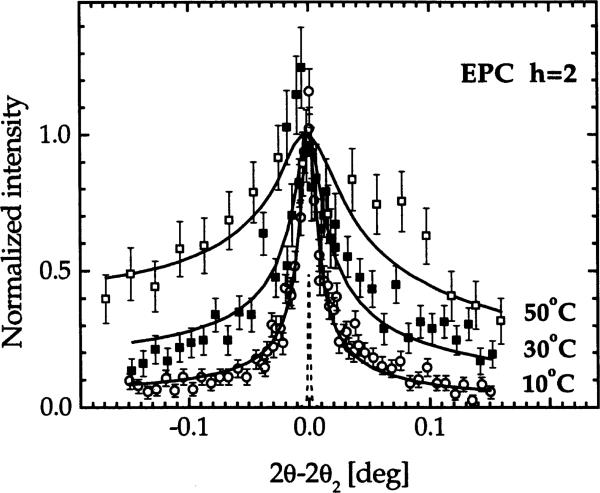
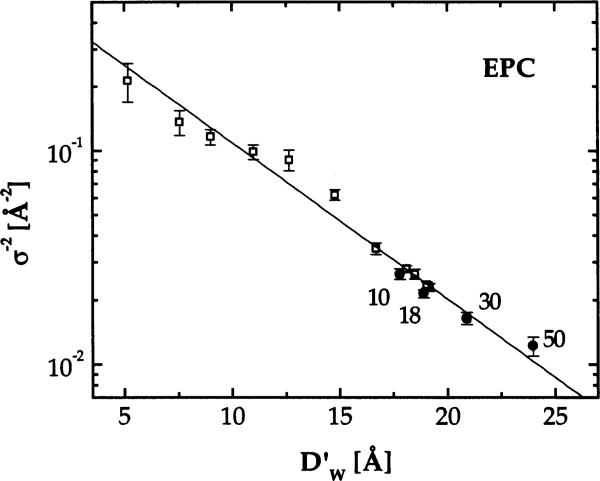
This section focuses exclusively on EPC because temperature (T) can be varied over a wider range in the F phase than for DMPC. We monitored only fully hydrated samples because we planned to focus on the fluctuations rather than on electron density profiles and bilayer thickness, which were studied for EPC by Simon et al. (1995). Fig. 5 shows the normalized peak shapes for the second order. Clearly, the tails of the peaks increase with T and this requires that η₁ increases with T to fit the data. In Fig. 6 we plot the inverse mean square water space fluctuation, σ⁻² (see Eq. (1)), on a logarithmic scale versus water spacing $D_W^{\prime }$ for samples at P = 0 for T = 10, 18, 30 and 50°C. For T = 30°C we obtained $D_W^{\prime }$ at P = 0 as explained in Section 3.3. For other temperatures we used the T dependence of the bilayer thickness of Simon et al. (1995), which was about 0.084 Å/°C to estimate $D_B^{\prime }$ which was then subtracted from our D to obtain $D_W^{\prime }$. The temperature dependence of σ⁻² in Fig. 6 clearly shows that interbilayer fluctuations increase with increasing T.

Fig. 5.

Comparison of h = 2 data for EPC at different temperatures. The solid lines show the fits, which also fit the first order data (not shown), with η₁ = 0.088, 0.137, 0.175 for T = 10, 30, 50°C, respectively. The dashed peak shows the instrumental resolution function.

Fig. 6.

σ⁻² versus $D_{\mathrm{W}}^{\prime }$ for EPC samples under various osmotic pressures at T = 30°C (open symbols) and for fully hydrated samples at T = 10,18,30 and 50°C (solid symbols).

Fig. 6 also shows σ⁻² for other samples at T = 30°C subject to various osmotic pressures P. The motivation for plotting σ⁻² on a logarithmic scale in Fig. 6 comes from our recent analysis of interbilayer interactions (Petrache et al., 1998) where we showed that the fluctuational contribution to the free energy is given by

$$F_{fl}={\left(\frac{k_{B}T}{2\pi }\right)}^2\frac{1}{K_c{\sigma }^2},$$ (12)

where K_C is the bending modulus, which is expected to be a function of T but not of osmotic pressure P. The T = 30°C EPC data shown in Fig. 6, as well as data for three other lipids (Petrache et al., 1998; Tristram-Nagle et al., 1998), are all reasonably well represented by an exponential. This is consistent with the theoretical prediction (Podgornik and Parsegian, 1992) that the fluctuation pressure P_fl has an exponential decay with ${\mathrm{D}}_{\mathrm{W}}^{\prime }$. Surprisingly, σ⁻² for other values of T also appear to fit on the same line in Fig. 6.

The other basic interactions between bilayers are the usual sum of hydration and van der Waals forces (Rand and Parsegian, 1989)

$$\begin{array}{cc}\hfill & V\left(D_W^{\prime }\right)=P_h\lambda {\mathrm{e}}^{-D_W^{\prime }∕\lambda }-\frac{H}{12\pi }\hfill \\ \hfill & \left(\frac{1}{D_W^{\prime 2}}-\frac{2}{{(D_W^{\prime }+D_B^{\prime })}^2}+\frac{1}{{(D_W^{\prime }+2D_B^{\prime })}^2}\right).\hfill \end{array}$$ (13)

Minimizing with respect to $D_W^{\prime }$ the total free energy F, which is the sum of Eq. (12) and Eq. (13), then gives the water spacing $D_{W0}^{\prime }$ when P = 0. Results of Simon et al. (1995) indicated only very small T dependences of the parameters P_h, λ and H that, within the quoted errors could have been constant. The estimates given for the Hamaker parameter H suggested about 10% decrease from 5 to 50°C, but theory suggests that H should increase (Parsegian and Ninham, 1971). Also, the values of λ ≈ 1.1 Å given by Simon et al. (1995) are much smaller than other values (Petrache et al., 1998; Rand and Parsegian, 1989), so we have used our values (Petrache et al., 1998) of λ = 1.94 Å, P_h = 1.07 × 10⁹ dyn cm⁻³ and H = 4.73 × 10⁻¹⁴ erg as constants at all T. Then, we have found the value of K_C for which the total free energy F has the minimum at values of $D_{W0}^{\prime }$ shown with solid symbols in Fig. 6. The results are presented in the second column of Table 3. The third column of Table 3 also shows the values of K_C that are predicted if K_C = 0.55 × 10¹² ergs at T = 30°C and if K_C is proportional to the square of the hydrocarbon chain thickness, which is a likely dependence for K_C (Simon et al., 1995).

Table 3.

Temperature dependence of bending modulus K_C

T (°C)	KC	KC
10	0.61	0.62
18	0.57	0.59
30	0.55a	0.55a
50	0.53	0.50

^aFrom Petrache et al. (1998)

Units of K_C are 10⁻¹² erg. Values at T = 30°C were fixed from other studies. K_C was obtained from fitting the water spacing at P = 0, and ${\widehat{K}}_C$ was obtained assuming quadratic dependence upon hydrocarbon chain thickness.

4. Discussion

The main structural results in this paper are the areas A^F for the fully hydrated biologically relevant L_α phase of EPC bilayers and DMPC bilayers. Our result $A_{\mathrm{EPC}}^F=69.4{\mathrm{Å}}^2$ at T = 30°C is smaller than 74 Ų obtained at T = 25°C using the Luzzati gravimetric method (Lis et al., 1982). The gravimetric method typically overestimates A because, contrary to the assumption in that method, not all the weighed water goes between the bilayers until the excess water phase begins to form (Klose et al., 1988; Koenig et al., 1997). The gravimetric method was later modified (Rand and Parsegian, 1989) to use data taken on samples under osmotic pressure together with a compressibility modulus K_A = 145 dyn cm⁻¹ which was not measured for EPC but estimated from DMPC (Evans and Needham, 1987); the revised value 69.5 Ų agrees very well with our value of 69.4 Ų. The agreement would not be quite so good if we also used this same value of K_A instead of our best K_A = 116 dyn cm⁻¹ nor if thermal expansion from T = 25−30°C were taken into account. Using an area dilation of 5 × 10⁻³/°C (Evans and Needham, 1987) would add about 1 Ų to $A_{\mathrm{EPC}}^F$. However, our K_A has a large uncertainty, and this propagates a range of uncertainty 68.3−70.5 Ų in our A. Since a similar range of uncertainty applies to the modified gravimetric result, we suggest that there is agreement for EPC that $A_{\mathrm{EPC}}^F=69.4\pm 1.1{\mathrm{Å}}^2$ in the T = 25−30°C range.

Our result $A_{\mathrm{DMPC}}^A=59.7{\mathrm{Å}}^2$ for DMPC at T = 30°C is lower than the value 65 Å obtained from the unmodified Luzzati gravimetric method (Lis et al., 1982) and even somewhat lower than the 61.7 Å obtained from modified gravimetric method (Rand and Parsegian, 1989), both at T = 27°C. Recently, the gravimetric method has been further modified by combining it with NMR S_CD order parameter data as a function of osmotic pressure (Koenig et al., 1997). There is uncertainty in converting S_CD data into absolute values of A (Nagle, 1993; Koenig et al., 1997), but Koenig et al. (1997) argue that changes in A are accurately obtained. By using the gravimetric method to obtain A at low hydration, where it is likely that most of the water does go between the bilayers, and by using the K_A obtained from NMR, Koenig et al. (1997) obtained $A_{\mathrm{DMPC}}^F=59.5\pm 0.2{\mathrm{Å}}^2$ at T = 30°C. This is excellent agreement between the results of two different methods that involve quite different assumptions. We suggest that there is agreement that $A_{\mathrm{DMPC}}^F=59.6\pm 0.2{\mathrm{Å}}^2$.

The large differences in $A_{\mathrm{DMPC}}^F$ and $A_{\mathrm{EPC}}^F$ imply that the hydrocarbon chains have a considerable influence on A^F. In addition to the contrast between DMPC and EPC, we have also recently obtained $A_{\mathrm{DPPC}}^F=62.9\pm 1.3{\mathrm{Å}}^2$ (Nagle et al., 1996) and $A_{\mathrm{DOPC}}^F=72.2\pm 1.1{\mathrm{Å}}^2$ (Tristram-Nagle et al., 1998). Not surprisingly, unsaturation leads to larger A^F. Clearly, there is a ‘fluidity’ spectrum, and not just one generic brand of fluid chains.

Our present result A^F = 59.6 Ų for DMPC at T = 30°C is clearly smaller than our earlier result A^F = 62.9 Ų for DPPC at T = 50°C. These results are different from the result (Tristram-Nagle et al., 1993) that A^G is nearly constant as a function of chain length for saturated lecithins in the gel phase. This is not surprising because the mechanism for maintaining constant A in the gel phase is the constraint of packing headgroups at their steric limit of A^G = 47−48 Ų; such a constraint would not be expected to play a role at the larger values of A^F in the fluid phase. Our A^F results also do not conform to an earlier conclusion (Lewis and Engelman, 1983) that A^F for the fluid phase remains nearly constant with chain length with values near A^F = 66 Ų. Although comparison is complicated by different temperatures (Lewis and Engelman used T = 36°C for DMPC and T = 44°C for DPPC), Evans and Needham (1987) found the coefficient of areal thermal expansion α to be about 0.005 deg⁻¹ and this only reduces their A^F to about 64 Ų for DMPC, still considerably larger than ours and it increases A^F for DPPC to about 68 Ų. More importantly, thermal expansion explains why A^F for DPPC at 50°C should be greater than A^F for DMPC at 30°C as follows. First, according to a theory of Flory (1956) hydrocarbon chain conformations in the fluid phase are determined by absolute temperature, not by temperature relative to the phase transition. Therefore, in first approximation, one should expect A^F for DMPC and DPPC to be equal at the same T and therefore differ by (αA) (20°C) = 6 Ų, even larger than our measured difference of 3 Ų. Of course, this is only a first approximation that does not account for the competition between the headgroup and the chains that would quite likely reduce this effect. Therefore, our measured differences between DMPC and DPPC appear to be quite reasonable.

The basic assumption in our method of obtaining A^F is that phosphatidylcholine headgroup dimensions are the same for different PC lipids in different phases. Now that the agreement with Koenig et al. (1997) lends support for this assumption, it is worth looking at these dimensions’ as visualized in Fig. 3. A new thickness corresponds to that part of the headgroup that extends from the average hydrocarbon layer, defined as D_C, to the peak in the electron density profile; we define this as D_H1 = (D_HH/2)–D_C. For PC head groups (which in our definition include the glycerol group and the carbonyls), Table 2 gives D_H1 = 4.1 Å (Note that D_H1 appears a bit larger in Fig. 3 because of the correction to D_HH due to Fourier truncation.) Once D_H1 and V_H are known for a given headgroup type, there is a simplified way to obtain A which is equivalent to the method developed in Eq. (6) in Section 3.2. First, one obtains D_C = (D_HH/2)–D_H1 from D_H1 and the corrected D_HH. Then, one obtains A = V_C/D_C where V_C is the hydrocarbon volume obtained using V_C = V_L–V_H, and of course, V_L is measured. It may also be noted that the basic assumption in this paragraph can be addressed with simulations that would determine how much D_H1 varies for different PC lipids in different phases.

Because we could not obtain enough orders of diffraction for fully hydrated F phase lipids, we applied osmotic pressure P which reduces the fluctuations. This meant that we had to extrapolate to P = 0 to obtain fully hydrated structure. This necessarily led us to obtain estimates for the area compressibility K_A (see Fig. 2). Although our estimates for K_A are not as accurate for DMPC as obtained by others (Koenig et al., 1997; Evans and Needham, 1987), they do agree. Furthermore, our errors for A^F remain small even though our errors for K_A are large, as can be seen in Fig. 2. In this context it should be mentioned that, if we had not corrected the head-head thickness D_HH following Sun et al. (1996), the slopes in Fig. 2 and the values of K_A would have been very large or even negative, which is physically unrealistic.

Bechinger and Seelig (1991) have reported NMR order parameter data showing that the conformation of the alpha and beta carbons between the phosphate and the choline change conformation as the system is dehydrated. This does not affect our analysis to obtain A^F above because the choline part of the headgroup has electron density 0.35e/ų that is very similar to that of water 0.33e/ų, as can be obtained from the determination of component volumes of lipids (Petrache et al., 1997). Therefore, a conformational change results in an exchange with water which does not change the electron density profiles. Furthermore, the choline is located in the outer part of the headgroup, not the part that is included in the D_H1 region required for the above analysis.

Figs. 1 and 3 show electron density profiles on an absolute scale and equivalently Fig. 4 shows the continuous transform on an absolute scale. This was accomplished by using the basic idea that A₁H₁ = A₂H₂ must be the same for different lipids and/or different phases, identified by the subscripts 1 and 2, provided that the headgroups are the same. Only H₁ contains the unknown instrumental scale factor. Once H₁ is known absolutely, the unknown scale factor for lipid 2 is determined such that H₂ = H₁A₁/A₂. It may also be noted that the headgroup region must have different amounts of water for different A. This is not expected to affect significantly the values of D_HH used in the determination of A because there is little difference in electron density between water and the hydrocarbon region, so the primary effect is to reduce the headgroup peak in the electron density profile, which is the property used here to obtain absolute electron density scales.

From the plot of the absolute electron density profiles shown in Fig. 1 we observe that EPC, which is a mixture of fatty acid chains, has more disorder at the bilayer center compared to DMPC and DPPC, for both of which the methyl trough in the electron density profile is narrower and deeper, suggesting that the methyl groups at the chain ends are better localized than in EPC. Recent results for DOPC (Tristram-Nagle et al., 1998) indicate more methyl disorder than for DPPC but less than for EPC. Although details of this kind may be obviated by Fourier truncation error, it nevertheless seems that the terminal methyls could be more delocalized for lipids containing unsaturated fatty acids, in agreement with the results of Holte et al. (1995).

Our analysis that determines A^F and K_A requires that there be no drastic structural changes over the range of P applied because extrapolation to P = 0 would then be invalidated. The fact that the data for all P fall close to the continuous transform in Fig. 3 confirms no large scale structural change. The small, systematic deviations of the h = 2 form factors for high and low P in Fig. 3 are consistent with small changes of order 1.5 Ų in D_B due to osmotic compression, as can be verified by varying the thickness in models (Torbet and Wilkins, 1976; McIntosh and Simon, 1986b; Nagle and Wiener, 1989) of electron density profiles.

Our data were mostly for T = 30°C, but we explored the issue of how fluctuations depend upon T for EPC by measuring the Caillé fluctuation parameter η₁. Our data directly confirm the hypothesis of Simon et al. (1995) that fluctuations increase with increasing T. Simon et al. (1995) also suggested that this is due to a decrease in bending modulus K_C. Assuming, following Simon et al. (1995), that the other interactions, van der Waals and hydration force, are independent of T, our data are consistent with a small decrease in K_C. However, we note that there is also a factor of T² in the fluctuation pressure that plays a non-negligible role in increasing the fluctuations. Although this factor is usually thought to be negligible, it can cause a substantial increase in water spacing D_W at full hydration (P = 0) because the minimum in the bare interbilayer potential is so shallow. As shown in Table 3 the T dependence of K_C is a little less than if K_C scaled as the square of the hydrocarbon chain thickness as measured by Simon et al. (1995). Therefore, our direct data for the T dependence of the fluctuations are basically consistent with the overall picture of T dependence of interbilayer interactions proposed by Simon et al. (1995).