Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2009 Sep 29.
Published in final edited form as: Neurosurgery. 2006 Nov;59(5):1094–1101. doi: 10.1227/01.NEU.0000245599.92322.53

A Model System for Mapping Vascular Responses to Complex Hemodynamics at Arterial Bifurcations In Vivo

Hui Meng 1,2, Daniel D Swartz 3,4, Zhijie Wang 5,6, Yiemeng Hoi 7,8, John Kolega 9,10, Eleni M Metaxa 11,12, Michael P Szymanski 13,14, Junichi Yamamoto 15,16, Eric Sauvageau 17, Elad I Levy 18,19
PMCID: PMC2754158  NIHMSID: NIHMS134414  PMID: 17143243

Abstract

Objective

Cerebral aneurysms are preferentially located at arterial bifurcation apices with complex hemodynamics. To understand disease mechanisms associated with aneurysm initiation, we attempted to establish a causal relationship between local hemodynamics and vascular responses.

Methods

Arterial bifurcations were surgically created from native common carotid arteries in two dogs, angiographically imaged 2 weeks and 2 months later, and then excised. We characterized local morphological changes in response to specifically manipulated hemodynamics. Computational fluid dynamics simulations were performed on the in vivo images and results mapped onto histological images.

Results

Local flow conditions, such as high wall shear stress and high wall shear stress gradient, were found to be associated with vascular changes, including an intimal pad in the flow impingement region and a “groove” bearing the characteristics of an early aneurysm.

Conclusion

This novel method of histohemodynamic micromapping reveals a direct correlation between an altered hemodynamic microenvironment and vascular responses consistent with aneurysm development.

Keywords: Arterial bifurcation, Cerebral aneurysms, Hemodynamics, Vascular remodeling

Since the early 1970s, studies of arterial bifurcation morphology have suggested linkage between hemodynamic stresses and vascular remodeling (2, 16). It is generally accepted that blood flow patterns and hemodynamic stresses associated with such morphology contribute to the development of vascular pathologies (4, 5, 11). Cerebral aneurysms are preferentially located near arterial bifurcations or along the outer curvature of arteries on or near the Circle of Willis (10, 15). The local hemodynamics at such sites are complex, presenting impinging flow, regions of high wall shear stress (WSS), gradients in wall shear stress (WSSG), combinations of both, as well as “disturbed flow” (1, 8, 18). Yet, these relationships between hemodynamic conditions at an arterial bifurcation and pathological vascular remodeling leading to aneurysms are not well understood.

Recent developments in computational fluid dynamics (CFD) enable detailed characterization of three-dimensional (3-D) flow fields in arteries of humans and larger animals (6). Thus, angiographic imaging and CFD can provide detailed flow fields from which measured hemodynamics can be correlated spatially and temporally with specific tissue responses in local microenvironments. Such hemodynamic-vascular response correlations constitute a model system for studying disease mechanisms that are mediated by altered hemodynamics.

In this study, we present a new method for correlating morphological changes in the vascular wall with the local hemodynamics in a surgically created arterial bifurcation in dogs. To study how arterial tissue adapts to the complex hemodynamic environment of impinging flow, we created the bifurcation from native arterial segments and studied how the morphology of the vascular wall changed in response to altered hemodynamics. The major benefit of using a created bifurcation is to establish a cause and effect relationship between the altered hemodynamics (specifically, the flow impingement normally associated with a bifurcation) and remodeling of the vascular wall at the cellular level. Here, the naïve vessel wall had never before been exposed to the type of impingement flow. New morphology that develops after the bifurcation has been created can thus be attributed to hemodynamic insult resulting from manipulated exposure of the naïve vessel wall to impinging flow. Our observations provide insight into how complex hemodynamic conditions near the apex of an arterial bifurcation (including flow impingement, WSS and spatial variations, or gradients, of WSS) could affect vascular remodeling processes, including those that go awry. The changes observed have important implications concerning the fundamental mechanisms of aneurysm initiation.

Methods

Bifurcation Creation

All procedures conformed to current regulations and guidelines for animal experiments and were approved by the Institutional Animal Care and Use Committee. Two mongrel female dogs weighing 20 to 25 kg were fed a high-salt diet (0.4 g NaCl/kg per day) to increase systemic arterial pressure, beginning 6 weeks before surgery and continuing until sacrifice (one animal was sacrificed 2 wk after the surgical procedure and the other 2 mo after surgery). Although the dogs were fed a high-salt diet for 8 to 14 weeks, their blood pressure did not increase significantly. The mean blood pressure at the time of sacrifice was 117 ±3 mmHg. Both common carotid arteries (CCAs) were exposed and isolated. Baseline flow was measured in both CCAs (under anesthesia) using a perivascular flow probe (Transonic System, Inc., Ithaca, NY). The left CCA was transected proximally, and the distal segment (L2 in Fig. 1) was mobilized under the trachea to the right side. Then, the right CCA was proximally and distally closed with atraumatic clips and divided. The distal segment of the right carotid (R2 in Fig. 1) was anastomosed end to end to the contralateral left distal carotid segment (L2). An arteriotomy was performed on that connected segment, and the right proximal carotid (R1 in Fig. 1) was anastomosed, resulting in a Y-shaped bifurcation. After removal of all clips, arterial patency was documented by routine angiography. Crystal radiopaque markers (Sonometrics Corp, London, Canada) were then placed around each bifurcation segment as reference points for subsequent 3-D angiography and histological mapping of the flow fields.

FIGURE 1.

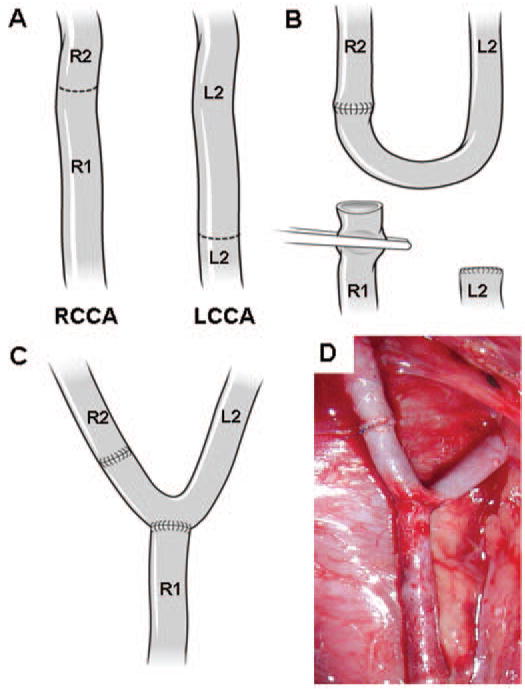
FIGURE 1

Open in a new tab

Creation of bifurcation. A–C, illustrations showing the arteries and their rearrangement. D, photograph showing anastomosis of the CCAs immediately after the completion of the anastomosis procedure. R1, proximal segment of the right CCA; R2, distal segment of the right CCA; L1, proximal segment of the left CCA; L2, distal segment of the left CCA.

Image Acquisition and Flow Measurement

Immediately before sacrifice, the bifurcation was imaged using 3-D digital subtraction angiography (Infinix vs-i; Toshiba America Medical Systems, Inc., New York, NY). Flow rates in the feeding artery and bifurcation branches were recorded (under anesthesia) using the flow probe mentioned above, and the pulsatile waveform of the feeding artery was represented by a six-term Fourier series as the inlet condition for CFD. The ratio of the average flow rates in the two branches provided an additional boundary condition in the CFD model.

Image Reconstruction and CFD

Because blood vessels move after the removal of surgical clips, closure of the surgical site, and recovery of the animal, the geometry of the created bifurcation in vivo is likely to differ from the photograph taken at the time of creation (Fig. 1D). Therefore, for CFD simulations and comparison with histological images, the 3-D lumen of the arterial bifurcation (Fig. 2A) was reconstructed from the rotational angiograms acquired at the time of sacrifice using the Angiosuite software (Infinix vs-i). CFD analysis also used the flow data acquired at the time of sacrifice.

FIGURE 2.

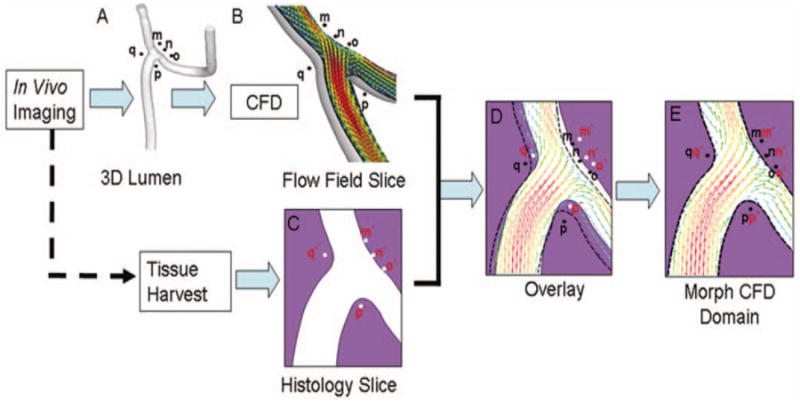
FIGURE 2

Open in a new tab

Steps involved in mapping CFD flow fields with the histological images. 3-D lumen geometry and reference points (m, n, o, p, q) were reconstructed (A) from in vivo rotational angiographic images acquired immediately before sacrifice. Then, CFD analysis was performed on this 3-D geometry, and the CFD solution was “sectioned” (B) in the same planes as the histology slides (C). These CFD slices were then superimposed onto the corresponding histological images (D). Mismatch of the two luminal geometries in D was caused by distortions on the histology slides introduced during tissue imbedding and sectioning. Using radiopaque markers (m, n, o, p, q) and arterial intersection as reference points, the CFD domain was then morphed to coincide with the histology domain (E).

In the CFD simulations, we assumed Newtonian fluid (μ = 0.0035 Pa·s) and incompressible, laminar flow (density = 1060 kg/m3) in a rigid-wall model. Approximately 1.6 million tetrahedral and prism grids were generated with ICEM-CFD software (Ansys, Berkeley, CA). The CFD solutions of both steady-state (Reynolds number = 730) and pulsatile flow conditions (Womersley number = 2.68) were obtained through commercial software Star-CD (CD-Adapco, Melville, NY). A traction-free boundary condition was applied to both outlets.

Histology

Vessels were perfused immediately after sacrifice with phosphate-buffered saline and pressure fixed in situ at 150 mmHg with 10% buffered neutral formalin for 30 minutes. The vessels were fixed at this slightly elevated pressure to prevent vasospasm and to compensate for the shrinkage that is associated with the fixation process. After fixation, the bifurcation was excised and embedded in paraffin. Before sectioning, the crystal radiopaque markers were removed. The indentations created by them served as reference points in the vessel wall for mapping the flow fields with histology. Next, the bifurcation was sectioned longitudinally. Adjacent, 4 μm-thick sections from the median plane of the bifurcation were stained with hematoxylin and eosin, van Gieson, and trichrome.

Mapping Flow Fields with Histology

Histological images were digitized from the histological sections and used as the basis for correlation with the hemodynamic microenvironment given by the CFD solution for the bifurcation at peak systole. The steps involved in mapping CFD solutions with the histological images are shown in Figure 2. First, 3-D–CFD analysis was performed based on the geometry and flow data acquired in vivo immediately before sacrifice. The 3-D–CFD solution was “sectioned” (Fig. 2B) in the same planes as the histology slides (Fig. 2C). These CFD slices were then superimposed on the corresponding histological images (Fig. 2D). Although pressurized fixation improved the preservation of lumen geometry, small distortions inevitably occurred during embedding and sectioning. Therefore, the two domains in Figure 2D do not match exactly. Next, a mesh grid was attached to the CFD domain. With use of the radiopaque markers (m, n, o, p, q) and arterial intersection as reference points, the mesh grid was deformed to make the CFD domain coincide with the histology domain (Fig. 2E).

It was important that the CFD simulations were performed on the in vivo geometry and not on the distorted geometry of the histology sections to ensure the accuracy of the flow field solutions. Once the flow field solutions were obtained, it was necessary to morph the solution grid along with the vessel geometry to map the solutions onto the histology slides to compensate for any postmortem distortions on the vessel geometry introduced by tissue preparation and histology sectioning. Morphological indications of the biological properties of the cells in the regions of interest were retained in the histological sections. Our goal was to relate these biological properties to the hemodynamic environments the cells experienced in situ.

Results

To examine how a vessel wall responds to the special hemodynamic environment occurring at a bifurcation, arterial bifurcations were surgically created in vivo from native CCAs (Fig. 1). Dogs were used because their relatively large arteries permit accurate imaging, flow computation, and tissue mapping. Extracranial vessels were chosen for ease of surgical access and placement of radiopaque markers for mapping in vivo flow fields onto histological sections. The hemodynamic microenvironment and tissue responses were examined 2 weeks and 2 months after creation.

Hemodynamic Microenvironment

Local flow fields in created bifurcations were determined by CFD analysis, which was based on rotational angiography and flow rates measured in vivo, and were aligned with vascular morphology revealed by histology (Fig. 3A). CFD also gave the velocity field, surface distributions of relative pressure on the wall, luminal WSS, and WSSG. Maps of luminal WSS and WSSG (Fig. 3, B and C) show the complex hemodynamic environment at the apex of the created bifurcation, which can be divided into three regions with different flow characteristics.

FIGURE 3.

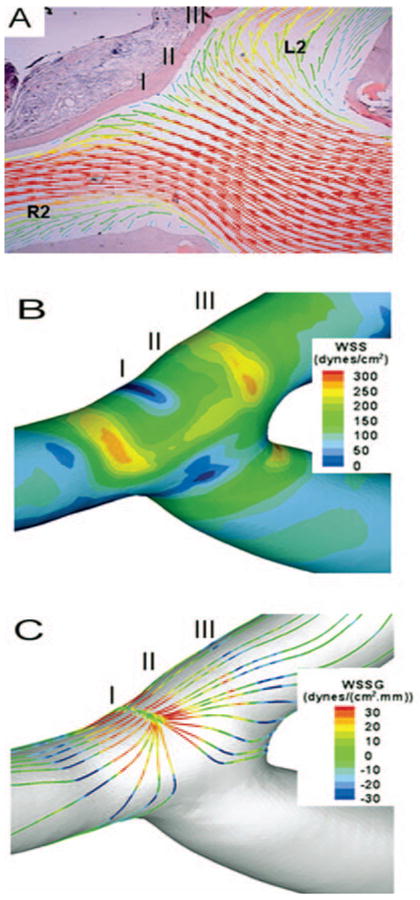
FIGURE 3

Open in a new tab

Mapping of hemodynamics. A, calculated velocity field on the plane overlaid on a histological image; vectors indicate the velocity direction and magnitude; colors also indicate velocity magnitude. B, surface distribution of luminal WSS. C, surface distribution of luminal WSSG along the flow streamlines. R2, distal segment of the right CCA; L2, distal segment of the left CCA.

Impingement Region

Where flow impinged upon the vessel wall opposite the feeding vessel, there was a stagnation point at which flow stopped as it changed direction. At the stagnation point, the velocity was less than 0.05 m/s (blue in Fig. 3B), but, immediately adjacent to the stagnation, blood accelerated into the branches so that shear stress (WSS) increased rapidly along the wall to the normal physiological level of 15 to 20 dynes/cm2 as observed in nonbranching vessels. This resulted in a high WSSG (spatial gradient of shear stress) at the apex of the bifurcation.

Acceleration Region

Flow continued to accelerate distal to the impingement region until it reached maximum velocity (thus maximal WSS), creating an extended region where the vessel wall experienced both high WSS (>20 dynes/cm2) and high WSSG.

Recovery Region

Once flow reached maximum velocity and WSS distal to the stagnation, it started to decelerate, and the WSS dropped down gradually to the normal physiological level further downstream along the wall. This region was defined as the recovery region.

Vessel Wall Remodeling

Mapping flow fields onto histological images of the created bifurcation (Fig. 3A) revealed distinct tissue responses in the three hemodynamic regions. The artery in the impingement region (I) developed an “intimal pad,” evident both 2 weeks (data not shown) and 2 months after creation (Fig. 4, A, A1, B, and B1). The wall in the acceleration region (II) at the left branch developed a “groove” at 2 months (Fig. 4, A, A2, B, and B2), whereas the recovery region (III) showed a normal morphology similar to the vessel before surgery (Fig. 4, A, A3, B, and B3). “Pad” and “groove” formation resembled early aneurysm development in the hypertensive rat model (7).

FIGURE 4.

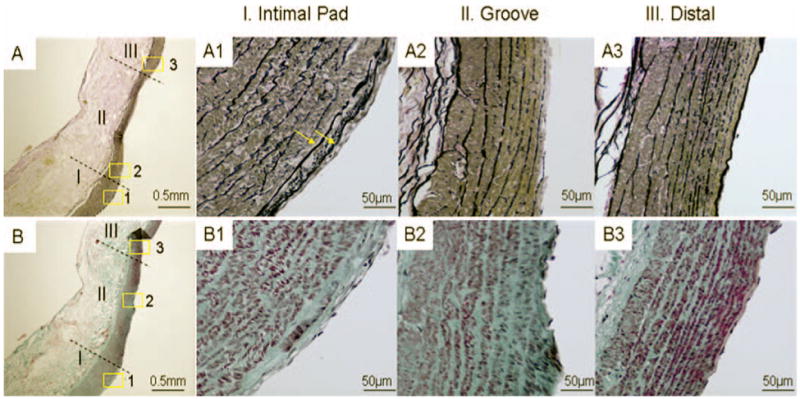
FIGURE 4

Open in a new tab

Histological images of impingement (I), acceleration (II), and recovery (III) regions on the left branch of bifurcation 2 months after creation. A–A3, van Gieson staining. B–B3, trichrome staining. A and B, gross morphology showing an intimal pad bordering a “groove” (original magnification, ×40). Insets 1 to 3 in A and B are shown at a higher magnification (×400) in A1 to A3 and B1 to B3. A1 and B1, more elastin deposition (A1, arrows; multiple layers of internal elastic lamina) and more collagen deposition (B1) within the intima hyperplasia in region I, indicating a more mature intimal pad compared with the bifurcation created at 2 weeks (data not shown). The “groove” in region II is characterized by disrupted endothelium and internal elastic lamina and a thinned media (A2) with smooth muscle cell depletion (B2). These are indications of early aneurysm. A3 and B3, region III (distal region on the left branch) shows normal morphology similar to that observed in the vessel before surgery (not shown).

At 2 weeks, the intimal pad showed intimal hyperplasia with dramatically increased cell numbers and deposition of extracellular matrix based on hematoxylin-eosin and trichrome staining (not shown). At 2 months, the number of cells in the hyperplastic region decreased slightly, but elastin (Fig. 4A1) and collagen (Fig. 4B1) deposition increased. Also, there seemed to be more than one internal elastic lamina layer (Fig. 4A1, arrows), the orientation of smooth muscle cells changed from circumferential to longitudinal (not shown), and the media beneath the intimal pad was thicker than the adjacent media (Fig. 4, A and B).

The “groove” immediately distal to the intimal pad at 2 months was characterized by disrupted endothelium and internal elastic lamina and a thinned media (Fig. 4A) with smooth muscle cell depletion (Fig., 4, B and B2). These are characteristics of the vessel wall where cerebral aneurysms are beginning to develop in hypertensive rats (3, 7).

The vascular responses of the “pad” or “groove” are induced by the altered hemodynamic environment and not directly by the surgical procedure. Examination of the regions close to the sutures of the anastomosis showed that tissue immediately adjacent to the anastomosis was normal. The three hemodynamic regions described above were more than 20 mm distant from the surgically damaged tissue. Furthermore, we found no remodeling of the vessel wall in the straight segment immediately distal to the end-to-end anastomosis (R2 in Fig. 1C). This segment thus serves as an “internal control.” Thus, the distinct morphological changes of the regions described above would not be a direct response to the surgery itself but rather to the altered hemodynamics secondary to the surgical manipulation.

Discussion

Flow-mediated vascular disease results from the complex interplay between mechanical insult and compromised biological response. Because cerebral bifurcations are particularly susceptible to aneurysm formation, it is important to understand the complex hemodynamic environment at these locations using appropriate models. Our study presents a new method for directly correlating flow microenvironment with vascular responses by spatial mapping in vivo. This approach is the first to spatially resolve the complex hemodynamic environment at an arterial bifurcation and examine accompanying cellular changes in vivo.

In this study, we adopted a number of assumptions to render the CFD simulations mathematically and computationally manageable. These assumptions include, in particular, Newtonian fluid and rigid walls. It is widely accepted that such simplifying assumptions on blood rheology and blood vessels contribute only second-order effects to the flow dynamics in large arteries, as compared with the predominant influence of geometry, and, secondarily, flow pulsatility (17, 18). Perktold and Hofer (13) and Xu et al. (19) reported slightly higher WSS values using a non-Newtonian versus Newtonian fluid model for blood, with the overall WSS distribution preserved by the Newtonian simulations. Numerical modeling by Perktold et al. (14) showed that non-Newtonian rheology had little effect on flow in a bifurcation aneurysm model, whereas a wall distensibility of 6% induced changes only in secondary flow characteristics during systole in a lateral aneurysm model (12). Using compliant wall models, Zhao et al. (20) and Karner et al. (9) observed a reduction of WSS magnitude, but the same global characteristics of the flow and WSS pattern when compared with rigid wall models. Taking the Newtonian fluid and rigid wall assumptions together, we think these effects are minor in our model and that the present study provided a reasonable first-order approximation. We think that higher-order effects can, in principle, be included in future studies to increase the accuracy of the simulation results. However, the cost can be prohibitive, and further assumptions must be introduced, such as the stress-strain relationships of the local vessel wall. Strictly speaking, modeling should include iterative fluid-structure biology three-way interaction. Such techniques are not yet developed.

By combining high-resolution in situ imaging, CFD, and postmortem histology, we were able to visualize, at the cellular level, the complex hemodynamics at the created bifurcations. Cells along the apex wall experienced three distinct sets of hemodynamic conditions: 1) low to normal WSS and high WSSG in the impingement region, 2) combined high WSS (>20 dynes/cm2 and high WSSG in the distal acceleration region, and 3) gradually decreasing WSS in the further distal recovery region. The complex hemodynamic environment at the bifurcation apex elicited correspondingly complex biological responses. The impingement region, which experienced low to normal WSS and high WSSG, formed an intimal pad, whereas the acceleration region, which experienced a combination of high WSS and high WSSG, developed a “groove.”

The intimal pad in the 2 month bifurcation was very similar to the intimal pad at the apex of a naturally occurring bifurcation (between the internal and external carotid arteries) excised from a similar dog. Meanwhile, the “groove” in the 2 month bifurcation was histologically very similar to an early stage aneurysm in hypertensive rats (3, 7): the internal elastic lamina was disrupted, the endothelial layer was missing, the media was thinned, and the number of smooth muscle cells was reduced. Furthermore, a “groove” immediately distal to an intimal pad is a pattern found both in the rat model and clinically in human bifurcation aneurysms (7, 10). We do not yet know whether or not the tissues in our created bifurcations would have ultimately undergone permanent synthetic and structural changes to form healthy bifurcations or full-blown aneurysms. However, this model system allows detailed investigation of how hemodynamics affects the processes that ultimately lead to long-term remodeling of the vessel wall.

The feasibility of applying this model system in smaller animals, such as rabbits, has been explored. In preliminary experiments, we have successfully created the same anastomosis in rabbits, albeit with limitations of the current methodology: 1) reduced success rate of quality bifurcations because of the fragility and small sizes of rabbit vessels, and 2) decreased accuracies in geometry construction and CFD calculations because of small vessel sizes and limited imaging resolution.

In summary, we demonstrated a new method to directly correlate the up- and downstream events for flow-mediated vascular responses. We characterized local morphological changes in response to specifically manipulated hemodynamics at a surgically created vessel bifurcation. The hemodynamic microenvironment was characterized in detail via image-based CFD calculations and correlated with histology of the remodeled vessel wall. We pinpointed specific aspects of the complex hemodynamics at the wall opposing an impinging flow and its role in the observed vascular responses. The impingement region was characterized by low to normal WSS and high WSSG and associated with development of an intimal pad; the adjacent flow acceleration region, subjected to both high WSS and high WSSG, was associated with the formation of a “groove” showing features of an early aneurysm.

Acknowledgments

This work was supported by the NIH under Grant NS047242, the NSF under Grant BES-0302389, and by the Cummings Foundation. We thank L. Nelson Hopkins, M.D. for inspiring the support that made this multidisciplinary work possible; William L. Young for critical suggestions on this manuscript; Ann Marie Paciorek for assistance in animal surgery and care; Ling Gao, Ph.D. for contributions to the article; Scott W. Woodward, Paul H. Dressel, and Debra J. Zimmer for technical assistance; and Rekha V. Tranquebar and Petru M. Dinu for assistance with image reconstruction.

Footnotes

Disclosure: John Kolega is a consultant for Boston Scientific (for a project not directly related to the topic of this article). Elad I. Levy has received industry grant support from and is Speaker Honoraria for Boston Scientific and Cordis.

Contributor Information

Hui Meng, Departments of Neurosurgery and Mechanical and Aerospace Engineering, University at Buffalo, State University of New York, Buffalo, New York Toshiba Stroke Research Center, University at Buffalo, State University of New York.

Daniel D. Swartz, Departments of Pediatrics and Neurosurgery, University at Buffalo, State University of New York, Buffalo, New York Toshiba Stroke Research Center, University at Buffalo, State University of New York.

Zhijie Wang, Department of Mechanical and Aerospace Engineering, University at Buffalo, State University of New York, Buffalo, New York Toshiba Stroke Research Center, University at Buffalo, State University of New York.

Yiemeng Hoi, Department of Mechanical and Aerospace Engineering, University at Buffalo, State University of New York, Buffalo, New York Toshiba Stroke Research Center, University at Buffalo, State University of New York.

John Kolega, Department of Pathology and Anatomical Sciences, University at Buffalo, State University of New York, Buffalo, New York Toshiba Stroke Research Center, University at Buffalo, State University of New York.

Eleni M. Metaxa, Department of Mechanical and Aerospace Engineering, University at Buffalo, State University of New York, Buffalo, New York Toshiba Stroke Research Center, University at Buffalo, State University of New York.

Michael P. Szymanski, Department of Mechanical and Aerospace Engineering, University at Buffalo, State University of New York, Buffalo, New York Toshiba Stroke Research Center, University at Buffalo, State University of New York.

Junichi Yamamoto, Department of Neurosurgery, University at Buffalo, State University of New York, Buffalo, New York Toshiba Stroke Research Center, University at Buffalo, State University of New York.

Eric Sauvageau, Department of Neurosurgery, University at Buffalo, State University of New York, Buffalo, New York

Elad I. Levy, Departments of Neurosurgery and Radiology, University at Buffalo, State University of New York, Buffalo, New York Toshiba Stroke Research Center, University at Buffalo, State University of New York.

References

  • 1.Cebral JR, Castro MA, Appanaboyina S, Putman CM, Millan D, Frangi AF. Efficient pipeline for image-based patient-specific analysis of cerebral aneurysm hemodynamics: Technique and sensitivity. IEEE Trans Med Imaging. 2005;24:457–467. doi: 10.1109/tmi.2005.844159. [DOI] [PubMed] [Google Scholar]
  • 2.Flaharty FV, Pierce J. Localizing factors in experimental atherosclerosis. In: Likoff WSB, Insull W, editors. Atherosclerosis and Coronary Heart Disease. New York: Grune & Stratton; 1972. pp. 40–84. [Google Scholar]
  • 3.Fukuda S, Hashimoto N, Naritomi H, Nagata I, Nozaki K, Kondo S, Kurino M, Kikuchi H. Prevention of rat cerebral aneurysm formation by inhibition of nitric oxide synthase. Circulation. 2000;101:2532–2538. doi: 10.1161/01.cir.101.21.2532. [DOI] [PubMed] [Google Scholar]
  • 4.Gibbons GH, Dzau VJ. The emerging concept of vascular remodeling. N Engl J Med. 1994;330:1431–1438. doi: 10.1056/NEJM199405193302008. [DOI] [PubMed] [Google Scholar]
  • 5.Glagov S, Zarins C, Giddens DP, Ku DN. Hemodynamics and atherosclerosis. Insights and perspectives gained from studies of human arteries. Arch Pathol Lab Med. 1988;112:1018–1031. [PubMed] [Google Scholar]
  • 6.Hassan T, Timofeev EV, Saito T, Shimizu H, Ezura M, Matsumoto Y, Takayama K, Tominaga T, Takahashi A. A proposed parent vessel geometry-based categorization of saccular intracranial aneurysms: Computational flow dynamics analysis of the risk factors for lesion rupture. J Neurosurg. 2005;103:662–680. doi: 10.3171/jns.2005.103.4.0662. [DOI] [PubMed] [Google Scholar]
  • 7.Hazama F, Kataoka H, Yamada E, Kayembe K, Hashimoto N, Kojima M, Kim C. Early changes of experimentally induced cerebral aneurysms in rats. Light-microscopic study. Am J Pathol. 1986;124:399–404. [PMC free article] [PubMed] [Google Scholar]
  • 8.Jou LD, Wong G, Dispensa B, Lawton MT, Higashida RT, Young WL, Saloner D. Correlation between lumenal geometry changes and hemodynamics in fusiform intracranial aneurysms. AJNR Am J Neuroradiol. 2005;26:2357–2363. [PMC free article] [PubMed] [Google Scholar]
  • 9.Karner G, Perktold K, Hofer M, Liepsch D. Flow characteristics in an anatomically realistic compliant carotid artery bifurcation model. Comput Methods Biomech Biomed Engin. 1999;2:171–185. doi: 10.1080/10255849908907986. [DOI] [PubMed] [Google Scholar]
  • 10.Krex D, Schackert HK, Schackert G. Genesis of cerebral aneurysms-an update. Acta Neurochir (Wien) 2001;143:429–448. doi: 10.1007/s007010170072. [DOI] [PubMed] [Google Scholar]
  • 11.Ku DN. Blood flow in arteries. Annu Rev Fluid Mech. 1997;29:399–434. [Google Scholar]
  • 12.Low M, Perktold K, Raunig R. Hemodynamics in rigid and distensible saccular aneurysms: A numerical study of pulsatile flow characteristics. Biorheology. 1993;30:287–298. doi: 10.3233/bir-1993-303-413. [DOI] [PubMed] [Google Scholar]
  • 13.Perktold K, Hofer M. Mathematical modeling of flow effects and transport processes in arterial bifurcation models. In: Xu XY, Collins MW, editors. The Haemodynamics of Arterial Organs: Comparison of Computational Predictions with in Vivo and in Vitro Data. Southampton: WIT; 1999. pp. 43–84. [Google Scholar]
  • 14.Perktold K, Peter R, Resch M. Pulsatile non-Newtonian blood flow simulation through a bifurcation with an aneurysm. Biorheology. 1989;26:1011–1030. doi: 10.3233/bir-1989-26605. [DOI] [PubMed] [Google Scholar]
  • 15.Sekhar LN, Heros RC. Origin, growth, and rupture of saccular aneurysms: A review. Neurosurgery. 1981;8:248–260. doi: 10.1227/00006123-198102000-00020. [DOI] [PubMed] [Google Scholar]
  • 16.Steiger HJ. Pathophysiology of development and rupture of cerebral aneurysms. Acta Neurochir Suppl (Wien) 1990;48:1–57. [PubMed] [Google Scholar]
  • 17.Steinman DA. Image-based computational fluid dynamics modeling in realistic arterial geometries. Ann Biomed Eng. 2002;30:483–497. doi: 10.1114/1.1467679. [DOI] [PubMed] [Google Scholar]
  • 18.Steinman DA, Milner JS, Norley CJ, Lownie SP, Holdsworth DW. Image-based computational simulation of flow dynamics in a giant intracranial aneurysm. AJNR Am J Neuroradiol. 2003;24:559–566. [PMC free article] [PubMed] [Google Scholar]
  • 19.Xu XY, Collins MW, Jones CJ. Flow studies in canine artery bifurcations using a numerical simulation method. J Biomech Eng. 1992;114:504–511. doi: 10.1115/1.2894102. [DOI] [PubMed] [Google Scholar]
  • 20.Zhao SZ, Xu XY, Hughes AD, Thom SA, Stanton AV, Ariff B, Long Q. Blood flow and vessel mechanics in a physiologically realistic model of a human carotid arterial bifurcation. J Biomech. 2000;33:975–984. doi: 10.1016/s0021-9290(00)00043-9. [DOI] [PubMed] [Google Scholar]

RESOURCES