Validation of CFD Simulations of Cerebral Aneurysms With Implication of Geometric Variations

Background

Computational fluid dynamics (CFD) simulations using medical-image-based anatomical vascular geometry are now gaining clinical relevance. This study aimed at validating the CFD methodology for studying cerebral aneurysms by using particle image velocimetry (PIV) measurements, with a focus on the effects of small geometric variations in aneurysm models on the flow dynamics obtained with CFD. Method of Approach. An experimental phantom was fabricated out of silicone elastomer to best mimic a spherical aneurysm model. PIV measurements were obtained from the phantom and compared with the CFD results from an ideal spherical aneurysm model (S1). These measurements were also compared with CFD results, based on the geometry reconstructed from three-dimensional images of the experimental phantom. We further performed CFD analysis on two geometric variations, S2 and S3, of the phantom to investigate the effects of small geometric variations on the aneurysmal flow field. Results. We found poor agreement between the CFD results from the ideal spherical aneurysm model and the PIV measurements from the phantom, including inconsistent secondary flow patterns. The CFD results based on the actual phantom geometry, however, matched well with the PIV measurements. CFD of models S2 and S3 produced qualitatively similar flow fields to that of the phantom but quantitatively significant changes in key hemodynamic parameters such as vorticity, positive circulation, and wall shear stress. Conclusion. CFD simulation results can closely match experimental measurements as long as both are performed on the same model geometry. Small geometric variations on the aneurysm model can significantly alter the flow-field and key hemodynamic parameters. Since medical images are subjected to geometric uncertainties, image-based patient-specific CFD results must be carefully scrutinized before providing clinical feedback.

Introduction

Flow dynamics is a key player in the initiation and progression of vascular diseases such as atherosclerosis and cerebral aneurysms [1–4]. Numerous hemodynamic parameters, such as wall shear stress (WSS), pressure, oscillatory shear index, wall shear stress gradient, impingement size on the arterial wall, and residence time of blood, have been postulated to indicate the tendency for initiation or progression of these vascular pathologies and to evaluate the effectiveness of medical devices in the treatments of such diseases [1–4]. However, in vivo measurements of these hemodynamic parameters for patients are difficult and often cost prohibitive. The combination of noninvasive diagnostic tools (e.g. MRI, CT, or ultrasound) and image-based computational fluid dynamics (CFD) techniques provides an alternative to in vivo measurements to estimate these patient-specific hemodynamic parameters [5–12]. Such image-based CFD analysis has the potential to provide key hemodynamic feedback for prospective studies of vascular diseases and to plan for individual therapeutic options [6,11,13].

Although the application of image-based CFD is rapidly advancing, the ever-present uncertainties in CFD analysis need to be evaluated. In particular, CFD outputs such as WSS or WSS gradients are extremely sensitive to the acquired in vivo geometry. The accuracy and reproducibility of the image-based CFD geometries depend on the orientation of the subject, physiological condition of the subject, variation in vascular structure, contrast-media injection techniques, and operator-dependent decisions in converting the medical images to CFD models [14,15]. Such variations produce poor geometric renditions that can generate as much as 60% variation in hemodynamic parameters obtained using CFD, especially in complex flow regions such as bifurcation apexes, anastomoses, flow separation zones, and aneurysm inflow zones [8,15–17]. Smoothing can reduce poor geometric renditions [16], but the process is somewhat subjective, resulting in an unknown deviation from the true in vivo geometry and subsequent in vitro and CFD models. In addition, the validity of CFD results relies heavily on both temporal and spatial boundary conditions [17–19], which are not routinely available in clinical practice. Significant efforts have been made to improve image-based CFD techniques [8,14,16,20–22], but there have been insufficient efforts to validate the CFD results with experiments.

In vitro experimental studies have often been employed to investigate the hemodynamics of vascular diseases and mechanical treatment devices, as well as assisting the development of CFD techniques. Rhee et al. and Imbesi et al. explored the influence of aneurysm geometry and intervention through flow visualization techniques [23,24]. Particle image velocimetry (PIV) and particle tracking velocimetry have been utilized to study the influence of intervention on aneurysmal flow [25–29]. Direct in vivo measurements of blood flow through x-ray imaging, MRI, and ultrasound techniques have also been explored [10,30–33]. MRI and ultrasound allow noninvasive measurement of instantaneous velocities in the 3D domain. Based on the field data, velocity gradients and strain rates are obtained to determine shear stresses and shear stress gradients. However, to date, in vitro studies have been limited to 2D flow fields and scaled-up models that provide optical access. These studies experience significant difficulties in reproducing the in vivo geometries [23] and in vivo biological environments. Direct in vivo measurements pose technical shortcomings, such as inadequate resolutions to derive the flow velocity near the wall, uncertainties in wall positions and insufficient velocity vectors to estimate the derivatives in complex flow regions [10,11,30,31,34–36].

One of the clinical applications of CFD is cerebral vascular diseases such as cerebral aneurysms. Subarachnoid hemorrhage following cerebral aneurysm rupture is often catastrophic, resulting in 12.4% of patient death before patients receive medical attention [37]. Recent studies using aneurysm geometry to predict the risks of aneurysm rupture relied heavily on the imaged aneurysm geometry [38–41]. Prospective patient-specific aneurysm studies that combine medical imaging, CFD analysis, and knowledge of biological responses to hemodynamics forces can provide insight into the hemodynamics of cerebral aneurysms, scientific assessments on therapeutic planning and, ultimately, positive clinical outcomes. However, quantitative validation of image-based CFD analysis against experimental and in vivo data has, to date, not been fully addressed. Following a prior CFD study, which focused on the characteristics of the hemodynamics in an aneurysm located on a curved vessel [42], a PIV validation effort was undertaken in our lab, leading to the investigation of flow sensitivity to aneurysm geometric variations. The goals of this study were to validate our CFD results with PIV experiments using an experimental aneurysm phantom and to quantify the influence of geometric variations on the aneurysmal flow dynamics.

Method of Approach

Aneurysm Phantom Creation

A negative mold intended to mimic a spherical aneurysm was fabricated. A low melting temperature, i.e., 70°C, alloy (Cerro^®), was cast into the mold, resulting in a positive image of the vasculature. Silicone elastomer, Sylgard^® 184 (Dow Chemical), was cast around the Cerro^®. The Cerro^® was then melted out, resulting in a high quality optically accessible silicone model for PIV measurement and micro-cone-beam computer tomography (micro-CT) scanning. The dimensions of the aneurysm phantom were carefully measured. Evidently, the created phantom aneurysm was not a perfect sphere. Rather, it was slightly oblate, with the major diameter parallel to the major axis of the aneurysm orifice. Its minor diameter was 10% or 2.32 mm less than the major diameter. Such geometric imperfections arose due to tolerances in the mold fabrication and casting processes.

Reconstruction of Experimental Phantom

To conduct a CFD analysis of the experimental aneurysm phantom, we used a micro-CT system that was developed in-house to scan and reconstruct the lumen of the phantom [43–47]. With the high-resolution micro-CT system, images of phantoms were acquired at a resolution of approximately 43 μm at 2° intervals for the full 360° of rotation [43–47]. The images were processed to reconstruct the 3D lumen of the phantom [45,46]. We compared the dimensions of the reconstructed aneurysm model with the original phantom and found insignificant differences between them. The micro-CT reconstructed phantom geometry was then used as input for the CFD analysis of the model (Fig. 1).

Fig. 1.

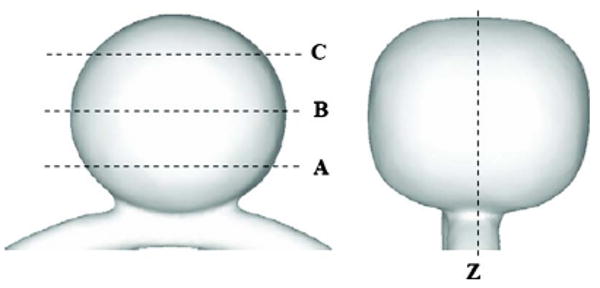
Geometry of the experimental phantom. A, B, C, and Z denote the PIV imaging planes. Plane Z is the meridian plane. Plane A is 0.25d below the center of the aneurysm. Plane B is at the center of the aneurysm, and Plane C is 0.25d above the center of aneurysm, where d is the major diameter.

Flow Loop and PIV Experiment

We performed a series of PIV experiments on the phantom to validate the CFD analysis of this model. A schematic diagram of the flow loop is shown in Fig. 2. An ultrasonic flow meter (Transonic, NY) was located in the parent vessel downstream from the phantom to measure the steady-state flow rate. The refraction of the light sheet passing through the complex, curved model surfaces was eliminated by fine tuning a 60% glycerine and 40% distilled water mixture. The working fluid was seeded with fluorescent particles (diameter 10–20 μm, Dantec, Denmark, ∼30 particles/mm³) in the PIV measurements.

Fig. 2.

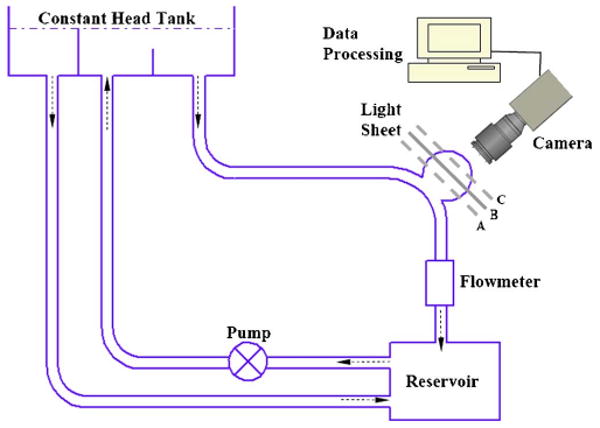
Schematic diagram of the experimental setup, with Plane B being imaged. Imaging Planes A and C required parallel shifts of the laser light sheet, and imaging Plane Z required turning the model block 90° so that the meridian plane faced the camera.

A continuous laser beam that was generated by an Argon laser passed through a Bragg cell to generate double laser pulses (∼2 ms apart). The laser light then passed though a cylindrical lens to create a light sheet with a thickness of approximately 1 mm. The light sheet intercepted the phantom and illuminated the fluorescent particles in the test region. A digital CCD camera (1280 × 1024 pixels) was placed perpendicular to the light sheet. To increase the signal-to-noise ratio, a 580-nm filter was placed in front of the camera to capture the fluorescing particle signals. The displacement of particles (approximately 10 pixels) over the double-pulse interval was computed from the 250 image pairs for every interrogation cell (40 × 40 pixels) using the Provision PIV image-processing program (IDT, Florida). Two sets of measurements were made with PIV, the first on the meridian plane (Plane Z) and the second on the three horizontal planes (Planes A, B, and C) (Fig. 1). Plane B is located on the major axis of the aneurysm dome. Plane A is 0.25d below Plane B, and Plane C is 0.25d above Plane B, where d is the major diameter of the aneurysm. Our PIV measurements yielded consistent results over repeated experiments. Numerous additional planes and orientations (not discussed here) were obtained to further validate the CFD results.

CFD Technique

Commercial mesh generation software (ICEM-CFD, NY) was used to generate hybrid meshes, consisting of both prism and tetrahedral grids. The Navier-Stokes equations were solved using commercial finite volume software (StarCD^®, CD-adapco, NY) with second-order accuracy. Grid independence was achieved with several refinements of grids, resulting in a grid size of approximately 0.5 mm with 600,000 cells. Near the wall, we refined the grids to 0.05 mm in order to better capture the near wall flow dynamics. We assumed steady state, incompressible, laminar flow of a Newtonian fluid in a rigid wall model. A fluid density of 1151 kg/m³ and viscosity of 12.88 cP, which were the same as the PIV experimental values, were used in the CFD simulation. These fluid properties were not aimed at matching those of blood but, rather, to match the index of refraction of the phantom model in the PIV experiment. We then used the same fluid properties in the CFD simulations to enable direct comparison with the PIV results. A Reynold's number of 160 in the parent vessel, typical of cerebral circulation, was used in all CFD simulations and PIV experiments. To account for the differences in fluid properties between the experiment and physiological condition, the equivalent physiological WSS values were calculated from the WSS values using the CFD simulations according to the laws of fluid dynamic similarity

$${\tau }_{\text{wss},\text{physio}}=\frac{{\rho }_F}{{\rho }_B}{\left(\frac{{\mu }_B}{{\mu }_F}\right)}^2{\tau }_{\text{wss},\text{CFD}}[\text{dyn}/{\text{cm}}^2],$$ (1)

where τ_wss,physio is physiological WSS value; τ_wss,CFD is WSS value from CFD results; ρ is density; μ is viscosity; subscripts B and F denote the properties of blood and working fluid in CFD simulations, respectively.

To evaluate the flow differences between models, we calculated the positive circulation in each of the planes of interest. The values of CFD-derived hemodynamic parameters were given as a percentage difference from the PIV measured values in the phantom. The percentage differences in the hemodynamic parameters were calculated based on the differences in hemodynamic parameters between the aneurysm models and phantom, reference to the phantom.

CFD Aneurysm Geometries

To explore flow sensitivity in aneurysm geometric variations, three idealized aneurysm geometries were investigated using CFD in addition to the reconstructed phantom. These included an ideal spherical aneurysm (S1) and two slightly oblate spheroid aneurysms (S2 and S3) that were similar to the experimental phantom. All of the aneurysms were located on an identical cylindrical curved parent vessel. The parent vessel diameter was 4.75 mm, the parent vessel curvature was 0.0667 mm⁻¹, and the aneurysm neck size (major axis of the orifice) was 12.56 mm. The geometric parameters of all four models are given in Table 1.

Table 1. Dimensions of the aneurysm geometry.

	S1 (Sphere)	Phantom (oblate spheroid)	S2 (oblate spheroid)	S3 (oblate spheroid)
Major aneurysm diameter (mm)	21.30	21.53	21.53	22.00
Minor aneurysm diameter (mm)	21.30	19.21	19.21	19.63
Aneurysm volume (mm3)	5092	4970	4588	4970

The major diameter was measured on the major axis of the spheroid, parallel to the major axis of the aneurysm orifice. Aneurysm S1 was a perfect sphere. Aneurysm S2 had the same major and minor diameters as the experimental phantom. Aneurysm S3 had the same volume as the experimental phantom. Both S2 and S3 had the same neck size as the phantom. The other geometric parameters were kept unchanged from the phantom.

Flow Parameters

To compare the flow fields in the phantom from the PIV measurements with the flow fields in the aneurysm geometries from the CFD results, we evaluated important flow parameters that could be obtained from the PIV measurements. The PIV results only provided the in-plane velocity vectors of the phantom geometry. From these in-plane velocity vectors, we derived the vorticity contours of the phantom geometry. Similarly, from the CFD results, we also plotted the velocity vectors and vorticity contours of all the aneurysm models and compared them against the PIV results (Figs. 3–5). Moreover, a global, physically meaningful, and easily measurable flow quantity would facilitate a simple definitive comparison between the flow fields in different aneurysm models. To this end, we considered the positive circulation (Γ+) in each plane of interest. The positive circulation is defined as

Fig. 3.

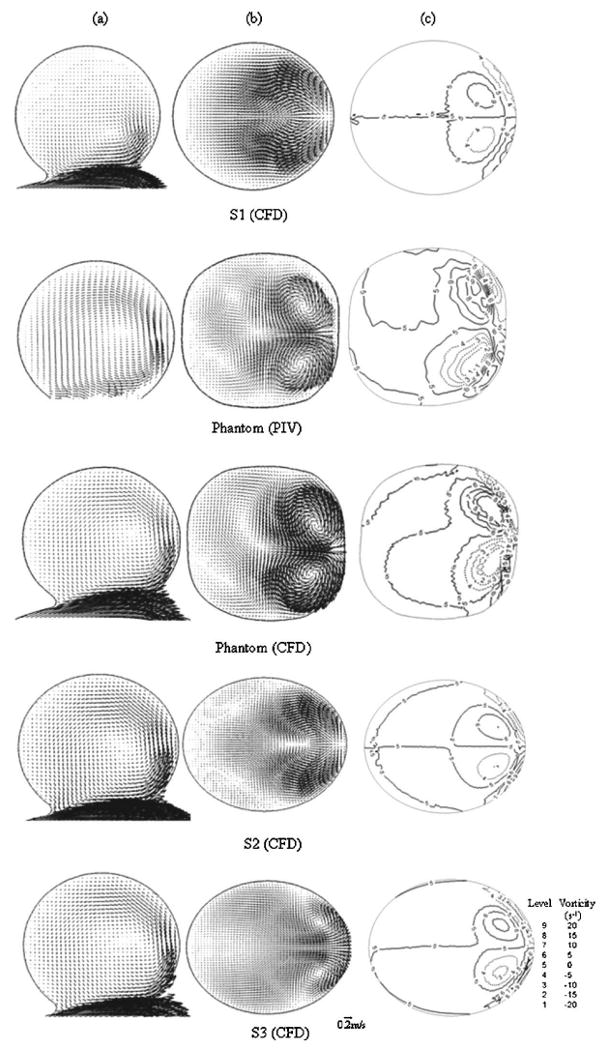
Comparison of (a) velocity fields in Plane Z, (b) velocity fields, and (c) vorticity contours in Plane B for various models

Fig. 5.

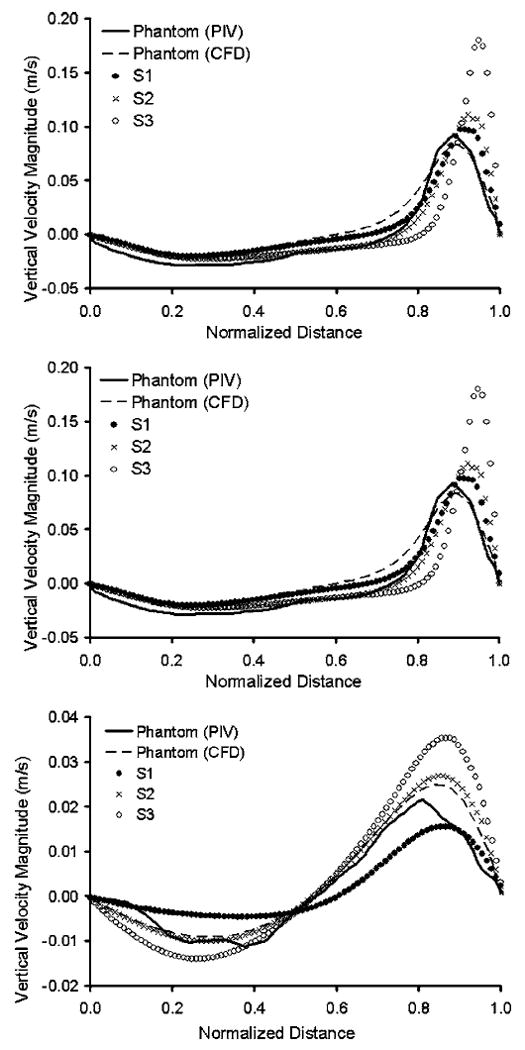
(a)–(c) Variations of magnitude of vertical velocity component in Plane Z, along three horizontal lines, marked as A, B, and C, obtained from intersection with Planes A, B, and C

$$\Gamma +=\int [(\nabla \times \text{V})\cdot \widehat{n}{]}_{\text{positive}}dA[{\text{m}}^{\text{2}}/\text{s}]$$ (2)

where V is the velocity and nˆ is the normal vector to the plane enclosed by the boundary. The integration path was along the aneurysm boundary. We chose to measure only the positive circulation and not the total circulation enclosed by the aneurysm wall, since the latter is inevitably zero due to the zero velocity at the wall. Negative circulation has a different direction but the same magnitude as positive circulation. The positive circulation is a measure of the strength of the counterclockwise vortices in the plane and is a direct measure of the integrated counterclockwise rotation of the aneurysmal flow. Finally, we compared the values of positive circulation in different planes and used them as a measure of the differences in flow patterns as a result of geometric variations.

Results and Discussion

Validation of CFD of an Ideal Spherical Aneurysm Model Using an Imperfect Phantom

In our initial attempt to validate our CFD results of the ideal spherical aneurysm S1, we conducted PIV measurements on the phantom, which were intended to mimic S1. The CFD results on S1 and the PIV results on the phantom are compared in the top two rows of Fig. 3. As seen from their velocity fields in the meridian plane Z (Fig. 3(a)), in both cases, flow entered the aneurysm at the distal neck, formed a coherent vortex, and exited the aneurysm at the proximal neck. This primary flow structure is consistent with observations by other researchers [26,27]. Furthermore, our PIV result in Plane B of the phantom also revealed pronounced secondary flow structures in the aneurysm cavity as shown in the second row of Fig. 3(b). Here, a secondary flow impinged on the distal side of the aneurysm wall, split symmetrically, and rolled up into a pair of counter-rotating vortices situated near the distal side of the aneurysm. Next to these counter-rotating vortices, weak tertiary vortex structures can be seen. These structures were quite different from the CFD results for S1, where these impingement-roll-up type of structures were absent in the velocity field in Plane B (Fig. 3(b), top row). To identify vortex structures more precisely, we plotted vorticity contours in Plane B for all models (Fig. 3(c)). The vortices in Plane B of S1 (Fig. 3(c), top row) were much weaker than the vortices in Plane B of phantom (PIV) (Fig. 3(c), second row).

Further quantitative comparisons between the idealized spherical aneurysm and experimental phantom were made for Planes A and C as well. Figure 4 shows the vorticity contours in Planes A, B and C, with the top two rows being S1 (CFD) and the phantom (PIV). It is clear that the dominant vortex structures in S1 were weaker than those in the phantom in Planes A to C parallel to the orifice. The positive circulation values in S1 were significantly smaller as compared to the values in the phantom geometry in Planes A to C. The differences in positive circulations between the two models, normalized by the value of the phantom (PIV), are given in Table 2, second column.

Fig. 4.

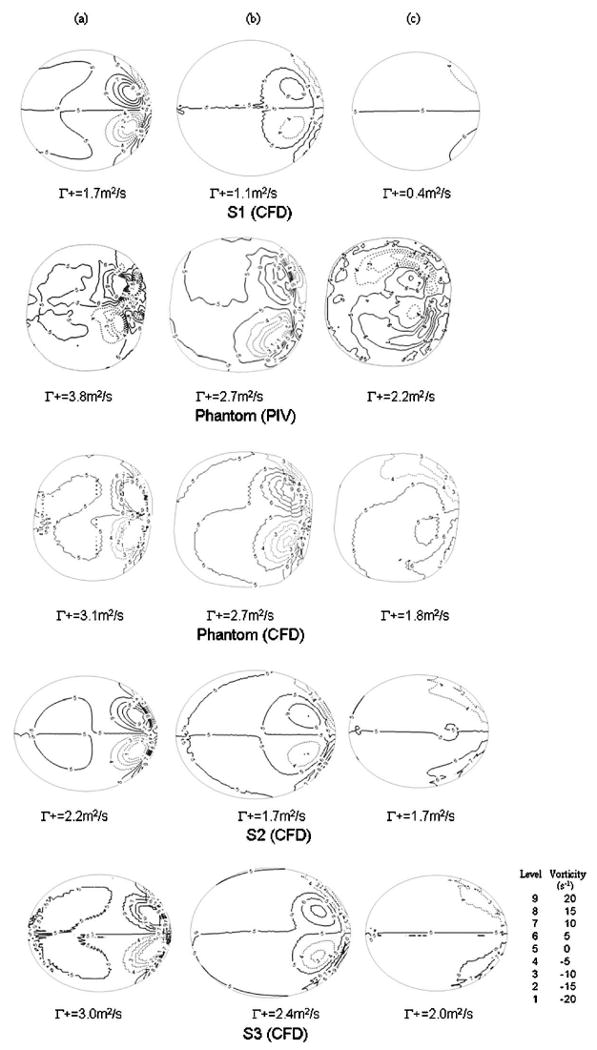
In-plane vorticity contours and positive circulation values in (a) Plane A, (b) Plane B, and (c) Plane C for various models. (Solid lines represent positive vortex; dashed lines represent negative vortex).

Table 2. Differences in positive circulation between the aneurysm geometries in Planes A, B, and C, normalized by the values in Phantom (PIV).

	S1 vs phantom (PIV)	Phantom (CFD) vs phantom (PIV)	S2 vs phantom (PIV)	S3 vs phantom (PIV)
Plane A	−56%	−18%	−42%	−21%
Plane B	−59%	0%	−37%	−11%
Plane C	−82%	−18%	−23%	−9%

Besides comparisons of the in-plane vorticity contours and positive circulation, which highlighted the secondary flow structure in horizontal planes, we also examined the primary aneurysmal flow structure in the meridian plane Z. In Fig. 5, we plotted the magnitude of the vertical velocity component in Plane Z along three horizontal lines marked as A, B, and C, obtained from intersection with Planes A, B, and C. A solid line represents the phantom (PIV) results, while closed circles represent the S1 (CFD) results. Clearly, the phantom (PIV) had a stronger flow on both the upward motion on the distal side and the downward motion on the proximal side (Figs. 5(b) and 5(c)).

We postulated that the discrepancies observed in the flow between the CFD of S1 and the PIV measurements were caused mostly by the different geometries of S1 and the experimental phantom. Therefore, if one relies on experimental measurements of an imperfect replica of the computational geometry to validate CFD simulations, the comparison results will be confusing and probably misleading.

Validation of CFD Results Using Actual Phantom Geometry

With a focus on checking the validity of our CFD techniques, we eliminated the geometric inconsistencies by performing CFD simulations on the phantom geometry itself. The computational geometry was obtained from micro-CT imaging of the phantom [44,45,47,48]. The geometric differences between the reconstructed aneurysm model and the original phantom were insignificant. The CFD results of the phantom geometry were then validated against PIV measurements.

As shown in Fig. 3, the CFD results of the phantom (Fig. 3, third row) captured the same primary and secondary vortex flow patterns as the PIV measurements (Fig. 3, second row), providing much better agreement with the PIV measurements than the CFD did for the S1 geometry. Furthermore, we plotted the vorticity contours and the values of positive circulation of the phantom (CFD) in Planes A, B, and C in the third row of Fig. 4. Their agreement with the PIV measurements was also quite good. Differences in the positive circulation between the CFD and PIV results of the phantom in these planes are given in the third column of Table 2. In addition, we plotted the magnitude of the vertical velocity component along lines A, B, and C in Plane Z for the phantom (CFD) in the dashed lines in Fig. 5. Clearly, it agreed very well with the PIV measurements (solid lines). From these comparisons, we are confident that our CFD provided a reasonably accurate description of the aneurysmal flow in the experimental geometry.

Exact agreement between CFD and PIV results is nearly impossible due to experimental uncertainties. For example, there could be misalignment in the positions and orientations of the planes of interest in the PIV and CFD results. Further reduction in the discrepancies between the CFD and PIV results of the phantom would be difficult and not worth pursuing.

Sensitivity to Small Geometric Variations

To study the sensitivity of flow to small geometric variations, we conducted CFD analysis on two variations of the phantom (S2 and S3) and compared these results with the PIV measurements of the original phantom. Results were displayed in the bottom two rows in Fig. 3 and 4 and plotted in Fig. 5 using crosses and open circles. From these plots, we could see gross similarity among phantom (PIV), phantom (CFD), S2 (CFD), and S3 (CFD). All of these aneurysm models presented a pair of counter-rotating vortices in Planes A, B, and C with consistent signs. In Fig. 4, the values of positive circulation in all aneurysm models decreased from Plane A to C. Such distributions of positive circulation showed that the strength of the secondary flow became weaker and the vortices were damped as the flow moved further away from the aneurysm neck towards the aneurysm dome. Despite the similarity in flow field among the phantom, S2 and S3, differences were revealed in closer examinations.

In S2, the volume of the aneurysm cavity was 8% less than that of the phantom. Its positive circulations in Planes A, B, and C were 42%, 37%, and 23% less than the phantom (PIV), respectively (Table 2). In S3, both the major and minor diameters were 2% more than those of the phantom (PIV) and its positive circulations were 21%, 11%, and 9% less than the phantoms in Planes A to C, respectively (Table 2).

Because of its significance in vascular remodeling and pathogenesis, we further examined WSS from the CFD results of the phantom, S2 and S3. We found that the maximum WSS was located at the distal side of the aneurysm neck in all models, but the values differ significantly, as shown in Table 3. Model S2, although having the same major and minor diameters of the phantom, produced greater differences in maximum WSS than model S3. Upon closer examination of the orifice shapes, we found that the orifice shape of S3 is actually closer to the phantom, despite that its orifice size is slightly larger than both the phantom and S2. This shows that WSS is very sensitive to the local geometry shape.

Table 3. Wall shear stress and WSS differences between aneurysm geometries of Phantom, S2 and S3. (WSS values were scaled to physiological conditions.).

	Maximum WSS (dy/cm2)	Difference with phantom (CFD)
Phantom (CFD)	59.8
S2 (CFD)	34.7	−42%
S3 (CFD)	42.7	−29%

Although the geometric differences among S2, S3, and the phantom were rather small, variations in the flow-field and the hemodynamic parameters from the CFD results were quite appreciable. Between S2 and S3, we found that S3 (which preserved the volume of the phantom) had a flow field, positive circulation, and WSS that were closer to those of the phantom.

Importance of Geometry

Our data illustrate the importance of producing an exact experimental replica of the computational geometry for validation. A slight geometrical variation in the experimental replica can result in appreciable changes in the flow field and even more in velocity derivatives and hemodynamic parameters. Near-wall hemodynamic parameters such as WSS are especially sensitive to variations in geometry [17,49]. Thus, to validate the CFD results, it is important to adopt the correct geometry. In addition, clinical diagnostic imaging techniques and the process of image reconstruction may also remove small details from the true vascular geometry [9,16,20,21,40]. Such differences between the image-based CFD geometry and the true vascular geometry could easily exceed the differences among the experimental phantom, S1, S2, and S3 in this study. Consequently, the CFD analysis of patient-specific geometry may not accurately predict the in vivo hemodynamic values [16,21,50]. If clinicians are to be guided by image-based CFD results, reasonable bounds need to be placed on the accuracy of such feedback.

Inherent Limitations of CFD

CFD techniques have other inherent limitations besides the high sensitivity to geometry, which our results underscore. The finite number of grids is unable to fully resolve the actual surface of the model. Inaccurate pulsatile waveforms used as boundary conditions, rigid wall assumptions, uncertainties in flow rate among the vessel branches, limited accuracy of the algorithms, inadequate temporal resolution in pulsatile flow, and the Newtonian fluid assumptions may all affect the accuracy of CFD results to various degrees [6,19,35,13]. However, computational geometry is the single most important factor in determining the accuracy of flow-field predictions [6,8,35,50]. The validity of image-based CFD results relies on whether the computational domain accurately represents the anatomy of vasculature. Any manual or semi-automatic process in constructing the geometry from medical images can introduce geometric variations [9,20,21,33]. Hence, validation of patient image-based CFD results is particularly challenging due to geometric uncertainties.

Conclusions

Our CFD results on the aneurysm phantom compared very well with PIV measurements. CFD simulation results can closely match by experimental measurements, as long as both were performed on the same model. Small geometric variations on the aneurysm model can significantly alter the flow-field and key hemodynamic parameters. Since medical images are subjected to geometric uncertainties, image-based patient-specific CFD results must be carefully scrutinized before providing clinical feedback.