Absolute Metabolite Concentrations and Implied Enzyme Active Site Occupancy in Escherichia coli

Abstract

Absolute metabolite concentrations are critical to a quantitative understanding of cellular metabolism, as concentrations impact both the free energies and rates of metabolic reactions. Here we use liquid chromatography-tandem mass spectrometry to quantify more than 100 metabolite concentrations in aerobic, exponentially growing E. coli with glucose, glycerol, or acetate as the carbon source. The total observed intracellular metabolite pool is approximately 300 mM. A small number of metabolites dominate the metabolome on a molar basis, with glutamate most abundant. Metabolite concentration exceeds K_m for most substrate-enzyme pairs. An exception is lower glycolysis, where concentrations of intermediates are near the K_m of their consuming enzymes and all reactions are near equilibrium. This may facilitate efficient flux reversibility given thermodynamic and osmotic constraints. The data and analyses presented here highlight the ability to identify organizing metabolic principles from systems-level absolute metabolite concentration data.

Introduction

Chromatography-mass spectrometry technologies enable simultaneous measurement of numerous intracellular metabolites from extracts of cultured cells^1–3. This capability is being increasingly widely applied to map relative changes in cellular metabolite concentrations induced by genetic and environmental perturbations^4–7. While relative concentration changes can be informative, knowledge of absolute metabolite concentrations is a critical complement, and as such, there is an increasing focus on determining absolute intracellular concentrations^8–10.

Flux directions depend on absolute metabolite concentrations based on the equation

$$\mathrm{\Delta }\mathrm{G}=\mathrm{\Delta }{\mathrm{G}}^{0,}+\text{RT}\text{ln}\mathrm{Q}$$

where Q is the reaction quotient, i.e., the ratio of the chemical activities of products and reactants within the compartment where the reaction is occurring. The second law of thermodynamics dictates that net flux occurs in the direction of ΔG < 0. Thus, flux direction is fundamentally and directly controlled by absolute metabolite concentrations (and the associated chemical activities of metabolites).

The relationship between metabolite concentrations and flux directions opens the door to inferring unknown flux directions from metabolite concentrations, and similarly to applying known flux directions and metabolite concentrations to place bounds on unknown metabolite concentrations. These concepts are formalized in network-embedded thermodynamic analysis^11–13 (NET) and thermodynamics-based metabolic flux analysis^{14, 15} (TMFA), which can be used to relate cellular metabolite concentrations and flux directions in a comprehensive manner by taking into account every annotated metabolite and enzymatic reaction in an organism’s genome. Resulting assessments of reaction thermodynamics may be applied to identify potential sites for metabolic regulation, based on the heuristic that regulated reactions are typically highly thermodynamically favored, and therefore functionally irreversible¹³.

In addition to enabling thermodynamic analysis of steady-state metabolism, absolute metabolite concentrations are critical to understanding metabolic dynamics. Absolute metabolite quantitation is necessary for the direct determination of flux^{16, 17}. Relaxation times of metabolic pools after small perturbations from steady-state occur with half-times related directly to fluxes and inversely to concentrations^{18, 19}. Absolute metabolite concentrations also dictate whether enzyme sites are largely filled or empty, and thus the sensitivity of reaction rates to changes in the concentrations of substrates, products, and competitive inhibitors.

Knowledge of both relaxation times (the time it takes a metabolite pool to turn over) and enzyme saturation levels are critical to modeling metabolic dynamics. Understanding relaxation times can allow one to combine reactions that are reliably fast relative to the cellular phenotype of interest, treating rapidly converting metabolite pools as a single pool.¹⁹ Understanding the extent of saturation can allow one to reduce Michaelis-Menten equations into simpler expressions, by omitting (taking as unity) terms for substrates that are reliably saturating, and by simplifying terms for substrates that are never saturating as first-order approximations. This facilitates otherwise intractable parameter identification challenges in building dynamic Michaelis-Menten models of metabolism^{20, 21}. Prokaryotic cells are particularly well suited to global thermodynamic analysis, as well as to assessing enzyme site saturation, because interpretation of absolute metabolite concentration data from eukaryotic cells is complicated by their extensive compartmentalization. In particular, in eukaryotic cells, flux directions and extent of enzyme saturation may vary between compartments. To provide a useful reference data set of absolute cellular metabolite concentrations, we accordingly selected the gram-negative bacterium E. coli, which is among the best-studied organisms from a metabolic perspective.^22–24

We elected to focus on core metabolism: reactions and metabolites that play an essential role in growth, are found in a diversity of organisms, and carry substantial flux. Using a measurement approach that enables fast metabolism quenching and applies isotopic internal standards throughout the measurement process, we obtain quantitative data on more than 100 metabolites, finding that a small number of compounds dominate the metabolome on a molar basis. We then use these absolute concentrations to examine the free energy of metabolic reactions and to determine the extent of substrate saturation of metabolic enzymes. Through these analyses, we begin to identify principles underlying the absolute abundance of different intracellular metabolites.

Results

Measurement approach

Metabolites were quantified by liquid chromatography-tandem mass spectrometry using an isotope ratio-based approach⁸. As isotope-labeled standards for many metabolites are not available, we used uniformly ¹³C-glucose media to label the intracellular metabolome of E. coli²⁵. This enabled the use of commercially available unlabeled compounds as internal standards. As many metabolites can react in solution (e.g., amines with carbonyl-containing compounds), metabolite standard mixtures were prepared freshly within 4 h of use and maintained at −20°C. To minimize the risk of standard degradation, stock solutions were limited to single metabolites, stored at −80°C, and used within 3 days of initial preparation from powder.

Absolute quantitation of the cellular species was performed by extracting labeled cells in the presence of unlabeled standards of known concentration. Internal standards were included directly in the quenching solvent. Thus, cellular metabolites and internal standards experienced similar opportunities for absorptive losses and degradation. As labeling of compounds that assimilate bicarbonate was found to be incomplete (Supplementary Table 1 and 2 online), concentrations were corrected for incomplete labeling²⁶ (see Methods). The extracts of ¹³C-glucose-grown cells were used as internal standards for quantifying the metabolome of E. coli grown on unlabeled glycerol and acetate.

To enable fast quenching of metabolism, E. coli were grown atop filters on an agarose-media support. Nutrients diffused through the agarose and filter to the cells, which grew with doubling times (77, 89, and 139 minutes in glucose (1), glycerol (2), and acetate (3)) similar to, but slightly slower than, those in comparable liquid media (Supplementary Fig. 1 online). Cells were separated from most growth media and quenched by transfer of the filter into cold organic solvent.

The solvent mixture of 40:40:20 acetonitrile:methanol:water with 0.1% formic acid was selected to minimize degradation of high energy metabolites such as ATP (4) and NADH (5) during the quenching and extraction process^{27, 28}. The procedure thereby enabled quantitation of energy charge and redox state. In all carbon sources, adenylate energy charge, defined as (ATP + 0.5 ADP (6))/(ATP + ADP + AMP (7)), was found to be high (> 0.9) and the NAD⁺ (8) pool was found to be substantially (~95%) oxidized.

Composition of the core E. coli metabolome

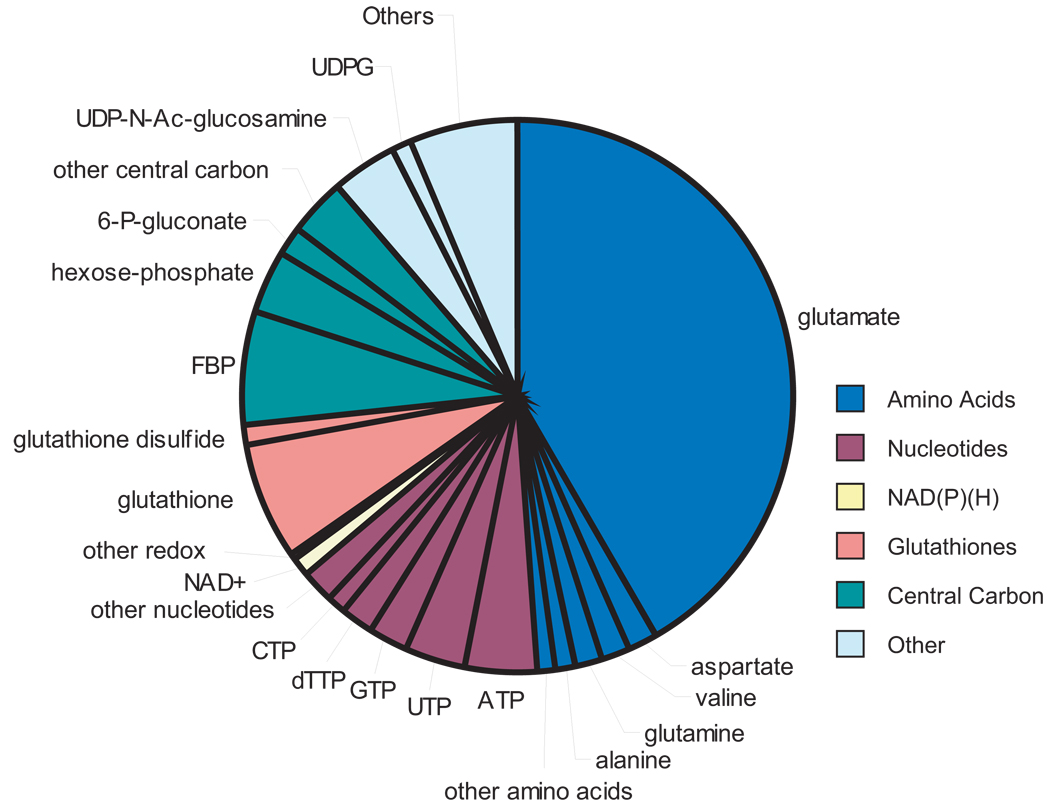
The absolute cellular concentrations of 103 metabolites were determined in glucose-fed cultures, and most were also determined in glycerol- and acetate-fed cultures (for glucose-grown cells only, see Table 1; for complete data, including error estimates, see Supplementary Table 3 online). Measured metabolites were more than 90% intracellular, not extracellular, with a few exceptions (Supplementary Table 4 online). The intracellular metabolome was dominated, on a molar basis, by a small number of abundant compound classes: amino acids (49%), nucleotides (mainly ribonucleotide triphosphates, 15%), central carbon intermediates (15%), and redox cofactors and glutathiones (9%) (Fig. 1). Glutamate (9) was the most abundant compound in each growth condition, followed in glucose-grown E. coli by glutathione (10), fructose-1,6-bisphosphate (FBP, 11), and ATP. Together the 10 most abundant compounds comprised 77% of the total molar concentration of the measured metabolome, whereas the less abundant half of measured metabolites together comprised only 1.3%. The large set of low-abundance metabolites includes metabolites of all classes.

Table 1. Intracellular metabolite concentrations in glucose-fed, exponentially growing E. coli.

For error estimates and comparable data in glycerol-fed and acetate-fed E. coli, see Supplementary Table 3 online.

metabolite	moles/L	metabolite	moles/L	metabolite	moles/L
glutamate	9.6 × 10−2	UDP-glucaronate (51)	5.7 × 10−4	N-acetyl-ornithine (79)	4.3 × 10−5
glutathione	1.7 × 10−2	ADP	5.6 × 10−4	gluconate (80)	4.2 × 10−5
fructose-1,6-bisphosphate	1.5 × 10−2	asparagine (52)	5.1 × 10−4	malonyl-CoA (81)	3.5 × 10−5
ATP	9.6× 10−3	α-ketoglutarate	4.4 × 10−4	cyclic-AMP (82)	3.5 × 10−5
UDP-N-acetyl-glucosamine (29)	9.2 × 10−3	lysine (53)	4.1 × 10−4	dCTP (83)	3.5 × 10−5
hexose-Pa	8.8 × 10−3	proline (54)	3.9 × 10−4	tyrosine (84)	2.9 × 10−5
UTP (30)	8.3 × 10−3	dTDP (55)	3.8 × 10−4	inosine-diphosphate (85)	2.4 × 10−5
GTP (31)	4.9 × 10−3	dihydroxyacetone-phosphate	3.7 × 10−4	GMP (86)	2.4 × 10−5
dTTP	4.6 × 10−3	homocysteine (56)	3.7 × 10−4	acetoacetyl-CoA (87)	2.2 × 10−5
aspartate	4.2 × 10−3	CMP (57)	3.6 × 10−4	riboflavin (88)	1.9 × 10−5
valine (32)	4.0 × 10−3	deoxyribose-5-P (58)	3.0 × 10−4	phenylalanine (89)	1.8 × 10−5
glutamine	3.8 × 10−3	isoleucine(59)+leuicine (60)	3.0 × 10−4	cis-aconitate (90)	1.6 × 10−5
6-phosphogluconate	3.8 × 10−3	AMP	2.8 × 10−4	dATP (91)	1.6 × 10−5
CTP (33)	2.7 × 10−3	inosine-monophosohate (61)	2.7 × 10−4	cytosine	1.4 × 10−5
alanine (34)	2.6 × 10−3	PRPP (62)	2.6 × 10−4	shikimate (92)	1.4 × 10−5
NAD+	2.6 × 10−3	succinyl-CoA (63)	2.3 × 10−4	histidinol (93)	1.3 × 10−5
UDP-glucose (35)	2.5 × 10−3	inosine-triphosphate (64)	2.1 × 10−4	tryptophan (94)	1.2 × 10−5
glutathione disulfide (36)	2.4 × 10−3	guanine (65)	1.9 × 10−4	dihydroorotate (95)	1.2 × 10−5
uridine (37)	2.1 × 10−3	phosphoenolpyruvate	1.8 × 10−4	quinolinate (96)	1.2 × 10−5
citrate	2.0 × 10−3	S-adenosyl-L-methionine (66)	1.8 × 10−4	ornithine (97)	1.0 × 10−5
UDP (38)	1.8 × 10−3	threonine (67)	1.8 × 10−4	dAMP (98)	8.8 × 10−6
malate (39)	1.7 × 10−3	FAD (68)	1.7 × 10−4	adenosine-phosphosulfate (99)	6.6 × 10−6
3-phosphoglycerateb	1.5 × 10−3	methionine (69)	1.5 × 10−4	myo-inositol (100)	5.7 × 10−6
glycerate (40)	1.4 × 10−3	2,3-Dihydroxybenzoic acid (70)	1.4 × 10−4	propionyl-CoA (101)	5.3 × 10−6
coenzyme A (41)	1.4 × 10−3	NADPH	1.2 × 10−4	ADP-glucose (102)	4.3 × 10−6
citrulline (42)	1.4 × 10−3	fumarate (71)	1.2 × 10−4	anthranilate (103)	3.5 × 10−6
pentose-Pc	1.3 × 10−3	phenylpyruvate (72)	9.0 × 10−5	deoxyadenosine (104)	2.8 × 10−6
Glucosamine-6-phosphate (43)	1.2 × 10−3	NADH	8.3 × 10−5	cytidine (105)	2.6 × 10−6
acetylphosphate (44)	1.1 × 10−3	N-acetyl-glucosamine-1P (73)	8.2 × 10−5	NADP+	2.1 × 10−6
gluconolactone (45)	1.0 × 10−3	serine (74)	6.8 × 10−5	guanosine (106)	1.6 × 10−6
GDP (46)	6.8 × 10−4	histidine (75)	6.8 × 10−5	adenine (107)	1.5 × 10−6
acetyl-CoA (47)	6.1 × 10−4	flavin mononucleotide (76)	5.4 × 10−5	deoxyguanosine (108)	5.2 × 10−7
carbamyl-aspartate (48)	5.9 × 10−4	4-hydroxybenzoate (77)	5.2 × 10−5	adenosine (109)	1.3 × 10−7
arginine (49)	5.7 × 10−4	dGMP (78)	5.1 × 10−5
succinate (50)	5.7 × 10−4	glycerol-3-phosphate	4.9 × 10−5

^ahexose-P denotes the combined pools of fructose-6-phosphate (110), glucose-6-phosphate (111) and glucose-1-phosphate (112)

^b3-phosphoglycerate concentration may be overestimated due to degradation of 1,3-diphosphoglycerate to 3-phosphoglycerate during sample handling.

^cpentose-P denotes the combined pools of ribose-5-phosphate (113), ribulose-5-phosphate (114), and xyulose-5-phosphate (115)

Figure 1. Composition of the measured metabolome.

The pie graph shows the molar abundance of different metabolites in glucose-fed cells. Amino acids are shown in dark blue, nucleotides in rust, NAD(P)(H) in yellow, glutathiones in pink, central carbon metabolites in dark green, and all other metabolites in light blue. Abundant metabolites are labeled. Abrevations used: ATP, adenosine-5'-triphosphate; UTP, uridine-5'-triphosphate; GTP, guanosine 5'-triphosphate; dTTP, thymidine 5'-triphosphate; CTP, cytidine-5'-triphosphate; NAD⁺, nicotinamide adenine dinucleotide; FBP, fructose-1,6-bisphosphate; 6-P-gluconate, 6-phospho-gluconate; Hexose-P, the combined pools of glucose-6-phosphate, glucose-1-phosphate, and fructose-6-phosphate; UDP-N-Ac-Glucosamine, uridine-5'-diphosphate N-acetyl-glucosamine; UDPG, uridine-5'-diphosphate glucose.

With respect to metabolite concentration changes between carbon sources, a majority of metabolites were present at significantly different concentration in glucose-fed cells than in cells fed glycerol or acetate (81% and 67% in glycerol and acetate respectively at false discovery rate < 0.05) (Supplementary Table 3 online), consistent with the presence of the preferred carbon source (glucose) having a substantial impact on metabolome composition. Somewhat fewer changed significantly between glycerol- and acetate-fed cells (51%). With a few exceptions, these changes did not reshape the overall molar metabolome composition: only four abundant metabolites (absolute concentration > 2 mM in any carbon source) changed more than 5-fold between carbon sources: 6-phosphogluconate (12), FBP, and dTTP (13) were highest in glucose-fed cells and citrate (14) was highest in acetate-fed cells. Notably, 6-phosphogluconate and FBP are only two reactions downstream of glucose assimilation and citrate only two reactions downstream of acetate assimilation.

Thermodynamics-based metabolic flux analysis (TMFA)

The availability of absolute concentration data on 103 metabolites enabled assessment of the feasible flux directions at a system level. TMFA was applied using free energies as described in reference ¹⁴ along with the metabolite concentration data and error estimates (Supplementary Table 3 online) to determine free energy ranges for all known metabolic reactions in E. coli in each carbon source. Flux direction was considered to be determined when the 95% confidence limits of ΔG excluded zero. The available data were sufficient to determine flux direction for ~ 25% of reactions. In general these reactions were strongly forward driven, with ΔG > 10 kJ/mol in ~ 66% of cases.

A reaction was considered to be feasible when the 95% confidence limits of ΔG included negative values. All reactions required for optimal biomass yield per glucose consumed were feasible. The same was true for acetate. Optimal biomass yield for growth on glycerol was not feasible, however, due to the inability to generate NADPH (15) via glycerol-3-phosphate dehydrogenase. This reaction (which is generally thought to synthesize glycerol-3-phosphate (16), rather than degrade it²⁹) was impossible, given the necessary NADP⁺(17)/NADPH ratio to allow biosynthetic reactions to proceed. However, near-optimal biomass yield using either a ubiquinone (18) dependent glycerol-3-phosphate dehydrogenase³⁰ or glycerol dehydrogenase^{31, 32} for glycerol assimilation was found to be feasible.

Growth on glucose or glycerol involves net flux from dihydroxyacetone phosphate (DHAP, 19) to phosphoenolpyruvate (PEP, 20). Growth on acetate involves the reverse. As the same enzymes are used in all cases, the thermodynamically favored flux direction must change. Because reaction free energies are invariant physical properties, this can arise only from changes in reaction quotient. The reaction quotient for DHAP forming PEP is

$$\mathrm{Q}=([\text{PEP}][\text{ATP}][\text{NADH}])/([\text{DHAP}][\text{ADP}][{\mathrm{P}}_{\mathrm{i}}][{\text{NAD}}^{+}][{\mathrm{H}}^{+}])$$

Three fundamental ratios control the flux direction: [PEP]/[DHAP], [ATP]/([ADP][P_i]), and [NADH]/([NAD⁺][H⁺]). The latter two ratios are similar in all carbon sources (assuming intracellular [P_i] and pH, which were not measured, do not change much). E. coli grown in glucose has a substantially lower [PEP]/[DHAP] ratio than cells grown in glycerol or acetate, favoring glycolytic flux; however, the [PEP]/[DHAP] ratio for cells growing on glycerol is similar to the acetate case, despite glycerol growth involving net flux towards PEP and acetate away from it. Indeed, Q_glycerol is (within error) indistinguishable from Q_acetate. This indicates that lower glycolysis is near equilibrium on both carbon sources, with ΔG approximately zero. Small changes in Q are accordingly adequate to tip the thermodynamically favored flux direction.

Given the near equilibrium of lower glycolytic reactions, properly assigning flux direction across carbon sources requires precise definition of standard free energies. In this respect, literature ΔG^0’ values may not be adequate, especially given the strong dependence of ATP hydrolysis and NADH oxidation energies on pH and ion concentrations^33–36. This led us to define a metric of standard free energy under cellular conditions that is consistent with observed metabolite concentrations and known flux directions, which we term ΔG^0,_ec for E. coli. ΔG^0,_ec is analogous to ΔG^0,, but at the intracellular pH and ionic composition of exponentially growing E. coli. We compared possible values of ΔG^0,_ec based on the metabolite concentration data (Supplementary Table 3 online) with literature values of ΔG^0, (Table 2). The literature values of ΔG^0, (Supplementary Table 5 online) and the calculated values of ΔG⁰ _ec overlap for the reactions from FBP to DHAP and from 3-phosphoglycerate (3PG, 21) to PEP, but not for the reactions converting DHAP to 3PG with concomitant ATP formation and NAD+ reduction (possibly due to mismeasurement of 3PG, see Table 2). We determined suggested values of ΔG⁰ _ec and resulting free energies of glycolytic and gluconeogenic reactions (Supplementary Table 6 online). These values result in ΔG < 0 for the forward fluxes on each carbon source, except for DHAP forming 3PG in glycerol-fed cells (where values of ΔG < 0 fall within the estimated 95% confidence interval of ΔG). For glucose-fed cells, but not glycerol- or acetate-fed ones, most reactions are clearly forward driven (95% confidence limits excluding zero). The only glycolytic reactions that were strongly forward driven (ΔG < −5 kJ/mol) were FBP formation by phosphofructokinase and its hydrolysis by fructose-1,6-bisphosphatase, and these reactions were strongly forward driven in each carbon source.

Table 2. Comparison of ΔG^0’ from literature and ΔG⁰_ec calculated from metabolite concentrations.

All calculations assume a concentration of 20 mM inorganic phosphate⁴⁷, and that intracellular pH is the same (for literature values, pH 7) in all three culture conditions. All values are in kJ/mole.

		from concentrations		Literature		Overlap
From	To	min ΔG0ec(kJ/mol)	max ΔG0ec(kJ/mol)	min ΔG0’(kJ/mol)	max ΔG0’(kJ/mol)	Min	Max
F6P + ATP	FBP + ADP	N/Aa	9.3	−22.1	−14.2	−22.1	−14.2
FBP	F6P + Pi	N/Aa	−2.2	−14.1	−10.0	−14.1	−10.0
FBP	DHAPb	21.5	29.3	10.3	23.1	21.5	23.1
DHAP + NAD + ADP + Pi	3PG + NADH +ATP	−22.9c	−40.1c	−12.6	−0.30	-	-
3PG	PEP	−2.32	4.3	−1.0	8.0	−1	4.3

^aN/A: There is no lower bound on ΔG⁰_ec using concentrations, as the reactions only need to work in one direction.

^bkJ/mole for FBP and kJ/(2 mole) for DHAP

^cA possible explanation for the requirement for a large negative ΔG⁰_ec value for this reaction is mismeasurement of one or more reactants or products. A particular possibility is that 1,3-diphosphoglycerate is hydrolyzed to 3PG during metabolome extraction, leading to erroneously high measured 3PG concentration.

Enzyme saturation

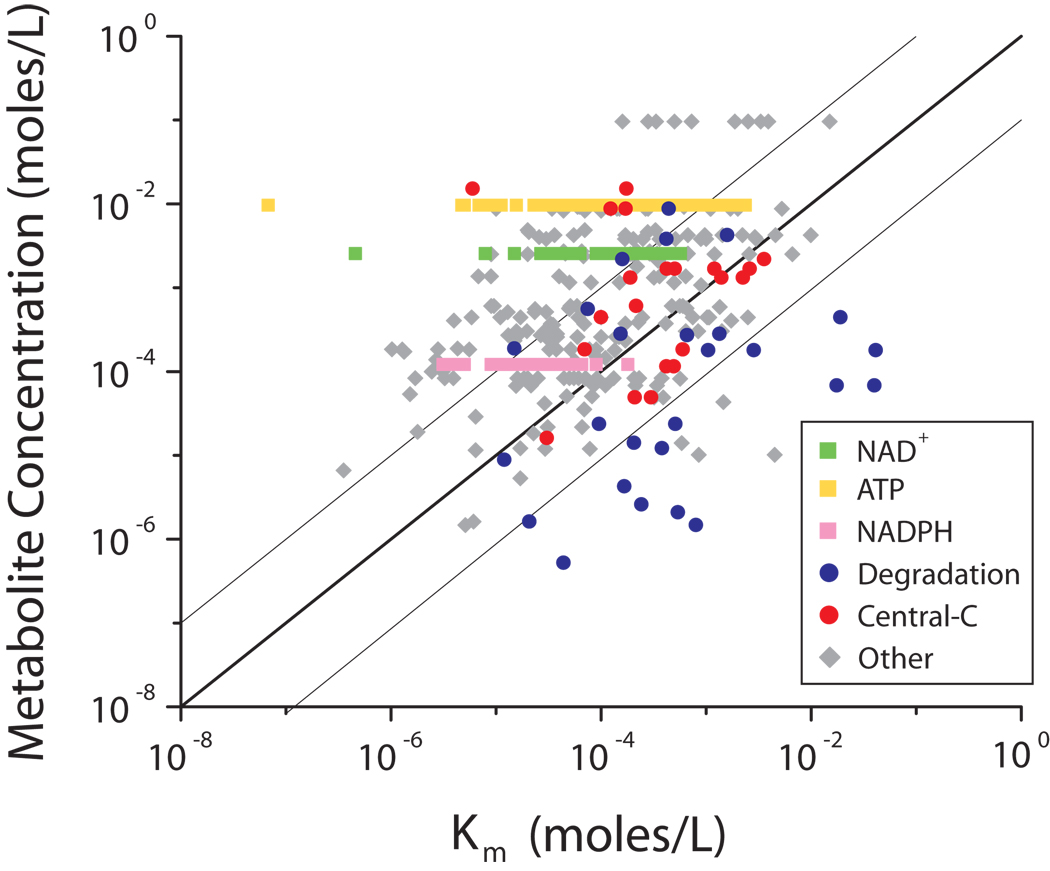
The absolute concentration of metabolites in glucose-grown cultures (Table 1) was employed to assess the extent of saturation of enzymes by their substrates, by comparing the measured concentrations to K_m values taken from the BRENDA database (Fig. 2, Supplementary Table 7 online). In a standard Michaelis-Menten enzyme mechanism, K_m is the concentration at which an enzyme active site is half-saturated with substrate. Each concentration-K_m pair that falls above and to the left of the line of unity indicate cases where the metabolite concentration exceeds K_m, and therefore the enzyme is anticipated to be > 50% saturated with substrate. A large majority of points (83%) fall to the upper-left of the line, with 59% having a concentration more than 10-fold higher than the K_m, indicating a trend towards saturation of most enzyme active sites.

Figure 2. Implied enzyme active site saturation.

The relationship of metabolite concentration and K_m of their consuming enzymes in glucose-grown E. coli. NAD⁺ is shown as green squares, ATP as yellow squares, NADPH as pinksquares, degradation reactions as blue circles, and reactions in central carbon metabolism (glycolysis, the pentose-phosphate pathway, and the TCA cycle) as orange circles. All other data are shown as grey diamonds. The dark line is the line of unity (where concentration = K_m) and the light lines denote a 10-fold deviation from the line of unity.

To gain further insight into which types of enzyme sites tended to be saturated, we examined the nature of each metabolite-enzyme pair. This revealed that the fundamental cofactors ATP and NAD⁺, which together account for 26% of the studied enzyme sites, are reliably saturating, with their concentrations typically exceeding the associated K_m values by more than 10-fold. Thus, at least under the present growth conditions, availability of these cofactors as substrates does not seem to limit enzymatic activity. NADPH, an analogous cofactor, is not as reliably saturating.

Substrate-enzyme pairs where concentration fell short of K_m (i.e., where the enzyme active site is anticipated to be largely unfilled) were dominated by enzymes catalyzing nucleotide, nucleoside, nucleobase, and amino acid degradation reactions. For example, the measured concentration of cytosine (22) was 70-fold lower than the K_m of the degradation enzyme, cytosine deaminase. Of the 26 degradation reactions in the data set, 19 had a concentration that was below the K_m of the consuming enzyme, a significant enrichment (p < 10⁻⁹ by hypergeometric test), and 14 were more than 10-fold lower than the K_m (p < 10⁻¹⁴ by hypergeometric test).

An intermediate case involved central carbon metabolic reactions (those in glycolysis, TCA cycle and the pentose-phosphate pathway), where substrate concentration and K_m tended to be similar. A notable aspect of these reactions is that many switch net flux direction depending on nutrient availability. Quantitatively, enzyme-substrate pairs from central carbon metabolism were enriched in the region of Fig. 2 between the light lines, where substrate concentration is within 10-fold of K_m (p < 0.0002 by hypergeometric test).

Discussion

Here we report systems level analysis of absolute intracellular metabolite concentrations in E. coli. The analytical approach obtained high sensitivity and specificity via MS/MS while minimizing systematic error by flash-quenching metabolism and including isotope-labeled internal standards throughout. A limitation of the analytical approach was the inability to differentiate free and macromolecule-bound metabolites, as both could be released via organic extraction. As the measured total metabolome concentration of 300 mM (100 million metabolites/cell) greatly exceeded the reported total protein concentration of 7 mM (2.4 million proteins/cell)³⁷, it is likely that the measured values largely reflect free metabolites. Consistent with this, the dataset was validated as thermodynamically feasible using TMFA. These factors give confidence in the reliability of the measured concentrations.

A striking feature of the observed data was the domination of the metabolome on a molar basis by a small number of compounds, with glutamate comprising over 40% of the total measured intracellular metabolome. Glutamate is the major nitrogen donor in the cell, distributing ~88% of the total nitrogen that ends up in biomass, largely via transamination reactions³⁸. As transamination reactions have standard free energies near zero, the high concentration of glutamate may be important for driving these reactions forward. Glutamate, however, also has an additional role as the major intracellular counter-ion to potassium³⁹. The second most abundant metabolite, glutathione, functions as an antioxidant. Thus, the two most abundant “metabolites” each have functions beyond serving as enzyme substrates. For metabolites whose sole role is to serve as enzyme substrates, concentrations were uniformly less than 22 mM, and under 1 mM in 70% of cases. Low concentrations are favorable for avoiding osmotic stress and disadvantageous spontaneous reactions.

The crowded nature of the cytosol, combined with the high costs of protein biosynthesis, favors achieving the metabolic fluxes required for growth with minimal enzyme concentrations, i.e., maximizing flux per enzyme⁴⁰. Thus, maintaining substrate concentrations high enough to saturate enzyme active sites should theoretically be beneficial. Consistent with this, most measured metabolites had concentrations that were higher than the K_m of their consuming enzymes. This was particularly true of the ubiquitous cofactors ATP and NAD⁺, but also true for measured metabolites more generally. A potential caveat is that the 103 metabolites measured here, and the associated 377 metabolite-enzyme pairs, may not be representative of the entire metabolome, as the measured compounds may be biased towards more abundant ones.

A consequence of maintaining substrate concentrations well above enzyme K_m is relative insensitivity of flux to substrate concentration. Such insensitivity could potentially lead to large swings in metabolite concentrations: flux would not be strongly activated when substrate accumulates, nor terminated when substrate concentration falls. To avoid large swings in metabolite concentrations, flux regulation by competitive inhibition, allostery, covalent modification, or control of enzyme concentrations (e.g., via transcriptional regulation) is accordingly important. Notably, competition for enzyme active sites has the potential to restore sensitivity of flux to substrate concentration, even when substrate is present at substantially above the nominal enzyme K_m. For an irreversible reaction with competitive inhibition, half-maximal reaction velocity occurs at a substrate concentration equal to K_m(1+ [I]/K_i), where [I] is the concentration of the competitive inhibitor and K_i is its dissociation constant. Such competition is a reasonable possibility, given the structural similarity of many metabolites and the ubiquitous possibility of enzyme inhibition by its product. Currently, insufficient K_i values are readily available in literature to systematically analyze the extent of competitive inhibition in E. coli. We have, however, identified a few cases where active site competition appears to occur. These include glutamate and α-ketoglutarate (23) competing for the active site of aspartate aminotransferase (with K_m of 0.90 mM and K_i of 0.15 mM respectively)⁴¹ and glutamine (24), glutamate, and aspartate (25) competing for the active site of glutamate synthase (with K_m of 0.25 and K_i of 28.0 and 1.75 mM respectively)⁴². Looking forward, the present data set provides the physiologically relevant concentrations of metabolites at which to test competitive and allosteric effects biochemically.

Given the general principle that, for desirable reactions, substrate concentrations are maintained above enzyme K_m to avoid “wasting” enzyme active sites, it is notable that substrate concentrations are close to K_m for many reactions of central carbon metabolism. We believe that this reflects constraints imposed by the bidirectional nature of central carbon metabolic pathways. One constraint involves the need for fast enzymes (i.e., ones with high k_cat) to rapidly release product. For bidirectional reactions, this precludes a very low K_m, as fast release of product in one direction implies fast release of substrate in the other (i.e., high K_m). Thus, to enable reasonably fast flux in both directions, substrate K_m in both directions must be reasonably large.

Others constraints, including thermodynamics, osmotic stress, and harmful side-reactions (like DHAP or glyceradlehyde-3-phosphate (26) forming the toxic compound methylglyoxal (27)^{43, 44}) preclude raising substrate concentrations above the relatively large K_m values required for fast bidirectional catalysis. Because the reactions from FBP to PEP are not strongly forward driven in any of the studied carbon sources, increases in the concentrations of downstream metabolites must be matched by increases in upstream ones to maintain the thermodynamic driving force. Due to the 2:1 stoichiometry between trioses and FBP, a ten-fold increase in a triose like DHAP (desirable to enhance enzyme saturation) would require a 100-fold increase in FBP to avoid changing the pathway thermodynamics. FBP is already the third most abundant compound in glucose-fed E. coli (15 mM intracellular), therefore such an increase would result in osmotic problems. The 15 mM concentration of FBP may have been evolutionarily selected to optimize the tradeoff between enzyme saturation and osmotic impact.

Consistent with the hypothesis that bidirectional enzymes are less reliably substrate-saturated than unidirectional ones, only four enzymes in central carbon metabolism are saturated with their carbon substrates, and three of these operate in only glycolysis or gluconeogenesis (not both): fructose-bisphosphatase, phosphofructokinase, and fructose-bis-phosphate aldolase A. Some putatively unidirectional enzymes of central carbon metabolism (citrate synthase, α-ketoglutarate dehydrogenase, phosphoenolpyruvate carboxylase) are not substrate saturated, however. Citrate synthase and α-ketoglutarate dehydrogenase sit at metabolic branch points between central carbon metabolism and biosynthesis. Phosphoenolpyruvate carboxylase consumes PEP, which is also used to transport carbon into the cell. Accordingly, the relatively high K_m of the central carbon metabolic enzyme may be advantageous for directing flux towards biosynthesis or transport when substrate becomes scarce. Consistent with this, the K_m of glutamate synthase for α-ketoglutarate is 17-fold lower than is the K_m of glutamate for α-ketoglutarate dehydrogenase. Data for the competing reactions in the other two cases are not available.

A more straightforward example of high enzyme K_m being advantageous for flux control arises in degradation pathways. Such pathways enable cells to catabolize end products (e.g., amino acids, nucleosides) that they scavenge from the environment or generate via macromolecule degradation, but have little utility to cells growing exponentially in minimal media. For cells grown on minimal media, we found that K_m typically exceeds substrate concentration for degradation enzymes. This provides a double check (in addition to transcriptional regulation) against disadvantageous futile cycling.

These examples highlight an emerging ability to understand the principles underlying the absolute concentrations of metabolites and the affinities of enzymes for their substrates in E. coli. A basic rule is to keep enzymes saturated without letting metabolites build up enough to have osmotic effects. Exceptions arise when the K_m values of enzymes that consume the same substrate vary in order to prioritize certain reactions or prevent deleterious ones. For the bidirectional pathways of central carbon metabolism, the need to rapidly release product in both directions and simultaneously conform to thermodynamic constraints prevents substrate concentration from climbing significantly above enzyme K_m.

Methods

Liquid chromatography-tandem mass spectrometry

Two different LC separations were coupled by electrospray ionization (ESI) to Thermo TSQ Quantum triple quadrupole mass spectrometers operating in multiple reaction monitoring (MRM) mode. The LC method coupled to positive mode ESI was hydrophilic interaction chromatography on an aminopropyl column¹; in negative mode ESI it was reversed phase chromatography with an amine-based ion pairing agent³. MRM scans were as previously reported¹. For details, see Supplementary Methods online.

Strain, media, and culture conditions

Wild-type K-12 strain NCM3722 of E. coli⁴⁵ was cultured in Gutnick minimal complete medium⁴⁶ with 4g/L of glucose, glycerol, or acetate as the carbon source. Growth of cells was as previously reported²⁶. Preparation of filter cultures is described in Supplementary Methods online. For ¹³C-glucose cultures, uniformly ¹³C-glucose (> 99% ¹³C from Cambridge Isotope Laboratories) was used for the overnight culture and the liquid and filter cultures, resulting in at least 10 doublings on uniformly ¹³C-glucose media.

Metabolite extraction

The filter cultures were grown to OD₆₅₀ of 0.35, at which point metabolism was quenched and cells extracted by dropping the filters directly into 2.5 mL of −20°C 40:40:20 acetonitrile:methanol:water with 0.1 M formic acid (acid is useful to ensure rapid and complete protein denaturation²⁸). After 15 min, filters were washed with an additional 1 mL of extraction solvent. The combined extract was neutralized with ammonium hydroxide to avoid acid-catalyzed metabolite degradation. For quantification of metabolites from cells grown on U-¹³C-glucose, metabolite standards were added to the initial 2.5 mL of extraction solution, but not the subsequent 1 mL. For other experiments (quantification of glycerol and acetate cells, determination of unlabelled fraction, and determination of metabolite excretion), standard was not added to either solution.

Quantification of glucose-grown cells

Quantification of metabolite concentrations in glucose-grown cells was largely as previously reported²⁶. Initial experiments determined appropriate concentrations of internal standards to match endogenous compound concentrations closely (maximal deviation < 10-fold). Then, on two separate days, two filter cultures were grown using U-¹³C glucose as the carbon source and extracted with a solution of 15–20 internal standards at a time in 40:40:20 acetonitrile:methanol:water with 0.1M formic acid (prepared as described in Supplementary Methods online). Quantitation was performed based on the mass spectrometry data from these four cultures, with the intracellular concentration of each metabolite determined using the ratio of the ¹³C-peak height to the ¹²C-peak height.

A complication in determining absolute metabolite concentrations based on ¹³C-labeling of endogenous species is the possibility for incomplete labeling. In closed cultures, this can generally be avoided by sufficiently prolonged labeling. In our open filter culture system, however, assimilation of unlabeled bicarbonate persistently occurs. To correct for such assimilation, we determined the fraction of each metabolite that was completely labeled. To avoid measurement error that would occur in quantitating low abundance species, we focused on high abundance compounds. The extent of labeling of these compounds can be used to deduce the extent of labeling of all compounds, based on the known connectivity of the metabolic network (Supplementary Table 2 and 8 online). The fractional labeling of these species was determined in two ways, which gave equivalent results: (1) monitoring every isotopic form in ¹³C-fed cultures and (2) comparing signal of fully ¹²C-compound from unlabeled culture to fully ¹³C-compound from ¹³C-fed culture. Details on methods for determining fractional labeling are described in detail elsewhere²⁶.

Calculation of intracellular concentration was according to the equation:

$$C_{\mathit{\text{avg}}}=\frac{R}{L}\times S\times V_1\times \frac{{\mathit{\text{DW}}}_{\mathit{\text{cell}}}}{{\mathit{\text{DW}}}_{\mathit{\text{tot}}}\times {\mathit{V}}_{\mathit{\text{cell}}}}$$

where R is the geometric mean of the ratio of the U-¹³C-metabolite peak height to the unlabeled standard peak height from replicate experiments (N ≥ 4), L is the geometric mean of all measurements of the fraction of the metabolite that was U-¹³C-labeled, S is the concentration of the standard in the extraction solution, V₁ is the volume of extraction solution containing the internal standard (2.5 mL), DW_cell is the cell dry weight (3.0 × 10⁻¹³ g), DW_tot is the total cell dry weight of the filter culture (8 × 10⁻⁴ g), and V_cell is the aqueous volume of one E. coli (3.0 × 10⁻¹³ g)²⁶. Unlabeled standard peak heights were corrected prior to the above calculation to correct for the natural abundance of carbon-13 by dividing the ¹²C-peak height by 0.989^C where 0.989 is the natural abundance of carbon-12 and C is the number of carbon atoms in the molecule. For metabolites that were ≥ 10% extracellular, reported concentrations were corrected for the fraction intracellular (see Supplementary Methods online).

Error in concentration measurements was determined by propagation of the uncertainty in R and L as standard errors in logarithmic space. The upper and lower bounds of the 95% confidence interval of the cellular metabolite concentration were calculated previously described²⁶:

$$C_{\mathit{\text{bound}}}=\text{exp}\left(\text{ln}\left(C_{\mathit{\text{avg}}}\right)\pm 1.96\times {\mathit{\text{SE}}}_{\text{ln}C}\right)$$

Quantitation of glycerol- and acetate-grown cells

To generate an internal standard for the quantification of metabolites in other growth conditions, we extracted four independent E. coli filter cultures grown on U-¹³C-glucose, and mixed the resulting extracts to obtain a cellular ¹³C-labeled internal standard. Using this internal standard (whose contents were quantified as per the procedure above), we measured the intracellular concentrations of metabolites in cells growing on acetate or glycerol as the carbon source by extracting unlabeled acetate- or unlabeled glycerol-fed filter cultures and mixing each extract in a 1:1 ratio with the cellular ¹³C-labeled internal standard. For calculations of concentrations and tests of significance, see Supplementary Methods online.

Thermodynamic Metabolic Flux Analysis

TMFA was performed largely as originally described.¹⁴ Measured metabolite concentrations (Supplementary Table 3 online) were used to constrain the TMFA model. For compounds that were quantitated in glucose-grown cells, but not glycerol- or acetate-grown cells, the upper bound for the concentration in the glycerol- or acetate-fed cells was set to 10 times the measured upper bound of the 95% confidence interval in glucose-grown cells. Unmeasured compounds were assumed to be between 1 µM and 20 mM in concentration, except for 1,3-diphosphoglycerate (27), which was assumed to be between 1 µM and 50 mM. The increased upper bound was necessary in order to allow glycolytic flux in glucose- and glycerol-fed cultures.

Figure 3.