Investigating the depth electrode-brain interface in deep brain stimulation using finite element models with graded complexity in structure and solution

Abstract

Deep brain stimulation (DBS) is an increasingly used surgical therapy for a range of neurological disorders involving the long-term electrical stimulation of various regions of the human brain in a disorder-specific manner. Despite being used for the last 20 years, the underlying mechanisms are still not known, and disputed. In particular, when the electrodes are implanted into the human brain, an interface is created with changing biophysical properties which may impact on stimulation. We previously defined the electrode-brain interface (EBI) as consisting of three structural elements: the quadripolar DBS electrode, the peri-electrode space and the surrounding brain tissue. In order to understand more about the nature of the EBI, we used structural computational models of this interface, and estimated the effects of stimulation using coupled axon models. These finite element models differ in complexity, each highlighting a different feature of the EBI’s effect on the DBS induced electric field. We show that the quasi-static models are sufficient to demonstrate the difference between the acute and chronic clinical stages post-implantation. However, the frequency-dependent models are necessary as the waveform shaping has a major influence on the activation of neuronal fibres. We also investigate anatomical effects on the electric field, by taking specific account of the ventricular system in the human brain. Taken together, these models allow us to visualise the static, dynamic and target specific properties of the DBS induced field in the surrounding brain regions.

Introduction

In recent years, deep brain stimulation (DBS) has become a widely used surgical procedure for treating a number of movement disorders and an increasing number of neurological and psychological disorders (Benabid et al., 1994;Nuttin et al., 2003;Vidailhet et al., 2005;Mayberg et al., 2005;Deuschl et al., 2006;Kupsch et al., 2006). The procedure involves the implantation of one or two quadripolar electrodes (e.g. model 3387/3389 ™, Medtronic Inc, Minneapolis, MN, USA). These electrodes are placed in condition-defined targets within the patient’s brain, and used to stimulate the brain via a train of electrical pulses which is defined by intensity, frequency and pulse-width parameters (Benazzouz et al., 2000;Rizzone et al., 2001;Benabid et al., 2002;Vitek, 2002;Dostrovsky and Lozano, 2002;Kuncel and Grill, 2004;Montgomery, Jr. and Gale, 2008;Birdno et al., 2008). However, despite the clinical success of the therapy (for a recent review, see (Benabid, 2007), its further development and application to other disorders or targets has been slowed by a number of limiting factors. Primarily, the mechanisms which elicit the observed therapeutic improvement in patients remain elusive (Lozano et al., 2002;Benabid, 2007;Kringelbach et al., 2007), despite the increasingly popular use of this treatment. This is in part due to the lack of systematic lab-based research preceding the initial use of the treatment, which was translated from ablative procedures via investigation in the operating theatre (Benabid et al., 1987). This lack of understanding slows and complicates further development and optimisation of the current procedure.

When the electrodes are implanted into the human brain for DBS, this also allows the possibility of recording neuronal activity via the implanted stimulation electrode in the form of local field potentials (Liu, 2003;Brown and Williams, 2005). In both depth recording and stimulation, an electrical signal, either from, or to the electrode, may conduct between the metal electrode and the surrounding brain volume across the electrode-brain interface (EBI). The DBS related depth EBI can be defined as consisting of (1) the implanted depth electrode; (2) the surrounding brain tissue; and (3) a peri-electrode space (PES), which is independent from the brain target and the disorder for which the electrodes are implanted for. The peri-electrode space has been shown to be a major component of the EBI, particularly as its biophysical properties are not static but evolve over time. At the acute stage post-implantation, the electrode is surrounded by cerebral spinal fluid (CSF) to form an electrode-electrolyte interface (EEI) of an electrical double layer (Rockwood, 1986) which is dynamically modulated under physiological conditions by brain pulsation (Xie et al., 2006;Priori et al., 2006). In contrast, at the chronic stage the peri-electrode space is replaced by giant cell growth (Moss et al., 2004) or the formation of microglia (Griffith and Humphrey, 2006). This encapsulation process is usually stabilized over a period of 6 - 8 weeks post-implantation.

Understanding the biophysical properties and the impact of the EBI on the signals crossing into and out of the brain is clearly an important first step to understanding more about the mechanisms underlying DBS and deep brain recording (DBR) and has clear significance for improving the signal to noise ratio of depth recording, investigating the neuronal mechanisms of DBS, and optimising the process of setting the stimulation parameters. However, investigation of the EBI in vivo is constrained by technical and ethical factors. In order to supplement physiological and morphological studies on DBS in situ, recent work has focussed on investigating the depth EBI in DBS using computational modelling to understand more about the nature of the EBI and the influence on the stimulation induced electric field (Butson and McIntyre, 2005;Butson et al., 2006;Yousif et al., 2007). This process involves at its core the use of a structural finite element (FEM) model of the geometry of the EBI which allows the quantitative visualisation of the stimulation induced electric field in the surrounding tissue. The structural model was validated by replicating experimental evidence showing that the shape and extent of the electric field created by DBS is modulated by physiological (Xie et al., 2006;Priori et al., 2006) and pathological (Moss et al., 2004;Griffith and Humphrey, 2006) factors affecting the EBI.

The primary objective of the present study is to develop FEM models of different complexity to investigate the depth EBI, and its changing properties over time post-implantation in DBS. In this paper we systemically describe the techniques of constructing a FEM model of the EBI, comparing different approaches so that others may use and extend the technique for other investigations. Computational models necessarily encompass assumptions and limitations, and as such a computational model needs not be a precise replica but ought to simplify the complexity of the system under scrutiny. The choice of the complexity of a computational model must be made based on the questions that will be studied using it. In the present study, we describe some FEM models which may be solved at different levels of complexity, and can involve the combination with additional computational models to address different features of the EBI. For instance, the very basic model was initially constructed as a quasi-static solution of the Laplace equation, therefore only accounting for the resistive properties of the tissue, which was further simplified to be homogenous and isotropic (Yousif et al., 2007;Yousif and Liu, 2007;Yousif et al., 2008a;Yousif et al., 2008b). However, as the DBS stimulation applies periodic electric pulses, the time dependence is an extremely important aspect to be modelled. For this reason the initial model needs to be expanded into the frequency domain, and focus on the solution of the Laplace equation with complex conductivity, i.e. the so-called Fourier FEM approach. This model further revealed how the features of the EBI impact not only on the amplitude, but also on the shape of this stimulus waveform in the tissue.

Furthermore, we would like to address the methodological reasons for constructing a 2 or 3-dimensional FEM model with a particular level of complexity in structure, and for increasing the complexity of the surrounding tissue in our models and looking beyond the usual DBS targets in the basal ganglia and thalamus for movement disorders (Benabid et al., 1987;Deuschl et al., 2000;Vidailhet et al., 2005;Kupsch et al., 2006) to other DBS targets such as the periventricular/periaqueductal gray regions for pain suppression (Bittar et al., 2005), and included new anatomical features of the surrounding tissue such as the ventricular system. The significance of this is highlighted by previous studies indicating that regions filled with high conductivity CSF may significantly attenuate the current spread in surrounding tissue (Astrom et al., 2006;Yousif et al., 2007), and hence 3-dimensional models of the electrode in the vicinity of ventricles were constructed. Such models demonstrate that the inhomogeneity of brain tissue has an important effect on the stimulation induced electric field.

Finally, in order to investigate the effects of the extracellular stimulation on the surrounding neuronal structures, we extended our initial approach of examining the potential distribution and isofield lines, to coupling the results of our FEM models with compartmental models of myelinated axons which is an accepted and widely used paradigm in the literature (Butson and McIntyre, 2006;Butson et al., 2006;Sotiropoulos and Steinmetz, 2007). This allowed us to estimate the volume of tissue activated by different stimulation paradigms in different implantation sites and at different post-implantation stages. While also discussing the limitations and assumptions which are inherent to these approaches, we show how our method of tailoring the model to the particular question at hand provides an efficient manner of investigating the EBI in DBS.

Materials and Methods

Definition of the depth EBI related to DBS

The generic depth EBI in our studies has been defined based on physiological recordings via the implanted DBS electrode of the physiologically modulated electrode potentials specifically related to the EBI, histological images of the region around the implanted depth electrodes, and post-mortem examination of the stimulation site in patients. The EBI consists of: (i) the implanted DBS electrode(s) based on the manufacturer’s description of the quadripolar electrode (model 3389/3387, Medtronic, MN, USA); (ii) the surrounding brain tissue; (iii) a layer of peri-electrode space surrounding the implanted electrode, which is filled with extracellular fluid in the acute post-implant stage, and reactive cells in the chronic stage. In the following sections, we describe the evolution of the basic EBI model (Figure 1) which we have constructed to study different aspects of DBS and DBR.

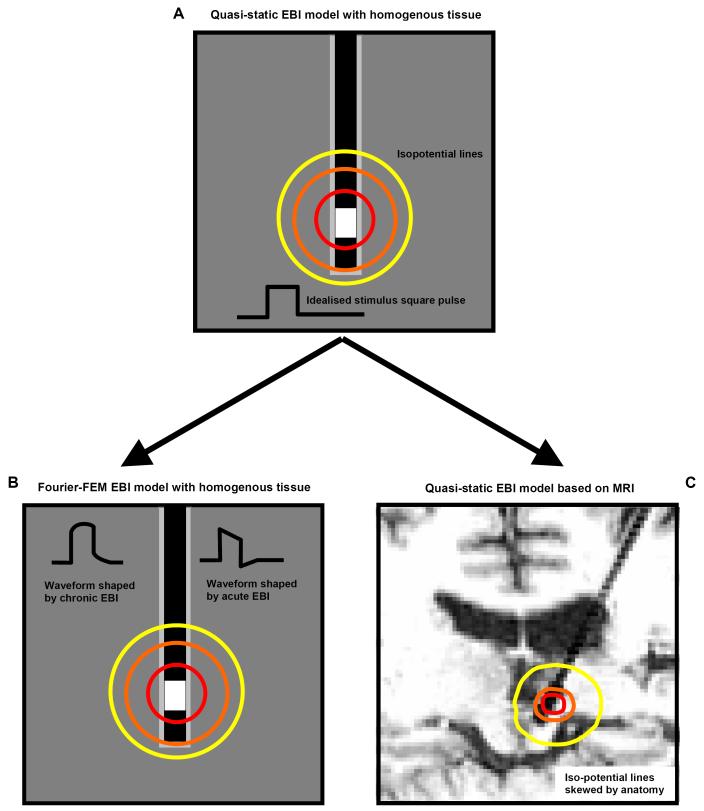
Figure 1.

The process of developing the model of the EBI in the FEM formulism is schematised here. The starting point is the simplistic quasi-static model (A). This assumes that the solution has no frequency or time dependence. This can be extended into a Fourier FEM model to allow for the frequency dependence of tissue, and therefore represent the waveform shaping over time (B). The geometry of the model can also account for the anatomical features of the implantation site as obtained from a post-operative MRI scan (C).

The basic structural model

The modelling package COMSOL Multiphysics 3.3 was used to create a two- or three-dimensional geometrical representation of the interface (Figure 2). The precise electrode dimensions were used for either the 3387 or the 3389 Medtronic electrode, the surrounding tissue was modelled as a rectangle (in two-dimensions) or cylinder (in three-dimensions) with a width or radius of 100mm, and the peri-electrode space was arbitrarily defined as 0.25mm thick. The size of these tissue areas/volumes were chosen to be comparable to the size of the human head, such that the boundary conditions (see below) correspond to the real case. The defined geometry is meshed using the default Delaunay triangulation method in COMSOL. The adaptive mesh option was then used in order to refine the mesh at the regions within the geometry where the potential changes most over space. This improves the accuracy of the solution in such regions, which are in fact in the vicinity of active electrode contacts.

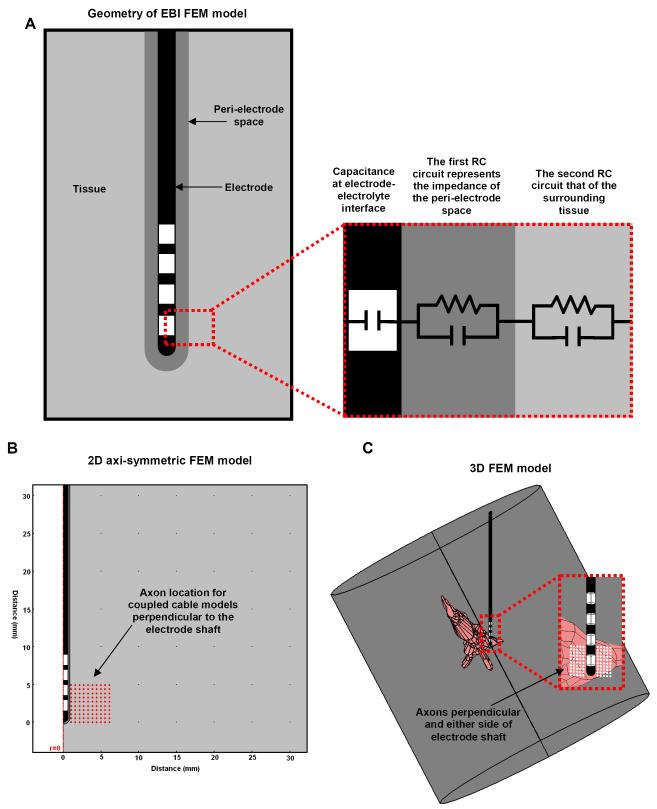
Figure 2.

(A) Schematic representation of the electrode-brain interface (EBI). We defined the EBI as consisting of the DBS electrode, the surrounding tissue, and a peri-electrode space whose properties change over time. The EBI can also be represented by an equivalent circuit (A right). (B) This can be modelled using a 2-dimensional axi-symmetric representation as this geometry is symmetrical along the axis of the electrode, which has the advantage of using less computational power to simulate. (C) However, a 3-dimensional model represents the precise geometry of the electrode, located within a cylinder of surrounding tissue which is centred on the tip of the electrode but orientated along the axis of the anatomical details included, in this case the third ventricle and cerebral aqueduct. Such FEM models were combined with axon models, which can be orientated perpendicular to both the electrode shaft, and the plane of the axi-symmetric model (red/white circles).

Representing the 3rd ventricle and aqueduct

In order to study the impact of the different conductivities of different anatomical regions surrounding the electrode, we can also use the anatomical data from patients’ MRI images to modify the geometry of the finite element model. The importance of this issue can be largely enhanced in some clinical cases. For instance, in contrast to DBS for movement disorders, in which the DBS electrode is implanted into brain targets in the basal ganglia and thalamus, where the electrode is surrounded by solid anisotropic and inhomogeneous brain structures of gray and white matter with different conductivity and reactivity values, DBS for suppressing neuropathic pain (e.g. (Bittar et al., 2005;Green et al., 2006), the electrodes are implanted in the periventricular/periaqueductal gray (PVG/PAG) region and are usually situated laterally very close to the third ventricle and the cerebral aqueduct. These structures are filled with cerebrospinal fluid (CSF), which has a much higher conductivity and lower reactivity than that of brain tissue (Rabbat, 1990). We hypothesised that the fluid filled ventricles would have an effect on the electric field distribution. As fluid filled regions show up clearly as low-signal regions on MR images, 2-dimensional slices taken in the plane of the electrode shaft were segmented by hand using a function called “roipoly” in Matlab (Version 7.0, Mathworks Inc., Natick, MA, USA), allowing the 3^rd ventricle and the aqueduct to be represented by curves. This function interactively allows the user to trace out a polygon by clicking the boundary points in an image. Therefore we were able to trace the anatomical region, and Matlab created a curve describing this shape. Each curve was converted into a 2-dimensional geometrical object in COMSOL Multiphysics 3.3 (COMSOL AB, Stockholm, Sweden) using the “flim2curve” command, and then into a 3-dimensional solid using the “loft” command. A similar procedure was utilised for the electrode artefact in the image, and the artefact was replaced by a geometrically accurate representation of the DBS electrode model 3387™ (Medtronic Inc, Minneapolis, MN, USA) which has four 1.5mm long platinum iridium contacts with three 1.5mm long separations on a 1.27mm diameter lead. The resulting model geometry therefore consisted of a 3-dimensional representation of the electrode and the surrounding anatomy, and the quasi-static Laplace equation (see below) was solved over this geometry. It is impossible to represent this using a 2-dimensional model, as the anatomy is not spherically symmetric, and simplifying the geometry to 2-dimensions would not have allowed accurate estimation of the volume of tissue activated (VTA) please see section “axon models” below.

Quasi-static model

The description of electric and magnetic fields can be obtained from Maxwell’s equations (Malmivuo and Plonsey, 1995). In the case of DBS, we can make the assumption that the fields and their sources vary slowly, as the frequency range is below 1000Hz, and the equations reduce to the Laplace equation. This implies that the medium is purely resistive and is referred to as the quasi-static model. The potential distribution induced by stimulation was calculated by solving the Laplace equation:

$$\nabla .\sigma \nabla V=0$$

where V is the potential (measured in V), σ is the conductivity (measured in S/m) and is constant for different tissue types, and ∇ is the gradient of the potential, such that $\nabla V(x,y,z)=(\frac{\partial V}{\partial x},\frac{\partial V}{\partial y},\frac{\partial V}{\partial z})$ thus resulting in a vector field, and ∇. is the divergence, representing the sum of the partial derivatives in each spatial coordinate such that for a vector F, $\nabla F=(\frac{\partial F_x}{\partial x}+\frac{\partial F_y}{\partial y}+\frac{\partial F_z}{\partial z})$. The mean conductivity values of the brain tissue were defined based on previous biological studies (Table 1). Active contacts were set to the desired stimulating potential in volts, and the outer boundary of the surrounding tissue (which is 100mm from the surface of the electrode) was constrained to 0V via Dirichlet boundary conditions. For monopolar stimulation this boundary condition represents the stimulator case which is far from the electrode contact being grounded, as in clinical practice. For bipolar stimulation, two of the electrode contacts are activated with opposite polarity. The non-active contacts and insulating parts of the implanted electrode were bound using Neumann conditions, constraining the derivative of the electric potential through these boundaries to be zero, i.e. there is no current flow through these boundaries.

Table 1.

Parameters used in the finite element models of the electrode brain interface. In the quasi-static model only the conductivity parameters are used to describe the tissue properties. When solving the complex Laplace equation, the permittivity of the surrounding tissue is also accounted for

	Conductivity (S/m)	Relative permittivity
Grey matter	0.2	1×107
White matter	0.125	1×107
CSF	1.7	109
Encapsulation	0.125	1×107

Fourier-FEM model

This approach provides a method to estimate the time-dependent effects of stimulation on the electric field induced in the surrounding neural tissue (Butson and McIntyre, 2005). Our method to the Fourier-FEM approach has been previously described (Yousif et al., 2008a), and is summarised here: The stimulus waveform which consists of the high-frequency square pulse is constructed in the time domain, then transformed into the frequency domain using a discrete Fourier transform (DFT) both steps using Matlab (Mathworks, Natick, MA, USA). The complex finite element model is solved at 513 frequencies in COMSOL Multiphysics, and the resulting complex electric potential is scaled and shifted by the DFT to yield the waveform in the tissue. Finally the waveform is transformed back into the time domain using an inverse DFT. We used a time range of 0-1 ms, and performed the DFT at 1024 steps. Therefore, we solved the FEM model at 513 frequencies from 0 Hz to 512 kHz.

The complex Laplace equation is defined as:

$$\nabla .{\sigma }^{\ast }\nabla V=0$$

with

$${\sigma }^{\ast }=\sigma -i\omega {\epsilon }_0{\epsilon }_r$$

where σ is the conductivity (measured in Siemens per metre), i is $\sqrt{-1}$, ω is the angular frequency or 2π f, where f is the frequency, ε₀ is a constant known as the permittivity of free space (8.85 × 10^-12 Farads per metre), ε_r is the relative permittivity, which is a material specific parameter and ∇ and ∇. are the gradient and divergence as defined above.. Parameters were taken directly from previous measurements in the literature, and are given in Table 1. Boundary conditions remain identical to the quasi-static case.

Equivalent electronic circuit models

In order to understand the electrical nature of the interface in more detail we can couple the FEM model to models of the equivalent electric circuit using a modelling environment for designing and simulating electronic circuits called PSPICE (Cadence, San Jose, CA, USA), therefore allowing us to investigate the specific contribution of each electrical part of the interface. Using an equivalent electrical circuit to describe the system is also an important way to understand how much charge is delivered to the tissue, which is significant in the consideration of patient safety in terms of changes occurring to the tissue and the electrode material, the stimulation of surrounding neurons, and of energy consumption. This circuit (Figure 2) is based upon previous studies of the electrode- electrolyte interface, which represent the interface as an RC circuit (Geddes, 1972). Assuming that the electrode is perfectly polarisable, the electrode can be modelled as a capacitor (Butson and McIntyre, 2005). In addition, each additional compartment of our EBI model, the PES and the surrounding neural tissue, are represented by an RC pair (Neuman, 1997) so that each component of the interface can be manipulated individually. Therefore the circuit consisted of a square pulse voltage source in series with a capacitor representing the electrode- electrolyte interface, which in turn is in series with an RC pair for the PES, and the tissue, as shown in Figure 2A. Parameters for each of the components in this model were calculated as described in (Yousif et al., 2008a) and are given in Table 2.

Table 2.

The parameters used for the circuit model of the electrode brain interface. The electrode-electrolyte component of the circuitry is simplified to a capacitance, under the assumption that no charge transfer occurs. The peri-electrode space and the surrounding tissue are each represented by an RC circuit

	EEI	PESacute	PESchronic	Tissue
Resistance (Ω)		25	334	1480
Capacitance (F)	0.6×10-6	2.3×10-11	2.1×10-6	2.99×10-7

Axon models

In order to estimate the effect that stimulation has on the surrounding neural structures (Rattay, 1989), and in addition to visualising the potential distribution, isofield lines, and activation function, an established approach is to couple the results of the FEM models with compartmental models of myelinated unconnected axons using cable theory, applying the FEM results as an extracellular stimulus to these axons. The location of axons which fire at the stimulating frequency is then taken as an activated point in the neural tissue. Although this method is based on the assumption that the mechanisms underlying DBS are mainly related to action potential generation in axons, which has neither been verified nor refuted, this method can be used to visualise the VTA by different stimulation paradigms. The model we used is that of McIntyre et al. (Butson et al., 2006), and is briefly described here. Double-cable models represent both the myelin sheath and the axolemma, with explicit representation of the nodes of Ranvier, paranodal and internodal segments. Implementing the models in NEURON v6.2, we used the 5.7μm diameter axons, which contain a fast sodium conductance, a persistent sodium conductance, and a slow potassium conductance at the nodes. We modelled 100 such axons in a 10×10 configuration, which were stimulated extracellularly using the induced electric potential estimated by the FEM model at the locations shown in Figure 2B.

Results

Quasi-static approach

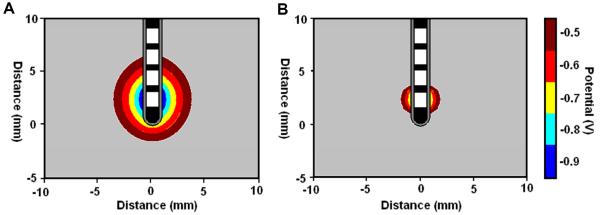
Use of the quasi-static model allows us to probe many features of the EBI and the stimulation induced field. In particular, we considered the biophysical properties of the interface at the different stages post-implantation, and what effect these changes have on the efficacy of stimulation. In the acute stage, the peri-electrode space is filled with fluid, and this in turn has a relatively high conductivity compared to grey matter (Table 1). The simulations of the EBI model show that as a result of the fluid filled layer, the induced current can spread further into the surrounding tissue in the acute compared to the chronic stage (Figure 3). The isopotential lines plotted in Figure 3, demonstrate that the -0.5V isopotential reaches 3.0mm away from the electrode, but in the acute stage this is reduced to 1.1mm.

Figure 3.

Quasi-static model solutions showing the effects of the changing biophysics of the EBI induced in the acute (A) and the chronic (B) stages post-implantation on the induced potential distribution with a stimulus amplitude of -1V.

Dynamic FFEM model

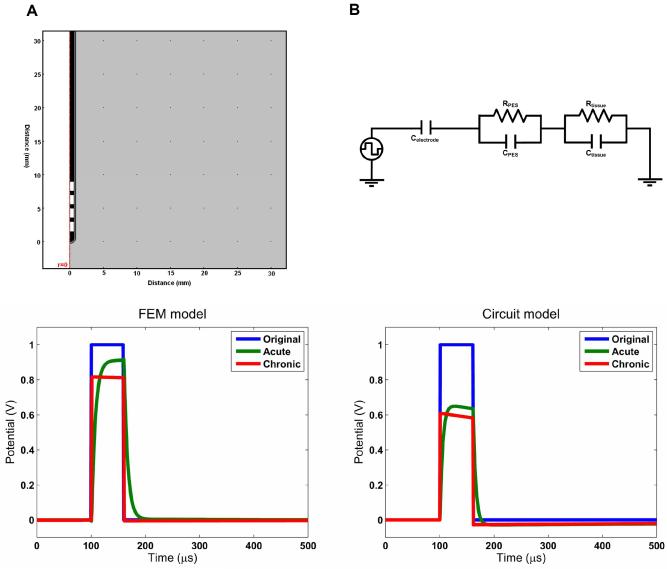
However, it has been understood for a long time that biological tissue has a reactive as well as a resistive component to its impedance. Therefore we took into account these frequency-dependent properties by solving the complex Laplace equation at the component frequencies as described above. Figure 4 shows the axi-symmetric model used and the resulting waveforms estimated to be induced in the surrounding tissue. These results indicate that the waveform shaping which occurs due to the electrical properties of the interface is also dependent on time-stage post implantation. In the acute stage, the high conductivity low capacitance ECF acts as a low-pass filter for the square pulse by smoothing the high frequency components of the square wave which occur at the start and the end of the pulse. However, in the chronic stage the low conductivity high capacitance encapsulation layer has an effect mainly on the amplitude of the waveform, and less so on the shape of the waveform.

Figure 4.

Both the Fourier-FEM model and the equivalent circuit model reveal the frequency dependent effects of the interface on the stimulus waveform. The circuit model represents the complex impedance of the peri-electrode space and the tissue using a RC circuit for each compartment. In the FEM model, these properties are represented by the conductivity and the permittivity of the regions in the geometry. The electrode is assumed to be perfectly polarisable and is consequently modelled as a pure capacitance. In both cases, the acute interface demonstrates low-pass filtering behaviour, whereas in the chronic stage the effect is mainly a reduction in amplitude. The charge delivered can be measured by the area under the curve, and the FEM model results show that 93% of the charge in the original waveform is delivered in the acute case, but only 76% in the chronic case. In the circuit model these values are 89% and 52%.

Representing the 3^rd ventricle and aqueduct

We studied the effect of a macroscopic anatomical feature in the brain on the attenuation of electric field distribution by modelling a clinical case of stimulating the peri-ventricular gray for alleviating neuropathic pain based on the post-operative MRI scans. The modelling demonstrates that in particular regions of the 3^rd ventricle and aqueduct filled with CSF of high conductivity values compared to the brain tissue significantly attenuate the stimulus-induced electric field distribution. The potential distribution was skewed compared to the homogenous case (Figure 1C) as the electric field lines are drawn towards the high conductivity ventricles.

Equivalent circuit model

The equivalent circuit which was used to understand these wave-shaping effects in more detail is shown in Figure 4. This model qualitatively replicated the FFEM model results very well, with a main difference seen in the amplitude of the results. The extra attenuation effect is due to the capacitance of the EEI in the circuit model, which is not represented in the FFEM model. However, once more we see the typical low-pass effect in the acute circuit, and the mainly attenuating effect in the chronic circuit. Removing the capacitance from the circuit reduces it back to the quasi-static case, and no waveform shaping is observed.

Estimating the VTA

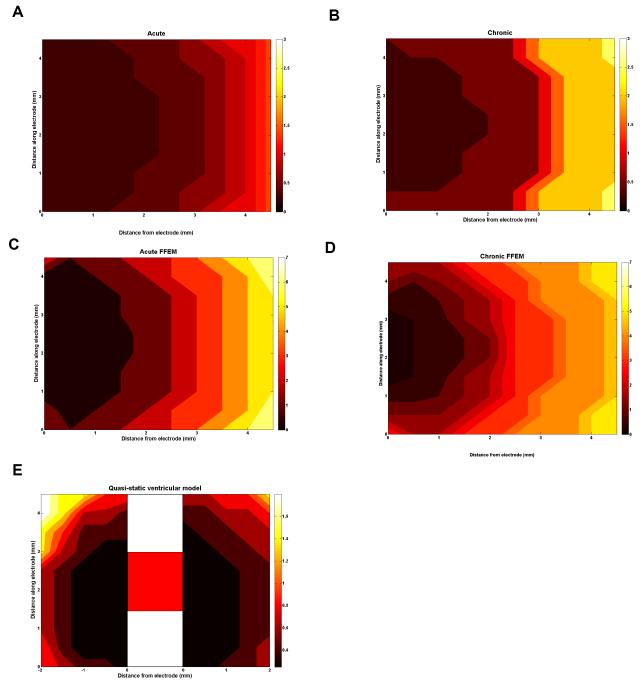
Finally, in order to appreciate the effect that the induced fields will have on the neuronal fibres in the surrounding tissue, we used the axon method to estimate the volume of tissue activated. Figure 5 shows the plot of the threshold potential required to stimulate the axons at the locations around the electrode for all of the modelled cases above. These plots show that the quasi-static models predict that potentials up to around 3 Volts are needed to fire action potentials in axons up to 4.5mm away, and that in the acute case lower amplitude potentials (Fig. 5A) than the chronic case (Fig. 5B) are necessary. However, if we consider the more accurate FFEM models, the potentials required are up to 7 Volts in amplitude, due to the effect on the pulse shaping. Note that in the FFEM case the acute EBI requires lower amplitude potentials (Fig. 5C) than the chronic case (Fig. 5D) to stimulate axons as in the quasi-static case. In the anatomical model with the 3^rd ventricle and cerebral aqueduct (see figure 2C), 50 axons were placed on the ventricle side of the electrode up to 2.5mm away (left side of VTA), and 50 on the other side, to examine the asymmetry of the electric field relative to the electrode shaft by comparing the ventricular with the contralateral sides. This shows potential amplitudes up to 1.5V required to stimulate fibres in the tissue between the electrode and the ventricles, and the VTA (Fig. 5E) is not symmetrical about the electrode, as the left hand side of the VTA is the ventricle side and the right hand side is the opposite side of the electrode which occurs due to the asymmetry in the anatomy. The presence of the ventricle on the medial side of the electrode causes the potential to spread further due to the high conductivity of the CSF, this results in a lower second spatial derivative of potential, which subsequently induced a decreased VTA. A comparison of the maximum distance from electrode surface at which an axon can be stimulated with a 1V amplitude pulse is given in Table 3.

Figure 5.

These plots show the potential amplitude required in monopolar stimulation to stimulate axons in the surrounding tissue. For each axon location, the potential threshold is plotted for each model presented: the quasi-static model acute (A) and chronic (B), FFEM acute (C) and chronic (D), and the anatomical model of the peri-ventricular gray (E). In all cases the axons are orientated perpendicular to the electrode. As the first 4 models predict a symmetric electric field, the axons are only located to one side of the electrode, as shown in figure 2B. In the ventricle case (E), the field is not symmetric and therefore, the axons are located either side of the electrode (shown schematically in the centre) for comparison, as the left hand side of the VTA is the ventricle side and the right hand side is the opposite side of the electrode. The potential thresholds rely greatly on the state of the EBI, as well as the surrounding anatomical details.

Table 3.

The maximum distance from the electrode surface at which an axon can be stimulated with a -1V amplitude pulse

	Maximum distance (mm)
Quasi-static model
acute	3.5
chronic	3.0
FFEM model
acute	1.5
chronic	1.5
Anatomical model of the peri-ventricular gray
acute	±2.5

Discussion

In the present study, we reported our computational modelling approach to studying the depth EBI specifically related to therapeutic DBS. These FEM models differed in complexity; each highlighting a different feature of the EBI’s effect on the DBS induced electric field (Yousif et al., 2007;Yousif et al., 2008a;Yousif et al., 2008b). DBS is increasingly becoming a treatment of choice for movement disorders, and neurological and psychiatric disorders (Benabid et al., 1994;Nuttin et al., 2003;Vidailhet et al., 2005;Mayberg et al., 2005;Deuschl et al., 2006;Kupsch et al., 2006). If we understood the mechanisms which underlie the observed improvements in patients, the process of optimising this treatment will be immeasurably benefited. When electrodes are implanted, an interface with the brain is immediately created, and it has been shown that this interface is changing over time (Moss et al., 2004;Xie et al., 2006;Yousif et al., 2008b). We hypothesized that understanding the EBI would be a crucial step in understanding the mechanisms of DBS and how the induced electric field will interact with the surrounding neuronal tissue.

Our finite element approach began with a quasi-static homogenous model of the electric field to simulate both the acute and the chronic post-implant stages, showing how the biophysical properties of this peri-electrode space are central to the spread of current, and therefore to accurately depicting the electric field induced by DBS. We show that the quasi-static models are sufficient to demonstrate the difference between the acute and chronic stages of implantation. Furthermore, the frequency-dependent models are necessary as the stimulus waveform shaped by the EBI is a major influential factor on the activation of neuronal fibres. In addition, we also investigate anatomical effects on the DBS induced field, by taking specific account of the ventricular system in the human brain. Taken together, these models allow us to visualise the static, dynamic and target specific properties of the DBS induced electric field. While we discuss the assumptions and limitations and which are inherent to these models, we emphasise that tailoring a specific model to a particular question at hand provides an efficient manner of investigating the EBI in DBS.

The quasi-static versus time-dependent models

The simplest quasi-static models showed that the peri-electrode space and its changing physical properties significantly affected the induced potential distribution, such that surrounding fibres required higher potentials to maintain the same level of activation in the chronic stage. This quasi-static model is derived from Maxwell’s equations (Malmivuo and Plonsey, 1995) under the assumption that the fields and their sources vary slowly as the frequency range is below 1000Hz. Therefore the full set of equations reduces to the Laplace equation which is capable of describing the electric field induced in DBS. This simple model has implications for parameter settings over time, and indicates that the potential amplitude may need to be increased as the implanted electrode is encapsulated with fibrous tissue (Yousif et al., 2007), particularly since the extent of this effect is impossible to quantify in vivo.

If we went on to take into account the effect of the frequency dependent electrical properties of the tissue, i.e. the capacitivity, the models showed that the idealised square pulse was shaped by these biophysical tissue properties. Once again this effect changed with the changing peri-electrode space (Yousif et al., 2008a). In the acute stage the fluid filled layer acted as a low-pass filter, whereas in the chronic stage the main effect was that of attenuation of the potential amplitude. This waveform shaping had a dramatic effect on the potential amplitude required to stimulate surrounding neuron fibres, which was consistent with previous work (Butson and McIntyre, 2005). These different effects may also impact on the recording from such electrodes, as previously indicated by our group (Yousif et al., 2008b).

Constructing structural models based on clinical imaging

We also considered the impact of large scale brain anatomy on the induced potential distribution by looking specifically at a case where the DBS targets lie particularly close to CSF-filled 3^rd ventricles and aqueduct regions in comparison with the brain targets in the ‘solid’ basal ganglia, we found that the presence of high conductivity regions in the vicinity of the electrode had a dramatic effect on the potential threshold required to stimulate fibres. A reduced potential amplitude was sufficient, in this case, to generate firing in nearby fibres. This result is crucial for such structural models of DBS, as it indicates that the volume of tissue activated may be very different to that previously appreciated, due to the presence of fluid-filled ventricular system in the human brain. Specifically, the VTA will not be symmetric about the axis of the electrode but will be skewed towards to the ventricle on one side, therefore the extent of the VTA would depend precisely on the location of the electrode relative to the anatomy. This is supported with the empirical observation that moving the electrode away laterally by a couple of millimetres can dramatically influence the clinical outcome in patients (Green et al., 2005; Green et al., 2006).

While we chose a method of defining the borders of the ventricles by manual segmentation, which is straightforward due to the high contrast difference between CSF and brain tissue on MR images, alternative methods of introducing anatomical details into the geometry of a FEM model of DBS have thus far been reported in the literature. Butson et al (Butson et al., 2007) first reported the idea of using information from diffusion tensor imaging by using an idea introduced by Tuch et al, which directly related the diffusion tensor to the conductivity of the tissue (Tuch et al., 2001). In this way it is possible to use such data to provide the parameters required to solve the Laplace equation. Sotiropoulous and Steinmetz achieved their anatomical detail from the segmentation of a stereotactic atlas, which is not patient-specific, but reliable and well documented. A recent paper by Vasques et al, (Vasques et al., 2009) used the expertise of a surgeon to delineate the border of the GPi from an MRI.

Tailoring a specific model to a particular question of investigating the EBI in DBS

The modelling study presented here is reliant on a number of assumptions and simplifications. The quasi-static models do not account for frequency dependence, and hence the Fourier-FEM models are introduced to account for that. The anatomic models account for some of the inhomogeneity in the brain, but do not represent the isotropy of conductivity due to fibre tracts in the brain. Indeed, these models are not meant to deliver precise estimations of every aspect of neuronal activation in patients’ brains. In this sense, this modelling strategy is very effective for understanding the general principles which underlie DBS. The work here can be further extended to account for inhomogeneity and isotropy in 3-dimensions combined with the frequency-dependent tissue properties within single unified models. This would allow a more accurate depiction of the DBS-induced electric field in individual patients’ brains. In addition, careful consideration of how to estimate the effect on surrounding neurons is needed, as the use of unconnected axons is a simplification based on the assumption that the mechanisms of DBS depend on stimulating surrounding axons, and that the effect on cell bodies and dendrites is arbitrarily ignored.

Validation of the models

With any theoretical model the most difficult and yet one of the most important parts of the evaluation of the results is to consider the validity of the findings with reference to empirical observations. A recent paper (Miocinovic et al., 2009) from the McIntyre group has aimed to directly compare the potential distribution predicted from a FEM model to that measured both in vitro in a saline tank, and in vivo in a monkey brain. The results in this paper indicate that for a -0.3V potential pulse, the maximum recorded potential in primate STN stimulation at 1mm distance from the electrode would be approximately -0.02V depending on the electrode impedance (their Figure 4). Our quasi-static FEM model, predicts that the induced potential with a -0.3V pulse (after amplitude adjustment by 57% following the methods in Miocinovic et al) is -0.099V (data not shown). This difference can be attributable to the lack of both inhomogeneity and anisotropy in our model, as well as the fact that we model the human DBS electrode and not the primate version. Such direct calibration to measurements is an important aim for validation of model results and is discussed further below.

Clinical data is always limited, and there is an issue of ethics when making recordings specifically for the purpose of validating modelling work from patients. Hence in vivo data from patients is not easy to acquire so that models cannot always be constructed based on clinical data (Yousif et al., 2007;Yousif et al., 2008a). Another interesting method to quantify the extent of the electric field was proposed by the Grill group (Kuncel et al., 2008). They measured the voltage amplitude required to induce motor side-effects in patients which had thalamic DBS. As this required the stimulation effects to reach a neighbouring thalamic nucleus, and as the location of the electrode was known, as was the distance to the neighbouring nucleus, they could use this to quantify the range of the field, which can be compared to theoretical predictions. Furthermore, this original method could be extended to other DBS targets where large stimulus amplitudes are known to cause side-effects.

Once again, this procedure requires a great deal of experimental effort, and goes beyond the normal clinical practice therefore prompting ethical issues. One useful indirect way of validating results is to compare the findings and predictions made by such FEM models, for example about the change in the VTA with changes in stimulation settings, and compare this to clinical and experimental observations in patients. One such example is to correlate the difference predicted between monopolar and bipolar fields to the empirical observation that bipolar stimulation requires higher amplitudes to induce the same clinical outcome (Yousif et al., 2007). In this way, theoretical model findings can be directly validated and used to aid clinical practice in a crucially needed manner.

Concluding remarks

The depth electrode-brain interface created during the clinical treatment of DBS, is crucial to understand how the stimulus impacts on the surrounding tissue, as its properties which are not static but changing over time in the post-operative period, affect the electric field induced. Therefore, understanding the bio-physical properties of this interface using electrophysiological (Xie et al., 2006), pathological (Moss et al., 2004) and theoretical (Yousif et al., 2007;Yousif et al., 2008a;Yousif et al., 2008b) techniques has been important to elucidate the multi-faceted nature of the EBI. In particular, the computational modelling studies described here have demonstrated the importance of including the EBI for both visualising the stimulation induced electric field, and making predictions of the effect of the field on surrounding neuronal structures. This accurate description of the EBI will also allow us to explore what stimulation paradigms can maximise therapeutic benefit while minimising energy use and damage at the interface.