Interpreting ‘Dose-Response’ Curves Using Homeodynamic Data: With an Improved Explanation for Hormesis

Abstract

A re-interpretation of the ‘dose-response’ curve is given that accommodates homeostasis. The outcome, or overall effect, of toxicity is the consequence of toxicity that is moderated by homeodynamic responses. Equilibrium is achieved by a balance of opposing forces of toxic inhibition countered by a stimulatory response. A graphical model is given consisting of two linked curves (response vs concentration and effect vs concentration), which provide the basis for a re-interpretation of the ‘dose-response’ curve. The model indicates that such relationships are non-linear with a threshold, which is due to homeodynamic responses. Subthreshold concentrations in ‘dose-response’ curves provide the sum of toxic inhibition minus the homeodynamic response; the response itself is unseen in serving its purpose of neutralizing perturbation. This interpretation suggests why the α- and β-curves are non-linear. The β-curve indicates adaptive overcorrection to toxicity that confers greater resistance to subsequent toxic exposure, with hormesis as an epiphenomenon.

INTRODUCTION

The ‘dose-response’ relationship does not reveal the responses that tend to counteract, or neutralize toxicity; it only indicates the outcome or overall effect. The ‘dose-response’ concept tends to obscure such an interpretation, as the term ‘response’ is misused in describing the outcome, rather than the organism’s response to toxicity. Clearly the reaction to toxicity and its outcome are not the same.

There are various adaptive responses to toxicity, which are typically of two kinds: the first is the response of an organism to toxic agents which may be detoxified by binding to metallothioneins, while organic compounds are typically degraded into water soluble forms by the MFO (mixed function oxygenase) system and then excreted. The second is the response of homeodynamic systems that react non-specifically in regulating processes affected by any agent that deviates a controlled process from its goal setting. The ubiquity of homeostasis is often overlooked, yet homeodynamic systems are found at all levels of organization, from the molecular to the ecological. Data presented as ‘dose-response’ curves often represent some integral of the output of homeostatic mechanisms (eg. growth rates). Even lethality as an endpoint is preceded, if not caused, by loss of homeostatic capacity.

Here the aim is to consider the moderation of toxicity by homeodynamic systems and accommodate them in ‘dose-response’ relationships. This has been achieved by a hypothetical coupling of the concentration-response curve to the concentration-effect curve (= ‘dose-response’), using published homeodynamic data. Elsewhere an interpretation of hormesis has been provided using dynamic control data with respect to time, representing the output of control mechanisms (Stebbing, 2000, 2003).

Here the earlier explanation of hormesis is presented with time-integrated data, that reduces the dependence upon the output of feedback mechanisms and control theory. The evidence for hormesis has grown rapidly over the last 20 years. Responsibility for our greater awareness of the evidence for hormesis is due largely to Dr E Calabrese and his coworkers. Now over 6000 examples of hormesis have been assembled in a single database to corroborate the generality of hormesis. A series of comprehensive reviews of hormesis have been published, covering the occurrence of hormesis in different fields (Calabrese and Baldwin, 2000, 2001, 2003; Calabrese, 2005a & b). The data have been gathered in support of the hypothesis that hormesis is a general phenomenon: meaning its generality across the major taxa of plants and animals, the toxic and stress-inducing agents that cause it, and the biological indices that exhibit it. It can now be accepted that hormesis is a well-defined and a general phenomenon, but the lack of a satisfactory explanation is an obstacle to its wider acceptance. In recent times it has been accepted that the mechanism for hormesis relates to some kind of overcorrection in response to low concentrations of toxic agents, which has been noted by others (see Calabrese, 1999). A cybernetic hypothesis was proposed by the author (Stebbing 1981a,b, 1982, 1998), and has gained some support (Calabrese, 1999; Calabrese and Baldwin, 2003), but it has been embedded in ideas on control theory (Stebbing, 2000) that are not yet widely accepted. Here a more accessible explanation is provided to consolidate the earlier hypothesis. The homeodynamic model for this interpretation is that developed by the author for the effects of toxic agents upon the control of growth in colonial hydroids and yeast.

THE ‘DOSE-RESPONSE’ RELATIONSHIP

There is an important features of ‘dose-response’ relationships that is overlooked (Figure 1b). The descending arm is the dominant feature, indicating that toxicity increases with concentration. This is as would be expected, but another feature has a less obvious interpretation. Over a range of concentrations, depending on the design of the experiment, low levels of the toxic agent have no apparent effect below the threshold at which toxicity first becomes apparent. But why is toxicity not proportional to concentration, and linear (without a threshold) from the origin of the graph? This is the kind of contentious ‘dose-response’ relationship that is assumed for radiation, and some highly toxic substances, in a ‘dose-response’ relationship known as the linear-no threshold hypothesis. As toxicologists, the evidence shows that linear-no-threshold curves are invalid, because ‘dose-response’ relationships are typically not linear. There has been a debate regarding the use of the linear-no-threshold hypothesis, opposed, particularly by those who recognize that the β-curve1 exhibiting hormesis is common, if not more usual (Calabrese and Baldwin, 2003). It is equally justifiable to question the validity of the linear-no-threshold hypothesis in relation to more usual ‘dose-response’ or α-curves. Both the α- and β-curves are non-linear and require explanation for their departure from the simpler explanation which is linear and implies proportionality. Let us first consider why the α-curve is non-linear. It will be shown that the plateau of subthreshold levels appears unperturbed, due to a balance of opposing forces between toxic inhibition and stimulatory counter response. The β-curve will be discussed separately in relation to the interpretation of hormesis.

FIGURE 1.

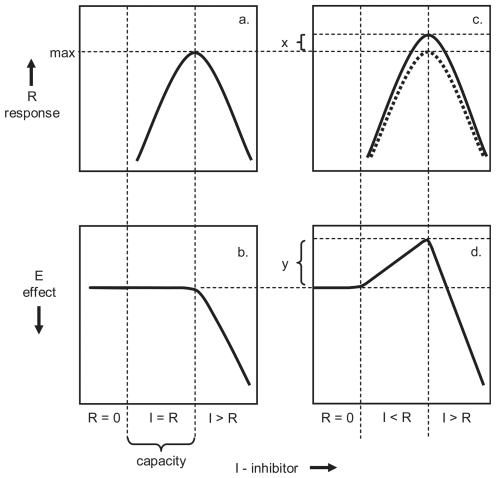
A graphic interpretation of the α- and β-curves based on a homeodynamic responses to toxic inhibition. The α-curve is indicated by a and b, and the β-curve by c and d. The responses (R) are indicated by a and c and the effects (E) by b and d. The inhibitor (I) applies to all graphs. The adjustment in rate due to sustained exposure x results cumulatively in an increase in growth y (see text for further explanation).

The author began to study the output of homeodynamic mechanisms responsible for the control of growth rates of hydroids exposed to low metal levels. ‘Dose-response’ relationships were also established for a series of metals, before later moving onto the effects of reduced salinity and later some organic compounds (Stebbing, 1976, 1981a,c). In all such relationships, subthreshold concentrations elicited control responses with oscillatory behaviour characteristic of such mechanisms, which restore equilibria following perturbation. The feedback mechanism maintains growth rate at the level of unperturbed organisms. It is proposed that at subthreshold concentrations of toxic agents, homeodynamic response effectively neutralizes toxic inhibition. It establishes an equilibrium between inhibition and a counter response, such that the inhibitor has no effect.

This interpretation is confirmed by experimental data showing that at subthreshold concentrations, growth control mechanisms are active in counteracting inhibition (freshwater Hydra littoralis, Stebbing and Pomroy, 1978; marine hydroid Laomedea flexuosa, Stebbing 1981a; marine yeast Rhodotorula rubra, Stebbing et al. 1984). That such an equilibrium exists can be seen by the sudden removal of the inhibitor, which briefly reveals the counter-response as a relaxation stimulation (Stebbing, 1981a). At even lower concentrations, the inhibitor is undetectable to the organism, and elicits no counter response.

Such control activity is non-specific, responding to inhibition in the same way, independently of its cause, because homeodynamic mechanisms respond to the inhibition that is caused and not the agent that causes it. The non-specificity of homeodynamic responses is important because, in effect, organisms are pre-adapted to counteract toxic inhibition, whatever the causes.

The ability to counteract toxic inhibition defers inhibition to a higher concentration, causing a threshold in the ‘dose-response’ curve, which explains why it is not linear.

THE α-CURVE AND HOMEODYNAMIC RESISTANCE TO INHIBITION

Homeodynamic systems have evolved with the inbuilt purpose of maintaining a goal setting, which is achieved by neutralizing deviations in the controlled process due to environmental perturbation.

The purpose of homeodynamic control is often perceived as merely to maintain constancy, but in doing so the effects of those external disturbances, that would deviate the process from its goal setting, are counteracted. It follows that the interpretation of toxicity is not a simple cause and effect relationship that can be defined by a single ‘dose-response’ curve, as it ignores the homeodynamic response of the organism. Toxicity is the outcome of the effect of some toxic agent, and those responses that act to moderate toxicity by counteracting inhibitory effects. The opposition of these forces is hidden, to the extent that integration over time in ‘dose-response’ curves obscures the reaction between inhibitor and a stimulatory counter response.2 Such behaviour is seen in the oscillatory output of homeodynamic mechanisms (Stebbing, 2000). The observed toxic effect (E) can be simply expressed as the outcome of the exposure of an organism to some toxic inhibitor (I), which is countered by a homeodynamic response (R) to growth inhibition, such that E = I – R (Stebbing, 1981a). Each term can be expressed as some function of concentration (C) such that C_{toxic effect} = C_inhibition – C_response. The inhibition due to some toxic inhibitor is opposed by a stimulatory response, such that within limits, inhibition is neutralized. The ultimate effect, or outcome of opposing forces, is given by the ‘dose-response’ relationship, which provides a threshold concentration, marking the onset of inhibition. Dynamic output data reveal that with rising concentrations, the loading of the control mechanism shows a trend, and a sequence of transitions with increasing concentration. They progress from overcorrection and rapid equilibration to low levels of load, to loads that requires longer periods of oscillation for equilibrium to be achieved, then loads too great for equilibration to be restored, and leading to overload and high output failure as the limit of the capacity to resist inhibition is exceeded (Stebbing, 2000, 2003).

It was only recently recognized by the author that this interpretation is little different from W. Ross Ashby’s Law of Requisite Variety (Ashby, 1958). In referring to disturbances (d), responses (r) and outcomes (o), he used the collective term ‘variety’ (V), such that V_(o) = V_(d) – V_(r). Later he recognized that the term ‘variety’ was misleading, and used the term ‘quantity’ rather than ‘variety’ of disturbance (Ashby, 1960). His law is not significantly different from that given above. There is therefore a requirement to restate Ashby’s homeodynamic law in a way that is not constrained by the limitations of set theory, as he ultimately meant something different from the form in which it was first stated.

The relationships of response and effect, in relation to concentrations of some toxic agent cannot be represented by a single ‘dose-response’ curve. Instead a linked pair of curves are used to provide a conceptual representation of this homeodynamic law (Figure 1). A typical form of ‘dose-response’ curve indicates the observed effect of a range of concentrations of toxic inhibitor (Figure 1b). The curve coupled to it represents the response to inhibition, as the relationship between the inhibitor and homeodynamic response (Figure 1a). The existence of such a homeodynamic response is known from published data cited above, but its form is inevitably hypothetical because the response cannot be generated without some disturbance or inhibition for it to oppose. As the counter response cannot be induced without a load for it to work against, the response is hidden within the final outcome (Figure 1b). Nevertheless, it is possible to deduce the form that the cryptic response curve takes.

The typical ‘dose-response’, or α-curve, indicates that there is no effect until the concentration exceeds the threshold of inhibition, whereupon inhibition increases linearly with concentration (Figure 1b). The response curve is given by a hypothetical inverted V-shaped curve (Figure 1a). At the lowest concentrations toxic inhibition is not detected, as the control mechanism output does not depart from the baseline (R = 0). At slightly higher concentrations, and extending to the threshold of inhibition, the response increases as inhibition is opposed by a neutralizing response (I ≤ R), such that there is no effect. At still higher concentrations of inhibitor, the response approaches a maximum (R_max), such that no further increase in concentration elicits any greater response (Figure 1a). Beyond this point the growth control mechanism experiences ‘high output failure’. As the response fails (R = 0) and the inhibition becomes unopposed, and the inhibitory effect curve falls in proportion to the concentration of inhibitor (E ∝ I) (Figure 1b).

The implications of this interpretation are that the threshold, and the onset of inhibition (Figure 1b) are due to overloading the homeodynamic mechanism (R_max). Up to that point, there is no effect because the increasing inhibition is neutralized by the counter response. Above that point the process is no longer protected by the response (I > R), and the inhibitory effect increases with concentration. The threshold in the effect curve is therefore a consequence of the homeodynamic capacity being exceeded. The crucial point for both curves is that at which the counter response reaches its maximum and then fails (Figure 1a), because it also determines the threshold in the effect curve and the onset of toxicity (Figure 1b).

The difficulty with this model is that the response curves (Figure 1a and c) cannot be isolated and plotted, so must be inferred. At sub-threshold concentrations, the response rises to match increasing levels of inhibition, but on reaching a maximum, the V-shaped curve reaches its apogee, and inhibition ensues in proportion to the concentration of inhibitor (Figure 1b). Where toxic inhibition and the response coincide in time, the counter response is not apparent, because it has served its purpose in neutralizing inhibition. In counteraction, inhibition and the stimulatory counter response become equivalent though opposite, and so cancel one another out. It is only when the capacity to neutralize inhibition is exceeded above threshold levels that an inhibitory effect is observed.

The form of a response curve has been deduced from other dynamic data (see Figure 14c, Stebbing 1981a). Following equilibration of a homeodynamic system to any sustained inhibitory load, the equilibrium represents a balance of opposing forces. If the inhibitor is suddenly removed, the counter response is briefly observed as a stimulatory peak, which lasts for as long as the lag in the control mechanism to correct it. The height of such peaks provide a measure of the stimulatory response that had been necessary to establish the equilibrium (Figure 1a). Such data provide evidence for the ascending arm of the response curve; the descending arm is assumed to decline with the effect curve, once the counter response fails at R_max (Stebbing, 2000).

CAPACITY TO COUNTERACT INHIBITION

It is apparent that the homeodynamic response has a capacity to counter inhibition (Figure 1a, b). The range of concentrations over which inhibition can be neutralized provides a measure of this homeodynamic capacity. At the lowest concentrations there is no response, as inhibition is not detected by the control mechanism (R = 0 in Figure 1b). Above a level of detection, a counter response is initiated and oscillations are observed in the control output, indicating the initiation of a counter response (Stebbing, 2000). The subthreshold range of detectable concentrations over which no effect is observed provides the measure of the capacity to counter inhibition (Figure 1b).

The threshold of inhibition marks the upper limit of the capacity to resist inhibition, such that any concentration above the threshold will cause failure due to overload. Conversely, any concentration less than the threshold will be counteracted. The capacity to resist is a measure of the health of the homeodynamic mechanism, and indirectly the health of the organism. Predictably, the less healthy, or partially loaded the control mechanism, renders the organism more vulnerable to overload, because the residual capacity is reduced.

The neutralization of inhibition contributes to fitness, which can be quantified as the capacity of the system. For experiments with copper on hydroids, the range amounts to an order of magnitude in concentration (Stebbing, 1981a), which is more than adequate to accommodate the range of variation in the hydroids’ estuarine habitat (Stebbing et al., 1983).

THE β-CURVE, ACQUIRED RESISTANCE AND HORMESIS

The β-curve is a second kind of ‘dose-response’ curve, with the principle feature of a stimulatory peak, referred to as hormesis. The form of such curves has been described and defined by Calabrese and Baldwin (1997). It is now believed that the β-curve is so common that it may be the predominant form of ‘dose-response’ curve (Calabrese and Baldwin, 2003).

In the foregoing case of the ‘dose-response’ or α-curve (Figure 1a,b), it has been argued that an inhibitory effect of toxic agents is neutralized by a stimulatory response, such that the opposing forces create an equilibrium (I = R) at subthreshold concentrations. When the toxic load upon the homeodynamic mechanism exceeds the capacity to neutralize inhibition, there is overload (I > R). Overcorrection occurs where the response exceeds the load to be neutralized (I < R). Such overcorrection is a feature of an adaptive response to subinhibitory concentrations that increases resistance (acquired tolerance) to subsequent and greater levels of inhibition (Stebbing, 2003).

Two factors contribute to hormesis. The first is due to a feedforward loop that elicits a rapid maximal, if transient, response irrespective of load. Later the response becomes proportional to load and an equilibrium is established. The second is due to another feedforward loop that results in an adjustment that increases the goal growth rate (Stebbing 1981a). Though the adjustment to the goal rate is small (~10%), the outcome in size becomes large (~50%), when the data are integrated over time (Figure 8 in Stebbing,2003). This is reflected in the adjustment in response (x in Figure 1c), resulting in a large hormetic effect (y in Figure 1d).

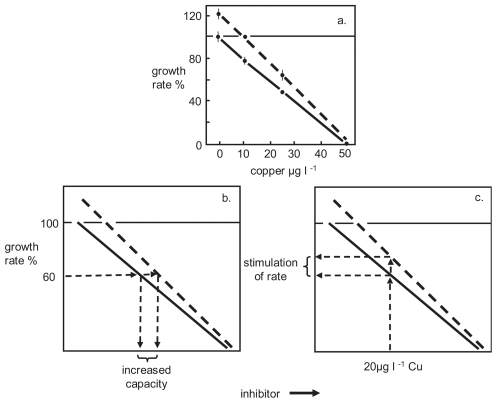
The adjustment in rate is adaptive in conferring increased resistance to future exposure to toxic inhibition. Acquired resistance to toxic exposure is best seen in experiments designed for the purpose (see Figure 7 in Stebbing, 2000). Hydroid colonies were pre-exposed (3 weeks at 10μg.ℓ⁻¹ copper). The effect of sustained exposure of hydroid colonies is demonstrated by comparing their sensitivity with other colonies not pre-exposed (Figure 2a). The two groups were then compared in an experiment to determine their growth rates when exposed to copper concentrations ranging from 0 to 50 μg. ℓ ⁻¹. It can be seen that the group pre-exposed to copper exhibited greater resistance across the range of sublethal concentrations. It is notable that although the pre-exposure concentration was 10μg. ℓ ⁻¹, significantly increased resistance occurred at 25 μg. ℓ ⁻¹, so pre-exposure confers resistance to higher concentrations than that used for pre-conditioning.

FIGURE 2.

Acquired resistance due to pre-exposure. a. the results of an experiment using hydroids, showing the effects of copper on growth rate. The colonies indicated by the dashed line were pre-exposure to copper (10μg. ℓ ⁻¹ for 3 weeks) and the control group had not (redrawn from Stebbing, 1981a); b. indicates how at a given level of inhibition, the capacity to resist the effect of copper is enhanced by pre-exposure; c. indicates how at a given concentration of copper, growth rate is increased as a result of pre-exposure.

The results can be interpreted in two ways. If the graph is read from the y-axis for an arbitrary inhibition of growth rate, say 40%, it can be seen that the pre-exposed group had a greater capacity to resist the effect of copper, such that inhibition occurs at a concentration ~10μg. ℓ ⁻¹ higher than those hydroids not pre-exposed (Figure 2b). If one then reads the same graph from the x-axis, for an arbitrary copper concentration of 20μg. ℓ ⁻¹, hydroids that are pre-exposed show 18% less inhibition than those not pre-exposed (Figure 2c). The enhanced increase in growth rate is converted to a counteractive response that neutralizes inhibition. In the second interpretation, it becomes obvious that acquired tolerance relates directly to increases in growth rate that will later, and more effectively, oppose toxic inhibition. Not only does this stimulation neutralize inhibition, but when it is held in anticipation, the rate-adjustment results in the stimulation of growth, causing hormesis.

If the α- and β-curves are compared, it becomes clear that the responses of the system to toxic inhibition are similar (Figure 1a & c), but the outcomes are different (Figures 1b & d). In the case of the α-curve, the stimulatory response is immediately taken up in neutralizing toxic inhibition, so the curve indicates no effect or deviation at sub-threshold concentrations (Figure 1b). The β-curve has a response curve of a slightly different form (Figure 1c), but an effect curve that is markedly different (Figure 1d). The β-curve shows a stimulatory effect, because the response to inhibition has adjusted to increase resistance to some future inhibition. The baseline about which growth rate oscillates is raised such that added stimulation becomes an anticipatory adaptation. The mechanism of adaptation involves the adjustment of preferred growth rates to a higher level (Stebbing 1981a, 2003). Any increase in growth rate inevitably results in a cumulative increase in size over time. This demonstrates that acquired resistance and hormesis are due to the same process of adaptive adjustment in growth rate.

The difference in what creates the α- and β-curves is that on the α-curve the stimulatory response is equal to the inhibition (I = R) (Figure 1b). The β-curve is different in that the stimulatory response is greater than the inhibition to be neutralized at the time. It is an overcorrection that requires a feedforward loop to adjust the goal setting of the control mechanism to a higher level, to neutralize some future inhibition more effectively (Figure 1c). This has two consequences. The first is that a raised baseline for growth rate develops and is maintained, providing an increase in the capacity to resist future exposure to toxic inhibition (Figure 1c). The second is that the sustained adjustment in growth rate has the consequence that size increases over the range of concentrations that adaptation applies (Figure 1d). When a similar toxic inhibition recurs later, the prior adjustment in growth rate comes into effect, providing an enhanced capability to counter inhibition (Figure 2a). The enhanced growth rate is capable of neutralizing an amount of inhibition, equivalent to the adjustment made. Should there be no later toxic exposure, the adjustment in growth rate has the inevitable consequence of stimulating growth, so creating a β-curve. Given this interpretation, hormesis becomes an epiphenomenon, due to the latent rate-adjustment.

It is of interest that pre-exposure at one concentration elicits enhanced resistance over a wide range of concentrations (Figure 2). It also appears that the range of concentrations which exhibit hormesis, is the same range that may be expected to acquire tolerance due to pre-exposure to toxic agents. This also implies that hormesis generally is a byproduct of acquired tolerance to toxic agents, such that the occurrence of hormesis alone is likely to indicate that resistance is being acquired.

When the development of this adaptation is monitored over time, what begins as an α-curve becomes transformed into a β-curve, as the adjustment in rates is made, and as the products of growth accumulate (Stebbing, 2000, 2003). It is not to be assumed therefore that the α- and β-curves are alternative or competing explanations of ‘dose-response’; it seems they are successive stages in the development of the same interpretation. Assuming an adequate range of concentrations, this interpretation suggests that ‘dose-response’ curves of the α-form are derived from experiments too short to allow the development of acquired tolerance and hormesis. With time, adjustment occurs and a β-curve begins to develop as the increase in growth rate results in a cumulative increase in size (see Figure 2 in Stebbing, 2003).

DISCUSSION

One of the difficulties is the use of the word ‘response’ in ‘dose-response’ curves. (Strictly speaking the term ‘dose’ is also contentious, as many species are exposed to a concentration of a toxic agent, rather that given a dose in the strict sense.) For too long the name has implied that such relationships represent a measure of response. In biological contexts a response is a reply or reaction that has evolved to moderate external challenges causing stress. Toxic inhibition results in a homeodynamic response, which is not the same as the outcome or effect. It is the effect that is usually represented by the misnamed ‘dose-response’ curve. To confuse ‘response’ with ‘effect’ has had misleading consequences, particularly with our understanding of adaptive responses, and their contribution to moderating toxic inhibition.

The aim here has been to re-interpret ‘dose-response’ curves (α- and β-curves) in a way that incorporates the part played by homeodynamic responses in countering toxic inhibition. A key feature of ‘dose-response’ curves is their non-linearity and threshold, which, it is concluded here, are due to homeodynamic mechanisms that maintain the biological index at an unperturbed level. Were this not the case, ‘dose-response’ curves would reveal toxic effects proportional to the concentration of the toxic agent, and conform to the linear-no-threshold hypothesis.

The idea of re-interpreting the ‘dose-response’ relationship followed access to the output of growth control mechanisms using perturbation with toxic agents (Stebbing, 1981a). Earlier published versions of the graphical model (Figure 1) were inaccurate with respect to the form of the cryptic response curve. Here a more realistic inverted V-shape response curve (Figure 1a & c) is coupled with the effect curve (Figure 1b,d). Such curves are not uncommon in the literature and have a similar explanation. For example, enzymes exposed to a range of pH levels and temperature also stimulate enzyme activity at low levels of pH until an optimum is reached, and inhibit them by denaturing the enzyme at higher levels (N.J. Berrill in Schmidt-Nielsen, 1979). The Yerkes-Dodson Law from biopsychology is still generally accepted and applied (Yerkes & Dodson, 1908). It is also depicted as an inverted V-shaped curve relating arousal or stress to performance or response. The effect of low levels of stress is to stimulate the response, but at high levels it has a negative effect and a decreased performance. The Yerkes-Dodson Law saw a revival in the 1960s and has found many applications in psychology (Teigen, 1994). Such curves are typical of adaptive responses that are first induced and then inhibited by over-stimulation, similar to the curve proposed here.

The counter response to inhibition creates the threshold that characterizes the α-curve, in which the subinhibitory, horizontal part of the curve indicates the range of concentrations over which control is maintained. Where proportionality is assumed, as in the linear-no-threshold hypothesis, its ability to predict toxicity has been found to be wanting, as it overlooks the action of homeodynamic counter responses. The response to toxic inhibition in the control of growth is of necessity stimulatory, and only when these two forces are not in equilibrium do inhibitory or stimulatory effects occur, providing explanations for overload and overcorrection.

CONCLUSIONS

Homeodynamic responses to toxic inhibition provide explanations for their non-linearity, and the differences between α- and β-curves. The subthreshold parts of the α- and β- curves are explained in terms of homeodynamic responses to toxic inhibition; the α-curve occurs where a response is equivalent and neutralizes toxic inhibition, and the β-curve occurs where the response exceeds toxic inhibition. The second has the primary purpose of conferring increased resistance to subsequent toxic inhibition, and until that occurs, increased growth rates stimulate growth creating a β-curve. It is the adjustment in growth rate and added resistance to toxic inhibition that is adaptive. Hormesis itself is almost certainly an epiphenomenon, as the rate-adjustment that causes it is shown to be adaptive. Acquired resistance to toxicity and hormesis are causally linked as consequences of homeodynamic responses to toxicity.