Chromophore concentrations, absorption and scattering properties of human skin in-vivo

Abstract

Absorption and reduced scattering coefficients of in-vivo human skin provide critical information on non-invasive skin diagnoses for aesthetic and clinical purposes. To date, very few in-vivo skin optical properties have been reported. Previously, we reported absorption and scattering properties of in-vivo skin in the wavelength range from 650 to 1000nm using the diffusing probe in the “modified two-layer geometry”. In this study, we determine the spectra of skin optical properties continuously in the range from 500 to 1000nm. It was found that the concentration of chromophores, such as oxy-hemoglobin, deoxy-hemoglobin, and melanin, calculated based on the absorption spectra of eighteen subjects at wavelengths above and below 600nm were distinct because of the inherent difference in the interrogation region. The scattering power, which is related to the average scatterer’s size, demonstrates a clear contrast between skin phototypes, skin sites, and wavelengths. We also applied venous occlusion on forearms and found that the concentrations of oxy- and deoxy-hemoglobin as assessed at wavelengths above and below 600nm were different. Our results suggest that diffuse reflectance techniques with the visible and near infrared light sources can be employed to investigate the hemodynamics and optical properties of upper dermis and lower dermis.

1. Introduction

The absorption coefficient µ_a, the scattering coefficient µ_s′, and chromophore concentrations of skin are fundamental properties of tissue that can provide essential information for many aesthetic, therapeutic, and diagnostic applications such as monitoring of skin blood oxygenation, melanin concentration, detection of cancer with fluorescence, laser surgery, and photodynamic therapy.[1–4] Many researchers have quantified the optical properties of skin tissue and most of them used ex-vivo skin samples and integrating sphere techniques. For example, Troy and Thennadil determined the optical properties of 22 human skin samples ex-vivo in the wavelength range from 1000 to 2200nm using double integrating sphere measurements.[5] Simpson et al. measured samples of dermis of five subjects (four Caucasians and one Negroid) ex-vivo and obtained the optical properties in the wavelength range from 625 to 1000nm using integrating sphere measurements.[6] Bashkatov et al. have characterized optical properties of 21 skin samples ex-vivo in the wavelength range from 400 to 2000nm using an integrating sphere approach.[7] Salomatina et al. have determined and compared the ex-vivo optical properties of human skin samples with those of non-melanoma skin cancers in the spectral range from 370 to 1600nm.[8]

Although the integrating sphere based techniques can be used to investigate ex-vivo optical properties of epidermis, dermis, and subcutaneous tissue, the need to take biopsies from subjects limits their applicability in the clinic. Furthermore, once tissue has been excised, it is no longer part of the living organism; oxy- and dexoy-hemoglobin concentrations begin to diverge from physiologic quantities and if not carefully handled, the hydration of the tissue begins to change.

Photon diffusion theory derived from the radiative transport equation is usually employed as an forward model to determine optical properties of in-vivo samples at source-detector separation longer than five mean-free-paths, where mean-free-path is defined as 1/(µ_a+µ_s′). It has been proven to be a not adequate model for source-detector separations longer than five mean-free-paths, because boundary conditions and the assumption of multiple scattering in a turbid medium cannot be satisfied.[9, 10] However, in order to limit interrogation to superficial tissue volumes, such as skin, source-detector separations shorter than five mean-free-paths are more favorable. To the best of our knowledge, in-vivo techniques which employ alternative forward models to determine optical properties of skin do exist, but have some important limitations. For example, Zhang et al. determined optical properties of in-vivo skin using visible reflectance spectroscopy with a multi-layer skin model and a genetic optimization algorithm.[11] A multi-layer skin model and a number of fitting parameters, such as layer thickness, chromophores, and scattering properties for each layer, and their corresponding ranges must be chosen carefully in advance to avoid non-uniqueness in the solution space. Zonios and Dimou proposed a model to extract optical properties from diffuse reflectance spectra collected from human skin in-vivo.[12] Their technique requires that all of the chromophores contributing to the measured signals are known in advance and the reduced scattering coefficient has a linear relation to the wavelength in order to separate absorption and reduced scattering coefficients from measured reflectance. For the case where all constituent chromophores cannot be determined, the absorption spectra cannot be recovered. In addition, for the case where the reduced scattering coefficient does not have a linear dependence on wavelength, the empirical mathematical model will not recover tissue optical properties properly.

Previously, we used the diffusing probe that has a “modified two layer geometry” in conjunction with the Steady-State Frequency Domain Photon Migration (SSFDPM) technique to quantify the in-vivo skin optical properties of 15 subjects (five Caucasians, five Asians, and five African-Americans) in the wavelength range from 650 to 1000nm.[13] The facilitating technologic innovation of this probe is the presence of a highly diffusing Spectralon layer at the input side that enables a diffusion model for small source-detector distances (less than three mean-free-paths), and, thus, the absorption and reduced scattering coefficients of the superficial volumes of samples can be separated and quantified.

In this study, the probe design has been adjusted into multiple source-detector pairs so that it can employ a white light source to obtain continuous spectra of absorption and reduced scattering coefficients. The advantages of this multi source-detector separation probe include relative low instrument cost and self-calibration for instrument response (by using the reflectance of one source detection pair as the reference and normalizing the reflectance of other source detector separation pairs to the reference). The normalized reflectance versus source-detector separation is then fit to a diffusion model by a least square minimization algorithm to determine the absorption and reduced scattering spectra. The recovered absorption spectra are fit linearly with known chromophore absorption spectra to extract chromophore concentrations, and the reduced scattering spectra are fit to a scattering power law to obtain the scattering power.[14]

The goal of this paper was to use this new diffusing probe to determine the skin optical properties of 18 subjects of different skin phototypes and also extract the chromophore concentrations and the scattering power of skin. It is found that performing the “two-region chromophore fitting” to the absorption spectrum would result in the best fit with minimal residuals. By two-region chromophore fitting, we mean that the skin absorption spectrum is fit to a set of known chromophore absorption spectra at wavelengths between 500 nm and 600 nm and again fit separately between 600 nm and 1000 nm. The rationale for performing the two-region fitting is that the skin has very different optical properties in the visible and the NIR wavelength regions, and thus the sampling volumes at these two regions are quite different. Monte Carlo simulation results were generated to support this assumption. Likewise, the best fittings for reduced scattering coefficients of skin were obtained when the reduced scattering spectra were fit in the region below and above 600nm separately. This suggests that the average scatterer sizes of skin determined in the visible and the NIR regions are much different. Results from the measurements carried out here also indicate that the scattering power is not only dependent to anatomical location but also on skin phototype. Finally, experimental results obtained from measuring 10 subjects with forearm venous occlusion were provided. We recovered significantly different hemoglobin concentration at the region below and above 600nm. Our results agree with those reported by other researchers and support that our proposed probe and fitting method are capable of studying in-vivo superficial tissue at different depths simultaneously.

2. Materials and methods

2.1 Instrumentation

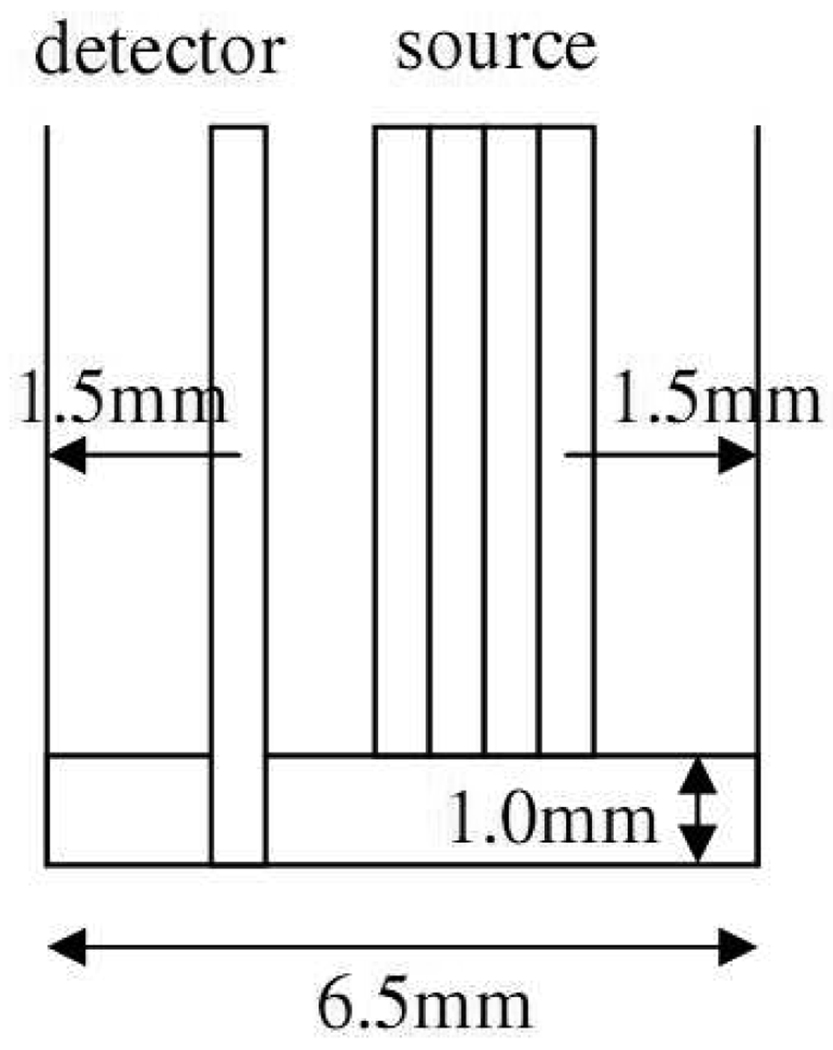
The diffusing probe used in this study is similar in design to the one we presented in our previous paper that was designed for SSFDPM instruments.[13] The geometry of this probe is illustrated in Fig. 1. The fibers employed in this probe are 480µm diameter low OH multimode fibers (core diameter=440µm) with numerical aperture of 0.22. The diameter of the Spectralon (Labshpere, NH, USA) disc is 6.5mm. The detection fiber penetrates the 1mm thick Spectralon layer so that it is flush with the lower surface of the Spectralon. There are four source fibers placed on the upper surface of the Spectralon and their distances from the detection fiber are 1.44mm, 1.92mm, 2.4mm, and 2.88mm, respectively. There are two 480µm spacer fibers placed in between the detection fiber and the first source fiber. The presence of the detection fiber in the Spectralon disturbs the photon propagation in the Spectralon that cannot be properly described by the diffusion theory. This phenomenon is severe when the source is close to the detector. Experimentally, we found that the reflectance measured with the source-detector pair of 0.48mm and 0.96mm separation cannot match with the theoretically calculated one. Therefore, in order to make the diffusion model work with our current probe, the shortest source-detector separation was chosen as 1.44mm. The probe was fabricated by RoMack Fiber Optics, VA, USA.

Fig. 1.

Configuration of the diffusing probe.

The detection fiber was connected to a spectrometer equipped with a back-thinned CCD (Model# BTC613, B&W TEK, DE, USA). An 1*4 optical switch (Piezosystem jena, MA, USA) was employed to switch between one fiber that is connected to a broadband Tungsten Halogen light source (Model# HL2000, Ocean Optics, FL, USA) and four source fibers of the diffusing probe. Because of the limitation imposed by the weak light source intensity below 600nm, the wavelength range in this study spanned from 500nm to 1000nm for subjects with skin type I–IV and spanned from 600nm to 1000nm for subjects with skin type V–VI. The optical switch and the spectrometer were connected to a computer and were coordinated and controlled by Labview (National Instruments, TX, USA). At each measurement, four reflectance spectra associated with four source-detector pairs were sequentially acquired and stored into one file. The average time required to take one complete measurement is about 10~20 seconds depending on skin pigmentation.

By using the reflectance from the 1.44mm source-detector pair as the reference, the reflectance from other source-detector pairs was normalized with respect to the reference reflectance. Thus, a normalized reflectance versus source-detector separation curve was generated. A modified two-layer diffusion model which has been described elsewhere was employed as a forward model to generate normalized reflectance versus source-detector separation curves to solve this inverse problem.[9][15] For completeness, we will provide a brief model derivation in the next subsection. The curve obtained from the experiment was then fit to the forward model to solve this inverse problem. The “lsqcurvefit” function in MATLAB (MathWorks, MA, USA) was used to perform the least-squares fittings to recover absorption and reduced scattering coefficients. With a personal computer equipped with an Intel Q6600 processor, absorption and reduced scattering spectra from a single sample can be determined within 10 seconds.

2.2 Modified two-layer model

The modified two-layer model was adopted from the two-layer photon diffusion model proposed by Kienle et al.[9][15] The derivation of the equation for calculating the reflectance at the detector in a modified two-layer geometry is briefly described here. In a two-layer turbid medium system, the diffusion equation can be written as:

$$\left[\frac{1}{c_i}\frac{\partial }{\partial t}+{\mu }_{ai}-\nabla [D_i(r)\nabla ]\right]{\mathrm{\Phi }}_i(r,t)=S_i(r,t)$$ (1)

, where D=1/3(µ_a+µ_s’) and Φ are the diffusion constant and the fluence rate, respectively. S is the source term, c is the speed of light in the medium, and i=1,2 is the number of the layer. The light source from the source fiber can be approximated as S₁=δ(x,y,z−z₀) and S₂=0, where z₀=1/(µ_a+µ_s’). By applying proper boundary conditions, where we employ the extrapolated boundary condition and assume the fluence and the flux are continuous at the boundary, the fluence rate of the diffusion equation system can be solved in the Fourier domain. In the modified two-layer geometry, one needs the fluence rate at the boundary of the first layer and the second layer to calculate the detected reflectance. The fluence rate at the boundary has the following form in the Fourier domain:

$${\varphi }_2(z,s)=\frac{\text{sinh}[{\alpha }_1(z_b+z_0)]}{D_1{\alpha }_1\text{cosh}[{\alpha }_1(l+z_b)]+D_2{\alpha }_2\text{sinh}[{\alpha }_1(l+z_b)]}$$ (2)

, Where ${\varphi }_2(z,s)={\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }{\mathrm{\Phi }}_2(x,y,z)\text{exp}\left[i\right(s_{1}x+s_{2}y\left)\right]\mathit{\text{dxdy}},{{\alpha }_2}^2=(D_2{s}^2+{\mu }_{a2}+j\omega /c)/D_2}}$, ω is the source modulation frequency, l is the thickness of the first layer, and s² = s₁² + s₂². By performing inverse Fourier transform to the solution numerically, we can obtain the fluence rate at the boundary. The spatially resolved reflectance can be calculated as the integral of the radiance L₂ at the boundary, where L₂ = φ₂ + 3D₂(∂Φ₂/∂z)cos θ, over the backward hemisphere:

$$R(\rho )={\displaystyle {\int }_{2\pi }[1-R_{\mathit{\text{fres}}}(\theta )]\text{cos}\theta (L_2/4\pi )d\mathrm{\Omega }}$$ (3)

Here $\rho =\sqrt{x^2+y^2}$, and R_fres (θ) is the Fresnel reflection coefficient for a photon with an incident angle θ elative to the normal to the boundary.

2.3 In-vivo skin measurements

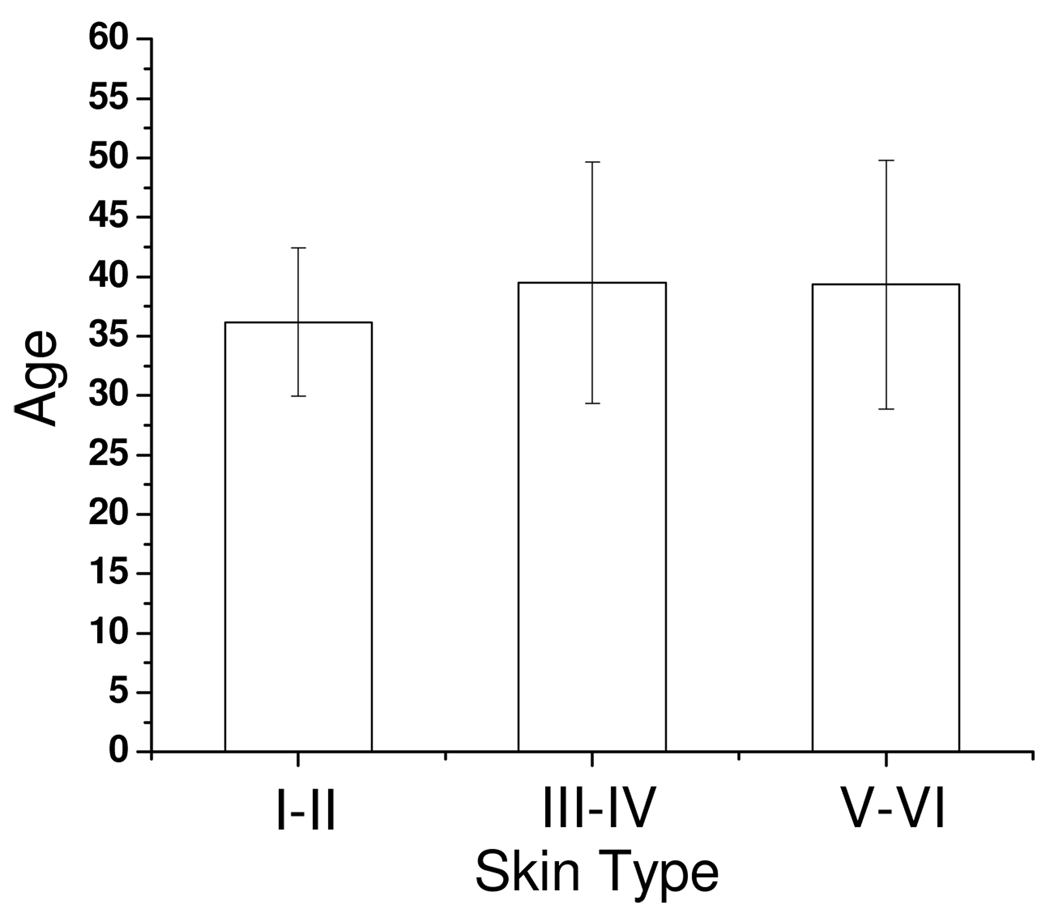
In this study, six subjects in skin type I–II, six subjects in skin type III–IV, and six subjects in skin type V–VI were recruited. The protocol was approved by the Institutional Review Board and the written informed consent was obtained from all subjects prior to the measurements. Measurement sites included the dorsal aspect of forearm and the upper inner arm. Three measurements were taken at each anatomic site on each subject, and the probe was physically removed and replaced on each site for each measurement. Because the dorsal forearm is usually a sun-unprotected site while the upper inner arm is relatively a sun-exposed site, we have chosen these locations for the first in-vivo experiments. The mean and the standard deviation of the age of the subjects in each skin photo-type category are shown in Fig. 2. There is no statistically significant difference in age between each group; therefore, the influence of intrinsic ageing on the optical properties is minimal.

Fig. 2.

Average and standard deviation of age of 6 subjects in each skin photo-type category.

2.4 Interrogation depth of diffusing probe

The diffusing probe was designed to investigate superficial volume of tissues. In order to interpret our results, the interrogation depth of this probe geometry needs to be carefully characterized in advance. The details of interrogation depth depend on wavelength dependent optical properties of the sample as well as source-detector separations. Monte Carlo simulations were used to obtain a detailed understanding of the interrogation region and depth of this diffusing probe. Since skin absorption and reduced scattering coefficients at 500nm are much higher than those at 900nm, the skin optical properties at 500nm and 900nm (data will be presented later in this paper) were used as input parameters in the Monte Carlo simulations. Moreover, the source-detector separations were set to 1.5mm and 3mm in the simulations to encompass the range of source-detector separations of our probe. Therefore, four sets (two s-d distances, two sets of optical properties) of Monte Carlo simulation results will be shown.

The Monte Carlo code used here is an extension of the general multi-layer, three dimensional, weighted photon Monte Carlo code developed by Wang et al.[16] In order to visualize the distribution of detected photon packets in the superficial diffusing probe geometry, two dimensional fluence distribution maps were generated using Monte Carlo simulations. When a photon packet encounters a collision, a fraction of energy of the photon packet, which is proportional to the weight of the photon packet and the absorption of the medium, is deposited to a local voxel in a three dimensional Cartesian coordinate system. Local fluence (J/mm²) is calculated by dividing the deposited energy by the local absorption coefficient. A three dimensional photon fluence distribution map is obtained by accumulating the fluence distribution of all photon packets arriving at the detector. The three dimensional map is converted to a two dimensional x–z map by binning along the y axis. The maps are normalized by the number of photon packets launched, the volume of a voxel, and the maximal fluence in the map.

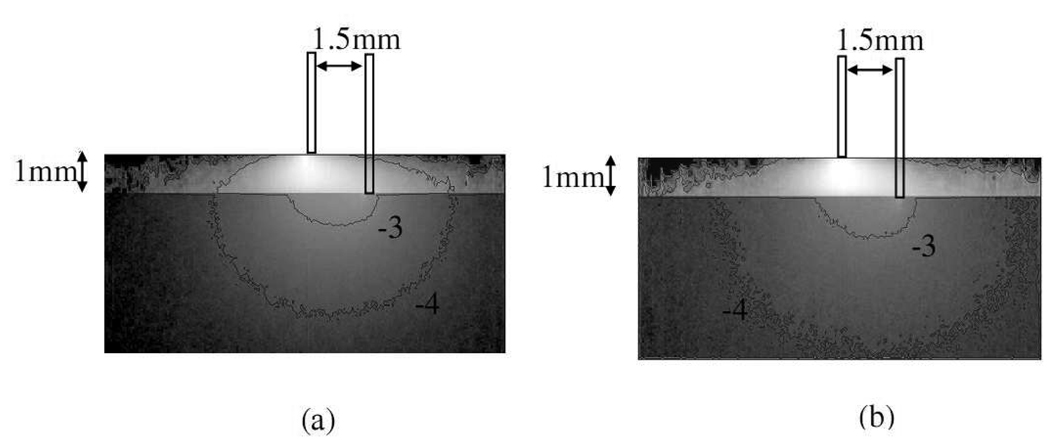
In the simulations, we used modified two-layer geometry in which the detection fiber penetrated the top high scattering layer and in contact with the semi-infinite sample layer. The optical properties were set as µ_a=1e−5/mm and µ_s′=50/mm for the high scattering top layer, and the source-detector separation was 1.5mm. The indices of refraction of the high scattering layer and the sample were 1.35 and 1.33, respectively. The index of refraction of the source fiber and the detection fiber was not considered in the simulations. The numerical aperture of the fibers was 0.22. Five million of photon packets were launched in each simulation. To simulate the effect of wavelength dependent optical properties on the size of the interrogation region, we used two sets of optical properties for the sample: µ_a=0.05/mm, µ_s′=1.5/mm to simulate light complexion skin at 900nm, and µ_a=0.1/mm, µ_s′=3/mm to simulate light complexion skin at 500nm. The distribution maps generated based on these parameters are shown in Fig. 3 and they are presented here as the logarithm base 10 of the original maps for greater ease of visualization. The fluence map illustrated in Fig. 3(a) represents photon distribution in light complexion skin at 500nm and Fig. 3(b) represents photon distribution in light complexion skin at 900nm. Comparing Fig. 3(a) and 3(b) qualitatively, it can be seen the “−4” contour line in Fig. 3(b) is wider and deeper than that in Fig. 3(a). This means the diffusing probe has deeper interrogation depths at 900nm compared to the interrogation depths at 500nm.

Fig. 3.

Normalized photon fluence distribution maps of the diffusing probe with (a) a light source of 500nm wavelength and (b) a light source of 900nm wavelength. Whiter region represent higher fluence rate area. Note that the contour line “−4” in (b) encloses larger region than that in (a). Please refer to text for the parameters used.

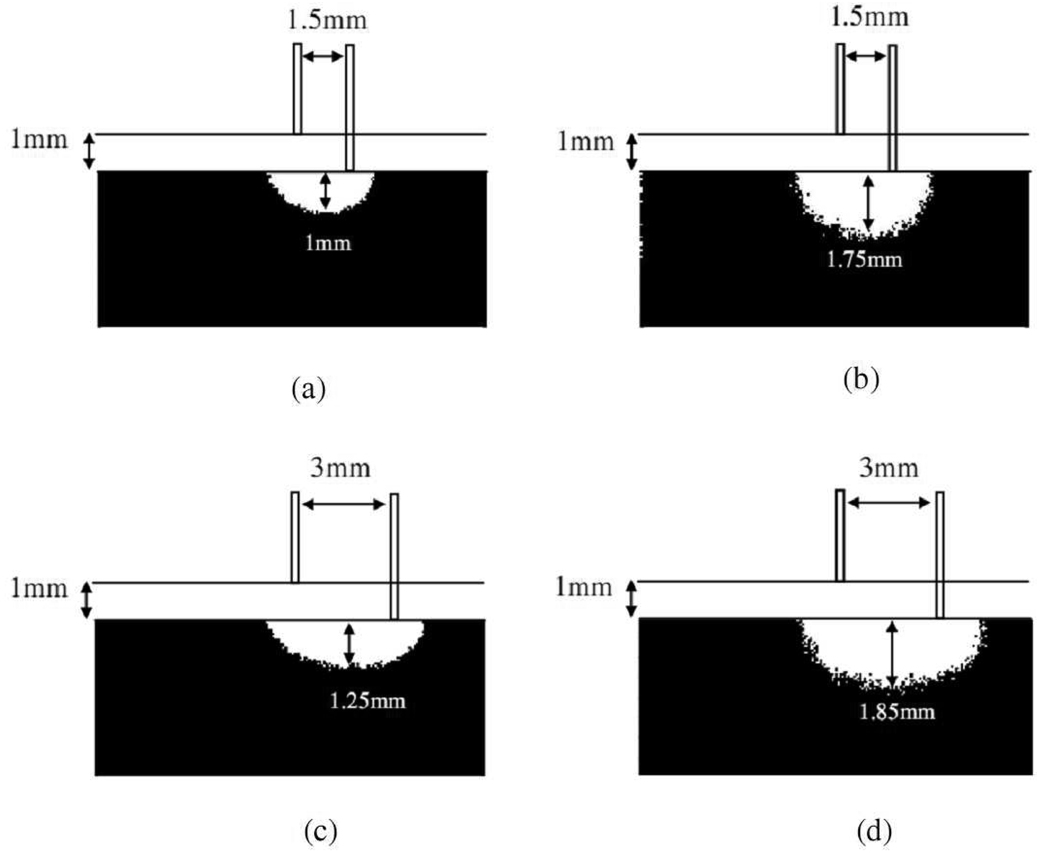
To compare the interrogation depth and region quantitatively, threshold maps were generated, as illustrated in Fig. 4, based on the fluence maps. The threshold maps shown in Fig. 4 illustrate only the sample layer and do not include the high scattering layer. The white area in the threshold maps denotes the voxels that have top 50 % greatest fluence values, and black area denotes otherwise. The interrogation depth of a 1.5 mm source-detector separation diffusing probe defined by the threshold map shown in Fig. 4(a) is about 1000µm at 500 nm while that defined by Fig. 4(b) is about 1750µm at 900 nm. The increase in interrogation depth is about 75% as the light source wavelength is changed from 900nm to 500nm. Similarly, the threshold maps were generated for a diffusing probe with source-detector separation of 3mm and they are illustrated in Fig. 4(c) and 4(d). The interrogation regions are larger in Fig. 4(c) and 4(d) than in 4(a) and 4(b). The interrogation depths defined by Fig. 4(c) and 4(d) are 1250µm and 1850µm, respectively, which represents 48% increase in interrogation depth as the wavelength is changed from 900nm to 500nm.

Fig. 4.

50% threshold maps for the diffusing probe of 1.5mm source-detector separation with (a) 500nm light source and (b) 900nm light source, and for the diffusing probe of 3mm source-detector separation with (c) 500nm light source and (d) 900nm light source. White region in the tissue sample represents the area that has top 50% fluence rate. Please refer to text for the parameters used.

In addition to the interrogation depth defined above, since the Monte Carlo simulations can tally the travel histories of all detected photons, the average interrogation depth of simulation can also be defined as following: Let $P_i=W_i/{\displaystyle {\sum }_{i=1}^n{W}_i}$, where W_i is the final weight of a detected photon packet and n is the number of photon packets launched. The average interrogation depth of a simulation is determined as $\overline{z}={\displaystyle {\sum }_{i=1}^n{P}_i{\left(z_{\mathit{\text{ave}}}\right)}_i}$, where $z_{\mathit{\text{ave}}}={\displaystyle {\sum }_{j=1}^m{d}_j/m}$ is the average penetration depth of a detected photon packet, d_j is the depth at which a collision happens in the sample, and m is the total collision number in the sample of the detected photon packet. Based on this definition, the average interrogation depth for the light complexion skin at 500nm is 646µm while that for the light complexion skin at 900nm is 947µm for the diffusing probe with 1.5mm source-detector separation. The average interrogation depth is 1100µm and 1601µm at wavelengths of 500nm and 900nm, respectively, for the diffusing probe with 3mm source-detector separation. Therefore the average interrogation depth of the diffusing probe has a 45%–47% increase as the light source wavelength is varied from 900nm to 500nm. Hence, the interrogation depth and interrogation region are significantly modulated by the light wavelength, whichever definition of interrogation depth is used. The interrogation region of the probe includes epidermis and upper dermis at wavelength of 500nm. As the wavelength increases to 900nm, the interrogation region includes epidermis, dermis, and a portion of subcutaneous lipid layer. The optical properties determined would be the average properties of the volume under investigation. This information will be used in the next few sections to help interpret the in-vivo data obtained and support the analyses applied to the data.

3. Results and discussions

3.1 Optical properties of in-vivo skin of various skin phototypes

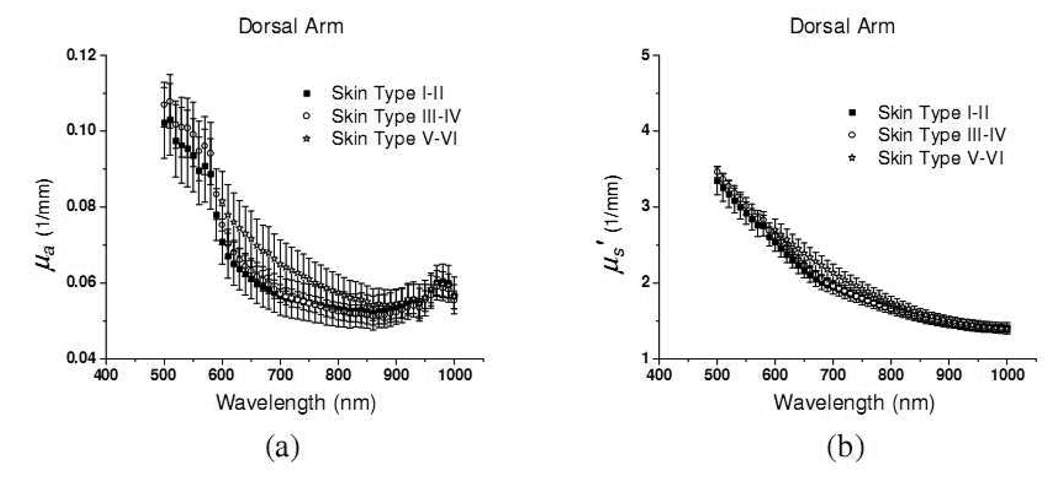
The absorption and reduced scattering coefficients of in-vivo dorsal forearm of eighteen subjects are demonstrated in Fig. 5. The data shown in Fig. 5 are in good agreement with those obtained from ex-vivo measurements and the in-vivo data reported earlier.[6] In Fig. 5(a), the absorption coefficients of the dorsal forearm of skin type I–II and III–IV increase steeply by a factor of two as the wavelength decreases from 600nm to 500nm. Hemoglobin and melanin both contribute to the increase in the absorption in this region. From ex-vivo measurement of extinction coefficients of hemoglobin, the abrupt increase at 600nm is one of the signatures of hemoglobin.[17] The optical properties of the dorsal forearm of skin type V–VI in the region from 500 to 600nm are not shown here since the skin was too absorbing and the measured reflectance were too noisy to recover accurate optical properties.

Fig. 5.

(a) absorption coefficient and (b) reduced scattering coefficient of in-vivo dorsal forearm of 18 subjects. Each skin phototype group has 6 subjects. Solid squares, open circles, and open stars represent optical properties of skin type I–II, III–VI, and V–VI, respectively.

In the 600–800nm region, the absorption coefficients decrease monotonically as the wavelength increases, and both hemoglobin and melanin contribute to this trend. Overall, the absorption spectra of dorsal forearms of skin type V–VI have greater slope in this wavelength region compared to the skin type I–II and III–IV. This should be caused by the difference in melanin concentration in various skin types, assuming other chromophore concentrations are similar. At wavelengths longer than 900nm, the absorption coefficients of three skin type groups have almost the same magnitude and the prominent absorption peak induced by water absorption at 980nm can clearly be observed.

The reduced scattering coefficients of the dorsal forearm of eighteen subjects are illustrated in Fig. 5(b). The average reduced scattering coefficients of the three groups are very similar. The average reduced scattering coefficients of the skin type V–VI group are is 1–10% higher than those of the skin type I–II and III–IV groups. This phenomenon may due to the fact that the density of scatterers in skin, such as melanin, is higher in the skin type V–VI group than skin type I–II and III–IV groups. In addition, the scattering spectra are not smooth over the whole wavelength region. Specifically, the scattering spectra have a very minor peak at 580nm which coincide with the absorption peak of oxy-hemoglobin. This phenomenon is very likely caused by the cross talk between µ_a and µ_s′ in the diffusion theory. Nevertheless, in the data reported by Bashkatov et al. and Salomatina et al., the coupling between absorption and reduced scattering coefficients is also evident.[7] They employed the inverse adding doubling technique, which should have smaller µ_a and µ_s′ cross talk than the diffusion theory, to recover the optical properties of human tissues. These observations reflect the fact that the structures which are commonly associated with absorbing chromophores could also play a role in light scattering.

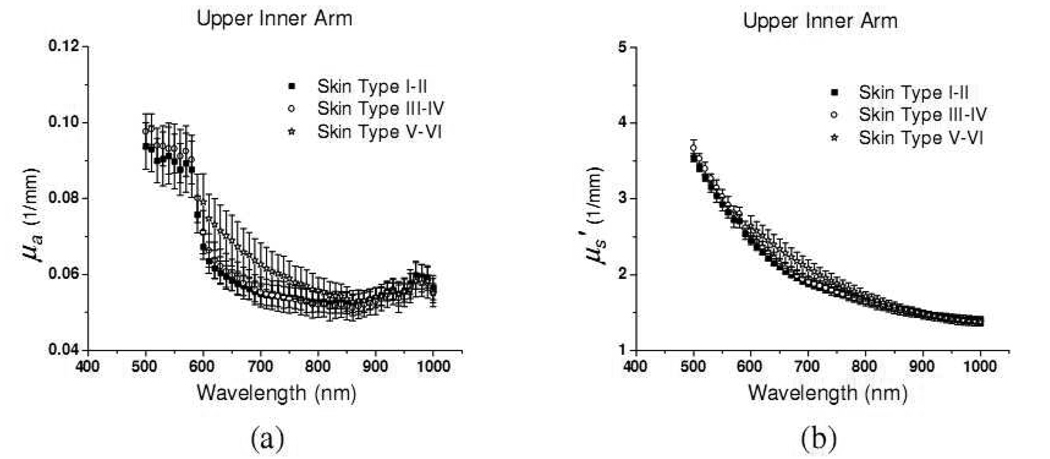
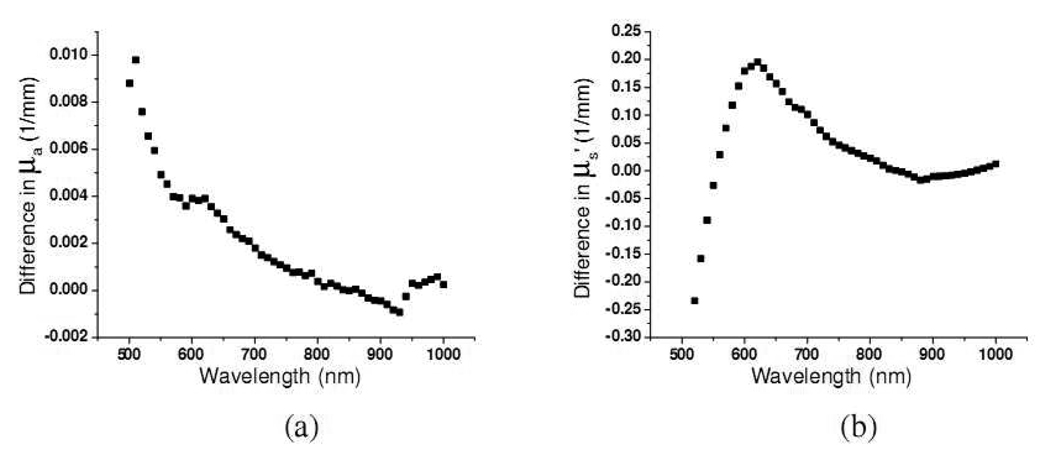
The absorption and reduced scattering coefficients of unexposed upper inner arm of eighteen subjects are illustrated in Fig. 6(a) and 6(b), respectively. The absorption coefficients of upper inner arm are generally lower than those of dorsal forearm within each skin type group in the wavelength range from 500 to 900nm. This can be attributed to higher melanin concentration at the dorsal forearm than upper inner arm, since, as mentioned before, the dorsal forearm is usually a sun-exposed site while the upper inner arm is usually a sun-protected site. By subtracting the mean absorption spectrum of the upper inner arm from that of the dorsal forearm of twelve subjects of skin type I–IV, the differential spectrum is shown in Fig. 7(a). The differences increase as the wavelength decreases from 900nm to 500nm, and this trend resembles those of ex-vivo and in-vivo melanin reported by Jacques et al. and Kollias et al.[18][19] However, because our probe has larger sampling volumes at longer wavelengths, melanin volume density is not constant over the wavelength region. Moreover, the differential spectrum shown in Fig. 7(a) may contain contributions from other chromophores such as hemoglobin. In addition, the lower subcutaneous fat absorption at 930nm of dorsal forearm compared to upper inner arm is illustrated.

Fig. 6.

(a) absorption coefficient and (b) reduced scattering coefficient of in-vivo upper inner arm of 18 subjects. Each skin phototype group has 6 subjects. Solid squares, open circles, and open stars represent optical properties of skin type I–II, III–VI, and V–VI, respectively.

Fig. 7.

The difference between the (a) mean absorption coefficient, and (b) mean reduced scattering coefficient of dorsal forearm and upper inner arm of twelve subjects of skin type I–IV. (The mean coefficient of upper inner arm is subtracted from that of dorsal forearm)

The differential spectrum obtained by subtracting the mean reduced scattering coefficient of upper inner arm from that of dorsal forearm of twelve subjects of skin type I–IV is plotted in Fig. 7(b). Unlike the differential absorption spectrum shown in Fig. 7(a), the differential reduced scattering spectrum first increases gradually as the wavelength decreases from 800nm to 580nm and then decreases precipitously for wavelengths shorter than 580nm. The mean reduced scattering coefficients for the dorsal forearm and the upper inner arm are very similar in the range from 800 to 1000nm. The bending of the curve at 580nm represents that the mean scatterer sizes at the two anatomical locations are different. Specifically, the mean scatterer size at the dorsal forearm is larger than that at the upper inner arm. Mourant et al. have demonstrated the similar trend using 0.05 and 0.1-µm-radius polystyrene spheres (Fig. 5). [20] From the Monte Carlo study, we understand that the diffusing probe has a much more superficial interrogation volume at short wavelengths than at long wavelengths. Therefore, we might conjecture that the size of the scatterers located at superficial skin, such as melanin dust, of the dorsal forearm is larger than that of the upper inner arm. We will discuss and perform analyses on the reduced scattering coefficients at wavelength regions covering 500–600nm and 600–1000nm in the following section.

3.2 Calculating skin chromophore concentrations using two-region fitting

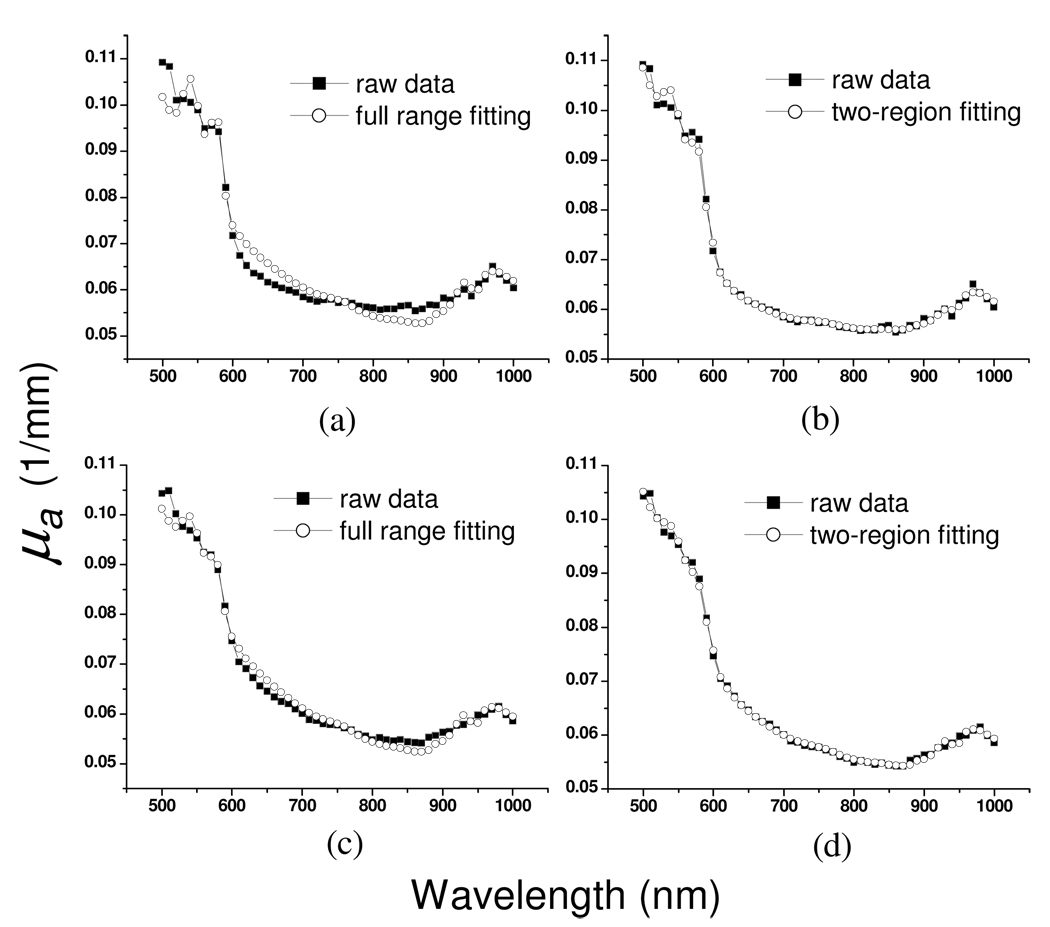
From our Monte Carlo simulation results, it can be inferred that the spectrum at 500–600nm derives from shallower skin layers than does the spectrum for the 600–1000nm region. Because of this reason, we have investigated the effect of fitting the chromophore extinction coefficients to the absorption coefficients in two wavelength regions independently versus fitting the entire wavelength region alone. Two fitting examples are demonstrated in Fig. 8. First, the skin absorption spectra ranging from 500nm to 1000nm were linearly fit with positive constraint to a set of chromophore spectra consisting of the extinction coefficients of oxy-hemoglobin, deoxy-hemoglobin, melanin, water and lipid. The fitting results of two absorption spectra are shown in Fig. 8(a) and 8(c). Linear fits with positive constraint were then performed to the same skin absorption spectra in 500–600nm and 600nm–1000nm regions independently. In the 500–600nm regional fitting, the water and lipid in the chromophore spectra set were excluded since their absorption coefficients are at least four orders of magnitude weaker than those of hemoglobin and melanin. The two-region fit results are shown in Fig. 8(b) and 8(d). Overall, it can be seen that the two-region fit performs better than the full range fit. The chromophore fit results of eighteen subjects are listed in Table 1 and Table 2 for dorsal forearm and upper inner arm, respectively.

Fig. 8.

Two typical chromophore fitting examples with full range fitting method and two-region fitting method. (a) and (b) demonstrate the fitting results of two fitting methods with the same raw data. (c) and (d) demonstrate another example. Solid squares represent raw data and open circles represent fit spectra.

Table 1.

Chromophore concentrations of dorsal forearm of 18 subjects recovered with two-regional fitting. Standard deviations were calculated to illustrate the deviation of recovered chromophore concentrations of 6 subjects within each group. Res.full represents the fitting residual of full wavelength range (500–1000nm) fitting, and Res.reg represents the fitting residual of two-regional fitting.

	500–600nm			600–1000nm
Dorsal forearm	deoxyHb [µM]	oxyHb [µM]	Melanin [%]	deoxyHb [µM]	oxyHb [µM]	Melanin [%]	H2O [%]	Lipid [%]	Res. full	Res. Reg
I–II	0.26 ±0.19	0.81 ±0.42	1.65 ±0.18	0.12 ±0.51	7.74 ±3.15	0.87 ±0.18	21.42 ±2.59	27.74 ±5.01	0.00165	0.00066
III–IV	0.31 ±0.28	0.84 ±0.30	1.98 ±0.09	0.08 ±0.26	9.47 ±3.41	1.15 ±0.09	22.46 ±2.46	26.12 ±6.04	0.00149	0.00069
V–VI	-	-	-	0.02 ±0.10	2.72 ±2.40	1.65 ±0.23	18.66 ±3.17	16.56 ±8.23	-	0.00104

Table 2.

Chromophore concentrations of upper inner arm of 18 subjects recovered with two-regional fitting. Standard deviations were calculated to illustrate the deviation of recovered chromophore concentrations of 6 subjects within each group. Res.full represents the fitting residual of full wavelength range (500–1000nm) fitting, and Res.reg represents the fitting residual of two-regional fitting.

	500–600nm			600–1000nm
Upper inner arm	deoxyHb [µM]	oxyHb [µM]	Melanin [%]	deoxyHb [µM]	oxyHb [µM]	Melanin [%]	H2O [%]	Lipid [%]	Res. full	Res. Reg
I–II	0.28 ±0.22	0.86 ±0.34	1.56 ±0.18	0.09 ±0.41	8.15 ±2.06	0.64 ±0.04	18.68 ±1.34	30.72 ±3.79	0.00203	0.00061
III–IV	0.42 ±0.29	0.82 ±0.39	1.66 ±0.24	0.31 ±0.60	9.57 ±2.78	0.82 ±0.09	19.23 ±2.29	33.69 ±5.46	0.00200	0.00067
V–VI	-	-	-	0.02 ±0.08	4.44 ±3.17	1.33 ±0.23	16.99 ±2.20	30.20 ±6.52	-	0.00086

The mean of the residual of full range fit and two-region fit is displayed in Table 1 and Table 2. The mean residual is defined as follows. Let r_i be the fit residual at wavelength λ_i; the average residual equals ${\displaystyle {\sum }_{i=1}^n\left|r_i\right|/n}$, where n is the number of wavelengths. The mean residual for the two-region fit is about one third of that for the full range fit in all cases.

The oxy-hemoglobin concentrations obtained in the 600–1000nm range are an order of magnitude higher than those obtained in the 500–600nm range. This suggests that the blood concentration in skin increases as depth increases, and this finding agrees with the general skin model that assumes vessel diameter increases from the upper plexus in the papillary dermis to the lower plexus at the dermal-subcutaneous interface. Braverman indicated that the vessel diameter at the lower plexus is generally about two to three times larger than that at the upper plexus in the dermis.[21]

The average oxygen saturation of hemoglobin StO₂ can be calculated from table 1 and table 2. The average StO₂ is in the range of 97–99% at the wavelength region 600–1000nm. This is a reasonable range for the blood vessels at the lower plexus in the dermis, since they are connected to the arteries coming from the subcutaneous fat layer and the muscle layer. In contrast, the average StO₂ is in the range of 66–75% for dorsal forearm or upper inner arm of skin type I–II and III–IV at the wavelength region 500–600nm. Our finding indicates that the blood flow and hemoglobin dynamics at the upper and lower plexuses are quite different. Nishidate et al. employed noninvasive optical method to investigate skin property and reported that the StO₂ of skin of arm at rest was about 60% using wavelength from 400–700nm.[1] Since the 500–600nm wavelength range we used in our study for determining the upper plexus StO₂ is located at the center of the 400–700nm range that Nishidate et al. used in their study, their result is an excellent support to our finding.

On the other hand, melanin concentrations recovered at 500–600nm are significantly higher than those recovered at 600–1000nm at both measurement sites of skin type I–II and III–IV. Since the melanin is localized in the epidermis, as the interrogation region becomes larger at 600–1000nm, the derived melanin concentrations are diluted and thus smaller compared to those derived at 500–600nm. Jacques et al. reported that the volume fraction of melanin in the epidermis is 1 to 3% for light-skinned Caucasians, 11 to 16% for Mediterranean types, and 18–43% for darkly pigmented Africans.[22] In table 1 and 2, the trend of the melanin percentage versus the skin phototype number correspond reasonably well with those reported by Jacques et al. Note that the melanin fraction determined at 500–600nm region is about 40–50% higher than those determined at 600–1000nm region. This result is consistent with the wavelength dependent reduction in interrogation volume as indicated by our Monte Carlo simulation results (45% increase in interrogation depth as the wavelength increases from 500nm to 900nm).

In this study, we also determined the concentration of water and lipid using their absorption features at 980nm and 930nm, respectively. By fitting NIR absorption spectra to chromophore spectra, Taroni et al. obtained the water volume percentage of forearms to be in the range from 13–32%.[23] The source-detector separation employed in their study was 2cm; thus, the water volume percentage determined by them represented the average value of the bulk tissue. The water volume fractions presented in this study are in the range from 16–22% as demonstrated in Table 1 and Table 2. Since we employed the wavelength region near 980nm to recover the water concentration, the interrogation depth is relatively deep and thus our results reasonably agree with those reported by Taroni et al. However, our results are not consistent with the skin water content (~65%) determined by skin desiccation.[24] We speculate that this discrepancy may come from two sources. First, the whole interrogation region of our probe most likely covers the epidermis, the dermis, and part of the subcutaneous layer of skin at the wavelength of 980nm. Hence, we have recovered the skin lipid concentration in the range from 16 to 30% as shown in Table 1. Since the subcutaneous layer has very low water content (~18% as indicated by Reinoso et al.), the skin water concentration determined by our method is lower than that reported by Reinoso et al. using desiccation method where they employed skin samples that were separated from the subcutaneous tissue.[24] Furthermore, it can be seen from Table 1 and 2 that the skin water concentration decreases as the skin melanin concentration increases. This means that the water concentration recovered by our algorithm could be affected by the melanin content of skin. Because water has only one prominent absorption feature at 980nm in the wavelength range of concern in this study, the accuracy of the skin water concentration determined using our algorithm strongly relies on the correctness of the chromophore absorption spectra near 980nm. The melanin absorption spectrum employed in our algorithm was adopted from the power law equation proposed by Jacques, which was an approximated equation derived from the data reported by various researchers at several wavelengths.[18] The uncertainty of this power law equation is high at wavelengths longer than 800nm since there is only one data point in this range. The uncertainty of the melanin absorption spectrum near 980nm could be another source for underestimating the water concentration of skin. The problem of underestimating skin water concentration caused by the two factors mentioned above could be alleviated by extending the upper bound of the experiment wavelength range to above 1000nm. Since there are more water absorption features and the melanin absorption is weaker in the wavelength range above 1000nm, the water concentration can be reliably recovered with minimum influence from melanin absorption. Moreover, the absorption coefficient of skin rapidly increases with the wavelength in the wavelength range above 1000nm due to strong water absorption in this range. Therefore, the interrogation depth of our probe decreases as the wavelength increases in this range, which will in turn diminish the contribution of the subcutaneous tissue to the measurement results. Extending the measurement wavelength range is one of the subjects of our continued research in an effort to develop a probe that can more accurately and reliably be used to deduce skin chromophore concentrations.

3.3 Two-region scattering power law least-square fit

We have illustrated in the previous section that the chromophore fitting quality can be improved by performing a two-region fit. In this section we will perform a two-region scattering power law fit to the reduced scattering spectra of skin.

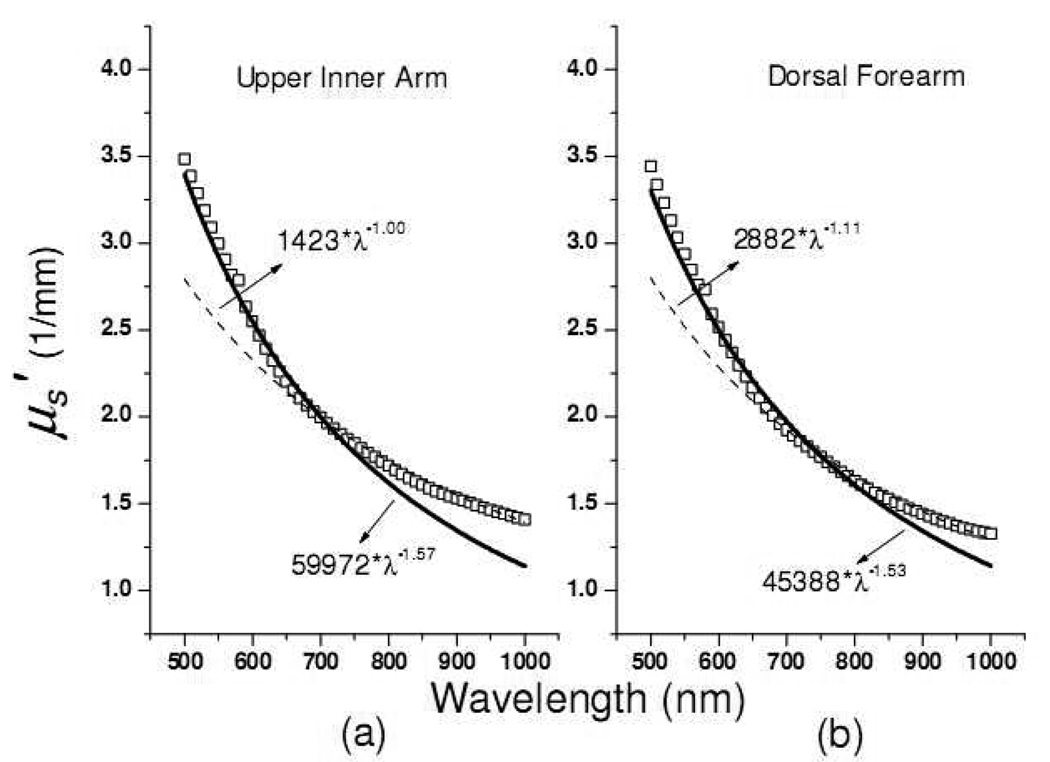
Mourant et al. used a power law a * λ^−b to fit the reduced scattering spectra of samples, and found that the scattering power −b was correlated to the scatterers’ average size in tissue phantoms: the smaller the value of −b, the smaller the average size of scatterers.[20] In fitting the skin reduced scattering spectra to a scattering power law, we found that a single scattering power law did not produce good fit results over the wavelength range of 500–1000nm. A two-region scattering power law fit to the skin reduced scattering spectrum was performed in which the reduced scattering spectrum at 500–700nm was fit with one scattering power law and that at 700–1000nm was fit with a separate scattering power law. An example is shown in Fig. 9, which demonstrates the two-region fit of the reduced scattering spectra of the dorsal forearm and upper inner arm of a subject. It can be seen in Fig. 9 that either spectrum cannot be well fit by a single scattering power law. We performed two-region fitting to the reduced scattering spectra of dorsal forearm and upper inner arm of eighteen subjects and summarized the calculated scattering power in the Fig. 10.

Fig. 9.

Two-region power law fitting of the reduced scattering spectra of the (a) dorsal forearm and (b) upper inner arm of a subject. Open squares represent raw data. Solid lines are the power law fitting to the raw data in 500nm to 600nm range while the dash lines are the power law fitting results in the 600nm to 1000nm range.

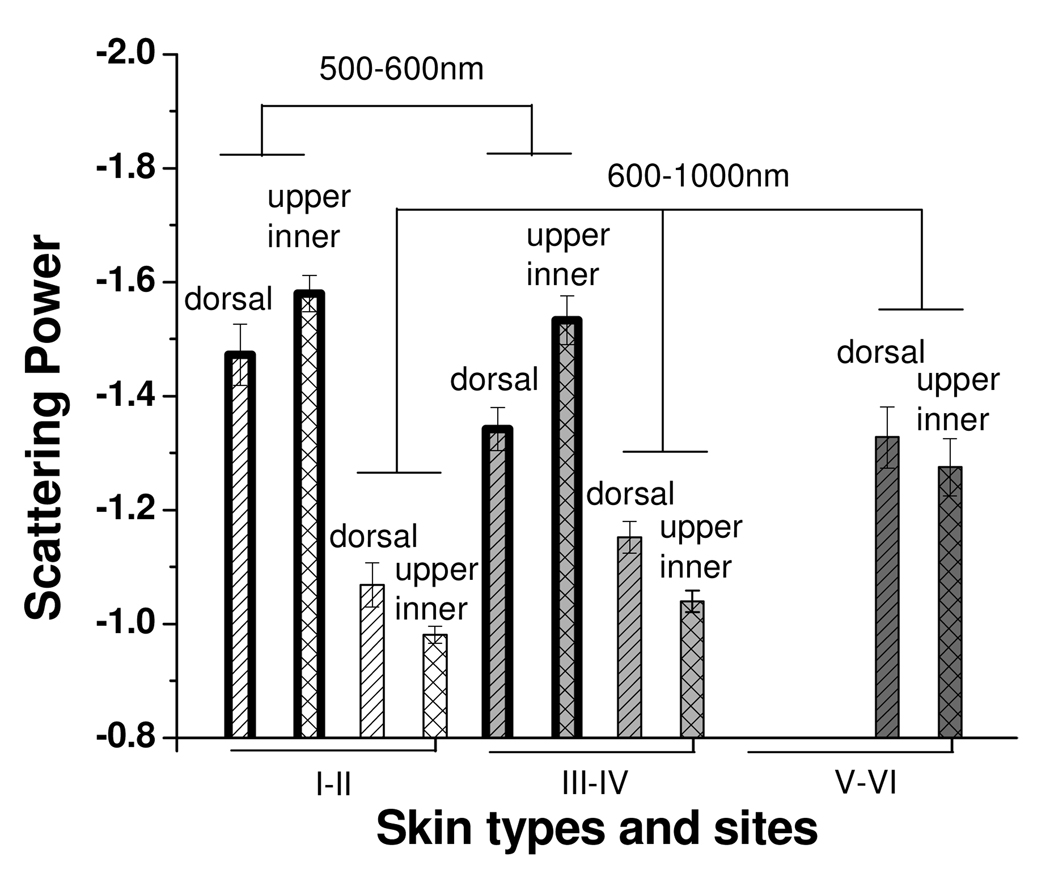
Fig. 10.

Scattering power calculated from two-region fitting to the reduced scattering spectra of dorsal forearm and upper inner arm of 18 subjects. Each skin phototype group has 6 subjects.

One of the first noteworthy features that are apparent in Fig. 10 is that the scattering power at 500–600nm is smaller than that at 600–1000nm for dorsal forearm and upper inner arm of skin type I–II and III–IV. Bashkatov et al. used two scattering power law to fit the skin reduced scattering spectra from 400nm to 2000nm, and concluded the scattering at wavelengths shorter than 600nm was attributed to the small Rayleigh scatterers, such as melanin dust and structural cell components, (size<<300nm) while the scattering at wavelengths longer than 600nm came from large Mie scatterers, such as collagen and elastin bundles, (size~1–8µm).[7] They reported scattering power of skin was −1.1 for the spectral range of 500–1200nm. In our data, we find that the reduced scattering of skin type I–II and III–IV at the wavelength range of 600–1000nm has scattering power of −1.15~−1.0 which is similar to the values obtained by Bashkatov et al. At wavelengths shorter than 600nm, we obtain scattering power in the range from −1.35~−1.6. The scattering power of this range corresponds to the medium size Rayleigh-Gans scatterers, such as cells and melanocytes, (size~300–600nm).[7, 25] In the 400–600nm range, Bashkatov et al. reported scattering power of –4, which was induced by Rayleigh scattering (size<100nm). The difference between our results and Bashkatov’s results in the wavelength shorter than 600nm may be caused by different fitting wavelength ranges and/or the inherent differences between in-vivo and ex-vivo samples, such as tissue hydration that affects the matrix surrounding the scattering bodies which in turn affects the scattering process.

As shown in Fig. 10, in the wavelength from 600–1000nm, the mean scattering power of dorsal forearm is lower than that of upper inner arm for all skin types. Considering the average interrogation depth is about 1000µm in this wavelength range, the dermis dominates the whole interrogation volume. Assuming the main difference between the two sites is the degree of sun exposure, the difference of the scattering power of the two sites is resulted mainly from the sun exposure altered dermis scattering property and partly from the sun exposure altered epidermis scattering property. Several researchers reported skin collagen structure could be affected by chronic UV exposure. Kollias et al. found that the fluorescence from the collagen cross-links in dermis decrease with chronic UVB exposure.[26] Miyamae concluded that the changes in the dermis property with photoaging are tied to the collapse of dermal collagen and the degeneration of elastic fibers.[27] Since the dermis dominates the interrogation volume of this probe, we speculate that the collagen and elastin bundles at the chronically sun-exposed site, such as dorsal forearm, may have smaller size than those at the sun-protected site, such as upper inner arm, which causes the mean scattering power of dorsal forearm is smaller than that of upper inner arm. In addition, sun exposure induces skin melanin production; therefore, the interrogation depth will be shallower in the relatively high melanin, high absorption dorsal forearm compared to the low melanin, low absorption upper inner arm. This will also make the scattering power move to smaller values at higher absorption site, since the size of the dominant scatterers in the epidermis, melanosome and cell structure, is much smaller than that of the dominant scatterers in the dermis, collagen and elastin bundles. Note that in this wavelength range, the scattering power decreases as the skin type number increases. Again, this phenomenon comes from the gradually more significant influence of the small size scatterers at epidermis on the overall scattering power as the skin type number and skin absorption increases.

In contrast, the mean scattering power of upper inner arm is smaller than that of dorsal forearm for skin type I–II and III–IV at 500–600nm. Melanin, which has index refraction of about 1.7[28], is generated and stored in the melanosome in the epidermis. Because the diffusing probe has average interrogation depths less than 500µm at wavelengths shorter than 600nm and melanin particles are very strong scatterers, the diffusing probe is sensitive to scattering introduced by melanin particles stored in the melanosome. Since solar radiation stimulates melanin generation, a sun-exposed site would have more melanin dust clustered in the melanosome compared to a sun-protected site. Therefore, the equivalent scatterer size in the epidermis of sun-exposed dorsal forearms may be larger than that of sun-protected upper inner arms which causes this trend shown in our data for skin type I–II and III–IV. Furthermore, it is seen that the mean scattering power in this wavelength region increases as skin type increases (I–II to III–IV) for both measurement sites in this study. Brenner and Hearing reported that the major elliptical axis of melanosome in Black skin is longer than that in White skin (roughly 800nm versus 400nm).[29] Their result is a strong support to our finding which demonstrates that, in the 500–600nm wavelength region, the mean scatterer size increases as skin type number increases (I–II to III–IV) for both anatomic sites. This also implies that at 500–600nm region our probe is sensitive to the epidermal scattering structure.

3.4 Determining hemoglobin concentrations of forearm skin with occlusion using two-region fitting

To demonstrate that the two-region chromophore fitting method can be used to monitor the variation of in-vivo skin chromophore concentrations at different depths, venous occlusion was induced on the forearm of 10 subjects who were enrolled in the previous study and had skin type I–IV. A pneumatic cuff was placed on the upper arm of the subjects and three baseline measurements were taken with the diffusing probe on the volar forearm of each subject. The pneumatic cuff was then inflated to a pressure of 50mm-Hg to induce venous occlusion. After the pressure was applied on the upper arm for 30 seconds, the volar forearm of each subject was measured once with the diffusing probe. The pressure was kept constant at 50mmHg over the course of measurement.

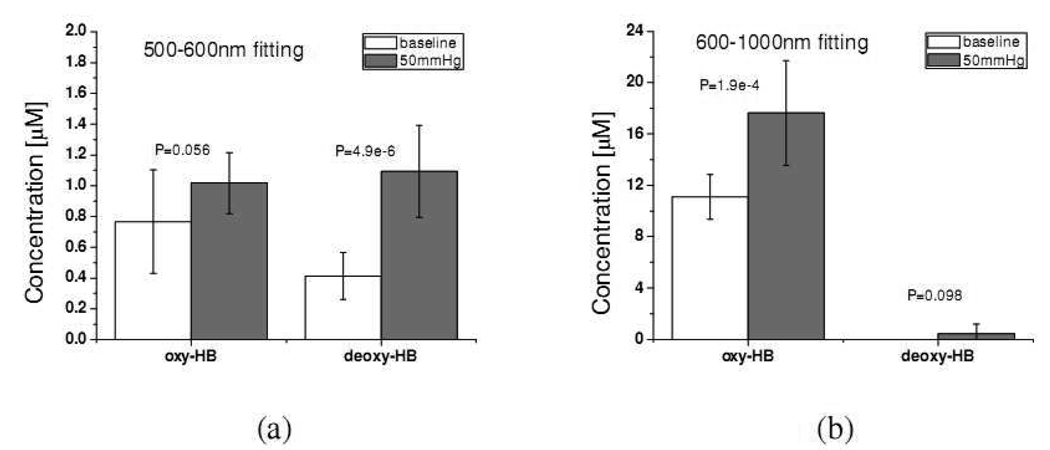
The average oxy-hemoglobin and deoxy-hemoglobin concentrations before and after venous occlusion recovered at the 500–600nm and 600–1000nm regions of 10 subjects are plotted in Fig. 11. It can be seen in Fig. 11(a), the deoxy-hemoglobin concentration of upper dermis after occlusion is statistically higher (p-value=4.9e-6) than that before occlusion, while the oxy-hemoglobin concentration of the upper dermis before and after occlusion have no statistically significant difference (p-value=0.056). This indicates that the accumulation of deoxy-hemoglobin in the vessels locating at the upper dermis when venous occlusion occurs. On the other hand, as shown in Fig. 11(b), the oxy-hemoglobin concentration at deeper dermis has higher value after occlusion than before occlusion (p-value=1.9e-4), while the deoxy-hemoglobin has no statistically significant difference before and after occlusion (p-value= 0.098). The rise of oxy-hemoglobin concentration in the deeper dermis provoked by venous occlusion can be attributed to the inflow of the arterial blood.

Fig. 11.

Oxy- and deoxy-hemoglobin concentration of volar forearm before (white bars) and after (gray bars) applying 50mmHg venous occlusion recovered at (a) 500–600nm region and (b) 600–1000nm region. “P” stands for the P-value.

It is noted that in Fig. 11(b) that the concentration of deoxy-hemoglobin is zero before occlusion. In addition, the uncertainty of the deoxy-hemoglobin concentration after occlusion is very high compared to the mean value. A reasonable explanation to this result is that the concentration of deoxy-hemoglobin is very low compared to those of oxy-hemoglobin and melanin, and our method for extracting chromophore concentrations is not sensitive enough to accurately pick up the small amount of deoxy-hemoglobin concentration in the wavelength range from 600 to 1000nm. In this wavelength range, the absorption of deoxy-hemoglobin decreases with wavelength, and this trend is similar to the property of melanin absorption. In addition, deoxy-hemoglobin has absorption peaks at 760nm, which coincides with the absorption peak of lipid. These factors combined make the uncertainty of the skin deoxy-hemoglobin concentration determined in the wavelength range from 600 to 1000nm with our method very high. In contrast, because lipid has an additional dominant absorption peak at 930nm, the concentration of lipid can be properly recovered.

Stamatas and Kollias employed diffuse reflectance spectroscopy to study the dependence of hemoglobin concentration of forearm skin on the pressure applied on the upper arm.[30] The probe used for light delivery and collection consisted of multiple, tightly packed, randomly arranged optical fibers with 50µm core diameter. The wavelength range used to recover hemoglobin concentration was from 500nm to 580nm. The pressure applied to induce venous occlusion was in the range from 20 to 60mmHg. They found that the deoxy-hemoglobin concentration increased with the pressure and the oxy-hemoglobin concentration was independent from the applied pressure. From the probe geometry and the wavelength range used to extract hemoglobin concentration, it is reasonable to estimate the interrogation region in their study was limited in the upper dermis. The results shown in Fig. 11(a) agree with Stamatas and Kollias’s results.

Wolf et al. used intensity-modulated laser at 830 and 758nm to determine the hemoglobin flow in calf muscle when the venous occlusion was induced on the leg with a pressure of 60mmHg.[31] The source-detector separation they used was 3cm. The data they obtained also demonstrated that the oxy-hemoglobin concentration increased with time at a rate about 4 times higher than that of deoxy-hemoglobin concentration. As shown in Fig. 11(b), we obtained statistically higher oxy-hemoglobin concentration after venous occlusion while the average deoxy-hemoglobin concentration was higher after venous occlusion but was statistically insignificant from that of the baseline measurement. Although our probe is not measuring the hemoglobin concentration of muscle, it is clear that the trend of dramatic increase in oxy-hemoglobin concentration in deeper dermis after occlusion coincides with the trend of oxy-hemoglobin concentration in muscle reported by Wolf et al.

We did not find that scattering power, melanin concentration, lipid concentration and water concentration of each individual had statistically significant change after applying venous occlusion for the 10 subjects we measured (P<0.05). The observation of different trends of hemoglobin concentration variation recovered at 500–600nm and 600– 1000nm regions induced by the venous occlusion validates our proposed probe combined with the two-region fitting method are applicable to monitor physiological dynamics of in-vivo superficial tissue at two different depths at the same time.

4. Conclusion

In this paper, we reported the optical properties of in-vivo skin of skin phototypes I–VI in the wavelength from 500nm to 1000nm. We conducted Monte Carlo simulations and generated photon fluence distribution maps to characterize the interrogation region of the diffusing probe in typical skin. The results of these simulations indicate that the interrogation depth at 500nm is at least 46% shallower than that at 900nm for skin. We can extrapolate this to mean that the skin optical properties obtained with this probe at wavelengths shorter than 600nm are more relevant to the upper dermis and the epidermis while those obtained at wavelengths longer than 600nm are more relevant to the lower dermis. We used the results of these simulations to assist with the analysis of absorption and reduced scattering spectra of in-vivo skin. We performed two-region chromophore fit to the absorption spectra of skin and found that the hemoglobin oxygen saturation was about 60–70% in the upper dermis and about 97–99% in the lower dermis. In addition, the concentration of oxy-hemoglobin in the lower dermis is one order of magnitude higher than that in the upper dermis. Thus the effect of the wavelengths on the interrogation region cannot be overlooked.

We also used scattering power law to fit the reduced scattering spectra of dorsal forearm and upper inner arm skin. Our analyses of the scattering power of skin reveal that dorsal forearm skin may have smaller mean scatterer size than upper inner arm skin in the lower dermis. This could be caused by the difference in collagen and elastin bundle size and/or melanin content that are introduced by skin photoaging. On the other hand, the dorsal forearm skin may have larger mean scatterer size than upper inner arm skin in the upper dermis and epidermis, for all skin types. This is possibly the result of different melanin cluster size in the melanosome at different sites.

Finally, we demonstrated that our diffusing probe combined with the two-region fitting method was capable of monitoring the variation in hemoglobin concentration of in-vivo skin at different depths simultaneously. We obtained that the deoxy-hemoglobin concentration at upper dermis and oxy-hemoglobin concentration at deeper dermis increased when venous occlusion of 50mmHg was applied on the forearm. Our results agree with those reported by other researchers and thus further support and validate our proposed method. In the future, we will employ this probe to study skin photoaging and in-vivo skin melanin synthesis. We will be able to study the modulation of mean scatterer size as well as chromophore concentrations in the epidermis and dermis introduced by UV radiation.