Joint Sulcal Detection on Cortical Surfaces With Graphical Models and Boosted Priors

Abstract

In this paper, we propose an automated approach for the joint detection of major sulci on cortical surfaces. By representing sulci as nodes in a graphical model, we incorporate Markovian relations between sulci and formulate their detection as a maximum a posteriori (MAP) estimation problem over the joint space of major sulci. To make the inference tractable, a sample space with a finite number of candidate curves is automatically generated at each node based on the Hamilton–Jacobi skeleton of sulcal regions. Using the AdaBoost algorithm, we learn both individual and pairwise shape priors of sulcal curves from training data, which are then used to define potential functions in the graphical model based on the connection between AdaBoost and logistic regression. Finally belief propagation is used to perform the MAP inference and select the joint detection results from the sample spaces of candidate curves. In our experiments, we quantitatively validate our algorithm with manually traced curves and demonstrate the automatically detected curves can capture the main body of sulci very accurately. A comparison with independently detected results is also conducted to illustrate the advantage of the joint detection approach.

I. INTRODUCTION

One of the most intriguing and difficult problems in brain imaging is identifying and registering the convolution patterns of the cortex. It is generally agreed that a set of major sulci are relatively stable [1] and they have been used as landmark curves for registration and locating structural and functional areas on cortices [2], [3]. On the other hand, the automated detection of these sulci is still a challenging problem due to the complexity and variability of the convolution patterns and the different forms these sulci may have in the folding patterns. Thus, manual annotation remains the gold standard in brain mapping practice. In this paper, we propose a novel approach for the joint detection of major sulci via the solution of an inference problem on graphical models [4], which we construct with boosting techniques [5] to incorporate prior knowledge from manual tracing.

Previous work on sulcal detection mostly focused on detecting each sulcus separately. Curvature features were first used to develop semi-automated algorithms [6]–[8] with user specification of start/end points. Depth features with respect to a shrink wrap surface were also used to study sulcal regions on cortical surfaces [9] or find their line representations [10]. Based on the idea of skeletons [11], [12] and digital topology [13]–[15], medial models, or sulcal ribbons, of sulcal regions were constructed from volume images [16]–[21], but user inputs are still required to label specific sulcus from these results.

To automate the sulcal detection process, prior models were introduced to alleviate the difficulty of the problem. The principal component analysis (PCA) of point sets [22] was used to model the centroids of sulcal basins and help with the labeling [23]. Based on spherical maps of cortical surfaces, a hierarchical contour evolution scheme was developed using a PCA model of major sulci [24]. Graphical models were constructed with neural networks in [25] for simple surfaces, which are subsets of major sulci, computed with the skeletonization algorithm in [16], and then annealing techniques were used to label them. Based on a learning technique called probabilistic boosting trees [26], an automated approach was proposed in [27] to detect sulci from volume images, but each curve was treated separately.

In this work, we propose a joint detection approach that realizes sulcal detection via inference over graphical models of major sulci. We assume that each major sulcus is represented as a continuous curve on the cortical surface following a manual tracing protocol [28]. While this assumption may omit some interruptions over gyral regions, it is useful in improving the regularity when these curves are used to guide the mapping of cortical surfaces across population [3]. Based on boosting techniques, we not only incorporate the individual shape prior of each sulcal curve, but also model joint shape priors between neighboring sulci and integrate this information through belief propagation. From the practice of manual annotation, the use of pairwise shape priors seems a natural idea. For example, the precentral sulcus usually needs to cross a gyrus to ensure it follows a route as parallel as possible to the central sulcus. In fact, such local dependencies are utilized fairly commonly to handle complicated situations in protocols for manual tracing [28].

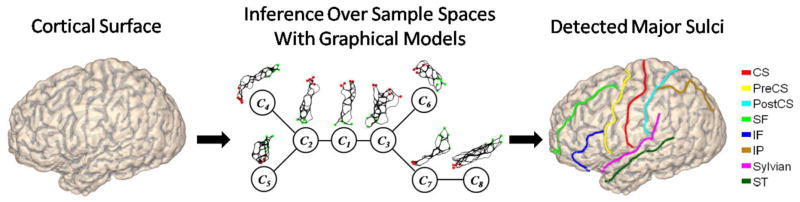
As an illustration, we provide an overview of our method in Fig. 1. In this example, the goal is to detect a set of eight major sulci on a cortical surface: the central sulcus (CS), precentral sulcus (PreCS), postcentral sulcus (PostCS), superior–frontal sulcus (SF), inferior–frontal sulcus (IF), intraparietal sulcus (IP), sylvian fissure (Sylvian), and the superior–temporal sulcus (ST). An undirected graphical model of eight nodes is used to represent the Markovian relations of these sulci. Since the random variable at each node is a sulcal curve that lives in an infinitely dimensional shape space, it is generally difficult to perform inference directly over such spaces. We overcome this challenge by constructing a sample space containing a finite number of candidate curves, as plotted over each node in the graph in Fig. 1, greatly reducing the search range for each variable. To incorporate both individual and pairwise shape priors, we use boosting techniques to learn discriminative shape models and use them to define potential functions on the graphical model. Finally the max-product algorithm of belief propagation is used to find the MAP estimation from the joint sample spaces of the eight sulci as the sulcal detection results.

Fig. 1.

An overview of our joint sulcal detection approach. The automatically detected sulci are plotted over the cortical surface with the color map on the right.

Compared with PCA models adopted in previous work [23], [24], the boosting approach we use does not need to impose the Gaussian assumption on shape models and can automatically select and fuse a large set of informative features to model both individual and pairwise shape priors. Our prior models are learned automatically from training data and there is no parameter to tune for different sulcal curves. Our method also works directly on cortical surfaces and does not need spherical maps of cortical surfaces [24].

Our work is most related to the sulci labeling algorithm proposed in [25], where the nodes of the graph are simple surfaces that oversample the major sulci and their labeling is realized by matching with a template graph learned from training data. In our work, we model each major sulcus as a continuous curve. In addition, the learning techniques and inference algorithms used in our work are different.

The rest of the paper is organized as follows. In Section II, we first present the general framework for joint sulcal detection. After that, we develop the algorithm for generating sample spaces of candidate sulcal curves in Section III. A learning-based approach for constructing potential functions of graphical models is proposed in Section IV to model priors of sulcal curves. Experimental results are presented in Section V on a data set of 40 surfaces. Finally, we discuss possible future extensions in Section VI.

II. Joint Detection Framework

In this section, we present our general framework for the joint detection of major sulci on cortical surfaces. By using a graphical model to represent Markovian relations of neighboring sulci, we realize automated sulcal detection by performing a MAP estimation over the sample spaces of sulcal lines.

Let ℳ denote the cortical surface and C₁, C₂,…, C_N be the set of major sulci to be detected on ℳ. To represent the Markovian relation among these sulci, we use an undirected graphical model G = (V, E), where V = {C₁, C₂,…, C_N} are the set of nodes, and E is the set of edges in the graph. As an example, a graphical model is shown in Fig. 1 for the eight major sulci: CS (C₁), PreCS (C₂), PostCS (C₃), SF (C₄), IF (C₅), IP (C₆), Sylvian (C₇), and ST (C₈). As the number of major sulci is typically small, we can construct such graph structures easily to encode desirable Markovian priors and it only needs to be done once for the same detection task.

Besides the graph structure, we need to specify the sample space for the random variable defined at each node and the potential functions to completely characterize the probabilistic graphical model. At each node in V, the random variable is a sulcal line and it can take values in a shape space of curves that is generally infinitely dimensional and difficult to analyze. One possible solution is to use dimension reduction techniques such as PCA models of curves [22] to generate each sulcal line as a linear combination of several basis functions. But the PCA models make the restrictive assumption of Gaussian distributions and there is no guarantee that the generated parametric curves will follow the sulcal regions. To overcome this problem, we develop a novel algorithm, which will be described in detail in Section III, to automatically generate a set of candidate curves for each node by combining geometric features of sulcal regions and machine learning techniques. These curves are guaranteed to be on the cortical surface and they span a wide variety of possible routes for each sulcus of interest. With these candidate curves as the sample space S_i of each node C_i, we convert the sulcal detection problem to a tractable inference problem over a set of discrete random variables with the goal of selecting the best from the candidate curves.

Based on the sample spaces of candidate sulcal curves, we define two types of potential functions to complete the construction of the graphical model: the local evidence function φ_i: S_i → ℝ at each node C_i and the compatibility function ψ_i,j: S_i × S_j → ℝ for each edge (C_i, C_j) ∈ E. Given a candidate curve from S_i, the local evidence function φ_i gives the likelihood of this curve being the desirable sulcus to be detected. The compatibility function φ_i,j, represents joint shape priors for two neighboring sulci (C_i, C_j) and measures how likely any two curves from S_i × S_j can co-exist as neighbors. To incorporate such individual and joint shape priors, we propose a discriminative approach based on AdaBoost [5] in Section IV to learn both types of potential functions from manually annotated training data. With the discriminative approach, we can use a flexible and large set of features derived from training data and selectively combine them with boosting techniques to form the potential functions, so there is no need of specifying parametric forms for either the individual or joint shape prior models of sulcal lines.

The undirected graphical model defined above is a Markov random field, so the joint distribution of all the sulci can be factorized as a product of potential functions

$$p(C_1,\dots ,C_N)=\frac{1}{Z}\prod _{(C_i,C_j)\in E}{\psi }_{i,j}(C_i,C_j)\prod _{C_i\in V}{\phi }_i(C_i)$$ (1)

where Z is the partition function for normalization. The task of finding the optimal set of curves ( $C_1^{\ast },C_2^{\ast },\dots ,C_N^{\ast }$) in the space S₁ × S₂ × ··· × S_N is then a MAP estimation problem defined as follows:

$$(C_1^{\ast },C_2^{\ast },\dots ,C_N^{\ast })=\underset{C_l,C_2,\dots ,C_N}{\text{argmax}}p(C_1,\dots ,C_N).$$ (2)

To solve this inference problem over graphical models, we use the max-product algorithm of belief propagation [4], [29] because it can efficiently compute the optimal solution for tree-structured graphs and also demonstrated very good performance on graphs with cycles in various applications [30], [31]. With belief propagation, each node in the graph receives and sends out messages at every iteration of the algorithm. For a node (C_i, the message it sends to its neighbor C_j is defined as

$$m_{i,j}(C_j)=\underset{C_i\in S_i}{max}{\psi }_{i,j}(C_i,C_j){\phi }_i(C_i)\times \prod _{C_k\in \mathcal{N}(C_i)\backslash C_j}{m}_{k,i}(C_i)$$ (3)

where (C_i) are neighbors of C_i in the graph. This message takes into account not only the local evidence φ_i and the compatibility function ψ_i,j, but also the messages the node C_i received from its neighbors except C_j. As an illustration, we show in Fig. 2 the flow of messages from the node C₆ and C₇ to C₃, and then to C₁ in the graphical model shown in Fig. 1. After the message passing procedure converges, we obtain the final belief at each node of the graph as

Fig. 2.

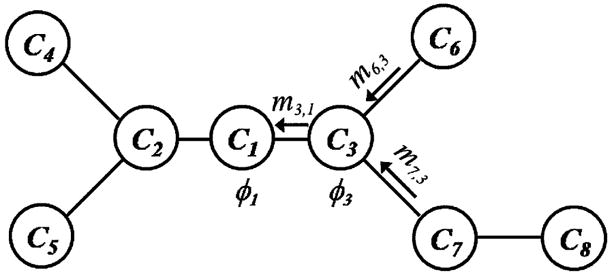
An example of message passing in the graphical model of Fig. 1.

$$b_i(C_i)={\phi }_i(C_i)\prod _{C_j\in \mathcal{N}(C_i)}{m}_{j,i}(C_i)i=1,2,\dots ,N$$ (4)

and also the pairwise belief of each edge as

$$\begin{array}{l}{b}_{i,j}(C_i,C_j)={\phi }_i(C_i){\phi }_j(C_j){\psi }_{i,j}(C_i,C_j)\\ \times \prod _{C_k\in \mathcal{N}(C_i)\backslash C_j}{m}_{k,i}(C_i)\prod _{C_k\in \mathcal{N}(C_j)\backslash C_i}{m}_{k,j}(C_j).\end{array}$$ (5)

Based on the final beliefs, we find an optimal configuration of major sulci with the following procedure [32], [33].

1. Start from a node C_i and pick the optimal sulcus $C_i^{\ast }$ at this node as the one that maximizes b_i (·).

2. For each node C_i visited, if it has a neighbor C_j unvisited, find the optimal solution for C_j by maximizing the pairwise belief function $C_j^{\ast }={\text{argmax}}_{C_j}{b}_{i,j}(C_i^{\ast },C_j)$. Repeat step 2 until all nodes are visited.

For tree-structured graphs, the above algorithm guarantees to find the globally optimal solution for the MAP estimation problem in (2). It is possible that more than one solution achieves global optimality for MAP estimation over graphs, but in our experience this does not happen in any of our sulci detection experiments. Nevertheless, we choose to fix the starting node as the one corresponding to the central sulcus in step 1 of the above procedure to remove the potential ambiguity that exists theoretically.

III. Sample Space Generation

Given a cortical surface ℳ represented as a genus zero triangular mesh, which we assume is a left hemispheric surface aligned in a standard ICBM space [34] with a nine-parameter affine registration including independent scaling in x-, y-, and z- directions to account for brain size differences, there are four main steps in our algorithm to generate a sample space for each node in the graphical model: 1) extract the skeleton of the sulcal regions; 2) partition the surface into the lateral and medial part; 3) compute a set of possible start/end points and route-control segments of candidate curves with a learning-based approach; 4) generate candidate curves via random walks on a graph built from the start/end points and route-control segments.

A. Sulcal Skeleton Extraction

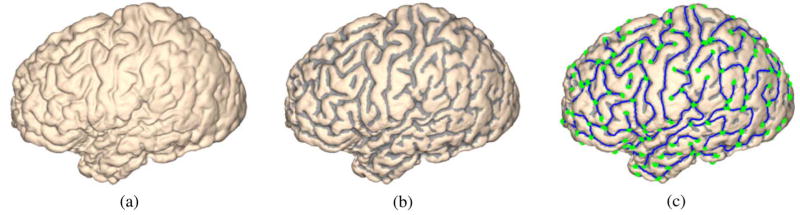
As a first stage toward sample space generation, we use the algorithm of computing Hamilton–Jacobi skeletons on cortical surfaces [35] to extract the skeleton of sulcal regions on ℳ. For completeness, we briefly describe the main steps of computing the sulcal skeletons as illustrated in Fig. 3. Using the mean curvature of the cortical surface ℳ, it is first partitioned into sulcal and gyral regions using graph cuts [36], [37] and the result is shown in Fig. 3(b). After that, the Hamilton–Jacobi skeleton method [38] is extended to triangular meshes to compute the skeleton of sulcal regions. A pruning process is finally applied to eliminate small branches with length below a specific threshold, which is 10 mm in all our experiments. The sulcal skeletons are decomposed into a set of branches as shown in Fig. 3(c), where we have plotted the main body of the branches in blue and the end points in green. From the results we can see these sulcal skeletons capture the major folding patterns fairly well and provide a compact summary of cortex geometry.

Fig. 3.

Main steps in computing the sulcal skeletons of a cortical surface, (a) The cortical surface, (b) The partition of the surface into sulcal and gyral regions. (c) The Hamilton–Jacobi skeleton of the sulcal regions. End points of each branch are marked as green dots.

B. Lateral/Medial Side Partition

In the second stage we partition the hemispheric cortical surface ℳ into lateral and medial parts with a graph-cut algorithm. The resulting boundary between the lateral and medial side is then used to compute a set of features with the aim of providing intrinsic information about sulcal features in addition to absolute coordinates (in millimeter) in the ICBM space and improving the robustness to pose variations.

Before we apply the graph-cut algorithm, we first find a set of seed points for both the lateral and medial side. Since ℳ is a left hemispheric surface in the ICBM space, where the x-coordinate increases from left to right, we find a set of seed points X_l for the lateral side as vertices visible from the left side, i.e., the “x” direction, using the Z-buffer algorithm for visible surface determination in computer graphics. Similarly, the set of seed points X_m for the medial side are determined as vertices visible from the right side, i.e., the “-x” direction.

Because there are hidden regions invisible from either the left or right side, the two sets X_l and X_m do not form a complete partition of the surface. To achieve this goal, we minimize the following energy function to separate ℳ into the lateral side R_l and the medial side R_m:

$$\begin{array}{l}E(R_l,R_m)=\sum _{{\mathcal{V}}_i\in R_l}{d}_{\mathcal{M}}(X_l,{\mathcal{V}}_i)+\sum _{{\mathcal{V}}_i\in R_m}{d}_{\mathcal{M}}(X_m,{\mathcal{V}}_i)\\ +\lambda \sum _{i=1}^K\sum _{{\mathcal{V}}_j\in \mathcal{N}({\mathcal{V}}_i)}\delta ({\mathcal{V}}_i,{\mathcal{V}}_j)\end{array}$$ (6)

where _i and _j are vertices on ℳ, K is the total number of vertices, d_ℳ(·, ·) denote the geodesic distance between two point sets on ℳ that can be computed numerically with the fast marching algorithm on triangular meshes [39], and the delta function δ is defined as one when _i and 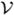_j, a vertex in its one-ring neighborhood 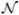( 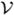_i), belong to different regions and zero otherwise. The first two energy terms require R_l and R_m to be close to their seed points, the third energy term provides regularization for boundary smoothness and the nonnegative parameter λ controls the weight of regularization. To minimize the energy, the same graph-cut algorithm used in stage one for partitioning ℳ into sulcal and gyral regions is applied to find the solution. Since this is a binary optimization problem, the graph-cut technique ensures the global optimality of the separation result [36], [37].

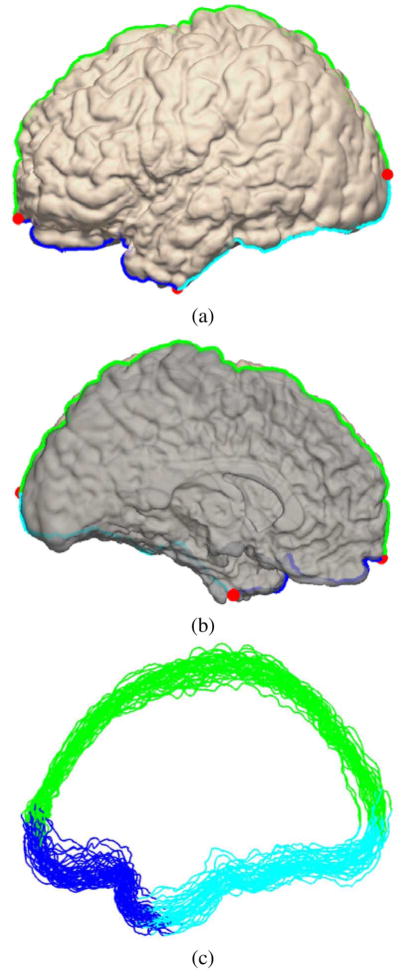
As an example, we show in Fig. 4 the partition results for the surface in Fig. 3(a). Choosing a proper regularization parameter ensures there will be no holes in R_l and R_m and their boundary is a simple curve. In our experience, the parameter λ = 10 gives very robust performance. With this parameter, our algorithm is able to successfully partition all of the 40 cortical surfaces used our experiments into only two connected components corresponding to the lateral and medial parts.

Fig. 4.

The result of partitioning the cortical surface in Fig. 3(a) into the lateral(bright) and medial(dark) side, (a) The lateral view, (b) The medial view. The boundary between the two regions is divided into three curves: BC₁ (green), BC₂ (blue), and BC₃ (cyan), (c) The landmark curves from 40 cortical surfaces.

Once we have the partition results R_l and R_m, we find three boundary vertices, shown as red dots in Fig. 4, that have the largest y-coordinate, the smallest y-coordinate, and the smallest z-coordinate, respectively, and use them to divide the boundary between R_l and R_m into three curves BC₁, BC₂, BC₃ shown as the green, blue, and cyan curve in Fig. 4(a) and (b). We have also plotted the three curves from all 40 surfaces used in our experiments in Fig. 4(c). We can see these curves are clustered fairly closely in the ICBM space and this helps demonstrate the robustness of our partition algorithm. Using these three curves, we can compute the landmark context feature [40] defined at each vertex as LC = [d_BC1, d_BC2, d_BC3] to provide an intrinsic characterization of locations on ℳ, where d_BCj (j = 1,2,3) is the geodesic distance to the curve BC_j. While the landmark context feature is not necessarily unique over the surface, it provides very intuitive characterizations of the intrinsic locations of major sulci on the cortical surface using distances to the three curves. For example, the distance to the curve BC₁ is useful in describing the almost parallel path to the medial wall the SF sulcus usually takes. This distance is also useful to describe the medial-to-lateral trend of the CS, PreCS, and PostCS. The distance to the curve BC₂ is valuable in characterizing the intrinsic location of the frontal part of the SF, IF, ST sulcus and the sylvian fissure. With the distance to the curve BC₃, we can quantify effectively the almost parallel relation between the ST sulcus and the sylvian fissure. In the next stage, we will use both the ICBM coordinate and the landmark context feature to characterize relative locations on ℳ for the learning algorithms.

C. Compute Start/End Points and Route-Control Segments

By computing the skeleton of sulcal regions, we greatly reduce the search range for the start point $X_i^s$ and end point $X_i^e$ of a sulcal curve C_i. Let us denote the set of end points for the branches of sulcal skeletons, i.e., the green dots in Fig. 3(c), as 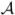. For each branch of the skeleton, we also divide it into ⎣ℒ/10⎦ segments of equal length around 10 mm, where ℒ is the length of the branch and ⎣x⎦ represents the largest integer less than or equal to x. We denote the set of such segments from all the branches as ℬ. In this third stage of our sample space generation algorithm, we use classifiers learned from training data to pick out a set of candidate points from the set 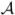for $X_i^s$ and $X_i^e$, and a set of segments from ℬ, which we denote as route-control segments, that help better control the intermediate path the sample curves should follow from $X_i^s$ to $X_i^e$.

To train these classifiers, we derive training data from a set of 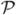cortical surfaces with manually traced sulci and use AdaBoost [5] as our learning algorithm because it is easy to implement, flexible to incorporate various features, and robust to over fitting. As listed in Table I, the main idea of boosting is to form a strong classifier by combining a series of weak classifiers with their weights chosen adaptively based on their classification performance. In order to train the classifier for the start/end point of a sulcal curve C_i, we form the training data as follows by using the start point of C_i as an example. For each of the 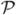cortical surfaces in the training data, we compute the set 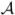of end points of sulcal skeletons. On each surface there is a manually labeled start point for the sulcal curve C_i and we compute the distance between this point and all points in 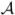. For each point in 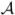, if this distance is less than 5 mm, we assign the label +1. For all other points in 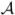, we assign a label −1. Combining all the results from the P surfaces, we form the training data for the start point of the sulcal curves C_i. The training data for its end point can be formed similarly. The features we use in our learning algorithm include the ICBM coordinate, the landmark context, and their individual components. For 1-D features, we learn a decision stump as the weak classifier. For 3-D features, we learn a perception using the pocket algorithm with rachet [41] as the weak classifier. Both the decision stump and perceptron are linear classifiers in the form

TABLE I.

AdaBoost Algorithm [5]

Given training data: (x1,y1, $w_1^1$), · · ·,(xn,yn, $w_n^1$) where xi are the sample data, yi ∈ {−1, 1} are the corresponding class labels, and $w_i^1$ are the initial weights.For t = 1, · · ·, T Train a weak classifier ht given the current weights. Compute the weighted error rate ∈t of the classifier ht. Update the weights: $$w_i^{t+1}=\frac{w_i^t{e}^{-{\alpha }_t{y}_i{h}_t(x_i)}}{Z_t}$$where αt = log((l − ∈t)/∈t)/2 and Zt is a normalization constant such that ${\sum }_{i=1}^n{w}_i^{t+1}=1$.Output the final classifier H = sign(f) with the decision function $f={\sum }_{t=1}^T{\alpha }_t{h}_t$.

$$h(x)=\{\begin{array}{ll}1,\hfill & \text{if}{\mu }^{T}x+\xi >0\hfill \\ -1,\hfill & \text{else}\hfill \end{array}$$ (7)

where x is the feature in ℝ¹ for the decision stump, and ℝ³ for the perception. For the decision stump, (μ, ξ) are coefficients of a 1-D linear classifier. In the case of the perceptron, they are coefficients of a 3-D linear classifier. While the perceptron seems sufficient for 3-D features such as the ICBM coordinates and landmark context, we have chosen to also include the decision stump for the individual components of these 3-D features because the training data is noisy and the 3-D classifier may not be as specific as the 1-D classifier in learning information that can be better captured by 1-D features. So the decision stump can be viewed as a robust version of the perceptron useful to learn explicitly 1-D information such as the distance to the medial wall. The AdaBoost algorithm is then used to selectively combine information from these features and form the final classifier.

For each sulcus C_i, we also use AdaBoost to train a classifier to pick out a set of route-control segments from the set ℬ that should be on the sample curves. For each of the P cortical surface in the training data, we first compute the set ℬ of skeleton segments. For every segment in ℬ, we then compute its Hausdorff distance to the manually traced curve on this surface. If the Hausdorff distance is less than 5 mm, we assign a label +1 to this segment; otherwise, a label −1 is assigned. Repeating the above procedure for all the P cortical surfaces, we form the training data for the route-control segments of C_i. For each segment, we compute the mean and difference of the ICBM coordinates, the landmark context features, and their individual components at its two end points as the features used for classification. The same learning algorithm described above is then used to learn the classifier for route-control segments.

D. Candidate Curve Generation via Random Walks

In this fourth stage, we generate sample curves based on random walks over a directed graph constructed from the candidate start/end points and route-control segments for a major sulcus C_i. Given a pair of candidate start point $X_i^s$ and end point $X_i^e$, we order all the route-control segments of C_i according to their geodesic distance to $X_i^s$, which we denote as RC = {Q₁, Q₂, … Q_J} and a segment Q_j1 is closer to $X_i^s$ than Q_j2 if jl < j2. Similarly, we also order the two end points of a segment Q_j and denote them as $Q_j^s$ and $Q_j^e$ such that $d_{\mathcal{M}}(X_i^s,Q_j^s)\le d_{\mathcal{M}}(X_i^s,Q_j^e)$, where d_ℳ(·,·) denotes the geodesic distance between two points on ℳ as in (6).

The directed attributed graph G⃗ = (V⃗, E⃗) for generating sample curves from $X_i^s$ to $X_i^e$ is composed of a set of nodes $\overrightarrow{V}=\{X_i^s,Q_1,Q_2,\dots ,Q_J,X_i^e\}$ and a set of direct edges $\overrightarrow{E}=\overrightarrow{E_1}\cup \overrightarrow{E_2}\cup \overrightarrow{E_3}$. Then set $\overrightarrow{E_1}=\{\overrightarrow{X_i^s{Q}_j}\mid j=1,2,\dots ,J\}$ are directed edges from $X_i^s$ to all the segments in RC and their weights are defined as $1/d_{\mathcal{M}}(X_i^s,Q_j^s)$. The set $\overrightarrow{E_2}=\{\overrightarrow{Q_j{X}_i^e}\mid j=1,2,\dots ,J\}$ are directed edges from all the segments in RC to $X_i^e$ and their weights are defined as $1/d_{\mathcal{M}}(Q_j^e,X_i^e)$. The set $\overrightarrow{E_3}=\{\overrightarrow{Q_{j1}{X}_{j2}}\mid \text{if}{d}_{\mathcal{M}}(X_i^s,Q_{j1}^e)<d_{\mathcal{M}}(X_i^s,Q_{j2}^s),1\le j1,j2\le J\}$ are composed of directed edges $\overrightarrow{Q_{j1}{Q}_{j2}}$ between segments in RC. To ensure there are no loops in the graph, we require the end point of Q_j1 to be closer to $X_i^s$ than the start point of Q_j2. The weights for edges in $\overrightarrow{E_3}$ are defined as $1/d_{\mathcal{M}}(Q_{j1}^e,Q_{j2}^s)$.

To generate a sample curve, we perform a random walk in G⃗ to find a path from $X_i^s$ to $X_i^e$. Starting from the node $X_i^s$, we pick the next node by randomly choosing an edge from all the direct edges starting from $X_i^s$ with a probability in proportion to the weights of these edges. The process is repeated until we reach the node $X_i^e$. Because we have defined the weights of edges inversely proportional to the geodesic distance between neighboring nodes, edges connecting closer nodes will have a higher chance of being visited in the random walk. Since there are no loops in G⃗ and all the router-control segments are connected to $X_i^s$ and $X_i^e$, any random walk starting from $X_i^s$ is guaranteed to stop at $X_i^e$. By repeating the random walk multiple times, we can generate sample curves covering various routes from the start point to the end point. This is important as the major sulci are not necessarily the shortest path from $X_i^s$ to $X_i^e$.

Suppose the path of the random walk in the graph G⃗ is $X_i^s\to Q_{j1}\to Q_{j2}\to \cdots \to Q_{jn}\to X_i^e$, we generate the sample curve by connecting a series of curve segments: $\overline{(X_i^s,Q_{j1}^s)}\to Q_{j1}\to \overline{(Q_{j1}^e,Q_{j2}^s)}\to Q_{j2}\to \cdots \to Q_{jn}\to \overline{(Q_{jn}^e,X_i^e)}$, where (·, ·) represents a weighted geodesic path connecting two points on ℳ. Because it is possible to jump from a curve segment to a relatively far away curve segment during the random walk, we need to design the weighted geodesies to ensure the path connecting them passes through sulcal regions whenever possible. Thus, we define the weight function for computing the geodesic as

$$F=e^{-D}$$ (8)

where D is the distance transform of the sulcal skeletons, so points closer to the skeleton will have higher speeds. To find each path numerically, we use the fast marching algorithm on triangular meshes [39] to solve the Eikonal equation on ℳ:

$$\nabla d^{w}F=1$$ (9)

and trace backward along the gradient direction of d^w to find the geodesic path.

As an example, we show in Fig. 5(b) the sample curves between a start point (the red dot) and end point (the green dot) generated with random walks on the graph constructed with the route-control segments shown in Fig. 5(a). For each pair of start/end points, we typically generate 30 candidate curves in our experiments. In this case, there are five start and five end points, so we obtain a sample space of 750 candidate curves as shown in Fig. 5(c). Similarly, we can generate the sample space for other major sulci of interest. The sample spaces of the eight sulci in the graphical model of Fig. 1 are plotted in Fig. 5(d) with the color map in Fig. 1. In this case, the usefulness of the random walking process can be best illustrated in the sample space generated for the IF sulcus as the shortest path is clearly not the most desirable. It is clear that most of the sample curves shown in Fig. 5(d) are not neuro-biologically valid sulci. There are also overlaps between candidate curves of different sulci as it is possible for some curve segments being classified as route-control segments by multiple sulci. To ensure that the belief propagation algorithm can handle these cases correctly, we learn the potential functions of the graphical model from training data to incorporate prior knowledge about individual and neighboring sulci.

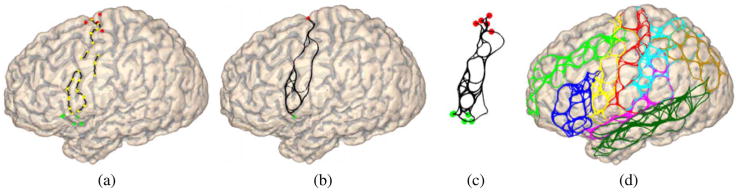
Fig. 5.

The process of sample space generation, (a) The candidate start (red) and end (green) points of the precentral sulcus, and its route-control segments whose both ends are marked as yellow dots, (b) The sample curves generated with 30 random walks between a pair of start and end points of the precentral sulcus. (c) The sample space of precentral sulcus as composed of curves connecting all the start and end points, (d) The sample spaces of all eight major sulci in the graphical model of Fig. 1 are plotted with the same color map in Fig. 1.

IV. Learning Potential Functions

In this section, we describe our learning-based approach to construct both the local evidence functions φ_i and compatibility functions ψ_i,j over the sample spaces of sulcal curves. For each potential function, we compute a large set of features and let the boosting technique automatically pick out the most informative features to model the individual and pairwise shape priors. Using the classifier learned by AdaBoost, we then define the potential function based on its connection to logistic regression [42].

For both the local evidence functions and compatibility functions, we assume a training data set of 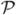cortical surfaces in the ICBM space with manually labeled sulcal lines. For each surface, we compute the sample space S_i for each node C_i in the graphical model.

A. Local Evidence Functions

To learn the local evidence function φ_i for a sulcus C_i, we form its training data as follows. We assign all the manually traced curves on the 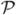surfaces the label +1. For a curve from S_i of each surface, we assign it the label −1 if more than 50% of the points on the curve have a minimum distance of 10 mm to the corresponding manually traced sulcus.

To characterize these curves, we use the Haar wavelet transform to compute a set of multiscale features. More specifically, we uniformly sample each curve into L_Harr = 32 points. The Haar wavelet transform is then computed for the ICBM coordinates, landmark context features, and their individual components defined at these uniformly sample points. As a result, we have 2L_Haar 3-D features from the ICBM coordinates and landmark context features, and 6L_Haar 1-D features from their individual components. This large set of features provides a multi-scale description of the location and orientation of the curves.

Using these features, the AdaBoost algorithm combines a series of weak classifiers to form a final decision function for a curve C_i ∈ S_i

$$f(C_i)=\sum _{t=1}^T{\alpha }_t{h}_t(C_i)$$ (10)

where h_t is the tth weak classifier, which is a decision stump for 1-D features and perceptron for 3-D features, α_t is the weight for this classifier, and T is the total number of weak classifiers. It is shown in [42] that AdaBoost approximates logistic regression and the learned decision function can be used to estimate the probability of a class label, thus we follow [42] and define the local evidence function as

$${\phi }_i(C_i)=\frac{e^{2f(C_i)}}{1+e^{2f(C_i)}}\forall C_i\in S_i.$$ (11)

The range of the local evidence function is between (0,1) and it approaches 1 when f(C_i) is large for a curve C_i ∈ S_i, which suggests this curve bears strong similarity to manually traced sulcal lines in the training data. On the other hand, it approaches zero for curves with negative decision function values.

B. Compatibility Functions

For two nodes C_i, and C_j in the graphical model G, we follow a similar process to learn their compatibility function ψ_i,j, but with a different set of features to capture their joint shape priors. Given a cortical surface, we generate the sample spaces S_i and S_j for these two sulci, and the value ψ_i,j(C_i, C_j) measures how compatible a pair of curves (C_i, C_j) ∈ S_i × S_j being the two major sulci. The training data to learn ψ_i,j thus are also composed of curve pairs (C_i, C_j) that we form as follows. For the 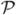pairs of manually traced sulci for C_i and C_j on the 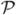surfaces in the training data, we assign a label +1. For each of the 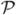surface, we compute the sample space S_i and S_j and assign a label −1 for the set of curve pairs (C_i, C_j) generated by associating each curve C_i ∈ S_i with a randomly picked curve C_j ∈ S_j with the goal of representing possible cases of incompatible curves. By repeating the above procedure for each edge in the graphical model G, we can generate different training data for other neighboring sulci.

As inputs to the weak classifiers used in AdaBoost, we design a set of multiscale features to model the joint configuration for each pair of curves (C_i, C_j). Let ϒ denote the maximum number of levels we want to compute the features. We resample each curve C_i and C_j into 2^ϒ + 1 equally spaced points. Let p₀, p₁, … p_2^ϒ be the 2^ϒ +1 points on C_i, we then approximate it with a set of 2ⁿ straight line segments at the level 0 ≤ η ≤ ϒ

$$\text{MC}(\eta )=\{\overline{p_{k{2}^{\mathrm{\Upsilon }-\eta }}{p}_{(k+1)2^{\mathrm{\Upsilon }-\eta }}}\mid 0\le k<2^{\eta }\}$$ (12)

where $\overline{p_{k{2}^{\mathrm{\Upsilon }-\eta }}{p}_{(k+1)2^{\mathrm{\Upsilon }-\eta }}}$ denote the line segment connecting the two points p_k2^ϒ−η and p_{(k+1)2^ϒ−η}. As shown in Fig. 6, line segments at the coarse scale captures the global trend of each curve, while the line segments at finer scales provide more local information. Similarly, the curve C_j is also decomposed into the same number of levels and we use the relation between line segments from these two curves to characterize their configuration at each level. More specifically, for each line segment LS₁ of C_i and LS₂ of C_j at a level η, we compute the angle between them and the shortest displacement vector from points on LS₁ to LS₂. Repeat this procedure for all levels, we obtain a set of multiscale features to describe the relative position of curves. The AdaBoost algorithm is then used to learn a strong classifier for the curve pair (C_i, C_j). Similar to the definition of local evidence functions, we define the compatibility function between C_i and C_j as

Fig. 6.

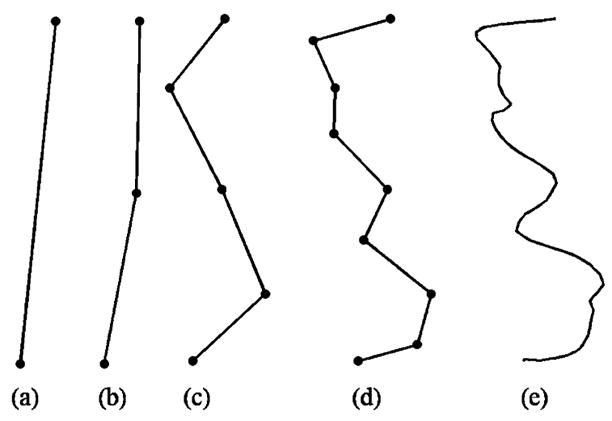
The multilevel decomposition of a curve, (a) η = 0. (b) η = 1. (c) η= 2. (d) η= 3. (e) The original curve.

$${\psi }_{i,j}(C_i,C_j)=\frac{e^{2f(C_i,C_j)}}{1+e^{2f(C_i,C_j)}}\forall (C_i,C_j)\in S_i\times S_j$$ (13)

where f(·, ·) is the decision function learned with AdaBoost using features described above.

Applying the above learning algorithms to each node and every pair of neighboring sulci in a graphical model, we can learn all the local evidence and compatibility functions, which complete the construction of the graphical model. After that, the belief propagation algorithm can be applied to detect sulci jointly on cortical surfaces from the sample spaces of major sulci.

V. Experimental Results

In this section, we present experimental results to demonstrate our joint sulcal detection algorithm on a data set of 40 left hemispheric surfaces. These surfaces represent the boundary between the gray matter and cerebrospinal fluid (CSF), and were generated from MRI images in the ICBM space using a surface extraction algorithm [43] and they all have genus zero topology. While these surfaces may not capture the deepest parts of sulcal regions, the regularity they share makes it easier to compare across population and perform group studies. More details on the MRI imaging and postprocessing protocols can be found in [44]. A set of eight major sulci were manually labeled on each surface for training and validation, which include the central sulcus (CS), precentral sulcus (PreCS), postcentral sulcus (PostCS), superior–frontal sulcus (SF), inferior–frontal sulcus (IF), intraparietal sulcus (IP), sylvian fissure (Sylvian), and the superior–temporal sulcus (ST).

In our experiments, we use the graphical model in Fig. 1 to demonstrate the joint detection method. As a common practice in graph-based estimation, belief propagation is also often applied to graphs with loops. This may allow us to incorporate more neighboring priors between sulcal curves, but no theoretical guarantee of global optimality exists for graphs with loops. So there is a tradeoff between using more complicated models and the tractability in obtaining the optimal solution. We have chosen to use tree-structured graphical models in our experiments as this allows us to focus more on the construction of sample spaces of candidate curves and shape priors.

In the first experiment, we learn from a set of training data the classifiers used in sample space generation and the potential functions in the graphical model, and then demonstrate the sulcal detection algorithm on surfaces in the training data. After that we apply the joint detection algorithm to a set of testing data and validate its performance quantitatively. In our third experiment, we demonstrate the advantage of the joint detection approach by comparing with results obtained without using the graphical model.

A. Graphical Model Training

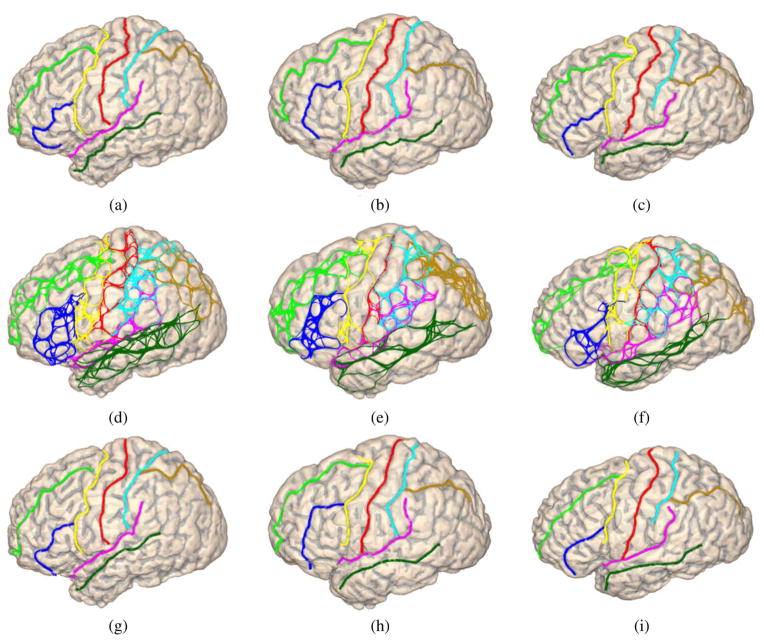
Among the 40 surfaces in our data we randomly pick 20 surfaces, together with their manually traced sulci, as the training data. As an illustration, we show three examples from the training data in Fig. 7(a)–(c). The other 20 surfaces are used as the testing data to evaluate the performance of the joint sulcal detection algorithm.

Fig. 7.

Three surfaces in the training data, (a)–(c) Cortical surfaces with manually traced sulcal curves. (d)–(f) Sample spaces of the eight sulci. (g)–(i) Automatically detected sulcal curves plotted on surfaces. (All curves are plotted with the color map in Fig. 1).

In this learning stage, we first compute the sulcal skeletons for all the surfaces in the training data. After that the landmark context features derived from the boundary of the lateral/medial partition are computed with the graph-cut approach developed in Section III-B. Using results obtained in these two steps, the AdaBoost algorithm is applied to learn the classifiers for the start/end points and route-control segments of each sulcal curve as described in Section III-C. On every surface, we then run the random-walk algorithm in Section III-D for each sulcal curve, or node of the graphical model, to generate its sample space of candidate curves. For the surfaces in Fig. 7(a)–(c), the corresponding sample spaces of the eight major sulci are plotted in Fig. 7(d)–(f). Finally the potential functions in the graphical model are learned following the procedure in Section IV.

As a first step to examine the graphical model we learned from training data, we perform MAP estimation on the sample spaces of each surface in training data using the belief propagation algorithm described in Section II. By presenting results from the training data, we demonstrate the ability of our learning-based approach in capturing shape priors from manual tracing. These results will also be used to compare with results from the testing data to illustrate the generalization ability of our method. For the three examples in Fig. 7, we have plotted in Fig. 7(g)–(i) the detected sulci. Compared with the manually traced curves in Fig. 7(a)–(c), we can see the detected sulci travel mostly along the same routes through sulcal regions. The geometric relations of neighboring sulci, such as the junctions between the IF and PreCS, are also correctly followed because both angle and displacement features are used in modeling the compatibility functions of these neighboring sulci.

Besides the visual results, we next present more detailed quantitative measures to compare automatically detected sulci with manual results. In previous works [19], [24], [27], statistics such as the mean and standard deviation of distances between points on detected sulci and manually traced curves were used. We extend these measures and use more detailed quantile statistics in our experiments. With quantile statistics, we can characterize how well the detected curves align with the main body of the major sulci at different levels, which maybe anatomically more reasonable considering the difficulty and the resulting variability in deciding the starting and ending parts of sulcal curves even for human tracers.

To compute the quantile statistics, we first calculate two distances between automatically detected curves and manual results. For each point on an automatically detected curve, we compute its minimum distance to the corresponding manually traced curve and denote this kind of distance as d_am. For each point on the manually traced curve, we also compute its minimum distance to the automatically detected curve and denote this distance as d_ma. For each major sulcus, we use the 20 pairs of automatically detected and manually traced curves on all the surfaces in training data to compute the quantile statistics of d_am and d_ma at the 50th, 70th, and 90th percentile.

The results for all eight sulci are listed in Table II. Each distance value in the table represents a cut-point on the cumulative distribution function (CDF) of either d_am or d_ma for a certain sulcus. For example, the last number in the column of central sulcus means that 90% of points on the manually traced curve have a distance d_ma ≤ 2.09 mm to the automatically detected curve. For all eight sulci, we can see the 50th percentile of both d_am and d_ma are less than 1.5 mm, and the 70th percentile are less than 3.5 mm. Even for highly variable sulci such as PostCS and IF, the 90th percentile of both d_am and d_ma are around 10 mm. So the results in Table II show that very good alignment has been achieved between the main body of automatically detected curves and manually traced ones.

TABLE II.

Quantile Statistics of d_am and d_ma From Sulci Detected in Training Data. All Distances are in Millimeters

		CS	PreCS	PostCS	SF	IF	IP	Sylvian	ST
dam	50th percentile	0.70	1.05	1.01	1.24	1.15	0.97	0.93	1.04
	70th percentile	0.98	1.91	1.86	2.25	3.28	2.01	1.58	1.94
	90th percentile	1.66	6.35	9.76	8.92	8.26	6.87	4.60	8.54
dma	50th percentile	0.75	1.18	1.14	1.38	1.31	1.12	1.05	1.26
	70th percentile	1.14	2.30	2.19	2.55	3.34	2.18	1.95	2.56
	90th percentile	2.09	8.15	12.75	9.29	8.62	7.35	6.62	11.21

B. Validation With Testing Data

In our previous experiment, we demonstrated very good sulcal detection results in Fig. 7 and Table II. For practical purposes, however, it is more important to examine the generalization abilities of the algorithm, i.e., its performance on testing data. In this experiment, we apply our algorithm to the 20 surfaces in the testing data and evaluate the results quantitatively with manually labeled sulcal lines.

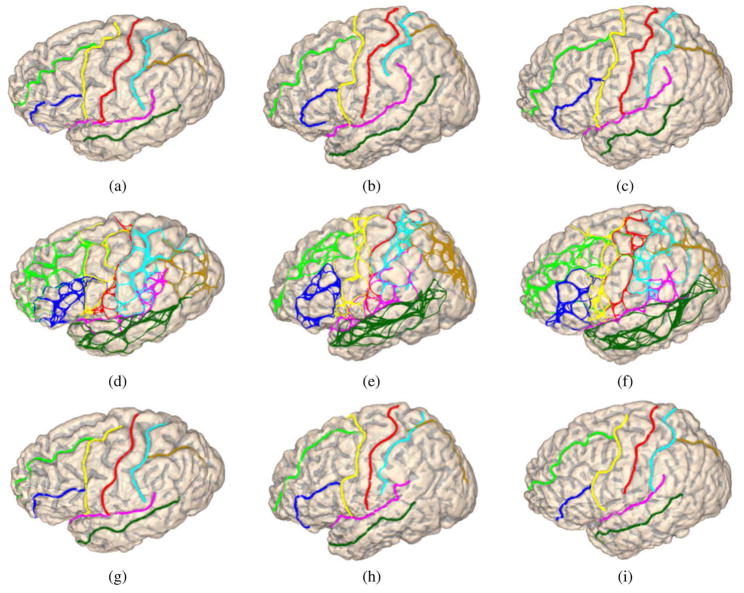
There are two main steps in applying our algorithm to testing data. In the first step, we generate a sample space of candidate curves for each sulcus on a cortical surface. During this stage, the classifier for start/end points and route-control segments learned from training data are used. After that, belief propagation is applied to pick out the best combination of sulcal curves from their sample spaces. Using the classifiers learned from training data, there are very few parameters to tune when we apply the two steps to the testing data. The only parameter we need to adjust is the number of sample curves to generate for each pair of start/end points of a sulcal curve at the first step. When we increase this number, we get larger sample spaces covering more routes a sulcal curve can follow, but it also increases the computational cost because more random walks need to be performed. In our experiments, we set this parameter to 30 curves as in the example shown in Section III-D. This usually generates a sample space containing around 1000 curves for each major sulcus. No significant gains are observed if we further increase this parameter. As an illustration, we visualize the results from these two steps on three surfaces in the testing data, as shown in Fig. 8(a)–(c). The sample spaces generated for each of the eight major sulci are plotted on the surfaces in Fig. 8(d)–(f) using the same color map in Fig. 1. The detected sulcal curves are plotted on the surfaces in Fig. 8(g)–(i). By comparing the automatically detected sulci with manually traced curves in Fig. 8(a)–(c), we can see the automatically detected curves overall capture the main body of the sulci and agree with manual results very well.

Fig. 8.

Sulcal detection results on three cortical surfaces in the testing data, (a)–(c) Cortical surfaces with manually traced sulci. (d)–(f) Sample spaces of the eight sulci. (g)–(i) Automatically detected sulcal curves plotted on surfaces. (All curves are plotted with the color map in Fig. 1.)

To measure quantitatively the performance of our sulcal detection algorithm on testing data, we compute the same statistics as in the first experiment. For each major sulcus, we use the 20 pairs of automatically detected and manually traced curves in testing data to calculate the quantile statistics of d_am and d_ma at the 50th, 70th, and 90th percentile. The results for the eight sulci are listed in Table III. For all eight sulci, the 50th percentile of both d_am and d_ma are less than 2 mm, and the 70th percentile are less than or around 5 mm. Besides the central sulcus, the 90th percentile of d_am and d_ma are around 10 mm, which is slightly worse than the performance on training data and this is mainly due to the high variability in the starting and ending parts of sulcal curves. One good example in illustrating this difficulty is the superior end of the PostCS. Following the tracing protocol [28], the manual tracer is able to consistently pick the posterior route whenever there are more than one choices in determining this part of the PostCS such as the example in Fig. 7(a). Our automated approach, however, may sometimes get confused and follow a posterior route that actually jumps across a gyrus as in Fig. 8(h). Another example is the difficulty in capturing the frontal part of the IF sulcus that usually bends backward. This is mainly because that the IF sulcus does not necessarily follow a weighted geodesic that we use to generate candidate curves. These kinds of situations contribute to the largest errors in the quantile statistics and point out directions of future improvements.

TABLE III.

Quantile Statistics of d_am and d_ma From Sulci Detected Jointly in Testing Data. All Distances Are in Millimeters

		CS	PreCS	PostCS	SF	IF	IP	Sylvian	ST
dam	50th percentile	0.70	1.23	1.05	1.46	1.55	0.92	1.34	1.33
	70th percentile	0.97	2.42	2.11	3.25	3.99	1.74	2.84	2.75
	90th percentile	1.70	8.07	9.32	8.98	9.17	8.60	7.36	7.64
dma	50th percentile	0.74	1.44	1.23	1.63	1.97	1.12	1.77	1.66
	70th percentile	1.14	3.32	2.93	3.38	5.16	2.24	4.13	4.19
	90th percentile	2.38	9.06	10.77	9.44	11.50	11.05	11.02	10.75

Overall the results in Table III show that our algorithm generalizes very well on testing data and the detected curves are able to capture the main body of major sulci accurately, which is especially encouraging for those sulci (PostCS, IF) that are highly variable.

C. Comparison With Sulci Detected Separately

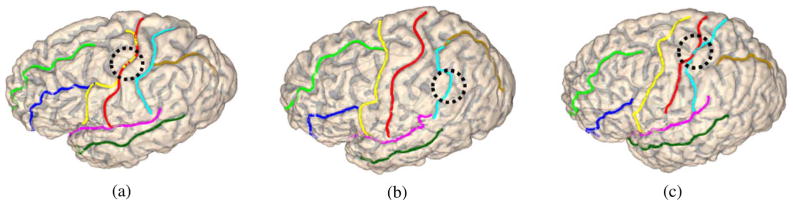
In this experiment, we compare the joint detection results in Section V-B with sulci detected separately without taking into account pairwise priors between neighboring sulci, which is realized by choosing the curve in each sample space that maximizes the associated local evidence function.

For the three surfaces in Fig. 8(a)–(c), we plot the independently detected sulci in Fig. 9(a)–(c), respectively. To highlight the differences between the detection results in Figs. 8 and 9, we have annotated with a dotted circle to identify one place on each surface in Fig. 9 where the independently detected curve failed to locate the corresponding sulcus accurately. On the contrary, these kinds of mistakes were avoided in the results shown in Fig. 8(g)–(i) because pairwise priors are incorporated. This demonstrates the value of the compatibility functions in improving sulci detection with joint shape priors.

Fig. 9.

Sulcal detection results without using graphical models. (All curves are plotted with the color map in Fig. 1).

Following the quantitative evaluation procedure in Section V-B, we also compare independently detected sulci with manually annotated sulcal curves on the 20 surfaces in our testing data by computing the same quantile statistics. The results are listed in Table IV. From the numbers in Tables III and IV, we can clearly see the advantage of the joint detection approach as it performs better on 40 of the 48 distance measures. For the 6 measures that the independent detection approach generated better results, it outperforms the joint detection method only by a slight margin of less than 0.1 mm. The performance gain with the use of the graphical model is especially significant for more variable sulci such as the PostCS and IF as demonstrated by their quantile statistics at the 70th percentile for both d_am and d_ma in Tables III and IV.

TABLE IV.

Quantile Statistics of d_am and d_ma From Sulci Detected Separately in Testing Data. All distances Are in Millimeters

		CS	PreCS	PostCS	SF	IF	IP	Sylvian	ST
dam	50th percentile	0.69	1.23	1.56	1.71	2.34	0.88	1.33	1.34
	70th percentile	0.99	2.96	7.52	4.87	7.29	1.65	2.86	3.24
	90th percentile	2.04	10.32	13.68	11.13	11.56	10.59	9.15	8.63
dma	50th percentile	0.74	1.54	1.90	1.83	2.42	1.13	1.71	1.78
	70th percentile	1.15	4.01	9.02	4.57	8.46	2.29	4.27	4.87
	90th percentile	2.82	10.95	16.42	11.10	13.52	12.61	11.79	11.65

VI. Discussion and Conclusion

In this paper, we proposed a joint detection framework for the automated labeling of major sulci on cortical surfaces. By generating sample spaces of candidate curves for the major sulci, we are able to convert sulcal detection into a tractable inference problem over discrete random variables. To capture both individual and joint shape priors of sulcal curves, we use graphical models in our framework to encode Markovian relations between neighboring sulci and learn the potential functions automatically with AdaBoost.

With the aim of providing stable landmark curves for the mapping of cortical surfaces across population, we represent each major sulcus as a continuous curve in our work, which is useful for the analysis of anatomical quantities defined on cortical surfaces such as gray matter densities. On the other hand, this assumption simplifies the interruptions of the sulci over gyral regions that exist naturally. So when the sulcal anatomy is the target of analysis, it might be beneficial to study the detailed configuration of sulcal regions directly.

In our experiments, we demonstrated the training of a graphical model and applied it to automatically detect a set of eight major sulci on hemispheric cortical surfaces. These sulci are on the lateral surface of the cortex, but our method is general and can also be applied to detect other major sulci on the medial surface such as the calcarine sulcus. For the detection of secondary sulci that may or may not be present, for example the secondary cingulate sulcus, however, we cannot apply our method directly. A model selection process might be necessary to first determine the proper graphical model to use and then apply the joint detection algorithm we develop here.

As noted in our experiments, there are still difficulties in accurately detecting sulcal lines that tend to bend backward. To address this problem, we will improve in the future work the sample space generation algorithm for these sulci to ensure their sample spaces contain valid candidate curves. For example, we can train an additional classifier for the IF sulcus to detect a route-control segment corresponding to the most frontal part of the sulcal line and use it to capture the bending between the start and end points.

A large set of features derived from the ICBM coordinates and landmark context features have been combined with AdaBoost to model shape priors of sulcal curves in our current work. The ability of this approach in modeling joint shape priors was demonstrated via comparisons with results detected without using graphical models. An interesting direction of future research is to include a feature selection process [45], [46] in our algorithm as many features contain redundant information. This may improve the effectiveness of our model. For example, this process could make the compatibility function of the PostCS and IP sulcus more sensitive to the spatial configuration between the closest line segments in their multilevel decompositions and help eliminate artifacts such as the slight overlap of these two sulcal curves in Fig. 8(h).

We have chosen to use tree-structured graphical models in our experiments because the belief propagation algorithm can efficiently compute the globally optimal solution on such models. This is, however, at the expense of leaving out potentially useful neighboring priors. To incorporate more joint shape priors, we will study the use of graphical models with loops in our future work. The same learning process developed here can still be used to construct the sample spaces of candidate curves and potential functions on such models, but the belief propagation algorithm has to be used with caution as there is no guarantee of global optimality anymore. More sophisticated optimization strategies such as the tree-reweighted message passing algorithm [47] and the primal-dual graph cut algorithm [48] will be investigated for MAP estimation on these graphical models with loops.