Electrostatic potential of point charges inside dielectric prolate spheroids

Abstract

The exact solution to an electrostatic problem of finding the electric potential of point charges inside a dielectric prolate spheroid is discussed in this note by using the classical electrostatic theory, where the prolate spheroid is embedded in a dissimilar dielectric medium. Such a problem may find its application in hybrid solvent biomolecular simulations, in which biomolecules and a part of solvent molecules within a dielectric cavity are explicitly modeled while a surrounding dielectric continuum is used to model bulk effects of the solvent beyond the cavity. Numerical experiments have demonstrated the convergence of the proposed series solutions.

1. A general electrostatic problem

A finite number of point charges are set inside a dielectric cavity of electric permittivity ε_i, which is embedded in a homogeneous, isotropic dielectric medium of electric permittivity ε_o. The point charges will polarize the surrounding dielectric medium, which in turn makes a contribution, called the reaction field, to the electric field throughout the cavity. The electric field inside the cavity is thus expressed asΨ_in = Ψ_s + Ψ_RF, where Ψ_s is the Coulomb potential which can be simply calculated by the well-known Coulomb’s Law, and Ψ_RF is the reaction field which will dominate the computational cost for calculating the electric field inside the cavity. Such a problem could be encountered in many applications such as hybrid explicit/implicit solvent biomolecular dynamics simulations [1–3]. In particular, in this note we are interested in the exact solution of the problem when the dielectric cavity is either a sphere or a prolate spheroid, and the surrounding medium is either the pure water solvent or an ionic solvent of low ionic strength.

By the principle of linear superposition, the electrostatic problem with a single source charge q inside a dielectric cavity only needs to be considered. It is then well-known that the total electric potential Ψ_in(r) inside the cavity is given by the solution of the Poisson equation

$$\nabla ·({\epsilon }_{\text{i}}\nabla {\mathrm{\Psi }}_{\text{in}}(\mathbf{r}))=-4\pi q\delta (\mid \mathbf{r}-{\mathbf{r}}_{\text{s}}\mid ),$$

where r_s represents the location of the point charge, and δ(r) the Dirac delta function. Outside the cavity, on the other hand, by assuming that the mobile ion concentration follows the Debye–Hückel theory, the electric field Ψ_out(r) is then given by the solution of the linearized Poisson–Boltzmann equation (LPBE)

$${\nabla }^2{\mathrm{\Psi }}_{\text{out}}(\mathbf{r})-{\lambda }^2{\mathrm{\Psi }}_{\text{out}}(\mathbf{r})=0,$$ (1)

where λ is the inverse Debye screening length which is proportional to the square root of the ionic concentration c_s measured in molar units [4] (λ = 0 for the pure water solvent). On the interface Γ of the dielectric prolate spheroid and its surrounding dielectric medium, the continuity of the tangential component of the electric field and the normal component of the displacement field requires that

$${\mathrm{\Psi }}_{\text{out}}{\mid }_{\mathrm{\Gamma }}={\mathrm{\Psi }}_{\text{in}}{\mid }_{\mathrm{\Gamma }}\text{and}{{\epsilon }_{\text{o}}\frac{\partial {\mathrm{\Psi }}_{\text{out}}}{\partial \mathbf{n}}\mid }_{\mathrm{\Gamma }}={\epsilon }_{\text{i}}{\frac{\partial {\mathrm{\Psi }}_{\text{in}}}{\partial \mathbf{n}}\mid }_{\mathrm{\Gamma }},$$ (2)

where n is the outward normal of the interface Γ.

2. A point charge inside a dielectric sphere

In the case of a spherical dielectric cavity, the problem can be solved very easily. Without loss of any generality, let us consider a dielectric sphere of radius a with a point charge q being located on the x-axis at a distance r_s < a from the center of the sphere, as shown in Fig. 1.

Fig. 1.

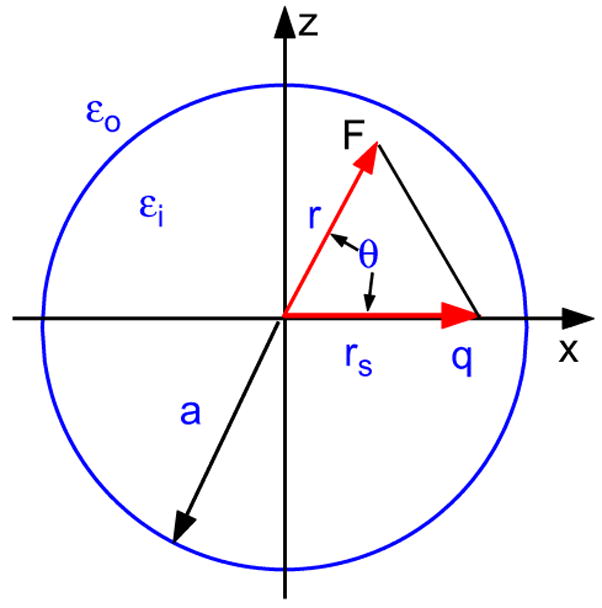
A point charge and a dielectric sphere.

When λ = 0, the analytical solution to this classical electrostatic problem by the famous Kirkwood expansion [5] is well-documented in the literature. More precisely, with respect to a spherical coordinate system (r, θ, ϕ) with its origin at the center of the sphere (the pole is denoted by the x-axis in this note), due to the azimuthal symmetry, the electrostatic potential at an observation point r=(r, θ, ϕ) is

$$\begin{array}{l}{\mathrm{\Psi }}_{\text{in}}(\mathbf{r})=\frac{q}{{\epsilon }_{\text{i}}\mid \mathbf{r}-{\mathbf{r}}_{\text{s}}\mid }+\frac{q}{{\epsilon }_{\text{i}}a}\sum _{n=0}^{\infty }\left(\frac{{\epsilon }_{\text{i}}(n+1)-{\epsilon }_{\text{o}}(n+1)}{{\epsilon }_{\text{i}}n+{\epsilon }_{\text{o}}(n+1)}\right)\\ \times {\left(\frac{r}{r_{\text{K}}}\right)}^n{P}_n(cos\theta ),\end{array}$$ (3)

$${\mathrm{\Psi }}_{\text{out}}(\mathbf{r})=\frac{q}{{\epsilon }_{\text{i}}r}\sum _{n=0}^{\infty }\left(\frac{{\epsilon }_{\text{i}}(2n+1)}{{\epsilon }_{\text{i}}n+{\epsilon }_o(n+1)}\right){\left(\frac{r_{\text{s}}}{r}\right)}^n{P}_n(cos\theta ),$$ (4)

where P_n(x) is the Legendre polynomial, and r_K = a²/r_s.

When λ ≠ 0, the problem can be solved analytically [6,7] by using the classical electrostatic theory as well. The exact solution is in fact given as

$$\begin{array}{l}{\mathrm{\Psi }}_{\text{in}}(\mathbf{r})=\frac{q}{{\epsilon }_{\text{i}}\mid \mathbf{r}-{\mathbf{r}}_{\text{s}}\mid }+\frac{q}{{\epsilon }_{\text{i}}a}\sum _{n=0}^{\infty }\left(\frac{{\epsilon }_{\text{i}}(n+1)k_n(u)+{\epsilon }_{\text{o}}u{k}_n^{\prime }(u)}{{\epsilon }_{\text{i}}n{k}_n(u)-{\epsilon }_{\text{o}}u{k}_n^{\prime }(u)}\right)\\ \times {\left(\frac{r}{r_{\text{K}}}\right)}^n{P}_n(cos\theta ),\end{array}$$ (5)

$${\mathrm{\Psi }}_{\text{out}}(\mathbf{r})=\frac{q}{{\epsilon }_{\text{i}}a}\sum _{n=0}^{\infty }\left(\frac{{\epsilon }_{\text{i}}(2n+1)}{{\epsilon }_{\text{i}}n{k}_n(u)-{\epsilon }_{\text{o}}u{k}_n^{\prime }(u)}\right){\left(\frac{r_{\text{s}}}{a}\right)}^n{k}_n(\lambda r)P_n(cos\theta ),$$ (6)

where u = λa, and k_n(r) is the modified spherical Hankel function of order n (also called the modified spherical Bessel function of the second or third kind) defined as [8]

$$k_n(r)=\sqrt{\frac{\pi }{2r}}{K}_{n+1/2}(r)=\frac{\pi }{2r}{\text{e}}^{-r}\sum _{k=0}^n\frac{(n+k)!}{k!(n-k)!}\frac{1}{{(2r)}^k}n\ge 0,$$ (7)

where K_n(x) is the modified Bessel function of the third kind.

Moreover, it has been shown in Ref. [7] that, when the ionic strength of the solvent, or equivalently the inverse Debye screening length λ, tends to zero, Eqs. (5) and (6) can be identified with Eqs. (3) and (4), respectively.

3. A prolate spheroid immersed in the pure water solvent

To the best of the author’s knowledge, the exact solution to the electrostatic problem that a point charge is set inside a dielectric prolate spheroid embedded in a dissimilar dielectric has not been published. Since this is a basic electrostatic problem, and most importantly, since it has potential applications in hybrid explicit/implicit solvation simulations [1–3] for bio-macromolecules of irregular shapes, the exact solution should be made known. It should be mentioned, however, that the exact solution to a similar electrostatic problem in which the point charge is set outside a dielectric or conducting prolate spheroid can be found in [9–11]. In addition, the electric potential arising from uniform charge distributions bounded by ellipsoids has been treated on many occasions [12], and potential and energy of much more complicated spheroidal charge distributions have been investigated in Refs. [13–15].

Let us consider a dielectric prolate spheroid of permittivity ε_i centered at the origin and embedded in a homogeneous dielectric medium of permittivity ε_o. The interfocal distance of the spheroid is assumed to be a; see Fig. 2.

Fig. 2.

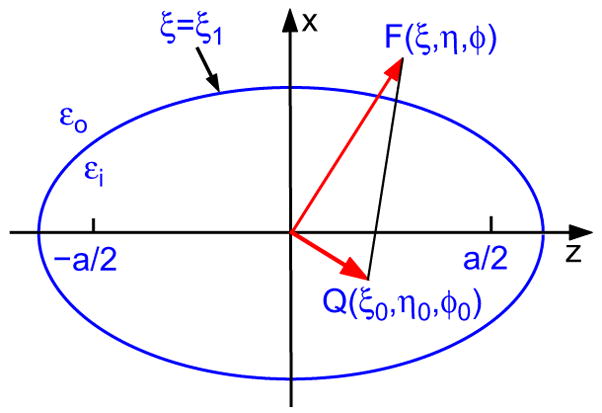
A point charge and a dielectric prolate spheroid.

There are several definitions of prolate spheroidal coordinates, and in this note, the prolate spheroidal coordinates (ξ, η, ϕ) are defined through

$$\begin{array}{l}x=\frac{a}{2}\sqrt{\left({\xi }^2-1\right)(1-{\eta }^2)}cos\phi ,\\ y=\frac{a}{2}\sqrt{\left({\xi }^2-1\right)(1-{\eta }^2)}sin\phi ,z=\frac{a}{2}\xi \eta ,\end{array}$$

where ξ ∈ [1, ∞) is the radial variable, η ∈ [−1, 1] is the angular variable, and ϕ ∈ [0, 2π] is the azimuthal variable. Also, the surface of constant ξ is a prolate spheroid with interfocal distance a (ξ = 1 corresponds to the line between the foci), the surfaces of constant η are the two sheets of a hyperboloid of revolution with foci z = ± a/2, and the surface of constant ϕ is a plane through the z-axis at an angle ϕ to the x–z plane.

Without loss of generality, let the point charge q be located at the point r_s = (ξ₀, η₀, ϕ₀ = 0) on the x–z plane inside the dielectric spheroid defined by the equation ξ = ξ₁ (so ξ₁ > ξ₀ ≥ 1); see Fig. 2. Outside the spheroid (ξ₁ ≤ ξ), the potential must be finite. By the usual procedure of the separation of variables, it is not difficult to conclude that the electrostatic potential outside the spheroid takes the form

$${\mathrm{\Psi }}_{\text{out}}(\mathbf{r})=\frac{q}{{\epsilon }_{\text{i}}a}\sum _{n=0}^{\infty }\sum _{m=0}^n(A_{mn}cosm\phi +B_{mn}sinm\phi )P_n^m(\eta )Q_n^m(\xi ),$$ (8)

where $P_n^m(x)$ and $Q_n^m(x)$ are the associated Legendre functions of the first and the second kind, respectively, and A_mn and B_mn are the unknown coefficients.

On the other hand, the potential inside the spheroid (1 ≤ ξ ≤ ξ₁) due to the source point charge q alone is q/ε_i|r − r_s|. We must superimpose on this a finite reaction potential due to the polarization of the dielectric. In fact, the total potential inside the spheroid takes the form

$$\begin{array}{l}{\mathrm{\Psi }}_{\text{in}}(\mathbf{r})=\frac{q}{{\epsilon }_{\text{i}}\mid \mathbf{r}-{\mathbf{r}}_{\text{s}}\mid }+\frac{q}{{\epsilon }_{\text{i}}a}\sum _{n=0}^{\infty }\sum _{m=0}^n(C_{mn}cosm\phi +D_{mn}sinm\phi )\\ \times P_n^m(\eta )P_n^m(\xi ),\end{array}$$ (9)

where C_mn and D_mn are the unknown expansion coefficients.

Note that the general expansion of 1/|r − r_s| in prolate spheroidal coordinates is given by [16–18]

$$\begin{array}{l}\frac{1}{\mid \mathbf{r}-{\mathbf{r}}_s\mid }=\frac{1}{a}\sum _{n=0}^{\infty }\sum _{m=0}^n{H}_{mn}cosm\phi P_n^m({\eta }_0)P_n^m(\eta )\\ \times \{\begin{array}{ll}{P}_n^m({\xi }_0)Q_n^m(\xi ),\hfill & \xi >{\xi }_0,\hfill \\ P_n^m(\xi )Q_n^m({\xi }_0),\hfill & \xi <{\xi }_0,\hfill \end{array}\end{array}$$

where

$$H_{mn}=2(2n+1)(2-{\delta }_{m0}){(-1)}^m{\left[\frac{(n-m)!}{(n+m)!}\right]}^2.$$

Here δ_m0 is the Kronecker delta. Therefore, the total potential inside the spheroid can also be expressed as

$$\begin{array}{l}{\mathrm{\Psi }}_{\text{in}}(\mathbf{r})=\frac{q}{{\epsilon }_{\text{i}}a}\sum _{n=0}^{\infty }\sum _{m=0}^n(C_{mn}cosm\phi +D_{mn}sinm\phi )P_n^m(\eta )P_n^m(\xi )\\ +\frac{q}{{\epsilon }_{\text{i}}a}\sum _{n=0}^{\infty }\sum _{m=0}^n{H}_{mn}cosm\phi P_n^m({\eta }_0)P_n^m(\eta )\\ \times \{\begin{array}{ll}{P}_n^m({\xi }_0)Q_n^m(\xi ),\hfill & \xi >{\xi }_0,\hfill \\ P_n^m(\xi )Q_n^m({\xi }_0),\hfill & \xi <{\xi }_0.\hfill \end{array}\end{array}$$ (10)

The expansion coefficients A_mn, B_mn, C_mn and D_mn in Eqs. (8) and (9) are to be determined by the boundary condition of Eq. (2) which, under the prolate spheroidal coordinates, becomes

$${\mathrm{\Psi }}_{\text{out}}({\xi }_1,\eta ,\phi )={\mathrm{\Psi }}_{\text{in}}({\xi }_1,\eta ,\phi ),$$ (11)

$${\epsilon }_{\text{o}}{\left(\frac{1}{h_{\xi }}\frac{\partial {\mathrm{\Psi }}_{\text{out}}}{\partial \xi }\right)}_{\xi ={\xi }_1}={\epsilon }_{\text{i}}{\left(\frac{1}{h_{\xi }}\frac{\partial {\mathrm{\Psi }}_{\text{in}}}{\partial \xi }\right)}_{\xi ={\xi }_1},$$ (12)

where h_ξ is the radial scale factor. Then, by using the orthogonality of cos mϕ and sin mϕ as well as that of $P_n^m(x)$, from Eq. (11) one can obtain

$$Q_n^m({\xi }_1)A_{mn}-P_n^m({\xi }_1)C_{mn}=H_{mn}{P}_n^m({\eta }_0)P_n^m({\xi }_0)Q_n^m({\xi }_1),$$ (13)

$$Q_n^m({\xi }_1)B_{mn}-P_n^m({\xi }_1)D_{mn}=0.$$ (14)

On the other hand, further by using the recursion formula

$$\begin{array}{l}(x^2-1)\frac{\text{d}{p}_n^m(x)}{\text{d}x}=(n-m+1)P_{n+1}^m(x)-(n+1)x{P}_n^m(x),\\ (x^2-1)\frac{\text{d}{Q}_n^m(x)}{\text{d}x}=(n-m+1)Q_{n+1}^m(x)-(n+1)x{Q}_n^m(x),\end{array}$$

from Eq. (12) one can get

$${\epsilon }_{\text{o}}{\widehat{Q}}_n^m({\xi }_1)A_{mn}-{\epsilon }_{\text{i}}{\widehat{P}}_n^m({\xi }_1)C_{mn}={\epsilon }_{\text{i}}{H}_{mn}{P}_n^m({\eta }_0)P_n^m({\xi }_0){\widehat{Q}}_n^m({\xi }_1),$$ (15)

$${\epsilon }_{\text{o}}{\widehat{Q}}_n^m({\xi }_1)B_{mn}-{\epsilon }_{\text{i}}{\widehat{P}}_n^m({\xi }_1)D_{mn}=0,$$ (16)

where

$$\begin{array}{l}{\widehat{P}}_n^m({\xi }_1)=(n-m+1)P_{n+1}^m({\xi }_1)-(n+1){\xi }_1{P}_n^m({\xi }_1),\\ {\widehat{Q}}_n^m({\xi }_1)=(n-m+1)Q_{n+1}^m({\xi }_1)-(n+1){\xi }_1{Q}_n^m({\xi }_1).\end{array}$$

From Eqs. (14) and (16), it follows that

$$B_{mn}=0,D_{mn}=0.$$

And solving Eqs. (13) and (15) leads to

$$A_{mn}=H_{mn}{P}_n^m({\eta }_0)P_n^m({\xi }_0)·\frac{{\epsilon }_{\text{i}}\left[P_n^m({\xi }_1){\widehat{Q}}_n^m({\xi }_1)-Q_n^m({\xi }_1){\widehat{P}}_n^m({\xi }_1)\right]}{{\epsilon }_{\text{o}}{P}_n^m({\xi }_1){\widehat{Q}}_n^m({\xi }_1)-{\epsilon }_{\text{i}}{Q}_n^m({\xi }_1){\widehat{P}}_n^m({\xi }_1)},$$

and

$$C_{mn}=H_{mn}{P}_n^m({\eta }_0)P_n^m({\xi }_0)·\frac{({\epsilon }_{\text{i}}-{\epsilon }_{\text{o}})Q_n^m({\xi }_1){\widehat{Q}}_n^m({\xi }_1)}{{\epsilon }_{\text{o}}{P}_n^m({\xi }_1){\widehat{Q}}_n^m({\xi }_1)-{\epsilon }_{\text{i}}{Q}_n^m({\xi }_1){\widehat{P}}_n^m({\xi }_1)}.$$

In summary, the total potential inside the spheroid is given by

$$\begin{array}{l}{\mathrm{\Psi }}_{\text{in}}(\mathbf{r})=\frac{q}{{\epsilon }_{\text{i}}\mid \mathbf{r}-{\mathbf{r}}_s\mid }+\frac{q}{{\epsilon }_{\text{i}}a}\sum _{n=0}^{\infty }\sum _{m=0}^n({\epsilon }_{\text{i}}-{\epsilon }_{\text{o}})H_{mn}{P}_n^m({\eta }_0)P_n^m({\xi }_0)\\ \times Q_n^m({\xi }_1){\widehat{Q}}_n^m({\xi }_1)K_{mn}^{-1}cosm\phi P_n^m(\eta )P_n^m(\xi ),\end{array}$$ (17)

while the potential outside the spheroid is

$$\begin{array}{l}{\mathrm{\Psi }}_{\text{out}}(\mathbf{r})=\frac{q}{{\epsilon }_{\text{i}}a}\sum _{n=0}^{\infty }\sum _{m=0}^n{\epsilon }_{\text{i}}{H}_{mn}{P}_n^m({\eta }_0)P_n^m({\xi }_0)\\ \times \left[P_n^m({\xi }_1){\widehat{Q}}_n^m({\xi }_1)-Q_n^m({\xi }_1){\widehat{P}}_n^m({\xi }_1)\right]K_{mn}^{-1}cosm\phi P_n^m(\eta )Q_n^m(\xi ),\end{array}$$ (18)

where

$$K_{mn}={\epsilon }_{\text{o}}{P}_n^m({\xi }_1){\widehat{Q}}_n^m({\xi }_1)-{\epsilon }_{\text{i}}{Q}_n^m({\xi }_1){\widehat{P}}_n^m({\xi }_1).$$

In a special case, when the prolate spheroid approaches a sphere, Eqs. (17) and (18) should reduce to Eqs. (3) and (4), respectively, which in fact can be demonstrated in a similar way as used in Ref. [9].

4. A prolate spheroid immersed in an ionic solvent

The LPBE has been solved analytically for systems with a spheroidal geometry for simple boundary conditions, like constant surface charge or potential, or for a mix of these [19–21]. To the best of the author’s knowledge, however, the exact solution to the electrostatic problem that a point charge is set inside a dielectric prolate spheroid immersed in an ionic solvent has never been discussed in the literature, perhaps for the reason that the solution is rather cumbersome.

Using the spheroidal coordinates, the LPBE of Eq. (1) can be written as

$$\begin{array}{l}\frac{\partial }{\partial \xi }\left[\left({\xi }^2-1\right)\frac{\partial \mathrm{\Psi }}{\partial \xi }\right]+\frac{\partial }{\partial \eta }\left[\left(1-{\eta }^2\right)\frac{\partial \mathrm{\Psi }}{\partial \eta }\right]+\frac{{\xi }^2-{\eta }^2}{\left({\xi }^2-1\right)(1-{\eta }^2)}\frac{{\partial }^2\mathrm{\Psi }}{\partial {\phi }^2}\\ -c^2\left({\xi }^2-{\eta }^2\right)\mathrm{\Psi }=0,\end{array}$$

where c = (a/2)λ is the spheroidal parameter. By means of the separation of variables with

$$\mathrm{\Psi }(\xi ,\eta ,\phi )=S_{mn}(ic,\eta )R_{mn}(ic,\xi )\left(\begin{array}{l}cosm\phi \\ sinm\phi \end{array}\right),$$

where m and n are zero or positive integers with n ≥ m, we obtain the ordinary differential equations

$$\frac{\text{d}}{\text{d}\eta }\left[\left(1-{\eta }^2\right)\frac{\text{d}{S}_{mn}(ic,\eta )}{\text{d}\eta }\right]+\left[{\lambda }_{mn}(ic)+c^2{\eta }^2-\frac{m^2}{1-{\eta }^2}\right]S_{mn}(ic,\eta )=0,$$ (19)

$$\frac{\text{d}}{\text{d}\xi }\left[\left({\xi }^2-1\right)\frac{\text{d}{R}_{mn}(ic,\xi )}{\text{d}\xi }\right]-\left[{\lambda }_{mn}(ic)+c^2{\xi }^2+\frac{m^2}{{\xi }^2-1}\right]R_{mn}\left(ic,\xi \right)=0,$$ (20)

where S_mn(ic, η) and R_mn(ic, ξ) are the eigenfunctions associated with the eigenvalue λ_mn(ic). As being discussed later, these two equations are those solved by prolate spheroidal wave functions but with c being replaced by ic. It should be pointed out that, although the equation governing the angular function S_mn(ic, η), Eq. (19), and that governing the radial function R_mn(ic, ξ), Eq. (20), are similar to each other, R_mn(ic, ξ) may not take a form similar to that of S_mn(ic, η). This is because their domains are different: 1 ≤ ξ < ∞ for the former, and −1 ≤ η ≤ 1 for the latter.

4.1. The angular function S_mn(ic, η)

In the standard theory, the prolate spheroidal angular wave function S_mn(c, η) satisfies the equation

$$\frac{\text{d}}{\text{d}\eta }\left[\left(1-{\eta }^2\right)\frac{\text{d}{S}_{mn}(c,\eta )}{\text{d}\eta }\right]+\left[{\lambda }_{mn}(c)-c^2{\eta }^2-\frac{m^2}{1-{\eta }^2}\right]S_{mn}(c,\eta )=0.$$ (21)

We only consider the angular functions of the first kind $S_{mn}^{(1)}(c,\eta )$ since they are regular at η = ± 1, but the angular functions of the second kind $S_{mn}^{(2)}(c,\eta )$ are not. Moreover, since when c vanishes, Eq. (21) becomes the equation which is satisfied by the associated Legendre functions, it follows that the angular functions of the first kind must reduce to the associated Legendre functions of the first kind, as c goes to zero. Therefore, the eigenvalues λ_mn(c) for which Eq. (21) admits solutions that are finite at η = ± 1 satisfy

$${\lambda }_{mn}(0)=n(n+1),$$

and the spheroidal angular functions of the first kind are usually expanded into the associated Legendre functions of the first kind as follows

$$S_{mn}^{(1)}(c,\eta )={\sum _{r=0,1}^{\infty }}^{\prime }{d}_r^{mn}(c)P_{m+r}^m(\eta ).$$ (22)

Here and in the sequel, the prime over the summation sign indicates that the summation is over only even values of r when n − m is even, and over only odd values of r when n − m is odd.

The eigenvalues λ_mn(c) and the angular expansion coefficients $d_r^{mn}(c)$ satisfy the following recursion formula for r ≥ 0 [22]

$$A_r^m(c)d_{r+2}^{mn}(c)+(B_r^m(c)-{\lambda }_{mn}(c))d_r^{mn}(c)+C_r^m(c)d_{r-2}^{mn}(c)=0,$$ (23)

in which

$$A_r^m(c)=\frac{(2m+r+2)(2m+r+1)c^2}{(2m+2r+3)(2m+2r+5)},$$ (24)

$$\begin{array}{l}{B}_r^m(c)=(m+r)(m+r+1)\\ +\frac{2(m+r)(m+r+1)-2m^2-1}{(2m+2r-1)(2m+2r+3)}{c}^2,\end{array}$$ (25)

$$C_r^m(c)=\frac{r(r-1)c^2}{(2m+2r-3)(2m+2r-1)}.$$ (26)

The eigenvalues are determined by the condition that $d_r^{mn}(c)\to 0$ as r → ∞, and various methods have been proposed to calculate the eigenvalues and the expansion coefficients; see Refs. [22–30] and references therein.

It has been found that when c is small, the dominant coefficient for given m and n is $d_{n-m}^{mn}(c)$. In particular, as c → 0, the only nonzero angular coefficient is then $d_{n-m}^{mn}(c)$, and hence the spheroidal angular function collapses to $P_n^m(\eta )$. Moreover, the expansion coefficients may be normalized so that each spheroidal angular function reduces exactly to the corresponding associated Legendre function when c becomes zero, which can be ensured by requiring $S_{mn}^{(1)}(c,0)=P_n^m(0)$ when n − m is even and ${S_{mn}^{(1)}}^{\prime }(c,0)={P_n^m}^{\prime }(0)$ when n − m is odd [22,23]. Then it follows that the functions of $S_{mn}^{(1)}(c,\eta )$ form an orthogonal set on the interval (−1,1), namely,

$${\int }_{-1}^1{S}_{mn}^{(1)}(c,\eta )S_{m{n}^{\prime }}^{(1)}(c,\eta )\text{d}\eta ={\delta }_{n{n}^{\prime }}\left(2{\sum _{r=0,1}^{\infty }}^{\prime }\frac{(r+2m)!{(d_r^{mn}(c))}^2}{(2r+2m+1)r!}\right).$$

The angular solution S_mn(ic, η) to Eq. (19) that is regular at η = ± 1 can be obtained from the standard prolate spheroidal angular wave function $S_{mn}^{(1)}(c,\eta )$ with c being replaced by ic, namely, the corresponding angular expansion coefficients $d_r^{mn}(ic)$ are obtained from those of the standard angular expansion coefficients $d_r^{mn}(c)$ by replacing c by ic in the recursion formula in Eqs. (23)–(26).

4.2. The radial function R_mn(ic, ξ)

In the standard theory, the prolate spheroidal radial wave function R_mn(c, ξ) satisfies the equation

$$\frac{\text{d}}{\text{d}\xi }\left[\left({\xi }^2-1\right)\frac{\text{d}{R}_{mn}(c,\xi )}{\text{d}\xi }\right]-\left[{\lambda }_{mn}(c)-c^2{\xi }^2+\frac{m^2}{{\xi }^2-1}\right]R_{mn}\left(c,\xi \right)=0.$$

The standard spheroidal radial functions are usually expanded in a basis of spherical Bessel functions. The expansions are quite simple, because the radial expansion coefficients are proportional to the angular expansion coefficients. A given set of spherical basis radial functions (Bessel, Neumann, or Hankel) has corresponding spheroidal radial functions. In general, the radial functions are written in the form [22]

$$\begin{array}{l}{R}_{mn}^{(k)}\left(c,\xi \right)=\frac{1}{{\rho }_{mn}(c)}{\left(\frac{{\xi }^2-1}{{\xi }^2}\right)}^{\frac{m}{2}}\\ \times {\sum _{r=0,1}^{\infty }}^{\prime }{i}^{r+m-n}{d}_r^{mn}(c)\frac{(2m+r)!}{r!}{z}_{m+r}^{(k)}\left(c\xi \right),\end{array}$$

where the normalization factor ρ_mn(c) is given by

$${\rho }_{mn}(c)={\sum _{r=0,1}^{\infty }}^{\prime }{d}_r^{mn}(c)\frac{(2m+r)!}{r!},$$

and $z_n^{(k)}(x)$ is the kth kind of spherical Bessel function of order n, i.e., $z_n^{(1)}(x)\equiv j_n(x),z_n^{(2)}(x)\equiv n_n(x),z_n^{(3)}(x)\equiv h_n^{(1)}(x)$, and $z_n^{(4)}(x)\equiv h_n^{(2)}(x)$, respectively.

Consequently, the radial solution R_mn(ic, ξ) to Eq. (20) can be expanded in the modified spherical Bessel functions [19]

$$R_{mn}^{(1)}\left(ic,\xi \right)=\frac{1}{{\rho }_{mn}(ic)}{\left(\frac{{\xi }^2-1}{{\xi }^2}\right)}^{\frac{m}{2}}{\sum _{r=0,1}^{\infty }}^{\prime }{d}_r^{mn}(ic)\frac{(2m+r)!}{r!}{i}_{m+r}\left(c\xi \right),$$

and

$$R_{mn}^{(3)}\left(ic,\xi \right)=\frac{1}{{\rho }_{mn}(ic)}{\left(\frac{{\xi }^2-1}{{\xi }^2}\right)}^{\frac{m}{2}}{\sum _{r=0,1}^{\infty }}^{\prime }{d}_r^{mn}(ic)\frac{(2m+r)!}{r!}{k}_{m+r}\left(c\xi \right),$$ (27)

where k_n(r) is the modified spherical Bessel function of the third kind as defined in Eq. (7), and i_n(r) the modified spherical Bessel function of the first kind defined as

$$i_n(r)=\sqrt{\frac{\pi }{2r}}{I}_{n+1/2}(r).$$

Here, I(x) is the modified Bessel function of the first kind. The fact that the radial functions can be expanded in the modified spherical Bessel functions can also be understood by noting that, as a → 0, Eq. (20) reduces to the following modified spherical Bessel equation

$$r^2\frac{{\text{d}}^{2}R}{\text{d}{r}^2}+2r\frac{dR}{dr}-\left({\lambda }^2{r}^2+n(n+1)\right)R=0,$$

indicating that the radial functions should reduce to the modified spherical Bessel functions.

Note that spheroidal wave functions are needed only for expressing the electric potential outside the prolate spheroid where ξ ≥ ξ₁ >1, which should vanish at infinity. Since only $R_{mn}^{(3)}(ic,\xi )$ is finite at ξ = ∞, we shall, therefore, use the radial function $R_{mn}^{(3)}(ic,\xi )$ to represent the potential outside the prolate spheroid.

For convenience, we refrain from appending superscripts (1) and (3) to, as well as including ic in, the symbols for the angular and the radial functions. Instead, we simply denote $S_{mn}^{(1)}(ic,\eta )$ by S_mn(η), $R_{mn}^{(3)}(ic,\xi )$ by R_mn(ξ), and $d_r^{mn}(ic)$ by $d_r^{mn}$ for the rest of this note.

4.3. Series representation of the potential

Let us consider again a point charge q located at the point r_s = (ξ₀, η₀, ϕ₀ = 0) on the x–z plane inside the dielectric spheroid defined by the equation ξ = ξ₁ (so ξ₁ > ξ₀ ≥ 1); see Fig. 2. Inside the spheroid, the total potential still takes the forms in Eqs. (9) and (10). On the other hand, since the potential outside the spheroid (ξ₁ ≤ ξ) must be finite and vanishes at ξ = ∞, it should take on the form

$${\mathrm{\Psi }}_{\text{out}}(\mathbf{r})=\frac{q}{{\epsilon }_{i}a}\sum _{n=0}^{\infty }\sum _{m=0}^n(A_{mn}cosm\phi +B_{mn}sinm\phi )S_{mn}(\eta )R_{mn}(\xi ),$$ (28)

where A_mn and B_mn are the unknown expansion coefficients.

Once again, by using the orthogonality of cos mϕ and sin mϕ together with the boundary conditions of Eqs. (11) and (12), we get on the interface Γ

$$\begin{array}{l}\sum _{n=m}^{\infty }[S_{mn}(\eta )R_{mn}({\xi }_1)A_{mn}-P_n^m(\eta )P_n^m({\xi }_1)C_{mn}]\\ =\sum _{n=m}^{\infty }{H}_{mn}{P}_n^m(\eta )P_n^m({\eta }_0)P_n^m({\xi }_0)Q_n^m({\xi }_1),\end{array}$$ (29)

$$\sum _{n=m}^{\infty }[S_{mn}(\eta )R_{mn}({\xi }_1)B_{mn}-P_n^m(\eta )P_n^m({\xi }_1)D_{mn}]=0.$$ (30)

and

$$\begin{array}{l}\sum _{n=m}^{\infty }\left[{\epsilon }_{\text{o}}{S}_{mn}(\eta )R_{mn}^{\prime }({\xi }_1)A_{mn}-{\epsilon }_{\text{i}}{P}_n^m(\eta )P_n^{m^{\prime }}({\xi }_1)C_{mn}\right]\\ =\sum _{n=m}^{\infty }{\epsilon }_{\text{i}}{H}_{mn}{P}_n^m(\eta )P_n^m({\eta }_0)P_n^m({\xi }_0)Q_n^{m^{\prime }}({\xi }_1),\end{array}$$ (31)

$$\sum _{n=m}^{\infty }\left[{\epsilon }_{\text{o}}{S}_{mn}(\eta )R_{mn}^{\prime }({\xi }_1)B_{mn}-{\epsilon }_{\text{i}}{P}_n^m(\eta )P_n^{m^{\prime }}({\xi }_1)D_{mn}\right]=0.$$ (32)

First of all, from Eqs. (30) and (32), it follows that

$$B_{mn}=0,D_{mn}=0.$$

It is observed, however, that the left- and right-hand sides of Eqs. (29) and (31) cannot be matched term by term due to different basis functions on both sides. Nevertheless, using Eq. (22), we can rewrite S_mn(η) in series of $P_n^m(\eta )$, and then it is possible to make use of the orthogonality of the associated Legendre polynomials $P_n^m(\eta )$ to arrive at equations for the expansion coefficients.

Recall that the associated Legendre polynomials $P_n^m(\eta )$ have the following orthogonality [18]

$${\int }_{-1}^1{P}_n^m(\eta )P_{n^{\prime }}^m(\eta )\text{d}\eta ={\delta }_{n{n}^{\prime }}{W}_{mn},$$

where

$$W_{mn}=\frac{(n+m)!}{(n+\frac{1}{2})(n-m)!}.$$

Also, note that

$$\begin{array}{l}{\int }_{-1}^1{S}_{mn}(\eta )P_{n^{\prime }}^m(\eta )\text{d}\eta ={\int }_{-1}^1\left({\sum _{r=0,1}^{\infty }}^{\prime }{d}_r^{mn}{P}_{m+r}^m(\eta )\right)P_{n^{\prime }}^m(\eta )\text{d}\eta \\ =\{\begin{array}{ll}{d}_{n^{\prime }-m}^{mn}{W}_{m{n}^{\prime }},\hfill & \text{if}n-n^{\prime }\text{even},\hfill \\ 0,\hfill & \text{if}n-n^{\prime }\text{odd}.\hfill \end{array}\end{array}$$

Then from Eqs. (29) and (31), we have for n ≥ m

$$\begin{array}{l}{\sum _{r=0,1}^{\infty }}^{\prime }{d}_{n-m}^{m(m+r)}{R}_{m(m+r)}({\xi }_1)A_{m(m+r)}-P_n^m({\xi }_1)C_{mn}\\ =H_{mn}{P}_n^m({\eta }_0)P_n^m({\xi }_0)Q_n^m({\xi }_1),\end{array}$$ (33)

$$\begin{array}{l}{\epsilon }_{\text{o}}{\sum _{r=0,1}^{\infty }}^{\prime }{d}_{n-m}^{m(m+r)}{R}_{m(m+r)}^{\prime }({\xi }_1)A_{m(m+r)}-{\epsilon }_{\text{i}}{P}_n^{m^{\prime }}({\xi }_1)C_{mn}\\ ={\epsilon }_{\text{i}}{H}_{mn}{P}_n^m({\eta }_0)P_n^m({\xi }_0)Q_n^{m^{\prime }}({\xi }_1),\end{array}$$ (34)

For a fixed value of m, Eqs. (33) and (34) for all n = m, m + 1,… constitute a system of an infinite set of equations, but the system can be completely decoupled into two independent systems, one for A_mm, A_m(m+2),…, C_mm, C_m(m+2),…, and the other for A_m(m+1), A_m(m+3),…, C_m(m+1), C_m(m+3),…. To solve for the unknown expansion coefficients, it is more convenient to cast the systems in matrix forms. For i, r = 0, 1, 2,…, let

$$\begin{array}{l}{a}_{ir}=d_i^{m(m+r)}{R}_{m(m+r)}({\xi }_1),\\ {\widehat{a}}_{ir}=d_i^{m(m+r)}{R}_{m(m+r)}^{\prime }({\xi }_1),\\ b_i=P_{m+i}^m({\xi }_1),\\ {\widehat{b}}_i=P_{m+i}^{m^{\prime }}({\xi }_1),\\ g_i=H_{m(m+i)}{P}_{m+i}^m({\eta }_0)P_{m+i}^m({\xi }_0)Q_{m+i}^m({\xi }_1),\\ {\widehat{g}}_i=H_{m(m+i)}{P}_{m+i}^m({\eta }_0)P_{m+i}^m({\xi }_0)Q_{m+i}^{m^{\prime }}({\xi }_1).\end{array}$$

Then we can write Eqs. (33) and (34) for all n = m, m +1,… as

$${\mathcal{M}}_{\sigma }{\mathit{U}}_{\sigma }={\mathit{V}}_{\sigma },\sigma =0,1,$$ (35)

where

$${\mathcal{M}}_{\sigma }=\left[\begin{array}{cccccc}{a}_{\sigma ,\sigma }& a_{\sigma ,\sigma +2}& \cdots & b_{\sigma }& 0& \cdots \\ {\epsilon }_{\text{o}}{\widehat{a}}_{\sigma ,\sigma }& {\epsilon }_{\text{o}}{\widehat{a}}_{\sigma ,\sigma +2}& \cdots & {\epsilon }_{\text{i}}{\widehat{b}}_{\sigma }& 0& \cdots \\ a_{\sigma +2,\sigma }& a_{\sigma +2,\sigma +2}& \cdots & 0& b_{\sigma +2}& \cdots \\ {\epsilon }_{\text{o}}{\widehat{a}}_{\sigma +2,\sigma }& {\epsilon }_{\text{o}}{\widehat{a}}_{\sigma +2,\sigma +2}& \cdots & 0& {\epsilon }_{\text{i}}{\widehat{b}}_{\sigma +2}& \cdots \\ ⋮& ⋮& \ddots & ⋮& ⋮& \ddots \end{array}\right],$$

and

$$\begin{array}{l}{\mathit{U}}_{\sigma }=\left(\begin{array}{c}{A}_{\sigma }\\ C_{\sigma }\end{array}\right),{\mathit{V}}_{\sigma }=\left(\begin{array}{c}{g}_{\sigma }\\ {\epsilon }_{\text{i}}{\widehat{g}}_{\sigma }\\ g_{\sigma +2}\\ {\epsilon }_{\text{i}}{\widehat{g}}_{\sigma +2}\\ ⋮\end{array}\right),{\mathit{A}}_{\sigma }=\left(\begin{array}{c}{A}_{m,m+\sigma }\\ A_{m,m+\sigma +2}\\ A_{m,m+\sigma +4}\\ ⋮\end{array}\right),\\ {\mathit{C}}_{\sigma }=\left(\begin{array}{c}{C}_{m,m+\sigma }\\ C_{m,m+\sigma +2}\\ C_{m,m+\sigma +4}\\ ⋮\end{array}\right).\end{array}$$

Let further

$$k_{ij}={\epsilon }_{\text{i}}{a}_{ij}{\widehat{b}}_i-{\epsilon }_{\text{o}}{\widehat{a}}_{ij}{b}_i,$$

$$f_i={\epsilon }_{\text{i}}\left(g_i{\widehat{b}}_i-{\widehat{g}}_i{b}_i\right).$$

Then eliminating C_σ in Eq. (35) leads to

$${\mathcal{K}}_{\sigma }{\mathit{A}}_{\sigma }={\mathit{F}}_{\sigma },\sigma =0,1,$$ (36)

where

$${\mathcal{K}}_{\sigma }=\left[\begin{array}{cccc}{k}_{\sigma ,\sigma }& k_{\sigma ,\sigma +2}& k_{\sigma ,\sigma +4}& \cdots \\ k_{\sigma +2,\sigma }& k_{\sigma +2,\sigma +2}& k_{\sigma +2,\sigma +4}& \cdots \\ k_{\sigma +4,\sigma }& k_{\sigma +4,\sigma +2}& k_{\sigma +4,\sigma +4}& \cdots \\ ⋮& ⋮& ⋮& \ddots \end{array}\right],{\mathit{F}}_{\sigma }=\left(\begin{array}{c}{f}_{\sigma }\\ f_{\sigma +2}\\ f_{\sigma +4}\\ ⋮\end{array}\right).$$

Once having solved Eq. (36) for the expansion coefficients A_σ, the expansion coefficients C_σ are then calculated by

$${\mathcal{B}}_{\sigma }{\mathit{C}}_{\sigma }={\mathcal{N}}_{\sigma }{\mathit{A}}_{\sigma }-{\mathit{G}}_{\sigma },\sigma =0,1,$$ (37)

where B_σ is a diagonal matrix given by

$${\mathit{B}}_{\sigma }=\text{diag}(b_{\sigma },b_{\sigma +2},b_{\sigma +4},\cdots ),$$

and

$${\mathcal{N}}_{\sigma }=\left[\begin{array}{cccc}{a}_{\sigma ,\sigma }& a_{\sigma ,\sigma +2}& a_{\sigma ,\sigma +4}& \cdots \\ a_{\sigma +2,\sigma }& a_{\sigma +2,\sigma +2}& a_{\sigma +2,\sigma +4}& \cdots \\ a_{\sigma +4,\sigma }& a_{\sigma +4,\sigma +2}& a_{\sigma +4,\sigma +4}& \cdots \\ ⋮& ⋮& ⋮& \ddots \end{array}\right],{\mathit{G}}_{\sigma }=\left(\begin{array}{c}{g}_{\sigma }\\ g_{\sigma +2}\\ g_{\sigma +4}\\ ⋮\end{array}\right).$$

4.4. Numerical approximation

For each value of m and each value of σ = 0, 1, the system in Eq. (36) consists of an infinite set of linear equations. However, the series expansion of the angular function S_mn(η), Eq. (22), is presumed to be a convergent representation. Hence, one can perform the computation based on a finite set of equations. The fact that the coefficients $d_r^{mn}$ peak sharply about the value of $d_{n-m}^{mn}$ means that the coupling between the finite set of equations and the infinite set of equations is very small.

Let us assume that, to calculate the electric potentials numerically, the series expansions of the potentials are truncated as

$${\mathrm{\Psi }}_{\text{out}}(\mathbf{r})\approx \frac{q}{{\epsilon }_{\text{i}}a}\sum _{n=0}^N\sum _{m=0}^n{A}_{mn}cosm\phi S_{mn}(\eta )R_{mn}(\xi ),$$ (38)

and

$${\mathrm{\Psi }}_{\text{in}}(\mathbf{r})\approx \frac{q}{{\epsilon }_{\text{i}}\mid \mathbf{r}-{\mathbf{r}}_{\text{s}}\mid }+\frac{q}{{\epsilon }_{\text{i}}a}\sum _{n=0}^N\sum _{m=0}^n{C}_{mn}cosm\phi P_n^m(\eta )P_n^m(\xi ),$$ (39)

where N is an imposed upper limit of n which must be large enough to make the truncation error negligible for a certain physical application. Then for each fixed m, one needs to evaluate S_m,m(η), S_m,m+1(η),…, S_m,N(η), and calculate the expansion coefficients A_m,m, A_m,m+1,…, A_m,N as well as C_m,m, C_m,m+1,…, C_m,N.

More specifically, for each fixed m (0 ≤ m ≤ N), the regular prolate spheroidal wave functions S_mn(η), n = m, m + 1,…, N are truncated as

$$S_{mn}(\eta )\approx {\sum _{r=0,1}^{r_{mn}}}^{\prime }{d}_r^{mn}{P}_{m+r}^m(\eta ),$$ (40)

where r_mn = (N − m) − σ. Here σ = 0 if N − n is even, and σ = 1 if N − n is odd.

On the other hand, the expansion coefficients A_m,m, A_m,m+1,…, A_m,N are obtained by solving the following truncated form of the system in Eq. (36)

$${\breve{\mathcal{K}}}_{\sigma }{\breve{\mathit{A}}}_{\sigma }={\breve{\mathit{F}}}_{\sigma },\sigma =0,1,$$ (41)

where

$${\breve{\mathcal{K}}}_{\sigma }=\left[\begin{array}{cccc}{k}_{\sigma ,\sigma }& k_{\sigma ,\sigma +2}& \cdots & k_{\sigma ,\sigma +2N_m^{(\sigma )}}\\ k_{\sigma +2,\sigma }& k_{\sigma +2,\sigma +2}& \cdots & k_{\sigma +2,\sigma +2N_m^{(\sigma )}}\\ ⋮& ⋮& \ddots & ⋮\\ k_{\sigma +2N_m^{(\sigma )},\sigma }& k_{\sigma +2N_m^{(\sigma )},\sigma +2}& \cdots & k_{\sigma +2N_m^{(\sigma )},\sigma +2N_m^{(\sigma )}}\end{array}\right],$$

and

$${\breve{\mathit{A}}}_{\sigma }=\left(\begin{array}{c}{A}_{m,m+\sigma }\\ A_{m,m+\sigma +2}\\ ⋮\\ A_{m,m+\sigma +2N_m^{(\sigma )}}\end{array}\right),{\widehat{\mathit{F}}}_{\sigma }=\left(\begin{array}{c}{f}_{\sigma }\\ f_{\sigma +2}\\ ⋮\\ f_{\sigma +2N_m^{(\sigma )}}\end{array}\right).$$

Here $N_m^{(\sigma )}$ is defined as

$$N_m^{(0)}=N_m^{(1)}=\frac{N-m-1}{2}$$

if N − m is odd, and as

$$N_m^{(0)}=\frac{N-m}{2},N_m^{(1)}=\frac{N-m-2}{2}$$

if N − m is even. Note that when N − m is even, the size of the second system given in Eq. (41) is one smaller than that of the first system. In particular, $N_N^{(0)}=0$ and $N_N^{(1)}=-1$, which corresponds to the case of m = N. In this case, only A_NN is to be calculated.

Accordingly, the expansion coefficients C_m,m, C_m,m+1,…, C_m,N can be calculated using the truncated form of Eq. (37)

$${\breve{\mathcal{B}}}_{\sigma }{\breve{\mathit{C}}}_{\sigma }={\breve{\mathcal{N}}}_{\sigma }{\breve{\mathit{A}}}_{\sigma }-{\breve{\mathit{G}}}_{\sigma },\sigma =0,1,$$

where

$$\begin{array}{l}{\breve{\mathcal{B}}}_{\sigma }=\text{diag}\left(b_{\sigma },b_{\sigma +2},\cdots ,b_{\sigma +2N_m^{(\sigma )}}\right),\\ {\breve{\mathcal{N}}}_{\sigma }=\left[\begin{array}{cccc}{a}_{\sigma ,\sigma }& a_{\sigma ,\sigma +2}& \cdots & a_{\sigma ,\sigma +2N_m^{(\sigma )}}\\ a_{\sigma +2,\sigma }& a_{\sigma +2,\sigma +2}& \cdots & a_{\sigma +2,\sigma +2N_m^{(\sigma )}}\\ ⋮& ⋮& \ddots & ⋮\\ a_{\sigma +2N_m^{(\sigma )},\sigma }& a_{\sigma +2N_m^{(\sigma )},\sigma +2}& \cdots & a_{\sigma +2N_m^{(\sigma )},\sigma +2N_m^{(\sigma )}}\end{array}\right],\end{array}$$

and

$${\breve{\mathit{C}}}_{\sigma }=\left(\begin{array}{c}{C}_{m,m+\sigma }\\ C_{m,m+\sigma +2}\\ ⋮\\ C_{m,m+\sigma +2N_m^{(\sigma )}}\end{array}\right),{\breve{\mathit{G}}}_{\sigma }=\left(\begin{array}{c}{g}_{\sigma }\\ g_{\sigma +2}\\ ⋮\\ g_{\sigma +2N_m^{(\sigma )}}\end{array}\right).$$

As stated in Section 1, the more general problem in which the dielectric cavity contains a finite number of point charges can be solved by means of linear superposition. More precisely, let a total of L point charges q₁, q₂,…, q_L be located at L arbitrary points r_l = (ξ_l, η_l, ϕ_l), l = 1, 2,…, L inside the prolate spheroid, although in hybrid explicit/implicit solvent biomolecular simulations [1–3], these point charges are in general uniformly distributed in the dielectric cavity. Then at a point r = (ξ, η, ϕ) outside the spheroid the potential takes on the form

$${\mathrm{\Psi }}_{\text{out}}(\mathbf{r})=\sum _{l=1}^L\left(\frac{q_l}{{\epsilon }_{\text{i}}a}\sum _{n=0}^{\infty }\sum _{m=0}^n{A}_{mn}^{(l)}cosm(\phi -{\phi }_l)S_{mn}(\eta )R_{mn}(\xi )\right),$$ (42)

and correspondingly at a point inside the spheroid it takes on the form

$${\mathrm{\Psi }}_{\text{in}}(\mathbf{r})=\sum _{l=1}^L\left(\frac{q_l}{{\epsilon }_{\text{i}}\mid \mathbf{r}-{\mathbf{r}}_l\mid }+\frac{q_l}{{\epsilon }_{\text{i}}a}\sum _{n=0}^{\infty }\sum _{m=0}^n{C}_{mn}^{(l)}cosm(\phi -{\phi }_l)P_n^m(\eta )P_n^m(\xi )\right),$$ (43)

where for each point charge q_l, the associated expansion coefficients $A_{mn}^{(l)}$ and $C_{mn}^{(l)}$ are determined by the system in Eqs. (33) and (34). Note that the coefficient matrix of the system in Eqs. (33) and (34) depends on only the spheroidal surface but not the point charge location. Therefore, the expansion coefficients $A_{mn}^{(l)}$ and $C_{mn}^{(l)}$ for all charges q_l can be obtained simultaneously by solving the system in Eqs. (33) and (34) with the same coefficient matrix but different right-hand sides.

4.5. Discussions

In a special case, when the dielectric spheroid approaches a sphere, namely, when the interfocal distance of the spheroid a tends to zero, Eq. (28) shall reduce to Eq. (6) and Eq. (9) shall reduce to Eq. (5), respectively. In order to avoid unnecessary complications, we shall consider the case when the charge q is set on the positive z-axis. Since now the problem is axially symmetrical, only terms with m = 0 remain in the expansions in Eqs. (9) and (28). Moreover, for a point with prolate spheroidal coordinates ((ξ, η, ϕ) and spherical coordinates (r, θ, ϕ), in the limit a → 0 one has (a/2)ξ → r and η → cos θ and consequently cξ → λr. (Note that for the points on the z-axis, outside the line between the foci of the spheroid, one has exactly (a/2)ξ = r and η = cos θ, regardless of the value of a.) Also, when a → 0, ξ, ξ₁ and ξ₀ all tend to infinity.

Note that $S_{mn}(ic,\eta )\to P_n^m(\eta )$ as c = (a/2)λ → 0. By using $P_n^0(x)=P_n(x)$, we have S_0n(ic, η) → P_n(cos θ). Furthermore, since $d_r^{mn}(0)=0$ when r ≠ n − m, from Eq. (27) one can see that

$$R_{0n}^{(3)}(ic,\xi )=\frac{1}{{\rho }_{0n}(ic)}{\sum _{r=0,1}^{\infty }}^{\prime }{d}_r^{0n}(ic)k_r(c\xi )\to k_n(\lambda r),\text{as}c\to 0.$$ (44)

Therefore, in this case the expansion in Eq. (28) reduces to a series in terms of the same basis functions as used in Eq. (6)

$${\mathrm{\Psi }}_{\text{out}}(\mathbf{r})=\sum _{n=0}^{\infty }{A}_n{k}_n(\lambda r)P_n(cos\theta ).$$ (45)

On the other hand, as a → 0, (a/2)ξ → r so ξ → 2r/a → ∞. Therefore,

$$P_n(\xi )\to \frac{(2n)!}{2^n{(n!)}^2}{\xi }^n=\frac{(2n)!}{a^n{(n!)}^2}{r}^n,\text{as}\xi \to \infty .$$ (46)

Accordingly, the expansion in Eq. (9) reduces to a series in terms of the same basis functions as used in Eq. (5)

$${\mathrm{\Psi }}_{\text{in}}(\mathbf{r})=\frac{q}{{\epsilon }_{\text{i}}\mid \mathbf{r}-{\mathbf{r}}_{\text{s}}\mid }+\sum _{n=0}^{\infty }{C}_n{r}^n{P}_n(cos\theta ).$$ (47)

Therefore, we can conclude that Eq. (28) will reduce to Eq. (6) and Eq. (9) to Eq. (5), respectively, after the boundary conditions in Eqs. (11) and (12) being applied. This can be demonstrated in detail by further assuming, like in Ref. [9], that the point charge q is set on the positive z-axis at z = (a/2)ξ₀ (note that then η₀ = 1) and applying the facts that $Q_n^0(x)=Q_n(x)$ and

$$Q_n(\xi )\to \frac{2^n{(n!)}^2}{(2n+1)!{\xi }^{n+1}},\text{as}\xi \to \infty .$$ (48)

Finally, as pointed out in Ref. [21], if cξ is small (for example when λ is very small), k_n(cξ) approaches infinity and the expansion in Eq. (27) diverges. In this case another expression for $R_{mn}^{(3)}(ic,\xi )$ is necessary. It is however not the aim of this note to discuss this expansion in detail, which can be found rather in Refs. [20,21].

4.6. Numerical examples

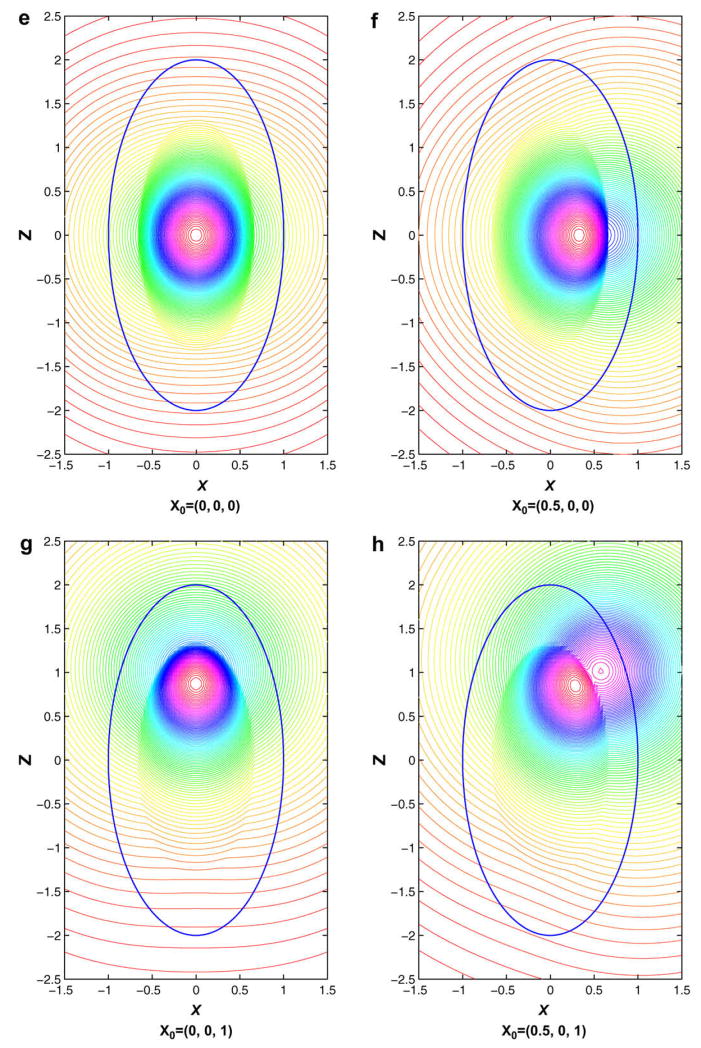
To illustrate the simulated behavior of the electrostatic potential distribution of point charges inside a prolate spheroid, we choose the dielectric prolate spheroid given by x² + y² + z²/4 = 1 of dielectric constant ε_i = 2, which is embedded in a dissimilar dielectric medium of high dielectric constant ε_o = 8. We first consider the situation that this dissimilar dielectric medium is a nonionic solvent, in which the electrostatic potential due to a point charge inside the dielectric prolate spheroid is calculated using the direct series expansions in Eqs. (17) and (18). Fig. 3(a)–(d) shows the contour graphs of the electrostatic potential distribution on the x–z plane due to unit point charges inside this prolate spheroid at four different locations x₀ = (0, 0, 0), x₀ = (0.5, 0, 0), x₀ = (0, 0, 1) and x₀ = (0.5, 0, 1), respectively, and on the other hand, Fig. 3(e)–(h) displays the contour graphs of the potential distribution on the y = 0.75 plane due to the same point charges. The results are obtained by including in the approximate expansions those terms given by n = 0, 1,…, N and m = 0, 1,…, n with N = 20. As been exhibited for all cases, the electric potential is continuous but its normal derivative is discontinuous across the spheroidal surface.

Fig. 3.

The contour graphs of the electrostatic potential distribution on either the x–z or the y = 0.75 plane due to a unit point charge at x₀ inside a prolate spheroid of dielectric constant ε_i = 2. The spheroid is embedded in a nonionic solvent of high dielectric constant ε_o = 8. Panels (a)–(d): on the x–z plane; panels (e)–(h): on the y = 0.75 plane.

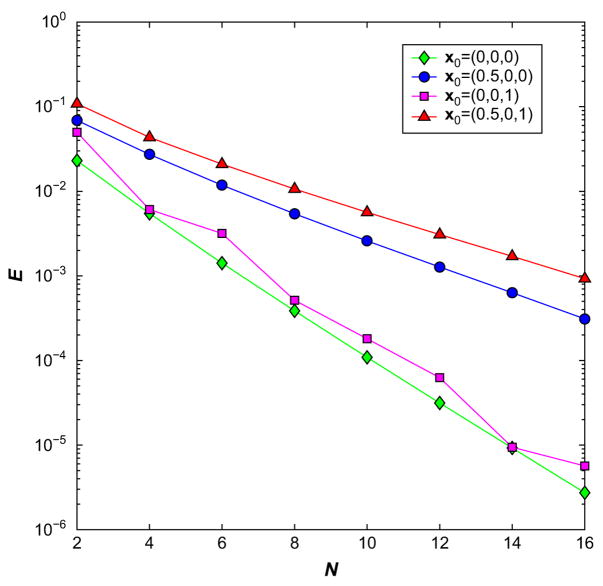
As can be seen clearly from Eqs. (3)–(6), for the spherical case the series expansions of the electric potentials in Eqs. (3)–(6) all converge as N → ∞, but the convergence rate depends not only on the location of the source charge but also on that of the observation point. In particular, in the case that the source charge is close to the spherical boundary, when calculating the electric potential at an observation point also close to the spherical boundary, the convergence rate by the direct series expansions in Eqs. (3)–(6) shall be slow, requiring a great number of terms to achieve high accuracy in the potential field. For the prolate spheroidal case, the series expansions in Eqs. (17) and (18) have been shown numerically convergent, and similarly, the convergence rate depends on the locations of both the source and the observation point. For example, the L₂ norm of the relative error E of the computed electric potential Ψ̄ (x_i) at 101³ observation points x_i uniformly located inside the rectangular box [−1.5,1.5]² × [−2.5, 2.5] for various N values are shown in Fig. 4, where

Fig. 4.

The relative error E of the computed electric potential for the nonionic-solvent case.

$$E={\left(\frac{{\sum }_{i=1}^{{101}^3}\mid \mathrm{\Psi }({\mathbf{x}}_i)-\overline{\mathrm{\Psi }}({\mathbf{x}}_i){\mid }^2}{{\sum }_{i=1}^{{101}^3}\mid \mathrm{\Psi }({\mathbf{x}}_i){\mid }^2}\right)}^{1/2}.$$

Here Ψ(x_i) represents the potential at x_i obtained by using the series expansions with N = 20. As shown in Fig. 4, the series solution converges for all four cases, and the error decreases monotonically as N increases. Moreover, it is very clear that the convergence rate is faster for the x₀ = (0, 0, 0) (ξ₀ = 1) or x₀ = (0, 0, 1) (ξ₀ = 1) case than that for the x₀ = (0.5, 0, 0) (ξ₀ = 1.04083) or x₀ = (0.5, 0, 1) (ξ₀ = 1.05769) case.

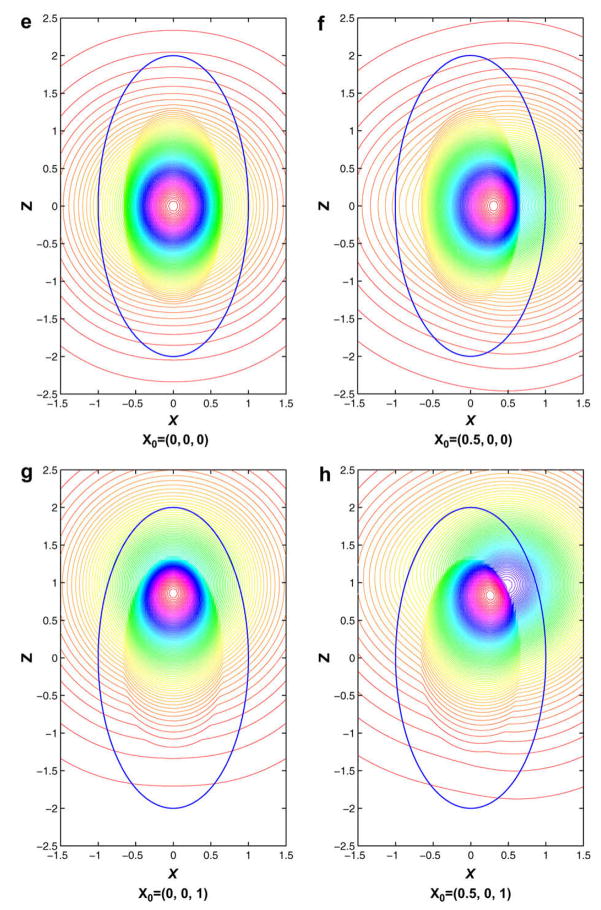
We then consider the situation that the dissimilar dielectric medium outside the dielectric prolate spheroid is an ionic solvent with the inverse Debye screening length λ = 4/a (so the spheroidal parameter c = 2), in which the electrostatic potential due to a point charge inside the prolate spheroid is approximated using the direct expansions in Eqs. (38) and (39). Fig. 5(a)–(d) shows the contour graphs of the electrostatic potential distribution on the x–z plane due to unit point charges inside this prolate spheroid again at four different locations x₀ = (0, 0, 0), x₀ = (0.5, 0, 0), x₀ = (0, 0, 1) and x₀ = (0.5, 0, 1), respectively, and on the other hand, Fig. 5(e)–(h) displays the contour graphs of the potential distribution on the y = 0.75 plane due to the same point charges. The results are obtained by including in the approximate expansions those terms given by n = 0, 1,…, N and m = 0, 1,…, n with N = 20.

Fig. 5.

The contour graphs of the electrostatic potential distribution on either the x–z or the y = 0.75 plane due to a unit point charge at x₀ inside a prolate spheroid of dielectric constant ε_i = 2. The spheroid is embedded in an ionic solvent of high dielectric constant ε_o = 8 and the inverse Debye screening length λ = 4/a. Panels (a)–(d): on the x–z plane; panels (e)–(h): on the y = 0.75 plane.

Likewise, the series expansions in Eqs. (38) and (39) have been shown numerically convergent, and similarly, the convergence rate depends on the locations of both the source and the observation point. For instance, the L₂ norm of the relative error E of the computed electric potential at 101³ observation points uniformly located inside the rectangular box [−1.5, 1.5]² × [−2.5, 2.5] for various N values are shown in Fig. 6, where again the results obtained by using the series expansion with N = 20 are treated as the exact solutions to calculate the errors of various approximations. As shown in Fig. 6, the series solution converges for all four cases, and the convergence rate is faster for the x₀ = (0, 0, 0) (ξ₀ = 1) or x₀ = (0, 0, 1) (ξ=₀ = 1) case than that for the x₀ = (0.5, 0, 0) (ξ₀ = 1.04083) or x₀ = (0.5, 0, 1) (ξ₀ = 1.05769) case. Moreover, the nonionic- and the ionic-solvent cases have comparable accuracy and convergence rate, although the former appears to be a little more accurate.

Fig. 6.

The relative error E of the computed electric potential for the ionic-solvent case.

5. Conclusions

In this paper, by using the classical electrostatic theory, the series expansions of the electric potential of point charges inside a dielectric prolate spheroid are obtained in terms of the associated Legendre functions or the spheroidal wave functions, depending on whether the surrounding dissimilar dielectric medium of the spheroid is ionic or nonionic. Numerical experiments have demonstrated that the series solutions are convergent, and the convergence rate is faster when point charges are near the center than when the point charges are close to the boundary of the prolate spheroid.