Abstract
We develop novel methods for recognizing and cataloging conformational states of RNA, and for discovering statistical rules governing those states. We focus on the conformation of the large ribosomal subunit from Haloarcula marismortui. The two approaches described here involve torsion matching and binning. Torsion matching is a pattern-recognition code which finds structural repetitions. Binning is a classification technique based on distributional models of the data. In comparing the results of the two methods we have tested the hypothesis that the conformation of a very large complex RNA molecule can be described accurately by a limited number of discrete conformational states. We identify and eliminate extraneous and redundant information without losing accuracy. We conclude, as expected, that four of the torsion angles contain the overwhelming bulk of the structural information. That information is not significantly compromised by binning the continuous torsional information into a limited number of discrete values. The correspondence between torsion matching and binning is 99% (per residue). Binning, however, does have several advantages. In particular, we demonstrate that the conformation of a large complex RNA molecule can be represented by a small alphabet. In addition, the binning method lends itself to a natural graphical representation using trees.
INTRODUCTION
RNA can both encode genetic information and catalyze chemical reactions (1). As the only biological macromolecule capable of such diverse activities, it has been proposed that RNA preceded DNA and protein in early evolution (2). Therefore, developing methods for recognizing conformational states of RNA and for discovering statistical rules governing conformation may help answer basic biological and biochemical questions including those related to the origins of life. Here we describe two novel methods for describing and recognizing patterns of RNA conformation. Although we are not attempting to develop methods to predict three-dimensional structure of RNA, that effort (3,4) may ultimately be aided by the results described here.
Traditionally, linear sequence databases have been the primary focus of informaticians, although three-dimensional structures of proteins have not been ignored (5). Recent increases in the size and complexity of the Nucleic Acid Database (6), which contains three-dimensional structures of RNA molecules, suggests to us the utility of pattern-recognition approaches. Here we describe two new approaches to exploit that database.
Our approaches allow one to efficiently locate, count, characterize, compare and describe RNA conformational states. As a test of our analytical methods we focus in this paper on a very large RNA molecule of known three-dimensional structure. The crystal structure of the large ribosomal subunit from Haloarcula marismortui has been determined to high resolution by Moore, Steitz and co-workers (7,8). The atomic positions of the vast majority of the 23S rRNA of HM LSU are well-characterized. The HM 23S rRNA, with >2500 residues, constitutes a large database with a rich omnibus of RNA conformation and interactions. The size and complexity of the HM 23S rRNA render manual analysis with a graphics program problematic, but make it an ideal target for automated pattern-recognition approaches.
The two approaches described in detail here involve torsion matching and binning. The torsion-matching method is a rigorous brute-force approach while the binning method is more elegant and efficient. In comparing the results of the two methods we have tested the hypothesis that the conformation of a very large complex RNA molecule can be described accurately by a limited number of discrete conformational states. The goals are to identify and eliminate extraneous and redundant information without losing accuracy, and to quantitatively assess the degree of success.
MATERIALS AND METHODS
Torsion space
Both conformational pattern recognition processes described in this paper are conducted in torsional space (9), rather than Cartesian space (e.g. a PDB file). One primary advantage of representing conformational information in torsion space is that direct and rapid determination of similarity/dissimilarity of conformational states of any pair or group of RNA fragments is accomplished without requirement for further transformation or superimposition of RNA fragments or for a reference state. In Cartesian space a very large number of superimpositions would be required with changing fragment lengths, etc. In torsion space, the comparison of every contiguous fragment of HM 23S rRNA with every other contiguous fragment of lengths from 3 to 20 residues, in addition to determinations of statistics of similarity, the output of similar sets, comparison with library, etc., requires less than 30 s on a modest desktop PC running in LINUX.
We have calculated the backbone (α, β, γ, …) and the glycosidic (χ) torsion angles (Fig. 1) and ribose pseudorotation phase angle (P) for each residue of the HM 23S rRNA ‘database’. The angle α of residue i is the O3′i–1-Pi-O5′i-C5′i torsion angle, β is the Pi-O5′i-C5′i-C4′i torsion angle, etc., as generally defined for nucleic acids (10). For computational efficiency the usual torsional format of –180° to +180° was converted to 0–360°. The conformation of an n-residue RNA molecule is specified by n sets of (α, β, γ, … P), with some angles absent from the terminal residues. The HM 23S rRNA torsional information is contained in a matrix of 2754 rows (∼200 residues of the 23S RNA are disordered and so are absent from the original coordinate file and from the torsion matrix). Each row of the torsion matrix has 10 elements (residue number, residue type, α, β, γ, … χ, P). The 10 elements of a given row combine to specify the location in primary sequence, the residue type (C, G, A or U) and the conformation of that residue.
Figure 1.
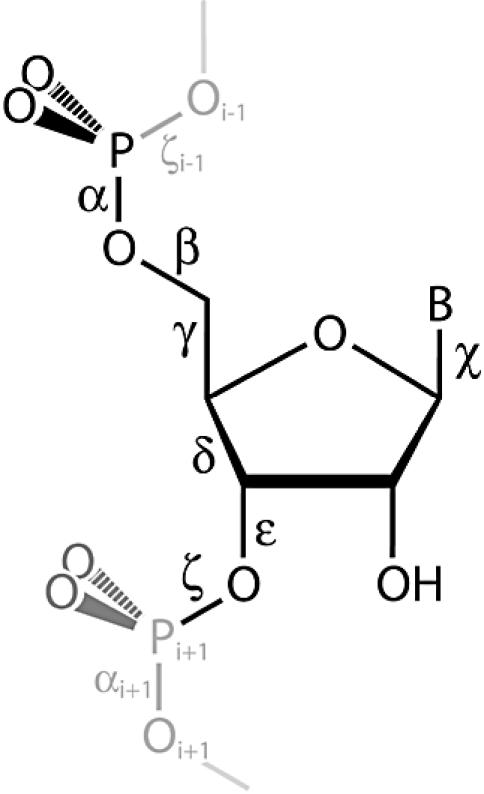
Ribonucleotide torsion angles used to specify conformation. The ribose pseudorotation phase angle (P) is not indicated.
Torsion matching
Repeating conformational states were identified by a computer program that searches for repetitive patterns of angles in the HM 23S rRNA torsion angle matrix. As previously noted by Olson (11), it is reasonable to use bond rotations to specify conformation, and to ignore variation in bond lengths and angles. Therefore α, β, γ, … χ, P were used to define the conformation of a given residue. A block of α(l), β(l), γ(l)… χ(l), P(l) extending over contiguous residues l, l+1, l+2… l+n with values that are repeated m times corresponds to a conformational state of length n that is repeated m times. More specifically, two fragments of HM 23S rRNA were taken to be in a similar conformational state if the matrix entries α(1,1),β(1,1),γ(1,1), … χ(1,1),P(1,1) (residue 1, fragment 1) are similar to α(1,2),β(1,2),γ(1,2), … χ(1,2),P(1,2) (residue 1, fragment 2) and the matrix entries α(2,1),β(2,1),γ(2,1), … χ(2,1),P(2,1) (residue 2, fragment 1) are similar to α(2,2),β(2,2), γ(2,2), … χ(2,2),P(2,2) (residue 2, fragment 2), etc., to a minimum of three residues, but with the possibility of extension to any number of residues. The definition of similarity places limits on relationships between fragments, but not within fragments. No a priori assumptions about preferred or acceptable conformational states are made. We have validated our torsional definition of conformational similarity by direct superimpositions in Cartesian space (Fig. 2) and by calculations of deviations of atomic positions.
Figure 2.
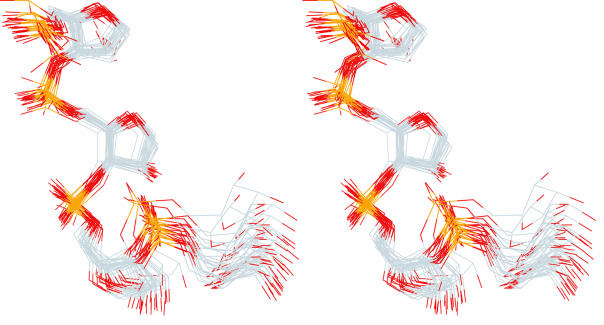
Tetraloops. Stereoview of the superimposition of the 25 RNA fragments within the tetraloop family are shown here. Only backbone atoms were used for the superimposition. Only backbone atoms are shown. The atoms are colored using the CPK standard.
The similarity cutoff angles (i.e. the definition of similarity) for each angle are given in Table 1. These cutoff angles are roughly related to intrinsic variability. For example, as shown in Table 1, torsion angles β and ζ show the greatest variability and have the largest cutoffs. The angles γ and δ show the least variability and have the smallest cutoffs. To evaluate the cutoff parameters, we generated distribution plots for all α, β, γ, … χ, P within the HM 23S rRNA ‘database’. As noted below each torsion angle tends to cluster within one or a few distribution envelopes. The envelopes are well separated, suggesting that as long as the cutoffs are sufficiently small so as not to include residues contained within two envelopes, and sufficiently large so as to not slice into an envelope, the result should remain essentially constant. Each cutoff parameter was empirically tuned by finding the range where its variation has minimal effect on outcome, then setting the cutoff to the minimum of that range. The fundamental conclusions of the analysis (below) are insensitive to moderate changes in cutoffs.
Table 1. Torsion matching fingerprints.
| α | β | γ | δ | ε | ζ | χ | P | RMSD (Å)a | |
|---|---|---|---|---|---|---|---|---|---|
| Cutoff limitsb | 35c | 40 | 12.5 | 12.5 | 40 | 40 | 40 | 20 | |
| Mean A-helix | 295 (6)d | 174 (9) | 54 (4) | 80 (2) | 209 (8) | 289 (9) | 198 (7) | 15 (4) | |
| Mean tetraloop | |||||||||
| Residue i | 297 (8) | 178 (8) | 52 (4) | 81 (3) | 215 (12) | 291 (7) | 201 (7) | 15 (4) | 0.39 |
| Residue i+1 | 295 (6) | 174 (10) | 52 (3) | 80 (2) | 219 (7) | 292 (8) | 204 (7) | 19 (5) | 0.28 |
| Residue i+2 | 165 (8) | 156 (12) | 53 (3) | 84 (2) | 223 (6) | 290 (6) | 197 (12) | 14 (3) | 0.51 |
| Residue i+3 | 296 (4) | 164 (6) | 58 (4) | 85 (3) | 215 (14) | 288 (12) | 211 (12) | 15 (4) | 0.89 |
aRMSDs of backbone atomic positions broken down by residue after superimposing all backbone atoms of 25 tetraloops. The overall RMSD for all backbone atoms of all tetraloops is 0.52 Å.
bThese are the cutoff angles used in the torsion-matching algorithm: α, 295 ± 35; β, 174 ± 40; γ, 54 ± 12.5, etc. are required to score a residue as A-helical.
cDegrees.
dThe numbers in parentheses are the standard deviations taken over all members of the family within the HM 23S rRNA.
If more than a minimal number of RNA fragments are observed in a common conformational state, their mean conformation, as given by their mean torsion angles, is defined as the ‘parent’ of the conformational family. The computer program compares the torsion angles of each parent against a user-defined library thus automating the identification of known conformational families such as A-helices, tetraloops, E-loop motifs, etc. The program identifies 18 A-helical regions of length >9 (Table 2) and 25 tetraloops (Table 3).
Table 2. Eighteen A-helices of length >9 residues identified by the torsion matching and binning methods.
| Length | Starting residue | Sequence (5′→3′)a | ASCII code | |
|---|---|---|---|---|
| 1 | 24 | 1535 | GCCCUGGGGUCGAUCACGCUGGGC | paaaaaaaaaaaaaaaaaaaaaaaawb |
| 2 | 16 | 1508 | CCGUGCCACUAUGCAG | taaaaaaaaaaaaaaaa* |
| 3 | 15 | 1262 | CCUGUCCGUACCACU | *aaaaaaaaaaaaaaao |
| 4 | 14 | 1014 | ACUUACAGACGCCG | ueaaaaaaaaaaaaaec |
| 5 | 13 | 606 | CGAUGUUCUGUCG | oaaaaaaaaaaaaan |
| 6 | 12 | 520 | AAUCAGUUGGCG | aaaaaaaaaaaaae |
| 7 | 10 | 98 | AACCAUGGAU | raaaaaaaaaae |
| 8 | 10 | 294 | CCGUCUCGAC | uaaaaaaaaaae |
| 9 | 10 | 346 | UACUCGAGAC | haaaaaaaaaae |
| 10 | 10 | 593 | ACUCACGGGA | eaaaaaaaaaa* |
| 11 | 10 | 748 | CCAUGUGGAC | aaaaaaaaaaae |
| 12 | 10 | 796 | AAGCGUGCCG | raaaaaaaaaao |
| 13 | 10 | 1301 | CGCUCUAAUU | aaaaaaaaaaai |
| 14 | 10 | 1909 | AACACCUCGU | eaaaaaaaaaa* |
| 15 | 10 | 1930 | AAGGACCUGU | aaaaaaaaaaae |
| 16 | 10 | 2260 | ACCGAUAGCC | taaaaaaaaaae |
| 17 | 10 | 2542 | CGGUUCCCUC | 9aaaaaaaaaar |
| 18 | 10 | 2621 | UAGACCGUCG | saaaaaaaaaao |
aTotal composition of the 18 longest A-helical regions is 55 G (26%), 71 C (33%), 43 A (20%) and 45 U (21%).
bThe ASCII characters of the 5′ and 3′ flanking residues are included.
cResidues that are not characterized equivalently by the torsion matching and binning methods are in bold.
Table 3. Tetraloops identified by the torsion matching and binning methods.
| Starting residue | Sequencea | Binning ASCII code | |
|---|---|---|---|
| 1 | 252 | CUCAC | aaoa |
| 2 | 313 | UGGAA | aaoa |
| 3 | 468 | UGUGA | aaoa |
| 4 | 505 | CGAAA | aaoa |
| 5 | 624 | UUUGA | aaoa |
| 6 | 690 | GGAAA | aaoa |
| 7 | 804 | CGAAA | aaoa |
| 8 | 1054 | GGUAA | aaoa |
| 9 | 1197 | GUAAC | aaoa |
| 10 | 1326 | UGAAA | aaoa |
| 11 | 1388 | UGAGA | aaoa |
| 12 | 1468 | GCAAC | aaoa |
| 13 | 1499 | UUAAU | aaoa |
| 14 | 1595 | GUAAU | aaoa |
| 15 | 1628 | GGAAA | aaoa |
| 16 | 1706 | GGCGA | aaoeb |
| 17 | 1748 | UUCGG | aaoa |
| 18 | 1793 | CGGAA | aaoa |
| 19 | 1808 | CGCAG | aaoa |
| 20 | 1862 | CGCAA | aaoa |
| 21 | 1991 | AUCAG | aaoa |
| 22 | 2248 | CGGGA | aaoa |
| 23 | 2411 | CGAAA | aaoa |
| 24 | 2629 | CGUGG | aaoa |
| 25 | 2695 | CGAGA | aaoa |
aResidues that deviate from the BKNRA consensus sequence are in bold.
bThe residue that is not characterized equivalently by the torsion matching and binning methods is in bold.
Our torsion-matching method leads to an operational definition of an A-helix that requires at least three contiguous residues in the same conformational state. In that conformational state the torsion angles must be within the specified cutoff ranges of the target values as given in Table 1. The mean values over all A-helices describe the A-helix parent, which is the average obtained for the most populated conformational state in the HM 23S rRNA, with the standard deviations of the torsion angles of the members of that family given in parentheses. In this operational definition an A-conformation helical strand may or may not be paired to a second A-conformation helical strand. This operation definition therefore differs from the standard definition of A-form helical RNA, which indicates two paired strands.
Torsion angle distributions
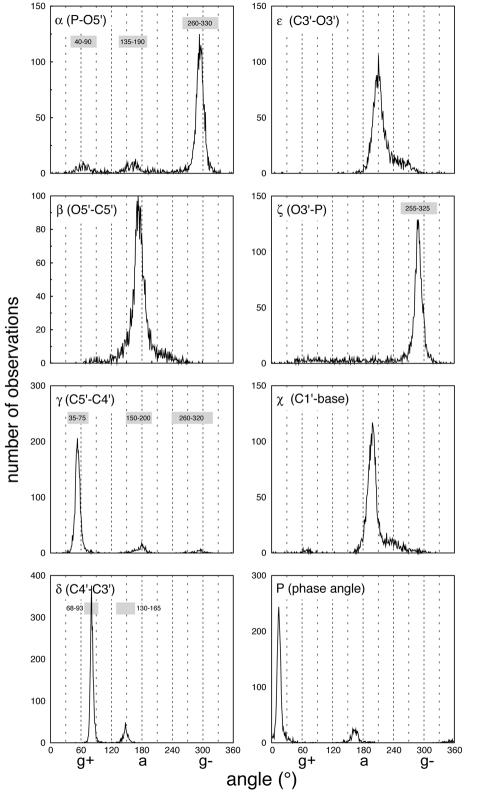
From hard-sphere calculations, potential energy calculations and empirical measurements, it is known that some regions of nucleotide conformational space are accessible while others are not (11–16). We have created plots of torsion angle versus frequency of observation for each of the torsion angles of the HM 23S rRNA, as illustrated in Figure 3. The distributions are generally in agreement with those described previously (11–13,16). For example a comparison of the frequency observed in Figure 3 in this report with Olson’s hard-sphere calculations (see figure 3 in ref. 11) shows a good correspondence. In the most substantial discrepancy, it was previously concluded that the two P-O torsion angles α and ζ (formerly ω and ω′) give similar frequency distributions, each with three maxima. In HM 23S rRNA the torsion angle α does indeed show the expected three maxima. However the torsion angle ζ gives only a single maximum in the gauche– region, accompanied by a broad featureless distribution extending from 60° into the primary peak centered near 230° (Fig. 3).
Figure 3.
Plots of angle versus frequency of observation of the backbone and glycosidic torsion angles and the pseudorotation phase angle (P) of HM 23S rRNA. The symbols g+, a, and g– at the bottom of the graph refer to gauche+, anti and gauche–, respectively. The shaded regions indicate the binning limits for the four ‘conformational identifier’ torsion angles.
Binning
The distinct near-Gaussian envelopes of the frequency distributions suggests a natural way of partitioning the angles into discrete bins. The limits of each envelope are determined by where the probability of observation drops to zero. Our method of empirical binning differs from previous methods that use ranges defined by equivalent limits on either side of ideal torsion angles (11). Thus, the descriptions anti, gauche+ and gauche– are not fully equivalent to the bins used here. Each torsion angle of a given residue was empirically ‘binned’ by allocating it to the appropriate envelope. Then, by assigning each envelope a discrete integer value, the continuous torsion angle data was converted into integers, which specify the correspondence of torsion angle to Gaussian envelope. The assumption that we make and test here is that each envelope can be reduced to a discrete state, when in fact torsion angles are continuous. With this assumption, the combined torsional states (α, β, γ, … χ, P) of a given residue are reduced to a small series of integers, which define the conformational state of that residue with reasonable accuracy.
By definition, torsion angles with single-peak distributions cannot be readily separated into distinct bins, because essentially all the angles are contained under a single Gaussian envelope. Thus, β, ε and χ are assumed not to contribute information to the conformational description, and are ignored. An analysis of rare conformations, found outside the primary Gaussians used here, is the subject of future work. Because of their multi-peaked nature, the remaining four torsion angles and P allow a straightforward separation into distinct configuration classes. However, δ and P are correlated, both by geometric definition (11,13), and from analysis of the HM 23S rRNA data. Thus, to avoid redundancy, we eliminate P and consider only four torsion angles, α, γ, δ and ζ. These four ‘conformational identifier’ angles are the same torsion angles similarly identified as variable (11–15). This reduction in parameters leads to a four-digit structural representation of the conformation of a given residue. Each residue is assigned a sequence of four intergers nα, nγ, nδ, nζ, where each digit denotes the Gaussian envelope to which a torsion angle belongs. The range of each envelope for the four identifier angles is given in Table 4. An additional class is also used to signify that a torsion angle belongs to no Gaussian envelope, as indicated by ‘other’. These definitions lead to 4 × 4 × 3 × 2 = 96 possible conformational states. However only 37 of these states are populated in the HM LSU 23S rRNA (bins occupied by more than five residues are considered to be populated). Seventeen of the populated bins correspond to single conformations, whereas 24 of the populated bins correspond to variable conformations (Table 5).
Table 4. Bin assignments and torsion ranges.
| Bin 1 | Bin 2 | Bin 3 | Bin 4 | |
|---|---|---|---|---|
| α | 40–90 | 135–190 | 260–330 | other |
| γ | 35–75 | 150–200 | 260–320 | other |
| δ | 68–93 | 130–165 | other | |
| ζ | 255–325 | other |
Table 5. ASCII symbols, bin numbers and observation frequencies.
| Ascii lettera | Bin number | Frequency |
|---|---|---|
| a | 3111 | 1709 |
| e | 3112 | 169 |
| r | 3122 | 124 |
| i | 2211 | 103 |
| o | 2111 | 58 |
| t | 4111 | 48 |
| n | 1111 | 37 |
| s | 2122 | 34 |
| l | 1211 | 31 |
| c | 3121 | 30 |
| u | 4211 | 28 |
| d | 1121 | 26 |
| p | 4122 | 21 |
| m | 1122 | 21 |
| h | 3411 | 18 |
| g | 1322 | 18 |
| b | 1112 | 14 |
| f | 3211 | 14 |
| y | 4112 | 13 |
| w | 2212 | 11 |
| k | 4121 | 11 |
| v | 3212 | 10 |
| x | 3222 | 10 |
| z | 1331 | 9 |
| j | 4222 | 9 |
| q | 3321 | 8 |
| 1 | 1212 | 8 |
| 2 | 3422 | 8 |
| 3 | 4311 | 8 |
| 4 | 4411 | 8 |
| 5 | 2121 | 7 |
| 6 | 3322 | 7 |
| 7 | 2222 | 7 |
| 8 | 2411 | 7 |
| 9 | 1311 | 7 |
| 0 | 1221 | 7 |
| + | 3311 | 6 |
aThe assignment of characters to configuration classes was made by frequency of observation. The choice of letter assignment was taken from http://www.askoxford.com/asktheexperts/faq/aboutwords/frequency. All bins with less than five residues are denoted by * and are omitted from this table.
The most highly occupied binned state for a single residue in the HM LSU 23S rRNA is the 3111 configuration. In this configuration, α is found within the third Gaussian envelope, and γ, δ and ζ are contained in the first envelopes of their respective distributions. Each of these envelopes are the largest (most populous) of their respective distributions. Approximately 65% of all residues are in the 3111 configuration, which corresponds to A-helical conformation. The second most common configuration is the 3112 class. The third most common configuration is the 3122 class. The population of each class is given in Table 5.
Binning allows the three-dimensional structure of the HM 23S rRNA to be represented by a simple ASCII string. Each of the various configurations can be represented by a distinct ASCII symbol. We have used a representation where the most common configuration (3111) is represented by the character ‘a’, and in general the associations of character to configuration are determined by frequency of observation. The associations of all 37 observed conformations with 37 ASCII characters are given in Table 5. By scanning the resulting character representation for repeating character subsequences, even with text editor, it is trivial to find various conformational motifs. Conformational motifs are repeating conformational states, which appear as repeating strings ASCII characters. For example, a common character string consists of a series of ‘a’s broken by a single residue, typically ‘o’. Inspection of the three-dimensional structure of the HM LSU 23S rRNA indicates that these character strings are characteristic of RNA tetraloops.
RESULTS
Torsion-matching: A-helices
The torsion-matching approach successfully identifies and counts repetitive conformational states, and groups RNA fragments with similar conformations. With the torsion-matching approach, we observe a total of 184 A-helices with an average length of 6.3 residues, consuming 41% of the HM 23S rRNA. An A-helix, defined by our torsion-matching approach, is a series of contiguous residues, each with torsion angles within the specified cutoffs of the mean A-helix torsion angles (Table 1). By definition, the minimum length of an A-helical region is three residues. The A-helical family is used here as one standard for comparing our two pattern recognition methods. The 18 longest A-helices observed in the HM 23S rRNA are listed in Table 2. The longest A-helix is 24 residues, initiating at residue 1535. There is one helix each of length 16, 15, 14, 13 and 12. There are 12 helices of length 10. The torsion-matching approach makes no assumptions about base composition or sequence, and does not search sequence-space. Sequence and base composition are output as dependent variables. We observe that C is over-represented in long A-helices, composing 33% of residues in A-helices of length >9 residues (Table 2).
Torsion-matching: tetraloops
A group of four-residue fragments in the HM 23S rRNA are identified as members of the tetraloop conformational family (17–21) by our torsion-matching method. The tetraloop family is used here for evaluating the relationships between similarity in torsion space and similarity in Cartesian space, and as a second standard for comparing our two pattern recognition methods. Torsional similarity indicates that 25 four-residue RNA fragments belong to the tetraloop conformational family. Residues i and i+1 of this family are characterized by torsion angles very near to A-conformation (Table 1). Residue i+2, the ‘U turn residue’ deviates substantially from A-conformation, with the largest deviation in torsion angle α (165°) and a smaller deviation in β (156°). Residue i+3 shows more moderate deviations from A-conformation, in β, γ and χ. The root mean square deviations (RMSD) of all backbone atomic positions in this family is 0.52 Å. The RMSDs are broken down for each residue in Table 1. The observed deviations in atomic positions are well within ranges used to define similar conformations, e.g. see Klein et al. (7). A superimposition of the backbone atoms of these 25 RNA tetramers is shown in Figure 2. As is apparent in Figure 2, residue i+3 shows the greatest variability of backbone atomic positions, with an RMSD of 0.89 Å (Table 1). Residue i+2 shows the second greatest variability backbone atomic positions (RMSD of 0.64 Å). These two residues also show the greatest deviations in torsion angles, with at least two torsion angles of each residue showing a SD of >11°. Only one torsion angle in residues i and i+2 combined shows a torsion angle with SD of >11°. If each of the cutoff limits indicated in Table 1 are halved, the number of tetraloops scored in the HM 23S rRNA database decreases from 25 to 19. Halving the cutoff limits causes the RMSDs of atomic positions of the tetraloops to decrease, along with the SDs of some of the torsion angles. Although the SDs of some torsion angles increase, the decreases are more numerous and are larger in magnitude than the increases.
Torsion matching: sequence output
The torsion-matching method provides an independent basis for comparison of RNA motif sequences with those found from phylogenetic and mutagenic approaches (18,22). A description of tetraloop consensus sequences is contained in the discussion section below.
Binning: A-helices
We have devised a second method, termed ‘binning’, for identifying conserved conformation, and for grouping RNA fragments with similar conformation. The binning method makes substantial simplifications and assumptions, the validity of which require rigorous assessment. The degree of accuracy of the binning method is determined here by specific comparisons with torsion-matching results, which are obtained with no assumptions or simplifications. In the binning method, RNA residues in the A-conformational state are identified by the ASCII letter ‘a’. The 24-residue A-helix observed by torsion-matching is identified by the binning method and is indicated by a string of 24 ‘a’ characters, flanked by the non-A-helical characters ‘p’ on the 5′-end and ‘w’ on the 3′-end (Table 2). The correspondence between A-helices observed by torsion-matching and binning is not perfect, but is extremely high. If one scores equivalently characterized A-helical residues for the longest 18 A-helices, including non-A-helical residues on the 3′- and 5′-termini of each A-helix, the agreement between torsion matching and binning is excellent. The conformations of 245 of 250 A-helical residues are characterized equivalently.
Binning: tetraloops
The binning ASCII code for a four-residue tetraloop motif is ‘aaoa’. This pattern is observed 24 times in the HM 23S rRNA (Table 3). Each of these tetraloops is also identified as such by torsion matching. Torsion matching identifies one tetraloop (initiates at residue 1706) that is characterized by the ASCII code aaoe. Of the 100 residues contained in 25 tetraloops identified by torsion matching, 99 are equivalently characterized by the binning approach. The 3′ residue of the anomalous aaoe tetraloop, residue 1709, has been binned into 3112 rather than 3111 as for the other tetraloops. The angle ζ is outside of the 255–325° range of the first bin (Table 4). Indeed torsion angle ζ of residue 1709 is 252°, just 3° outside the range of the first bin but just 4° inside the torsion-matching threshold of 248° (288–40; Table 1). It appears that if one attempted to tune the two approaches, one may be able to improve the correspondence between torsion matching and binning.
Tree structure diagrams
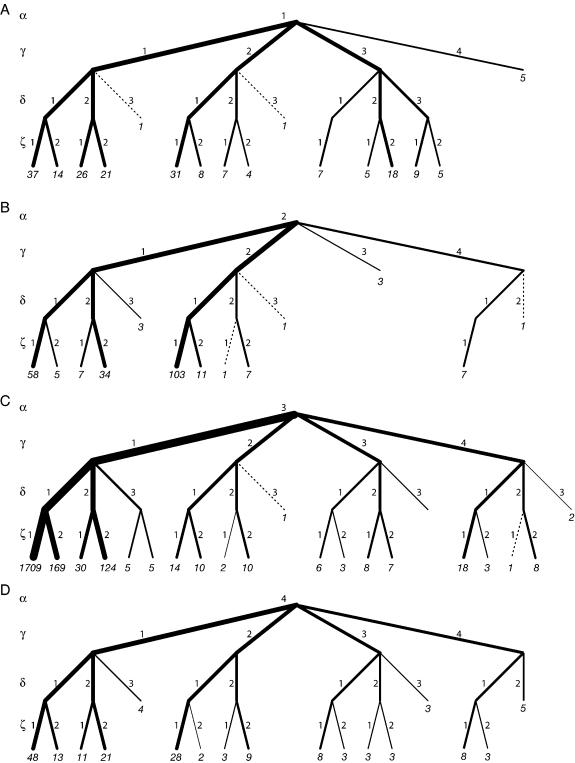
The binning method lends itself to a natural statistical representation using trees. The tree diagram for HM 23S rRNA is shown in Figure 4. The root node of the tree, which is the top level, has the number of residues in the RNA. The second generation, which is the next level down in the tree, has the populations for each of the three α classes, which are the four α bins. Each α node is split at the next level down to give the populations in the four γ nodes, which in turn bifurcate to give the populations in the three δ nodes, which in turn bifurcate to give the populations in the two ζ nodes. For simplicity of representation in Figure 4, we separated the four α branches into four different trees. The line widths within the trees are proportional to the log of the number of the residues in that bin. In this manner, the population of each branch can be seen, and the tree gives a signature to RNA conformation. This tree representation enables recognition of the correlation relations among the identifier torsion angels and may provide a visual fingerprint of large RNA conformation classes.
Figure 4.
The tree representation of the conformation of HM 23S rRNA. The four different α branches are represented in A–D. The bin numbers correspond to branch numbers (indicated). The numbers in italics represent the populations of the binned states. Line widths are weighted by the logarithms of the populations. Dashed lines indicate a population of one.
DISCUSSION
We have developed a torsion matching program that parses a three-dimensional database and locates, characterizes and catalogs RNA conformation states. The database used here is the three-dimensional structure of HM 23S rRNA, with over 2500 residues. The torsion matching program identifies 18 A-helices over nine residues in length and 25 tetraloops. The expected correlations are observed in torsional and Cartesian descriptions of conformational similarity. Torsion matching appears to be a fast, robust and easily tunable method of conformational similarity searching. Although it is beyond the scope of the current work, we observe additional conformational families in the HM 23S rRNA. Some, such as E-loop motifs (23) have been previously characterized, and others not. Additional motifs will be discussed in detail in a future publication.
Tetraloops
The four residue definition of a tetraloop obtained here is shifted one residue in the 5′ direction relative to previous definitions. This 5′ shift is required, when using conformation as the criterion, to obtain the most precise and general definition of the tetraloops of the HM 23S rRNA. Twenty-five tetraloops are scored by conformation (Table 3), such that 25 tetraloop sequences are obtained as output. There appears to be a single sequence class among the 25 tetraloops, which is BKNRA (where B = U/C/G, K = G/U, N = any residue, R = purine, Y = pyrimidine, the fifth site is not part of the conformational definition, but is part of previous sequence-based definitions). A is observed at the first site of only a single tetraloop. A residue other than U or G is observed at the second site of only a single tetraloop. A superimposition shows that the positions of the O6 atoms of Gs and the O4 atoms of Us of site two are highly localized. Sixteen of the 25 tetraloops fit the BKNRA sequence definition exactly. Seven tetraloops deviate from this sequence at a single site, with those deviations limited to one of the termini of the BKNRA consensus sequence. Two tetraloops deviate from the consensus sequence at two positions. Note that the methods described here address an issue articulated by Pyle, who observed a need to characterize RNA structure objectively and quantitatively rather than visually or anecdotally (24). Table 1 gives well-defined and easily accessible yet quantitative definitions of A-form and tetraloop RNA. Analogous definitions are obtained for any repetitive RNA conformational state.
Binning
As with the φ and ψ torsion angles that define protein backbone conformation (25), RNA torsion angles are restricted and interdependent (11,13,16). Therefore we have tested the hypothesis that the conformation of a large RNA molecule as described rigorously by torsion angles contains redundant and extraneous information that can be eliminated without sacrificing accuracy and utility. The goal is to reduce information as far as possible without sacrificing accuracy to make simple and efficient the process of describing and analyzing the RNA conformation. Our approach is an extension of tRNA conformational wheels (15,26), which can simultaneously represent sequence and all of torsion space. To enable analysis of very large RNA molecules, we have eliminated the sequence information and compressed the torsional information previously displayed in conformational wheels. The approach described here is distinct from, and possibly complementary to, the virtual bond (or pseudo-bond) treatments of Olson (14) and Duarte and Pyle (24). Those methods compress information in Cartesian space before conversion to torsion space. The relative merits of the various approaches have yet to be fully investigated.
Specifically we have transformed continuous conformational information (torsion angles) to a limited number of discrete descriptors. For example, the torsion angle α falls in one of three roughly Gaussian envelopes centered at 300, 165 and 70° (16). The probability of finding α outside one these three envelopes is vanishingly small. Therefore α was ‘binned’, i.e. reduced from a continuous variable to a variable with one of three discrete values (300, 165 or 70°). The centers of the Gaussians allow one to determine a natural set of discrete native states. The widths of each Gaussian allow one to determine natural cutoff parameters to allocate the continuous values into the discrete bins. This approach allows conformational states to be classified into a relatively small number of categories which can be represented symbolically. Thus, the conformation of a large complex RNA molecule can be represented by a small ASCII alphabet.
We conclude, as expected (12,13,15), that four of the torsion angles contain the overwhelming bulk of the structural information, which is not compromised by binning the continuous torsional information into a limited number of discrete values. Analysis of A-helical regions and tetraloops indicates that the correspondence between torsion matching and binning is 99% (per residue). Thus, the binning method appears to be an efficient, accurate, powerful and useful tool for identifying conformational features of RNA. Our methods do not consider or incorporate interactions between residues. However, it should be possible to combine our binning method with the methodology developed by Leontis and Westhof (27) to simultaneously display and utilize both types of information.
Trees
The binning method for describing RNA conformation lends itself to a natural statistical representation using trees (Fig. 4). The tree representation gives a visual fingerprint of conformation. The tree representation devised here suggests an alternative to the two-dimensional Ramachandran plots used for proteins. Such an alternative is especially useful for RNA, where the backbone torsion angle space has more than two dimensions. Furthermore, such a graphical tool can be useful for studying correlations among torsion angles. The tree representation shows for example that conformation 3111 (A-form) is the most highly populated state of HM 23S rRNA (as indicated by the thick lines in Fig. 4C).
This report illustrates the utility of torsion space for representing, decomposing and compressing conformational information. Torsion space yields objective definitions, and direct and rapid determination of similarity/dissimilarity of conformational states of any pair or group of RNA fragments. Conformation matching is accomplished without requirement for further transformation or superimposition of fragments or for a reference state. The primary limitation of torsion space as a descriptor of nucleic acid structure, is that torsions can be conceptually impenetrable, hampering structural visualization. Addition limitations might arise from a differential sensitivity of global conformation to various torsions and the ability of two or more torsion angles to vary in a compensatory fashion that conserves global conformation. We are presently investigating methods to overcome these limitations. We will also characterize and catalog novel conformational families of RNA, and are exploring statistical relationships between RNA conformation and molecular interactions. For example, our approach allows facile exploration of relationships between RNA conformation and interactions with proteins and metals, etc. In addition we will seek to improve the utility of the binning method by automating the partitioning of the torsion angle distribution functions into envelopes. This would make it possible to consider the joint probability distribution function of all the torsion angles, allowing the incorporation of correlation effects into our binning method. Furthermore, one can also extend the binning method to work with groups of residues, allowing the incorporation of inter-residue couplings.
Acknowledgments
ACKNOWLEDGEMENTS
This work was partially supported by grants from NSF, AFOSR, ARO, MURI and NIH. The authors thank Drs Nick Hud, Jane Richardson and Laura Murray for helpful discussions.
REFERENCES
- 1.Cech T.R. (2001) Ribozymes, the first 20 years. Biochem. Soc. Trans, 30, 1162–1166. [DOI] [PubMed] [Google Scholar]
- 2.Joyce G.F. (2002) The antiquity of RNA-based evolution. Nature, 418, 214–221. [DOI] [PubMed] [Google Scholar]
- 3.Stagg S.M., Mears,J.A. and Harvey,S.C. (2003) A structural model for the assembly of the 30S subunit of the ribosome. J. Mol. Biol., 328, 49–61. [DOI] [PubMed] [Google Scholar]
- 4.Kidd-Ljunggren K., Zuker,M., Hofacker,I.L. and Kidd,A.H. (2000) The hepatitis B virus pregenome: prediction of RNA structure and implications for the emergence of deletions. Intervirology, 43, 154–164. [DOI] [PubMed] [Google Scholar]
- 5.Buchan D.W., Rison,S.C., Bray,J.E., Lee,D., Pearl,F., Thornton,J.M. and Orengo,C.A. (2003) Gene3d: structural assignments for the biologist and bioinformaticist alike. Nucleic Acids Res., 31, 469–473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Berman H.M., Olson,W.K., Beveridge,D.L., Westbrook,J., Gelbin,A., Demeny,T., Hsieh,S.-H., Srinivasan,A.R. and Schneider,B. (1992) The nucleic acid database. A comprehensive relational database of three-dimensional structures of nucleic acids. Biophys. J., 63, 751–759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Klein D.J., Schmeing,T.M., Moore,P.B. and Steitz,T.A. (2001) The kink-turn: a new RNA secondary structure motif. EMBO J., 20, 4214–4221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ban N., Nissen,P., Hansen,J., Moore,P.B. and Steitz,T.A. (2000) The complete atomic structure of the large ribosomal subunit at 2.4 Å resolution. Science, 289, 905–920. [DOI] [PubMed] [Google Scholar]
- 9.Bucourt R. (1974) The torsion angle concept in conformational analysis. In Eliel,E.L. and Allinger,N.L. (eds), Topics in Stereochemistry. John Wiley & Sons, New York, NY, Vol. 8, pp. 159–224. [Google Scholar]
- 10.Saenger W. (1984) Principles of Nucleic Acid Structure. Springer-Verlag, New York, NY. [Google Scholar]
- 11.Olson W.K. (1982) Theoretical studies of nucleic acid conformation: Potential energies, chain statistics and model building. In Neidle,S. (ed.), Topics in Nucleic Acid Structure, Part 2. Macmillan Press Inc., London, UK, pp. 1–79. [Google Scholar]
- 12.Sundaralingam M. (1969) Stereochemistry of nucleic acids and their constitutents. Allowed and preferred conformations of nucleosides, nucleoside mono-, di-, tri-, tetraphosphates. Nucleic acids and polynucleotides. Biopolymers, 7, 821–860. [Google Scholar]
- 13.Sundaralingam M. (1973) Conformation of biological molecules and polymers. In Bergmann,E.D. and Pullman,B. (eds), The Jerusalem Symposium on Quantitative Chemistry and Biochemistry. Academic Press, New York, NY, Vol. 5, pp. 417–456. [Google Scholar]
- 14.Olson W.K. (1975) Configuration statistics of polynucleotide chains. A single virtual bond treatment. Macromolecules, 8, 272–275. [DOI] [PubMed] [Google Scholar]
- 15.Olson W.K. and Srinivasan,A.R. (1980) Yeast tRNAPhe conformational wheels: a novel probe of the monclinic and orthorhombic models. Nucleic Acids Res., 8, 2307–2329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Murthy V.L., Srinivasan,R., Draper,D.E. and Rose,G.D. (1999) A complete conformational map for RNA. J. Mol. Biol., 291, 313–327. [DOI] [PubMed] [Google Scholar]
- 17.Woese C.R. and Gutell,R.R. (1989) Evidence for several higher-order structural elements in ribosomal-RNA. Proc. Natl Acad. Sci. USA, 86, 3119–3122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Gutell R.R., Weiser,B., Woese,C.R. and Noller,H.F. (1985) Comparative anatomy of 16-S-like ribosomal RNA. Prog. Nucleic Acid Res. Mol. Biol., 32, 155–216. [DOI] [PubMed] [Google Scholar]
- 19.Michel F. and Westhof,E. (1990) Modelling of the three-dimensional architecture of group I catalytic introns based on comparative sequence analysis. J. Mol. Biol., 216, 585–610. [DOI] [PubMed] [Google Scholar]
- 20.Jucker F.M. and Pardi,A. (1995) GNRA tetraloops make a U-turn. RNA, 1, 219–222. [PMC free article] [PubMed] [Google Scholar]
- 21.Butcher S.E., Dieckmann,T. and Feigon,J. (1997) Solution structure of a GAAA tetraloop receptor RNA. EMBO J., 16, 7490–7499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Woese C.R., Winker,S. and Gutell,R.R. (1990) Architecture of ribosomal-RNA—constraints on the sequence of tetra-loops. Proc. Natl Acad. Sci. USA, 87, 8467–8471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Leontis N.B. and Westhof,E. (1998) A common motif organizes the structure of multi-helix loops in 16 S and 23 S ribosomal RNAs. J. Mol. Biol., 283, 571–583. [DOI] [PubMed] [Google Scholar]
- 24.Duarte C.M. and Pyle,A.M. (1998) Stepping through an RNA structure: a novel approach to conformational analysis. J. Mol. Biol., 284, 1465–1478. [DOI] [PubMed] [Google Scholar]
- 25.Ramachandran G.N. and Sasisekharan,V. (1968) Stereochemistry of polypeptide chain configurations. Adv. Protein Chem., 23, 283–437. [DOI] [PubMed] [Google Scholar]
- 26.Srinivasan A.R. and Yathindra,N. (1977) A novel representation of the conformational structure of transfer RNAs. Correlation of the folding patterns of the polynucleotide chain with the base sequence of the nucleotide back bone torsions. Nucleic Acids Res., 4, 3969–3979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Leontis N.B. and Westhof,E. (2001) Geometric nomenclature and classification of RNA base pairs. RNA, 7, 499–512. [DOI] [PMC free article] [PubMed] [Google Scholar]