Abstract
Genes and proteins are organized on the basis of their particular mutual relations or according to their interactions in cellular and genetic networks. These include metabolic or signaling pathways and protein interaction, regulatory or co-expression networks. Integrating the information from the different types of networks may lead to the notion of a functional network and functional modules. To find these modules, we propose a new technique which is based on collective, multi-body correlations in a genetic network. We calculated the correlation strength of a group of genes (e.g. in the co-expression network) which were identified as members of a module in a different network (e.g. in the protein interaction network) and estimated the probability that this correlation strength was found by chance. Groups of genes with a significant correlation strength in different networks have a high probability that they perform the same function. Here, we propose evaluating the multi-body correlations by applying the superparamagnetic approach. We compare our method to the presently applied mean Pearson correlations and show that our method is more sensitive in revealing functional relationships.
INTRODUCTION
Biological systems are functionally organized in different related networks defined by the type of their particular interaction, such as metabolic or signaling pathways and protein interaction, regulatory or co-expression networks. Metabolic networks are known to be subjected to conditional activity control, implemented by a variety of mechanisms such as transcript regulation, chemical modification, protein–protein interaction or signal cascades. No clearly separated networks exist in the cell. While metabolic pathways often contain protein complexes with strong protein–protein interactions, they are regulated by product feedback inhibition and are subject to common transcriptional regulation.
Single biomolecular networks are currently investigated in terms of topology (1,2), motifs (3), correlation structure (4) and modular properties (5–7) which are related to function. A functional module (5) is defined as a group of genes or their products which are related by one or more genetic or cellular interactions, e.g. co-regulation, co-expression or membership of a protein complex, of a metabolic or signaling pathway or of a cellular aggregate (e.g. chaperone, ribosome, protein transport facilitator, etc.). An important property of a module is that its function is separable from other modules (5) and that its members have more relations among themselves than with members of other modules, which is reflected in the network topology. The separability may stem from, for example, cellular localization or specific interaction of proteins or specific regulation of genes. Modules can be understood as a separated substructure of a network or pathway, e.g. the complex of fatty acid synthetase subunits may serve as an example of a module of the fatty acid biosynthesis pathway and the protein complex is a module of a protein interaction network (6). In principle, the large-scale cellular networks are robust due to their hierarchical, scale-free organization (2). Genes with related functions may have similar expression profiles, i.e. may be members of a module of the co-expression network. Co-expression is regulated in yeast by the modular action of transcription factors showing a strong correlation with gene function (8).
Presently, large amounts of data related to functional properties of genomes, e.g. gene expression and protein interaction data, are being generated. Expression data are analyzed in an unsupervised way by finding a similarity measure between gene expression profiles by clustering or biclustering the data with hierarchical, k-means clustering or more appropriate clustering like CLICK (9) and superparamagnetic clustering (10,11).
To obtain more reliable information than using these distinct data sets alone and to obtain insights into functional modules we integrate independent but biologically related data sets or different genetic and molecular networks (12). So far, an integrative data analysis has been performed with correlation mapping (13) and mean Pearson correlations (14,15). The main drawbacks are that the present integrative methods rely on clustering procedures which are not sufficiently robust against noise, fail for complex non-spherical data structures, or are dependent on external parameters like the predefined number of clusters. Furthermore, multi-body correlations are often estimated by averaging, but averaging does not reflect any realistic correlation structure of the data.
The integration could be done, on the one hand, by combining each binary interaction (16). On the other hand, we can find clusters, structures or modules in one particular network and see if the components (proteins or genes) of these structures are significantly related in any other network. In the present paper we propose a method for the latter strategy which can be used to integrate genetic, metabolic and regulatory information as well as functional classification (17) to find functional modules.
Outline of the method
Our method can be used: (i) to reduce the rate of false functional assignments; (ii) to analyze expression data in a more sensible way compared to statistical evidence only; (iii) to find hypotheses for functional modules and new complexes and to assign unknown genes a function. To provide an example we integrated protein interaction and co-expression networks. Having identified a module of the protein interaction network or using a protein complex we calculated the significant correlation strength of the corresponding gene expression profiles. For this purpose we employed the definition of the correlation of superparamagnetic clustering (18), a very successful algorithm (19,20), very effective for expression analysis (10,11) and clustering of genetic networks (32). Besides its advantageous features, including its robustness against noise, it is able to define the correlation strength of a group of gene expression profiles or, more generally, of a group of nodes in a sparse network such as the co-expression network (Materials and Methods). The corresponding P value (probability that the correlation strength is a random coincidence) is calculated according to the rationale described in Jansen et al. (14). We calculated the distribution (a histogram) of the correlation strengths of all possible groups with the same number of genes. The area of the distribution greater than the correlation strength of our module consisting of the same number of genes is then the definition of our P value (see Materials and Methods). In contrast to Jansen et al. (14), we include the structure of the co-expression network. Its nodes are the genes which are connected for the most similar pairs of expression profiles. With the help of the superparamagnetic approach we looked for significant substructures. Highly significant correlation may be resulting in direct neighborhood of two nodes or membership of a larger (dense) substructure of the coexpression network where the gene expression profiles of the resulting complex are connected by a transitivity relation (21). In contrast to Jansen et al. (14), our method is not only applicable in the supervised mode, introducing prior knowledge, it can subsequently be used in an unsupervised way. First, the protein interaction network and its clusters are tested for significant co-expression, leading to a hypothesis of protein complexes and, second, we obtain not only the most significant co-expressed protein complexes but also their corresponding gene expression profiles.
MATERIALS AND METHODS
Expression data and co-expression network
We used two independent yeast expression data sets to evaluate our method. The first one is data on cell cycle-related profiles using alpha, cdc15 and cdc28 synchronization (22,23). Each time series was used separately. The second is the Rosetta Compendium, which includes 300 deletion and drug treatment experiments (24). The expression data is available in the form of a matrix having N rows and D columns. The columns represent the tissues in a special condition and the rows represent the gene profiles. The data used in the calculations had already been preprocessed. We normalized them in a z-score fashion such that the average expression ratio of one profile is 0 and the standard deviation is 1. From the expression data a sparse co-expression network was constructed using the K mutual nearest neighbor criterion (25). For every gene expression profile a list of the K nearest neighbor profiles was produced. The nearest neighbor of one expression profile is defined as the most similar profile measured, for example, as the Euclidean distance. Two nodes were connected if they were on each others’ list. The optimal K is ∼15, as discussed in Agrawal and Domany (26).
Protein interaction data
The protein interaction data set is taken from the MIPS database (17). As an example we used the yeast two-hybrid (Y2H) data of Ito et al. (27) and von Mering et al. (28) as well as the complex catalog (17). The correlation structure has been investigated by Maslov and Sneppen (4). In principle, protein complexes and modules can be found by clustering the protein interaction network (29,32) or by clustering according to functional assignments (30). A protein in a complex is a densely connected subnetwork, but a member directly interacts with no more than a few members of the same complex.
The superparamagnetic approach
Superparamagnetic clustering (18) has been successfully applied to artificial and real data (19,20) as well as to expression data (10,11) and is based on a physical analog, the magnetic phase transitions of spin systems. We briefly describe the algorithm which is able to partition a network into clusters, i.e. highly connected subgraphs. The algorithm is very suitable for our analysis because it establishes a hierarchy of clusters, a dendrogram. A dendrogram is formed if we are looking at a system with different resolutions: at low resolution the whole network is one cluster. At higher resolutions it decays into multiple other clusters until at the highest resolution every node is its own cluster. There exists a particular resolution where a cluster disappears, which we call the critical resolution. With the help of the algorithm we determined the correlation for a number of nodes in the network (see below), which is the probability that the nodes belong to a common cluster. We define the correlation strength of a module or group of nodes as the critical resolution where its correlation drops to zero. Finally, we calculated the distribution of the correlation strength of all pairs, triplets, etc. of nodes.
After having constructed the co-expression network according to the K mutual nearest neighbor criterion (see above), we assigned every node an integer label Si = 1…q (equivalent to a Potts spin with q different states), where q is an integer. The nodes representing the expression profiles i and j are connected with edges weighted with the coupling constant Jij, for which we use a fast decreasing Gaussian decay (10)
Jij =(1/K)exp[–(dij2/2 d̄2)].
Here, dij is the Euclidean distance between the gene expression profiles of gene or node i and j, d̄ is the mean distance between all neighbors and K is the mean number of neighbors. The coupling is only non-zero for connected nodes. For unweighted networks, e.g. the protein interaction network, Jij may be 1 or 0.
We calculate the correlation of a certain number of nodes (gene expression profiles) of the network using a Monte-Carlo simulation, the Swendsen–Wang algorithm (31). Starting from a random configuration (random label Si = 1…q on each node i), the algorithm assigns node i and j the same label with the probability pij = 1 – exp(Jij/τ), where Jij/τ is the effective coupling between node i and j and τ (the temperature of the physical spin system) is defined as the resolution (see above) with which we investigate the system. Having gone over all edges of the network, every area with the same label forms a cluster. The integer q is not related to the number of clusters. A new configuration is generated by giving every node in a cluster a new random label. Averaging over several of these configurations gives the probability of a number of nodes being in the same cluster, which is defined as the correlation function. The algorithm includes a transitivity rule: if node A has the same label as B and A the same as C, then B and C also have the same label; A, B and C are strongly correlated. Increasing the resolution τ we decrease the effective coupling Jij/τ, which leads to hierarchically related nodes. The effective coupling and thus the correlation of a group of nodes decreases with increasing resolution. We define their correlation strength TM as the critical resolution where the correlation of a group of nodes drops to 0 (the correlation as a function of the resolution is actually a step function). It is dependent on the coupling of two or more nodes and is a collective measure as well. The more densely connected these nodes are the higher is their correlation strength.
To assess the correlation strength of genes which are members of the same module of a different genetic network we define a P value which gives the probability that the strength of the correlation was found by chance. Therefore, we calculate the distribution ρ or histogram of the correlation strength T of all possible groups with the same number of genes. The one-sided P value is then defined as the area of the distribution ρ above the correlation strength of the module, divided by the normalization ρ0 (the number of all possible modules),
P(TM) = (1/ρ0) ∫TpTM ρ(T)dT
where TM is the correlation strength of the tested module and Tp the maximal possible correlation strength in the network.
RESULTS
We constructed a graph of co-expressed genes (see Materials and Methods) for the cell cycle as well as the Rosetta data set, in which the nodes are the genes. Two nodes are connected if they fulfill the mutual nearest neighbor criterion (see Materials and Methods). Such networks have been investigated in detail in Agrawal (25). The definition of the co-expression network is similar to the transitivity relations of Zhou et al. (21). We adopted the definition of the collective multi-body correlations from the superparamagnetic clustering (18) and calculated the correlation strength for modules of random genes described in detail in Materials and Methods.
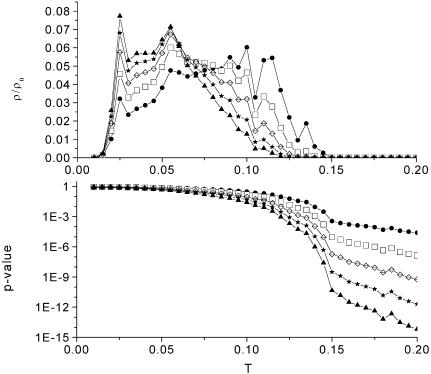
A distribution or histogram of the correlation strength is displayed in Figure 1 (top) for groups of two to six gene expression profiles for the cell cycle experiment (α arrest). In Figure 1 (bottom) we show the corresponding one-sided P value which is defined similarly to in Marcotte et al. (12) (see Materials and Methods). As expected, the weight of the distribution is shifted to the left if the number of members of a module increases. Most of the larger modules have a lower correlation strength, but to find a large group with a high correlation strength gives a lower P value than for finding a smaller module.
Figure 1.
Normalized distribution ρ/ρ0 or histogram of the critical resolution or correlation strength T (top) and P value (bottom) for groups of two to six (circle, square, diamond, star and triangle) expression profiles. The weight of the distribution is shifted to the left side. The larger the group the lower the correlation strength.
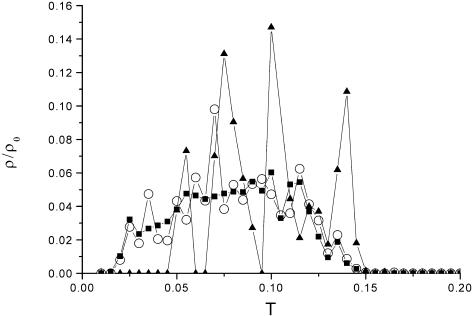
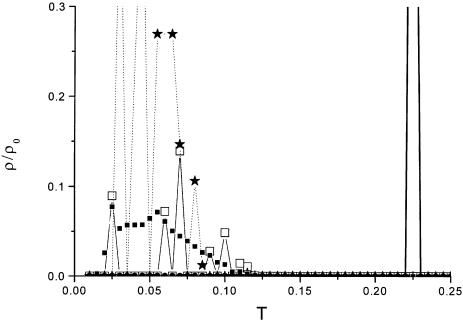
Given the distribution of the correlation strength based on the expression data we were able to test the protein interaction data for significant co-expression. First, we tested the binary data of Hughes et al. (24) and von Mering et al. (28) and, second, the complex data. Figure 2 shows the distribution of the correlation strength (co-expression) of members of Y2H data and members of a ribosome complex in comparison to the random background. The Y2H data shows, in accord with Marcotte et al. (12), almost no deviation from the random background, although the distribution is slightly shifted to the right to a higher correlation strength. By choosing a certain P value it is possible to obtain a significantly co-expressed part of the protein interaction network (see below). The situation is different in that only the open reading frames (ORFs) of the ribosome were chosen. As shown in Figure 2, most of the ribosome is highly co-expressed and so the weight of the distribution is shifted to a higher correlation strength. Figure 3 displays the distribution of the correlation strength of six gene expression profiles (with squares representing the random background). It is clearly shown that the nucleosomal complex and parts of the ribosome are highly significantly co-expressed.
Figure 2.
Distribution of the correlation strength for pairs of expression profiles which are members of a ribosome protein complex (triangle), a Y2H interaction (circle) (27) and the random control (square).
Figure 3.
Distribution of the correlation strength of a group of six expression profiles for the α cell cycle data which are members of the small mitochondrial ribosome subunit (star), large mitochondrial ribosome subunit (empty square), the nucleosome complex (thick line) and the random control (filled square). The correlation strength of the complex data is shifted to the right. The correlation strength of the complexes is much higher compared to the random control. The highest correlation strength is found for the nucleosome complex with the peak at T = 0.225.
Details of single complexes are annotated in Table 1 for the Rosetta Compendium and the alpha, cdc15 and cdc28 synchronization time series. Only complexes which have a P value <1E – 3 are displayed. Mainly those complexes are significant which are constantly needed in the cell, as expected, using an expression profile over many experiments or during the cell cycle. A part of the cycline complex is co-expressed in the α, cdc15 and cdc28 experiments. They are not significant in the Rosetta Compendium, which does not include any cell cycle synchronization and thus averages over the cell cycle. The nucleosomal protein complex is also very tightly co-expressed. It is co-regulated in all the expression experiments as well as parts of the cytochrome c oxidase, the mitochondrial and the cytoplasmic ribosomes. The respiration chain complex F0/F1 ATP synthase is only significantly co-expressed in the Rosetta Compendium. In summary, we found significant co-expression in many permanent complexes, similar to Jansen et al. (14). Since we did not average over the correlation of all members, we immediately obtained those parts of the complexes with the highest correlation strength. In agreement with Jansen et al. (14), we found that transient complexes mostly have no significant co-expression. The significant co-expression of the 20S proteasome and of the 19/22S regulator was found for the cell cycle data but not in the Rosetta data. We found a qualitatively similar result as Jansen et al. (14). Quantitative differences are related to the fact that we included transitive similarities of expression profiles (not directly similar, but similar to the same set of profiles).
Table 1. List of protein complexes with more than two open reading frames (ORF) with significant co-expression (P < 0.001).
| Complex | n | alpha | Cdc15 | Cdc28 | Rosetta |
|---|---|---|---|---|---|
| Alpha, al-treh. anchor (50) | 4 | 75% | 75% | ||
| AnaPromCom (60) | 11 | 27% | |||
| Cacinerum B (100) | 3 | 67% | 67% | ||
| Chaperone containing T-complex TRiC (130) | 8 | 50% | 25% | ||
| CDc28p (133.10) | 10 | 20% | 50% | 20% | |
| Pho85p (133.20) | 6 | 33% | |||
| Actin-associated proteins (140.20.20) | 24 | 25% | |||
| Glycine decarboxylase (200) | 3 | 67% | |||
| ATPase (210) | 4 | 100% | 50% | ||
| ATPase (220) | 15 | 27% | 40% | ||
| TRAPP (260.60) | 10 | 40% | |||
| Vps4p ATPase (260.70) | 3 | 67% | |||
| Arp2p complex (260.90) | 6 | 33% | |||
| TOM (290.10) | 9 | 22% | |||
| Nucleosome protein (320). | 8 | 100% | 87% | 37% | 75% |
| 20 S proteasome (360.10.10) | 15 | 13% | 40% | 33% | |
| 19/22S regulator (360.10.20) | 18 | 17% | 28% | 44% | |
| Replication complex (410.35) | 13 | 39% | 23% | 15% | |
| Cytochrome bc1 complex (420.30) | 9 | 44% | 78% | 78% | |
| Cytochrome c oxidase (420.40) | 8 | 50% | 38% | 88% | 50% |
| F0/F1 ATP synthase (complex V)(420.5) | 15 | 60% | |||
| Ribonucleoside reductase (430) | 4 | 50% | |||
| Nuclear processing (440.10.10) | 5 | 40% | |||
| Cytoplasmic ribosome large subunit (500.40.10) | 81 | 33% | 21% | 21% | 47% |
| Small subunit (500.40.20) | 57 | 37% | 16% | 18% | 49% |
| Mitochondrial ribosome large subunit (500.60.10) | 32 | 16% | 53% | 43% | 31% |
| Small subunit (500.60.20) | 14 | 14% | 42% | 21% | 29% |
| RNA polymerase I (510.10) | 8 | 38% | 38% | 50% | |
| RNA polymerase II (510.40.10) | 9 | 44% | |||
| RNA polymerase III (510.120) | 12 | 17% | 33% | 17% |
The percentage of the ORFs which are significant is indicated. The table lists, from left to right, the name and MIPS classification number, the number of ORFs and the percentage of ORFs which are significant for the alpha, cdc15, cdc28 and Rosetta data set. Not displayed are non-significant protein complexes, e.g., SAGA complex, CCR4 complex, SWI/SNF transcription activator, TAFIIs and RSC complex.
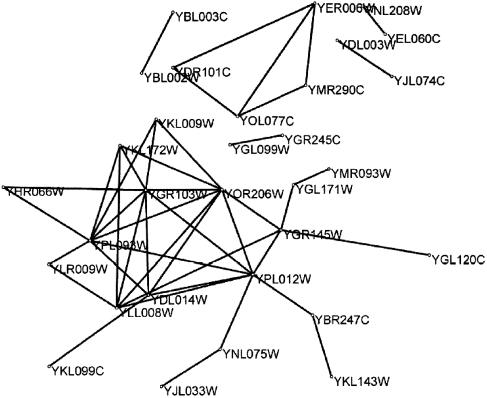
Our approach has the advantage that it is possible: (i) to display the result as a substructure of the co-expression network, e.g. to detect those profiles which are transitively related; (ii) to find parts of the protein interaction network with a significant correlation strength in the co-expression network. As an example we show two subnetworks in Figures 4 and 5. The result is a subnetwork of the protein interaction network (28) which is related to cell cycle (alpha) expression data (Fig. 4) where only the highest significant correlation strength (lowest P value) is taken into account. This network is still connected and mirrors parts of a RNA metabolism complex, nucleosomal protein complex and a protein synthesis turnover complex. Interactive interfaces to the data can be used to obtain hypotheses of protein complexes and to find essential parts of the protein interaction network, reducing its high false positive rate.
Figure 4.
Y2H data (28) which are highly significantly co-expressed. A network which is part of a RNA metabolism complex, a nucleosome protein complex and a protein synthesis turnover complex are identified. The nodes are the ORFs and the edges represent protein interaction.
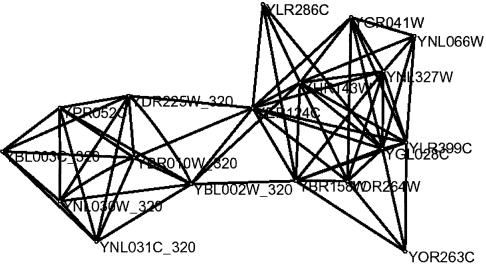
Figure 5.
Co-expression cluster of the nucleosome protein complex (ORFs are labeled 320) which are significant in the Rosetta data set. Co-expressed with the complex are unclassified genes, a non-histone and genes which are cell cycle related. All genes except YLR286 (endochitinase) are localized in the nucleus. The nodes are the ORFs and the edges indicate co-expression.
The parts of the co-expression network that we display in Figure 5 correspond to the subnetwork of the Rosetta expression data, which includes the six genes of the significant nucleosome protein complex. The correlations that we found can be mapped to known and unknown functional interactions. For instance, a non-histone protein and genes with unknown function, as well as cell cycle genes and genes related to budding, correlate with the gene expression profiles of the complex. One gene is annotated as an endochitinase (17), a function that does not fit into the experimental context.
CONCLUSION
It remains a challenging task to interpret expression data in the context of known functional relations. Systematic approaches which integrate different types of functional information representing cellular networks are still needed in the post-genomic sector to understand the functional context of genes and to uncover functional modules. Almost no protein or gene performs its function in isolation, thus most of the existing interactions have to be discovered or confirmed. Currently, groups of gene expression profiles are clustered according to their similarity and are related to function or protein interaction afterwards. Our method starts from different groups with known interacting proteins and looks at whether they are also significantly related in other experimental data. In the case that a group or subset of the data correlates in a dense co-expression subnetwork, unknown genes that are members of such a subnetwork are candidates for interaction.
We integrated cellular networks with gene expression based on the correlation defined in the superparamagnetic approach, a very successful clustering procedure (10,11,32), which includes transitive co-expression. Furthermore, the method is robust against noise and is able to calculate multi-body correlations and their strength. Having defined in our examples a module or complex in the protein interaction network, we evaluated the correlation strength of this module in the co-expression network. By calculating the distribution of the correlation strength of all groups of gene expression profiles (nodes of the co-expression network) we were able to evaluate P values for any module of a given size. Since the set of the known or predicted correlations is small compared to the combinatorial number of all possible correlations, we generally avoided most false positive signals by calculating the strength of a correlation to all groups and comparing it to the strength of any chosen module. The P value is the probability that the observed strength was by random coincidence.
The main advantage of the method is the use of multi-body correlations in contrast to the averaging used earlier (14,15). The latter mixes strong with weak correlations, which does not reflect the network structure of the data. In addition, when compared to the Pearson correlation, the superparamagnetic approach takes into account the co-expression network. For instance, some pair could have a low Pearson correlation but could be a member of the same process because the partners are related by transitivity (21). The superparamagnetic approach would not miss these correlations.
We applied our new method to combine protein interaction and expression data from independent experiments. The correlation of protein complexes significantly overlapping with interaction data appears to be a logical consequence of the need to co-express tightly interacting and functionally dependent proteins. However, in most cases such correlations are found by intuition rather than statistical correlation. It has been shown that we can map correlated structures, e.g. complexes, to correlated structures of the co-expression network, which leads to the identification of functional modules. We provide a systematic, generally applicable approach which integrates different genetic information and expression profiles and which is able to test and reveal hypothetical functional modules. These features cannot be supplied by other frequently applied methods like mean Pearson correlations (14) or mapping of clusters (13). With a growing number of known interactions and co-expression, a larger number of hypotheses can be tested. In addition, we employed confidence values correlating to the nature of the interaction data (e.g. high for many known complexes but low for Y2H data).
The method is well suited to application to other combinations and is directly extendable to any set of cellular and genetic network data. Future work will be directed at systematic application of the method to the different functional classifications available (e.g. 17). Starting from well-known correlations we will attempt to define, for example, co-expressed modules exhibiting significant P values, and to annotate them as experimentally confirmed functional dependencies. Our method provides a framework and generator of hypotheses to be confirmed or rejected. It is applicable to the large amount of experimental high-throughput functional data to come.
Acknowledgments
ACKNOWLEDGEMENTS
We thank A. Manolescu for his help concerning the algorithm, M. Münsterkötter and U. Güldener concerning the data, G. Kastenmüller, A. Facius and K. Mayer for useful discussions and S. Rudd for critical reading of our manuscript. The research was supported by the BMBF (FKZ01KW9928 and 031U118A).
REFERENCES
- 1.Barabasi A.-L. and Albert,R. (1999) Emergence of scaling in random networks. Science, 286, 509–512. [DOI] [PubMed] [Google Scholar]
- 2.Jeong H., Tombor,B., Albert R., Oltvai,Z.N. and Barabási,A.-L. (2000) The large scale organisation of metabolic networks. Nature, 407, 651–654. [DOI] [PubMed] [Google Scholar]
- 3.Shen-Orr S., Milo,R., Mangnan,S. and Alon,U. (2002) Network motifs in the transcriptional regulation network of Eschericha coli. Nature Genet., 31, 64–68. [DOI] [PubMed] [Google Scholar]
- 4.Maslov S. and Sneppen,K. (2002) Specificity and stability in topology of protein networks. Science, 296, 910–913. [DOI] [PubMed] [Google Scholar]
- 5.Hartwell L.H., Hopfield,J.J., Leibler,S. and Murray,A.W. (1999) From molecular to modular cell biology. Nature, 402 (suppl.), C47–C52. [DOI] [PubMed] [Google Scholar]
- 6.Rives A.W. and Galitski,T. (2003) Modular organization of cellular networks. Proc. Natl Acad. Sci. USA, 100, 1128–1133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Oltvai Z.N. and Barabasi,A.-L. (2002) Life’s complexity pyramid. Science, 298, 763–764. [DOI] [PubMed] [Google Scholar]
- 8.Lee T.I., Rinaldi,N.J., Robert,F., Odom,D.T., Bar-Joseph,Z., Gerber,G.K., Hannett,N.M., Harbison,C.T., Thompson,C.M., Simon,I. et al. (2002) Transcriptional regulatory networks in Saccharomyces cerevisiae, Science, 298, 799–804. [DOI] [PubMed] [Google Scholar]
- 9.Sharan R. and Shamir,R. (2000) CLICK: a clustering algorithm with application to gene expression analysis. In Proceedings of the 8th ISMB, pp. 260–268. [PubMed] [Google Scholar]
- 10.Getz G., Levine,E., Domany,E. and Zhang,M.Q. (2000) Super-paramagnetic clustering of yeast expression profiles. Physica, A279, 457–464. [Google Scholar]
- 11.Getz G., Levine,E. and Domany,E. (2000) Coupled two-way clustering analysis of gene microarray data. Proc. Natl Acad. Sci. USA, 97, 12079–12084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Marcotte E.M., Pellegrini,M., Thompson,M.J., Yeates,T.O. and Eisenberg,D. (1999) A combined algorithm for genome-wide prediction of protein function. Nature, 402, 83–86. [DOI] [PubMed] [Google Scholar]
- 13.Ge H., Church,G.M. and Vidal,M. (2001) Correlation between transcriptome and interactome mapping data from Saccharomyces cerevisiae. Nature Genet., 29, 482–486. [DOI] [PubMed] [Google Scholar]
- 14.Jansen R., Greenbaum,D. and Gerstein,M. (2002) Relating whole-genome expression data with protein–protein interaction. Genome Res., 12, 37–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Pavlidis P. Weston,J., Cai,J. and Noble,W.S. (2002) Learning gene functional classifications from multiple data types. J. Comput. Biol., 9, 474–485. [DOI] [PubMed] [Google Scholar]
- 16.Hanisch D., Zien,A., Zimmer,R. and Lengauer,T. (2002) Co-clustering of biological networks and gene expression data. Bioinformatics, 18, S145–S154. [DOI] [PubMed] [Google Scholar]
- 17.Mewes H.W., Frishman,D., Gueldner,U. Mannhaupt,G., Mayer,K., Mokrejs,M., Morgenstern,B. Munsterkotter,M., Rudd,S. and Weil,B. (2002) MIPS: a database for genomes and protein sequences. Nucleic Acids Res., 30, 31–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Blatt M, Wiseman,M. and Domany,E. (1996) Superparamagnetic clustering of data. Phys. Rev. Lett., 76, 3251–3255. [DOI] [PubMed] [Google Scholar]
- 19.Domany E. (1999) Superparamagnetic clustering of data. The definitive solution of an ill posed problem. Physica, A263, 158–169. [Google Scholar]
- 20.Vendruscolo M., Paci,E., Dobson,C.E. and Karplus,M. (2001) Three key residues from critical network in a protein folding transition state. Nature, 409, 641–645. [DOI] [PubMed] [Google Scholar]
- 21.Zhou X., Kao,M.-C.J. and Wong,W.H. (2002) Transitive functional annotation by shortest-path analysis of gene expression data. Proc. Natl Acad. Sci. USA, 99, 12783–12788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Spellman P.T., Sherlock,G., Zhang,M.Q., Iyer,V.R., Anders,K., Eisen,M.B., Brown,P.O., Botstein,D. and Futcher,B. (1998) Comprehensive identification of cell cycle-regulated genes of yeast Saccharomyces cerevisiae by microarray hybridization. Mol. Biol. Cell, 9, 3273–3297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Cho R.J., Campbell,M.J., Winzeler,E.A., Steinmetz,L., Conway,A., Wodicka,L., Wolfsberg,T.G., Gabrielian,A.E., Landsman,D., Lockhart,D.J. et al. (1998) A genome-wide transcriptional analysis of the mitotic cell cycle. Mol. Cell, 2, 65–73. [DOI] [PubMed] [Google Scholar]
- 24.Hughes T.R., Marton,M.J., Jones,A.R., Roberts,C.J., Stoughton,R., Armour,C.D., Bennett,H.A., Coffey,E., Dai,H., He,Y.D. et al. (2000) Functional discovery via a compendium of expression profiles. Cell, 102, 109–126. [DOI] [PubMed] [Google Scholar]
- 25.Agrawal H. (2002) Extreme self-organization in networks constructed from gene expression data. Phys. Rev. Lett., 89, 268702–268706. [DOI] [PubMed] [Google Scholar]
- 26.Agrawal H. and Domany,E. (2003) Potts ferromagnets on coexpressed gene networks: identifying maximally stable partitions. Phys. Rev. Lett., 90, 158102–158106. [DOI] [PubMed] [Google Scholar]
- 27.Ito T., Chiba,T., Ozawa,R., Yoshida,M., Hattori,M. and Sakaki,Y. (2001) A comprehensive two-hybrid analysis to explore the yeast protein interactome. Proc. Natl Acad. Sci. USA, 98, 4569–4574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.von Mering C., Krause,R., Snel,B., Cornell,M., Oliver,S.G., Fields,S. and Bork,P. (2002) Comparative assessment of large-scale data sets of protein–protein interactions. Nature, 417, 399–403. [DOI] [PubMed] [Google Scholar]
- 29.Gavin A.C., Bosche,M., Krause,R., Grandi,P., Marzioch,M., Bauer,A., Schultz,J., Rick,J.M., Michon,A.M., Cruciat,C.M. et al. (2002) Functional organization of the yeast proteome by systematic analysis of protein complexes. Nature, 415, 141–147. [DOI] [PubMed] [Google Scholar]
- 30.Fellenberg M., Albermann,K., Zollner,A., Mewes,H.W. and Hani,J. (2000) Integrative analysis of protein interaction data. In Proceedings of the 8th ISMB, pp. 152–161. [PubMed] [Google Scholar]
- 31.Swendsen R.H. and Wang,J.S. (1987) Nonuniversial critical dynamics in Monte Carlo simulations. Phys. Rev. Lett., 58, 86–88. [DOI] [PubMed] [Google Scholar]
- 32.Spirin V. and Mirny,L.A. Protein complexes and function modules in molecular networks. Proc. Natl Acad. Sci., 2003 Sep 29 [Epub ahead of print], 10.1073/pnas.2032324100. [DOI] [PMC free article] [PubMed] [Google Scholar]