Abstract
The coupling of various chemical microseparation methods with small-scale NMR detection is a growing area in analytical chemistry. The formation of enlarged flow cells within the active volume of the NMR detector can significantly increase the coil filling factor and hence the signal-to-noise ratio of the NMR spectra. However, flow cells can also lead to deterioration of the separation efficiency due to the development of complex flow patterns, the form of which depend on the particular geometry of the flow cell and the flow rate used. In this study, we investigated the flow characteristics in different flow cell geometries relevant to the coupling of capillary liquid chromatography and NMR. Computational fluid dynamics was used to simulate fluid flow inside flow cells with a volume of ~ 1 µL. Magnetic resonance microimaging was used to measure experimentally the velocity fields inside these flow cells. The results showed good agreement between experiment and simulation and demonstrated that a relatively gradual expansion and contraction is necessary to avoid areas of weak recirculation and strong radial velocities, both of which can potentially compromise separation efficiency.
An essential component in the purification and analysis of unknown compounds is efficient separation of individual components from an often complex chemical or biological system. Advances in microseparations, include techniques such as capillary liquid chromatography (cLC),1 capillary electrophoresis (CE),2 and capillary electrochromatography3 have played a large role in improving the separation efficiency. The chromatographic dilution (D) of cLC, for example, is given by
| (1) |
where C0 is the initial concentration of the analyte, Cmax is the final compound concentration at the peak maximum, r is the column radius, ϵ is the column porosity, k is the retention factor, L is the column length, H is the column plate height, and Vinj is the injected sample volume. Equation 1 shows that a smaller column radius results in less chromatographic dilution and higher concentration elution peaks. The smaller scale is also much more amenable to very rapid separations. In addition to these general benefits of microseparations, in electrophoretic separations the high surface area-to-volume ratio of the small capillaries used in CE systems, for example, dissipates Joule heating effectively, and therefore allows substantially higher electrophoresis voltages to be used, resulting in higher separation efficiency.
The coupling of various chemical microseparation methods with small-scale nuclear magnetic resonance (NMR) detection has developed rapidly in recent years.4–12 The mass sensitivity (Sm), defined as the minimum amount of analyte detectable, of NMR can be expressed as
| (2) |
where ω0 is the operating frequency of the NMR system, M is the number of moles of analyte within the observe volume of the NMR detector, t is the total data acquisition time, and dc is the diameter of the NMR radio frequency coil, which is usually either a solenoid or saddle geometry. Equation 2 shows that one ideally performs experiments at the highest magnetic field strength, with the maximum concentration of analyte, and the smallest diameter NMR coil.
Since most separation systems contain a considerable number of magnetic components, a long “transfer line” is required to connect the separation instrument to the NMR probe inside the magnet.4,6,7 The inner diameter of such a capillary is generally chosen to be between 50 and 100 µm to minimize peak dispersion and column broadening after the separation. If the inner diameter of the capillary is too small, it can act as a separation column itself, and back pressures can be very large for long lengths of the transfer capillary. If the inner diameter of the capillary is too large, on the other hand, peak dispersion due to diffusion can destroy the separation.
Due to its intrinsic low sensitivity, even using high magnetic fields and very small detector coils, on-line NMR analysis requires a reasonably large sample volume, particularly for analytes at low concentrations. To address the dual requirements for a large detector volume and a small diameter transfer capillary, enlarged flow cells, also termed “bubble cells”, can be formed and the NMR detector placed directly around these cavities in the capillary.6 An example of such a flow cell is shown in Figure 1a. These types of bubble cells, also produced commercially by Agilent Technologies under the description of extended light-path capillaries, are used extensively in UV-detected CE separations. In terms of minimizing the peak dispersion, an ideal flow cell should have a rapid expansion from the smaller inner diameter of the transfer capillary. In practice, however, such a geometry can result in complex fluid flow patterns,13–15 which degrade the efficiency of the separation. In addition, the quality of the NMR spectrum is affected directly by the flow rate. For on-line NMR measurements, flow during data acquisition causes spectral broadening of the NMR peaks, resulting in a full width-half-maximum line width (LW) given by16
| (3) |
where τ is the residence time of the fluid within the flow cell and the line width in the absence of flow is given by . Therefore, very fast flow rates result in very broad lines and the loss of information in the NMR spectrum.
Figure 1.
Photographs of the flow cells showing the reference positions (black arrows) used for microimaging. (a) Flow cell with a gradual transition region and (b) flow cell with an abrupt transition. (c) shows the form of the solenoidal coil used for imaging wrapped around the flow cell.
In this study, numerical simulations were conducted to investigate the effect of the geometry of flow cells on flow patterns. As experimental verification, a series of magnetic resonance (MR) microimaging measurements were taken of the velocity fields of fluid flow inside flow cells with various geometries at different flow rates.
EXPERIMENTAL SECTION
Numerical Simulations
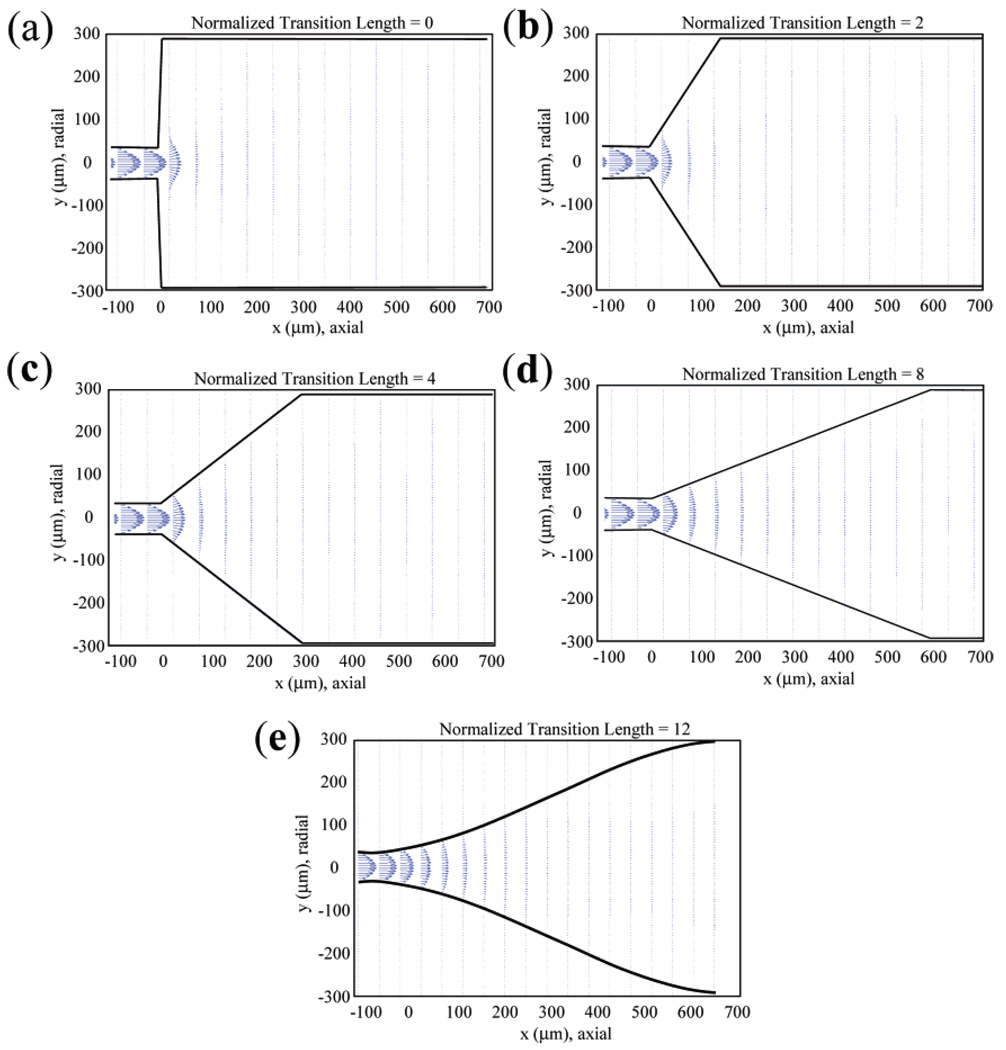
The behavior of Newtonian viscous fluid flow can be described by the Navier–Stokes equations.17 Even though the equations can be simplified when dealing with incompressible and steady-state flow, analytical solutions are available only for a few cases.18 These nonlinear partial differential equations may be solved numerically by using finite difference methods provided that proper boundary conditions and iteration methods are applied.19 Such simulation methods have been applied by Takemitsu20 and Xia et al.:21 in these papers, the underlying equations are described in detail, and in ref 21, experimental results were obtained using MR microimaging that were in reasonable agreement with the simulations. Nevertheless, to address complex geometry and calculation stability issues, finite element methods (FEM) are used in most practical cases, as is the case in this work. The general-purpose FEM analysis software ANSYS (Version 6.1, Canonsburg, PA.) was used to perform the fluid flow simulations. The following boundary conditions were used throughout the simulations: zero axial and radial velocities at the capillary walls, zero radial velocity along the centerline of the long-axis of the flow cell (since the radial velocity is positive above the axis and negative below the axis, from its axial symmetry the radial velocity has to be zero along the centerline), fully developed laminar (Hagen–Poiseuille) flow at the inlet, and a fluid temperature of 298 K. The lengths of the upstream and the downstream capillaries were set to 20 times the inner diameter of the capillary for these boundary conditions to be valid. The flow cells were characterized by the ratio of the lengths of the “transition” region to the inner diameter of the transfer capillaries, here termed the normalized transition length. Simulations were performed on flow cells with normalized transition lengths of 0, 2, 4, 8, and 12. The number of nodes used in the meshing procedure was ~36 000, which produced a simulation resolution of 3 µm × 8 µm. It took ~8 h per simulation using a Sun Blade 1000 Workstation (Sun Microsystems, Santa Clara, CA).
Flow Cell Formation
Two different flow cells, corresponding to normalized transition lengths of 0 and 12, were constructed for MR microimaging studies. One, shown in Figure 1a, was made with a gradual transition using localized etching with hydrofluoric acid. The dimensions of this flow cell were an inner diameter (i.d.) of 600 mm and length of 3.9 mm from the beginning of the expansion to the end of the contraction. It was created within a length of 75-µm-i.d./800-µm-o.d. quartz capillary (VitroCom). The quartz capillary was connected to a capillary system driven by a syringe pump (Harvard Apparatus) and was rinsed with acetone, 10% HCl, 10% NaOH, and water, successively, to clean its interior surface. A piece of aluminum foil was wrapped tightly around the position where the flow cell was to be formed. A heating coil of the same length was constructed by winding resistance heating wire (Omega Engineering, Stamford, CT) onto the foil-wrapped portion of the capillary. A water bath was used to provide chilled water (4 °C) to cool the parts of the capillary immediately adjacent to the two ends of the heating coil to produce a large temperature gradient. The heating coil was separated from the chilled water by two pieces of thin glass (Corning Glass Works), one at either end of the coil. The voltage applied to the heating coil was adjusted so that the temperature on the surface of the heating coil was roughly 90 °C throughout the etching process. The surface temperature was monitored using a digital thermometer (Omega Engineering). HF (10% in water) was pumped through the capillary system using the syringe pump at a flow rate of 1 mL/min for 60 min, and for another 60 min in the opposite direction to eliminate tapering toward the end of the flow cell due to the decrease in HF concentration as a result of etching.
The second flow cell was made with abrupt transitions. It had an i.d. of 672 mm and length of 3.4 mm, as shown in Figure 1b, and was created by carefully inserting and gluing two pieces of 188-mm-i.d. capillaries into the two ends of a larger capillary with i.d. 672 mm. For both flow cells, the lengths of straight capillary upstream and downstream of the flow cell were at least 20 times the diameter of the capillaries in order to ensure fully developed laminar flows within the inlet and the outlet capillaries.
NMR Microimaging of Flow
Of the many methods for measuring flow, MRI has the advantage that three-dimensional velocity fields can be measured directly. Many MR flow imaging methods have been developed based on principles of inflow/outflow, spin-tagging, time of flight, and phase contrast.22 However, in the microscopic regime, the diffusion of fluid molecules must also be taken into account, otherwise a significant source of error is introduced for flow with small Reynolds numbers.23,24 Measurements of both diffusion and flow can be encoded in a so-called q-space imaging experiment.25–27 In its most common implementation, a standard pulsed-field gradient spin–echo (PGSE) experiment is used.28 The signal in the PGSE experiment, E, is given by
| (4) |
where v is the flow velocity, Δ is the time between the two gradient pulses, D is the diffusion coefficient, and q is defined as
| (5) |
where γ is the gyromagnetic ratio of the nuclear spins and g and δ are the amplitude and the width of the gradient pulses, respectively,. The first term on the right-hand side of eq 4 represents a phase shift in the signal, and the second term an attenuation of the signal amplitude. To measure spatially resolved velocity maps, a series of MR images are acquired using the PGSE sequence, each image acquired with gradient pulses successively incremented by a value ginc, and then inverse Fourier transformation in q-space is performed for each pixel in the image. This results in a Gaussian-shaped function, P̄s(z,Δ), given by
| (6) |
This function is centered at a value kv given by
| (7) |
where nD is the number of increments of the strength of velocity/diffusion encoding gradient pairs and N is the digital array size for the q-space transformation. The full width half-maximum, kfwhm, of the Gaussian function is related to the value of D by25
| (8) |
Compared to time-of-flight and the phase-contrast methods, the q-space PGSE method provides much higher accuracy and the ability to measure velocity and diffusion simultaneously. The major drawback of this method is that, depending on the number of flow-encoding measurements in q-space, it takes much longer to acquire the data.
MR microimaging was performed with a 14.1-T (600-MHz) imaging spectrometer (Varian, Palo Alto, CA) using custom-built solenoidal coils (3.2 mm long, 12 turns of wire) wrapped around the flow cells as shown in Figure 1c. As described above, a set of 21 flow images were acquired with equal spacing in q-space, with a maximum strength of the flow-encoding gradient of 40 G/cm. To eliminate such effects as eddy currents and imperfections in the gradient waveforms, two sets of images were acquired–one with the flow on and the other with the flow off. The in-plane spatial resolution of the images was 15.6 µm × 15.6 µm with a slice thickness of 200 µm. The slices were oriented perpendicular to the long axis of the flow cell, at between 100- and 2000-µm distances from the reference positions shown in Figure 1. The total data acquisition time was 6 h. In this study, a flow rate of 5 µL/min was used, since this is a typical value used in cLC separations.11 For the flow cells used in the experiment, this flow rate corresponds to a residence time of ~6 s for an rf coil 2 mm in length, such as might typically be used for microseparations. Assuming a static line width of 1 Hz, the additional line-broadening introduced by flow, as described by eq 3, is negligible being only ~0.05 Hz.
RESULTS AND DISCUSSION
Simulated velocity fields for flow cells with different normalized transition lengths are shown in Figure 2. For Figure 2a and b, where the normalized transition lengths are 0 and 2, respectively, the short transition length results in a central high-velocity spike. Although decaying rapidly, this high-velocity spike, together with nearby regions with very low velocity, effectively produces regions of “dead flow” near the reentrant corners. In contrast, for the case of normalized transition lengths of 4 and 8, corresponding to Figure 2c and d, there is no high-velocity spike or indeed any regions of dead flow. The simulated velocity fields shown in Figure 2e correspond to the gradual flow cell used in the experimental studies, with a normalized transition length of 12: flow here is virtually laminar.
Figure 2.
Simulated velocity fields for flow cell geometries with different normalized transition lengths. (a–d) Normalized transition lengths of 0, 2, 4, and 8, respectively. (e) Normalized transition lengths of 12 used in the experimental studies. The velocities are represented as vectors, with both magnitude and direction indicated by the arrows.
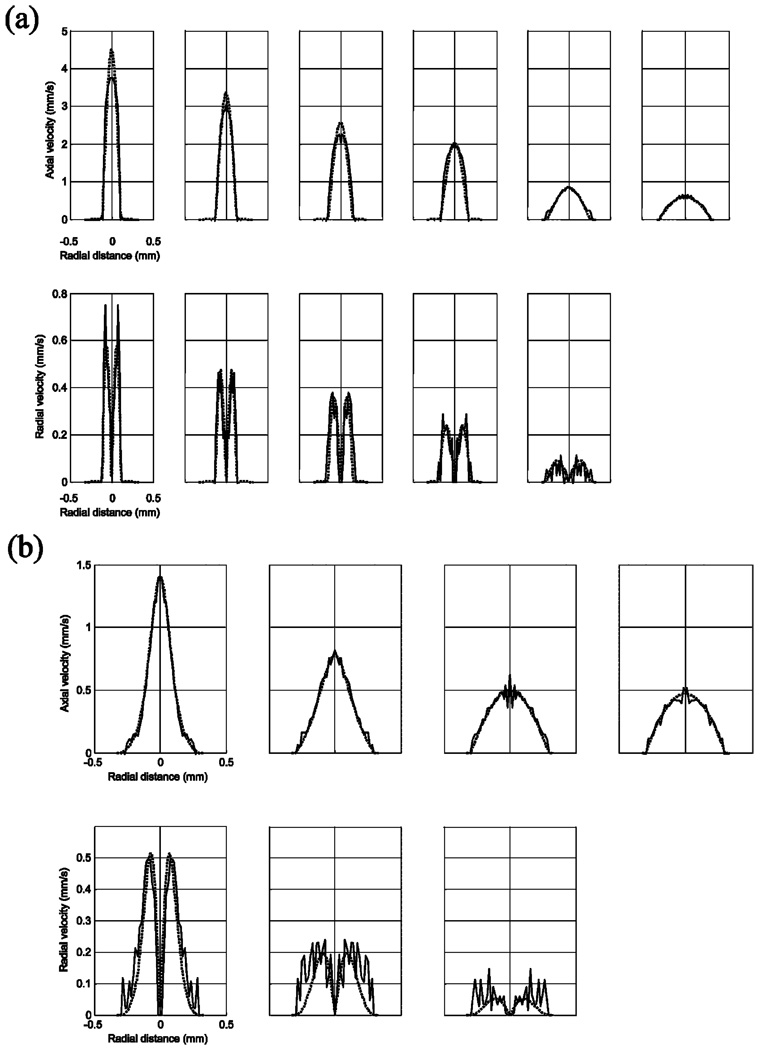
Figure 3 shows results from the MR microimaging experiments of the axial and radial velocities inside each of the two flow cells as a function of distance along the flow cell and the corresponding simulation results. Cross-sectional magnitude plots of the same set of data are shown in Figure 4. Due to the azimuthal symmetry of the flow, the velocity field is azimuthally “average- and-replicated”21 in order to increase the signal-to-noise ratio of the measurements: thus, the exact symmetrical nature of the experimental results is artificial. Simulations were performed at the point corresponding to the center of the imaging slice. The axial flow profile inside the gradual flow cell, shown in Figure 3a and Figure 4a, resembles fully developed laminar flow much more than the flow profile inside the abrupt flow cell, shown in Figure 3b and Figure 4b. This demonstrates that the gradual flow cell has a more homogeneous velocity field, i.e., less disturbance to the flow, than the abrupt one. Comparing Figure 4a and b, the ratio of axial to radial velocities for the gradual flow cell is much larger than that of the abrupt flow cell: this indicates the flow inside the former is less divergent than the latter. Figure 4a shows that the experimental velocity measurements are slightly below the simulated values, whereas the radial values are slightly higher. This is a result of “velocity averaging” over the relatively thick slice required for the experiments. For the abrupt transition flow cell, these effects were not seen, and there is excellent agreement between simulation and experiment. For the flow cell with abrupt transitions, simulations also indicated that there were regions with weak recirculation existing near reentrant corners at the inlet and the outlet. However, such weak recirculation was more than 3 orders of magnitude smaller than the velocity at the center of the slice, which was beyond the accuracy of the MR flow imaging (see Results and Discussion).
Figure 3.
Comparison of measured and simulated velocity fields of the two flow cells. (a) shows 2D velocity maps in the gradual flow cell and (b) maps in the abrupt flow cell. In (a), each column from the left to the right are slices centered at 100, 200, 300, 400, 600, and 2000 microns from the reference position shown in Figure 1a, as indicated by the gray bars. In (b), columns from the left to the right are slices centered at 100, 200, 300, and 500 microns from the reference position shown in Figure 1b.
Figure 4.
Cross-sectional magnitude plots of the measured and the simulated velocity fields of (a) the gradual and (b) the abrupt flow cell for the data shown in Figure 3. The thin lines are experimental data, and the thick lines are simulated. No data are shown for the case where the radial velocity map was below the noise level.
Simulation and measurement (data not shown) also suggested that the flow pattern was insensitive to flow rates within a practical range of interest (5–50 µL/min) due to the small Reynolds numbers involved. For example, at a flow rate of 5 µL/min, the maximum velocity at the center of the gradual flow cell was 0.6 mm/s, which corresponds to a Reynolds number of 0.35.
The experimental results obtained using q-space MR micro-imaging agree well with the simulations, as shown in Figure 3 and Figure 4, showing the utility of the technique, even for the very small size dimensions required in this study. A number of other researchers have investigated fluid flow in systems geometrically similar to that presented here. Xia et al.21 used PGSE to study fluid flow through a rapid contraction (from 2.9 to 1.8 mm) and, by inverting the direction of flow, a rapid expansion. Moser et al.32 studied flow through a model of stenosis with a ~9.5-mm narrow cylinder representing a step function for fluid flowing via a 19.05-mm-diameter cylinder. Han et al.33 studied flow inside a pipe, whose diameter decreased smoothly from 5.1 to 3.5 mm over a distance of 11 mm. In all cases, the characteristic radial dimension of the flow structures was of the order of millimeters, with a relatively moderate change of radius. In this work, flow imaging was conducted at a much smaller scale: the diameter of the capillary changes from 75 to 600 µm over a distance of 1 mm for the gradual-transition flow cell. This represents a change in diameter of a factor of 8, which corresponds to a change of average flow velocities of a factor of 64. In addition, this work shows that MR microimaging of velocity fields can be performed in very small samples at very high spatial resolution, in this case, in-plane resolution of 15 × 15 µm.
As with all techniques, it should be noted that there are a number of intrinsic limitations to velocity measurement using MRI. First, the “velocity resolution” is limited by the finite number of q-space images acquired and also by the Nyquist criterion in the velocity dimension, requiring that phase shifts produced by the fastest and slowest flows not differ by more than 2π rad/gradient increment. A potential source of error in estimating velocities is phase accumulation due to acceleration, which is not accounted for in these experiments, although it can potentially either be measured using MRI29 or compensated for by using suitable second-moment nulling gradient waveforms.30 A positive acceleration makes the apparent velocity larger than its actual value, and the error due to acceleration can be significant if the flow rate is high. The finite slice thickness is one of the most important sources of error due to the small dimensions of the flow cells. As seen in Figure 2c and d, the flow pattern almost returns to a fully developed laminar flow ~500 µm from the start of the transition zone of the tapered flow cell. Therefore, given that the slice thickness used in these experiments was 200 µm, considerable velocity averaging occurs. The thickness of the slice was limited by the S/N of the image, particularly at high q-values. As shown by Wassenius and Callaghan,31 the velocity determination error (δv) is given by
| (9) |
where A/δP is the S/N of the measurement of P̄s(z,Δ). Finally, there is a potential error due to misalignment of the flow cell and the gradient coordinate system. From measurements it was estimated that any rotation of the flow cell with respect to the gradient coordinate system was ~1°. Given that the magnitude of axial velocity is far greater than radial velocity, such a small misalignment has little impact on the accuracy of axial velocity field. However, for the radial velocity field, it would result in a larger systematic error. In practice, however, since the measured velocities are averaged azimuthally, such an error is much less than the lower limit of the velocity measurement accuracy.
One of the disadvantages of the MR velocity measurements is the long data acquisition time. However, it has been shown that, with appropriate imaging sequences and data processing, and assuming cylindrical symmetry in the flow patterns, the two-dimensional imaging process can be reduced to that of acquiring one-dimensional projections.34,35 This type of technique could potentially be used either to decrease the data acquisition time or to acquire full three-dimensional velocity maps with much thinner slice thicknesses than presented here.
In conclusion, the results obtained show good agreement between MR microimaging experiments and computational fluid dynamics simulations and demonstrate that a relatively gradual expansion and contraction is necessary in flow cells to avoid areas of weak recirculation and strong radial velocities, both of which can potentially compromise separation efficiency.
ACKNOWLEDGMENT
This work was supported by National Institutes of Health (R01 EB02343), an N.S.F. CAREER award (DBI 97-22320), and the Alexander von Humboldt Foundation.
References
- 1.Vissers JP. J. Chromatogr., A. 1999;856:117–143. doi: 10.1016/s0021-9673(99)00692-5. [DOI] [PubMed] [Google Scholar]
- 2.Altria KD, Elder D. J Chromatogr., A. 2004;1023:1–14. doi: 10.1016/j.chroma.2003.10.054. [DOI] [PubMed] [Google Scholar]
- 3.Feltink S, Rozing GP, Kok WT. Electrophoresis. 2003;24:3935–3961. doi: 10.1002/elps.200305638. [DOI] [PubMed] [Google Scholar]
- 4.Albert K, editor. On-line LC-NMR and Related Techniques. Chichester, NY: Wiley; 2002. [Google Scholar]
- 5.Jayawickrama DA, Sweedler JV. J. Chromatogr., A. 2003;1000:819–840. doi: 10.1016/s0021-9673(03)00447-3. [DOI] [PubMed] [Google Scholar]
- 6.Pusecker K, Schewitz J, Gfrorer P, Tseng L-H, Albert K, Bayer E. Anal. Chem. 1998;70:3280–3285. doi: 10.1021/ac980063o. [DOI] [PubMed] [Google Scholar]
- 7.Lacey ME, Tan ZJ, Webb AG, Sweedler JV. J. Chromatogr., A. 2001;922:139–149. doi: 10.1016/s0021-9673(01)00912-8. [DOI] [PubMed] [Google Scholar]
- 8.Gfrorer P, Tseng L-H, Rapp E, Albert K, Bayer E. Anal. Chem. 2001;73:3234–3239. doi: 10.1021/ac0100392. [DOI] [PubMed] [Google Scholar]
- 9.Kautz RA, Lacey ME, Wolters AM, Foret F, Webb AG, Kargar BL, Sweedler JV. J. Am. Chem. Soc. 2001;123:3159–3160. doi: 10.1021/ja005537r. [DOI] [PubMed] [Google Scholar]
- 10.Wolters AM, Jayawickrama DA, Larive CK, Sweedler JV. Anal. Chem. 2002;74:2306–2313. doi: 10.1021/ac015744p. [DOI] [PubMed] [Google Scholar]
- 11.Krucker M, Lienau A, Putzbach K, Grynbaum MD, Schuler P, Albert K. Anal. Chem. 2004;76:2623–2628. doi: 10.1021/ac030379i. [DOI] [PubMed] [Google Scholar]
- 12.Jayawickrama DA, Sweedler JV. Anal. Bioanal. Chem. 2004;378:1528–1535. doi: 10.1007/s00216-003-2421-0. [DOI] [PubMed] [Google Scholar]
- 13.Sylvester ND, Rosen SL. AIChE J. 1970;16:964–972. [Google Scholar]
- 14.Vrentas SR, Duda JL. Appl. Sci. Res. 1973;28:241–260. [Google Scholar]
- 15.Sisavath S, Jing X, Pain CC, Zimmerman RW. J. Fluids Eng. 2002;124:273–278. [Google Scholar]
- 16.Laude D, Wilkins C. Anal. Chem. 1984;56:2471–2475. doi: 10.1021/ac00271a025. [DOI] [PubMed] [Google Scholar]
- 17.White F. Viscous fluid flow. New York: McGraw-Hill; 1991. [Google Scholar]
- 18.Wang CY. Annu. Rev. Fluid Mech. 1991;23:159–177. [Google Scholar]
- 19.Roache P. Computational fluid dynamics. Albuquerque, NM: Hermosa Publishers; 1972. [Google Scholar]
- 20.Takemitsu NJ. Comput. Phys. 1985;61:499–518. [Google Scholar]
- 21.Xia Y, Callaghan PT, Jeffrey K. AIChE J. 1992;38:1408–1420. [Google Scholar]
- 22.Haake EM, Brown RW, Thompson MR, Venkatesan R. Magnetic Resonance Imaging. New York: John Wiley; 1999. Chapter 24. [Google Scholar]
- 23.Callaghan PT. Rep. Prog. Phys. 1999;62:599–670. [Google Scholar]
- 24.Fukushima E. Annu. Rev. Fluid. Mech. 1999;31:95–123. [Google Scholar]
- 25.Callaghan PT, Eccles CD, Xia Y. J. Phys. E. 1998;21:820–822. [Google Scholar]
- 26.Callaghan PT, MacGowan D, Packer KJ, Zelaya FO. J. Magn. Reson. 1990;90:177–182. [Google Scholar]
- 27.Callaghan PT, Xia Y. J. Magn. Reson. 1991;91:326–352. [Google Scholar]
- 28.Stejskal EO, Tanner JE. J. Chem. Phys. 1965;42:288–292. [Google Scholar]
- 29.Li T-Q, Ödberg L, Powell RL, McCarthy MJ. J. Magn. Reson. Ser. B. 1995;109:213–217. [Google Scholar]
- 30.Pipe JG, Chenevert TL. Magn. Reson. Med. 1991;19:175–179. doi: 10.1002/mrm.1910190116. [DOI] [PubMed] [Google Scholar]
- 31.Wassenius H, Callaghan PT. J. Magn. Reson. 2004;169:250–256. doi: 10.1016/j.jmr.2004.05.005. [DOI] [PubMed] [Google Scholar]
- 32.Moser KW, Kutter EC, Georgiadis JG, Buckius RO, Morris HD, Torczynski JR. Exp. Fluids. 2000;29:438–447. [Google Scholar]
- 33.Han S, Stapf S, Blümich B. J. Magn. Reson. 2000;146:169–180. doi: 10.1006/jmre.2000.2145. [DOI] [PubMed] [Google Scholar]
- 34.Gibbs SJ, Haycock DE, Frith WJ, Ablett S, Hall LD. J. Magn. Reson. 1997;125:43–51. doi: 10.1006/jmre.1996.1084. [DOI] [PubMed] [Google Scholar]
- 35.Hanlon AD, Gibbs SJ, Hall LD, Haycock DE, Frith WJ, Ablett S. Magn. Reson. Imaging. 1998;16:953–961. doi: 10.1016/s0730-725x(98)00089-7. [DOI] [PubMed] [Google Scholar]