Estimating Cerebral Blood Volume with Expanded Vascular Space Occupancy Slice Coverage

Abstract

A model for quantifying cerebral blood volume (CBV) based on the vascular space occupancy (VASO) technique and varying the extent of blood nulling yielding task-related signal changes with various amounts of blood oxygenation level-dependent (BOLD) and VASO weightings was previously described. Challenges associated with VASO include limited slice coverage and the confounding inflow of fresh blood. In this work, an approach that extends the previous model to multiple slices and accounts for the inflow effect is described and applied to data from a multi-echo sequence simultaneously acquiring VASO, cerebral blood flow (CBF) and BOLD images. This method led to CBV values (7.9 ± 0.3 and 5.6 ± 0.3 mL blood/100 mL brain during activation and rest, respectively) consistent with previous studies using similar visual stimuli. Furthermore, an increase in effective blood relaxation (0.65 ± 0.01) compared to the published value (0.62) was detected, likely reflecting inflow of fresh blood. Finally, CMRO₂ estimates using a multiple compartment model without assumption of CBV_REST led to estimates (18.7 ± 17.0 %) that were within published ranges.

Introduction

Blood oxygenation level-dependent (BOLD) contrast based functional MRI (fMRI) has been the most widely used functional neuroimaging method for the last 15 years. Despite its wide utilization, there are two important limitations related to the BOLD contrast. First, the contrast is dependent on a combination of physiological parameters, including cerebral blood flow (CBF), cerebral blood volume (CBV) and cerebral metabolic rate of oxygen (CMRO₂) and therefore produces relative, not absolute, measures that vary longitudinally for reasons outside the realm of neuronal activity dynamics (1). Second, the magnitude of the signal change is largely dependent on brain vasculature because the BOLD signal originates from the venous concentration of deoxyhemoglobin (2). Therefore, the localization of “activation” is aligned more with draining veins than neurons. Furthermore, the regional magnetic effect of deoxyhemoglobin exaggerates spatial extent of the measured contrast because it produces a bulk susceptibility difference between the vessels and surrounding tissue so image voxels in extravascular space also exhibit the BOLD contrast. While this susceptibility enhances BOLD sensitivity (a main reason for BOLD's ease of utilization), spatial localization is not as specific as methods based on other types of contrast such as CBF and CBV (2).

The low longitudinal consistency and spatial specificity of the BOLD contrast have motivated the development of noninvasive measures of CBF and CBV. While initial MRI methods for CBF imaging relied on contrast agents (3), arterial spin labeling (ASL) enables absolute CBF measurement without any exogenous agents by using magnetically labeled arterial blood water as an endogenous tracer (4-10). Similarly, a recent technique was introduced to image CBV by measuring the extravascular water signal without the use of contrast agents. This technique detects changes in vascular space occupancy (VASO) by acquiring images when the blood signal is selectively nulled (11). While the original VASO technique provides CBV-weighted signal changes between rest and activation states, it relies on the assumption of absolute CBV for quantification. More recently, one group developed a biophysical model allowing for decomposition of BOLD and CBV weighting enabling CBV quantification by varying the extent of blood nulling. (12) However, this approach does not account for the inflow of fresh blood spins that are not nulled, confounding the steady-state magnetization and in turn, the VASO contrast (13). Furthermore, this model has only been applied to single slice acquisition.

The present model extends this approach to multiple slices and accounts for inflow effects. Furthermore, the application of this model to data from a multi-echo sequence simultaneously acquiring VASO, CBF and BOLD enables CMRO₂ estimation. Many studies estimating CMRO₂ use a single-compartment model, calibrating the BOLD-CBF relationship with induced hypercapnia (14-17) and deriving ΔCBV from ΔCBF based Grubb's relationship using PET (18). However, this assumption may not be accurate across brain regions and species, especially in pathological conditions. To avoid the potential errors arising from using Grubb's relationship, Lu et al. introduced a multi-compartment method, separating the BOLD signal into intravascular and extravascular components, that included VASO measurement (19). Specifically, they acquired CBF, BOLD and VASO images with separate sequences, assuming stimulus-induced changes in the visual cortex were constant across scans. Relative ΔCBV is estimated from CBV-weighted changes, or ΔVASO, by assuming a resting state blood volume fraction. This introduces some uncertainty as CBV_REST could vary between brain regions and subjects and CMRO₂ estimation could be confounded by the use of separate scans for each contrast. A recent study utilizes this model in combination with simultaneous acquisition, also assuming CBV_REST to derive ΔCBV from traditional VASO measurements (20).

While these models have provided viable methods for estimating CMRO₂ in the healthy population, the assumptions of CBV-CBF relationship or absolute CBV_REST makes their application to patient and/or elderly population difficult. One study incorporated explicit CBV measurement by complementing fMRI with diffuse optical imaging (DOI) to better define the subject-specific relationship between CBF and CBV. However, DOI requires the assumption of baseline hemoglobin concentrations from published literature for quantification, has low spatial resolution and may reflect responses from different volumes of tissue relative to MR observations (21). It is therefore desirable to have an entirely MR-based approach for estimating CMRO₂ without assuming CBF-related CBV dynamics or absolute CBV_REST. For this reason, the current method's ability to noninvasively quantify CBV during simultaneous BOLD and CBF acquisition can enhance CMRO₂ estimation, particularly in patient populations where the CBV-CBF relationship is unknown.

The current work seeks two main objectives in this context by extending a previous modeling approach (12). First, quantification of CBV_REST and CBV_ACT is extended beyond a single slice and in conjunction with simultaneous VASO, CBF and BOLD acquisition (22). Second, this approach accounts for the inflow of fresh blood by modeling the effective R_1,BLOOD, addressing the confound of VASO-based CBV quantification. Finally, CMRO₂ is estimated using a multi-compartment model (19) without the assuming CBV_REST.

Materials and Methods

A total of four normally sighted males (age 23-36) participated in this study. Written consent was acquired for all subjects and all experiments were approved by Emory University's Internal Review Board.

Modified Biophysical Model

The previous CBV quantification model acquires VASO images at multiple inversion times (TI), the time between inversion and transverse excitation, to provide varied CBV and BOLD weightings (12). In their study, Gu et al. used the singular VASO sequence (11) and applied a biophysical model to data from 14 different TIs to quantify CBV_REST and CBV_ACT. Once the relative signal changes, ΔS/S = (S_ACTIVATION - S_REST)/ S_REST, are calculated for each TI, Gu et al. employed two steps of data fitting to the model to obtain four unknown parameters: fraction of cerebral-spinal fluid (F_CSF), CBV_REST, CBV_ACT and average blood oxygenation during activation (Y_B,ACT). For the first step, an admissible range of F_CSF was determined by focusing on the two TI values to either side of the blood nulling point. In this step, CBV_REST, CBV_ACT and Y_B,ACT were assumed to locate an admissible range of F_CSF. The second step is a three-parameter non-linear fitting using a Levenberg–Marquardt algorithm applied to the remaining TI values to obtain CBV_REST, CBV_ACT and Y_B,ACT for each of these F_CSF values selecting the parameters resulting in minimal residual errors (12).

The present work builds upon this model by quantifying CBV during simultaneous acquisition of VASO, CBF and BOLD, leveraging the varying TIs required for the model to expand to multiple slice coverage and modeling the inflow of fresh blood spins. The main difference between the standard VASO and multi-echo sequences in the context of quantifying CBV involves the difference in longitudinal steady state magnetization. With the singular VASO sequence, the signal dependence on longitudinal relaxation rate (R1) can be calculated as follows:

$$M(TI)=1-2\cdot e^{(-TI\cdot R_1)}+e^{-R_1(TR)}$$ [1]

where TR is the repetition time and TI is the inversion time (22). With two excitations in the sequence used in this study (Fig. 1), one must consider the second inversion time (TI₂), or the time between inversion and the second excitation, when calculating this signal dependence:

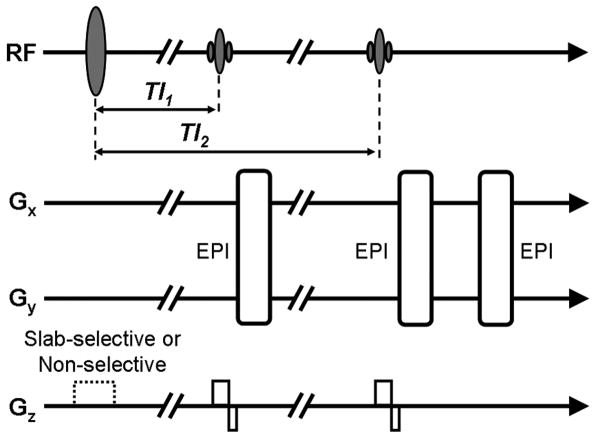
Figure 1.

Multi-echo sequence acquires VASO image from first excitation and ASL and BOLD images from second excitation. (Sequence from (22))

$$M({\mathit{\text{TI}}}_1)=1-2\cdot e^{(-{\mathit{\text{TI}}}_1\cdot R_1)}+e^{-R_1(TR+{\mathit{\text{TI}}}_2-{\mathit{\text{TI}}}_1)}$$ [2]

However, steady state magnetization for either the singular VASO or multi-echo sequence is confounded by the inflow of fresh blood. To account for this, R_1,BLOOD is assumed to be a variable that is determined by experimental data (as well as CBV_REST, CBV_ACT, F_CSF and Y_B,ACT). Using an ROI of suprathreshold VASO voxels, an exhaustive search of these parameters minimized the sum of squares of the difference between empirical and simulated ranges of ΔS/S. As with the previous model, the two data points on either side of the zero-crossing were omitted because they are mainly sensitive to CSF as opposed to CBV.

The biophysical model was separately applied to each slice and averaged over the ROIs in all the slices to yield estimates for each subject's active 3-dimensional ROI. By fitting the data for CBV_REST, CBV_ACT, F_CSF, Y_B,ACT and R_1,BLOOD, CBV quantification can be more accurately estimated for several slices and utilized for CMRO₂ modeling.

MRI Experiments

All data were acquired on a Siemens 3T Tim Trio scanner (Siemens Medical Solutions, Malvern, PA) with a multi-echo sequence utilizing an inversion recovery sequence with two excitations (2 sec TR, 11/11/33 ms TE for VASO/CBF/BOLD, 250 mm FOV, 75% k-space coverage, 3.9 × 3.9 mm in plane resolution for five ascending 5 mm thick slices) for a total scanning time of approximately 21 minutes. (22). As shown in Fig. 1, spins are inverted by a 180° pulse before excitation and VASO acquisition. A second excitation pulse prepares for two additional gradient echo images, CBF (short TE) and BOLD (long TE). The interleaved slab-selective/non-selective gradient is used for labeled/control CBF images, respectively. For VASO imaging, a relatively thick slab (>100 mm) for the selective gradient is required to minimize the inflow of uninverted spins. On the other hand, excessive slab thickness could reduce perfusion signal due to the reduced amount of labeled spins. CBF and VASO contrasts are balanced based on empirical comparisons of acquisitions at slab inversion thickness of 500, 150, 125, 100 and 50 mm (22) which demonstrated that a slab thickness of 125 mm provided the best balance of CBF and VASO contrasts.

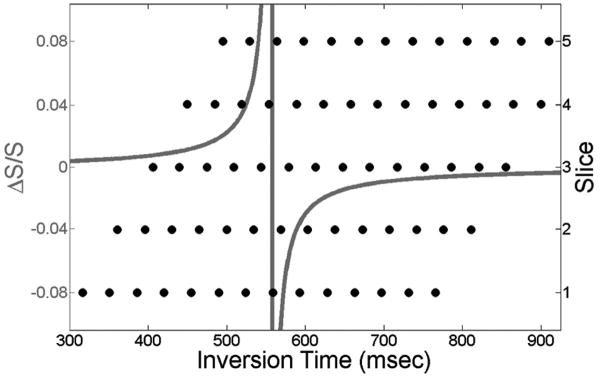
For traditional VASO acquisition, the delay between the inversion pulse and the first excitation pulse (TI₁) is selected at the blood nulling point to yield a minimized signal from voxels containing blood. As indicated above, the present study instead collects 14 scans with different TI₁ values to vary the level of blood nulling. (12) This strategy, which allows for an increase in slice coverage relative to traditional VASO experiments, yields a different set of TI₁ values for each slice, but each sufficiently covers the range of blood nulling required to apply the biophysical model (Fig. 2). The time between the 180° inversion and the second excitation pulse (TI₂) is also slightly different for each slice, but the model accounts for this difference.

Figure 2.

Simulated ΔS/S for range of TI₁ (gray) and TI₁ coverage for slices 1-5 (black).

Visual Stimulation

Visual stimuli were delivered using a back-projection system (40 degree viewing angle), where a projection screen is installed behind the subject's head while a mirror mounted on a head coil reflects the screen to the subject. A projector equipped with a long throw replacement lens displayed computer input on an in-bore screen. Visual paradigms were programmed in Presentation™ (www.neuro-bs.com), while a serial response box (Current Designs™, www.curdes.com) was used for synchronization with the MR scanner. For each TI, stimulus consisted of 24 seconds of fixation on a cross followed by 48 seconds of a flashing checkerboard (8 radial degrees of the visual field) with reversing contrast at 8 Hz and ended with another 20 seconds of fixation.

Data Processing

VASO, CBF and BOLD data were preprocessed and statistically analyzed using SPM2 (Wellcome Department, University College of London, UK). All raw data were corrected for motion before adding (VASO and BOLD) or subtracting (CBF) control and label images. Subtracted images were quantified using the following equation (23):

$$\mathit{\text{CBF}}=\frac{\lambda \mathrm{\Delta }{\mathit{\text{CBF}}}_{\mathit{\text{weighted}}}}{2\alpha M_0\tau e^{-({\mathit{\text{TI}}}_2/T_{1a})}}$$ [3]

where T_1a is the longitudinal relaxation time of blood and τ (700 ms) and TI₂ (1000 ms) are the labeling duration and image acquisition time, respectively. Prior to statistical analysis, CBF and VASO data were spatially smoothed with a 6 mm kernel to improve signal-to-noise. Data from all 14 scans were used for BOLD analysis but data from only the first 5 scans were used for CBF analysis. This is because when the time between VASO/ASL selective inversion and VASO excitation approaches 700 ms, uninverted blood, critical for ASL contrast, could reach the imaging region and be affected by the VASO excitation pulse. VASO data from each scan (corresponding to each TI₁) were separately analyzed, generating fourteen t-maps with varied BOLD/VASO weighting (positive/negative correlation to task). These individual maps were combined using multiple dataset analysis (12,24) by utilizing the inverse normal cumulative distribution function (Φ) and p-values (P_i) corresponding to test statistics for each voxel from each scan. Specifically, maps from each TI₁ were thresholded using absolute value (due to TI₁-dependent BOLD/VASO weighting) of the t-statistic corresponding to p<0.05 before applying

$$T_C=\sum _{i=1}^N\frac{{\phi }^{-1}(1-P_i)}{\sqrt{N}}$$ [4]

where T_c is the cumulative statistic and N is the number of individual activation maps included in the calculation. Voxels with a T_c larger than 5 and contiguous cluster size of at least 8 voxels were considered active for the VASO contrast at multiple TI₁ values. All maps were masked with SNR threshold of 5 derived from VASO data collected at the blood nulling point to exclude large vessel effects (25).

Assessment of Fitting Accuracy

Fitting results and quality were assessed by comparing the results of the original model (12) which assumes R_1,BLOOD to be 0.62 and our revised model which assumes R_1,BLOOD to a fitting parameter. The inclusion of this additional parameter reduces degrees of freedom. Models were tested for statistical difference by comparing the residual variance of their fits using the “extra sum-of-squares” principle (26):

$$F=\frac{{\mathit{\text{SS}}}_1-{\mathit{\text{SS}}}_2}{({\mathit{\text{df}}}_1-{\mathit{\text{df}}}_2)(SS2/{\mathit{\text{df}}}_2)}$$ [5]

where SS₁ and SS₂ are the sum of squares with degrees of freedom df₁ and df₂ for the current and original models, respectively. The F-ratio is used to assess the decrease in sum-of-squared error relative to decrease in degrees of freedom for the more complex model.

Assessment of CBF – CBV Relationship

As described above, many experiments estimate CMRO₂ by deriving stimulus-related CBV and CBF changes with the following equation (18):

$$\frac{\mathit{\text{CBV}}}{{\mathit{\text{CBV}}}_0}={\left(\frac{\mathit{\text{CBF}}}{{\mathit{\text{CBF}}}_0}\right)}^{\alpha }$$ [6]

where α is assumed to be 0.38. We evaluated this relationship empirically by calculating α with relative CBV changes derived from the model and simultaneously acquired relative CBF changes.

Estimation of CMRO₂

The multi-compartment model does not rely on calibration or parameter assumption by utilizing CBV to calculate OEF en route to CMRO₂ estimation (19). First, this model separates microvasculature into two compartments, arteriolar (a, 30%) and venular (v, 70%). The BOLD signal is therefore described with the equation

$$S\sim \underset{\mathit{\text{arteriolar}}\mathit{(}a\mathit{)}}{0.3\cdot x\cdot M_a{e}^{-R_{2a}^{\ast }TE}}+\underset{\mathit{\text{venular}}\mathit{(}v\mathit{)}}{0.7\cdot x\cdot M_a{e}^{-R_{2v}^{\ast }TE}}+\underset{\mathit{\text{tissue}}\mathit{(}t\mathit{)}}{(1-x)\cdot M_t{e}^{-R_{2t}^{\ast }TE}}$$ [7]

where S denotes BOLD signal, x is the water fraction of the blood in the voxel, and M_i and R_2i* (i=a,v,t) describe magnetization and transverse relaxation, respectively. Upon neuronal activation, the BOLD signal change can be characterized as follows:

$$\frac{\mathrm{\Delta }S}{S}=\frac{0.3\cdot (\mathrm{\Delta }x)\cdot M_a{e}^{-R_{2a}^{\ast ,\mathit{\text{rest}}}TE}+0.7\cdot M_v(x^{\mathit{\text{act}}}\cdot e^{-R_{2v}^{\ast ,\mathit{\text{act}}}TE}-x^{\mathit{\text{rest}}}\cdot e^{-R_{2v}^{\ast ,\mathit{\text{rest}}}TE})+M_t{e}^{-R_{2t}^{\ast ,\mathit{\text{rest}}}TE}[e^{-\mathrm{\Delta }{R}_{2t}^{\ast }TE}(1-x^{\mathit{\text{act}}})-(1-x^{\mathit{\text{rest}}})]}{0.3\cdot x^{\mathit{\text{rest}}}\cdot M_a{e}^{-R_{2a}^{\ast ,\mathit{\text{rest}}}TE}+0.7\cdot x^{\mathit{\text{rest}}}\cdot M_a{e}^{-R_{2v}^{\ast ,\mathit{\text{rest}}}TE}+(1-x^{\mathit{\text{rest}}})\cdot M_t{e}^{-R_{2t}^{\ast ,\mathit{\text{rest}}}TE}}$$ [8]

In this equation, Δx, the stimulus-induced change in water fraction of blood, is typically obtained from the VASO signal and assumed CBV_REST (19,20) as follows:

$$\mathrm{\Delta }x=x^{\mathit{\text{act}}}-x^{\mathit{\text{rest}}}=\left(\frac{C_{\mathit{\text{par}}}-{\mathit{\text{CBV}}}_{\mathit{\text{REST}}}{C}_{\mathit{\text{blood}}}}{C_{\mathit{\text{par}}}}\right)\cdot \frac{\mathrm{\Delta }\mathit{\text{VASO}}}{\mathit{\text{VASO}}}$$ [9]

where C_par=0.89 and C_blood=0.87, the water contents in mL water/ mL substance for parenchyma and blood, respectively, and relating CBV and VASO changes with the following equation (19,20):

$$\frac{\mathrm{\Delta }\mathit{\text{CBV}}}{\mathit{\text{CBV}}}=-\left(\frac{C_{\mathit{\text{par}}}}{C_{\mathit{\text{blood}}}{\mathit{\text{CBV}}}_{\mathit{\text{REST}}}}-1\right)\cdot \frac{\mathrm{\Delta }\mathit{\text{VASO}}}{\mathit{\text{VASO}}}$$ [10]

In the present study, Δx was determined without VASO or assumption of CBV_REST using absolute CBV derived from experimental data. These parameters were also used to determine $R_{2t}^{\ast }$ as follows:

$$\mathrm{\Delta }{R}_{2t}^{\ast }=R_{2t}^{\ast ,\mathit{\text{act}}}-R_{2t}^{\ast ,\mathit{\text{rest}}}=0.7\cdot \gamma \cdot B_0\cdot \frac{4}{3}\pi \cdot \mathrm{\Delta }\chi \cdot \mathit{\text{Hct}}\cdot ({\mathit{\text{CBV}}}_{\mathit{\text{act}}}\cdot (1-Y_v^{\mathit{\text{act}}})-{\mathit{\text{CBV}}}_{\mathit{\text{rest}}}\cdot (1-Y_v^{\mathit{\text{rest}}}))$$ [11]

where Hct is the hematocrit fraction of blood in microvasculature (0.36), Δχ is the susceptibility difference between fully oxygenated and deoxygenated blood (0.2 ppm)(12), and B₀ is the strength of the magnetic field (3 Tesla).

Because $R_{2a}^{\ast }$ does not change during activation $(Y_a^{\mathit{\text{rest}}}=Y_a^{\mathit{\text{act}}})$, the only remaining unknown in Eq. 8 is R_2v*,^act (assuming Y_a =1 and Y_v^rest =.61) which can be determined by using the measured BOLD signal change, ΔS/S. This enabled calculation of Y_v^act using Eq. 11, followed by OEF calculation at both rest and activation using

$$(1-Y_v)=1-Y_a+\mathit{\text{OEF}}\cdot Y_a$$ [12]

and calculating the change in OEF during activation as follows:

$$\mathrm{\Delta }\mathit{\text{OEF}}=\left(\frac{Y_a-Y_V^{\mathit{\text{act}}}}{Y_a}-\frac{Y_a-Y_V^{\mathit{\text{rest}}}}{Y_a}\right)$$ [13]

Task-related change in OEF was normalized to baseline with

$$\frac{\mathrm{\Delta }\mathit{\text{OEF}}}{\mathit{\text{OEF}}}=\left(\frac{Y_V^{\mathit{\text{rest}}}-Y_V^{\mathit{\text{act}}}}{Y_a-Y_V^{\mathit{\text{rest}}}}\right)$$ [14]

and used in conjunction with normalized ΔCBF to estimate ΔCMRO₂ as follows (19):

$$\left(1+\frac{\mathrm{\Delta }\mathit{\text{OEF}}}{\mathit{\text{OEF}}}\right)\cdot \left(1+\frac{\mathrm{\Delta }\mathit{\text{CBF}}}{\mathit{\text{CBF}}}\right)=\left(1+\frac{\mathrm{\Delta }{\mathit{\text{CMRO}}}_2}{{\mathit{\text{CMRO}}}_2}\right)$$ [15]

Similarly, the single-compartment model (17) was adapted to include CBV measurement as follows:

$$M=\frac{\frac{\mathrm{\Delta }\mathit{\text{BOLD}}}{{\mathit{\text{BOLD}}}_0}}{1-\left(\frac{\mathit{\text{CBV}}}{{\mathit{\text{CBV}}}_0}\right){\left(\frac{{\mathit{\text{CMRO}}}_2}{{\mathit{\text{CMRO}}}_2{|}_0}\right)}^{\beta }{\left(\frac{\mathit{\text{CBF}}}{{\mathit{\text{CBF}}}_0}\right)}^{-\beta }}$$ [16]

where β is a constant reflecting the influence of deoxyhemoglobin concentration (1.5) and M is typically estimated by inducing hypercapnia (17,27) or hyperoxia (28). While our experiment did not induce hypercapnia, we used estimated ΔCMRO₂ from the multi-compartment model to solve for M in the single-compartment model.

Results

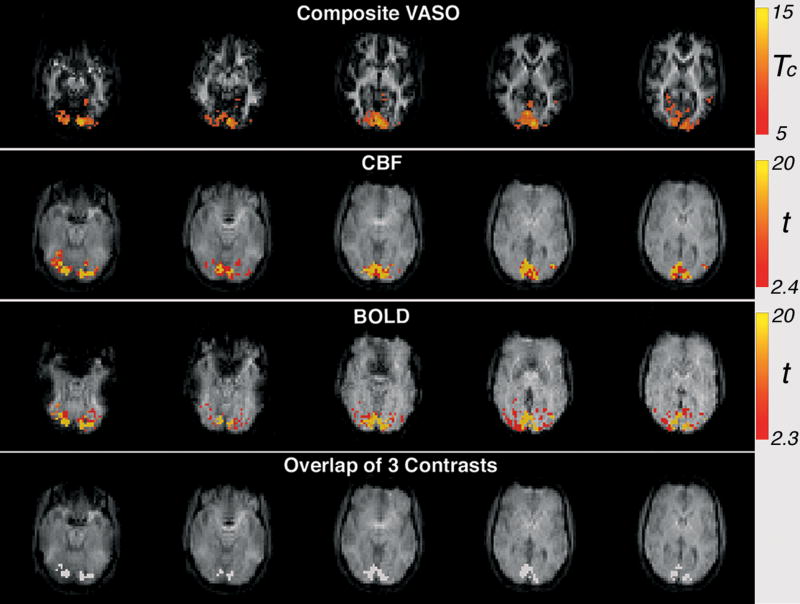
For all subjects, robust activation maps were derived from VASO, CBF and BOLD contrasts. As shown in Fig. 3, activation for each contrast demonstrated bilateral activation in the occipital lobe, consistent with the flashing checkerboard presented to both visual fields. As expected, BOLD activation was more extensive than CBF and VASO, which are known to have better spatial specificity (11,29). Although this study focuses on quantifying and expanding coverage of the VASO contrast, the ability to maintain CBF and BOLD contrast detection using this method is critical for estimating CMRO₂ (16,17).

Figure 3.

An example of brain activation for the composite VASO, CBF and BOLD contrasts (contiguous voxels > 8, T_c > 5 for VASO, p < 0.01 for BOLD and CBF), as well as overlap of all three contrasts (subject 3).

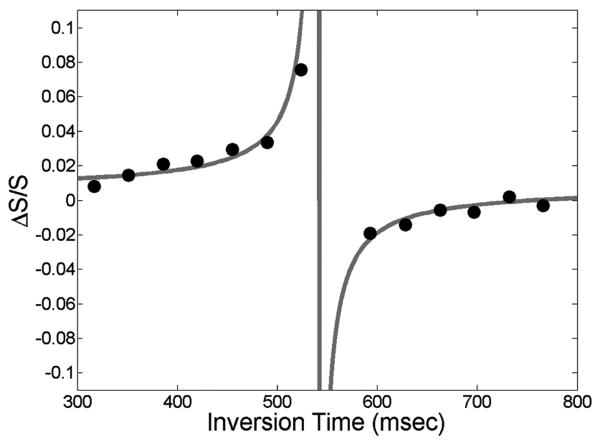
Modeling yielded close alignment of experimental and simulated ΔS/S, as demonstrated in Fig. 4. In addition to finding fits with low residuals, all estimated parameters were fairly consistent between subjects and within expected ranges (12). For instance, R_1,BLOOD was higher (0.65 ± 0.01) than the intrinsic blood R1 (0.62) (30) for all subjects, suggesting that the inflow of uninverted blood spins increase the effective relaxation rate (Table 1). Estimating CBV with R_1,BLOOD set to 0.62 yielded different results. Specifically, CBV_REST derived with fixed R_1,BLOOD differed from the corresponding values derived by our model by -4 to 7%, CBV_ACT by -12 to 4% and %ΔCBV by -4 to 18%. Relative to the original model, fitting with our model was significantly improved for the bottom slice, which is closest to blood inflow, across subjects (F-ratio = 3.9, p-value = 0.05). Across slices, fit for our model was significantly improved for subject 1 (F-ratio = 6.3, p-value = 0.02). While differences in other fits were not significant, our model consistently reduced sum-of-squared error.

Figure 4.

Simulated ΔS/S for range of TI₁ (gray) and experimental points (black).

Table 1. CBF, BOLD and model results for CBV_REST, CBV_ACT, %ΔCBV, Y_B,ACT and R_1,BLOOD.

Subject	CBFREST (mL blood / 100 mL brain / min)	CBFACT (mL blood / 100 mL brain / min)	ΔCBF	ΔBOLD	ΔCBV derived from ΔCBF	α (Based on ΔCBF and model ΔCBV)	CBVREST (mL blood / 100 mL brain)	CBVACT (mL blood / 100 mL brain)	ΔCBV derived from model	Yb,ACT	R1,BLOOD
1	63.1	119.4	89.2%	1.5%	27.4%	0.58	5.6	8.0	44.4%	0.772	0.64
2	36.2	79.3	119.1%	1.2%	34.7%	0.50	5.2	7.8	48.5%	0.748	0.66
3	75.5	159.7	111.5%	2.4%	32.9%	0.45	6.0	8.4	39.7%	0.745	0.63
4	41.8	81.7	95.7%	1.9%	29.1%	0.46	5.6	7.6	36.1%	0.745	0.64
Mean ± S.D.	54.1 ± 18.4	110.0 ± 37.9	103.9 ± 13.8%	1.7 ± 0.6%	31.0 ± 3.4%	0.50 ± 0.06	5.6 ± 0.3	7.9 ± 0.3	42.2 ± 5.4%	0.753 ± 0.013	0.65 ± 0.01

Using our model, absolute CBV values were 7.9 ± 0.3 and 5.6 ± 0.3 mL blood/100 g tissue for CBV_ACT and CBV_REST, respectively, and %ΔCBV was 42.2 ± 5.4 % (Table 1). Quantified CBF at rest and during activation were 54.1 ± 18.4 and 110.0 ± 37.9 mL blood/100 g tissue/min, respectively, and relative changes in CBF and BOLD were 103.9 ± 13.8 % and 1.7 ± 0.6 %, respectively. CBV changes derived from our method (42.4 ± 5.4%) are higher than those derived from CBF changes using Grubb's relationship (31.0 ± 3.4%) assuming an α of 0.38. This difference can be further probed by calculating α from the modeled CBV estimated measured CBF changes (α = 0.50 ± 0.06).

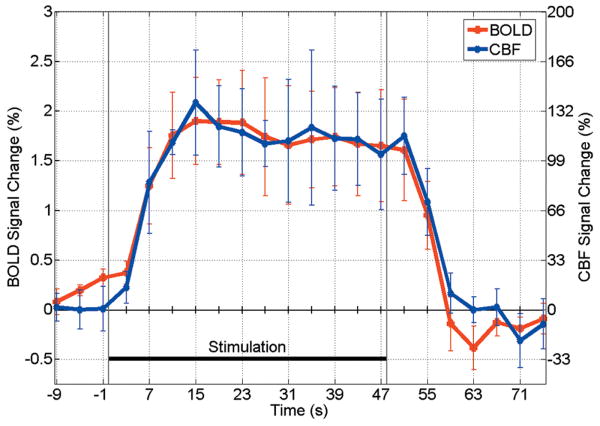
While our model yields a single CBV estimate for group of scans, CBF and BOLD changes are calculated at each time point (Fig.5). A distinct post-stimulus undershoot is evident in BOLD but not CBF, consistent with a previous study of fMRI signal dynamics with visual stimuli (19).

Figure 5.

Average time courses for BOLD and CBF (n=4).

The multi-compartment model led to CMRO₂ values shown in Table 2. The average change in CMRO₂ (18.7%) is consistent with literature values and variability is consistent with some prior studies (14). Interestingly, estimation of M using these CMRO₂ values in the single-compartment model yielded consistent values (M = 0.05 ± 0.006).

Table 2. Relative changes in CMRO₂ using the multi-compartment model and associated M values from the single-compartment model.

Subject	ΔCMRO2	M
1	16.9%	0.051
2	43.3%	0.057
3	6.8%	0.047
4	7.9%	0.043
Mean ± S.D.	18.7 ± 17.0	0.050 ± 0.006

Discussion and Conclusions

This work expands a previous model estimating CBV from VASO by acquiring multiple slices, incorporating simultaneous acquisition of VASO, CBF and BOLD, and accounting for inflow of blood by estimating effective R_1,BLOOD. The determination of longitudinal blood relaxation based on experimental data can improve accuracy of CBV quantification for the singular VASO sequence and is even more critical for the multi-echo sequence because a thinner inversion slab, important for CBF detection, is associated increased inflow of fresh blood spins.

In addition to the confounding effect of fresh blood inflow, our method addresses several challenges of the VASO technique including reliance on precise blood signal nulling, assumption of CBV_REST to estimate ΔCBV from ΔVASO and limited slice coverage. First, varying TI accounts for inexact blood nulling; in contrast to traditional VASO, the current method intentionally varies the extent of blood nulling so subject-specific TI is not required. Furthermore, the desire to vary TI enables multiple slices to be acquired. Second, by modeling CBV empirically, our method does not assume CBV_REST for the quantification of relative VASO changes. This avoids error related to inter-subject or inter-regional differences and also does not require the use of Grubb's relation.

One recent study utilized global saturation immediately after single slice acquisition to avoid the confounding effect of fresh blood inflow (31). This approach accounts for blood inflow, as the current approach does, but unlike the current method, still relies on assumed CBV_REST to estimate ΔCBV from VASO-related changes. Another study also relies on this assumption to quantify ΔCBV and estimate CMRO₂ (19). However, this study is also limited by single slice coverage and does not simultaneously acquire CBF and BOLD as the current study does. The study upon which the present method was based varies TI to avoid assumptions of CBV_REST, CBF-related changes in CBV and exact blood nulling TI (12). Our approach builds upon this method by expanding to multiple slices, incorporating simultaneous BOLD and CBF acquisition and accounting for the inflow of fresh blood spins. Finally, another method quantified CBV using VASO by acquiring images before and after contrast agent injection (32). This method is critically different because the present method is non-invasive.

To evaluate our method's ability to quantify CBV without assuming a direct relationship with CBF or absolute CBV_REST we compare our model results to previous findings. Our CBV estimates (∼7.9 and ∼5.6 mL blood/100 g tissue for CBV_ACT and CBV_REST, respectively) and %ΔCBV (∼42.2%) are slightly higher than the previous study (12) which assumed R_1,BLOOD for the model (∼6.6 and ∼5 mL blood/100 g tissue for CBV_ACT and CBV_REST, respectively, and ∼32.4 %ΔCBV). However, our CBV_REST estimates are very similar to previously measured values from PET (33) and fMRI (34) studies which both reported baseline CBV of approximately 5.5 mL blood / 100 mL tissue. When typical %ΔVASO (∼2.15% in (11)) is used with this value of CBV_REST, estimated CBV_ACT is in the range of our findings. Similarly, our estimated Y_B,ACT (∼0.753) is within one standard deviation of the original model (0.787 ± 0.059 in (12)). Furthermore, the inclusion of R_1,BLOOD improves fitting accuracy to a greater extent than it reduces degrees of freedom, revealing differences in CBV quantification and %ΔCBV. Fitting the data with our model significantly improved fitting for the bottom slice (across subjects) and subject 1 (across slices) demonstrating that some slices and subjects benefit more from our model. Furthermore, because the fitting was not degraded in any subjects or slices with our model, future studies can use our model to improve overall fit quality. Mean sum-of-squared error was lower for the first 3 slices (0.0005) than slices 4 and 5 (0.0009) due to TI ranges that were more balanced around the blood nulling point. Future studies can acquire 14 slices using a similar protocol (14 separate scans) each with a different slice order (scan 1: slice 1 first; scan 2: slice 2 first; etc.) to provide a balanced and consistent TI coverage with further expansion of slice coverage and empirical determination R_1,BLOOD.

While we attribute the higher R_1,BLOOD to the inflow of fresh blood resulting in an increase in effective R_1,BLOOD there are reasons inherent R_1,BLOOD could also be different. Typically, longitudinal blood relaxation is based on bovine blood matched for common human Hct levels which are typically 0.38 to 0.46 in humans (30,35). However, actual R_1,BLOOD is dependent on the exact Hct level which could vary between subjects. Modeling R_1,BLOOD is particularly useful when Hct levels are unknown in certain populations, as studies have found altered Hct in patients with cardiac disease (36) and hypertension (37). Furthermore, that study found temperature to affect relaxation times ∼20 ms/°C so scanner temperature can play a role in relaxation rates. Also, radiation damping can increase R_1,BLOOD which can be more problematic as fMRI experiments are conducted at higher fields. While dephasing could reduce the effect of damping (30), there still will be damping during the delay of the RF pulse and the spoiling gradient (38). For these reasons, it is difficult to compare R_1,BLOOD from our model to published values; uncertainly of longitudinal blood relaxation suggests that our model's empirical derivation of R_1,BLOOD is appropriate.

Quantified CBF at rest (∼54.1 mL blood/100 g tissue/min) was slightly lower than grey matter CBF in a similar experiment (∼66.4 and ∼67.2 mL blood/100 g tissue/min using multi-echo and traditional ASL in (22)) but similar to another fMRI study using a separate labeling coil (48 – 62 mL blood/100 g tissue/min in (39)) which has better SNR due to the absence of magnetization transfer. ROIs in our study contained some white matter voxels which have lower CBF (25.2 and 24.6 mL blood/100 g tissue/min using multi-echo and traditional ASL, respectively, in (22)), resulting in lower CBF_REST. Relative change in CBF in our study (∼110.0 %) was higher than the previous study (∼50-80 % for both multi-echo and traditional ASL in (22)). In addition to lower baseline CBF, higher %ΔCBF in our study could be attributed to a thinner inversion slab (125 mm) relative to the previous study (150 mm in (22)).

Assessing the CBF-CBV relationship, α was found to be 0.50 ± 0.06, while it is typically assumed a priori in other studies (0.38 in (18) or 0.50 in (40)). The consistency between the derived α with those measured or assumed in other studies validates our approach in situations where the assumed value may be inaccurate, such as in elderly or patient populations. CMRO₂ estimates (18.7 ± 17.0 %) were within the range and inter-subject variability of previous studies (6 to 47.7% in (14)). The ability to experimentally determine ΔCBV without assuming a CBF-CBV relationship could reduce uncertainty in CMRO₂ estimation. In addition, our model does not require assuming the value of CBV_REST. A more comprehensive comparison between CMRO₂ estimation methods with more subjects will be required to appropriately validate our method.

The present method enables quantitative VASO imaging with simultaneous CBF and BOLD image acquisition. This approach is less reliant on assumptions related to CBV quantification and accounts for the fresh inflow of uninverted blood. Future applications can involve more subjects to quantify CBV in conjunction with CBF and BOLD measurement to better understand CMRO₂ estimation accuracy.