Abstract
Ultrasound motion estimation is a fundamental component of clinical and research techniques that include color flow Doppler, spectral Doppler, radiation force imaging and ultrasound-based elasticity estimation. In each of these applications, motion estimates are corrupted by signal decorrelation that originates from nonuniform target motion across the acoustic beam. In this article, complex principal component filtering (PCF) is demonstrated as a filtering technique for dramatically reducing echo decorrelation in blood flow estimation and radiation force imaging. We present simulation results from a wide range of imaging conditions that illustrate a dramatic improvement over simple bandpass filtering in terms of overall echo decorrelation (≤99.9% reduction), root mean square error (≤97.3% reduction) and the standard deviation of displacement estimates (≤97.4% reduction). A radiation force imaging technique, termed sonorheometry, was applied to fresh whole blood during coagulation, and complex PCF operated on the returning echoes. Sonorheometry was specifically chosen as an example radiation force imaging technique in which echo decorrelation corrupts motion estimation. At 2 min after initiation of blood coagulation, the average echo correlation for sonorheometry improved from 0.996 to 0.9999, which corresponded to a 41.0% reduction in motion estimation variance as predicted by the Cramer-Rao lower bound under reasonable imaging conditions. We also applied complex PCF to improve blood velocity estimates from the left carotid artery of a healthy 23-year-old male. At the location of peak blood velocity, complex PCF improved the correlation of consecutive echo signals from an average correlation of 0.94 to 0.998. The improved echo correlation for both sonorheometry and blood flow estimation yielded motion estimates that exhibited more consistent responses with less noise. Complex PCF reduces speckle decorrelation and improves the performance of ultrasonic motion estimation.
Keywords: Acoustic radiation force imaging, Blood velocity estimation, Complex principal component filtering, Motion estimation, Time delay estimation
INTRODUCTION
Determining the relative motion between reference and shifted signals is a common procedure in application areas including radar, sonar, speech processing and medical imaging. Referred to as time delay estimation (TDE), this technique is also central to many medical ultrasound modalities. Notable motion estimation applications include blood flow estimation (Bohs et al. 1993; Bonnefous and Pesque 1986; Embree and O’Brien 1990; Jensen 1996; Kasai et al. 1985; Loupas et al. 1995), phase aberration correction (Flax and O’Donnell 1988; Ng et al. 1994; Nock and Trahey 1992; Sumino and Waag 1991), tissue elasticity estimation (O’Donnell et al. 1994; Ophir et al. 1991; Skovoroda et al. 1995) and acoustic radiation force imaging (Bercoff et al. 2004; Fatemi and Greenleaf 1999; Nightingale et al. 2002; Viola and Walker 2003; Viola et al. 2004; Walker et al. 2000). Because of its broad application, many algorithms for TDE have been devised. These methods aim to optimize accuracy, precision, computational efficiency, delay range and noise performance, among other criteria.
In general, TDE algorithms use pattern-matching functions to estimate the optimal delay between two or more discretely sampled signals (Giunta 1999; Jacovitti and Scarano 1993). Regardless of the particular pattern-matching function used, all TDE algorithms exhibit an intrinsic bias and variance. The bias of an estimator is defined as the difference between the expected value of that estimator and the true value of the variable that is being estimated. The estimator variance is a function of two types of errors: false peak errors and jitter errors. False peak errors occur at integer multiples of the signal periods and generally occur with low probability under reasonable imaging parameters and conditions. Because of the low probability that these errors will happen and because they are easily distinguishable, they may be readily identified and removed. In contrast, jitter errors are generally small in magnitude and represent a fundamental limit on performance for a given set of imaging parameters, signal-to-noise ratio (SNR) and signal correlation. For an unbiased estimator, the minimum achievable variance can be predicted theoretically using the Cramer-Rao lower bound, which was derived for medical ultrasound by Walker and Trahey (1995) after previous work by Carter (1987), as follows:
| (1) |
where Δt is the true time delay, Δ̂t is the estimated time delay, f0 is center frequency, T is kernel length, B is fractional bandwidth, ρ is signal correlation, and SNR is electronic signal-to-noise ratio. Equation (1) indicates that given a set of imaging parameters (f0, B and T), the performance of an unbiased TDE estimator is highly dependent on the signal correlation and electronic SNR.
Whereas both electronic noise and signal decorrelation degrade TDE performance, they result from different physical phenomena and generally possess different frequency spectra. Electronic noise, which is generally considered to be a random process, originates from thermal noise in resistors, quantization noise in analog-to-digital converters and intrinsic amplifier noise. Because electronic noise is considered to be random, it is typically modeled as additive noise with a uniform power spectrum. In contrast, echo decorrelation results from the varying echo contributions from different scatterers between different signal acquisitions. In radiation force imaging, for example, a gradient of deformations across the point spread function causes signal decorrelation that, in turn, leads to corruption of TDE estimates and an underestimation of peak displacement (McAleavey et al. 2003; Palmeri et al. 2006; Viola and Walker 2002). Echo decorrelation from radiation force application is shown schematically in Fig. 1. Differential scatterer motion corrupts the echo data, leading to errors in the displacement estimates.
Fig. 1.
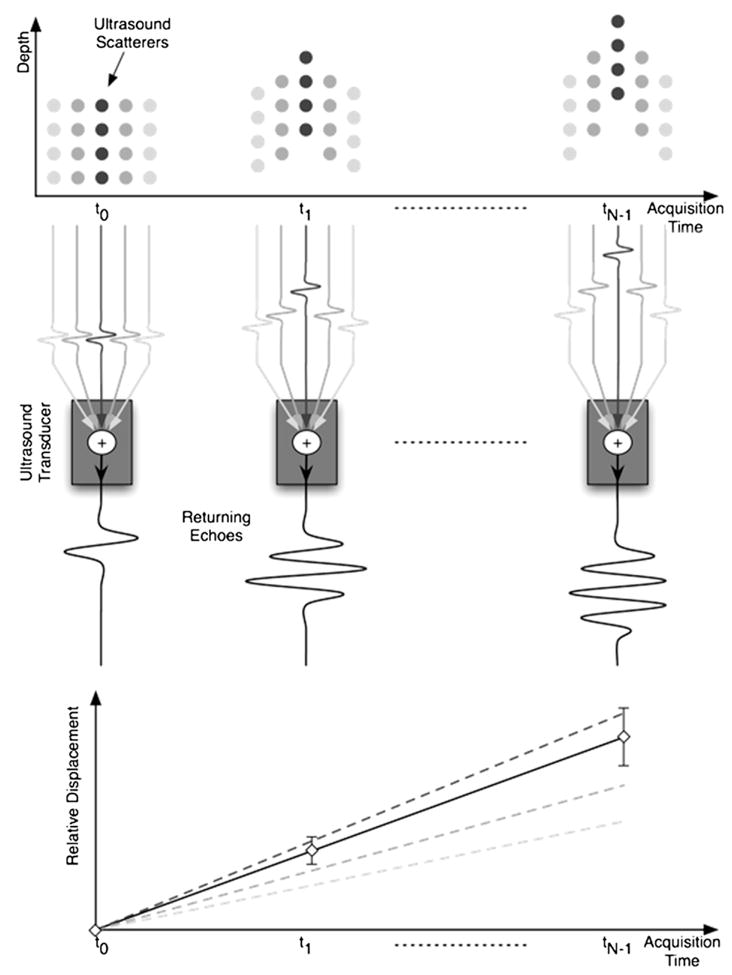
A depiction of the relationship between differential scatterer motion and uncertainty in displacement estimation. A spatially varying acoustic radiation force field is applied to a set of targets over N acquisitions from time t0 to tN−1. The nonuniform force field induces a gradient of scatterer displacements across the point spread function (PSF). In the illustration, different displacements are associated with different shades of gray circles (scatterers) in the target field. The echo signals from all scatterers across the PSF are summed to give the resulting received echo. The delays in echo signals from different sets of scatterers are illustrated prior to the summation node at the transducer. As the gradient of displacements increases through acquisition time, the correlation between successive received echoes decreases, which results in increasing uncertainty in displacement estimates. The displacement profile estimated from the received echo signal is illustrated as the solid line with error bars, indicating uncertainty in the displacement estimate. The dashed lines correspond to the different sets of scatterers and indicate the actual displacements of these scatterers.
In applications where deformations are larger, such as blood flow estimation and elastography, decorrelation originates not only from a gradient of displacements across the acoustic beam, but also from targets moving into and out of the acoustic beam. Unlike electric noise, echo decorrelation is typically modeled by adding noise sources that contain the same frequency spectrum as the primary signal of interest (Walker 2001). In this study, decorrelation was modeled as the superposition of a desirable displacement signal of larger magnitude with two undesirable displacement signals of lower magnitude. All signal components exhibited the same shaped power spectrum. In addition, random Gaussian noise was included to simulate the contribution from electronic SNR.
To minimize the effects of noise and decorrelation and therefore improve TDE performance, signal separation techniques may be used before TDE. Finite impulse response (FIR) and infinite impulse response (IIR) filters are widely used to improve SNR. However, these frequency domain–based techniques are unable to separate signals with overlapping spectra and, therefore, are generally ineffective in reducing signal decorrelation. In contrast, regression filters offer an alternative approach that assumes signals are the summation of polynomials in the time domain (Kadi and Loupas 1995). The utility of regression depends heavily on the selection of the polynomial constituents forming the signal basis. Although the polynomial basis for regression filtering can be formed from an a priori model of previous data examples, this strategy is typically not feasible in medical ultrasound in which different tissue structures and imaging parameters dramatically change the statistical structure of received data. Instead, adaptively forming the polynomial signal basis is a more appropriate approach.
In medical ultrasound, adaptive regression filtering has been demonstrated via blind source separation (BSS) techniques applied to clutter rejection and filtering physiological motion, radiation force–induced displacements and blood velocity profiles (Gallippi and Trahey 2002, 2004; Gallippi et al. 2003; Kruse and Ferrara 2002; Ledoux et al. 1997). Similarly, Yu and Cobbold (2008) have applied eigen-based decomposition techniques to estimate flow using a technique called the Matrix Pencil. BSS has also been employed with data mining techniques to automate the identification of tissue structures exhibiting similar displacement responses to acoustic radiation force excitation (Mauldin et al. 2008).
In this study, we will examine a specific instance of BSS called complex principal component filtering (PCF) as a method for improving echo correlation and SNR and, thus, improving overall TDE performance.
Complex PCF
Mathematically, principal component analysis (PCA) is defined as an orthogonal linear transformation of the data onto a new coordinate system such that the projection of the data onto the first coordinate (called the first principal component [PC]) has the greatest variance. Likewise, the second PC, which is orthonormal to the first, has a projection with the second greatest variance, and this trend persists for all new PC coordinates. When applied to ensembles of radiofrequency (RF) data, the goal of PCA is to separate source signals of interest from undesired secondary source signals and noise. To filter the undesirable source signals using PCF, the input data matrix is mapped onto a new signal subspace that spans only the PC coordinates of interest.
To illustrate the application of complex PCF to ensembles of echo data, first consider the matrix of complex echo data X (with dimensions [M × N]). The matrix X has been mean reduced so that each column has zero mean and the matrix contains a single ensemble of A-lines. Columns of X represent the N number of A-lines in the ensemble, each containing M samples. The M samples span the “fast time” dimension with time intervals determined by the sampling rate after complex demodulation. Conversely, the rows of X are oriented in the “slow time” dimension, so that there are N samples with periods determined by the pulse repetition frequency (PRF). With this orientation, there are M observations (rows) and N variables (columns). Filtering is performed in the observation or row dimension, which corresponds to slow time in our application. The first complex PC, v1 (with dimensions [N × 1]), may be expressed as follows (Jolliffe 2002):
| (2) |
where indicates that the argument is maximized under the condition that vk is a unit vector, var denotes variance, and E denotes expectation value. Therefore, the first PC, v1, is the unit vector that maximizes the variance of the projection onto X. Similarly, the kth PC coordinate may be found recursively, as follows:
| (3) |
| (4) |
where v* is the conjugate transpose of v.
An alternative approach to computing principal components, which is used in this article, is a linear algebra approach called the covariance method. Given that the covariance matrix of the mean-reduced ensemble of echo data is typically unknown, the sample covariance matrix Ĉ (with dimensions [N × N]) can be computed as follows:
| (5) |
The PCs can then be calculated by performing an eigenvalue decomposition to diagonalize Ĉ, as follows:
| (6) |
where V is an N × N matrix of eigenvectors arranged in columns, which are the computed PCs. The diagonal matrix Λ contains eigenvalues that are arranged to correspond with the associated PCs in V.
To perform complex PC-based filtering, the orthonormal PCs that correspond to the signal of interest are adaptively selected to form a matrix W (with dimensions [N × L]), where L represents the number of selected PCs. The projection operator, Pk (with dimensions [N × N]) is then formed to map the input data matrix X onto the new signal subspace retaining only the PCs of interest as follows:
| (7) |
| (8) |
where Y (with dimensions [M × N]) is the output signal of the complex PC filter and W* is the conjugate transpose of W. Therefore, a reduced rank approximation of the original data set can be computed to form an adaptively filtered output (Strobach 1996). In this study, the echo data were made complex using the Hilbert transform applied to RF echo data. Only the real part of the filtered RF data, Y, was used for TDE. The advantage of allowing PCF to operate on complex echo data is that trends in displacement can be captured with the first, most energetic principal component. In contrast, when PCF operates on real echo data, even small shifts through ensemble length require multiple principal components. Visual inspection is generally required when deciding which real PCs to retain, whereas complex PCF does not require user input.
The primary objective of this study is to test the efficacy of complex PCF for overcoming speckle decorrelation and improving motion estimation. The first aim is to determine whether PCF improves echo decorrelation and time delay estimates in synthetic ultrasound data that are simulated with decorrelation and noise. The PCF method is compared to the typical bandpass filtering approach, and the performance of each method is quantified in terms of time delay root mean square (RMS) error, time delay standard deviation and echo correlation. The second aim is to validate the applicability of PCF for improved TDE in sonorheometry and blood flow estimation.
MATERIALS AND METHODS
Simulation methods
To assess the performance of the proposed technique, broadband ultrasound signals were simulated with varied SNR, delay, TDE window length and PCF window length. Synthetic ensemble data were constructed by summing a desirable, peak delay signal with two undesirable, lower energy signals that mimicked a range of displacements across the acoustic beam. These simulations were analyzed to determine the ability of complex PCF to separate the desired, peak displacement signal from the undesirable and decorrelating signals present in the lateral regions of the tracking beam. An illustration of the physical basis for the decorrelation model is shown in Fig. 1.
Time delay estimation was applied to simulated data that had undergone bandpass filtering, PCF or both. TDE performance was analyzed in terms of signal correlation, standard deviation and RMS error between the estimated and true delay profile. In both simulated and experimental data, only the first PC was retained. This PC corresponded to a matrix W (with dimensions [N × 1]) as shown in filtering eqns (7) and (8). The dimension N corresponded to slow time or the number of transmissions in the ensemble. Furthermore, PCF operated on complex echo data in all instances via the Hilbert transform. Because the amount of echo shift is retained in phase information, it was preferable for PCF to operate on complex data, which contains phase information, rather than the real component of the echo data.
Unless otherwise noted, simulations used the default values summarized in the Table. The PCF kernel length TPCF represents a typical value suitable for the radiation force imaging application sonorheometry. When PCF is applied to clinical RF echo data, it is advantageous to use longer kernel lengths if the displacements within the kernel window are approximately stationary. Furthermore, although an ensemble length of 400 echo lines may not be appropriate for blood flow imaging, it is typical in the sonorheometry application. The SNR reported in the Table reflects the ratio of signal to additive Gaussian distributed white noise. Synthetic, broadband ultrasound signals were generated in MATLAB (The MathWorks, Natick, MA, USA) by convolving Gaussian distributed white noise with a Gaussian weighted sinusoidal ultrasound pulse given as follows:
| (9) |
| (10) |
where B is fractional bandwidth, f0 is center frequency, and 0.42466 relates the full width at half maximum value of a Gaussian to its standard deviation.
Table 1.
Default simulation parameters
| Parameter | Value |
|---|---|
| Center frequency (f0) | 10 MHz |
| Sampling frequency (fs) | 65 MHz |
| Signal-to-noise ratio (SNR) | 20 dB |
| Fractional bandwidth (BW) | 50% |
| TDE kernel length (T) | 3 periods |
| PCF kernel length (TPCF) | 20 periods |
| Ensemble length | 400 echo lines |
| Displacement | 3 samples |
TDE = time delay estimation, PCF = principal component filtering.
To model a sum of different target deformations across the acoustic beam, the default ensemble sT (with dimensions [M × N]) was defined as the sum of three independent ensembles of echo data, each with different weighting coefficients and constant velocity, as follows:
| (11) |
where w are weighting coefficients (w1 > w2 > w3), and s represents independent M × N matrices (s1, s2 and s3) of simulated ensemble data. The ensemble with the greatest weighting coefficient also corresponded to the ensemble with the greatest time delay, so that if d is the peak delay for ensemble s then:
| (12) |
Within this simulation framework, the goal of complex PCF is to reject random noise across all frequencies and to reject the undesirable signals s2 and s3 while retaining the most energetically significant signal s1. By keeping only the most energetic signal (corresponding to the greatest time delay), correlation of echo signals should improve, and bias and standard deviation in TDE measurements should be reduced. Simulations were also performed in which s1 corresponded to the signal with the lowest velocity rather than the highest. Another set of simulations was performed with exponential rather than linear velocity, five signal components rather than three and more narrow velocity separation between components.
TDE was performed on ensembles of simulated echo data after either frequency-based or regression filtering. A schematic of the different processing approaches is illustrated in Fig. 2. The bandpass filtering method is represented in the left column, and the complex PCF method is represented in the right column.
Fig. 2.
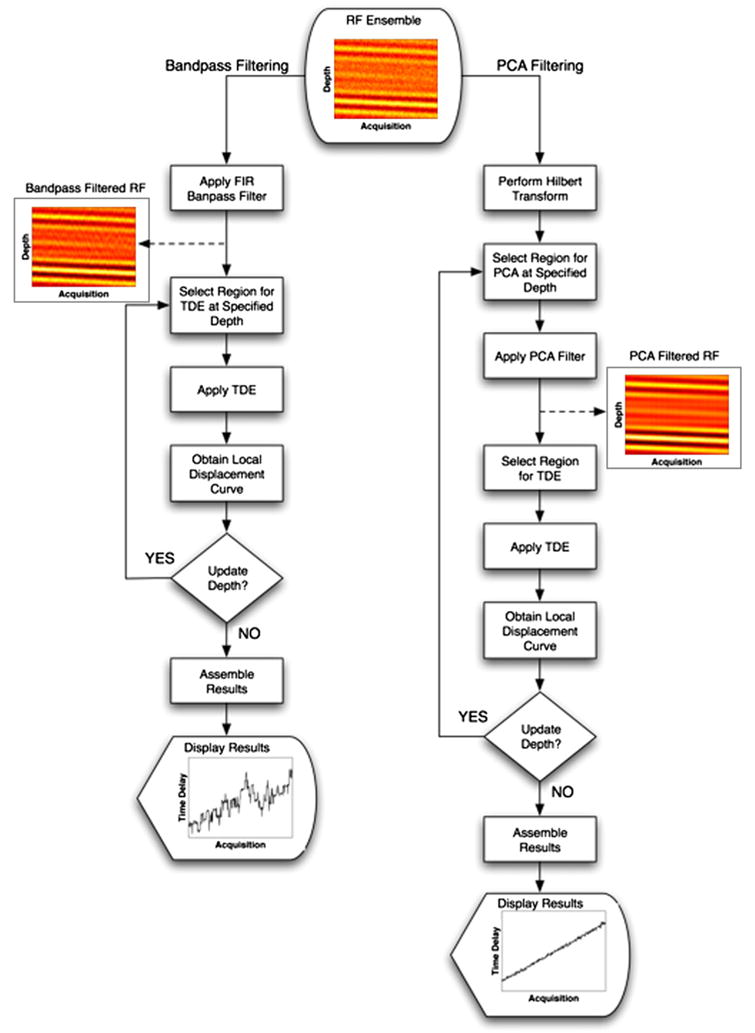
Two RF filtering algorithms for motion estimation are illustrated with simulated echo data and resulting displacement profiles for each method. The left branch illustrates the application of bandpass filtering on an ensemble of RF data to estimate displacements. The right branch illustrates the steps taken when complex PCF is applied to the same ensemble of RF data to estimate displacements. RF data were simulated at an SNR of 5 dB, and displacement profiles were estimated by the spline TDE technique and the N to N−1 delay profile estimation method.
In the case of the complex PCF approach, echo data were first processed to generate a complex representation via the Hilbert transform. Next, the complex data were windowed over a predefined PCF kernel length and then filtered in the acquisition time or slow time dimension. In this way, the resulting PCs represented echo delays across the length of the ensemble. Only the first PC was retained, so that matrix W was a vector of the first PC and filtering was performed via eqns (7) and (8). Time delays were estimated from the real part of the reduced rank output of our complex PC filter. In all simulation instances, the FIR bandpass filter was 50 taps and had a center frequency of 10 MHz with a fractional bandwidth of 50%.
The spline-based TDE algorithm described by Viola and Walker (2005) was used to estimate time delays. The delay profiles through ensemble length were formed using two different variations: N to 1 delay estimation and N to N−1 delay estimation. A delay profile is defined as a vector representing the cumulative time delay across ensemble length. The N to 1 delay technique determined the Nth time delay (Δt̂N) by estimating the delay between the first reference signal (e1) of the ensemble and the Nth shifted signal (eN) as follows:
| (13) |
Conversely, the N to N−1 delay technique computed the Nth time delay as the addition of the delay between signal N−1 and the Nth shifted signal and the previously computed N−1 delay (Δt̂N−1) as follows:
| (14) |
| (15) |
Because the N and N−1 echoes are consistently spaced in time (assuming constant PRF) and generally exhibit small relative shifts, the N to N−1 delay profile technique has the advantage of decreased and more constant decorrelation across the ensemble. In contrast, the N to 1 method will tend to have increased decorrelation as the time between the first and Nth echo grows. The improved correlation of the N to N−1 method is offset by an accumulation of error. This accumulation of error is illustrated in eqns (14) and (15) in which the Nth delay is dependent on the previous N−1 delay. In contrast, the N to 1 method from eqn (13) exhibits no dependence on previous delay values. Another important difference between the N to N−1 and N to 1 methods is their associated computational load. Whereas the N to 1 delay profile method only requires one spline operation per delay profile, the N to N−1 method requires N−1 transformations of the discretely sampled echo signals to continuous spline representations.
Under a given set of simulation conditions, performance statistics were computed over 1000 trials. The RMS error over a single estimated delay profile was computed as follows:
| (16) |
where Δt and Δt̂ are the true and estimated time delays, respectively, and N is the ensemble length.
Experimental application I: Complex PCF for sonorheometry displacement estimation
By observing the dynamic displacements induced in blood by acoustic radiation force, sonorheometry has been shown to provide a noncontact means for assessment of blood coagulation in vitro (Viola et al. 2004). In sonorheometry, radiation force ultrasound was used to transfer momentum to coagulating blood and ultrasound tracking methods were used to track resulting displacement. As a means to improve echo correlation and displacement estimation in sonorheometry, complex PCF was applied to experimental RF data.
Radiofrequency data were acquired using a 10 MHz, 1.0-cm diameter, single piston transducer (model V327, GE Panametrics, Waltham, MA, USA) with a 4.0-cm focal length. The piston transducer was coupled to a custom-designed sonorheometry system, which consisted of two transmit channels, four receive channels, a field-programmable gate array and power supply circuitry (Viola et al. 2007). Received echoes were bandpass filtered, digitized at 65 MHz with 12 bits precision, and then transferred via a USB 2.0 cable to a laptop computer where the data were processed in MATLAB (The MathWorks). Experiments were performed using 1 mL of the fresh blood samples placed in polystyrene cuvettes, which were modified as described below. Blood samples were obtained via a 20-gauge intravenous catheter placed in a peripheral arm vein of a healthy 39-year-old male subject. The initial 3 mL of blood was discarded; 1-mL blood samples were then obtained, and 10 experiments were performed on each of these samples.
Each cuvette was modified by drilling a 7-mm diameter hole through the front and back and sealing both holes with a 250-μm polydimethylsiloxane film. The hole and film allowed the acoustic beam to propagate through the blood sample with minimal attenuation. Blood was then mixed with 125 μl of 0.1% kaolin solution to initiate the clotting process, with the first acquisition taking place 30 s after adding kaolin. An ensemble of sonorheometry data consisted of 400 pulses transmitted at a PRF of 400 Hz for a total duration of 1 s. A single experiment consisted of a series of ensembles repeated every 6 s for 8 min. Experiments were performed with written consent from all subjects and in accordance with the protocol approved by the Institutional Review Board at the University of Virginia.
Time delay estimations were made using the spline TDE algorithm after either FIR bandpass or complex PC filtering. Complex PCF was applied to the experimental RF in the same way that it was applied to the simulated echo data. The PC kernel window length was identical to the simulation default, which corresponded to 20 periods or approximately 1.5 mm. Displacement profiles of coagulating blood were calculated, and the material properties were estimated by fitting displacement responses to a discrete viscoelastic model. The model used in this study was a modified Voigt model with an added mass, which has been shown to characterize the response of coagulating blood to a step excitation of acoustic radiation force (Viola et al. 2004). The differential equation governing this viscoelastic model, with acoustic radiation force modeled as a step function with magnitude A can be written as follows:
| (17) |
where u(t) is the unit step function, x(t) is the resulting displacement, k is the elastic constant, μ is the coefficient of viscosity, and m is an inertial constant. Two mechanical parameters of interest in this article are the time constant parameter τ and the steady-state displacement parameter xss, which can be expressed, respectively, as follows:
| (18) |
| (19) |
Experimental application II: Complex PCF for improved blood velocity estimation
Complex PCF was also applied to M-mode RF data obtained in the left carotid artery of a 23-year-old healthy male subject. In this experimental setting, ensembles of raw RF echo data were collected at a sampling frequency of 40 MHz, a PRF of 10 kHz and a center frequency of 5 MHz using an Ultrasonix Sonix RP scanner and a L14-5 linear array transducer (both obtained from Ultrasonix, Vancouver, BC, Canada). The scanner was modified to acquire an ensemble of 156 A-lines from transmitted pulses with a fractional bandwidth of ~25%. Returning echoes from the carotid artery were arranged into 13 ensembles with 12 A-lines per ensemble. Wall filtering was performed across the slow time dimension with a 50-tap, digital FIR high-pass filter that had a cutoff frequency of 120 Hz. The ensembles were then processed using a conventional blood velocity estimation technique that included a bandpass filter and the TDE algorithm described by Loupas et al. (1995), which is called the “Loupas TDE algorithm.” This technique was compared to the PCF method with the same Loupas TDE algorithm. In the PCF instance, the PCF kernel window length corresponded to 10 periods. A TDE kernel length corresponding to 3 periods was utilized in both bandpass and PCF instances. Because the center frequency in blood flow experiments (5 MHz) was half of the center frequency used for sonorheometry (10 MHz), the spatial extent of the PCF kernel window corresponded to ~1.5 mm in both instances. Just as there are tradeoffs to consider when choosing kernel lengths for TDE, there are similar tradeoffs between PCF performance and spatial sensitivity when choosing the appropriate PCF kernel length. These tradeoffs are further addressed in the Discussion.
RESULTS
Simulation results
The default simulation values, which are listed in the Table, include a 10-MHz center frequency, 65-MHz sampling frequency, 20-dB SNR, 50% fractional bandwidth, 3 period TDE kernel window length, 20-period PC kernel window length, an ensemble length of 400 Alines and maximum delay per ensemble length of three samples.
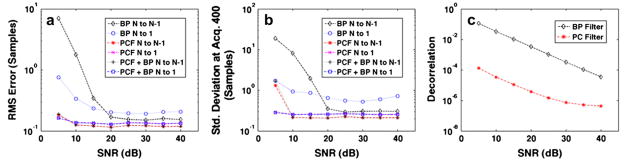
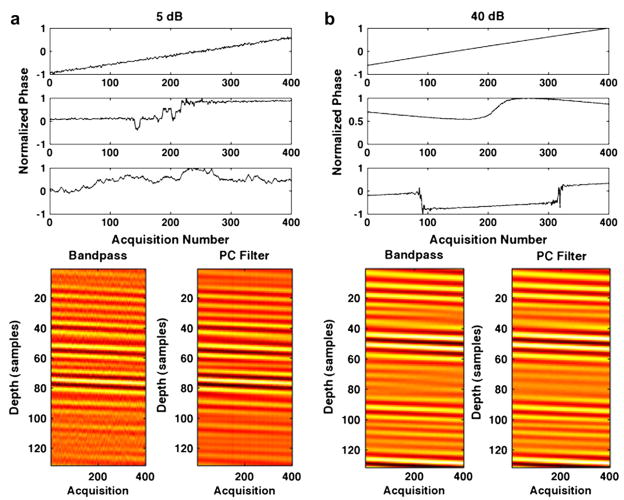
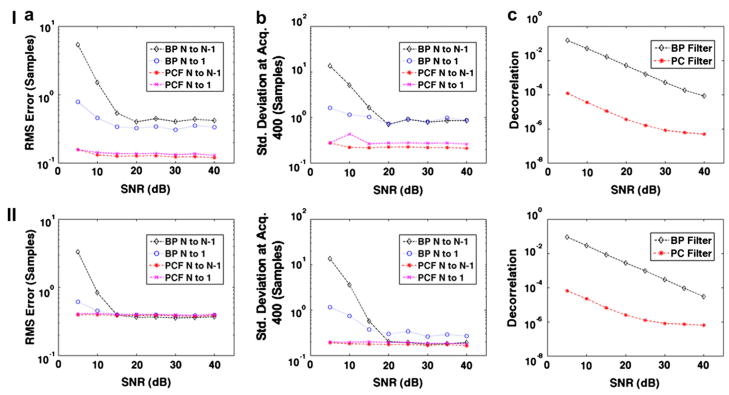
Results in Fig. 3 show (a) RMS error, (b) standard deviation at acquisition 400 and (c) the average decorrelation between consecutive echoes (average N to N−1 decorrelation) when SNR was varied and all other simulation parameters were held constant. Results are illustrated for bandpass, complex PCF and bandpass with complex PCF methods, which were used in conjunction with either the N to 1 or N to N−1 methods for delay profile estimation. As viewed in Figs. 3a and b, there is a negligible difference between bandpass and PCF combined versus PCF alone. Therefore, through the remainder of this article, we omit results for combined complex PCF with bandpass filtering. In Fig. 3b, the average standard deviation was calculated for the 400th time delay estimate. As the Table indicates, the peak time delay for the simulated ensemble was three samples and, therefore, Fig. 3b represents the standard deviation for spline TDE at a shift of three samples. Sample PCs and simulated RF from the variable SNR simulations are displayed in Fig. 4. In Fig. 4a, normalized PC phases (top) for PCs 1, 2 and 3 (from top to bottom) with the corresponding simulated echo data (bottom) are illustrated for an SNR of 5 dB. The simulated echo data are shown across the PC kernel window length of 20 periods or 130 samples for each of the 400 echo acquisitions. The simulated RF after a 50-tap bandpass filter is shown on the left; simulated RF after complex PCF is displayed on the right. Similarly, Fig. 4b illustrates the normalized PC phase and the simulated RF over a range of 130 samples at 40-dB SNR.
Fig. 3.
Simulation results over 1000 trials when SNR is varied from 5 dB to 40 dB. Plots display (a) RMS error, (b) standard deviation at acquisition 400 and (c) average decorrelation between consecutive echoes (average N to N−1 decorrelation). Results are shown for the bandpass (BP) filter, complex PCF and combined bandpass filter and complex PCF techniques. The RF data filtering methods were applied in conjunction with either the N to N−1 or N to 1 delay profile estimation technique.
Fig. 4.
Filtered ensembles of RF are illustrated after either bandpass filtering (left) or complex PCF (right) applied to ensembles of RF simulated with (a) 5-dB SNR (bottom) and (b) 40-dB SNR (bottom). The normalized phase of associated PCs are displayed for (a) the 5-dB SNR instance (top) and (b) the 40-dB SNR instance (top). The PCs are shown with the first, most energetic PC on the top and the third PC on the bottom.
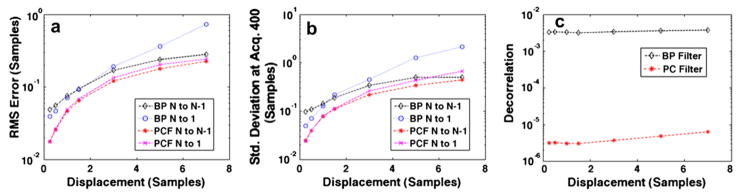
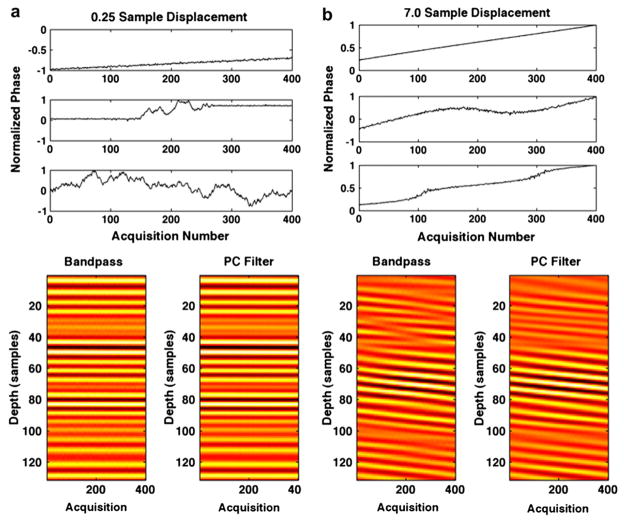
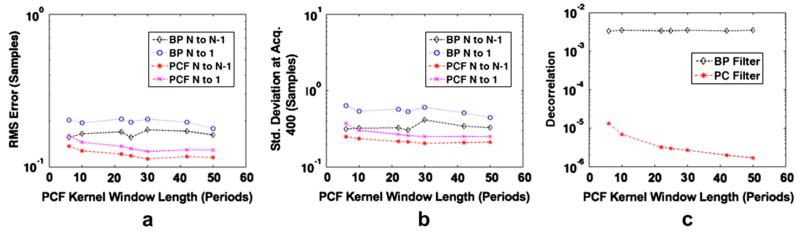
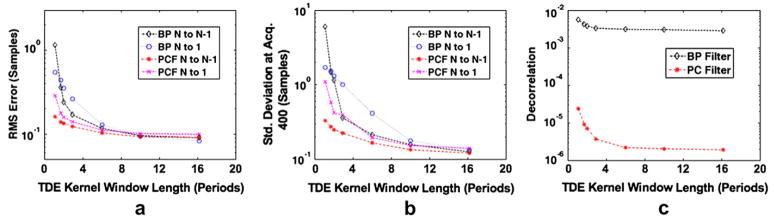
Figure 5 displays simulation results obtained from 1000 trials in which maximum displacement over the ensemble was variable and all other simulation parameters were held constant. Root mean square error, standard deviation at acquisition 400 and N to N−1 decorrelation are displayed, respectively, in Figs. 5a through c. The maximum displacement per ensemble was varied between 0.25 and 7 samples, and results are displayed for bandpass filtering and PCF techniques with both N to 1 and N to N−1 estimates used to form delay profiles. In Fig. 6a, the normalized phase of PCs 1, 2 and 3 (from top to bottom) with 0.25 maximum displacement are displayed at the top with corresponding bandpass filtered RF (left) and complex PCF filtered RF (right). In the same manner, Fig. 6b displays the normalized phase of PCs 1, 2 and 3, accompanied by bandpass filtered RF (left) and complex PCF RF (right) when simulated RF data had a maximum displacement of seven samples. RF data are shown over a 130-sample window, which corresponds to the PC kernel window length used in the simulation. Figures 7 and 8 display the RMS error, standard deviation at acquisition 400 and decorrelation trends observed over the course of 1000 trials when only PC kernel window and TDE kernel window lengths, respectively, were varied.
Fig. 5.
Simulation results over 1000 trials when maximum displacement per ensemble is varied from 0.25 samples to 7.0 samples. Plots display (a) RMS error, (b) standard deviation at acquisition 400 and (c) average decorrelation between consecutive echoes (average N to N−1 decorrelation). Results are shown for the bandpass (BP) filter and complex PCF. The RF filtering methods were used in conjunction with either the N to N−1 or N to 1 delay profile estimation technique.
Fig. 6.
Filtered ensembles of RF data are illustrated after either bandpass filtering (left) or complex PCF (right) applied to ensembles of RF data that were simulated with (a) 0.25 samples of displacement across the ensemble (bottom) and (b) 7.0 samples of displacement across the ensemble (bottom). The normalized phase of associated PCs are displayed for (a) the 0.25 sample simulation (top) and (b) the 7.0 sample simulation (bottom). The PCs are shown with the first, most energetic PC on the top and the third PC on the bottom. By summing uncorrelated signal components of different shifts, decorrelation was induced in simulated RF.
Fig. 7.
Simulation results over 1000 trials when PCF kernel length is varied from 6 periods to 50 periods. Plots display (a) RMS error, (b) standard deviation at acquisition 400 and (c) average decorrelation between consecutive echoes (average N to N−1 decorrelation). Results are shown for the bandpass (BP) filter and complex PCF techniques. The RF filtering methods were applied in conjunction with either the N to N− or N to 1 delay profile estimation technique.
Fig. 8.
Simulation results over 1000 trials when TDE kernel length is varied from 1 period to 16 periods. Plots display (a) RMS error, (b) standard deviation at acquisition 400 and (c) average decorrelation between consecutive echoes (average N to N−1 decorrelation). Results are shown for the bandpass (BP) filter and complex PCF techniques. The RF filter methods were used in conjunction with either the N to N−1 or N to 1 delay profile estimation technique.
Figure 9 shows simulation results similar to Fig. 3 depicting (a) RMS error, (b) standard deviation at acquisition 400 and (c) the average decorrelation between consecutive echoes when SNR is varied from 5 to 40 dB. In row I of Fig. 9, simulated ensembles of echo data were formed where the signal of interest s1 had the lowest velocity of the three signal components as given by the following:
| (20) |
Fig. 9.
Simulation results over 1000 trials when SNR is varied from 5 dB to 40 dB. Plots display (a) RMS error, (b) standard deviation at acquisition 400 and (c) average decorrelation between consecutive echoes (average N to N−1 decorrelation). In row I, simulations were performed when the desired signal component corresponded to the smallest velocity given by eqn (20). In row II, simulations were performed with five signal components, which followed the exponential trend depicted in eqn (21). The simulated velocity of the signal components are given by eqn (22). Results are compared between bandpass (BP) filtering and complex PCF techniques. The RF data filtering methods were applied in conjunction with either the N to N−1 or N to 1 delay profile estimation technique.
In row II of Fig. 9, simulated ensembles of echo data were formed with five signal components rather than three. Furthermore, rather than a constant velocity, the component displacement profiles followed an exponential trend where υn(t) is displacement through time, d is the steady-state displacement, t is time from 0 to 1 s, and τ is the time constant set to 0.25 s, as follows:
| (21) |
The five signal components also had a lesser separation in velocity than other simulations performed in this study. The steady-state displacement of each signal component for Fig. 9 (row II) were given as follows:
| (22) |
Sonorheometry results
A total of 10 sonorheometry experiments were performed using 1-mL blood samples from a healthy 39-year-old male volunteer. In an individual experiment, a single interrogation consisted of 400 A-lines obtained at a PRF of 400 Hz for a total interrogation time interval of 1 s. This process was repeated every 6 s; results are displayed from 0.5 min to approximately 6.5 min, relative to the time at which the kaolin solution was added to the blood. In Fig. 10a, the average N to N−1 RF decorrelation is shown for both bandpass and complex PCF techniques across 10 sonorheometry experiments at the same interrogation depth. Error bars indicate the addition or subtraction of the standard deviation from the mean. Sample displacement profiles resulting from either the bandpass filter technique or the complex PCF technique are displayed in Fig. 10b, where delay profiles were formed using the N to N−1 method described in eqns (14) and (15). The corresponding RF data, from which the profiles in Fig. 10b were generated, are shown in Fig. 10c after a bandpass filter (left) or complex PCF (right). The phase, normalized by the maximum phase value, of the first three PCs associated with the RF data in Fig. 10c are shown in Fig. 10d.
Fig. 10.
The average decorrelation between consecutive echoes (average N to N−1 decorrelation) is presented for both bandpass filtering and complex PCF techniques. Error bars indicate the standard deviation added to (top) or subtracted from (bottom) the average decorrelation. Decorrelation values are averaged over 10 sonorheometry experiments from 1-mL fresh blood samples of a healthy 39-year-old male subject. Example displacement profiles are illustrated in (b) after either bandpass (BP Filter) or complex PCF (PC Filter) methods. The filtered RF data from which the profiles in (b) were rendered are shown in (c) with bandpass filtered RF on the left and PC filtered RF on the right. (d) The normalized phase of PCs 1 through 3 (from top to bottom) rendered from complex PCF are displayed. Only the first PC was retained during filtering.
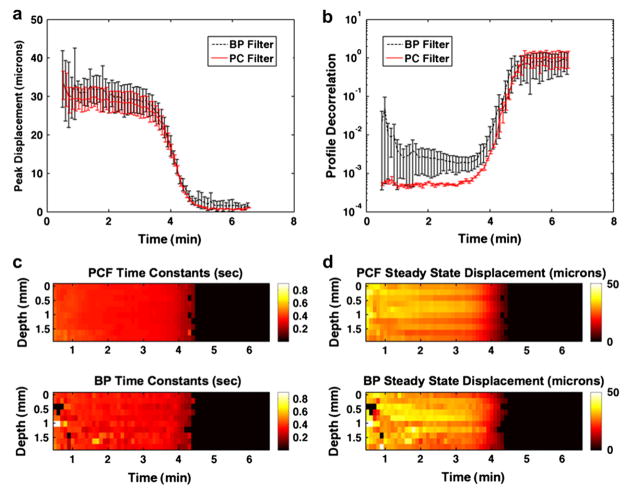
Example sonorheometry results are shown in Fig. 11. Displacement profiles were calculated every 0.2 mm across a 2-mm range for a total of 10 displacement profiles; profiles were formed using the N to N−1 method. In Fig. 11a, the average peak displacement plus or minus the standard deviation across the same 2-mm range in depth is illustrated when profiles were calculated from RF data that were filtered with either the bandpass technique or the complex PCF technique. The steep drop in displacement from approximately 30 microns to 0 microns reflects the rapid clotting of the blood sample. To model the relevant viscoelastic characteristics of the blood response to acoustic radiation force, the displacement profiles were fit to a viscoelastic Voigt model with an added mass term as illustrated by eqn (17). The average decorrelation, or 1 minus correlation, between the model fit and the actual displacement profile generated from either bandpass filtered or complex PCF RF is displayed in Fig. 11b. Error bars indicate the mean plus or minus the standard deviation over 10 depths spanning a 2-mm range. The time constant parameter, which is independent of force as expressed by eqn (18), was extracted from the viscoelastic model fits of the displacement profiles across depth.
Fig. 11.
(a) The average peak displacement from 10 displacement profiles rendered across a 2-mm window in depth are displayed. Average peak displacements are shown for each sonorheometry interrogation, which occurred every 6 s and are displayed from 0.5 min to 6.5 min. Results illustrate the peak displacement values obtained via bandpass filtering (BP Filter) versus complex PCF (PC Filter) of the RF data prior to TDE. Error bars indicate the standard deviation added to (top) or subtracted from (bottom) the average over 10 ranges. (b) Average decorrelation values (one minus correlation) between the displacement profiles and a viscoelastic Voigt model with added mass are illustrated; error bars indicate the mean ± the standard deviation over 10 depths. Images are rendered across a 2-mm window of the blood sample for (c) time constants and (d) steady-state displacement. Viscoelastic parameters determined after complex PCF are shown on top, and derived parameters after bandpass filtering are shown on bottom. Parameter values in (c) and (d) are masked when the displacement profile fit the viscoelastic model with < 0.95 correlation.
Images of time constant values across the 2 mm window are illustrated in Fig. 11c, where complex PCF-rendered parameters are shown on the top and bandpass filtered parameters are shown on the bottom. Similarly, images of steady-state displacement values, calculated from eqn (19), are illustrated in Fig. 11d for PCF-derived (top) and bandpass-derived (bottom) displacement profiles. In the images shown in Figs. 11c and d, the parameters are masked when the fit between the displacement profile and the viscoelastic model achieve a correlation value <0.95.
Blood flow results
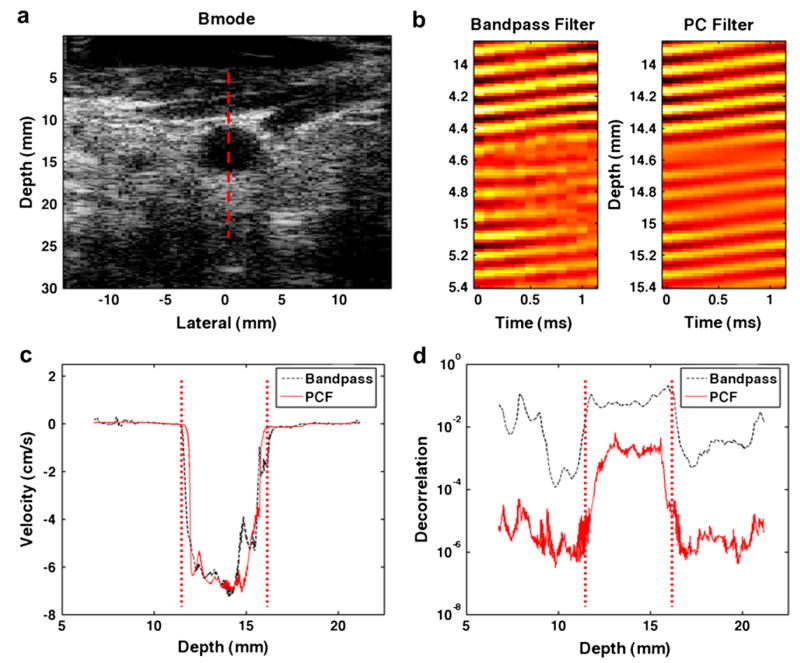
The axial component of blood velocity was estimated in the left carotid artery of a healthy 23-year-old male subject. A B-mode image of the artery is shown in Fig. 12a; the dotted red line shows the line of interrogation for 156 M-mode acquisitions. The M-mode data were organized into 13 ensembles of 12 A-lines each, and blood velocities were estimated with either the bandpass and Loupas techniques or the complex PCF and spline techniques. Sample RF data for the same range in depth are illustrated in Fig. 12b after a bandpass filter (left) or complex PCF (right) was applied to the acquired RF. In Fig. 12c, blood velocity profiles are shown for the two techniques, with negative velocity indicating blood motion toward the transducer. Velocity profiles in Fig. 12c were calculated using either bandpass filtering or PCF methods from an ensemble of 12 A-lines that spanned a duration of 1.2 ms. Maximum blood velocities are shown to reach as much as 7 cm/s, and the vertical, dotted red lines indicate the proximal (left) and distal (right) walls of the carotid artery. The average N to N−1 RF decorrelation across the 12 ensembles versus imaging depth is displayed in Fig. 12d. The RF decorrelation is compared between the bandpass and Loupas techniques versus the PCF and Loupas techniques, where the red dotted lines indicate the location of the carotid proximal and distal walls.
Fig. 12.
(a) A B-mode image from the left carotid artery of a healthy 23-year-old male volunteer is illustrated, with the red, dotted line marking the line of interrogation for acquired M-mode data. (b) Sample RF data after either a bandpass filtering (left) or complex PCF (right) is illustrated. (c) Estimated velocity profiles are shown for either bandpass or complex PCF technique. The red, dotted lines indicate the location of proximal and distal vessel walls. (d) Average decorrelation between consecutive echoes (average N to N−1 decorrelation) versus interrogation depth are illustrated, with red, dotted lines indicating the proximal and distal vessel walls.
DISCUSSION
The advantage of allowing PCF to operate on complex echo data can be understood if we first consider the characteristics of observations in both complex and real echo data instances. In our typical motion estimation environment, as illustrated in Fig. 1, returning echoes are shifted through acquisition time. The ensemble of returning echoes is arranged for PCF, so that an observation at a given depth (or M fast time value) is composed of N real or complex values. These values correspond to the returning echo values at N acquisition times. When PCF operates on real echo data, these observations follow the oscillatory behavior of the returning echoes. Because the set of M real observations are zero mean, eqn (2) is satisfied with the first PC reflecting some constant offset. Thus, when operating on real echo data, PCF requires maintaining multiple PCs to capture echo delay through acquisition time. In contrast, the observations from the complex echo data instance follow the characteristics of complex exponentials with accumulating phase across acquisition time. Because the phase of the complex valued observations is not zero mean, PCF can capture the desirable signal component (echo delay through acquisition time) with only the first PC. As reflected in eqn (2), this approach of selecting only the first PC is based on the assumption that the desirable signal component is also the most energetic.
Simulation
Simulations were performed by generating artificial ensemble data, which were the sum of three signal components: s1, s2 and s3. The primary signal of interest s1 had the maximum delay, whereas signals s2 and s3 had less delay and energy and added decorrelation to our signal model. As explained by eqn (1), decorrelation and additive noise in the ensemble data present fundamental limitations on TDE performance. Therefore, the objective of these simulations was to assess which signal separation technique, frequency-based bandpass filtering or regression-based complex PCF, provides the best means for reducing the decorrelation and noise constraints on TDE performance.
In Fig. 3, the effects of PCF for reduced echo decorrelation and noise were examined against the alternative frequency-based filtering approach for varied levels of additive noise. The first apparent trend in the data was that PCF with bandpass filtering provided no additional benefit than PCF alone. From these results, it was concluded that the combined approach provided no additional benefit, and so it was omitted from later simulation comparisons. The next apparent trend was that, for SNR values between 5 dB and 40 dB, the PCF technique resulted in TDE estimates with lower bias, as reflected in RMS error values in Fig. 3a, and lower TDE standard deviation, as reflected in Fig. 3b. This trend was independent of whether the N to 1 or N to N−1 delay profile estimation technique was utilized. An explanation for this trend may be found in the N to N−1 decorrelation values, which are shown in Fig. 3c. With higher correlation between successive echo signals, eqn (1) predicts that the PCF method would exhibit a lower standard deviation in delay estimates, which was verified in Fig. 3b. Furthermore, with the lower RMS error seen in Fig. 3a, it may be concluded that complex PCF is more efficacious at rejecting random noise along with undesirable signal components s2 and s3 than the bandpass filtering technique across a range of 5 dB to 40 dB SNR. It is also apparent from Fig. 3 that the relative improvement in TDE performance with complex PCF increased as SNR decreased.
The last apparent trend from Fig. 3 is that, for either the bandpass or the PCF technique, there was a crossover point between which the delay profile method exhibited a lower RMS error and standard deviation. When the bandpass filtering technique operated on the simulated RF, the N to N−1 delay profile method had a lower standard deviation and RMS error at SNR values of ≤ 20 dB, but the N to 1 performed better at SNR values < 20 dB. For complex PCF, this switch occurred between 5 dB and 10 dB SNR — 10 dB lower than the bandpass instance. Due to error accumulation with the N to N−1 instance, the N to 1 technique is preferred under low SNR. The lower SNR value at which the N to 1 method becomes preferable in the complex PCF case illustrates that complex PCF rejected a larger amount of noise than bandpass filtering.
Example PCs and RF data from the SNR simulations are illustrated in Fig. 4 for SNR values of 5 dB and 40 dB. For both SNR values, it is clear that the first PC, which was the only PC retained for filtering, was also the only PC that represented the desired signal component of constant velocity across the ensemble. The second and third PCs, which were orthonormal to PC 1, represented noise and energy from the undesired and decorrelating signal components. As reflected in Fig. 3, the difference between the RF data after a bandpass filter (left) and PC filter (right) was more visible at lower SNR values.
By varying the slope of delay across the ensemble, simulations were performed to examine the impact of delay magnitude on the PCF technique; results are shown in Fig. 5. There are two dominant trends present in the data. First, given the same delay profile estimation technique, either N to N−1 or N to 1, the RMS error, standard deviation and decorrelation was always lower for complex PCF. Second, for bandpass filtering, there was a shift in optimal delay profile technique, where the N to 1 technique had a lower RMS error and standard deviation at total shifts < 1.5 samples. Conversely, the N to N−1 method exhibited superior performance at total shifts ≤ 1.5 samples. This trend, which is similar to what was observed in Fig. 3, can be explained by a larger amount of decorrelation across the ensemble with larger total shifts. Because the N to N−1 technique performed better under greater decorrelation, this delay profile estimation method was preferable for greater displacements.
Increased decorrelation with larger shift is apparent in the RF data of Fig. 6. In Fig. 6a, with a maximum shift of 0.25 samples, random noise represents the only visible cause of signal corruption. In Fig. 6b, however, with a maximum shift of seven samples, the data were visibly corrupted by decorrelation. The bandpass filtered data (left) exhibits significantly more signal decorrelation than the complex PCF data (right). Further, the PCs shown in Figs. 6a and b illustrate the same characteristics as those in Fig. 4 in which the first PC (top) represents the desired signal component with constant delay across the ensemble and PCs 2 and 3 (below) represent undesired signal components.
In Figs. 7 and 8, the impact of kernel lengths for PCA filtering TPCF and spline TDE T are shown, respectively. When only TPCF was varied and all other simulation parameters were held constant, the complex PCF method provided better results with longer TPCF as displayed in Fig. 7. Because a larger TPCF, corresponding to a larger number of observations, allowed for a better estimate of the sample covariance matrix, superior filter performance resulted. Figure 8 shows that the advantage of complex PCF over bandpass filtering is negligible with increased TDE kernel lengths. Although decorrelation is dramatically reduced by PCF at greater values of T, as shown in Fig. 8c, the RMS error and standard deviation differences are minimal. Equation (1) suggests that decorrelation no longer dominates TDE performance at large values of T, where TDE kernel length dominates performance.
Although larger TDE kernel lengths produced lower error and standard deviation, there are costs associated with larger TDE kernel lengths in practical applications, including increased computational cost and decreased sensitivity to displacement changes through depth. Because clinical data often exhibit a large range of displacement magnitudes and profiles through depth, it is preferable to be sensitive to these displacement changes by selecting a smaller T. Thus, there is a practical tradeoff, and one must select a T that balances these effects. There is a similar tradeoff with respect to TPCF when complex PCF is applied to clinical RF data. Although increasing TPCF results in a better estimate of the covariance matrix, it only does so when the displacement profile is stationary across the analysis window. If the RF data at different ranges exhibit differing displacement profiles, the shape of the first PC retained during complex PCF may be impacted. In this way, a very large TPCF could provide biased results. This possibility is especially true when different regions within the window exhibit differing gains, which is common under frequency-dependent attenuation. For this reason, it is desirable to choose a large TPCF only if the echo data within the interval are approximately stationary.
Figure 9 illustrates the (a) RMS error (b) standard deviation at acquisition 400 and (c) average decorrelation for simulations when SNR was varied, but other simulation parameters were held constant. Rather than the desirable signal component s1 also having the greatest velocity, simulations illustrated in row I of Fig. 9 assigned the lowest velocity to the desirable signal component as given by eqn (20). The results show that PCF performs at least as well in terms of RMS error and standard deviation under these circumstances as in Fig. 3, when s1 was assigned the greatest velocity given by eqn (12). Thus, we conclude that the efficacy of our PCF algorithm does not rely on the desirable signal component having the greatest displacement, but only that our signal of interest is the most energetic.
Furthermore, row II of Fig. 9 shows the performance of PCF versus bandpass filtering when there are five signal components that exhibit nonuniform velocity through ensemble length and a smaller difference between velocity magnitudes. By simulating the echo data with signal components that had more similar velocity trends, the resulting simulated RF did not contain as much decorrelation. Thus, PCF did not offer gains in RMS error and standard deviation as large as those reported in Fig. 3. However, as expected, PCF still produced large gains in TDE performance at lower SNR levels. Thus, simulation results summarized in row II of Fig. 9 illustrate that the PCF methods do not rely on a specific number of components, constant velocity or a specified difference between magnitudes of component velocities. However, these results do indicate that PC filtering will offer larger gains in TDE performance when there is more decorrelation and noise present in the echo data.
Complex PCF has been demonstrated to outperform the conventional bandpass filtering technique when ultrasound echo data were simulated with decorrelation and noise over a wide range of imaging conditions. Therefore, the first specific aim of this study was achieved.
Application I: Sonorheometry
The application of complex PCF to sonorheometry achieved superior performance over typical bandpass filtering. As shown in Fig. 10a, the average RF decorrelation over 10 trials decreased by at least an order of magnitude under complex PCF. For example, at 2 min after initiation of blood coagulation, correlation improved from 0.996 to 0.9999. Example displacement profiles, illustrated in Fig. 10b, exhibited much less noise and a more well-behaved response. Figure 10c shows ensembles of RF from which the displacement profiles of Fig. 10b were calculated. The RF displayed less decorrelation and noise under PCF (right). Following the simulation trends, Fig. 10d shows that the first PC computed from the RF data is the only PC with the desired delay characteristics.
In Fig. 11a, the peak displacement values obtained with PCF showed a much smoother response. Further, the results in Fig. 11b illustrate that PCF yields a better fit between displacement profiles and the viscoelastic model. This trend was especially true prior to blood clotting, which occurred at approximately 4 min. After blood clotted, there was no displacement, and therefore, the correlation between the estimated displacement profile and the viscoelastic model tends toward zero. Results from Figs. 11c and d show much more consistent results when viscoelastic parameters were extracted from PC filtered displacement profiles (top) versus bandpass filtered profiles (bottom).
Application II: Blood velocity estimation
In clinical blood velocity estimation, complex PCF was applied to ensembles of 12 interrogations with a TPCF length of five periods. In this setting, complex PCF improved RF correlation and provided apparently less noisy velocity profiles. The dramatic improvement in correlation is illustrated in Fig. 12b, where the PC-filtered RF shows a marked reduction in data corruption from decorrelation. In addition, Fig. 12d illustrates the reduction in decorrelation across interrogation depth, and Fig. 12c displays velocity profiles from both bandpass and Loupas methods or PCF and Loupas methods. At the peak velocity depth of ~14 cm as displayed in Fig. 12c, correlation between echoes N and N−1 improved from an average of 0.94 with bandpass filtering to an average of 0.998 with complex PCF. Because the interrogation angle was not factored into our blood velocity measurements, the values reported in Fig. 12c do not represent the true blood velocity in the carotid artery. Instead, it is likely that these velocities are underestimated.
Thus, if the angle of interrogation between the transducer and the vessel wall were assumed to be 15°, our measurements would represent blood velocities in the carotid artery of approximately 27 cm/s. Figure 12c shows that the PCF and Loupas techniques produced cleaner velocity profiles, which appeared more physiological. This observation included a peak velocity near the center of the vessel and decreasing velocity toward the vessel walls. In contrast, the bandpass and Loupas methods showed a velocity profile with a much rougher response through depth and an unanticipated hump in the velocity profile ~15 mm in depth.
In contrast to the sonorheometry application, the highest energy signal in blood flow estimation is not necessarily the desired signal from blood. If the received echo data are corrupted by clutter or reverberation signal that is greater in amplitude than signal from the blood, then complex PCF will not capture the blood velocity characteristics with the first PC. Instead the first PC will reflect the higher energy signal from reverberations or clutter. In this study, this problem is avoided by applying a wall filter before performing complex PCF. A similar assumption of clutter rejection applies to the Loupas algorithm (Loupas et al. 1995). However, this assumption of the highest energy signal corresponding to signal from blood is not necessary for complex PCF to operate in blood flow estimation. For instance, if there is no wall filter applied to the echo data, then complex PCF could be applied to blood velocity estimation by retaining only the second PC, which would correspond to the next highest energy signal or blood in this example. These alternative methods will be examined in future work.
By validating the applicability of PCF in two experimental applications of TDE – sonorheometry and blood flow estimation – the second aim of this study was achieved.
Computational efficiency
An important consideration when examining complex PCF, especially when applied to real-time filtering applications, is the associated computational load. For an ensemble of echo data with dimensions M × N, bandpass filtering requires an estimated (2MlogM + M2)N number of operations. In this example, M is the number of samples through fast time, whereas N is the number of A-lines acquired through ensemble length, or slow time. If the ensemble is windowed by TPCF, so that the PCF subset of echo data has dimensions T × N, then PCF requires approximately (2TN + N + N2)NP number of operations for P number of depths. Therefore, dimensions of M, N, T and P must be considered when comparing the computational efficiency of either filtering approach.
For example, if we consider the default parameters used in simulation, and considering M equal to 1000, then the bandpass filtering approach becomes more computationally efficient only if P is greater than 4. Alternatively, if we consider N equal to 12, as in the blood flow application, then bandpass filtering becomes more computationally efficient only if P is greater than 484. Whereas a small P and larger N is more suitable for the sonorheometry application, a larger P and smaller N is more suitable for applications such as blood velocity estimation and acoustic radiation force impulse imaging.
CONCLUSION
Complex PCF was demonstrated in TDE simulation and two different experimental applications. Simulations using synthetic ultrasound data showed that complex PCF dramatically reduced decorrelation and noise, thus reducing TDE error and standard deviation compared to conventional bandpass filtering. Simulation results illustrated greater gains in standard deviation and RMS error from complex PCF than bandpass filtering in environments with high noise levels and decorrelation. Furthermore, complex PCF showed greater gains in standard deviation and RMS error than bandpass filtering when the TDE kernel window was reduced and when the PCF kernel window was increased. When echo data were simulated with lower levels of noise but higher decorrelation, the N to N−1 method, where delays were computed from consecutive lines of RF, showed lower RMS error and standard deviation. In sonorheometry, complex PCF reduced RF decorrelation by at least an order of magnitude and displacement profile noise was clearly reduced. Similarly, when complex PCF was applied to blood velocity estimation, the RF correlation was improved, which resulted in cleaner velocity profiles. This investigation supports the use of complex PCF for overcoming speckle decorrelation in TDE applications.
Acknowledgments
The authors acknowledge StarFish Medical, Victoria, BC, Canada for technical support in the design of the sonorheometry data acquisition board. We thank Ultrasonix Medical Corporation for their technical support. This work was funded by the National Institutes of Health (grant R01 EB005433-01).
References
- Bercoff J, Tanter M, Fink M. Supersonic shear imaging: A new technique for soft tissue elasticity mapping. IEEE Trans Ultrason Ferroelect Freq Contr. 2004;51:396–409. doi: 10.1109/tuffc.2004.1295425. [DOI] [PubMed] [Google Scholar]
- Bohs L, Friemel B, McDermott B, Trahey G. A real time system for quantifying and displaying two-dimensional velocities using ultrasound. Ultrasound Med Biol. 1993;19:751–761. doi: 10.1016/0301-5629(93)90092-3. [DOI] [PubMed] [Google Scholar]
- Bonnefous O, Pesque P. Time domain formulation of pulse-Doppler ultrasound and blood velocity estimation by cross correlation. Ultrason Imaging. 1986;8:75–85. doi: 10.1177/016173468600800201. [DOI] [PubMed] [Google Scholar]
- Carter G. Coherence and time delay estimation. Proc IEEE. 1987;75:236–255. [Google Scholar]
- Embree PM, O’Brien WR. Volumetric blood flow via time-domain correlation: Experimental verification. IEEE Trans Ultrason Ferroelect Freq Contr. 1990;37:176–189. doi: 10.1109/58.55307. [DOI] [PubMed] [Google Scholar]
- Fatemi M, Greenleaf J. Application of radiation force in noncontact measurement of the elastic parameters. Ultrason Imaging. 1999;21:147–154. doi: 10.1177/016173469902100205. [DOI] [PubMed] [Google Scholar]
- Flax S, O’Donnell M. Phase-aberration correction using signals from point reflectors and diffuse scatterers: Basic principles. IEEE Trans Ultrason Ferroelect Freq Contr. 1988;35:758–767. doi: 10.1109/58.9333. [DOI] [PubMed] [Google Scholar]
- Gallippi C, Trahey G. Adaptive clutter filtering via blind source separation for two-dimensional ultrasonic blood velocity measurement. Ultrason Imaging. 2002;24:193–214. doi: 10.1177/016173460202400401. [DOI] [PubMed] [Google Scholar]
- Gallippi C, Nightingale K, Trahey G. BSS-based filtering of physiological and ARFI-induced tissue and blood motion. Ultrasound Med Biol. 2003;29:1583–1592. doi: 10.1016/j.ultrasmedbio.2003.07.002. [DOI] [PubMed] [Google Scholar]
- Gallippi C, Trahey G. Complex blind source separation for acoustic radiation force impulse imaging in the peripheral vasculature, in vivo. IEEE Ultrason Symp. 2004;1:596–601. [Google Scholar]
- Giunta G. Fine estimators of two-dimensional parameters and application to spatial shift estimation. IEEE Trans Signal Process. 1999;47:3201–3207. [Google Scholar]
- Jacovitti G, Scarano G. Discrete time techniques for time delay estimation. IEEE Trans Signal Process. 1993;41:525–533. [Google Scholar]
- Jensen J. Estimation of blood velocities using ultrasound: A signal processing approach. New York: Cambridge University Press; 1996. [Google Scholar]
- Jolliffe IT. Principal component analysis (Springer series in statistics) 2. New York: Springer; 2002. [Google Scholar]
- Kadi A, Loupas T. On the performance of regression and step-initialized IIR clutter filters for color Doppler systems in diagnostic medical ultrasound. IEEE Trans Ultrason Ferroelect Freq Control. 1995;45:837–851. [Google Scholar]
- Kasai C, Namekawa K, Koyano A, Omoto R. Real-time two-dimensional blood flow imaging using autocorrelation technique. IEEE Trans Sonics Ultrason. 1985;32:458–463. [Google Scholar]
- Kruse D, Ferrara K. A new high resolution color flow system using an eigendecomposition-based adaptive filter for clutter rejection. IEEE Trans Ultrason Ferroelect Freq Contr. 2002;49:1384–1399. doi: 10.1109/tuffc.2002.1041080. [DOI] [PubMed] [Google Scholar]
- Ledoux L, Brands P, Hoeks A. Reduction of the clutter component in Doppler ultrasound signals based on singular value decomposition: A simulation study. Ultrason Imaging. 1997;19:1–18. doi: 10.1177/016173469701900101. [DOI] [PubMed] [Google Scholar]
- Loupas T, Peterson R, Gill R. Experimental evaluation of velocity and power estimation for ultrasound blood flow imaging, by means of a two-dimensional autocorrelation approach. IEEE Trans Ultrason Ferroelect Freq Contr. 1995;42:689–699. [Google Scholar]
- Mauldin F, Zhu H, Behler R, Nichols T, Gallippi C. Robust principal component analysis and clustering methods for automated classification of tissue response to ARFI excitation. Ultrasound Med Biol. 2008;34:309–325. doi: 10.1016/j.ultrasmedbio.2007.07.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McAleavey SA, Nightingale KR, Trahey GE. Estimates of echo correlation and measurement bias in acoustic radiation force impulse imaging. IEEE Trans Ultrason Ferroelect Freq Contr. 2003;50:631–641. doi: 10.1109/tuffc.2003.1209550. [DOI] [PubMed] [Google Scholar]
- Ng G, Worrell S, Freiburger P, Trahey G. A comparative evaluation of several algorithms for phase aberration correction. IEEE Trans Ultrason Ferroelect Freq Contr. 1994;41:631–643. [Google Scholar]
- Nightingale K, Soo M, Nightingale R, Trahey G. Acoustic radiation force impulse imaging: In vivo demonstration of clinical feasibility. Ultrasound Med Biol. 2002;28:227–235. doi: 10.1016/s0301-5629(01)00499-9. [DOI] [PubMed] [Google Scholar]
- Nock L, Trahey G. Synthetic receive aperture imaging with phase correction for motion and for tissue inhomogeneities-Part II: Effects of and correction for motion. IEEE Trans Ultrason Ferroelect Freq Contr. 1992;39:496–501. doi: 10.1109/58.148540. [DOI] [PubMed] [Google Scholar]
- O’Donnell M, Skovoroda A, Shapo B, Emelianov S. Internal displacement and strain imaging using ultrasonic speckle tracking. IEEE Trans Ultrason Ferroelect Freq Contr. 1994;41:314–325. [Google Scholar]
- Ophir J, Cespedes I, Ponnekanti H, Yazdi Y, Li X. Elastography: A quantitative method for imaging the elasticity of biological tissues. Ultrason Imaging. 1991;13:111–134. doi: 10.1177/016173469101300201. [DOI] [PubMed] [Google Scholar]
- Palmeri ML, McAleavey SA, Trahey GE, Nightingale KR. Ultrasonic tracking of acoustic radiation force-induced displacements in homogeneous media. IEEE Trans Ultrason Ferroelect Freq Contr. 2006;53:1300–1313. doi: 10.1109/tuffc.2006.1665078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skovoroda A, Emelianov S, O’Donnell M. Tissue elasticity reconstruction based on ultrasonic displacement and strain images. IEEE Trans Ultrason Ferroelect Freq Contr. 1995;42:746–765. [Google Scholar]
- Strobach P. Low-rank adaptive filters. IEEE Trans Signal Process. 1996;44:2932–2947. [Google Scholar]
- Sumino Y, Waag R. Measurements of ultrasonic pulse arrival time differences produced by abdominal wall specimens. J Acoust Soc Amer. 1991;90:2924–2930. doi: 10.1121/1.401766. [DOI] [PubMed] [Google Scholar]
- Viola F, Walker W. Ultrasound echo decorrelation due to acoustic radiation force. IEEE Ultrason Symp. 2002;2:1903–1906. [Google Scholar]
- Viola F, Walker W. Radiation force imaging of viscoelastic properties with reduced artifacts. IEEE Trans Ultrason Ferroelect Freq Control. 2003;50:736–742. doi: 10.1109/tuffc.2003.1209564. [DOI] [PubMed] [Google Scholar]
- Viola F, Kramer M, Lawrence M, Oberhauser J, Walker W. Sonorheometry: A noncontact method for the dynamic assessment of thrombosis. Ann Biomed Eng. 2004;32:696–705. doi: 10.1023/b:abme.0000030235.72255.df. [DOI] [PubMed] [Google Scholar]
- Viola F, Walker W. A spline-based algorithm for continuous time-delay estimation using sampled data. IEEE Trans Ultrason Ferroelect Freq Contr. 2005;52:80–93. doi: 10.1109/tuffc.2005.1397352. [DOI] [PubMed] [Google Scholar]
- Viola F, Mauldin F, Tropello S, Macik B, Lawrence M, Walker W. Sonorheometry: A new method for assessing coagulation potential. IEEE Ultrason Symp. 2007;1:1001–1004. [Google Scholar]
- Walker W, Trahey G. A fundamental limit on delay estimation using partially correlated speckle signals. IEEE Trans Ultrason Ferroelect Freq Contr. 1995;42:301–308. [Google Scholar]
- Walker W, Fernandez F, Negron L. A method of imaging viscoelastic parameters with acoustic radiation force. Phys Med Biol. 2000;45:1437–1447. doi: 10.1088/0031-9155/45/6/303. [DOI] [PubMed] [Google Scholar]
- Walker W. The significance of correlation in ultrasound signal processing. Proc SPIE. 2001;4325:159. [Google Scholar]
- Yu A, Cobbold R. Single-ensemble-based eigen-processing methods for color flow imaging – part II. The matrix pencil estimator. IEEE Trans Ultrason Ferroelect Freq Contr. 2008;55:573–587. doi: 10.1109/TUFFC.2008.683. [DOI] [PubMed] [Google Scholar]