1 Introduction
The introduction of residual dipolar couplings (RDCs) for protein structure determination over 10 years ago has energized development of NMR methods. Robust automation of the complete NMR structure determination procedure has been a long-standing goal, and RDC-based algorithms may increase the consistency and reliability of NMR structural studies. It has also been recognized that structure determination based primarily on orientational restraints could be quicker and more accurate than traditional distance-restraint methods. Furthermore, NMR is increasingly important in applications where structural information is already available, so that methods which effectively automate NMR assignment of known structures would also be a substantial contribution.
Since RDCs are measured in a global coordinate frame, they enable molecular replacement-like methods that perform assignments using structural priors. Furthermore, recent methods for structure determination have exploited novel RDC equations, which combine RDC data and protein kinematics. Under fairly mild assumptions, the dihedral torsional angles of a protein can be analytically expressed as roots of these low-degree monomials. Solving these equations exactly has enabled a departure from earlier stochastic methods, and led to linear-time, combinatorially-precise algorithms for NMR structure determination. These algorithms are optimal in terms of combinatorial (but not algebraic) complexity, and show how structural data can be used to produce a deterministic, optimal solution for the protein structure in polynomial time.
The coefficients of the RDC equations are determined by the data. An RDC error bound therefore defines a range of coefficients, which, in turn, yield a range of roots representing the structural dihedral angles. Hence, the RDC equations define an analytical relationship between the RDC error distribution, and the coordinate error of the ensemble of structures that satisfy the experimental restraints. Precise methods that relate the experimental error to the coordinate error of the computed structures therefore appear within reach. This article reviews these and other recent advances in NMR assignment and structure determination based on sparse dipolar couplings.
1.1 Background
While automation is revolutionizing many aspects of biology, the determination of three-dimensional (3D) protein structure remains a harder, more expensive task. Novel algorithms and computational methods in biomolecular NMR are necessary to apply modern techniques such as structure-based drug design and structural proteomics on a much larger scale. Traditional (semi-) automated approaches to protein structure determination through NMR spectroscopy require a large number of experiments and substantial spectrometer time, making them difficult to fully automate. A chief bottleneck in the determination of 3D protein structures by NMR is the assignment of chemical shifts and nuclear Overhauser effect (NOE) restraints in a biopolymer.
The introduction of residual dipolar couplings (RDCs) for protein structure determination enabled novel attacks on the assignment problem, to enable high-throughput NMR structure determination. Similarly, it is difficult to determine protein structures accurately using only sparse data. New algorithms have been developed to handle the increased spectral complexity encountered for larger proteins, and sparser information content obtained either in a high-throughput setting, or for larger or difficult proteins. The overall goal is to minimize the number and types of NMR experiments that must be performed and the amount of human effort required to interpret the experimental results, while still producing an accurate analysis of the protein structure.
This review is tempered by our recent experiences in automated assignments [79, 82, 83, 118, 153, 174], novel algorithms for protein structure determination [152, 156, 117, 89, 110, 151, 155, 154], characterization of protein complexes [118, 99] and membrane proteins [117], and fold recognition using only unassigned NMR data [82, 83, 78, 80]. Recent algorithms for automated assignment and structure determination based on sparse dipolar couplings represent a departure from the stochastic methods frequently employed by the NMR community (e.g., simulated annealing/molecular dynamics (SA/MD), Monte Carlo (MC), etc.) A corollary is that such stochastic methods, now routinely employed in NMR structure determination pipelines [60, 53, 91, 64], should be reconsidered in light of their inability to assure identification of the unique or globally-optimal structural models consistent with a set of NMR observations. In this vein, our review focuses on sparse data. While SA/MD may perform adequately in a data-rich, highly-constrained setting, it is difficult to determine protein structures accurately using only sparse data. Sparse data arises not only in high-throughput settings, but also for larger proteins, membrane proteins [117], symmetric protein complexes [118], and difficult systems including denatured or disordered proteins [154]. Sparse-data algorithms require guarantees of completeness to ensure that solutions are not missed and local minima are evaded.
We caution that in the context of NMR, “high-throughput” is relative, and currently not as rapid as, for example, gene sequencing or even crystallography. Hence the term “batch mode” may be more appropriate. The challenge is to develop new algorithms and computer systems to exploit sparse NMR data, demonstrating the large amount of information available in a few key spectra, and how it can be extracted using a blend of combinatorial and geometric algorithms. Moreover, because of their (relative) experimental simplicity, we hypothesize that the computational advantages offered by such approaches should ultimately obtain an integrated system in which automated assignment and calculation of the global fold could be performed at rates comparable to current-day protein screening for structural genomics using 15N-edited heteronuclear single quantum coherence spectroscopy (15N-HSQC).
This article reviews how sparse dipolar couplings can be exploited to address key computational bottlenecks in NMR structural biology. The past few years have yielded rapid progress in automated assignments, novel algorithms for protein structure determination, characterization of protein complexes and membrane proteins, and fold recognition using only unassigned NMR data. We review recent algorithms that assist these advances, including: (1). Sparse-data algorithms for protein structure determination from residual dipolar couplings (RDCs) using exact solutions and systematic search; (2). RDC-based molecular replacement-like techniques for structure-based assignment; (3). Structure determination of membrane proteins and complexes, especially symmetric oligomers, enabled by RDCs; and (4). Automated assignment of NOE restraints in both monomers and complexes, based on backbones computed primarily using sparse RDC restraints.
These define the four main themes in our review:
-
It is difficult to determine protein structures accurately using only sparse data. Sparse data arises not only in high-throughput settings, but also for larger proteins, membrane proteins, and symmetric protein complexes. For de novo structure determination, there are now roots-of-polynomials approaches to compute exact solutions, by systematic search, for internuclear bond vectors and backbone dihedral angles using as few as 2 recorded RDCs per residue (for example NH in two media, or NH and Hα-Cα in one medium). By combining systematic search with exact solutions, it is possible to efficiently compute accurate backbone structures using less NMR data than in traditional approaches.
De novo structure determination from sparse dipolar couplings can exploit structure equations derived by Wang and Donald [152, 151]. These include a quartic equation to compute the internuclear (e.g., bond) vectors from as few as 2 recorded RDCs per residue, and quadratic equations to subsequently compute protein backbone (ϕ, ψ) angles exactly [152, 151]. The structure equations make it possible to compute, exactly and in constant time, the backbone (ϕ, ψ) angles for a residue from very sparse RDCs. Simulated annealing, molecular dynamics, energy minimization, and distance geometry are not required, since the structure is computed exactly from the data. Novel algorithms build upon these exact solutions, to perform protein structure determination, using mostly RDCs but also sparse NOEs. For example, the rdc-exact algorithm employs a systematic search with provable pruning, to determine the conformation of helices, strands, and loops and to compute their orientations using exclusively the angular restraints from RDCs [152, 156]. Then, the algorithm uses very sparse distance restraints between these computed segments of structure, to determine the global fold.
-
Algorithms using sparse dipolar couplings can accelerate protein NMR assignment and structure determination by exploiting a priori structural information. By analogy, in X-ray crystallography, the molecular replacement (MR) technique allows solution of the crystallographic phase problem when a “close” or homologous structural model is known, thereby facilitating rapid structure determination. In contrast, a key bottleneck in NMR structural biology is the assignment problem — the mapping of spectral peaks to tuples of interacting atoms in a protein. For example, peaks in a 3D nuclear Overhauser enhancement spectroscopy (NOESY) experiment establish distance restraints on a protein's structure by identifying pairs of protons interacting through space. An automated procedure for rapidly determining NMR assignments given an homologous structure, can similarly accelerate structure determination. Moreover, even when the structure has already been determined by crystallography or computational homology modeling, NMR assignments are valuable because NMR can be used to probe protein-protein interactions and protein-ligand binding (via chemical shift mapping or line-broadening), and dynamics (via, e.g., nuclear spin relaxation). Molecular replacement-like approaches for structure-based assignment of resonances and NOEs, including structure-based assignment (SBA) algorithms, can be applied when an homologous protein is known. Moreover, to find structural homologs, it is possible to apply (filter) modules of SBA to a structure database (as opposed to a single structure). This technique performs rapid fold recognition by correlating structural geometry vs. distributions of unassigned NMR data, enabling detection of homologous structures before assignments [82, 83, 78, 145, 97, 80]. Hence, the algorithm finds candidate homologs using only unassigned spectra; then SBA algorithms perform assignments given the structural homolog.
Several algorithms have been proposed for structure-based assignment using RDCs [4, 3, 63, 82, 83, 79, 67, 64]. For example, Nuclear Vector Replacement (NVR) [79] exploits RDCs to perform structure-based assignment (backbone and NOEs) of proteins when a homologous structure is known, and requires only 15N labeling. NVR was a step in developing a molecular replacement-like method for NMR (useful because many NMR studies, especially in drug design and pharmacology, are of homologous proteins). NVR exploits a priori structural information. Automated procedures for rapidly determining NMR assignments given an homologous structure, can accelerate structure determination, since assignments must generally be obtained before NOEs, chemical shifts, RDCs, and scalar couplings can be employed for structure determination/refinement. NVR offers a high-throughput mechanism for the required assignment process. However, the spectral assignment produced by NVR is itself an important product: even when the structure has already been determined by x-ray crystallography or computational homology modeling, NMR assignments are valuable for structure-activity relation (SAR) by NMR [133, 54] and chemical shift mapping [18], which compare assigned NMR spectra for an isolated protein and a protein:ligand or protein:protein complex. Both are used in high-throughput drug activity screening to determine binding modes. Assignments are also necessary to determine the residues implicated in the dynamics data from nuclear spin relaxation (e.g. [113, 112, 71]). Building on NVR [79], the algorithm gd [78] performs rapid fold recognition (via geometric hashing against a protein structural database) to correlate distributions of unassigned NMR data. gd exploits novel approaches for alignment tensor estimation from unassigned RDCs [78, 82, 83], to perform maximum-likelihood resonance and NOE assignment [80] (in the NVR framework) against the PDB, to detect the fold even before assignments.
In contrast to traditional methods, the set of NMR experiments required by NVR and rdc-exact is smaller, and requires less spectrometer time. While these algorithms have exploited uniform 13C-/15N-labeling [151, 156], NVR and rdc-exact have been successfully applied to experimental spectra from different proteins using only 15N-labeling, a cheaper process than 13C labeling (cf. Wüthrich [166]: “A big asset with regard to future practical applications… [is] … straightforward, inexpensive experimentation. This applies to the isotope labeling scheme as well as to the NMR spectroscopy…”)
-
We will review recent algorithms that assist in determining membrane protein structures. In such systems RDCs serve several functions. First, RDCs enable accurate subunit backbone structure calculation in complexes. Second, in symmetric homo-oligomers, the RDCs aid in determining the symmetry axis [2, 168]. These two advantages enable complete algorithms for NOE assignment and structure determination that overcome limitations of the simulated annealing/molecular dynamics (SA/MD) methodology when the data are sparse. Several methods, including symbrane and Ambipack, cast the problem of structure determination for symmetric homo-oligomers (such as many membrane proteins) into a systematic search of symmetry configuration space, automatically assigning NOEs and handling NOE ambiguity while provably characterizing the uncertainty in the structural ensemble [117, 118].
Membrane proteins present experimental and computational challenges. Structural studies can be difficult if a protein is hard to crystallize (for X-ray) or is not well-behaved in an artificial membrane (for NMR). Many membrane proteins are symmetric oligomers. In an n-mer, identical electronic environments obtain identical chemical shifts, thereby boosting each signal approximately n-fold. However it is not possible to distinguish signals from symmetric atoms in different subunits. The ambiguity in inter-subunit NOEs (with identical chemical shifts) adds to the usual chemical shift ambiguity in assigning NOEs in monomers (with ‘merely’ similar shifts). While the latter could, in principle, be resolved experimentally (for example using 4D NOESY [21]), the former is inherent in the symmetry and cannot currently be resolved by experimental methods: computational solutions are required. On the other hand, the symmetry (which is known to exist from the signal overlap) can be used as an explicit kinematic constraint during structure determination. symbrane is both complete, in that it evaluates all possible conformations, and data-driven, in that it evaluates conformations separately for consistency with experimental data and for quality of packing. Completeness ensures that the algorithm does not miss the native conformation, and being data-driven enables it to assess the structural precision possible from data alone. symbrane performs a branch-and-bound search in the symmetry configuration space. It eliminates structures inconsistent with intersubunit NOEs, and then identifies conformations representing every consistent, well-packed structure. symbrane has been used to determine the complete ensemble of NMR structures of unphosphorylated human cardiac phospholamban [117], a pentameric membrane protein. symbrane addresses some of the challenges of protein complex determination, larger proteins, and the difficulties arising from symmetry and NOE ambiguity. By running symbrane using different priors (starting structures) encoding the putative oligomeric number, one can determine, solely from NMR data, the maximum-likelihood oligomeric state.
Since accurate protein backbone structures can be computed from RDCs, these backbones can then be used to bootstrap NOE assignment. Novel techniques, including the algorithms triangle [153] and Hana [174], exploit the accurate, high-throughput backbone structures obtained exactly using sparse RDCs. NOE assignment can be difficult to fully automate, and structure determination of symmetric membrane proteins by NMR can be challenging. We review how, by combining these two difficult problems, recent results indicate an algorithm that solves both simultaneously, and that enjoys guarantees on its completeness and complexity [117, 118].
An overview of the major steps to automated assignment and structure determination using sparse RDCs is given in Fig. 1. The figure suggests how these algorithms and software tools could be developed into a set of integrated programs for automated fold recognition, assignment, monomeric and oligomeric structure determination. For each of the modules in the figure, there are algorithms and implementations reported by several groups working on NMR methodology. One example for each module is shown in the figure, and should be interpreted as a representative for a class of algorithms (reviewed below) with similar function. Fold recognition [82, 83, 78, 145, 97, 80, 128] denotes correlation of unassigned NMR distributions (e.g., RDCs) against a database of known folds. Structure-based assignment (SBA) [4, 3, 63, 82, 83, 79, 67, 64] denotes automated assignment given priors on the putative structure(s) of the protein. Note that, like sparse data and completeness, SBA is a crosscutting theme: NVR uses priors on putative homologs (detected by gd) to assign resonances (and unambiguous HN-HN NOEs). Algorithms for protein structure determination based on exact solutions to the RDC equations include [122, 159, 152, 151, 156, 154, 155, 174]. rdc-exact is one such algorithm [151, 152, 156]. While the algorithms of [38, 69, 167] are not exact, it is likely that a roots-of-polynomials exact solutions version of these algorithms could be derived, although possibly not in closed-form. triangle uses backbone structure (computed by rdc-exact) to assign ambiguous backbone and side-chain NOEs. Several algorithms exist to determine the structure of symmetric homo oligomers using a combination of RDCs, NOEs, and other NMR data [150, 117, 118, 129, 168]. symbrane [117, 118] and Ambipack [150] exploit the subunit (monomer) structure to assign intermolecular NOEs and determine the complex structure. Finally, note that assignment (NVR) and Fold Recognition (gd) operate entirely on unassigned data. Structure Determination by rdc-exact operates on assigned data.
Figure 1.
Overview of the major modules in automated NMR assignment and protein structure determination using sparse dipolar coupling constraints. One example for each module is shown in the figure, and should be interpreted as a representative for a class of algorithms (reviewed in the text) with similar function. gd performs rapid fold determination from unassigned NMR data. NVR performs structure-based assignment. rdc-exact determines backbone structure de novo, from 2 RDCs per residue plus sparse NOEs. triangle assigns the NOESY spectra, allowing determination of a high-resolution monomer structure. symbrane assigns intermolecular NOEs and determines the oligomeric number and complex structure. Each of these modules takes as input NMR data that can be collected in a high-throughput fashion. The major data sources are shown; complete descriptions of the data requirements are in the text. The solid arrows show the data flow for the molecular replacement-like method for NMR. Dashes show an alternative pathway for de novo assignment and structure determination in the case where a completely novel fold is detected (by gd) from unassigned NMR data. apaces, brgraph and cjigsaw are ab initio assignment algorithms [22, 105, 149, 70, 148, 12]. Right solid arrows show the data flow from structure to assignments. Downward arrows show the data flow from assignments to structure. dsymbrane simultaneously performs assignment and structure determination.
This article concentrates upon the information content of the NMR experiments, and the methods for assignment and structure determination, with an emphasis, where possible, on provable algorithms with guarantees of soundness, completeness, and complexity bounds. A number of excellent articles have appeared on the experimental aspects of RDCs; we recommend [160] for a good introduction to RDCs and the interplay between experimental and computational challenges.
Rather than describing a competition between computer programs, this review tries to evaluate the strengths and weaknesses of the underlying ideas (algorithms). There are several reasons. First, we believe no one will be using the same programs in 10 years (and if we are, that would reflect poorly on the field). However, the underlying mathematical relationships between the data and the structures should prove enduring, warranting a characterization of the completeness, soundness, and complexity of structure determination algorithms exploiting sparse dipolar couplings.
2 The Power of Exact Solutions
Let us consider an analogy. A point-mass p is fired from a cannon with velocity v, where v is a tangent vector to Euclidean three-dimensional space ℝ3. Assuming Newtonian dynamics, when, and where, will it hit the ground?
This problem can be solved by numerical forward-integration of the dynamical equations of motion, or by random guessing (also known as Monte Carlo sampling), simulated annealing, neural networks, genetic algorithms, systematic grid search, or a host of other techniques. However, the following simple technique, from middle-school physics, suffices. The trajectory of the mass p is given by a quadratic equation in one scalar variable (time). By solving this equation simultaneously with the plane of the ground, z = 0, the solution to our problem may be calculated exactly, in closed form, and in constant-time (using only a constant number of computer operations). In this case, “closed-form” means using only the field operations (addition, subtraction, multiplication, and division) plus calculating roots . In this case, j ≤ 2.
A similar trick is available to assist in protein structure determination, (Figs. 2- 7) when we have measured dipolar couplings (Fig. 6). A simplified example will be helpful to understand the idea. The example arises in protein structure determination from RDCs measured in one medium, using exact solutions.
Figure 2.
The scalar component of the residual dipolar coupling. ħ is Planck's constant, μ0 is the magnetic permeability of vacuum, γa and γb are the gyromagnetic ratios of two nuclei a and b, and θ is the angle between the external magnetic field B0 and the internuclear vector v (from a to b) in the weakly-aligned anisotropic phase. is the ensemble average of the second Legendre polynomial of cosθ. ra,b is the distance between nuclei a and b. Here, a and b are assumed to be covalently bonded, and therefore the ensemble average in the denominator is replaced with the single scalar . In classical solution-state NMR, proteins tumble rapidly and isotropically and therefore the dipolar couplings average to zero. RDCs are measured by introducing a dilute alignment medium which biases the orientational distribution of the protein so that dipolar couplings can be measured. In contrast to NOEs, whose magnitude is proportional to the interatomic distance to the inverse sixth power, RDCs are proportional to . The alignment tensor S represents the molecular alignment in the anisotropic phase. It is convenient to express the residual dipolar coupling in Yan-Donald tensor notation [82, 83], as DmaxvTSv.
Figure 7.

Protein backbone kinematics and RDC restraints.
Figure 6.

Key ingredients to a structure determination algorithm exploiting exact solutions and systematic search.
Suppose we have recorded RDCs (Figs. 2- 4) in a single alignment medium for NH and Cα-Hα bond vectors (Fig. 7), and that secondary structure regions have been identified using either chemical shifts, short-range NOEs, or scalar coupling experiments such as HNHA or J-doubling to measure the ϕ bond angles. Consider the simplified problem of computing the orientation and conformation of a secondary structure element (helix or strand) h containing k residues, and that a good estimate of the alignment tensor is available. As described in [152, 151, 156], an initial estimate of the alignment tensor may be obtained by fitting parametric ideal helical geometry to RDCs from a secondary structure element such as a helix. The alignment tensor can be subsequently refined in an iterative fashion [152].
Figure 4.
It is convenient to express the internuclear vector as a unit vector of the form v, corresponding to its direction cosines. The RDC r can be expressed in Yan-Donald tensor notation [82, 83], as r = DmaxvTSv, or in a principal order frame that diagonalizes the alignment tensor, namely r = Sxxx2 + Syyy2 + Szzz2. Here, Sxx, Syy and Szz are the three diagonal elements of a diagonalized Saupe matrix S (the alignment tensor), and x, y and z are, respectively, the x, y, z-components of the unit vector v in a principal order frame (POF) which diagonalizes S.
Henceforth we will simply refer to the Cα-Hα bond as a CH bond, and to a Cα-Hα RDC as a CH RDC. Let us assume standard protein backbone geometry (Fig. 7); our example proceeds by analogy with the mathematical concept of strong induction. Assume we have already computed the structure of the first i − 1 < k residues of h starting at the N-terminus. In this case, the (i − 1)st peptide plane (between residues i − 1 and i) is known (Fig. 7). As the ith ϕ dihedral angle, ϕi rotates, the orientation of the ith Cα-Hα bond vector will move in a circle (Figs. 7- 8). Under any change of coordinate system, this circle will transform to an ellipse, E, on the two-dimensional sphere S2. Such an ellipse is shown in green in Fig. 8.
Figure 8.

Given NH and Cα-Hα RDCs measured in one medium, the Wang-Donald Structure Equations yield exact solutions for the (φ, ψ) backbone dihedral angles.
For each RDC r, the dipolar coupling is given by the top equation in Fig. 2, as shown in [140, 142]. It is convenient to express the residual dipolar coupling in Yan-Donald tensor notation [82, 83], as
| (1) |
where Dmax is the dipolar interaction constant, v is the internuclear vector orientation relative to an arbitrary substructure frame, and S is the 3 × 3 Saupe order matrix [130] (Fig. 2). S is a symmetric, traceless, rank 2 tensor with 5 degrees of freedom, which describes the average substructure alignment in the weakly-aligned anisotropic phase (Figs. 2- 3). The measurement of five or more independent RDCs in substructures of known geometry allows determination of S [92].
Figure 3.
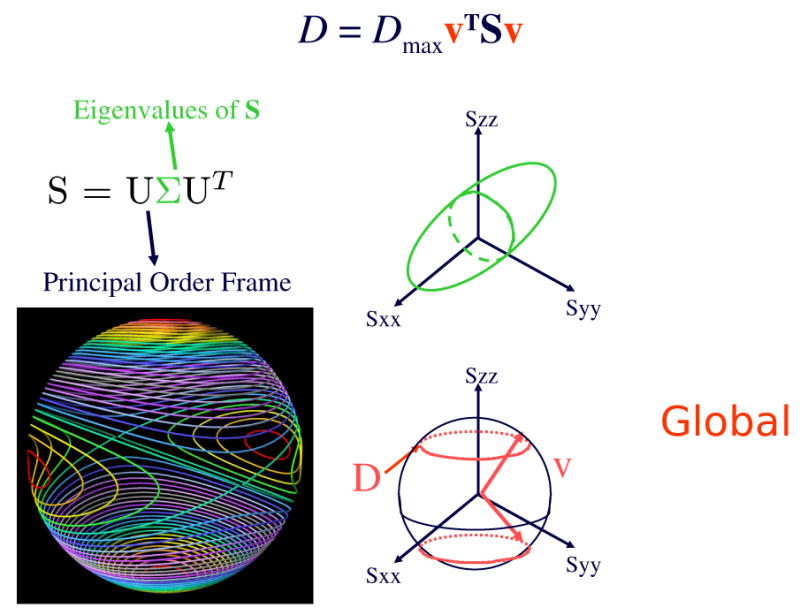
The alignment tensor S is a symmetric second-rank tensor that may be represented by a real-valued 3 × 3 matrix that is symmetric and traceless. Hence S has 5 degrees of freedom and may be decomposed using singular value decomposition (SVD) into a rotation matrix U, called the principal order frame, and a diagonal matrix Σ encoding its eigenvalues. The principal axes of U encode the eigenvectors. For a fixed experimental RDC D, the possible orientations of the corresponding internuclear vector v must lie on one of two RDC curves on the two-dimensional sphere S2. Each curve is the intersection of an ellipsoidal cone with S2. Lower left: RDCs curves are shown spaced at 1 Hz intervals (figure courtesy of Vincent Chen and Tony Yan.)
Now, if the RDC has been measured for the CH bond vector in residue i, then the RDC equation (1) constrains the bond vector orientation to lie on one of two curves R = R1 ∪ R2. Each of these curves is the intersection of S2 with an ellipsoidal cone. One such curve is shown in orange in Fig. 8.
Therefore, the ϕi angles that simultaneously satisfy protein backbone kinematics and the CH RDC data are given by the intersection of curves E and R, shown as the green and orange ellipses, respectively, in Fig. 8. Generically, this intersection will be a set of 0, 2, or 4 points (the 1-point solution in non-generic), as shown in Fig. 8. Wang and Donald showed that these points are the roots of a quartic monomial equation [151, 152] and hence may be computed exactly and in closed-form. (Technically, we compute exact solutions for the sine and cosine of this angle ϕi, which completely determine the angle ϕi, which, if desired, can then be computed numerically using the 2-argument arctangent function atan2).
Now, a solution is chosen for ϕi from amongst these multiple exact solutions, and the procedure continues along the polypeptide chain. With ϕi fixed, we find ourselves in a symmetrical situation. As the ψi bond angle rotates, the orientation of the NH vector of residue i + 1 will move in an ellipse E′ (Fig. 8). Similarly, if the RDC has been measured for this NH bond then its orientation will similarly be constrained to lie on curves R′ on S2. Therefore, the orientation of the (i + 1)st NH bond vector must lie on the intersection of the curves E′ and R′, and the ψi angles satisfying this constraint can similarly be solved for exactly and in closed-form, as done previously for ϕi.
Again, a solution is chosen for ψi from amongst these multiple exact solutions, which defines the ith peptide plane (between residues i and i + 1), and the procedure continues along the polypeptide chain.
Every exact solution precisely satisfies the data. Since there are multiple solutions for each backbone dihedral angle a choice must be made, and this defines a discrete combinatorial search for the structure of the secondary structure element h. A scoring function is used to choose the correct root, and hence the correct backbone dihedral angle. The scoring function can use the Ramachandran diagram, molecular mechanics energies, and any of the usual components of an empirical scoring function [152, 151, 156, 154]. By structuring the search into a conformation tree [152, 88, 156, 45] and using a depth-first search with backtracking [152], or A* search [45], the optimal solution over the entire secondary structure element h can be found (Fig. 9). Henceforth, we will call such a secondary structure element h a fragment.
Figure 9.

A conformation tree is a data structure used in depth-first search over the exact solution (roots of polynomials) with backtracking or A* search, to optimally compute the backbone dihedral angles that globally best-fit the RDC data and an empirical scoring function.
The RDC RMSD term in the scoring function calculates the sum of the squared differences between the experimental RDCs and the back-computed RDCs over all k residues of the secondary structure element h [152]. Minimizing the scoring function over the combinatorial number of choices of the polynomial roots representing the backbone dihedral angles, will yield in the structure that optimally fits the data [152, 156]. Unlike some traditional methods (SA/MD, MC, etc.) that can only compute local minima, this technique is guaranteed to compute the globally optimal solution for h. We discuss this point below.
2.1 Computing the Globally-Optimal Solution
It is important to note that the choice of backbone dihedral angle is not made locally solely using the RDC information for that residue. Rather, the scoring function includes an RDC RMSD term, so that the global optimum is computed over the entire fragment [152, 156]. By global optimal we mean the minimum of the scoring function, where the minimum is taken over all (ϕ, ψ) angles in the fragment that are zeroes of the structure equations. While a grid search over all (discretized) (ϕ, ψ) angles is not computationally feasible, a complete search with full backtracking that considers all possible exact solutions for all possible dihedral angles is possible over secondary structure elements of up to about 20 residues [152, 156, 174]. Typical scoring functions over this tree search have included terms for: RDC RMSD, Ramachandran suitability, and hydrogen bonds [152, 156, 174] or van der Waals packing [154], but any empirical molecular mechanics energy function would be feasible. Note that while an exhaustive search over the entire tree is theoretically necessary in the worst-case, in practice, combinatorial speed-up can be obtained since when a node is pruned, the entire subtree below it is eliminated [152, 156]; see Fig. 9.
This gives a procedure to compute the structure of h that optimally fits the data under the scoring function. Now, the procedure is exponential in k, the length of h. This exponential dependence provides a combinatorial obstruction to simply proceeding along the polypeptide chain for the entire protein. To overcome this problem, the following algorithm is used. The protein is partitioned into secondary structure regions. The orientation and conformation of each secondary structure element is solved using the techniques described above. Each may be solved independently and in parallel since, under suitable assumptions about the dynamics, they all share the same alignment tensor. This allows the algorithm to divide and conquer: for a protein with n residues, there could, in principle, be at most n secondary structure elements. However, each will have only constant length (k = O(1)). Therefore the problem is divided into a series of Θ(n) subproblems, each of constant size. Each of these can be solved in constant time since the exponential of a constant is also a constant.
When RDCs are recorded in a single medium there is a fourfold orientational ambiguity between a pair of secondary structure elements. This cannot be disambiguated solely using the RDCs. However, not all combinations need to be tried. The secondary structure elements can be assembled sequentially using sparse NOEs to pack them together (Fig. 10). For example if the secondary structure elements, whose orientations (up to the symmetry of the dipolar operator) and conformations have been optimally determined are (h1, h2, …, hm), that the algorithm would first pack h2 to dock with h1, and then pack h3 to dock with the packed substructure (h1, h2), and then pack h4 to dock with the packed substructure (h1, h2, h3), and so forth. Each of these packing operations can determine the optimal packing including the orientational ambiguity. This may be done using a complete algorithm as described by [117, 152, 156, 174]. Note that although there could be Θ(n) secondary structure elements, the packing and assembly problem is not exponential since it is transformed into a linear-sized sequence of constant-sized packing problems. The requirements on the NOEs are fairly mild since the conformation of the secondary structure elements is determined up to translation (and the fourfold discrete orientational degeneracy). This means that the translation between the oriented secondary structure elements is not determined using RDCs alone. Therefore a small number of sparse NOEs will suffice to pack the secondary structure elements [152].
Figure 10.

The orientations and conformations of secondary structure elements (SSEs) can be calculated using sparse RDCs. Then the SSEs are packed using sparse NOEs. Packings are scored separately for data fit and molecular mechanics energies [117] to avoid bias. The packing by NOEs also disambiguates the discrete 4-fold orientational degeneracy due to the symmetry of the dipolar operator.
Once the global fold has been determined by packing together the secondary structure elements based on the RDCs and sparse NOEs, loops must be determined to connect them. This problem is similar to the kinematic loop closure problem in x-ray crystallography. The similarity arises because once the core structure of the secondary structure elements has been computed, it defines orientations and positions for the helices and strands. Models of loops must be built that close these kinematic gaps, to connect the secondary structure elements. The kinematic loop closure problem is combined with the RDC restraints that are measured for the loop residues, to compute an ensemble of loops that simultaneously satisfies the closed-chain kinematics and the polynomial equations arising from the RDCs [152, 174].
Finally, it is possible to model error in the input RDCs. In the simplest method, a distribution is placed over the input data, and that distribution can be sampled [152, 151]. This sampling results in a set of perturbed RDCs. The combinatorially-precise, exact algorithms above are run for different sets of the sampled RDCs, resulting in different solutions to the structure. Out of this ensemble of solutions, the maximum-likelihood solution can be computed [152, 151, 156]. Alternatively, an ensemble of structures that fit the data can be returned [154]. In the case that sampling is undesirable, it is possible, in principle, to use algebraic algorithms (polynomial arithmetic) to push the RDC error intervals through the RDC equations, and obtain a representation of the probability density function over backbone dihedral angles [156].
In general, when different RDCs (at least 2) have been measured per residue, a similar algebraic and kinematic derivation holds to obtain exact solutions. The case for NH RDCs recorded in two media is shown in Fig. 5. In all cases, the coefficients of the RDC equations are determined by the data [151]. An RDC error bound therefore defines a range of coefficients, which, in turn, yield a range of roots representing the structural dihedral angles. Hence, the RDC equations define an analytical relationship between the RDC error distribution, and the coordinate error of the ensemble of structures that satisfy the experimental restraints [156]. Precise methods that relate the experimental error to the coordinate error of the computed structures therefore appear within reach.
Figure 5.
A cartoon of the geometry and algebra of RDCs measured in two independent aligning media. If the two principal order frames (POFs) are independent, then the internuclear unit vector v is constrained to simultaneously lie on the blue RDC curve (from the blue POF) and the red RDC curve (from the red POF). Generically, the blue and red RDC curves will intersect at 0, 2, 4, or 8 points. Here, only one of the two RDC curves is shown for each POF. Suppose that r is the red RDC and that the diagonalized red POF can be represented as (Sxx, Syy, Szz). Let , where x is the x-component of v and a2 = (r − Szz)/(Sxx − Szz); see Eq. (6) below and [152, p. 238]. The discrete points corresponding to the RDC curve intersections are calculated exactly by solving a quartic monomial equation in u, of the form f4u4 + f3u3 + f2u2 + f1u + f0 = 0 [152], which is also a quartic monomial equation in x2.
Of course, whenever exact solutions exist, there usually are also excellent numerical algorithms [37] (as opposed to exact algorithms), that stably solve the same analytical equations (7,10 below) not exactly, but up to the accuracy of the floating-point representation. In our motivating example of a point-mass fired from a cannon, these numerical algorithms include (for example), the eponymous Newton's method. Such techniques, born in the field of numerical analysis and scientific computation [37], enable provably-good approximation algorithms for our structure determination problem.
2.2 Limitations and Extensions
The approach described above assumes that dynamics can be neglected, although recent studies indicate that modest dynamic averaging can be tolerated, albeit with reduced accuracy in the determined orientations of internuclear bond vectors [69]. In addition, it is assumed that the alignment tensor can be estimated initially by fitting parametric secondary structure geometry (helices and β-strands) to the RDCs to obtain the alignment [152], and that the alignment parameters can be optimized in an iterative fashion by alternating the roots-of-polynomials exact solutions approach to structure determination (given an alignment tensor) with fitting the alignment tensor to RDCs and the just-determined nascent partial structure (using SVD) [152, 151, 156]. While good results have generally been obtained from this methodology [152, 151, 156, 174], if inaccurate tensors are used, the resulting structures may have innaccuracies [69]. We observe that the RDCs are scaled by the order parameter S. Suppose order parameters S2 are measured for the same bond vectors as the RDCs, using, for example, relaxation experiments. In this case, neglecting dynamics outside the timescale of the dynamics measurements, one may heuristically assume that when S2 is high enough (close to 1), then the dynamic averaging due to S in the RDC measurement is safe to use for structure determination.
3 NMR Structure Determination Algorithms Using sparse RDCs
Several papers [152, 151, 156, 154, 155, 174] make contributions (1–8, below) to the method of determining protein structures by solution NMR spectroscopy using RDCs as the main restraints. These contributions may be valuable not only to the NMR community in particular and structural genomics in general, but also to structural biologists more broadly. This is because in both experimental and computational structural biology, exact computational methods have been, for the most part, elusive to date. Second, rigorous comparisons of structures derived from NMR vs. X-ray crystallography are made possible by these techniques, and these comparisons should be of general interest.
One algorithm, rdc-exact (Fig. 6), requires the following experimental NMR data: (a) two RDCs of backbone internuclear vectors per residue (e.g., assigned NH RDCs in two media or NH and CH RDCs in a single medium); (b) identified α-helices and β-sheets with known hydrogen bonds (H-bonds) between paired strands, and (c) a few NOE distance restraints. The implementation in [152, 151, 156, 174] uses this experimental data, and allows for missing data as well. In contrast to NOE assignment, RDCs can be recorded and assigned on the order of hours. Additionally, it is relatively straightforward to rapidly obtain the few (three or four), unambiguous NOEs required for the packing algorithm (see Section 2) from a standard NOESY spectrum, or by using, for example, the labeling strategy of Kay and coworkers [40]. The secondary structure types of residues along the backbone can be determined by NMR from experimentally-recorded scalar coupling HNHA [16, pages 524–528] data, or J-doubling [31] data for larger proteins (these experiments report on the ϕ backbone angles). NMR chemical shifts [163, 165, 164, 94, 25] or automated assignment [12] can also be used. Hydrogen bonds can be determined by NMR from experimentally-recorded data [24, 157], or, for example, by using backbone resonance assignment programs such as Jigsaw [12]. In the remainder of this review, we discuss the algorithm rdc-exact assuming that we are given assigned NH RDCs in two media (Fig. 5). However, the results also hold for the case of NH and CH RDCs in one medium with slight modifications to the equations in Section 9.1 as shown in ref. [151], and as illustrated in Section 2 above.
Most traditional algorithms focus on using NOE restraints to determine protein structure. This approach has been shown to be NP-hard [131], essentially due to the local nature of the constraints. The most notable characteristic of NP-hard problems is that no fast solution to them is known [162]; that is, the time required to solve the problem using any currently-known algorithm increases very quickly as the size of the problem grows. As a result, the time required to provably solve even moderately large versions of many of these problems becomes prohibitive using any currently-available amount of computing power. Here, this implies that no algorithm for computing a structure that globally satisfies a dense network of NOE constraints can be mathematically proven to produce a satisfactory solution in a reasonable time. This is an undesirable property for structure determination software. In particular, in the case of algorithms such as SA/MD and Monte Carlo, no guarantees of soundness, efficiency, or completeness can be made. In contrast, it is remarkable that by primarily using RDCs instead of NOEs, provably polynomial-time algorithms can be obtained, that have guarantees of soundness, efficiency, and completeness.
In practice, approaches such as molecular dynamics and simulated annealing [15, 52], which lack both combinatorial precision and guarantees on running time and solution quality, are used routinely for structure determination. Several structure determination approaches do use RDCs, along with other experimental restraints such as chemical shifts or sparse NOEs [6, 32, 46, 62, 125, 139], yet remain heuristic in nature, without guarantees on solution quality or running time. Unlike previous approaches ([14] is a notable exception), which have either no theoretical guarantees [15, 52, 6, 32, 46, 62, 125, 139], or run in worst-case exponential time [131, 29, 28, 55, 56], recent methodology has shown that it is possible to exploit RDC data, which gives global restraints on the orientation of internuclear bond vectors, in conjunction with very sparse NOE data, to obtain an algorithm that runs in polynomial time and provably computes the structure that agrees best with the experimental data.
These results are consistent with earlier observations [140, 142, 139, 38, 120, 6, 32, 46, 62, 125, 159] that, empirically, RDCs increase the speed and accuracy of biomacromolecular structure determination: rdc-exact formally quantifies the complexity-theoretic benefits of employing globally-referenced angular data on internuclear bond vectors. The main contributions of this work were as follows.
To derive low-degree monomial equations that can be solved exactly and in constant time, to determine backbone (ϕ, ψ) angles from experimentally-recorded RDCs. Only two RDCs per residue are required. For example, after measuring RDCs corresponding to a single internuclear vector v in two different aligning media, the easily-computable exact solutions eliminate the need for one-dimensional grid-search previously employed [159] to compute the direction of v or two-dimensional grid-search [46, 139, 158, 93] to compute (ϕ, ψ) angles. The main results also hold for the case of NH and CH RDCs in one medium with slight modifications to the Wang-Donald equations in Section 9.1, as shown in [151, 156, 174] (see Section 2). Furthermore, these equations are very general and can be extended to compute other backbone and side-chain dihedral angles. The method can be applied mutatis mutandis to derive similar equations for computing dihedral angles from RDCs in nucleic acids.
The first NMR structure determination algorithm that simultaneously uses exact solutions, systematic search and only two RDCs per residue. (A systematic search is a search over all possible conformations (solutions) that employs a provable pruning strategy which guarantees pruned conformations need not be considered further).
The first combinatorially precise, polynomial-time algorithm for structure determination using RDCs, secondary structure type, and very sparse NOEs.
The first provably polynomial-time algorithm for de novo backbone protein structure determination solely from experimental data (of any kind).
An implementation of the algorithm that is competitive in terms of empirical accuracy and speed, but requires much less data than, previous NMR structure determination techniques.
-
Testing and results of the algorithm on protein NMR data.
Representative results from rdc-exact, including RMSD to high-resolution crystal structures and NMR structures, are shown in Figs. 11–12. In addition to these studies several blind tests of rdc-exact were performed, in which the structure was not known ahead of time [174]. NMR data were recorded for the ubiquitin-binding zinc finger domain of the human DNA Y-polymerase eta (polη). [174] used NH and Hα-Cα RDCs recorded in one medium, with typically 10-15% missing data (but up to 32%) in one secondary structure region, plus 9 NOEs between the helix and β-strands. The structure of polη was then computed by rdc-exact, and is shown in Fig. 13L. The rdc-exact structure [174] was compared with the structure being determined (by conventional techniques) in Dr. Pei Zhou's laboratory (Fig. 13C). The core structure (helix and sheet) computed by rdc-exact was 1.28 Å RMSD from the Zhou lab structure (Fig. 13C). In a second test, the same suite of NMR data [174] was obtained for a second protein, the human Set2-Rpb1 interacting (SRI) domain. The global fold of human SRI was determined by rdc-exact, similarly using NH and Hα-Cα RDCs recorded in one medium, plus sparse NOEs. The resulting core structure (a 3-helix bundle) had an RMSD of 1.61 Å to the reference structure (see Fig. 13R). Both reference structures were determined using traditional methods (Xplor [15]) requiring a much larger set of experimental spectra. The accuracy of rdc-exact on these blind tests is comparable to the accuracy achieved in the retrospective studies (Figs. 11–12). The ability of rdc-exact to determine the global fold of polη and human SRI with reasonable accuracy, using only a minimal suite of experiments, that could be collected in a high-throughput fashion, supports the feasibility of the exact solutions approach for structure determination.
rdc-exact can compute β-sheets from RDC data alone, which fundamentally extends previous methods [38] targeting only entirely helical proteins. Unlike α-helices, β-strands are often twisted in globular proteins so it is important to refine them accurately from RDC data. rdc-exact can determine the backbone structures of proteins consisting of either α-helices, β-sheets, or both, and thus has wider application since most proteins have both α-helices and β-sheets.
rdc-exact was the first demonstration that the conformations and orientations of both α-helices and β-strands can be computed accurately and efficiently using exclusively RDCs measured on a single bond vector type (NH) in only two aligning media [152]. Similar accuracies and efficiency were obtained using only NH and CH RDCs in one medium [151, 156, 174]. With a minimum number of additional distance restraints a three-dimensional structure could be computed consequently [152, 156, 174].
Figure 11.
Results of rdc-exact. (a) experimental RDC data for ubiquitin (PDB ID: 1D3Z), Dini (PDB ID: 1GHH) and Protein G (PDB ID: 3GB1) were taken from the Protein Data Bank (PDB). (b) number of residues in α-helices or β-sheets, versus the total number of residues. (c) the total number of experimental RDCs (note that RDCs are missing for some residues). (d) RDCS from different experimental datasets (for different bond vectors) were used. (e) number of hydrogen bonds used. (f) number of NOEs used. (g) RMSD (for Cα, N, and C′ backbone atoms) between the oriented and translated secondary structure elements (excluding loop regions) computed by rdc-exact to reference structures: ubiquitin to a high-resolution X-ray structure (PDB ID:1UBQ); Dini to an NMR structure (PDB ID: 1GHH); and Protein G to an NMR structure (PDB ID: 3GB1).
Figure 12.
Top: Structure of ubiquitin backbone with loops. The ubiquitin backbone structure (blue) was computed by extending rdc-exact to handle loop regions along the protein backbone [156]. The structure was computed using 59 NH and 58 CH RDCs (117 out of 137 possible RDCs, 20 are missing), 12 H-bonds and 2 unambiguous NOEs. Our structure has a backbone RMSD of 1.45 Å with the high-resolution X-ray structure (PDB ID: 1UBQ, in magenta) [147]. Bottom: Comparison of rdc-exact with previous approaches. (a) References to previously-computed ubiquitin backbone structures (including loop regions), (b) Algorithmic technique; (c) Data requirements; (d) Backbone RMSD of structure (for Cα, N, and C′ backbone atoms) compared to the X-ray structure (1UBQ). The structure computed by rdc-exact includes loops and turns, as shown at top. eReferences [152, 151, 156, 155].
Figure 13.

Left: The global fold of polη, computed by rdc-exact using 2 RDCs per residue measured in one medium plus 9 NOEs between the helix and β-strands. Center: Comparison of polη to the reference structure, PDB id: 2I5O. The RMSD of the secondary structure elements is 1.28 Å. Right: Global fold of human SRI, computed by rdc-exact (thick lines) using two RDCs per residue measured in one medium plus sparse NOEs. The reference structure is shown in thin lines (PDB id: 2A7O [86]).
Structure determination using sparse data is an underconstrained problem. Additional constraint may be obtained using structure prediction [73, 126] or homology modeling [121]. The former reduces to decoy detection, pruned by NMR data. The second reduces to biasing the structure determination using the PDB. In both approaches, sparse RDCs can be employed, but, compared with conventional protocols, the resulting structures obtain their authority less from the data and more from modeling or homology. In contrast, the exact solutions technique admits algorithms that can extract more structural information from less NMR data, than had been previously exploited. This can be done using a combination of computer algebra, computational geometry, and statistical methods. Compared with previous algorithms for computing backbone structures using RDCs, rdc-exact achieves similar accuracies but requires less data, relies less on statistics from the PDB and does not depend on molecular dynamics or simulated annealing (Figs. 11–13). Since RDCs can be acquired and assigned much more quickly than NOEs in general, the results show it is possible to compute structures rapidly and inexpensively using mainly RDC restraints.
4 Nuclear Vector Replacement for Automated NMR Assignment and Structure Determination
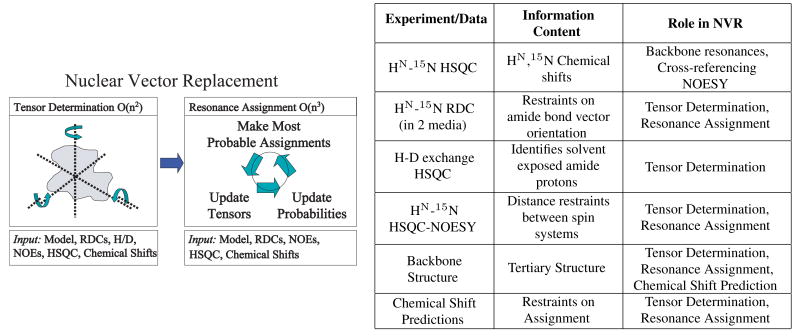
High-throughput NMR structural biology can play an important role in structural genomics. Recent results have generalized and extended structure-based assignment algorithms such as jigsaw [12], to obtain an automated procedure for high-throughput NMR resonance assignment for a protein of known structure, or of an homologous structure [79, 82, 83, 78, 8]. Nuclear Vector Replacement (NVR) uses Expectation/Maximization (EM) to compute assignments (Fig. 14L). NVR is an RDC-based algorithm, which computes assignments that correlate experimentally-measured RDCs, chemical shifts, HN-HN NOEs (which are called dNNs) and amide exchange rates to a given a priori 3D backbone structural model. The algorithm requires only uniform 15N-labeling of the protein, and processes unassigned HN-15N HSQC spectra, HN-15N RDCs, and sparse dNNs, all of which can be acquired in a fraction of the time needed to record the traditional suite of experiments used to perform resonance assignments (Fig. 14R). NVR could form the basis for “Molecular Replacement (MR) by NMR”. RDCs provide global orientational restraints on internuclear bond vectors, (see Eq.(1) and Figs. 2- 3 above). Once the alignment tensor S has been determined, RDCs may be simulated (back-calculated) given any other internuclear vector vi. In particular, suppose an (HN,15N) peak i in an HN-15N HSQC (subsequently termed simply “HSQC”) spectrum is assigned to residue j of a protein, whose crystal structure is known. Let ri be the measured RDC value corresponding to this peak. Then the RDC ri is assigned to amide bond vector vj of a known structure, and we should expect that (although noise, dynamics, crystal contacts in the structural model, and other experimental factors will cause deviations from this ideal).
Figure 14.
Nuclear Vector Replacement. Left: Schematic of the NVR algorithm for resonance assignment using EM. The NVR algorithm takes as input a model of the target protein and several unassigned spectra, including the 15N-HSQC, HN-15N RDC, 15N-HSQC NOESY, and an H-D exchange-HSQC to measure amide exchange rates. In the first phase, NVR computes the alignment tensors for both media using chemical shift prediction, dNNs, H-D exchange-exchange rates and the Expectation/Maximization (EM) algorithm. This step takes time O(n2), where n is the number of residues. In the second phase, chemical shift predictions, dNNs, RDCs in two media and the EM algorithm are used to assign all remaining peaks. This entire process runs in minutes, and is guaranteed to converge in time O(n3). NVR Experiment Suite: Right: The 5 unassigned NMR spectra used by NVR to perform resonance assignment. The HSQC provides the backbone resonances to be assigned. HN-15N RDC data in two media provide independent, global restraints on the orientation of each backbone amide bond vector. The H-D exchange HSQC identifies fast exchanging amide protons. These amide protons are likely to be solvent-exposed and non-hydrogen bonded and can be correlated to the structural model. A sparse number of unambiguous, unassigned dNNs can be obtained from the NOESY. These dNNs provide distance constraints between spin systems which can be correlated to the structural model. Chemical shift predictions are used as a probabilistic constraint on assignment.
SBA approaches use unassigned NMR data, such as RDCs. Note that, in contrast, assigned RDCs have also been employed by a variety of structure refinement [19] and structure determination methods [62, 6, 159], including: orientation and placement of secondary structure to determine protein folds [38], pruning an homologous structural database [7, 96], de novo structure determination [125], in combination with a sparse set of assigned NOEs to determine the global fold [100], and a method for fold determination that selects heptapeptide database fragments best fitting the assigned RDC data [32]. Bax and co-workers termed their technique “molecular fragment replacement” [32], by analogy with x-ray crystallography MR techniques. Unassigned RDCs have been successfully used to expedite resonance assignments [176, 32, 139].
The idea of correlating unassigned experimentally measured RDCs with bond vector orientations from a known structure was first proposed by Al-Hashimi and Patel [4] and subsequently demonstrated by Al-Hashimi et al. [3] who considered permutations of assignments for RNA, and also in reference [63]. Brüschweiler and co-workers [63] successfully applied RDC-based maximum bipartite matching to structure-based resonance assignment. Their technique requires RDCs from several different bond types which, in turn, requires 13C-labeling of the protein and triple resonance experiments. NVR builds on these works and offers some improvements in terms of isotopic labeling, spectrometer time, accuracy and computational complexity. NVR algorithms have addressed the following hypothesis: Are backbone amide RDCs and dNNs sufficient for performing resonance assignment? Like the techniques of Hus et al. [63], NVR calls optimal bipartite matching as a subroutine, but within an Expectation/Maximization (EM) framework that offers some benefits, described below. Previous methods (and later algorithms [67, 64]) required 13C-labeling and RDCs from many different internuclear vectors (for example, C′-15N, C′-HN, Cα-Hα, etc.). NVR uses a different algorithm and requires only amide bond vector RDCs, no triple-resonance experiments, and no 13C-labeling. Moreover, NVR is more efficient. The combinatorial complexity of the assignment problem is a function of the number n of residues (or bases in a nucleic acid) to be assigned, and, if a rotation search is required, the resolution k3 of a rotation-space grid over the Lie group SO(3) of 3D rotations. The time-complexity of the RNA-assignment method, named CAP [3] grows exponentially with n. In particular, CAP performs an exhaustive search over all permutations, making it difficult to scale up to larger RNAs. The method presented in reference [63] runs in time O(In3), where O(n3) is the complexity of bipartite matching [76] and I is the number of times that the bipartite matching algorithm is called. I may be bounded by O(k3), the time to search for the principal order frame (POF) over SO(3). Thus, the full time-complexity of the algorithm presented in reference [63] is O(k3n3). Version 1 of NVR [82, 83, 78] also performed a discrete grid search for the POF over SO(3), but used a more efficient algorithm with time-complexity O(nk3). Once the POF has been computed, resonance assignments are made in time O(n3). Thus, the total running time of NVR Version 1.0 [82, 83] is less: O(nk3 + n3). Zweckstetter and Bax [175] estimated alignment tensors (but not assignments) using permutations of assignments on a subset of the residues identified using either selective labeling or 13Cα/β chemical shifts. If m residues can be thus identified a priori, then this method provides an O(nm6) tensor estimation algorithm that searches over all possible assignment permutations.
NVR Version 2.0 [79] requires neither a search over assignment permutations, nor an explicit rotation search over SO(3). Rather, EM [33] is used to correlate the chemical shifts of the HN-15N HSQC resonance peaks with the structural model. In practice, the application of EM on the chemical shift data is sufficient to uniquely assign a small number of resonance peaks, and directly determine the alignment tensor by singular value decomposition (SVD) – see Fig. 3. NVR 2.0 eliminates the rotation grid-search over SO(3), and hence any complexity dependence on a grid or its resolution k, running in O(n3) time, scaling easily to proteins in the middle NMR size range (n = 56 to 129 residues) [79]. Moreover, NVR elegantly handles missing data (both resonances and RDCs).
NVR adopts a sparse-data, or minimalist approach [12], demonstrating the large amount of information available in a few key spectra. By eliminating the need for triple resonance experiments, NVR saves spectrometer time. The required data (Fig. 14R) can be acquired in about one day of spectrometer time using a cryoprobe. NVR runs in minutes and efficiently assigns the (HN,15N) backbone resonances as well as the sparse dNNs from the 3D 15N-NOESY spectrum. NVR was tested on NMR data from 3 proteins using 20 different alternative structures, all determined either by X-ray crystallography or by different NMR experiments (without RDCs) (Table 1). When NVR was run on NMR data from the 76-residue protein, human ubiquitin (matched to four structures, including one mutant/homolog), it achieved 100% assignment accuracy. Similarly good results were obtained in experiments with the 56-residue streptococcal protein G (SPG) (99%) and the 129-residue hen lysozyme (100%) when they were matched by NVR to 16 3D structural models. Table 1 summarizes the performance of NVR using alternative structures of ubiquitin, SPG, and lysozyme, none of which were refined using RDCs. 1UD7 is a mutant form of ubiquitin where 7 hydrophobic core residues have been altered (I3V, V5L, I13V, L15V, I23F, V26F, L67I). It was chosen to test the effectiveness of NVR when the model is a (close) homolog of the target protein. This success in assigning the mutant 1UD7, suggests that NVR could be applied more broadly to assign spectra based on homologous structures [79, 8]. Thus, NVR could play a role in structural genomics.
Table 1. Backbone Amide Resonance Assignment Accuracy using NVR.
Accuracies report the percentage of correctly-assigned backbone HSQC peaks. aStructural model used. bAccuracy of NVR on the NMR data shown in Fig. 14R for Ubiquitin (i), SPG (ii), and Lysozyme (iii-iv). The 96% accuracy for 2GB1 reflects a single incorrect assignment.
| PDB IDa | Accuracyb |
|---|---|
| 1G6J [10] | 100% |
| 1UBI [123] | 100% |
| 1UBQ [147] | 100% |
| 1UD7 [66] | 100% |
| (i) Ubiquitin | |
| 1GB1 [50] | 100% |
| 2GB1 [50] | 96% |
| 1PGB [39] | 100% |
| (ii) SPG | |
| 193L [146] | 100% |
| 1AKI [9] | 100% |
| 1AZF [90] | 100% |
| 1BGI [106] | 100% |
| 1H87 [47] | 100% |
| 1LSC [77] | 100% |
| 1LSE [77] | 100% |
| (iii) Lysozyme | |
| 1LYZ [35] | 100% |
| 2LYZ [35] | 100% |
| 3LYZ [35] | 100% |
| 4LYZ [35] | 100% |
| 5LYZ [35] | 100% |
| 6LYZ [35] | 100% |
| (iv) Lysozyme | |
5 Protein Fold Determination via Unassigned Residual Dipolar Couplings
Sequence homology can be used to predict the fold of a protein, yielding important clues as to its function. However, it is possible for two dissimilar amino acid sequences to fold to the “same” tertiary structure. For example, the RMSD between the human ubiquitin structure (PDB Id: 1D3Z) and the structure of the Ubx Domain from human Fas-associated factor 1 (Faf1; PDB Id: 1H8C) is quite small (1.9 Å), yet they have only 16% sequence identity. Detecting structural homology given low sequence identity poses a difficult challenge for sequence-based homology predictors. Is there a set of fast, cheap experiments that can be analyzed to rapidly compute 3D structural homology? A new method for homology detection has been developed, called gd, that exploits high-throughput solution-state NMR. This algorithm extends the NVR technique to perform protein 3D structural homology detection, demonstrating that NVR and its generalization gd, are able to identify structural homologies between remote amino acid sequences from a database of structural models. The first paper on protein fold determination using unassigned RDCs was published in RECOMB in April, 2003 [82]. Other papers on this topic include [78] and [83, 80]. One goal of structural genomics is the identification of new protein folds. gd is an automated procedure for detecting 3D structural homologies from sparse, unassigned protein NMR data, and could aid in prioritizing unknown proteins for structure determination. gd identifies the 3D structural models in a protein structural database whose “unassigned geometries” best fit the unassigned experimental NMR data. It does not use sequence information and is thus not limited by sequence homology. gd can also be used to confirm or refute structural predictions made by other techniques such as protein threading or sequence homology.
gd runs in O(pnk3) time, where p is the number of proteins in the database (2,456 in [82, 78, 83]), n is the number of residues in the target protein, and k is the resolution of a rotation search. gd requires only uniform 15N-labeling of the protein and processes unassigned HN-15N RDCs, which can be acquired rapidly. Experiments on NMR data from 5 different proteins demonstrated that gd identifies closely related protein folds, despite low-sequence homology between the target protein and the computed model [82, 78, 83, 80]. The overall rankings of the top predicted homologs are good (Fig. 15). Human Faf1 (1H8C) (discussed above) was identified as a structural homolog of ubiquitin (Fig. 15U). gd does best on lysozyme, where the native structure and 5 homologous structures occupied the top 6 places (Fig. 15L).
Figure 15.

GD, Representative Results. gd was tested on unassigned HN-15N RDCs for 5 proteins [78]; representative scatter plots of RMSD vs. the score computed by GD are shown for human ubiquitin (Top Left) and hen lysozyme (Top Right). Only proteins within 10% of the target protein's length are plotted. Open circles are data points for the native structure (1D3Z for ubiquitin; 1E8L for lysozyme) and five homologous structures (Tables U and L). The + signs are the data points associated with non-homologous proteins. The diamond is the 2D mean of the +'s while the triangle is the 2D mean of the open circles. The trend line shows the correlation between the score computed by gd and RMSD for all the data points. The scores associated with the native fold and the 5 homologs are statistically significantly lower than the scores of unrelated proteins (p-values < 2.7 × 10−5). Tables: GD Results for (U) ubiquitin and (L) lysozyme. The sequence identity and RMSD of these 2 test proteins with their respective top 5 homologs are shown. aThe rank of each model, out of 2,456 proteins in the database, using the score computed by gd. bThe Ubx Domain from human Faf1 (see Sec. 5) was ranked 11th.
gd [82] represented the first systematic algorithm to exploit an unassigned “fingerprint” of RDCs for rapid protein fold determination. After Langmead et al. [82], a similar idea was independently proposed and extended by number of researchers including Prestegard [145, 128], Baker [97], [98], and coworkers. gd was later extended to demonstrate high-throughput inference of protein-protein interfaces using only unassigned NMR data [99], which should be valuable in structural proteomics.
6 Automated NOE Assignment Using a Rotamer Library Ensemble and RDCs
Despite recent advances in RDC-based structure determination (see Sections 2- 3), NOE distance restraints are still important for computing a complete three dimensional solution structure including sidechain conformations. In general, NOE restraints must be assigned before they can be used in a structure determination program. NOE assignment is very time-consuming to do manually, challenging to fully automate, and has become a key bottleneck for high-throughput NMR structure determination. The difficulty in automated NOE assignment is ambiguity: there can be tens of possible different assignments for an NOE peak based solely on its chemical shifts. Most automated NOE assignment approaches [103, 57, 59, 68, 60, 53, 91] rely on an ensemble of structures, computed from a subset of all the NOEs, to iteratively filter ambiguous assignments. Despite this progress, there is room for improvement since previous methods require quite high quality input data. For example, they typically require initializing the assignment/structure determination/assignment cycle with a large number of unambiguous or manually-assigned NOE peaks (e.g., > 5 NOEs per residue in [103]), > 85% complete resonance assignments (including side chains), almost complete aromatic side-chain assignments, a low percentage of noise peaks, and only small errors in chemical shifts (≤ 0.03 ppm for 3D NOESY spectra). Moreover, previous algorithms are heuristic in nature, provide no guarantees on solution quality or running time, and consume many hours to weeks of computation time.
Sparse dipolar couplings have enabled the development of new NOE assignment algorithms, including triangle [153] and Hana [174]. An in-depth understanding of Hana would require a review of the minimum Hausdorff distance [37] and Chernov tail bounds [174], which are beyond the scope of this review. Therefore, we describe the conceptually-simpler triangle algorithm; since the information content of the input data is identical, triangle will illustrate the basic paradigm. The interested reader can consult Zeng et al. [174] for a description of Hana, which extends triangle and is more general and robust. triangle begins with known resonance assignments and an accurate backbone structure computed using rdc-exact (Sections 2- 3, [152, 151, 156]). In principle, another structure determination algorithm could be used instead. However, rdc-exact is the only algorithm that can compute a complete protein backbone structure de novo using only two RDCs per residue. triangle uses the backbone structure determined by rdc-exact to boot-strap the automated assignment of NOEs: the assignment proceeds by filtering the experimentally-measured NOEs based on consistency with the backbone structure.
One novel feature of triangle is the use of a rotamer-library-derived ensemble of intraresidue vectors between the backbone atoms and side-chain protons to reduce the ambiguity in the assignment of NOE restraints involving side-chain protons, especially aliphatic protons. The rotamer database was built from ultra-high resolution structures (<1.0 Å) in the PDB [153]. triangle merges this ensemble of intra-residue vectors, together with internuclear vectors from the computed backbone structure. For example, consider the putative assignment of an NOE to an (HN,Hδ) pair of protons. The triangle relationship (Fig. 16L) defines a decision procedure to filter NOE assignments by fusing information from RDCs (vNβ), rotamer modeling (vβδ), and NOEs (|vNδ|). More details of the triangle algorithm are provided in [153, 174] and Section 9.3 below.
Figure 16.
Left: The triangle relationship, defines a decision procedure to filter NOE assignments by fusing information from structure (vNβ), modeling (vβδ), and experiment (|vNδ|). An accurate backbone structure is first computed using only 2 RDCs per residue (Section 3). The vector vNβ is computed from this backbone structure, vβδ is a rotamer ensemble-based intra-residue vector mined from the PDB. The computed length of vNδ is compared with the experimental NOE distance dN (measured using NOE crosspeak intensities) to filter ambiguous NOE assignments. The complexity of NOE assignment is O(n2 log n), where n is the number of protons in the protein. One cycle of NOE assignment suffices when a well-defined backbone structure is computed using rdc-exact. In practice, it took less than one second to assign 1783 NOE restraints from the NOE peak list picked from both the 3D 15N-edited and 13C-edited NOESY spectra of human ubiquitin. Right and Center: The NMR structures computed from the automatically-assigned NOEs. The middle panel shows the 12 best NMR structures with no NOE distance violation larger than 0.5 Å. The side-chains are blue; the backbone is magenta. The right panel is the overlay of the NMR average structure (blue) with the 1.8 Å x-ray structure (magenta) [147].
In [153], rdc-exact was first employed to compute an accurate backbone structure of ubiquitin using only two backbone RDCs per residue (Fig. 12L, [152, 151, 156]). Next, triangle was successfully applied to assign more than 1,700 NOEs, with better than 90% accuracy on the experimental 15N- and 13C-edited 3D NOESY spectra for ubiquitin [153]. The result of the automated assignment is summarized in Table 2. Out of the 1153 NOE peaks picked from the 15N-edited NOESY spectrum, 1083 originate from backbone amide protons, the remaining 50 are from side-chain amide protons. Only 420 NOE peaks originating from backbone Hα protons could be picked from the 13C-edited NOESY spectrum. triangle was able to assign 1053 NOE peaks from the 1083 peaks picked from 15N-edited NOESY spectrum and 393 peaks from the 420 peaks picked from 13C-edited NOESY spectrum. The assigned NOE distance restraints are divided into two classes: sequential NOEs and medium/long-range NOEs (Table 2). The number of assigned NOE distance restraints is larger than the number of assigned peaks since it is possible that more than one NOE restraint could be assigned to a single peak. It took less than one second on a 2.4 GHz single-processor Linux workstation for triangle to compute the assignments.
Table 2. NOE restraints automatically assigned by triangle.
(a) NOEs between residue i and i + 1, (b) NOEs between residue i and i + j where 1 < j < 4, and (c) NOEs between residue i and i + j where j ≥ 4. No.: Number
| Spectrum | No. of Peaks | No. of Assigned NOEs | No. of Sequential NOEs(a) | No. of Medium(b), long-range NOEs(c) |
|---|---|---|---|---|
| 15N-NOESY | 1083 | 1288 | 822 | 466 |
| 13C-NOESY | 420 | 495 | 228 | 167 |
To test the quality of the 1783 NOE restraints automatically generated and assigned by triangle (Table 2), [153] then used these restraints to calculate the structure of ubiquitin, using a hybrid distance-geometry and SA protocol (xplor [15]). No RDC restraints were used. In the resulting ensemble of 70 structures, 163 restraints had NOE violations larger than 0.5 Å in 50 structures. However, none of the NOE violations was larger than 2.5 Å. After these 163 restraints were deleted from the NOE list, Xplor was invoked for a second time to compute the structures using the remaining 1620 NOE restraints. Twelve structures out of 70 total computed structures had no NOE violations larger than 0.5 Å. Thus, the NOE assignment algorithm had an accuracy of 91%, and the incorrect assignments could easily be detected and removed. The 12 best NMR structures (Fig. 16C) can be overlayed with a pairwise RMSD of 1.18 ± 0.16 Å for backbone atoms and a pairwise RMSD of 1.84 ± 0.19 Å for all heavy atoms. The accuracy of the structures computed using the automatically-assigned NOEs from triangle is in the range of typical high- to medium-resolution NMR structures. The average structure (Fig. 16R) computed from the best 12 structures has a 1.43 Å backbone RMSD and 2.13 Å all heavy-atom RMSD from the 1.8 Å ubiquitin X-ray structure [147]. Hana, a successor to triangle, was tested on additional proteins, resulting in similarly good accuracies [174].
7 NMR Structure Determination of Symmetric Homo-oligomers
Symmetric homo-oligomers play pivotal roles in complex biological processes including ion transport and regulation, signal transduction, and transcriptional regulation. RDCs were recently used in studies of phospholamban, a symmetric homo-pentameric membrane protein that regulates the calcium levels between cytoplasm and sarcoplasmic reticulum and hence aids in muscle contraction and relaxation [111]. Ion conductance studies [75] also suggest that phospholamban might have a separate role as an ion channel. To understand the dual function of phospholamban and other such symmetric homo-oligomers, a combined experimental-computational approach, symbrane [117, 118], determined their structures using sparse inter-subunit NOE distance restraints and van der Waals (vdW) packing. In this case, the RDCs were used to refine the subunit structure.
symbrane is complete in that it tests all possible conformations, and it is data-driven in that it first tests conformations for consistency with data and only then evaluates each of the consistent conformations for vdW packing. Completeness in a structure determination method is a key requirement since it ensures that no conformation consistent with the data is missed. This avoids any bias in the search, as well as any potential for becoming trapped in local minima, problems inherent in energy minimization-based approaches. (rdc-exact, described above in Sections 2- 3, is also complete). The data-driven nature of symbrane allows one to independently quantify the amount of structural constraint provided by data alone, versus both data and packing. This avoids overreliance on subjective choices of parameters for energy minimization, and consequent false precision in determined structures. Analogously to single particle analysis in cryoelectron microscopy [107], symbrane also allows determination of the oligomeric number of the complex. symbrane was the first approach that determines the oligomeric number of a symmetric homo-oligomer from inter-subunit NOE distance restraints. The complete ensemble of NMR structures of the human cardiac phospholamban pentamer, determined by symbrane, was reported by Potluri et al. [117] and deposited in the PDB (id: 2HYN).
symbrane exploits the observation that, given the structure of a subunit, the structure of a symmetric homo-oligomer is completely determined by the parameters (position and orientation) of its symmetry axis. Thus we can formulate structure determination as a search in the space of all symmetry axis parameters, symmetry configuration space (SCS). symbrane performs a branch-and-bound search in the SCS, which defines all possible Cn homo-oligomeric complexes for a given subunit structure. It eliminates those symmetry axes inconsistent with NOE distance restraints and then identifies conformations representing any consistent, well-packed structure.
symbrane consists of two phases. The first phase performs a complete, data-driven search in SCS and returns consistent regions in SCS, that is, regions representing all conformations consistent with (i.e., satisfying) the data. In the second phase, all satisfying structures are evaluated for vdW packing. symbrane computes a set of well-packed satisfying (WPS) structures that are not only consistent with data, but also have high-quality vdW packing. symbrane explicitly quantifies the uncertainty in determined structures using the size of the regions in SCS and the variations in atomic coordinates in the structures. The difference in uncertainty between the satisfying structures and the WPS structures illustrates the relative precision that is possible from data alone, versus data and packing together. symbrane simultaneously assigns the intermolecular NOEs during the SCS search for structure determination [118]. This assignment resolves the ambiguity as to which pairs of protons generated the observed NOE peaks, and thus should be restrained in structure determination.
For inter-subunit NOEs in symmetric homo-oligomers, the ambiguity includes both the identities of the protons and the identities of the subunits to which they belong. symbrane resolves both ambiguities to determine its structures, and returns all structures consistent with the available data (ambiguous or not). However, while symbrane is complete, it avoids explicit enumeration of the exponential number of combinations of possible assignments. symbrane geometrically prunes SCS regions and NOE assignments that are mutually inconsistent. Pruning occurs only due to provable inconsistency and thereby avoids the pitfall of local minima that could arise from best-first sampling-based approaches. Ultimately, symbrane returns a mutually-consistent set of conformations and NOE assignments. symbrane can draw two types of conclusions not possible under previous methods: (a) that different assignments for an NOE would lead to different structural classes, or (b) that it is not necessary to assign an NOE since the choice of assignment would have little impact on structural precision.
In contrast to previous techniques, symbrane separately quantifies the amount of structural constraint provided by data alone, versus data and packing (Fig. 18d). For the human phospholamban pentamer in dodecylphosphocholine micelles, using the structure of one subunit determined from a subset of the experimental NMR data, symbrane identifies a diverse set of complex structures consistent with the nine inter-subunit NOE restraints [117]. The distribution of structures determined in the ensemble (PDB Id 2HYN) provides an objective characterization of structural uncertainty: incorporating vdW packing reduced the structural diversity by 29% and average variance in backbone atomic coordinates by 44%.
Figure 18.

symbrane Algorithm. (a) Given the subunit structure, the relative position t ∈ ℝ2 and orientation a ∈ S2 of the symmetry axis uniquely determines structure. Structure determination is a search problem in 4-dimensional symmetry configuration space (SCS), S2 × ℝ2. An NOE is shown between protons p and q′. (b) The branch-and-bound algorithm proceeds as a tree search in SCS. The 4D SCS is represented as two 2D regions, a sphere representing the orientation space S2 and a square representing the translation space ℝ2. The dark shaded regions at each node of the tree represent the region in SCS being explored (A × T ⊂ S2 × ℝ2). Ultimately (bottom left of the tree) the branch-and-bound search returns regions in 4D space representative of structures that possibly satisfy all the restraints. At each node, we test satisfaction of each restraint of form pq′ ≤ d by testing intersection between the ball of radius d centered at p and the convex hull bounding possible positions of q′. If there exists an intersection between the ball and the convex hull for each restraint, further branching is done (node 1); otherwise, the entire node and its subtree are pruned (node 2). (c) Representative results: Complete ensemble of NMR structures of the unphosphorylated human Phospholamban pentamer, PDB id: 2HYN [117]. (d) Phospholamban restraint satisfaction score vs. packing score for all structures. The vertical and horizontal lines indicate the cutoffs for WPS structures: 1 Å for the satisfaction score and 0 kcal/mol for the packing score. The green stars and the blue crosses indicate the set of satisfying structures. The magenta points indicate the set of non-satisfying structures that have been pruned. The green stars indicate the set of WPS structures and the red star indicates the reference structure.
By comparing data consistency and packing quality in a search using different assumptions of oligomeric number, symbrane identified the C5 pentamer as the most likely oligomeric state of phospholamban, demonstrating that it is possible to determine oligomeric number directly from NMR data. Additional tests on six other homo-oligomers, from dimer to heptamer, similarly demonstrated the power of symbrane to provide unbiased determination and evaluation of homo-oligomeric complex structures [117, 118].
8 Applications and Connections to Other Biophysical Methods
Both NVR and symbrane are structure-based (in that they exploit priors on the monomer structure) and have clear analogies to molecular replacement (MR) in X-ray crystallography, and its leverage of subunit structure and non-crystallographic symmetry (NCS). At the heart of NVR is a novel rotation search (over 3D rotation space, SO(3)), and at the core of symbrane is novel exploitation of the kinematics of Cn symmetry. It is possible to generalize and apply these algorithms to help expedite structure determination even using very different experiments (crystallography). To analyze NCS in MR-based X-ray diffraction data of biopolymers, one must “recognize” a finite subgroup of SO(3) out of a large set of molecular orientations. This problem may be reduced to clustering in SO(3) modulo a finite group, and solved efficiently by “factoring” into a clustering on the unit circle followed by clustering on the 2-sphere S2, plus some group-theoretic calculations [89]. This yields a polynomial-time algorithm, crans, that is efficient in practice, and which enabled determination of the structure of dihydrofolate reductase-thymidylate synthase (DHFR-TS) from Cryptosporidium hominis, PDB id: 1QZF [110, 109, 89]. Cryptosporidium is an organism high on the bioterrorism list of the Centers for Disease Control, a Category B bioterrorist threat. There is currently no drug therapy for cryptosporidosis. The enzyme DHFR-TS is in the sole de novo biosynthetic pathway for the pyrimidine deoxyribonucleotide dTMP, and therefore an attractive drug target. Solving the structure of DHFR-TS from C. hominis enabled species-specific drug design [5, 116], exploiting structural differences between the human enzyme and C. hominis DHFR-TS.
In general, algorithms like NVR and symbrane are often promiscuous, in that such tools can be applied to many problems in structural biology. The crans NCS method for MR [89, 110, 109] in X-ray crystallography generalized NVR rotation search algorithms that were originally proposed for a different problem, NMR assignment [82, 83, 78, 79]. Similarly, work in target selection for structural and functional genomics [84, 81, 87] has applied algorithms from NMR signal processing such as maximum entropy spectral analysis. Recent work on enzyme redesign in the non-ribosomal peptide synthetase pathway [88, 136, 45, 44] (using crystallography and site-directed mutations) generalized algorithms for modeling NMR ensembles [49, 11] and rotamers for NOE assignment [153, 174]. These rotamer optimization algorithms [88, 45, 44] can, in turn, be used as a tool in structure determination as discussed below in Sections 9.3–9.4.
9 Looking Under the Hood: How the Algorithms Work, and Outlook for Future Developments
In the future, one expects improvements and extensions to the algorithms described above. In particular, the primary goals focus on robustness and scaling. We wish the algorithms to be more robust to noise and missing data. We want the implemented systems to scale to run successfully on more proteins, and larger proteins. A number of smaller steps and subgoals are forseen to achieve these goals. In this section, we describe in more detail how the algorithms work so the reader can develop an appreciation both for their scope and how they may be extended and improved.
In general, but particularly for rdc-exact, it is useful for the algorithms and software to allow users a choice: to record either (i) one type of backbone RDC (such as NH RDCs) in two aligning media, or (ii) two types of backbone RDCs (such as NH and CH RDCs) in a single medium. This flexibility allows application to a wider range of proteins. Experimental NH RDCs in two media require only an 15N-labeled sample, which is an order of magnitude cheaper to prepare than a doubly-labeled 15N/13C sample. However, it is not always straightforward to find two aligning media for a protein; in this case the algorithm can use use NH and CH RDCs in a single medium since recording an extra set of RDCs in the same medium requires only slightly more spectrometer time. New methods [127] will be very useful for measuring RDCs in multiple alignment media.
9.1 Exact solutions for computing backbone dihedral angles from RDCs
rdc-exact is an exact solution, systematic search-based algorithm for structure determination. We now describe the outlook for such algorithms, focusing on robustness and scaling. We wish the algorithm to be more robust to noise and missing data, and to run successfully on more proteins, and larger proteins. In this section, we describe in more detail how the algorithms work, so the reader can develop an appreciation both for their scope, and how they may be extended and improved.
rdc-exact was developed both as a de novo structure determination algorithm and as a tool in “MR for NMR.” In particular, NVR assignments are structure-based. However, rdc-exact does not currently exploit (or require) structural priors. Thus, a naïve implementation of the MR-like pathway in Fig. 1 might ignore the structural homolog found by gd, and hence lose information. However, rdc-exact could use the structural homologs found by gd as a bias in structure determination. More specifically: rdc-exact is currently a de novo structure determination method, starting with resonance assignments. Those assignments could either come from NVR or from conventional triple-resonance experiments. Indeed, in the case where gd detects (from unassigned NMR data) a novel fold, not in the database (Fig. 1), one can use algorithms for de novo assignment, that process either triple-resonance experiments or sequential connectivities deduced from short-range NOEs [22, 105, 149, 70, 148, 12]. However, for a non-novel fold, the structural model determined by gd can be exploited to bias the choice in rdc-exact of polynomial roots representing the backbone dihedral angles. Initially these were chosen by Ramachandran fitness; we now describe an improved version of rdc-exact that exploits bias towards a priori structure in the regions of regular secondary structure and low dynamics. A series of filters can be employed to choose between the discrete, finite roots representing conformations. These filters (which may be viewed as a fitness function) combine the fit to the data, modeling (Ramachandran fitness), and structural homology (from gd). In the case of missing data [156], or for denatured or disordered proteins [154], one can introduce into the fitness function van der Waals or molecular mechanics energies [114, 15, 117]. This increases reliance on modeling, using an empirical energy function to compensate for missing data. Such fitness functions may combine sources of data and modeling using relative weights. The choice of these weights can be problematic [124]. By converting each term of the fitness function to a Bayesian probability (proposed by Nilges [124], and successfully employed in characterizing denatured structures [154] and automated assignments [105]) the resulting probabilities can be combined as log likelihood (the sum of the logarithms of the probabilities), without explicit weights, thereby reducing subjectivity.
When 13C chemical shifts are available, talos [25] can be used for secondary structure determination and to provide restraint on the polynomial roots representing (ϕ,ψ) angles. Once rdc-exact has used sparse RDCs to determine the conformations and orientations of elements of secondary structure, these fragments are rigidly translated using sparse NOEs [152, 174] or PREs [154]. Connecting loops between these elements can then be solved (as shown in Fig. 12L and [156, 174]). Without NMR data, this would reduce to the kinematic loop closure problem (KLCP), which can be addressed using computer algebra or optimization techniques [74, 134, 104, 26, 27]. With RDC data, the polynomial system of the KLCP can be combined with the quartic and quadratic RDC monomials (Eqs. 7,10 below) to simultaneously find satisfying solutions (conformations) to the KLCP and the RDC equations. This simultaneous bicriterion optimization search requires solving higher-degree polynomials, which can be approximated using homotopy continuation or solved exactly using multivariate resultant or Gröbner basis methods, as presented in [37]. Since the Ramachandran plot is less informative for loops, the enhanced filters above, that incorporate packing and empirical molecular mechanics energies, are helpful outside regions of regular secondary structure. One can also employ a modified version of the robotics-based CCD algorithm [174]. One can represent the loop residues as a conformation tree (Fig. 9) [152, 88, 156, 174], and filter/search it for the loop ensemble that best fits the experimental RDCs (and any available long-range NOEs). Recent results suggest that this search can return a structural loop ensemble with good stereochemistry that simultaneously solves the KLCP consistent with the experimental NMR measurements [156, 174].
rdc-exact should be particularly useful for the studies of large protein complexes because backbone resonances and associated RDCs can be readily assigned and measured even in a very large protein, such as the 82 kDa malate synthase G [144, 143]. The rdc-exact algorithm computes backbone dihedral angles from two RDCs per residue, in constant time per residue. It is possible to derive, from the physics of RDCs, low-degree monomials (with degree at most 4) whose solutions give the backbone (ϕ,ψ) angles.
We describe the methodology and protocol for exact solutions assuming that we are given assigned NH RDCs in two media. These methods also hold for the case of NH and CH RDCs in one medium with slight modifications to the equations below, as shown in Section 2 and reference [151]. For ease of exposition, we assume that the dipolar interaction constant Dmax is equal to 1. By considering a global coordinate frame that diagonalizes the alignment tensor, Eq. (1) becomes:
| (2) |
where Sxx, Syy and Szz are the three diagonal elements of a diagonalized Saupe matrix S (the alignment tensor), and x, y and z are, respectively, the x, y, z-components of the unit vector v in a principal order frame (POF) which diagonalizes S. Now, S is a 3 × 3 symmetric, traceless matrix with five independent elements [140, 142]. Given NH RDCs in two aligning media, the associated NH vector v must lie on the intersection of two conic curves [135, 159]. We now derive the Wang-Donald Equations (Eqs. 7, 10, and 13) below), that permit the (ϕ,ψ) backbone dihedral angles to be solved exactly and in closed-form, given protein kinematics and two RDCs per reside. Very similar equations have been derived for NH and CαHα RDCs measured in a single medium (see Section 2 and reference [151]).
Proposition 1 [152]
Given the diagonal Saupe elements Sxx and Syy for medium 1, and for medium 2 and a relative rotation matrix R between the POFs of medium 1 and 2, the square of the x-component of the unit vector v satisfies a monomial quartic equation.
The following is a sketch of the proof. The methods for the computation of the seven parameters (Sxx, Syy, , and R12) and the full expressions for the polynomial coefficients and temporary variables (a2, b2, c1, etc.) can be found in reference [152].
Proof Sketch
Fix a backbone NH vector v along the backbone and let r (Eq. 2) and be the experimental RDCs for v in the first and second medium, respectively. We have (x′ y′ z′)T = R(x y z)T, where x, y, z are the 3 components of v in a POF of medium 1, r′ and x′, y′, z′ are the corresponding variables for medium 2. Let R = (Rij)i,j=1,…, 3. Eliminating x′, y′ and z′ we have
| (3) |
| (4) |
where , , and a1, b1, b2, c0, …, c4 are similar constants; full details are given in reference [152].
Eliminating z from Eq. (3) we obtain
| (5) |
where , and d7, d6, …, d0 are analogously defined; these are fully specified in [152]. Eq. (5) is a degree 8 monomial in x after direct elimination of y using Eq. (4). However, it can be reduced to a quartic equation by substitution since all terms have even degree. Introducing new variables t and u such that
| (6) |
and through algebraic manipulation we finally obtain the Wang-Donald Equation of type I for NH vectors from RDCs in 2 media:
| (7) |
The full expressions for coefficients a, b, f0, f1, f2, f3, f4 are given in reference [152]. Since Eq. (7) is also a quartic equation in x2.
Similar equations to Eq. (7) have been derived for NH and CαHα RDCs measured in a single medium (see Section 2 and reference [151]). The y-component of v can be computed directly from Eq. (6). Due to two-fold symmetry in the RDC equation the number of real solutions for v is at most 8. We will refer to the bond vector between the N and Cα atoms as the NCα vector. Given two unit vectors in consecutive peptide planes we can use backbone kinematics to derive quadratic equations to compute the sines and cosines of the (ϕ, ψ) angles:
Proposition 2 [152]
Given the NH unit vectors vi and vi+1 of residues i and i + 1 and the NCα vector of residue i the sines and cosines of the intervening backbone dihedral angles (ϕ, ψ) satisfy the trigonometric equations sin (ϕ + g1) = h1 and sin (ψ + g2) = h2, where g1 and h1 are constants depending on vi and vi+1, and g2 and h2 depend on vi, vi+1, sin ϕ and cos ϕ. Furthermore, exact solutions for sin ϕ, cos ϕ, sin ψ, and cos ψ can be computed from a quadratic equation by tangent half-angle substitution.
The following is a sketch of the proof. Full expressions for the polynomial coefficients and temporary variables (x1, y1, z1, x2, y2, z2, g1, h1, g2, h2) introduced in the proof are given in reference [152].
Proof Sketch
Using backbone inverse kinematics, the two NH vectors vi and vi+1 can be related by 8 rotation matrices between two coordinate systems in peptide planes i and i + 1:
| (8) |
The definitions of the coordinate systems, the expressions for the rotation matrices Rx, Ry and Rz and the definitions of the six backbone angles (θ1, θ3, θ5, θ6, θ7 and θ8) are given in reference [152]. The backbone (ϕ, ψ) angles are defined according to the standard convention. Given the values of these six angles Rl = Rx(θ7)Ry(θ6)Rx(θ5) and Rr = Ry(θ8)Rx(θ1) are two 3 × 3 constant matrices. Define two new vectors w1 = (x1, y1, z1) = Rl−1vi and w2 = (x2, y2, z2) = Rrvi+1 to obtain
| (9) |
By Eq. (9) we can then obtain the Wang-Donald Equation of type II for the ϕ dihedral angle from RDCs in 2 media:
| (10) |
where
| (11) |
and g1 is a similar constant; see reference [152] for details. The values of sin ϕ and cos ϕ can be computed from a quadratic equation by the substitution
| (12) |
Substituting the computed sin ϕ and cos ϕ into Eq. (9) we can obtain the analogous Equation of type II for the ψ dihedral angle from RDCs in 2 media [152]; it is another simple trigonometric equation:
| (13) |
Hence, sin ψ and cos ψ can be computed similarly from a quadratic equation where both g2 and h2 ≤ 1 are computed from y1, x2, y2, z2, θ3, sin ϕ and cos ϕ.
Similar equations to Eqs. (10–13) have been derived for NH and CαHα RDCs measured in a single medium (see Section 2 and reference [151]).
The structures computed by rdc-exact may be slightly different from structures computed using traditional protocols (Section 3), which use different data, more data, and rely more upon modeling. In contrast to, for example, simulated annealing approaches, rdc-exact is built upon the exact solutions for computing backbone (ϕ, ψ) angles from RDC data and systematic search. rdc-exact is guaranteed to compute the global minimum (the best fit, or maximum likelihood solution to the data) and hence is provable in terms of completeness, correctness, and complexity. We caution that in the context of rdc-exact, the term ‘provably correct’ refers to the computational correctness of the algorithm. It is not meant to imply that the rdc-exact structures computed using the above modeling assumptions (i.e., standard protein covalent geometries, pruning of (ϕ, ψ) solutions using the Ramachandran plot and steric clashes) will always compute biologically correct structures. More precisely, the proofs guarantee accuracy (of the computed structures) and optimality (of the maximum likelihood structure) up to, but only up to the accuracy of the modeling assumptions. One can relax the modeling assumptions and improve their accuracy, as outlined above. However, a helpful first step has been to develop an algorithm that is provably correct up to the limitations of the initial model. It is unusual for protein structure determination algorithms to have guarantees of computing the optimal structure, in polynomial time. rdc-exact has both these desirable properties [156], and hence promises significant advantages as a method to compute structures accurately using only very sparse restraints.
For smaller proteins it may be possible to collect side-chain RDCs, in which case rdc-exact can be extended to compute side-chain conformations. One can extend the algorithms to compute complete protein structures (including side-chains), since exact equations analogous to Eqs. (7,10) can be derived mutatis mutandis to compute the side-chain dihedral angles χ1, χ2, … from side-chain RDCs. In this case, the average or Ramachandran angles used as root-filters in [152], may be replaced with modal side-chain rotamer library angles χa,1, χa,2, … One can also expedite protein structure determination using pseudocontact shift restraints [72] or carbonyl chemical shift anisotropy upon alignment [167], since similar equations can be derived for computing the corresponding vector orientation and dihedral angles.
9.2 Nuclear Vector Replacement and Fold Recognition using Unassigned RDCs
NVR-like algorithms for automated assignment form a cornerstone for molecular-replacement (MR) type methods for NMR starting with only unassigned data. Since gd can be viewed as the application (filtering) of NVR modules to a database (as opposed to a single structure), improvements to NVR will, mutatis mutandis, improve the accuracy and performance of gd. Note that unlike MR (in crystallography), NVR/gd is sufficiently efficient computationally that it can be applied to thousands of template structures in a short time.
NVR uses two classes of constraints: geometric and probabilistic (Fig. 14). The HN-15N RDC, H-D exchange and 15N-NOESY each provide independent geometric constraints on assignment. A sparse number of dNNs are extracted from the unassigned NOESY after the diagonal peaks of the NOESY are cross-referenced to the peaks in the HSQC. These dNNs provide distance restraints for assignments. In general, there are only a small number of unambiguous dNNs that can be obtained from an unassigned 3D 15N-edited NOESY. The amide exchange information probabilistically identifies the peaks in the HSQC corresponding to non hydrogen bonded, solvent-accessible backbone amide protons. RDCs provide probabilistic constraints on each backbone amide-bond vector's orientation in the POF. Finally, chemical shift prediction is employed [79] to compute a probabilistic constraint on assignment. NVR exploits the geometric and probabilistic constraints by combining them within an Expectation/Maximization framework.
NVR can be improved by exploiting different, but still efficient experiments. Currently, NVR uses amide exchange experiments to distinguish surface from buried residues [79]. This “inside/outside” information is correlated with the structural model, and increases assignment accuracy. When these experiments may be impractical for larger proteins, one can, in principle, employ paramagnetic quenching [172] or “water HSQC” experiments [41, 51], which identify fast-exchanging or solvent-exposed backbone protons. Since this information is complementary to the slow-exchange protons identified by H-D exchange, it likely could be integrated into NVR by complementing the corresponding edge weights in a bipartite graph, which we shall discuss below. Similarly, it is probable that assignment accuracy will improve by incorporating CH RDCs into NVR and gd, since in helices the Cα-Hα bond vector orientations are less degenerate than NH vectors, thereby both improving tensor accuracy in the bootstrapping phase and increasing disambiguation of helical RDCs in the assignment phase. 4-dimensional 15N-,15N- and 13C-,15N-edited NOESY experiments [21] from singly and doubly labeled samples, respectively, will reduce the ambiguity in both spin systems and assignments, and facilitate matching of NOE restraints to structural models. While the acquisition time for 4D NOESY is longer, the direct polar Fourier transformation holds great potential to speed up data collection significantly, by producing quantitatively accurate spectra from radial and concentric sampling [23, 13].
The ultimate goal is to make NVR useful in an analogous manner to molecular replacement (MR) in crystallography. To do this NVR has been extended to operate on more distant structural homologs [8]. The relative sensitivity of RDCs to structural noise is evident in Eq. (1), from the quadratic dependence on the bond vector v versus the linear dependence on the alignment tensor S. In the NVR scoring function, the M step of the EM algorithm uses edge weights to compute the joint probability of the resonance assignments in an ensemble of bipartite graphs. This score is a maximum likelihood estimator of assignment accuracy, and as parameters and inputs to the algorithm (such as the structural model and alignment tensor) are varied, its log likelihood may be optimized. As cross-validation, an alternative scoring function, proposed in [79], employs the mean tensor consistency computed from an ensemble of subsets of assignments against the structural model. In principle, both methods allow a parametric family of structural models to be explored about the putative homolog, enabling NVR to bootstrap assignments analogously to the role of MR, starting with a structural homolog in crystallography. Indeed, traditional (X-ray) MR had previously been extended to solve phase problems from more distant models by using normal mode analysis (NMA) [138, 137]. Analogously, one can perform a geometric exploration of conformation space to generate an ensemble of neighboring structures to the initial homolog using NMA [8].
NMA can be performed as described traditionally [58, 17] or with a Gaussian network model [141]. It would also be valuable to compare and geometrically simulate diffusive motions to sample the internal mobility of the protein using alternative techniques such as froda, first, and rock [65, 173, 161], that are based on graph rigidity theory. The structures that maximize the likelihood of assignment accuracy can then be used for NVR [8]. An allied idea was used earlier by Baker and co-workers for decoy detection in the context of pruning structure predictions by NMR data [97]. NVR-NMA ensembles [8] are different in that they systematically represent the deformation space for equilibrium protein motions, rather than a family that mixes correct and incorrect structures. It appears that as in [138], the NMA-like approaches above can adequately sample the necessary convolution of structural variation, noise, and dynamics around the target structure [8].
We now review a number of technical and algorithmic features of NVR. NVR uses a variation of the EM algorithm [79], which is a statistical method for computing the maximum likelihood estimates of parameters for a generative model. EM has been a popular technique in a number of different fields, including machine learning and image understanding. It has been applied to bipartite matching problems in computer vision [30]. Bipartite matching is extremely sensitive to noise in the edge weights. There is evidence that sophisticated algorithms such as EM or NVR must be employed if bipartite matching is to be used as a subroutine on data that is sparse or noisy [79, 8]. In the EM framework there are both observed and hidden (i.e., unobserved) random variables. In the context of structure-based assignment, the observed variables are the chemical shifts, unassigned dNNs, amide exchange rates, RDCs, and the 3D structure of the target protein. Let X be the set of observed variables.
The hidden variables Y = YG∪YS are the true (i.e., correct) resonance assignments YG, and YS, the correct, or ‘true’ alignment tensors. Of course, the values of the hidden variables are unknown. Specifically, YG is the set of edge weights of a bipartite graph, G = {K, R, K × R}, where K is the set of peaks in the HSQC and R is the set of residues in the protein. The weights YG represent correct assignments, therefore encode a perfect matching in G. Hence, for each peak k ∈ K (respectively, residue r ∈ R), exactly one edge weight from k (respectively r) is 1 and the rest are 0.
The probabilities on all variables in Y are parameterized by the ‘model’, which is the set Θ of all assignments made so far by the algorithm. Initially, Θ is empty. As EM makes more assignments, Θ grows, and both the probabilities on the edge weights YG and the probabilities on the alignment tensor values YS will change. The goal of the EM algorithm is to estimate Y accurately to discover the correct edge weights YG, thereby computing the correct assignments. The EM algorithm has two steps; the Expectation (E) step and the Maximization (M) step. The E step computes the expectation E (Θ ∪ Θ′|Θ) = E(log P(X, Y|Θ ∪ Θ′)). Here, Θ′ is a non-empty set of candidate new assignments that is disjoint from Θ. The M step computes the maximum likelihood new assignments . Then the master list of assignments is updated, Θ ← Θ ∪ Θ*.
The alignment tensors are re-computed at the end of each iteration, using all the assignments in Θ. Thus, the tensor estimates will be continually refined during the run of the algorithm. The algorithm terminates when each peak has been assigned.
Care must be taken to implement the probabilistic EM framework efficiently; for details see [79]. In brief: Individual bipartite graphs are constructed for each of the 7 sources of data (See Table 14. NVR operates on bipartite graphs between peaks and residues. The edge weights from each peak to all residues form a probability distribution. The probabilities are derived from 1) “inside/outside” experiments (H-D exchange, paramagnetic quenching), 2) dNNs, 3) chemical shift predictions based on average chemical shifts from the BMRB [132], 4) chemical shift predictions made by the program shifts [169], 5) chemical shift predictions made by the program shiftx [101], and 6-7) constraints from RDCs in two media).
Data (1-7) above are converted into constraints on assignment. The difference between the experimentally-determined chemical shifts and the set of predicted chemical shifts are converted into assignment probabilities. Let S1 and S2 be the alignment tensors computed from unassigned data as described in Section 4 and references [79, 82, 83, 78]. The amide bond vectors from the structural model are used to back-compute a set of RDCs using Eq. (1). The difference between each back-computed RDC and each experimentally recorded RDC is converted into a probability on assignment. Let Dm be the set of observed RDCs in medium m, and Fm be the set of back-computed RDCs using the model and Sm. Two bipartite graphs M1 and M2 are constructed on the peaks in K and residues in R. The edge weights are computed as probabilities as follows: w(k, r) = P(k ↦ r|Sm) = g(k, r) where k ∈ K and r ∈ R. Here, g(k, r) =  (dm(k) − bm(r), σm) where dm(k) ∈ Dm, bm(r) ∈ Fm. The probabilities are computed using a 1-dimensional Gaussian distribution
, with mean dm(k) − bm(r) and standard deviation σm. Langmead et al. [79] used σ = L/8 Hz in their experiments (Section 4), where L is the range of the RDCs in that medium (the maximum-valued RDC minus the minimum valued RDC). If an RDC is missing in medium i for a peak k, then we set the weight w(k, r) = 1/n0 in graph Mi, for each residue r of the n0 remaining (i.e., unassigned) residues. The details of how the chemical shifts, dNNs and amide exchange rates are converted into constraints on assignment are analogous, see [79].
(dm(k) − bm(r), σm) where dm(k) ∈ Dm, bm(r) ∈ Fm. The probabilities are computed using a 1-dimensional Gaussian distribution
, with mean dm(k) − bm(r) and standard deviation σm. Langmead et al. [79] used σ = L/8 Hz in their experiments (Section 4), where L is the range of the RDCs in that medium (the maximum-valued RDC minus the minimum valued RDC). If an RDC is missing in medium i for a peak k, then we set the weight w(k, r) = 1/n0 in graph Mi, for each residue r of the n0 remaining (i.e., unassigned) residues. The details of how the chemical shifts, dNNs and amide exchange rates are converted into constraints on assignment are analogous, see [79].
NVR uses a unique voting scheme for combining multiple sources of information [79, 8]. For each possible combination of data (1-7) above, a combined graph is constructed whose edge weights are the joint probabilities of the edges in the single-spectra graphs. NVR then constructs a new bipartite graph V, called the expectation graph, whose edge weights are initialized to 0. For each combined graph c, we compute a maximum bipartite matching. Let Hc ⊂ E be the matching computed on c. For each edge e ∈ Hc NVR increments the weight on the same edge in the expectation graph, V, by 1. This is done for all combined graphs. Hence, each bipartite matching “votes” for a set of edges. Thus, edge weights in V record the number of times a particular edge was part of a maximum bipartite matching. Note that the edge weights are probabilities in the bipartite graphs. Thus, a bipartite matching gives a maximum likelihood solution on that graph, which in turn maximizes the expected log-likelihood of the average edge weight.
Let w0 be the largest edge weight in V. The M step is computed, and assignments are made by Θ ← Θ ∪ w−1(w0). As previously stated, each of the constituent votes used to construct V is a maximum likelihood solution. Hence, it maximizes the expected edge weight in the matching. Therefore, in the bipartite graph V, those edges with maximum votes have the highest expected values over all combinations of the data, thus correctly computing the maximum likelihood new assignments Θ* as the argmax in the M-Step described above.
When an assignment is made, the associated nodes k ∈ K and r ∈ R are removed from -BNOE, the NOE graph. The geometric NOE restraints are applied to prune matching. The three graphs for chemical shift prediction are synchronized with BNOE so that all graphs have the same set of zero-weight edges. Each graph is then re-normalized so that the edge weights from each peak form a probability distribution. This completes a single iteration of the EM algorithm.
Recently, a new version of the gd module of NVR, called hd, improved the accuracy of NVR/gd [80]. In particular, hd eliminates the false-positives evident in Fig. 15, even against a larger database of 4,500 folds (vs. only 2,456 in gd [78]); see Fig. 17 and [80]. Furthermore, it has been found that combining hd with NMA ensembles (described above) can boost the assignment accuracy using distant structural homologs (3–7 Å backbone RMSD) by up to 22% [8].
Figure 17.
Improved fold detection from unassigned NMR data [80]: (A) score computed by hd vs. backbone RMSD (Å). The line is a least-squares fit to the data. The correlation coefficient is -0.75. Open diamonds are homologous structures with low sequence similarity, detected by hd score ≥ −10 (Table (B)). Solid diamonds are structures classified as non-homologs by hd score < −10 (Table (C)). Tables (B-C): (a) 3 test proteins: (i) Ubiquitin, (ii) GαIP, (iii) SPG. bPDB/chain Id for the structures detected by HD. cSequence identity of the 3 test proteins(a) vs. the primary sequence of the structure.b dBackbone RMSD between the structuresb and the native structures of the test proteins.(a) eScore computed by our algorithm hd. Higher hd-scores (closer to 0) indicate closer structural similarity. Table (B) does not include those structures detected by hd that have > 30% sequence identity.
The advantage of NVR over maximum bipartite matching lies in its iterative nature. NVR takes a conservative approach, making only likely assignments, given the current information. After making these assignments, the edge weights between the remaining unassigned peaks and residues are updated. Suppose that, during the ith iteration of the algorithm, peak k is assigned to residue r. The edge weight between peak k and residue r is then set to 1, indicating the certainty of that assignment. The edge weights form a probability distribution. Accordingly, the edge weight between peak k and any other residue is set to 0. Similarly, the weights on the edges from any other peak to r are immediately set to 0. The (non-zero) edge weights from each remaining unassigned peak are re-normalized prior to the next iteration. Thus, a peak whose assignment may be ambiguous in iteration i may become unambiguous in iteration i + 1.
Somewhat surprisingly, results of perturbation studies [79, pp. 120–130] suggest that NVR is not very sensitive to the quality of the initial tensor estimates, because the additional, non-RDC lines of evidence (chemical shift prediction, amide-exchange, dNN′s) can overcome these inaccuracies. The NVR voting algorithm (see above and references [79, 8]) used to integrate different lines of evidence is essentially a means to increase the signal-to-noise ratio. Here the signal is the computed likelihood of the assignment between a peak and the (correct) residue. The noise is the uncertainty in the data, where the probability mass is distributed among multiple residues. Each line of evidence (i.e., experiment) has noise, but the noise tends to be random and thus cancels when the lines of evidence are combined. Conversely, the signals embedded in each line of evidence tend to reinforce each other, resulting in (relatively) unambiguous assignments. Hence, even if the two initial tensor estimates are poor, it is unlikely that they can conspire (by voting together) to force an incorrect assignment. More generally, given the NVR voting scheme (above, and [79, 8]), any pair of lines of evidence is unlikely to outvote the majority. Finally, the iterative update (described above) by the alignment tensors at each cycle of the EM, allows the tensor accuracy to improve as more assignments are made [79].
9.3 Automated NOE Assignment
triangle is discussed for illustrative purposes; the interested reader is referred to Hana [174] for a more sophisticated algorithm with the same flavor. The triangle [153] and HANA [174] algorithms for automated NOE assignment use a rotamer library ensemble and RDCs. Both algorithms employ a rotamer-library-derived ensemble of intra- and inter-residue vectors between the backbone atoms and side-chain protons to reduce the ambiguity in the assignment of NOE restraints involving side-chain protons, especially aliphatic protons. For example, consider the putative assignment of an NOE to an (HN,Hδ) (respectively, (Hα,Hδ) pair of protons. The triangle relationship (see Fig. 16L) defines a decision procedure to filter NOE assignments by fusing information from RDCs (vNβ), rotamer modeling (vβδ), and NOEs (|vNδ|). Specifically,
Proposition 3 [153]
Given the vector vβδ from a Cβ atom to a side-chain proton S (e.g. Hδ), and the vector vNβ from the backbone HN to the Cβ, (respectively the vector vαβ from the Hα atom to Cβ), the vector vNS from the HN to S (respectively the vector vαS from the Hα to S) can be computed by: vNS = vNβ+ vβδ, vαS = vαβ + vβδ.
vNβ, and vαβ are computed directly from the backbone structure determined by rdc-exact and can be inter- or intra-residue. The vectors vNS, vNβ and vβδ form three sides of a triangle (Fig. 16), where vNβ is computed from the backbone structure and vβδ lies in a finite set of vectors, mined from the PDB rotamers. Hence, for each side-chain proton, vβδ lies in a finite set of vectors. Consequently, there is a finite set VN (respectively Vα) of vectors containing vNS (respectively vαS). The triangle relationship (Proposition 3) is then used to filter the assignment of NOE peaks involving side-chain protons. The algorithm first estimates the NOE distances, dN and dα, using the NOE intensities from, respectively, the experimental NOE peaks picked from the 3D 15N- and 13C-NOESY spectra. triangle tests dN and dα to see whether they satisfy the constraints: min |vNS| − εN ≤ dN ≤ max |vNS| + εN, min |vαS| − εα ≤ dα ≤ min |vαS| + εα, where min and max for vNS (respectively vαS) are both computed over vNS ∈ VN (respectively vαS ∈ Vα). εN and εα are the NOE distance error bounds for the corresponding 3D 15N- (respectively 13C-) edited NOESY peaks.
Tests of triangle and Hana are described in Section 6 and references [153, 174]. In the future, it will be important to quantify any possible bias introduced by the rotamer library, using both rotamer subsampling and rotamer energy minimization (generalizing prior work on rotamer optimization [88, 45, 44]), and comparison to conventional assignments. For example, one can use a subsampled rotamer library that is >6,000-times finer than the library in [153]. In preliminary tests on ubiquitin NOE spectra, the finer library resulted in modest improvements in assignment accuracy (about 5%) at a considerable computational cost (two hours vs. one second). This suggests that the optimal number of rotamers should lie in between.
Further study is required of the effect of spin diffusion on cross-peak intensity and the NOE distance |vNδ| in the triangle relationship (Fig. 16L) for assignment pruning. An extension of triangle has been used with rdc-exact to assign the NOEs and compute structures, including side-chains [174]. It will be valuable to extend triangle to account for the various labeling patterns necessary in large proteins to solve the structures of such large systems. These labeling strategies can sometimes vitiate the HCCH-TOCSY [108] for side-chain resonance assignments. One can extend triangle to assign NOEs involving these ambiguous proton resonances, by replacing their side-chain assignment with a set of possible labels (analogous to [1]). The labels, which represent competing assignments for the indirect 1H dimension, can be pruned using Proposition 3. The resulting NOESY assignments from triangle would provide side-chain resonance assignments as a byproduct. This extension to triangle would not only reduce the dependence of NOE assignment algorithms upon the (less sensitive) TOCSY experiments, but also increase their tolerance of incomplete side-chain resonance assignments.
Side-chain/side-chain NOEs may be assigned by ‘lifting’ triangle's rotamer-based ensemble of internuclear vectors (via Cartesian product). 4D NOESY experiments can expedite triangle's computation of these assignments. A discussion of the information content of 4D NOESY vs. selective labeling is therefore warranted. triangle and its successor, Hana [174], employ a ‘symmetry check’ [60] to increase assignment confidence using ‘back’ NOEs. Consider a putative assignment for an NOE, 15N-HN↔ 1H, where ω(1H) is assigned to 1Hδ of F16. If the assignment is correct then we should see a symmetric NOE in the 13C-NOESY: HN↔ 1Hδ-13Cδ of F16. Finding this peak requires searching a box in the 3D 13C-NOESY, about the (HN, 1H, 13Cδ) shifts. Since the ‘back’ NOE might be missing and there might be other peaks in this box, the symmetry check must be treated inferentially, as changing the Bayesian probability of the assignment. Using a 4D NOESY reduces this ambiguity, and in principle the symmetric interaction will always be observed. As a pruning condition, back NOEs and 4D NOEs complement the Triangle Relationship (Proposition 3) by integrating the geometric and spectral constraint of the additional observed 13Cδ. However, under some isotopic labeling schemes, 4D NOEs to protons bonded to 12C will not be observed, and the set-of-labels strategy above must be employed. Finally, triangle and Hana should be helpful to assist with proposed experimental methods for 24-65 kDa proteins that currently use manual 4D NOE assignment (e.g., [170]), which could then be automated, saving time and reducing subjectivity.
9.4 NMR Structure Determination of Symmetric Oligomers
Many experimental challenges exist for determining the structure of membrane protein complexes. Current algorithms in this area, including symbrane (Section 7) do not address all of these problems, and make a number of assumptions. Most importantly, it can sometimes be assumed that the overall fold of a subunit can be obtained from RDCs and other NMR measurements in the holo state, and that inter-subunit NOEs can be distinguished from intra-subunit NOEs using isotope filtering, as was done for phospholamban [111, 117]. In particular, the automated ambiguous inter-subunit NOE assignment in symbrane relies on these assumptions [118].
One wishes to extend and relax these assumptions; although a long-term goal is to develop algorithms for general membrane proteins, this review focuses next on the challenges of symmetric oligomers, which include many biomedically important systems. Moreover, RDCs can play a crucial role for such complexes, not only in determining the conformation and orientation of the individual subunits, but also in computing the symmetry axis. The overall scheme of symbrane is shown in Fig. 18. In contrast, traditional protocols [102] for structure determination of protein complexes from NMR data use simulated annealing (SA) and molecular dynamics (MD). However, the SA/MD mechanism is not complete and could get trapped in local minima. Furthermore, the precision in the determined structure is strongly affected by the temperature. symbrane avoids temperature dependence and local minima problems, and does not suffer from “false precision” in characterizing the diversity of determined structures. symbrane's search in the symmetry configuration space (SCS) takes advantage of the ‘closed-ring’ constraint of a symmetric homo-oligomer. Ambipack [150] used a branch-and-bound algorithm to compute rigid body transformations satisfying potentially ambiguous inter-subunit distance restraints. In contrast, symbrane uses the oligomeric number to enforce an a priori symmetry constraint. In this sense it is analogous to the manner in which non-crystallographic symmetry is handled in molecular replacement for x-ray crystallography [89]. By formulating the structure determination problem in the SCS rather than in the space of atom positions, symbrane is able to exploit directly the kinematics of the ‘closed-ring’ constraint, and thereby derive an analytical bound for pruning, which is tighter and more accurate than previous randomized numerical techniques [150]. symbrane's guarantees of completeness should be especially important for membrane proteins (where sparse data is a particularly important problem), but should also prove useful for water-soluble oligomers.
symbrane simultaneously assigns NOEs and determines structure (by identifying regions in SCS), and is guaranteed to find all consistent assignments and structures [118]. Let R be a set of (possibly ambiguous) NOEs. Let rkl represent the lth possible assignment of the kth NOE rk of R, and let skl ⊂ S2 × ℝ2(see Fig. 18a) be the region of the SCS in which distance restraint rkl is satisfied. An assignment specifies the subunit and the protons involved in the NOE. A determined structure must satisfy all ambiguous NOEs; it satisfies each by satisfying one or more of its possible assignments. In the SCS, this translates into finding the region
| (14) |
where tk is the number of possible assignments for rk, the kth NOE.
Using Eq. (14), the algorithm computes redundant and inconsistent NOEs and assignments, via unions and intersections of geometric sets in SCS. Let Q ⊂ R be a set of NOEs. Let rk be an (arbitrary) ambiguous NOE (not in Q) with tk assignments. We compute that NOE assignment rkl is redundant with respect to Q if and only if p(Q) ⊂ skl. Similarly, we compute that rkl is inconsistent with respect to Q if and only if p(Q) ∩ skl = ∅, where ∅ is the empty set. We can extend these algorithms from assignments to NOEs as follows. Let be the region of the SCS which satisfies at least one assignment of rk. We then compute that rk is redundant with respect to Q if and only if p(Q) ⊂ Sk, and compute that rk is inconsistent with respect to Q if and only if p(Q) ∩ Sk = ∅. symbrane eliminates inconsistent NOEs and assignments, and is able to detect redundant ones. symbrane's approach to identifying the mutually-consistent, complete set of NOE assignments and SCS regions is summarized in Figure 19 and described in detail in reference [118].
Figure 19.

symbrane strategy to resolve ambiguous NOEs in structure determination of symmetric homo-oligomers. Top: Different possible assignments for one ambiguous NOE are illustrated for a trimer. The NOE could be ordered between subunits as 1-2-3 or 1-3-2, and has chemical shift degeneracy between protons a, b, and c. The former is called “subunit ambiguity” and the latter “atom ambiguity.” Phase 1: Consistent regions in the SCS are obtained using a branch-and-bound algorithm [117], taking a subset of available NOEs (typically atom-unambiguous NOEs, if any) as input. The 4-dimensional SCS is cartoon-represented as in Fig. 18b. Phase 2: symbrane uses the consistent regions output from the branch-and-bound search plus possible assignments of the ambiguous NOEs, to determine a mutually-consistent, complete set of NOE assignments and ambiguity consistent regions (ACR) in SCS. Bottom: Pseudocode for symbrane's ambiguity resolution algorithm. Each NOE's score is the average of the scores of all of its possible assignments (the line marked (*), Bottom). This score provides an ordering criterion for NOE assignment. [118] shows that the order does not affect the completeness, results, or accuracy, but can improve the efficiency.
When RDCs can be obtained in combination with NOEs, then structure determination of symmetric homo-oligomers reduces to an inverse kinematics problem that can be solved exactly (analogously to the procedures in Section 3), without resorting to the branch-and-bound search used in references [117, 118]. It is likely that ambiguous NOE assignment [118] will also be improved since the ensemble of exact solutions will be smaller, increasing the structural precision that geometrically prunes the assignments. symbrane currently allows for limited uncertainty in the subunit structure: symbrane computes satisfying structures using rigid monomers, but energy scores allowing side-chain minimization [117]. This allows for some side-chain flexibility, but is subject to local minima and is not systematic. Instead, one could use a rotamer library to systematically sample different distinct conformational side-chain states, exploiting recent advances in rotamer optimization [88, 45, 44], particularly in the presence of provable rotamer energy minimization [45, 44]. Considering rotamers increases the complexity of the hierarchical subdivision scheme, but techniques such as dead-end elimination (DEE) [34, 85, 48, 115, 44] and minimized DEE [45, 44] can be used to prune rotamers and compute solutions more quickly. It may also be possible to derive exact or analytic solutions for NOE assignment when RDCs are available. While more difficult, backbone flexibility could also be incorporated in a DEE-like search [42, 43]. Allowing greater uncertainty in the subunit structure, would make symbrane more robust and eventually useful for multimers with a more intricate folding topology.
Two novel features of symbrane are of particular note: (1) the ability to assign inter-subunit NOEs in a complete search that avoids exhaustive, exponential enumeration [118]; and (2) the ability to determine the oligomeric number using NMR data alone [117]. Specifically:
Errors in resolving inter-subunit NOE ambiguities have led to incorrect NMR structures [20]. Beyond the importance of this particular problem in NMR data analysis, symbrane represents a departure from the stochastic methods frequently employed by the NMR community. A corollary is that such stochastic methods, now routinely employed, should be reconsidered in light of their inability to assure identification of the unique or globally-optimal structural models consistent with a set of NMR observations. symbrane can provide more confident answers to these problems.
In general, the oligomeric state of the complex includes the symmetry type (Cn, Dn, etc.) as well as the oligomeric number (n = 2, 3, 4, …). In addition to assigning the intermolecular NOEs and determining the complex structure, symbrane tests whether the available data suffices to determine the oligomeric number for Cn symmetry. For each possible symmetry type and oligomeric number, symbrane can determine a set Y of WPS structures. For some oligomeric states, Y = ∅: we can place higher confidence on the oligomeric state that (a) has some WPS structures (i.e., Y ≠ ∅, and (b) affords better vdW packing. Thus we can determine the oligomeric state using the NMR data and vdW packing. symbrane provides for an independent verification of the oligomeric state (which is typically determined using experiments such as chemical cross-linking followed by SDS-PAGE, or by equilibrium sedimentation). The results from symbrane show how novel algorithms can draw conclusions from NMR data that were previously possible only using additional biophysical experiments. Such algorithms can reduce experimental time and provide cross-validation of structure and assembly.
Acknowledgments
We would like to thank our colleagues for collaborations and assistance in NMR methodology, without which this article would not have been possible: Chris Bailey-Kellogg, Jeffrey Boyles, James Chou, Jeff Hoch, Dan Keedy, Shobha Potluri, David and Jane Richardson, Chittu Tripathy, Gerhard Wagner, Tony Yan, Anna Yershova, and Pei Zhou. We thank the following colleagues for helpful discussions, which greatly improved this article: Marcelo Berardi, Vincent Chen, David Cowburn, Brian Hare, Terry Oas, Tomás Lozano-Pérez, Art Palmer, Len Spicer, Bruce Tidor, Ron Venters, and Peter Wright. We thank all members of the Donald laboratory, past and present, for helpful discussions and comments. We thank the Duke University NMR Center for their assistance and support. The authors are supported by NIH grant GM-65982 to B.R.D.
Glossary of Abbreviations
- NMR
Nuclear Magnetic Resonance
- ppm
parts per million
- RMSD
mean square deviation
- HSQC
Heteronuclear Single Quantum Coherence spectroscopy
- NOE
Nuclear Overhauser Effect
- RDC
Residual Dipolar Coupling
- PDB
Protein Data Bank
- pol η
zinc finger domain of the human DNA Y-polymerase Eta
- CH
Cα-Hα
- hSRI
human Set2-Rpb1 interacting domain
- FF2
FF Domain 2 of human transcription elongation factor CA150 (RNA polymerase II C-terminal domain interacting protein)
- POF
Principal Order Frame
- SA
Simulated Annealing
- MD
Molecular Dynamics
- SSE
secondary structure element
- C′
carbonyl carbon
- WPS
well-packed satisfying
- vdW
van der Waals
- DOF
degrees of freedom
Footnotes
Color versions of the figures in this paper are available online at http://www.sciencedirect.com/science/journal/00796565.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Eiso AB, Pugh DJR, Kaptein R, Boelens R, Bonvin AMJJ. Direct use of unassigned resonances in NMR structure calculations with proxy residues. J Am Chem Soc. 2006;128(23):7566–7571. doi: 10.1021/ja058504q. [DOI] [PubMed] [Google Scholar]
- 2.Al-Hashimi HM, Bolon PJ, Prestegard JH. Molecular symmetry as an aid to geometry determination in ligand protein complexes. J Magn Reson. 2000;142:153–158. doi: 10.1006/jmre.1999.1937. [DOI] [PubMed] [Google Scholar]
- 3.Al-Hashimi HM, Gorin A, Majumdar A, Gosser Y, Patel DJ. Towards Structural Genomics of RNA: Rapid NMR Resonance Assignment and Simultaneous RNA Tertiary Structure Determination Using Residual Dipolar Couplings. J Mol Biol. 2002;318:637–649. doi: 10.1016/S0022-2836(02)00160-2. [DOI] [PubMed] [Google Scholar]
- 4.Al-Hashimi HM, Patel DJ. Residual dipolar couplings: Synergy between NMR and structural genomics. J Biomol NMR. 2002;22(1):1–8. doi: 10.1023/a:1013801714041. [DOI] [PubMed] [Google Scholar]
- 5.Anderson AC. Two crystal structures of dihydrofolate reductase-thymidylate synthase from Cryptosporidium hominis reveal protein-ligand interactions including a structural basis for observed antifolate resistance. Acta Crystallograph Sect F Struct Biol Cryst Commun. 2005;61(Pt 3):258–262. doi: 10.1107/S1744309105002435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Andrec M, Du P, Levy RM. Protein backbone structure determination using only residual dipolar couplings from one ordering medium. J Biomol NMR. 2001;21(4):335–347. doi: 10.1023/a:1013334513610. [DOI] [PubMed] [Google Scholar]
- 7.Annila A, Aitio H, Thulin E, Drakenberg T. Recognition of protein folds via dipolar couplings. J Biomol NMR. 1999;14:223–230. [Google Scholar]
- 8.Apaydin S, Conitzer V, Donald BR. Structure-based protein NMR assignments using native structural ensembles. J Biomol NMR. 2008;40:263–276. doi: 10.1007/s10858-008-9230-x. [DOI] [PubMed] [Google Scholar]
- 9.Artymiuk PJ, Blake CCF, Rice DW, Wilson KS. The Structures of the Monoclinic and Orthorhombic Forms of Hen Egg-White Lysozyme at 6 Angstroms Resolution. Acta Crystallogr B Biol Crystallogr. 1982;38:778. [Google Scholar]
- 10.Babu CR, Flynn PF, Wand AJ. Validation of Protein Structure from Preparations of Encapsulated Proteins Dissolved in Low Viscosity Fluids. J Am Chem Soc. 2001;123:2691. doi: 10.1021/ja005766d. [DOI] [PubMed] [Google Scholar]
- 11.Bailey-Kellogg C, Kelley JJ, III, Lilien R, Donald BR. Physical geometric algorithms for structural molecular biology. Proceedings IEEE International Conference on Robotics and Automation (ICRA-2001); Special Session on Computational Biology & Chemistry; May, 2001. pp. 940–947. [Google Scholar]
- 12.Bailey-Kellogg C, Widge A, Kelley JJ, III, Berardi MJ, Bushweller JH, Donald BR. The NOESY Jigsaw: Automated protein secondary structure and main-chain assignment from sparse, unassigned NMR data. Jour Comp Biol. 2000;3–4(7):537–558. doi: 10.1089/106652700750050934. [DOI] [PubMed] [Google Scholar]
- 13.Coggins BE, Zhou P. Sampling of the NMR time domain along concentric rings. J Magn Reson. 2007;184(2):207–221. doi: 10.1016/j.jmr.2006.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Berger B, Kleinberg J, Leighton FT. Reconstructing a three-dimensional model with arbitrary errors. Journal of the ACM. 1999;46(2):212–235. [Google Scholar]
- 15.Brünger AT. XPLOR: A system for X-ray crystallography and NMR. Yale University Press; New Haven: 1993. [Google Scholar]
- 16.Cavanaugh J, Fairbrother WJ, Palmer AG, III, Skelton NJ. Protein NMR Spectroscopy: Principles and Practice. Academic Press; 1995. [Google Scholar]
- 17.Cavasotto CN, Kovacs JA, Abagyan RA. Representing receptor flexibility in ligand docking through relevant normal modes. J Am Chem Soc. 2005;127(26):9632–9640. doi: 10.1021/ja042260c. [DOI] [PubMed] [Google Scholar]
- 18.Chen Y, Reizer J, Saier MH, Jr, Fairbrother WJ, Wright PE. Mapping of the binding interfaces of the proteins of the bacterial phosphotransferase system, HPr and IIAglc. Biochemistry. 1993;32(1):32–37. doi: 10.1021/bi00052a006. [DOI] [PubMed] [Google Scholar]
- 19.Chou JJ, Li S, Bax A. Study of conformational rearrangement and refinement of structural homology models by the use of heteronuclear dipolar couplings. J Biom NMR. 2000;18:217–227. doi: 10.1023/a:1026563923774. [DOI] [PubMed] [Google Scholar]
- 20.Clore GM, Omichinski JG, Sakaguchi K, Zambrano N, Sakamoto H, Appella E, Gronenborn AM. Interhelical angles in the solution structure of the oligomerization domain of p53: Correction. Science. 1995;267(5203):1515–1516. doi: 10.1126/science.7878474. [DOI] [PubMed] [Google Scholar]
- 21.Coggins BE, Venters RA, Zhou P. Filtered backprojection for the reconstruction of a high-resolution (4,2)D CH3-NH NOESY spectrum on a 29 kDa protein. J Am Chem Soc. 2005;127(33):11562–11563. doi: 10.1021/ja053110k. [DOI] [PubMed] [Google Scholar]
- 22.Coggins BE, Zhou P. PACES: Protein sequential assignment by computer-assisted exhaustive search. J Biomol NMR. 2003;26(2):93–111. doi: 10.1023/a:1023589029301. [DOI] [PubMed] [Google Scholar]
- 23.Coggins BE, Zhou P. Polar Fourier transforms of radially sampled NMR data. J Magn Reson. 2006;182(1):84–95. doi: 10.1016/j.jmr.2006.06.016. [DOI] [PubMed] [Google Scholar]
- 24.Cordier F, Rogowski M, Grzesiek S, Bax A. Observation of through-hydrogen-bond 2hJHC′ in a perdeuterated protein. J Magn Reson. 1999;40(2):510–512. doi: 10.1006/jmre.1999.1899. [DOI] [PubMed] [Google Scholar]
- 25.Cornilescu G, Delaglio F, Bax A. Protein backbone angle restraints from searching a database for chemical shift and sequence homology. J Biomol NMR. 1999;13:289–302. doi: 10.1023/a:1008392405740. [DOI] [PubMed] [Google Scholar]
- 26.Coutsias EA, Seok C, Jacobson MP, Dill KA. A kinematic view of loop closure. J Comput Chem. 2004;25(4):510–528. doi: 10.1002/jcc.10416. [DOI] [PubMed] [Google Scholar]
- 27.Coutsias EA, Seok C, Wester MJ, Dill KA. Resultants and loop closure. Internatl J Quant Chemi. 2006;106(1):176–189. [Google Scholar]
- 28.Crippen G. Chemical distance geometry: Current realization and future projection. Journal of Mathematical Chemistry. 1991;6:307–324. [Google Scholar]
- 29.Crippen GM, Havel TF. Distance Geometry and Molecular Conformations. Wiley; 1988. [Google Scholar]
- 30.Cross ADJ, Hancock ER. Graph Matching With a Dual-Step EM Algorithm. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1998;20(11):1236–1253. [Google Scholar]
- 31.del Rio-Portílla F, Blechta V, Freeman R. Measurement of poorly-resolved splittings by J-doubling in the frequency domain. J Magn Reson. 1994;111a:132–135. [Google Scholar]
- 32.Delaglio F, Kontaxis G, Bax A. Protein structure determination using molecular fragment replacement and NMR dipolar couplings. J Am Chem Soc. 2000;122(9):2142–2143. [Google Scholar]
- 33.Dempster A, Laird N, Rubin D. Maximum Likelihood from incomplete data via the EM algorithm. (B).Journal of the Royal Statistical Society. 1977;39(1):1–38. [Google Scholar]
- 34.Desmet J, DeMaeyer M, Hazes B, Lasters I. The dead-end elimination theorem and its use in protein side chain positioning. Nature. 1992;356:539–542. doi: 10.1038/356539a0. [DOI] [PubMed] [Google Scholar]
- 35.Diamond R. Real-space refinement of the structure of hen egg-white lysozyme. J Mol Biol. 1974;82:371–391. doi: 10.1016/0022-2836(74)90598-1. [DOI] [PubMed] [Google Scholar]
- 36.Donald BR. Proceedings of the Sixth International Workshop on the Algorithmic Foundations of Robotics (WAFR) Utrecht/Zeist, The Netherlands: University of Utrecht; Jul, 2004. Plenary lecture: Algorithmic challenges in structural molecular biology and proteomics; pp. 1–10. [Google Scholar]; Erdmann M, Overmars M, Hsu D, van der Stappen AF, editors. Algorithmic Foundations of Robotics VI, Springer Tracts in Advanced Robotics. Vol. 17. Springer; Berlin: 2005. pp. 1–10. [Google Scholar]
- 37.Donald BR, Kapur D, Mundy J. Symbolic and Numerical Computation for Artificial Intelligence. Academic Press, Harcourt Jovanovich; London: 1992. [Google Scholar]
- 38.Fowler AC, Tian F, Al-Hashimi HM, Prestegard JH. Rapid determination of protein folds using residual dipolar couplings. J Mol Bio. 2000;304(3):447–460. doi: 10.1006/jmbi.2000.4199. [DOI] [PubMed] [Google Scholar]
- 39.Gallagher T, Alexander P, Bryan P, Gilliland GL. Two crystal structures of the B1 immunoglobulin-binding domain of streptococcal protein G and comparison with NMR. Biochemistry. 1994;33:4721–4729. [PubMed] [Google Scholar]
- 40.Gardner KH, Kay LE. Production and incorporation of 15N, 13C, 2H (1H-δ1 methyl) isoleucine into proteins for multidimensional NMR studies. J Am Chem Soc. 1997;119(32):7599–7600. [Google Scholar]
- 41.Gemmecker G, Jahnke W, Kessler H. Measurement of fast proton exchange rates in isotopically labelled compounds. J Am Chem Soc. 1993;115(24):11620–11621. [Google Scholar]
- 42.Georgiev I, Donald BR. Dead-end elimination with backbone flexibility. Bioinformatics. 2007;23(13) doi: 10.1093/bioinformatics/btm197. [DOI] [PubMed] [Google Scholar]; Special issue on papers from the International Conference on Intelligent Sys for Mol Biol (ISMB 2007) Vienna, Austria: Jul 21-25, 2007. [Google Scholar]
- 43.Georgiev I, Keedy D, Richardson J, Richardson D, Donald BR. Algorithm for backrub motions in protein design. Bioinformatics. 2008 Jul;22:e174–183. doi: 10.1093/bioinformatics/btn169. [DOI] [PMC free article] [PubMed] [Google Scholar]; Special issue on papers from International Conference on Intelligent Sys for Mol Biol (ISMB 2008) Toronto, CA: Jul, 2008. [Google Scholar]
- 44.Georgiev I, Lilien R, Donald BR. Improved pruning algorithms and divide-and-conquer strategies for dead-end elimination, with application to protein design. Bioinformatics. 2006;22(14):e174–183. doi: 10.1093/bioinformatics/btl220. [DOI] [PubMed] [Google Scholar]; Special issue on papers from the Int'l Conf on Intelligent Sys for Mol Biol (ISMB 2006) Fortaleza, Brazil: [Google Scholar]
- 45.Georgiev I, Lilien R, Donald BR. The minimized dead-end elimination criterion and its application to protein redesign in a hybrid scoring and search algorithm for computing partition functions over molecular ensembles. Journal of Computational Chemistry. 2008;29(10):1527–1542. doi: 10.1002/jcc.20909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Giesen AW, Homans SW, Brown JM. Determination of protein global folds using backbone residual dipolar coupling and long-range NOE restraints. J Biomol NMR. 2003;25:63–71. doi: 10.1023/a:1021954812977. [DOI] [PubMed] [Google Scholar]
- 47.Girard E, Chantalat L, Vicat J, Kahn R. Gd-HPDO3A, a Complex to Obtain High-Phasing-Power Heavy Atom Derivatives for SAD and MAD Experiments: Results with Tetragonal Hen Egg-White Lysozyme. Acta Crystallogr D Biol Crystallogr. 2001;58:1–9. doi: 10.1107/s0907444901016444. [DOI] [PubMed] [Google Scholar]
- 48.Goldstein R. Efficient rotamer elimination applied to protein side-chains and related spin glasses. Biophys J. 1994;66:1335–1340. doi: 10.1016/S0006-3495(94)80923-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Gorczynski MJ, Grembecka J, Zhou Y, Kong Y, Roudaiya L, Douvas MG, Newman M, Bielnicka I, Baber G, Corpora T, Shi J, Sridharan M, Lilien R, Donald BR, Speck NA, Brown ML, Bushweller JH. Allosteric inhibition of the protein-protein interaction between the leukemia-associated proteins RUNX1 and CBFβ. Chemistry & Biology. 2007;14(10) doi: 10.1016/j.chembiol.2007.09.006. [DOI] [PubMed] [Google Scholar]
- 50.Gronenborn AM, Filpula DR, Essig NZ, Achari A, Whitlow M, Wingfield PT, Clore GM. A novel, highly stable fold of the immunoglobulin binding domain of streptococcal protein G. Science. 1991;253:657. doi: 10.1126/science.1871600. [DOI] [PubMed] [Google Scholar]
- 51.Grzesiek S, Bax A. Measurement of amide proton exchange rates and NOEs with water in 13C/15N-enriched calcineurin B. J Biomol NMR. 1993;3(6):627–638. doi: 10.1007/BF00198368. [DOI] [PubMed] [Google Scholar]
- 52.Güntert P, Mumenthaler C, Wüthrich K. Torsion angle dynamics for NMR structure calculation with the new program DYANA. J Mol Biol. 1997;273:283–298. doi: 10.1006/jmbi.1997.1284. [DOI] [PubMed] [Google Scholar]
- 53.Guntert Peter. Automated NMR structure calculation with CYANA. Methods Mol Biol. 2004;278:353–378. doi: 10.1385/1-59259-809-9:353. [DOI] [PubMed] [Google Scholar]
- 54.Hajduk PJ, Meadows RP, Fesik SW. Drug design: Discovering high-affinity ligands for proteins. Science. 1997;278:497–499. doi: 10.1126/science.278.5337.497. [DOI] [PubMed] [Google Scholar]
- 55.Hendrickson B. Conditions for unique graph realizations. SIAM Journal on Computing. 1992;21:65–84. [Google Scholar]
- 56.Hendrickson B. The molecule problem: Exploiting structures in global optimization. SIAM Journal on Optimization. 1995;5:835–857. [Google Scholar]
- 57.Herrmann T, Güntert P, Wüthrich K. Protein NMR structure determination with automated noe assignment using the new software CANDID and the torsion angle dynamics algorithm DYANA. J Mol Biol. 2002;319:209–227. doi: 10.1016/s0022-2836(02)00241-3. [DOI] [PubMed] [Google Scholar]
- 58.Hinsen K. Course and Lecture Notes. Centre de Biophysique Molculaire (CNRS); Orleans, France: 2000. Normal mode theory and harmonic potential approximations. http://dirac.cnrs-orleans.fr/∼hinsen/ [Google Scholar]
- 59.Huang YJ, Swapna GV, Rajan PK, Ke H, Xia B, Shukla K, Inouye M, Montelione GT. Solution NMR structure of ribosome-binding factor a (RbfA), a coldshock adaptation protein. Escherichia coli J Mol Biol. 2003;327:521–536. doi: 10.1016/s0022-2836(03)00061-5. [DOI] [PubMed] [Google Scholar]
- 60.Huang YJ, Tejero R, Powers R, Montelione GT. A topology-constrained distance network algorithm for protein structure determination from NOESY data. Proteins. 2006;62(3):587–603. doi: 10.1002/prot.20820. [DOI] [PubMed] [Google Scholar]
- 61.Hus JC, Marion D, Blackledge M. De novo determination of protein structure by NMR using orientational and long-range order restraints. J Mol Bio. 2000;298(5):927–936. doi: 10.1006/jmbi.2000.3714. [DOI] [PubMed] [Google Scholar]
- 62.Hus JC, Marion D, Blackledge M. Determination of protein backbone using only residual dipolar couplings. J Am Chem Soc. 2001;123:1541–1542. doi: 10.1021/ja005590f. [DOI] [PubMed] [Google Scholar]
- 63.Hus JC, Prompers J, Bruschweiler R. Assignment strategy for proteins of known structure. J Mag Res. 2002;157:119–125. doi: 10.1006/jmre.2002.2569. [DOI] [PubMed] [Google Scholar]
- 64.Korukottu J, Bayrhuber M, Montaville P, Vijayan V, Jung YS, Becker S, Zweckstetter M. Fast High-Resolution Protein Structure Determination by Using Unassigned NMR Data. Angew Chem Int Ed Engl. 2007;46:1176–1179. doi: 10.1002/anie.200603213. [DOI] [PubMed] [Google Scholar]
- 65.Jacobs DJ, Rader AJ, Kuhn LA, Thorpe MF. Protein flexibility predictions using graph theory. Proteins. 2001;44(2):150–165. doi: 10.1002/prot.1081. [DOI] [PubMed] [Google Scholar]
- 66.Johnson EC, Lazar GA, Desjarlais JR, Handel TM. Solution structure and dynamics of a designed hydrophobic core variant of ubiquitin. Structure Fold Des. 1999;7:967–976. doi: 10.1016/s0969-2126(99)80123-3. [DOI] [PubMed] [Google Scholar]
- 67.Jung YS, Zweckstetter M. Backbone assignment of proteins with known structure using residual dipolar couplings. J Biomol NMR. 2004;30(1):25–35. doi: 10.1023/B:JNMR.0000042955.14647.77. [DOI] [PubMed] [Google Scholar]
- 68.Juszewski K, Schwieters CDS, Garrett DS, Byrd RA, Tjandra N, Clore GM. Completely Automated, Highly Error-Tolerant Macromolecular Structure Determination from Multidimensional Nuclear Overhauser Enhancement Spectra and Chemical Shift Assignments. J Am Chem Soc. 2004;126:6258–6273. doi: 10.1021/ja049786h. [DOI] [PubMed] [Google Scholar]
- 69.Ruan K, Briggman KB, Tolman JR. De novo determination of internuclear vector orientations from residual dipolar couplings measured in three independent alignment media. J Biomol NMR. 2008;41(2):61–76. doi: 10.1007/s10858-008-9240-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Kamisetty H, Bailey-Kellogg C, Pandurangan G. An efficient randomized algorithm for contact-based NMR backbone resonance assignment. Bioinformatics. 2006;22(2):172–180. doi: 10.1093/bioinformatics/bti786. [DOI] [PubMed] [Google Scholar]
- 71.Kay LE. Protein dynamics from NMR. Nature Structural Biology. 1998;5:513–517. doi: 10.1038/755. [DOI] [PubMed] [Google Scholar]
- 72.Kemple MD, Ray BD, Lipkowitz KB, Prendergast FG, Rao BD. The use of lanthanides for solution structure determination of biomolecules by NMR: Evaluation of the methodology with EDTA derivatives as model systems. J Am Chem Soc. 1988;110(25):8275–8287. [Google Scholar]
- 73.Kim DE, Chivian D, Baker D. Protein structure prediction and analysis using the Robetta server. Nucleic Acids Res. 2004;32(Web Server issue):526–531. doi: 10.1093/nar/gkh468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Kolodny R, Guibas L, Levitt M, Koehl P. Inverse kinematics in biology: the protein loop closure problem. International J Robotics Research. 2005;24:151–163. [Google Scholar]
- 75.Kovacs RJ, Nelson MT, Simmerman HK, Jones LR. Phospholamban forms Ca2+-selective channels in lipid bilayers. J Biol Chem. 1988;263:18364–18368. [PubMed] [Google Scholar]
- 76.Kuhn HW. Hungarian method for the assignment problem. Nav Res Logist Quarterly. 1955;2:83–97. [Google Scholar]
- 77.Kurinov IV, Harrison RW. The influence of temperature on lysozyme crystals - structure and dynamics of protein and water. Acta Crystallogr D Biol Crystallogr. 1995;51:98–109. doi: 10.1107/S0907444994009261. [DOI] [PubMed] [Google Scholar]
- 78.Langmead C, Donald BR. Proceedings of the IEEE Computer Society Bioinformatics Conference (CSB) Stanford; Aug, 2003. 3D structural homology detection via unassigned residual dipolar couplings; pp. 209–217. PMID: 16452795. [PubMed] [Google Scholar]
- 79.Langmead C, Donald BR. An expectation/maximization nuclear vector replacement algorithm for automated NMR resonance assignments. Jour Biomolecular NMR. 2004;29(2):111–138. doi: 10.1023/B:JNMR.0000019247.89110.e6. [DOI] [PubMed] [Google Scholar]
- 80.Langmead C, Donald BR. Proceedings of the IEEE Computational Systems Bioinformatics Conference (CSB) Stanford; CA: Aug, 2004. High-throughput 3D structural homology detection via NMR resonance assignment; pp. 278–289. PMID: 16448021. [PubMed] [Google Scholar]
- 81.Langmead C, McClung CR, Donald BR. A maximum entropy algorithm for rhythmic analysis of genome-wide expression patterns. Proceedings of the IEEE Computer Society Bioinformatics Conference (IEEE CSB) 2002 August;:237–245. PMID: 15838140. [PubMed] [Google Scholar]
- 82.Langmead C, Yan A, Lilien R, Wang L, Donald BR. Proceedings of The Seventh Annual International Conference on Research in Computational Molecular Biology (RECOMB) Berlin, Germany: ACM Press; Apr, 2003. A polynomial-time nuclear vector replacement algorithm for automated NMR resonance assignments; pp. 176–187. [Google Scholar]
- 83.Langmead C, Yan A, Lilien R, Wang L, Donald BR. A polynomial-time nuclear vector replacement algorithm for automated NMR resonance assignments. Jour Comp Biol. 2004;11(2-3):277–298. doi: 10.1089/1066527041410436. [DOI] [PubMed] [Google Scholar]
- 84.Langmead C, Yan A, McClung CR, Donald BR. Phase-independent rhythmic analysis of genome-wide expression patterns. Journal of Computational Biology. 2003;10(3-4):521–536. doi: 10.1089/10665270360688165. [DOI] [PubMed] [Google Scholar]
- 85.Lasters I, Desmet J. The fuzzy-end elimination theorem: correctly implementing the side chain placement algorithm based on the dead-end elimination theorem. Protein Eng. 1993;6:717–722. doi: 10.1093/protein/6.7.717. [DOI] [PubMed] [Google Scholar]
- 86.Li M, Phatnani HP, Guan Z, Sage H, Greenleaf AL, Zhou P. Solution structure of the Set2-Rpb1 interacting domain of human Set2 and its interaction with the hyperphosphorylated C-terminal domain of Rpb1. Proc Natl Acad Sci U S A. 2005;102(49):17636–17641. doi: 10.1073/pnas.0506350102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Lilien R, Farid H, Donald BR. Probabilistic disease classification of expression-dependent proteomic data from mass spectrometry of human serum. Journal of Computational Biology. 2003;10(6):925–946. doi: 10.1089/106652703322756159. [DOI] [PubMed] [Google Scholar]
- 88.Lilien R, Stevens B, Anderson A, Donald BR. A novel ensemble-based scoring and search algorithm for protein redesign, and its application to modify the substrate specificity of the Gramicidin Synthetase A phenylalanine adenylation enzyme. Journal of Computational Biology. 2005;12(6-7):740–761. doi: 10.1089/cmb.2005.12.740. [DOI] [PubMed] [Google Scholar]
- 89.Lilien RH, Bailey-Kellogg C, Anderson AC, Donald BR. A subgroup algorithm to identify cross-rotation peaks consistent with non-crystallographic symmetry. Acta Crystallographica Section D: Biological Crystallography. 2004;60(6):1057–1067. doi: 10.1107/S090744490400695X. [DOI] [PubMed] [Google Scholar]
- 90.Lim K, Nadarajah A, Forsythe EL, Pusey ML. Locations of bromide ions in tetragonal lysozyme crystals. Acta Crystallogr D Biol Crystallogr. 1998;54:899–904. doi: 10.1107/s0907444998002844. [DOI] [PubMed] [Google Scholar]
- 91.Lopez-Mendez B, Guntert P. Automated protein structure determination from nmr spectra. J Am Chem Soc. 2006;128(40):13112–13122. doi: 10.1021/ja061136l. [DOI] [PubMed] [Google Scholar]
- 92.Losonczi JA, Andrec M, Fischer MW, Prestegard JH. Order matrix analysis of residual dipolar couplings using singular value decomposition. J Magn Reson. 1999;138(2):334–342. doi: 10.1006/jmre.1999.1754. [DOI] [PubMed] [Google Scholar]
- 93.Bryson M, Tian F, Prestegard JH, Valafar H. REDCRAFT: a tool for simultaneous characterization of protein backbone structure and motion from RDC data. J Magn Reson. 2008;191(2):322–34. doi: 10.1016/j.jmr.2008.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Marin A, Malliavin TE, Nicolas P, Delsuc MA. From NMR chemical shifts to amino acid types: Investigation of the predictive power carried by nuclei. J Biomol NMR. 2004;30(1):47–60. doi: 10.1023/B:JNMR.0000042948.12381.88. [DOI] [PubMed] [Google Scholar]
- 95.Meiler J, Blomberg N, Nilges M, Griesinger C. A new approach for applying residual dipolar couplings as restraints in structure elucidation. Journal of Biomolecular NMR. 2000;16:245–252. doi: 10.1023/a:1008378624590. [DOI] [PubMed] [Google Scholar]
- 96.Meiler J, Peti W, Griesinger C. DipoCoup: A versatile program for 3D-structure homology comparison based on residual dipolar couplings and pseudocontact shifts. J Biom NMR. 2000;17:283–294. doi: 10.1023/a:1008362931964. [DOI] [PubMed] [Google Scholar]
- 97.Meiler J, Baker D. Rapid protein fold determination using unassigned NMR data. Proc Natl Acad Sci U S A. 2003;100(26):15404–15409. doi: 10.1073/pnas.2434121100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Meiler J, Baker D. The fumarate sensor DcuS: progress in rapid protein fold elucidation by combining protein structure prediction methods with NMR spectroscopy. J Magn Reson. 2005;173(2):310–316. doi: 10.1016/j.jmr.2004.11.031. [DOI] [PubMed] [Google Scholar]
- 99.Mettu R, Lilien R, Donald BR. High-throughput inference of protein-protein interfaces from unassigned NMR data. Bioinformatics. 2005;21(Suppl. 1):i292–i301. doi: 10.1093/bioinformatics/bti1005. [DOI] [PubMed] [Google Scholar]
- 100.Mueller GA, Choy WY, Yang D, Forman-Kay JD, Venters RA, Kay LE. Global folds of proteins with low densities of NOEs using residual dipolar couplings: application to the 370-residue maltodextrin-binding protein. J Mol Biol. 2000;300(1):197–212. doi: 10.1006/jmbi.2000.3842. [DOI] [PubMed] [Google Scholar]
- 101.Neal S, Nip AM, Zhang H, Wishart DS. Rapid and accurate calculation of protein 1H, 13C and 15N chemical shifts. J Biomol NMR. 2003;26:215–240. doi: 10.1023/a:1023812930288. [DOI] [PubMed] [Google Scholar]
- 102.Nilges M. A calculation strategy for the structure determination of symmetric dimers by 1H NMR. Proteins. 1993;17(3):297–309. doi: 10.1002/prot.340170307. [DOI] [PubMed] [Google Scholar]
- 103.Nilges M, Macias M, Odonoghue S, Oschkinat H. Automated NOESY interpretation with ambiguous distance restraints: The refined NMR solution structure of the pleckstrin homology domain from β-spectrin. J Mol Biol. 1997;269:408–22. doi: 10.1006/jmbi.1997.1044. [DOI] [PubMed] [Google Scholar]
- 104.Noonan K, O'Brien D, Snoeyink J. Probik: protein backbone motion by inverse kinematics. International J Robotics Research. 2005;24(11):971–982. [Google Scholar]
- 105.Vitek O, Bailey-Kellogg C, Craig B, Vitek J. Inferential backbone assignment for sparse data. J Biomol NMR. 2006;35(3):187–208. doi: 10.1007/s10858-006-9027-8. [DOI] [PubMed] [Google Scholar]
- 106.Oki H, Matsuura Y, Komatsu H, Chernov AA. Refined structure of orthorhombic lysozyme crystallized at high temperature: correlation between morphology and intermolecular contacts. Acta Crystallogr D Biol Crystallogr. 1999;55:114. doi: 10.1107/S0907444998008713. [DOI] [PubMed] [Google Scholar]
- 107.Okorokov AL, Sherman MB, Plisson C, Grinkevich V, Sigmundsson K, Selivanova G, Milner J, Orlova EV. The structure of p53 tumour suppressor protein reveals the basis for its functional plasticity. EMBO J. 2006;25(21):5191–5200. doi: 10.1038/sj.emboj.7601382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Olejniczak ET, Xu RX, Fesik SW. A 4D HCCH-TOCSY experiment for assigning the side chain 1H and 13C resonances of proteins. J Biomol NMR. 1992;2(6):655–659. doi: 10.1007/BF02192854. [DOI] [PubMed] [Google Scholar]
- 109.O'Neil R, Lilien R, Donald BR, Stroud R, Anderson A. The crystal structure of dihydrofolate reductase-thymidylate synthase from Cryptosporidium hominis reveals a novel architecture for the bifunctional enzyme. Jour Eukaryotic Microbiology. 2003;50(6):555–556. doi: 10.1111/j.1550-7408.2003.tb00627.x. [DOI] [PubMed] [Google Scholar]
- 110.O'Neil R, Lilien R, Donald BR, Stroud R, Anderson A. Phylogenetic classification of protozoa based on the structure of the linker domain in the bifunctional enzyme, dihydrofolate reductase-thymidylate synthase. Jour Biol Chem. 2003;278(52):52980–52987. doi: 10.1074/jbc.M310328200. [DOI] [PubMed] [Google Scholar]
- 111.Oxenoid K, Chou JJ. The structure of phospholamban pentamer reveals a channel-like architecture in membranes. PNAS. 2005;102:10870–10875. doi: 10.1073/pnas.0504920102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Palmer AG. Probing Molecular Motion By NMR. Current Opinion in Structural Biology. 1997;7:732–737. doi: 10.1016/s0959-440x(97)80085-1. [DOI] [PubMed] [Google Scholar]
- 113.Palmer AG, Williams J, McDermott A. Nuclear Magnetic Resonance Studies of Biopolymer Dynamics. Journal of Physical Chemistry. 1996;100:13293–13310. [Google Scholar]
- 114.Pearlman DA, Case DA, Caldwell JW, Ross WS, Cheatham TE, DeBolt S, Ferguson D, Seibel G, Kollman P. AMBER, a package of computer programs for applying molecular mechanics, normal mode analysis, molecular dynamics and free energy calculations to simulate the structures and energies of molecules. Comp Phy Comm. 1995;91:1–41. [Google Scholar]
- 115.Pierce N, Spriet J, Desmet J, Mayo S. Conformational splitting: a more powerful criterion for dead-end elimination. J Comput Chem. 2000;21:999–1009. [Google Scholar]
- 116.Popov VM, Chan DCM, Fillingham YA, Yee WA, Wright DL, Anderson AC. Analysis of complexes of inhibitors with Cryptosporidium hominis DHFR leads to a new trimethoprim derivative. Bioorg Med Chem Lett. 2006;16(16):4366–4370. doi: 10.1016/j.bmcl.2006.05.047. [DOI] [PubMed] [Google Scholar]
- 117.Potluri S, Yan A, Chou JJ, Donald BR, Bailey-Kellogg C. Structure determination of symmetric homo-oligomers by a complete search of symmetry configuration space using NMR restraints and van der Waals packing. Proteins: Structure, Function and Bioinformatics. 2006;65(1):203–219. doi: 10.1002/prot.21091. [DOI] [PubMed] [Google Scholar]
- 118.Potluri S, Yan A, Donald BR, Bailey-Kellogg C. A complete algorithm to resolve ambiguity for inter-subunit NOE assignment in structure determination of symmetric homo-oligomers. Protein Science. 2006;16(1) doi: 10.1110/ps.062427307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Prestegard JH. New techniques in structural NMR – anisotropic interactions. Nature Structural Biology. 1998:517–522. doi: 10.1038/756. [DOI] [PubMed] [Google Scholar]
- 120.Prestegard JH, Bougault CM, Kishore AI. Residual dipolar couplings in structure determination of biomolecules. Chem Rev. 2004;104(8):3519–3540. doi: 10.1021/cr030419i. [DOI] [PubMed] [Google Scholar]
- 121.Qu Y, Guo JT, Olman V, Xu Y. Protein fold recognition through application of residual dipolar coupling data. Pac Symp Biocomput. 2004:459–470. doi: 10.1142/9789812704856_0043. [DOI] [PubMed] [Google Scholar]
- 122.Bertram R, Quine JR, Chapman MS, Cross TA. Atomic refinement using orientational restraints from solid-state NMR. J Magn Reson. 2000;147:9–16. doi: 10.1006/jmre.2000.2193. [DOI] [PubMed] [Google Scholar]
- 123.Ramage R, Green J, Muir TW, Ogunjobi OM, Love S, Shaw K. Synthetic, structural and biological studies of the ubiquitin system: the total chemical synthesis of ubiquitin. J Biochem. 1994;299:151–158. doi: 10.1042/bj2990151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124.Rieping W, Habeck M, Nilges M. Inferential structure determination. Science. 2005;209(5732):303–306. doi: 10.1126/science.1110428. [DOI] [PubMed] [Google Scholar]
- 125.Rohl CA, Baker D. De Novo determination of protein backbone structure from residual dipolar couplings using Rosetta. J Am Chem Soc. 2002;124(11):2723–2729. doi: 10.1021/ja016880e. [DOI] [PubMed] [Google Scholar]
- 126.Rohl CA. Protein structure estimation from minimal restraints using Rosetta. Methods Enzymol. 2005;394:244–260. doi: 10.1016/S0076-6879(05)94009-3. [DOI] [PubMed] [Google Scholar]
- 127.Ruan K, Tolman JR. Composite alignment media for the measurement of independent sets of NMR residual dipolar couplings. J Am Chem Soc. 2005;127(43):15032–15033. doi: 10.1021/ja055520e. [DOI] [PubMed] [Google Scholar]
- 128.Bansal S, Miao X, Adams MW, Prestegard JH, Valafar H. Rapid classification of protein structure models using unassigned backbone RDCs and probability density profile analysis (PDPA) J Magn Reson. 2008;192(1):60–8. doi: 10.1016/j.jmr.2008.01.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Rumpel S, Becker S, Zweckstetter M. High-resolution structure determination of the CylR2 homodimer using paramagnetic relaxation enhancement and structure-based prediction of molecular alignment. J Biomol NMR. 2008;40(1):1–13. doi: 10.1007/s10858-007-9204-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130.Saupe A. Recent results in the field of liquid crystals. Angew Chem. 1968;7:97–112. [Google Scholar]
- 131.Saxe JB. Embeddability of weighted graphs in k-space is strongly NP-hard. Proceedings of the 17th Allerton Conference on Communications, Control, and Computing. 1979:480–489. [Google Scholar]
- 132.Seavey BR, Farr EA, Westler WM, Markley JL. A relational database for sequence-specific protein NMR data. Journal of Biomolecular NMR. 1991;1:217–236. doi: 10.1007/BF01875516. [DOI] [PubMed] [Google Scholar]
- 133.Shuker SB, Hajduk PJ, Meadows RP, Fesik SW. Discovering high-affinity ligands for proteins: SAR by NMR. Science. 1996;274:1531–1534. doi: 10.1126/science.274.5292.1531. [DOI] [PubMed] [Google Scholar]
- 134.Singh R, Berger B. ChainTweak: sampling from the neighbourhood of a protein conformation. Pacific Symposium on Biocomputing; 2005; 2005. pp. 54–65. [PubMed] [Google Scholar]
- 135.Skrynnikov NR, Kay LE. Assessment of molecular structure using frame-independent orientational restraints derived from residual dipolar couplings. J Biomol NMR. 2000;18(3):239–252. doi: 10.1023/a:1026501101716. [DOI] [PubMed] [Google Scholar]
- 136.Stevens B, Lilien R, Georgiev I, Donald BR, Anderson A. Redesigning the PheA domain of Gramicidin Synthetase leads to a new understanding of the enzyme's mechanism and selectivity. Biochemistry. 2006;45(51):15495–15504. doi: 10.1021/bi061788m. [DOI] [PubMed] [Google Scholar]
- 137.Suhre K, Sanejouand YH. ElNemo: a normal mode web server for protein movement analysis and the generation of templates for molecular replacement. Nucleic Acids Res. 2004;32(Web Server issue):610–614. doi: 10.1093/nar/gkh368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 138.Suhre K, Sanejouand YH. On the potential of normal-mode analysis for solving difficult molecular-replacement problems. Acta Crystallogr D Biol Crystallogr. 2004;60:796–799. doi: 10.1107/S0907444904001982. Pt 4. [DOI] [PubMed] [Google Scholar]
- 139.Tian F, Valafar H, Prestegard JH. A dipolar coupling based strategy for simultaneous resonance assignment and structure determination of protein backbones. J Am Chem Soc. 2001;123(47):11791–11796. doi: 10.1021/ja011806h. [DOI] [PubMed] [Google Scholar]
- 140.Tjandra N, Bax A. Direct measurement of distances and angles in biomolecules by NMR in a dilute liquid crystalline medium. Science. 1997;278:1111–1114. doi: 10.1126/science.278.5340.1111. [DOI] [PubMed] [Google Scholar]
- 141.Tobi D, Bahar I. Structural changes involved in protein binding correlate with intrinsic motions of proteins in the unbound state. Proc Natl Acad Sci U S A. 2005;102(52):18908–18913. doi: 10.1073/pnas.0507603102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 142.Tolman JR, Flanagan JM, Kennedy MA, Prestegard JH. Nuclear magnetic dipole interactions in field-oriented proteins: Information for structure determination in solution. Proc Natl Acad Sci USA. 1995;92:9279–9283. doi: 10.1073/pnas.92.20.9279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 143.Tugarinov V, Choy WY, Orekhov VY, Kay LE. Solution NMR-derived global fold of a monomeric 82-kDa enzyme. Proc Natl Acad Sci U S A. 2005;102(3):622–627. doi: 10.1073/pnas.0407792102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 144.Tugarinov V, Muhandiram R, Ayed A, Kay LE. Four-dimensional NMR spectroscopy of a 723-residue protein: chemical shift assignments and secondary structure of malate synthase g. J Am Chem Soc. 2002;124(34):10025–10035. doi: 10.1021/ja0205636. [DOI] [PubMed] [Google Scholar]
- 145.Valafar H, Prestegard JH. Rapid classification of a protein fold family using a statistical analysis of dipolar couplings. Bioinformatics. 2003;19(12):1549–1555. doi: 10.1093/bioinformatics/btg201. [DOI] [PubMed] [Google Scholar]
- 146.Vaney MC, Maignan S, Ries-Kautt M, Ducruix A. High-resolution structure (1.33 angstrom) of a HEW lysozyme tetragonal crystal grown in the APCF apparatus. Data and structural comparison with a crystal grown under microgravity from SpaceHab-01 mission. Acta Crystallogr D Biol Crystallogr. 1996;52:505–517. doi: 10.1107/S090744499501674X. [DOI] [PubMed] [Google Scholar]
- 147.Vijay-Kumar S, Bugg CE, Cook WJ. Structure of ubiquitin refined at 1.8 Å resolution. J Mol Biol. 1987;194:531–544. doi: 10.1016/0022-2836(87)90679-6. [DOI] [PubMed] [Google Scholar]
- 148.Vitek O, Bailey-Kellogg C, Craig B, Kuliniewicz P, Vitek J. Reconsidering complete search algorithms for protein backbone NMR assignment. Bioinformatics. 2005;21 2:ii230–ii236. doi: 10.1093/bioinformatics/bti1138. [DOI] [PubMed] [Google Scholar]
- 149.Vitek O, Vitek J, Craig B, Bailey-Kellogg C. Model-based assignment and inference of protein backbone Nuclear Magnetic Resonances. Stat Appl Genet Mol Biol. 2004;3(1) doi: 10.2202/1544-6115.1037. [DOI] [PubMed] [Google Scholar]
- 150.Wang CE, Pérez TL, Tidor B. AMBIPACK: A systematic algorithm for packing of macromolecular structures with ambiguous distance constraints. Proteins: Structure, Function, and Genetics. 1998;32:26–2. doi: 10.1002/(sici)1097-0134(19980701)32:1<26::aid-prot5>3.0.co;2-c. [DOI] [PubMed] [Google Scholar]
- 151.Wang L, Donald BR. Proceedings of the IEEE Computational Systems Bioinformatics Conference (CSB) Stanford; CA: Aug, 2004. Analysis of a systematic search-based algorithm for determining protein backbone structure from a minimal number of residual dipolar couplings; pp. 319–330. PMID: 16448025. [DOI] [PubMed] [Google Scholar]
- 152.Wang L, Donald BR. Exact solutions for internuclear vectors and backbone dihedral angles from NH residual dipolar couplings in two media, and their application in a systematic search algorithm for determining protein backbone structure. Jour Biomolecular NMR. 2004;29(3):223–242. doi: 10.1023/B:JNMR.0000032552.69386.ea. [DOI] [PubMed] [Google Scholar]
- 153.Wang L, Donald BR. Proceedings of the IEEE Computational Systems Bioinformatics Conference (CSB) Stanford; CA: Aug, 2005. An efficient and accurate algorithm for assigning nuclear Overhauser effect restraints using a rotamer library ensemble and residual dipolar couplings; pp. 189–202. PMID: 16447976. [DOI] [PubMed] [Google Scholar]
- 154.Wang L, Donald BR. Proceedings of the LSS Computational Systems Bioinformatics Conference (CSB) Stanford; CA: Aug, 2006. A data-driven, systematic search algorithm for structure determination of denatured or disordered proteins; pp. 68–78. PMID: 17369626. [PubMed] [Google Scholar]
- 155.Wang L, Mettu R, Donald BR. Proceedings of the IEEE Computational Systems Bioinformatics Conference (CSB) Stanford; CA: Aug, 2005. An algebraic geometry approach to protein backbone structure determination from NMR data; pp. 235–246. PMID: 16447981. [DOI] [PubMed] [Google Scholar]
- 156.Wang L, Mettu R, Donald BR. A polynomial-time algorithm for de novo protein backbone structure determination from NMR data. Journal of Computational Biology. 2006;13(7):1276–1288. doi: 10.1089/cmb.2006.13.1267. [DOI] [PubMed] [Google Scholar]
- 157.Wang YX, Jacob J, Cordier F, Wingfield P, Stahl SJ, Lee-Huang S, Torchia D, Grzesiek S, Bax A. Measurement of 3hJNC connectivities across hydrogen bonds in a 30 kDa protein. J Biomol NMR. 1999;14(2):181–184. doi: 10.1023/a:1008346517302. [DOI] [PubMed] [Google Scholar]
- 158.Wang YX, Marquardt JL, Wingfield P, Stahl SJ, Lee-Huang S, Torchia D, Bax A. Simultaneous measurement of 1H-15N, 1H-13C′, and 15N-13C′ dipolar couplings in a perdeuterated 30 kda protein dissolved in a dilute liquid crystalline phase. J Am Chem Soc. 1998;120(29):7385–7386. [Google Scholar]
- 159.Wedemeyer WJ, Rohl CA, Scheraga HA. Exact solutions for chemical bond orientations from residual dipolar couplings. J Biomol NMR. 2002;22:137–151. doi: 10.1023/a:1014206617752. [DOI] [PubMed] [Google Scholar]
- 160.Weidong H, Wang L. Residual dipolar couplings: Measurements and applications to biomolecular studies. Annual Reports on NMR Spectroscopy. 2006;58:231–303. [Google Scholar]
- 161.Wells S, Menor S, Hespenheide B, Thorpe MF. Constrained geometric simulation of diffusive motion in proteins. Phys Biol. 2005;2(4):127–136. doi: 10.1088/1478-3975/2/4/S07. [DOI] [PubMed] [Google Scholar]
- 162.Wikipedia. NP-completeness. Wikipedia, the Free Encyclopedia. 2008 September; Available online: http://en.wikipedia.org/wiki/NP-complete.
- 163.Wishart DS, Sykes BD. The 13C chemical shift index: A simple method for the identification of protein secondary structure using 13C chemical shift data. Journal of Biomolecular NMR. 1994;4:171–180. doi: 10.1007/BF00175245. [DOI] [PubMed] [Google Scholar]
- 164.Wishart DS, Sykes BD, Richards FM. Relationship between nuclear magnetic resonance chemical shift and protein secondary structure. Journal of Molecular Biology. 1991;222(2):311–33. doi: 10.1016/0022-2836(91)90214-q. [DOI] [PubMed] [Google Scholar]
- 165.Wishart DS, Sykes BD, Richards FM. The 13C chemical shift index: A fast and simple method for the identification of protein secondary structure using 13C chemical shift data. Biochemistry. 1992;31(6):1647–1651. doi: 10.1021/bi00121a010. [DOI] [PubMed] [Google Scholar]
- 166.Wuthrich K. Protein recognition by NMR. Nat Struct Biol. 2000;7(3):188–189. doi: 10.1038/73278. [DOI] [PubMed] [Google Scholar]
- 167.Choy WY, Tollinger M, Mueller GA, Kay LE. Direct structure refinement of high molecular weight proteins against residual dipolar couplings and carbonyl chemical shift changes upon alignment: an application to maltose binding protein. J Biomol NMR. 2001;21(1):31–40. doi: 10.1023/a:1011933020122. [DOI] [PubMed] [Google Scholar]
- 168.Wang X, Bansal S, Jiang M, Prestegard JH. RDC-assisted modeling of symmetric protein homo-oligomers. Protein Sci. 2008;17(5):899–907. doi: 10.1110/ps.073395108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 169.Xu XP, Case DA. Automated prediction of 15N, 13C′alpha′, 13C′beta′ and 13C′ chemical shifts in proteins using a density functional database. J Biomol NMR. 2001;21:321–333. doi: 10.1023/a:1013324104681. [DOI] [PubMed] [Google Scholar]
- 170.Xu Y, Zheng Y, Fan JS, Yang D. A new strategy for structure determination of large proteins in solution without deuteration. Nat Methods. 2006;3(11):931–937. doi: 10.1038/nmeth938. [DOI] [PubMed] [Google Scholar]
- 171.Yan A, Langmead C, Donald BR. A probability-based similarity measure for Saupe alignment tensors with applications to residual dipolar couplings in NMR structural biology. International Journal of Robotics Research. 2005;24(2–3):165–182. Special Issue on Robotics Techniques Applied to Computational Biology. [Google Scholar]
- 172.Zamoon J, Mascioni A, Thomas DD, Veglia G. NMR solution structure and topological orientation of monomeric phospholamban in dodecylphosphocholine micelles. Biophysical Journal. 2003;85(4):2589–2598. doi: 10.1016/s0006-3495(03)74681-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 173.Zavodszky MI, Lei M, Thorpe MF, Day AR, Kuhn LA. Modeling correlated main-chain motions in proteins for flexible molecular recognition. Proteins. 2004;57(2):243–261. doi: 10.1002/prot.20179. [DOI] [PubMed] [Google Scholar]
- 174.Zeng J, Tripathy C, Zhou P, Donald BR. Proceedings of the LSS Computational Systems Bioinformatics Conference (CSB) Stanford; CA: Aug, 2008. A Hausdorff-based NOE assignment algorithm using protein backbone determined from residual dipolar couplings and rotamer patterns; pp. 169–181. PMID. [PubMed] [Google Scholar]
- 175.Zweckstetter M. Determination of molecular alignment tensors without backbone resonance assignment: Aid to rapid analysis of protein-protein interactions. J Biomol NMR. 2003;27(1):41–56. doi: 10.1023/a:1024768328860. [DOI] [PubMed] [Google Scholar]
- 176.Zweckstetter M, Bax A. Single-step determination of protein substructures using dipolar couplings: aid to structural genomics. J Am Chem Soc. 2001;123(38):9490–9491. doi: 10.1021/ja016496h. [DOI] [PubMed] [Google Scholar]