Adjusting power for a baseline covariate in linear models

SUMMARY

The analysis of covariance provides a common approach to adjusting for a baseline covariate in medical research. With Gaussian errors, adding random covariates does not change either the theory or the computations of general linear model data analysis. However, adding random covariates does change the theory and computation of power analysis. Many data analysts fail to fully account for this complication in planning a study. We present our results in five parts. (i) A review of published results helps document the importance of the problem and the limitations of available methods. (ii) A taxonomy for general linear multivariate models and hypotheses allows identifying a particular problem. (iii) We describe how random covariates introduce the need to consider quantiles and conditional values of power. (iv) We provide new exact and approximate methods for power analysis of a range of multivariate models with a Gaussian baseline covariate, for both small and large samples. The new results apply to the Hotelling-Lawley test and the four tests in the “univariate” approach to repeated measures (unadjusted, Huynh-Feldt, Geisser-Greenhouse, Box). The techniques allow rapid calculation and an interactive, graphical approach to sample size choice. (v) Calculating power for a clinical trial of a treatment for increasing bone density illustrates the new methods. We particularly recommend using quantile power with a new Satterthwaite-style approximation.

1. INTRODUCTION

1.1. Motivation

Medical studies often use a random baseline covariate to increase precision and statistical power. Although of no consequence in data analysis, including any random predictors substantially complicates the theory and computation of power. Failing to account for randomness of predictors may distort power analysis and lead to a poor choice of sample size.

Regression and analysis of variance (ANOVA) models express a random response as a function of one or more predictors. Describing each predictor as fixed or random requires careful consideration of the study design. A scientist decides what values fixed predictors have before the study begins. For example, dose levels of a drug are usually fixed. In contrast, a scientist discovers values of random predictors only after collecting the data. Although errors in measurement could introduce additional randomness in both fixed and random predictors, we assume that the scientist measures all predictors without appreciable error.

In general, random predictors require more complex theory than do fixed predictors [1]. Optimal parameter estimates and hypothesis tests result from treating all of the predictors fixed. However, power analysis used to plan future studies must account for the random distribution of predictors. Computing the average power over all possible realizations of a particular study design [1] leads to what may be called unconditional power. Power calculated for a particular set of predictor values is described as (a particular) conditional power. With random predictors, the non-centrality parameter is a random variable. Quantile power equals the conditional power value that corresponds to a non-centrality value of specified probability. Each non-centrality value typically encompasses many predictor configurations.

1.2. Literature review

Power analysis with a baseline covariate, or any other type of random predictor, has received little attention. Univariate linear models of Gaussian responses and random discrete predictors have been popular in genetics [2] Soller and Genizi [3, 4] suggested large sample power approximations for such studies. Sampson [1] reviewed the relationships between correlation theory and regression models with multivariate Gaussian responses and predictors, defined unconditional power, and provided expressions for power in the univariate case. Gatsonis and Sampson [5] provided computational formulae and tables for exact (small sample) power of the test of zero multiple correlation with Gaussian predictors and response.

Many authors have studied the power of tests of independence between two sets of Gaussian variables. Most results involve asymptotic properties and use zonal polynomial forms [6-16].

Muller et al. [17] reviewed power calculations for the general linear multivariate model (GLMM) with fixed predictors. They recommended approximations due to Muller and Peterson [18] and Muller and Barton [19]. O'Brien and Shieh (Pragmatic, unifying algorithm gives power probabilities for common F tests of the multivariate general linear hypothesis, unpublished manuscript, University of Florida, 1992) suggested some modifications. The various approximations achieve roughly two decimal places of accuracy [19] (O'Brien and Shieh, unpublished manuscript as before).

1.3. Why not run a simulation?

Computer simulations provide a general tool for power analysis. However, the approach has many disadvantages, including programming time and the burden of certifying the accuracy of the results. Power analysis simulation can never be easier than data analysis. Equally importantly, power analysis typically involves considering an extensive range of design variations. Each change requires a new simulation. The common desire for the hundreds or thousands of power values needed for plots makes simulations troublesome at best. Although we use simulations for power analysis on occasion, it stands as our last resort.

1.4. Why worry about random predictors?

The following example illustrates the many concerns that may arise with random predictors. Cystic fibrosis typically decreases bone mineral density (BMD). Ontjes (unpublished proposal, University of North Carolina at Chapel Hill, 1994) planned to measure spine BMD at baseline, six months, and one year. Stratified by gender, patients were randomly assigned to treatment with a drug designed to increase bone density. Clearly baseline BMD has great appeal as a covariate. Without knowing exactly what values of BMD will occur, how can power be calculated? Is knowing the distribution sufficient? What if the study involves a few tens of subjects, as typically happens in phase I and II clinical trials? What impact do covariates have on the power of tests of fixed effects, such as drug dose? Do repeated measures or multivariate tests change the conclusions? Are there important interactions between two or more such complications? The new results allow answering these questions for many situations.

Although many other choices have practical value, we restrict attention to continuous predictors with Gaussian distributions. The restriction reffects particular interest in models with a baseline covariate.

2. A TAXONOMY OF MODELS AND HYPOTHESES

2.1. The GLMM(F, G, D)

We introduce a taxonomy in order to simplify discussion and separate known power results from those remaining to be discovered. Write the GLMM(F, G, D) as

$$\begin{array}{cc}\hfill \underset{N\times p}{\overset{\mathit{Y}}{}}& =\underset{N\times q\times p}{\overset{\mathit{XB}}{}}+\underset{N\times p}{\overset{\mathbb{E}}{}}\hfill \\ \hfill & =\underset{N\times q_F\times p}{\overset{{\mathit{FB}}_F}{}}+\underset{N\times q_G\times p}{\overset{{\mathit{GB}}_G}{}}+\underset{N\times q_D\times p}{\overset{{\mathit{DB}}_D}{}}+\underset{N\times p}{\overset{\mathbb{E}}{}}\hfill \end{array}$$ (1)

in which q_F, q_G and q_D are the number of columns of fixed, Gaussian and random discrete variables, respectively. Here q_F + q_G + q_D = q. The N rows of Y, X and 𝔼 correspond to independent sampling units, referred to as subjects, for convenience. We assume that X and each of its submatrices, F, G and D, have full rank, that B contains fixed parameters (which are known for power analysis), and that 𝓔([Y G 𝔼])=[FB_F 0 0]. Rows of G and 𝔼 are assumed to independently follow non-singular (finite) Gaussian distributions. As in [1], ${\mathit{B}}_G={\Sigma }_G^{-1}{\Sigma }_{GY}$ and ${\Sigma }_{\mathbb{E}}={\Sigma }_Y-{\Sigma }_{YG}{\Sigma }_G^{-1}{\Sigma }_{GY}$ imply ${\Sigma }_{\mathbb{E}}={\Sigma }_Y-{\mathit{B}}_G^{\prime }{\Sigma }_G{\mathit{B}}_G$. Also

$$\mathcal{v}=\left\{{\mathrm{row}}_i{\left(\left[\mathit{Y}\mathit{G}\mathbb{E}\right]\right)}^{\prime }\right\}=\left[\begin{array}{ccc}{\Sigma }_Y\hfill & {\Sigma }_{\mathit{YG}}\hfill & {\Sigma }_{\mathbb{E}}\hfill \\ {\Sigma }_{\mathit{GY}}\hfill & {\Sigma }_G\hfill & 0\hfill \\ {\Sigma }_{\mathbb{E}}\hfill & 0\hfill & {\Sigma }_{\mathbb{E}}\hfill \end{array}\right]$$ (2)

For fixed Σ_G and Σ_Y, diagonal elements of diagonal elements of Σ_𝔼 decrease with increasing correlation between the outcomes and the predictors. If q_G =1, then write g and ${\sigma }_g^2$ rather than G and Σ_G.

Depending on the choice of predictors and distributional assumptions, several different simplifications of the full model arise. The classical GLMM has only fixed predictors, and in our notation is called the GLMM(F). Similarly, we call a model with fixed and multivariate Gaussian predictors a GLMM(F, G), and so on.

For the BMD example, both gender and drug treatment represent fixed effects, while the baseline BMD measure serves as a random predictor. Let d_j indicate a vector of bone mineral density measurements at month j ∈ {0, 6, 12}. With m for male, f for female, t for treatment, and p for placebo, a reference cell coding allows writing the model as

$$\left[\begin{array}{cc}\hfill {\mathit{d}}_6\hfill & \hfill {\mathit{d}}_{12}\hfill \end{array}\right]=\left[\begin{array}{ccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\mathbf{d}}_{0,\mathrm{mp}}\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill {\mathbf{d}}_{0,\mathrm{mt}}\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\mathbf{d}}_{0,\mathrm{fp}}\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill {\mathbf{d}}_{0,\mathrm{ft}}\hfill \end{array}\right]\left[\begin{array}{cc}\hfill {\beta }_{0,6}\hfill & \hfill {\beta }_{0,12}\hfill \\ \hfill {\beta }_{\mathrm{f},6}\hfill & \hfill {\beta }_{\mathrm{f},12}\hfill \\ \hfill {\beta }_{\mathrm{t},6}\hfill & \hfill {\beta }_{\mathrm{t},12}\hfill \\ \hfill {\beta }_{\mathrm{ft},6}\hfill & \hfill {\beta }_{\mathrm{ft},12}\hfill \\ \hfill {\beta }_{1,6}\hfill & \hfill {\beta }_{1,12}\hfill \end{array}\right]+\mathbb{E}$$ (3)

In this design there are no random categorical predictors (D does not exist) and

$${\mathit{FB}}_F+{\mathit{gB}}_G=\left[\begin{array}{cccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \end{array}\right]\left[\begin{array}{cc}\hfill {\beta }_{0,6}\hfill & \hfill {\beta }_{0,12}\hfill \\ \hfill {\beta }_{\mathrm{f},6}\hfill & \hfill {\beta }_{\mathrm{f},12}\hfill \\ \hfill {\beta }_{\mathrm{t},6}\hfill & \hfill {\beta }_{\mathrm{t},12}\hfill \\ \hfill {\beta }_{1,6}\hfill & \hfill {\beta }_{1,12}\hfill \end{array}\right]+\left[\begin{array}{c}\hfill {\mathit{d}}_{0,\mathrm{mp}}\hfill \\ \hfill {\mathit{d}}_{0,\mathrm{mt}}\hfill \\ \hfill {\mathit{d}}_{0,\mathrm{fp}}\hfill \\ \hfill {\mathit{d}}_{0,\mathrm{ft}}\hfill \end{array}\right]\left[{\beta }_{1,6}{\beta }_{1,12}\right]$$ (4)

2.2. The General Linear Hypothesis (GLH)

With both fixed and random predictors, hypothesis tests may involve only random, only fixed, or both fixed and random predictors. Assume C, U and Θ₀ are fixed and known, with C of full row rank and U of full column rank. With Θ=CBU, an a × b matrix, every general linear hypothesis may be stated as H₀:Θ=Θ₀. For the GLMM(F, G), a GLH(F) has C =[C_F 0], with C_F a × q_F. The GLH(G) has C =[0C_G] with C_G a × q_G. A test of both random and fixed predictors, the GLH(F, G), has C =[C_F C_G].

Power may be computed in terms of a small collection of intermediate expressions, especially

$$\mathit{M}=\mathit{C}{\left({\mathit{X}}^{\prime }\mathit{X}\right)}^{-1}{\mathit{C}}^{\prime }$$ (5)

$$\mathit{H}={(\Theta -{\Theta }_0)}^{\prime }{\mathit{M}}^{-1}(\Theta -{\Theta }_0)$$ (6)

$${\Sigma }_{\ast }={\mathit{U}}^{\prime }{\Sigma }_{\mathbb{E}}\mathit{U}$$ (7)

$$\Omega =\mathit{H}{\Sigma }_{\ast }^{-1}$$ (8)

s= min(a, b), and s_* =rank(Ω) ≤ s. Also define $\epsilon ={\left[\mathrm{tr}\left({\Sigma }_{\ast }\right)\right]}^2∕\left[b\mathrm{tr}\left({\Sigma }_{\ast }^2\right)\right]$ a measure of discrepancy from sphericity used for repeated measures tests. See reference [17] for more details. For power analysis, assume that C , B, U, Θ₀, Σ_G and Σ_Y are known constants. If any component of X is random, then so are M, H and Ω.

The cystic fibrosis study focused on the test of gender-by-treatment interaction. Using a MANOVA approach asks if the interaction predicts any linear combination of the BMD at six or twelve months, adjusting for baseline. Define C=[0 0 0 1 0], U =I₂, Θ₀ =0. This is a GLH(F), which is often the most interesting sort of test in a clinical trial.

3. SMALL SAMPLE POWER

3.1. Known results for fixed predictor power and conditional power

Any method giving power for fixed predictors also gives power for models including a particular realization of random predictors. For example, in the BMD study, consider computing power using baseline values from a previous study. Hence power for fixed predictors equals conditional power, as defined earlier. We consider the multivariate Hotelling-Lawley trace statistic (HLT), as well as the tests for the univariate approach to repeated measures (Geisser-Greenhouse, Huynh-Feldt, Box conservative, and uncorrected). See the Appendix for detailed formulae. All reduce to the usual univariate test if b=1, which requires either only one outcome measure, or a univariate contrast among responses. As an example, for the BMD study, testing only the linear trend across the repeated measures gives b=1.

The O'Brien and Shieh modification of the Muller and Peterson [18] approximation for conditional power of the HLT uses McKeon's [20] F-approximation for the null. If t₁ = (N - q)² - (N - q)(2b + 3) + b(b + 3), t₂ =(N - q)(a + b + 1) - (a + 2b + b² - 1), then d:f :(H)=4 + (a + b + 2)t₁/t₂. Let $f_{\mathrm{crit},H}=F_F^{-1}[1-\alpha ;ab,d.f.\left(H\right)]$ and ${\omega }_{\mathrm{H}}=\mathrm{tr}\left(\mathit{H}{\Sigma }_{\ast }^{-1}\right)$. Conditional power is approximated by 1 - F_F[f_crit,H; ab,d.f.(H), ω_H].

Muller and Barton [19] described approximations for conditional power of the conservative, Geisser-Greenhouse, Huynh-Feldt and uncorrected tests. The tests estimate ε as 1/b, $\widehat{\epsilon }$, $\tilde{\epsilon }$ and 1, respectively, with $\widehat{\epsilon }$ and $\tilde{\epsilon }$ the MLE and Huynh-Feldt estimates. For test T∈{C, GG, HF, Un}, define $f_{\mathrm{crit},T}=F_F^{-1}[1-\alpha ;abm\left(\mathrm{T}\right),(N-q)bm\left(\mathrm{T}\right)]$, with m(T) equal to 1/b, an approximate value of 𝓔($\left(\widehat{\epsilon }\right)$), an approximate value of 𝓔($\left(\widehat{\epsilon }\right)$), or 1. Conditional power is approximated by 1 - F_Ft[f_crit,T; abε, b(N - q)ε ω_U], with ω_U = εtr(H)/tr(Σ_*). The uncorrected test and power calculations are exact whenever sphericity holds (ε=1).

Examination of the conditional power approximations allows concluding that they depend on random predictors only through scalar non-centrality values. In particular, ω_H and ω_U become random variables as functions of random X. Hence unconditional power may be computed by deriving the density of the random non-centrality parameter and integrating over all possible values.

3.2. New results for unconditional power: distributions of non-centrality for q_G =1

The special case with q_G = 1 and q_D = 0 reduces the design matrix to

$$\mathit{X}=\left[\mathit{F}\mathit{g}\right]$$ (9)

and also implies

$$\mathit{C}=\left[{\mathit{C}}_F{\mathit{c}}_g\right]$$ (10)

with C and C_F assumed to be of rank a and c_g of rank 0 or 1. For example, the test of treatment effect in the BMD study analysis is a special case. In turn, the presence of random g in

$${\omega }_{\mathrm{H}}=\mathrm{tr}\left[{(\Theta -{\Theta }_0)}^{\prime }{\left(\left[{\mathit{C}}_F{\mathit{c}}_g\right]{\left[\begin{array}{cc}\hfill {\mathit{F}}^{\prime }\mathit{F}\hfill & \hfill {\mathit{F}}^{\prime }\mathit{g}\hfill \\ \hfill {\mathit{g}}^{\prime }\mathit{F}\hfill & \hfill {\mathit{g}}^{\prime }\mathit{g}\hfill \end{array}\right]}^{-1}\left[\begin{array}{c}\hfill {\mathit{C}}_F^{\prime }\hfill \\ \hfill {\mathit{c}}_g^{\prime }\hfill \end{array}\right]\right)}^{-1}(\Theta -{\Theta }_0){\Sigma }_{\ast }^{-1}\right]$$ (11)

and

$${\omega }_{\mathrm{U}}=\frac{b\epsilon }{\mathrm{tr}\left({\Sigma }_{\ast }\right)}\mathrm{tr}\left[{(\Theta -{\Theta }_0)}^{\prime }{\left(\left[{\mathit{C}}_F{\mathit{c}}_g\right]{\left[\begin{array}{cc}\hfill {\mathit{F}}^{\prime }\mathit{F}\hfill & \hfill {\mathit{F}}^{\prime }\mathit{g}\hfill \\ \hfill {\mathit{g}}^{\prime }\mathit{F}\hfill & \hfill {\mathit{g}}^{\prime }\mathit{g}\hfill \end{array}\right]}^{-1}\left[\begin{array}{c}\hfill {\mathit{C}}_F^{\prime }\hfill \\ \hfill {\mathit{c}}_g^{\prime }\hfill \end{array}\right]\right)}^{-1}(\Theta -{\Theta }_0)\right]$$ (12)

makes both random.

Lemma 1

Assume h_H,1 and h_U,1 are constant, and q₁ q₂, q_3H and q_3U are scaled χ² random variables. For a GLMM(F, g), and a GLH(F, g) or a GLH(F), the random non-centrality for power approximation for the HLT test is exactly

$${\omega }_{\mathrm{H}}=h_{\mathrm{H},1}-q_{3\mathrm{H}}∕(q_1+q_2)$$ (13)

and for the `univariate' approach to repeated measures tests is exactly

$${\omega }_{\mathrm{U}}=h_{\mathrm{U},1}-q_{3\mathrm{U}}∕(q_1-q_2)$$ (14)

See the Appendix for details of the notation and a proof. Standard results for quadratic forms allow proving that q₁ is independent of q₂, q_3H, and q_3U, while q₂ is not independent of q_3H or q_3U. Also, neither q_3H nor q_3U are independent of q₁ + q₂.

Lemma 2

The non-centralities described in Lemma 1 may each be expressed exactly as weighted sums of independent χ² random variables. See the Appendix for a proof.

3.3. Unconditional power approximations

Theorem 1

For a GLMM(F, g) and a GLH(F, g) or a GLH(F), with C and C_F of rank a, ω_H is absolutely continuous, with Pr{0≤h_H,0≤ω_H≤h_H,1}=1. Hence the unconditional power for the Hotelling-Lawley trace may be approximated by

$$\begin{array}{cc}\hfill P_{u,\mathrm{H}}=& 1-{\int }_{h\mathrm{H},0}^{h\mathrm{H},1}{F}_F[f_{\mathrm{crit},\mathrm{H}};\mathit{ab},\mathrm{d}f\left(\mathrm{H}\right),t]f_{{\omega }_{\mathrm{H}}}\left(t\right)\mathrm{d}t\hfill \\ \hfill =& 1-\left\{F_F[f_{\mathrm{crit},\mathrm{H}};\mathit{ab},\mathrm{d}f\left(\mathrm{H}\right),t]f_{{\omega }_{\mathrm{H}}}\left(t\right)\mid \underset{t=h_{\mathrm{H},0}}{\overset{t=h_{\mathrm{H},1}}{}}-{\int }_{h\mathrm{H},0}^{h\mathrm{H},1}{F}_{{\omega }_{\mathrm{H}}}\left(t\right)\frac{\partial F_F[f_{\mathrm{crit},\mathrm{H}};\mathit{ab},\mathrm{d}f\left(\mathrm{H}\right),t]}{\partial t}\mathrm{d}t\right\}\hfill \\ \hfill =& 1-F_F[f_{\mathrm{crit},\mathrm{H}};\mathit{ab},\mathrm{d}f\left(\mathrm{H}\right),h_{\mathrm{H},1}]\hfill \\ \hfill & -\frac{1}{2}{\int }_{h_{\mathrm{H},0}}^{h_{\mathrm{H},1}}{F}_{{\omega }_{\mathrm{H}}}\left(t\right)\left\{F_F[f_{\mathrm{crit},\mathrm{H}};\mathit{ab},\mathrm{d}f\left(\mathrm{H}\right),t]-F_F\left[\frac{f_{\mathrm{crit},\mathrm{H}}\mathit{ab}}{\mathit{ab}+2};\mathit{ab}+2,\mathrm{d}f\left(\mathrm{H}\right),t\right]\right\}\mathrm{d}t\hfill \end{array}$$ (15)

The power may be approximate for three reasons. Conditional power is approximate for s = min(a, b)>1. Numerical calculation of the integral may reduce accuracy. Finally, an approximation (as in Section 3.5) may be preferred to Davies' [21] method for calculating F_ωH(t) if s_*>1. The results are exact (except for inaccuracy due to numerical integration) if s=1. This special case arises in comparing only two groups, as in many clinical trials. If s_* =1 then F_ωH(t) can be expressed exactly in terms of a possibly non-central F CDF, even if s>1.

Theorem 2

Let T index the conservative, Geisser-Greenhouse or Huynh-Feldt test. For a GLMM(F, g), and a GLH(F, g), with C and C_F of rank a, the approximate unconditional power for the univariate approach to repeated measures statistics is given by

$$\begin{array}{cc}\hfill P_{u,\mathrm{U}}=& 1-{\int }_0^{\infty }{F}_F[f_{\mathrm{crit};\mathrm{T}};\mathit{ab}\epsilon ,b(N-q)\epsilon ,{\omega }_{\mathrm{U}}]\mathbf{d}{\mathit{F}}_{{\omega }_{\mathrm{U}}}\hfill \\ \hfill & =1-F_F[f_{\mathrm{crit};\mathrm{T}};\mathit{ab}\epsilon ,b(N-q)\epsilon ,h_{\mathrm{U},1}]\hfill \\ \hfill & -\frac{1}{2}{\int }_{h_{\mathrm{U},0}}^{h_{\mathrm{U},1}}{F}_{{\omega }_{\mathrm{U}}}\left(t\right)\{F_F[f_{\mathrm{crit},\mathrm{T}};\mathit{ab}\epsilon ,b(N-q)\epsilon ,t]\phantom{\}}\hfill \\ \hfill & \phantom{\{}-F_F\left[\frac{f_{\mathrm{crit},\mathrm{T}}\mathit{ab}\epsilon }{\mathit{ab}\epsilon +2};\mathit{ab}\epsilon +2,b(N-q)\epsilon ,t\right]\}\mathrm{d}t\hfill \end{array}$$ (16)

The logic and most details of the proof are the same as for theorem 1 (see the Appendix).

The power may be approximate for three reasons. Conditional power is approximate if b>1. Numerical integration may introduce some inaccuracy. Finally, an approximation (as in Section 3.5) may be preferred for calculating F_ωH(t) if s_*>1. The results are exact (except for inaccuracy due to numerical integration) if b=1. This case arises with hypotheses involving only one response dimension, such as a linear trend, and any univariate hypothesis. If s_* = 1 then F_ωU(t) can be expressed exactly in terms of a possibly non-central F CDF, even if s>1.

3.4. Quantile power approximations

In addition to unconditional power, quantile power is of interest. Let ω_Hq be a number such that Pr{ω_H<ω_Hq}=F_ωH(ω_Hq)=q. A non-centrality parameter that small or smaller occurs in only 100q per cent of all realizations of possible experiments. Define quantile power for the Hotelling-Lawley test to be the power obtained conditional on observing a non-centrality parameter of ω_Hq:

$$P_{q,\mathrm{H}}=1-F_F[f_{\mathrm{crit},\mathrm{H}};\mathit{ab},\mathrm{d}f\left(\mathrm{H}\right),{\omega }_{{\mathrm{H}}_q}]$$ (17)

Quantile powers for the four tests with the `univariate' approach to repeated measures are defined similarly.

3.5. Computational techniques and approximations

Calculating a numerical value for quantile power will be illustrated by considering the Hotelling-Lawley test:

1. Fix q. For example, to nd the 25th percentile, q=0:25.

2. Find the qth percentile of non-centrality, ${\omega }_{\mathrm{H}q}=F_{{\omega }_{\mathrm{H}}}^{-1}\left(q\right)$, by numerical inversion of the equation F_ωH(ω_Hq)=q. A simple bisection method works, with Davies' algorithm for exact calculation of the CDF's of ω_H and ω_U.

3. Compute P_q,H with equation [17]. The QUAD function [22] or algorithm 5.1.2 in Thisted (reference [23], p. 271) were used for integration. Davies' algorithm was used to calculate exact CDF's of ω_H and ω_U.

To improve calculation speed, we developed an algorithm based on Satterthwaite approximations. For a GLH(F), equations [A6] and [A9] express Pr{ω_T≤w}, the CDF of the (random) non-centrality for test statistic T ∈ {H,U}, in terms of the CDF of

$$S_{\mathrm{T}}\left(w\right)=\sum _{k=0}^a{\lambda }_{\mathrm{T}k}{\chi }_k^2\left({\nu }_k\right)$$ (18)

Note that the set of λ_Tk are functions of w. Let

$${\nu }_{\ast \mathrm{T}1}={\left(\sum _{\{k:{\lambda }_{\mathrm{T}k}>0\}}{\lambda }_{\mathrm{T}k}{\nu }_k\right)}^2/\sum _{\{k:{\lambda }_{\mathrm{T}k}>0\}}{\lambda }_{\mathrm{T}k}{\nu }_k$$ (19)

$${\nu }_{\ast \mathrm{T}1}=\sum _{\{k:{\lambda }_{\mathrm{T}k}>0\}}{\lambda }_{\mathrm{T}k}^2{\nu }_k/\sum _{\{k:{\lambda }_{\mathrm{T}k}>0\}}{\lambda }_{\mathrm{T}k}{\nu }_k$$ (20)

and define ν_*T2 and λ_T2 as similar sums over the set {k : λ_Tk<0}, but with λ_Tk replaced by |λ_Tk| Note that ν_*T1, ν_*T2, λ_*T1 and λ_*T2 all depend on w through the set of λ_Tk. If {k: λ_Tk>0} is empty, F_ωT(w)=0, and if {k: λ_Tk<0} is empty, F_ωT(w)=1. Otherwise, a Satterthwaite type of approximation is given by

$$F_{{\omega }_{\mathrm{T}}}\left(w\right)\approx F_F\left(\frac{{\nu }_{\ast \mathrm{T}2}{\lambda }_{\ast \mathrm{T}2}}{{\nu }_{\ast \mathrm{T}1}{\lambda }_{\ast \mathrm{T}2}};{\nu }_{\ast \mathrm{T}1},{\nu }_{\ast \mathrm{T}2}\right)$$ (21)

The approximation can be used for both unconditional and quantile power.

4. LARGE SAMPLE POWER

For all of the multivariate tests, conditional power approaches 1 as sample size approaches ∞ (reference [14], p. 330). In turn, unconditional power also approaches 1, since it is an average conditional power. Here we focus on quantized limits, in the spirit of those in Anderson (reference [14], p. 330). See the Appendix for details. For a positive integer, m, define N(m)=mN, with N fixed. Evaluation of quantized limits centres on local Pitman-type alternatives (reference [14], p. 330; reference [24], p. 238). This leads to basing the test statistics on B/√{N (m)},(Θ - Θ₀)/√{N (m)}, and H_LA = H/N(m), and considering N(m)→∞.

With W and F_e as defined in the Appendix, asymptotic limits of the approximations to unconditional power may be expressed in terms of ${\mathit{M}}_{\mathrm{LA}}=N{C}_F{\left({\mathit{F}}_e^{\prime }{\mathit{WF}}_e\right)}^{-1}{\mathit{C}}_F^{\prime }={\mathit{C}}_F{\left({\mathit{F}}^{\prime }\mathit{F}\right)}^{-1}{\mathit{C}}_F^{\prime }$ and

$${\mathit{Q}}_{\mathrm{LA}}={(\Theta -{\Theta }_0)}^{\prime }[{\mathit{M}}_{\mathrm{LA}}^{-1}-{({\sigma }_g^2+{\mathit{c}}_g^{\prime }{\mathit{M}}_{\mathrm{LA}}^{-1}{\mathit{c}}_g)}^{-1}{\mathit{M}}_{\mathrm{LA}}^{-1}{\mathit{c}}_g{\mathit{c}}_g^{\prime }{\mathit{M}}_{\mathrm{LA}}^{-1}](\Theta -{\Theta }_0)$$ (22)

Lemma 3

For a GLMM(F, g) and a GLH(F, g), under a sequence of Pitman local alternatives indexed by m

$$H_{\mathrm{LA}}\underrightarrow{p}{\mathit{Q}}_{\mathrm{LA}}$$ (23)

See the Appendix for a proof.

Theorem 3

Consider the limits of the unconditional power approximations given in theorems 1 and 2 under a sequence of Pitman local alternatives indexed by m. Define ${\omega }_{H,\mathrm{LA}}=\mathrm{tr}\left({\mathit{Q}}_{\mathrm{LA}}{\Sigma }_{\ast }^{-1}\right)$ and ω_U,LA =bε tr(Q_LA)/tr(Σ_*), and let $c_{\mathrm{crit}}\left(\nu \right)=F_{{\chi }^2}^{-1}(1-\alpha ;\nu )$ be the 1 - α quantile of a χ² variable with ν degrees of freedom. Then the limits of the unconditional power approximations for the tests are given in Table I. See the Appendix for a proof.

Table I.

Limits of unconditional power under local alternatives

	Test	Limit
Univariate	Conservative	1 - Fχ2 [bεccrit(a); abε, ωU, LA]
	Geisser-Greenhouse	1 - Fχ2 [ccrit(abε); abε, ωU, LA]
	Huynh-Feldt (unbounded)	1 - Fχ2 t[ccrit(abε); abε, ωU, LA]
Multivariate	All tests coincide	1 - Fχ2 [ccrit(ab); ab, ωH, LA]

5. NUMERICAL RESULTS

We conducted a number of simulations to assess the accuracy of the approximations and to compare the speed of calculations to a Monte Carlo approach. Unconditional and quantile power, with s_* =1 and s_*>1, for HLT and the Geisser-Greenhouse tests were evaluated.

We illustrate the results with a simulation based on p=4, q_F = 3 and q_G = 1. Cell mean coding for a balanced design gave F_e = I_qF and F=I_qF ⊗1_N/qF. This led to

$$\mathit{Y}=\left[\begin{array}{cc}\hfill \mathit{F}\hfill & \hfill \mathit{g}\hfill \end{array}\right]\left[\begin{array}{c}\hfill {\mathit{B}}_F\hfill \\ \hfill {\mathit{B}}_g\hfill \end{array}\right]+\mathbb{E}$$ (24)

We chose Σ_Y = I_p, ${\sigma }_g^2=1$, B_F = Δg(1,2,0_qF-2), and ${\mathit{B}}_g=\rho 1_p^{\prime }$. The hypothesis involved α=0:05, C =[-1_qF-1 I_qF-1 0], U =I_p and Θ₀ = 0, which gave Ω two non-zero eigenvalues. The parameter Δ scales differences between two group intercepts (and means), while ρ is the slope for the covariate. We chose ρ=0:5 and N ∈ {15, 75, 150}. For each N, we selected three values of Δ so that exact median quantile power, p_q,H, was 0.20, 0.50 or 0.80. We also calculated the Satterthwaite approximate 0.50 quantile power (P_S,0.50,H).

Table II contains numerical power values and times. All calculations allowed a maximum error of 0.001. To find empirical quantile power, for fixed values of N, Σ_g, Σ_Y, Δ and ρ, we generated 1000 values of g. The SAS NORMAL function [22] produced pseudo-random spherical Gaussian data which were transformed to obtain realizations of g. For each g, we generated 1000 values of Y, and calculated 𝔼. Then LINMOD [25] was used to calculate test statistics and p-values. For each g, the empirical quantile power was the total number of times that the null hypothesis was rejected, divided by 1000. The empirical quantile power was the median of the 1000 empirical powers. Times for both quantile and unconditional power illustrate the dramatic speed advantage of the new methods over simulation, and the approximations over exact. For the examples considered, the results for non-centrality CDF's differ from those calculated with Davies' algorithm only in the third decimal place. All other inaccuracy arose from the conditional power approximations. The univariate approach to repeated measures conditional power approximations introduced errors as large as 0.05 for some cases with N = 15.

Table II.

Calculated and empirical HLT power

N	Δ	Median			Unconditional (mean)
		Exact	Approximate	Empirical	Exact	Approximate	Empirical
15	0.4997	0.200	0.200	0.194	0.195	0.195	0.193
	0.8076	0.500	0.500	0.502	0.487	0.487	0.491
	1.0976	0.800	0.800	0.809	0.784	0.784	0.796
75	0.1651	0.200	0.200	0.199	0.198	0.198	0.200
	0.2623	0.500	0.500	0.498	0.497	0.497	0.500
	0.3508	0.800	0.800	0.798	0.797	0.797	0.798
150	0.1142	0.200	0.200	0.200	0.199	0.199	0.200
	0.1813	0.500	0.500	0.498	0.498	0.498	0.499
	0.2424	0.800	0.800	0.798	0.802	0.798	0.798
Total CPU minutes		0.063	0.001	627.461	24.223	0.130	627.461

A limited number of cases were examined to assess the formulae given for asymptotic unconditional power. In those cases, a sample size of at least 1000 was required to ensure roughly two digits of accuracy. The same accuracy can apparently be achieved by using, for HLT for example, the rst term, and neglecting the integral term, in equation [15]. The integral term was never seen to be more than roughly 0.05.

6. POWER ANALYSIS EXAMPLE

A power analysis was conducted for the cystic fibrosis example using our new methods. Plausible values for B_G, Σ_Y and Σ_G were based on pilot data in the grant proposal [20]. It was assumed that the variances of the baseline, six and twelve month BMD's were equal, and that the correlation between any pair of measurements was equal. Sample sizes of 13 and 39 were considered, and a range of differences between means examined.

At the small sample size, substantial differences can be seen in Figure 1 among unconditional power, the lower 0.025 quantile (corresponding to a 95 per cent confidence level), and the traditional conditional power approximation based on adjusting the error covariance. The upper 0.975 quantile points lie roughly at the same values as the conditional approximation.

Figure 1.

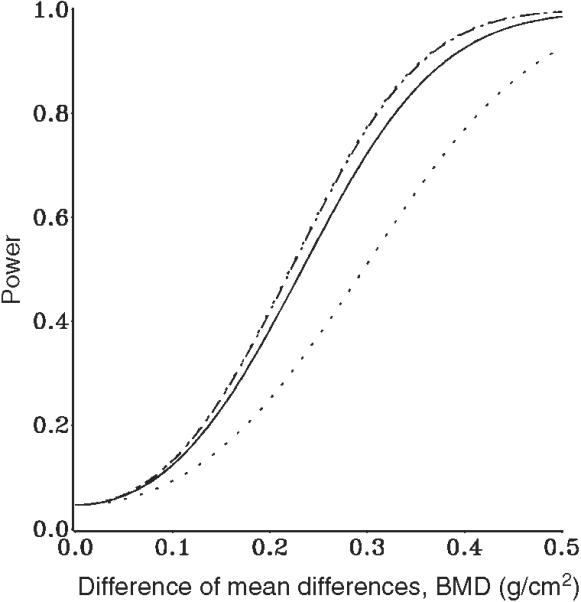
Geisser-Greenhouse power for gender × treatment, N = 13: … 95 per cent Cl; —unconditional; — - —conditional.

For N = 39 (see Figure 2), for the hypothesis and sample size of interest, the choice of quantile has a modest effect on power. Similar results were found for a range of related designs, tests and hypotheses.

Figure 2.

Geisser-Greenhouse power for gender × treatment, N = 39: … 95 per cent Cl; —unconditional; — - —conditional.

7. CONCLUSIONS

The presence of a baseline covariate substantially complicates power calculations of treatment effects in univariate and multivariate ANCOVA settings. New exact and approximate results allow conveniently computing power in the presence of a Gaussian covariate. We recommend computing quantile power for studies with random predictors. The choice of which quantile depends on the ethical and monetary features of the application.

Power methods vary substantially in convenience and speed. Simulations were the slowest, with methods based on numerical integration being next slowest. The Satterthwaite-style approximation is essentially as fast as the simple adjustment with conditional power methods, while being nearly as accurate in the integration technique. Hence the simple adjustment should be avoided, except possibly in large samples. We recommend using the Satterthwaite-style approximation as the best combination of accuracy and computational speed.

Many unanswered questions remain for power analysis with random covariates. In particular, the test of interaction between a random continuous predictor and a fixed predictor seems very important, but is not covered by known results. In the BMD example, testing for equality of baseline slopes in each treatment group falls into this category. More generally, non-Gaussian predictors seem important for practice, yet are not covered by known results.

APPENDIX

A.1. Distributions and approximations

As needed, a matrix is described as constant, random, or a realization of a random matrix. The Kronecker product is A⊗B = {a_ij·B}. Graybill's (reference [26], p. 309) definition for vec is used. Let Dg({λ₁,λ₂,…,λ_n}) indicate a diagonal matrix. Let χ²(ν,ω) indicate a chi-squared random variable with ν degrees of freedom and non-centrality ω (reference [27], chapter 28). Write the cumulative distribution function (CDF) of random variable Z as F_Z(z; θ₁, θ₂,…, θ_p), with pth quantile $F_Z^{-1}(p;{\theta }_1,{\theta }_2,\dots ,{\theta }_p)$. For the non-central F (reference [27], chapter 30) this gives F_F(x; a, b, ω).

Let K be the number of groups of subjects in F, with N_k subjects in each group. Assume that K, N_k and the maximum entry in F are all finite. The actual variables of interest are assumed to be available, and no surrogate variables are used. None of the data may be missing.

Proof of Lemma 1

A standard result for the inverse of a partitioned matrix (reference [28], p. 67) gives

$${\left[\begin{array}{cc}\hfill {\mathit{F}}^{\prime }\mathit{F}\hfill & \hfill {\mathit{F}}^{\prime }\mathit{g}\hfill \\ \hfill {\mathit{g}}^{\prime }\mathit{F}\hfill & \hfill {\mathit{g}}^{\prime }\mathit{g}\hfill \end{array}\right]}^{-1}=\left[\begin{array}{cc}\hfill {\mathit{B}}_{11}\hfill & \hfill {\mathit{b}}_{12}\hfill \\ \hfill {\mathit{b}}_{12}^{\prime }\hfill & \hfill b_{22}\hfill \end{array}\right]$$ (A1)

with B₁₁ =(F′F)^-1 + (F′F)^-1F′gb₂₂g′F(F′F)^-1, b₁₂ =-(F′F)^-1F′gb₂₂ and $b_{22}={\left\{{\mathit{g}}^{\prime }[\mathit{I}-\mathit{F}{\left({\mathit{F}}^{\prime }\mathit{F}\right)}^{-1}{\mathit{F}}^{\prime }]\mathit{g}\right\}}^{-1}=q_1^{-1}$. Then, with P =C_F(F′F)^-1F′ and g_* =Pg - c_g

$$\begin{array}{cc}\hfill \mathit{M}& =\left[\begin{array}{cc}\hfill {\mathit{C}}_F\hfill & \hfill {\mathit{c}}_g\hfill \end{array}\right]\left[\begin{array}{cc}\hfill {\mathit{B}}_{11}\hfill & \hfill {\mathit{b}}_{12}\hfill \\ \hfill {\mathit{b}}_{12}^{\prime }\hfill & \hfill b_{22}\hfill \end{array}\right]\left[\begin{array}{c}\hfill {\mathit{C}}_F^{\prime }\hfill \\ \hfill {\mathit{c}}_g^{\prime }\hfill \end{array}\right]\hfill \\ \hfill & ={\mathit{PP}}^{\prime }+b_{22}{\mathit{g}}_{\ast }{\mathit{g}}_{\ast }^{\prime }\hfill \end{array}$$ (A2)

Using the Bartlett formula for the inverse of a partitioned matrix (reference [28], p. 69), define ${\mathit{T}}_1=\left({\mathit{PP}}^{\prime }\right)={\left[{\mathit{C}}_F{\left({\mathit{F}}^{\prime }\mathit{F}\right)}^{-1}{\mathit{C}}_F^{\prime }\right]}^{-1}$, $q_2={\mathit{g}}_{\ast }^{\prime }{\mathit{T}}_1{\mathit{g}}_{\ast }$ and

$$\begin{array}{cc}\hfill {\mathit{M}}^{-1}& ={({\mathit{PP}}^{\prime }+b_{22}{\mathit{g}}_{\ast }{\mathit{g}}_{\ast }^{\prime })}^{-1}\hfill \\ \hfill & ={\left({\mathit{PP}}^{\prime }\right)}^{-1}-\frac{b_{22}}{1+b_{22}{\mathit{g}}_{\ast }^{\prime }{\left({\mathit{PP}}^{\prime }\right)}^{-1}{\mathit{g}}_{\ast }}{\left({\mathit{PP}}^{\prime }\right)}^{-1}{\mathit{g}}_{\ast }{\mathit{g}}_{\ast }^{\prime }{\left(P{P}^{\prime }\right)}^{-1}\hfill \\ \hfill & ={\mathit{T}}_1-{\mathit{T}}_1{\mathit{g}}_{\ast }{\mathit{g}}_{\ast }^{-1}{\mathit{T}}_1∕(q_1+q_2)\hfill \end{array}$$ (A3)

If $q_{3\mathrm{H}}={\mathit{g}}_{\ast }^{\prime }{\mathit{T}}_1(\Theta -{\Theta }_0){\Sigma }_{\ast }^{-1}{(\Theta -{\Theta }_0)}^{\prime }{\mathit{T}}_1{\mathit{g}}_{\ast }$ and $h_{\mathrm{H},1}=\mathrm{tr}\left[{(\Theta -{\Theta }_0)}^{\prime }{\mathit{T}}_1(\Theta -{\Theta }_0){\Sigma }_{\ast }^{-1}\right]$, then

$$\begin{array}{cc}\hfill {\omega }_{\mathrm{H}}& =\mathrm{tr}\left[{(\Theta -{\Theta }_0)}^{\prime }{\mathit{T}}_1(\Theta -{\Theta }_0){\Sigma }_{\ast }^{-1}\right]-\frac{1}{q_1+q_2}\mathrm{tr}\left[{(\Theta -{\Theta }_0)}^{\prime }{\mathit{T}}_1{\mathit{g}}_{\ast }{\mathit{g}}_{\ast }^{-1}{\mathit{T}}_1(\Theta -{\Theta }_0){\Sigma }_{\ast }^{-1}\right]\hfill \\ \hfill & =h_{\mathrm{H},1}-\mathrm{tr}\left[{\mathit{g}}_{\ast }^{\prime }{\mathit{T}}_1(\Theta -{\Theta }_0)\sum _{\ast }^{-1}{(\Theta -{\Theta }_0)}^{\prime }{\mathit{T}}_1{\mathit{g}}_{\ast }\right]∕(q_1+q_2)\hfill \end{array}$$ (A4)

Independence among some q_j's may be proven as follows. If z ~ N_N(0, I_N), then, $\mathit{g}={\sigma }_g\mathit{z}~{\mathrm{N}}_N(0,{\sigma }_g^2{\mathit{I}}_N)$. If m_g =P′ (PP′)^-1c_g and m_z = m_g/σ_g then g_* = P (g - m_g) = σ_gP(z - m_z). Define symmetric and psd A₁ = I - F(F′F)^-1F′, A₂ = P′ T₁P, and ${\mathit{A}}_{3\mathrm{H}}={\mathit{P}}^{\prime }{\mathit{T}}_1(\Theta -{\Theta }_0){\Sigma }_{\ast }^{-1}{(\Theta -{\Theta }_0)}^{\prime }{\mathit{T}}_1\mathit{P}∕h_{H,1}$. Here A₁ is idempotent, rank ν₁ = N - q_F, A₂ is idempotent, rank a and A_3H is not idempotent, with rank of s_*≤s. Also $q_1={\sigma }_g^2{\mathit{z}}^{\prime }{\mathit{A}}_1\mathit{z}$, $q_2={\sigma }_g^2{(\mathit{z}-{\mathit{m}}_z)}^{\prime }{\mathit{A}}_2(\mathit{z}-{\mathit{m}}_z)$ and $q_{3\mathrm{H}}={\sigma }_g^2{(\mathit{z}-{\mathit{m}}_z)}^{\prime }{\mathit{A}}_3(\mathit{z}-{\mathit{m}}_z)$ proving that each q_j is a quadratic form in independent Gaussians. Hence A₁A₂ = A₁A_3H = 0, and A₂A_3H ≠ 0 implies independence of corresponding q_j pairs [29].

For the univariate tests, h_U,1 = bεtr^-1(Σ_*)tr[(Θ - Θ₀)′T₁(Θ - Θ₀)]. Replacing ${\Sigma }_{\ast }^{-1}$ by bεtr^-1(Σ_*)I_b defines A_3U in lieu of A_3H, which in turn leads to q_3U in lieu of q_3H. Therefore

$$\begin{array}{cc}\hfill {\omega }_{\mathrm{U}}& =b\epsilon {\mathrm{tr}}^{-1}\left({\Sigma }_{\ast }\right)\mathrm{tr}\left[{(\Theta -{\Theta }_0)}^{\prime }{\mathit{T}}_1(\Theta -{\Theta }_0)-\frac{1}{q_1+q_2}{(\Theta -{\Theta }_0)}^{\prime }{\mathit{T}}_1{\mathit{g}}_{\ast }{\mathit{g}}_{\ast }^{\prime }{\mathit{T}}_1(\Theta -{\Theta }_0)\right]\hfill \\ \hfill & =h_{\mathrm{U},1}-q_{3\mathrm{U}}∕(q_1+q_2)\hfill \end{array}$$ (A5)

Proof of Lemma 2

Let F_ωH(w)=Pr{ω_H≤w} and b₀=1 - w/h_H,1, with 0≤b₀≤1. Then

$$\begin{array}{cc}\hfill F_{{\omega }_{\mathrm{H}}}\left(w\right)& =\mathrm{Pr}\{h_{\mathrm{H},1}-q_{3\mathrm{H}}∕(q_1+q_2)\le w\}\hfill \\ \hfill & =\mathrm{Pr}\{b_0\le (q_{3\mathrm{H}}∕h_{\mathrm{H},1})∕(q_1+q_2)\}\hfill \\ \hfill & =\mathrm{Pr}\left\{b_0\le \frac{{\sigma }_g^2}{{\sigma }_g^2}\frac{{(\mathit{z}-{\mathit{m}}_z)}^{\prime }{\mathit{A}}_{3\mathrm{H}}(\mathit{z}-{\mathit{m}}_z)}{{\mathit{z}}^{\prime }{\mathit{A}}_1\mathit{z}+{(\mathit{z}-{\mathit{m}}_z)}^{\prime }{\mathit{A}}_2(\mathit{z}-{\mathit{m}}_z)}\right\}\hfill \\ \hfill & =\mathrm{Pr}\{b_0{\mathit{z}}^{\prime }{\mathit{A}}_1\mathit{z}+{(\mathit{z}-{\mathit{m}}_z)}^{\prime }(b_0{\mathit{A}}_2-{\mathit{A}}_{3\mathrm{H}})(\mathit{z}-{\mathit{m}}_z)\le 0\}\hfill \\ \hfill & =\mathrm{Pr}\{S_{\mathrm{H}}\le 0\}\hfill \end{array}$$ (A6)

Define A_dH =(b₀A₂ - A_3H). The fact that A₁A₂ = A₁A_3H = 0 implies A₁A_dH = 0. With ${\mathit{T}}_1={\mathit{F}}_{T1}{\mathit{F}}_{T1}^{\prime }$ and ${\mathit{F}}_{T1}^{\prime }(\Theta -{\Theta }_0){\Sigma }_{\ast }^{-1}{(\Theta -{\Theta }_0)}^{\prime }{\mathit{F}}_{T1}∕h_{H,1}={\mathit{V}}_{s\mathrm{H}}\mathrm{Dg}\left({\lambda }_{s\mathrm{H}}\right){\mathit{V}}_{s\mathrm{H}}^{\prime }$, it follows that

$$\begin{array}{cc}\hfill {\mathit{A}}_{d\mathrm{H}}& =b_0{\mathit{P}}^{\prime }{\mathit{F}}_{T1}{\mathit{F}}_{T1}^{\prime }\mathit{P}-{\mathit{P}}^{\prime }{\mathit{F}}_{T1}{\mathit{F}}_{T1}^{\prime }(\Theta -{\Theta }_0){\Sigma }_{\ast }^{-1}{(\Theta -{\Theta }_0)}^{\prime }{\mathit{F}}_{T1}{\mathit{F}}_{T1}^{\prime }\mathit{P}∕h_{\mathrm{H},1}\hfill \\ \hfill & ={\mathit{P}}^{\prime }{\mathit{F}}_{T1}[b_0{\mathit{I}}_a-{\mathit{V}}_{s\mathrm{H}}\mathrm{Dg}\left({\lambda }_{s\mathrm{H}}\right){\mathit{V}}_{s\mathrm{H}}^{\prime }]{\mathit{F}}_{T1}^{\prime }\mathit{P}\hfill \\ \hfill & ={\mathit{P}}^{\prime }{\mathit{F}}_{T1}{\mathit{V}}_{s\mathrm{H}}[b_0{\mathit{I}}_a-\mathrm{Dg}\left({\lambda }_{s\mathrm{H}}\right)]{\mathit{V}}_{s\mathrm{H}}^{\prime }{\mathit{F}}_{T1}^{\prime }\mathit{P}\hfill \end{array}$$ (A7)

If V_dH+ = P′F_T1V_sH, then ${\mathit{V}}_{d\mathrm{H}+}^{\prime }{\mathit{V}}_{d\mathrm{H}+}={\mathit{I}}_a$ and A_dHV_dH+ = V_dH+[b₀I_a - Dg(λ_sH)]. Hence the first a eigenvectors of A_dH are V_dH+. Also A_dH has at most a non-zero eigenvalues, namely {b₀ - λ_sH,k}. Define ${\mathit{m}}_{z\mathrm{H}}={\mathit{V}}_{d\mathrm{H}+}^{\prime }{\mathit{m}}_z={\mathit{V}}_{s\mathrm{H}}^{\prime }{\mathit{F}}_{T1}^{\prime }{\mathit{c}}_g∕{\sigma }_g(a\times 1)$. Then

$$S_{\mathrm{H}}=b_0{\chi }_0^2(N-q_F)+\sum _{k=1}^{s_{\ast }}(b_0-{\lambda }_{s\mathrm{H},k}){\chi }_k^2(1,m_{z\mathrm{H},k}^2)+b_0\sum _{k=s_{\ast }+1}^a{\chi }_k^2(1,m_{z\mathrm{H},k}^2)$$ (A8)

with all χ² random variables independent of each other, which completes the proof. All coefficients are positive unless b₀ - λ_sH,1>0, which implies w>h_H,0 =h_H,1(1 - λ_sH,1).

Many special cases arise. If c_g = 0 then all χ²'s are central. Note that b₀ ∈(0,1) and λ_sH,k ∈(0,1). If λ_sH,k ≡ λ_sH>b₀, which is guaranteed by s_* = 1, then Pr{S_H≤0} can be expressed in terms of the CDF of a possibly doubly non-central F. If c_g = 0, s_* = 1 and N_* = N - q_F + a - 1, then λ_sH = 1, $S_{\mathrm{H}}=b_0{\chi }_0^2\left(N_{\ast }\right)+(b_0-1){\chi }_1^2\left(1\right)$, f_* = w/[N_*(h_H,1 - w)] and Pr{S_H≤0} = F_F(f_*;N_*,1).

Replacing ${\Sigma }_{\ast }^{-1}$ by bεtr^-1(Σ_*)I_b gives the parallel result for ω_U. In particular

$$\begin{array}{cc}\hfill F_{{\omega }_{\mathrm{U}}}& =\mathrm{Pr}\{b_0\le (q_{3\mathrm{U}}∕h_{\mathrm{U},1})∕(q_1+q_2)\}\hfill \\ \hfill & =\mathrm{Pr}\{b_0{\mathit{z}}^{\prime }{\mathit{A}}_1\mathit{z}+{(\mathit{z}-{\mathit{m}}_z)}^{\prime }(b_0{\mathit{A}}_2-{\mathit{A}}_{3\mathrm{U}})(\mathit{z}-{\mathit{m}}_z)\le 0\}\hfill \\ \hfill & =\mathrm{Pr}\{S_{\mathrm{U}}\le 0\}\hfill \end{array}$$ (A9)

With ${\mathit{F}}_{T1}^{\prime }(\Theta -{\Theta }_0){(\Theta -{\Theta }_0)}^{\prime }{\mathit{F}}_{T1}b\epsilon ∕\left[\mathrm{tr}\left({\Sigma }_{\ast }\right)h_{U,1}\right]={\mathit{V}}_{s\mathrm{U}}\mathrm{Dg}\left({\lambda }_{s\mathrm{U}}\right){\mathit{V}}_{s\mathrm{U}}^{\prime }$, the first a eigenvectors of A_dU=(b₀A₂ - A_3U) are P′F_T1V_sU. If ${\mathit{m}}_{z\mathrm{U}}={\mathit{V}}_{s\mathrm{U}}^{\prime }{\mathit{F}}_{T1}^{\prime }{\mathit{Pm}}_z={\mathit{V}}_{s\mathrm{U}}^{\prime }{\mathit{F}}_{T1}^{\prime }{\mathit{c}}_g∕{\sigma }_g(a\times 1)$ then

$$S_{\mathrm{U}}=b_0{\chi }_0^2(N-q_F)+\sum _{k=1}^{s_{\ast }}(b_0-{\lambda }_{s\mathrm{U},k}){\chi }_k^2(1,m_{z\mathrm{U},k}^2)+b_0\sum _{k=2_{ast}+1}^a{\chi }_k^2(1,m_{z\mathrm{U},k}^2)$$ (A10)

Proof of Theorem 1

Unconditional power equals the expected value of conditional power over all possible realizations of the experiment. Using the law of total probability, unconditional power can be approximated by integrating approximate conditional power with respect to ω_H.

For any G, ${\omega }_{\mathrm{H}}=\mathrm{tr}\left(\mathit{H}{\Sigma }_{\ast }^{-1}\right)\ge 0$ implies h_H,1 ≥q_3H/(q₁ + q₂). Also, q_j ≥ 0 and q_3H/(q₁ + q₂) ≥ 0. Finite N, Θ, C_F and 0<|Σ_*|<∞ ensure finite h_H,1. Hence ∞>h_H,1 ≥ q_3H/(q₁+q₂) ≥ 0, which implies h_H,1 ≥ ω_H ≥ 0. See the proof of lemma 2 for the derivation of h_H,0. As a smooth function of absolutely continuous random variables, ω_H is also absolutely continuous (and has a density). Use an expression for ∂F_F(f;ν₁,ν₂,t)=∂t [30, 30.46] and integration by parts to complete the proof.

A.2. Local alternatives and quantized limits

In a GLMM(F), the experimenter decides a priori to select a certain number of subjects from each of K groups. Write the predictor matrix as

$$\mathit{F}={\left[\begin{array}{cccc}\hfill {\mathit{f}}_1\otimes 1_{N_1}^{\prime }\hfill & \hfill {\mathit{f}}_2\otimes 1_{N_2}^{\prime }\hfill & \hfill \cdots \hfill & \hfill {\mathit{f}}_k\otimes 1_{N_K}^{\prime }\hfill \end{array}\right]}^{\prime }\left[\begin{array}{c}\hfill {\mathit{f}}_1\otimes 1_{N_1}^{\prime }\hfill \\ \hfill {\mathit{f}}_2\otimes 1_{N_2}^{\prime }\hfill \\ \hfill \cdots \hfill \\ \hfill {\mathit{f}}_k\otimes 1_{N_K}^{\prime }\hfill \end{array}\right]$$ (A11)

with f_k a q_F × 1 vector of values for a subject in group k. Define the essence matrix, F_e, as that matrix which contains one and only one copy of each unique row of F [31]:

$$\underset{K\times q_F}{\overset{{\mathit{F}}_e}{}}={\left[\begin{array}{cccc}\hfill {\mathit{f}}_1\hfill & \hfill {\mathit{f}}_2\hfill & \hfill \cdots \hfill & \hfill {\mathit{f}}_k\hfill \end{array}\right]}^{\prime }$$ (A12)

Let W be a diagonal K × K matrix with diagonal entries {N₁/N,N₂/N,…,N_k/Nt}. Then $N={\Sigma }_{k=1}^K{N}_k$ and ${\mathit{F}}^{\prime }\mathit{F}=N{\mathit{F}}_e^{\prime }{\mathit{WF}}_e$.

For a positive integer m, let N(m)= mN. As m →∞, then N(m)→∞ in a sequence of quantized steps, each of size N, a quantized limit process. The sequences used in the limits here are in the same spirit as those in Anderson (reference [14], p. 330). Also define F(m) = F ⊗ 1_m. Then $\mathit{F}{\left(m\right)}^{\prime }\mathit{F}\left(m\right)=N\left(m\right){\mathit{F}}_e^{\prime }{\mathit{WF}}_e$. Note that W, F_e and N remain fixed as N (m) increases.

We assume row_i(G_m)′ = N_N(m)(0,Σ_G), with independent rows. Both F(m) and G_m increase by N rows at each step, which corresponds to drawing a larger random sample for G_m.

Proof of Lemma 4

Consider

$$\underset{N\left(m\right)\to \infty }{\overset{\lim }{}}{\left[N\left(m\right)\right]}^{-1}{\mathit{M}}^{-1}=\underset{N\left(m\right)\to \infty }{\overset{\lim }{}}{[{\mathit{T}}_1∕N\left(m\right)]}^{-1}-\underset{N\left(m\right)\to \infty }{\overset{\lim }{}}\left([N\left(m\right){\sigma }_g^2∕(q_1+q_2)]\left\{{\left[N\left(m\right)\right]}^{-2}{\sigma }_g^{-2}{\mathit{T}}_1{\mathit{g}}_{\ast }{\mathit{g}}_{\ast }^{\prime }{\mathit{T}}_1\right\}\right)$$ (A13)

First

$$\begin{array}{cc}\hfill \underset{N\left(m\right)\to \infty }{\overset{\lim }{}}{[{\mathit{T}}_1∕N\left(m\right)]}^{-1}& =\underset{N\left(m\right)\to \infty }{\overset{\lim }{}}{\{{\mathit{C}}_F{\left[N\left(m\right){\mathit{F}}_e^{\prime }\mathit{W}{\mathit{F}}_e\right]}^{-1}{\mathit{C}}_F^{\prime }∕N\left(m\right)\}}^{-1}\hfill \\ \hfill & ={\mathit{M}}_{\mathrm{LA}}^{-1}\hfill \end{array}$$ (A14)

Next write

$$\underset{N\left(m\right)\to \infty }{\overset{\lim }{}}\left[\frac{{\sigma }_g^{2}N\left(m\right)}{q_1+q_2}\right]=\underset{N\left(m\right)\to \infty }{\overset{\lim }{}}\frac{1}{{\left[N\left(m\right){\sigma }_g^2\right]}^{-1}{q}_1+{\left[N\left(m\right){\sigma }_g^2\right]}^{-1}{q}_2}$$ (A15)

and use lemma 19.9 of Arnold (reference [32], p. 365) to show ${\lim }_{N\left(m\right)\to \infty }{\left[N\left(m\right){\sigma }_g^2\right]}^{-1}{q}_1=1$ As the Gaussian in q₂ converges in probability to a point mass, $q_2∕N\left(m\right)\stackrel{p}{\to }{\mathit{c}}_g^{\prime }{\mathit{M}}_{\mathrm{LA}}^{-1}{\mathit{c}}_g∕{\sigma }_g^2$. Finally

$${\mathit{T}}_1{\mathit{g}}_{\ast }{\mathit{g}}_{\ast }^{\prime }{\mathit{T}}_1{\left[{\sigma }_{g}N\left(m\right)\right]}^{-2}={\mathit{T}}_1{\mathit{g}}_{\ast }{\mathit{g}}_{\ast }^{\prime }{\left[{\sigma }_{g}N\left(m\right)\right]}^{-2}{\mathit{T}}_1$$ (A16)

with ${\mathit{T}}_1={\left\{{\mathit{C}}_F{\left[N\left(m\right){\mathit{F}}_e^{\prime }{\mathit{WF}}_e\right]}^{-1}{\mathit{C}}_F^{\prime }\right\}}^{-1}$. Since the Gaussian vector in ${\mathit{T}}_1{\mathit{g}}_{\ast }{\mathit{g}}_{\ast }^{\prime }{\mathit{T}}_1$ converges in probability to a point mass

$${\mathit{T}}_1{\mathit{g}}_{\ast }{\mathit{g}}_{\ast }^{\prime }{\mathit{T}}_1{\sigma }_g^{-2}{\left[N\left(m\right)\right]}^{-2}\underrightarrow{p}{\mathit{M}}_{\mathrm{LA}}^{-1}{\mathit{c}}_g{\mathit{g}}_g^{\prime }{\mathit{M}}_{\mathrm{LA}}^{-1}{\sigma }_g^{-2}$$ (A17)

and the result follows.

Proof of Theorem 3

For the HLT, approximate unconditional power is defined in equation (15). By lemma 4, ${\mathit{H}}_{\mathrm{LA}}\stackrel{p}{\to }{\mathit{Q}}_{LA}$. Thus ${\lim }_{N\left(m\right)\to \infty }{\omega }_{\mathrm{H}}={\omega }_{H,\mathrm{LA}}$. The result follows by lemma 1 in Glueck and Muller [33]. For the univariate tests, convergence of H_LA implies that lim_N(m)→∞ω_U=ω_U,LA, and the CDF of non-centrality becomes a point mass. Similar arguments apply to the Pillai-Bartlett and Wilks' tests. Hence they have the same asymptotic unconditional power under local alternatives.