Newtonian Kinetic Isotope Effects. Observation, Prediction, and Origin of Heavy-Atom Dynamic Isotope Effects

Abstract

Intramolecular ¹³C kinetic isotope effects were determined for the dimerization of cyclopentadiene. Substantial isotope effects were observed in three positions, despite the C₂ symmetry of the cycloaddition transition state and the absence of dynamical bottlenecks after this transition state. The observed isotope effects were predicted well from trajectory studies by extrapolating the outcomes of trajectories incorporating superheavy isotopes of carbon, ranging from ²⁰C to ¹⁴⁰C. Trajectory studies suggest that the isotope effects are unrelated to zero-point energy or the geometrical and momentum properties of the transition state. However, steepest-descent paths in mass-weighted coordinates correctly predict the direction of the isotope effects, supporting a novel origin in Newton’s second law of motion.

Newton’s second law of motion provides that lighter masses accelerate more in response to a constant force. This effect is routinely used to separate isotopes, for example in mass spectrometry, but the fractionation of isotopes associated with chemical reactivity originates mainly in quantum effects such as zero-point energy (ZPE) and tunneling. We describe here the observation of unusual heavy-atom kinetic isotope effects (KIEs) in a familiar reaction, an approach to the difficult problem of quantitatively predicting these KIEs, and a discussion of their apparent origin in classical mechanics.

Many simple reactions pass through symmetrical transition states to afford without barrier products of lower symmetry.¹ Diverse calculational methods place the Diels-Alder dimerization of cyclopentadiene in this category,^2,3 involving a C₂-symmetric transition structure 1 on its way to the asymmetric product. The branching accompanying the symmetry breaking leads to two equivalent structures. With isotopic substitution, the products are isotopomeric and distinguishable. For example, 1 containing a ¹³C at the starred carbon a may afford either 2 or 3. Their ratio constitutes an intramolecular KIE and represents the selectivity among trajectory outcomes on the “bifurcating energy surface” of the reaction. Five intramolecular ¹³C KIEs may be observed in the dimerization of cyclopentadiene, as five pairs of isotopomeric products may arise from labeling in positions a, b, c, d, and e of 1.

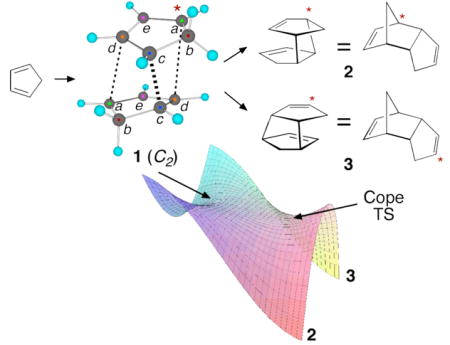
To measure these KIEs, the relative ¹³C content in the five paired positions of dimer formed at 25 °C was determined at natural abundance by an indirect procedure. Dicyclopentadiene undergoes a degenerate [3,3]-sigmatropic (Cope) rearrangement at temperatures below its normal cracking temperature,⁴ and this rearrangement equilibrates the isotopomeric pairs formed in the dimerization process. The difference in the isotopic composition of equilibrated (140 °C, 6 h) versus unequilibrated dicyclopentadiene (“kinetic dimer”) reflects the departure of the kinetic dimer from its equilibrium composition, and this difference is readily determined by NMR methodology.⁵ The intramolecular KIEs were obtained by correcting the raw results for small equilibrium isotope effects, calculated from the harmonic B3LYP/6-311+G** frequencies.³ The average results from seven independent determinations, each based on six spectra for each equilibrated and kinetic dimer sample, are summarized in Figure 1.

Figure 1.

¹³C distribution and intramolecular ¹³C KIEs in the dimerization of cyclopentadiene. Numbers in parentheses represent 95% confidence limits in the last digit. The intramolecular KIEs are defined as k_12C/k_13C(a)/k_12C/k_13C (a′), k_12C/k_13C (b)/k_12C/k_13C (b′), etc.

The intramolecular ¹³C KIEs observed are comparable in magnitude to ordinary ¹³C KIEs, despite the absence of a barrier between 1 and the five pairs of isotopomeric products. The KIEs in the a/a′ and d/d′ positions correspond to a preference for ¹²C to be incorporated into the newly formed σ bond. The direction of these KIEs is interestingly in line with expectations for a highly unsymmetrical transition state, though calculations weigh strongly against this explanation.^2,3 The c/c′ KIE does not fit with an unsymmetrical transition state and is enigmatic from any conventional perspective.

The KIEs cannot be predicted from conventional transition state theory because the pairs of products arise from a single transition state. Lluch has proposed that variational transition state theory can be applied in such cases.⁶ However, the Lluch approach requires the existence of dynamical bottlenecks along steepest-descent paths leading to the products. Applying the Lluch procedure, B3LYP/6-31G* and CCSD(T)/6-311+G**//B3LYP/6-31G* paths show no bottleneck.

Repetitive randomized trajectories could in principle be used to predict these KIEs,⁷ but the ≈10⁶ trajectories required for sufficient precision would be impractical in DFT calculations. We reasoned that this problem may be avoided by using, in silico, much heavier isotopes of carbon. Toward that end, quasiclassical direct-dynamics⁸ trajectories on a B3LYP/6-31G* energy surface were initiated from isotopologues of 1 containing a single ²⁰C, ²⁸C, ⁴⁴C, ⁷⁶C, or ¹⁴⁰C (12 + 2^N amu, N=3, 4, 5, 6, or 7). Each normal mode in 1 was given its ZPE plus a Boltzmann sampling of additional energy appropriate for 25 °C, with a random phase and sign for its initial velocity. The transition vector was given a Boltzmann sampling of energy ‘forward’ from the col. Employing a Verlet algorithm, 1-fs steps were taken until the product was formed (median time 80 fs), and the trajectories affording product with the superheavy carbon in the a versus a′, b versus b′, etc. positions were counted (Table 1).

Table 1.

Trajectories started from 1 employing superheavy carbons.

Labeled position	isotope weight	results	KIE 95% confid. range	extrapolated KIE for 13C
a	140	151 a, 269 a′	1.80 ± 0.28	1.018(8)
	76	157 a, 245 a′	1.58 ± 0.25
	44	192 a, 256 a′	1.34 ± 0.19	[exp.: 1.020(6)]
	28	205 a, 251 a′	1.23 ± 0.14
	20	272 a, 296 a′	1.09 ± 0.13
b	140	237 b, 249 b′	1.06 ± 0.13
	76	227 b, 223 b′	0.99 ± 0.13
c	140	205 c, 115 c′	0.57 ± 0.10	0.988(4)
	76	166 c, 112 c′	0.68 ± 0.11
	44	315 c, 243 c′	0.77 ± 0.09	[exp.: 0.991(3)]
	28	286 c, 254 c′	0.89 ± 0.10
	20	282 c, 262 c′	0.93 ± 0.10
d	140	314 d, 226 d′	0.72 ± 0.09	0.982(4)
	76	284 d, 216 d′	0.76 ± 0.09
	44	168 d, 140 d′	0.84 ± 0.14	[exp.: 0.983(4)]
	28	907 d, 777 d′	0.86 ± 0.06
	20	687 d, 627 d′	0.91 ± 0.07
e	140	252 e, 234 e′	0.93 ± 0.11
	76	318 e, 334 e′	1.05 ± 0.11

The trajectory results parallel experiment closely. Superheavy carbons in 1 preferentially move to the a′, c, and d positions of the product, and the preference increases as the mass increases. No statistically significant preference for b versus b′ or e versus e′ positions was observed, even with ¹⁴⁰C. Extrapolation of the results to ¹³C (see the Supporting Information) leads to predicted KIEs for the a, c, and d positions of 1.018, 0.988, and 0.982, respectively, in striking agreement with the experimental KIEs. This supports the idea that the underlying physics leading to the KIEs with the superheavy carbons is the same as with ¹³C experimentally.

The ability of trajectory studies to predict these KIEs solves one part of the problem, but such studies provide no direct or intuitively satisfying explanation of their origin. In weighing the origin of the KIEs, we considered five ways in which isotopic substitution desymmetrizes the system: A. the ZPE-derived motion of the ‘competing’ carbon atoms will differ at the transition state; B. the energy surface including ZPE becomes unsymmetrical; C. the transition state hypersurface becomes unsymmetrical in coordinate space from the desymmetrization of the normal modes; D. the transition state becomes unsymmetrical in momentum space due to the motions associated with the desymmetrized normal modes; and E. as per Newton’s second law, the lighter of competing carbons responds more quickly to the forces pulling atoms toward the product geometry after the transition state. This last factor is tautologically equivalent to recognizing that the potential energy surface between the transition state and the products is unsymmetrical in mass-weighted coordinates.

A series of observations gauge the importance of these factors to the origin of the observed KIEs. First, the calculated KIEs are unchanged in fully classical trajectory simulations. This weighs strongly against ZPE as a substantial contributor to the KIEs. We also note that ZPE-derived explanations do not fit with the c/c′ KIE; at no point along a steepest-descent path to product (obtained by the Lluch procedure⁶) is there a significant difference in the ZPE for substitution of ¹³C at c versus c′. The asymmetry of the transition state hypersurface was assayed directly by Boltzmann-weighted integrations with ¹⁴⁰C in the various positions. In each case, no significant difference was found in the relative areas closer in Cartesian space to a versus a′, b versus b′, etc. As an indirect measure of the transition state hypersurface, the KIEs disappear in simulations that use initial conditions based on the normal modes with ¹⁴⁰C but use ¹²C as the mass for propagating trajectories. In contrast, trajectories initialized with ¹²C but propagated with ¹⁴⁰C exhibit the regular KIEs. These observations are inconsistent with an origin of the KIEs in the geometrical or momentum properties of the transition state.

By elimination, this leads to Newton’s second law as the source of the KIEs. In support of this idea, steepest descent paths in mass-weighted coordinates started from 1 containing ¹³C in positions a, c, and d desymmetrize rapidly and lead in each case to the major product. The origin of this desymmetrization (and by extension the KIEs) for a and d is recognizably associated with the greater distance these carbons must travel from 1 to form a σ bond in the product. More subtly, the steepest-descent path with a heavy isotope at c holds back motion of the adjacent d toward σ bond formation, accounting for the isotope effect at c. In contrast, ¹³C in positions b, and e engender no significant desymmetrization of the paths.

None of this should be surprising; though real trajectories do not follow IRCs,⁹ the role of Newton’s second law in determining products is subtly assumed in the multitude of calculational papers employing IRCs. The results here simply show for the first time that this principle of classical motion can lead to KIEs in ordinary reactions.