Dynamic Conditionally Linear Mixed Models for Longitudinal Data

Summary

We develop a new class of models, dynamic conditionally linear mixed models, for longitudinal data by decomposing the within-subject covariance matrix using a special Cholesky decomposition. Here ‘dynamic’ means using past responses as covariates and ‘conditional linearity’ means that parameters entering the model linearly may be random, but nonlinear parameters are nonrandom. This setup offers several advantages and is surprisingly similar to models obtained from the first-order linearization method applied to nonlinear mixed models. First, it allows for flexible and computationally tractable models that include a wide array of covariance structures; these structures may depend on covariates and hence may differ across subjects. This class of models includes, e.g., all standard linear mixed models, antedependence models, and Vonesh–Carter models. Second, it guarantees the fitted marginal covariance matrix of the data is positive definite. We develop methods for Bayesian inference and motivate the usefulness of these models using a series of longitudinal depression studies for which the features of these new models are well suited.

1. Introduction

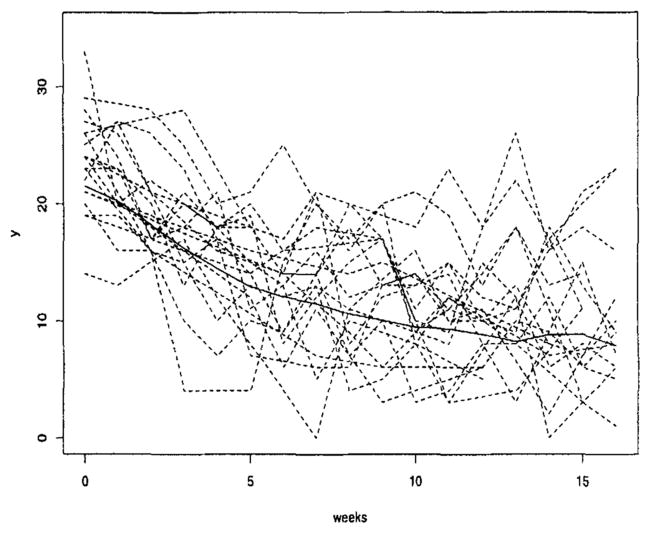
In clinical trials and observational studies, repeated measures on the same subject over time are correlated. In this article, we explore the dependence structure of longitudinal data from a series of five depression studies conducted in Pittsburgh from 1982 to 1992 (Thase et al., 1997). Patients were assigned active treatment and measured weekly for 16 weeks. Earlier work (Thase et al., 1997) explored the time to recovery from depression. Here we will examine the rate of improvement and dependence in weekly depression scores over this 16-week period for the 549 subjects with no missing baseline covariates (Figure 1). Three main questions of interest for this analysis were as follows: (1) Is the combination drug/psychotherapy treatment more effective than the psychotherapy-only treatment in improving patients’ depression? (2) Is initial severity an important predictor of patient improvement? (3) Do treatment and initial severity interact in their impact on the rate of improvement? This last question relates to practice guide-lines for treatment of major depression, which emphasizes the importance of symptom severity in determining the need for antidepressant drugs (Thase et al., 1997).

Figure 1.

Trend in depression scores over the 16-week treatment period. The solid line is the line through the observed mean at each week. The dashed lines are the observed curves for a random sample of 20 subjects.

For these 549 patients, about 30% (2840) of the possible measurements were missing mostly intermittently. There are several reasons for the missingness. Several of the studies measured depression biweekly for part or all of the active phase of treatment, so we have some observations missing by design. Some subjects dropped out (about 16%). Of the dropouts, some were missing completely at random (MCAR) while some were related to treatment, such as side effects or being so depressed they would need an alternative treatment (Patricia Houck, personal communication). Previous analyses with these data and analyses of similar data (Gibbons et al., 1993) have assumed the missingness was at random (MAR). Within our modeling framework, discussed below, the MAR assumption implies that dropout is explained by measured covariates in the model and/or observed responses prior to dropout (e.g., poor performance early in the study). Future work will examine the sensitivity of inferences to this assumption using pattern mixture models (e.g., Hogan and Laird, 1997), where we use the class of models developed here for each missing data pattern; however, this is beyond the scope of the current article.

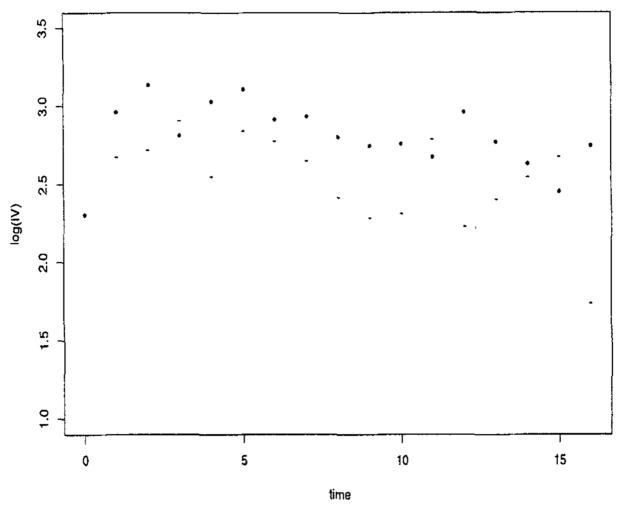
We develop a class of models with the following features: (1) flexibility in modeling the covariance structure parsimoniously and (2) ease in allowing the covariance structure to vary across subjects. The first feature is motivated by the fact that a 17 × 17 covariance matrix has 153 parameters and one needs to reduce the number of parameters to be estimated. The second feature is motivated by preliminary exploration of components of the covariance matrix, which suggests that the covariance structure may differ by the initial severity of depression in the patient. In particular, the variances for the severely depressed patients (defined at baseline) are higher than those not severely depressed (see Figure 2). Our class of models includes random effects models with residual auto-correlation, which has been used previously in the analysis of depression data (Gibbons et al., 1993).

Figure 2.

Logarithm of innovation variances versus time for low (−) and high (*) severity.

Having motivated the features of this class of models for analyzing the depression dataset, we review some models for longitudinal data in the current literature and, in the process, introduce our model in more detail. Many methods for handling dependence are introduced as an afterthought in conjunction with the desire to model accurately the marginal means of the responses within the framework of generalized linear models (McCullagh and Nelder, 1989, Chapter 9; Diggle, Liang, and Zeger, 1994). A notable example is the linear mixed models (Laird and Ware, 1982),

$${\mathit{y}}_i=X_i\beta +Z_i{b}_i+{\epsilon }_i,i=1,\dots ,m,$$ (1)

where y_i is an n_i × 1 vector of responses measured on the ith subject, β is the vector of unknown fixed effects parameters, b_i is a q × 1 vector of unknown random effects parameters, and X_i and Z_i are known n_i × p and n_i × q design matrices, respectively. The roles of the random term Z_ib_i in modeling the individual effects (conditional means) and covariances simultaneously carry over to our more general treatment of dependence if one views Z_ib_i as a stochastically weighted sum of the columns of the design matrix Z_i. Lately, there is a growing tendency to view the repeated measures on a subject over time as a curve and model it using certain extensions of latent curve analysis (Rao, 1958) and multivariate growth curve models (Potthoff and Roy, 1964). The key mathematical tool in this framework is the spectral decomposition (Karhunen-Loève expansion) of a covariance matrix Σ (stochastic process), with its eigenspace taking the place of the column space of Z_i (Rice and Silverman, 1991; Ramsay and Silverman, 1997; Brumback and Rice, 1998; Wang, 1998; Scott and Handcock, 1999; Verbyla et al., 1999). The close relationships between the linear mixed models and its predecessor, the multivariate growth curve models and its more recent reincarnation as functional data analysis (Ramsay and Silverman, 1997), are established by Mikulich et al. (1999) and Scott and Handcock (1999), respectively. These developments reveal the salient feature of the linear mixed models as a source for flexible and powerful models for capturing dependence in the repeated measure data; for its limitations, however, see Lindsey (1999, p. 119).

An extension of (1) known as conditionally linear mixed models (Vonesh–Carter models) is given by

$${\mathit{y}}_i=f(X_i,\beta )+Z_i{b}_i+{\epsilon }_i,i=1,2,\dots ,m,$$ (2)

with every component as in (1) except that now f is a known nonlinear function of its arguments (Vonesh and Carter, 1992). This model, which is linear in the random effects and nonlinear in the fixed effects, subsumes many earlier models and is closely related to the Sheiner, Rosenberg, and Melmon (1972) and Beal and Sheiner’s (1982) models.

Our focus in this article is on the accurate modeling of the covariance matrix of the responses. We show that another generalization of (2) called dynamic conditionally linear mixed models is universal for modeling dependence in the sense that it can handle essentially any dependence structure. The key idea is that the covariance matrix Σ of a mean-zero random vector y = (y₁,…,y_n) can be diagonalized by a lower triangular matrix constructed from the regression coefficients when y_t is regressed on its predecessors y₁,…,y_t−1. More precisely, for t = 2,…,n, we have

$$y_t=\sum _{j=1}^{t-1}{\varphi }_{tj}{y}_j+{\epsilon }_t,T\mathrm{\sum }{T}^{\prime }=D,$$ (3)

where T and D are unique matrices, T is a unit lower triangular having ones on its diagonal and −ϕ_tj at its (t, j) th position, j < t, and D is diagonal with ${\sigma }_t^2=var({\epsilon }_t)$ as its diagonal entries (Pourahmadi, 1999, 2000). We show that, after accounting for the means, (3) leads to representing the vector y_i of repeated measurements on the ith subject with covariance Σ_i as a model similar to (2) with two additional design matrices, both random, depending on the response y_i and, in addition, depending nonlinearly on the fixed effect parameters β and linearly on the random mean parameters b_i. The resulting marginal covariance matrices are guaranteed to be positive definite and can differ across individuals through either explained (covariates) or unexplained (random effects) heterogeneity.

The outline of the article is as follows. Section 2 reviews dynamic conditionally linear mixed models. These models allow for a wide selection of covariance structures within the frame-work of a simple, conditionally linear mixed model. Section 3 discusses Bayesian inference, including computational details and model comparisons. Section 4 offers a complete analysis of the depression dataset and, in the process, introduces some of the types of covariance structures that can be modeled in this framework. For these data, model 5 in Table 1 stands out as a clear indication of the degree of flexibility one has in modeling covariances using the factorization (3).

Table 1.

The DIC and design matrices for several models fitted to the depression data. The DIC of the best fitting model is in bold type. Design matrices: Z_i: * = (poly_t(2)); A_i: + = (I_t−j=1 × severity_i, I_t−j=2), + + = (I_t−j=1, I_t−j=2, I_t−j=3, I _t−j=4), + + + = (poly_t(1) × I _t−j=1, poly_t−j(4) × I_{t−j > l}), + + + + = (poly_t(1) × I_t−j=1 × drug_i, poly_t−j(4) × I_t−j>l × drug_i); U_i: * = (I_{t−j = l}); L_i: + = (severity_i × I_t=0, I_t>0 × I_severityi=1, I_t>0 × I_severityi=0 × poly_t(3)).

Model	Zi	Ai	Ui	Li	DIC*	DIC	D̄	D(θ̄)	pD
ID		—	—	—	28,677	28,542	28,512	28,481	31
UN	—	—	—	—	25,536	25,045	24,931	24,817	114
1	*	—	—	—	25,408	25,249	25,212	25,175	37
2	*	+	—	+	25,024	24,934	24,913	24,892	21
3	—	++	—	+	25,069	24,956	24,930	24,905	26
4	—	+++	*	+	25,174	24,910	24,850	24,789	61
5	—	++++	—	+	25,025	24,886	24,855	24,823	32

2. Dynamic Mixed Models for Longitudinal Data

In this section, we introduce a dynamic extension of (2) that offers considerable conceptual and computational flexibility in modeling the covariance of correlated data. Consider a longitudinal study where m subjects enter the study. Let y_i = (y_i1,…,y_i,ni)′ stand for the vector of repeated measurements on subject i, y_it be the response measured at (not necessarily equidistant) times indexed by t = 1,…,n_i (i = 1,…,m), and x_it = (x_1it,…,x_pit)′ be the covariates. Often it is of interest to assess the effects of the covariates on the response of interest using regression models while accounting for the dependence among the repeated measurements.

Let Σ_i = cov(y_i) be the covariance matrix of the measurements on the ith subject and $T_i{\mathrm{\sum }}_i{T}_i^{\prime }=D_i$ be its Cholesky decomposition as in (3). Following Pourahmadi (1999) and Daniels and Pourahmadi (2001), the nonredundant entries of T_i and D_i, denoted by ϕ_i,tj, which will be called the generalized autoregressive parameters (GARP), and ${\sigma }_{it}^2$, which will be called the innovation variances (IV), can be modeled using time and/or subject-specific covariate vectors a_i,tj and l_i,t by setting

$${\varphi }_{i,tj}=a_{i,tj}^{\prime }\gamma ,log{\sigma }_{it}^2={\ell }_{i,t}^{\prime }\lambda ,$$ (4)

where γ and λ are q₁ × 1 and q₂ × 1 vectors of unknown dependence and variance parameters, respectively. Then the dynamic model (3) for the ith subject takes the form $y_{it}={\mathrm{\sum }}_{j=1}^{t-1}{\varphi }_{i,tj}{y}_{ij}+{\epsilon }_{it}$. Upon substituting for ϕ_i,tj from (4), it reduces to

$$y_{it}=A_{it}^{\prime }\gamma +{\epsilon }_{it},$$ (5)

where $A_{it}={\mathrm{\sum }}_{j=1}^{t-1}{a}_{i,tj}{y}_{ij}$ is a stochastically weighted sum of the covariates a_i,tj with y_ij’s as the weights, reminiscent of the random term Z_ib_i in (1).

If the levels, variations, and shapes of subject-specific trajectories vary considerably across subjects (Figure 1), then one may replace γ by γ + g_i, which is random and subject dependent, and add the effect of the covariates x_it to (5), as in (2). To this end, we introduce two new design matrices and parameter vectors, (Z_i, bi) and (U_i, g_i), and additionally allow the flexibility for the marginal mean to be nonlinear in the fixed parameters β through f (·) by considering the model

$${\mathit{y}}_i=f(X_i,\beta )+Z_i{b}_i+A_i\gamma +U_i{g}_i+{\epsilon }_i,i=1,2,\dots ,m,$$ (6)

where ε_i ~ N(0, D_i), b_i ~ N(0, G_b), g_i ~ N(0, G_g), and A_i = (A_i1,…,A_ini) and U_i = (U_i1,…,U_ini) are dynamic design matrices constructed from the a_i,tj and u_i,tj (subset of a_i,tj associated with the random components of γ, g_i), respectively, as in (5), but with y_it replaced by y_it − f (x_it, β) − z_itb_i. Such centering of the design matrix is needed for the identification of the mean parameters (β, b_i) and the covariance parameters (γ, g_i) (see (7) below).

We call (6) a dynamic conditionally linear mixed model. Special cases of this model include all nonlinear mixed effects models in Vonesh and Carter (1992), where g_i and γ equal zero; random coefficient autoregressive models (Rahiala, 1999), where b_i equals zero, f(·) is the identity function, and A_i and U_i are not centered; and hence the random coefficient polynomial and growth curve models. The model in (6) allows the flexibility of fitting many complex covariance structures using the conceptual and computational tools often used to fit the standard linear mixed models.

Alternatively, for computational convenience, we rewrite (6) as

$${\mathit{y}}_i=f(X_i\beta )+Z_i{b}_i+{\epsilon }_i^{\ast },i=1,2,\dots ,m,$$ (7)

where ${\epsilon }_i^{\ast }\sim \text{N}(0,{\mathrm{\sum }}_i)$ and ${\mathrm{\sum }}_i^{-1}=T(\gamma ,g_i)D_i^{-1}(\lambda )T^{\prime }(\gamma ,g_i)$. This formulation also makes apparent how computations can be done very simply using the Gibbs sampler and induces a marginal covariance structure on y_i of the familiar form $Z_i{G}_b{Z}_i^{\prime }+{\mathrm{\sum }}_i$. This model allows the covariance matrix to vary across subjects using either subject-specific covariates, a_i,tj and l_i,t, and/or random effects, g_i. While we have arrived at this extension of (2) via a purely algebraic factorization of a covariance matrix, historically, (2) had appeared first in the literature of pharmacokinetics (Sheiner et al., 1972; Beal and Sheiner, 1982) using linearization methods to approximate nonlinear mixed models with a form additive in the random effects and individual errors. A major motivation for such approximations was the desire to adapt the existing estimation and inferential procedure and software packages for the linear mixed models. For a detailed review of the linearization methods and the relevant software, see Davidian and Giltinan (1995, Chapter 6).

A referee has pointed out that, in models (2) and (6), the fixed and random effects appear on different scales. Though these models have some limitations, they are useful in approximating more general nonlinear mixed models, and in some case studies, they are motivated by the substantive knowledge and are supported by the data; see Heitjan (1991).

3. Bayesian Inference

In this section, we discuss prior specifications and model fitting using the Gibbs sampler. In addition, we discuss model comparison using the output from the Gibbs sampler.

3.1 Priors and Computations

We propose independent, noninformative normal priors on β γ, and λ, with large variances and inverse Wishart priors on G_b and G_g, with degrees of freedom equal to dim(G_b) and dim(G_g), respectively. To sample from the posterior distribution of the parameters, we develop a simple Gibbs sampler. The full conditional distributions of all parameters have known forms, either normals, inverse Wisharts, or inverse gammas, except for λ. Specifically, when sampling from the full conditional distribution of G_b, β, b_i, and the missing data, we use formulation (7); when sampling γ, g_i, and D(λ), we use formulation (6). To sample λ, we implement a Metropolis–Hastings algorithm, using a normal approximation to the full conditional distribution of λ as the candidate distribution. For the models with f (·) not the identity function, nonlinear models in the fixed mean parameters, the full conditional distribution of β will not be a known form. Here we also implement a similar Metropolis–Hastings algorithm. More details of the Bayesian implementation can be found in Davidian and Giltinan (1995, Chapter 8) and Daniels and Pourahmadi (2001).

We use data augmentation (Tanner and Wong, 1987) to integrate over the missing data. Operationally, this involves imputing the missing responses using equation (7) and assumes the missing responses are MAR. More specifically, the complete set of 17 observations for subject i are divided into its observed components (y_obs) and missing components (y_mis), so that y_i = (y_obs, y_mis). Given that y_i conditional on all the mean and covariance parameters is multivariate normal, the conditional distribution of y_mis | y_obs will also be multivariate normal. This distribution is the full conditional of the missing data for subject i given the observed data.

3.2 Model Comparison

The complexity of these models make standard model comparisons using the AIC and BIC difficult since both the sample size and the dimension of the parameter space are not obvious. Consequently, to compare models with or without random effects in the mean or covariance parameters, we will use the recent deviance information criterion (DIG) (Spiegelhalter et al., 2001). The structure of this statistic allows for automatic computation of the dimension of the parameter space and has a form similar to the Akaike information criterion (AIC): a goodness-of-fit term, the deviance evaluated at the posterior mean of the parameters, and a penalty term, two times the effective number of parameters, computed as the mean deviance minus the deviance evaluated at the posterior mean. Thus,

$$\text{DIC}=\text{dev}(\overline{\theta })+2p_D,$$ (8)

where θ̄ is the posterior mean of θ and $p_D=\overline{\text{dev}}-\text{dev}(\overline{\theta })$, where $\overline{\text{dev}}$ is the posterior mean of the deviance.

However, we point out that the DIC has a problem similar to the AIC; when the sample size gets large, it favors models with too many parameters. As a result, we might alter the DIC to a form similar to the BIC,

$${\text{DIC}}^{\ast }=\text{dev}(\overline{\theta })+p_{D}log(m),$$ (9)

where m is the number of subjects. We will use both DIC and DIC* for model comparison in Section 4.

4. Longitudinal Depression Data

4.1 Model Building and Selection

The Hamilton Rating Scale for Depression (HRSD), measured weekly, was used as the measure of depression for these studies. Similar to Thase et al. (1997), we pooled the data across studies. We did not include indicators of study in our model, which was motivated by the fact that they were confounded with age and gender so we adjusted for study by including these covariates in the model. For our analysis, we modeled the rate of improvement of HRSD over the 17 weeks (baseline + 16 weeks of treatment). The main questions of interest were addressed in the Introduction.

We restricted ourselves to the dynamic conditionally linear mixed models (6) with f (·) the identity function. As discussed in Section 2, this class of models allows the covariance structure to vary across subjects, either through random parameters of the covariance and/or covariates, i.e., through the design matrices A_i and U_i. These models were fit using Gibbs sampling algorithm described in Section 3.1. To compare the different covariance models, we used the DIC and DIC*. Here we defined the deviance as

$$\text{dev}(\theta )=-2\times \text{loglik}(\theta \mid y_{\text{obs}}),$$ (10)

where $\theta =(\beta ,{\mathrm{\sum }}_i^{-1}(g_i,\gamma ,\lambda ,G_g))$ as in (7), y_obs is the observed data, and the other parameters and missing data have been integrated out. We also mention that p_D depends on how we parameterize θ Fortunately, in our analysis, similar conclusions were drawn when we set θ = (β, g_i, γ λ G_g). This explains, e.g., why p_D for the unstructured model in Table 1 is not 167, the number of parameters in the unstructured covariance matrix plus the 14 fixed mean parameters (β).

4.2 Exploratory Analysis

Our exploratory work on these data is presented next. A quadratic trend in weekly Hamilton scores (see Figure 1) fit well. We considered interactions of this trend with the four possible combinations of the two binary covariates: initial severity of depression in the patient, with two levels, high versus low; and treatment (drug), with two levels, drug and psychotherapy versus only psychotherapy. Estimation and testing of these interactions addresses one of the questions of this analysis—how treatment and severity affect the rate of improvement. To account for the differences between studies, we also included age and gender of the patient. Thus, the design vector x_it for the ith patient at time t is 14 × 1, x_it = (poly_t(2), drug_i × poly_t(2), severity_i × poly_t(2), drug_i × severity_i × poly_t(2), gender_i, age_i), where poly_a (k) is a kth-order orthogonal polynomial in a.

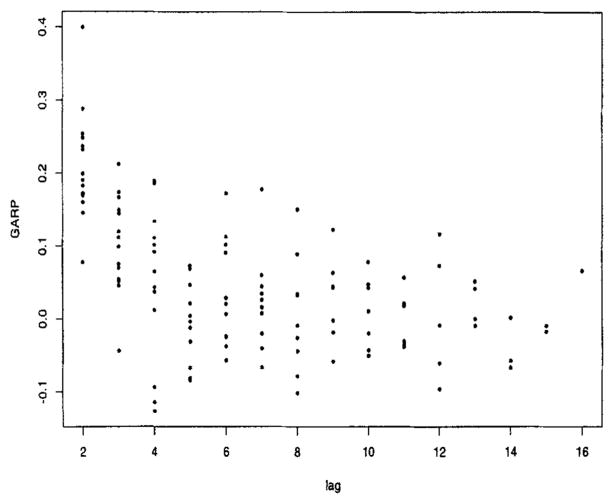
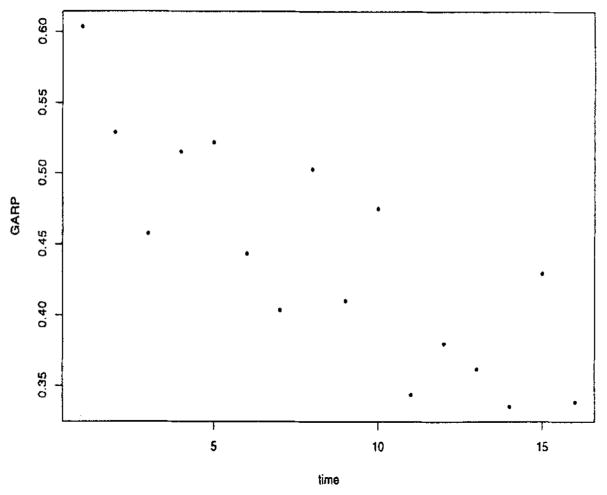
We then explored the covariance structure. First, we examined the plot of $log{\sigma }_t^2$ versus time (Figure 2). The variability at baseline, ${\sigma }_0^2$, was much lower than at the other time points, and the variability for the low severity patients was consistently lower than the high severity patients. Based on this plot and examination of credible intervals of coefficients and the DIC, we fit a separate intercept at baseline for each category of severity and a flat line for high severity from weeks 1 to 16 and a cubic for low severity over the same time period. Conditional on this model for the log ${\sigma }_t^2$, we then explored models for the generalized autoregressive parameters (GARP). Empirical regressograms (Pourahmadi, 1999) of the GARP appear in Figures 3 and 4, namely the plot of the estimated ϕ_t,,t−j in (3) versus j and the plot of ϕ_t,t−1 versus t, respectively. Figure 4 suggests the lag-1 GARP ϕ_t,t−1 has a roughly linear relationship with time. No apparent patterns were obvious for the other ϕ_t,t−j over time. Figure 3 suggested that lag-1, -2, -3, and -4 GARPs were relatively large and important and that a fourth-order polynomial, poly_t−j, (4), fit the data well. These observations were used to suggest parametric models for ϕ_t,,j’s giving rise to structured (parametric) models for GARP. In addition, there was an important interaction between the GARP models and treatment (drug) (not shown in figures). These exploratory plots along with examination of 95% credible intervals and the DIC were used to guide our analysis.

Figure 3.

GARP versus lag.

Figure 4.

Lag-1 GARP versus time.

As a comparison with more standard approaches to modeling the covariance structure, we also fit an independence model, an unstructured covariance matrix model, a random effects model, i.e., with random quadratic curves (Z_i, = poly_t(2)), and a random effects model with residual auto-correlation and a structured model on ${\sigma }_t^2$ (four parameters corresponding to the two levels of severity and baseline versus weeks 1–16).

4.3 Results

The DICs for a subset of models we fit, including the best fitting ones, appear in Table 1. Clearly, the independence (ID) model fits poorly and the unstructured (UN) model fits better.

Model 5 fit best overall. For the GARP, this model included a fourth-order polynomial in t − j, j ≥ 2, for ϕ_t,t−j first-order polynomial in t for ϕ_t,t−j, with both sets of coefficients depending on drug. For the innovation variances, the model included a third-order polynomial in t for log ${\sigma }_t^2$, t = 1,…, 16, and a separate parameter for ${\sigma }_0^2$ for low-severity patients and two intercepts for t = 0 and t = 1,…,16, respectively, for high-severity patients. Model 4, which allows for unexplained heterogeneity, with a random intercept in ϕ_t,t−1, was less competitive. Model 2, the random effects model with residual autocorrelation and a structured model for ${\sigma }_t^2$, with both the dependence and variance parameters depending on severity, fit about as well as the best model without a random quadratic curve (model 5). In general, the best fitting models support the covariance structure differing by either severity or drug or both.

Table 2 shows the estimates of the mean parameters for the best fitting model, model 5. Using this table, we address the three main questions of interest for this analysis: (1) There was not a significant effect of drug and psychotherapy versus psychotherapy only in terms of rate of improvement, although the sign of the coefficients suggested those on the combination therapy did better. (2) Initial severity was an important predictor of rate of improvement. Those patients who were severely depressed at the start of the studies improved more quickly than those not so severely depressed (95% credible interval for the severity by linear interaction excluded zero). In addition, the magnitude of effects were larger for initial severity than for treatment. (3) There were no significant interactions between treatment and severity on rate of improvement. However, the signs of the coefficients suggested the rate of improvement was most rapid for those with high initial severity and on the combination drug/psychotherapy treatment. Age and gender were not statistically significant.

Table 2.

Posterior means and 95% credible intervals for the coefficients in model 5 from Table 1

Covariate	Estimate
Intercept	11.0 (10.3, 11.8)
Linear	−0.59 (−0.67, −0.52)
Quadratic	0.014 (0.009, 0.019)
Severity	3.35 (2.30, 4.37)
Severity × linear	−0.20 (−0.33, −0.08)
Severity × quadratic	0.0062 (−0.0014, 0.014)
Drug	−0.74 (−1.77, 0.26)
Drug × linear	−0.084 (−0.19, 0.022)
Drug × quadratic	0.0013 (−0.0058, 0.0081)
Severity × drug	−0.92 (−2.29, 0.48)
Severity × drug × linear	−0.12 (−0.27, 0.035)
Severity × drug × quadratic	0.0068 (−0.0028, 0.016)
Age	0.013 (−0.0016, 0.028)
Gender	−0.017 (−0.46, 0.42)

5. Discussion

We have proposed a class of models and a unified method to fit these, which allows the user to fit a wide variety of potentially parsimonious covariance structures to unbalanced longitudinal data including models in which there is heterogeneity in the covariance structure across subjects, either explained or unexplained by covariates. In addition, we have suggested a simple approach to compare these models within the Bayesian paradigm using the DIC; however, we recommend using the DIC only as a guide to finding better fitting covariance structures. In the depression example, we found initial severity to be an important determinant of both the improvement rate and the covariance structure in depressed patients and drug to be less important. For these data, model 5 stands out as a clear indication of the degree of flexibility one has in modeling covariances using the factorization (3) and the ensuing dynamic conditionally linear model (6).

Future work on these models will address the impact of heterogeneity in the covariance structure on estimation of β; Daniels and Kass (2001) discuss gains in mean squared error for estimating β when the covariance structure is properly modeled for nonheterogeneous situations. In terms of the depression data, models that allow for nonignorable missingness (dropout) will be explored as detailed in the Introduction. In addition, the sensitivity of the overall inferences to individual studies might be addressed by using a cross-validation approach (Thase et al., 1997). Finally, we are currently exploring using the modified Cholesky decomposition to smoothly incorporate covariates into a random effects matrix.

Résumé

Nous développons une nouvelle classe de modèles, les modèles mixtes dynamiques conditionnellement linéaires, pour des données longitudinales, en déomposant la matrice de covariance intra-sujet par une décomposition de Cholesky particulière. Dans notre approche, dynamique se réfère à l’utilisation des réponses passées comme covariables, et la linéarité conditionnelle signifie que les paramètres linéaire du modèle peuvent être aléatoires tandis que les paramètres non-linéaires sont non aléatoires. Ce dispositif offre plusieurs avantages, et est étonnamment similaire aux modèles obtenus par une méthode de linéarisation au premier ordre appliquée aux modèles mixtes non linéaires. Tout d’abord il s’applique à des modèles flexibles, accessibles aux calculs et incluant une large gamme de structures de covariance; ces structures peuvent dépendre des covariables et par là-même varier entre sujets. Cette classe de modèles inclut par exemple tous les modèles linéaires mixtes standard, les modèles d’antédépendance, et les modèles de Vonesh-Carter. Ensuite, il garantit que la matrice de covariance marginale ajustée soit définie positive. Nous développons des méthodes pour l’inférence bayésienne, et nous justifions l’intérêt de ces modèles en utilisant une série d’études longitudinales sur la dépression pour lesquelles les caractéristiques de ces nouveaux modèles sont particulièrement bien adaptées.