A Bayesian hierarchical nonlinear model for assessing the association between genetic variation and drug cytotoxicity

Abstract

Non-tumor cell based model systems have recently gained interest in pharmacogenetic research as a hypothesis generating tool. The hypotheses generated from these model systems can be followed up in functional studies, or tested in individuals taking the same investigational agents. The current cellular phenotypes (e.g. cytotoxicity) of interest in these studies are based on effects of an individual dosage of a drug on the cell lines, or a summary of results at many dosages of a drug (e.g. dose that inhibits 50% of cell growth, GI50). A more complete analysis of the impact of genetic variation on all aspects of the dose-response curve may lend additional insight into the pharmacogenomics of a particular drug. This paper illustrates the use of a Bayesian hierarchical nonlinear model for the analysis of pharmacogenomic data with cytotoxicity endpoints. The model is illustrated with cytotoxicity and expression data collected on cell lines from a pharmacogenomic study of the drug gemcitabine. By completing an analysis based on the entire dose-response curve, we were able to detect additional genes that affect not only the GI50, but also the slope of the curve, which reflects the therapeutic index of the drug. Simulation studies also demonstrate that in comparison to the analyses based on the commonly used summary measure GI50, investigation of the impact of genetic variation on all aspects of the cytotoxicity dose-response curve are more informative, and more powerful with respect to detecting the effect of gene expression on cytotoxicity.

1. INTRODUCTION

Recently, there has been an increased interest in “individualized medicine” in the research and treatment of cancer. This in turn has increased awareness of the study of pharmacogenetics and pharmacogenomics in cancer research. Pharmacogenetics is the study of the role of inheritance in individual variation in response to drugs, nutrients and other xenobiotics [1, 2]. In this post-genomic era, pharmacogenetics has evolved into pharmacogenomics, a discipline that has been heralded as one of the first major clinical applications of the striking advances that have occurred and continue to occur in human genomic science (http://www.fda.gov/cder/genomics/genomic_biomarkers_table.htm)[3–7]. Pharmacogenomics is the study of the influence of genetic variation across the entire genome on drug response (e.g., efficacy, toxicity) in patients.

In the late 1980s, the National Cancer Institute (NCI) developed a collection of human tumor cell lines (NCI60) from a variety of common solid tumors, such as lung, colon and breast, for anti-cancer drug screening [8]. Recently, pharmacogenomic research has incorporated non-tumor cell-based model systems [9–12]. The use of these non-tumor cell lines are gaining in popularly due to greater availability of samples. Hypotheses generated with the cell-based model system can then be tested in individuals treated with the drug, or followed-up in functional studies.

Currently, investigation of the genomic relationship with drug concentration endpoints from cell lines is often completed by either analyzing a drug concentration endpoint measured at a single drug dosage or a summary measure of the dose-response curve of the concentration endpoints (e.g., dose that inhibits 50% of cell growth, GI50). Drug concentration endpoints are any measurable cellular phenotypes that are related to drug concentration, one example being cytotoxicity (measured as the percent of surviving cells after exposure to the drug). An analysis of the impact of genetic variation on all aspects of the dose-response curve may lead to more insight into the pharmacogenomics of a particular drug. For example, by investigating the impact of genetic variation on the slope of the dose-response curve, one may be able to determine genetic variation responsible for differences in therapeutic index, the comparison of the amount of a therapeutic drug that causes the therapeutic effect to the amount that causes toxic effects, between subjects treated with the drug.

Although numerous methods exist to evaluate subject-specific effects on nonlinear dose response curves, application to pharmacogenomic studies has been lacking. One possible method, used in the past for the analysis of population pharmacokinetic studies, is a Bayesian hierarchical nonlinear model fit using Markov chain Monte Carlo (MCMC) [13–16]. Bennett, Racine-Poon and Wakefield (1996) give a nice overview of MCMC methods for hierarchical nonlinear models in Markov Chain Monte Carlo in Practice [17]. For a review of non-Bayesian estimation of nonlinear mixed effects model, the reader is refer to Davidian and Giltinan [16].

Over the last few decades, applications of Bayesian methods by Markov chain Monte Carlo (MCMC) [18,19], and in particular the Gibbs Sampler [20], have increased with the advancement of computers and computational methods, particularly with their application to genetic data [21]. Use of a Bayesian hierarchical nonlinear model, allows determination of the impact of genetic variation on all aspects of the dose-response curve, along with possible incorporation of prior knowledge into the model. In addition, by analyzing the data within a hierarchical nonlinear model, researchers are able to partition the variation in response to the drug into: genetic variation, unexplained “between-subject” variation, and within-subject variation (inter-observation-time variation, and residual random error). Understanding the magnitude of these various sources of variation has important clinical implications. For example, a large amount of unexplained between-subject variation in cytotoxicity can imply that a drug will be difficult to use in a heterogeneous population because of uncontrolled toxicity. Hence, the Bayesian hierarchical nonlinear model can offer insights into the understanding of the pharmacogenomics of a particular drug.

This paper outlines a Bayesian hierarchical nonlinear model for analysis of pharmacogenomic-cytotoxicity studies involving the use of a cell based “model system”[22]. We begin by describing the motivating pharmacogenomic study involving the anti-cancer drug gemcitabine, used to treat a variety of solid cancer tumors such as pancreatic and breast cancer. This pharmacogenomic study will be used in the application of a Bayesian hierarchical nonlinear model to determine if mRNA expression for genes within the gemcitabine pathway is related to cytotoxicity. In addition, three simulation studies are presented comparing the findings from the hierarchical nonlinear model to the results from the analysis using the GI50, a commonly used summary measure of the curve.

2. METHODS AND MATERIALS

2.1. Description of Gemcitabine Pharmacogenomic Cytotoxicity Data

Pancreatic cancer is a rapidly fatal disease with a 5-year survival rate of less than 5% [23,24]. Gemcitabine is the standard chemotherapy for pancreatic cancer, drug response varies widely among individuals. Genetic variation at each step within the gemcitabine metabolic pathway including: transport, metabolism, and drug target could potentially influence: the quantity of drug transported into the cell, the rate of active drug formation, and the quantity of active drug reaching its target(s) resulting in metabolic inactivation of the drug. The goal of this pharmacogenomic study is to identify genetic variation, in the form of gene expression levels, associated with response to gemcitabine treatment (measured as cytotoxicity) through the use of a cell line model system.

2.1.1. Cell lines, Drug and Cytotoxicity Assays

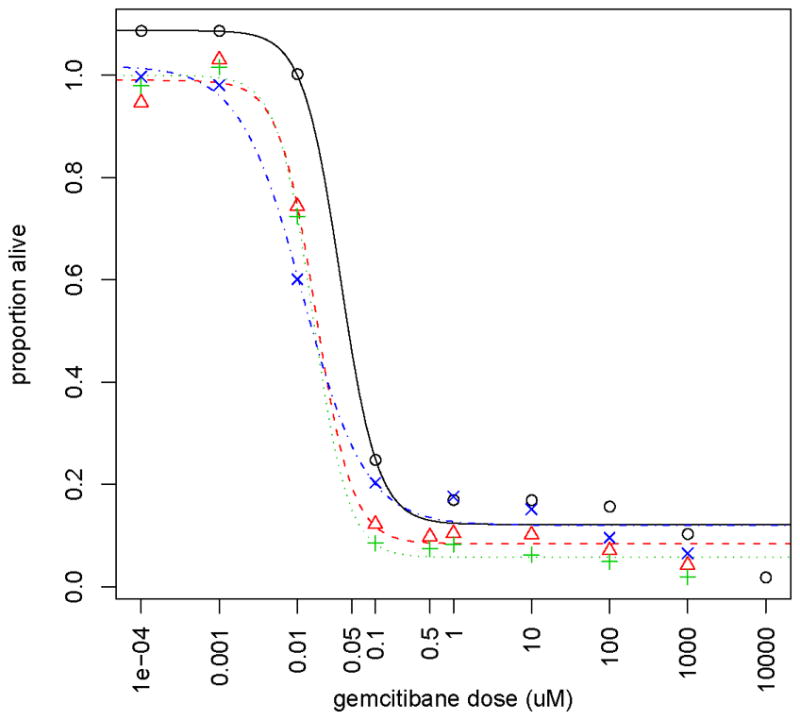
194 EBV-transformed B lymphoblastoid cells (39.7% male) derived from 60 Caucasian-American (CA), 52 African-American (AA) and 59 Han Chinese-American (HCA), as well as 23 CEPH (also CA) subjects were purchased from the Coriell Institute (Camden, NJ). These cell lines were obtained from the Coriell at different times, as far as 20 years apart, 79 (40.7%) obtained greater than 10 years prior to the experiment. The drug gemcitabine (dFdC) was provided by Lilly. Cytotoxicity assays were performed with the human lymphoblastoid cells using the CellTiter 96 AQueous Non-Radioactive Cell Proliferation Assay (Promega Corporation). Gemcitabine cytotoxicity data (measured as percent of surviving cells) were collected at drug dosages 1000, 100, 10, 1, 0.1, 0.01, 0.001, and 0.0001 uM for the entire set of cell lines. An example of the gemcitabine cytotoxicity data for a subset of four different cell lines is shown in Figure 1.

Figure 1.

Dose-response curves for a subset of 4 cell lines. The different symbols and line types represent data for 4 different cell lines. The symbols represent the observed proportion of cells alive at the various doses of the drug gemcitabine and with the lines representing the fitted dose-response curves.

2.1.2. Basal Affymetrix U133 Plus2.0 GeneChip gene expression data

Whole Genome expression data for cell lines was obtained with Affymetrix U133 plus 2.0 expression array chip. The RNA extraction and the expression array assay were performed following the Affymetrix GeneChip® expression technical manual (Affymetrix, Inc., Santa Clara, CA). Before the assay, RNA quality was tested using an Agilent 2100 Bioanalyzer. The Affymetrix GeneChip® contains over 54,000 probe sets designed based on build 34 of the Human Genome Project. Each probe set containing 11 probes of which nucleotide sequence is specifically designed to hybridize the targeted gene. The mRNA expression array data were normalized on the log₂ scale using GCRMA methodologies [25–27]. For illustration of the Bayesian hierarchical nonlinear model, only the 30 probe sets within the gemcitabine metabolic pathway were analyzed.

2.2. Bayesian Hierarchical Nonlinear Model for Pharmacogenomic Cytotoxicity and Expression Data

Often, pharmacogenomic measurements taken at different concentrations may best be characterized by a nonlinear model. Although non-linearity can sometimes be removed by different data-transformations, the resulting models lose the structural dose-response relationship that makes sense to clinical pharmacologists, particularly when planning drug-dosing experiments, along with interpretation on the original scale. The nonlinear model for the relationship between the response (Y_i) and the drug concentration (D_i) is Y_i = f (β, D_i) + ε_i, where f (β, D_i) is a function that is nonlinear in terms of β.

Let there be N cell lines in which J doses of the drug are applied to each cell line. In addition to drug dosage, additional covariates of gender, ethnicity and mRNA gene expression values are recorded for each cell line. In general, the relationship between the cytotoxicity response and drug dosage exhibits a sigmoidal shape that can be modeled with a four parameter logistic function. The four parameter logistic model is the most common model fit to in-vitro dose response data and is the recommended function for use by the NIH Chemical Genomics Center (http://www.ncgc.nih.gov/guidance/section3.html). Following is the Bayesian hierarchical nonlinear model (HNLM) used to assess the effect of mRNA gene expression for genes within the gemcitabine pathway on the gemcitabine cytotoxicity dose-response curve using a four parameter logistic function, where cytotoxicity is measured as proportion of cells alive at each dose of the drug. For situations in which the four parameter logistic function is inadequate, the model can be modified using a different nonlinear function.

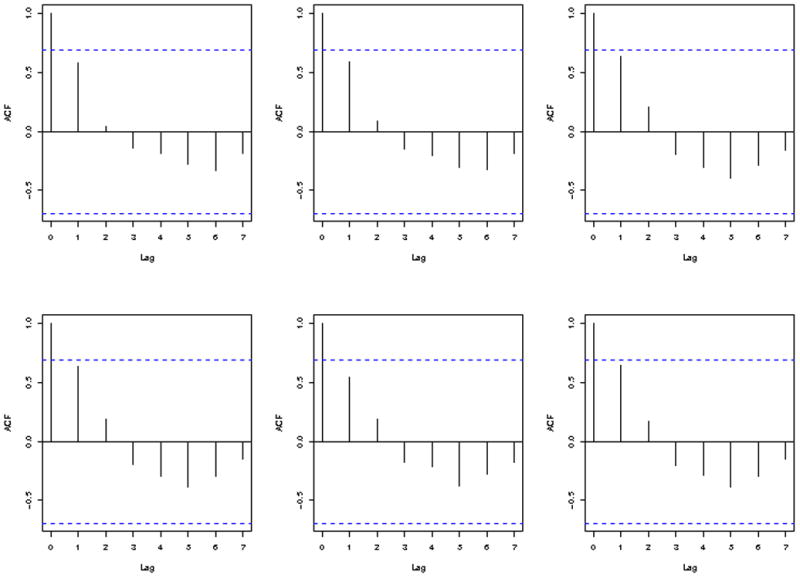
Let Y_ij represent the response for cell line i at dose j (D_j), i = 1,…, N and j =1,…, 8 with Y_ij ~ N(η_ij, σ²) and ${\eta }_{ij}={\beta }_{1i}+\frac{({\beta }_{2i}^{\ast }-{\beta }_{1i})}{1+exp\{{\beta }_{4i}(log(D_j)-{\beta }_{3i})\}},{\beta }_{1i},{\beta }_{2i}^{\ast }>0$. The responses at infinite and zero concentration are represented by β_1i and ${\beta }_{2i}^{\ast }$, respectively. The parameterβ_3i represents the log(EC50) with EC50 representing the effective concentration that kills 50% of the cell or refers to the concentration of a drug which induces a response halfway between the baseline and maximum. In the four parameter logistic model, the EC50 is equivalent to the GI50. For other nonlinear functions, the GI50 may or may not be represented by a parameter in the nonlinear model. Lastly, β_4i represents the slope of the dose-response curve. For computational issues, we have re-parameterized the model such that ${\beta }_{2i}={\beta }_{2i}^{\ast }-{\beta }_{1i}$. We have chosen not to explicitly model the dependency within each individual response due to the limited number of measurements for each cell line. As discussed by Davidian and Giltinan [16], due to numerous parameters involved in HNLM, without tremendous amount of data it is difficult to sort out the intra- and inter-individual covariance components, and thus modeling within-individual correlation should be approached with caution. There appears to be autocorrelation between dosages, seen in a lag plot (Figure 2) of 6 randomly selected cell lines. To verify the adequacy of the model that does not model the within-subject correlation, model checking was completed as outlined in section 2.3. The results of model checking, as described in section 3.1., indicated that fitting a model assuming no within-individual correlation was adequate.

Figure 2.

Lag plots of cytotoxicity measurements for six randomly selected cell lines. The y-axis show the measure of auto-correlation and the x-axis show the lag in time measurements. The figures show positive autocorrelation for measurements within 2 lags of each other and negative autocorrelation for measurements with 3 or more lags between them.

Next, we let β_1i = exp{α_1i}, β_2i = exp{α_2i}, β_3i = α_3i + γ₃ (GE_i), and β_4i = α_4i + γ₄ (GE_i), where GE_i represents the mRNA gene expression for cell line i. For the analysis of gemcitabine cytotoxicity, only the effect of mRNA gene expression on the log(EC50) and the slope is modeled, as there appears to be little variation in response at zero or infinite drug dosage for gemcitabine. If relevant for the drug of interest, the model could be extended to allow for the gene expression to impact β_1i and/or β_2i.

A multivariate normal distribution is used to model the curve parameters, allowing dependency amongst the parameters (e.g., as the log(EC50) increases, so may the slope). That is, α_i = (α_1i,α_2i,α_3i,α_4i)^T ~ MVN(μ, V) with μ = (μ₁, μ₂, μ_3, μ₄)^T ~ MVN(μ₀,Σ) and V⁻¹ ~ Wishart(R,4). To specify a non-informative Wishart prior on V⁻¹, the degrees of freedom were set equal to the rank of V, rank(V) = 4, where in general the smaller the degrees of freedom, the less informative the prior. A non-informative, diffuse prior for μ was set, in which, μ₀ was set to (2.3, 4.5, −3, 1.5) based on both biological knowledge and visual inspection of individual dose-response curves for the 194 cell lines treated with gemcitabine and Σ = c×Idenity matrix with c = 100². Lastly, non-informative, diffuse proper priors were placed on the remaining parameters in the model (e.g., γ₃ ~ N(0,100²), γ₄ ~ N(0,100²), and1/σ² ~ Gamma(0.001,0.001)).

2.3. Model Diagnostics

With inferences based on posterior distribution, which in turn are based on the specified probability model, model diagnostics is critical in Bayesian analyses. It is often the case that multiple models will fit the data reasonably well and provide consistent answers to the scientific question/hypothesis. The main question is “How much do the posterior distributions change if another, reasonable, model is assumed?” As outlined by Gelman et al [19], the posterior predictive distribution was utilized to check the fit of the model using discrepancy measures. The discrepancy measures of the posterior predictive distribution utilized to assess model fit for the HNLM were: the minimum, median, and maximum of the simulated replicate data. The distributions of these discrepancy measures where then compared to: the minimum, median, and maximum values in the observed phenotypic data. In addition to these three measures, we also compared the simulated data to the observed data by visually displaying and assessing the residuals (simulated replicate data minus the observed data). Convergence of the MCMC was monitored using the convergence measure $\sqrt{R}$, as discussed by Gelman et al [19], along with trace plots. The measure $\sqrt{R}$ converges to 1 as number of iterations of MCMC approaches ∞, where $\sqrt{R}<1.2$ indicates the chain has converged.

2.4. Simulation Study

mRNA gene expression data was simulated from a normal distribution with mean 0 and variance 3. For the simulation study designed to access the power to detect an expression effect on log(EC50), the cytotoxicity values for each cell line were simulated from a multivariate normal distribution MVN(ω,ψ) with mean

$$\mathbf{\omega }={\beta }_1+\frac{{\beta }_2-{\beta }_1}{1+exp\{{\beta }_4(log(\mathbf{D})-{\beta }_3)\}},$$

withβ₁ = 10, β₂ = 95, β₄ = 1.5 and β₃ = −3+0.055(mRNA expression) and covariance matrix; ψ that has an auto correlation structure with lag of 1 with variance τ²= 100 and auto-correlation parameter ρ = 0.65. The vector D contains the eight drug concentrations of 1000, 100, 10, 1, 0.1, 0.01, 0.001, and 0.0001, selected to mimic the drug concentrations for the gemcitabine study. One-hundred datasets, each containing 250 subjects/cell-lines, were generated in which each subject/cell line had 8 simulated cytotoxicity measurements, and one simulated value for an expression probe set.

Each simulated dataset was analyzed using both the HNLM described in section 2.2 and an analysis based on the summary measure GI50. For the analysis of the association of the GI50 with expression, Pearson correlation coefficients were calculated for GI50 and expression levels and a Wald test was used to test the null hypothesis of no correlation or association. For the Bayesian models, a significant effect was noted if the 95% credible interval for the parameter does not contain 0. For the frequentist analysis of GI50, we defined a significant effect if the two-side p-value ≤ 0.05. Power was estimated as the proportion of simulations that a method correctly detected the simulated expression effect. False positive rates were estimated likewise as the proportion of falsely detected effects when no expression effect was simulated.

The simulation study to assess the power to detect expression effects on the slope was completed in a similar manner as for the simulation study for log(EC50) with β₁ = 10,β₂ = 95, β₃ = −3, and β₄ = 1.75+0.1(mRNA expression). Lastly, 100 null dataset with 250 subjects/cell lines each were simulated with no effect of expression on any aspect of the curve.

3. RESULTS

3.1. Gemcitabine Pharmacogenomic Study

The GCRMA normalized log₂ expression data was regressed on gender, race, and the storage time of each cell lines, or time since submission of each cell line to Coriell (dichotomized at 10 years). The binary variable of storage time was included to adjust for the differences observed in expression values with respect to time since Coriell submission of each cell line. The residuals from this regression model were then standardized, resulting in a standardized, adjusted, GCRMA normalized mRNA expression value. GI50 summary cytotoxicity values were log transformed, and then in a similar fashion adjusted for gender, race, and storage time as above before standardizing. Pearson correlation coefficients for the relationship between the standardized adjusted GI50 with each of the 30 standardized, adjusted, GCRMA normalized, expression probe sets within the gemcitabine pathway were calculated. A test of the null hypothesis of no correlation was conducted using a Wald test.

For analyses using the HNLM, the adjusted, normalized, log₂ mRNA expression values and unadjusted cytotoxicity data were model as outlined in section 2.2, using WinBUGS 1.4.3 [28,29]. In addition to the expression effects modeled for β_3i and β_4i, race, gender and storage time were also included as covariate effects on all level-two parameters (β_1i, β_2i, β_3i β_4i). For each of the 30 probe sets within the gemcitabine pathway, three independent chains were run with different starting values, each for 60,000 iterations. The first 10,000 iterations were subsequently removed for burn-in, and every 5^th iteration was kept in order to reduce serial correlation, and save on storage space. Convergence was checked using trace plots, and the $\sqrt{R}$ values, as outlined in section 2.3. After removing the beginning of the chain for burn-in, the trace-plots, and $\sqrt{R}$ indicated convergence for each of the 30 analyses.

Probe sets deemed to have a mRNA expression effect based on either: the 95% credible interval not containing zero for log(EC50) (γ₃), or slope (γ₄) parameters in HNLM; or p-value ≤ 0.05 from a standard analysis based on GI50 summary are shown in Table 1. As Table 1 illustrates, the two probe sets found to be significant at the 0.05 level using the summary measure GI50 were also detected with the HNLM. In addition, the HNLM detected two probe sets with an impact on log(EC50), and another two probe sets with an effect on the slope of the dose response curve that were not found using the standard analysis. The two probes sets detected to have an effect on the slope using the hierarchical model did not have significant p-values from the analyses based on GI50, as expected, since the phenotype GI50 does not reflect the slope. Therefore, by using all the cytotoxicity data collected on the cell lines in one hierarchical nonlinear model, researchers are able to detect expression probe sets that are missed with the analysis based on GI50.

Table 1.

Probe sets with 95% credible intervals for γ₃ or γ₄ that do not contain 0 based on the HNLM or probe sets with p value < 0.05 based on analysis of summary measure of curve (GI50).

	Bayesian Hierarchical Nonlinear Model		Analysis with GI50
Probe	Interval forγ3, Log(EC50)	Interval for γ4, Slope	P-Value
201801_s_at	(−0.251, −0.052)	(−0.305, 0.047)	0.002
209155_s_at	(0.028, 0.224)	(−0.107, 0.224)	0.096
217870_s_at	(−0.185, 0.022)	(−0.397, −0.019)	0.269
223178_s_at	(0.010, 0.199)	(−0.014, 0.323)	0.081
223298_s_at	(0.186, 0.356)	(−0.009, 0.334)	1.6e-07
243100_at	(−0.053, 0.136)	(−0.236, −0.001)	0.726

Since all analyses used the same model and observed cytotoxicity data in which only the covariate of mRNA expression varying from analysis to analysis, model checking was completed for only one probe set (probe set 201801_s_at). Three chains with different starting values were used, in which each chain is run for 35,000 iterations, removing the first 10,000 iterations for burn-in, and keeping every 5^th iteration. Model checking was completed as outlined in section 2.3 using replicate data simulated from the model. The distributions of minimum, maximum, and median of the simulated replicate data are presented in Figure 3. The proportion of simulations with minimum, maximum, and median more extreme than the observed minimum, maximum, and median is 0.05, 0.13 and 0.21, respectively. Figure 4 displays the 2.5%-tile, and 97.5%-tile of the residuals comparing the replicate and observed data for the last 1,000 simulations from each chain. In Figures 3 and 4 the vast majority of distributions are centered at 0, implying there is no large systematic bias, or model inadequacy. However, there are five cell lines with two (out of eight) of their residual distributions that do not contain zero, and one cell line with three distributions that do not contain zero. On further investigation, the individually estimated dose-response curves for these six cell lines were distinct from the dose-response curves for the majority of the cell lines (e.g., dose relationship more linear than sigmoidal, large amount of variation in cytotoxicity data). Therefore, overall, we feel the model fit is adequate.

Figure 3.

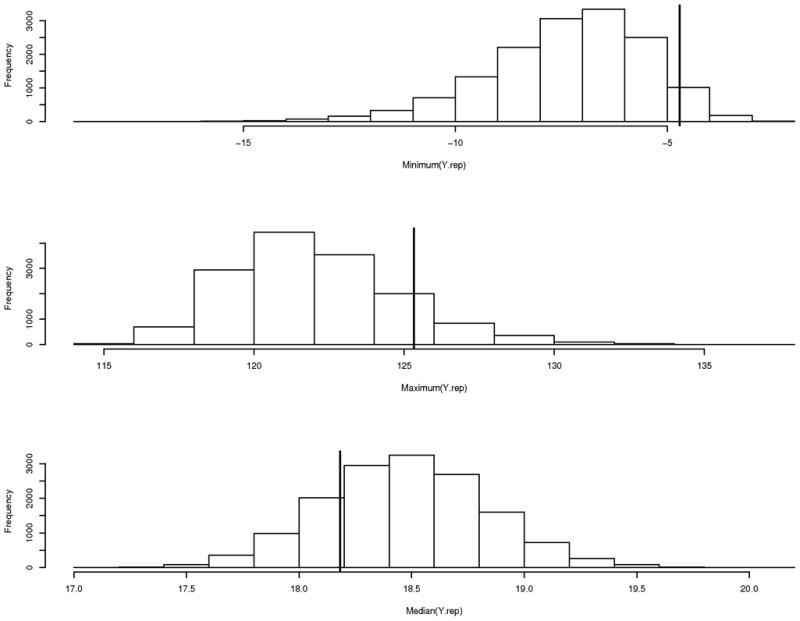
Histograms of discrepancy measures (minimum, maximum and median) utilized to assess model fit. The solid vertical line represents the observed value in the cell line data. The proportion of simulations with minimum, maximum and median more extreme than the observed minimum, maximum and median is 0.05, 0.13 and 0.21, respectively.

Figure 4.

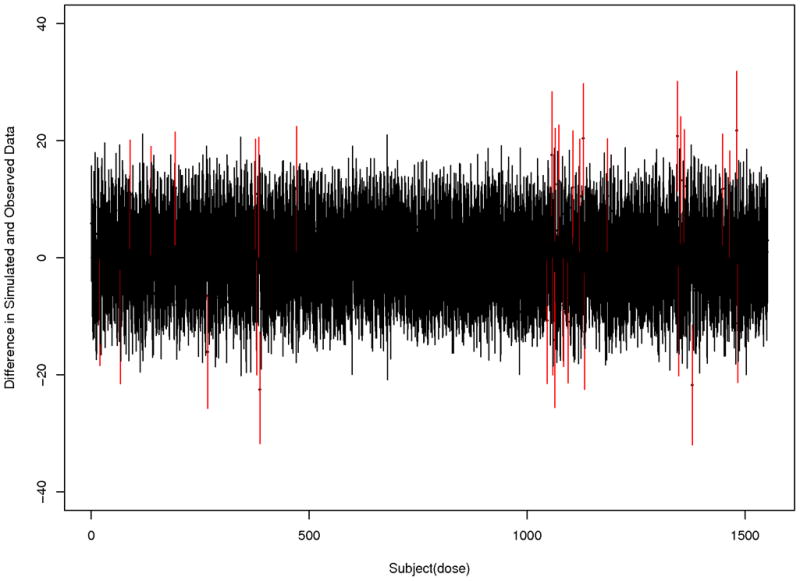
Plot of the mean difference, with 2.5% and 97.5%-tiles, for difference in simulated replicate data and observed data for the 194 cell lines at 8 drug doses. The red lines indicate situations in which zero is not contained in the middle 95% of the residual distribution.

3.2. Simulation Study

The 100 datasets simulated with an effect of expression on log(EC50), but not slope, were analyzed with both the Bayesian hierarchical nonlinear model, and the standard method based on GI50, the summary measure of the curve. For the HNLM defined in section 2.2., WinBUGS 1.4.3 [28,29] was utilized. Three chains with different starting values were run for 30,000 iterations, removing the first 10,000 for burn-in, keeping every 5^th iteration to reduce serial correlation, and save on storage space. Of the 100 simulations, 95 of the 100 simulations detected the expression effect on the log(EC50) (i.e., the 95% credible interval for γ₃ did not contain 0). In only one out of the 100 simulations was there an effect on slope (γ₄) detected, note worthy is that a log(EC50) effect was also detected.

For each of the 100 simulated datasets, the posterior mean was estimated for key parameters of interest. A summary of the posterior means across the 100 simulated datasets is presented in Table 2. As the table illustrates, the average estimate of expression effect on log(EC50), γ₃, across the 100 simulations was 0.055, which coincides with the true value used in the simulation of the data.

Table 2.

Average of the summary measures across the 100 simulated datasets simulated with an expression effect on log(EC50).

Parameter	Simulation value	Mean	SD	2.5%	50%	97.5%	$\sqrt{R}$
γ3	0.055	0.055	0.015	0.026	0.055	0.083	1.002
γ4	0.000	−0.003	0.021	−0.043	−0.003	0.039	1.002
μ1	2.300	2.130	0.055	2.014	2.127	2.229	1.003
μ2	4.550	4.430	0.008	4.419	4.435	4.451	1.003
μ3	−3.000	−3.020	0.026	−3.070	−3.018	−2.968	1.003
μ4	1.500	1.540	0.043	1.464	1.543	1.632	1.008

Analyses of the simulated datasets with an expression effect on log(EC50) were also computed using the commonly used method based on GI50. For each of the simulated datasets, GI50 was computed for each cell line, and then correlated with the simulated expression variable. The mean p-value across the 100 analyses based on the GI50 summary measure was 0.02, with a standard deviation of 0.055. Of the 100 simulated datasets, 89 out of the 100 analyses based on GI50 produced a p-value less than 0.05. Of the analyses that produced p-values greater than 0.05, the p-values ranged from 0.055 to 0.334. In comparison, six out of eleven of these effects were detected with the HNLM using the entire dose-response curve. Lastly, the five simulation datasets in which the HNLM was unable to detect the simulated expression effect were also datasets with signals not detected by the analyses based on GI50.

The simulation study designed to assess the power to detect a gene expression effect on the slope of the dose response curve found that 95% of the simulated effects were detected with the HNLM (i.e., 95% credible interval for γ₄ did not contain 0). The average estimate for γ₄ was 0.092, which is close to the truth of 0.10 used to simulate the data (Table 3). Additionally, eight out of the 100 analyses also detected a gene expression effect for log(EC50), of which, all eight detected an effect for slope. This is in part due to the correlation between these two parameters. In a similar manner as completed for the log(EC50) simulation study, analyses of the 100 datasets from the slope simulation study were also completed using the summary measure GI50. For the analyses based on GI50, only ten out of the 100 simulated expression effects on the slope were detected (i.e., p-value < 0.05). Of the ten detected with the analysis of GI50, all expression effects were also detected with the HNLM. Lastly, all effects not detected with the Bayesian model were also not detected with the analysis based on GI50. That is, all effects detected with the analysis of GI50 were also detected with the HNLM, with the HNLM detecting an additional 85% gene effects on the slope of the dose-response curve.

Table 3.

Average of the summary measures across the 100 simulated datasets simulated with an expression effect on slope.

Parameter	Simulation value	Mean	SD	2.5%	50%	97.5%	$\sqrt{R}$
γ3	0.000	−0.006	0.016	−0.037	−0.006	0.024	1.004
γ4	0.100	0.093	0.029	0.037	0.092	0.151	1.005
μ1	2.300	2.124	0.055	2.013	2.126	2.227	1.002
μ2	4.550	4.434	0.008	4.418	4.434	4.449	1.003
μ3	−3.000	−3.021	0.028	−3.076	−3.021	−2.966	1.004
μ4	1.750	1.807	0.060	1.697	1.804	1.933	1.011

The analyses of the 100 null simulated datasets were completed in a similar manner as completed for the datasets simulated with an expression effect on log(EC50), or slope. For the analyses based on the HNLM, seven and three of the 100 simulated datasets had a 95% credible interval for γ₃ and γ ₄ that did not contain 0, respectively. Of these significant findings, two of the probe sets had a significant association for both γ₃ and γ₄. When compared to the analyses based on the GI50, eight out of the 100 analyses resulted in a p-value for a probe set effect less than 0.05, of which, five out of the eight probe sets were also detected with the HNLM.

Since the same model, with the exception of the expression effect, was utilized to simulate the datasets, diagnostics were conducted for only one of the datasets simulated with an expression effect on log(EC50). If the model was determined to be adequate for one of the simulated datasets, it was considered adequate for all simulated datasets. With the three chains having different starting values, it was determined that the chain had converged to the stationary distribution, as the three chains converging to the same point in the trace plots, as well $\sqrt{R}<1.20$ for all parameters in the model (data not shown). Model checking was completed as outlined in section 2.3.

4. DISCUSSION and CONCLUSIONS

This study presented a Bayesian hierarchical nonlinear model (HNLM) for the pharmacogenomic analysis of drug dose-response cytotoxicity curves, and mRNA expression data. The analysis of the pharmacogenomic study of gemcitabine, and simulation study illustrated that an analysis of the dose-response curve (i.e., repeated measurements) is more informative, and appears to be more powerful in detecting the effect of gene expression on cytotoxicity than the analyses based on the commonly used GI50 summary measure of the curve. Finally, analysis of the simulated null data showed similar false positive rates between the analyses based on the HNLM, and analyses based on the GI50 summary measure. However, these conclusions are based on a relatively small simulation study of 100 replicates. A larger simulation study involving over 1,000 replicates is needed to definitively conclude the analysis of the entire dose response curve is more powerful than an analysis based on a summary measure of the curve.

Due to the computational nature of the HNLM, it is currently impractical to run the HNLM for all mRNA expression probe sets on a genome-wide Affymetrix expression array panel (approximately 54,000 probe sets). Therefore, the analysis of genetic variation has been focused within a biological pathway of interest. Future work is needed to develop adequate statistical screening methods that can be quickly analyzed using standard statistical methodology. One option would be to use a phenotype that captures various differences between the dose response curves, for example, the area under the curve (AUC). For each cell line, integration could be completed to determine the computed phenotype of AUC. This computed phenotype would then be associated with genome-wide SNP and/or mRNA expression data using standard statistical methods. Any SNP, or expression probe set found to be moderately associated with AUC would then be analyzed using the HNLM to assess which, if any, aspect of the curve is impacted by genetic variation.

In addition to the development of an adequate screening method, future research is needed to extend the HNLM to incorporate SNPs, and haplotype effects, as well to jointly model the effects of gene expression, and SNPs on various aspects of the dose-response curve. This HNLM can be extended to studies in which a class of drugs is the unit of interest, as opposed to a single drug. For example, gemcitabine and the drug cytosine arabinoside (AraC) are in the same class of drugs called cytidine analogues. The models can be extended to answer questions dealing with which genes impact a class of drugs, and whether the relationships between the gene and the cytotoxicity of the drugs are similar. These models could provide insight for understanding how a set of drugs in the same drug class differ from one another. Lastly, the HNLM can be easily modified to incorporate the use of different nonlinear functions beyond the four parameter logistic, and biological information via informative proper priors.

To summarize, investigating the impact of genetic variation on all aspects of the dose-response cytotoxicity curve within a Bayesian hierarchical nonlinear model appears to be more informative, and powerful at detecting the genetic effect on all aspects of the dose response curve in comparison to the analyses based on the commonly used summary measure GI50. In addition to the analysis of the entire dose-response curve being more powerful, for many drugs, one may be interested in all aspects of the curve, particularly the slope or bottom asymptote. For example, when studying the drug mycophenolic acid (MPA) used in organ transplant [30,31], one may be interested in all aspects of the curve, particularly the bottom asymptote, as the goal of the drug is to reduce rejection of the organ, due to an immune system attack, but not to reduce the immune systems ability to fight off infection if needed (i.e., wish to lower cytotoxicity to a point, but not too low). Findings from these analyses will guide our understanding of the pharmacogenomic nature of drugs, and lead to better understanding of the complex nature of the relationship between genetic variation and drug response, with the ultimate goal of “individualized medicine” for patients.