Abstract
The details of melting of DNA immobilized on a chip or nanoparticle determines the sensitivity and operating characteristics of many analytical and synthetic biotechnological devices. Yet, little is known about the differences in how the DNA melting occurs between a homogeneous solution and that on a chip. We used molecular dynamics simulations to explore possible pathways for DNA melting on a chip. Simulation conditions were chosen to ensure that melting occurred in a submicrosecond timescale. The temperature was set to 400 K and the NaCl concentration was set to 0.1 M. We found less symmetry than in the solution case where for oligomeric double-stranded nucleic acids both ends melted with roughly equal probability. On a prepared silica surface we found melting is dominated by fraying from the end away from the surface. Strand separation was hindered by nonspecific surface adsorption at this temperature. At elevated temperatures the melted DNA was attracted to even uncharged organically coated surfaces demonstrating surface fouling. While hybridization is not the simple reverse of melting, this simulation has implications for the kinetics of hybridization.
Keywords: DNA, melting, and microarray
1. Introduction
The recent availability of complete genomic sequences from many organisms coupled with commercial microarray platforms give ample opportunity to conduct gene expression analysis [5]. DNA microarrays are analytical devices designed to rapidly determine the composition of multicomponent solutions of nucleic acids at relatively low cost [41]. Lately, they also have become an interesting topic in nanotechnology and various biosensor technologies [29, 35]. Oligonucleotide arrays most often have the DNA tethered to surfaces with longer target DNA molecules in the solution. While the number of uses of DNA chips is impressive, the understanding of the physical chemistry of these devices, both experimental and theoretical aspects, lags behind the technological applications [19].
Recent progress has been made on developing simple analytical models that take into account several parameters common to many of the experiments. Among the required parameters are the probes’ lengths, densities, spacers, and grafting procedures, as well as, the targets’ lengths, preparation protocols, and the hybridization solution conditions [13, 36–40, 49]. Such theories have sufficient accuracy for many applications but lack atomic detail and the concomitant mechanistic insights. All-atom molecular dynamics simulations of DNA on a surface have also been performed to provide more insight into the structure of DNAs and their interactions [44, 45, 47]. But, little is known about the atomic details of DNA melting near surfaces.
DNA melting and hybridization are fundamental biological processes as well as crucial steps in many modern biotechnological applications. The separation of double-stranded DNA (dsDNA) into single-stranded DNA (ssDNA) is fundamental to replication in living organisms, and to the polymerase chain reaction (PCR). At equilibrium, DNA will separate when the free energy of the separated ssDNA is lower than that of the dsDNA. In most biochemical studies of DNA separation, the strands separate upon increasing the temperature of the sample until the DNA melts (thermal separation). In living organisms, however, DNA separation is not thermally driven, rather enzymes and other proteins induce the two strands apart. Experimental investigations of dsDNA separation using force-induced techniques, at temperatures where the dsDNAs are stable, have recently been performed (mechanical separation) [10].
Aspects of melting of duplex DNA have been studied for decades [15]. For short DNA with fewer than 12 base pairs, melting and hybridization can often be described by a two-state thermodynamic model as an equilibrium between single-and double- stranded DNA [7]. For longer DNA, the melting curve exhibits a multi-step behavior consisting of plateaus with different sizes separated by sharp jumps [24]. A popular description for these longer molecules is the zipper model [8], which allows for partially open (intermediate) states. End effects and sequence design also control the nature of the melting transition for DNA oligomers [24].
Although many of the thermodynamic properties of melting of free DNA are known, DNA melting in a constrained space, such as on surfaces, is still poorly understood [25]. DNA confined on surfaces exhibits a behavior different from that in free solutions. Surfaces order the solvent, cosolvents and salts in solution, sometimes strongly. Differences in solvent and salt activity are well known to induce structural changes in nucleic acids [22, 47, 48]. Experiments on DNA arrays have revealed substantial differences in the thermodynamics of hybridization for DNA free in solution versus surface-tethered DNA. The main observations include a surface dependent change, often a decrease, in the thermodynamic stability of the DNA duplex on the surface with a concomitant suppression of the thermal denaturation temperature of the duplex into single strands, and a dramatic broadening of the thermal denaturation duplex melting curve [12]. More detailed experiments demonstrated that these effects change as the surface density of probes increases [26,31,42], which is in agreement with theory [38].
Vainrub et al. [36] developed a mean field model of the Coulomb effects for surface bound DNA to understand the binding isotherms and thermal denaturation characteristics of the double helix. They found that the electrostatic repulsion of the assayed nucleic acid from the array of DNA probes dominates the binding thermodynamics, and thus causes a Coulomb blockage of hybridization. The results explain, for DNA microarrays, the dramatic peak in the hybridization efficiency and the thermal denaturation curve broadening as the probe surface density increases [3, 38–40].
The system of DNA-capped gold nanoparticles exhibits unique phase transitions and represents a new class of complex fluids. The melting temperature of the DNA duplex attached to gold nanoparticle surfaces is in some cases lower than that of free DNA and the melting transition is much sharper [33]. Melting curves of DNA on a solid support have previously been obtained for optical fibers [27], optical wave guides [32], optical scan arrays [17], and temperature-gradient assays [23].
Most DNA melting experiments measure only the kinetic or average dynamical behavior, being deprived of (losing) information about intermediate states and sub-population variations. In order to provide some insight into the structure and the conformations of dsDNA on surfaces at high temperature, and to study the effect of the microarray surface on DNA melting, we performed an all-atom molecular dynamics simulation of a duplex tethered to a surface at an elevated temperature of 400 K. This temperature, though high, was chosen to ensure melting within the submicrosecond timescale.
2. Methods
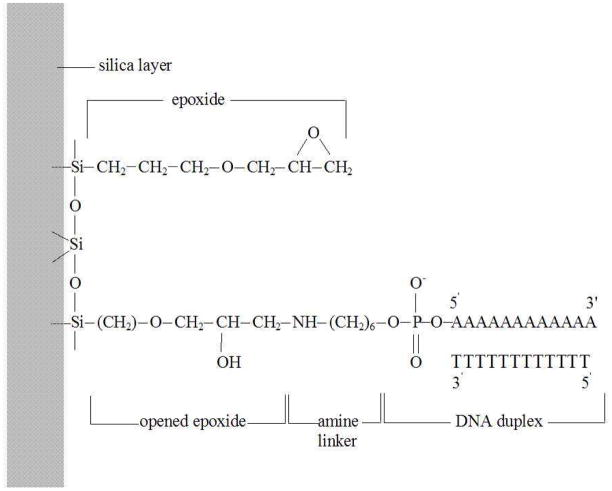
The model design chosen is similar to ones used in previous work from this laboratory [44,45,47]. The system consisted of a silicon dioxide (β-cristobalite) surface coated with an epoxide monolayer, a 12-base-pair (A12·T12) B-DNA duplex tethered to one of the surface epoxides through its 5′-amine linker, and a surrounding solution of 0.1 M NaCl.
Following the earlier work of Wong and Pettitt [43], we modeled the glass substrate by a layer of β-cristobalite [9] with 240 silicon and 420 oxygen atoms. 120 epoxides were bonded to the silicon atoms of the surface. The resulting surface density was 4.5 nm−2 for the epoxides and 0.04 nm−2 for the DNA, which represents a fairly dense system [38]. As illustrated in Fig. 1, the terminal of one of the epoxides was modified and connected to the 5′-amine linker of the homooligomeric (A12·T12) DNA duplex. The force field parameters for the silica layer were adopted from the consistent valence force field (CVFF) [1, 28], and the parameters for the epoxides, the amine linker, and the DNA were adopted from the all-atom CHARMM22 proteins [21] and CHARMM27 nucleic acids [11] force fields.
Figure 1.
The chemical structure of the unreacted epoxides on the silica surface, the opened epoxide which bonds with the amine linker, and the DNA duplex.
TIP3P [11,16] water molecules were used, of which 43 were randomly chosen and replaced by 33 sodium and 10 chloride ions [6]. The additional 23 sodium ions were included to balance the negative charges on the DNA phosphates thus producing a neutral simulation box. The final system of dimension 5.1 × 5.3 × 8.0 nm3 contained 19,040 atoms; including 5367 water molecules. The initial orientation of the epox-ides and the amine linker were set so as to point towards the positive z-direction but were randomly oriented in the x- and y-directions. The DNA duplex, built in canonical B-form with the NAB [20] progam, was also initially oriented in the positive z-direction.
The molecular dynamics program ESP [30], which includes the glide-plane boundary condition [43], was used for this calculation. Given the periodicity parallel to the surface and the model design described above, this setup is well suited to a DNA-coated interface [18]. The ensemble type was microcanonical (NVE) and the electrostatic interactions were evaluated using the Ewald summation [2]. During the simulation, all bond lengths and water bond angles were constrained by the RATTLE algorithm [4] and all silica atoms were fixed. The equations of motion were solved by the velocity Verlet integrator [34] with a time step of 2 fs. The simulation was started with 30 steps of steepest descent minimization followed by equilibration during which the velocities of atoms were scaled periodically to give a temperature of 400 K. The production calculation followed and the coordinates and velocities of the atoms were saved every 0.1 ps for analysis and a total simulation time of 82 ns.
3. Results and discussion
During the simulation, the duplex, which was started in the positive z-direction, fluctuated between various conformations that were dependent on the number of separated base pairs. These orientational fluctuations differed from those in the previous simulation of a duplex DNA tethered to a surface [45]. In that room temperature simulation the DNA was found to swing in random directions on the nanosecond time scale. The DNA tilted with a polar angle fluctuation around 55° and oscillated between a well tilted structure and an upright structure relative to the surface. The linker, between the DNA and the surface, also exhibited conformational oscillations relative to the surface.
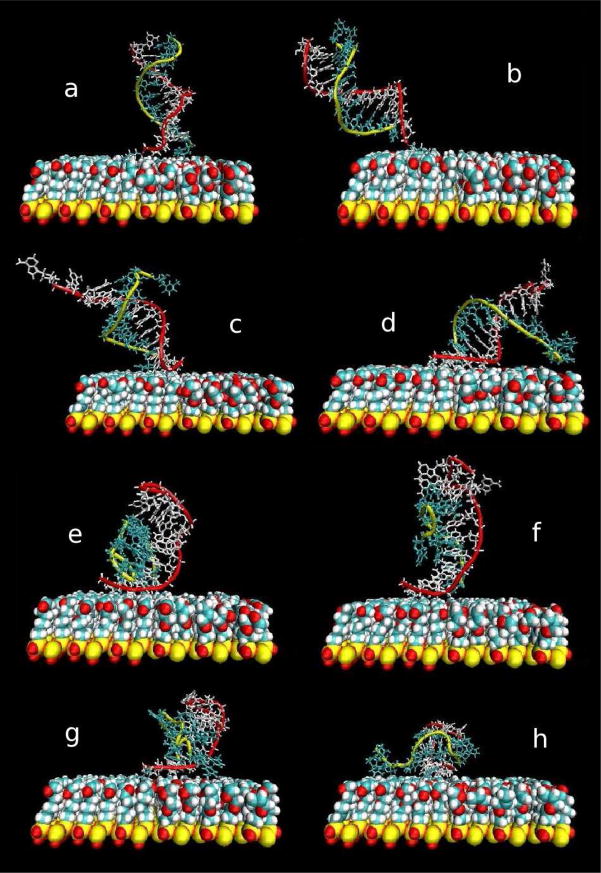
In the present simulation at 400K, the DNA did not tilt in a manner similar to the room temperature calculation. Instead, the oscillations were accompanied by fraying at the end furthest from the surface, the non-tethered end. This should be entropically favorable. Snapshots of the orientational fluctuations and duplex separation along the time course of this computer experiment are illustrated in Fig. 2. From the beginning the relatively hydrophobic linker between the DNA and the surface collapsed, pulling the DNA towards the surface and helping it to maintain an upright position as shown in Fig. 2a. As time progressed, in less than 5 ns, fraying was observed at the “free”, i.e., not tethered end, of the duplex. Within 10 ns there was significant separation of the strands (Fig. 2b and c) that was not observed in the previous simulation at 300 K [44].
Figure 2.
Snapshots of the simulation at (a) 0.2 ns, (b) 2.4 ns, (c) 7.4 ns, (d) 18.4 ns, (e) 26 ns, (f) 27.6 ns, (g) 38.4 ns, and (h) 82 ns.
As the strands began to separate the duplex was also changing its orientation relative to the surface (Fig. 2c and d). Occasionally, the untethered strand oriented its separated bases towards the surface and made direct interactions and contact with the surface as shown in Fig. 2d. We can also see in this snapshot the increase in fraying at the end of the duplex; within 15 ns three base pairs are completely separated. After about 20 ns the canonical DNA duplex structure began to become unspecifically coiled. After about 25 ns the two strands were half base-paired, as in Fig. 2f, but still associated with each other, where the lower six base pairs were still intact.
As the simulation continued the two strands continued to fluctuate, gradually loosing base pairing. Around the half way point, 40 ns, we observe that the two strands were mostly coiled nonspecifically together, even in the regions where base-pairing was lost. Indeed, the two ends of the untethered strand began nonspecifically associating with the surface, as seen in Fig. 2g. After this time and continuing to the end of the simulation the two strands stacked together and interacted as two single strands on a surface. Figure 2h shows the final snapshot of the simulation at 82 ns.
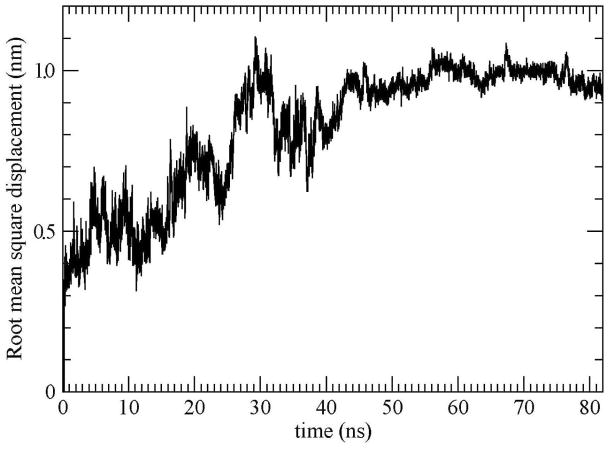
In order to help quantify the conformational changes of the DNA during the simulation, we calculated the root mean square displacement (RMSD) of the DNA with respect to the starting structure. The initial structure was translated and rotated to best fit the DNA conformation at each time step. Figure 3 shows the RMSD as a function of time. Within the first nanosecond it can be seen that there were large accommodations of the room temperature structure to the computational T-jump. It can be seen from the figure that after the initial sharp rise from zero, during the T-jump, the RMSD reached a plateau in the first nanosecond. Following, large fluctuations in the RMSD which grew during the simulation are evident. In the melting period between 0 and 50 ns most of the Watson-Crick base pairs were separated, which we can use as a melting indicator.
Figure 3.
Root mean square displacement of the DNA relative to the first snapshot as a function of time.
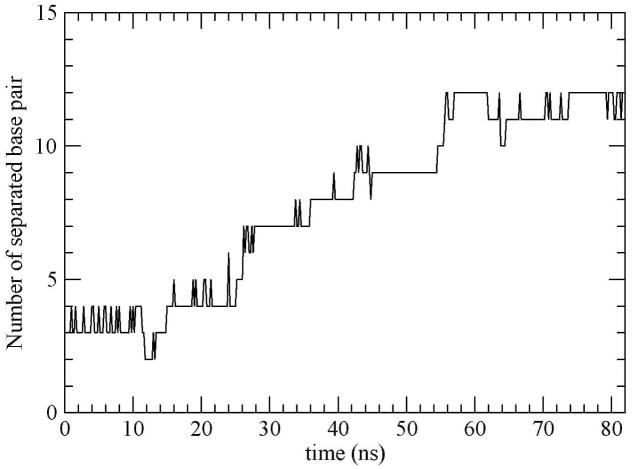
Melting of DNA duplex is a process by which two strands unbind upon heating (this case) or mechanical strain. The number of base pairs as a function of time is a good measure of melting of the DNA duplex, which also helps to understand the variations of the RMSD in Fig. 3. Figure 4 shows the number of separated Watson-Crick base pairs as a function of time. It can be seen that the system exhibits a multi-step behavior consisting of plateaus with different sizes separated by sharp jumps in agreement with other studies [10,33]. This type of fluctuation is observed in experimental studies of the unzipping of duplex DNA [10].
Figure 4.
Number of separated Watson-Crick base pairs as a function of time.
It is easy to see the strong correlation between the RMSD in Fig. 3 and the number of separated base pairs in Fig. 4. During the first 15 ns of the simulation, the strands of the DNA were bound by 9 base pairs and the average RMSD was only 0.5 nm; this is after the sharp T-jump. Between 15 and 26 ns there is another rise in the RMSD with fluctuations around an average value of ~ 0.68 nm with a maximum of ~ 0.75 nm at ~ 19.9 ns. During this period the DNA was bound by 8 base pairs indicating the loss of another Watson-Crick pair. Between the 26th. and 36th. ns the DNA was bound by 5 base pairs having lost 3 additional base pairings, and the RMSD exhibited another rise with fluctuations around an average of ~ 0.94 nm and a maximum of 1.08 nm at 29.2 ns. In the 36 to 42.4 ns period there was a fluctuation around an average of ~ 0.85 nm during which the DNA had 4 base pairs having now lost two thirds of its complementary base-pairings. From 42.4 to 54.6 ns, the fluctuations of the DNA was smaller relative to the earlier ones and occurred around an average of ~ 0.97 nm. In this period the two strands of the DNA associated with the surface and only had 3 remaining base pairs. Later, the two strands behaved as separate ones, nonspecifically binding to the surface and interacting with each other with non-Watson-Crick H-bonds.
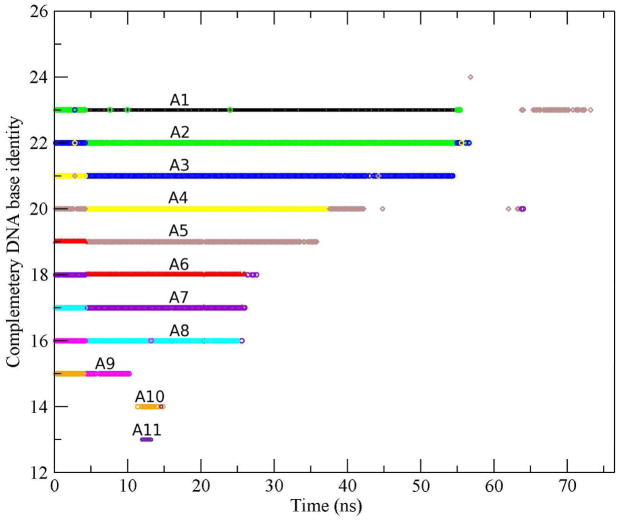
In order to explore the temporal variations of base-pairing between the strands during melting of the duplex, we plotted the base number of the thymine base-paired to each adenine as a function of time in Fig. 5. The color corresponding to each adenine can be deducted easily from the fact that in the initial structure of the duplex, A1 base-paired with T24, A2 base-paired with T23, etc. Hence, A1 is black, A2 is green, A3 is deep blue, A4 is yellow, etc. From Fig. 5 we can observe that, from near the beginning of the simulation, there was a separation of three base pairs: A12-T13 and A11-T14 at the end far from the surface, and A1-T24 at the tethered end.
Figure 5.
Base number of the thymine complementary to each adenine as a function of time. Each color represents one adenine, e.g., black is A1, green is A2, deep blue is A3, etc. Note the global shift between 4 and 5 ns.
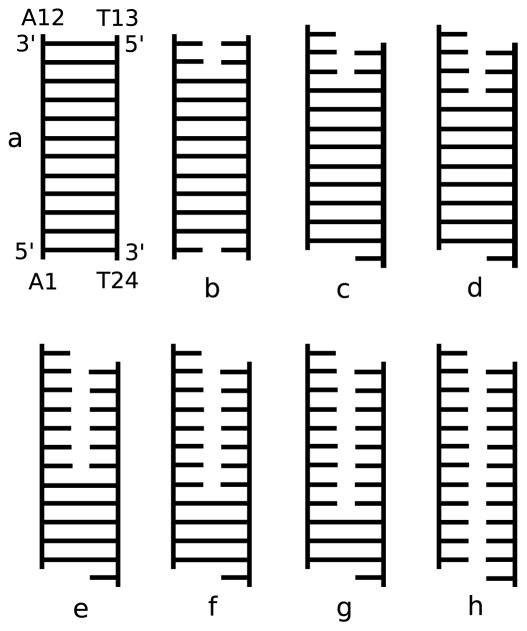
Searching for complementary base pairing along strands was found to be important in oligomeric DNA melting in isotropic solution. [46] Here, between 4 and 5 ns, a searching shift occurred between the two strands relative to the initial B-form such that bases A12 and T24 became single dangling bases at the 3 ′-ends. Thus, after the shift, A1 base-paired with T23, A2 base-paired with T22, etc. Base pairs also broke and remade along the plateaus of Fig. 4. For example, base pairs A10-T14 and A11-T13 remade and separated more than once between 11 and 15 ns. To illustrate the average base pairs of the DNA duplex, we used the information from Fig. 5 to draw a schematic illustration of the DNA duplex during the simulation and it is shown in Fig. 6. Note the shift of base pairs between Fig. 6b and c.
Figure 6.
Schematic illustration of the DNA in various time intervals: (a) the initial B-form DNA duplex and the most dominant structures for the DNA duplex, (b) from 0 to 4.4 ns, (c) 4.4 to 15 ns, (d) 15 to 26 ns, (e) 26 to 36 ns, (f) 36 to 42.4 ns, (g) 42.4 to 54.6 ns, and (h) 54.6 to 82 ns.
The melting temperature can be related to the temperature at which one half of the DNA is denatured or no longer base-paired. After 26 ns we can consider the DNA duplex as past the mid-point of melting. During the last step in the separation curve, which is represented by the period between 54.6 and 82 ns, almost all the base pairs were unpaired as shown in Fig. 6h. The corresponding structure shows the two strands of the DNA duplex stacked and nonspecifically associated together as two single strands on a surface.
Surfaces order the solvent and salts in solution, sometimes strongly. As a result the spatial distributions of water molecules and ions near the surface are very different from the bulk, which leads to a distinct screening environment and modifies the kinetics and thermodynamics of DNA hybridization and/or melting near the surface compared to homogeneous bulk solution. Differences in solvent and salt activity are well known to induce structural changes in nucleic acids [48].
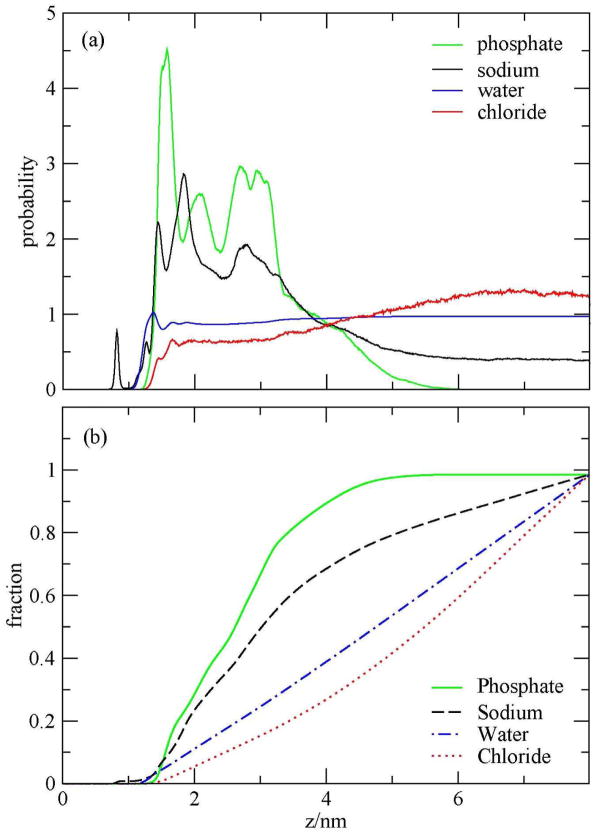
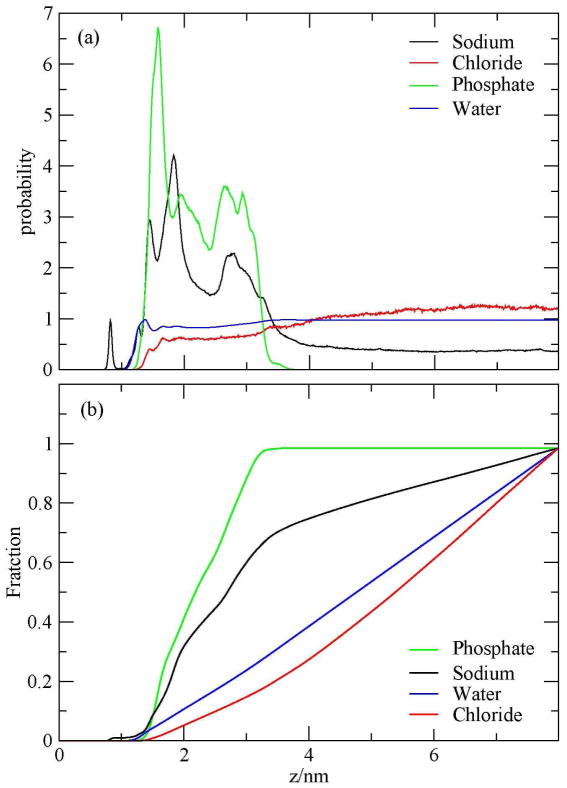
Figure 7a represents the average probability distribution function of water oxygen, sodium ions, chloride ions, and phosphate during the 82 ns simulation as a function of z, the distance measured from the edge of the simulation cell. As a reference, the epoxides extended over the surface up to ~ 1 nm from the edge of the simulation box. From this view it can be seen that the density of phosphates near the surface has a first peak near 1.58 nm and a smaller one at 2.08 nm. The density of sodium ions near the surface has a complicated structure, including peaks associated with the surface and peaks correlated with the phosphates of the DNA. The water and chloride ions densities exhibit less structure in the probability near the surface. Due to the repulsion by the DNA charge, chloride ions density remains below the bulk value up many nanometers.
Figure 7.
(a) Probability distributions and (b) fractions of sodium ions, chloride ions, water oxygen, and phosphates as a function of z during the 82-ns simulation.
Figure 7b shows the fractions of sodium ions, chloride ions, phosphates, and water oxygens during the entire simulation. Within 3 nm from the edge of the simulation box, 70% of the phosphates and 50% of sodium ions were found. To analyze the density of phosphates near the surface, we calculated the densities and fractions of sodium ions, chloride ions, phosphates, and water in two periods of the simulation. The first one is during the first 28 ns, which represents the first half of the melting event. The results are shown in Fig. 8. The second period when the duplex is considered as melted is shown in Fig. 9. Figure 8a shows that the density of phosphates near the surface has a strong split peak near 1.5 nm and another further out. The sodium ions density has two peaks at 1.26 and 1.44 nm. Thus we see here a lack of penetration for the sodium ions through the epoxide layer in the early part of the simulation. The fraction of the phosphates and sodium ions within 3 nm from the edge of the simulation box were 45% and 38%, as shown in Fig. 8b, which are smaller than the average.
Figure 8.
(a) Probability distributions and (b) fractions of sodium ions, chloride ions, water oxygen, and phosphates as a function of z during the first 28 ns of the simulation, which represents the melting period for the DNA duplex.
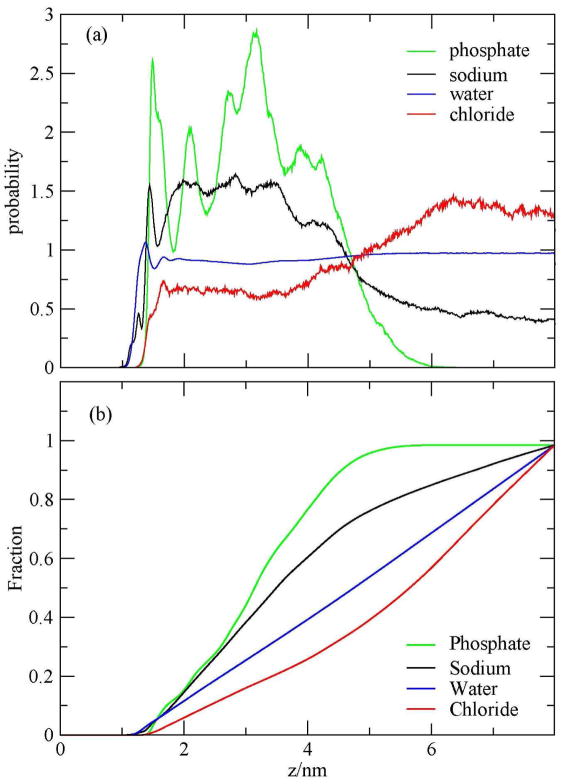
Figure 9.
(a) Probability distributions and (b) fractions of sodium ions, chloride ions, water oxygen, and phosphates as a function of z during the last 39 ns of the simulation, during which the DNA is considered as a melted one.
Figure 9a shows that the density of phosphates near the surface has two peaks at 1.58 and 1.93 nm; both of them are significant. The density of sodium ions near the surface has two small peaks: the first one is near 0.82 nm, which corresponds to the penetration of the sodium ions to the epoxide layer.
Figure 9b shows that the fractions of the phosphates and sodium ions, within 3 nm from the edge of the simulation box, were 89% and 60%, respectively. The water and chloride densities in the two periods exhibit similar trends. From these results it can be concluded that the large density of phosphates near the surface originates from the melted, surface associated DNA during the last interval of the simulation, when its two strands interact with the surface.
4. Conclusions
In this work we simulated the melting of DNA near a surface at an elevated temperature of 400 K. The DNA was found to behave differently than in homogeneous solution [46]. The strands clearly came apart with higher probability at the end away from the surface versus the rather more equal probability of end dissociation for oligomers in homogeneous solution. At such high temperatures surface fouling occurred and was clearly evident in our atomic models.
The difference in the mechanism of melting between isotropic solution and surfaces is perhaps not surprising. Both the thermodynamics and kinetics are known to differ. A critical question for the quantitative use of such systems in biotechnology related tasks is whether such profound differences can be controlled through the design of appropriate surfaces.
Nonspecific surface association of DNA in hybridization for beads or chips has long been thought to be a kinetic hindrance. The higher the temperature the worse the surface association or fouling. This competition between strand dissociation and nonspecific surface adsorbtion will be explored in future works.
Acknowledgments
KQ would like to express her grateful thanks for a Fulbright fellowship and the hospitality of the Pettitt group and the assistance from all the group members during her stay in Houston. We gratefully acknowledge the National Institutes of Health, and the Robert A. Welch Foundation for partial financial support. This research was performed in part using the Molecular Science Computing Facility (MSCF) in the William R. Wiley Environmental Molecular Sciences Laboratory, a national scientific user facility sponsored by the U.S. Department of Energy’s Office of Biological and Environmental Research and located at the Pacific Northwest National Laboratory, operated for the Department of Energy by Battelle. Part of this work was also supported by the National Science Foundation through TeraGrid resources provided by SDSC and PSC. Some figures were prepared with VMD [14] and Tachyon.
References
- 1.Molecular Simulations. San Diego, CA: May, 1996. Discover 2.9.8/96.0. [Google Scholar]
- 2.Allen MP, Tildesley DJ. Computer Simulations of Liquids. Clarendon Press; Oxford: 1992. [Google Scholar]
- 3.Ambia-Garrido J, Pettitt BM. Free energy calculations for DNA near surfaces using an ellipsoidal geometry. Comm Comput Phys. 2008;3:1117–1131. [PMC free article] [PubMed] [Google Scholar]
- 4.Andersen HC. Rattle : a ”velocity” version of the Shake algorithm for molecular dynamics calculations. J Comput Phys. 1983;52:24–34. [Google Scholar]
- 5.Barrett JC, Kawasaki ES. Microarrays: the use of oligonucleotides and cDNA for the analysis of gene expression. Drug Discov Today. 2003;8:134–141. doi: 10.1016/s1359-6446(02)02578-3. [DOI] [PubMed] [Google Scholar]
- 6.Beglov D, Roux B. Finite representation of an infinite bulk system: Solvent boundary potential for computer simulations. J Chem Phys. 1994;100:9050–9063. [Google Scholar]
- 7.Bloomfield VA, Crothers DM, Tinoco I., Jr . Nucleic acids : structures, properties, and functions. University Science Books; Sausalito, CA: 2000. [Google Scholar]
- 8.Cantor CR, Schimmel PR. Biophysical chemistry. W. H. Freeman; San Francisco: 1980. [Google Scholar]
- 9.Chuang IS, Maciel GE. A detailed model of local structure and silanol hydrogen bonding of silica gel surfaces. J Phys Chem B. 1997;101:3052–3064. [Google Scholar]
- 10.Danilowicz C, Coljee VW, Bouzigues C, Lubensky DK, Nelson DR, Prentiss M. DNA unzipped under a constant force exhibits multiple metastable intermediates. Proc Natl Acad Sci USA. 2003;100:1694–1699. doi: 10.1073/pnas.262789199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Foloppe N, MacKerell AD., Jr All-atom empirical force field for nucleic acids: I. parameter optimization based on small molecule and condensed phase macromolecular target data. J Comput Chem. 2000;21:86–104. [Google Scholar]
- 12.Forman JE, Walton ID, Stern D, Rava RP, Trulson MO. Thermodynamics of duplex formation and mismatch discrimination on photolithographically synthesized oligonucleotide arrays. In: Leontis NB, SantaLucia J Jr, editors. Molecular Modeling of Nucleic Acids. American Chemical Society; Washington, DC: 1998. pp. 206–228. [Google Scholar]
- 13.Halperin A, Buhot A, Zhulina EB. On the hybridization isotherms of DNA microarrays: the Langmuir model and its extension. J Phys Condens Matter. 2006;18:S463–S490. [Google Scholar]
- 14.Humphrey W, Dalke A, Schulten K. VMD - visual molecular dynamics. J Molec Graphics. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 15.John SantaLucia J, Hicks D. The thermodynamics of dna structural motifs. Annu Rev Biophys Biomol Struct. 2004;33:415–440. doi: 10.1146/annurev.biophys.32.110601.141800. [DOI] [PubMed] [Google Scholar]
- 16.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulating liquid water. J Chem Phys. 1983;79:926–935. [Google Scholar]
- 17.Khomyakova EB, Dreval EV, Tran-Dangs M, Potier MC, Soussaline FP. Innovative instrumentation for microarray scanning and analysis: application for characterization of oligonucleotide duplexes behavior. Cell Mol Biol. 2004;50:217–224. [PubMed] [Google Scholar]
- 18.Lamture JB, Beattie KL, Burke BE, Eggers MD, Ehrlich DJ, Fowler R, Hollis MA, Kosicki BB, Reich RK, Smith SR, Varma RS, Hogan ME. Direct detection of nucleic acid hybridization on the surface of a charge coupled device. Nucleic Acids Res. 1994;22:2121–2125. doi: 10.1093/nar/22.11.2121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Levicky R, Horgan A. Physicochemical perspectives on DNA microarray and biosensor technologies. Trends Biotechnol. 2005;23:143–149. doi: 10.1016/j.tibtech.2005.01.004. [DOI] [PubMed] [Google Scholar]
- 20.Macke TJ, Case DA. Modeling unusual nucleic acid structures. In: Leontis NB, SantaLucia J Jr, editors. Molecular Modeling of Nucleic Acids. American Chemical Society; Washington, DC: 1998. pp. 379–393. [Google Scholar]
- 21.MacKerell AD, Jr, Bashford D, Bellott M, Dunbrack RL, Jr, Evanseck JD, Field MJ, Fischer S, Gao J, Guo H, Ha S, Joseph-McCarthy D, Kuchnir L, Kuczera K, Lau FTK, Mattos C, Michnick S, Ngo T, Nguyen DT, Prodhom B, Reiher WE, III, Roux B, Schlenkrich M, Smith JC, Stote R, Straub J, Watanabe M, Wiórkiewicz-Kuczera J, Yin D, Karplus M. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J Phys Chem B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 22.Makarov V, Pettitt BM, Feig M. Solvation and hydration of proteins and nucleic acids: A theoretical view of simulation and experiment. Acc Chem Res. 2002;35:376–384. doi: 10.1021/ar0100273. [DOI] [PubMed] [Google Scholar]
- 23.Mao H, Holden MA, You M, Cremer PS. Reusable platforms for high-throughput on-chip temperature gradient assays. Anal Chem. 2002;74:5071–5075. doi: 10.1021/ac025851z. [DOI] [PubMed] [Google Scholar]
- 24.Montrichok A, Gruner G, Zocchi G. Trapping intermediates in the melting transition of DNA oligomers. Europhys Lett. 2003;62:452–458. [Google Scholar]
- 25.Naef F, Lim DA, Patil N, Magnasco M. DNA hybridization to mismatched templates: A chip study. Phys Rev E. 2002;65:040902. doi: 10.1103/PhysRevE.65.040902. [DOI] [PubMed] [Google Scholar]
- 26.Peterson AW, Heaton RJ, Georgiadis RM. The effect of surface probe density on DNA hybridization. Nucleic Acids Res. 2001;29:5163–5168. doi: 10.1093/nar/29.24.5163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Piunno PAE, Watterson JH, Kotoris CC, Krull UJ. Alteration of the selectivity of hybridization of immobilized oligonucleotide probes by co-immobilization with charged oligomers of ethylene glycol. Anal Chim Acta. 2005;534:53–61. [Google Scholar]
- 28.Rovere M, Ricci MA, Vellati D, Bruni F. A molecular dynamics simulation of water confined in a cylindrical SiO2 pore. J Chem Phys. 1998;108:9859–9867. [Google Scholar]
- 29.Rusling JF, editor. Biomolecular Films : Design, Function, and Applications. Marcel Dekker; New York: 2003. [Google Scholar]
- 30.Smith PE, Holder ME, Dang LX, Feig M, Wong K-Y, Pettitt BM. ESP. University of Houston; 1996. [Google Scholar]
- 31.Steel AB, Herne TM, Tarlov MJ. Electrochemical quantitation of DNA immobilized on gold. Anal Chem. 1998;70:4670–4677. doi: 10.1021/ac980037q. [DOI] [PubMed] [Google Scholar]
- 32.Stimpson DI, Hoijer JV, Hsieh W, Jou C, Gordon J, Theriault T, Gamble R, Baldeschwieler JD. Real-time detection of DNA hybridization and melting on oligonucleotide arrays by using optical wave guides. Proc Natl Acad Sci USA. 1995;92:6379–6383. doi: 10.1073/pnas.92.14.6379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Sun Y, Harris NC, Kiang CH. Melting transition of directly linked gold nanoparticle DNA assembly. Physica A. 2005;350:89–94. [Google Scholar]
- 34.Swope WC, Andersen HC, Berens PH, Wilson KR. A computer simulation method for the calculation of equilibrium constants for the formation of physical clusters of molecules: application to small water clusters. J Chem Phys. 1982;76:637–649. [Google Scholar]
- 35.Tarlov MJ, Steel AB. DNA-based sensors. In: Rusling JF, editor. Biomolecular Films : Design, Function, and Applications. ch 12. Marcel Dekker; New York: 2003. pp. 545–608. [Google Scholar]
- 36.Vainrub A, Pettitt BM. Thermodynamics of association to a molecule immobilized in an electric double layer. Chem Phys Lett. 2000;323:160–166. [Google Scholar]
- 37.Vainrub A, Pettitt BM. Coulomb blockage of hybridization in two-dimensional DNA arrays. Phys Rev E. 2002;66:041905. doi: 10.1103/PhysRevE.66.041905. [DOI] [PubMed] [Google Scholar]
- 38.Vainrub A, Pettitt BM. Sensitive quantitative nucleic acid detection using oligonucleotide microarrays. J Am Chem Soc. 2003;125:7798–7799. doi: 10.1021/ja035020q. [DOI] [PubMed] [Google Scholar]
- 39.Vainrub A, Pettitt BM. Surface electrostatic effects in oligonucleotide microarrays: Control and optimization of binding thermodynamics. Biopolymers. 2003;68:265–270. doi: 10.1002/bip.10271. [DOI] [PubMed] [Google Scholar]
- 40.Vainrub A, Pettitt BM. Theoretical aspects of genomic variation screening using DNA microarrays. Biopolymers. 2004;73:614–620. doi: 10.1002/bip.20008. [DOI] [PubMed] [Google Scholar]
- 41.Wang J. From DNA biosensors to gene chips. Nucleic Acids Res. 2000;28:3011–3016. doi: 10.1093/nar/28.16.3011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Watterson JH, Piunno PAE, Wust CC, Krull UJ. Effects of oligonucleotide immobilization density on selectivity of quantitative transduction of hybridization of immobilized DNA. Langmuir. 2000;16:4984–4992. [Google Scholar]
- 43.Wong KY, Pettitt BM. A new boundary condition for computer simulations of interfacial systems. Chem Phys Lett. 2000;326:193–198. [Google Scholar]
- 44.Wong KY, Pettitt BM. A study of DNA tethered to surface by an all-atom molecular dynamics simulation. Theor Chem Acc. 2001;106:233–235. [Google Scholar]
- 45.Wong KY, Pettitt BM. Orientation of DNA on a surface from simulation. Biopolymers. 2004;73:570–578. doi: 10.1002/bip.20004. [DOI] [PubMed] [Google Scholar]
- 46.Wong KY, Pettitt BM. The pathway of oligomeric DNA melting investigated by molecular dynamics simulations. Biophys J. 2008;95:5618–5626. doi: 10.1529/biophysj.108.141010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Wong KY, Vainrub A, Powdrill T, Hogan M, Pettitt BM. A non-Watson-Crick motif of base-pairing on surfaces for untethered oligonucleotides. Mol Sim. 2004;30:121–129. [Google Scholar]
- 48.Yang L, Pettitt BM. B to a transition of DNA on the nanosecond time scale. J Phys Chem. 1996;100:2564–2566. [Google Scholar]
- 49.Zhang L, Miles MF, Aldape KD. A model of molecular interactions on short oligonucleotide microarrays. Nat Biotechnol. 2003;21:818–821. doi: 10.1038/nbt836. [DOI] [PubMed] [Google Scholar]