Drug Effect Unveils Inter-head Cooperativity and Strain-dependent ADP Release in Fast Skeletal Actomyosin

Abstract

Amrinone is a bipyridine compound with characteristic effects on the force-velocity relationship of fast skeletal muscle, including a reduction in the maximum shortening velocity and increased maximum isometric force. Here we performed experiments to elucidate the molecular mechanisms for these effects, with the additional aim to gain insight into the molecular mechanisms underlying the force-velocity relationship. In vitro motility assays established that amrinone reduces the sliding velocity of heavy meromyosin-propelled actin filaments by 30% at different ionic strengths of the assay solution. Stopped-flow studies of myofibrils, heavy meromyosin and myosin subfragment 1, showed that the effects on sliding speed were not because of a reduced rate of ATP-induced actomyosin dissociation because the rate of this process was increased by amrinone. Moreover, optical tweezers studies could not detect any amrinone-induced changes in the working stroke length. In contrast, the ADP affinity of acto-heavy meromyosin was increased about 2-fold by 1 mm amrinone. Similar effects were not observed for acto-subfragment 1. Together with the other findings, this suggests that the amrinone-induced reduction in sliding velocity is attributed to inhibition of a strain-dependent ADP release step. Modeling results show that such an effect may account for the amrinone-induced changes of the force-velocity relationship. The data emphasize the importance of the rate of a strain-dependent ADP release step in influencing the maximum sliding velocity in fast skeletal muscle. The data also lead us to discuss the possible importance of cooperative interactions between the two myosin heads in muscle contraction.

Muscle contraction, as well as several other aspects of cell motility, results from cyclic interactions between myosin II motors and actin filaments. These force-generating interactions are driven by the hydrolysis of ATP at the myosin active site as outlined in Scheme 1 (1–3). In the absence of actin, the P_i and ADP release steps (k₄ and k₅) are rate-limiting for the entire cycle at high (>12 °C) and low temperatures, respectively (4–6). In the presence of actin, the rate of P_i release increases significantly, and the overall cycle is accelerated more than 2 orders of magnitude. The sliding velocity of myosin-propelled motors is generally believed to be rate-limited by actomyosin dissociation (rate constant k′₅, k′₆, or k′₂ in Scheme 1) (7). Alternatively, some studies (8, 9) have suggested that the sliding velocity is determined by the fraction of myosin heads in the weak-binding states, AM⁴ ATP and AM ADP P_i. However, it is worth emphasizing that K_T is very low under physiological conditions (1, 3) with low population of these states. For the same reason, the rate of dissociation of the AM complex is governed by K′₁ and k′₂.

SCHEME 1.

Simplified kinetics scheme for MgATP turnover by myosin (lower row) and actomyosin (upper row). Inorganic phosphate is denoted by P_i; MgATP is denoted by ATP, and MgADP is denoted by ADP; myosin is denoted by M. The states AM*ADP and AM ADP correspond to myosin heads with their nucleotide binding pocket in a partially closed and open conformation, respectively (7, 52). Rate constants are indicated by lowercase letters (rightward transitions, k₂ − k₅ and k′₂ − k′₅, or leftward transitions, k₋₂ − k₋₅ and k′₋₂ − k′₋₅) and equilibrium constants by uppercase letters (K₁, K′₁, K_T, K₃, K′₃, K₆, k′₆, and K_DP). The equilibrium constants are association constants except for simple bimolecular reactions where they are defined as k_i/k_−i.

For the study of contractile mechanisms in both muscle and other types of cells, drugs may be useful as pharmacological tools affecting different transitions or states in the force-generating cycle. Whereas the use of drugs as tools may be less specific than site-directed mutagenesis, it also has advantages. The motor protein function may be studied in vivo, with maintained ordering of the protein components, e.g. as in the muscle sarcomere, allowing more insight into the relationship between specific molecular events and contractile properties of muscle. A drug that has been used quite extensively in this context is butanedione monoxime. The usefulness of this drug is based on firm characterization of its effect on actomyosin function on the molecular level (3, 10–13). More recently other drugs, like N-benzyl-p-toluene sulfonamide (14, 15) and blebbistatin (16), have been found to affect myosin function, and their effects at the molecular level have also been elucidated in some detail (14, 15, 17, 18). Both these drugs appear to affect the actomyosin interaction in a similar way as butanedione monoxime by inhibiting a step before (or very early in) the myosin power stroke, leading to the inhibition of actomyosin cross-bridge formation and force production.

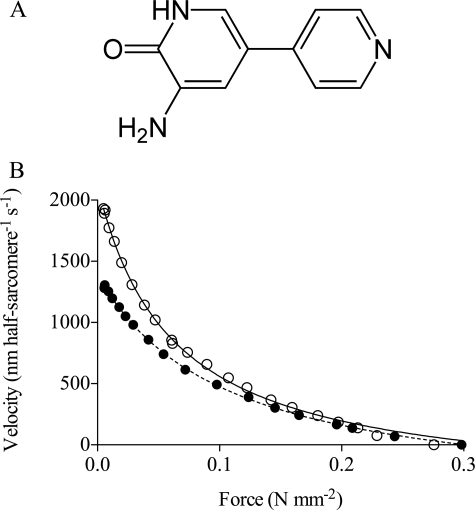
In contrast to the reduced isometric force, caused by the above mentioned drugs, the bipyridine compound amrinone (Fig. 1A) has been found to increase the isometric force production of fast intact skeletal muscles of the frog (19, 20) and mouse (21) and also of fast (but much less slow) skinned muscle fibers of the rat (22). In all the fast myosin preparations, the effect of about 1 mm amrinone on isometric force was associated with characteristic changes of the force-velocity relationship (Fig. 1B), including a reduced maximum velocity of shortening (19–22) and a reduced curvature of the force-velocity relationship (19–22). The latter effect was accompanied (20, 21) by a less pronounced deviation of the force-velocity relationship from the hyperbolic shape (23) at high loads. There have been different interpretations of the drug effects. It has been proposed (20–22) that amrinone might competitively inhibit the MgATP binding by myosin. However, more recently, results from in vitro motility assay experiments (24) challenged this idea. These results showed that amrinone reduces the sliding velocity (V_max) at saturating MgATP concentrations but not at MgATP concentrations close to, or below, the K_m value for the hyperbolic relationship between MgATP concentration and sliding velocity. Such a combination of effects is consistent with a reduced MgADP release rate (24) but not with competitive inhibition of substrate binding. However, effects of amrinone on the MgADP release rate have not been directly demonstrated. Additionally, in view of the uncertainty about what step actually determines the sliding velocity at saturating [MgATP] (see above and Refs. 7–9), it is of interest to consider other possible drug effects that could account for the data of Klinth et al. (24). These include the following: 1) an increased drag force, e.g. because of enhancement of weak actomyosin interactions; 2) a reduced step length; and 3) effects of the drug on the rate of MgATP-induced dissociation of actomyosin.

FIGURE 1.

A, structure of amrinone. B, experimental force-velocity data obtained in the presence (filled symbols) and absence (open symbols) of 1.1 mm amrinone. The data, from intact single frog muscle fibers, were obtained at 2 °C and fitted by Hill's (42) hyperbola (lines) for data truncated at 80% of the maximum isometric force. Filled line, equation fitted to control data, a/P₀* = 0.185; P₀*/P₀ = 1.196. Dashed line, amrinone, a/P₀* = 0.347; P₀*/P₀ = 1.009. Force-velocity data were obtained in collaboration with Professor K. A. P. Edman. Same data as in Fig. 8 of Ref. 20. Note a decrease in maximum sliding velocity and curvature of the force-velocity relationship at low force, in response to amrinone. Also note that amrinone caused increased isometric force and a reduced deviation of the force-velocity relationship from the Hill's hyperbola at high force. All changes of the force-velocity relationship were statistically significant (20), and similar changes were later also observed in intact mouse muscle and skinned rat muscle fibers. Data in Fig. 1 are published by agreement with Professor K. A. P. Edman.

To differentiate between these hypotheses for the amrinone effects, and to gain more general insight into fundamental aspects of muscle function (e.g. mechanisms underlying the force-velocity relationship), we here study the molecular effects of amrinone on fast skeletal muscle myosin preparations in the presence and absence of actin.

In vitro motility assay studies at different ionic strengths suggest that drag forces, caused by increased fraction of myosin heads in weak binding states, are not important for the effect of amrinone on sliding velocity. Likewise, optical tweezers studies showed no effect of the drug on the myosin step length. Finally, ideas that amrinone should reduce sliding velocity by reduced rate of MgATP-induced dissociation could be discarded because the drug actually increased the rate of this process. Instead, we found an amrinone-induced increase in the MgADP affinity of heavy meromyosin (HMM) in the presence of actin. Interestingly, similar effects of amrinone were not observed using myosin S1. As discussed below, this result and other results point to an amrinone-induced reduction in the rate of a strain-dependent MgADP release step. Simulations, using a model modified from that of Edman et al. (25), support this proposed mechanism of action. The results are discussed in relation to fundamental mechanisms underlying the force-velocity relationship of fast skeletal muscle, including which step determines shortening velocity and the possible importance of inter-head cooperativity.

MATERIALS AND METHODS

Protein Preparations

Actin was prepared from rabbit skeletal muscle (26) as described previously and, for some experiments, labeled with pyrene (27) and phalloidin or with TRITC-Ph (Invitrogen) (28). Myosin was purified from fast rabbit skeletal muscle (either white leg or psoas muscles).

For the in vitro motility assay and steady-state MgATP turnover experiments, fresh myosin was cleaved by α-chymotrypsin to obtain HMM (24, 28) or by papain (in the presence of Mg²⁺) (28) to obtain papain subfragment 1 (papain S1). Aliquots of both HMM and S1 were frozen in liquid nitrogen and stored at −80 °C until use.

For transient kinetics experiments, S1 and HMM were prepared by α-chymotryptic digestion of rabbit skeletal muscle myosin based on the protocols of Weeds and Taylor (29) and Margossian and Lowey (30). Papain S1 for transient kinetics and optical tweezers studies was prepared according to Margossian and Lowey (30). Both HMM and S1 for the kinetics experiments were purified by ion exchange on DEAE-Sephacryl using a linear KCl gradient. Protein concentrations were measured spectrophotometrically (28).

Myofibrils

Myofibrils were prepared from rabbit psoas muscle (10, 31) and stored at 4 °C for up to 3 days in a storage buffer (50 mm Tris, 100 mm potassium acetate, 5 mm KCl, 2 mm magnesium acetate, 2 mm dithiothreitol, 0.5 mm sodium azide, 0.2 mm phenylmethylsulfonyl fluoride, 10 μm leupeptin, and 5 μm pepstatin, adjusted to pH 7.4 at room temperature with acetic acid). Pyrene-labeled myofibrils were prepared as described by Ma and Taylor (32), and myosin head concentration was measured according to Houadjeto et al. (33). Control experiments showed that the steady-state ATPases in the presence of Ca²⁺ or EGTA for pyrene-labeled myofibrils are the same as for the unlabeled myofibrils (34) suggesting the lack of major myofibril function alteration with pyrene labeling.

Amrinone Solutions

Stock solutions of amrinone were prepared in lactic acid (24). Several control experiments (e.g. myosin ATPase, motility assays; see also Klinth et al. (24)) suggested that lactic acid per se did not affect actomyosin or myosin function (provided that pH was controlled). However, despite this fact we took care to ensure similar concentrations of lactic acid in solutions with and without amrinone.

Steady-state ATPase

The steady-state ATPase activity of myosin or HMM was obtained by the method of Kodama et al. (35) (room temperature, 20–25 °C in different experiments). Myosin or HMM was diluted in a buffer (Buffer A: 50–500 mm KCl, 20 mm MOPS, 10 mm MgCl₂ (pH 7.2)). The final protein concentration was 1 mg ml⁻¹ (2 μm) for myosin or 120 μg ml⁻¹ (0.34 μm) for HMM. The reaction was initiated by addition of MgATP to a final concentration of 1 mm (pH 7.2) and was quenched after different time periods by addition of perchloroacetic acid at a final concentration of 0.3 m. A “zero time blank” was obtained for each concentration of amrinone by adding perchloroacetic acid to the mixture of myosin, drug, and MgATP immediately after addition of MgATP to the myosin/drug mixture. After centrifugation for 1 min at 17,900 × g, a sample was withdrawn from each perchloroacetic acid-treated reaction solution. This sample was transferred to a 96-well plate and allowed to react with malachite green-molybdate reagent (35) followed by reading of absorbance at 620 nm. In each experiment the absorbance was related to that of a phosphate standard where a solution of KH₂PO₄ (P_i) at different concentrations had been mixed and allowed to react with the malachite green-molybdate reagent as described above. Generally, the relationship between [P_i] and absorbance was highly linear (r² > 0.998) and not affected by the presence of lactic acid or amrinone. For studies of calcium-ATPase, MgCl₂ was exchanged for CaCl₂. The ionic strength was calculated using the software winmaxc 3.2, version 2.05, with stability constants for metal complexes obtained from the NIST Standard Reference Data base 46 version 8.0 (NIST Standard Reference Data, Gaithersburg, MD).

Transient Kinetics, Chymotryptic S1 in the Absence of Actin

Transient kinetics with S1 were carried out in a home-built, thermostatically controlled, rapid quench flow apparatus (5). The procedure was to mix S1 with [γ-³²P]ATP in the apparatus. With ADP displacement technique, the procedure was to preincubate S1 and ADP and to mix them with [γ-³²P]ATP. In both experimental conditions, the reaction mixtures were quenched at different times in acid (22% trichloroacetic acid, 1 mm KH₂PO₄), and the total P_i concentrations were determined by the filter paper method (36). This type of experiment allows the measurement of the kinetics of total P_i formation, i.e. free P_i plus myosin head bound P_i. The kinetics was fitted using linear or nonlinear regression. It is important to note that the measurement error estimated from the residuals of the fits is lower than total experimental error, including mass and volume imprecision during S1 suspension and ATP solution preparations. To minimize this source of error, amrinone and control experiments were performed on the same day with the same buffers and preparations.

Transient Kinetics with Actin, Myofibrils, HMM, and S1

All kinetic measurements were done with a High-Tech Scientific SF-61 DX2 stopped-flow system. Experiments on acto-HMM or acto-S1 were performed at 20 °C in 20 mm MOPS, 100 mm KCl, 5 mm MgCl₂, and 1 mm azide (pH 7), unless indicated otherwise. Pyrene actin fluorescence was excited at 365 nm, and emission was detected after passing through a KV389 nm cutoff filter (Schott, Mainz, Germany). The stated concentrations of reactants are those after mixing in the stopped-flow observation cell unless indicated otherwise.

For studies of myofibrils, changes in either pyrene fluorescence or tryptophan fluorescence were observed. In the latter case the excitation wavelength was 295 nm, and emission was higher than 320 nm. A series of 20–30 shots was performed and averaged for each experimental condition. The dependences of rate constant of the fast component (k_obs) on the MgATP concentration were hyperbolic and fitted using the equation k_obs = k_obs(max) × [ATP]/(K_0.5 + [ATP]), where K_0.5 is the concentration of ATP giving 50% of the k_obs(max) value. Stopped-flow data were analyzed using the software provided by Hi-Tech (KinetAsyst, Bradford-on-Avon, UK) and the Origin software (OriginLab Corp.).

In Vitro Motility Assay

Flow cells were prepared, and motility assays were performed essentially as described previously (24, 37), using assay solutions of the following composition (with or without amrinone): 20 mm MOPS (pH 7.2), 1 mm Na₂ATP, 2 mm MgCl₂, 5–150 mm KCl, 0.1 mm EGTA, 10 mm dithiothreitol, and an anti-photobleach mixture of 3 mg ml⁻¹ glucose, 20 units ml⁻¹ glucose oxidase, 920 units ml⁻¹ catalase (24). In assay solutions of ionic strength >40 mm, methylcellulose was added at a final concentration of 0.6%. For rinsing between incubation steps, a wash solution of the following composition was used: 25 mm imidazole-HCl (pH 7.4), 4 mm MgCl₂, 25 mm KCl, 1 mm EGTA, 1 mm dithiothreitol. In vitro motility assay experiments were retained for analysis only if the fraction of motile filaments in the control solution exceeded 0.60, and generally, this fraction was >0.8. The temperature varied between 23 and 30 °C between experiments as described below but was constant to within ±0.7 °C during a given experiment. Filament sliding was recorded by a Nikon Eclipse TE300 inverted microscope equipped with a cooled CCD camera (37), and the sliding velocities were analyzed as described previously (24, 38).

Optical Tweezers Experiment

The optical tweezers transducer was built around a Zeiss Axiovert microscope (39). Experiments were performed with flow cells made from a microscope slide and pieces of coverslip. Glass beads (2 μm diameter) were applied to the coverslip surface as a suspension in 0.1% (w/v) nitrocellulose/amyl acetate. Papain S1 was allowed to bind to the coverslip surface, with 0.5 mg ml⁻¹ of protein in buffered salt solution (containing (in mm): 25 KCl, 25 imidazole, 4 MgCl₂, 1 EGTA (pH 7.4), 23 °C). The solution was replaced by one containing TRITC-Ph-labeled actin filaments and 1.1-μm diameter polystyrene beads that had been precoated with N-ethylmaleimide-modified myosin. The salt solution was supplemented with (in mm) 2 creatine phosphate, 20 dithiothreitol, 0.01 to 0.1 ATP, and (in mg ml⁻¹) 1 creatine phosphokinase, 0.5 bovine serum albumin, 3 glucose, 0.1 glucose oxidase, 0.02 catalase. An actin filament (average length ∼4 μm) was bound at either end to 1.1-μm polystyrene beads held in optical tweezers. A pretension of ∼2 pn was applied to the suspended actin filament by moving one of the traps in parallel to the actin filament axis. The bead-actin-bead assembly was then positioned in the vicinity of a surface-bound glass bead. Interactions between actin filament and myosin were recorded by casting the image of the polystyrene beads onto four-quadrant photodetectors. With the actin filament pulled taut but in the absence of myosin binding, the root mean square amplitude of the thermal motion was (k_bT/2κ_trap)^0.5 ∼12 nm, with k_bT being the thermal energy and κ_trap being the optical tweezers stiffness = 0.015–0.02 pn·nm⁻¹. When myosin bound to actin, the motion of the beads parallel to the actin filament axis was restrained by the trap stiffness κ_trap plus an additional stiffness κ_add, which reduced the root mean square amplitude of thermal motion to (k_bT/κ_tot)^0.5, with κ_tot = 2κ_trap + κ_add (39, 40). Brownian motion of the trapped beads showed a Lorentzian power density distribution with a roll-off frequency f_c = κ_tot/2πβ ∼500 Hz (where β = 6πηr; η = solution viscosity, r = bead radius = 0.55 μm). Data were collected at 1 kHz, whereas a 100-nm amplitude sine wave oscillation was applied to one of the traps (41). Changes in the amplitude in this signal pick up were used as a sensitive indicator of system stiffness, i.e. myosin binding events. All experiments were carried out at 23 °C.

Simulation of Force-Velocity Data of Muscle

The model of Edman et al. (25), in its original form, accounts for the nonhyperbolic shape of the force-velocity relationship as well as for isometric tension transients and the time course of tension development during an isometric tetanus. For the present purposes, the model was modified as described in the supplemental material. To simulate steady-state force-velocity data, systems of ordinary differential equations were solved (25) by numerical integration using the fourth order Runge-Kutta-Fehlberg method implemented in the software Simnon (version 1.3; SSPA, Gothenburg, Sweden). Increasing the time step in the numerical integration 10 times did not appreciably affect the outcome of the simulations. For further details, see supplemental material and Edman et al. (25).

Statistical Analysis and Graphics

Experimental and simulated force-velocity data were fitted to the Hill (42) hyperbolic equation for forces <80% of the maximum (isometric) force as shown in Equation 1,

Here, v is shortening velocity; P is measured force, and P₀* is the maximum force obtained by extrapolation of the Hill equation to the force axis. The quantities a and b are constants that are related to the curvature of the force-velocity relationship. Here we use the ratio a/P₀* as a measure of this curvature. Moreover, we use the ratio P₀*/P₀ as a measure of the deviation of the force-velocity relationship from the Hill hyperbola at high force (see Ref. 20). As P₀ is the measured maximum (isometric) force, a large value of the ratio, P₀*/P₀, suggests a large deviation of the force-velocity data from a hyperbola.

If not otherwise stated, statistical analyses, including linear and nonlinear regression (Levenberg-Marquardt algorithm), were performed using the GraphPad Prism software (versions 4.0 and 5.0 GraphPad Software, San Diego). Data are given as means ± S.E. unless otherwise stated.

RESULTS

Amrinone Increases Basal MgATPase of HMM

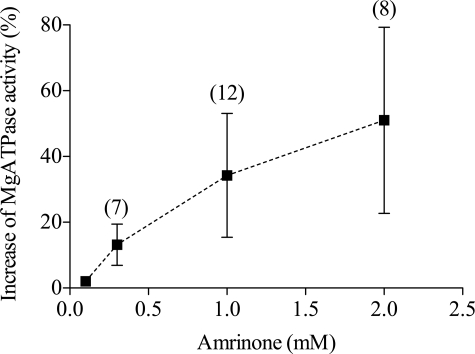
Fig. 2 shows that the basal MgATPase activity of HMM (fast leg muscle) exhibited a concentration-dependent increase in response to amrinone. The effects of the drug on the MgATPase activity of HMM and full-length myosin were compared in separate experiments and were found to exhibit quantitatively similar magnitude and concentration dependence (data not shown).

FIGURE 2.

Effects of amrinone on HMM MgATPase. Effect of amrinone concentration (error bars, 95% confidence intervals) on basal MgATPase of HMM (white rabbit leg muscle). Because altered ionic strength did not influence the amrinone effect (supplemental Fig. 1), data from experiments at ionic strengths of 130 and 500 mm were pooled. The number of experiments is indicated within parentheses. Temperature, 20–25 °C.

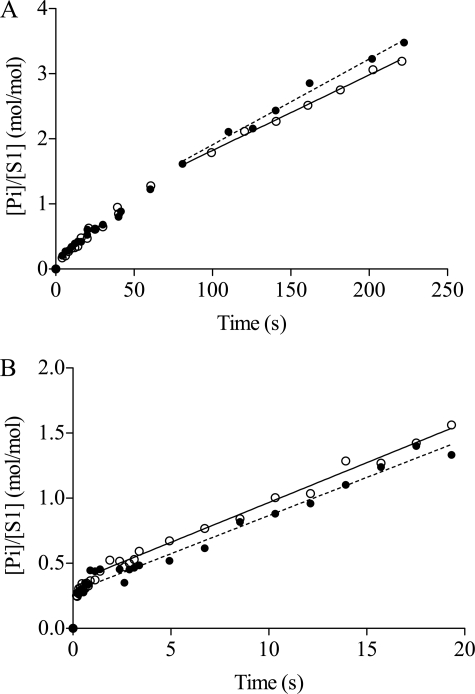
Detailed studies in the absence of actin were performed using chymotryptic S1, and the results have been summarized in supplemental Table 2. Quench flow studies at low temperature (see supplemental Figs. 2 and 3) suggested that the rate constant of the transition limiting MgADP release (k₅) increases slightly, from 0.016 s⁻¹ to 0.026 s⁻¹ upon addition of amrinone (1–2 mm). There was also a small effect on the rate constant of P_i release (k₄), which increased from 0.087 s⁻¹ (no amrinone) to 0.108 s⁻¹ (with amrinone). Rapid quench flow experiments with MgADP displacement from chymotryptic S1 were conducted at 4 and 25 °C (Fig. 3). Each curve is biphasic; a P_i burst phase that is followed by a steady-state turnover phase. The presence of 1 mm amrinone did not alter the P_i burst phase either at 4 (Fig. 3A) or 25 °C (Fig. 3B) suggesting that amrinone has no effect on the actual MgADP release step (K₆ in Scheme 1) (10). Neither was there a significant effect of amrinone on the steady-state turnover phase (Fig. 3), consistent with very small effects of amrinone on both k₄ and k₅. To summarize, the main results of this section are that amrinone increases the basal MgATPase activity of HMM, but the effects on MgATP turnover by S1 are less consistent.

FIGURE 3.

Displacement of MgADP from S1 by MgATP. Data in the control solution (○) and in the presence of 1 mm amrinone (●) at 4 °C (A) and 25 °C (B) S1 (2 μm) plus MgADP (5 μm) were mixed with [γ-³²P]MgATP with or without amrinone. The reaction mixtures were aged for the times indicated and then quenched in acid followed by P_i determination. Straight lines were fitted by linear regression to data in the steady-state phase. At 4 °C the slopes were 0.0116 ± 0.0004 and 0.0132 ± 0.0007 s⁻¹ in the presence and absence of amrinone, respectively. At 25 °C the slopes were 0.0586 ± 0.0025 and 0.0612 ± 0.0017 s⁻¹, in the presence and absence of amrinone.

Amrinone Enhances Actomyosin Dissociation

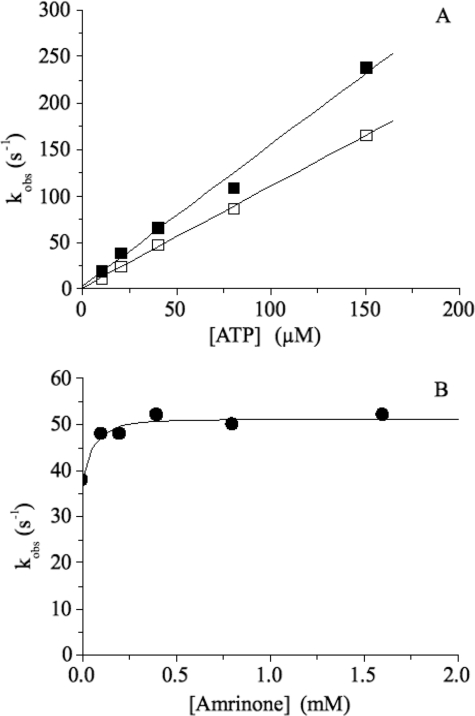
The effect of amrinone on the MgATP-induced dissociation of acto-S1 (chymotryptic S1) is depicted in Fig. 4. Here 0.5 μm acto-S1 (using pyrene-labeled actin) in the presence or absence of 1 mm amrinone was rapidly mixed with various MgATP concentrations. The pyrene fluorescence signal could be fitted to a single exponential, and the resulting rate constant, k_obs, is plotted as a function of ATP concentration (Fig. 4A). From the slope, one can determine the MgATP-induced dissociation rate constant K′₁k′₂. This was increased from 1.09 ± 0.02 μm⁻¹ s⁻¹ in the absence of drug to 1.52 ± 0.09 μm⁻¹ s⁻¹ in the presence of 1 mm amrinone. Fig. 4B shows the results after incubating acto-S1 with variable amounts of amrinone before rapidly mixing with 25 μm ATP. In the presence of amrinone, the observed rates (k_obs) increased slightly from k_obs = 38 s⁻¹ (no amrinone present) to k_obs = 52 s⁻¹ (1.6 mm amrinone). The measured amplitudes were reduced at high amrinone concentrations, because of an inner filter effect of amrinone at 365 nm (data not shown). The increase of the MgATP-induced dissociation rates in the presence of amrinone was also seen with HMM using MgATP concentrations in the range 25–100 μm (data not shown).

FIGURE 4.

Effect of amrinone on the MgATP-induced dissociation of acto-S1. A, 0.5 μm acto-S1 in the presence (■) or absence (□) of 1 mm amrinone was rapidly mixed with various MgATP concentrations. The fluorescence signal could be fitted to a single exponential, and the resulting k_obs values are depicted as a function of [ATP]. From the slope, the MgATP-induced dissociation constant K′₁k′₂ can be obtained, which is slightly higher in the presence of amrinone (K′₁k′₂ = 1.52 ± 0.09 μm⁻¹ s⁻¹) compared with K′₁k′₂ = 1.09 ± 0.02 μm⁻¹ s⁻¹ without amrinone present. B, 0.25 μm acto-S1 + variable concentrations of amrinone were reacted with 25 μm MgATP. In the presence of amrinone the observed rates (k_obs) increased slightly from k_obs = 38 s⁻¹ (no amrinone present) to k_obs = 52 s⁻¹ (1.6 mm amrinone). Temperature, 20 °C.

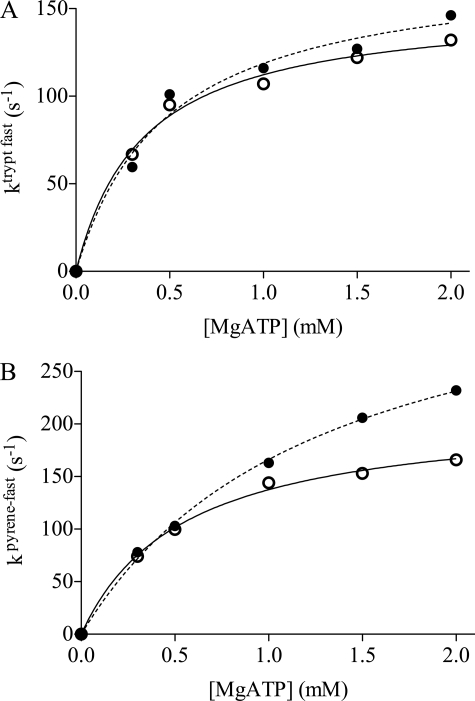
The increase in ATP-induced dissociation in the presence of amrinone was corroborated using stopped-flow studies of myofibrils at low temperature (4 °C). After rapidly mixing myofibrils (3 μm; myosin head concentration) in the presence or absence of amrinone (100 μm) with variable amounts of MgATP, the intrinsic tryptophan fluorescence signal could be fitted to a double exponential. The fast component of tryptophan fluorescence kinetics gives information about myosin head detachment induced by the MgATP binding, whereas the slow component is because of the ATP cleavage step (step 3 in Scheme 1) (8). The maximum amrinone concentration that could be studied using intrinsic tryptophan fluorescence changes was 100 μm because higher concentrations markedly decreased the signal magnitude due to an inner filter effect caused by amrinone at 295 nm. At 100 μm amrinone, no effect could be determined for the slow component. However, for the fast phase, an increase in MgATP-induced dissociation rate was found, compared with controls (Fig. 5A). To test the effect of higher amrinone concentrations (2 mm) on MgATP-induced detachment, pyrene-labeled myofibrils were used because the dependences of pyrene rate and tryptophan fast rate constants are very similar and report the same phenomenon, i.e. cross-bridge detachment. There was no slow phase in the pyrene signal. A fit to a hyperbola (Fig. 5B) suggests that 2 mm amrinone increases k_obs(max) from 213 ± 7 to 381 ± 18 s⁻¹. These values would be expected to correspond directly to the rate constant k′₂ in Scheme 1. The hyperbolic fits also show that 2 mm amrinone increase the constant K_0.5 to 1.29 ± 0.12 mm from the control value of 0.55 ± 0.06 mm, corresponding to an ∼2-fold reduction in the association constant K′₁ (Scheme 1). The key result of this section is the finding that amrinone increases the rate constant k₂′.

FIGURE 5.

Effect of amrinone on the ATP-induced actomyosin dissociation in myofibrils, measured using intrinsic tryptophan fluorescence (A) or pyrene fluorescence (B). A, myofibrillar tryptophan fluorescence fast rate constants as a function of MgATP concentration in the presence of 100 μm amrinone (●) compared with controls (○). B, pyrene fluorescence rate constant as a function of MgATP concentration in the presence of 2 mm amrinone compared with controls. Reaction mixtures contained myofibrils with a myosin head concentration of 3 μm. Lines represent hyperbolas (see “Materials and Methods”) fitted to the data by nonlinear regression. Filled lines, control; dashed lines, amrinone. For the results of the fits, see text. Temperature, 4 °C.

Amrinone Increases MgADP Affinity of HMM but Not of S1

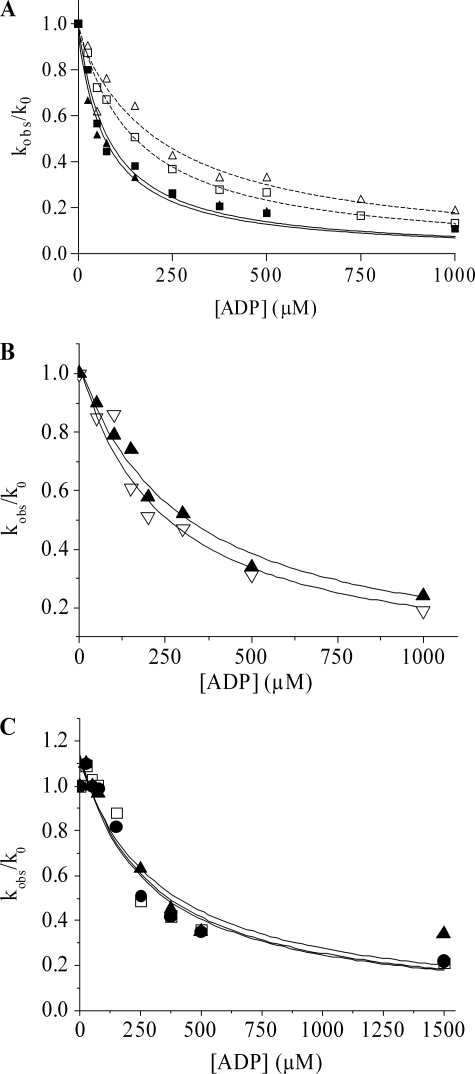
The effect of amrinone on the MgADP affinity (K_AD) of actomyosin was investigated using stopped-flow techniques. Here K_AD is related to K′₆ (association constant) and K′₅ = k′₅/k′₋₅. In the experiments (Fig. 6A), 0.25 μm pActo-HMM, incubated with or without amrinone, was rapidly mixed with 100 μm MgATP and varying concentrations of MgADP. Without amrinone, the change in pyrene fluorescence could be fitted to a double exponential with k_obs = 158 s⁻¹ for the fast phase (amplitude = 32%) and 21 s⁻¹ for the slow phase (amplitude = 3.3%), and both fast and slow rate constants decreased with increasing MgADP concentration. In the presence of 1 mm amrinone the fluorescence change could also be fitted to a double exponential, resulting in slightly faster rates for the fast and the slow phase compared with the rates measured in the absence of amrinone (about 20% increase in both k_obs). Plots of the relative rate constant (k_obs/k₀) versus MgADP concentration are shown in Fig. 6A. Without amrinone present, the K_AD value was 152 ± 7 and 227 ± 41 μm for the fast and slow phase, respectively. The presence of 1 mm amrinone resulted in an ∼2-fold increase of the MgADP affinity, i.e. the K_AD was 81 ± 10 μm for the fast phase and 78 ± 11 μm for the slow phase.

FIGURE 6.

Effect of amrinone on the ADP affinity of rabbit psoas HMM (A), papain S1 (B), and chymotryptic S1 (C). A, 0.25 μm phalloidin-stabilized pyrene-labeled actin was incubated with HMM (containing an equimolar amount of myosin heads) in the presence or absence of 1 mm amrinone before rapidly mixing with 100 μm ATP and various MgADP concentrations. The fluorescence signal could be fitted to a double exponential with a fast (■) and a slow (▲) phase. The plots of the relative rate constant (k_obs/k₀) versus ADP concentration could be fitted against a hyperbola, resulting in a K_AD = 152 ± 7 μm for acto-HMM (fast phase) and 227 ± 41 μm (slow phase) in the absence of amrinone (open symbols), whereas in the presence of 1 mm amrinone (filled symbols) the K_AD was 81 ± 10 μm for the fast phase and 78 ± 11 μm for the slow phase. Data were based on two independent experiments. B, as described in A but using papain-S1 resulting in K_AD = 242 ± 39 μm without amrinone (open symbols) and K_AD = 299 ± 30 μm with 1 mm amrinone (filled symbols). C, as described in A but using chymotryptic S1 resulting in K_AD = 285 ± 68 μm without amrinone (open squares) and K_AD = 279 ± 78 μm with 0.4 mm amrinone (▲) and K_AD = 331 ± 78 μm with 0.8 mm amrinone (●). Temperature, 20 °C.

The effect of amrinone on the MgADP affinity was also investigated using chymotryptic S1 (without the regulatory light chain) or papain S1 (with intact regulatory light chains). The pyrene-labeled acto-S1 complex, in the presence or absence of amrinone, was rapidly mixed with 100 μm MgATP and varying concentrations of MgADP. The observed pyrene fluorescence signal could also be fitted to a double exponential with a fast phase (amplitude = 48%) and a slow phase (amplitude = 4.5%). Both fast and slow rate constants decreased with increasing MgADP concentration as depicted in Fig. 6, B and C, for the two S1 complexes. For clarity, only the fast phase is shown because it has a relative amplitude >90%.

In contrast to the situation with HMM, the MgADP affinity (K_AD) of the acto-S1 complexes was very similar in the presence and absence of 1 mm amrinone. This can be seen for papain S1 in Fig. 6B and for chymotryptic S1 in Fig. 6C. Thus, amrinone increases MgADP affinity of acto-HMM but not of acto-S1.

Amrinone Reduces Actin Filament Sliding Velocity

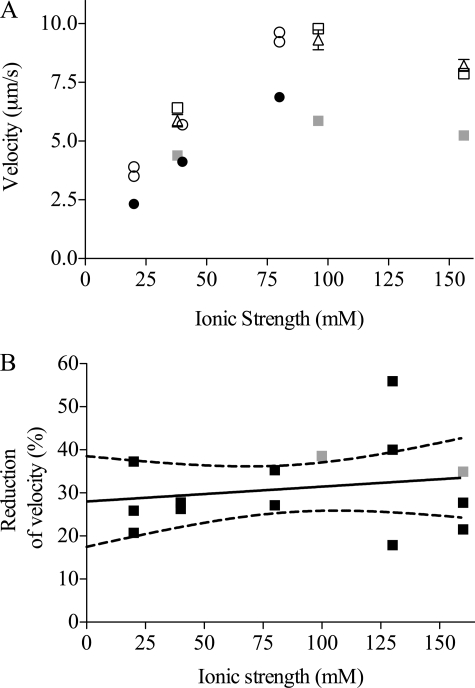
The effect of amrinone on actin filament sliding velocity was studied using in vitro motility assays and HMM from fast leg muscle isoforms IIx and IIb (24). The presence of amrinone reduced the sliding velocity significantly, as is depicted in Fig. 7 at various ionic strengths. It can be seen in Fig. 7A that 1–2 mm amrinone reduced the sliding velocity at all ionic strengths studied, from control values ranging from 3.5 μm s⁻¹ at the lowest ionic strength to ∼10 μm s⁻¹ at 100 mm ionic strength. The percentage reduction of sliding velocity (mean, 31.0 ± 2.5%; n = 15 experiments) in the presence of 1 mm amrinone was similar at different ionic strengths (20–160 mm) of the assay solution (Fig. 7B). It is also shown in Fig. 7A that the effect of amrinone was fully reversible. Thus sliding velocities measured in a given flow cell were virtually identical in a control assay solution before and after incubation of the cell with an amrinone-containing assay solution.

FIGURE 7.

Effects of 1–2 mm amrinone on the HMM-induced actin filament sliding velocity at pH 7. 2. A, sliding velocities at different ionic strengths of the assay solution without amrinone (open symbols) and in the presence of the drug (filled symbols; 1 mm amrinone, black; 2 mm amrinone, gray). Each symbol represents data from a given flow cell (circles) or alternatively obtained using a given flow cell for both amrinone and control solution (first control assay solution (open squares), followed by an assay solution with 2 mm amrinone (filled squares), and then a control assay solution again (open triangles). Between incubations in the different assay solutions, the flow cell was rinsed with wash buffer (see “Materials and Methods”) and TRITC-Ph-labeled actin filaments. Mean velocity was calculated from 64 to 138 filament paths. Standard error of the mean was generally smaller than the size of the symbols. B, percentage of amrinone-induced reduction in sliding velocity at different ionic strengths of the assay solution (black squares, 1 mm amrinone; gray squares, 2 mm amrinone). Full line was obtained by linear regression. Dashed lines, 95% confidence interval for regression line. Regression coefficient (0.034 ± 0.048% mm⁻¹) not significantly different from zero. Each data point refers to mean sliding velocities based on 26–262 filament paths. HMM incubation concentration, 60 μg ml⁻¹. Temperature, 29–30 °C.

By reducing the pH from 7.2 to 6.7, the solubility of amrinone was increased, allowing studies at higher drug concentrations (supplemental Table 1). At pH 6.7 we found a similar decrease in sliding velocity at 1 mm amrinone (average reduction 28.3 ± 10.4%) as at pH 7.2. At higher amrinone concentrations (3 mm) there was a moderate further increase in sliding velocity. This indicates that the effect of amrinone may not be fully saturated at the concentration of 1–2 mm, as used throughout in the present work for practical reasons.

Data from in vitro motility assay experiments at 23 and 29 °C are compared in a Table 1 both for HMM from fast leg muscles (MHC IIb and MHC IIx) (24) and psoas muscle (MHC IIx) (43). It can be seen that amrinone (1 mm) reduced the sliding velocity by ∼30% at both temperatures (see also Fig. 7) for HMM from leg muscle. The effect of the drug on the sliding velocity for two HMM preparations (two different myosin preparations) from musculus psoas major, was slightly lower than for the leg muscle, an effect that was enhanced at the lowest temperature. In vitro motility assays were also performed using two different papain-S1 preparations from psoas muscles (29 °C). The average sliding velocity in the control solution was 3.35 ± 0.08 μm s⁻¹ (n = 4 experiments), and there was a reduction in velocity in response to amrinone. Although the effect of 1 mm amrinone was small (reduction by 7.8 ± 3.6%), it occurred in all experiments. Moreover, as shown in one experiment, the effect was fully reversible. In this case the velocity was reduced from 3.57 ± 0.05 μm s⁻¹ (n_f = 27 filaments) in the control solution to 3.35 ± 0.05 μm s⁻¹ (n_f = 26) in 1 mm amrinone and then back to 3.58 ± 0.04 μm s⁻¹ (n_f = 49) after re-immersion in amrinone-free solution.

TABLE 1.

In vitro motility data using HMM and showing the effect of myosin isoform composition and temperature on the amrinone-induced reduction in sliding velocity

HMM preparation	% reduction of sliding velocity at two temperaturesa
	28.6 °C	22.9 °C
	%	%
Fast leg muscleb	28.9	31.3
Musculus psoas majorc, prepared April, 2007	20.7	13.3
M. psoas majorc, prepared October, 07	17.3	11.5

^a Each numerical value was based on more than 147 filament paths in both test and control.

^b Similar amounts of MHC IIx and MHC IIb according to Ref. 24 and confirmed in the present work (data not shown).

^c This muscle contains almost exclusively MHC IIx (43).

To conclude this section, amrinone reduces the sliding velocity of actin filaments propelled by both HMM and S1. Whereas the effect was larger with HMM, it was reversible with both HMM and S1. The effect of amrinone on sliding velocity was similar over a range of ionic strengths.

Optical Tweezers Experiments

Optical tweezers experiments were performed to elucidate the effects of amrinone on the working stroke produced by the interactions of a single muscle myosin motor head (papain S1) with F-actin. Fig. 8 shows that the drug had no clear effect on the amplitude of the myosin working stroke or on the rate constant of MgATP-induced detachment. Consistent with other results in this work, there was a slight increase of the MgATP-dependent rate constant for detachment in the presence of amrinone (from 3.5 to 4.1 μm⁻¹ s⁻¹).

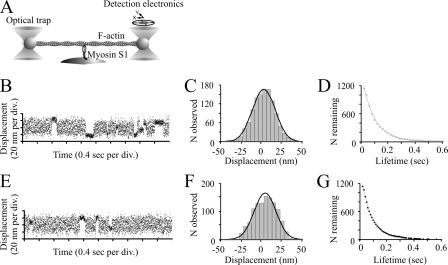
FIGURE 8.

Optical tweezers study. A, schematic representation of the three-bead assay used in the single molecule mechanical experiments. A single actin filament is suspended between two 1.1-μm polystyrene beads, held in the optical tweezers. The actin filament is brought into the vicinity of a 2-μm bead coated with skeletal muscle myosin S1 on the surface of the experimental chamber. Single actomyosin interactions are observed by monitoring the position of one trapped bead using a four quadrant photodetector. B–D, displacement data obtained at 3 μm ATP in the presence of 1 mm lactic acid but in the absence of amrinone. The mean displacement was 4.1 ± 0.4 nm (n = 1137). The average lifetime of attachment events corresponds to a rate constant of 10.6 ± 0.3 s⁻¹ and a second-order rate constant for ATP-induced detachment of 3.5 μm⁻¹ s⁻¹. E–G, displacement data obtained at 3 μm ATP in presence of 1 mm amrinone. The mean displacement was 4.2 ± 0.4 nm (n = 1164). The average lifetime of attachment events corresponds to a rate constant of 12.3 ± 0.4 s⁻¹ and a second-order rate constant for ATP-induced detachment of 4.1 μm⁻¹ s⁻¹. Temperature, 23 °C.

Modeling of the Force-Velocity Relationship

The three attached cross-bridge states in the modified version of the model of Edman et al. (25) (Fig. 9 and supplemental material) may be readily identified with the AMADP·P_i, (A₀) AM*ADP (A₁) and AMADP/AM/AMATP (A₂) states in Scheme 1 (see Ref. 44). Attempts to use the original version of the model (25) to account for the amrinone effects were not successful. We therefore introduced minor modifications (supplemental material). Simulation of amrinone effects by a mechanism involving a reduced rate constant of a strain-dependent MgADP release step could be achieved in either of two ways. Thus, either the free energy of the A₁ (AM*ADP) state is reduced, or the free energy of the A₂ (AM ADP, AM, and AM ATP) state is increased (Fig. 9). Both changes predict the main effects of amrinone on the force-velocity relationship (supplemental material). However, the increase in free energy of the A₂ state is also, in a straightforward way, consistent with an increased rate of MgATP-induced detachment of actomyosin. It can be seen in Fig. 10, A and B, that an increase in free energy of the state A₂ both predicts a reduced maximum velocity of shortening and an increased maximum isometric tension. Moreover, there is a tendency toward a reduced curvature of the force-velocity relationship at low forces, and there is a reduced deviation of the force-velocity relationship from a hyperbolic form (23, 42) at high forces. In this simulation it was assumed that k′₆ ≪ k′₂ leaving the effect of amrinone on k′₂ without any appreciable effect on the rate function k₂₃(x) in the model (see further supplemental material and “Discussion”).

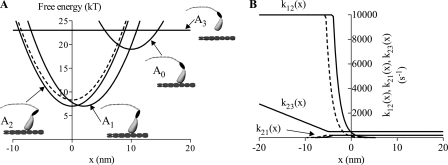
FIGURE 9.

Free-energy diagrams (A) and important rate constants (B) in modified cross-bridge model of Edman et al. (25). A, state A₀ is assumed to correspond to biochemical state AM ADP P_i, whereas the detached state A₃ would correspond to the M ATP and M ADP P_i states in Scheme 1 (where M indicates myosin). Furthermore, the state A₁ corresponds to AM*ADP and the state A₂ corresponds to the AM, AM ADP, and AM ATP states. The free energy diagrams for the control situation are illustrated by the full lines, whereas the change in free energy of state A₂, assumed to be caused by amrinone, is illustrated by the dashed line. The schematic drawings of the myosin head indicate differences in head configuration at the equilibrium positions (free-energy minima) of each state. B, amrinone-induced change in the free-energy of the state A₂ leads to the changes in the rate constant k₁₂(x) that governs the transition from A₁ to A₂ (filled line, control; dashed line, amrinone). Also the reverse rate constant k₂₁(x) is changed at low x values to be consistent with the free energy diagrams in A. However, it is not assumed that amrinone affects the detachment rate constant k₂₃(x), i.e. we assume that k′₆ ≪ k′₂ (see supplemental material).

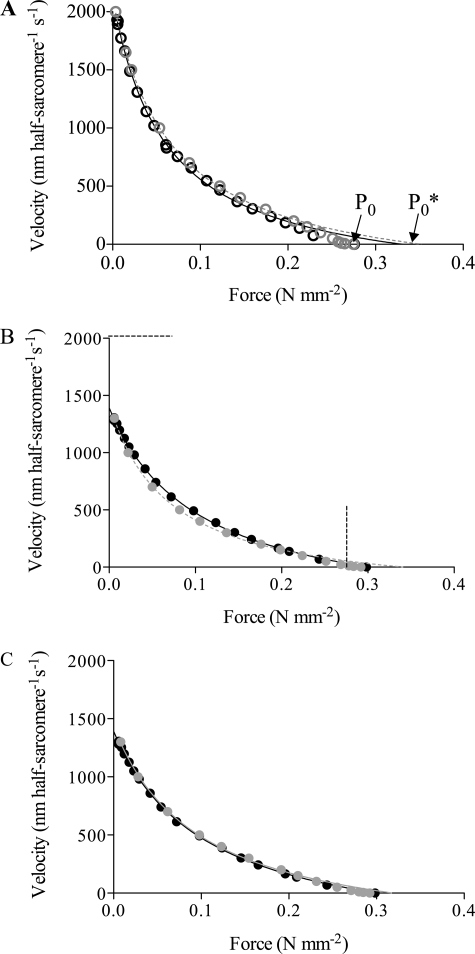
FIGURE 10.

Simulation of the force-velocity relationship of muscle on basis of modified cross-bridge model of Edman et al. (25) designed to simulate mechanical properties of frog muscle fibers. A, simulated force-velocity data for control conditions (gray open circles) superimposed on the experimental data in Fig. 1 (black open circles). Both simulated and experimental data fitted by Hill's (42) hyperbolic equation truncated at forces ≥80% of maximum. Fits to simulated data (dashed gray line) gave a/P₀* = 0.190; P₀*/P₀ = 1.284. For experimental data (filled line), see Fig. 1. B, amrinone conditions simulated by increased free energy of the state A₂ (AM ADP, AM, and AM ATP) by 1.3 kT (Fig. 9A) without further changes. The magnitude of the change was chosen to account for the reduction in the maximum sliding velocity. The simulated data (gray filled circles) are superimposed on the experimental amrinone data from Fig. 1 (black filled circles). Lines represent fits of the Hill equation to experimental (filled line) and simulated data (dashed gray line; a/P₀* = 0.20; P₀*/P₀ = 1.14), as described above. Dashed straight lines indicate magnitudes of maximum isometric force and the maximum shortening velocity under control conditions. C, amrinone conditions (gray filled circles) simulated by increased free energy of state A₂ by 1.3 kT (Fig. 9A) and increase of attachment rate function k₃₀(x, v) by 33% (compared with simulation in B) for high (but not low) velocities. Black full lines and gray dashed lines represent the Hill equation fitted to the experimental and simulated data (a/P₀* = 0.30; P₀*/P₀ = 1.07), respectively. Note increased isometric force, reduction in the maximum sliding velocity, and reduced deviation of force-velocity relationship from hyperbola for simulated data in both B and C. Moreover, note reduced curvature of the force-velocity relationship. Simulated force data scaled to P₀ in control experiment. For details see supplemental material.

In the model of Edman et al. (25), and also in the modified model used here, the rate constant of cross-bridge attachment is increased with the sliding velocity (supplemental Fig. 4F). The assumption of an amrinone-induced increase of the rate constant of cross-bridge attachment during shortening (but not in isometric contraction) leads to improved model behavior in certain important respects. Thus the model better reproduces both the amrinone-induced reduction in curvature of the force-velocity relationship at low forces (with a higher ratio a/P₀* in the Hill equation (42)) and the reduced deviation of the force-velocity relationship from the Hill hyperbola at high forces (Fig. 10C).

DISCUSSION

In accordance with earlier results for the CaATPase (22) and preliminary studies of basal MgATPase activity (24), amrinone moderately increased the MgATP turnover rate of myosin and HMM in the absence of actin. This suggests (see Introduction) that amrinone increases the rate constant k₄ (Scheme 1). Whereas a small increase in the basal MgATPase activity cannot, per se, cause lower sliding velocity, the combination of reduced velocity and an increased basal MgATPase have been observed in response to several point mutations within the myosin motor domain (45–47). A similar combination of effects has also been observed by exchanging regular MgATP for a fluorescent MgATP analogue (48). The different effects of amrinone on HMM and S1 is considered in the supplemental material.

The fact that the 30% reduction in HMM-induced sliding velocity was independent of the ionic strength of the assay solution indicates that the effect on velocity is not because of drag forces caused by myosin cross-bridges in weak binding states (9, 34). Such forces are expected to increase at reduced ionic strength, which would have resulted in greater reduction of sliding velocity by amrinone under these conditions (49).

The studies of actomyosin kinetics focused on dissociation from strongly bound, force-producing states. Thus the steps in this process (1′–2′ and 5′–6′ in Scheme 1) have been implicated (7, 50) as important determinants of the maximum sliding speed. Results with myofibrils, HMM and S1, suggest that amrinone produces a small to moderate increase of the rate constant, k′₂, for ATP-induced detachment. Clearly such an effect cannot account for the amrinone-induced reduction in sliding velocity. However, it may play a modulatory role (supplemental material). For example, for psoas myosin there are suggestions (7) that the rate-limiting step for actomyosin dissociation may change from k′₆ to k′₂ at temperatures below about 25 °C. This may be related to the generally lower effect of amrinone on sliding velocity with the psoas preparation (Table 1). The finding that amrinone does not affect the myosin step length is consistent with previous conclusions (24) from studies of sliding velocity at different ATP concentrations.

An amrinone-induced increase of the MgADP affinity was observed with HMM but not with papain S1 (which, like HMM, has an intact regulatory light chain region). This is consistent with the view that mechanically strained myosin heads, with MgADP at the active site, are important for the amrinone effect. In solution, such strained heads would exist only with two-headed myosin motor fragments (51). In contrast, strain occurs also with one-headed motor fragments in the in vitro motility assay because several surface-immobilized S1 motors can act asynchronously on the same actin filament. Therefore, amrinone effects on a strain-dependent MgADP release step can account for the amrinone-induced reduction in actin sliding velocity also with S1.

The lack of amrinone effects on the MgADP affinity of S1 agrees with the idea that the drug does not affect the actual MgADP release step (k′₆ in Scheme 1; related to K′₆ = k′₋₆/ k′₆) but alters the preceding isomerization step (k′₅/k′₋₅). The existence of such an isomerization between a state with a closed (AM*ADP) and open (AM ADP) nucleotide pocket has been explicitly incorporated into statistical cross-bridge models of muscle contraction (44, 52, 53). It has also been proposed to account for the strain sensitivity and slow MgADP release of several slow myosin II isoforms (54–56). As proposed for these slow isoforms (7), the AM*ADP-AM ADP transition may also influence the measured value of K_AD. Thus, the idea that amrinone affects this transition would be consistent with the drug-induced reduction of K_AD for acto-HMM. Preliminary transient kinetics results with acto-HMM are consistent with this conclusion (supplemental material). These results suggest that 1 mm amrinone markedly alters the multiexponential time course of acto-HMM dissociation following displacement of MgADP at the active site with MgATP. Amrinone increased the amplitude of slow exponential processes at the expense of fast ones and reduced the slow rates but not the fast rates.

In general agreement with the idea of a mechanically strained AM*ADP state, an MgADP-induced structural change in angle of the myosin light chain binding domain has been observed for slow muscle myosin isoforms and for non-muscle myosin classes (57–62). Moreover, in a series of optical tweezers studies (40, 63–65), slow muscle myosin isoforms as well as non-muscle myosins (classes I, V, and VI) were all found to exhibit a power stroke in two steps, probably coupled to the release of P_i and MgADP. Furthermore, single molecule mechanical experiments on smooth muscle and non-muscle myosin class V showed that the dwell time preceding the second step of the working stroke is load-dependent (40, 66). This is consistent with the idea of a load-dependent isomerization preceding the MgADP release step.

The presence of two actomyosin ADP states in skeletal muscle has been implicated before (67, 68), but the properties of these states have been largely unknown (55). Thus, in contrast to the situation for various slow myosin classes, MgADP-induced ultrastructural changes have not been observed for fast skeletal muscle myosin (58, 59). Neither could the existence of a second step be detected in previous optical tweezers studies (63). As pointed out earlier (55), this does not necessarily mean that such a step does not exist. Instead, the population of the state may be low (because of an unfavorable equilibrium), and the kinetics may be fast. Consistent with these ideas, recent optical tweezers studies with improved time resolution (69) have demonstrated two-step force generation also in fast skeletal muscle myosin. The idea that the second step represents the above mentioned isomerization in skeletal muscle was discussed (69) but could not be unambiguously verified. Here, amrinone might be of value as a pharmacological tool in future studies.

The above discussion suggests that the AM* ADP state becomes more heavily populated during muscle contraction in the presence of amrinone. This is in accordance with the increased isometric force production in response to the drug (19–22) because the AM* ADP state is likely to be the main force-producing state (40, 63, 69). Amrinone also affects the shape of the force-velocity relationship (see Introduction and Fig. 1) (19–21). The amrinone effects were well simulated by the modified model of Edman et al. (25) (see Figs. 9 and 10). Here amrinone was assumed to reduce the rate constant, k′₅, of the AM*ADP to AM ADP transition as a result of increased free energy of the state A₂. The amrinone effects were well reproduced (Fig. 10) without any extensive attempts for optimization of the model. Indeed, the only experimental parameter quantitatively fitted in the simulations was the reduction in maximum sliding velocity.

Simulation of the amrinone effects by increased free energy of the state A₂ rather than by reduced free energy of the state A₁ was favored. In this way both the increase of the rate constant k′₂ and the reduction of the rate constant k′₅ may be accommodated without the need to postulate that the drug affects the free energy of more than one state (see supplemental material). The fact that the amrinone effect on k′₂, unlike the effect on K_AD (related to K′₅ and K′₆), was observed in both one- and two-headed motor fragments does not preclude that both effects are due to binding to the same site (see supplemental material). Thus, even if an effect on k′₅ exists also with S1 (cf. in vitro motility assay data above) a two-headed myosin fragment is needed in solution experiments to significantly populate the AM*ADP state, thus enabling the probing of the strain-dependent AM*ADP-AM ADP transition.

The potential importance of cooperativity between the two heads of skeletal muscle myosin II is emphasized by the difference in the amrinone effects between S1 and HMM. In analogy with these effects, amrinone might also modulate cooperative effects existing in shortening muscle (e.g. due to prolonged binding of one head in the AM*ADP state positioning the other head for rapid binding to the next actin site). It is therefore interesting to note that an improved fit of the force-velocity data in the presence of amrinone was obtained by the assumption of an increase of the attachment rate constant at high sliding velocity in the presence of the drug. Whether this corresponds to effects of the drug on inter-head cooperativity deserves further investigation. (cf. Refs. 70, 71).

In conclusion, this study not only addresses the mechanism of action of the myosin inhibitor amrinone but also elucidates several long standing issues of general relevance for mechanistic insight into skeletal muscle biochemistry and physiology. Of particular interest is the finding that the amrinone-induced reduction in sliding velocity can be attributed to inhibition of a strain-dependent MgADP release step. Such a step, associated with a significant population of the AM* ADP state, has not previously been convincingly demonstrated in fast skeletal muscle. Incorporation of this idea into a simple statistical model allowed faithful simulation of the unique set of amrinone effects on the force-velocity relationship. This provides general support for the validity and explanatory power of the statistical model used and deeper insight into fundamental mechanisms of muscle contraction. It is important to point out that those results that are of greatest general relevance to the understanding of muscle function do not rely on knowledge of the exact binding site of amrinone. Moreover, because determination of this site is very challenging (see supplemental material), it is outside the scope of the present investigation but may be of interest to elucidate in future studies.