Abstract
The temperature-dependent rotation of F1-ATPase γ subunit was observed in Vmax conditions at low viscous drag using a 60-nm gold bead (Nakanishi-Matsui, M., Kashiwagi, S., Hosokawa, H., Cipriano, D. J., Dunn, S. D., Wada, Y., and Futai, M. (2006) J. Biol. Chem. 281, 4126–4131). The Arrhenius slopes of the speed of the individual 120° steps and reciprocal of the pause length between rotation steps were very similar, indicating a flat energy pathway followed by the rotationally coupled catalytic cycle. In contrast, the Arrhenius slope of the reciprocal pause length of the γM23K mutant F1 was significantly increased, whereas that of the rotation rate was similar to wild type. The effects of the rotor γM23K substitution and the counteracting effects of βE381D mutation in the interacting stator subunits demonstrate that the rotor-stator interactions play critical roles in the utilization of stored elastic energy. The γM23K enzyme must overcome an abrupt activation energy barrier, forcing it onto a less favored pathway that results in uncoupling catalysis from rotation.
F-ATPase (FoF1), consisting of the catalytic sector F1 (α3β3γδϵ) and the transmembrane proton transport sector Fo (ab2c10), synthesizes or hydrolyzes ATP coupled with proton transport (for reviews, see Ref. 1–6). As Abrahams et al. (7) discovered in the first high resolution x-ray structure, a critical feature of the F1-ATPase is the inherent asymmetry of the three β subunits in different conformations, βTP, βDP, and βE, referring to the nucleotide bound in each catalytic site, ATP, ADP, or empty, respectively. A rotational mechanism has been firmly established mostly based on direct observation in single molecule experiments of the behavior of the rotor complex ϵγc10, relative to the stator complex α3β3δab2 (reviewed in Ref. 1). ATP hydrolysis-dependent rotation of the γ and ϵ subunits in purified bacterial F1 (8, 9), the ϵγc10 complex in detergent solubilized FoF1 (10–13), and the ϵγc10 complexin FoF1 in lipid bilayers (14) were shown experimentally by single molecule observations using fluorescent actin filament as a probe. Relative rotation of the single copy Fo a subunit was also shown in F0F1, which was immobilized through the ring of ∼10 c subunits, suggesting that the rotor and stator are interchangeable mechanical units (14). ATP synthesis by F-ATPase is believed to follow the reverse mechanism of ATP hydrolysis because mechanically induced rotation of the γ subunit in immobilized F1 in the presence of ADP and Pi results in net ATP synthesis (15, 16). There remain many questions about the mechanism of coupling between catalysis and transport via mechanical rotation. In particular, the mechanism of coupling H+ transport to rotation of the subunit c10 ring is still not well understood (4).
In contrast, there is considerably more information on the mechanism of coupling catalysis to γ and ϵ subunit rotation. Observations of γ subunit rotation in the catalytic F1 sector are consistent with Boyer's binding change model (17); thus coupling between the chemistry and rotation can be assessed by studies of the soluble F1, and these findings relate to the mechanism of the entire ATP synthase complex. The γ subunit rotates relative to the α3β3 hexamer in distinct 120° steps. A 120° rotation step consisting of pause and rotation substeps appears to correspond to the hydrolysis of one ATP, assuming that three ATP molecules are hydrolyzed per 360° revolution (18). Additional pauses observed at low ATP concentrations are attributed to the “ATP waiting” dwell (19). Yasuda et al. (19) and Shimabukuro et al. (20) further resolved that each 120° step occurred in two substeps: an 80° substep whose onset was dependent upon the Mg·ATP concentration, and a 40° substep, which was not affected by substrate concentration (19). The pause before the 80° substep, the ATP waiting dwell became shorter with increasing [Mg·ATP]. In contrast, the pause duration before the 40° rotation step was modulated by the slow hydrolysis rate of ATPγS2 or by the catalytic site mutant βE190D (in the Bacillus PS3 F1), which was found to significantly increase the length of the catalytic dwell (20). These data together indicate that the dwell before the 40° step is the “catalytic dwell” (20) and defines the order of the substeps during the 120° rotation step observed in high Mg·ATP concentrations (21).
In this paper, we address the question of when the rate-limiting step of steady state catalysis occurs, with respect to the rotational behavior. Pre-steady state analysis of the burst kinetics of ATP hydrolysis at nearly Vmax conditions demonstrated that the rate-limiting transition state occurs after the reversible hydrolysis/synthesis step and before release of phosphate (Pi) (22, 23). The rate-limiting step is likely associated with a rotation step because a γ-β cross-linked enzyme is still able to undergo the initial ATP hydrolysis, but the rotation-impeded enzyme is unable to release Pi (23). Significantly, the kinetics of steady state hydrolysis can only be assessed when the Mg·ATP concentration is high enough to fill all three catalytic sites. The only model consistent with these data is one that involves all three catalytic sites. During each 120° catalytic cycle, one site binds ATP, a different site carries out reversible hydrolysis/synthesis, and the third site releases product Pi and ADP (22, 23).
Steady state analyses, which take advantage of a particular γ subunit mutation γM23K (24), are consistent with this model. Replacement of the conserved γMet-23 with lysine causes an uncoupling between catalysis and γ subunit rotation caused by altered interactions between γ and β subunits (25). Importantly, Al-Shawi and Nakamoto (26) and Al-Shawi et al. (25, 27) found that the γM23K mutation strongly affected the rate-limiting transition state of steady state ATP hydrolysis and ATP synthesis. The slope of the Arrhenius plots and thus the energy of activation were significantly increased in the mutant enzyme. Several second site suppressor mutations, mostly in the γ subunit (28, 29) but also in the β subunits (30, 31), were genetically identified because they restored coupled ATP synthesis. Significantly, all were in the γ-β interface. Thermodynamic analyses found that the second site suppressors generally compensated for the primary γM23K mutations by reducing the increased activation energy (25, 27, 31). Although most of the second site mutations were found distant from the γM23K site, the x-ray crystal structures (7) suggested that γM23K may directly interact with conserved βGlu-381. As expected, replacement of βGlu-381 with aspartate also suppressed the uncoupling effects of γM23K (31).
To identify the rate-limiting transition state step in the rotational behavior, we analyzed the temperature dependence of the γM23K mutant in Vmax conditions observed in single molecule experiments. Interestingly, direct observation of this mutant using the micron-length actin filaments did not detect differences in the rotation behavior at room temperature (9). In contrast, we find in the data presented here that there is dramatic effect of the mutation on the temperature dependence of the length of the catalytic dwell or pause between the 120° rotation steps. This is likely because of two factors: first, we used a bead small enough not to invoke a drag on the rotation (32), and second, the temperature dependence of the rate of the rotation steps is critical for the analyses of the mechanism.
EXPERIMENTAL PROCEDURES
Preparations and Materials
γM23K (γ subunit methionine 23 changed to lysine), βE381D (β subunit glutamate 381 changed to aspartate), and the γM23K/βE381D double mutation were introduced into the atp operon on a derivative of plasmid pBWU13 (33). Wild-type or mutant FoF1 complexes were expressed in the atp-deleted Escherichia coli strain DK8 (ΔatpB-C) (34). The cells were grown with glycerol as the sole carbon source and disrupted in a French pressure cell, the membranes were collected by ultracentrifugation, and the F1 sector was dissociated and purified as described previously (32). The mutant and wild-type F1 were more than 95% pure and contained α, β, γ, and ϵ subunits as judged from gel electrophoresis. Pyruvate kinase and lactate dehydrogenase were obtained from Roche Applied Science. The other materials used were the highest grade commercially available.
Assay methods
Wild-type and mutant ATPase activities were assayed under the conditions used for the rotation assay (32). Briefly, ATP hydrolysis was followed at the indicated temperatures for ∼10 min using a pyruvate kinase/lactate dehydrogenase enzyme-coupled system by following the decrease in NADH absorbance at 340 nm as previously described (35). The F1 concentration used for the assay was ∼0.1 nm, the ϵ subunit is largely dissociated from F1, and the pyruvate kinase and lactate dehydrogenase were used at sufficient levels so that they were not limiting the reaction rates at any of the assay temperatures. Concentrations of protein (32) and Mg·ATP (36) were determined as previously described.
Direct Observation of γ Subunit Rotation
Rotational behavior was tracked using a 60-nm diameter gold bead (British Biocell International, Cardiff) connected to the γ subunit of E. coli F1 complex immobilized in a flow cell (30 μm deep). We used the same experimental set-up as that previously described (32, 37). The reaction mixture contained 2 mm ATP, 2 mm MgCl2, 10 mm MOPS-KOH, 50 mm KCl, 50 μg/ml pyruvate kinase, 1 mm phosphoenol pyruvate, and 10 mg/ml bovine serum albumin at pH 7.0. Images of beads illuminated with laser light were obtained on a dark field microscope (BX51WI CDEVA-F; Olympus, Tokyo, Japan) and recorded with a C-MOS camera at 4,000 or 8,000 frames/s. The data were analyzed using Image J (National Institutes of Health) (37). The assay temperature was controlled by Thermoplate (Tokai Hit Co. Ltd., Shizuoka, Japan) attached to the objective. In addition, the room temperature was adjusted to help obtain steady sample temperatures. Actual temperatures were measured by a thermister placed in the immersion oil between the objective and flow cell (Anritu Co. Ltd., Kanagawa, Japan).
Unless otherwise specified, bead rotation was monitored for 2 s, which is the maximum data collection period for our experimental set-up. The detection frequency of rotating beads was ∼20% of those observed. The rotation rate was determined by taking the reciprocal of the geometric means of the full 360° rotation time (single revolution time). The rates were also estimated from the arithmetic mean simply by calculating the number of revolutions/s. In this case, we did not include any long pauses lasting longer than 0.1 s (see “Results”).
RESULTS
Direct Observation of Rotation Using a 60-nm Gold Bead Attached to F1 γ Subunit
Continuous high speed rotation was followed using a 60-nm gold bead attached to the γ subunit of F1 complex bound to a glass substrate. Certainly, the small bead exhibited much faster rates than the actin filaments used previously. The ∼1-μm actin filament rotated at ∼10 revolutions/s compared with ∼400 revolutions/s of a 40-nm-diameter bead attached to the same point on the γ subunit (32). The 60-nm bead size was previously found to be small enough not to impart a significant drag and thus does not slow the rate of ATP hydrolysis-driven rotation (32). In tests with a range of beads from 40 to 200 nm in diameter, the rates of 40- and 60-nm beads were similar, suggesting that the observed rates were close to that of the γ subunit without the probe attached. The rotations rates were slower in the presence of the ϵ subunit, which is consistent with its ATPase inhibitory activity (32).
In the experiments described here, the reaction conditions include 2 mm ATP plus 2 mm MgCl2, which gives a Mg·ATP concentration of ∼1.6 mm, ∼30–60-fold higher concentration than the Km for Mg·ATP in steady state hydrolysis determined in bulk phase assay conditions (32, 35). Furthermore, the free Mg2+ concentration is relatively low (<0.4 mm) to reduce its inhibitory effects (38). The beads occasionally exhibited long pauses (>0.1 s), which play a role in the bulk steady state ATPase activity (21) (also see below). They were not considered in the present study because we are only analyzing the partial reactions of continuous rotational catalysis, which includes the rate-limiting step.
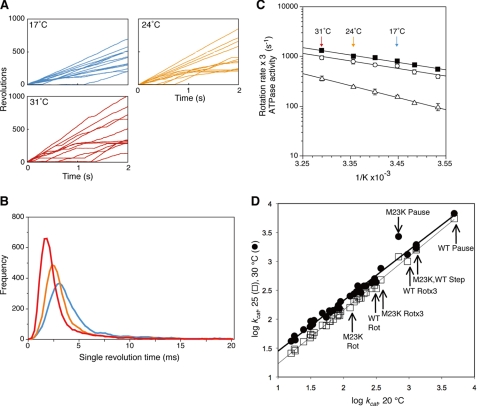
With our optimized single molecule assay in Vmax conditions, we determined the temperature dependence of the ATP-driven rotation to assess the rate-limiting step of the rotational behavior. As can be observed in the positional traces (time courses) shown in Fig. 1A, the beads rotate at slower rates with decreasing temperature. First, we collected data recording the time required for full 360° revolutions and reported these data as single revolution times in the frequency plot in Fig. 1B. All of the rotation events include the short pauses and 120° steps. Because the frequency plots for records of individual beads and those of multiple beads are very similar as was previously observed (21), we use the data from ∼10 randomly selected beads to calculate the single revolution time in a given condition. As can be seen in Fig. 1B, the single revolution time clearly becomes longer and the distribution becomes broader with decreasing temperature. The frequency plots also show the stochastic nature of the rotation behavior, which we have previously concluded is an intrinsic characteristic of the F1-ATPase mechanism (21).
FIGURE 1.
Effect of temperature on the γ subunit rotation in F1. A, time courses of 60-nm gold bead rotation attached to the γ subunit were followed for 2 s at the indicated temperatures. B, single revolution times (time required for full 360° rotations) were obtained from ∼10 gold beads rotating at 17 °C (blue), 24 °C (orange), or 31 °C (red). C, Arrhenius analysis of rotation rates, obtained from the reciprocals of the geometric means of single revolution times (closed squares) or from arithmetic average of the number of rotations in 2 s (open circles). The rotation rates are reported based on the assumption that three ATP are hydrolyzed per 360° rotation, equivalent to ATPase activities (three times the number of rotations). Temperature dependence of bulk phase steady state ATPase activities is also shown (open triangles, the F1 used was the same as the rotation experiments but without the gold bead attached). The error bars show the standard error. D, linear free energy relationship of the ATP synthase. Linear free energy relationships between activities at 20 °C on the x axis compared with 25 °C (open squares) or 30 °C (closed circles) on the y axis. ATPase and ATP synthesis data are taken from a wide variety of sources as reported elsewhere (27, 39). The lines are linear regressions for each data set: the goodness of fit values, R2, for the 20–25 °C and the 20–30 °C data sets are 0.997 and 0.991, respectively. The arrows indicate the new data for wild-type (WT) and γM23K F1 rotations rates with or without multiplying by three (WT or M23K Rot or WT or M23K Rotx3, respectively), speed of the 120° step (M23K, WT Step), or pause durations (WT or M23K Pause).
Arrhenius Analysis of Rotation and ATP Hydrolysis
We used the reciprocal of the geometric mean of the single revolution time to give the rotation rate, which is plotted in the Arrhenius plots in Fig. 1C (closed squares). We also determined the rotation rates by taking the arithmetic mean by simply averaging the number of rotations over a period of time for randomly selected beads (Fig. 1C, open circles). Again, these averages do not include the long pauses that last longer than 0.1 s. Note that the rotation rates are plotted in terms of the expected rates of ATP hydrolysis. Assuming that the hydrolysis of three ATP drives each 360° revolution and the ATPase is efficiently coupled to rotation, three times the rotation rate should correspond to the rate of ATP hydrolysis for a single molecule. We also point out that the plots of the rotation rates obtained from reciprocal single revolution time are essentially the same as those from arithmetic means, indicating that the data are internally self-consistent.
It is not possible as yet to directly measure ATP hydrolysis in a single molecule. Thus, we must compare the rotation rates to the bulk phase ATP hydrolysis rates measured in the same conditions as the rotation experiments. We previously found (32) that the ATPase turnover calculated from the rotation experiments was three to five times faster than that from bulk steady state hydrolysis measurements (Fig. 1C, closed squares and open circles representing the ATP hydrolysis rate based on the rotation rates compared with the bulk steady state ATPase determinations, shown by open triangles). We note that ∼20% of the beads in a given 2-s observation window were rotating (Fig. 1A), and the frequency of rotating beads increased with longer observation time. As shown in Fig. 1A, some beads initiate rotation in the middle of the 2-s observation (those that arise from “0” during the 2-s observation window), whereas other beads rotated for significant time but then paused. We note that the behavior of such beads is missed in the rotation data if the observation window is limited to 1 s. Thus, approximately a third to a fifth of F1 molecules rotate at any one time, whereas the other molecules are in pauses, which can last longer than 2 s (21). We have observed pauses longer than 2 s when an observation window of 10 s was used (data not shown.) The prolonged pauses of the beads probably account for the bulk phase ATPase rates that are lower than what is expected based on the observed rotation rates (21).
The slope of the Arrhenius plots gives the activation energy, EA, for the reaction. Significantly, the Arrhenius plot of the bulk phase steady state ATP hydrolysis rates has a slightly steeper slope than the ATPase rates based on the rotation rates (Fig. 1C). Because the rotation rates do not consider the long pauses, it is not surprising that the activation energy for the rotational behavior is slightly lower. On the other hand, we also note that the rate-limiting step appears to be the same kinetic step for both rotation and for bulk steady state ATPase. The linear free energy relationship (Fig. 1D) for steady state ATPase activity of a wide range of wild-type and mutant F1 and FoF1 enzymes clearly shows that these enzymes share the same rate-limiting step and a common transition state structure (27, 39). Importantly, the rotation rates also fall on the same line, showing that the rotation behavior has the same rate-limiting step as the steady state ATP hydrolysis cycle.
Effect of Temperature on the Steps of Rotation
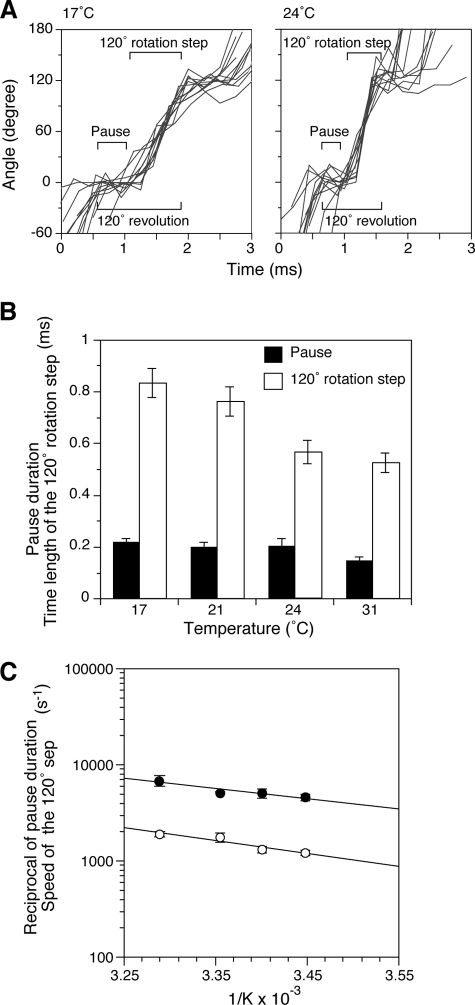
Using a data collection rate of 4,000–8,000 frames/s allows us to detect the intervening short pauses between 120° rotation steps during continuous rotation behavior (Fig. 2A). We previously concluded that ATP hydrolysis occurs during the short pause and is thus called the catalytic dwell (21). This dwell corresponds to the pause between the 80° and 40° substeps as observed by Yasuda et al. (19). The duration of the catalytic dwell became slightly shorter with increasing temperature; for example, the average dwell lengths at 17 and 31 °C were 0.22 ± 0.014 and 0.15 ± 0.016 ms, respectively (Fig. 2B, black bars). The time length for a 120° rotation step was longer than the pause duration and also became shorter with increasing temperature: 0.84 ± 0.055 ms at 17 °C and 0.53 ± 0.037 ms at 31 °C (Fig. 2B, open bars). The reciprocal of the step time is used to calculate the speed of the 120° step, which increased with increasing temperature: 1206 ± 80 s−1 at 17 °C and 1917 ± 127 s−1 at 31 °C (Fig. 2C, open circles).
FIGURE 2.
Effect of temperature on pause duration and the speed of the 120° step. A, observation of the pause duration (catalytic dwell) and the speed of the 120° step. Examples are shown of aligned 120° rotation steps for 17 and 24 °C experiments (data collection rate, 4,000 frames/s). B, effect of temperature on pause duration and time length of the 120° rotation step. Rotations of gold beads were followed for 2 s at the indicated temperatures. The average time required for the 120° revolution (as shown in A) includes the short pause and 120° step. Time for the pause duration was determined by subtracting the time for 120° rotation step from the time for the 120° revolution. These values were determined over 900 120° revolutions, and the average pause duration (black bars) and time length of 120° rotation steps (open bars) are shown. Essentially, the same values were obtained using 8,000 frames/s. The error bars indicate standard errors. C, Arrhenius plots of speed of the 120° step (in s−1) determined from the time lengths of the steps (open circles) and the reciprocal of the pause duration (closed circles).
The Arrhenius plots of the reciprocal of the average pause duration (closed circles) and the speed of the 120° step (open circles) are shown in Fig. 2C. Both lines are linear and similar to the overall rotation rates taken from Fig. 1C (squares), indicating that they have the same activation energy and the same rate-limiting step between 17 and 31 °C. Significantly, both the reciprocal of the pause duration and the speed of the 120° step also conform to the linear free energy relationship (Fig. 1D). These results suggest that there is no overall distinguishable rate-limiting transition state and that the energy pathway of the multi-site steady state reaction is flat, thus preventing the enzyme from having to overcome large activation energies.
Rotational Behavior of the γM23K Mutant
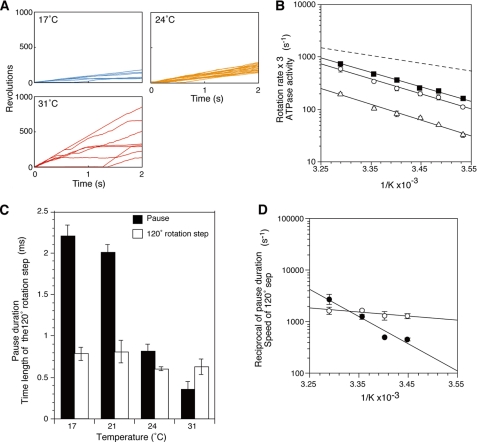
To further delineate the role of the rate-limiting step in ATP-driven rotation, we turned to analysis of a well characterized mutant F1 with an amino acid replacement in the rotor-stator interface, γM23K (24–29). Al-Shawi et al. (25–27) showed that the γM23K substitution caused a significant increase in the activation energy of the steady state reaction. This is a direct effect of the positively charged lysine at a key position where each of the β subunits interacts with the rotor γ subunit in a manner that dictates the conformation of the catalytic site during rotation. In the rotation experiments shown in Fig. 3A, the time courses clearly show that the γM23K F1 rotates at slower overall rates than wild type at saturating Mg·ATP. Similar to steady state ATPase activity, the γM23K rotation rates were ∼2–3.5-fold slower than that of wild type between 10 and 31 °C, respectively. Like wild type, the plots obtained from single revolution times (Fig. 3B, closed squares) and from rotation rates (Fig. 3B, open circles) for the γM23K enzyme were very similar. The difference in temperature effect on γM23K rotation is clearly seen in the steeper Arrhenius plots compared with wild type (Fig. 3B, compare with wild type (dashed line) cited from Fig. 1C). In contrast to the wild-type enzyme where the activation energy, EA, is lower for the rotation than the bulk steady state ATPase, the temperature dependence of the mutant rotation rates is almost parallel to that of the ATPase activity, showing that EA is the same for rotation and bulk ATPase. In the case of the rotation experiments, this result indicates that the rate-limiting step dominates the kinetics of the rotation behavior in the γM23K mutant enzyme. These results are consistent with our previous finding that the steady state ATPase activity of the γM23K mutant enzyme requires significantly higher EA than wild type (25).
FIGURE 3.
Effect of temperature on rotation, pause duration and speed of the 120° step of the γM23K mutant F1. A, examples of 2-s time courses of randomly selected gold beads attached to the γM23K γ subunit at 17, 24, and 31 °C. B, Arrhenius plots of γM23K mutant F1 rotation rates. Time courses of gold beads at different temperature were recorded for 2 s, and rotation rates were determined from the reciprocal of the geometric mean of the single revolution times (closed squares) or the arithmetic average of rotation rates (open circles). The γM23K F1 bulk phase steady state ATPase activities are also shown (open triangles). The linear regression line of the wild-type rotation rate data from Fig. 1C is indicated by the dashed line. C, effect of temperature on the pause duration (black bars) and the time length of the 120° rotation step (open bars) of γM23K F1. Pause duration and time length of the 120° rotation step were obtained as described for Fig. 2B. The rates were determined as in Fig. 2C. The error bars indicate standard errors. D, Arrhenius plots of the speed (in s−1) of the γM23K F1 determined from the time lengths of the 120° rotation steps (open circles) and the reciprocal of the pause duration (closed circles).
Effects of Temperature on the Speed of the 120° Step and Pause Duration of the γM23K
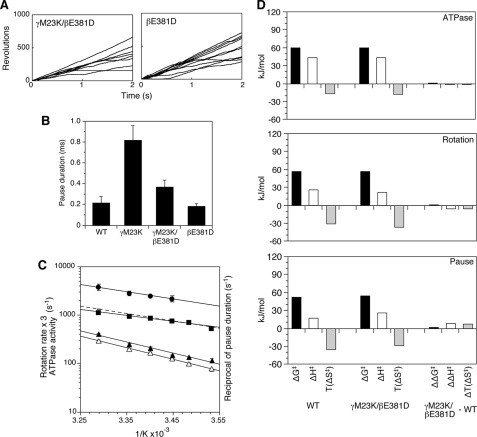
The time length of the 120° step of γM23K over the temperatures of 17–31 °C (Fig. 3C) is similar to those of wild type (compare with Fig. 2B). In contrast, the γM23K pause duration (or catalytic dwell) is strongly affected by temperature (Fig. 3C compared with Fig. 2B) and has much steeper temperature dependence than wild type (Fig. 3D, closed circles). The average pause duration of γM23K was 2.2 ms at 17 °C compared with 0.4 ms at 31 °C (Fig. 3C), whereas those of the wild type were 0.21 ms at 17 °C and 0.16 ms at 31 °C (Fig. 2B).
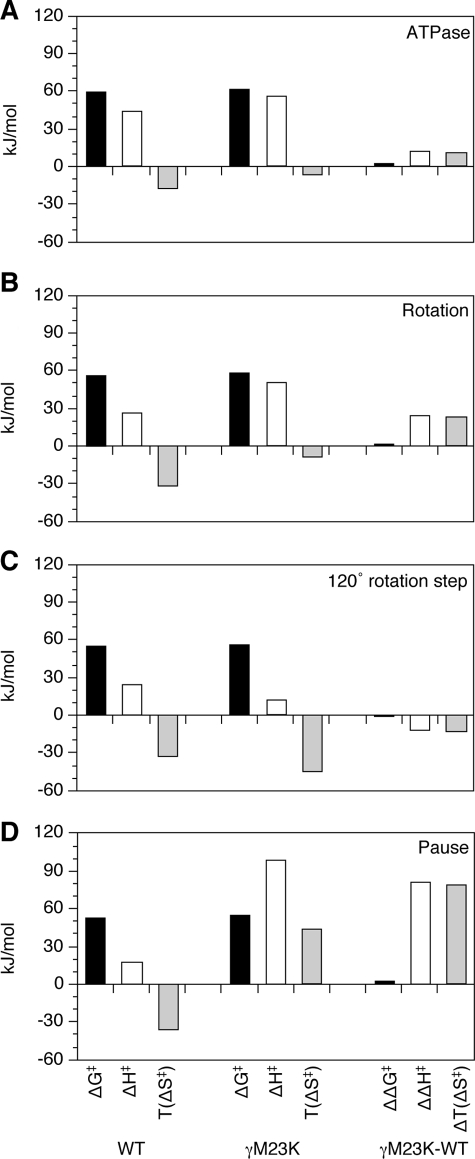
The differences between the γM23K mutant and wild-type enzymes are summarized by the transition state thermodynamic parameters calculated from the Arrhenius plot data (Fig. 4). Based on the rotation rates and compared with the wild type, the γM23K enzyme has a more positive ΔH‡ and less negative ΔS‡, which compensate to give a similar ΔG‡ (Fig. 4, the ΔΔ comparisons are in the right column). The differences in the thermodynamic parameters for the transition state are very similar to those obtained from measurement of bulk steady state ATPase and ATP synthesis reactions (25, 27).
FIGURE 4.
Transition state thermodynamic parameters at 31 °C for wild-type and γM23K F1 rotation. Transition state thermodynamic parameters were calculated from the Arrhenius data for: bulk steady state ATPase activity (A), rotation rate (B), speed of the120° step (C), and reciprocal of the pause duration (D). The differences in the parameters between γM23K and wild-type (WT) F1 enzymes are shown as ΔΔ values on the right.
Significantly, the transition state thermodynamic parameters calculated for the speed of the 120° step and the pause duration show the dramatic effect of the γM23K on the catalytic dwell. Whereas the thermodynamic parameters for the speed of the 120° step were very similar (Fig. 4C), the parameters calculated for the pause duration, ΔH‡ and TΔS‡, were significantly increased by ∼80 kJ/mol for γM23K compared with the wild type (Fig. 4D). These data clearly demonstrate that the mutant enzyme has a dominant rate-limiting step during the catalytic dwell. The prolonged dwell indicates the much larger EA the enzyme faces to start the rotation step.
Effects of βE381D on γM23K
Previously, we hypothesized that the effect of the γM23K replacement was on altered interactions of the γ subunit with the conserved 380βDELSEED386 motif of the β subunit. A critical component of this hypothesis is the counteracting effect of several second site amino acid replacements in regions of γ-β interaction including changes of residue βGlu-381 in the 380βDELSEED386 motif (31). The βE381D single mutation was also tested here in the rotation experiments (Fig. 5A). As expected, the γM23K/βE381D double mutant has bulk steady state ATPase activity similar to that of wild type. Importantly, the mutant γM23K/βE381D has single revolution times (not shown) and pause durations (Fig. 5B) similar to wild type. Accordingly the double mutant has very similar Arrhenius slopes of the rotation rate, ATPase activity, and reciprocal of the pause duration (Fig. 5C). Also, the double mutant has very similar thermodynamic parameters compared with wild type, in particular for the pause duration (Fig. 5D). Enzyme with only the βE381D mutation also had properties very similar to wild type (data not shown). The effects of the γM23K enzyme are dramatically counteracted by the β subunit mutation. These results demonstrate that the specific interactions between γ and β subunits play a critical role in establishing the transition state structure of the enzyme.
FIGURE 5.
Effect of temperature on γM23K/βE381D rotation. A, time courses of 60-nm gold bead rotation at 24 °C attached to the γ subunit of the γM23K/βE381D F1 (left) or βE381D F1 (right). B, average length of the pause duration of mutant F1 at 24 °C. The error bars indicate standard errors. C, Arrhenius analysis of the rotation data for γM23K/βE381D F1; the reciprocal of the pause duration (closed circles) and the rotation rates (closed squares) obtained from the reciprocals of the geometric means of single revolution times. The linear regression line from the rotation rates of wild-type F1 from Fig. 1C is shown for comparison (dotted line). The rotation rates are reported, as in Fig. 1, based on the assumption that three ATP are hydrolyzed per 360° rotation, equivalent to ATPase activities (three times the number of rotations). Temperature dependence of bulk phase steady state ATPase activities of the γM23K/βE381D F1 (open triangles) and βE381D F1 (closed triangles) are also shown. The error bars show the standard error. D, thermodynamic parameters of the γM23K/βE381D F1 compared with wild-type F1 calculated at 31 °C from Arrhenius data for bulk phase steady state ATPase activity, rotation rate, and the pause duration.
DISCUSSION
The present single molecule studies add an important dimension to an enzyme that has had extensive and elaborate mechanistic studies done (see Refs. 5 and 6 for reviews). Because E. coli is a mesophilic organism, its F1-ATPase is appropriate for analyzing mechanism in the experimentally accessible temperature range of 15–40 °C. Similar studies were recently published (40) using the thermophilic Bacillus PS3 enzyme, which has a normal growth temperature of 85 °C. Interestingly, the rates of rotation of this enzyme were apparently independent of temperature between 20 and 50 °C. The behavior may have been due to the reaction conditions because other investigators (41) find steady state ATPase activities of the FoF1 complex to be temperature-dependent in the range of 25–50 °C. Alternatively, it is possible that γ subunit rotation of the PS3 enzyme may be uncoupled or regulated differently in this temperature range.
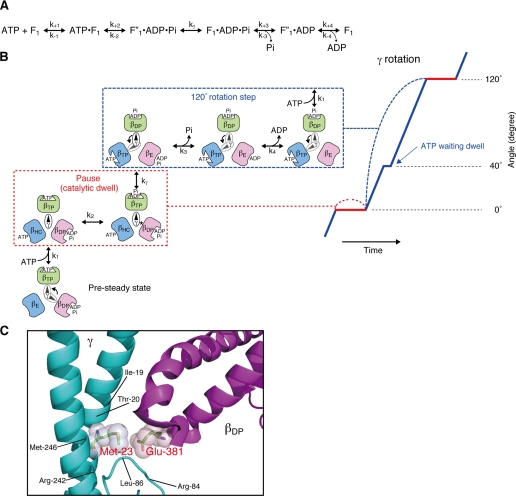
Because the rotation experiments presented in this paper were done using 60-nm gold beads, small enough not to impart a viscous drag to slow ATP hydrolysis-dependent rotation, and high levels of Mg·ATP, the enzyme is operating at Vmax with a tri-site mechanism, in which all three catalytic sites are occupied with nucleotide most of the time. A kinetic model for the steady state rotational catalytic pathway based on pre-steady analyses of E. coli F1-ATPase was recently published (22, 23) and is shown in Fig. 6A with coordination of the partial reactions to the 40° and 80° rotation substeps in Fig. 6B. The rate constants for each step are found in Scanlon et al. (22, 23). With the enzyme in Vmax conditions, we only observe the pauses at the 120° positions (32). This pause is also called the catalytic dwell, which occurs after the 80° and before the 40° subrotation steps, because the reversible hydrolysis/synthesis reaction (k2; Fig. 6, A and B) occurs during this dwell (13, 42). The pause duration of the ATP-waiting dwell (after the 40° and before the 80° subrotation steps (19)) is minimized and not resolved in our rotation experiments (Figs. 1A and 3A). Mg·ATP binding is relatively fast with an association rate constant slightly slower than diffusion limited (22), and the onset of the 80° rotation occurs almost immediately (19). The ATP-dependent dwell appears to occur at a constant rapid rate at saturating Mg·ATP and does not have the stochastic fluctuation over a broad distribution of time lengths that is characteristic of the catalytic dwell (21, 32). Thus, at saturating Mg·ATP, we observe the contiguous 40° and 80° rotation substeps as a single 120° rotation step.
FIGURE 6.
Proposed scheme of rotational catalysis in F1. A, basic reaction pathway as defined by the pre-steady state and steady analyses of Scanlon et al. (22, 23). kγ is the rate-limiting step that follows hydrolysis and precedes Pi release. B, proposed schematic model for the relationship of the catalytic steps to the β subunit conformation and the position of the γ subunit during the catalytic dwell (or pause, outlined in the red dotted box) and the 120° rotation steps (outlined in the blue dotted box) at saturating Mg·ATP. The angular position of the γ subunit during the dwell (red) and the 120° rotation step (blue) is represented on the right. The catalytic dwell involves the reversible hydrolysis/synthesis of ATP in the βTP conformer, as well as the rate-limiting transition state, kγ‡. The transition state is greatly increased in the γM23K mutant enzyme. The 120° rotation step includes phosphate and ADP release from βDP and ATP binding to βE (indicated by the arrow). Note that the γ-β subunit interactions are different for each β subunit (see “Discussion”). C, proximity of the conserved γMet-23 to βGlu-381 in the βDP conformer. The coiled coil region of the γ subunit is shown in teal, and the conserved 380βDELSEED386 loop is in purple. Residues whose side chains are within 5 Å from γMet-23 are shown. This figure was based on the bovine mitochondrial F1 structure of Bowler et al. (47). This figure was generated using PyMol (Delano).
Previously, we have argued that the rate-limiting transition state of the steady state reaction occurs during the catalytic dwell. The pre-steady state hydrolysis of ATP could only be fit with a kinetic model where the rate-limiting step, referred to as kγ, occurs after the reversible hydrolysis/synthesis step (k2 in Fig. 6A) and before Pi release (k3) (22, 27). Consistent with this notion, an F1 constrained from rotation by a disulfide cross-link between γ and one of the β subunits is able to undergo reversible hydrolysis/synthesis of ATP but is unable to release Pi (23). These results demonstrate that a rotation step (the 40° rotation) is necessary for decreasing the affinity for Pi and occurs with the conversion of βDP to βE.
Significantly, the slope of the Arrhenius plot for both the pause length and the rotation rate of the wild-type F1 were very similar (Fig. 2), showing that these steps have similar activation energies. This result implies that there is no single distinct rate-limiting step in the steady state cycle. Clearly, the wild-type rotational catalytic mechanism follows an energy pathway that is relatively flat, thus preventing the enzyme from having to overcome large activation energies. Rather than having a single transition state with a large activation energy, the energetics of the pathway are balanced so that there are multiple, lower activation energies to overcome throughout the pathway. This conclusion is consistent with the analyses of Wang and Oster (43), who predicted that the energy pathway of the steady state reaction is smoothed by small steps over the positions of the γ subunit by the storage and utilization of elastic energy. Previous analyses have found that energy gained from substrate binding in the low affinity βHC site is used to drive the rotation of γ subunit, causing the conformation changes of the catalytic sites (44). As mentioned above, our pre-steady state analysis reveals that the enzyme has a relatively slow step in kγ, which we refer to as rate-limiting. However, our kinetic simulations also show that this step is not slow enough to cause a significant dwell before proceeding to the release of Pi (k3) that occurs closely associated with the 40° rotation step (22).
In contrast to the wild type, the γM23K mutant F1 causes a greatly increased activation energy of kγ. The increase in the EA for kγ was previously shown by steady state analyses (25, 27) and is shown here by the temperature dependence of the pause length, which causes an increase of the EA of ∼80 kJ/mol greater than wild type (Fig. 4). The mutation does not appear to affect other partial reactions of the steady state. The speed of the 120° step is similar to wild type, and we do not detect an additional dwell (Fig. 3). Furthermore, we have previously shown that the reversible hydrolysis/synthesis rates (k2/k-2), which occur at the beginning of the catalytic dwell, are not affected in this mutant (26). The increased activation energy of the γM23K enzyme causes a distinct rate-limiting step to occur during the catalytic dwell, showing that kγ occurs during the dwell.
The mutant phenotype is only obtained by replacement of the conserved γMet-23 with a positively charged amino acid, with lysine having the stronger effect (24). As we previously have shown, the γM23K mutant F1 still conforms to the linear free energy relationship, as shown in Fig. 1D. This is strong evidence that the mutant enzyme pathway passes through the same transition state structure as the wild-type enzyme (26, 27). Because the effect of the γM23K enzyme transition state has the same structure as the wild type, we conclude that the γM23K residue is exactly in the necessary position to perturb the catalytic dwell directly in the pathway toward achieving the transition state. Based on the high resolution crystal structure (7), we previously proposed that the lysine causes an extra interaction between the rotor γ subunit and the conserved acidic β subunit motif, 380βDELSEED386 (25, 27, 31) (Fig. 6C). The extra interaction occurs each time one of the three β subunit 380βDELSEED386 motifs passes the positive charge of the lysine. Because it follows the same energy pathway, the effect of the γM23K substitution can be used to define the timing and relationship of the transition state to the partial reactions and rotational behavior of the steady state. In the case of the wild type, the enzyme normally has adequate stored elastic energy to achieve the transition state and then undergoes the 40° power stroke rotation to move the reaction smoothly forward. In the γM23K enzyme, the energy required for the activation is achieved less frequently, and the enzyme stalls in the dwell.
The effect of the γM23K mutation clearly shows that the interactions between the γ and β subunits are critical in creating a flat energy pathway in the rotational mechanism. This is in contrast to other amino acid substitutions that affect the ability to store energy. For example, the β subunit mutation, S174F, reduces the ATP hydrolysis-induced torque, indicating that it directly affects the storage of elastic energy (45). It also causes prolonged catalytic dwells because of the inability to achieve the transition state (21). However, this is in contrast to the γM23K substitution, which appears to affect specifically the efficient utilization of elastic strain that is stored in the structure of the complex. The interactions between the rotor and stator are important for efficient utilization of this stored energy as is demonstrated by the large number of second site mutations that counteract the effects of the γM23K primary mutation (28–31). All of the suppressor mutations fall in regions of γ-β interactions and include specific interactions with the conserved 380βDELSEED386 motif. As observed in the results here as well in many other examples (see Ref. 46 for a review), perturbations of the rotor-stator interactions disrupt the thermodynamics and kinetics of the rotational mechanism as well as the efficiency of coupling between transport and catalysis. We hypothesize that the altered energy landscape and kinetics of the mutant catalytic mechanism allow the enzyme to take alternative pathways that are uncoupled between catalysis of ATP hydrolysis/synthesis and γ subunit rotation.
Acknowledgments
We thank S. Yano, M. Kudo, S. Kashiwagi, and T. Ubukata for expert technical assistance and Dr. H. Hosokawa for critical discussions.
This work was supported, in whole or in part, by National Institutes of Health Grants RO1 GM50957 (to R. K. N.) and RO1 GM52502 (to M. K. S.). This work was also supported by Core Research for Evolutional Science and Technology, (CREST) the Japan Science and Technology Agency, the Japanese Ministry of Education, Culture, and Science, funds from Daiichi Pharmaceutical Co., Ltd. and Eisai Co., Ltd., and funds from the Terumo Life Science Foundation (to M. N.-M.).
- ATPγS
- adenosine 5′-O-(3-thiotriphosphate) MOPS, 3-(N-morpholino)propanesulfonic acid.
REFERENCES
- 1.Boyer P. D. (1997) Annu. Rev. Biochem. 66, 717–749 [DOI] [PubMed] [Google Scholar]
- 2.Weber J., Senior A. E. (1997) Biochim. Biophys. Acta 1319, 19–58 [DOI] [PubMed] [Google Scholar]
- 3.Stock D., Gibbons C., Arechaga I., Leslie A. G., Walker J. E. (2000) Curr. Opin. Struct. Biol. 10, 672–679 [DOI] [PubMed] [Google Scholar]
- 4.Fillingame R. H., Angevine C. M., Dmitriev O. Y. (2003) FEBS Lett. 555, 29–34 [DOI] [PubMed] [Google Scholar]
- 5.Futai M., Sun-Wada G. H., Wada Y. (2004) in Handbook of ATPases: Biochemistry, Cell Biology, Pathophysiology (Futai M., Wada Y., Kaplan J. eds) pp. 237–260, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany [Google Scholar]
- 6.Nakamoto R. K., Baylis Scanlon J. A., Al-Shawi M. K. (2008) Arch. Biochem. Biophys. 476, 43–50 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Abrahams J. P., Leslie A. G., Lutter R., Walker J. E. (1994) Nature 370, 621–628 [DOI] [PubMed] [Google Scholar]
- 8.Noji H., Yasuda R., Yoshida M., Kinosita K., Jr. (1997) Nature 386, 299–302 [DOI] [PubMed] [Google Scholar]
- 9.Omote H., Sambonmatsu N., Saito K., Sambongi Y., Iwamoto-Kihara A., Yanagida T., Wada Y., Futai M. (1999) Proc. Natl. Acad. Sci. U.S.A. 96, 7780–7784 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sambongi Y., Iko Y., Tanabe M., Omote H., Iwamoto-Kihara A., Ueda I., Yanagida T., Wada Y., Futai M. (1999) Science 286, 1722–1724 [DOI] [PubMed] [Google Scholar]
- 11.Pänke O., Gumbiowski K., Junge W., Engelbrecht S. (2000) FEBS Lett. 472, 34–38 [DOI] [PubMed] [Google Scholar]
- 12.Tanabe M., Nishio K., Iko Y., Sambongi Y., Iwamoto-Kihara A., Wada Y., Futai M. (2001) J. Biol. Chem. 276, 15269–15274 [DOI] [PubMed] [Google Scholar]
- 13.Ueno H., Suzuki T., Kinosita K., Jr., Yoshida M. (2005) Proc. Natl. Acad. Sci. U.S.A. 102, 1333–1338 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Nishio K., Iwamoto-Kihara A., Yamamoto A., Wada Y., Futai M. (2002) Proc. Natl. Acad. Sci. U.S.A. 99, 13448–13452 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Itoh H., Takahashi A., Adachi K., Noji H., Yasuda R., Yoshida M., Kinosita K. (2004) Nature 427, 465–468 [DOI] [PubMed] [Google Scholar]
- 16.Rondelez Y., Tresset G., Nakashima T., Kato-Yamada Y., Fujita H., Takeuchi S., Noji H. (2005) Nature 433, 773–777 [DOI] [PubMed] [Google Scholar]
- 17.Boyer P. D. (1979) in Membrane Bioenergetics (Lee C. P., Schatz G., Ernster L. eds) pp. 461–479, Addison-Wesley Publishing Co., Reading, MA [Google Scholar]
- 18.Yasuda R., Noji H., Kinosita K., Jr., Yoshida M. (1998) Cell 93, 1117–1124 [DOI] [PubMed] [Google Scholar]
- 19.Yasuda R., Noji H., Yoshida M., Kinosita K., Jr., Itoh H. (2001) Nature 410, 898–904 [DOI] [PubMed] [Google Scholar]
- 20.Shimabukuro K., Yasuda R., Muneyuki E., Hara K. Y., Kinosita K., Yoshida M. (2003) Proc. Natl. Acad. Sci. U.S.A. 100, 14731–14736 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Nakanishi-Matsui M., Kashiwagi S., Ubukata T., Iwamoto-Kihara A., Wada Y., Futai M. (2007) J. Biol. Chem. 282, 20698–20704 [DOI] [PubMed] [Google Scholar]
- 22.Scanlon J. A., Al-Shawi M. K., Le N. P., Nakamoto R. K. (2007) Biochemistry 46, 8785–8797 [DOI] [PubMed] [Google Scholar]
- 23.Scanlon J. A., Al-Shawi M. K., Nakamoto R. K. (2008) J. Biol. Chem. 283, 26228–26240 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Shin K., Nakamoto R. K., Maeda M., Futai M. (1992) J. Biol. Chem. 267, 20835–20839 [PubMed] [Google Scholar]
- 25.Al-Shawi M. K., Ketchum C. J., Nakamoto R. K. (1997) J. Biol. Chem. 272, 2300–2306 [DOI] [PubMed] [Google Scholar]
- 26.Al-Shawi M. K., Nakamoto R. K. (1997) Biochemistry 36, 12954–12960 [DOI] [PubMed] [Google Scholar]
- 27.Al-Shawi M. K., Ketchum C. J., Nakamoto R. K. (1997) Biochemistry 36, 12961–12969 [DOI] [PubMed] [Google Scholar]
- 28.Nakamoto R. K., Maeda M., Futai M. (1993) J. Biol. Chem. 268, 867–872 [PubMed] [Google Scholar]
- 29.Nakamoto R. K., al-Shawi M. K., Futai M. (1995) J. Biol. Chem. 270, 14042–14046 [DOI] [PubMed] [Google Scholar]
- 30.Jeanteur-De Beukelaer C., Omote H., Iwamoto-Kihara A., Maeda M., Futai M. (1995) J. Biol. Chem. 270, 22850–22854 [DOI] [PubMed] [Google Scholar]
- 31.Ketchum C. J., Al-Shawi M. K., Nakamoto R. K. (1998) Biochem. J. 330, 707–712 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Nakanishi-Matsui M., Kashiwagi S., Hosokawa H., Cipriano D. J., Dunn S. D., Wada Y., Futai M. (2006) J. Biol. Chem. 281, 4126–4131 [DOI] [PubMed] [Google Scholar]
- 33.Moriyama Y., Iwamoto A., Hanada H., Maeda M., Futai M. (1991) J. Biol. Chem. 266, 22141–22146 [PubMed] [Google Scholar]
- 34.Klionsky D. J., Brusilow W. S., Simoni R. D. (1984) J. Bacteriol. 160, 1055–1060 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Sun-Wada G. H., Imai-Senga Y., Yamamoto A., Murata Y., Hirata T., Wada Y., Futai M. (2002) J. Biol. Chem. 277, 18098–18105 [DOI] [PubMed] [Google Scholar]
- 36.Fabiato A., Fabiato F. (1979) J. Physiol. 75, 463–505 [PubMed] [Google Scholar]
- 37.Abramoff M. D., Magelhaes P. J., Ram S. J. (2004) Biophotonics Int. 11, 36–42 [Google Scholar]
- 38.Kanazawa H., Horiuchi Y., Takagi M., Ishino Y., Futai M. (1980) J. Biochem. 88, 695–703 [DOI] [PubMed] [Google Scholar]
- 39.Peskova Y. B., Nakamoto R. K. (2000) Biochemistry 39, 11830–11836 [DOI] [PubMed] [Google Scholar]
- 40.Furuike S., Adachi K., Sakaki N., Shimo-Kon R., Itoh H., Muneyuki E., Yoshida M., Kinosita K., Jr. (2008) Biophys. J. 95, 761–770 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Mnatsakanyan N., Krishnakumar A. M., Suzuki T., Weber J. (2009) J. Biol. Chem. 284, 11335–11345 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Shimabukuro K., Muneyuki E., Yoshida M. (2006) Biophys. J. 90, 1028–1032 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Wang H., Oster G. (1998) Nature 396, 279–282 [DOI] [PubMed] [Google Scholar]
- 44.al-Shawi M. K., Parsonage D., Senior A. E. (1990) J. Biol. Chem. 265, 4402–4410 [PubMed] [Google Scholar]
- 45.Iko Y., Sambongi Y., Tanabe M., Iwamoto-Kihara A., Saito K., Ueda I., Wada Y., Futai M. (2001) J. Biol. Chem. 276, 47508–47511 [DOI] [PubMed] [Google Scholar]
- 46.Nakamoto R. K., Ketchum C. J., al-Shawi M. K. (1999) Annu. Rev. Biophys. Biomol. Struct. 28, 205–234 [DOI] [PubMed] [Google Scholar]
- 47.Bowler M. W., Montgomery M. G., Leslie A. G., Walker J. E. (2007) J. Biol. Chem. 282, 14238–14242 [DOI] [PubMed] [Google Scholar]