Robust passive dynamics of the musculoskeletal system compensate for unexpected surface changes during human hopping

Abstract

When human hoppers are surprised by a change in surface stiffness, they adapt almost instantly by changing leg stiffness, implying that neural feedback is not necessary. The goal of this simulation study was first to investigate whether leg stiffness can change without neural control adjustment when landing on an unexpected hard or unexpected compliant (soft) surface, and second to determine what underlying mechanisms are responsible for this change in leg stiffness. The muscle stimulation pattern of a forward dynamic musculoskeletal model was optimized to make the model match experimental hopping kinematics on hard and soft surfaces. Next, only surface stiffness was changed to determine how the mechanical interaction of the musculoskeletal model with the unexpected surface affected leg stiffness. It was found that leg stiffness adapted passively to both unexpected surfaces. On the unexpected hard surface, leg stiffness was lower than on the soft surface, resulting in close-to-normal center of mass displacement. This reduction in leg stiffness was a result of reduced joint stiffness caused by lower effective muscle stiffness. Faster flexion of the joints due to the interaction with the hard surface led to larger changes in muscle length, while the prescribed increase in active state and resulting muscle force remained nearly constant in time. Opposite effects were found on the unexpected soft surface, demonstrating the bidirectional stabilizing properties of passive dynamics. These passive adaptations to unexpected surfaces may be critical when negotiating disturbances during locomotion across variable terrain.

during gaits like running, hopping, and trotting, animals bounce along the ground in a springlike manner (6, 11, 12, 23). These gaits can be modeled using a simple spring-mass system, consisting of a single linear “leg spring” and a point mass that is equivalent to body mass (2, 10, 23). The stiffness of the leg spring represents the average pseudostiffness of the overall musculoskeletal system during the ground contact phase. In the literature, this leg stiffness is calculated as the ratio of the peak ground reaction force to the maximum vertical displacement of the center of mass (COM) (12, 23).

It has been shown that human hoppers and runners adjust leg stiffness when expecting a transition in surface stiffness (15, 16). This adjustment results in similar COM dynamics, regardless of surface stiffness. Ferris et al. (16) suggested that neural pathways were responsible for this leg stiffness adjustment.

A study by Moritz and Farley (24) has shown that even when hoppers are surprised by a change in surface stiffness, their leg stiffness changes very soon after touchdown. Leg stiffness changed as early as 52 ms after landing on an unexpected hard surface, while electromyographic (EMG) data did not change until 68–188 ms after landing (24). The authors argued that the rapid change in leg stiffness after landing on an unexpected surface resulted from passive mechanisms, meaning that no neural feedback was necessary for this change.

Several mechanisms have been proposed to explain this passive leg stiffness adjustment. Moritz and Farley (24) suggested that changes in leg stiffness on an unexpected hard surface are due to changes in orientation of the leg segments. The unexpected hard surface forces the joints into more flexed positions, which, in turn, causes a decrease in leg stiffness (13, 14). Similar passive adaptations in leg stiffness as a result of leg orientation have been shown to occur in Guinea fowls running over surfaces that unexpectedly changed in height (7, 8). Intrinsic muscle properties, such as force-length and force-velocity relations, can also provide zero-lag stabilizing effects after perturbations (28), which have been termed “preflexes” (22), for example in standing (32), knee bending (31), and arm function (4). Recently, Hurst et al. (20) proposed another mechanism for passive adaptation to surface stiffness changes in running and hopping robots. They showed that a passive spring, in conjunction with a preprogrammed actuator that adjusts the set point trajectory of this spring as a function of time (and thereby its effective stiffness), has stabilizing effects on the limit cycle of running. Similar mechanisms could play a role in muscle-tendon complexes (MTCs) of human hoppers, with preprogrammed muscle activation changing muscle force over time, independent of the surface underfoot.

Although a number of studies thus suggest that passive mechanisms play a role in adaptations to surfaces with unexpected stiffness (7, 8, 24), it is difficult to fully exclude the effects of neural feedback in experimental studies. The fastest reflexes in hopping take only 35–45 ms (9, 17), and small changes in muscle stimulation might not be detectable with EMG data. Forward dynamic musculoskeletal modeling allows us to examine the effects of passive mechanisms in isolation, since neural feedback loops can be excluded from the model. Furthermore, using a realistic model, including activation dynamics and Hill-type muscle properties, we can study the behavior of the individual elements of the musculoskeletal system during hopping. In this way, we can see how individual muscles and their components react to an unexpected change in surface stiffness.

The goal of this simulation study was first to study whether leg stiffness can change passively, i.e., without neural control adjustments, when a musculoskeletal model lands on an unexpected hard or compliant (soft) surface, and, second, to determine what mechanisms are responsible for this change in leg stiffness. We simulated hopping on soft, hard, and unexpected surfaces and compared the results with experimental data (24).

METHODS

Outline of the simulation study.

The musculoskeletal model used for the simulations is schematically shown in Fig. 1. The model had as input STIM(t), the stimulation of nine muscles of the lower extremity as a function of time, and as output the muscle forces and the resulting kinetics and kinematics of body segments. The interaction with the surface was modeled as a nonlinear spring, in parallel with a damper. STIM(t) was optimized using the sum of squared differences between simulated and measured kinematics of the contact phase of an actual hop (24) as criterion. This was done separately for the contact phase of one representative hop on a soft surface and one on a hard surface. Subsequently, the optimal stimulation pattern for hopping on the soft surface was applied to the musculoskeletal model hopping on the hard surface and vice versa. In this way, it was determined how the mechanical interaction of the model with the unexpected surface affected overall leg stiffness, leg segment dynamics, and muscle function. More details on the model and the optimization procedures are provided below.

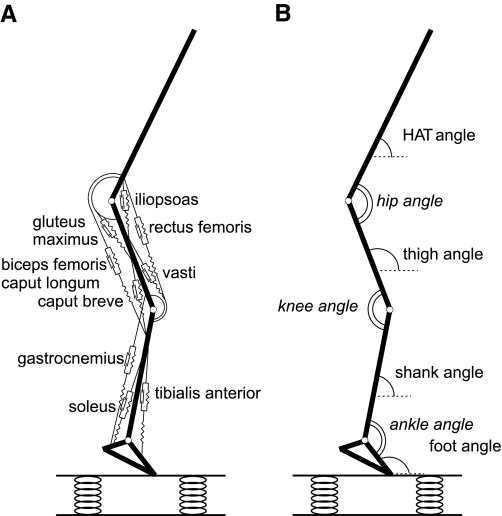
Fig. 1.

A: schematic representation of the musculoskeletal model used in this study. B: definition of joint and segment angles. HAT, head-arm-trunk segment.

Description of the musculoskeletal model.

We used a two-dimensional, forward-dynamic musculoskeletal model, which has been extensively described elsewhere (28, 30). This model has been used successfully in simulation studies of, for example, human vertical jumping and cycling (26, 30). The model consisted of two submodels: a skeletal submodel of four interconnected rigid segments, and a muscular submodel consisting of Hill-type muscles. In the present study, we included m. gastrocnemius, m. soleus, m. tibialis anterior, mm. vasti, m. rectus femoris, m. biceps femoris caput longum, m. biceps femoris caput breve, m. gluteus maximus, and m. iliopsoas (Fig. 1).

The skeletal submodel consisted of a chain of four rigid segments, representing feet, lower legs, upper legs, and head-arms-trunk. The segments were interconnected by frictionless hinge joints. Parameter values for the skeletal model were estimated from the mean anthropometric data of six well-trained male volleyball players (3). The Newtonian dynamic equations of motion of the skeletal submodel were formulated so that the acceleration of the skeletal model could be calculated as a function of position and velocity of the segments, external forces (including gravitational and ground reaction forces), and net muscle moments at the joints (5).

In the muscular submodel, each muscle consisted of a contractile element (CE), a series elastic element (SEE), and a parallel elastic element (PEE). The behavior of SEE and PEE was described by a quadratic force-length relationship, with a strain of 4% at maximum isometric muscle force. For instance, the ankle plantar flexors had a SEE length of 0.24 m (m. soleus) and 0.38 m (m. gastrocnemius), with a peak stretch of ∼1 and 1.5 cm, respectively. The behavior of the CE was more complex: contraction velocity of the CE was determined by CE length, active state q (the relative amount of calcium bound to troponin), and force, with force being directly related to SEE length. SEE length was derived from CE length and MTC length, with the latter being directly related to joint angles. STIM(t) was a one-dimensional representation of the recruitment and firing rate of α-motoneurons and could range between zero and one. Following Hatze (19), active state was related to STIM using a first-order differential equation. In this relation, a correction for length-dependent calcium sensitivity was included (21). Short-range elastic stiffness was not included in our muscle model. However, it has been shown that standard Hill-type models predict muscle force well, also during eccentric contractions, by capturing some effects of short-range stiffness (27). Furthermore, during hopping, we see relatively large changes in joint angles. Therefore, we expect that the effect of short-range elastic stiffness is relatively small. All muscle parameter values of the model were identical to those used previously in the study of van Soest et al. (29).

In total, the model was mathematically described by a set of 28 coupled nonlinear first-order differential equations. Given the initial state and STIM as a function of time, the resulting movement could be calculated through numerical integration. The numerical integration routine used was a variable order, variable step size, Adams-Bashford predictor, and Adams-Moulton corrector (25).

Experimental data.

In the study of Moritz and Farley (24), 10 subjects hopped on a continuous hard surface, a continuous soft surface, and once on an unexpected hard surface. Experimental kinematic and kinetic data from one representative subject of that study were used as reference data to model the foot-surface interaction, to calculate initial conditions, and to serve as a criterion for optimization of STIM(t) on the hard and the soft surface. See Ref. 24 for more details about the data collection and processing.

Description of the foot-surface interaction.

To make the model represent human hopping on different surfaces, we simulated the viscoelastic interaction between foot and surface on both the soft and the hard surface. The coefficients for these equations were based on an optimized fit of the subject's fifth metatarsophalangeal joint (MTP5) movement after touchdown as a function of the ground reaction force. The following equations were derived.

1) Soft surface:

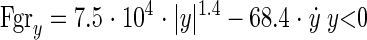2) Hard surface:

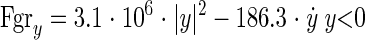where y is the vertical displacement (m) of the base of the model (representing MTP5) relative to the initial surface position, and Fgr_y is the vertical ground reaction force (N).

Calculating the initial conditions.

Initial values for segment angles, angular velocities, and vertical velocity of the base (MTP5) were derived from the experimental data. To calculate initial values for the state of the muscles, an equilibrium situation (constant CE length and active state q) was defined using the experimental net joint moments of the subject at touchdown, which were close to zero. As an infinite number of muscle stimulation combinations could have produced these joint moments, we defined the following optimization criterion. The initial muscle stimulation had to result in 1) net joint moments that were close to zero, and 2) simulated segment angles for the first 30 ms that best resembled the movement of the subject, without changing the muscle stimulation, according to:

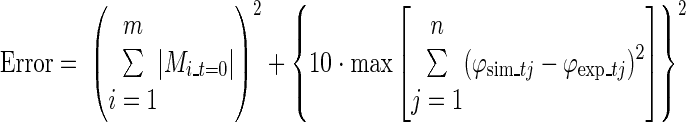where m is the number of joints, M_{i_t=0} is the moment at joint i at touchdown, n is the number of segments, ϕ_{sim_tj} is the angle of segment j for the first few time steps t of 0.01 s from 0 to 0.03 s after touchdown, and ϕ_{exp_tj} is the angle of segment j at time step t of the experiment (sample frequency 100 Hz). The first term was only included when |M_{i_t=0}| for at least one of the joints exceeded 2 Nm.

Optimization of STIM(t).

After setting up the initial conditions, STIM(t) was optimized to match the kinematics, mechanical energy, and duration of the experimental hops. The optimization criterion was a weighted sum of 1) the difference in segment angles over time between the model and the subject, 2) the difference in ground contact time between the model and the subject, and 3) the difference in total mechanical energy due to height and vertical velocity of the COM between touchdown and takeoff. This mechanical energy was the sum of the gravitational potential energy and the kinetic energy of the COM due to vertical velocity. These criteria were combined in the following objective function:

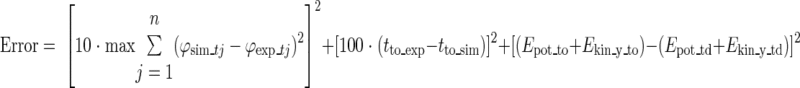where n is the number of segments; ϕ_{sim_tj} and ϕ_{exp_tj} are the angles of segment j at time step t of the model (sim) and the experiment (exp) respectively; t_{to_exp} and t_{to_sim} are the instants of toe-off (to) of the experiment and the model; E_{pot_to} and E_{kin_y_to} are the potential (pot) and kinetic (kin) energy of the model at toe-off; and E_{pot_td} and E_{kin_y_td} are the potential and kinetic energy at touch down (td). The weighting of the factors (i.e., 10 and 100) was added to make all values of the same order of magnitude. The optimization criteria and weighing factors were chosen such that a good fit with experimental data was achieved, both in terms of kinematics, kinetics, and energetics. Due to the numerical intensity of the simulations, we were unable to perform a full sensitivity analysis to these optimization criteria and weighing factors. We did, however, perform extensive pilot simulations to be confident that our main findings did not depend on the exact parameter choices made. The dynamic optimization problem was solved using simulated annealing (18).

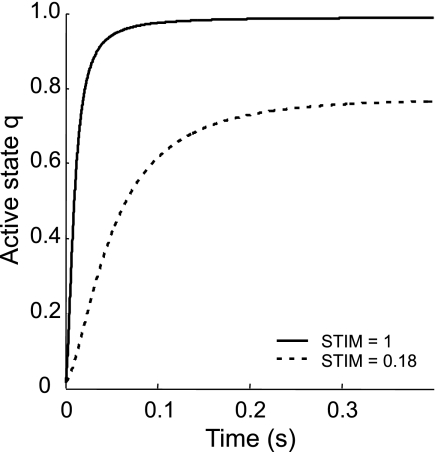
The STIM for each muscle was allowed to switch twice, instantaneously, either to 0.18 (“on”) or to 0 (“off”). This intermediate value of STIM was chosen to match the kinetics observed during human hopping, which is a submaximal activity. While previous studies of maximal height jumping have used a STIM value of 1.0 (e.g., Refs. 3, 30), such maximal muscle activation resulted in the ground reaction force increasing much faster than observed in hopping subjects. Extensive pilot simulations showed that a value of 0.18 resulted in a realistic rate of increase of ground reaction force and the closest fit with experimental kinematic data. This value of 0.18 resulted in slower rise of active state q with only 25% reduction in maximal active state q (Fig. 2) due to the nonlinear activation dynamics (19). Thus we achieved a more realistic force rise with little change in peak force amplitude.

Fig. 2.

Active state q vs. time. At time 0, STIM (stimulation of nine muscles of the lower extremity) changes from 0 to either 1 or 0.18. Note that, when STIM is 0.18, the active state q rises slower than when STIM is 1 and reaches a steady state of ∼0.8.

Surfaces of unexpected stiffness.

After STIM(t) had been optimized separately for the hard and the soft surface, hopping on the unexpected surfaces was simulated. The model with STIM(t) optimized for the soft surface (expected soft) was put on a hard surface without changing initial geometry, initial muscle stimulation, or STIM(t) during ground contact (unexpected hard). Analogously, the model optimized for the hard surface (expected hard) was put on a soft surface (unexpected soft).

Definitions.

Leg compression, (pseudo) leg stiffness, joint stiffness, and muscle stiffness were defined following others (12, 23). Leg compression was defined as the decrease in distance between COM and toes and calculated by subtracting the surface displacement from the vertical displacement of the COM. Leg stiffness was defined as the slope of the relationship between ground reaction force and leg compression; joint stiffness as the slope of the relationship between net joint moment and joint angle, and muscle stiffness as the slope of the relationship between muscle force and MTC length. Changes in leg, joint, and muscle stiffness were qualitatively compared between conditions. Midstance was defined as the instant that COM reached its lowest value.

RESULTS

Hopping on expected surfaces.

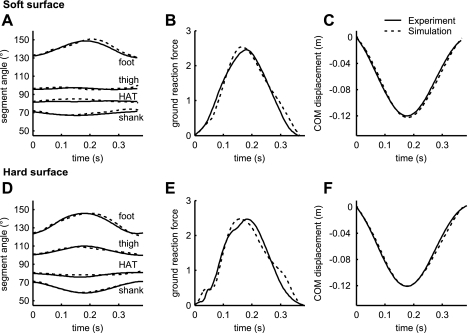
Kinematics, ground contact time, and mechanical energy of optimal hops of the model on the expected soft and hard surfaces corresponded well with experimental data, showing that the model could replicate experimental data (Fig. 3). The root mean square (RMS) error of the segment angles averaged over the four segments was 1.69° for the hop on the soft surface and 1.19° for the hop on the hard surface (Fig. 3, A and D). The ground contact time of the model was similar to experimental data, both on the soft surface (368 vs. 365 ms) and on the hard surface (376 vs. 385 ms; Fig. 3, B and E). The mechanical (potential + vertical kinetic) energy at toe-off was close to the energy at touchdown on both surfaces; the change in energy for both the soft and the hard surface was <0.1%, indicating that there was virtually no increase or decrease in hopping height.

Fig. 3.

Time histories of segment angles with respect to the horizontal (A and D), ground reaction force normalized to body weight (B and E), and center of mass (COM) displacement (C and F). Experimental data are derived from hops of one representative subject, with a low-pass filtering of the marker data at 7 Hz (24). Simulation data are derived by optimizing muscle stimulation STIM(t) to make the model match the experimental data, separately for a soft (A–C) and a hard surface (D–F).

Ground reaction force and COM displacement also corresponded well with experimental data. The RMS errors for the ground reaction force normalized to body weight were 5.9% of the maximal force value for the soft surface and 8.1% of maximal force for the hard surface, respectively (Fig. 3, B and E). The RMS error for COM displacement was 3.5 mm on the soft surface and 3.2 mm on the hard surface (Fig. 3, C and F). We concluded that the model satisfactorily represented the features of the real system that are salient for hopping.

Transition to unexpected hard and soft surfaces.

When the model with STIM(t) optimized for the soft surface landed on the unexpected hard surface, it passively adjusted and performed a successful hop. The same was true for the transition from the hard surface to the unexpected soft surface. In all conditions, anteroposterior displacement of the COM was small (<2 cm) and not notably affected by the unexpected surfaces. For clarity, the findings for the transition from the soft surface to the unexpected hard surface will first be described in detail, after which the findings for the transition from the hard surface to the unexpected soft surface will be summarized. The figures have been grouped so that both the unexpected hard surface data (Figs. 4–6, top) and unexpected soft surface data (Figs. 4–6, bottom) are shown together for comparison.

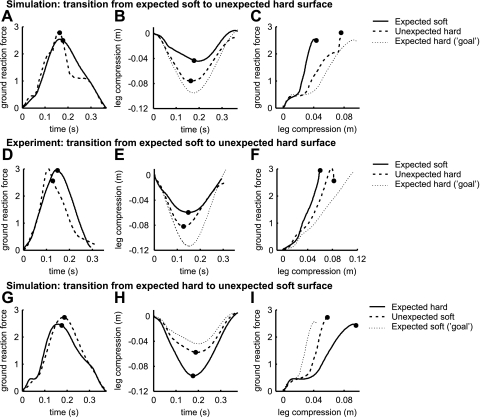
Fig. 4.

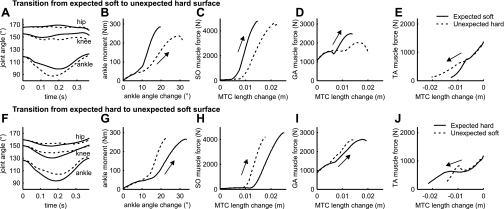
Time histories from touch down to toe-off of ground reaction force normalized to body weight (A, D, and G) and leg compression (B, E, and H). C, F, and I: ground reaction force vs. leg compression, plotted from touch down to midstance. D, E, and F: for comparison, experimental data are shown from Fig. 7A of Moritz and Farley (24). No experimental data were available on unexpected soft surfaces. •, Midstance.

Fig. 6.

Time histories from touch down to toe-off of joint angles (A and F), ankle moment vs. ankle angle change from touch down to midstance (B and G), and muscle force vs. muscle-tendon complex (MTC) length change for m. soleus (SO; C and H), m. gastrocnemius (GA; D and I), and m. tibialis anterior (TA; E and J). Arrows indicate the progression in time.

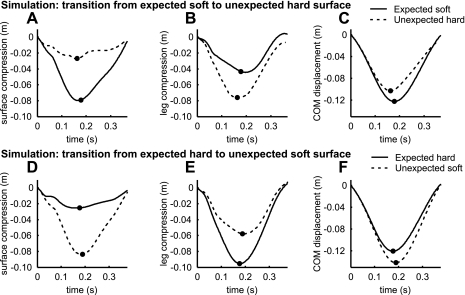
Upon landing on the unexpected hard surface, the leg stiffness passively decreased compared with the expected soft surface. The ground reaction force was only slightly higher in the first part of the hop on the unexpected hard surface than in the hop on the expected soft surface (Fig. 4A). The leg compression was substantially larger (Fig. 4B), so leg stiffness was lower when the model landed on the unexpected hard surface (Fig. 4C). The change in leg stiffness was comparable to the experimental results of Moritz and Farley (24) (Fig. 4, D–F). The increase in leg compression (also shown in Fig. 5B for better comparison) compensated almost entirely for the decrease in surface compression (Fig. 5A), which, summed together, resulted in a downward displacement of COM on the unexpected hard surface (Fig. 5C) that was close to that on the expected hard surface (Fig. 5F).

Fig. 5.

Time histories from touch down to toe-off of surface compression (A and D), leg compression (B and E) (similar to Fig. 4, B and E), and COM displacement (C and F).

Figures 4 and 5 also show the degree to which the model adapted to the unexpected hard surface, with no change in muscle activation. The thin dotted line in Fig. 4, B and C, shows the modeled data on the expected hard surface, which can be considered a perfect adjustment, or “goal”. The passive adaptation of the model to the unexpected surface covers more than one-half of the desired adjustment. If no adaptation in leg stiffness had occurred, then leg compression would have been similar to that on the expected soft surface (Figs. 4B and 5B), resulting in a COM displacement that would have been much smaller than desired.

The larger leg compression on the unexpected hard surface was a result of increased flexion in the ankle and knee joint and, to a lesser extent, in the hip joint (Fig. 6A). As a result, joint stiffness was lower at all joints. Because the reduction in stiffness was most pronounced at the ankle (Fig. 6B), and in line with literature (13, 14), we will focus on the ankle joint. Figure 6, C–E, shows the behavior of the muscles around the ankle. In all ankle muscles, the average slope of the force vs. MTC length curve, i.e., the effective “muscle stiffness”, was lower on the unexpected hard surface than on the expected soft surface. Thus the rise in muscle force, relative to the change in MTC length, was decreased on the unexpected hard surface. This will be explored further in the discussion.

The findings for transition from the expected hard surface to the unexpected soft surface were opposite to those for the transition from the expected soft surface to the unexpected hard surface, demonstrating that the model could passively adjust to both harder and softer surfaces. The unexpected soft surface decelerated the foot less, resulting in smaller joint flexions during early stance and a straighter and stiffer leg. On the unexpected soft surface, the initial ground reaction force was close to normal (Fig. 4G), but leg compression was much smaller than on the expected hard surface (Fig. 4H), resulting in higher leg stiffness than on the expected hard surface (Fig. 4I). Because of this increase in leg stiffness, the COM displacement did not change much, despite a large decrease in surface stiffness (Fig. 5, D–F). Also, the joints flexed less (Fig. 6F), and joint and effective muscle stiffness were larger (Fig. 6, G–J) than on the expected hard surface.

DISCUSSION

Our results show that leg stiffness passively adjusts to unexpected surface changes. The results of the transition from the expected soft to the unexpected hard surface are qualitatively similar to experimental results (24). This simulation study demonstrates that neural feedback is not a prerequisite for a change in leg stiffness, which could not be conclusively demonstrated in previous experimental studies. Moreover, this study demonstrates that passive adjustments are robust and occur on both unexpected hard and unexpected soft surfaces.

Our results support the argument of Moritz and Farley (24) that the rapid change in leg stiffness is the result of passive mechanisms and that neural feedback is not necessary for this change. What passive mechanism causes this change in leg stiffness? As mentioned in the Introduction, three candidate mechanisms have been suggested: 1) geometry effects (24); 2) “preflexes”, i.e., stabilizing effects of intrinsic muscle properties, such as force-length and force-velocity relations (22, 24, 28); and 3) stabilizing effects of a time-based actuator in series with a spring (20). The latter two both focus on joint stiffness that, together with leg geometry, determines leg stiffness (13). We will discuss all three possible mechanisms in more detail. For our explanation, we will focus on the unexpected hard surface compared with the expected soft surface. The same explanation, but with all changes in the opposite direction, holds for the transition from the expected hard to the unexpected soft surface.

Geometry of the leg has been shown to play an important role in determining leg stiffness (13). Farley et al. (13, 14) argue that greater joint flexion leads to a decrease in leg stiffness for two reasons. First, the ground reaction force has larger moment arms about the joints; and, second, a given joint angular displacement leads to a greater change in leg length, leading to a nonlinear softening mechanical advantage governed by the sine of the joint angle. Thus landing in a more flexed position leads to a large reduction in leg stiffness, which subjects choose as a compensation strategy when landing on stiffer surfaces (13). However, when landing on an unexpected surface, the leg geometry at touch down is not changed. The changes in geometry can only affect leg stiffness if the leg is flexed more than it would normally be on an expected surface. Certainly this occurred over time on the unexpected hard surface. Geometry effects cannot explain, however, the differences in stiffness among conditions at the same leg compression. The leg force-displacement curves (e.g., Fig. 4C) show that, at a given leg compression (e.g., 0.03 m), the leg stiffness (slope) is much less for the unexpected hard surface compared with the expected soft surface. With leg compression being closely related to leg geometry, this shows that leg stiffness changed independent of leg geometry. Since we are most interested in initial adaptations to the new surface occurring shortly after landing, we conclude that changes in muscle stiffness dominate the adaptations compared with the changes in leg geometry. The initial changes in leg stiffness must, therefore, result from changes in joint and (consequently) muscle stiffness, rather than from geometry effects.

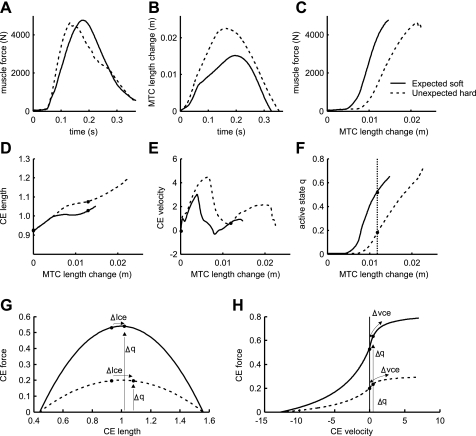
Force-length and force-velocity relationships have been shown to have a stabilizing effect in human motion (e.g., Refs. 4, 22, 28, 31, 32), by causing a zero-lag effect of changes in kinematics on changes in muscle and joint stiffness. In order for muscle stiffness to be lower on the unexpected hard surface, a smaller increase in muscle force must occur for a given change in MTC length. Figure 7 shows the model's m. soleus force (Fig. 7A) and MTC length change (Fig. 7B) vs. time, muscle force vs. MTC length change (Fig. 7C), as well as the underlying CE length and CE velocity vs. MTC length (Fig. 7, D and E), and the CE force-length and force-velocity relations (Fig. 7, G and H). CE length reaches higher values on the unexpected hard surface than on the expected soft surface (Fig. 7D). However, since CE length is around optimum, the muscle is in a relatively flat area of the force-length curve, and changes in CE length have very little influence on muscle force and thus on muscle stiffness (Fig. 7G). CE lengthening velocity is also higher on the unexpected hard surface than on the expected soft surface (Fig. 7E). In both cases, the stretch velocity rapidly increases and then decreases, with higher peak velocity on the unexpected hard surface. According to the force-velocity curve (Fig. 7H), this leads to an increase in the muscle force per MTC length change, followed by a decrease, as shown in Fig. 7H. Both effects are small and opposite, resulting in no net effect on the effective muscle stiffness.

Fig. 7.

Time histories of m. soleus force (A), MTC length change (B), and muscle force vs. MTC length change (C). D: contractile element (CE) length normalized to optimal length. E: CE velocity. F: active state q vs. MTC length change of m. soleus. Data in D–F are plotted as a function of MTC length change to highlight the effect on effective muscle stiffness shown in C. Force-length (G) and force-velocity (H) relationships for the active states q indicated in F are shown. These correspond to an MTC length change of 0.012 m relative to touch down. The effects of changes in CE length (Δlce) and CE velocity (Δvce) on muscle force are indicated along the force-length and force-velocity curves, whereas the effect of change in q (Δq) on muscle force is indicated by the height of the curve. Note that force rise as shown in C mainly depends on the rise in q (F).

The effect of muscle active state q (Fig. 7F) on force is much larger than the effects of muscle length or velocity. Muscle active state q rises as a result of stimulation STIM(t), which is fixed in time, and scales the force-length and force-velocity curves, as illustrated in Fig. 7, G and H. The force shifts along the force-length and the force-velocity curve due to changes in CE length and velocity, but at the same time the curves themselves increase rapidly in height due to changes in q. Muscle active state q increases the force so much that it overshadows the effects of CE length and velocity. This shows most clearly from the similarity between force (Fig. 7C) and active state q (Fig. 7F). On the unexpected hard surface, the joints flex more rapidly, resulting in faster muscle length changes. Since the rise in q is mainly fixed in time,1 and thus unaffected by ground stiffness changes, the more rapid joint flexion on the unexpected hard surface does not coincide with a matching increase in q. Thus, for a given change in joint angle, muscle force has risen less on the unexpected hard surface and joint moments are lower. In effect, the stiffness of the leg has been reduced.

This stabilizing effect of time-based q on muscle stiffness, and thereby on joint and leg stiffness, is similar to the mechanical mechanism as described by Hurst et al. (20). They developed dynamic models of two hoppers: one with a prismatic leg, and one with a linear rotational spring at the knee. The springs in both models were connected in series with a time-dependent set point adjustment, representing the net effect of leg muscle actuation. The set point trajectory was chosen such that the combined action of spring and actuator resulted in a springlike effect, with higher stiffness than the one actually present in the spring. In other words, the time-dependent actuator represented the “for-that-surface” preprogrammed muscle activation history. They found that this mechanism provided open-loop stabilizing effects in the first part of stance of a running spring-mass model, by effectively adjusting leg stiffness. Although in our simulation CE does not shorten but lengthens during the first part of stance (causing the overall MTC stiffness to be lower than the physically present tendon stiffness), it lengthens more on an unexpected hard surface than on an expected soft surface, thereby decreasing stiffness. Both in our simulations and in the paper of Hurst et al. (20), the time-dependent actuator in series with a tendon-spring results in passive leg stiffness adjustments to unexpected surfaces.

Passive adaptation to changes in surface stiffness may complement the role of neural pathways, which have been suggested by Ferris et al. (16) to be responsible for adjusting leg stiffness during running. They predicted that if an unexpected change in surface stiffness occurred, this would substantially disrupt a runner's movements. The present study, although performed on hopping, shows that leg stiffness can be changed passively, which may help to simplify the adaptation to sudden changes in surface. Neural responses are obviously helpful in the second part of stance (24), for example to prevent the energy content of the system from changing. Also, if the change in surface stiffness is foreseen, then active neural control can lead to anticipatory changes that can improve the adaptation to the new surface (24).

The passive adaptation of the musculoskeletal system to unexpected changes in surface stiffness demonstrates its intrinsic robustness to perturbations. It shows that it is the complexity of the musculoskeletal system compared with a simple spring-mass model that simplifies the neural control necessary to overcome perturbations. This result is in line with recent ideas that it is the interplay between neural control, body dynamics, and intrinsic muscle properties that together result in stable and agile locomotion on varying terrains (1). Moreover, our results show that the neural system does not need to control leg stiffness per se, since the same stimulation pattern can result in different leg stiffness values, dependent on the surface.

The passive adaptation to unexpected surfaces may be important when negotiating disturbances. In the presence of perturbations, controlled muscles do not operate as simple springs, but can passively adjust their stiffness. Therefore, modeling hopping or running with simple springs alone may not yield realistic behavior in the presence of unexpected surfaces or disturbances.

In conclusion, this study shows that, in simulated human hopping, leg stiffness passively adjusts to both unexpected hard and soft surfaces, which demonstrates that neural feedback is not necessary for this initial change. The passive changes in leg stiffness are not caused by geometry effects at touchdown, but by subsequent changes in joint angles and muscle length due to the interaction with the unexpected surface and the fixed timing of muscle stimulation. The preprogrammed muscle stimulation pattern results in increases in muscle force that are fixed in time and independent of surface stiffness, while leg compression is simultaneously altered by the interaction with the unexpected surface underfoot. The passive adaptation to unexpected surfaces may be important when negotiating disturbances, in which case preprogrammed muscle stimulation may combine with leg mechanics to create a robust system capable of rejecting a wide range of surface perturbations.

GRANTS

This research was supported by two Gerrit Jan van Ingen Schenau promising young scientist awards and the VU University Fund (to M. M. van der Krogt and W. W. de Graaf), by National Institute of Arthritis and Musculoskeletal and Skin Diseases Grant AR-44008 (to C. T. Farley), and by an American Society of Biomechanics Grant-in-aid (to C. T. Moritz).