On the Tilable Nature of Virus Capsids and the Role of Topological Constraints In Natural Capsid Design

Abstract

Virus capsids are highly specific assemblies that are formed from a large number of often chemically identical capsid subunits. In the present report we ask to what extent these structures can be viewed as mathematically tilable objects using a single two-dimensional tile. We find that spherical viruses from a large number of families – eight out of the twelve studied – qualitatively possess properties that allow their representation as two dimensional monohedral tilings of a bound surface, where each tile represents a subunit. This we did by characterizing the extent to which individual spherical capsids display subunit-subunit (1) holes, (2) overlaps and (3) gross structural variability. All capsids with T values greater than 1 from the Protein Data Bank, with homogeneous protein composition, were used in the study. These monohedral tilings, called canonical capsids due to their platonic (mathematical) form, offer for the first time a mathematical segue into the structural and dynamical understanding of not one, but a large number of virus capsids. From our data, it appears as though one may only break the long-standing rules of quasi-equivalence by the introduction of subunit-subunit structural variability, holes and gross overlaps into the shell. To explore the utility of canonical capsids in understanding structural aspects of such assemblies, we used graph theory and discrete geometry to enumerate the types of shapes that the tiles (and hence the subunits) must possess. We show that topology restricts the shape of the face to a limited number of five-sided prototiles, one of which is the “bisected trapezoid” that is a platonic representation of the most ubiquitous capsid subunit shape seen in nature (the trapezoidal jelly roll motif). This motif is found in a majority of seemingly unrelated virus families that share little to no host, size or amino acid sequence similarity. This suggests that topological constraints may exhibit dominant roles in the natural design of biological assemblies, while having little effect on amino acid sequence similarity.

I. Introduction

The genomic material of a majority of viruses is enclosed and protected by spherical capsids. These spherical capsids are icosahedral in symmetry and are composed of protein subunits that are often chemically identical. The number of subunits that exist in a capsid (i.e., the size) is generally described by the triangulation number T, where a spherical capsid of triangulation number T will possess 60T subunits. The T number must satisfy the equation T = h² + hk + k², where h and k are non negative integers (additionally h + k > 0). Often, capsid subunits of a specific virus family assemble into capsids of highly specific size or T value. For example, sesbania mosaic virus capsid subunits are known to spontaneously form T=3 spherical capsids [1], while the subunits belonging to the birnaviridae family form larger, T=13 capsids [2]. These rules of quasi-equivalence, which are at the core of describing the organization of such capsids, have been long standing and were proposed by Caspar and Klug in 1962 [3].

As indicated by the rules of quasi-equivalence, even the smallest virus capsids must be made up of at least sixty protein subunits, each containing thousands of atoms themselves, making the analysis of structural and dynamical properties of these systems in all-atom form computationally inapproachable. For example, state of the art numerical simulations of a T=1 all-atom STMV capsid were performed for more than 50 nanoseconds at the approximate rate of 1.1 nanoseconds per day on 48 processors [4]. Although a testament to parallel processivity, the simulation was also a testament to the current inadequacies, for virus capsids must be simulated for more than a millisecond (100,000 times more) to record important aspects such as assembly and structural changes. Furthermore, biochemical and biophysical laboratory studies of important events such as capsid maturation and assembly offer few clues to the dynamic mechanisms involved. These complications have motivated a plethora of theoretical attempts aimed at understanding virus capsids using necessary and simplifying geometric assumptions regarding the nature of capsid assemblies.

The use of simplified geometric models such as discs on a sphere [5, 6], simple van der Waals spheres [7], Stock-mayer fluids [8], trapezoidal subunits [9, 10], tiles [11] and simple bonding units [12–14] has enabled the application of physics and mathematics in the exploration of various capsid phenomena such as assembly kinetics, capsid subunit stoichiometry, quasi-equivalence and assembly nucleation events. Although many of these models accurately describe specific phenomenological aspects of a capsid (such as discs on a sphere explaining the emergence of icosahedral symmetry [5, 6]), a simplified capsid model that represents a broad array of properties of many natural capsids in an accurate manner (i.e., a model possessing “transferability”) has yet to be described.

We are interested in understanding the extent to which simplified models may represent spherical capsids in nature. This problem will be addressed in the first half of the paper, where we will show that a large number of virus capsids (“group 1” capsids, see I) found in nature can, indeed, be modeled as simplified two-dimensional tilings of a bound surface by a single prototile, i.e., we will show that a large number of virus capsids may be represented by monohedral tilings. Capsids which follow these monohedral tilability rules (along with the quasi-equivalent rules) we call canonical capsids. Mathematical studies of these monohedral tilings (canonical capsids) are expected to relate the physical and structural properties obtained directly to a large number of capsids found in nature (corresponding to the group 1 capsids).

As an example of one mathematical application, the second part of our paper asks: What are the shapes available to a spherical capsid subunit as dictated by topological rules? Since the subunit is directly represented by a canonical capsid prototile, one only needs to ask how topology dictates the types of tiles that the canonical capsid may have. This is answered using graph theory, tiling theory, and the rules of spherical capsid equivalence laid down by Caspar and Klug [3]. We show that the expected canonical capsid subunit shape strongly reflects the trapezoidal subunit shapes found in natural capsids.

II. Materials and Methods

Virus capsids analyzed

For our analyses, we used all capsids present in the VIPERdb virus capsid repository (as of April 2007)[15] comprised of chemically identical subunits with triangulation numbers greater than one. Capsids denoted by the following PDB IDs (also VIPERdb IDs) were used in the analysis (65 in number): 1aq3, 1aq4, 1auy, 1bms, 1c8n, 1cwp, 1ddl, 1dwn, 1dzs, 1e57, 1e7x, 1f15, 1f2n, 1f8v, 1frs, 1fr5, 1gav, 1gkv, 1gkw, 1ihm, 1js9, 1kuo, 1laj, 1mst, 1mva, 1mvb, 1ng0, 1nov, 1ohf, 1ohg, 1opo, 1qbe, 1qgt, 1qjz, 1sva, 1sid, 1sie, 1smv, 1u1y, 1w39, 1wce, 1×35, 1za7, 1zdh, 1zdi, 1zdj, 1zdk, 1zse, 2b2d, 2b2e, 2b2g, 2bbv, 2bu1, 2frp, 2fs3, 2fsy, 2ft1, 2gh8, 2ms2, 2tbv, 4sbv, 5msf, 6msf, 7msf, fhv. (The structure named fhv is not present in the PDB and was deposited into the VIPERdb as a personal communication.)

Definition of a monohedral tiling

We may say that a two-dimensional monohedral bound tiling is one where identically shaped (congruent) tiles come together onto a bound (sphere-like) surface such that no tile-tile overlaps and holes are found. In slightly more specific terms, the term “monohedral two dimensional tiling” refers to the classical strongly balanced tiling by a single prototile. Strongly balanced tiling means that each tile must be a topological disk (polygon), the assembled tilings must represent a 2-manifold (tiles must not overlap), edges can not be disconnected (i.e., its an edge-edge tiling), and they must be uniformly bounded and balanced (introduced by Grünbaum and Shepherd to preclude “paradoxical” tilings in their authoritative treatise on tilings and patterns [16]). Monohedrality imposes the need for just one tile shape to exist within the tiling, however, each instance of this shape need not be related by any symmetry operation. For an understanding of edge-to-edge monohedral tilings please refer to the review by Grünbaum and Shephard [17].

Characterizing tilability

We first need to characterize the extent to which virus capsids display holes and overlaps. Although this may be qualitatively done visually, we chose to develop a simple metric for quantitative characterization. In this method, we projected each protein atom present in the all-atom capsid structure onto a sphere whose radius equals the average radius of the capsid shell (depicted in Figure 1). We then cast a net of dots, or “dot matrix” onto the shell using a 1 Å grid, and calculated the percentage of dots that were present within holes and subunit-subunit overlaps. The volume of each subunit was defined by the van der Waals radii of the constituent atoms along with a 1.4 Å addition accounting for water. These percentages are obtained for each virus capsid.

Fig. 1.

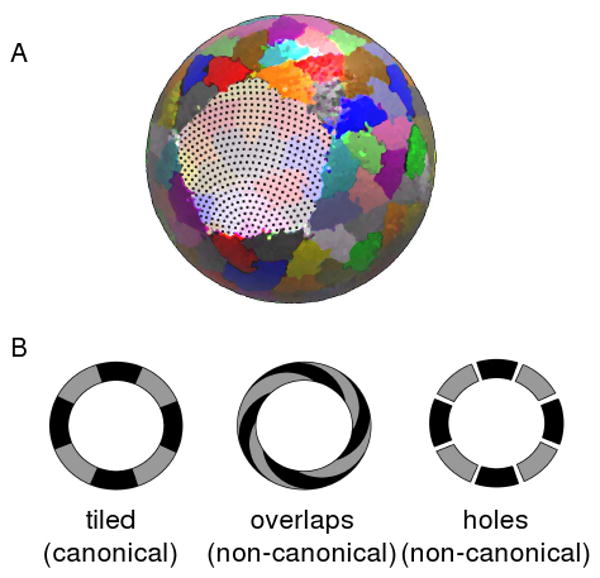
Analyzing the tilability of a capsid. (a) The three dimensional all-atom model is projected onto a sphere of average shell radius (colored to represent individual subunits) upon which a net, or dot matrix, is cast (visible in the subunit cleared area). These dots will be used in calculating the (area-wise) percentage of holes and overlaps in the capsid shell. (The above projected capsid was derived from PDB ID: 1smv). (b) The presence of either holes (right) or subunit-subunit overlaps (middle) will result in the inability to represent these structures as well behaved two dimensional tilings (left).

Characterizing monohedral tilability

Assuming that the capsid is tilable, monohedral tilability is found when the shape of each tile (or subunit) is the same (or congruent). To investigate tile congruence, we look at variability within subunits in a capsid, i.e,. we structurally compare subunits within the asymmetric unit of the crystal structure to each other (since the asymmetric unit possesses the maximally different structures within the crystal structure). Note that our interest lies in characterizing structural changes in the entire subunit, and not localized conformational changes which alter the inter-subunit interactions in an otherwise structurally rigid subunit, e.g., the order-disorder transitions in TBSV (reviewed in [18]). This is because those structural changes may be manifested in the tiling as dihedral angle changes.

Characterizing the shape of the capsid subunit

In the final section of this report, we use topology and tiling theory to compile a list of projected (two dimensional) shapes available to the spherical virus capsid subunit.

III. Results and Discussion

Tilability of natural spherical capsids

The extent to which capsids possess any of the three properties: (1) holes, (2) overlaps once projected onto a sphere, and (3) architectural variability is used as a metric for tilability.

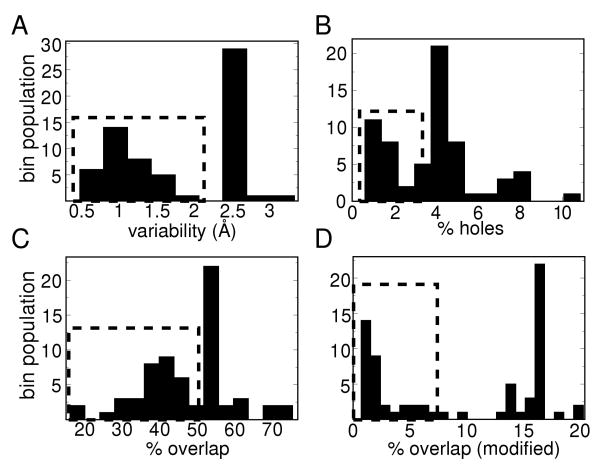
Using methods described in the previous section, four values were calculated for each capsid and plotted as histograms in Figure 2. The four graphs probe the following four properties: (a) monohedrality (subunit variability within a capsid measured by an averaged RMSD value in Å), (b) the amount of breaks within the capsid shell (% holes), (c) the percentage of subunit-subunit overlap within the capsid, and (d) the percentage of gross subunit overlap (which was calculated by first shrinking each pruned subunit [26] by a scaling factor of 0.83 and then calculating the percentage overlaps without the 1.4 Å addition). The last graph was used to differentiate between those capsids that have normal overlaps – caused by interdigitation of neighboring residues into each other at the subunit-subunit interfaces – and gross structural (subunit-subunit) overlaps. It is clear that even in the most well behaved 2D representable virus capsid, residue-residue interdigitations are inevitable; it is only the gross subunit-subunit overlaps that pose a hindrance to 2D tiling representations. In all of the metrics used, low values indicate that the capsid possess little structural variability, negligible holes or negligible overlaps.

Fig. 2.

There are a large number of spherical capsids (highlighted by the dashed rectangles), that possess one of the three requirements of monohedral tilability.

It is immediately evident from the histograms that there is one group of capsids (highlighted by the dashed squares), where at least one of the three properties of monohedral tilability are possessed. The next question is: do some capsids possess all three properties (making them representable by monohedral tilings)?

The average % overlap (modified), % holes and subunit structural variability were calculated for each virus family and these values were plotted against each other, resulting in the three graphs in Figure 3 a,b and c. These graphs indicate that all three properties are positively correlated with each other. Conversely, as we move away from any one of the three properties, the other two properties tend to weaken too, with the exception being the families tetraviridae and hepadnaviridae.

Fig. 3.

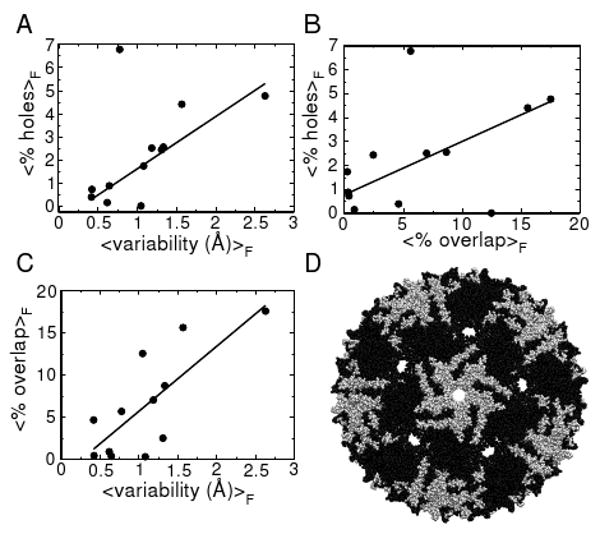
(a,b,c) The dependence of one of three requirements for monohedral tilability is plotted versus each of the others using family averaged values. The solid lines are added to emphasize the trends. (d) An example of a capsid belonging to the Leviviridae family (PDB ID: 1mst), which violates all of the requirements of monohedral tilability, as indicated by excessive overlap of black and white subunits and large holes at five- and pseudo six-fold symmetry axes (Subunit coloring: A,B: black; C: white).

It is evident that there are capsids (belonging to families in Group 2 in Table I) that present either high structural variability, subunit-subunit overlaps (tetraviridae), holes (hepadnaviridae), or all three characteristics (leviviridae and polyomaviridae) and prevent them from being represented as monohedral 2D bound tilings, or canonical capsids. A levivirus has been represented in Figure 3 d as an example of the holes and overlaps found in group 2 capsids.

Table I.

The list of families studied along with their triangulation numbers (T), average percentage (modified) overlap_m values (% O), average percentage holes values (% H) and average subunit variance in Angstrom units (V) within each family. The line divides the families into two groups: (1) families whose capsids are representable by monohedral tilings (with relatively low % O, % H, V), and (2) capsids that cannot be represented as monohedral tilings, i.e., capsids that possess holes, gross overlaps and subunit variability.

Group	Family name	T	%O	%H	V
1	Birnaviridae	13	0.350	0.870	0.648
	Caliciviridae	3	7.002	2.502	1.189
	Nodaviridae	3	4.632	0.382	0.421
	Sobemovirus	3	0.757	0.218	0.605
	Tombusviridae	3	0.421	0.717	0.426
	Tymoviridae	3	0.242	1.455	1.075
	Siphoviridae	7l	3.860	2.777	1.138
	Bromoviridae	3	2.253	3.916	1.175
2	Leviviridae	3	15.191	4.320	2.028
	Polyomaviridae	7d	16.943	5.033	2.524
	Tetraviridae	4	12.504	0.001	1.052
	Hepadnaviridae	4	5.653	6.769	0.780

Importantly, there are a large number of capsids (capsids belonging to 8 of the 12 families studied; the first group in Table I) that possess all three qualities of monohedral tilability and “reside” within all the dashed-line boxes in Figure 2. These capsids, may be represented by bound monohedral tilings that we call canonical capsids.

Our interest now is to show that predictions made about these discrete mathematical models (canonical capsids) can, indeed, be related back to the capsids belonging to families in Group 1 of Table I.

Definition of the canonical capsid

Canonical capsids are monohedral tilings/polyhedra where the tiles/faces within one polyhedron are related to each other under the rules of quasi-equivalence [3]. Spherical capsids adhering to this paradigm possess 60T number of subunits, and may also be thought of as groupings of 12 pentamers and 10(T − 1) hexamers. The manner in which one may go about making a Caspar-Klug capsid is by starting off with a hexagonal lattice and, based on a set of rules, converting specific hexagons into pentagons in a processes that introduces curvature (or a disclination) to the surface. With these concepts in mind, we can characterize the types of two dimensional (projected) shapes that a subunit must possess in order to assemble into a canonical capsid of a specific T value.

Characterizing the subunit shape

Characterizing the types of shapes available to the canonical capsid subunit will be attempted by sequentially answering two more tractable questions. First, we will find the number of edges (σ) that the canonical capsid prototile may possess. Then, we will ask what the number of tiling shapes that those σ-sided tiles may possess. However, we need to formulate a representation of the subunit that enables these questions to be answered.

Representing the subunit

Figure 4 (a) shows a representation of the prototile with one quasi-equivalent vertex (circled), two straight edges, and one curved edge. The curved edge may be bisected by any number of 3-valent vertices (allowing this structure to have an arbitrary number of edges/vertices). This has been done so as not to limit the number of shapes of the tile (dictated by the number of vertices or edges). Each quasi-equivalent vertex may be either five or six valent as reflected by the two clusters (capsomeres) that are either five or six in number (Figure 4 b and c). The number of vertices and edges (σ) may be dependent on various properties of the capsid such as the size or T value.

Fig. 4.

The canonical capsid subunit is represented (a) with a quasi-equivalent vertex or ‘centroid’ (that can be either five or six-valent), two non-bisectable straight edges (inter-capsomere edges), and one curved edge that may possess two or more vertices. The subunit may be associated in two quasi-equivalent configurations called capsomeres – comprising five-valent (b) and six-valent (c) clusters.

The allowance to describe capsids as monohedral tilings (or polyhedra) and our description of a σ-unrestricted subunit allows the canonical capsid to be systematically analyzed using simple topological tools such as the Euler's polyhedral formula.

I. The number of sides (σ)

All canonical capsids can be thought of, graph theoretically, as triangulations of the icosahedron. As the icosahedron is convex, it can be projected as a planar graph onto a two dimensional plane (as a Schlegel diagram, for example[19]). This, in turn, means that the graph representation of every canonical capsid is expected to be planar, whether or not the three-dimensional canonical capsid is convex. From which it follows that the graphs describing connectivity for canonical capsids must abide by Euler's polyhedral formula.

Euler's polyhedral formula shows that various elements within convex and certain non-convex polyhedra may be related to each other in a predictable manner. Specifically, the number of vertices (V), edges (E), and faces (F) of a such a polyhedron may be related through the following equation:

$$V-E+F=2$$ (1)

All tilings describing the canonical capsid must satisfy this equation. This offers a direct relationship between the number of subunits (F) and the allowable number of interactions/edges per tile (σ). We will be able to relate the two terms (F and σ) by relating V, E, and F to the number of sides, (σ) and the size of the capsid (T). From the general definitions of quasi-equivalent spherical virus capsids (discussed above), we will establish the relationships between V, E, F, σ and T to establish an expression for σ.

Since we know that the number of faces corresponds to the number of subunits in the canonical capsid, we have

$$F=60T$$ (2)

Also, as this is an edge-edge tiling, each edge is shared by exactly two faces. So, the number of edges is

$$E=F\sigma /2=30T\sigma$$ (3)

The Caspar and Klug rules of capsid assemblies shows that there are twelve 5-valent vertices and 10(T − 1) 6-valent vertices [3] within the canonical capsid (these vertices are called centroid vertices). So, the number of centroid vertices (V_C) is equal to

$$V_C=10(T-1)+12=10T+2$$ (4)

We know that each prototile must have exactly one centroid vertex. Also, from our earlier definition of the prototile, the rest of the (σ − 1) vertices are trivalent in nature. Therefore, The number of trivalent vertices are equal to

$$V_R=60T(\sigma -1)/3=20T(\sigma -1)$$ (5)

Finally, from Equations 4 and 5, we have the total number of vertices

$$V=V_R+V_C=2+20T\sigma -10T$$ (6)

Substituting equations 6, 3, and 2 in equation 1, we get

$$60T+40T+2+20T\sigma -10T=2$$ (7)

Further reducing this equation, we find

$$\sigma =5$$ (8)

A capsid invariant

Via simple topological relationships, we obtained an invariant geometric characteristic (σ) that is independent of the T value. Using the assumptions of a fixed number of faces, quasi-equivalence, and 3-valency for non quasi-equivalent vertices (i.e., modeling a 5/6,3-vertex polyhedron with 60T faces), topology dictates that only a five sided prototile will be able to assemble into any sized (T-valued) canonical capsid (with the modification of subunit-subunit interaction angles). The number of sides (σ) is invariant of the triangulation number (T), which shows that a subunit may be modified to assemble into capsids of non-native T values.

II. The shapes available to a five-sided canonical capsid subunit

Any prototile that can tile a bound canonical capsid should, by the rules of quasi-equivalence, also tile a two dimensional hexavalent lattice (a hexagonal lattice containing hexavalent vertices). So, our second query is simplified to: how many five-sided prototiles may assemble into a hexavalent lattice?

The tiling of 2D surfaces by convex pentagons has been a subject studied at least since the early twentieth century. In the early 80s, Grünbaum and Shepherd enumerated a list of thirteen known convex pentagonal tilings, and since then, one more has been added to that list [20, 21]. We searched the resulting catalogues as capitulated by Sugimoto and Ogawa [20] for convex pentagonal prototiles that can assemble into a hexavalent lattice, and found only one tiling to fit that criteria (known in [20] as Type 5; shown here in Figure 5 a). Therefore, only one type of tiling among the known ones (the Type 5 tiling) will be allowed to form a canonical capsid of any size.

Fig. 5. Pentagonal type 5 tilings.

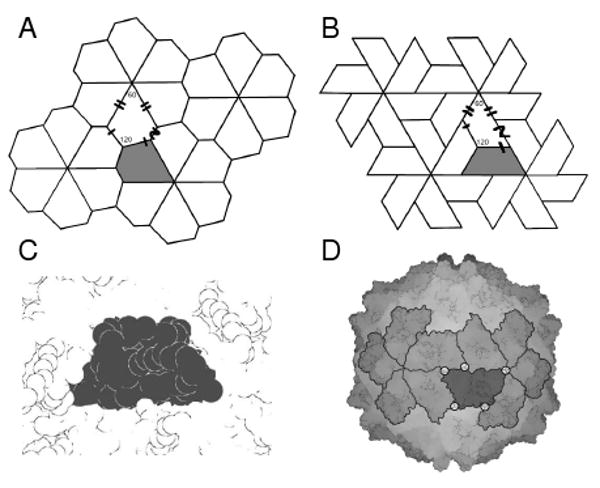
Type 5 tiles are the only five sided tiles that possess six-valent vertices. Furthermore, a version of this tile (b) resembles a very commonly seen subunit shape found in nature depicted as a space-filled subunits (a) and within its capsid environment (b) (Structure used: 1vak of the Sobemovirus family).

The ubiquitous trapezoid shape emerges

Interestingly, this tiling is equivalent (combinatorially) to the tiling seen in Figure 5 b, which represents a 2D projection of the trapezoid structure seen in nature. This subunit shape is highly ubiquitous in the spherical capsid world [22] and is found in virus families that differ greatly in sequence space (down to 0% sequence identity), host specificity (insects, birds, mammals) and capsid size (with recorded T values ranging from 1 through 13)[27]; An example of one of these subunits is shown in Figure 5 c and d. This suggests that topological constraints may play dominant roles in the natural design of the shape of virus capsid subunits. This, in turn, means that the chance that two proteins may have evolved from distinct lineages into the same structural shape can not be dismissed.

Rationalizing the need for a five-sided subunit

One could look at the need for a five-sided subunit intuitively from a symmetry-oriented standpoint. There are two kinds of icosahedral point group symmetries – full (or achiral) icosahedral symmetry and rotational (or chiral) icosahedral symmetry. Although both point group symmetries have the same number of 2, 3 and 5-fold axes of rotation, they differ in the number of mirror planes they possess; the full icosahedral symmetry group possesses fifteen mirror planes while the rotational icosahedral symmetry group possess none. Due to the chirality of biological macromolecules, it is evident that only the chiral icosahedral symmetry may exist.

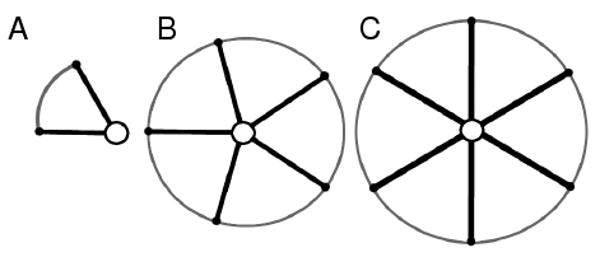
Figure 6 represents versions of the three, four and five sided prototile in its hexameric form (a), which is a precursor to the canonical capsid, and prototile itself (b). It is immediately evident that the number of possible mirror symmetries (shown as dotted lines) disappears at σ = 5. As chirality (or the absence of mirror symmetries) is crucial within the biological world, σ = 5 is the only viable option for virus capsid subunits; and from σ = 5, the trapezoid of the tiling is automatically obtained.

Fig. 6.

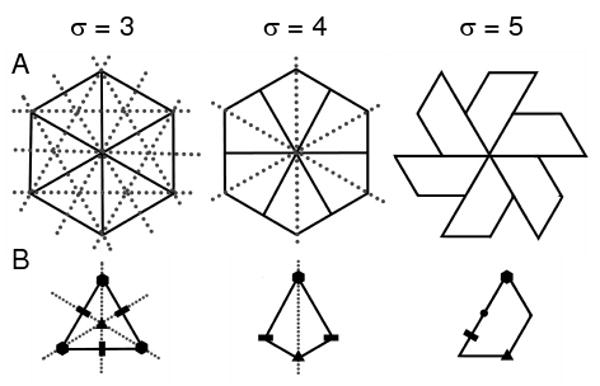
The relationship between mirror symmetries and the number of sides per tile (σ). This image illustrates trigonal, tetragonal and pentagonal tiles in (a) the hexavalent form and (b) as a single tile (along with the 2, 3 and 6-fold symmetry relationships denoted). The dotted lines in the figure indicate possible mirror planes cutting the plane of the paper perpendicularly. It is immediately evident that the hexameric cluster for only σ = 5 has no possible mirror symmetries, which is crucial in the chiral-centric biological world.

Canonical capsids do represent group 1 capsids

All capsids present within group 1 families described in Table I – the capsids representable by monohedral tilings – also possess trapezoidal shapes. This means that the predictions made by analyzing canonical capsids, and the empirical evidence obtained from the shapes of group 1 capsids indicate a congruence between the mathematical models and natural capsids. Thus, the canonical capsid may, in fact, be used to represent and study capsids belonging to group 1 families of Table I. Furthermore, it is interesting to note that capsids belonging to families such as picornaviridae and comoviridae that possess chemically distinct subunits in the capsid asymmetric unit, but that appear to have no gross structural overlaps and holes, also possess the familiar trapezoidal subunit motif.

Capsids that possess subunit-subunit holes, overlaps or structural variability (i.e., group 2 capsids) were found to possess, largely, non-trapezoidal shaped subunits. Most notable among these are the polyomaviridae family viruses that not only break the rules of monohedral tilability, but also break the otherwise longstanding rules of quasi-equivalence.

Divergence or convergence?

The trapezoidal subunit shape is seen within capsids sharing little to no similarity in amino acid sequence, host specificity, genome type (RNA, DNA), and size (T value). Our findings raise interesting questions about the evolutionary reason for this structure's prevalence among such diverse virus families. It is widely believed that all these capsids arose from a single proto-viral strain [22]. However, we show that the bisected-trapezoid is the only subunit shape (among other type 5 tilings) that is allowable within canonical capsids, i.e., it appears as though the trapezoid is the only shape available to a capsid that attempts to maximize, via edge-edge tilings, the amount of interactions while minimizing the extent of holes and simultaneously reducing design complexity by being relatively structurally invariant/monohedral (all of these features are acceptable from a free energetic point of view). Consequently, it is not improbable that distinct families evolved in parallel and encountered, independently, the trapezoidal-shaped jelly-roll architecture, i.e., convergent evolution is a distinct possibility, especially in systems with general but stringent constraints (such as topological constraints).

Future applications

Virus tiling theory, as pioneered by Twarock, has already been used to explain interesting assembly-related properties of capsids that break the rules of quasi-equivalence by displaying only pentamers and no hexamers [11, 23–25]. Specifically, they showed that capsids belonging to the polyomaviridae family must be represented as bound tilings formed from two distinct subunit shapes or tiles [11, 23], i.e., capsids from this family can not be represented by monohedral tilings, which corroborates the classification of these capsids as “group 2” in Table I. Importantly, Twarock and colleagues showed that one may characterize the “assembly pathways” of these tilings using mathematical methods [24, 25]. Those studies were primarily applied to capsids belonging to the polyomaviridae family.

Our findings show that canonical capsids – monohedral bound trapezoidal tilings that follow the rules of quasi-equivalence – may be used to represent a large number of capsids, allowing for a physical understanding of those capsids in a manner that builds upon the techniques introduced by Twarock and colleagues. Mathematical and physical investigations of these canonical capsids are currently being pursued.

IV. Conclusion

We have shown that a majority of capsids (comprising eight out of twelve structurally characterized families) may be represented as monohedral tilings (canonical capsids), thereby allowing the use of many fields of mathematics (such as topology, tiling theory, graph theory, etc.) to explain capsid structure and dynamics. We demonstrated that only a specific five-sided prototile is compatible with bound monohedral tilability and the definitions of quasi-equivalence of virus capsids. This we did using simple topology, graph theory, and symmetry concepts. Of the possible tilings, one – of trapezoidal shape – was found to be displayed by capsid subunits within every one of the eight tilable virus capsid families. This trapezoidal subunit shape is found in capsids sharing little to no sequence similarity, host specificity, genome type (RNA, DNA), and size (T value). These results raise interesting questions about the nature of the non-canonical capsids, and the divergent and convergent nature of the group 1 capsids with respect to evolution and design. More importantly, our result that the expected shape of the canonical capsid accurately reflects the shape of the group 1 capsid subunits found in nature lends credence to usefulness of the bound monohedral tiling model of capsids (the “canonical capsid”).