Abstract
We review insights from computational studies of affinities of ligands binding to proteins. The power of structural biology is in translating knowledge of protein structures into insights about their forces, binding, and mechanisms. However, the complementary power of computer modeling is in showing “the rest of the story” (i.e., how motions and ensembles and alternative conformers and the entropies and forces that cannot be seen in single molecular structures also contribute to binding affinities). Upon binding to a protein, a ligand can bind in multiple orientations; the protein or ligand can be deformed by the binding event; waters, ions, or cofactors can have unexpected involvement; and conformational or solvation entropies can sometimes play large and otherwise unpredictable roles. Computer modeling is helping to elucidate these factors.
Introduction: Computer Modeling Is an Important Tool for Understanding Ligand Binding to Proteins
Structure-based computer modeling of ligand-protein interactions is now a core component of modern drug discovery (Charifson and Kuntz, 1997). It is now difficult to imagine the drug discovery process without computation (Jorgensen, 2004). Computational methods have played a key role in the drug discovery process for a growing number of marketed drugs, including HIV protease inhibitors (Charifson and Kuntz, 1997; Greer et al., 1994; Jorgensen, 2004) and zanamivir (an antiviral neuraminidase inhibitor) (von Itzstein et al., 1993), and in the development of new drug candidates, such as HIV integrase inhibitors (Hazuda et al., 2004; Schames et al., 2004), hepatitis C protease inhibitors (Liverton et al., 2008; Thomson and Perni, 2006), and beta-secretase inhibitors (BACE-1) (Stauffer et al., 2007).
An early step in this field was the invention of the DOCK method in 1982 (Kuntz et al., 1982). There are now at least four classes of physical computer methods (listed from fastest to slowest, and least physical to most physical): (1) very fast molecular docking methods, including DOCK, Glide, AutoDock, FlexX, ICN, PMF, and GOLD, (2) approximate free energy methods, in which the solvent and protein motions are taken into account with fewer approximations, (3) relative binding free energy (RBFE) methods, which include full solvent and protein motions, but which require prior knowledge of the structure of a complex of the protein with a ligand that is similar to the one of interest, and (4) absolute binding free energy (ABFE) methods, which are the most expensive computationally, but which include the physics in the most rigorous way that is currently practical (see Figure 1). ABFE methods start from an unbound ligand and potentially the unbound structure of the protein to attempt to predict the structures, affinities, and thermal properties of the complexes of interest. Mining minima is another method that is very nearly in this last category and has provided insight into binding (Chang and Gilson, 2004; Gilson and Zhou, 2007; Head et al., 1997).
Figure 1. Relative Publication Numbers for Different Computational Methods.
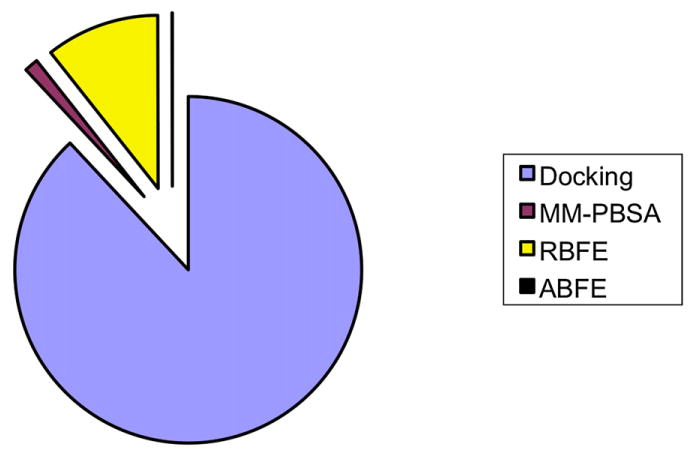
From Google Scholar (July 2008). MM-PBS, molecular-mechanics with Poisson-Boltzmann surface area; RBFE, relative binding free energy; ABFE, absolute binding free energy. Percentages, in the order listed in the legend, are 88%, 1%, 11%, and 0.04%.
Different Computer Methods Trade Off Speed versus Physical Accuracy
First, we define some terms. A lead compound is a molecule, typically in early-stage drug discovery, that can be further chemically modified to improve its properties as a possible drug candidate. A complex is a receptor and ligand bound together. A pose is one conformation of a ligand in a complex and specifies both the ligand conformation and its position relative to the receptor. A pose can refer either to a conformation that is known from an experimental structure of a complex, or to a hypothetical conformation generated in a computer model. The apo form refers to the structure of the protein that has no ligand bound to it. The holo form refers to the structure of the protein when it is complexed with ligand. The binding free energy, ΔG°, is the free energy of the complex minus the free energies of the ligand and apo protein separately in aqueous solution. The binding free energy is related to the equilibrium association constant, Ka, (in units of M−1) by ΔG° = −RT ln (C° Ka), where R is the gas constant, T is the absolute temperature, and C° is the standard concentration (1 M). The binding affinity, or dissociation constant, equals 1/Ka. The binding free has two components, ΔG = ΔH – TΔS, where H is the enthalpy and S is the entropy. Here are some of the key approaches used for studying binding.
Docking
Docking methods start with a known protein structure and a known ligand structure and aim to rapidly generate an optimal protein-ligand bound conformation. Docking was designed to be very rapid (seconds or less per compound), which is desirable for screening large libraries in the short times required for modern pharmaceutical lead discovery. Docking explores many ligand conformations and orientations, and in some cases even different potential binding sites. The different poses are rank ordered by a score, a quantity that ideally would correlate with the free energy of binding, and is obtained either from a physical or knowledge-based potential. Often, docking approaches treat the protein as completely rigid, having a single fixed receptor conformation. Other docking methods treat protein motions by moving only certain atoms out of the way. Though some modern docking approaches can allow for some motions of side chains or backbone (Corbeil et al., 2007; Cozzini et al., 2008; Leach, 1994; Meiler and Baker, 2006; Sherman et al., 2006; Wei et al., 2004), treating these degrees of freedom slows down the computations considerably. Docking is an appealing way to generate leads (Shoichet et al., 2002) because of its speed and ability to screen large libraries of potential leads (Huang and Jacobson, 2007; Babaoglu et al., 2008). But because docking trades off physical accuracy for speed, it is seldom accurate enough to predict binding affinities or rank-order compounds. Its power to discriminate binders from nonbinders varies widely depending on the target protein (Graves et al., 2008; Warren et al., 2006). But because of its speed, docking approaches are the method of choice for filtering out compounds that are likely nonbinders and for identifying native-like poses.
MM-PBSA/GBSA
MM-PBSA/GBSA is more physically rigorous than docking. The acronym stands for molecular mechanics with Poisson-Boltzmann + surface area or MM-GBSA (GB stands for Generalized Born), and the method was originated by the Kollman and Case labs in the late 1990s (Cheatham et al., 1998; Kollman et al., 2000; Srinivasan et al., 1998), with parallel work by others (Vorobjev and Hermans, 1999). It involves greater computational cost than docking (at least several hours per compound), but also is more physical in its more extensive conformational sampling. MM-PBSA aims to estimate the binding free energies, or relative binding free energies, of related compounds. Here, a computer generates representative bound and unbound structures by molecular mechanics simulations or by energy minimization of a protein-ligand complex, usually in explicit solvent. The goal is to estimate the change in enthalpy on binding by comparing the average enthalpy of bound and unbound states, but this would be a small difference of two large, noisy energies. So after the all-atom simulations, the water is removed and the enthalpies and binding free energies are estimated using an implicit (Poisson-Boltzmann or Generalized Born) representation of water. The binding free energy estimate includes the enthalpy change plus the change in salvation free energy from the implicit solvent model.
In many cases, an approximate value of the entropy is also estimated from these simulations. Because MM-PBSA/GBSA invests more effort in sampling and entropies, it is closer to a true free energy calculation. However, often, because of limitations in the approximations for estimating entropy (Gilson and Zhou, 2007), entropic contributions are omitted when estimating relative binding strengths, in the hope that these contributions will cancel when comparing similar ligands (Gilson and Zhou, 2007; Shirts et al., 2009).
Early results with the MM-PBSA method were quite promising (typically with mean-squared errors under 3 kcal/mol for the first several years) (Huo et al., 2002; Kuhn and Kollman, 2000; Mardis et al., 2001; Rizzo et al., 2004; Schwarzl et al., 2002; Shirts et al., 2009), but more recent studies have seen larger errors in some cases (Shirts et al., 2009). Applications have typically been limited to single targets, so it is difficult to evaluate how well the method does generally.
The drawbacks of MM-PBSA/GBSA are that it, too, is sometimes not predictive (Pearlman, 2005; Shirts et al., 2009; Steinbrecher et al., 2006) and it requires prior knowledge of a likely bound complex as a starting point, although such starting conformations can be taken from prior docking (Steinbrecher et al., 2006).
Relative Binding Free Energies
A still more rigorous approach uses the energetics of a physical force field and extensive conformational sampling from molecular dynamics simulations to actually compute differences in binding free energies between similar ligands. This can be done using computational alchemy to obtain the difference in binding free energies, ΔΔGA→B. This is the free energy of changing ligand A into ligand B in the receptor, minus the free energy of changing A into B in solution. To compute this free energy difference for just one pair of ligands binding to the same protein can cost several hundred CPU days. These relative free energies can be computed precisely—given sufficiently long molecular dynamics simulations—using one of several different analysis techniques (Shirts et al., 2007). Though the accuracy of the binding free energies obtained from this method depends on the accuracy of the underlying molecular mechanics force field, it does treat fully, at least in principle, free energies associated with conformational change as well as entropies.
The first alchemical calculations were performed in the 1980s in the McCammon lab (Tembe and McCammon, 1984; Wong and McCammon, 1986), and then by others (Hermans and Subramaniam, 1986; Warshel et al., 1986; Bash et al., 1987; Shirts et al., 2007). Limitations of these methods are the high computational costs and the need to know at least one bound structure of a similar ligand in the protein as a starting point. Accuracies are generally better than for MM-PBSA (Pearlman, 2005; Steinbrecher et al., 2006) and docking (Mobley et al., 2007b; Pearlman and Charifson, 2001), but few systematic comparisons have been done. These methods are only useful for comparing related ligands or receptors.
Absolute Binding Free Energies
The most powerful approach, in principle, is the method of absolute binding free energies (ABFE) (Boresch et al., 2003; Hermans and Wang, 1997; Roux et al., 1996). Like RBFE methods, ABFE methods also use full molecular dynamics simulations with fully detailed atomic force fields, and also involve separate sets of simulations for the solvated ligand, the solvated protein, and the complex. But ABFE methods do not require prior knowledge of the binding affinity of a related ligand, hence the term absolute. There have been two groups of ABFE approaches. The first begins with the structure of the ligand of interest bound to the protein. However, the ultimate goal is to begin with no prior knowledge of either the structure or affinity of the ligand complex. A second, more recent group replaces starting knowledge of the structure with one or more docking poses (Mobley et al., 2006, 2007b; Jayachandran et al., 2006). Various studies suggest that ABFE methods are fairly accurate, with good correlations to experimental binding affinities and with RMS errors often less than 3 kcal/mol (Deng and Roux, 2006; Fujitani et al., 2005; Jayachandran et al., 2006; Mobley et al., 2007b; Shirts et al., 2007; Wang et al., 2006), and sometimes much better.
Ligand Binding Is Described by Energy Landscapes, Not Just Single Structures
The enterprise of structural biology has given us powerful “eyes” to see single structures—specific native structures and specific bound complexes—and some of the driving forces that hold them together: hydrogen bonds, hydrophobic interactions, ion pairing, and van der Waals packing. However, “what you see” is not always “what you get.” Other equally important forces, namely the entropies, are not visible in native structures.
To capture both the observable and nonobservable contributions to the energetics, it is important to note that binding takes place on an energy landscape. Exploring energy landscapes often requires modeling and computer simulations. For binding, the energy landscape is the free energy of the system as a function of its degrees of freedom, which are many, and include translational, rotational, conformational, and solvation degrees of freedom.
Upon Binding, a Ligand Loses Translational and Rotational Entropy
Relative to a receptor, a ligand has three translational degrees of freedom (x, y, and z directions) and three orientational degrees of freedom. When bound, motion in these degrees of freedom becomes restricted. This loss of freedom results in an entropic and free energy cost, opposing binding and favoring the dissociated state (Chang et al., 2007; Chang and Gilson, 2004; Chen et al., 2004; Deng and Roux, 2006; Lee and Olson, 2006; Wang et al., 2006). The loss of freedom depends on the mobility remaining in the binding site, so that in a series of increasingly tightly bound structures there will be increasing losses in translational and rotational entropies, resulting in a contribution opposing binding.
Upon Binding, a Ligand Can Lose Internal Freedom and Entropy
Some simple models assume that the ligand entropy lost on binding correlates with the number of rotatable bonds in the ligand (Böhm, 1993; Gilson and Zhou, 2007; Huey et al., 2007; Laederach and Reilly, 2003; Taylor et al., 2002; Gohlke and Klebe, 2002). The ligand is envisioned to start in its unbound state having access to all possible conformers and to end in its bound state having a single conformer. However, interestingly, more rigorous recent computational studies in host-guest systems indicate that losses in ligand conformational entropy on binding are not strongly correlated with the number of rotatable bonds (Chang and Gilson, 2004; Chen et al., 2004; Guimaraes and Cardozo, 2008). Recent work on salvation free energies of small molecules has led to similar conclusions (Mobley et al., 2008). Not all small-molecule conformers are populated equally in solution. Thus computing accurate ligand affinities (and entropy losses) requires more accurate treatments of the different ligand populations in solution. Entropic contributions can also vary between different conformations of the same ligand in a particular receptor (Chen et al., 2004; Gilson and Zhou, 2007), which may be important even for docking (Ruvinsky and Kozintsev, 2005).
A Ligand Can Bind to a Receptor in Different Poses
A ligand can sometimes adopt multiple different conformations or orientations upon binding (see Figure 2). These different poses can be separated by energetic barriers. In some cases the different poses are due to ligand or protein symmetries. HIV-1 protease is a dimer with a nearly symmetric active site; as a result, many HIV protease inhibitors have two nearly identically binding modes (e.g., see Protein Data Bank [PDB] codes 1AXA, 1IZH, 1MUI, and 1U8G). Ligand symmetries can lead to trivial cases of multiple binding modes, which have significant entropic implications. Multiple binding modes are observed also when symmetries do not play a role. Computational studies show multiple distinct ligand binding modes in binding sites in T4 lysozyme (Mobley et al., 2006, 2007b), neutrophil elastase (Steinbrecher et al., 2006), estrogen receptor inhibitors (Oostenbrink and van Gunsteren, 2004), FKBP inhibitors (Jayachandran et al., 2006), biotin and streptavidin (Lazaridis et al., 2002), and cytochrome P450cam (Paulsen and Ornstein, 1992).
Figure 2. Hypothetical Ligand Binding Energy Landscape.
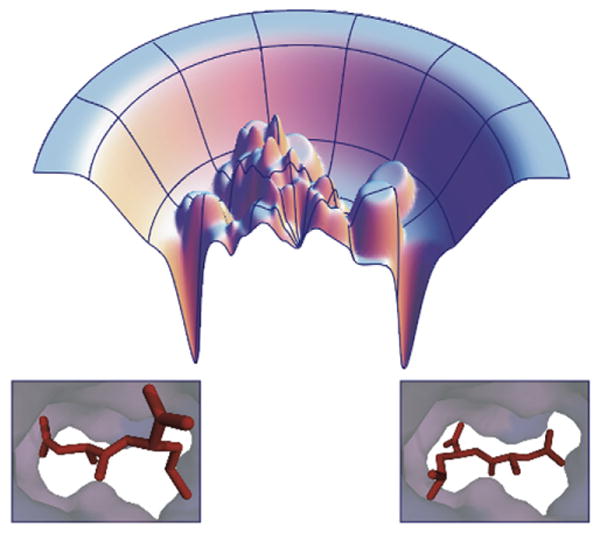
Ligand binding energy landscapes (top) can be rough, with multiple minima. These multiple minima can correspond to multiple distinct ligand binding conformations in the receptor (bottom).
Do experimental studies support these predictions of multiple ligand conformations? The challenge is that multiple conformers are difficult to determine experimentally. But there is at least some direct crystallographic evidence suggesting multiple relevant orientations: in T4 lysozyme (Graves et al., 2005; Mobley et al., 2006, 2007b), influenza neuraminidase (Stoll et al., 2003) and possibly in trypsin (Stubbs et al., 2002), where the binding mode is affected by pH. Multiple binding modes of fragment-like kinase inhibitors have also been observed (Constantine et al., 2008). Multiple orientations or binding modes have also been seen in thymidylate synthase (Montfort et al., 1990), in the binding of an HIV-1 cell entry inhibitor to the core of HIV-1 gp41 (Zhou et al., 2000), the binding of a transition state analog to an AmpC beta lactamase mutant (Chen et al., 2006), the binding of thiocamphor to cytochrome P450cam (Raag and Poulos, 1991), the binding of flavin to para hydroxybenzoate hydrolase (Gatti et al., 1994), and in the binding of some HIV-1 protease inhibitors (Murthy et al., 1992). There is additional evidence for multiple orientations in several other cases (Birdsall et al., 1989; Böhm and Klebe, 1996; Lazaridis et al., 2002; Mewshaw et al., 2005; Orville et al., 1997; Uytterhoeven et al., 2002). Spectroscopic data (Deng et al., 2001) and studies of drastically different binding modes of related inhibitors (Figure 3) (Stout et al., 1999; Badger et al., 1988; Böhm and Klebe, 1996; Kim, 2007a, 2007b; Pei et al., 2006; Reich et al., 1995; Stoll et al., 2003), some of which may have multiple binding modes (Montfort et al., 1990), suggest that multiple binding modes may be relatively common.
Figure 3. Small Changes in a Ligand May Modify the Binding Landscape.
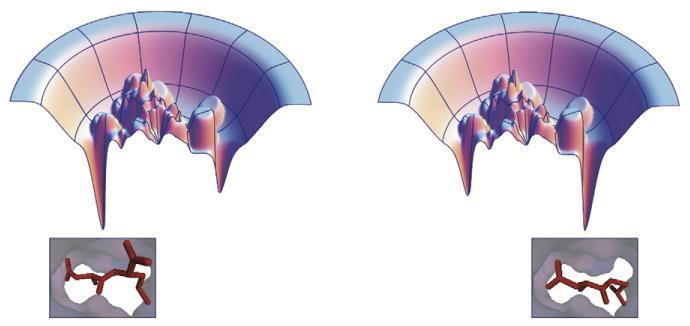
It is not uncommon to find that small modifications in a ligand (bottom) may lead to drastic changes in the observed binding mode (bottom) (Stout et al., 1999; Badger et al., 1988; Böhm and Klebe, 1996; Kim, 2007a, 2007b; Pei et al., 2006; Reich et al., 1995; Stoll et al., 2003). This can be explained by an energy landscape with multiple minima (top), which is altered slightly by minor modifications to the ligand (top left versus top right), leading to a substantial change in the binding mode.
Proteins Wiggle, and May Have Multiple Conformers in Both the Bound and Unbound States
It is not only ligands that can have multiple binding modes. Proteins can, too (Mobley et al., 2007a, 2007b). We refer here not to induced fit, where the ligand binding event causes a change in protein conformation. Rather, we focus on internal motions or freedom of the protein that occur either in the apo structure of the protein itself or in the complex itself. Comparisons of different apo structures of the same proteins show that there are some rotamer changes near binding sites even in the absence of the ligand (Najmanovich et al., 2000), suggesting that multiple rotameric states may be relevant; this is also supported by NMR data (Chou and Bax, 2001). Structural data in the apolar T4 lysozyme binding cavity suggests that helix F, which borders on the binding cavity, can undergo substantial motions of 1.5–2.5 Å with little free energy cost (Morton and Matthews, 1995); various other motions occur in T4 lysozyme as well (Zhang et al., 1995). DHFR appears to have multiple relevant conformations, both in isolation and when binding ligands, and the populations are modulated by pH (Birdsall et al., 1989); each state in the catalytic cycle appears to have at least partially occupied conformations that resemble those before or after it in the cycle (Boehr et al., 2006). Crystallographic evidence suggests multiple protein conformations due to domain motion in some cases (Ma et al., 2002). Multiple conformers are also seen in host-guest binding (Chang and Gilson, 2004; Chen et al., 2004) and can be critical for protein mechanisms such as enzyme catalytic motions (Eisenmesser et al., 2005; Arora and Brooks, 2007; Henzler-Wildman et al., 2007; Henzler-Wildman and Kern, 2007). Several other studies also have provided evidence for multiple protein conformations (Eisenmesser et al., 2002; Gerstein et al., 1994; Min et al., 2005a, 2005b; Fragai et al., 2006).
Strain: A Measure of the Free Energy of Deformation
Ligand binding to a protein may induce strain. Strain refers to an energy cost, usually associated with a deformation of some sort. To achieve the lowest free energy of binding in the complex, the protein and/or ligand may become deformed relative to its unbound state in solvent, which costs energy (strain). Computational studies in the apolar lysozyme model binding site have found that protein strain energies for a valine side-chain rotamer change can be 3–4 kcal/mol (Deng and Roux, 2006; Mobley et al., 2007a, 2007b). When such strain energies are not taken into account, it leads to errors in predicted binding free energies (Mobley et al., 2007a, 2007b).
Computational modeling suggests that ligand strain free energies can be significant. In a survey of 150 crystallographic protein-ligand complexes, Perola and Charifson (2004) used molecular mechanics scoring functions to assess strain energies and found that roughly 50% of ligands with 4–6 rotatable bonds had strain energies more than 3 kcal/mol, and, overall, 40% of ligands had strain energies more than 5 kcal/mol. Another study computed quantum mechanical torsional potentials for a variety of PDB ligands and found that typical strain energies could be on the order of 0.6 kcal/mol per torsion motif, amounting to roughly 3 kcal/mol for a ligand with five torsion motifs (Hao et al., 2007). Another study found, for several ligands, that free energy costs of restricting the ligand to the bound conformation could be a few kcal/mol (Tirado-Rives and Jorgensen, 2006). More recent work suggests that these values could be overestimates of the true strain, as crystal structures (from which strain is estimated) may be refined with a different force field than is used in estimating the strain, introducing artifacts. Nevertheless, strain energies often appear to be greater than several kT (Huang et al., 2006). See also Warren and Perola's (Warren and Perola, 2008) presentation on the topic from OpenEye's CUP meeting (http://www.eyesopen.com/about/events/cups-2008/pdfs-CUP/CUP9-Field-of-Extremes.pdf). Apparently, binding interactions can be strong enough to pay a substantial strain price for deforming one or both partners. Hence the true bound structure of a complex will not be the one that maximizes the interaction energy between the receptor and ligand, but rather the one that best balances the tradeoff between gaining additional favorable interactions while also inducing strain (Sharp, 2005).
Some experiments support this contention that strain free energies can be substantial. In an NMR study on maltose binding protein, Tang et al. (2007) found that the unbound protein was predominantly (roughly 95%) in the open apo conformation, and had a smaller (roughly 5%) population in a minor apo conformation that was more like the holo conformation, but with no evidence that it populated the holo conformation at all in the absence of the ligand. Thus the minor apo conformation is roughly 1.7 kcal/mol less favorable than the major apo conformation, and the holo conformation is probably still more unfavorable. In another instance, in NtrCr, a conformational switch in bacteria that undergoes a conformational change upon phos-phorylation, the active conformation has been shown to be partially populated even when the protein is unphosphorylated (Volkman et al., 2001), but with a smaller population. Based on the populations, this active-like conformation is about 2 kcal/mol less favorable than the norm in active conformation. So, functional protein conformational changes can make significant contributions to the thermodynamics.
Ligand Binding Can Cause Conformational Change in Protein Structures
When a ligand binds to a protein, it causes conformational changes in the protein. This may or may not be accompanied by strain in the protein, as strain is an (invisible) energy cost.
Ligand-induced protein conformational changes are not rare events. Comparisons of apo and holo structures from the PDB show that backbone conformational motions on ligand binding are relatively common; 20% of binding residues (Gutteridge and Thornton, 2005) and 25% of binding sites (Najmanovich et al., 2000) across a variety of proteins have backbone Cα motions more than 1 Å. And 15% of binding site residues have side-chain motions of more than 2 Å (Gutteridge and Thornton, 2005), whereas only 30%–40% of binding sites have been shown to undergo no side-chain rotamer changes (Najmanovich et al., 2000). More anecdotal reports of conformational changes on ligand binding are available for a wide range of systems; kinases, for example, are notoriously flexible (Noble et al., 2004; Vajpai et al., 2008; Weisberg et al., 2007), as are many other proteins (Böhm and Klebe, 1996; Kim, 2007a; Meiler and Baker, 2006; Teague, 2003). An extreme example may be natively disordered proteins in which large parts of the protein may become ordered upon interacting with binding partners (Hilser and Thompson, 2007; Radivojac et al., 2007; Wright and Dyson, 1999).
In addition, a given protein can adopt different conformations for different ligands. A PDB study of 206 binding site pairs (each pair consisting of two structures of the same protein with different, similar ligands in the binding site) showed that in 83% of the cases there were significant conformational changes in the binding sites between pair members (Bostrom et al., 2006); changes were judged significant if the RMSD for all side-chain atoms if at least one amino acid residue within 5 Å of the ligand is greater than 1.0 Å. The most frequent differences were changes in water architecture and side-chain conformation (both occurring in over 50% of the pairs). Significant backbone conformational changes occurred in only 7% of the set; changes were judged significant if the RMSD of at least one backbone heavy atom in three or more consecutive amino acids is more than 0.5 Å. A smaller study found examples of substantial conformational changes on binding similar ligands for a variety of systems as well (Kim, 2007a). It is even possible for a single ligand to bind to different protein conformations under different solution conditions (Miller and Dill, 1997). Thus, changes in binding site architecture, at least at the side-chain and water level, should be regarded as the rule, rather than the exception.
Small Changes in Conformation Can Cause Big Changes in Binding Affinities
Some computational studies predict that even when a binding site structure is not perturbed very much, its energetics can change substantially. For example, simulations show that neglecting even small protein motions can lead to large errors (RMS errors relative to experiment of nearly 20 kcal/mol when protein motions are not allowed), relative to much smaller errors (1.7 kcal/mol RMS) when protein motion is allowed. Even small relaxations of the protein reduced the RMS errors to 4–5 kcal/mol) (Mobley et al., 2007b). This is important for both conceptual and practical reasons. Conceptually, it means the strength or quality of binding interactions is sensitive to minute details of the bound structure and is not easily assessed by simple metrics like hydrogen bond counts or apparent fit. Practically, it means that free energy methods that include these protein conformational changes can potentially have much higher accuracy than docking methods that neglect them.
The conclusion that these small changes can make big differences in the energetics is supported by a variety of docking and (re)scoring studies that have looked at the effects of introducing small amounts of protein flexibility. Though scores do not necessarily improve for all ligands, they do typically change substantially, showing some improvement (Graves et al., 2008; Huang et al., 2006; Meiler and Baker, 2006; Sousa et al., 2006; Wei et al., 2004). But introducing protein flexibility without accounting for protein strain energies can potentially increase false positive rates by making binding sites too permissive (Graves et al., 2008; Sousa et al., 2006; Wei et al., 2004). This likely highlights the role of conformational change and strain.
Differences in Solvation Can Contribute to Binding Affinities
Several detailed binding free energy studies have suggested that differences in solvation may play an important role in differences in binding free energy between relatively similar compounds (Jiao et al., 2008; Reddy and Erion, 2001). Two molecules might have similar interactions with a protein, similar strain energies, etc., but have different solvation properties in water, leading to solvation-driven differences in binding free energies. These differences may not always be intuitive. For example, the N-methylacetamide/amine “problem” (Rizzo and Jorgensen, 1999) suggests that adding a hydrophobic methyl group to acetamide or ammonia increases the affinity for water, whereas subsequent methylations decrease the affinity.
The importance of solvation and desolvation is supported by an emerging trend toward including approximate estimates of solvation/desolvation energies in approximate docking methods for scoring protein-ligand binding. Including such estimates appears to result in improved scoring (Ferrara et al., 2004; Gilson and Zhou, 2007; Shoichet et al., 1999). Without these contributions, charged ligands can wrongly appear to bind better than polar ligands in a polar binding site. A charged ligand may make favorable electrostatic interactions in a polar binding site, but it also costs a huge amount of energy to remove it from water (Brenk et al., 2006; Gilson and Zhou, 2007; Shoichet et al., 1999). In other cases, a small modification to a ligand can potentially lead to affinity gains due to a change in the desolvation cost (Kangas and Tidor, 2001).
Bound Waters Usually Contribute Favorably to Ligand Binding, But Not Always, and Their Contributions Are Highly Variable
Computer simulations have been used to study the role of crystallographic waters in binding thermodynamics (Barillari et al., 2007; Hamelberg and McCammon, 2004; Lu et al., 2006; Olano and Rick, 2004; Zhang and Hermans, 1996; see also Helms and Wade [1995, 1998a, 1998b] for desolvation of a buried binding cavity). In many cases, binding or ordering of waters occurs concurrently with ligand binding, so it can be extremely difficult to experimentally assess the contribution of water binding to overall binding thermodynamics. Computational methods can directly compute the free energy of inserting or removing a water molecule from a binding site, providing key insight that is hard to obtain experimentally.
These computational studies indicate that bound waters contribute substantially to binding free energies, contributing as much as −10 kcal/mol for some waters (Barillari et al., 2007), but smaller values between −3 and −6 kcal/mol are more typical (Barillari et al., 2007; Hamelberg and McCammon, 2004; Lu et al., 2006; Olano and Rick, 2004; Zhang and Hermans, 1996). In some cases, crystallographic waters appear substantially unfavorable relative to bulk, raising the possibility of problems with refinement or force fields (Barillari et al., 2007; Olano and Rick, 2004). Perhaps ligands can be designed with improved affinities by recognizing nearby sites where waters can be easily displaced (Abel et al., 2008; Pan et al., 2007).
Sometimes ligand binding can involve concerted reordering of many water molecules. In some hydrophobic sites in proteins that bind fatty acids or lipids, whole networks of more than a half-dozen water molecules shift their structures to form a “hydrophobic” interface with the ligand (LaLonde et al., 1994; Sulsky et al., 2007).
Protonation States Can Change on Binding, Influencing Affinity
Binding free energies can also be affected by other unseen and unexpected factors. For example, protonation states can change on binding (Czodrowski et al., 2007; Dullweber et al., 2001; Gohlke and Klebe, 2002; Steuber et al., 2007), as can tautomeric states (Pospisil et al., 2003) and other factors. In some cases, multiple protonation or tautomeric states can be relevant, as observed crystallographically for one CDK2 inhibitor (Furet et al., 2002) and hypothesized in another instance (Lee et al., 1996). “Similar” ligands may also adopt different protonation states on binding (Dullweber et al., 2001).
Perspective
We have reviewed some recent computational studies of ligand binding to proteins. Ultimately, to predict accurate binding affinities, it will be necessary to go beyond predicting a single “dominant” conformation of the ligand complexed with the protein. Binding free energy is not driven by a single conformation, but rather by the free energy landscape. It is the shape of the energy landscape that is crucial, the shape and width of the minima influences entropies. Entropies are key contributors to binding thermodynamics and are not observable in single bound structures. Other factors about the full landscape also play key roles, such as multiple ligand poses, protein conformations, strain energies, changes in water structure, and solvation and protonation all play roles. And none of these are observable in single structures. Computational tools can help provide insight into the unseen landscape, so those doing crystallographic studies may want to complement their work by using computational tools to explore this landscape. And those relying on crystallographic data (e.g., in a drug design context) should be aware that there are various binding possibilities that might not be captured in a single crystal structure.
Acknowledgments
We thank Scott P. Brown (Abbott Laboratories), Sarah Boyce (University of California, San Francisco), John van Drie, and John D. Chodera (Stanford University), for help with references; Sarah Boyce, Eric Manas (GlaxoSmithKline), and Gabe Rocklin (University of California, San Francisco) for comments on the manuscript; and Sarina Bromberg for preparing figures. We acknowledge financial support of the National Institutes of Health (Grant GM34993 to K.A.D.).
References
- Abel R, Young T, Farid R, Berne BJ, Friesner RA. Role of the active-site solvent thermodynamics of factor Xa ligand binding. J Am Chem Soc. 2008;130:2817–2831. doi: 10.1021/ja0771033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arora K, Brooks CL., III Large-scale allosteric conformational transitions of adenylate kinase appear to involve a population-shift mechanism. Proc Natl Acad Sci USA. 2007;104:18496–18501. doi: 10.1073/pnas.0706443104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Babaoglu K, Simeonov A, Irwin JJ, Nelson ME, Feng B, Thomas CJ, Cancian L, Costi MP, Maltby DA, Jadhav A, et al. Comprehensive mechanistic analysis of hits from high-throughput and docking screens against beta-lactamase. J Med Chem. 2008;51:2502–2511. doi: 10.1021/jm701500e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Badger J, Minor I, Kremer MJ, Oliveira MA, Smith TJ, Griffith JP, Guerin DMA, Krishnaswamy S, Luo M, Rossmann MG, et al. Structural analysis of a series of antiviral agents complexed with human rhino-virus 14. Proc Natl Acad Sci USA. 1988;85:3304–3308. doi: 10.1073/pnas.85.10.3304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barillari C, Taylor J, Viner R, Essex JW. Classification of water molecules in protein binding sites. J Am Chem Soc. 2007;129:2577–2587. doi: 10.1021/ja066980q. [DOI] [PubMed] [Google Scholar]
- Bash PA, Singh UC, Brown FK, Langridge R, Kollman PA. Calculation of the relative change in binding free energy of a protein-inhibitor complex. Science. 1987;235:574–576. doi: 10.1126/science.3810157. [DOI] [PubMed] [Google Scholar]
- Birdsall B, Feeney J, Tendler SJB, Hammond SJ, Roberts GCK. Dihydrofolate reductase: multiple conformations and alternative modes of substrate binding. Biochemistry. 1989;28:2297–2305. doi: 10.1021/bi00431a048. [DOI] [PubMed] [Google Scholar]
- Boehr DD, McElheny D, Dyson HJ, Wright PE. The dynamic energy landscape of dihydrofolate reductase catalysis. Science. 2006;313:1638–1642. doi: 10.1126/science.1130258. [DOI] [PubMed] [Google Scholar]
- Böhm HJ. The development of a simple empirical scoring function to estimate the binding constant for a protein-ligand complex of known three-dimensional structure. J Comput Aided Mol Des. 1993;8:243–256. doi: 10.1007/BF00126743. [DOI] [PubMed] [Google Scholar]
- Böhm HJ, Klebe G. What can we learn from molecular recognition in protein-ligand complexes for the design of new drugs? Angew Chem Int Ed Engl. 1996;35:2588–2614. [Google Scholar]
- Boresch S, Tettinger F, Leitgeb M, Karplus M. Absolute binding free energies: a quantitative approach for their calculation. J Phys Chem A. 2003;107:9535–9551. [Google Scholar]
- Bostrom J, Hogner A, Schmitt S. Do structurally similar ligands bind in a similar fashion? J Med Chem. 2006;49:6716–6725. doi: 10.1021/jm060167o. [DOI] [PubMed] [Google Scholar]
- Brenk R, Vetter SW, Boyce SE, Goodin DB, Shoichet BK. Probing molecular docking at a charged model binding site. J Mol Biol. 2006;357:1449–1470. doi: 10.1016/j.jmb.2006.01.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang CE, Gilson MK. Free energy, entropy, and induced fit in host-guest recognition: calculations with the second-generation mining minima algorithm. J Am Chem Soc. 2004;126:13156–13164. doi: 10.1021/ja047115d. [DOI] [PubMed] [Google Scholar]
- Chang CE, Chen W, Gilson MK. Ligand configurational entropy and protein binding. Proc Natl Acad Sci USA. 2007;104:1534–1539. doi: 10.1073/pnas.0610494104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charifson PS, Kuntz ID. Recent successes and continuing limitations in computer aided drug design. In: Charifson PS, editor. Practical Application of Computer Aided Drug Design. New York: Dekker; 1997. [Google Scholar]
- Cheatham TE, Srinivasan J, Case DA, Kollman PA. Molecular dynamics and continuum solvent studies of the stability of polyG-polyC and polyA-polyT DNA duplexes in solution. J Biomol Struct Dyn. 1998;16:265–280. doi: 10.1080/07391102.1998.10508245. [DOI] [PubMed] [Google Scholar]
- Chen W, Chang CE, Gilson MK. Calculation of cyclodextrin binding affinities: energy, entropy, and implications for drug design. Biophys J. 2004;87:3035–3049. doi: 10.1529/biophysj.104.049494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y, Minasov G, Roth TA, Prati F, Shoichet BK. The deacylation mechanism of AmpC beta-lactamase at ultrahigh resolution. J Am Chem Soc. 2006;128:2970–2976. doi: 10.1021/ja056806m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chou JJ, Bax A. Protein side-chain rotamers from dipolar couplings in a liquid crystalline phase. J Am Chem Soc. 2001;123:3844–3845. doi: 10.1021/ja015660y. [DOI] [PubMed] [Google Scholar]
- Constantine KL, Mueller L, Metzler WJ, McDonnell PA, Todderud G, Goldfarb V, Fan Y, Newitt JA, Keifer SE, Gao M, et al. Multiple and single binding modes of fragment-like kinase inhibitors revealed by molecular modeling, residue type-selective protonation, and nuclear overhauser effects. J Med Chem. 2008;51:6225–6229. doi: 10.1021/jm800747w. [DOI] [PubMed] [Google Scholar]
- Corbeil CR, Englebienne P, Moitessier N. Docking ligands into flexible and solvated macromolecules. 1. Development and validation of FITTED 1.0. J Chem Inf Model. 2007;47:435–449. doi: 10.1021/ci6002637. [DOI] [PubMed] [Google Scholar]
- Cozzini P, Kellogg GE, Spyrakis F, Abraham DJ, Constntino G, Emerson A, Fanelli F, Gohlke H, Kuhn LA, Morris GM, et al. Target flexibility: an emerging consideration in drug discovery and design. J Med Chem. 2008;51:6237–6255. doi: 10.1021/jm800562d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Czodrowski P, Sotriffer CA, Klebe G. Atypical protonation states in the active site of HIV-1 protease: a computational study. J Chem Inf Model. 2007;47:1590–1598. doi: 10.1021/ci600522c. [DOI] [PubMed] [Google Scholar]
- Deng Y, Roux B. Calculation of standard binding free energies: aromatic molecules in the T4 lysozyme L99A mutant. J Chem Theory Comput. 2006;2:1255–1273. doi: 10.1021/ct060037v. [DOI] [PubMed] [Google Scholar]
- Deng H, Zhadin N, Callender R. Dynamics of protein ligand binding on multiple time scales: NADH binding to lactate dehydrogenase. Biochemistry. 2001;40:3767–3773. doi: 10.1021/bi0026268. [DOI] [PubMed] [Google Scholar]
- Dullweber F, Stubbs MT, Musil D, Sturzebecher J, Klebe G. Factorising ligand affinity: a combined thermodynamic and crystallographic study of trypsin and thrombin inhibition. J Mol Biol. 2001;313:593–614. doi: 10.1006/jmbi.2001.5062. [DOI] [PubMed] [Google Scholar]
- Eisenmesser EZ, Bosco DA, Akke M, Kern D. Enzyme dynamics during catalysis. Science. 2002;295:1520–1523. doi: 10.1126/science.1066176. [DOI] [PubMed] [Google Scholar]
- Eisenmesser EZ, Millet O, Labeikovsky W, Korzhnev DM, Wolf-Watz M, Bosco DA, Skalicky JJ, Kay LE, Kern D. Intrinsic dynamics of an enzyme underlies catalysis. Nature. 2005;438:117–121. doi: 10.1038/nature04105. [DOI] [PubMed] [Google Scholar]
- Ferrara P, Gohlke H, Price DJ, Klebe G, Charles L, Brooks Assessing scoring functions for protein-ligand interactions. J Med Chem. 2004;47:3032–3047. doi: 10.1021/jm030489h. [DOI] [PubMed] [Google Scholar]
- Fragai M, Luchinat C, Parigi G. “Four-dimensional” protein structures: examples from metalloproteins. Acc Chem Res. 2006;39:909–917. doi: 10.1021/ar050103s. [DOI] [PubMed] [Google Scholar]
- Fujitani H, Tanida Y, Ito M, Shirts MR, Jayachandran G, Snow CD, Sorin EJ, Pande VS. Direct calculation of the binding free energies of FKBP ligands. J Chem Phys. 2005;123:084108. doi: 10.1063/1.1999637. [DOI] [PubMed] [Google Scholar]
- Furet P, Meyer T, Strauss A, Raccuglia S, Rondeau JM. Structure-based design and protein X-ray analysis of a protein kinase inhibitor. Bioorg Med Chem Lett. 2002;12:221–224. doi: 10.1016/s0960-894x(01)00715-6. [DOI] [PubMed] [Google Scholar]
- Gatti DL, Palfrey BA, Lah MS, Entsch B, Massey V, Ballou DP, Ludwig ML. The mobile flavin of 4-OH benzoate hydroxylase. Science. 1994;266:110–114. doi: 10.1126/science.7939628. [DOI] [PubMed] [Google Scholar]
- Gerstein M, Lesk AM, Chothia C. Structural mechanisms for domain movements in proteins. Biochemistry. 1994;33:6739–6749. doi: 10.1021/bi00188a001. [DOI] [PubMed] [Google Scholar]
- Gilson MK, Zhou HX. Calculation of protein-ligand binding affinities. Annu Rev Biophys Biomol Struct. 2007;36:21–42. doi: 10.1146/annurev.biophys.36.040306.132550. [DOI] [PubMed] [Google Scholar]
- Gohlke H, Klebe G. Approaches to the description and prediction of the binding affinity of small-molecule ligands to macromolecular receptors. Angew Chem Int Ed. 2002;41:2645–2676. doi: 10.1002/1521-3773(20020802)41:15<2644::AID-ANIE2644>3.0.CO;2-O. [DOI] [PubMed] [Google Scholar]
- Graves AP, Brenk R, Shoichet BK. Decoys for docking. J Med Chem. 2005;48:3714–3728. doi: 10.1021/jm0491187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graves AP, Shivakumar DM, Boyce SE, Jacobson MP, Case DA, Shoichet BK. Rescoring docking hit lists for model cavity sites: predictions and experimental testing. J Mol Biol. 2008;377:914–934. doi: 10.1016/j.jmb.2008.01.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greer J, Erickson JW, Baldwin JJ, Varney MD. Application of the three-dimensional structures of protein target molecules in structure-based drug design. J Med Chem. 1994;37:1035–1047. doi: 10.1021/jm00034a001. [DOI] [PubMed] [Google Scholar]
- Guimaraes CRW, Cardozo M. MM-GB/SA rescoring of docking poses in structure-based lead optimization. J Chem Inf Model. 2008;48:958–970. doi: 10.1021/ci800004w. [DOI] [PubMed] [Google Scholar]
- Gutteridge A, Thornton J. Conformational changes observed in enzyme crystal structures upon substrate binding. J Mol Biol. 2005;346:21–28. doi: 10.1016/j.jmb.2004.11.013. [DOI] [PubMed] [Google Scholar]
- Hamelberg D, McCammon JA. Standard free energy of releasing a localized water molecule from the binding pockets of proteins: double-decoupling method. J Am Chem Soc. 2004;126:7683–7689. doi: 10.1021/ja0377908. [DOI] [PubMed] [Google Scholar]
- Hao MH, Haq O, Muegge I. Torsion angle preference and energetics of small-molecule ligands bound to proteins. J Chem Inf Model. 2007;47:2242–2252. doi: 10.1021/ci700189s. [DOI] [PubMed] [Google Scholar]
- Hazuda DJ, Anthony NJ, Gomez RP, Jolly SM, Wai JS, Zhuang L, Fisher TE, Embrey M, Guare JP, Jr, Egbertson MS, et al. A nap-thyridine carboxamide provides evidence for discordant resistance between mechanistically identical inhibitors of HIV-1 integrase. Proc Natl Acad Sci USA. 2004;101:11233–11238. doi: 10.1073/pnas.0402357101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Head MS, Given JA, Gilson MK. “Mining minima”: direct computation of conformational free energy. J Phys Chem A. 1997;101:1609–1618. [Google Scholar]
- Helms V, Wade RC. Thermodynamics of water mediating protein-ligand interactions in cytochrome P450cam: a molecular dynamics study. Biophys J. 1995;69:810–824. doi: 10.1016/S0006-3495(95)79955-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Helms V, Wade RC. Computational alchemy to calculate absolute protein-ligand binding free energy. J Am Chem Soc. 1998a;120:2710–2713. [Google Scholar]
- Helms V, Wade RC. Hydration energy landscape of the active site cavity in cytochrome P450cam. Proteins Struct Funct Genet. 1998b;32:381–396. [PubMed] [Google Scholar]
- Henzler-Wildman K, Kern D. Dynamic personalities of proteins. Nature. 2007;450:964–972. doi: 10.1038/nature06522. [DOI] [PubMed] [Google Scholar]
- Henzler-Wildman KA, Thai V, Lei M, Ott M, Wolf-Watz M, Fenn T, Pozharski E, Wilson MA, Petsko GA, Karplus M, et al. Intrinsic motions along an enzymatic reaction trajectory. Nature. 2007;450:838–844. doi: 10.1038/nature06410. [DOI] [PubMed] [Google Scholar]
- Hermans J, Subramaniam S. The free energy of xenon binding to myoglobin from molecular dynamics simulation. Isr J Chem. 1986;27:225–227. [Google Scholar]
- Hermans J, Wang L. Inclusion of the loss of translational and rotational freedom in theoretical estimates of free energies of binding. Application to a complex of benzene and mutant T4 lysozyme. J Am Chem Soc. 1997;119:2707–2714. [Google Scholar]
- Hilser VJ, Thompson EB. Intrinsic disorder as a mechanism to optimize allosteric coupling in proteins. Proc Natl Acad Sci USA. 2007;104:8311–8315. doi: 10.1073/pnas.0700329104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang N, Jacobson MP. Physics-based methods for studying protein-ligand interactions. Curr Opin Drug Discov Dev. 2007;10:325–331. [PubMed] [Google Scholar]
- Huang N, Kalyanaraman C, Bernacki K, Jacobson MP. Molecular mechanics methods for predicting protein-ligand binding. Phys Chem Chem Phys. 2006;8:5166–5177. [Google Scholar]
- Huey R, Morris GM, Olson AJ, Goodsell DS. A semiempirical free energy force field with charge-based desolvation. J Comput Chem. 2007;28:1145–1152. doi: 10.1002/jcc.20634. [DOI] [PubMed] [Google Scholar]
- Huo S, Wang J, Cieplak P, Kollman PA, Kuntz ID. Molecular dynamics and free energy analyses of cathepsin D-inhibitor interactions: insight into structure-based ligand design. J Med Chem. 2002;45:1412–1419. doi: 10.1021/jm010338j. [DOI] [PubMed] [Google Scholar]
- Jayachandran G, Shirts MR, Park S, Pande VS. Parallelized-over-parts computation of absolute binding free energy with docking and molecular dynamics. J Chem Phys. 2006;125:084901. doi: 10.1063/1.2221680. [DOI] [PubMed] [Google Scholar]
- Jiao D, Golubkov PA, Darden TA, Ren P. Calculation of protein-ligand binding free energy using a polarizable potential. Proc Nat Acad Sci USA. 2008;105:6290–6295. doi: 10.1073/pnas.0711686105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorgensen WL. The many roles of computation in drug discovery. Science. 2004;303:1813–1818. doi: 10.1126/science.1096361. [DOI] [PubMed] [Google Scholar]
- Kangas E, Tidor B. Electrostatic complementarity at ligand binding sites: application to chorismate mutase. J Phys Chem B. 2001;105:880–888. [Google Scholar]
- Kim KH. Outliers in SAR and QSAR: 2. Is a flexible binding site a possible source of outliers? J Comput Aided Mol Des. 2007a;21:421–435. doi: 10.1007/s10822-007-9126-y. [DOI] [PubMed] [Google Scholar]
- Kim KH. Outliers in SAR and QSAR: Is unusual binding mode a possible source of outliers? J Comput Aided Mol Des. 2007b;21:63–86. doi: 10.1007/s10822-007-9106-2. [DOI] [PubMed] [Google Scholar]
- Kollman PA, Massova I, Reyes C, Kuhn B, Huo S, Chong L, Lee M, Lee T, Duan Y, Wang W, et al. Calculating structures and free energies of complex molecules: combining molecular mechanics and continuum models. Acc Chem Res. 2000;33:889–897. doi: 10.1021/ar000033j. [DOI] [PubMed] [Google Scholar]
- Kuhn B, Kollman PA. Binding of a diverse set of ligands to avidin and streptavidin: an accurate quantitative prediction of their relative affinities by a combination of molecular mechanics and continuum solvent models. J Med Chem. 2000;43:3786–3791. doi: 10.1021/jm000241h. [DOI] [PubMed] [Google Scholar]
- Kuntz ID, Blaney JM, Oatley SJ, Langridge R, Ferrin TE. A geometric approach to macromolecule-ligand interactions. J Mol Biol. 1982;161:269–288. doi: 10.1016/0022-2836(82)90153-x. [DOI] [PubMed] [Google Scholar]
- Laederach A, Reilly PJ. Specific empirical free energy function for automated docking of carbohydrates to proteins. J Comput Chem. 2003;24:1748–1757. doi: 10.1002/jcc.10288. [DOI] [PubMed] [Google Scholar]
- LaLonde JM, Bernlohr DA, Banaszak LJ. X-ray crystallographic structures of adipocyte lipid-binding protein complexed with palmitate and hexadecanesulfonic acid. Properties of cavity binding sites. Biochemistry. 1994;33:4885–4895. doi: 10.1021/bi00182a017. [DOI] [PubMed] [Google Scholar]
- Lazaridis T, Matsunov A, Gandolfo F. Contributions to the binding free energy of ligands to avidin and streptavidin. Proteins. 2002;47:194–208. doi: 10.1002/prot.10086. [DOI] [PubMed] [Google Scholar]
- Leach AR. Ligand docking to proteins with discrete side-chain flexibility. J Mol Biol. 1994;235:345–356. doi: 10.1016/s0022-2836(05)80038-5. [DOI] [PubMed] [Google Scholar]
- Lee MS, Olson MA. Calculation of absolute protein-ligand binding affinity using path and endpoint approaches. Biophys J. 2006;90:864–877. doi: 10.1529/biophysj.105.071589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee H, Reyes VM, Kraut J. Crystal structures of Escherichia coli dihydrofolate reductase complexed with 5-formyltetrahydrofolate (folinic acid) in two space groups: evidence for enolization of pteridine O4. Biochemistry. 1996;35:7012–7020. doi: 10.1021/bi960028g. [DOI] [PubMed] [Google Scholar]
- Liverton NJ, Holloway MK, McCauley JA, Rudd MT, Butcher JW, Carroll SS, DiMuzio J, Fandozzi C, Gilbert KF, Mao SS, et al. Molecular modeling based approach to potent P2-P4 macrocyclic inhibitors of hepatitis C NS3/4A protease. J Am Chem Soc. 2008;130:4607–4609. doi: 10.1021/ja711120r. [DOI] [PubMed] [Google Scholar]
- Lu Y, Wang CY, Wang S. Binding free energy contributions of interfacial waters in HIV-1 protease/inhibitor complexes. J Am Chem Soc. 2006;128:11830–11839. doi: 10.1021/ja058042g. [DOI] [PubMed] [Google Scholar]
- Ma B, Shatsky M, Wolfson HJ, Nussinov R. Multiple diverse ligands binding at a single protein site: a matter of pre-existing populations. Protein Sci. 2002;11:184–197. doi: 10.1110/ps.21302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mardis KL, Luo R, Gilson MK. Interpreting trends in the binding of cyclic ureas to HIV-1 protease. J Mol Biol. 2001;309:507–517. doi: 10.1006/jmbi.2001.4668. [DOI] [PubMed] [Google Scholar]
- Meiler J, Baker DA. ROSETTALIGAND: protein-small molecule docking with full side-chain flexibility. Proteins. 2006;65:538–548. doi: 10.1002/prot.21086. [DOI] [PubMed] [Google Scholar]
- Mewshaw RE, Edsall RJ, Jr, Yang C, Manas ES, Xu ZB, Henderson RA, Keith JC, Jr, Harris HA. ERbeta ligands. 3 Exploiting two binding orientations of 2-phenylnapthalene scaffold to achieve ERbeta selectivity. J Med Chem. 2005;48:3953–3979. doi: 10.1021/jm058173s. [DOI] [PubMed] [Google Scholar]
- Miller DW, Dill KA. Ligand binding to proteins: the binding landscape model. Protein Sci. 1997;6:2166–2179. doi: 10.1002/pro.5560061011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Min W, English BP, Luo G, Cherayil BJ, Kou SC, Xie XS. Fluctuating enzymes: lessons from single-molecule studies. Acc Chem Res. 2005a;38:923–931. doi: 10.1021/ar040133f. [DOI] [PubMed] [Google Scholar]
- Min W, Luo G, Cherayil BJ, Kou SC, Xie XS. Observation of a power-law memory kernel for fluctuations within a single protein molecule. Phys Rev Lett. 2005b;94:198302. doi: 10.1103/PhysRevLett.94.198302. [DOI] [PubMed] [Google Scholar]
- Mobley DL, Chodera JD, Dill KA. On the use of orientational restraints and symmetry corrections in alchemical free energy calculations. J Chem Phys. 2006;125:084902. doi: 10.1063/1.2221683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mobley DL, Chodera JD, Dill KA. Confine-and-release method: obtaining correct binding free energies in the presence of protein conformational change. J Chem Theory Comput. 2007a;3:1231–1235. doi: 10.1021/ct700032n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mobley DL, Graves AP, Chodera JD, McReynolds AC, Shoichet BK, Dill KA. Predicting absolute ligand binding free energies to a simple model site. J Mol Biol. 2007b;371:1118–1134. doi: 10.1016/j.jmb.2007.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mobley DL, Dill KA, Chodera JD. Treating entropy and conformational changes in implicit solvent simulations of small molecules. J Phys Chem B. 2008;112:938–946. doi: 10.1021/jp0764384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montfort WR, Perry KM, Fauman EB, Finer-Moore JS, Maley GF, Hardy L, Maley F, Stroud RM. Structure, multiple site binding, and segmental accomodation in thymidylate synthase on binding dUMP and an anti-folate. Biochemistry. 1990;29:6964–6977. doi: 10.1021/bi00482a004. [DOI] [PubMed] [Google Scholar]
- Morton A, Matthews BW. Specificity of ligand binding in a buried nonpolar cavity of {T4} lysozyme: linkage of dynamics and structural plasticity. Biochemistry. 1995;34:8576–8588. doi: 10.1021/bi00027a007. [DOI] [PubMed] [Google Scholar]
- Murthy KHM, Winborne EL, Minnich MD, Culp JS, Debouck C. The crystal structures at 2.2-A resolution of hydroxyethylene-based inhibitors bound to human immunodeficiency virus type 1 protease show that the inhibitors are present in two distinct orientations. J Biol Chem. 1992;267:22770–22778. [PubMed] [Google Scholar]
- Najmanovich R, Kuttner J, Sobolev V, Edelman M. Side-chain flexibility in proteins upon ligand binding. Proteins. 2000;39:261–268. doi: 10.1002/(sici)1097-0134(20000515)39:3<261::aid-prot90>3.0.co;2-4. [DOI] [PubMed] [Google Scholar]
- Noble ME, Endicott JA, Johnson LN. Protein kinase inhibitors: insights into drug design from structure. Science. 2004;303:1800–1805. doi: 10.1126/science.1095920. [DOI] [PubMed] [Google Scholar]
- Olano LR, Rick SW. Hydration free energies and entropies for water in protein interiors. J Am Chem Soc. 2004;126:7991–8000. doi: 10.1021/ja049701c. [DOI] [PubMed] [Google Scholar]
- Oostenbrink C, van Gunsteren WF. Free energies of binding of polychlorinated biphenyls to the estrogen receptor from a single simulation. Proteins. 2004;54:237–246. doi: 10.1002/prot.10558. [DOI] [PubMed] [Google Scholar]
- Orville AM, Elango N, Lipscomb JD, Ohlendorf DH. Structures of competitive inhibitor complexes of protocatechuate 3,4-dioxy-genase: multiple exogenous ligand binding orientations within the active site. Biochemistry. 1997;36:10039–10051. doi: 10.1021/bi970468n. [DOI] [PubMed] [Google Scholar]
- Pan C, Mezei M, Mujtaba S, Muller M, Zeng L, Li J, Wang Z, Zhou MM. Structure-guided optimization of small molecules inhibiting human immunodeficiency virus 1 Tat association with the human coactivator p300/CREB binding protein-associated factor. J Med Chem. 2007;50:2285–2288. doi: 10.1021/jm070014g. [DOI] [PubMed] [Google Scholar]
- Paulsen MD, Ornstein RL. Predicting the product specificity and coupling of cytochrome P450cam. J Comput Aided Mol Des. 1992;6:449–460. doi: 10.1007/BF00130396. [DOI] [PubMed] [Google Scholar]
- Pearlman DA. Evaluating the molecular mechanics poisson-boltzmann surface area free energy method using a congeneric series of ligands to p38 MAP kinase. J Med Chem. 2005;48:7796–7807. doi: 10.1021/jm050306m. [DOI] [PubMed] [Google Scholar]
- Pearlman DA, Charifson PS. Are free energy calculations useful in practice? A comparison with rapid scoring functions for the p38 MAP kinase protein system. J Med Chem. 2001;44:3417–3423. doi: 10.1021/jm0100279. [DOI] [PubMed] [Google Scholar]
- Pei Z, Li X, Longenecker K, Geldern TW, Wiedeman PE, Lubben TH, Zinker BA, Stewart K, Ballaron SJ, Stashko MA, Mika AK, Beno DW, et al. Discovery, structure-activity relationship, and pharmacological evaluation of (5-substituted-pyrrolidinyl-2-carbonyl)-2-cyanopyrrolidines as potent dipeptidyl peptidase IV inhibitors. J Med Chem. 2006;49:3520–3535. doi: 10.1021/jm051283e. [DOI] [PubMed] [Google Scholar]
- Perola E, Charifson PS. Conformational analysis of drug-like molecules bound to proteins: an extensive study of ligand reorganization upon binding. J Med Chem. 2004;47:2499–2510. doi: 10.1021/jm030563w. [DOI] [PubMed] [Google Scholar]
- Pospisil P, Ballmer P, Scapozza L, Folkers G. Tautomerism in computer-aided drug design. Journal of Receptors and Signal Transduction. 2003;23:361–371. doi: 10.1081/rrs-120026975. [DOI] [PubMed] [Google Scholar]
- Raag R, Poulos TL. Crystal structures of cytochrome P-450CAM complexed with camphane, thiocamphor, and adamantane: factors controlling P-450 substrate hydroxylation. Biochemistry. 1991;30:2674–2684. doi: 10.1021/bi00224a016. [DOI] [PubMed] [Google Scholar]
- Radivojac P, Iakoucheva LM, Oldfield CJ, Obradovic Z, Uversky VN, Dunker AK. Intrinsic disorder and functional proteomics. Biophys J. 2007;92:1439–1456. doi: 10.1529/biophysj.106.094045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reddy MR, Erion MD. Calculation of relative binding free energy differences for fructose 1,6-bisphosphatase inhibitors using the thermodynamic cycle perturbation approach. J Am Chem Soc. 2001;123:6246–6252. doi: 10.1021/ja0103288. [DOI] [PubMed] [Google Scholar]
- Reich SH, Melnick M, II, Davies JF, Appelt K, Lewis KK, Fuhry MA, Pino M, Trippe AJ, Nguyen D, Dawson H, et al. Protein structure-based design of potent orally bioavailable, nonpeptide inhibitors of human immunodeficiency virus protease. Proc Natl Acad Sci USA. 1995;92:3298–3303. doi: 10.1073/pnas.92.8.3298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rizzo RC, Jorgensen WL. OPLS all-atom model for amines: resolution of the amine hydration problem. J Am Chem Soc. 1999;121:4827–4836. [Google Scholar]
- Rizzo RC, Toba S, Kuntz ID. A molecular basis for the selectivity of thiadiazole urea inhibitors with stromelysin-1 and gelatinase-A from generalized born molecular dynamics simulations. J Med Chem. 2004;47:3065–3074. doi: 10.1021/jm030570k. [DOI] [PubMed] [Google Scholar]
- Roux B, Nina M, Poms R, Smith JC. Thermodynamic stability of water molecules in the bacteriorhodopsin proton channel: a molecular dynamics free energy perturbation study. Biophys J. 1996;71:670–681. doi: 10.1016/S0006-3495(96)79267-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruvinsky AM, Kozintsev AV. New and fast statistical-thermodynamic method for computation of protein-ligand binding entropy substantially improves docking accuracy. J Comput Chem. 2005;26:1089–1095. doi: 10.1002/jcc.20246. [DOI] [PubMed] [Google Scholar]
- Schames JR, Henchman RH, Siegel JS, Sotriffer CA, Ni H, McCammon JA. Discovery of a novel binding trench in HIV integrase. J Med Chem. 2004;47:1879–1881. doi: 10.1021/jm0341913. [DOI] [PubMed] [Google Scholar]
- Schwarzl SM, Tschopp TB, Smith JC, Fischer S. Can the calculation of ligand binding free energies be improved with continuum solvent electrostatics and an ideal-gas entropy correction? J Comput Chem. 2002;23:1143–1149. doi: 10.1002/jcc.10112. [DOI] [PubMed] [Google Scholar]
- Sharp KA. Important considerations impacting molecular docking. In: Shoichet BK, Alvarez J, editors. Virtual Screening in Drug Discovery. Boca Raton, FL: CRC Press; 2005. [Google Scholar]
- Sherman W, Day T, Jacobson MP, Friesner RA, Farid R. Novel procedure for modeling ligand/receptor induced fit effects. J Med Chem. 2006;49:534–553. doi: 10.1021/jm050540c. [DOI] [PubMed] [Google Scholar]
- Shirts MR, Mobley DL, Brown SP. Free energy calculations in structure-based drug design. In: Merz KM, Ringe D, Reynolds CH, editors. Structure Based Drug Discovery. Cambridge: Cambridge University Press; 2009. [Google Scholar]
- Shirts MR, Mobley DL, Chodera JD. Alchemical free energy calculations: ready for prime time? Ann Rep Comput Chem. 2007;3:41–59. [Google Scholar]
- Shoichet BK, Leach AR, Kuntz ID. Ligand solvation in molecular docking. Proteins. 1999;34:4–16. doi: 10.1002/(sici)1097-0134(19990101)34:1<4::aid-prot2>3.0.co;2-6. [DOI] [PubMed] [Google Scholar]
- Shoichet BK, McGovern SL, Wei B, Irwin JJ. Lead discovery using molecular docking. Curr Opin Chem Biol. 2002;6:439–446. doi: 10.1016/s1367-5931(02)00339-3. [DOI] [PubMed] [Google Scholar]
- Sousa SF, Fernandes PA, Ramos MJ. Protein-ligand docking: current status and future challenges. Proteins. 2006;65:15–26. doi: 10.1002/prot.21082. [DOI] [PubMed] [Google Scholar]
- Srinivasan J, Cheatham TE, III, Cieplak P, Kollman PA, Case DA. Continuum solvent studies of the stability of DNA, RNA, and phosphor-amidate-DNA helices. J Am Chem Soc. 1998;120:9401–9409. [Google Scholar]
- Stauffer SR, Stanton MG, Gregro AR, Steinbeiser MA, Shaffer JR, Nantermet PG, Barrow JC, Rittle KE, Collusi D, Espeseth AS, et al. Discovery and SAR of isonicotinamide BACE-1 inhibitors that bind [beta]-secretase in a N-terminal 10s-loop down conformation. Bioorg Med Chem Lett. 2007;17:1788–1792. doi: 10.1016/j.bmcl.2006.12.051. [DOI] [PubMed] [Google Scholar]
- Steinbrecher T, Case DA, Labahn A. A multistep approach to structure-based drug design: studying ligand binding at the human neutrophil elastase. J Med Chem. 2006;49:1837–1844. doi: 10.1021/jm0505720. [DOI] [PubMed] [Google Scholar]
- Steuber H, Czodrowski P, Sotriffer CA, Klebe G. Tracing changes in protonation: a prerequisite to binding to aldose reductase. J Mol Biol. 2007;373:1305–1320. doi: 10.1016/j.jmb.2007.08.063. [DOI] [PubMed] [Google Scholar]
- Stoll V, Stewart KD, Maring CJ, Muchmore S, Giranda V, Gu YG, Wang G, Chen Y, Sun M, Zhao C, et al. Influenza neuraminidase inhibitors: structure-based design of a novel inhibitor series. Biochemistry. 2003;42:718–727. doi: 10.1021/bi0205449. [DOI] [PubMed] [Google Scholar]
- Stout TJ, Tondi D, Rinaldi M, Barlocco D, Pecorari P, Santi DV, Kuntz ID, Stroud RM, Shoichet BK, Costi MP. Structure-based design of inhibitors specific for bacterial thymidylate synthase. Biochemistry. 1999;38:1607–1617. doi: 10.1021/bi9815896. [DOI] [PubMed] [Google Scholar]
- Stubbs MT, Reyda S, Dullweber F, Moller M, Klebe G, Dorsch D, Mederski WWKR, Wurziger H. pH-dependent binding modes observed in trypsin crystals: lessons for structure-based drug design. Chem-biochem. 2002;3:246–249. doi: 10.1002/1439-7633(20020301)3:2/3<246::aid-cbic246>3.0.co;2-#. [DOI] [PubMed] [Google Scholar]
- Sulsky R, Magnin DR, Huang Y, Simpkins L, Taunk P, Patel M, Zhu Y, Stouch TR, Bassolino-Klimas D, Parker R, et al. Potent and selective biphenyl azole inhibitors of adipocyte fatty acid binding protein (aFABP) Bioorg Med Chem Lett. 2007;17:3511–3515. doi: 10.1016/j.bmcl.2006.12.044. [DOI] [PubMed] [Google Scholar]
- Tang C, Schweiters CD, Clore GM. Open-to-closed transition in apo maltose-binding protein observed by paramagnetic NMR. Nature. 2007;449:1078–1082. doi: 10.1038/nature06232. [DOI] [PubMed] [Google Scholar]
- Taylor RD, Jewsbury PJ, Essex JW. A review of protein-small molecule docking methods. J Comput Aided Mol Des. 2002;16:151–166. doi: 10.1023/a:1020155510718. [DOI] [PubMed] [Google Scholar]
- Teague SJ. Implications of protein flexibility for drug discovery. Nat Rev Drug Discov. 2003;2:527–541. doi: 10.1038/nrd1129. [DOI] [PubMed] [Google Scholar]
- Tembe BL, McCammon JA. Ligand-receptor interactions. Comput Chem. 1984;8:281–283. [Google Scholar]
- Thomson JA, Perni RB. Hepatitis C virus NS3-4A protease inhibitors: countering viral subversion in vitro and showing promise in the clinic. Curr Opin Drug Discov Devel. 2006;9:606–617. [PubMed] [Google Scholar]
- Tirado-Rives J, Jorgensen WL. Contribution of conformer focusing to the uncertainty in predicting free energies for protein-ligand binding. J Med Chem. 2006;49:5880–5884. doi: 10.1021/jm060763i. [DOI] [PubMed] [Google Scholar]
- Uytterhoeven K, Sponer J, Meervelt LV. Two 1:1 binding modes for distamycin in the minor groove of d(GGCCAATTGG) Eur J Biochem. 2002;269:2868–2877. doi: 10.1046/j.1432-1033.2002.02952.x. [DOI] [PubMed] [Google Scholar]
- Vajpai N, Strauss A, Cowan-Jacob SW, Manley PW, Crzesiek S, Jahnke W. Solution conformations and dynamics of ABL kinase-inhibitor complexes determined by NMR substantiate the different binding modes of imatinib/nilotinib and dasatinib. J Biol Chem. 2008;283:18292–18302. doi: 10.1074/jbc.M801337200. [DOI] [PubMed] [Google Scholar]
- Volkman BF, Lipson D, Wemmer DE, Kern D. Two-state allo-steric behavior in a single-domain signaling protein. Science. 2001;291:2429–2433. doi: 10.1126/science.291.5512.2429. [DOI] [PubMed] [Google Scholar]
- von Itzstein M, Wu WY, Kok GB, Pegg MS, Dyason JC, Jin B, Van Phan T, Smythe ML, White HF, Oliver SW, et al. Rational design of potent sialidase-based inhibitors of influenza virus replication. Nature. 1993;363:418–423. doi: 10.1038/363418a0. [DOI] [PubMed] [Google Scholar]
- Vorobjev YN, Hermans J. ES/IS: estimation of conformational free energy by combining dynamics simulations with explicit solvent with an implicit solvent continuum model. Biophys Chem. 1999;78:195–205. doi: 10.1016/s0301-4622(98)00230-0. [DOI] [PubMed] [Google Scholar]
- Wang J, Deng Y, Roux B. Absolute binding free energy calculations using molecular dynamics simulations with restraining potentials. Biophys J. 2006;91:2798–2814. doi: 10.1529/biophysj.106.084301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warren GL, Andrews CW, Capelli AM, Clarke B, LaLonde J, Lambert MH, Lindvall M, Nevins N, Semus SF, Sender S, et al. A critial assessment of docking programs and scoring functions. J Med Chem. 2006;49:5912–5931. doi: 10.1021/jm050362n. [DOI] [PubMed] [Google Scholar]
- Warren G, Perola E. Field of extremes: if you re-refine them, they will come down. Paper presented at CUP IX; March 16-19, 2008; Santa Fe, NM. 2008. Available online at http://www.eyesopen.com/about/events/cups-2008/pdfs-CUP/CUP9-Field-of-Extremes.pdf. [Google Scholar]
- Warshel A, Sussman F, King G. Free energy of charges in solvated proteins: microscopic calculations using a reversible charging process. Biochemistry. 1986;25:8368–8372. doi: 10.1021/bi00374a006. [DOI] [PubMed] [Google Scholar]
- Wei BQ, Weaver LH, Ferrari AM, Matthews BW, Shoichet BK. Testing a flexible-receptor docking algorithm in a model binding site. J Mol Biol. 2004;337:1161–1182. doi: 10.1016/j.jmb.2004.02.015. [DOI] [PubMed] [Google Scholar]
- Weisberg E, Manley PW, Cowan-Jacob SW, Hochhaus A, Griffin JD. Second generation inhibitors of BCR-ABL for the treatment of imatinib-resistant chronic myeloid leukaemia. Nat Rev Cancer. 2007;7:345–356. doi: 10.1038/nrc2126. [DOI] [PubMed] [Google Scholar]
- Wong CF, McCammon JA. Dynamics and design of enzymes and inhibitors. J Am Chem Soc. 1986;108:3830–3832. [Google Scholar]
- Wright PE, Dyson HJ. Intrinsically unstructured proteins: reassessing the protein structure-function paradigm. J Mol Biol. 1999;293:321–331. doi: 10.1006/jmbi.1999.3110. [DOI] [PubMed] [Google Scholar]
- Zhang L, Hermans J. Hydrophilicity of cavities in proteins. Proteins Struct Funct Genet. 1996;24:433–438. doi: 10.1002/(SICI)1097-0134(199604)24:4<433::AID-PROT3>3.0.CO;2-F. [DOI] [PubMed] [Google Scholar]
- Zhang XJ, Wozniak JA, Matthews BW. Protein flexibility and adaptability seen in 25 crystal forms of T4 lysozyme. J Mol Biol. 1995;250:527–552. doi: 10.1006/jmbi.1995.0396. [DOI] [PubMed] [Google Scholar]
- Zhou G, Ferrer M, Chopra R, Kapoor TM, Strassmaier T, Weissenhorn W, Skehel JJ, Oprian D, Schreiber SL, Harrison SC, Wiley DC. The structure of an HIV-1 specific cell entry inhibitor in complex with the HIV-1 gp41 trimeric core. Bioorg Med Chem. 2000;8:2219–2227. doi: 10.1016/s0968-0896(00)00155-3. [DOI] [PubMed] [Google Scholar]


