Generating Coherent Patterns of Activity from Chaotic Neural Networks

Abstract

Neural circuits display complex activity patterns both spontaneously and when responding to a stimulus or generating a motor output. How are these two forms of activity related? We develop a procedure called FORCE learning for modifying synaptic strengths either external to or within a model neural network to change chaotic spontaneous activity into a wide variety of desired activity patterns. FORCE learning works even though the networks we train are spontaneously chaotic and we leave feedback loops intact and unclamped during learning. Using this approach, we construct networks that produce a wide variety of complex output patterns, input-output transformations that require memory, multiple outputs that can be switched by control inputs, and motor patterns matching human motion capture data. Our results reproduce data on pre-movement activity in motor and premotor cortex, and suggest that synaptic plasticity may be a more rapid and powerful modulator of network activity than generally appreciated.

Introduction

When we voluntarily move a limb or perform some other motor action, what is the source of the neural activity that initiates and carries out this behavior? We explore the idea that such actions arise from the reorganization of spontaneous neural activity. This hypothesis raises another question: How can apparently chaotic spontaneous activity be reorganized into the coherent patterns required to generate controlled actions? Following, but modifying and extending, earlier work (Jaeger and Haas, 2004; Maass et al., 2007), we show how external feedback loops or internal synaptic modifications can be used to alter the chaotic activity of a recurrently connected neural network and generate complex but controlled outputs.

Training a neural network is a process through which network parameters (typically synaptic strengths) are modified on the basis of output errors until a desired response is produced. Researchers in the machine learning and computer vision communities have developed powerful methods for training artificial neural networks to perform complex tasks (Rumelhart and McClelland, 1986; Hinton et al., 2007), but these apply predominantly to networks with feedforward architectures. Biological networks tend to be connected in a highly recurrent manner. Training procedures have also been developed for recurrently connected neural networks (Rumelhart et al., 1986; Williams and Zipser, 1989; Pearlmutter, 1989; Atiya and Parlos, 2000), but these are more computationally demanding and difficult to use than feedforward learning algorithms, and there are fundamental limitations to their applicability (Doya, 1992). In particular, these algorithms generally will not converge if applied to recurrent neural networks with chaotic activity, that is, activity that is irregular and exponentially sensitive to initial conditions (Abarbanel et al., 2008). This limitation is severe because models of spontaneously active neural circuits typically exhibit chaotic dynamics. For example, spiking models of spontaneous activity in cortical circuits (van Vreeswijk and Sompolinsky, 1996; Amit and Brunel, 1997; Brunel, 2000), which can generate realistic patterns of activity, and the analogous spontaneously active firing-rate model networks that we use here have chaotic dynamics (Sompolinsky et al., 1988).

To develop a successful training procedure for recurrent neural networks, we must solve three problems. First, feeding erroneous output back into a network during training can cause its activity to deviate so far from what is needed that learning fails to converge. In previous work (Jaeger and Haas, 2004), this problem was avoided by removing all errors from the signal fed back into the network. In addition to the usual synaptic modification, this scheme required a mechanism for removing feedback errors, and it is difficult to see how this latter requirement could be met in a biological system. Furthermore, feeding back a signal that is identical to the desired network output prevents the network from sampling fluctuations during training, which can lead to stability problems in the final network. Here, we show how the synaptic modification procedure itself can be used to control the feedback signal, without any other mechanism being required, in a manner that allows fluctuations to be sampled and stabilized. For reasons given below, we call this procedure FORCE learning.

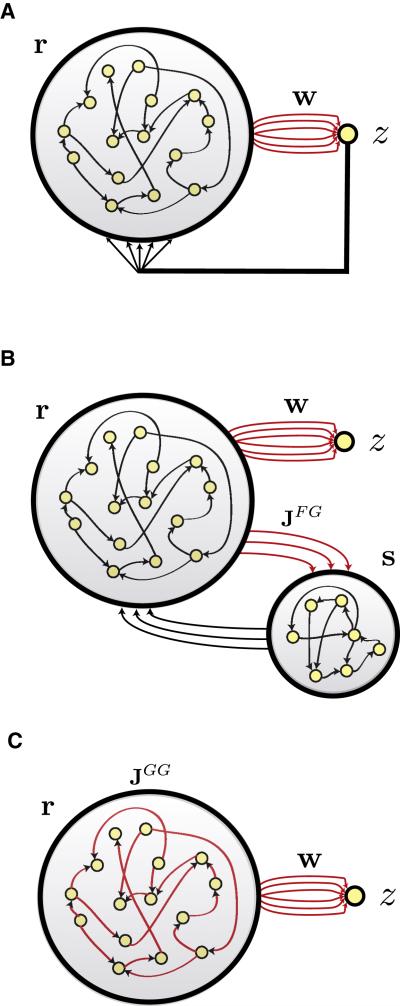
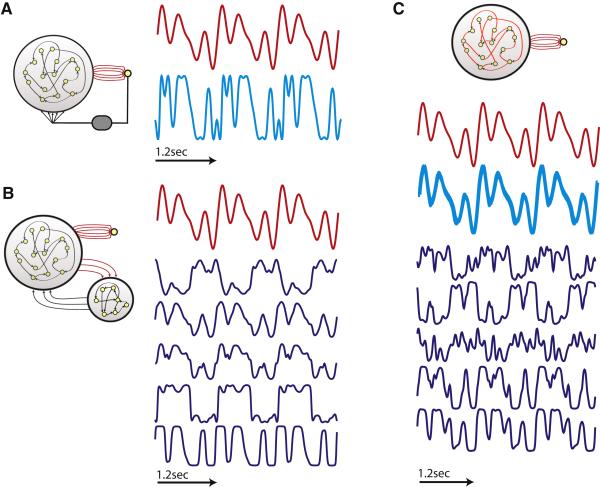
A second problem with training that is particularly severe in recurrent networks is credit assignment for output errors. Credit assignment amounts to figuring out which neurons and synapses are most responsible for output errors and therefore most in need of modification. This problem is particularly challenging for network units that do not produce the output directly. Jaeger and Haas (2004) dealt with this issue by restricting modification solely to synapses directly driving network output. Initially, we follow their lead in this, using the architecture of figure 1A. However, the power of FORCE learning allows us to train networks with the architectures shown in figures 1B and 1C, in which modifications are not restricted to network outputs. For reasons discussed below, these architectures are more biologically plausible than the network in figure 1A.

Figure 1.

Network architectures. In all three cases, a recurrent generator network with firing rates r drives a linear readout unit with output z through weights w (red) that are modified during training. Only connections shown in red are subject to modification. A) Feedback to the generator network (large network circle) is provided by the readout unit. B) Feedback to the generator network is provided by a separate feedback network (smaller network circle). Neurons of the feedback network are recurrently connected and receive input from the generator network through synapses of strength J^FG (red), which are modified during training. C) A network with no external feedback. Instead, feedback is generated within the network and modified by applying FORCE learning to the synapses with strengths J^GG internal to the network (red).

The third problem we address is training in the face of chaotic spontaneous activity. Jaeger and Haas (2004) avoided this problem by starting with networks that were inactive in the absence of input (which is the basis for calling them echo-state networks). As we show in the Results, there are significant advantages in using a network that exhibits chaotic activity prior to training. To exploit these advantages, however, we must avoid chaotic network activity during training. It turns out that the solution for learning in a recurrent network and for suppressing chaos turn out to be one and the same: synaptic modifications must be strong and rapid during the initial phases of training. This is precisely what the FORCE procedure achieves.

FORCE learning operates quite differently from traditional training in neural networks. Usually, training consists of performing a sequence of modifications that slowly reduce initially large errors in network output. In FORCE learning, errors are always small, even from the beginning of the training process. As a result, the goal of training is not significant error reduction, but rather reducing the amount of modification needed to keep the errors small. By the end of the training period, modification is no longer needed, and the network can generate the desired output autonomously.

From a machine learning point of view, the FORCE procedure we propose provides a powerful algorithm for constructing recurrent neural networks that generate complex and controllable patterns of activity either in the absence of or in response to input. From a biological perspective, it can be viewed either as a model for training-induced modification or, more conservatively, as a method for building functioning circuit models for further study. Either way, our approach introduces a novel way to think about learning in neural networks and to make contact with experimental data.

Results

The recurrent network that forms the basis of our studies is a conventional model in which the outputs of individual neurons are characterized by firing rates and neurons are sparsely interconnected through excitatory and inhibitory synapses of various strengths (Methods). Following ideas developed in the context of liquid-state (Maass et al., 2002) and echo-state (Jaeger, 2003) models, we assume that this basic network is not designed for any specific task, but is instead a general purpose dynamical system that will be co-opted for particular applications through subsequent synaptic modification. As a result, the connectivity and synaptic strengths of the network are chosen randomly (Methods). For the parameters we use, the initial state of the network is chaotic (figure 2A).

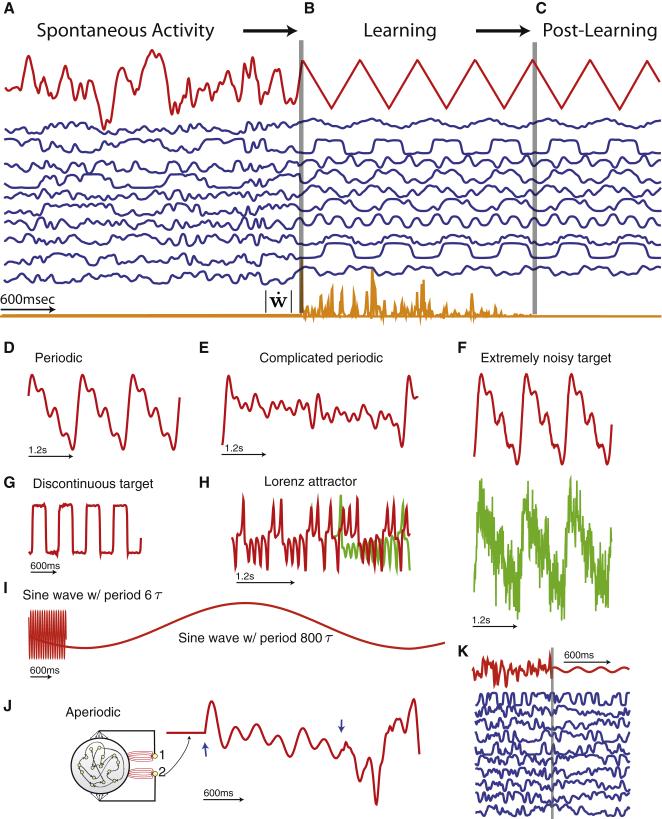
Figure 2.

FORCE learning in the network of figure 1A. A-C) The FORCE training sequence. Network output, z, is in red, the firing rates of 10 sample neurons from the network are in blue and the orange trace is the magnitude of the time derivative of the readout weight vector. A) Before learning, network activity and output are chaotic. B) During learning, the output matches the target function, in this case a triangle wave and the network activity is periodic because the readout weights fluctuate rapidly. These fluctuations subside as learning progresses. C) After training, the network activity is periodic and the output matches the target without requiring any weight modification. D-K) Examples of FORCE Learning. Red traces are network outputs after training with the network running autonomously. Green traces, where not covered by the matching red traces, are target functions. D) Periodic function composed of 4 sinusoids. E) Periodic function composed of 16 sinusoids. F) Periodic function of 4 sinusoids learned from a noisy target function. G) Square-wave. H) The Lorenz attractor. Initial conditions of the network and the target were matched at the beginning of the traces. I) Sine waves with periods of 60 ms and 8 s. J) A one-shot example using a network with two readout units (circuit insert). The red trace is the output of unit 2. When unit 1 is activated, its feedback creates the fixed point to the left of the left-most blue arrow, establishing the appropriate initial condition. Feedback from unit 2 then produces the sequence between the two blue arrows. When the sequence is concluded, the network output returns to being chaotic. K) A low amplitude sine wave (right of gray line) for which the FORCE procedure does not control network chaos (blue traces) and learning fails.

To specify a task for the networks of figure 1, we must define their outputs. In a full model, this would involve simulating activity all the way out to the periphery. In the absence of such a complete model, we need to have a way of describing what the network is “doing”, and here we follow another suggestion from the liquid- and echo-state approach (Maass et al., 2002; Jaeger, 2003; see also Buonomano and Merzenich, 1995). We define the network output through a weighted sum of its activities. Denoting the activities of the network neurons at time t by assembling them into a column vector r(t) and the weights connecting these neurons to the output by another column vector w, we define the network output as

$$z\left(t\right)={\mathbf{w}}^T\mathbf{r}\left(t\right).$$ (1)

Multiple readouts can be defined in a similar manner, each with its own set of weights, but we restrict the discussion to one readout at this point. Although a linear readout is a useful way of defining what we mean by the output of a network, it should be kept in mind that it is a computational stand-in for complex transduction circuitry. For this reason, we refer to the output-generating element as a unit rather than a neuron, and we call the components of w weights rather than synaptic strengths.

Having specified the network output, we can now define the task we want the network to perform, which is to set z(t) = f (t) for a pre-defined target function f (t). In most of the examples we present, the goal is to make a network produce the target function in the absence of any input. Later, we consider the more conventional network task of generating outputs that depend on inputs to the network in a specified way. Due to stability issues, this is an easier task than generating target functions without inputs, so we mainly focus on the no-input case.

In the initial instantiation of our model (figure 1A), we follow Jaeger and Haas (2004) and modify only the output weight vector w. All other network connections are left unchanged from their initial, randomly chosen values. The critical element that makes such a procedure possible is a feedback loop that carries the output z back into the network (figure 1A). Learning cannot be accomplished in a network receiving no external input without including such a loop. The strengths of the synapses from this loop onto the neurons of the network are chosen randomly and left unmodified. The strength of the feedback synapses is of order 1 whereas that of synapses between neurons of the recurrent network is of order 1 over the square root of the number of recurrent synapses per neuron. The feedback synapses are made stronger so that the feedback pathway has an appreciable effect on the activity of the recurrent network. Later, when we consider the architectures of figures 1B & 1C, we will no longer need such strong synapses.

FORCE Learning

Training in the presence of the feedback loop connecting the output in figure 1A back to the network is challenging because modifying the readout weights produces delayed effects that can be difficult to calculate. Modifying w has a direct effect on the output z given by equation 1, and it is easy to determine how to change w to make z closer to f through this direct effect. However, the feedback loop in figure 1A gives rise to a delayed effect when the resulting change in the output caused by modifying w propagates repeatedly along the feedback pathway and through the network, changing network activities. Because of this delayed effect, a weight modification that at first appears to bring z closer to f may later cause it to deviate away. This problem of delayed effects arises when attempting to modify synapses in any recurrent architecture, including those of figure 1B and 1C.

As stated in the Introduction, Jaeger and Haas (2004) eliminated the problem of delayed effects by clamping feedback during learning. In other words, the output of the network, given by equation 1 was compared with f to determine an error that controlled modification of the readout weights, but this output was not fed back to the network during training. Instead the feedback pathway was clamped to the target function f. The true output was only fed back to the network after training was completed.

We take another approach, which does not require any clamping or manipulation of the feedback pathway, it relies solely on error-based modification of the readout weights. In this scheme, we allow output errors to be fed back into the network, but we keep them small by making rapid and effective weight modifications. As long as output errors are small enough, they can be fed back without disrupting learning, i.e. without introducing significant delayed, reverberating effects. Because the method requires tight control of a small (first-order) error, we call it First-Order, Reduced and Controlled Error or FORCE learning. Although the FORCE procedure holds the feedback signal close to its desired value, it does not completely clamp it. This difference, although numerically small, has extremely significant implications for network stability. Small differences between the actual and desired output of the network during training allow the learning procedure to sample instabilities in the recurrent network and stabilize them.

A learning algorithm suitable for FORCE learning must rapidly reduce the magnitude of the difference between the actual and desired output to a small value, and then keep it small while searching for and eventually finding a set of fixed readout weights that can maintain a small error without further modification. A number of algorithms are capable of doing this (Discussion). All of them involve updates to the values of the weights at times separated by an interval Δt. Each update consists of evaluating the output of the network, determining how far this output deviates from the target function, and modifying the readout weights accordingly. Note that Δt is the interval of time between modifications of the readout weights, not the basic integration time step for the network simulation, which can be smaller than Δt .

At time t, the training procedure starts by sampling the network output, which is given at this point by w^T (t - Δt)r(t). The reason that the weights appear here evaluated at time t - Δt is that they have not yet been updated by the modification procedure, so they take the same values that they had at the end of the previous update. Comparing this output with the desired target output f (t), we define the error

$$e_{-}\left(t\right)={\mathbf{w}}^T(t-\Delta t)\mathbf{r}\left(t\right)-f\left(t\right).$$ (2)

The minus subscript signifies that this is the error prior to the weight update at time t . The next step in the training process is to update the weights from w(t - Δt) to w(t) in a way that reduces the magnitude of e_-(t). Immediately after the weight update, the output of the network is w^T (t)r(t), assuming that the weights are modified rapidly on the scale of network evolution (Discussion). Thus, the error after the weight update is

$$e_{+}\left(t\right)={\mathbf{w}}^T\left(t\right)\mathbf{r}\left(t\right)-f\left(t\right),$$ (3)

with the plus subscript signifying the error after the weights have been updated.

The goal of any weight modification scheme is to reduce errors by making |e₊(t)| < |e_-(t)| and also to converge to a solution in which the weight vector is no longer changing so that training can be terminated. This latter condition corresponding to making e₊(t)/e_-(t)→1 by the end of training. In most training procedures, these two conditions are accompanied by a steady reduction in the magnitude of both errors (e₊ and e_-) over time, which are both quite large during the early stages of training. FORCE learning is unusual in that the magnitudes of these errors are small throughout the learning process, although they are similarly reduced over time. This is done by making a large reduction in their size at the time of the first weight update, and then maintaining small errors throughout the training process that decrease with time.

If the training process is initialized at time t = 0, the first weight update will occur at time Δt. A weight modification rule useful for FORCE learning should make |e₊(Δt)|, the error after the first weight update has been performed, small, and then keep |e_-(Δt)| small while slowly increasing e₊(t)/e_-(t)→1. Given a small magnitude of e₊(t - Δt)), e_-(t), which is equal to e₊(t - Δt) plus a term of order Δt, is kept small by keeping the updating interval Δt sufficiently short. This means that learning can be performed with an error that starts and stays small.

As stated above, several modification rules meet the requirements of FORCE learning, but the recursive least squares (RLS) algorithm is particularly powerful (Haykin, 2002), and we use it here (see Discussion and Supplementary Materials for another, simpler algorithm). In RLS modification,

$$\mathbf{w}\left(t\right)=\mathbf{w}(t-\Delta t)-e_{-}\left(t\right)\mathbf{P}\left(t\right)\mathbf{r}\left(t\right),$$ (4)

where P(t) is an N × N matrix that is updated at the same time as the weights according to the rule

$$\mathbf{P}\left(t\right)=\mathbf{P}(t-\Delta t)-\frac{\mathbf{P}(t-\Delta t)\mathbf{r}\left(t\right){\mathbf{r}}^T\left(t\right)\mathbf{P}(t-\Delta t)}{1+{\mathbf{r}}^T\left(t\right)\mathbf{P}(t-\Delta t)\mathbf{r}\left(t\right)}.$$ (5)

The algorithm also requires an initial value for P , which is taken to be

$$\mathbf{P}\left(0\right)=\frac{\mathbf{I}}{\alpha },$$ (6)

where I is the identity matrix and α is a constant parameter. Equation 4 can be viewed as a standard delta-type rule (that is, a rule involving the product of the error and the presynaptic firing rate), but with multiple learning rates given by the matrix P , rather than by a scalar quantity. In this algorithm, P is a running estimate of the inverse of the correlation matrix of the network rates r plus a regularization term (Haykin, 2002), i.e. $\mathbf{P}={(\underset{t}{\mathbf{r}}\left(t\right){\mathbf{r}}^T\left(t\right)+\alpha \mathbf{I})}^{-1}$.

It is straightforward to show that the RLS rule satisfies the conditions necessary for FORCE learning. First, if we assume that the initial readout weights are zero for simplicity (this is not essential), the above equations imply that the error after the first weight update is

$$e_{-}\left(\Delta t\right)=-\frac{\alpha f\left(\Delta t\right)}{\alpha +{\mathbf{r}}^T\left(\Delta t\right)\mathbf{r}\left(\Delta t\right)}.$$ (7)

The quantity r^Tr is of order N , the number of neurons in the network, so as long as α = N, this error is small, and its size can be controlled by adjusting α (see below). Furthermore, at subsequent times, the above equations imply that

$$e_{+}\left(t\right)=e_{-}\left(t\right)(1-{\mathbf{r}}^T\left(t\right)\mathbf{P}\left(t\right)\mathbf{r}\left(t\right)),$$ (8)

The quantity r^TPr varies over the course of learning from something close to 1 to a value that asymptotically approaches 0, and it is always positive. This means that the size of the error is reduced by the weight update, as required, and ultimately e₊(t)/e_-(t)→1.

The parameter α , which acts as a learning rate, should be adjusted depending on the particular target function being learned. Small α values result in fast learning, but sometimes make weight changes so rapid that the algorithm becomes unstable. In those cases, larger α should be used (subject to the constraint α = N), but if α is too large, the FORCE algorithm may not keep the output close to the target function for a long enough time, causing learning to fail. In practice, values from 1 to 100 are effective, depending on the task.

In addition to dealing with feedback, FORCE learning must control the chaotic activity of the network during the training process. In this regard, it is important to note that the network we are considering is being driven through the feedback pathway by a signal approximately equal to the target function. Such an input can induce a transition between chaotic and non-chaotic states (Molgedey et al., 1992; Bertchinger and Natschläger, 2004; Rajan et al., 2008). This is how the problem of chaotic activity can be avoided. Provided that the feedback signal is of sufficient amplitude and frequency to induce a transition to a non-chaotic state (the required properties are discussed in Rajan et al., 2008), learning can take place in the absence of chaotic activity, even though the network is chaotic prior to learning.

Examples of FORCE Learning

Figure 2A-C illustrates how the activity of an initially chaotic network can be modified so that it ends up producing a periodic, triangle-wave output autonomously. Initially, with the output weight vector w chosen randomly, the neurons in the network exhibit chaotic spontaneous activity, as does the network output (figure 2A). When we start FORCE learning, the weights of the readout connections begin to fluctuate rapidly, which immediately changes the activity of the network so that it is periodic rather than chaotic and forces the output to match the target triangle wave (figure 2B). The progression of learning can be tracked by monitoring the size of the fluctuations in the readout weights (orange trace in figure 2B), which diminish over time as the learning procedure establishes a set of static weights that generate the target function without requiring modification. At this point, learning can be turned off, and the network continues to generate the triangle wave output on its own indefinitely (figure 2C). The learning process is rapid, converging in only four cycles of the triangle wave in this example.

FORCE learning can be used to modify networks that are initially in a chaotic state so that they autonomously produce a wide variety of outputs (Figure 2D-K). In these examples, training typically converges in about 1000τ, where τ is the basic time constant of the network, which we set to 10 ms. This means learning takes about 10 s of simulated time. Networks can be trained to produce periodic functions of different complexity and form (figures 2D-G and I), even when the target function is corrupted by noise (figure 2F). The dynamic range of the outputs that chaotic networks can be trained to generate by FORCE learning is impressive. For example, a 1000 neuron network with a time constant of 10 ms can produce sine wave outputs with periods ranging from 60 ms to 8 s (figure 2I).

FORCE learning is not restricted to periodic functions. For example, a network can be trained to produce an output matching one of the dynamic variables of the three-dimensional chaotic Lorenz attractor (Methods, see also Jaeger and Haas, 2004), although in this case, because the target is itself a chaotic process, a precise match between output and target can only last for a finite amount of time (figure 2H). After the two traces diverge, the network still produces a trace that looks like it comes from the Lorenz model.

FORCE learning can also produce a segment matching a one-shot, non-repeating target function (figure 2J). To produce such a one-shot sequence, the network must be initialized properly, and we do this by introducing a fixed-point attractor as well as the network configuration that produces the one-shot sequence. This is done by adding a second readout unit to the network that also provides feedback (Methods, network diagram in figure 2J). The first feedback unit induces the fixed point corresponding to a constant z output (horizontal red line in figure 2J), and then the second unit induces the target pattern (red trace between the arrows in figure 2J). As shown below, initialization can also be achieved through appropriate input.

As discussed above, FORCE learning must induce a transition in the network from chaotic to non-chaotic activity during training. This requires an input to the network, through the feedback loop in our case, of sufficient amplitude. If we try to train a network to generate a target function with too small an amplitude, the activity of the network neurons remains chaotic even after FORCE learning is activated (figure 2K). In this case, learning does not converge to a successful solution. There are a number of solutions to this problem. It is possible for the network to generate low amplitude oscillatory and non-oscillatory functions if these are displaced from zero by a constant shift. Alternatively, the networks shown in figure 1B and C can be trained to generate low amplitude signals centered near zero.

PCA Analysis of FORCE Learning

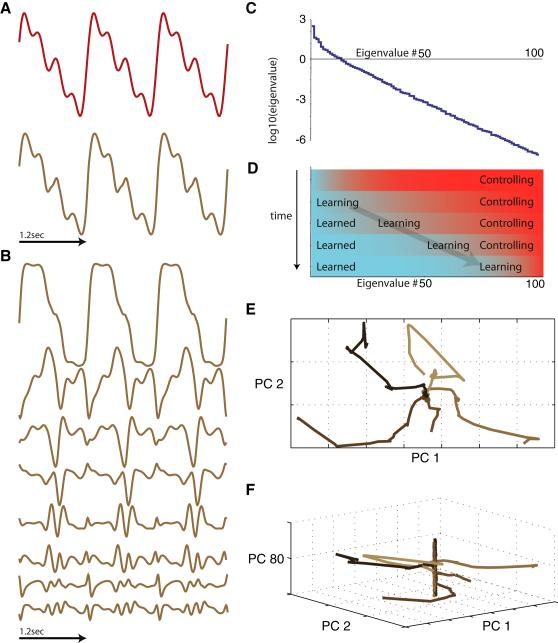
The activity of a network that has been modified by the FORCE procedure to produce a particular output can be analyzed by principal component analysis (PCA). For a network producing the periodic pattern shown in figure 3A, the distribution of PCA eigenvalues (figure 3C) indicates that the trajectory of network activity lies primarily in a subspace that is of considerably lower dimension than the number of network neurons. The projections of the network activity vector r(t) onto the PC vectors form a set of orthogonal basis functions (figure 3B) from with the target function is generated. An accurate approximation of the network output (brown trace in Figure 3A) can be generated using the basis functions derived from only the first 8 principal components (with components labeled in decreasing order of the size of their eigenvalues). These 8 components are not the whole story, however, because, along with generating the target function, the network must be stable. If we express the readout weight vector in terms of its projections onto the PC vectors of the network activity, we find that learning sets about the top 50 of these projections to uniquely specified values (figure 3E). The remaining projections take different values from one learning trial to the next, depending on initial conditions (figure 3F). This multiplicity of solutions greatly simplifies the task of finding successful readout weights.

Figure 3.

Principal component analysis of network activity. A) Output after training a network to produce a sum of four sinusoids (red), and the approximation (brown) obtained using activity projected onto the 8 leading principal components. B) Projections of network activity onto the leading eight PC vectors. C) PCA eigenvalues for the network activity that generated the waveform in A. Only the largest 100 of 1000 eigenvalues are shown. D) Schematic showing the transition from control to learning phases of learning as a function of time and of PC eigenvalue. E) Evolution of the projections of w onto the two leading PC vectors during learning starting from five different initial conditions. These values converge to the same point on all trials. F) The same weight evolution but now including the projection onto PC vector 80 as a third dimension. The final values of this projection are different on each of the 5 runs, resulting in the vertical line at the center of the figure. Nevertheless, all of these networks generate the output in A.

The uneven distribution of eigenvalues shown in figure 3C illustrates why the RLS algorithm works so well for FORCE learning. As mentioned previously, the matrix P acts as a set of learning rates for the RLS algorithm. This is seen most clearly by shifting to a basis in which P is diagonal. Assuming learning has progressed long enough for P to have converged to the inverse correlation matrix of r, the diagonal basis is achieved by projecting w and r onto the PC vectors. Doing this, it is straightforward to show that the learning rate for the component of w aligned with PC vector a after M weight updates is 1/(Mλ_a +α), where λ_a is the corresponding PC eigenvalue. This rate divides the RLS process into two stages, one when M <α/λ_a in which the major role of weight modification is to control the output (set it close to f), and another when M >α/λ_a in which the goal is learning, that is, finding a static weight that accomplishes the task. Components of w with large eigenvalues quickly enter the learning phase, whereas those with small eigenvalues spend more time in the control phase (figure 3D). Controlling components with small eigenvalues allows weight projections in dimensions with large eigenvalues to be learned.

The learning rate for all components during the control phase is 1/α. During the learning phase, the rate for PC component a is proportional to 1/λ_a. The average rate of change (as opposed to just the learning rate) of the projection of the output weight vector onto principal component a is proportional to $\sqrt{{\lambda }_a}∕(M{\lambda }_a+\alpha )$ because the factor of r in equation 4 introduces a term proportional to $\sqrt{{\lambda }_a}$, so the full rate of change for large M goes as $1∕\sqrt{{\lambda }_a}$. This is exactly what it should be, because in the expression for z, this change is multiplied by the projection of r onto PC vector a, which again has an amplitude proportional to $\sqrt{{\lambda }_a}$. Thus, RLS, by having rates of change of w proportional to $1∕\sqrt{{\lambda }_a}$ in the PC basis, allows all the projections to, potentially, contribute equally to the output of the network.

Comparison of Echo-State and FORCE Feedback

In echo-state learning (Jaeger and Haas, 2004), the feedback signal during training was set equal to the target function f (t). In FORCE learning, the feedback signal is z(t) during training. To compare these two methods, we introduce a mixed feedback signal, setting the feedback equal to γ f (t) + (1-γ)z(t) during training. Thus, γ = 0 corresponds to FORCE learning and γ =1 to echo-state learning, with intermediate values interpolating between these two approaches.

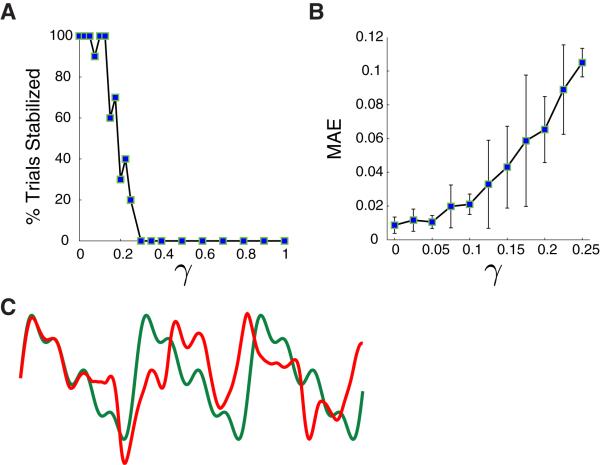
Training to produce the output of figure 3A, we find the network is only stable on the majority of trials when γ < 0.15, in other words close to the FORCE limit (figure 4A). Furthermore, in this γ range, the error in the output after training increases as a function of γ, meaning γ = 0 performs best (figure 4B). For a typical instability of pure echo-state learning, the output matches the target briefly after learning is terminated, but then it deviates away (figure 4C). Because this stability problem arises from the failure of the network to sample feedback fluctuations, it can be alleviated somewhat by introducing noise into the feedback loop during training (Jaeger and Haas, 2004, introduced noise into the network, which is less effective). Doing this, we find that pure echo-state learning converges on about 50% of the trials, but the error on these is significantly larger than for pure FORCE learning.

Figure 4.

Comparison of different mixtures of FORCE (γ = 0 and echo-state (γ =1) feedback. A) Percent of trials resulting in stable generation of the target function. B) Mean absolute error (MAE) between the output and target function after learning over the γ range where learning converged. C) Example run with output (red) and target function (green) for γ =1. The trajectory is unstable.

Advantages of Chaotic Spontaneous Activity

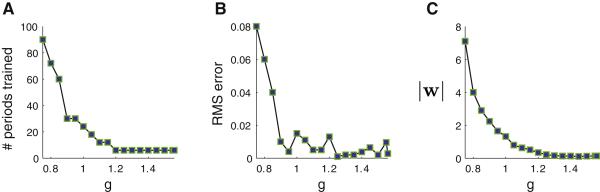
To study the effect of spontaneous chaotic activity on network performance, we introduce a factor g that scales the strengths of the recurrent connections within the network. Networks with g <1 are inactive prior to training, whereas networks with g >1 exhibit chaotic spontaneous activity (Sompolinsky et al., 1988) that gets more irregular and fluctuates more rapidly as g is increased beyond 1 (we typically use g =1.5).

The number of cycles required to train a network to generate the periodic target function shown in figure 3A drops dramatically as a function of g , continuing to fall as g gets larger than 1 (figure 5A). The average root-mean-square (RMS) error, indicating the difference between the target function and the output of the network after FORCE learning, also decreases with g (figure 5B). Another measure of training success is the magnitude of the readout weight vector |w| (figure 5C). Large values of |w| indicate that the solution found by a learning process involves cancellations between large positive and negative contributions. Such solutions tend to be unstable and sensitive to noise. The magnitude of the weight vector falls as a function of g and takes its smallest values in the region g > 1 characterized by chaotic spontaneous activity.

Figure 5.

Chaos improves training performance. Networks with different g values (Methods) were trained to produce the output of figure 3A. Results are plotted against g in the range 0.75 < g <1.56, where learning converged. A) Number of cycles of the periodic target function required for training. B) The RMS error of the network output after training. C) The length of the readout weight vector |w| after training.

These results indicate that networks that are initially in a chaotic state are quicker to train and produce more accurate and robust outputs than non-chaotic networks. Learning works best when g > 1 and, in fact, fails in this example for networks with g > 0.75. This might suggest that the larger the g value the better, but there is an upper limit. Recall that FORCE learning does not work if the feedback from the readout unit to the network fails to suppress the chaos in the network. For any given target function and set of feedback synaptic strengths, there is an upper limit for g beyond which chaos cannot be suppressed by FORCE learning. Indeed, the range of g values in figure 5 terminates at g = 1.56 because learning did not converge for higher g values due to this problem. Thus, the best value of g for a particular target function is at the “edge of chaos” (Bertchinger and Natschläger, 2004), that is the g value just below the point where FORCE learning fails to suppress chaotic activity during training.

Distorted and Delayed Feedback

The linear readout unit was introduced into the network model as a stand-in for a more complex, un-modeled peripheral system, in order to define the output of the network. The critical information provided by the readout unit is the error signal needed to guide weight modification, so its biological interpretation should be as a system that computes or estimates the deviation between an action generated by a network and the desired action. However, in the network configuration presented to this point (figure 1A), the readout unit, in addition to generating the error signal that guides learning, is also the source of feedback. Given that the output in a biological system is actually the result of a large amount of nonlinear processing and that feedback, whether proprioceptive or a motor efference copy, may have to travel a significant distance before returning to the network, we begin this section by examining the effect of introducing delays and nonlinear distortions along the feedback pathway from the readout unit to the network neurons.

The FORCE learning scheme is remarkably robust to distortions introduced along the feedback pathway (figure 6A). Nonlinear distortions of the feedback signal can be introduced as long as they do not diminish the temporal fluctuations of the output to the point where chaos cannot be suppressed. We have also introduced low-pass filtering into the feedback pathway, which can be quite extreme before the network fails to learn. Delays can be more problematic if they are too long. The critical point is that FORCE learning works as long as the feedback is of an appropriate form to suppress the initial chaos in the network. This means that the feedback really only has to match the period or the duration of the target function and roughly have the same frequency content.

Figure 6.

Feedback variants. A) Network trained to produce a periodic output (red trace) when its feedback (cyan trace) is 1.3tanh(sin(πz(t -100 ms)), a delayed and distorted function of the output z(t) (gray oval in circuit diagram). B) FORCE learning with a separate feedback network (circuit diagram). Output is the red trace, and blue traces show activity traces from 5 neurons within the feedback network. C) A network (circuit diagram) in which the internal synapses are trained to produce the output (red). Activities of 5 representative network neurons are in blue. The thick cyan traces are overlays of the component of the input to each of these 5 neurons induced by FORCE learning, $\underset{j}{}(J_{ij}\left(t\right)-J_{ij}\left(0\right))r_j\left(t\right)$ for i=1K 5.

FORCE Learning with Other Network Architectures

Even allowing for distortion and delay, the feedback pathway, originating as it does from the linear readout unit, is a non-biological element of the network architecture of figure 1A. To address this problem, we consider two ways of separating the feedback pathway from the linear readout of the network and modeling it more realistically. The first is to provide feedback to the network through a second neural network (figure 1B) rather than via the readout unit. To distinguish the two networks, we call the original network, present in figure 1A, the generator network and this new network the feedback network. The feedback network has nonlinear, dynamic neurons identical to those of the generator network, and is recurrently connected. Each unit of the feedback network produces a distinct output that is fed back to a subset of neurons in the generator network, so the task of carrying feedback is shared across multiple neurons. This repairs two biologically implausible aspects of the architecture of figure 1A: the strong feedback synapses mentioned above and the fact that every neuron in the network receives the same feedback signal.

When we include a feedback network (figure 1B), FORCE learning takes place both on the weights connecting the generator network to the readout unit (as in the architecture of figure 1A) and on the synapses connecting the generator network to the feedback network (red connections in figure 1B). Separating feedback from output introduces a credit-assignment problem because changes to the synapses connecting the generator network to the feedback network do not have a direct effect on the output. To solve this problem within the FORCE learning scheme, we treat every neuron subject to synaptic modification as if it were the readout unit, even when it is not. In other words, we apply equations 4 & 5 to every synapse connecting the generator network to the feedback network (Supplementary Materials), and we also apply them to the weights driving the readout unit. When we modify synapses onto a particular neuron of the feedback network, the vector r in these equations is composed of the firing rates of generator network neurons presynaptic to that feedback neuron, and the weight vector w is replaced by the strengths of the synapses it receives from these presynaptic neurons. However, the same error term that originates from the readout (equation 2) is used in these equations whether they are applied to the weights of the readout unit or synapses onto neurons of the feedback network (Methods). The form of FORCE learning we are using is cell autonomous, so no communication of learning-related information between neurons is required to implement these modifications, except that they all use a global error signal.

FORCE learning with a feedback network and independent readout unit can generate complex outputs similar to those in figure 4, although parameters such as α (equation 6) may require more careful adjustment. After training, when the output of these networks matches the target function, the activities of neurons in the feedback network do not, despite the fact that their synapses are modified by the same algorithm as the readout weights (figure 6B). This difference is due to the fact that the feedback network neurons receive input from each other as well as from the generator network, and these other inputs are not modified by the FORCE procedure. Differences between the activity of feedback network neurons and the output of the readout unit can also arise from different values of the synapses and the readout weights prior to learning.

With a separate feedback network, the feedback to an individual neuron of the generator network is a random combination of the activities of a subset of feedback neurons, summed through random synaptic weights. While these sums bear a certain resemblance to the target function, they are not identical to it nor are they identical for different neurons of the generator network. Nevertheless, FORCE learning works. This extends the result of figure 6A, showing not only that the feedback does not have to be identical to the network output, but that it does not even have to be identical for each neuron of the generator network.

Why does this form of learning, in which every neuron with synapses being modified is treated as if it were producing the output, work? In the example of figure 6B, the connections from the generator network to the readout unit and to the feedback network are sparse and random (Methods), so that neurons in the feedback network do not receive the same inputs from the generator network as the readout unit. However, suppose for a moment that each neuron of the feedback network, as well as the readout unit, received synapses from all of the neurons of the generator network. In this case, the changes to the synapses onto the feedback neurons would be identical to the changes of the weights onto the readout unit and therefore would induce a signal identical to the output into each neuron of the feedback network. This occurs, even though there is no direct connection between these two circuit elements, because the same learning rule with the same global error is being applied in both cases.

The explanation of why FORCE learning works in the feedback network when the connections from the generator network are sparse rather than all-to-all (as in figure 6B) relies on the accuracy of randomly sampling a large system (Sussillo, 2009). With sparse connectivity, each neuron samples a subset of the activities within the full generator network, but if this sample is large enough, it can provide an accurate representation of the leading principal components of the activity of the generator network that drive learning. This is enough information to allow learning to proceed. For figure 6B, we used an extremely sparse connectivity (Methods) to illustrate that FORCE learning can work even when the connections of the units being modified are highly non-overlapping.

The original generator network we used (figure 1A) is recurrent and can produce its own feedback. This means that we should be able to apply FORCE learning to the synapses of the generator network itself, in the arrangement shown in figure 1C. To implement FORCE learning within the generator network (Supplementary Materials), we modify every synapse in that network using equations 4-5. To apply these equations, the vector w is replaced by the set of synapses onto a particular neuron being modified, and r is replaced by the vector formed from the firing rates of all the neurons presynaptic to that network neuron. As in the example of learning in the feedback network, FORCE learning is also applied to the readout weights, and the same error, given by equation 2, is used for every synapse or weight being modified.

FORCE learning within the network can produce a complex target output (figure 6C). An argument similar to that given for learning within the feedback network can be applied to FORCE learning for synapses within the generator network. To illustrate how FORCE learning works, we express the total current into each neuron of the generator network as the sum of two terms. One is the current produced by the original synaptic strengths prior to learning, $\underset{j}{\overset{J_{ij}}{}}\left(0\right)r_j\left(t\right)$ for neuron i. The other is the extra current generated by the learning-induced changes in these synapses, $\underset{j}{}(J_{ij}\left(t\right)-J_{ij}\left(0\right))r_j\left(t\right)$. The first term, as well as the total current, is different for each neuron of the generator network because of the random initial values of the synaptic strengths. The second, learning-induced current, however, is virtually identical to the target function for each neuron of the network (figure 6C, cyan). Thus, FORCE learning induces a signal representing the target function into the network, just as it does for the architecture of figure 1A, but in a subtler and more biologically realistic manner.

Output patterns like those in figure 2 can be reproduced by FORCE learning applied within the generator or feedback networks. In the following sections, we illustrate the capacity of these forms of FORCE learning while, at the same time, introducing new tasks. All of the examples shown can be reproduced using all three of the architectures in figure 1, but for compactness we show results from learning in the generator network in figure 7 and learning in the feedback network in figure 8. For the interested reader, Matlab files that implement FORCE learning in the different architectures are included with the Supplementary Materials.

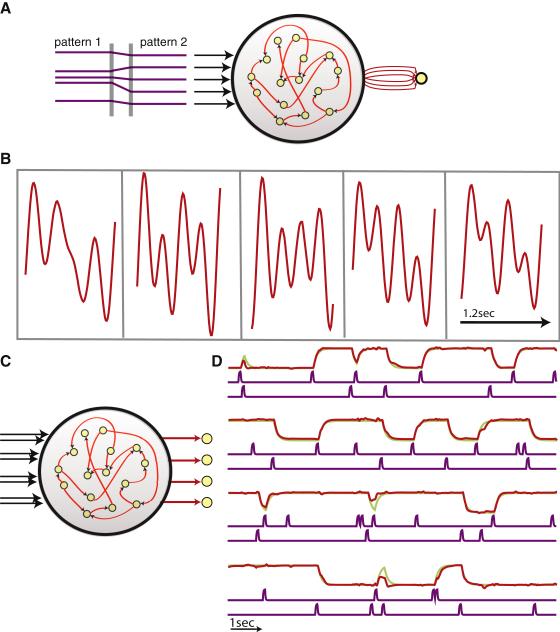
Figure 7.

Multiple pattern generation and 4-Bit memory through learning in the generator network. A) Network with control inputs used to produce multiple output patterns (synapses and readout weights that are modifiable in red). B) Five outputs (1 cycle of each periodic function made from 3 sinusoids is shown) generated by a single network and selected by static control inputs. C) A network with 4 outputs and 8 inputs used to produce a 4-bit memory (modifiable synapses and readout weights in red). D) Red traces are the 4 outputs, with green traces showing their target values. Purple traces show the 8 inputs, divided into ON and OFF pairs associated with the output trace above them. The upper input in each pair turns the corresponding output on (sets it to +1). The lower input of each pair turns the output off (sets it to -1). After learning, the network has implemented a 4-bit memory, with each output responding only to its two inputs while ignoring the other inputs.

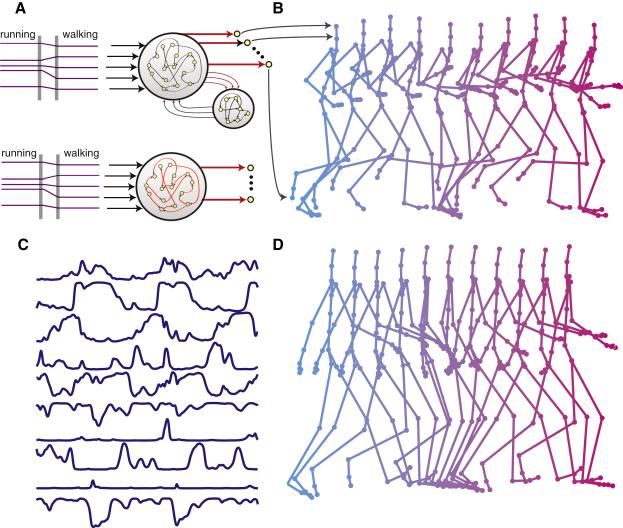
Figure 8.

Networks that generate both running and walking human motions. A) Either of these two network architectures can be used to generate the running and walking motions (modifiable readout weights shown in red), but the upper network is shown. Constant inputs differentiate between running and walking (purple). Each of 95 joint angles is generated through time by one of the 95 readout units (curved arrows). B) The running motion generated after training. Cyan frames show early and magenta frames late movement phases. C) Ten sample network neuron activities during the walking motion. D) The walking motion, with colors as in B.

Switching Between Multiple Outputs and Input-Output Mapping with Memory

The examples to this point have involved a single target function. We can train networks with the architecture of figure 1C in both sparse and fully connected configurations (we illustrate the sparse case) to produce multiple functions, with a set of inputs controlling which is generated at any particular time. We do this by introducing static control inputs to the network neurons (figure 7A) and pairing each desired output function with a particular input pattern (Methods). The constant values of the control inputs are chosen randomly. When a particular target function is being either trained or generated, the control inputs to the network are set to the corresponding static pattern and held constant until a different output is desired. The control inputs do not supply any temporal information to the network, they act solely as a switching signal to select a particular output function. The result is a single network that can produce a number of different outputs depending on the values of the control inputs (figure 7B).

Up to now, we have treated the network we are studying as a source of what are analogous to motor output patterns. Networks can also generate complex input/output maps when inputs are present. Figure 7C shows a particularly complex example of a network that functions as a 4-bit memory that is robust to input noise. This network has 8 inputs that randomly connect to neurons in the network and are functionally divided into pairs (Methods). The input values are held at zero except for short pulses to positive values that act as ON and OFF commands for the 4 readout units. Input 1 is the ON command for output 1 and input 2 is its OFF command. Similarly, inputs 3 and 4 are the ON and OFF commands for output 2, and so on. Turning on an output means inducing a transition to a state with a fixed positive value of 1, and turning it off means switching it to -1. After FORCE learning, the inputs correctly turn the appropriate outputs on and off with little crosstalk between inputs and inappropriate outputs (figure 7C). This occurs despite the random connectivity of the network, which means that the inputs do not segregate into different channels. This example requires the network to have, after learning, 16 different fixed point attractors, one for each of the 4² possible combinations of the 4 outputs, and the correct transitions between these attractors induced by pulsing the 8 inputs.

A Motion Capture Example

Finally, we consider an example of running and walking based on data obtained from human subjects performing these actions while wearing a suit that allows variables such as joint angles to be measured (also studied by Taylor et al., 2008 using a different type of network and learning procedure). These data, from the CMU Motion Capture Library, consist of 95 joint angles measured over hundreds of time steps.

We implemented this example using all the architectures in figure 1 in both sparse and fully connected configurations with similar results (we show a sparse example using the architecture of figure 1B). Producing all 95 joint angle sequences in the data sets requires that these networks have 95 readout units. For internal learning, subsets of neurons subjected to learning were assigned to each readout unit and trained using the error generated by that unit (Methods). Although running and walking might appear to be periodic motions, in fact the joint angles in the real data are non-periodic. For this reason, we introduced static control inputs to initialize the network prior to starting the running or walking motion. Because we wanted a single network to generate both motions, we also used the control inputs to switch between them, as in figure 7A. The successfully trained networks produced both motions (figure 8; for an animated demo showing all the architectures of figure 1 see the avi files included with the Supplementary Materials) demonstrating that a single chaotic recurrent network can generate multiple, high-dimensional, non-periodic patterns that resemble complex human motions.

Discussion

In the Introduction, we mentioned that FORCE learning could be viewed either as a model for learning-induced modification of biological networks or, more simply, as a method for constructing models of these networks. Our results should be evaluated in light of both of these interpretations.

FORCE learning solves some, but certainly not all, of the problems associated with applying ideas about learning from mathematical neural networks to biological systems. Biological networks exhibit complex and irregular spontaneous activity that probably has both chaotic and stochastic sources. FORCE learning provides an approach to network training that can be applied under these conditions (see, in particular, figure 2F). Furthermore, training does not require any reconfiguration of the network or changes in its dynamics other than the introduction of synaptic modification. Finally, the networks constructed by FORCE learning are more stable than in previous approaches.

FORCE learning relies on an error signal that, in our examples, is based on a readout unit that is not intended to be a realistic circuit element. It is not clear how the error is computed in biological systems. This is a problem for all models of supervised learning. In motor learning, we imagine that the target function is generated by an internal model of a desired movement and that circuitry exists for comparing this internal model with the motor signal generated by the network and for producing a modulatory signal that guides synaptic plasticity. The cerebellum has been proposed as a possible locus for such internal modeling (Miall et al., 1993). Examples like that of figure 8, which involve multiple outputs, require multiple error signals. For figure 8, we subdivided the network being trained into different regions in which plasticity was controlled by a different error signal. If the error is carried by a neuromodulator, this would require multiple pathways (though not necessarily multiple modulators) with at least some spatial targeting. If the error signal is transmitted as in the case of the climbing fibers of the cerebellum, multiple error signals are more straightforward to handle. Examples with a single output only require a single global error signal.

It is also not known how the error signal, once generated, controls synaptic plasticity. Again, this is a problem associated with all models of error- or reward-based learning. FORCE learning adds the condition that this modification act rather quickly compared to the timescale of the action being learned, at least during the initial phases of learning. Both because it is under the control of an error signal and because it acts rapidly, the plasticity required does not match that of typical long-term potentiation experiments, and it is a challenge raised by this work to uncover how such rapid plasticity can be realized biologically, or if it is realized at all. Whatever the plasticity mechanism, a key component of FORCE learning is producing the roughly correct output even during the initial stages of training. Analogously, people cannot learn fine manual skills by randomly flailing their arms about and having their movement errors slowly diminish over time, which would be analogous to more conventional network learning schemes. FORCE learning reminds us that motor learning works best when the desired motor action is duplicated as accurately as possible during training.

The RLS algorithm we have used is neuron-specific but not synapse-specific. By this we mean that the algorithm uses information about all the inputs to a given neuron to guide modification of its individual synapses. The algorithm requires some fairly involved calculations, although not matrix inversion. It is possible to use a simpler, synapse-specific weight modification procedure in which the matrix P is replaced by a single learning rate (Supplementary Material). Provided that this scalar rate is adapted over time, FORCE learning can work with such a simpler plasticity mechanism. Nevertheless, RLS is clearly a more powerful algorithm because it adapts the learning rate to the magnitude of different principal components of the network activity. It is possible that a scheme that is simpler and more biologically plausible than RLS can be devised that retains this desirable feature.

The architectures of figures 1B and 1C, where learning occurs within feedback or generator networks, match biological circuits better than that of figure 1A, where feedback comes directly from the readout unit. A key feature of learning in these cases is that network plasticity is accompanied by plasticity along the output or error-computing pathway. Plasticity in multiple areas (at least two, in these examples) coupled by a common error signal is a basic prediction of the model. It is a curious feature that performance is comparable for all three architectures in figure 1, despite that fact that the case of figure 1C involves changing many more synaptic strengths. We do not currently know whether changing synapses within a network offers advantages for the function-generation task. It may, but the modification algorithms developed thus far are not powerful enough exploit these advantages.

We now come to an analysis of FORCE learning as a model-building scheme. We have studied how spontaneously active neural networks can be modified to generate desired outputs, and how control inputs can be used to initiate and select among those outputs. Although this has most direct application to motor systems, it can be generalized to a broader picture of cognitive processing (Yuste et al., 2005; Buonomano and Maass, 2009), as our example of a 4-bit, input-controlled memory suggests.

Ganguli et al. (2008) have discussed the advantages of using an effective delay-line architecture in applications of networks to memory retention. Provided that a feedback loop from the output, as in figure 1A, is in place, a delay line structure within the generator network should be quite effective for function generation as well. However, because we were interested in networks that generate spontaneous activity even in the absence of the output feedback loop, we did not consider such an arrangement in any detail.

The two-step process by which we induced a chaotic network to produce a non-periodic sequence (figures 2J and 8) may have an analog in motor and premotor cortex. The brief fixed point that we introduced to terminate chaotic activity results in a sharp drop in the fluctuations of network neurons just before the learned sequence is generated. Churchland et al. (2006) and Churchland and Shenoy (2007a) have reported just such a drop in variability in their recordings from motor and premotor areas in monkeys immediately before they performed a reaching movement. Except in the simplest of examples, the activity of the generator neurons bears little relationship to the output of the network. Trying to link single-neuron responses to motor actions may thus be misguided. Instead, results from our network models suggest that it may be more instructive to study network-wide modes or patterns of activity extracted by principal components analysis of multi-unit recordings (Fetz, 1992; Robinson, 1992; Churchland and Shenoy, 2007b).

There are some interesting and perhaps unsettling aspects of the networks we have studied. First, the connectivity of the generator network in the architectures of figure 1A and 1B is completely random, even after the network has been trained to perform a specific task. It would be extremely difficult to understand how the generator network “works” by analyzing its synaptic connectivity. Even when the synapses of the generator network are modified (as in figure 1C), there is no obvious relationship between the task being performed and the connectivity, which is in any case not unique. The lesson here is that the activity, response properties and function of locally connected neurons can be drastically modified by feedback loops passing through distal networks. Circuits may need to be studied with an eye toward how they modulate each other, rather than how they function in isolation.

The architecture of figure 1B, involving a separate feedback network (basal ganglia or cerebellum), may be a way to keep plasticity from disrupting the generator network (motor cortex), a disruption that would be disastrous for all motor output, not merely the current task being learned. Modification of synapses in a second network (as in figure 1B) may dominate when a motor task is first learned, whereas changes within motor cortex (analogous to learning within the network of figure 1C) may be reserved for “virtuoso” highly trained motor actions. Our examples show the power of adding feedback loops as a way of modifying network activity. Nervous systems often seem to be composed of loops within loops within loops. Because adding a feedback loop leaves the original circuit unchanged, this is a non-destructive yet highly flexible way of increasing a behavioral repertoire through learning, as well as during development and evolution.

Methods

All the networks we use are based on firing-rate descriptions of neural activity. To encompass all the models, we write the network equations for the generator network as (note that, in the Results, we called the parameter labeled here as g_GG simply g)

$$\tau \frac{d{x}_i}{dt}=-x_i+{g_{GG}}_{j=1}^{N_G}{J}_{ij}^{GG}{r}_j+g_{Gz}{J}_i^{Gz}Z+{g_{GF}}_{a=1}^{N_F}{J}_{ia}^{GF}{S}_a{+}_{\mu =1}^{N_I}{J}_{i\mu }^{GI}{I}_{\mu }$$

for i =1,2,K ,N_G with firing rates r_i = tanh(x_i). For the feedback network,

$$\tau \frac{d{y}_a}{dt}=-y_a+{g_{FF}}_{b=1}^{N_F}{J}_{ab}^{FF}{S}_b+{g_{FG}}_{i=1}^{N_G}{J}_{ai}^{FG}{r}_i{+}_{\mu =1}^{N_I}{J}_{a\mu }^{FI}{I}_{\mu }$$

for a =1,2,K,N _F with firing rates s_a = tanh(y_a ). Equation 1 determines z and τ =10 ms. Sometimes we assign a sparseness p_z to the readout unit, meaning that a random fraction 1- p of the components of w are set and held to zero. The connection matrices are also assigned sparseness parameters, p, meaning that each element is set and held to 0 with probability 1-p_z. Nonzero elements of J^GG, J^GF, J^FG, J^FF are drawn independently from Gaussian distributions with zero means and variances equal to the inverses of p_GG N_G, p_GF N_F, p_FG N_G and p_FF N_F, respectively. Rows of J^GI and J^FI have a single non-zero element drawn from a Gaussian distribution with zero mean and unit variance. Elements of J^Gz are drawn from a uniform distribution between -1 and 1. Nonzero elements of w are set initially either to zero or to values generated by a Gaussian distribution with zero mean and variance 1/(p_zN).

For figures 2-5 and 6A

N_G = 1000, p_GG = 0.1, p_z =1, g_Gz = 1, g_GF = 0, α = 1.0, and N_I = 0. For figure 5, g_GG was varied, otherwise g_GG = 1.5 . For figure 2H, the standard Lorenz attractor model (see Strogatz, 1994) was used with σ = 10, β = 8/3, and ρ = 28. The target function was what is conventionally labeled as x divided by 10, to fit it roughly into the range of -1 to 1. For figure 2J, the two readouts and feedback loops are similar except for different random choices for the strengths of the feedback synapses onto the network neurons. The additional readout unit takes two possible states, one called active in which its output is determined by equation 1, and another called inactive in which its output is 0 . For further discussion of training in this case, see the Supplementary Materials.

For figures 6B

N_G = 20,000, N_F = 95, p_GG = 0.1, p_GF = 0.25, p_FG = 0.025, p_FF = 0.25, p_z = 0.025, g_GG =1.5, g_GF =1, g_FG =1, g_FF =1.2, α =1.0, and N_I = 0. RLS modification was applied to w and J^FG .

For figures 6C

N_G = 750, p_GG = 0.5, p_z = 0.5, g_GG = 1.5, g_GF = 0, α = 1.0, and N_I = 0. RLS modification was applied to w and J^GG .

For figure 7B

N_G =1200, p_GG = 0.8, p_z = 0.8, g_GG = 1.5, g_GF = 0, α = 80, and N_I = 100. The inputs I_μ where chosen randomly and uniformly over the range -2 to 2 for inputs generating initialization fixed points, and -0.5 to 0.5 for inputs control the choice of output function. RLS modification was applied to w and J^GG, but of the 1200 network neurons, 800 were subject to synaptic modification of their incoming synapses (due to memory considerations).

For figure 7D

N_G =1200, p_GG = 0.8, p_z =1, g_GG = 1, g_GF = 0, α = 40, and N_I = 8. The elements of the control input vector I_μ had OFF values of 0.0 and ON values of 0.375. RLS modification was applied to w and J^GG , with 800 of the network neurons subject to synaptic modification of their incoming synapses.

For figure 8

Although all network variants in figure 1 were implemented successfully, the following parameters are for the generator-feedback architecture: N_G = 5000, N_F = 285, p_GG = 0.05, p_GF = 0.5, p_FG = 0.185, p_FF = 0.5, p_z = 0.185, g_GG = 1.5, g_GF = 2.0, g_FG = 1.0, g_FF = 1.5, α = 2.0, and N_I = 50. RLS modification was applied to w and J^FG .

Motion capture data were downloaded from the Carnegie Mellon University Motion Capture Library (MOCAP) (http://mocap.cs.cmu.edu/). Data set 09_02.amc was used for the running example and data set 08_01.amc for the walking case. The data were preprocessed by a simple moving average filter to remove discontinuities and then interpolated to fill in to 10 times density, which works better for our continuous time models. The resulting joint angles were transformed into exponential form (see Taylor et al., 2006) and the means were removed. Movement through space was ignored, so we modeled a runner or walker on a treadmill. Four sets of control inputs were used, one each for running and walking and two for initial-value fixed points for these motions. Fixed-point inputs were chosen randomly and uniformly over the range -2 to 2 and control inputs over -0.25 to 0.25.