Modeling discrete heterogeneity in X-ray diffraction data by fitting multi-conformers

A new algorithm that automatically models discrete heterogeneity in X-ray data demonstrates that the variability observed at high resolution can be adequately represented by including correlated structural features in protein models. The algorithm is based on simultaneous exploration of a very large number of alternative interpretations of electron-density maps.

Abstract

The native state of a protein is regarded to be an ensemble of conformers, which allows association with binding partners. While some of this structural heterogeneity is retained upon crystallization, reliably extracting heterogeneous features from diffraction data has remained a challenge. In this study, a new algorithm for the automatic modelling of discrete hetero­geneity is presented. At high resolution, the authors’ single multi-conformer model, with correlated structural features to represent heterogeneity, shows improved agreement with the diffraction data compared with a single-conformer model. The model appears to be representative of the set of structures present in the crystal. In contrast, below 2 Å resolution representing ambiguous electron density by correlated multi-conformers in a single model does not yield better agreement with the experimental data. Consistent with previous studies, this suggests that variability in multi-conformer models at lower resolution levels reflects uncertainty more than co­ordinated motion.

1. Introduction

It has been proposed that the ‘native state’ of a protein should be regarded as an ensemble of conformers (Ma et al., 1999 ▶, 2002 ▶). Binding mechanisms of functional importance, as well as crystal packing, are explained by ensemble members interacting with complementary binding partners, with equilibrium shifting in favor of the complex (the conformational selection model; Huang & Wong, 2009 ▶). X-ray crystallography is a versatile experimental technique for determination of the three-dimensional structure of macromolecules, which has led to key insights into how proteins function inside the cell. Upon crystallization of the protein, some of this heterogeneity is preserved (Rejto & Freer, 1996 ▶). Indeed, the presence of distinct side-chain and main-chain conformations in a crystal has been observed on many occasions (Wilson & Brünger, 2000 ▶; van den Bedem et al., 2005 ▶; Davis et al., 2006 ▶) and the importance of accurately representing structural heterogeneity has long been recognized (Rejto & Freer, 1996 ▶; Wilson & Brünger, 2000 ▶; DePristo et al., 2004 ▶; Furnham et al., 2006 ▶; Berman et al., 2006 ▶) as even subtle conformational changes may have important functional consequences (Koshland, 1998 ▶).

However, while several programs are available for automatically building an accurate structural model into an electron-density map (Perrakis et al., 1999 ▶; Terwilliger, 2003a ▶,b ▶; Ioerger & Sacchettini, 2003 ▶; DiMaio et al., 2006 ▶, 2007 ▶), these methods utilize a single-conformer model at unit occupancy, where uncertainty is modeled with an isotropic Gaussian distribution of the position of each atom. This distribution, which is parameterized by the temperature factor, accounts for small vibrations about each atom’s equilibrium position. At high resolution, when experimental data are abundant, fitting an anisotropic (trivariate) Gaussian function becomes possible, requiring nine parameters per atom to be estimated to differentiate directional motion (Willis & Pryor, 1975 ▶). A sparser anisotropic but still harmonic parameterization involves partitioning the protein into rigid bodies undergoing independent displacements (translation, libration and screw; TLS; Schomaker & Trueblood, 1968 ▶). These harmonic error models are unable to accurately describe distinct conformational substates resulting from rotameric interconversions or multi-modal main-chain motion owing to their equilibrium-displacement nature (Kuriyan et al., 1986 ▶; Ichiye & Karplus, 1988 ▶; Wilson & Brünger, 2000 ▶).

It has been suggested that an ensemble of independent models would be a more suitable representation of a macromolecular crystal structure than a single model (Furnham et al., 2006 ▶). However, the interpretation of such an ensemble is the subject of contentious debate. DePristo et al. (2004 ▶) demonstrated that several distinct single-conformer models are each equally plausible interpretations of the diffraction data. It was proposed that differences arise from correlated changes throughout the molecule, as well as from imprecision in structure-determination techniques. Owing to the (partial) independence between the models, ensemble refinement of the alternate models led to better agreement with the diffraction data than any single model, except at high resolution. Knight et al. (2008 ▶) explored structural variability with a family of single-conformer models obtained with the help of a physics-based potential. They furthermore proposed a heuristic based on ensemble refinement to distinguish structural heterogeneity from uncertainty. Using synthetic data, Terwilliger et al. (2007 ▶) examined the relationship between alternate models and the contents of a synthetic crystal. The crystal structure was modeled as a set of 20 perfect structures obtained from random perturbation of a starting model. A single-conformer optimization program generated a diverse collection of structural models that were compatible with the data. It was established that the diversity among the range of structural models did not represent the heterogeneity in the crystal, but that such an ensemble instead represented the uncertainty (lack of knowledge) of the model. Also using synthetic data, Levin et al. (2007 ▶) juxtaposed this view by validating the use of ensemble refinement of independent models to represent heterogeneity in a synthetic crystal generated by molecular-dynamics trajectories. An ensemble of single-conformer starting models subjected to torsion-angle dynamics refinement better represented the atomic positions than a single conformation. It was furthermore shown that such ensemble refinement led to better agreement with the diffraction data for experimental structures over a wide range of resolutions. Gore & Blundell (2008 ▶) augmented molecular-dynamics ensemble refinement with combinatorial optimization of side-chain rotamers. However, the results did not improve agreement with the diffraction data compared with an unperturbed single-conformer starting model.

The lack of algorithms and software that can automatically and consistently model heterogeneity as correlated motion necessitated these studies to use families of a fixed number of independent models. This approach is unable to fully capture all heterogeneous substates or to distinguish between un­certainty and coordinated motion. Here, we present a new approach to automatically identify and model heterogeneity by fitting occupancies of a set of candidate conformations for each residue to the electron density. Our main result is that at high resolution data can be adequately explained by a single multi-conformer model with local correlated structural features representing discrete heterogeneity. At resolutions below 2 Å correlated multi-conformers in a single model do not yield better fitting statistics, demonstrating that elevated uncertainty in the data precludes coordinated motion from being accurately distinguished. Throughout this paper a ‘multi-conformer model’ denotes a model computed with our algorithm, i.e. a single model with local correlated structural features. An ‘ensemble’ denotes a family of a fixed number of independent models.

2. Description of the algorithm

Alternate side-chain conformations often involve anharmonic main-chain deviations (Davis et al., 2006 ▶). Our method uses a local sample-selection protocol to compute an occupancy-weighted set of main-chain and side-chain conformations that collectively best represents the electron density (Dhanik et al., 2008 ▶). Each sampling step generates a large set of candidate conformations. A subsequent selection step concurrently fits the occupancies of this set of samples to the electron-density map with an efficient convex optimization algorithm in real space. It typically assigns nonzero occupancy to at most a handful of samples. It should be emphasized that the algorithm infers the nonzero occupancies from the data; it has no prior knowledge about the number of conformations.

2.1. Sampling and selecting conformational subsets

The algorithm starts from a main chain, a ‘starting model’, with the side chain truncated at the C^β atom. A thermal ellipsoid is obtained from anisotropic refinement of this residue. Six trial positions for the C^α atom are selected from sampling the principal axes of its thermal ellipsoid at a surface of constant iso-probability. To position the C^α atom at the trial position, the ϕ and ψ dihedral angles of a seven-residue fragment centered around the trial atom are adjusted using an inverse-kinematics algorithm (van den Bedem et al., 2005 ▶; Lotan et al., 2005 ▶) to maintain ideal geometry and closure. For each trial C^α position, the side chain is added at rotameric positions (Lovell et al., 2000 ▶) and furthermore sampled in a small neighborhood around each χ angle. For smaller side chains the χ angles are currently discretized at 10° intervals. The temperature factors of side-chain atoms are set to in­crease with the number of bonds from the C^α atom and are slightly randomized. Electron-density maps for this set of side-chain conformations are then concurrently fitted to the observed electron-density map with a quadratic program (QP; Gärtner & Schönherr, 2000 ▶),

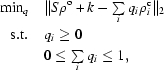where ρ^o is the observed electron-density map, ρ^c _i is the calculated electron-density map corresponding to conformer i, q_i is the occupancy of conformer i and S and k are scale factors. For side chains with more than two χ angles, aromatic rings and histidine this procedure is applied sequentially. Each χ angle in turn is discretized at 2.5° intervals. The collection of atoms that are invariant under rotation of χ angles with higher indices are fitted to the electron density with a QP. The set of angles with nonvanishing occupancy are built on for sampling the next χ angle. In a finalizing step for both smaller and large side chains, the complete set of all conformations with nonzero occupancy is subjected to a selection step with a resolution-dependent threshold constraint. A threshold constraint requires the reformulation of the optimization problem as a mixed-integer program rather than a QP program. Current implementations of mixed-integer programs are not sufficiently fast to allow a threshold constraint on the full set of conformations.

2.2. Modeling proteins

The contents of an asymmetric unit are modeled by running the algorithm independently and in parallel on each individual residue of the protein structure. Next, fragments of subsequent residues with alternate main-chain conformations are resubmitted to a selection step to obtain a constant number of conformations and occupancies over the length of the fragment. This step samples all combinations along the fragment and selects a subset that best represents the electron density. The atomic coordinates of the fragments together with remaining individual residues constituting the protein are refined with low weighting of the X-ray term (wxc_scale = 0.1 in phenix.refine). Finally, duplicate side chains, i.e. alternate side chains for which all atoms are within maximum-likelihood-based coordinate error of corresponding atoms of a second alternate side chain, are removed and occupancies are added to the atoms of the remaining side chain.

2.3. Refinement

All multi-conformer and reference models in this study were further subjected to identical automated refinement protocols with phenix.refine v.1.3 (Afonine et al., 2005b ▶) unless otherwise noted. The ligands and crystallographic waters of starting models were removed. Coordinates, (an)isotropic atomic displacement factors (ADPs) and occupancies were refined in the presence of experimental phases (where available) for five macro cycles, with automatic optimization of the X-ray and stereochemistry/ADP weights resulting in the lowest R _free factors. Longer refinement cycles did not appreciably alter the R _free or R values.

3. Validation with simulated data

We used simulated structure factors with Gaussian noise to validate the algorithm. The number of true conformational substates in simulated data is known, whereas for experimental data they are subject to interpretation by a crystallo­grapher. Data were calculated at various resolution cutoffs to examine the effect of data resolution on the results of the algorithm.

3.1. Preparation of simulated data

The crystal structure of an XisI-like protein (YP_324325.1) from Anabaena variabilis, solved at 1.30 Å resolution by the Joint Center for Structural Genomics (JCSG) and deposited in the Protein Data Bank (PDB; Berman et al., 2000 ▶) with PDB code 2nlv, is a dimer of 112 amino acids in length. 29 residues have an alternate conformer modeled, eight residues were truncated at various levels beyond the C^β atom, the C-termini were not modeled and two residues were missing at the N-­terminus of the B chain, giving a total of 212 residues. Crystallographic waters were removed and the PDB structure was subjected to isotropic refinement in the presence of experimental phases, with H atoms in riding positions, thus obtaining a reference model. The resulting temperature factors were retained, averaging 14.36 Ų. MolProbity (Davis et al., 2007 ▶), a widely used protein-structure quality-validation tool, reported three rotamer outliers for dual-conformer residues (Gln49B, Arg56B and Lys64B) and one for a single-conformer residue (Leu97B). Identification of such outliers is impeded by the nature of our algorithm, which relies on sampling neighborhoods of rotamers. Simulated structure factors were calculated from the reference model with a low-resolution cutoff corresponding to the experimental data of 29 Å and a bulk-solvent correction (Afonine et al., 2005a ▶) using phenix.pdbtools. Gaussian noise with a standard deviation of 10% of the magnitude of the calculated data was added to simulate experimental errors. To obtain a single-conformer model, the crystal structure was rebuilt into the simulated data with noise using phenix.autobuild (Terwilliger et al., 2008 ▶) at resolutions ranging from 1.1 to 2.4 Å. The rebuilt model was then used as a starting model for our algorithm.

3.2. Accuracy of the algorithm versus resolution

The resulting structural model at each resolution was compared with the reference model. A side chain was con­sidered to be modeled correctly if it was within 1 Å root-mean-square difference (r.m.s.d.) of the corresponding side chain in the reference model. R.m.s.d.s were calculated over all pertinent atoms starting at the C^β atom. Side chains with non-unique orientations (tyrosine, phenylalanine, glutamate, aspartate and arginine) had their final χ angle adjusted to minimize the r.m.s.d., as did side chains that are nearly identical (glutamine, asparagine and histidine). For the side chains of valine and threonine, a density profile can occasionally be adequately resolved by distinct combinations of rotamers owing to a correspondence between the χ₁ angle and the bond angle between the distal atoms of the side chain. R.m.s.d. values were calculated between equivalent atoms and did not correct for distinct but equivalent combinations of rotamers. Truncated residues as well as the first three residues at the N-­termini and the final three residues at the C-termini were excluded from r.m.s.d. calculations.

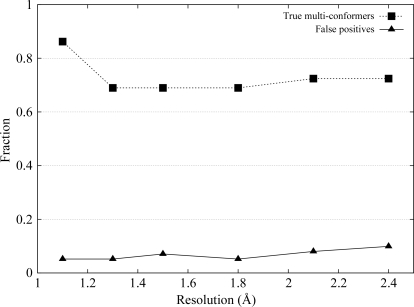
Fig. 1 ▶ summarizes the results. At very high resolution, the algorithm correctly identified and modeled 86% of 29 residues with alternate conformations. The success rate remained high at about 70% as the resolution decreased. Of the rotamer outliers, Gln49 was correctly modeled only at the highest resolution. Fewer outliers were correctly modeled towards lower resolutions, with all three modeled incorrectly at 2.1 Å.

Figure 1.

Validation of the algorithm. The fraction of the 29 multi-conformer side chains in the reference structure correctly identified and modeled by our algorithm (squares) and false positives (triangles) at resolution levels ranging from 1.1 to 2.4 Å are shown.

A less desirable side effect of identifying low-occupancy conformers is that ambiguous electron density can be falsely interpreted as a structural feature. A residue in our model was considered to be a false positive if the r.m.s.d. to its (closest) corresponding conformer in the reference structure exceeded 1 Å for any of its side-chain conformations. Thus, if a multi-conformer residue was modeled with one conformation within 1 Å and the other exceeding 1 Å, this residue was considered to be a false positive. The false-positive rate calculated for all 212 residues approximately doubled from 5% at high resolution to just below 10% at a resolution of 2.4 Å (Fig. 1 ▶). Outlier Leu97B was not correctly modeled at any of the resolutions.

In summary, the rate at which true multi-conformers are identified in electron-density maps is high and only mildly affected by resolution. When ambiguity in side-chain density increases towards lower resolution levels, which happens frequently at the protein surface, the algorithm introduces low-occupancy structural features at an incremental rate to account for electron density resulting in part from noise, analogous to the increase in variability towards lower resolution levels observed in Terwilliger et al. (2007 ▶).

4. Agreement with experimental data

We investigated the agreement of our models with experimental diffraction data from 16 crystal structures across a range of resolutions in the context of three refinement scenarios: a single-conformer isotropic model, an ensemble of independent (isotropic) models and a single-conformer anisotropic model. By analyzing data fits and model variability, we established the advantages and limitations of fitting correlated features in each scenario. It was found that our model better represented diffraction data at resolutions higher than 2 Å than the single-conformer isotropic model and more consistently improved the data fit than an ensemble. Below 2 Å a single-conformer model or an ensemble of independent models better explain the data. At resolutions where anisotropic refinement is common, our algorithm accurately discriminates anharmonic features from equilibrium displace­ment.

4.1. Improved structural models at high resolution

We employed our algorithm to identify and model structural heterogeneity in experimental data starting from single-conformer models obtained by rebuilding 16 final PDB-deposited models with phenix.autobuild. Nonprotein atoms were excluded in the rebuilding process. The rebuilt models were used to calculate 2mF _o − DF _c map coefficients from the experimental data (Read, 1986 ▶). The resulting map and model resembled what would typically be a starting point for manual refinement and served as input to our algorithm. Refinement statistics of the multi-conformer models together with those of the single-conformer models are shown in Table 1 ▶ and are summarized in Fig. 2 ▶. The geometry statistics, expressed as root-mean-square deviations of bond lengths and bond angles, of the multi-conformer model were comparable with those of the single-conformer model (data not shown).

Table 1. 16 structural models rebuilt and subjected to multi-conformer modeling.

Columns represent the PDB code of the model, resolution, number of residues in the asymmetric unit, number of reflections and R _free and R of the single-conformer reference model and our multi-conformer model.

				Single-conformer		Multi-conformer
PDB code	Resolution (Å)	No. of residues in ASU	No. of reflections	Rfree	R	Rfree	R
3eo6	0.97	212	216251	0.2748	0.2689	0.2532	0.2439
3f40	1.27	112	54373	0.2741	0.2691	0.2669	0.2595
2nlv	1.3	224	52774	0.2768	0.2662	0.2750	0.2533
3d02	1.3	303	133600	0.2426	0.2354	0.2365	0.2279
3e8o	1.4	238	63378	0.2668	0.2541	0.2641	0.2516
3f14	1.4	112	38973	0.2555	0.2566	0.2494	0.2515
3ccg	1.5	190	30978	0.2909	0.2577	0.2796	0.2403
2nvh	1.5	153	34800	0.2832	0.2689	0.2823	0.2639
1a0j	1.7	892	76148	0.2509	0.2205	0.2490	0.2147
3eby	1.75	153	34918	0.2806	0.2472	0.2740	0.2469
3en8	1.85	128	27989	0.2998	0.2565	0.3017	0.2489
3ecf	1.9	520	79131	0.2744	0.2444	0.2711	0.2399
2q7b	2.0	181	30620	0.2889	0.2281	0.2906	0.2504
3ele	2.1	1592	170242	0.2816	0.2544	0.2925	0.2577
3b7f	2.2	394	27216	0.2672	0.2345	0.2752	0.2372
9ilb	2.3	153	9535	0.2188	0.1658	0.2317	0.1778

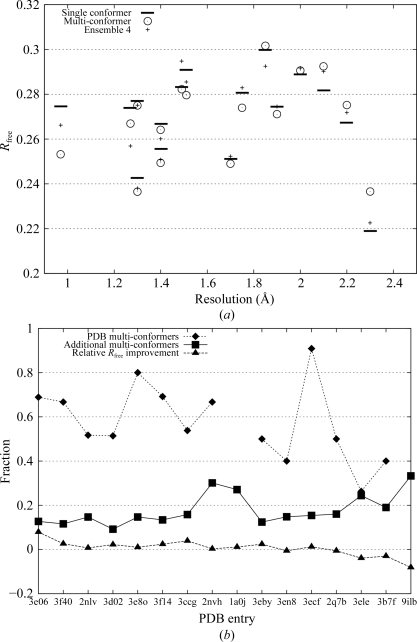
Figure 2.

Summary of the performance of the algorithm on experimental data. (a) shows R _free values of the reference models (horizontal bars), our multi-conformer models (circles) and an ensemble of four independent models (crosses) as a function of resolution. (b) is similar to Fig. 1 ▶, but with experimental data. The PDB codes of the 16 test structures are listed in order of decreasing resolution along the horizontal axis. The fraction of multi-conformer side chains in each of the 16 reference PDB structures correctly modeled by our algorithm is represented by diamonds. No alternate conformers were present in the PDB structures of 1a0j and 9ilb. Additional conformers are represented by squares. The triangles represent the relative improvement in R _free. A positive value indicates a drop in R _free.

At resolutions better than 2 Å the hold-out (cross-validation) residual R _free (Brünger, 1992 ▶) improved for all multi-conformer models (see Fig. 2 ▶ a) compared with the single-conformer models except for one (3en8). For this resolution range, the R _free values obtained from our models were on average 0.5% lower than those of the single-conformer model. For comparison, careful manual modeling of 36 discretely dis­ordered residues in a 1.0 Å structure of calmodulin lowered R _free by 1.19% (Wilson & Brünger, 2000 ▶). The improvement in R _free in our study suggests that heterogeneity is indeed represented well by a single multi-conformer model with correlated structural features and that such a model is representative of the set of structures present in the crystal. At resolutions worse than 2 Å, R _free no longer improved. Representing ambiguity in electron-density maps below this resolution with correlated structural features did not explain experimental data better than a single model plus an isotropic B factor.

The fraction of multi-conformer residues in the PDB entries for which the full set of alternate conformations was modeled to within 1 Å r.m.s.d. was only slightly below that observed in simulated data, ranging from approximately 50 to 80% at high resolution (see Fig. 2 ▶ b). Additional conformers were proposed for about 15% of residues (ranging from 10 to 30% and increasing as the resolution falls). Note that this fraction is elevated for PDB entries for which no alternate conformers were deposited (1a0j and 9ilb). Extrapolating from our results on simulated data, at lower resolutions an increasing fraction of additional conformers were likely to account at least partially for the increased uncertainty in the density. Combined with the deficient R _free values above, this suggests that below 2 Å ambiguity in electron-density maps is no longer dominated by correlated motion and that the variability in our model reflects uncertainty, consistent with the observations in Terwilliger et al. (2007 ▶).

4.2. Comparison with ensemble of independent conformers

Simultaneous refinement of an ensemble of multiple non-interacting near-copies of a structural model provides an alternative method of representing structural variability with few assumptions about the origin (uncertainty or correlated motion) of the disorder. Across a wide range of resolution levels, ensemble refinement has been shown to improve agreement with diffraction data over a single isotropic structural model (Burling & Brünger, 1994 ▶; Rader & Agard, 1997 ▶; Wilson & Brünger, 2000 ▶; Levin et al., 2007 ▶; Knight et al., 2008 ▶).

Four independent diverse structural models, each consistent with the experimental data, were obtained by rebuilding the PDB entries using the multiple_models option in phenix.autobuild. The four models were combined into a single ensemble of non-interacting conformers by fixing the occupancy of each model at 0.25. Table 2 in Levin et al. (2007 ▶) demonstrates that at resolution levels of 1.9 Å and higher, the best R _free statistic is attained at ensemble sizes of four or eight, with on average over 80% improvement of the value occurring at ensemble size two. Our ensemble size was fixed at four; fewer conformers in the ensemble would leave a potential for R _free to reach a substantial lower minimum, whereas increasing the number of conformers carries the risk of modeling noise. The isotropic temperature factors of the rebuilt models were retained. The ensemble was subjected to a refinement protocol identical to that of the single-conformer reference models and our multi-conformer models.

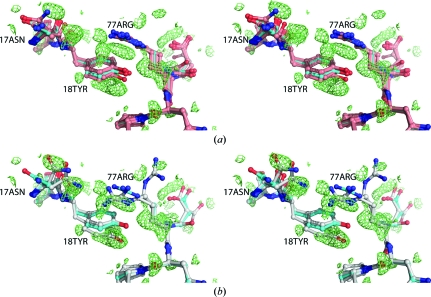
The R _free values resulting from ensemble refinement improved those of the reference model less consistently than the structural models obtained by our algorithm (see Fig. 2 ▶). For three models at resolutions better than 2 Å, the ensemble R _free values were worse than those of the reference model. In three cases the ensemble R _free was lower than our multi-conformer R _free, but an important limitation of ensemble refinement is that it only identifies the dominant conformer in cases where the electron density is spatially well separated for alternative conformations (Wilson & Brünger, 2000 ▶; Knight et al., 2008 ▶). Fig. 3 ▶(a) illustrates that while an ensemble model (shown in salmon) was quite heterogeneous and globally yielded slightly a lower R _free than our multi-conformer model, locally it failed to account for difference density corresponding to distinct side-chain conformations. Our multi-conformer model correctly identified the alternate conformations (Fig. 3 ▶ b). In particular, owing to the lack of a strong continuous gradient, ensemble refinement was unable to transition between rotameric positions.

Figure 3.

Stereo representation of a heterogeneous area around residues Tyr18 and Arg77 in 2nlv. (a) The single-conformer reference model is shown in cyan. Positive density of the mF _o − DF _c difference map corresponding to the single model, shown in lime, is contoured at 1.75σ. (b) Our multi-conformer model, shown in grey, neatly models alternate conformers of Asn17, Tyr18 and Arg77 in the positive density, albeit at the cost of a small misfit in the B conformer of Arg77. The algorithm did not find sufficient evidence for the Asn17 side-chain conformation of the reference model. Examination of the difference map reveals a substantial negative peak in this area (not shown).

As in the case of the single-conformer reference model, the R _free values of the ensemble model were better than our multi-conformer model below 2 Å resolution.

4.3. Anisotropic motion or discrete substates?

Side-chain motion that is highly anisotropic, i.e. for which the ratio of the shortest and the longest axis of the thermal ellipsoids of the atoms is substantially below unity, can easily be mistaken for discrete heterogeneity. The sampling conformers in our algorithm were calculated with an isotropic temperature factor and may therefore attempt to approximate highly anisotropic side chains with a small number of discrete substates. To investigate this, we refined the eight highest resolution multi-conformer models anisotropically and com­pared the R _free and mean anisotropy values with those obtained from anisotropically refined (single-conformer) reference models.

4.3.1. Improved anisotropic models at very high resolution

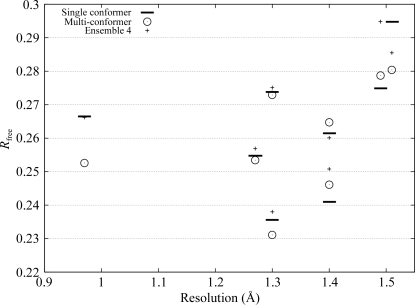
In contrast to ensemble refinement, the sparse parameterization of our multi-conformer model allowed anisotropic refinement against typical diffraction data at high resolution; the number of atoms per reflection for the multi-conformer models did not exceed 0.08 for the eight selected models. At resolutions of 1.3 Å and better, lower R _free values were obtained for the anisotropic multi-conformer models than for the anisotropic reference model (see Fig. 4 ▶), although the gap between the R _free values of the multi-conformer and reference models narrowed, as is to be expected when R _free values fall.

Figure 4.

Anisotropic R _free values of the eight highest resolution multi-conformer models (circles) and their single-conformer reference models (horizontal bars). Crosses represent the R _free values obtained from isotropic ensemble refinement of independent models, which are identical to those in Fig. 2 ▶.

Comparing the R _free values obtained from isotropic ensemble refinement of independent models with those from anisotropic refinement of our multi-conformer models, we observed that the latter were all lower, with one exception at 1.4 Å (see Fig. 4 ▶). [Note that the number of parameters was comparable between these two refinement scenarios; the isotropic ensembles had approximately 4 (models) × 4 (parameters) × N refinable parameters, whereas our multi-conformer models had r ⁻¹ × 9 × N parameters, where N is the number of atoms in the single-conformer reference model and r is the ratio of the number of single-conformer (reference) atoms to multi-conformer atoms. From Fig. 5 ▶, we see that the value of r is close to one half for most models.] This suggested that some discrete isotropic substates in the ensemble may be more appropriately represented by fewer anisotropic conformational states. Indeed, it has been observed that ensemble refinement can provide an overly isotropic view of disorder (Wilson & Brünger, 2000 ▶) and that high-resolution anisotropic refinement generally yields better R _free values than isotropic ensemble refinement (Wilson & Brünger, 2000 ▶; Levin et al., 2007 ▶).

Figure 5.

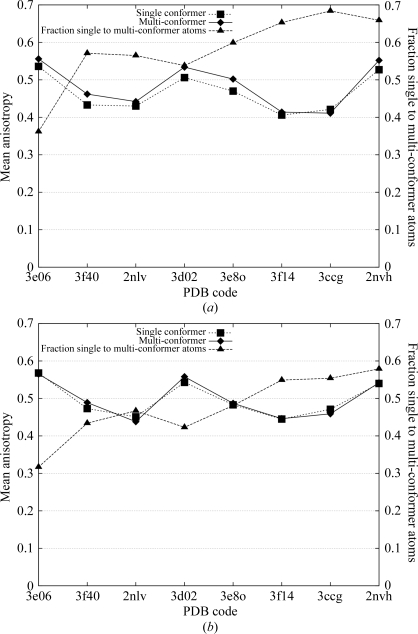
Mean main-chain (a) and side-chain (b) anisotropy for eight selected high-resolution structural models. Listed along the horizontal axis are the PDB codes of the eight test structures in order of decreasing resolution. The single-conformer reference models are represented by squares and our multi-conformer models by diamonds. Triangles depict the ratio of the number of single-conformer atoms to the number of multi-conformer atoms.

4.3.2. Anisotropic motion discriminated from discrete substates

In the single-conformer reference model, atomic displacement parameters are significantly correlated with positional parameters owing to missing atoms (Tickle et al., 2000 ▶), which may have resulted in an overly anisotropic interpretation of the data. For its part, our multi-conformer model may have given an overly isotropic representation by incorrectly modeling harmonic anisotropic features with closely spaced distinct con­formations. The mean anisotropy values, which are defined as the ratio of the minimum and maximum eigen­values of the atomic displacement tensor U averaged over all protein atoms (Trueblood et al., 1996 ▶), of the single-conformer model and the multi-conformer model were surprisingly similar, ranging from 0.43 to 0.56 for the eight models (data not shown; the mean anisotropy was calculated with PARVATI; Merritt, 1999 ▶). The mean anisotropy based on an analysis of structures from the PDB was found to be 0.45, with a standard deviation of 0.15 (Merritt, 1999 ▶). Thus, the single-conformer reference models did not appear to be overly anisotropic.

Comparing the mean anisotropy values of main-chain atoms and side-chain atoms separately, as shown in Fig. 5 ▶, we observe that the multi-conformer model yielded a slightly more isotropic interpretation of the main chain (Fig. 5 ▶ a; dia­monds) than the single-conformer reference model (squares), notwithstanding the higher ratio of single-conformer to multi-conformer atoms (triangles) than for side chains (Fig. 5 ▶ b). This was most likely to be a consequence of the limitations of the current implementation of the algorithm. The selection step of the algorithm is driven by side-chain conformations; a com­plete set of main-chain atoms (i.e. N, C^α, C, O) is introduced whenever necessary to support an alternate side chain, even if a subtle adjustment of main-chain bond angles and dihedral angles would accomplish a repositioning of just the C^α—C^β bond to support the alternate main chain. While a very minor effect, such extraneous closely spaced main-chain atoms would be suggestive of multi-modal main-chain motion, not all of which would be present in the crystal structure. The mean anisotropy values for the side-chain atoms were nearly indistinguishable, suggesting that in this case our algorithm correctly distinguished harmonic anisotropic features from anharmonic (multi-modal) features. Thus, an accurate fully anisotropic multi-conformer representation of the diffraction data is made possible by our algorithm and should be employed at high resolution to achieve the best possible description of harmonic and multi-modal disorder in structural models.

5. Comparison with alternate conformations modeled by crystallographers

In addition to agreement with diffraction data, we compared alternate conformations modeled by expert crystallographers with those modeled by our algorithm for the 16 structural models in the previous section. Visually identifying conformational substates in electron-density maps is challenging and subject to human interpretation. In contrast to our test with simulated data, the ‘true’ conformational substates of the residues are not known.

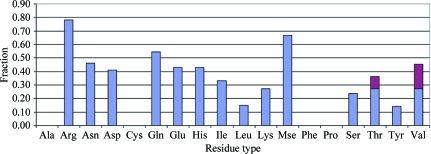
A total of 228 residues with multi-conformer side chains were found in the PDB entries of our test set of 16 structural models. The algorithm performed very well on small side chains with few dihedral angles (Cys, Ile, Leu, Pro, Ser and Thr), disagreeing with the full set of alternate conformations of these residues found in the PDB entries in at most about 25% of cases (see Fig. 6 ▶).

Figure 6.

Agreement with PDB multi-conformers. The fraction of all 228 multi-conformer residues among the 16 structural models for which the algorithm disagreed with one or more of the conformations in the PDB entry by residue type. The denominator is given by the total number of residues of a given type with two or more alternate conformations. The numerator is the number of residues of that type for which the algorithm failed to model the full set of alternate conformations to within 1 Å r.m.s.d. For Ala, Cys, Phe and Pro side chains no disagreement greater than 1 Å was found. The geometry of Thr and Val side chains allows near-equivalent explanation of electron density with distinct combinations of rotamers; the magenta top of the bars for these side chains indicates the fraction for which our algorithm models the density with a different combination than that found in the PDB entry. Gly is excluded and alternate conformations of Trp were not observed among the 16 models.

Side chains with more than two χ angles, aromatic rings and histidine were sampled in a sequential fashion, i.e. each χ angle in turn was sampled and subjected to the selection step. As the fit to the density relied on only a subset of atoms of the side chain, in most cases just one atom, performance was weaker for these side chains (Fig. 6 ▶).

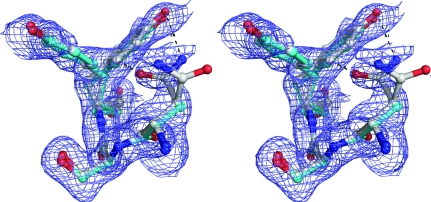
For the side chains of phenylalanine and tyrosine the algorithm capitalizes on the fact that the position of the C^ζ atom and O^η atom are invariant under rotation of χ₂. No disagreement was found for the two phenylalanine residues among our test set and only one of seven tyrosine residues disagreed with the corresponding PDB entry. Stereo Fig. 7 ▶ shows an example of main-chain and side-chain heterogeneity involving a tyrosine in PDB entry 3ccg. Note that the main chain of Tyr82 deviated considerably to accommodate the two conformations. Our model also accounts for difference density (not shown) at the carbonyl O atom, which is present in the PDB entry in a single conformation. In addition, Asn80 appeared to exhibit coordinated motion; the amide N atom interacted favorably with the hydroxyl group of Tyr82 at a distance of 3.1 Å, whereas Asn80 OD1 interacted with partially positively charged H atoms on the edge of the aromatic ring at a distance of 2.0 Å. MolProbity reported that a flip was preferred for the other Asn80 conformation. The side chain of Asn80 is truncated at the C^β atom in the PDB entry.

Figure 7.

Side-chain and main-chain heterogeneity. Stereo representation of residues Asn80, Ser81 and Tyr82 of 3ccg, with the PDB entry (cyan) and our model (grey) shown in 2mF _o − DF _c density contoured at 0.5σ. The two models overlap near-perfectly for this fragment.

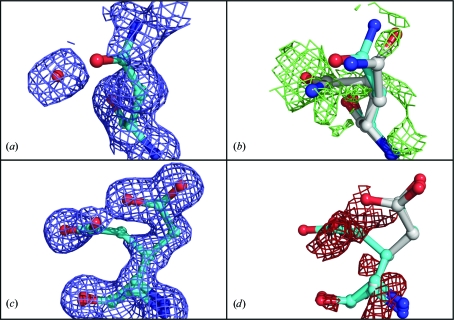
The results were less straightforward for the acidic side chains aspartate and glutamate and their amide counterparts asparagine and glutamine, disagreeing with the multi-conformer side chains found in the PDB entries in about 50% of cases. Density for these residues tended to be ambiguous and alternate conformations were sometimes difficult to distinguish from nearby solvent molecules, even for an expert crystallographer. Fig. 8 ▶ displays two examples of ambiguous electron density around these side chains. In the case of a glutamine at 1.5 Å, our algorithm found evidence for an alternate con­former, modeled at an occupancy of 0.47, where a water molecule was present in the PDB entry (Figs. 8 ▶ a and 8 ▶ b). Note that the difference density contoured at 1.1σ extended from the carbonyl group back to the C^γ atom of the added conformer. Also note that the amide of the original con­former flipped, which is the orientation that MolProbity preferred. The reverse situation was found for a glutamate at 1.3 Å, where an alternate conformation was present in the PDB entry which was not identified by our algorithm (Figs. 8 ▶ c and 8 ▶ d). Note the asymmetry in the density around the carboxyl group of the leftmost conformer in Fig. 8 ▶(c), which is possibly the result of a water molecule at partial occupancy. Our algorithm did not model the leftmost conformer. Evidence for this additional conformer appeared to be ambiguous, as indicated by negative difference density (Fig. 8 ▶ d).

Figure 8.

Ambiguous density around acidic side chains and their amide counterparts. (a) Residue Gln14 as modeled in PDB entry 2nvh, with a water molecule modeled in nearby 2mF _o − DF _c density. (b) Our model (grey) shown in mF _o − DF _c difference density calculated from the PDB entry with the water molecule removed. The difference density, contoured at 1.1σ, extends from the carbonyl group back to the C^γ atom of the added conformer. (c) Residue Glu13 as modeled in PDB entry 3d02, with two conformers at 0.5/0.5 occupancy in 2mF _o − DF _c density contoured at 0.75σ. (d) Our model (grey) in mF _o − DF _c difference density contoured at −1.5σ.

Disagreement was strongest for alternate conformations of the side chains of arginine and selenomethionine. The algorithm agreed with the full set of multi-conformers of an arginine side chain in fewer than 20% of cases. The length of arginine, with its four dihedral angles, together with the large number of rotameric conformations (34) that can overlap significantly, certainly contributes to the complexity of correctly selecting a handful that best explain the electron density. Lysine is of equal length with a similar number of rotamers, yet the algorithm performed very well on this side chain. Its elongated shape throughout is likely to reduce the number of overlapping rotamers. Of the 16 structural models, 13 were selenomethionine-labeled. One model (2nvh) contained a methionine in a dual conformation, which was renamed MSE for convenience. We hypothesize that the strong scattering of Se atoms easily washes out the electron-density profiles of neighboring C atoms, impacting on the performance of sequential sampling.

In summary, in cases where the algorithm can fit (nearly) complete side chains it agreed well with the manual interpretation. For longer side chains the results were more divergent, in part owing to more ambiguous density. In those cases it is often difficult to determine which interpretation is superior.

6. Improved estimation of model phases

It is imperative to accurately represent the data from the earliest stages of model building (DePristo et al., 2004 ▶). In a crystallographic experiment, the phase angle of the diffracted beam is lost. Only magnitudes are measured on the sensitive surface of the detector, but various techniques exist to enhance the experiment to determine the phase angles of the reflections. The phase angles of a macromolecular model are estimated and improved by building and interpreting successive electron-density maps using maximum-likelihood (ML) algorithms and can be validated by comparison with the experimentally determined phases. Disregarding structural heterogeneity in the successive electron-density maps or omitting fragments from a model altogether bias the phases in this procedure (Burling et al., 1996 ▶). In this section, we used an exceptionally accurate set of experimental phases to investigate whether our algorithm can model heterogeneity early in the structure-determination process and thereby improve phase estimates.

Brünger and coworkers obtained a set of highly accurate experimental phase angles for a 230-residue fragment of mannose-binding protein (Burling et al., 1996 ▶) at 1.8 Å resolution. Both a single-conformer structural model (PDB code 1ytt) and an ensemble consisting of eight non-interacting copies of the single-conformer model were built into the electron-density map. The reported mean difference between the phase angles calculated from the model and the experimental phase angles |ϕ_calc − ϕ_obs| over all reflections was smaller for the ensemble (26.2°) than for the single conformer (27.3°).

A multi-conformer model was obtained using the PDB entry as a (single-conformer) starting model and an electron-density map calculated from experimental phases as input for our algorithm. After following a refinement protocol similar to that reported in Burling et al. (1996 ▶), we found that our multi-conformer model reported a slightly smaller phase-angle difference (28.38°) as reported by PHISTATS (Collaborative Computational Project, Number 4, 1994 ▶) than the PDB entry (28.65°, waters removed). The difference reported by the ensemble model was smaller still (27.73°). The modest further decrease in the mean phase-angle difference of the ensemble came at the expense of a vastly greater number of parameters. The ensemble model consisted of 14 224 protein atoms compared with 2409 for our multi-conformer model (1778 for the PDB entry). Our model proposed alternate conformations for 97 residues (42%).

Thus, introducing correlated structural features early in the model-building process can improve phase estimates. In fact, while our model was built into the experimental electron-density map and subsequently refined without any human intervention, its phase set is slightly better than that of the carefully refined PDB entry. In (more typical) cases where experimental phases are less accurate, our algorithm would be a valuable contribution to iterative model-building and refinement procedures at high resolution.

7. Discussion and conclusions

Alternate conformations are often observed in high-resolution electron-density maps, but manually building them into disordered electron density is time-consuming and dependent on the experience of the crystallographer. As even the smallest conformational changes can drive functional mechanisms, accurately representing structural heterogeneity is important for biological and biomedical research relying on structural data deposited in the PDB. Correlated side-chain conformations could elucidate coordinated motion around, for instance, an active site (also termed dynamic close packing; Rader & Agard, 1997 ▶) and provide valuable insight for functional annotation or docking experiments.

The method presented in this study is based on a simultaneous exploration of a very large number of alternative interpretations of the experimental data, resulting in a single model with local occupancy-weighted alternate conformations that provide a near-optimal explanation of the electron density. Validation tests on simulated data with noise established that our algorithm identifies and models true multi-conformers at a consistently high rate, even as the resolution falls below 2 Å. The number of ‘false-positive’ conformers modeled by the algorithm incrementally rises towards low resolution as the ambiguity in the electron density increases. Our convex optimization method is known to identify the global optimum of the target function, i.e. within the limitation of a discrete set of samples the conformations with nonzero occupancy optimally explain the electron density. Hence, the elevated variability towards lower resolution is dominated by uncertainty rather than coordinated motion, which is consistent with the conclusion of Terwilliger et al. (2007 ▶).

Our study demonstrates that the limited specificity of model parameters at reduced resolution precludes differentation of multi-conformers resulting from coordinated motion, which is borne out by an increase in false positives (simulated data) and deficient cross-validation statistics (experimental data) below 2 Å resolution. While the threshold of 2 Å could perhaps be improved slightly, it is a characteristic of the data rather than the method. Indeed, the information that can be extracted from an electron-density map is limited. Stenkamp & Jensen (1984 ▶) proposed that individual atoms can only be optically resolved in (noiseless) electron-density maps when they are separated by a distance greater than 0.917d _min, where d _min is the minimum lattice distance, i.e. their overlapping density profiles are unimodal below this distance. At a resolution d _min of 1.8 Å or worse, most covalent-bond lengths in the structure exceed the optical resolution limit. The com­bined density profile of closely spaced larger features such as side chains are likely to have a unique signature exceeding this distance, allowing our method to identify multi-conformers beyond the optical resolution limit. Furthermore, at reduced resolutions the peak value of an electron-density profile is lowered and the width increases. The density profile of a low-occupancy conformer is then easily obscured by noise. Indeed, at occupancy levels of about 0.2 C atoms have only a slightly higher scattering power than a H atom at full occupancy. H atoms are typically only observed at very high resolution (<1.2 Å)

Our method is complementary to an ensemble representation in important ways. (i) For an ensemble model the parameterization is kept fixed and homogeneous throughout the model, whereas our algorithm sparsely introduces additional parameters locally as needed, resulting in a favorable parameters-to-observations ratio. (ii) Contrary to our method, an ensemble model requires a nonvanishing gradient between alternate conformers, in the absence of which it identifies only the dominant conformer. (iii) The (partial) independence of the structure factors of members of an ensemble improves the agreement with diffraction data by virtue of ‘averaging’. The atomic coordinates of conformers tend to accumulate in well resolved electron density, whereas scattering from spatially widely distributed coordinates in weak electron density are not easily distinguished from noise levels owing to their low occupancy levels. These observations suggest that lower resolution data, which are a result of lattice disorder and elevated protein mobility, are more suitably represented by an ensemble of independent models. Our method, which is designed to identify and model discrete heterogeneity with correlated multi-conformer features, is better suited to represent co­ordinated motion at high resolution.

A detailed analysis of the performance of the algorithm by residue type showed that it performed very well whenever it can fit complete or nearly complete structural features to the electron density, which is the case for smaller side chains and certain aromatic residues. It performed less well for side chains that are modeled with a sequential algorithm, which is more sensitive to the optical resolution limit. Fitting large side chains in their entirety would lead to combinatorially large sample sizes. Instead, using a fine-grained more extensive rotamer library (Xiang & Honig, 2001 ▶) without additional sampling could allow the fitting of larger structural features to the electron density, thus improving performance without increasing the computational complexity of the algorithm.

This work is only a step in the direction of automatically and consistently identifying structural heterogeneity in proteins. Few tools are currently available to automatically subject multi-conformer structural models to quality control or to use these snapshots of large-amplitude motions to infer functional mechanisms. Developing such tools is a priority, as improvement of experimental equipment and techniques continues to lead to an increase in high-resolution crystal structures. Furthermore, it will often be important at any resolution level to determine where variability in a structural model represents true heterogeneity, i.e. where correlated motion occurs in the crystal structures and where uncertainty dominates. The experimental data can be further exploited to accomplish this, but comparative analyses with structurally homologous protein models could highlight regions exhibiting similar heterogeneous features.

8. Implementation details

The software is implemented in C++ and uses the following packages: Clipper (Cowtan, 2003 ▶), LoopTK (Dhanik et al., 2007 ▶), CGAL (Computational Geometry Algorithms Library; http://www.cgal.org) and COIN-OR (Computational Infrastructure for Operations Research; http://www.coin-or.org). The software will be made available for download as well as through a web server at http://smb.slac.stanford.edu/~vdbedem.