Modeling Cardiac Action Potential Shortening Driven by Oxidative Stress-Induced Mitochondrial Oscillations in Guinea Pig Cardiomyocytes

Abstract

Ischemia-induced shortening of the cardiac action potential and its heterogeneous recovery upon reperfusion are thought to set the stage for reentrant arrhythmias and sudden cardiac death. We have recently reported that the collapse of mitochondrial membrane potential (ΔΨ_m) through a mechanism triggered by reactive oxygen species (ROS), coupled to the opening of sarcolemmal ATP-sensitive potassium (K_ATP) channels, contributes to electrical dysfunction during ischemia-reperfusion. Here we present a computational model of excitation-contraction coupling linked to mitochondrial bioenergetics that incorporates mitochondrial ROS-induced ROS release with coupling between the mitochondrial energy state and electrical excitability mediated by the sarcolemmal K_ATP current (I_K,ATP). Whole-cell model simulations demonstrate that increasing the fraction of oxygen diverted from the respiratory chain to ROS production triggers limit-cycle oscillations of ΔΨ_m, redox potential, and mitochondrial respiration through the activation of a ROS-sensitive inner membrane anion channel. The periods of transient mitochondrial uncoupling decrease the cytosolic ATP/ADP ratio and activate I_K,ATP, consequently shortening the cellular action potential duration and ultimately suppressing electrical excitability. The model simulates emergent behavior observed in cardiomyocytes subjected to metabolic stress and provides a new tool for examining how alterations in mitochondrial oxidative phosphorylation will impact the electrophysiological, contractile, and Ca²⁺ handling properties of the cardiac cell. Moreover, the model is an important step toward building multiscale models that will permit investigation of the role of spatiotemporal heterogeneity of mitochondrial metabolism in the mechanisms of arrhythmogenesis and contractile dysfunction in cardiac muscle.

Introduction

The regulation of cardiac function involves a variety of intrinsic (e.g., muscle length, stimulation frequency, and metabolic) and extrinsic (e.g., sympathetic and parasympathic regulation, circulating hormone levels, regional blood flow, workload) mechanisms that interact to match cardiac output to the energy demands of the body. A healthy heart can increase its workload significantly (four-to-six times), and normal contractile function is supported by continuously adjusting the rate of mitochondrial oxidative phosphorylation to maintain a steady supply of ATP for sarcomere shortening, Ca²⁺ cycling, and ion homeostasis (1). However, under disease conditions, such as ischemia-reperfusion, the exquisite regulation of metabolic and electrophysiological processes may become dysfunctional, often resulting in alterations in ionic balance and the abrupt loss of cardiac function in the form of fatal cardiac arrhythmias and/or contractile failure. Based on observations in isolated perfused hearts (2), we have proposed that the failure of the mitochondrial network to maintain ΔΨ_m underlies reperfusion arrhythmias.

More than a decade ago, we observed spontaneous self-sustaining oscillations of sarcolemmal adenosine triphosphate (ATP)-sensitive potassium current (I_K,ATP) in cardiac myocytes subjected to metabolic stress. These oscillations were correlated with transient decreases in NADH fluorescence and could be modulated by glucose (3). We proposed that such changes in I_K,ATP, by altering the cardiac action potential and refractory period, might contribute to an arrhythmogenic substrate during ischemia-reperfusion. Cardiac sarcolemmal ATP-sensitive K⁺ (K_ATP) channels (4) are comprised of an inwardly rectifying K⁺ channel, Kir6.2, and a regulatory sulfonylurea receptor, SUR2a (5,6). K_ATP channels are directly gated by intracellular ATP and Magnesium adenosine diphosphate (MgADP) and have low probability of opening under normal conditions. However, when the cellular ATP/ADP ratio decreases, open probability of these channels increases, setting membrane potential close to the equilibrium potential for K⁺ (7). Because I_K,ATP is a weak inward rectifier, the additional outward current hastens repolarization and increases the threshold for firing an action potential (AP), thus, K_ATP channels directly couple the cell's energy state to its electrical activity.

We have previously demonstrated that metabolic stress in the form of substrate deprivation or localized laser flash can trigger cellwide oscillations or collapse of mitochondrial membrane potential in isolated cardiomyocytes (3,8,9), which can be interrupted or prevented either by employing ROS scavengers or applying ligands of the mitochondrial benzodiazepine receptor, which are known inhibitors of an inner membrane anion channel (IMAC) (8). The coordinated behavior of mitochondria in the cardiac cell in these experiments led to the concept of mitochondrial criticality, in which the level of oxidative stress on the mitochondrial network builds to critical threshold, when ΔΨ_m either collapses or oscillates between the energized and deenergized states in a synchronized manner throughout the whole cell (8,10). The mechanism involves mitochondrial reactive oxygen species (ROS) triggering the activation of IMAC in a positive feedback loop causing energy dissipation and the uncoupling of oxidative phosphorylation. Because the mitochondrial F₁F_O ATPase is reversible, the uncoupled mitochondria consume intracellular ATP stores, driving the activation of the K_ATP channel (11) and consequently producing significant changes in the action potential duration (APD).

The underlying biological processes are highly nonlinear, and depend upon subcellular compartmentation and complex interactions between metabolic and electrophysiological networks that cannot be easily understood without a comprehensive model as a tool. Furthermore, it is technically very difficult to simultaneously measure metabolites, ions, metabolic fluxes, and currents in experiments on cardiomyocytes. Hence, this work was undertaken to study these interactions in a mathematical model. Specifically, a recently published integrated model of the cardiomyocyte (12) was further developed by incorporating a ROS-induced ROS release mechanism (RIRR) and sarcolemmal K_ATP channels. The model (ECME-RIRR) integrates mitochondrial energetics, ROS-induced ROS release, cellular electrophysiology, excitation-contraction coupling, and myofilament activation. The dynamics of ΔΨ_m, NADH, ROS, and respiration rate in response to oxidative stress are simulated, and the effects of these energetic changes on cytosolic ATP/ADP ratio, K_ATP current, and APs are investigated.

Methods

Model development

Our model is based on our previous model of mitochondrial energetics and excitation-contraction coupling (ECME) (12), which was modified to incorporate a mitochondrial ROS-dependent oscillator that we have described in experimental (8,10) and modeling studies (13). In addition, the sarcolemmal ATP-sensitive potassium current (I_K,ATP) (14) was incorporated to examine the relationship between mitochondrial energetic state and cellular electrical activity. The general scheme of E-C coupling, mitochondrial energetics, and ROS-induced ROS release (ECME-RIRR) is shown in Fig. 1. In the integrated model, the metabolic, electrophysiological, and mechanical components of the heart cell are linked through the high-energy phosphate pools, i.e., ATP, ADP, and phosphocreatine, as well as through ions, including Ca²⁺ and Na⁺ in the cytoplasm and mitochondrial matrix (Fig. 1).

Figure 1.

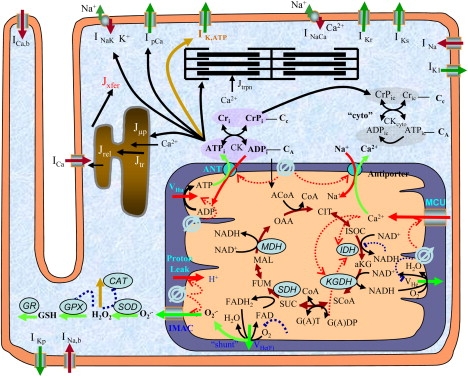
General scheme of the E-C coupling, mitochondrial energetics, and ROS-induced ROS release (ECME-RIRR) model. The electrophysiological module describes the major ion channels underlying the action potential (e.g., ATP-sensitive potassium channel) and the processes involved in Ca²⁺ handling (e.g., transport of Ca²⁺ across the sarcolemma, SR), and the inner mitochondrial membrane channels (e.g., Ca²⁺ uniport). The mitochondrial module accounts for the major components of mitochondrial energetics such as the TCA cycle and oxidative phosphorylation. The RIRR module describes ROS production (from the electron transport chain), transport (through IMAC), and scavenging (e.g., by the superoxide dismutase and glutathione peroxidase enzymes). The mitochondrial energetics and ROS are linked to cellular electrical activity through the K_ATP current, which is activated when the ADP/ATP increases.

The model development used a modular strategy, whereby the formulation of each process, such as an ionic current or metabolic reaction rate, was tested separately using MATLAB 7.0.1 (The MathWorks, Natick, MA) to assure that it reproduces the best available experimental data within the boundaries of the physiological parametric range. Once the behavior of each module proved satisfactory, cellular subsystems were then joined and tested before linkage with other model components. The general strategy of model development emphasizes the interactions between the various blocks in the model. The dynamics of each species/ion were described by mass balance equations, and the assembled integrative model was coded in C⁺⁺ in the development environment of Microsoft Visual Studio (Microsoft, Redmond, WA).

Mitochondrial ROS-induced ROS release

Under normal conditions, ROS produced by the electron transport chain serve as important signaling molecules that protect cells against injury (15–17). However, under pathological conditions, such as during ischemia-reperfusion, mitochondrial ROS can trigger a larger burst of ROS, or RIRR, a concept previously put forward to explain mitochondrial permeability transition pore-opening in response to laser illumination (18). This concept was also applied to explain the activation of IMAC, a mitochondrial ion channel inhibited by mitochondrial benzodiazepine receptor ligands, but not cyclosporin A (8). IMAC activation leads to the rapid discharge of ΔΨ_m in a synchronized and oscillatory fashion that is closely coupled to changes in the electrophysiology of the cardiac cell. Inhibition of mitochondrial collapse through this mechanism also prevented reperfusion arrhythmias after 30 min global ischemia in guinea-pig (2) or rabbit (19) hearts.

To quantitatively simulate the effect of mitochondrial ROS-induced oscillations on cellular electrophysiology and function, RIRR was incorporated into the model by

• 1.Shunting a fraction of the electrons of the respiratory chain toward the generation of O_2·⁻,
• 2.Adding a cytoplasmic ROS scavenging system, and
• 3.Adding a ROS-activated inner membrane anion channel, based on our previous work, to develop an isolated mitochondrial oscillator model (13).

Modeling the sarcolemmal K_ATP current

To quantitatively investigate the effect of mitochondrial energetics on cellular electrophysiology and cellular APs, a K_ATP current model was incorporated into the integrated ECME-RIRR model. This comprehensive K_ATP channel model has been described in detail by Ferrero et al. (14). Briefly, the total current density through the K_ATP channels was described as

$$I_{\text{K},\text{ATP}}=\sigma \times g_0\times p_0\times f_{\text{ATP}}\times \left(V_{\text{m}}-E_{\text{K},\text{ATP}}\right),$$

where σ is the channel density, g₀ is the unitary conductance, p₀ is the maximum channel open probability, f_ATP is the fraction of activated channels, V_m is the membrane potential, and E_K,ATP is the reversal potential of the channel. In the cardiomyocytes, f_ATP is strongly dependent upon the levels of [ATP]_i and free [ADP]_i,

$$f_{\text{ATP}}=\frac{1}{1+{\left({\left[\text{ATP}\right]}_{\text{i}}/K_{\text{m}}\right)}^{\text{H}}},$$

with

$$K_{\text{m}}=35.8+17.9\times {\left[\text{ADP}\right]}_{\text{i}}^{{\text{K}}_{\text{m},\text{KATP}}}$$

and

$$H=1.3+0.74\times e^{\left(-{\text{H}}_{\text{KATP}}\times {\left[\text{ADP}\right]}_{\text{i}}\right)},$$

where K_m,KATP and H_KATP are model parameters.

The dynamics of sarcolemmal membrane potential were modified from the original ECME model by adding the K_ATP current:

$$\frac{dV}{dt}\text{=}-\frac{1}{C_{\text{m}}}\left(\begin{array}{c}{\text{I}}_{\text{Na}}+I_{\text{Ca}}+I_{\text{Ca},\text{K}}+{\text{I}}_{\text{K}}+{\text{I}}_{{\text{K}}_1}+I_{\text{Kp}}+I_{\text{NaCa}}\\ +I_{\text{NaK}}+I_{\text{ins}\left(\text{Ca}\right)}+{\text{I}}_{\text{pCa}}+I_{\text{Ca,b}}+I_{\text{Na,b}}+I_{\text{K},\text{ATP}}\end{array}\right)\text{.}$$

The rate expressions of other currents included in this equation (such as I_Na and I_Ca) and metabolic reactions, as well as the mass or ion balance equations, were the same as those described in the ECME model (12) and are listed in the Supporting Material.

Simulation protocol

The complete model consists of 54 nonlinear ordinary differential equations (ODEs), which were integrated numerically by CVODE, a stiff ODEs solver in C developed by Cohen and Hindmarsh that uses variable coefficient Adams and BDF methods (http://citeseer.ist.psu.edu/1230.html). The model parameters were either obtained directly from the literature or determined by minimizing the differences between model simulations and experimental data. The parameters of the ECME model were same as in the original model (12) (parameter sets are included in the Supporting Material). The parameters of the RIRR model and K_ATP channel model were modified slightly from those in the original models, as listed in Tables 1 and 2, respectively. Before testing model responses to the external stimulation, the behavior of the resting cardiomyocyte was simulated to obtain steady-state values, which were used as initial conditions for all runs in a series of in silico experiments. Subsequently, the model was run for ∼400 s with pacing at various frequencies of 0.25, 0.5, 1, and 2 Hz. Oxidative stress was induced by increasing the fraction of ROS produced from the electron transport chain as a byproduct of respiration (shunt). Simulation results were analyzed using Microcal Origin 7.5 (Microcal Software, Northampton, MA). APD was defined as the interval between the time of the maximum upstroke velocity of the action potential, [dV/dt]_max, and 90% repolarization.

Table 1.

Parameters for ROS-induced-ROS-release model

af	1.0e4	Activation factor by cytoplasmic O2·−.
Kcc	0.01	Activation constant of IMAC by O2·− (mM).
G_L	0.035e-6	Leak conductance for IMAC (mM/ms/mV).
G_max	3.9085e-6	Integral conductance of IMAC at saturation (mM/ms/mV).
Kappa	0.07	Steepness factor (/mV).
Em	4	Potential at half-saturation (mV).
k1_SOD	1.2e3	Second-order rate constant of conversion between native oxidized and reduced SOD (mM/ms).
k5_SOD	0.25e-3	First-order rate constant for conversion between inactive and active oxidized SOD (/mM/ms).
k3_SOD	24	Second-order rate constant of conversion between native reduced SOD and its inactive form (/mM/ms).
etSOD	1.43e-3	Intracellular concentration of SOD (mM).
kki	0.5	Inhibition constant for H2O2 (mM).
k1_CAT	17	Rate constant of CAT (/mM/ms).
etCAT	0.01	Intracellular CAT concentration (mM).
fr	0.05	Hydrogen peroxide inhibition factor for CAT.
EtGPX	0.01	Intracellular GPX concentration (mM).
Phi1	0.5e-2	Constant for GPX activity (mM ms).
Phi2	0.75	Constant for GPX activity (mM ms).
K1_GR	5.0e-3	Rate constant of GR (/ms).
etGR	0.01	Intracellular GR concentration (mM).
Km_GSSG	0.06	Michaelis constant for oxidized glutathione of GR (mM).
Km_NADPH	0.015	Michaelis constant for NADH for GR (mM).
NADPH	1	Total NADH pool (mM).
GT	1	Total glutathione pool (mM).
shunt	0.02	Fraction of O2 to form superoxide.
j	0.1	Fraction of IMAC conductance.

SOD; superoxide dismutase, CAT; catalase, GPX; glutathione peroxidase, GR; glutathione reductase.

Table 2.

Parameters for sarcolemmal K_ATP channel model

σ	0.6	Channel density (channels/μm2).
g0	30.95	Channel unitary conductance.
p0	0.91	Maximum channel open probability.
EK-ATP	−94.02	KATP channel reversal potential (mV).
HKATP	−0.001	Hill coefficient constant.
Km,KATP	0.56	Km constant.
surf	104	Cell surface (μm2).

Results

Comparison of model-simulated K_ATP current with experimental data

The model of the K_ATP channel developed by Ferrero et al. (14) was tested separately before being incorporated into the ECME-RIRR model. The results were in accord with those obtained experimentally from isolated cardiomyocytes (20) (Fig. 2 A). K_ATP current was inhibited by an increase ATP and the ability of ATP to suppress K_ATP current was significantly reduced by increasing [ADP]_i; that is, increasing ADP concentration (e.g., from 0 to 300 μM) shifted the ATP versus I_K,ATP curve to the right. The K_ATP channel activity was also affected by the extracellular potassium concentration ([K]_o). As observed in experiments (21) and in our simulations, increasing [K]_o decreases the current, especially when the membrane potential is depolarized (Fig. 2 B).

Figure 2.

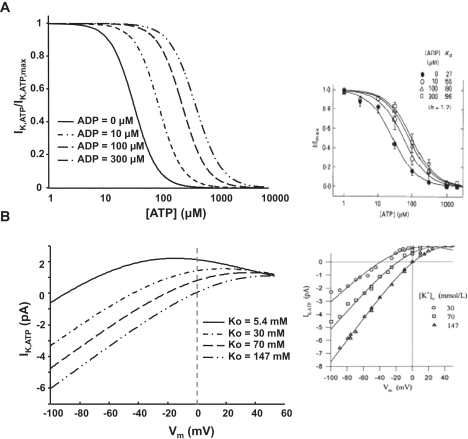
Model-simulated effects of ADP on the dose-response curve of K_ATP current to [ATP]_i (A) and effect of extracellular potassium concentration ([K]_o) on the K_ATP channel activity (B). The insets represent experimental data obtained from the literature, reprinted with permission from the Journal of Physiology (20) and Circulation Research (14).

Oxidative stress-induced mitochondrial oscillations

Our previous experimental studies showed that a highly localized laser flash could induce cell-wide mitochondrial oscillations in isolated cardiomyocytes, which involve depolarization of ΔΨ_m and ROS generation, with concomitant shortening of the cellular AP (8,10). To validate the integrated ECME-RIRR model, we simulated the responses of mitochondria to oxidative stress by increasing the ROS shunt from 0.02 to 0.10. Oxidative stress triggered sustained oscillations in [ROS]_i, [ROS]_m, ΔΨ_m, and [NADH], associated with bursts in the mitochondrial respiration rate (Fig. 3 C) and ROS production rate (data not shown). In addition, ΔΨ_m depolarization occurred in concert with oxidation of NADH (Fig. 3 B), with ROS concentration in both the cytoplasm and mitochondria peaking during the rapid uncoupling of oxidative phosphorylation (Fig. 3 A). Finally, when ΔΨ_m depolarizes, there is a significant decrease in the rate of mitochondrial ATP production, which switches over to net ATP consumption (Fig. 3 D), even while respiration rate increases (Fig. 3 C), indicating that uncoupled mitochondria deplete ATP and increase intracellular ADP/ATP ratio.

Figure 3.

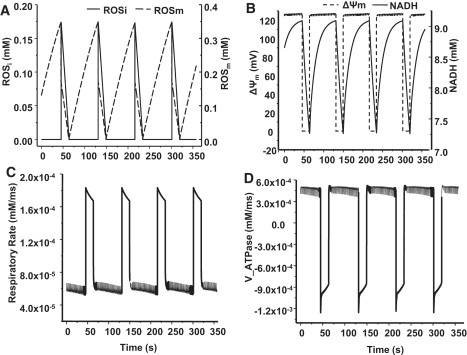
Simulation of mitochondrial oscillations in ROS (A), mitochondrial membrane potential (ΔΨ_m) and NADH (B), respiratory rate (C), and ATP synthase (complex V) flux (D) with the integrated model. The model parameters are listed in Table 1. The shunt was modified from 0.02 to 0.1 to initiate an oxidative stress. f = 0.5 Hz.

Shortening of APD during mitochondrial depolarization

ROS triggered oscillations in ΔΨ_m produced phasic changes in cytosolic ATP concentration, sarcolemmal K_ATP current, and APD (Fig. 4; for better visualization, an expanded view of the depolarization phase is shown). It is apparent that there is a moderate decrease in ATP concentration (from 7.9 mM to 7.08 mM) when ΔΨ_m is depolarized, but a much larger relative increase in the ADP concentration, given that ADP concentration is typically an order-of-magnitude lower than ATP, and the total adenine nucleotide pool is constant (8 mM) in the model. The threefold increase in the ADP/ATP ratio (from 0.018 to 0.056) was responsible for the activation of the K_ATP channels and the rapid increase in membrane current (Fig. 4 A, dotted line). These changes were reversible—when ΔΨ_m repolarized, the ADP/ATP ratio recovered, and the K_ATP channels were inactivated. The activation of K_ATP current during ΔΨ_m depolarization, as expected, caused significant shortening of the cardiac cell APD (from 170 ms to 43 ms, Fig. 4 B insets and Fig. 5 A). Further increases in K_ATP current resulted in more shortening of the ADP; an increase of K_ATP channel density from 0.6 to 1.2 channels/μm² resulted in an I_K,ATP increase from 2.11 to 3.82 nA and additional APD shortening from 43 to 23 ms. When the channel density was raised to 3.8 channels/μm², the cell became electrically inexcitable (green record, Fig. 5 A). The amplitude of the AP was also partially suppressed when I_K,ATP was very large (Fig. 5 A).

Figure 4.

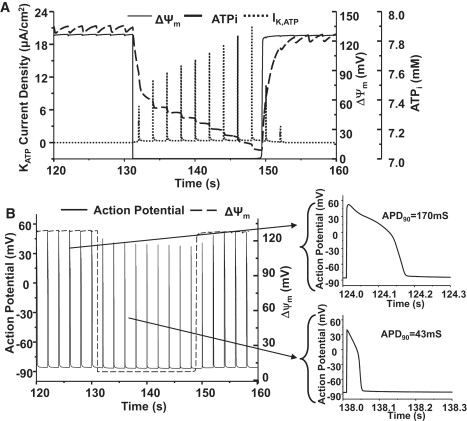
Simulations of ΔΨ_m, cytoplasmic ATP concentration ([ATP]_i) and sarcolemmal K_ATP current during oscillations triggered by oxidative stress (A) and comparison of action potentials during polarized and depolarized states (B). For clarity, only part of one oscillatory cycle is shown. Shunt = 0.1, f = 0.5 Hz.

Figure 5.

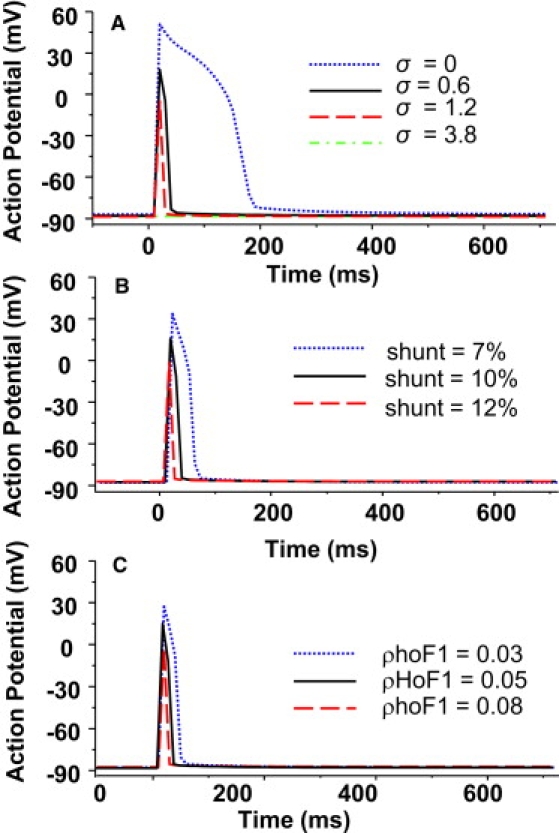
Simulated effects of model parameters on morphology of action potential. (A) K_ATP channel density (σ), (B) ROS production (shunt), and (C) mitochondrial ATP synthase activity (ρhoF1). f = 0.5 Hz and other parameters were as same as listed in Tables 1 and 2.

The action potential morphology was also affected by parameters that influenced mitochondrial RIRR. Increasing ROS production (shunt) over the range from 10% to 12% resulted in a decrease of APD in both the duration (from 43 to 18 ms) and amplitude during ΔΨ_m depolarization, while decreasing the shunt to 7% had the opposite effect (Fig. 5 B). ATP synthase activity (ρhoF1) also influenced the action potential, by determining the rate of ATP hydrolysis when the mitochondria depolarized. Increasing ρhoF1 by 60% shortened the APD from 43 to 28 ms, and decreasing ρhoF1 by 60%, on the contrary, significantly prolonged the APD and increased the AP amplitude (Fig. 5 C).

Effect of elevated energy demand on mitochondrial oscillations and cellular electrophysiology

A decreased energetic demand subsequent to the opening of sarcolemmal K_ATP channels has been proposed to be cardioprotective by reducing Ca²⁺ influx and contraction (22–24). Model simulations showed that force was suppressed when K_ATP current increased during ΔΨ_m depolarization (Fig. 6 A). To examine the effects of mitochondrial energy state on cardiac function, the effects of external electrical stimulation on cellular metabolic and electrophysiological activities were simulated by changing the pacing frequency from 0.25 to 0.5, 1.0, or 2 Hz. Increasing pacing frequency significantly decreased the dynamic and steady-state cytoplasmic ATP concentrations, especially at 2 Hz (Fig. 6 B).

Figure 6.

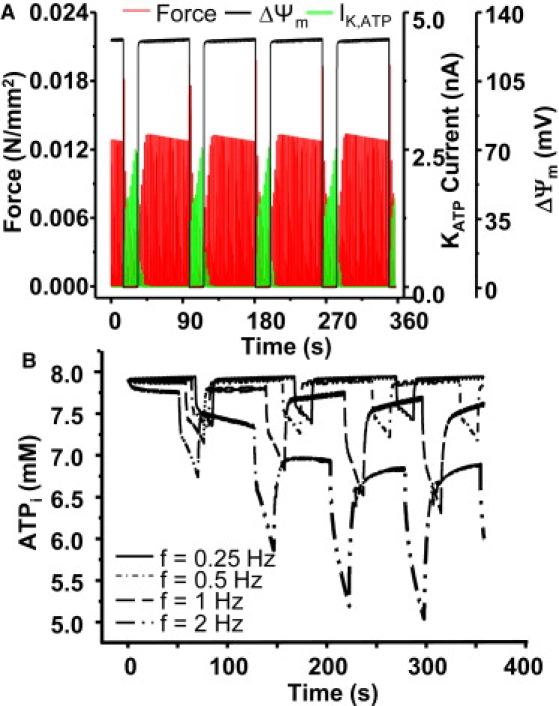
Effect of mitochondrial depolarization and resulting activation of K_ATP current on force (A) and the effect of pacing frequency on cytoplasmic ATP concentration (B). In panel A, f = 0.5 Hz and in panel B, the pacing frequency was 0.25, 0.5, 1, and 2 Hz, respectively. Shunt = 0.1.

Faster pacing shortened the cycle length of ΔΨ_m oscillation by abbreviating both the repolarization and depolarization phases, indicating faster mitochondrial oscillations (the oscillation period was reduced from 103 to 76 s when the frequency was raised from 0.25 to 2 Hz). The increased stimulation rates had minor effects on the amplitude of ΔΨ_m, but significantly increased the amplitude of K_ATP current, especially at the low end of the frequency range (e.g., 0.25 or 0.5 Hz) (Fig. 7, A and B). However, when the pacing frequency was higher (e.g., 1 or 2 Hz), the [ATP]_i was lower, even when ΔΨ_m was polarized, resulting in activation of K_ATP current (Fig. 7, C and D) and shortening of APD (data not shown).

Figure 7.

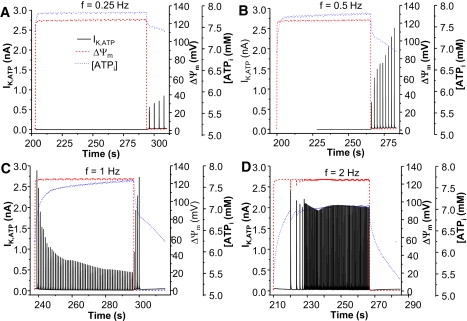
Model simulated effect of external stimulation on the mitochondrial membrane potential and K_ATP current. The pacing frequency was 0.25 (A), 0.5 (B), 1 (C), and 2 Hz (D), respectively. Shunt = 0.1.

Discussion

This work provides, for the first time to our knowledge, a computational framework to examine the nonlinear emergent properties of the cardiac cell under oxidative stress. Under metabolic stressors such as ischemia-reperfusion or antioxidant depletion, mitochondrial membrane potential (ΔΨ_m) has been shown to collapse abruptly, or to undergo slow period oscillation (∼0.01 Hz), both in isolated cardiomyocytes (3,8,25) and intact hearts (26). The remarkable interplay between the mitochondrial energy state and cellular electrical excitability is demonstrated by the model, manifested as synchronized oscillations in ΔΨ_m, ROS, NADH, and APD. The effect of changing stimulation frequency also revealed significant interactions between E-C coupling-mediated changes in ATP utilization and energetics.

Coupling between depolarization of ΔΨ_m, K_ATP current activation, and action potential morphology

K_ATP channels have a low open probability under physiological conditions, but are rapidly activated during ischemia or metabolic inhibition (4,22). The increased K⁺ conductance tends to lock the resting membrane potential close to the equilibrium potential for K⁺ (E_K); for example, after 10 min of ischemia, resting membrane potential is equal to E_K (27). K_ATP activation can occur even though total cellular ATP has not been fully depleted because the open probability is increased when cofactors like ADP, pH, and Mg²⁺ increase. Mitochondrial uncoupling accelerates K_ATP current activation because the drop in ΔΨ_m causes the ATP synthase to run in reverse, thus consuming cytoplasmic ATP and decreasing the phosphorylation potential. Tight coupling between the mitochondrial energy state and the sarcolemmal K_ATP current is facilitated by the high-energy phosphoryl transfer reactions of the cytoplasm (11). The close correspondence between APD and ΔΨ_m has been demonstrated in our previous work on myocytes exposed to local oxidative stress (8) and the model produced results that were very similar to the experimental observations. During the phase of mitochondrial depolarization, the AP shortened by almost 75% (Fig. 4) and the intracellular Ca²⁺ transient amplitude (not shown) and force production decreased (Fig. 6). The negative feedback on E-C coupling during ΔΨ_m depolarization in the simulation was primarily due to the action potential shortening, which decreases Ca²⁺ entry and sarcoplasmic reticulum Ca²⁺ loading on each beat. These results were in agreement with our previous experimental observations showing a decline in the Ca²⁺ transient amplitude during metabolic oscillations triggered by substrate deprivation (3).

A feedforward effect of pacing frequency on the mitochondrial oscillator was also observed (Fig. 6 B and Fig. 7). Higher frequency stimulation corresponded to a decreased period for the mitochondrial oscillator. This effect was due to the increased energy demand, which resulted in lower ATP levels at higher frequencies and higher mitochondrial respiration rates. The higher mitochondrial respiration rate also increased ROS production since the ROS shunt was described as a fraction of the total oxygen consumption. This model prediction requires experimental testing in the future.

Comparison with previous integrated models

The major advance of the ECME-RIRR model is that it explicitly accounts for mitochondrial energetics, cellular ATPase reactions, high energy phosphate buffers (e.g., the creatine kinase/phosphocreatine reaction), and the RIRR mechanism, which permits examination of the sequence of events that activate I_K,ATP during oxidative stress. There have been several previous attempts to model the interactions between mitochondrial bioenergetics and other cellular subsystems like Ca²⁺ cycling and plasmalemmal ion channels. To explain how glucose promotes bursting electrical behavior linked to insulin release in pancreatic beta cells, Keizer and Magnus (28) modeled mitochondrial ATP production linked to glucose oxidation in a whole-cell model that incorporated membrane ion channels and Ca²⁺ handling. An increase in the ATP/ADP ratio induced by glucose oxidation modulated the bursting and continuous spiking electrical activity via inhibition of K_ATP channels, which governed the resting membrane potential of the cell. Ca²⁺ cycling was a key component of the feedback loop regulating the burst durations, through a Ca²⁺-activated K⁺ conductance. The effects of K_ATP channel activation on the cardiac action potential were quantitatively investigated using the OXSOFT (D. Noble, Oxford University, UK) cardiac cell electrophysiological model by Nichols and Lederer (29) with corresponding experimental validation (30). Similarly, the effects of K_ATP current activation on simulated electrocardiograms using a whole cell model was investigated by Gima and Rudy (31), who demonstrated that K_ATP current activation underlies ST segment elevation during ischemia. A model by Ch'en et al. (32), took into account the biochemical changes in cytosolic ATP, pH and Ca²⁺ that occur during ischemia-reperfusion. Michailova and McCulloch (33) and Michailova et al. (34) further explored the role of free Mg²⁺, MgATP, and MgADP on I_K,ATP, I_Ca, and [Ca²⁺]_i in a canine cell model. Simulations from Michailova et al. (34) showed that either increases in free cytosolic Mg²⁺ (0.2–5 mM) with fixed Mg-nucleotide concentrations, or decreases in the ATP/ADP ratio with fixed total Mg²⁺, could activate I_K,ATP and systematically change the APD, Ca²⁺ current, and the Ca²⁺ transients (35).

The previous modeling studies provide important information about the interaction of multiple cytosolic factors in the regulation of metabolically sensitive ion channels; however, none of the cardiac cell models to date have incorporated realistic mathematical representations of mitochondrial energetics to drive the changes in ATP/ADP ratio, and the subsequent effects on integrated cell function. Moreover, the nonlinear interactions of the mitochondria and the cell during RIRR have never been examined in computational studies of the cardiac cell before this work, to our knowledge.

Implications of mitochondrial network depolarization for cardiac function

The teleological reason behind the activation of K_ATP channels during metabolic stress is not completely understood. Certainly, at the level of an isolated single cardiomyocyte, it can be viewed as a protective mechanism, i.e., decreasing electrical excitability, shortening the AP, and reducing Ca²⁺ cycling and contraction could reduce energy demand and prevent cell death (35,36). In the setting of exercise training, for example, it has been shown that K_ATP channel activation contributes to enhanced peak performance, based on comparisons between normal and knockout mice having reduced K_ATP channel proteins (37). This effect is not completely understood, but could possibly be related to K_ATP current shortening the duty cycle for resetting electrical and contractile activity at the high heart rates of the mouse. On the other hand, under more severe metabolic stress, such as ischemia-reperfusion, shutting down the function of myocytes in the cardiac syncytium would not be particularly beneficial. In this case, myocardial performance would be compromised even though the external workload remained. Moreover, local or regional changes in cardiomyocyte function could contribute to electromechanical dys-synchrony, further exacerbating the problem.

Regarding the negative implications of K_ATP channel opening, it has been reported that reperfusion arrhythmias in large animals are inhibited by K_ATP channel blockers (38) and we have shown that they are also prevented by agents that inhibit ΔΨ_m depolarization and eliminate the associated APD oscillations (2). Stabilization of ΔΨ_m effectively decreased the incidence of ventricular fibrillation even when applied only upon reperfusion (2,19). Based on these findings, we have proposed that the heterogeneous collapse of ΔΨ_m in clusters of cells in the myocardium during ischemia-reperfusion create metabolic sinks that would impact electrical wave propagation and introduce large gradients in the refractory periods of neighboring regions of the heart, thus creating a substrate for reentry. The altered electrical excitability would be a consequence of the excitation-contraction-bioenergetic coupling mechanisms described by the model. In fact, in preliminary studies in which we have expanded the ECME-RIRR single cell model to a two-dimensional monodomain model, we have observed significant effects of the periodic mitochondrial depolarizations on wave propagation, including complex reentrant activity (39), illustrating how the model could be applied to testing possible arrhythmogenic mechanisms in the future.

Model limitations and future directions

Although modeling of the heart began over 40 years ago, the field is still a long way from achieving a truly comprehensive computational model of the cardiac myocyte. Nevertheless, there have been many achievements in developing electrophysiological models (40–44), metabolic models (13,45–48), and mechanoelectrical models (49–51)—only very recently have models been developed to account for the interaction between electrophysiology, Ca²⁺ handling, and bioenergetics. The ECME-RIRR model developed here expedites this effort by integrating detailed descriptions of sarcolemmal and mitochondrial ion transport pathways, Ca²⁺ handling, and E-C coupling with mitochondrial energy metabolism and the ROS-induced-ROS-release mechanism, permitting us to begin to examine catastrophic events related to cellular injury. However, as with all models, there are limitations that suggest areas for further development in the future. These areas for expansion include adding pathways for higher level substrate oxidation (currently, acetyl CoA is the primary substrate representing the nexus of glycolytic and fatty acid pathways); a more detailed representation of factors known to change during ischemia-reperfusion including blood flow, oxygen uptake, and substrate transport (e.g., glucose and oxygen), pH, and Na⁺ homeostasis; and more comprehensive antioxidant pathway representations.

Another challenging problem for further model development is to take into account the important role of phosphotransfer networks in connecting cell metabolism with metabolite-sensitive channels, transporters, or sites of ATP consumption. Creatine kinase and adenylate kinase circuits take part in phosphotransfer networks that can rapidly transmit local changes in the rates of ATP consumption or synthesis across the cytoplasm to fine-tune the modulation of metabolically regulated targets while at the same time buffering the global levels of ATP and ADP (52,53). Sarcolemmal K_ATP channels are particularly sensitive to changes in ATP/ADP microdomains, as evidenced by the observation that they can be locally regulated by associated glycolytic enzymes (54), but can also be activated by mitochondrial uncoupling even when cells are internally dialyzed with high levels of MgATP via patch pipette (8,11). Moreover, the sensitivity of mitochondrial respiration to ADP varies depending on the mode of delivery; for example, a more efficient response is achieved when ADP is increased through the mitochondrially bound creatine kinase reaction than when is increased in the bulk myoplasm of the cardiac cell (55,56). Together, such observations support the idea that sites regulated by, or regulating, ATP level typically depend on localized near-membrane kinetic disequilibria. Computational descriptions of this aspect will require spatially distributed models of the enzyme transfer networks and a detailed representation of the cell architecture, which is beyond the scope of this article. However, to approximate some of these features without introducing partial differential equations, rapid mitochondrial responses to energy demand associated with E-C coupling and rapid ion channel responses to changes in mitochondrial energization are represented in the ECME-RIRR model by two nucleotide pools: the bulk cytosolic pool, which is largely buffered by creatine kinase and does not permit ADP to vary significantly; and a minimally buffered nucleotide pool in which ADP concentration can fluctuate according to the metabolic state. This was required to simulate I_KATP activation during mitochondrial ΔΨ_m depolarization and oscillation, in agreement with the available experimental data.

Finally, the next phase of model development will be to expand the cell models to two- and three-dimensional tissue models to investigate the effect of mitochondrial depolarization on cardiac electrophysiology and function at the tissue or organ levels.

In summary, the integrated ECME-RIRR model was capable of simulating the phenomenon of oxidative stress-induced mitochondrial oscillations and their effects on whole cardiomyocyte function, providing a new tool for examining how alterations in mitochondrial energetic state will impact the electrophysiology and electrical activities of the cardiac cell. The results demonstrate the power of combining the Ca²⁺ handling and electrophysiological and energy-producing subsystems of the cell into an integrated model to simulate the dynamics of metabolic and electrical processes of the heart under pathological conditions.

Supporting Material

Model and parameters are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01292-2.