Elastic Moduli of Collagen Gels Can Be Predicted from Two-Dimensional Confocal Microscopy

Abstract

We quantitatively compare data obtained from imaging two-dimensional slices of three-dimensional unlabeled and fluorescently labeled collagen gels with confocal reflectance microscopy (CRM) and/or confocal fluorescence microscopy (CFM). Different network structures are obtained by assembling the gels over a range of concentrations at various temperatures. Comparison between CRM and CFM shows that the techniques are not equally sensitive to details of network structure, with CFM displaying higher fidelity in imaging fibers parallel to the optical axis. Comparison of CRM of plain and labeled collagen gels shows that labeling itself induces changes in gel structure, chiefly through inhibition of fibril bundling. Despite these differences, image analyses carried out on two-dimensional CFM and CRM slices of collagen gels reveal identical trends in structural parameters as a function of collagen concentration and gelation temperature. Fibril diameter approximated from either CRM or CFM is in good accord with that determined via electron microscopy. Two-dimensional CRM images are used to show that semiflexible polymer theory can relate network structural properties to elastic modulus successfully. For networks containing bundled fibrils, it is shown that average structural diameter, rather than fibril diameter, is the length scale that sets the magnitude of the gel elastic modulus.

Introduction

Type I collagen is the most abundant structural protein in mammalian tissue. Collagen I based gels have been used widely as extracellular matrix approximations in biophysical experiments and as scaffolds in tissue engineering (1–3). In vivo, collagen undergoes self-assembly into fiber networks that are organized differently in different tissues (4). In vitro, collagen undergoes a very similar self-assembly process in which monomers assemble into fibrils that may bundle into fibers that assemble into a network. Different fibril microstructure and different overall network structure can be obtained by altering the pH, ionic strength, and temperature at which fibrillogenesis proceeds (5–10). Gel structure on both the fibril and network length scales is expected to impact the mechanical properties (and biological activity) of the resulting gels.

Turbidity studies and electron microscopy have long been used to investigate macroscopic and microscopic features of collagen gels, respectively (8,11–14). More recently, fibril and gel structure have been investigated via a variety of confocal microscopies including second harmonic generation (SHG) and multiphoton fluorescence (MFM) (6,7,15,16). One of the simplest microscopies currently used to image three-dimensional (3D) collagen gels is confocal reflectance microscopy (CRM) (9). This technique is used commonly in cell studies in which simultaneous, multimodal imaging of collagen (with CRM) and cells (with confocal fluorescence microscopy, CFM) is carried out to investigate cell-environment interactions (1,17,18). Like SHG and MFM (as it is typically carried out), CRM requires no potentially perturbative labeling, as contrast is generated through Rayleigh and Mie scattering. Unlike SHG and MFM, CRM imaging requires no specialized laser systems or microscope optics. The nonperturbative nature and uncomplicated experimental setup required thus make CRM a very attractive technique with which to image collagen gels. However, the anisotropy of Mie scattering results in a scattering intensity dependence on structural orientation (19). This may lead to incorrect interpretation of the 3D structure of the network; as such, fluorescent labeling followed by CFM on collagen networks has been reported recently (20). To date no comparison of CRM and CFM images from collagen gels has been described.

In this study, we quantitatively compare network structures extracted from two-dimensional (2D) CRM and CFM slices of 3D collagen I gels in a manner similar to that undertaken recently for SHG/MFM (7). In concert with the quantitative comparison of CRM and CFM, we also delineate how changes in collagen concentration and gelation temperature affect fibril structure, network structure, and gel stiffness. CRM images of unlabeled collagen gels and those labeled with fluorescein-isothiocyanate (FITC) are compared to evaluate whether FITC labeling of collagen monomers affects collagen self-assembly. CRM and CFM images from FITC-labeled collagen gels are compared to evaluate whether the two modalities are equally sensitive to details of network structure. We then show that network parameters extracted from 2D CRM images of 3D collagen networks are sufficient to predict storage moduli of the networks within the context of semiflexible polymer theory.

Materials and Methods

Materials

High concentration type I collagen extracted from rat tail tendon is obtained from BD Bioscience (San Jose, CA). The solution is delivered at ∼10 mg/mL in 0.01 M acetic acid. FITC-conjugate type I collagen is obtained from Sigma Aldrich (St. Louis, MO). The solution is supplied at 1 mg/mL in 0.01 M acetic acid. DMEM 10× solution and sterile NaOH (1 N) are purchased from Sigma Aldrich. Gibco HEPES buffer (1 M) is obtained from Invitrogen (Carlsbad, CA). Fixation supplies necessary for scanning electron microscopy (SEM) studies are obtained from Electron Microscopy Sciences (Hatfield, PA).

Preparation of collagen gels

Plain (FITC-labeled) collagen gel solutions are prepared by diluting the high concentration unlabeled collagen (and FITC-conjugate collagen). Appropriate amounts of high concentration collagen (∼10.0 mg/mL) and (for labeled gels) FITC-conjugate collagen (1.0 mg/mL), depending on the final concentration desired, are mixed at 4°C with 0.2 mL DMEM 10× solution and 50 μL HEPES buffer (1 M). NaOH (0.5 M) is added to bring the pH to 7.4. Deionized water is added to bring the total volume to 2.0 mL. Final ionic strength of gel solutions are I ∼ 0.13. Gel matrices are formed in situ during rheology or by incubation at 37°C or 32°C for 2 h or at 27°C or 22°C for 24 h.

Rheology

Rheological experiments are conducted on an AR-2000 rheometer with built-in temperature and gap calibration (TA Instruments, New Castle, DE). A 1° acrylic cone geometry with a solvent trap is used. All experiments are conducted in oscillatory mode at a fixed frequency of 1 Hz with a controlled strain amplitude of 0.8%. In all cases, 1 mL of collagen solution is neutralized and then applied to the measuring stage at 4°C. The solvent trap is added, and the measurement begins when the tool reaches the desired temperature. Storage modulus, G′ (Pa), and loss modulus, G″ (Pa), are monitored as the gel forms until plateaus are reached. Moduli are determined by averaging the last 10 points in the plateau regions. All tests are repeated at least three times.

SEM

Unlabeled collagen gels are fixed in 3% glutaraldehyde containing 3% paraformaldehyde and 2.5% dimethylsulphoxide in 0.1 M sodium cacodylate buffer (pH 7.4) for at least 12 h at room temperature. Gels are washed extensively with 0.1 M sodium cacodylate buffer (pH 7.4), dehydrated in a graded series of ethanol solutions, and critical-point dried from ethanol in CO₂. The dried gels are mounted on the SEM stub with silver conducting adhesive, sputter-coated with 10 nm gold-platinum, and examined in scanning electron microscope (Hitachi 4700, Brisbane, CA) at 10 kV.

Confocal microscopy

CRM images are recorded with an inverted confocal laser scanning microscope (Olympus Fluoview, Center Valley, PA) equipped with a 60×, NA = 1.2 water objective. An Ar⁺ laser at 488 nm is used to illuminate the sample, and the reflected light is detected with photomultiplier tube detectors. All images are taken ∼100 μm into the samples. CFM images are recorded using the same laser and objective as CRM images. A dichroic mirror and long-pass 510 nm emission filter are used to ensure rejection of reflected light at 488 nm. Three to five CRM/CFM images per gel are collected. For the same type of imaging (CRM or CFM), excitation power and detection settings are kept constant for all the gels. To reconstruct 3D CRM/CFM images, CRM/CFM slices are collected from ∼90 to ∼110 μm into the sample with a step size of 0.25 μm. Three-dimensional reconstructions of 2D CRM/CFM slices are generated using the Volume Viewer plug-in in NIH Image J software (Bethesda, MD).

Image analysis

Mesh size as well as number, length, and average diameter of visualized structures are quantified from processed CRM and/or CFM images of plain and FITC-labeled collagen gels. The image processing procedure is described in the Supporting Material. Mesh size is determined by two methods, and characteristic mesh size (ξ_cha) (21) and average mesh size (ξ_av) are calculated. All additional image analysis requires use of a fiber-finding algorithm slightly modified from that described previously (22). After the fiber-finding algorithm is carried out, number of structures identified (N_structure) is reported:

$$N_{\text{structure}}=\sum _i{N}_{\text{structure}}^i,$$ (1)

with Nⁱ_structure the number of found structures of width i = 1, 2, 4, 6, and 8 pixels. Additional details on mesh size calculation, fiber-finding, and N_structure determination are provided in the Supporting Material.

To determine collagen structure diameter, we take several approaches. First, fibril diameter (d_fibril,SEM) is measured manually from SEM images using the line-drawing feature of Image J. Only individually distinguishable fibrils, as opposed to fibrils comprising fibril bundles (i.e., fibers) are measured. A total of 200–400 fibrils are measured in each gel. Additionally, structural diameter is estimated from CRM and CFM images. Assuming the specific volume of a collagen structure is 0.73 cm³/g, the average diameter of identified structures in the image is given by

$$d_{\text{structure}}={((4\times 0.73\times c{V}_{\text{image}})/\left(\pi \sum _{i,j}{L}_j^i\right))}^{1/2},$$ (2)

where Lⁱ_j is the length of the jth structure of width i, c is the collagen concentration, and V_image is the imaged volume (20). For 2D CRM and CFM slices, we assume image thickness to be 1 μm. This calculation of average structural diameter assumes that width as measured in 2D confocal microscopy is proportional to actual structural width, which is supported by the linear relationship found between SHG and SEM determined width of collagen structures (6). It further assumes that fibrils and fibers have the same packing density. Given the almost crystalline packing of collagen molecules into fibrils, this likely overestimates fiber density and thus overestimates average structural diameter for systems in which bundled fibrils (fibers) are present.

A second approach allows independent calculation of fibril and fiber diameter from confocal images. This method does not require assumption of identical fibril and fiber density but does require other assumptions. We assume that found structures of i = 1 and i = 2 pixels are single fibrils. We make this assumption because our fiber-finding algorithm identifies most found structures in gels formed at 37°C as being 2 pixels in width. SEM imaging of gels formed at this temperature show little evidence of fibril bundling (Fig. S1 a), and we assume that all structures in gels formed at 37°C are individual fibrils. Gels formed at lower temperatures include structures in the confocal images that can be identified as individual structures with our fiber-finding algorithm only by allowing width in pixels to go up to 8. These structures are assumed to be fibers, i.e., composed of several fibrils (each of 2-pixel width).

Although many studies have detailed how collagen molecules pack in fibrils, very little information is available on how fibrils bundle into fibers. As such, we make the assumption made previously for other bundled biopolymers that fibers are packed such that the increase in fiber width goes as the square root of the number of fibrils in the bundle (23). This scaling is consistent with several different types of packing. For example, for a 4-fibril wide bundle, this equation describes both a square bundle (4 fibrils across and 4 fibrils deep) or a thicker bundle, anchored by a 4-fibril wide center, atop and below which are 3, 2, and 1 fibril layers. Other packings are also possible: if fibrils are organized in a flat layer, the assumed scaling would overestimate the number of fibrils in found structures of i = 4, 6, or 8. Hexagonal close packing is also possible, and then the assumed scaling may underestimate number of fibrils in a structure. SEM images of collagen gels prepared at 22°C (Fig. S1 b) show that such gels contain a diversity of fiber structures, and the quadratic scaling represents an average over likely bundle packings.

Given these assumptions, the diameter of a fibril can then be calculated as

$$d_{\text{fibril}}={((4\times 0.73\times c{V}_{\text{image}})/\left(\pi (\sum _{i=1,2;j}{L}_j^i+\sum _{i=4,6,8;j}{\left(\frac{i}{2}\right)}^2{L}_j^i)\right))}^{1/2},$$ (3)

where the factor of (i/2) captures the assumption that each fibril is 2 pixels in width and the squaring of this term captures the assumption about packing. At 37°C, where all found structures are 1–2 pixels in width, the two approaches give identical results and d_structure = d_fibril. Below, we use the terms “structure” and “fibril” interchangeably for gels constructed at 37°C. For gels formed at lower temperature, using the same assumptions described above, we can also estimate average diameter of the structures in these gels. We term this measure d_fiber to distinguish it from d_structure, although both variables average over fibrils and fibers. This diameter is given by

$$d_{\text{fiber},\text{calc}}=(\sum _{i\text{=}1,2}{N}_{\text{structure}}^i{d}_{\text{fibril}}+\sum _{i=4,6,8}\left(\frac{i}{2}\right)N_{\text{structure}}^i{d}_{\text{fibril}})/N_{\text{structure}}\text{.}$$ (4)

Alternately, a mixed approach using number of structures determined via confocal microscopy but using fibril diameter measured with SEM (d_fibril,SEM) is used to calculate this quantity:

$$d_{\text{fiber},\text{mixed}}=(\sum _{i=1,2}{N}_{\text{structure}}^i{d}_{\text{fibril},\text{SEM}}+\sum _{i=4,6,8}\left(\frac{i}{2}\right)N_{\text{structure}}^i{d}_{\text{fibril},\text{SEM}})/N_{\text{structure}}\text{.}$$ (5)

We note that detailed study of how rod-like structures of diameter ∼50 nm–>1 μm at all angles relative to the optical axis appear in 2D CRM and CFM, as well as how our fiber-finding algorithm most faithfully identifies images of those structures, would allow for a more accurate reporting of how apparent width in CRM and CFM relates to actual fibril and fiber width. In the absence of such a detailed study, we believe our approach includes reasonable assumptions given the complex nature of the system. This statement will be supported by results showing that d_structure and d_fiber are of very similar magnitude despite being based on somewhat different assumptions.

Results and Discussion

Fibril and network structure as a function of fluorescent labeling and collagen concentration

CRM images of plain collagen gels as well as CRM/CFM images of FITC-labeled collagen gels are compared as a function of collagen concentration at 37°C (Fig. 1). Collagen gels of increasing concentration (from 0.5 to 5.0 mg/mL) show increasing fibril number in all types of confocal images. Comparing CRM of unlabeled collagen (Fig. 1, column 1) and CRM of labeled collagen (Fig. 1, column 3), suggests that the addition of 3% FITC-labeled collagen subtly alters microstructure of the gels. Preliminary studies were carried out to determine the amount of labeled collagen to be used in preparing these gels. Weight percentages from 1% to 10% were examined, and 3% FITC-labeled collagen was used in all subsequent studies, as it was the lowest labeling density that led to CFM images with a high degree of colocalization with CRM images. The low level labeling also limited clumping and changes to fibril morphology that were evident in higher label density preparations. Even at this low labeling density, however, we find differences between CRM of plain collagen gels and CRM of FITC-labeled gels. Most notably, we find longer fibrils in CRM images of FITC-labeled collagen gels than in those of plain collagen gels.

Figure 1.

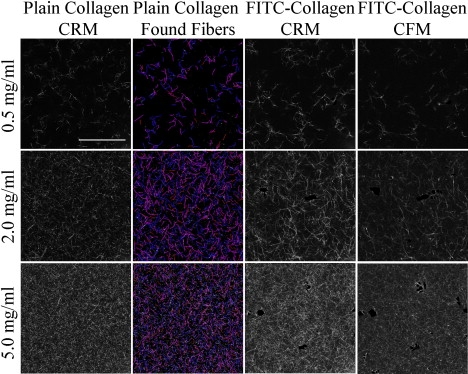
CRM images of unlabeled collagen (first column), fibrils identified from CRM images in the first column by the fiber-finding algorithm (second column), and CRM/CFM (third/fourth column) images of FITC-labeled collagen formed at 37°C. Collagen concentration is 0.5 mg/mL (first row), 2.0 mg/mL (second row), and 5.0 mg/mL (third row). In the second column, found fibers are either 1 pixel (in red, online) or 2 pixels (in blue and pink, online) in width. Scale bar = 50 μm.

Comparing CRM (Fig. 1, column 3) and CFM (Fig. 1, column 4) of FITC-labeled collagen shows additional differences. Excitation power and detection settings are set to provide maximum contrast between background and fibrillar structures without significant saturation for both CRM and CFM. At these settings, CRM reveals more and longer structures than CFM images of the same regions of FITC-labeled collagen gels. This comparison shows differences in the microscopic techniques rather than differences in the gels themselves. Several factors may contribute to these differences. Unlike isotropically emitted fluorescence, backscattered Mie and Rayleigh scattering intensity is orientation dependent, with scattering efficiency decreasing as the incident angle decreases relative to the scatterer (24,25). This would suggest CRM will underrepresent structures present, as it may miss entities at large angles to the x,y plane (out of plane structures). On the other hand, there are at least two forces countering this tendency for CRM to undercount fibers relative to CFM. First, the low level labeling we use could result in some fibrils being sparsely labeled enough to be undetectable in our CFM measurement. Additionally, we find in practice that the axial resolution of CFM appears better than that of CRM. This is consistent with the finding that point scatterers appear sharper in the axial dimension in CFM than CRM (19). As a result, structures nearly parallel to the optical axis appear as bright, isolated spots in CFM but as less bright, short structures in CRM. These entities are then identified by the fiber-finding algorithm carried out on CRM images but not CFM images.

To quantify network structures in images such as those presented in Fig. 1, we first calculate mesh size as a function of concentration (Fig. 2 a). As expected for both unlabeled and labeled collagen, as imaged with either CRM or CFM, characteristic mesh size, ξ_cha, and average mesh size, ξ_av, decrease with increasing collagen concentration. ξ_cha and ξ_av are very similar at all concentrations except 0.5 mg/mL. Here, ξ_cha is ∼60% larger than ξ_av, which is consistent with characteristic mesh size more heavily weighing the presence of large pores than does average mesh size. All additional network analysis carried out requires the fiber-finding algorithm described in Materials and Methods. Fibrils identified in the CRM images of unlabeled collagen shown in Fig. 1, column 1, are shown in Fig. 1, column 2. The algorithm is very effective in identifying collagen fibrils in CRM images for concentrations up to 4.0 mg/mL. For images of 4.0 and 5.0 mg/mL collagen, some dim fibrils identified by visual inspection are not identified by the algorithm. This is due to the increase of scattering entities in the excitation and detection paths that leads to noticeably decreased contrast in images of the high concentration gels.

Figure 2.

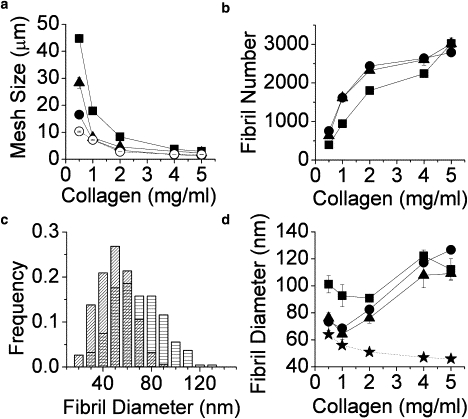
Fibril and network structure as shown by image analysis for gels formed at 37°C. (a) Characteristic mesh size ξ_cha (solid symbols) and average mesh size ξ_av (open symbol; only shown for unlabeled collagen), (b) fibril number, (c) distribution of fibril diameter measured from SEM images, d_fibril,SEM, at 0.5 mg/mL (bars with horizontal lines) and 5.0 mg/mL (hatched bars), and (d) d_fibril,SEM (★) and fibril diameter, d_fibril (= d_structure). In all panels, parameters quantified from CRM images of unlabeled collagen are represented by circles, those from CRM images of FITC-labeled collagen are triangles, and those from CFM images of FITC-labeled collagen are squares.

The number of fibrils identified with the fiber-finding algorithm (N_structure) increases as collagen concentration increases in all three types of images (Fig. 2 b). Except for the 5.0 mg/mL gel, the number of fibrils found in the CRM images of plain and FITC-labeled collagen of the same concentration is identical within error. Thus, although the fluorescent labeling seems to affect the morphology of fibrils somewhat, it does not seem to affect overall number of fibrils. On the other hand, fewer structures are typically identified in CFM images of FITC-labeled gels than in the corresponding CRM images of those gels. Although some of this discrepancy may be attributable to differences in detection settings between the two imaging configurations, a significant portion is likely due to differences between CRM and CFM described earlier.

Average fibril length as measured with the fiber-finding algorithm on CRM images of unlabeled and FITC-labeled collagen parallel each other but do not show clear trends as a function of collagen concentration (data not shown). In general, however, found fibrils in plain collagen gels are shorter than those in FITC-labeled collagen (as imaged with either CRM or CFM), which is consistent with visual inspection. At 2 mg/mL, average fibril length is 7.7 ± 0.2 μm for CRM of FITC-labeled gels, 7.0 ± 0.1 μm for CFM of FITC labeled gels, and 6.3 ± 0.1 μm for CRM of unlabeled gels. Histograms of fibril diameter distribution as measured by SEM (shown in Fig. 2 c for 0.5 and 5.0 mg/mL) show that mean fibril diameter decreases as collagen concentration increases, from 64 nm at 0.5 mg/mL to 46 nm at 5.0 mg/mL collagen. Fibril diameter (d_fibril = d_structure) is calculated as described in Materials and Methods and compared to fibril diameter measured from SEM images (d_fibril,SEM) in Fig. 2 d. This shows that d_fibril deviates increasingly from d_fibril,SEM as collagen concentration increases. This is due to the systematic undercounting of fibers that occurs at high collagen concentration. We note that although 2D confocal imaging clearly does not reproduce the trend in fibril diameter as a function of collagen concentration shown by SEM, maximum fibril diameter overestimation as calculated with the method described here is significantly smaller than the apparent overestimation reported from direct measurement from CRM or SHG images (6,9).

Fibril and network structure as a function of fluorescent labeling and gelation temperature

Although altering collagen concentration obviously alters collagen network structure, altering temperature, pH, and ionic strength at a given collagen concentration may also lead to different fibril and overall network structure. We investigated fibril and network structure of collagen gels as a function of decreasing gelation temperature from 37°C to 22°C. This is shown for collagen gels of 2.0 mg/mL in Fig. 3. Several trends are evident: mesh size increases, number of visualized structures decreases, and diameter of visualized structures increases with decreasing temperature. Comparing CRM of unlabeled collagen (Fig. 3, column 1) and CRM of FITC-labeled collagen (Fig. 3, column 3) shows that the presence of labeled collagen strongly inhibits the lateral bundling of fibrils into thicker structures that otherwise occurs at low gelation temperature. Given that the FITC-labeling occurs via covalent bonding to collagen lysine residues, the same residues at which neighboring collagen fibrils can chemically cross-link (4,26), it is not unexpected that labeling can affect the intricate self-assembly processes that occur during fibril and fiber formation. Comparing CRM (Fig. 3, column 3) and CFM (Fig. 3, column 4) of FITC-labeled collagen shows that CRM imaging reveals more structures in the image plane than does CFM, consistent with Fig. 1. This finding is supported by the presence of bright spots in CFM images that are absent in CRM images of the same region: these spots are cross sections of fibers intersecting the image plane at a large angle that scatter substantially into the plane in reflectance mode. Although such differences are evident in all imaged gels, the differences appear starkest at low gelation temperature, where fibril bundling (even the reduced fibril bundling as occurs in FITC-labeled gels) results in thick fiber cross sections. To further investigate differences between CRM and CFM of such samples, we collected 20 μm z-stacks from 2D CRM and CFM of FITC-labeled 2.0 mg/mL collagen gelled at 22°C. Fig. S2 presents projections and a 3D reconstruction from a location within a gel where numerous bright spots in one x,y slice of CFM were apparent. The differences seen in the x,y and y,z projections confirm that increased fiber number in 2D CRM images can emerge from out of plane fibers scattering into the plane. This accounts for the slightly larger mesh size, fewer structures, and larger structural diameter found from CFM images of FITC-labeled gels than the corresponding CRM images.

Figure 3.

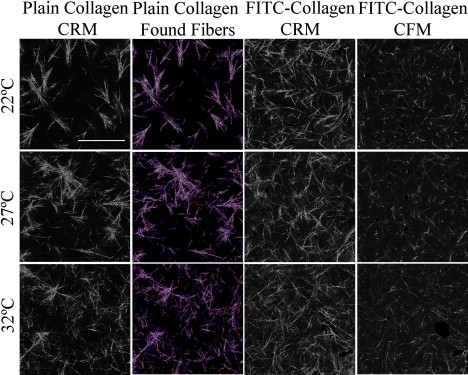
CRM images of plain collagen (first column), fibers identified from CRM images in the first column by the fiber-finding algorithm (second column), and CRM/CFM (third column/fourth column) images of FITC-labeled collagen of 2 mg/mL. Collagen gels formed at 22°C (first row), 27°C (second row), and 32°C (third row). In the second column, found fibers are either 1 pixel (in red, online), 2 pixels (in blue, online), or 4, 6, or 8 pixels (in pink, online) in width. Scale bar = 50 μm.

Returning to the bundling trends as a function of gelation temperature, clear bundling is found at low temperature, as has been noted previously (5,6). For identical collagen concentration, this results in a larger mesh size as a function of decreasing temperature. This is reflected in mesh size, which is plotted for 2 mg/mL collagen gels formed at temperatures between 37°C and 22°C (Fig. 4 a). To more fully assess network structure in these gels, fiber-finding is carried out on all confocal images. Found structures in CRM images of unlabeled collagen are illustrated (Fig. 3, column 2). The algorithm is effective in tracing structures at different gelation temperatures if diameter in pixels, i, is varied from 1 to 8 as described in Materials and Methods and the Supporting Material. This is in contrast to the images analyzed of gels formed at 37°C, where limiting i to 1 and 2 allows for almost complete colocalization between imaged and found structures. We note that the gels constructed at low temperature (particularly those at 22°C) contain some thick fiber bundles. Our fiber-finding algorithm identifies fibers within these bundles, and we determine diameter averaged over fibril and fiber structures in these gels via d_structure, d_fiber,calc, and d_fiber,mixed as described in Materials and Methods.

Figure 4.

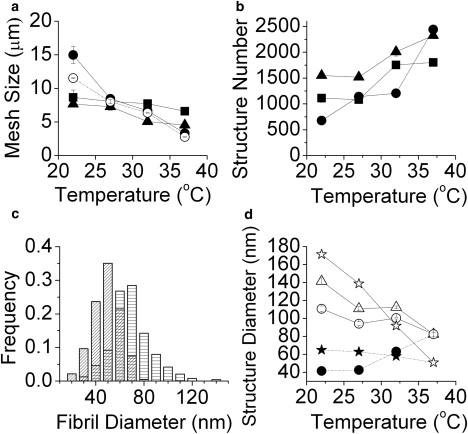
Fiber and network structure as revealed by image analysis as a function of gelation temperature for 2 mg/mL collagen gels. (a) Characteristic mesh size ξ_cha (solid symbols) and average mesh size ξ_av (open symbols; only presented for unlabeled collagen). (b) Number of identified structures. In a and b, parameters quantified from CRM images of unlabeled collagen are represented by circles, those from CRM images of FITC-labeled collagen are triangles, and those from CFM images of FITC-labeled collagen are squares. (c) Distribution of fibril diameter measured from SEM images of 2 mg/mL collagen gelled at 22°C (bars with horizontal lines) and 37°C (hatched bars). (d) Fibril diameter measured from SEM, d_fibril,SEM, (★) as well as various measures of structural diameter from CRM images of unlabeled collagen: fibril diameter (d_fibril) (●), structural diameter (d_structure) (▵), and fiber diameter (d_fiber,mixed, ○; d_fiber,calc, ☆).

The number of structures found in CRM images of plain collagen gels decreases dramatically as gelation temperature decreases due to the increased bundling of fibrils that occurs with decreasing temperature. Because FITC labeling inhibits bundling, the number of structures found in CRM and CFM images of FITC-labeled collagen decreases more slowly with decreasing temperature (Fig. 4 b). Fibril diameter of plain collagen is measured via SEM. Histograms of fibril diameter distribution show that not only bundling but also average diameter of single fibrils increases as the gelation temperature decreases, from 51 nm at 37°C to 65 nm at 22°C (Fig. 4 c). This is consistent with some (8,22) but not all (5,6) previous studies. Increase of fibril diameter with decreasing temperature is also consistent with the nucleation-growth mechanism of collagen self-assembly (27). Fibril diameter is determined during the nucleation step, by the rate of nucleation and the shape of the nuclei (11,27). At higher temperature and higher concentration, nucleation is faster, and more nucleation centers form and compete with each other for aggregation of remaining collagen molecules, resulting in slender fibrils (22,28). Although increased fibril thickness at low temperature is well explained by nucleation and growth, increased bundling is not. An explanation based on altered attractive and repulsive interactions has instead been proposed as a source of increased bundling at low temperature (6).

Despite the finding (from SEM) that fibril diameter increases with decreasing gelation temperature, calculated fibril diameter, d_fibril, from each of the three types of confocal imaging decreases somewhat with decreasing gelation temperature (shown for CRM of plain collagen in Fig. 4 d). As in high collagen concentration gels constructed at 37°C, the increased number of structures present at increasing gelation temperature results in an increased tendency to undercount structures for a given collagen concentration. Thus, the deviation of fibril diameter as measured with confocal microscopy from that measured via SEM at increasing temperature parallels that which occurs at increasing concentration at a given temperature. Despite this systematic error, calculated fibril diameter is within a factor of two of the SEM measured diameter for gels at 2 mg/mL at all temperatures investigated. In addition to calculating d_fibril, we also calculate and plot average structural diameter as a function of gelation temperature for gels of 2 mg/mL with the approaches described previously yielding d_structure, d_fiber,calc, and d_fiber,mixed (Fig. 4 d). The values of these variables increase by factors of 1.7, 1.3, and 3.4, respectively for gelation temperatures between 37°C and 22°C. These measures suggest a transition from single fibril gels to gels constructed of fibers of ∼4 fibrils (d_structure and d_fiber,calc) to ∼9 fibrils (d_fiber,mixed). In Fig. S1 b it is apparent that there is significant polydispersity in fiber size and structure, and an average structural diameter in the range of 4–9 fibrils is consistent with the SEM measurements. Because accurate knowledge of structural diameter is imperative in predicting elastic modulus within semiflexible polymer theory, the ability to accurately estimate these diameters from 2D confocal images is crucial in allowing mechanical properties to be predicted from such in situ 2D imaging.

Collagen gels formed at 37°C are consistent with semiflexible polymer theories

The storage moduli, G′, of unlabeled collagen gels from 0.5–5.0 mg/mL at 22°C and 37°C are measured by rheology. G′ is found to increase with collagen concentration, with G′ ∼ c^2.1 at 37°C and G′ ∼ c^2.8 at 22°C (Fig. 5 a). Whereas the rheological measurements were carried out at 1 Hz, frequency sweeps of gels from 0.5 to 2 mg/mL display the same frequency dependence (G′ ∼ ω^0.17–0.18), suggesting the scaling of modulus with concentration will be independent of particular frequency investigated (data not shown). The measured concentration dependence in this study is consistent with our previous measurement (22) although another recent study found a somewhat greater (G′ ∼ c^2.7) variation of storage modulus with concentration for collagen gels formed at 37°C (29). The concentration dependences measured in both studies are similar to those that have been found for other biopolymers, with tightly cross-linked actin displaying G′ ∼ c^2.5 (30). It is notable that the storage moduli of the 1–5 mg/mL collagen gels assembled at 22°C are larger than those of gels of the same concentration formed at 37°C. This increased elasticity occurs despite the increased mesh size in the gels formed at lower temperature. This result differs from a previous study that showed a monotonic decrease of G′ at decreasing temperature (37°C–4°C) for 4 mg/mL collagen gels (6). Monotonic decrease in moduli was also seen for collagen gels formed at decreasing pH values from 9.0 to 5.5 (7,9). In both cases, increasing mesh size at lower temperatures or pH values was the proposed cause of the decreased stiffness (6,7). Although increased mesh size in networks made of identical structures would be expected to decrease the value of elastic modulus, the increased thickness of the structures comprising the “struts” of the networks formed at low temperatures may increase gel stiffness, competing with any decrease due to increasing mesh size. In the temperature and concentration ranges explored here, it is clear that strut thickness must be considered as an important factor in setting magnitude of storage modulus. To further explore the relationship between G′ and the network structure of collagen, the dependence of G′ on temperature is investigated for 2.0 mg/mL collagen (Fig. 5 b). We find that maximum storage modulus for 2 mg/mL collagen gels occurs for gelation at 27°C, a temperature at which (at this concentration) there is a moderately large mesh size and moderately bundled fibrils.

Figure 5.

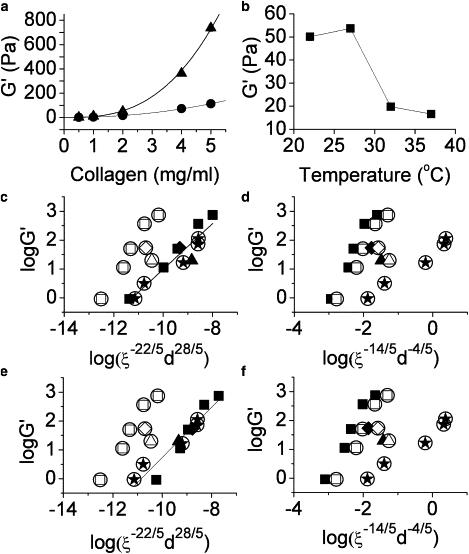
(a) Storage moduli, G′, of unlabeled collagen as a function of concentration for gels formed at 37°C (●) and 22°C (▴). G′ scales with collagen concentration as G′ ∼ c^2.1 at 37°C (solid curve) and as G′ ∼ c^2.8 at 22°C (dotted curve). (b) Storage modulus of 2 mg/mL collagen as a function of gelation temperature. (c–f) Scaling relationship between storage modulus and characteristic mesh size and structural diameter. Comparison to the (c and e) MacKintosh and (d and f) Morse models. Fits use ξ_av together with d_fibril,SEM (squares, diamonds, triangles, and stars, all within circles) and (c and d) d_structure (■♦▴), or (e,f) d_fiber,mixed (■♦▴). Data are obtained from 0.5, 1.0, 2.0, 4.0, and 5.0 mg/mL collagen gelled at 37°C (star within a circle) and 22°C (solid squares, and open squares within circles), and 2.0 mg/mL collagen gelled at 32°C (solid triangle, and open triangle within a circle) and 27°C (solid diamond, and open diamond within a circle). Fits for data points using (c) d_structure and (e) d_fiber,mixed for comparison with the MacKintosh (m = 0.79, R² = 0.89 and m = 0.87, R² = 0.91, respectively) model are shown as solid lines.

We assess the scaling relationship found for gelation at 37°C (G′ ∼ c^2.1) in the context of two models of semiflexible polymers. Although collagen fibrils may be expected to behave as rigid rods due to their high aspect ratio, we use models that have already successfully described some aspects of the elasticity of collagen as well as more flexible biopolymers (30–32). The first model used was developed by MacKintosh et al. (31) and proposed to describe chemically cross-linked or sterically entangled networks of semiflexible polymers (or worm-like chains (WLC)). Here, the storage modulus is expected to scale as G′ ∼ κ^7/5(c′l)^11/5, with κ the bending modulus, c′ the concentration of WLCs, and l the contour length of the chain (31). For collagen fibrils, κ has been experimentally shown to scale with the fourth power of fibril diameter (33). c′l can be expressed in terms of mesh size (ξ) with c′l = ξ⁻² when persistence length (l_p) is much greater than mesh size (31,34). Thus, we can express G′ in terms of mesh size and structural diameter, two quantities that can be assessed via confocal microscopy. The resulting expression is G′ ∼ ξ^−22/5d^28/5. The assumptions implicit in the MacKintosh model include affine deformation, the existence of dense entanglements or cross-links, and d << ξ < l_p, where d is chain diameter (collagen fibril or fiber diameter: ∼40–200 nm in this study), ξ is mesh size (∼1–40 μm in this study), and l_p is persistence length (∼1 cm for collagen fibers) (29,35). We assess this model, as well as the ability to estimate d and ξ from 2D CRM images, using two sources of mesh size and two sources of fibril diameter for CRM images of unlabeled collagen gels formed at 37°C (Fig. S2 a). Such measurements are also possible (and lead to similar results) for CRM/CFM of labeled collagen, but we focus on CRM results on unlabeled collagen because the morphological changes induced by the presence of fluorophores limit differences in collagen network structure that allow for fullest comparison of our results to model predictions.

The mesh size estimations used to assess the fitness of the MacKintosh model for describing collagen gels formed at 37°C are average mesh size, ξ_av, and characteristic mesh size, ξ_cha. We note that another pore size determination method for collagen gels was published recently, but this method is not appropriate for use on 2D images (36). The fibril diameters used are d_fibril (identical to d_structure for gels constructed at 37°C) and d_fibril,SEM. Although both ξ_av and ξ_cha give a linear relationship between log(G′) and log(ξ^-22/5d^28/5), ξ_av does so with a slope closer to one whether we use d_fibril or d_fibril,SEM in this assessment (Fig. S3 a). Thus, we use ξ_av for all further comparison to theory. To further assess the suitability of this model for describing collagen gel storage moduli, we will check for linearity between G′ and ξ^-22/5d^28/5 for collagen gels formed at lower temperatures.

In addition, we compare our results to a model developed by Morse (34,37) and formerly used to correlate collagen structural and mechanical properties (7). Like the MacKintosh model, the Morse model can describe tightly entangled solutions of semiflexible polymers; however the effect of cross-links is not included, and relatively free tangential motion of the WLCs is assumed (37). As such, the primary contribution to the (low-frequency) viscoelasticity of these systems is Brownian motion of the WLC along its contour, rather than stretching out of thermal fluctuations between cross-links. Given that very little is known about cross-links between fibrils in collagen networks, it is unclear whether cross-links will be important in the linear rheological response of collagen gels. Whereas the MacKintosh model predicts G′ ∼ ξ^−22/5d^28/5, the Morse model predicts G′ ∼ ξ^−14/5d^−4/5 (7). This relationship derives from the finding that G′ ∼ κ^-1/5(c′l)^7/5 (37). Comparing the Morse and MacKintosh descriptions of storage modulus in terms of mesh size and strut diameter, the most obvious difference is the sign and magnitude of the d dependence in these models. For gels formed at 37°C, we find the Morse model fits the measured data at least as well as does the MacKintosh model (Fig. S3 b). This is true whether we use d_fibril,_SEM or d_fibril (or the identical d_structure).

Collagen gels formed at low temperature distinguish between models

Although data collected from collagen gels formed at 37°C do not allow us to distinguish between the fitness of the Morse and MacKintosh models for describing the concentration dependence of the elastic modulus of collagen gels, data collected for collagen gels constructed at lower temperature clarify the situation. Fig. 5 compares measured G′ to both the MacKintosh (Fig. 5, c and e) and Morse (Fig. 5, d and f) models using measured ξ_av and d_fibril,SEM for 0.5–5.0 mg/mL gels formed at both 37°C (stars within circles) and 22°C (Fig. 5, squares within circles) as well as for 2.0 mg/mL gels constructed at 32°C (triangle within a circle) and 27°C (Fig. 5, diamond within a circle). It is evident that neither the MacKintosh nor Morse models well describes the measured storage moduli. However, when the structural diameter averaged over fibrils and fibers is used as the relevant length scale, the MacKintosh model does fit the data whereas the Morse model does not. We reiterate that at 37°C, fiber diameter and fibril diameter are identical, as we see little evidence for fibril bundling in either confocal imaging or SEM. For the comparison of the two investigated models at lower temperatures, we use both d_structure and d_fiber,mixed. We use d_fiber,mixed rather than d_fiber,calc (derived solely from CRM) to minimize effects from the spurious undercounting of fibers in high collagen concentration gels. When data from gels created at all four temperatures investigated is plotted using d_structure (Fig. 5, c and d) and d_fiber,mixed (Fig. 5, e and f), the linear relationship remains intact for comparison with the MacKintosh model (Fig. 5 c, m = 0.79, R² = 0.89, and Fig. 5 e, m = 0.87, R² = 0.91), but the fit is poor for comparison with the Morse model, where the data does not lay on a single line. We believe d_fiber,mixed results in a better fit than d_structure because like d_fiber,calc, d_structure contains some effects from systematic undercounting of fibers. However, the fact that d_structure fits the MacKintosh model almost as well as d_fiber,mixed suggests one can ascertain storage modulus from CRM imaging alone for gels of moderate fiber density, where undercounting in fiber-finding is not significant. We conclude that the MacKintosh model is consistent with all the data collected whereas the Morse model is not, suggesting that the effect of cross-links must be considered in describing collagen gels and showing that consideration of entropic stretching alone is sufficient to explain the data. Importantly, we find in cases in which fibril bundling is evident, average diameter averaged over both fibrils and fibers is the length scale that sets storage modulus in these systems. We note that this average diameter does not average over the thickest structures seen in collagen gels, fiber bundles, which appear in gels assembled at 27°C and 22°C. In CRM and CFM images, fiber bundles can be identified as structures composed of more than one fiber (structures that are 4–8 pixels wide) close to parallel along at least part of their length. Although we have not calculated average fiber bundle diameter in these gels, it is clearly larger than d_structure, d_fiber,calc, and d_fiber,mixed and thus using a structural diameter that includes fiber bundles would not be consistent with predictions of either the MacKintosh or Morse models.

Although we find that the MacKintosh model is consistent with our data, it is possible that the agreement emerges due to generic properties of the model rather than a fully accurate description of the physics of collagen networks. Indeed, it is not clear that entropic stretching out of individual filaments should accurately describe collagen gels. Other possibilities for the origin of elasticity in these gels that are not captured by either of the models explored here include bending of fibrils between cross-links (enthalpic elasticity), nonaffine deformations and geometric rearrangements of fibrils (29,38,39), and the presence of fibril bundles that are not fully coupled (23,40). Although some of these theories predict an overall storage modulus dependence on concentration that is weaker than that found in this study, others do predict G′ > c² and are thus alternate candidates for describing the rheological responses of collagen gels. Fuller investigation of the linear and nonlinear rheology should clarify the most appropriate model for describing the complex physico-chemical collagen networks.

Conclusion

We have quantified trends in collagen network structure as a function of collagen concentration and gelation temperature. Comparing CRM and CFM of FITC-labeled collagen gels shows that CFM allows for higher fidelity 3D reconstructions of network structure. Despite such differences, using a fiber-finding algorithm on 2D CRM or CFM images allows fibril diameter estimates that are in good agreement with those measured via SEM, especially at concentrations <4 mg/mL. Comparing 2D CRM images of unlabeled collagen gels to those of FITC-labeled collagen gels shows that FITC-labeling of collagen inhibits bundling and suppresses differences in structure and elastic modulus that otherwise occur in networks assembled at low temperature. The fact that fibrils, fibers, and fiber bundles can all be distinguished in CRM and that 2D CRM provides sufficient information to estimate fibril and fiber diameter confirms that 2D CRM is a viable, straightforward technique for revealing important structural parameters of collagen gels. Using 2D CRM images of collagen gels formed from 22°C (significant bundling) to 37°C (no bundling), we successfully estimate and relate network structural parameters to the storage moduli of these gels within the confines of semiflexible polymer theory. We show that in gels with bundled fibrils, fibril diameter is not the relevant length scale for setting elastic modulus, but an average over fibril and fiber diameters does fit predictions of the MacKintosh model. This shows that entropic considerations for cross-linked networks are sufficient to explain the variation of collagen gel storage modulus with network structure.

Supporting Material

Additional image analysis details and three figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01299-5.