Molecular Dynamics Simulations of DNA-Polycation Complex Formation

Abstract

Complexes formed from DNA and polycations are of interest because of their potential use in gene therapy; however, there remains a lack of understanding of the structure and formation of DNA-polycation complexes at atomic scale. In this work, molecular dynamics simulations of the DNA duplex d(CGCGAATTCGCG) in the presence of polycation chains are carried out to shed light on the specific atomic interaction that result in complex formation. The structures of complexes formed from DNA with polyethylenimine, which is considered one of the most promising DNA vector candidates, and a second polycation, poly-L-lysine, are compared. After an initial separation of ∼50 Å, the DNA and polycation come together and form a stable complex within 10 ns. The DNA does not undergo any major structural changes on complexation and remains in the B-form. In the formed complex, the charged amine groups of the polycation mainly interact with DNA phosphate groups, with polycation intrusion into the major and minor grooves dependent on the identity and charge state of the polycation. The ability of the polycation to effectively neutralize the charge of the DNA phosphate groups and the resulting influence on the DNA helix interaction are discussed.

Introduction

Complexation between negatively charged DNA and polycations has been a subject of great interest over the last decade because of its relevance to gene therapy (1,2), a promising treatment for many diseases in which a gene is delivered to cells to produce a missing or therapeutic protein. As naked DNA is degraded by nucleases outside of cells, successful gene therapy requires the use of a vector that is able to safely and efficiently deliver DNA into cells, while overcoming the many barriers that limit transgene expression. Early gene therapy techniques were based on packaging the DNA into viruses, which have evolved to successfully deliver foreign genes into cells. However, because of immunoresponses and other safety concerns caused by viral vectors (3,4), there has been a recent focus on developing nonviral gene therapy vectors. One group of highly studied nonviral vectors are polycations, which have the ability to condense negatively charged DNA through electrostatic forces.

A little over a decade ago, Boussif et al. (5) introduced the synthetic polymer polyethylenimine (PEI) as a potential gene delivery vector, and it has subsequently been shown to be one of the most promising synthetic vector candidates (1,2). In comparison with other polyamines, such as poly-L-lysine (PLL), PEI offers a higher transfection efficiency, while maintaining a relatively low cell toxicity (5,6). Much of the success of PEI as a gene therapy vector has been attributed to its ability to act as a proton sponge, aiding in the release of DNA-PEI complexes from endosomal compartments. Because every third atom along the backbone of PEI is a protonable nitrogen and only a fraction of these atoms are expected to be protonated at physiological pH, PEI is able to adsorb protons in the increasingly acidic endosome environments that are encountered in cells. The proton sponge ability of PEI has several possible effects that are advantageous to gene delivery, including causing an influx of chloride ions (7) that results in osmotic swelling and vesicle rupture, and buffering the endosomes so that the DNA is not exposed to very acidic environments (6,8). Additionally, it has been suggested that the swelling of endosomes is partially the result of changes in the structure of the polymer network as a result of the adsorption of protons by PEI (6). Several groups have linked the influence of the size of complexes formed with the observed transfection efficiency (9–11). They suggested that a more compact size of the formed complex favors a high uptake through cell endocytosis, and hence a potentially higher transfection efficiency. However, other factors such as the amount of secondary amine present also seem to play an important role in determining the transfection efficiency.

The complexation between DNA and polycations is related closely to another intriguing phenomenon, namely, DNA condensation by multivalent ligands. The capability of multivalent cations such as spermine and spermidine to condense extended DNA into small, compact particles with a characteristic toroidal structure, while monovalent cations like (Na⁺) lack such capability, has attracted considerable attention in the past 30 years (12–18). Because the mean-field theory based on Poisson-Boltzmann equation always predicts a repulsive interaction between two charged DNA helices, the observed condensation has inspired development of new theories for more than 20 years. It is now generally believed that when the negative charge around DNA helix is neutralized by the multivalent cations, short-range attractions would then dominate and lead to condensation. The origin of this short-range attraction, however, is of debate. The proposed origins include attractions caused by counterion fluctuations (19,20), the zipper-motif model (21), and hydration forces mediated by waters bridging between DNA helixes (22). Further delineation on the origin of the attraction has not been made and could be potentially achieved if atomistic structural details of DNA in the presence of counterions are made available.

Several atomistic molecular dynamics simulations have investigated the specific interactions that occur between DNA and monovalent cations, such as Na⁺, as well as short polyamines, such as spermine (23–28). These atomistic simulations focused on the binding of counterions with DNA helix and demonstrated that current computational methodologies to simulate DNA fragments in explicit water with counterions are reasonably reliable. Savelyey and Papoian compared the binding of Na⁺ and K⁺ to a 16 basepairs of DNA helix (25) and found that Na⁺ condensed around the DNA exterior and penetrate the DNA interior to a greater extent than K⁺, presumably because Na⁺ has a smaller size than K⁺. They found that both cations interacted with electronegative sites near the major and minor grooves of DNA as well as the oxygen atoms of the DNA phosphate group, with both cations having maximum occupancies in selected binding sites of ∼1 ns. A second comparison of the binding of Na⁺ and K⁺ to DNA (28) showed a preference for Na⁺ to remain near the DNA phosphate groups whereas the K⁺ showed greater binding to major and minor groove sites. Na⁺ organizes and immobilizes water structures around itself and near DNA whereas K⁺ has less tendency to organize water structures. There has also been interest in how binding of Na⁺ to groove sites may affect the groove structure (23,24,26,27). Although some of these reports have shown a correlation between the presence of Na⁺ in the minor groove on the minor groove width, a recent report (26) indicates that some of these correlations may be the result of false positives caused by the limited timescale of some previous simulations. Korolev et al. (29–34) have studied the interactions of short polyamines, such as spermine and spermidine, with three B-DNA decamers arranged in periodic hexagonal cell. Their simulations showed that flexible polyamines have several binding sites along DNA helix, interacting with both oxygen atoms of phosphate groups and the groove sites irregularly. This was used as a potential reason for the absence of spermine densities in the determined x-ray structures of DNA fibers where spermines were used to crystallize DNA. The competition of binding with DNA for spermine, sodium ion and water molecules in the same simulation has also been investigated. They found that spermine pushes water out of the minor grooves whereas Na⁺ ions tend to organize water molecules along DNA. The flexible polyamines such as spermine display a high presence in the minor grooves but do not form long-lived structurally defined complexes. Another group (35) studied the effect of spermine binding on the transition of DNA from the A to B form and found that A-DNA is stabilized by the binding of spermine to the major groove. None of these studies however have been able to shed light on the interaction between DNA helices in the presence of these counterions.

On another front, when DNA chains were modeled as bead-spring polyelectrolyte chain, the compaction of the DNA chain has been observed in the presence of trivalent or tetravalent counterions or in the presence of positively charged polyelectrolytes. Stevens (36), for example, observed toroids and rods formed from a bead-spring polyelectrolyte chain in the presence of trivalent and tetravalent counterions. He also observed that an increase in chain stiffness resulted in an increase of toroidal structures. The complexation of single, flexible polyanion, and polycation chains of identical length has also been studied with molecular dynamics simulations that showed compact glasslike condensate structures formed for systems when the columbic interaction between the chains was sufficiently strong and that the presence of counterions did not significantly affect complex formation (37). A separate investigation of the energetics of complex formation between two oppositely charged polyelectrolyte chains found that the driving force between the complexation of strong polyelectrolytes (such as DNA) is the entropy gain resulting from the release of counterions from the polyelectrolytes and that this release entropy is a function of the counterion salt concentration (38). Several groups have also investigated the structure of complexes formed in systems in which the number and lengths of the polyelectrolyte chains were varied, potentially producing systems that model shorter PEI in the presence of the longer DNA chains as found in gene therapy vector preparation. Dias et al. (39) found that compact structures formed in systems of a longer polyanion chain in the presence of several shorter polycations chains resulted from the polycations bridging between different sites of the polyanion. Although complete charge neutralization was not required for all compact structures, an increase in the number or length of the polycations resulted in greater collapse of the polyanion chain. Finally, in a series of Monte Carlo simulations, Hayashi et al. (40–42) studied the formation of polyplexes from a system of many polyanion and polycation chains and presented a set of simple rules that governed the number and size of the polyplexes. They found that the net charge and charge density of the polyplexes was minimized to reduce electrostatic repulsion, whereas the total number of polyplexes was maximized to maintain translational entropy.

Although these coarse-grained molecular dynamic and Monte Carlo simulations have been useful in providing understanding of the factors influencing the complexation between oppositely charged polyelectrolytes, they have, however oversimplified the structures of DNA and the condensing agents. A DNA double helix is a strong electrolyte, with −2e charge per 3.4 Å rise in the helix. The Bjerrum length l_B, which is the distance at which the electrostatic interaction between two unit charges becomes comparable to thermal energy, is ∼7 Å in water. The strength of electrostatic interaction between charged groups along the polyelectrolyte chain is usually quantified by the quantity, Γ = l_B/l₀, where l₀ is the linear charge distance along the polymer chain. In these coarse-grained simulations or theories, DNA double helix is often represented by a simple bead-spring model with a Γ ∼ 4.2. If one considers the atomic structure of DNA double helix, the separation of the two phosphate groups on the same side of the strand is actually ∼6.5–7.5 Å, about the same as the Bjerrum length. The distance between two phosphate groups on the opposite strand forming the basepair is even larger, ∼15 Å, the width of a B-form DNA helix. Most theories and coarse-grained simulations have ignored this fact and have assumed a linear charge density Γ = 4.2 for DNA helix. Therefore atomistic simulations examining DNA condensation like those reported in this study, though computationally costly, will provide understanding on some key issues that have been ignored in earlier studies.

To have a better understanding on how PEI and PLL may differ when they interact with DNA helix, we carried out atomistic molecular dynamics simulations of a single DNA duplex with the sequence d(CGCGAATTCGCG)₂ (43) in the presence of PEI or PLL polycation chains with explicit water and counterions. The spontaneous complex formation between DNA helix with PEI and PLL chains have been captured in the simulation. The simulation showed different binding characteristics of PEI-DNA system with PLL-DNA system. PEI chains, due to their flexibility and higher charge density, were able to neutralize the charge on DNA more effectively than PLL chains. The resulting impact on DNA helix interaction as well as the potential structures of condensed DNA-PLL and DNA-PEI systems was discussed.

Methods

All simulations were carried out using the Amber Parm99 (44) force field and the AMBER 8 (45) molecular dynamics software package. The canonical B-form DNA structure was created with the nucgen module of AMBER. The DNA sequence used in all simulations was the self-complementary Drew-Dickerson dodecamer, d(CGCGAATTCGCG)₂, with the first 12 bases belonging to strand 1 and the final 12 bases belonging to strand 2. Six different systems, which contained the species summarized in Table 1 in addition to the DNA duplex, were prepared with the polycations initially separated from the DNA. We investigated two types of polycations, PLL and PEI with PEI chain modeled in two different protonation states, namely all protonated or 50% protonated. More discussion on the rationale of using two protonation states is given in the next section. Monovalent counterions were added to the system using LEaP to neutralize the charges on polycations, except in the case of the 50%-PEI(20) system where five more ions of both Na⁺ and Cl⁻ were added so that the total number of monovalent salt ions was identical to the PEI(20) and PLL systems. For the Na⁺ system, 20 Na⁺ ions were placed in the same location as the nitrogen atoms of the PEI in the PEI(20) system, and the remaining Na⁺ and Cl⁻ were subsequently added using LEaP. This system was prepared as a control in case of major conformational changes in DNA structure and as a point of comparison in evaluating the ability of the polycations to neutralize the DNA charge. All systems were solvated in ∼25,000 TIP3P water molecules (46) in a rectangular box.

Table 1.

Properties of simulated systems

System number	System name	Dimensions of simulation box (Å)	Species present (concentration in M)	N/P ratio
I	PEI(20)	97 × 102 × 80	PEI with 20 repeating units, all protonated	1:1
			22 Na+ (0.05)
			20 Cl− (0.05)
II	PLL(20)	110 × 80 × 90	PLL with 20 lysine units, all protonated	1:1
			22 Na+ (0.05)
			20 Cl− (0.05)
III	50%-PEI(20)	95 × 100 × 80	PEI with 20 repeating units, 10 protonated	1:1
			27 Na+ (0.06)
			15 Cl− (0.04)
IV	50%-PEI(40)	107 × 117 × 70	PEI with 40 repeating units, 20 protonated	2:1
			22 Na+ (0.05)
			20 Cl− (0.05)
V	3-PEI(20)	107 × 100 × 110	Three PEI chains each with 20 repeating units with 10 protonated	3:1
			22 Na+ (0.03)
			30 Cl− (0.05)
VI	Na+	95 × 102 × 80	42 Na+ (0.09)	N/A
			20 Cl− (0.05)

The systems were first equilibrated with 2000 steps of energy minimization with harmonic restraints on the DNA and polycation atoms and, subsequently, 1000 steps of unrestrained minimization. The temperature was increased to 300 K over 20 ps of constant pressure simulation, with 10 kcal/mol × Å² restraints on the DNA and polycation, followed by 1.2 ns of simulation with restraints on the DNA and polycation at constant temperature (300 K) and pressure (1 bar) using Langevin temperature equilibration with a collision frequency of 1.0 ps⁻¹. The restraints were then removed and the production runs were carried out with constant temperature and pressure for 12–18 ns. A time step of 2 fs was used throughout all the simulations with SHAKE (47,48) constraints on covalent bonds with hydrogen atoms. The particle mesh Ewald method (49) was used to treat long-range electrostatic interactions with a 10 Å direct space cutoff. The systems were visualized using VMD 1.8.5 (50) and images were produced using the UCSF Chimera package (51).

The degree of protonation of polyethylenimine has been the subject of debate in the literature, and a clear consensus has yet to emerge. Some studies of PEI for use in gene therapy use the value of PEI protonation provided by titrations of branched PEI carried out by Suh et al. in 1994 (52), who found that only 10–20% of PEI amine groups are protonated at physiological pH (∼7.4). However, several other studies have found much higher degrees of protonation for both branched and linear PEI and shorter polyamine analogs. Nagaya et al. (53) reported that ∼30% of branched PEI amines are protonated at pH 7.4, whereas others (54,55) have reported chain length dependent pKa for a series of PEI samples in the range of 8.2–9.5, indicating that most PEI amine would be protonated at physiological pH. Borkovec and co-workers (56) and Koper et al. (57) have determined the degree of protonation for linear, star-like, and comb-like PEI using both experimental titrations and Ising-model based computational methods, with all forms having ∼50% of the PEI amine groups protonated at pH = 7.4. Finally, the pKa of polyamines with 2–6 protonatable sites has been reviewed, showing that polyamines with structures similar to PEI typically have ∼50% of the amine groups protonated at physiological pH (58). In this study, two protonation states have been used: a PEI with 50% of the amine groups protonated and a fully protonated PEI chain. A degree of protonation of 50% was chosen as this was in the intermediate range of the values reported in the literature for PEI at physiological pH, whereas the fully protonated PEI would allow for investigation into how increased PEI charge in more acidic endosomes impacts polyplex structure. The 50%-PEI(20) system was a chain of 20 ethylamine monomers, with 10 randomly selected to be protonated. Starting at the C-terminal end of PEI, amines of monomers 2, 4, 6, 7, 12, 13, 14, 16, 17, and 20 were protonated. The 50%-PEI(40) system was a chain of 40 ethylamine monomers, again with 20 selected randomly to be protonated. In the 3-PEI system, the three PEI chains are identical, each with alternating protonated and unprotonated amines along the chain. The partial charges used for the PEI chains were determined with the RESP (44,59) method using the Gaussian03 (60) program with the 6-31G^∗ basis set. Although both linear and branched PEI have been used as gene therapy vectors, this preliminary study used only linear PEI.

Results

Complex formation

Fig. 1 shows the distances between the centers of mass of the DNA and the polycation chains over the course of simulation for the first three systems, with time zero at the removal of restraints on DNA and polycation chains. These distances plateau over the first ∼2 ns, and then decrease rapidly, as the polycation approaches the DNA. The rates of complex formation for these three systems are nearly the same. The charge differences on polycations, such as 50%-PEI(20) with PEI(20), did not seem to affect the rate significantly. Runs with slightly different starting positions between DNA and polycations were carried out for these systems. The maximum rate, estimated based on derivatives from the smoothed data, was found to be sensitive to the initial distance between DNA helix and polycation chains. This is not surprising because for bimolecular reactions the apparent rate of association will be dependent on how easily the two molecules find each other. Fig. 2 presents similar results for 3-PEI(20) system, with the distance change for each chain presented separately. The three PEI chains bind to DNA at different times in this case. The first and second PEI chains approach DNA helix nearly at the same time. After these two chains bind, the charge around DNA helix is almost neutralized because each PEI carries +10 charge and the negative charge on DNA chain is −22. Nevertheless, we observe that the third PEI chain approaches DNA helix and forms the final complex. As will be shown shortly, the final complex is overcharged and the net charge around DNA helix is positive.

Figure 1.

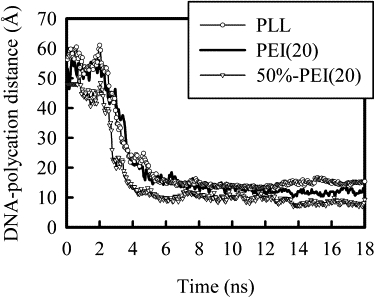
Plot of the distance between the centers of mass of DNA and the polycation chains as a function of simulation time for the first three systems, PEI(20), PLL(20), and 50%-PEI(20). Time zero corresponds to the moment when restraints on the chains were removed.

Figure 2.

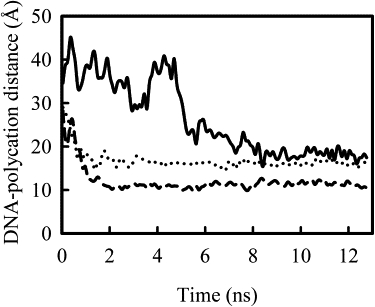
Same plot as in Fig. 1, but for system V (3-PEI(20)), with the distances between DNA and each of the three different PEI chains shown separately.

Visual inspection of the trajectories and analysis of monovalent counterions around DNA helix reveal that the association of the polycation with DNA is accompanied with the release of monovalent counterions around the DNA helix. Fig. 3 presents the change in the number of Na⁺ ions, and positive charged Nitrogen atoms from the PEI chain, that are within 10 Å away from the nearest atoms on DNA helix, as the simulation progresses (only shown for system I). The initial decrease in the number of Na⁺, from a value around 15 to ∼5–10, is associated with the equilibration of monovalent salts around DNA helix. In these simulations, Na⁺ and Cl⁻ counterions were initially placed in locations with the highest electrostatic potentials, typically very near DNA phosphate and polycation amine groups, resulting in complete charge balance of the polyelectrolytes within just a few angstroms of their surfaces. During the initial equilibration before the removal of restraints on DNA and PEI chains, the salt reorganizes around DNA helix. Earlier studies (24,25) suggested that a full equilibration is slow and may not be completed by the time we removed the restraint on DNA and PEI chains. As the PEI chain moves toward DNA, the number of Na⁺ ions is further reduced to a level <5. In comparison, the number of Na⁺ for system VI, which has exactly the same total positive and negative charges as in system I, remained between 5–10 over the course of entire simulation. Hence the further reduction in Na⁺ ions around DNA is due to the association of PEI with DNA. This release of monovalent counterion as the polycation binds has been observed in coarse-grained simulation and has been understood as the driving force in polyplex formation (38). However, in contrast with what seen in coarse-grained simulation (38) where the formation of polyplex led to an observable change in total electrostatic interaction, in our simulation, the total energy of the system and the total electrostatic interaction of the system did not show any change during the complex formation. In coarse-grained simulation, water is not explicitly included, rather is modeled as a continuum dielectric medium. Clearly, explicit water molecules included in our simulations are able to rearrange around DNA and polycations such that the total electrostatic interaction energy remains constant.

Figure 3.

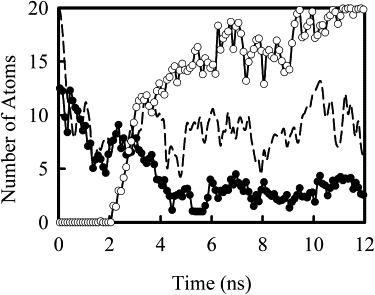
Plot of the number of Na⁺ ions (solid circles) and protonated amine nitrogens (open circles) for system I (PEI(20)) within 10 Å of any C1′ DNA atom as a function of time for system I (PEI(20)). The dashed line shows the number of Na⁺ ions for system VI as a reference. The number of Na⁺ ion around DNA helix is reduced as PEI chain approaches the DNA helix.

Although complexation of DNA with polycations has been shown to result in compaction of long DNA chains into characteristic toroidal structures (10), the short DNA helix in all of our simulations remained relatively stable and did not show major conformational changes. Analysis of the DNA structure with the program 3DNA (61) showed that the DNA remained in its initial B-form conformation after binding with the polycation, with riboses remaining in the C2^∗-endo conformations and intraphosphate and groove width distances that were, in general, consistent with a B-DNA double helix. This result is in agreement with experimental observation that DNA remains in the B-form when complexed with polycations (55,62). The same is true when DNA is condensed by multivalent cations. The compaction of long DNA chain into characteristic toroidal structure is due to structural change at much larger scale, when different sections of DNA helix, separated far along the chain, attract each other leading to compaction of whole DNA chain, similar to the coil/globule transition well-known for flexible polymer chain placed in a bad solvent. The molecular origin of this attraction between DNA helix however has been heavily debated and we will come back to this issue in the latter section. It is also possible that there were small changes in the DNA structure, such as a narrowing of minor grooves on the formation of the interactions between DNA and polycation atoms, similar to previous results for DNA interaction with short polyamine and monovalent cations (27,32), but these type of specific structural changes were not the focus of this work.

Atomic contacts between polycations and DNA

We examine the contacts made between polycations and DNA helix at atomic level. As has been shown previously for DNA interacting with Na⁺ and K⁺ (24–26), as well as short polyamines, such as spermine (29–31), cations typically interact predominantly with the phosphate groups of DNA, but also with electronegative atoms in the DNA major and minor grooves. Analysis of the hydrogen bonds formed during complex formation showed that the primary interactions in the polyplexes were between the polycation amine groups and the O1P and O2P atoms of the DNA phosphate groups. We have further analyzed the contacts made between polycations and DNA for the first three systems. Here, a contact is defined as when the distance between the DNA atom and a nitrogen atom of a polycation amine was <4 Å. Fig. 4, a–c, show contacts made with DNA phosphate groups, whereas Fig. 4, d and e, show the contacts made with the atoms in the major and minor grooves. In general the interactions formed between the DNA phosphate and polycation amine groups are stable and long-lasting on the timescale of the simulations. Once formed, most of these interactions are maintained throughout most of the trajectory, a phenomena that is also found for DNA interacting with spermine (35). In comparison, the interactions between DNA and Na⁺ ions (24,25) typically have much shorter lifetimes (also see our data presented in Fig. 5). It is also notable that in the PLL and PEI(20) systems, there are significant interactions with several phosphate groups on both strands of the DNA duplex throughout the entire simulation. In contrast, the interactions in 50%-PEI(20) are predominantly only with strand 2 of the DNA during the last 8 ns of the simulation. Fig. 4, d and e, shows the development of interactions between polycation amine groups and electronegative sites in the major and minor grooves of DNA. Following previous work, we monitored T_O2, C_O2, A_N3, and G_N3 in the minor groove and A_N7, G_N7, G_O6, and T_O4 in the major groove (25,29). Again, a 4 Å distance cutoff between the DNA atom and protonated polycation amine N was used to determine whether or not there was an interaction. The PEI(20) system did not have any contacts with the major or the minor groove and this was true in another separate run for PEI(20). Hence the corresponding panel for this system was absent. PLL and 50%-PEI(20), however, have contacts with the major/minor groove. Comparing Fig. 4, d and e, with Fig. 4, b and c, one can observe that the contacts with the phosphate group were formed before the contacts with the major and minor grooves. Both types of contacts, however, were long-lived, in contrast to what was seen for the Na⁺ binding. Detailed analysis of atomic contacts for the other systems were not done, but visual inspection of the structures of formed confirms the general trends observed here. In general, we found that decreasing the protonation states in PEI lead to more contacts with the major and minor grooves of DNA.

Figure 4.

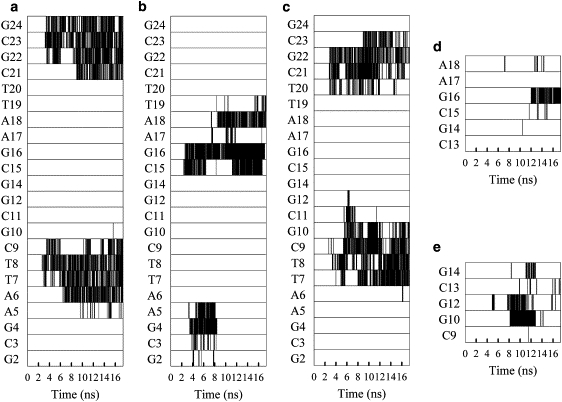
Development of interactions between polycation amine groups and DNA basepairs for the first three systems. (a–c) Interaction with DNA phosphorus atoms within 4 Å of any protonated amine.(a) PEI(20). (b) 50%-PEI(20). (c) PLL(20)). (d and e) Interactions between electronegative atoms in the major and minor grooves of DNA interacting with protonated amine. (d) (50%-PEI(20)). (e) PLL(20)). For d and e, only the DNA bases that are involved in an interaction at one point during the trajectory are shown.

Figure 5.

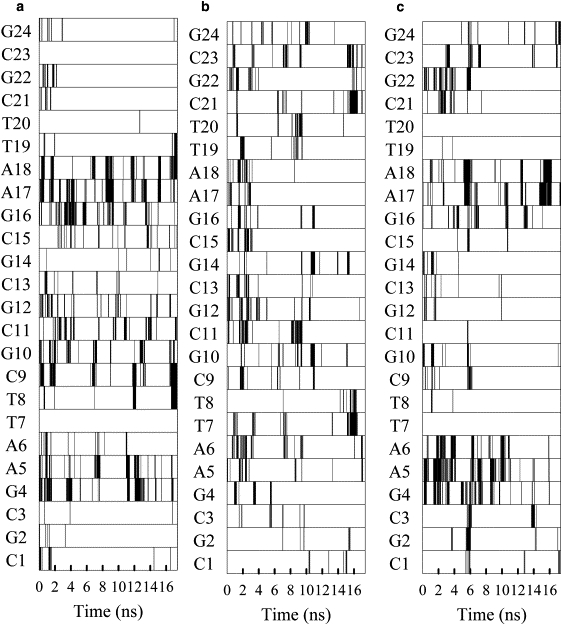
Development of interactions between sodium ions and interior DNA atoms for the first three systems: (a) PEI(20), (b) 50%-PEI(20), and (c) PLL(20).

Fig. 5 shows interactions between Na⁺ and electronegative atoms in the major and minor DNA grooves throughout the simulation using the same criteria as in Fig. 4, d and e, for the first three systems. Despite the presence of the polycation, the larger size and stiffness of the DNA allow for several sites where there is significant interaction with Na⁺. Similar to earlier results in the literature (23–28), interactions between DNA and Na⁺ are much shorter lived than DNA-polycation interactions. The longest lived interactions in Fig. 5 have lifetimes around 1 ns. In many cases, the binding of the polycation repels Na⁺ from interacting with that section of the DNA. For example, in the PEI(20) simulation, there is very little Na⁺ interaction with electronegative sites of the C21–G24 stretch of DNA that is bound to the polycation. However, there are some exceptions to this general trend. Toward the end of the PEI(20) simulation, a Na⁺ resides with minor groove sites of the T8 and C9 bases near a DNA phosphate-polycation amine interaction, and, in the PLL trajectory, a Na⁺ interacts with major groove sites of G22 and G23, whereas the polycation is bound to the minor groove side of these bases.

To show the average structural properties of the DNA-polycation complexes, the spatial distribution functions of the polycations around the DNA over the final 6 ns of the trajectories were calculated. Fig. 6 shows spatial distribution functions of the DNA complexes averaged with a grid spacing of 1 Å, as well as a typical snapshot from late in each simulation for the first three systems. As can be seen in the figure, the PEI(20) system has a well-defined structure with the PEI aligning with DNA phosphate groups of both strands of the DNA, while crossing over the DNA minor groove. The structure of the complex in the PLL system is less organized, with several of the amine groups of the PLL sticking away from the DNA surface. In contrast to PEI, in which the amine groups are along the polymer backbone, the amine groups of PLL are separated from the backbone by four methylene groups, providing a steric limit to the number of amine groups that can be directly near the DNA phosphate groups. As mentioned above, the 50%-PEI(20) complex, unlike the other two polyplexes, is primarily the result of interaction of the polycation with only one strand of the DNA, with a significant section of the polycation lying in the DNA major groove. The section of the 50%-PEI(20) in the major groove is mostly composed of unprotonated monomers of the PEI, with only one of the four monomers that occupy this region containing a protonated amine group. Examination of structures formed in other systems confirms that less protonated PEI chain makes more contacts with major and minor groove sites.

Figure 6.

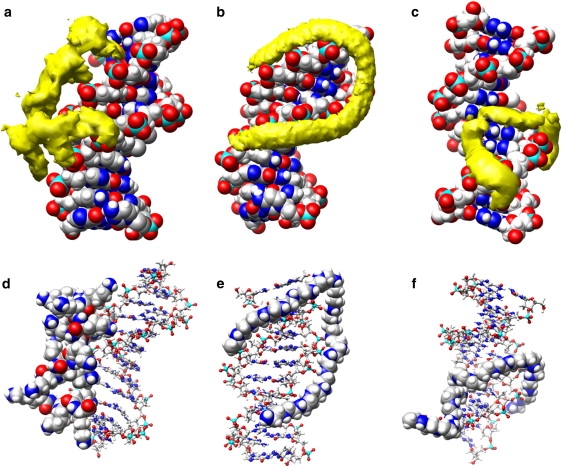
(a–c) Spatial distribution functions of polycations over the last 6 ns of simulation around an average DNA structure for (a) PLL(20), (b) PEI(20), and (c) 50%-PEI(20). Polycation density of >50% of the maximum polycation density is shown in yellow with DNA shown with a space-filling model. (d–f) Typical snapshots from late in the trajectory for (d) PLL(20), (e) PEI(20), and (f) 50%-PEI(20) simulations. The polycation is shown in a space-filling model, whereas the DNA is shown as sticks-and-balls.

Charge neutralization

We now examine the ability of the polycations to neutralize the charge of the DNA phosphate groups by calculating the number of protonated amine groups that interact with DNA phosphate group oxygen atoms. As shown in Fig. 7, radial distributions functions of the polycation amine nitrogen atoms around the O1P and O2P DNA atoms have two distinct peaks, one at ∼3 Å and one at ∼5 Å (note the distance is measured against oxygen atoms on the phosphate group). This first peak indicates primary interactions that result from direct contact between the amine and phosphate groups, such as the formation of a hydrogen bond between amine hydrogen atoms and the phosphate oxygen. Secondary interactions, which are included in the second radial distributions functions peak, are the results of water-mediated hydrogen bonding or other less direct interactions. As can be seen in Fig. 7, there are significant differences in both peak heights for the different polycations. To quantify these differences, the number of amine nitrogen atoms involved in a primary or secondary interaction with an O1P or O2P atom, averaged over the last 6 ns of the trajectory, was calculated and is presented in Table 2. The densely charged PEI(20) is able to surround the phosphate groups with a high number of positive charges, with >80% of the amines forming primary and secondary interactions with phosphate groups. Not only do the PEI(20) amines form more primary interactions than the other polycation, but closeness of the charges along the PEI(20) backbone results in over three times as many secondary interactions as primary interactions. In comparison, the PLL(20) system has fewer amine groups in overall interacting with DNA phosphates, and much fewer secondary interactions. As we have shown earlier, some of the lysine residues point away from the DNA helix. Although 50%-PEI(20) has only half as many positive charged N atoms as PLL, the total number of protonated amine groups near DNA phosphates is similar to PLL(20). Being intrinsically more flexible and less bulky at atomic scale, PEI is able to better neutralize the charge on DNA phosphate groups than PLL at the equivalent charged N/P ratio.

Figure 7.

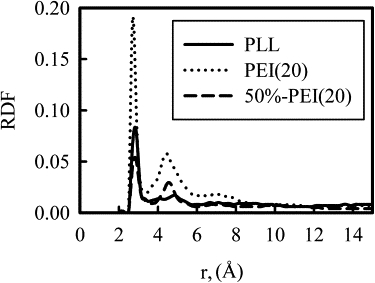
Radial distribution functions of polycation amine groups shown in figure legends around the O1P and O2P DNA atoms. In the case of the 50%-PEI(20) simulation, only charged amine groups are included.

Table 2.

Average number of amine groups of each polycation interacting with DNA O1P and O2P atoms averaged over the last 6 ns of each simulation

System name	Primary	Secondary
PLL(20)	4.06	2.23
PEI(20)	5.86	10.53
50%PEI(10)	2.97	2.90

The key issue to understanding DNA condensation is determining the charge distribution around the DNA helix. Manning (63) considered the counterion distribution around a strong polyelectrolyte chain and predicted an existence of Manning condensation when Γ > 1 (see the Introduction for the definition of Γ). Namely, there will be a fraction of counterions bound to the polyelectrolyte chain with an energy greater than k_BT, so that these counterions move together with the polyelectrolyte and the net charge of the polyelectrolyte appears to be reduced to Γ_c ∼ 1. If multivalent cations are present, the charge is further reduced to Γ_c/Z where Z is valency of the cation (64). Using this basic knowledge, Ngyuen et al. (64) have shown that electrostatic repulsion between DNA helix is significantly reduced when Z-valent cations are added into the solution. They have further shown that there exist two concentration thresholds, N_c and N_d. When the added Z-valent cation concentration N > N_c, the charge around DNA helix is reduced due to the binding of Z-valent cation and DNA helix condenses because of the short-range attraction. As the concentration of Z-valent cation further increases beyond N_d, the charge around DNA helix is inverted and DNA helix redissolves in solution due to the repulsion between overcharged helixes. The above physical picture is based on the solution to the Poisson-Boltzmann equation with water treated as a continuum medium with dielectric constant of 80. It would be of interest to see if such prediction holds in full atomistic simulations.

Fig. 8 shows the cumulative number of sodium ions within the given distance of any nearest C1′-DNA atom, averaged over the last 6 ns of the simulation trajectory. The C1′ atom is on the ribose ring connecting with the base, located inside the DNA helix ∼5 Å away from surface of DNA helix tube defined by the phosphorus atoms. As can be seen from Fig. 8, the closest approach of Na⁺ to the C1′ atom is ∼5 Å in all cases. From 5 Å to 25 Å, the presence of polycation chains greatly reduced the number of Na⁺ around the DNA helix. The reduction in Na⁺ ions depend on the total charge on the polycation. For example, 50%-PEI(20) carries the least positive charge on the polycation, and we see that the number of Na⁺ in this range is the highest among all systems with polycations, although it is much lower than the value seen in the absence of polycations (Na⁺ system). PLL and PEI(20) have nearly the same distribution of Na⁺ ions, except PLL system has a slightly lower value for the distance range from 15 Å to 25 Å.

Figure 8.

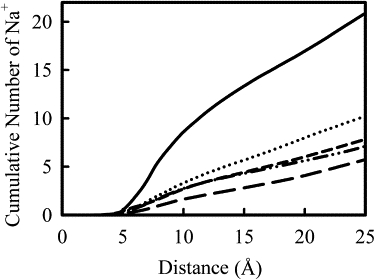
Cumulative number of sodium ions as a function of the distance from any C1′ DNA atom for each simulation. From the top line down, the Na⁺ (solid line), 50%-PEI(20) (dotted line), PEI(20) (short dashes), PLL (dots-dashes), and 50%-PEI(40) (long dashes) systems are shown.

Fig. 9 shows the net cumulative charge in the solution surrounding the DNA as a function of distance to the nearest DNA C1′ atoms, taking into account the charges of Na⁺, Cl⁻, and polycations, but not the charge of the DNA When the net cumulative charge of solution reaches +22, then the charge on DNA is neutralized. We first focus on the results for the Na⁺ system (system VI). The net charge in solution reached ∼80% of the charge on DNA at a distance 25 Å away from the C1′ atom (or 20 Å away from the DNA surface). According to Manning's theory, one should expect 76% of counterions bound to DNA helix with energy greater than k_BT. Currently, we have not determined at which distance these counterions should be considered as bound. A detailed comparison of ion distribution against continuum Poisson-Boltzmann theory will be presented in the future.

Figure 9.

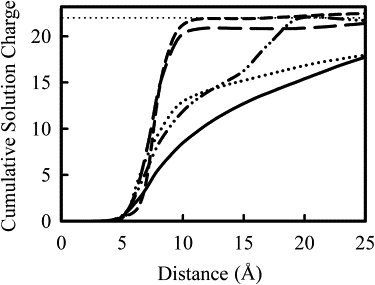
Cumulative solution charge around the DNA helix as a function of the distance from C1′ DNA atoms. The cumulative solution charge is calculated including the charges on polycation, sodium ion, and chloride ion within the given distance, but does not include the charges of the DNA. The line types follow Fig. 8, from the top line down at a distance of 15 Å: PEI(20) (short dashes), 50%-PEI(40) (long dashes), PLL (dots-dashes), 50%-PEI(20) (dotted), and Na⁺ (solid line). The horizontal dotted line indicates the solution charge needed to balance the charge on DNA helix.

The net charge in solution for PEI(20) rises sharply at a distance from 6 Å to 10 Å, and at ∼10 Å away from C1′ atom, the DNA charge is completely neutralized, which is ∼5 Å from the DNA surface. The 50%-PEI(40) system also exhibits a sharp rise around that distance range, although one can clearly notice that the initial rise in 50%-PEI(40) is slightly earlier than in PEI(20). This is because the PEI chain in 50%-PEI(40) system sit closer to DNA, making contacts with the atoms in grooves. The final plateau charge in 50%-PEI(40) is one unit charge less than in PEI(20) system, which we attribute to fluctuations. The PLL(20) system exhibit two transitions, the first rise from 5 Å to 12 Å, and followed by another rise from 15 Å to 20 Å. The first rise is attributed to the lysine residues that pointing toward DNA helix, whereas the second rise could be traced to those lysine side chains sticking out around DNA helix. All three systems reached nearly complete neutralization at distance 25 Å away from C1′ atom. The 50%-PEI(20), however, did not reach complete neutralization at 25 Å, it has a value similar to that Na⁺ system.

Fig. 10 presents the similar plot as in Figs. 8 and 9 but for 3-PEI(20) system. Now the solution charge exceeds the negative charge on DNA at a distance 7.5 Å and beyond. The charge then decays slowly to a value equal to the total negative charge on DNA. The mean-field Poisson-Boltzmann theory would not be able to predict this kind of overcharging behavior. Overcharging has also been recently observed in coarse grained simulations of condensation of polyelectrolyte by trivalent and tetravalent counterions (65,66). Overcharging has been suggested as the cause of the re-dissolution of DNA helix bundle at high salt concentration of Z-valent counterions. From our simulation, it is clear that electrostatic repulsion between overcharged DNA helix extends over a very long distance, at least 40 Å away from C1′ atom.

Figure 10.

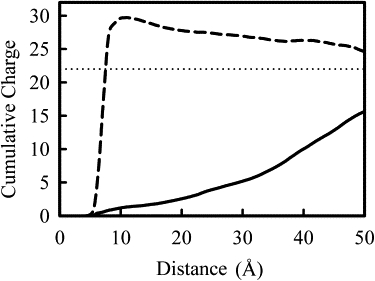
Cumulative number of Na⁺ ions (solid line) and cumulative solution charge (dashed line) for the 3PEI(20) system as a function of distance from C1′ DNA atoms. The horizontal dotted line indicates the solution charge needed to balance the charge on DNA helix. Overcharging of DNA helix is seen at distance >7 Å.

Discussion and Conclusion

With the above data, one can now discuss the potential interaction between DNA helix decorated with the polycations. If there is only monovalent salt concentration, we observe a slow decay of total charge around DNA helix extending over a distance at least 25 Å away from the surface of DNA helix. Under this condition, due to long-range electrostatic interaction, DNA helix will not be able to approach each other close enough such that the short-range attraction may lead to collapse. On the contrary, in PEI(20) system, the charge on DNA is neutralized at a surface ∼5 Å away. This implies that the DNA helix can approach each other at least ∼5 Å without experiencing electrostatic repulsion. At this close approach, short range attraction can play a role and lead to condensed helix phases. We also see that the concentration of PEI, and protonation states of the PEI chain could affect the charge distribution around the DNA helix dramatically, which in turn means that the interaction between DNA helix in the presence of PEI will be sensitive functions of these parameters. Unfortunately the exact protonation state of PEI is not clearly known and is a function of solution pH. If the protonation state is 50%, then at 1:1 N/P ratio (corresponding to system III) the formed complex will have negative charge. On increase the N/P ratio, overcharging will occur and the net charge appears to be positive. This observed phenomenon is in agreement with typical experimental observation. At low N/P ratio (1:1 or 2:1), the measured Zeta potential of the complex often is negative. On increasing N/P ratio, the measured Zeta potential became positive (6,67,68). Quantitative comparison against experimental results is hampered by the unknown percentage of protonation states in PEI.

We may also compare our simulation results with experimental results by DeRouchey et al. (69) who recently investigated the structures of condensed DNA helix phases in the presence of PEI, PLL and other condensing agents. They found that the condensed DNA helix is in a close-packed hexagonal arrangement. The polycations, being intrinsically much more flexible than DNA helix, act as a linker that wrap around or bridge over DNA helix strands. The close distance between DNA helix as well as the helix pitch were determined from the x-ray diffraction patterns. Notably, the center of closest DNA helices was 30.4 Å for PLL-condensed DNA and 28.0 Å for linear PEI-condensed DNA. Based on the atomic structures obtained in our simulation for PEI-DNA and PLL-DNA, one can easily appreciate that the closest distance between DNA helix decorated with PLL will be larger than DNA-PEI complex. Fig. 11 presents distances between atoms on polycations to the center of DNA helix determined as the mid-point between two C1′ atoms forming the basepairs. The maximum distance for atoms on the PLL chain to the center of DNA helix was ∼22 Å. If one brings two DNA helixes, each decorated with PLL chain, together, then the closest distance would be 44 Å, larger than the experimentally measured one. Therefore, we suggest that in this PLL-DNA close-packed condensed phase, there is only one PLL chain bridging between the two helixes. The lysine residues that stick out of one of the DNA helix interact with the other DNA helix. This would make the distance between DNA helixes around exactly 30.0 Å. For the PEI-DNA system, the largest distance between atoms on PEI chain to the center of DNA helix was found to be 14 Å. If one brings two DNA helixes each bound with one PEI chain together, the closest distance between two helixes will be just around 28 Å, in agreement with experimental reported helix distance. DeRouchey et al. (69) also found that the polycations were spaced along the DNA with distances near 36 Å, close to the pitch of the DNA axis. This result agrees with what we have observed in the simulations, specifically for the PEI(20) simulation where the polycation wrap along the DNA phosphate groups. Longer polycation chains would be able to make complete rotations around the DNA helix, making the polycation spaced by a distance close to the DNA helical pitch.

Figure 11.

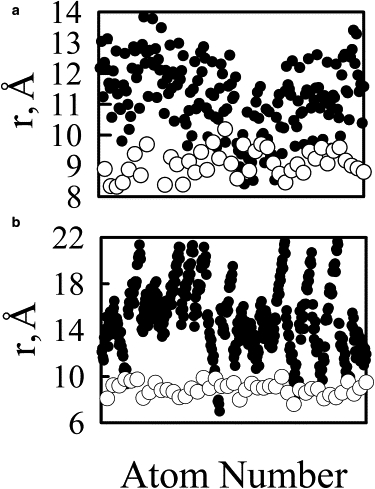
Minimum distance from each polycation atom (solid circles) and O1P and O2P DNA atom (open circles) to the center of DNA double helix as discussed in the text for the (a) PEI(20) and (b) PLL systems.

Additionally, our simulation results can be used to shed some insight into the effectiveness of PEI as a gene therapy vector. In comparison with PLL, PEI seems better able to neutralize the charge of DNA. The smaller and more densely charged PEI took up less space on the DNA, capable of condensing DNA to a greater extent than PLL. This observation, linked with experimental suggestion that a more compact size of the formed complex favors a high uptake through cell endocytosis, would then imply potentially higher transfection efficiency with PEI. The protonation state of PEI is a function of pH, where protonation state of PLL is not. Comparing the structures of PEI-DNA formed with different protonation states, we noticed that at a 50% protonation state, the PEI chain stayed closer to the DNA helix making contacts in the groove sites. The fully protonated PEI chain, on the other hand, did not make any contacts in the groove sites. Hence one may envision that when PEI changes its protonation state from a lower percentage to a high percentage, the DNA-PEI complex will expand and cause the complex to erupt. This may help the release of DNA from the endsome stage.

Although the spontaneous association of oppositely charged polyions is a well-known phenomenon, the complex formation between DNA and polycations at atomic scale has never been simulated or reported. Our atomistic simulation reported here offered what to our knowledge is a first glance at the atomic structures of these DNA-polycation complexes. Although our simulations have not been able to capture the DNA condensation by polycations, and probably capturing such process may still beyond the limit of current computing power, the understanding gained in this study are of great value both in terms of understanding DNA condensation process as well as in addressing the differences between PEI and PLL as gene delivery vectors. A more systematic investigation of ion distribution of multivalent cations around the DNA helix and simulation of condensation of PEI with DNA at different N/P ratio are planned. A detailed comparison of ion distribution against the solution of Poisson-Boltzmann equation will also be presented in the future.