Abstract
The copper-catalyzed N-arylation of amides, i.e., the Goldberg reaction, is an efficient method for the construction of products relevant to both industry and academic settings. Herein, we present mechanistic details concerning the catalytic and stoichiometric N-arylation of amides. In the context of the catalytic reaction, our findings reveal the importance of chelating diamine ligands in controlling the concentration of the active catalytic species. The consistency between the catalytic and stoichiometric results suggest that the activation of aryl halides occurs through a 1,2-diamine-ligated copper(I) amidate complex. Kinetic studies on the stoichiometric N-arylation of aryl iodides using 1,2-diamine ligated Cu(I) amidates also provide insights into the mechanism of aryl halide activation.
Introduction
The foundation of modern cross-coupling chemistry was built at the beginning of the twentieth century with the pioneering work of Fritz Ullmann and Irma Goldberg.1 Their explorations into new methods for the synthesis of C-C, C-N, and C-O bonds provided the conceptual breakthrough that allowed for the use of unactivated aryl halides to supplant the electron-poor aryl halides typically required for the classical nucleophilic aromatic substitution reaction. These advancements not only expanded the scope of substrates that could be utilized in aromatic substitution reactions, it changed the way chemists thought about constructing molecules containing aryl-N and aryl-O bonds. Further testimony for this achievement is the myriad of industrial processes that utilize this methodology, i.e., in the synthesis of pharmaceuticals, agrochemicals, and in polymer chemistry.2
Classic Ullmann and Goldberg protocols typically require harsh conditions such as high temperatures, extended reaction time, and in some cases stoichiometric amounts of copper. To circumvent these problems, chemists have referred to the more recently developed palladium-catalyzed C-N bond-forming reaction as a means to generate a diverse array of arylated amines.3 However, the palladium-catalyzed N-arylation also encounters some limitations. For example, substrates with functional groups containing free N-H moieties4 as well as amides5 and heterocycles4a,b, remain problematic.
The employment of chelating ligands has provided the major driving force behind the evolution of Cu-catalyzed C-N bond-forming processes. The first reports concerning the intentional use of exogenous ligands focused on 1,10-phenanthroline. For example, for N-arylation of imidazoles and synthesis of arylamines, catalyst systems based on 1,10-phenanthroline allowed for lower temperatures, shorter reaction times, and in nonpolar solvents in comparison to the classic Ullmann conditions.6 Also during the synthesis of triarylamines, the 1,10-phenanthroline/CuCl catalyst system was found to be the most effective, thus allowing the reactions to occur at much lower temperatures than those previously used.7 Moreover, soluble complexes of Cu(I) and 1,10-phenanthroline, i.e., LCu(PPh3)Br, and its derivatives based on neocuproine and 2,2′-bipyridine have been exploited in the synthesis of aryl amines.8 Other chelating ligands such as ethylene glycol,9 L-proline,10 N-methyl glycine,10 and diethylsalicylamide11 have also proven to be quite effective in the N-arylation of both aliphatic and aryl amines. One of the most general catalyst systems based on a chelating ligand, which is used in the N-arylation of amides and heterocycles as well as cyanation and halide exchange reactions, is that derived from inexpensive 1,2-diamines.12 This catalyst system allows for the efficient coupling of a wide variety of substrates, specifically, those containing free N-H and O-H as well as heterocycles. Despite these achievements, most of the copper-based catalyst systems have yet to achieve the high turnover numbers that are typically obtained in the complementary palladium chemistry.13 Moreover, reactions of less active substrates such as aryl chlorides and aryl sulfonates have thus far been relatively unsuccessful, especially in the latter case. Attempts to understand similar deficiencies in the related palladium chemistry have been investigated through a significant amount of mechanistic work; however, analogous studies on copper-catalyzed reactions are relatively scarce.13
Of the few mechanistic studies that have been performed on Cu-catalyzed C-N and C-O bond-forming reactions, the major emphasis has been on the empirical observations pertaining to which catalyst system, i.e., Cu(0), Cu(I) or Cu(II), provides the fastest reaction rate. Since the earliest work by both Ullmann and Goldberg and later Adkins, several different copper sources were found to be effective for the transformation, e.g., CuBr2, CuCl2, Cu(OAc)2, Cul, CuBr, CuCl, and even Cu(0).1,14 Copper sources from three different oxidation states provided nearly identical reaction rates in both N-and O-arylations, with Cu(I) salts providing slightly higher rates compared to those of Cu(0) and Cu(II). The initial hypothesis for this behavior was that a single catalytic species results from each of these precursors and the active oxidation state is Cu(I).15 Investigations by electron paramagnetic resonance (EPR) showed that indeed the Cu(II) species decays over time while in the presence of the amine, thereby producing Cu(I).16 This process was proposed to occur through oxidation of the ligand bound to Cu(II), either the alkoxide, phenolate, or amide. The only direct evidence for ligand oxidation occurred when tetraphenylhydrazine was isolated from the N-arylation of diphenylamine using CuBr2 or Cu(acac)2 as the precatalyst.17,18 With regard to the use of Cu(0) as a precatalyst, Paine has found through SEM imaging that the surface of Cu(0) is covered with a thin layer of Cu2O, which then possibly leaches into solution upon amine coordination.17 Taken together, these results do indeed support the primary role of Cu(I) in facilitating Ullmann-type reactions.
Several stoichiometric studies have been performed to remedy the cryptic nature of the active Cu(I) species. Initial experiments have implied that a simple metathesis reaction occurs between either the CuX2 or CuX salt and the metal alkoxide or amide, thus providing an explanation for the nearly identical reaction rates obtained with different copper salts.15 With regard to the copper-catalyzed C-O bond-forming reaction, an additional equivalent of alkoxide is then required to form the catalytically active species which is cuprate-like, i.e., M[Cu(OR)2] where M is Na (eq 1).18a In contrast, with studies using phthalimide as the nucleophile, the most reactive species was generated when the Cu(I):pthalimidate ratio was <1, suggesting that an anionic bis-amido Cu(I) species is unfavorable in this case (eq 2).19 Furthermore, both Whitesides20 and Yamamoto21 have shown that Cu(I) alkoxides and Cu(I) amidates can react with aryl halides when the Cu:nucleophile ratio is 1:1. Importantly, what these studies suggest is that a Cu(I)-nucleophile complex must form prior to aryl halide activation. Indeed, recent work by our laboratory22 and Hartwig's23 demonstrates that Cu(I) amidates can serve as intermediates during the N-arylation process. This recent work also indicates, as suggested by Bacon and Karim19, that the reactivity of Cu(I) amidates towards aryl halides is dependent on the number of amidates coordinated to the metal center, i.e., the N-arylation of aryl halides is not observed with anionic bis-amido Cu(I) species.23
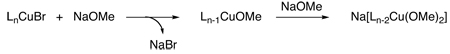 |
(1) |
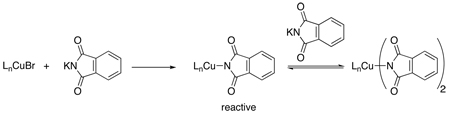 |
(2) |
To provide a more rational basis for the development of improved copper catalysts that promote either C-C or C-heteroatom bond-forming reactions, we have further investigated the mechanism of copper-catalyzed C-N bond-forming reactions. Much of this work has focused on the N-arylation of amides since this reaction remains the most versatile in the presence of Cu(I)/l,2-diamine catalyst systems. The results provide insights into the role of 1,2-diamines in controlling the coordination environment around Cu(I). The catalyst is more efficient at high concentrations of 1,2-diamine and high concentrations of amide, as revealed by a nonlinear dependence of the rate on 1,2-diamine concentration. Furthermore, we demonstrate that a 1,2-diamine ligated Cu(I)-amidate can serve as the reactive species that activates the aryl halide, which was established through both its chemical and kinetic competency in the stoichiometric N-arylation process. This behavior has important consequences for new catalyst development since the results show the significance of both the diamine and amide in modulating the overall reactivity of the system.
Results
Kinetics Studies: 1,2-Diamine and Catalyst Effects
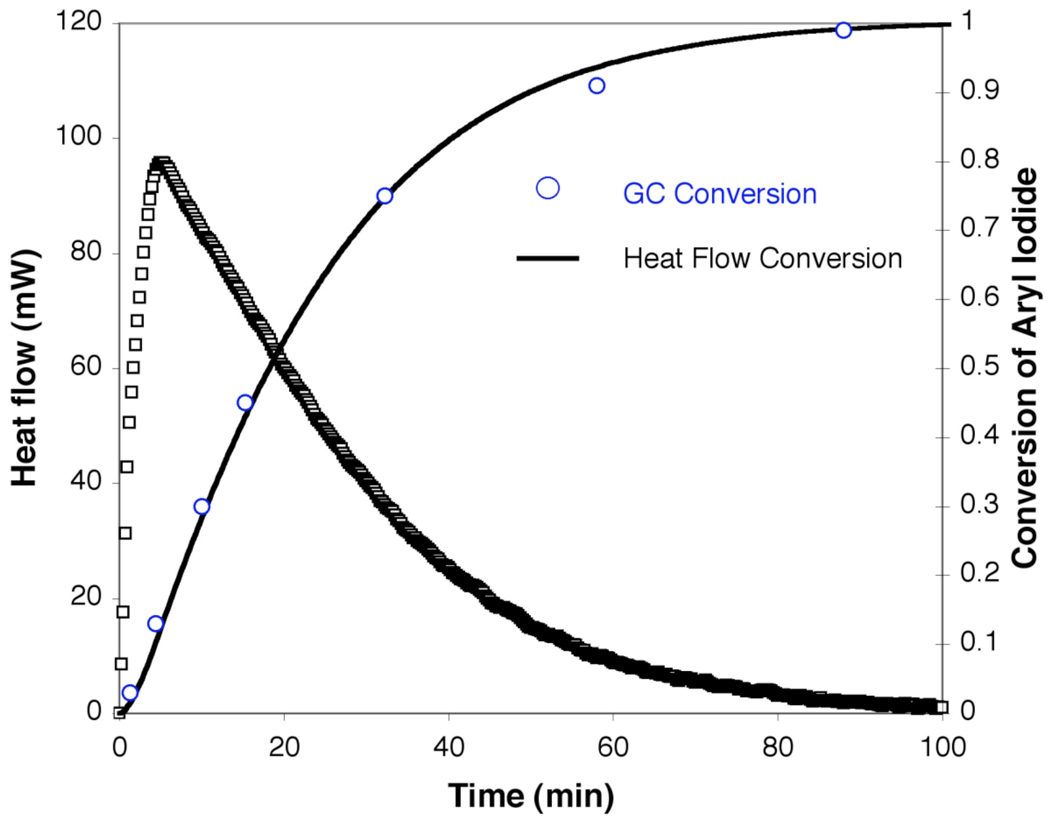
The N-arylation of 2-pyrrolidinone (2) with 3,5-dimethyliodobenzene (1) catalyzed by CuI/3 (5/10 mol %) (eq 3) proceeds to complete conversion within 2 h at 90 °C. An Omnical SuperCRC reaction calorimeter, which is a differential scanning calorimeter, was used to acquire kinetics of the catalytic reaction in situ by monitoring the heat flow as a function of time at a constant temperature. The reaction time-course (Figure 1) displays a temporal decrease in heat flow and lacks a significant induction period. There is, however, an apparent time lapse, albeit short, between the actual start of the reaction and the point at which the heat flow begins to decrease, which is inherent to measuring rates of reactions with calorimetry.24 On the basis of the temporal heat flow, the reaction rate (eq 4), the fractional conversion (eq 5), and the instantaneous concentrations of the reactants/products can be calculated. Conversion measured by GC analysis was compared to conversion measured by heat flow and the agreement between the two methods validates the use of reaction calorimetry to follow the copper-catalyzed amidation of aryl iodides.
Figure 1.
A representative heat flow versus time profile for the CuI/3 catalyzed N-arylation of 2-pyrrolidinone with 3,5-dimethyliodobenzene and comparison of conversion data obtained from heat flow to that obtained by GC measurements. Data sampling occurred at a rate of 4 min−1. Conditions: [1]0= 0.4 M, [2]0 = 0.8 M, [K3PO4]0 = 2.4 mmol25, [CuI] = 0.02 M, [3] = 0.04 M in 2.0 mL of toluene at 90 ° C.
 |
(3) |
| (4) |
| (5) |
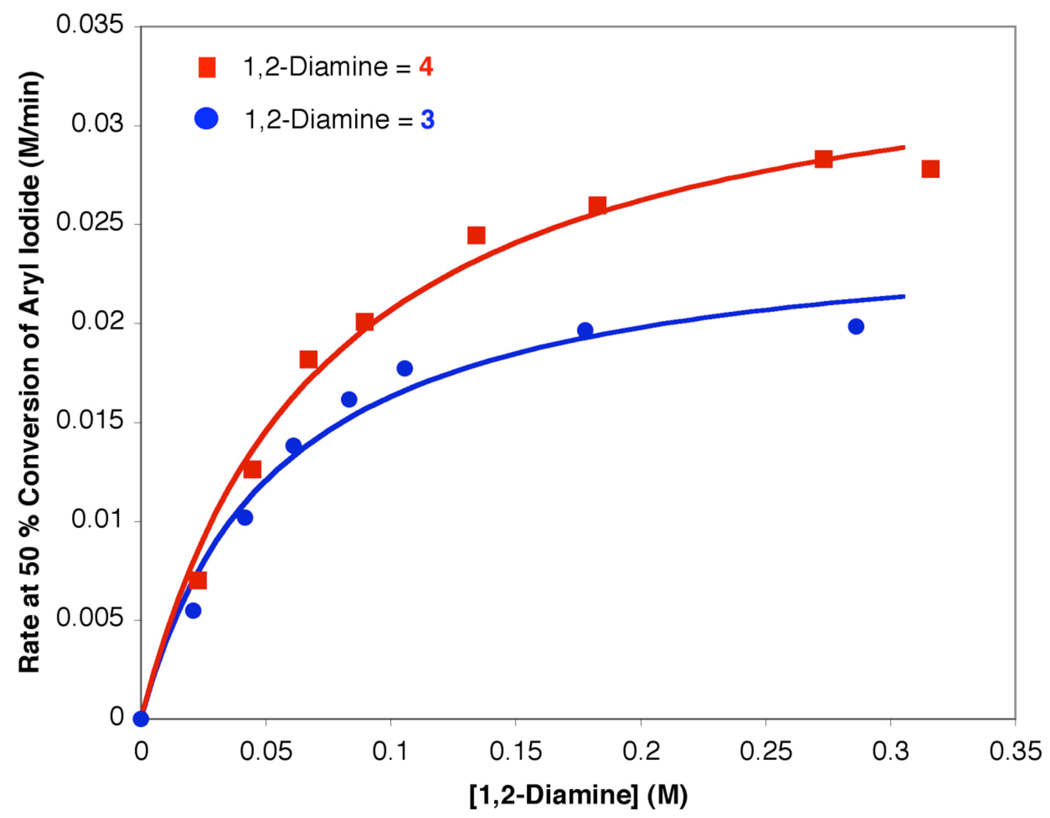
The initial kinetic studies focused on determining the precise role of the 1,2-diamine in this reaction. As shown in Figure 2, a nonlinear relationship between [1,2-diamine] and the reaction rate at 50 % conversion of 1 was observed over a 20-fold change in [1,2-diamine]. The data at 50 % conversion was chosen as a result of the non-linearity of the reaction rate vs. concentration profiles under certain conditions and the inherent time lapse in the calorimetric data. The data were fit using nonlinear least squares to an equation describing saturation with excellent agreement.26 Both catalyst systems, i.e., that based on ligand 3 and that based on ligand 4, provided nearly identical reactions rates with the catalyst based on 4 providing a slightly higher overall rate.
Figure 2.
Reaction rate at 50% conversion of 1 vs. [1,2-diamine] in the N-arylation of 2 (0.8 M) with 1 (0.4 M) using [CuI] (0.02 M) at 90 ° C. The curve fit reflects a nonlinear least squares fit to a function: rate = C1[l,2-diamine]/(C2 + [1,2-diamine])
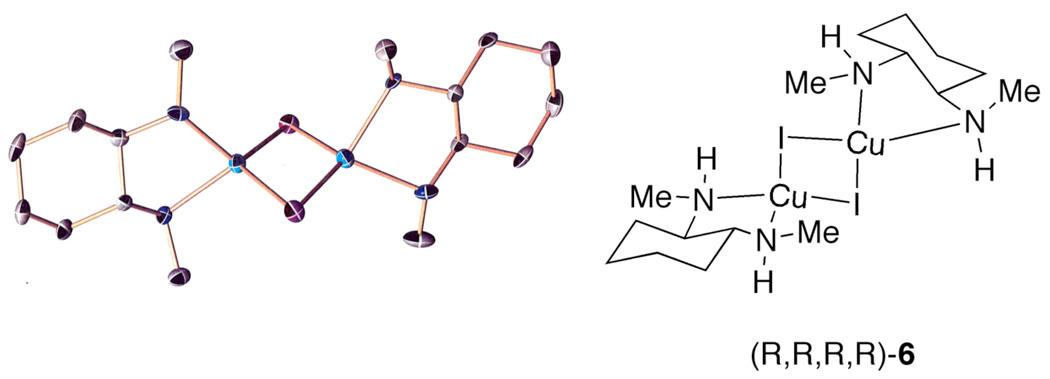
To determine whether the nonlinear rate dependence on [1,2-diamine] is a result of either catalyst solubility or catalyst deactivation, mixtures of CuI with 3 or 4 in toluene were examined. The observation that complete dissolution of the copper(I) salt occurs in a mixture containing CuI and 3 or 4 in a 1:1 ratio precludes an explanation for the saturation behavior based on a change in solubility of the active copper(I) species. Only upon layering a toluene solution of CuI and 3 with hexanes did a colorless precipitate form. Single-crystal X-ray diffraction analysis of these crystals revealed a dimeric complex 6 containing iodine atoms that bridge the two tetrahedrally coordinated copper(I) centers (Figure 3).27,28
Figure 3.
Crystal structure of the dimeric 1,2-diamine-ligated CuI complex.
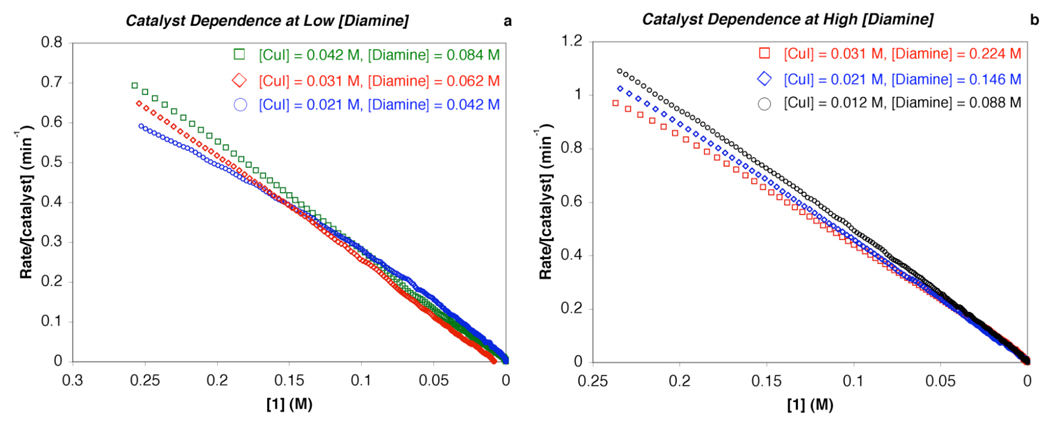
To examine whether catalyst deactivation could account for the saturation kinetics in [1,2-diamine] the reaction rate dependence on catalyst concentration was examined at both high and low [3]. If high [1,2-diamine] prevents bimolecular catalyst decomposition from occurring, then a nonlinear rate dependence on [catalyst] would be expected at low [3], whereas, at high concentrations of [1,2-diamine] a linear rate dependence on [catalyst] would be predicted. This is evidenced by the overlapping rate profiles in the plots of rate/[catalyst] versus [1] (Figure 4). In the event, a first-order dependence on [copper]total in reactions with Cu(I):3 ratios of both 1:2 and 1:7 also rules out a bimolecular catalyst decomposition process.29
Figure 4.
Dependence of the reaction rate on catalyst concentration at both (a) low [3] (Cu:3 =1:2) and (b) high [3] (Cu:3 = 1:7). In both cases the reaction rate displays a first-order dependence on catalyst concentration, i.e., rate ∝ [catalyst] or rate/[catalyst] = constant. Conditions: [CuI] = 0.01 – 0.04 M, [3] = 0.04 – 0.22 M, [1]o = 0.4 M, [2]o = 0.8 M, [K3PO4]o = 2.4 mmol, 2 mL of toluene, 90 °C.
Kinetics Studies: Amide, Aryl Iodide, and Base Effects
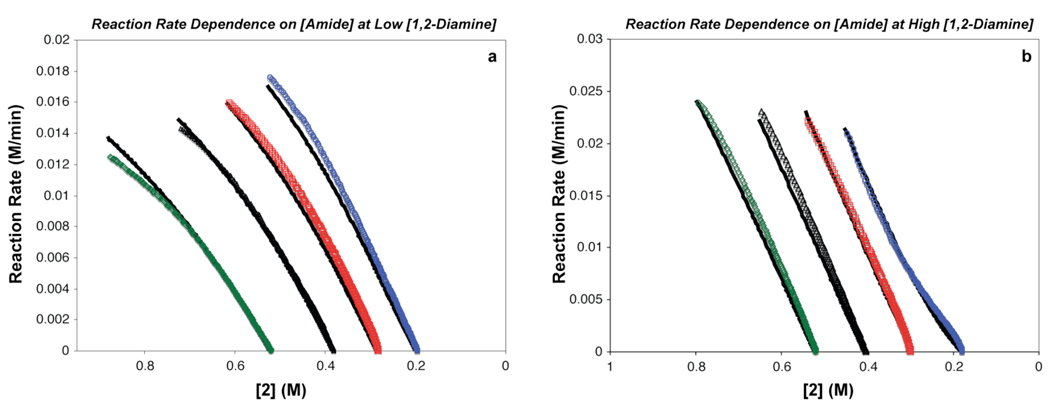
The dependence of the reaction rate on the amide concentration is a function of 1,2-diamine concentration (Figure 5). At low [1,2-diamine], the reaction rate decreases with increases in [amide] (Figure 5a). For example, comparing the rate profiles when [amide]o = 0.93 M to that when [amide]o = 0.6 M, indicates that at 0.93 M the initial rate (∼ 0.012 M/min) is nearly 25% lower (∼ 0.016 M/min) than at 0.6 M. Also, the slope of the rate curve at 0.93 M is smaller than that at 0.6 M. In contrast, at high [1,2-diamine] (Figure 5b) the reaction rate increases as the [amide] increases. Both the increasing slope of the rate curves as well as the higher initial reaction rates at higher [amide] reflect a positive-order reaction rate dependence on [amide] at high [1,2-diamine]. Thus at low [1,2-diamine] there is a positive-order rate dependence on [1,2-diamine] and an inverse dependence on [amide], and at high [1,2-diamine], there is a zero-order rate dependence on [1,2-diamine] and a positive-order dependence on [amide]. These relationships are expressed in equation 6a and equation 6b
| (6a) |
| (6b) |
Figure 5.
Dependence of the reaction rate on amide concentration ([2]) at both (a) low [3] (Cu:3 = 1:2) and (b) high [3] (Cu:3 = 1:10). Conditions: (a) [3] = 0.04 M and (b) [3] = 0.2 M, [CuI] = 0.02, [1]o = 0.4 M, [2]o = 0.93 M ( ), 0.8 M (△), 0.7 M (
), 0.8 M (△), 0.7 M ( ), 0.6 M (
), 0.6 M ( ), [K3P04]o = 2.4 mmol, 2 mL of toluene, 90 °C. The black curves represent the nonlinear least-squares fit to eq. 9. The kinetic parameters are: K1 = 0.85 ± 0.05, K2 = 2.0 ± 0.2, kact = 12 ± 3 M−1•min−1.
), [K3P04]o = 2.4 mmol, 2 mL of toluene, 90 °C. The black curves represent the nonlinear least-squares fit to eq. 9. The kinetic parameters are: K1 = 0.85 ± 0.05, K2 = 2.0 ± 0.2, kact = 12 ± 3 M−1•min−1.
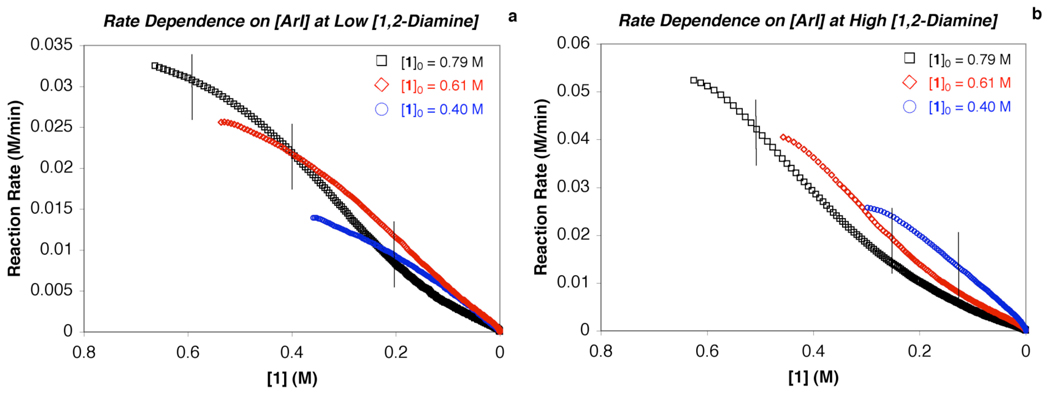
The reaction rate exhibits a positive-order dependence on the [aryl iodide] using both high and low [1,2-diamine] conditions (for a more comprehensive analysis of the reaction rate dependence see the Supporting Information). For simplicity, each of the vertical lines in Figure 6a and Figure 6b represent points at which the [amide] is the same for the three different initial [aryl iodide] used. With the [amide] the same, the reaction rates at various [aryl iodide] can be compared. At low [1,2-diamine] (Figure 6a), the reaction rates where the vertical lines are present correspond to 0.032 M/min, 0.021 M/min, and 0.0095 M/min, respectively. At these three points [aryl iodide] is 0.2 M, 0.4 M, and 0.6 M, thus, the reaction rates are almost directly proportional to the aryl iodide concentration (eq 6c). This is also the case at high [1,2-diamine] (Figure 6b), where the vertical lines represent points at which the rate is: 0.042 M/min when [aryl iodide] is 0.5 M, 0.02 M/min when [aryl iodide] is 0.25 M, and 0.011 M/min when [aryl iodide] is 0.125 M. Thus, the approximate first-order reaction rate dependence on [aryl iodide] can be extracted from the rate profiles in Figure 6
| (6c) |
Figure 6.
Dependence of the reaction rate on aryl iodide concentration ([1]) at both (a) low [3] = 0.04 M (Cu:3 = 1:2) and (b) high [3] = 0.2 M (Cu:3 = 1:10). Conditions: [CuI] = 0.02, [1]o = 0.4 M ( ), 0.61 M (
), 0.61 M ( ), 0.79 M (□), [2]o = 0.83 M, [K3PO4]o = 2.4 mmol, 2 mL of toluene, 90 °C.
), 0.79 M (□), [2]o = 0.83 M, [K3PO4]o = 2.4 mmol, 2 mL of toluene, 90 °C.
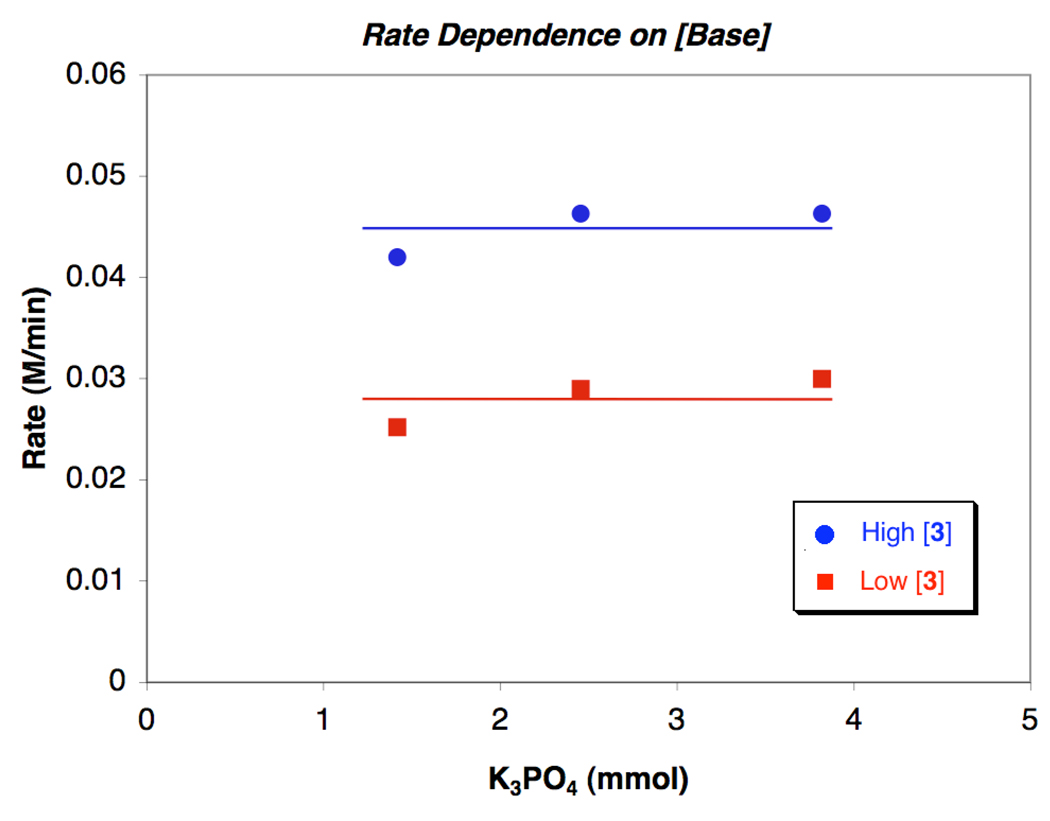
At both low and high [1,2-diamine], the reaction rate is not significantly influenced while changing the amount of K3PO4 by over 3-fold (Figure 7). This behavior presumably indicates that saturation of the inorganic base in a nonpolar solvent is occurring. These results further substantiate the claim that the reaction rate is not mass transfer limited, since a rate dependence on [K3PO4] may indicate otherwise.
Figure 7.
Dependence of the reaction rate on K3PO4 concentration at both (a) low [3] (Cu:3 =1:2) and (b) high [3] (Cu:3 = 1:10). Conditions: (a) [3] = 0.04 M and (b) [3] = 0.2 M, [CuI] = 0.02 M, [1]o = 0.4 M, [2]o = 0.83 M, [K3PO4]o = 1.4–3.8 mmol, 2 mL of toluene, 90 °C.
Kinetics Studies: Electronic Effects
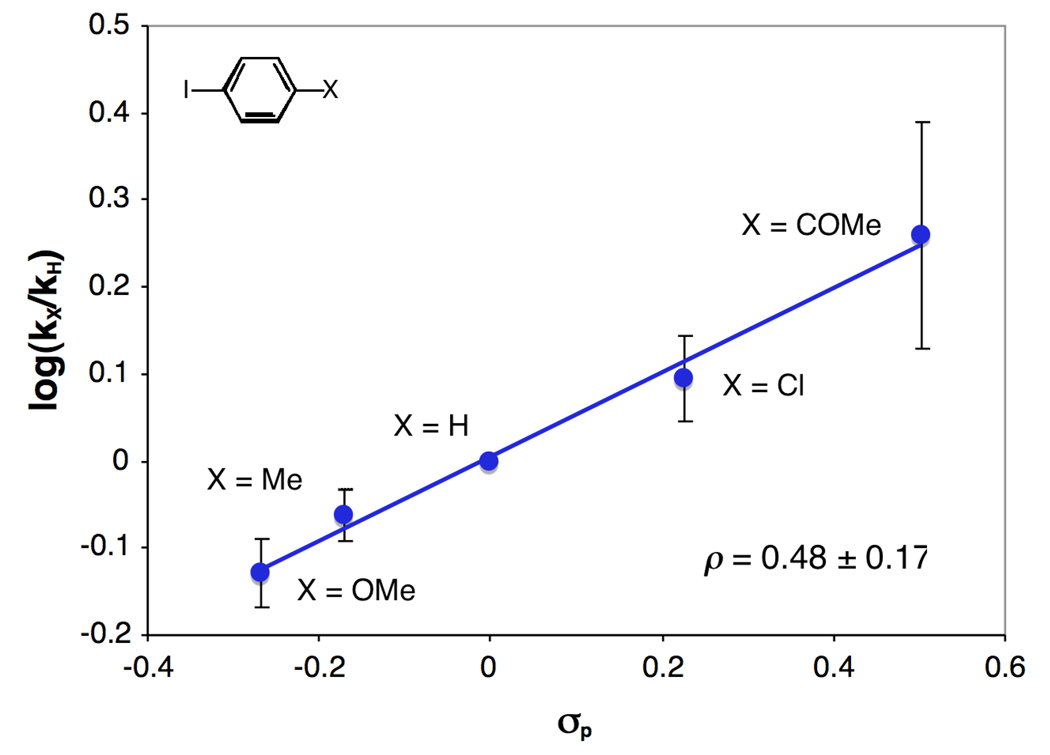
A series of para-substituted aryl iodides, X-C6H4I (X = COMe, Cl, H, Me, OMe) were used to investigate electronic effects on the catalytic turnover rate. The reaction rate exhibits a nonlinear dependence on [1,2-diamine] with each of the aryl iodides. However, the electronic effect does not change within statistical significance while varying [1,2-diamine]. Thus, at both high and low [1,2-diamine], electron-deficient analogues facilitate more rapid turnover rates (Figure 8, the combined ρ = +0.48 ± 0.17 is representative of the electronic effects at both high and low [1,2-diamine]).
Figure 8.
Hammett plot derived from the observed rate constants of the N-arylation of 2-pyrrolidinone (2) with a series of para-substituted aryl iodides. Conditions: [CuI] = 0.02, [3] = 0.04 and 0.2 M, [aryl iodide]o = 0.4 M, [2]o = 0.83 M, [K3PO4]o = 2.4 mmol, 2 mL of toluene, 90 °C. Each point is the average of the six experiments, three experiments at each high and low [3].
Synthesis and Characterization of Cu(I) Amidates
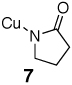
The Cu(I) amidate 7 was obtained from the reaction between dry, oxygen-free 2 and halide free mesitylcopper30 at room temperature in toluene under a nitrogen atmosphere (eq 7).31 Cu(I) amidate 7 is soluble in both toluene and 1,4-dioxane and less soluble in diethyl ether, THF, and hexanes. The Cu(I) amidate 7, which was obtained as a white solid upon removal of toluene under vacuum and washing with hexanes, hydrolyzes on contact with water and is rapidly oxidized by air. The ratio of amidate to Cu(I) was analyzed for the composition of 2-pyrrolidinone by gas chromatography through the hydrolysis of 7 upon addition of concentrated HCl to a solution of 7 in toluene; the Cu content was analyzed by iodometric titration. These analyses indicate that the ratio of amidate:Cu is approximately 1: 1.32
 |
(7) |
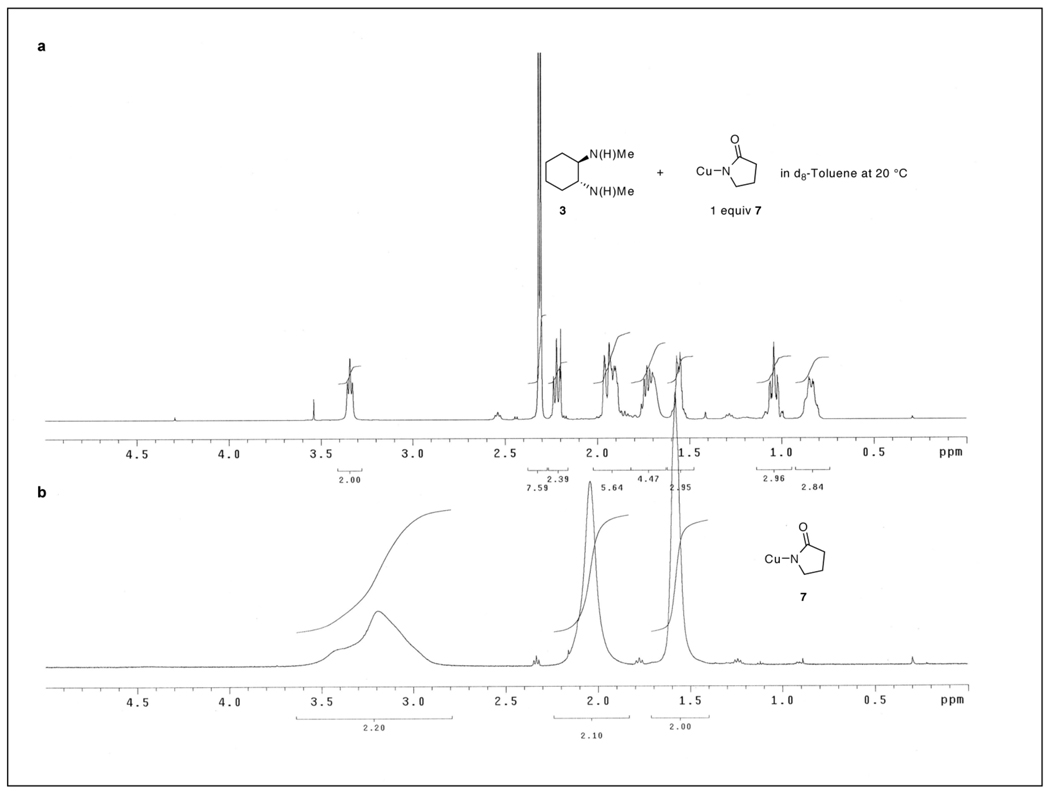
The solution structure of 7 is dependent on whether the chelating 1,2-diamine is present. In accordance with the solution behavior of Cu(I) alkoxides,21,33 Cu(I) amides,28 and CuCN,34 7 exists as a rapidly exchanging oligomeric species as evidenced by the broadened resonances in the room temperature 1H NMR spectrum (Figure 9b). However, upon addition of 3 to a solution of 7 in toluene, the resonances are sharpened in the 1H NMR spectrum, which is consistent with a structure where the 2-pyrrolidinoate moieties are no longer rapidly exchanging with other oligomeric forms (Figure 9a). This suggests that a single species results from the addition of 3 to 7.
Figure 9.
1H NMR spectra of a solution containing a) 7 and 3 and b) just 7 in d8 – toluene at 20 °C.
To further evaluate the solution structure of 7 in the same solvent in which the catalytic reaction is performed, molecular weight measurements were obtained using the Signer method in the presence and absence of the 1,2-diamine.35 As shown in Table 1, a solution of 7 in toluene yielded a molecular weight of 517. Since the Signer method measures the total amount of solute in solution, the solution structure of 7 in a nonpolar solvent is consistent with a species that is an average between a tetramer (MW 588, 147 per monomeric unit) and a trimer (MW 441). Upon addition of the 1,2-diamine (MW 142) to the solution of 7 in toluene using a Cu: 1,2-diamine ratio of 1:1, the measured molecular weight of the solute was 267 in comparison to the theoretical MW of 289 for the 1:1 complex. Although analysis of the latter solution by 1H NMR after completion of the molecular weight measurement revealed an identical spectrum to that shown in Figure 9a, a minor amount of free pyrrolidinone was present (less than 15 %), which can result in a number for the observed molecular weight that is lower than the actual value. The average molecular weight of a solution containing a 1:1 mixture of non-interacting 7 and 1,2-diamine is 222. In contrast, the observed molecular weight of 267 suggests that the solution structure is more consistent with the formation of a 1,2-diamine-ligated Cu(I) amidate monomeric complex (8, MW 289) from a mixture of 1 mmol each of 1,2-diamine and 7 (eq 8). This conclusion is further supported by the recent work of Hartwig and co-workers where they demonstrated, by X-ray crystallography, that a 1:1 mixture of 1,10-phenanthroline and Cu(I) phthalimidate results in a monomeric three-coordinate trigonal planar complex 9 similar to that proposed for 8.23
Table 1.
Molecular weight determinations by the Signer method.
N, degree of association.
MWcalc, molecular weight of oligomer nearest to the MWobs
used as a standard.
 |
(8) |
Kinetics Studies: N-Arylation of Cu(I) Amidate with Aryl Iodides
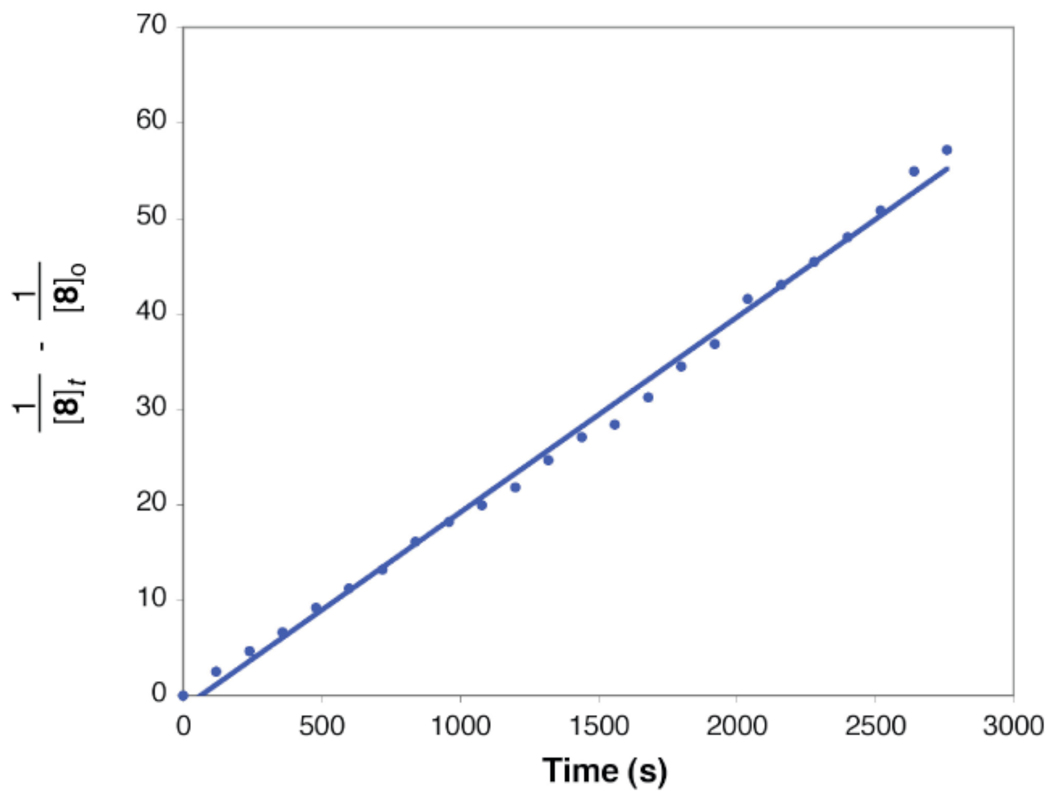
With the solution structure of the 1,2-diamine-ligated Cu(I) amidate (8) established, we sought to characterize the kinetic competency of 8 as a potential intermediate during the N-arylation process. The kinetics of the N-arylation of 8 were investigated by 1H NMR (eq 9) and the data is consistent with the reaction being first-order in both [1] and [8] (see Supporting Information for more details).36 It is important to note that the reaction rate for aryl iodide activation is independent of [3] at ratios of 3:Cu(I) amidate >1. As shown in Figure 10, the plot of 1/[8]t– 1/[8]o versus time furnishes a linear plot with slope equal to kapp for the N-arylation of 8 over 3 half-lives. The observation of a first-order dependence on the [8] is also consistent with 8 existing as a monomer in solution. Comparing ΔG‡ (obtained from the second-order rate constant, i.e., kapp) for the Cu(I) amidate based on ligand 3, i.e., 8, to that based on ligand 4 reveals a nearly identical activation energy; 19.4 kcal·mol−1 for the former and 19.5 kcal·mol−1 for the latter, respectively.
Figure 10.
Linear relationship between l/[8]t – l/[8]o and time (s) for the N-arylation of 8 (52 mM) with 1 (52 mM) in 1 mL of d8 – toluene at 20 °C; kapp = 2.04 × 10−2 M−1•s−1.
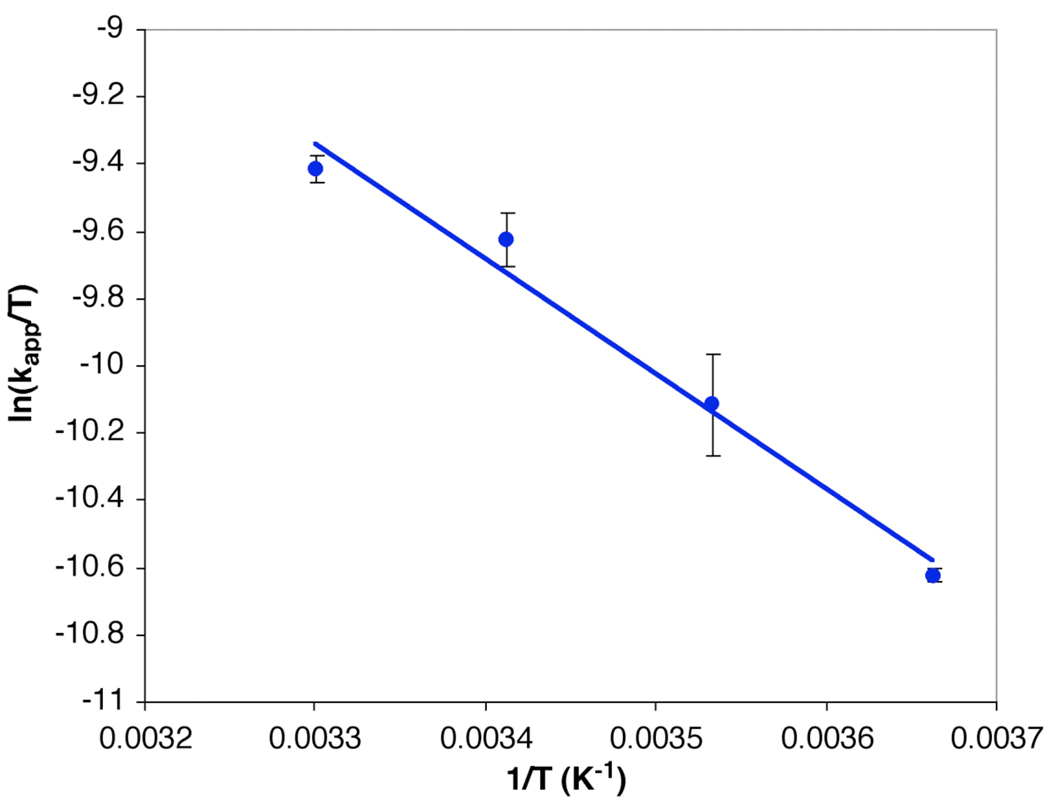
The activation parameters for the stoichiometric N-arylation process allowed for further characterization of the aryl iodide activation step. Measuring the second-order rate constant, kapp, over a 30 °C temperature range, i.e., 0 – 30 °C, provided a linear Eyring plot (Figure 11). The activation parameters were measured to be: ΔH‡ = 6.8 kcal·mol−1, ΔS‡ = − 43.3 eu, and ΔG‡ = 19.4 kcal/mol. Table 2 lists the individual rate constants (kapp) for each temperature. These results are consistent with the ΔG‡ of 18 kcal/mol recently reported for the N-arylation of 4-iodotoluene with the N, N’-dimethylethylenediamine-ligated Cu(I) pyrrolidinate.23
Figure 11.
Eyring plot for the N-arylation of 8 (52 mM) with 1 (52 mM) in 1 mL of toluene from 0 – 30 °C. Each point is the average of three experiments.
Table 2.
Individual rate constants (kapp) for each temperature.
| T(K) | kapp (M−1s−1) |
|---|---|
| 303 | 2.47±0.04 × 10−2 |
| 293 | 1.94±0.12 × 10−2 |
| 283 | 1.15±0.18 × 10−2 |
| 273 | 6.65±0.08 × 10−3 |
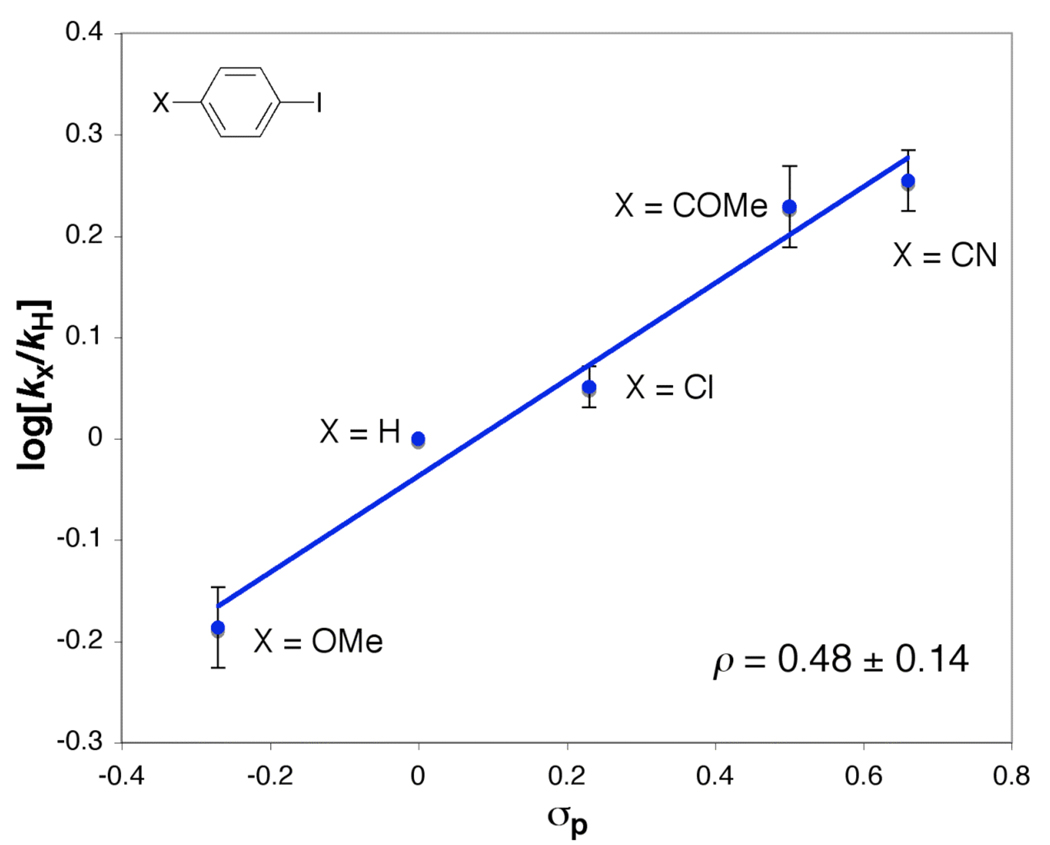
A series of para-substituted aryl iodides, X–C6H4I (X = OMe, H, CI, COMe, CN) were used to investigate electronic effect on the N-arylation of 8. As shown in Figure 12, a linear Hammett plot is obtained, which indicates that electron-deficient aryl iodides enhance the rate at which the aryl iodide activation occurs (ρ = +0.48 ± 0.14). Of importance, this result is similar to that obtained from the catalytic process.
Figure 12.
Hammett plot derived from the second-order rate constant, kapp, obtained from the N-arylation of (l,2-diamine)Cu(I) amidate (8) with a series of para-substituted aryl iodides. Conditions: [8] = 52 mM, [aryl iodide] = 52 mM, 1 mL of toluene, 20 °C. Each point is the average of three experiments.
Discussion
Catalytic Mechanism: Overview
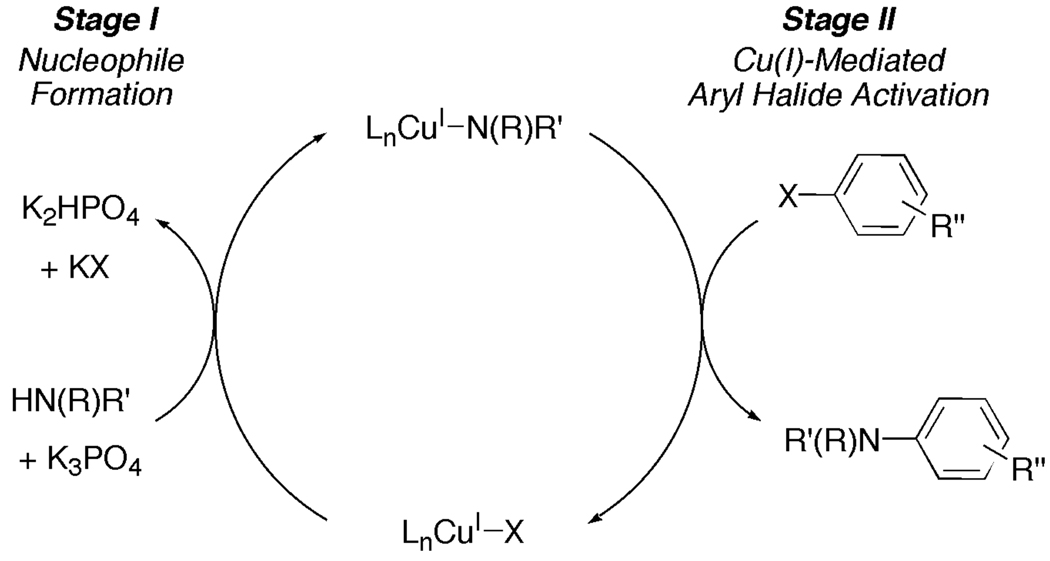
The Cu(I)-catalyzed C-N bond-forming reaction between N-nucleophiles and aryl halides proceeds by a Cu(I)-mediated nucleophilic aromatic substitution type mechanism in which the aryl halide activation and the nucleophile formation occur in two independent, sequential stages (Scheme 1). Consistent with this proposal, Cu(I) amidates promote the kinetically competent stoichiometric N-arylation.37
Scheme 1.
Simplified Catalytic Cycle Displaying the Two-Stage Cu(I)-Catalyzed N-Arylation Process.
Kinetic studies on the catalytic N-arylation of amides using the Cu(I)/l,2-diamine catalyst system reveal a positive-order rate dependence on aryl iodide concentration under conditions where the rate dependence on [amide] and [1,2-diamine] are changing, i.e., the studies carried out at high and low [1,2-diamine]. These results suggest that the Cu(I)-mediated aryl halide activation step (Stage II, Scheme 1), under all circumstances, is the rate determining step. The linear Hammett plot obtained under the changing dependencies on [amide] and [1,2-diamine] further substantiates this proposal.
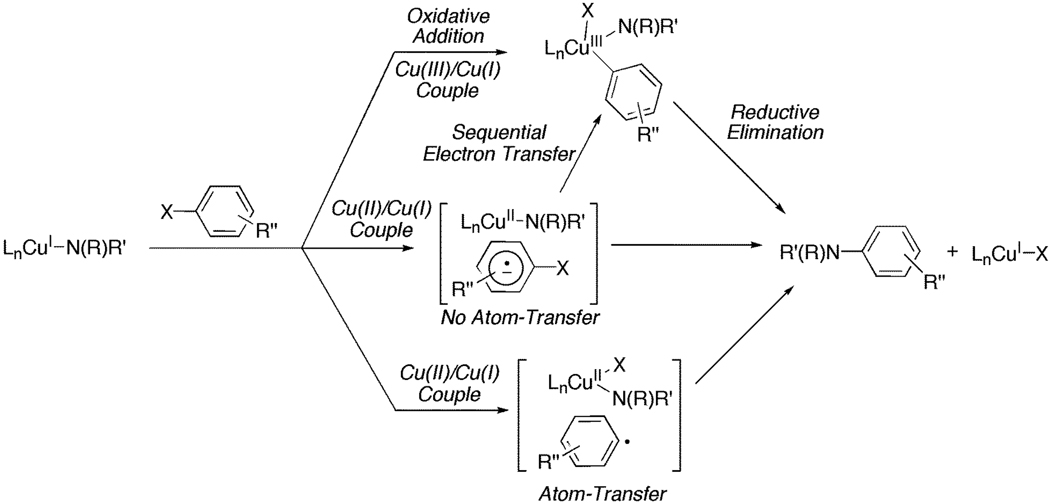
Evidence pinpointing a single mechanism for the Cu(I)-mediated aryl halide activation step (Stage II, Scheme 1) is relatively scarce. Previous research concerning the mechanism of the Ullmann C-N bond-forming reaction has suggested that the aryl halide activation step occurs through an oxidative addition process where the redox chemistry takes place between either a Cu(III)/Cu(I) couple or a sequential electron-transfer process involving all three oxidation states of copper, i.e., Cu(I), Cu(II) and Cu(II) (Scheme 2).2 Additionally, there are two plausible mechanisms for the “inner-sphere” electron transfer involving the Cu(II)/Cu(I) couple. The first involves a radical anion intermediate which forms without atom-transfer to Cu(II) prior to C-N bond formation, i.e., a SRNl-type mechanism,38 while the second involves an aryl radical which forms upon oxidation of Cu(I) to Cu(II) with concurrent atom-transfer (Scheme 2). All of these postulates originate from the pioneering work of Kochi,39 Whitesides,40 Johnson,41 and Cohen42 through their mechanistic investigations on alkyl radical additions to Cu(II), Ullmann C-C coupling, halogen-exchange, and organocuprate nucleophilic substitutions.
Scheme 2.
Mechanisms for the Cu(I)-Mediated Aryl Halide Activation Step.
There are two contrasting views for aryl halide activation during C-N bond-forming reaction.23,43,44 While studying the Ullmann condensation reaction of haloanthraquinone derivatives with 2-aminoethanol, Hida observed the oxidation of initial Cu(I) species to a Cu(II) species with the concomitant formation of a 1-bromoanthraquinone radical anion via EPR spectroscopy.43 This result supports an aryl halide activation process involving a Cu(II)/Cu(I) redox couple, but unfortunately due to the rate of subsequent steps the intermediacy of a Cu(III) species could not be established. In contrast, both Bethell44 and Hartwig23 have suggested that a Cu(III) intermediate is formed during the coupling reaction between aryl halides and amines/amides. In support of this, Huffman and Stahl have provided evidence for pathway involving a Cu(III)/Cu(I) couple by demonstrating that C-N bond-forming reductive elimination occurs rapidly from well-defined Cu(III)-aryl species.45
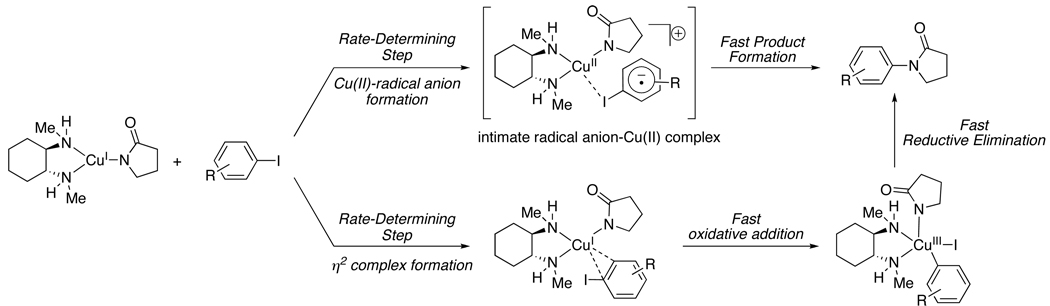
Considering the present mechanistic studies on the stoichiometric N-arylation of the Cu (I) amidate, a well-defined pathway for aryl iodide activation cannot be resolved. Comparing the activation parameters in addition to the ρ – value (ρ = +0.48) to those obtained from the oxidative addition of Pd(0) with aryl iodides suggests that the Cu(I) amidate-mediated aryl iodide activation does not involve a rate-determining oxidative addition process involving a Cu(III)/Cu(I) couple. For example, a ρ – value of 2.3 and enthalpy of activation (ΔH‡) of 18.4 kcal·mol−1 was obtained for the oxidative addition of Pd(0) with aryl iodides.46 In the latter case, the carbon-iodide bond is broken and a significant amount of negative charge is built up in the transition state. In contrast, during the activation of aryl iodides by the Cu(I) amidate, the relatively low ΔH‡ (6.8 kcal·mol−1) and ρ – value suggest that very little bond cleavage and build up of negative charge occurs during the rate-determining step. However, recent B3LYP level calculations on the oxidative addition of iodobenzene to [(dmeda)Cu(pyrrolidinone)] found that the ΔH‡ is 6 kcal·mol−1 and the ΔG‡ is 25 kcal·mol−1,23 which is congruent with the experimentally determined ΔH‡ and ΔG‡ obtained in this study. Although the latter consistency is a compelling argument for the possibility of an oxidative addition mechanism to occur during the Cu(I) amidate-mediated aryl iodide activation, the alternative mechanism whereby an inner sphere electron-transfer process occurs prior to the formation of the Cu(III) species can not be ruled out. A reaction taking place via such inner-sphere process would not be expected to show a dependence solely on the reduction potential of the aryl halide, as interactions between the metal and halide may be significant. Taken together, the data presented here is consistent with two possible mechanisms for aryl iodide activation (Scheme 3). The first route involves aryl iodide coordination to the Cu(I) amidate, a process facilitated by electron-donating groups in the para-position of the aryl iodide,47 followed by an inner-sphere single-electron transfer from Cu(I) to the aryl iodide generating a transient Cu(II) species in addition to an intimate radical anion without considerable changes in bonding; electron-deficient groups in the para-position of the aryl iodide facilitate the latter process. Subsequently, the fast product formation step could entail halide atom transfer to the Cu(II) intermediate (see Scheme 2), radical recombination to form a Cu(III) species and finally reductive elimination to afford the N-arylated amide. The second possible mechanism for aryl iodide activation involves the Cu(III)/Cu(I) redox couple. This reaction pathway, as suggested by Guo and co-workers, involves the formation of an η2 complex between the Cu(I) amidate and the aryl iodide during the rate-determining step (Scheme 3).48 In this case, the extent to which bond cleavage occurs is also minimal and electron-deficient aryl iodides would facilitate the formation of the η2 complex by lowering the LUMO of the aromatic ring.
Scheme 3.
Possible Mechanisms for the Cu(I) Amidate Promoted Aryl Iodide Activation.
Catalytic Mechanism: B) Controlling the Resting State of the Catalyst with the 1,2-Diamine Ligand
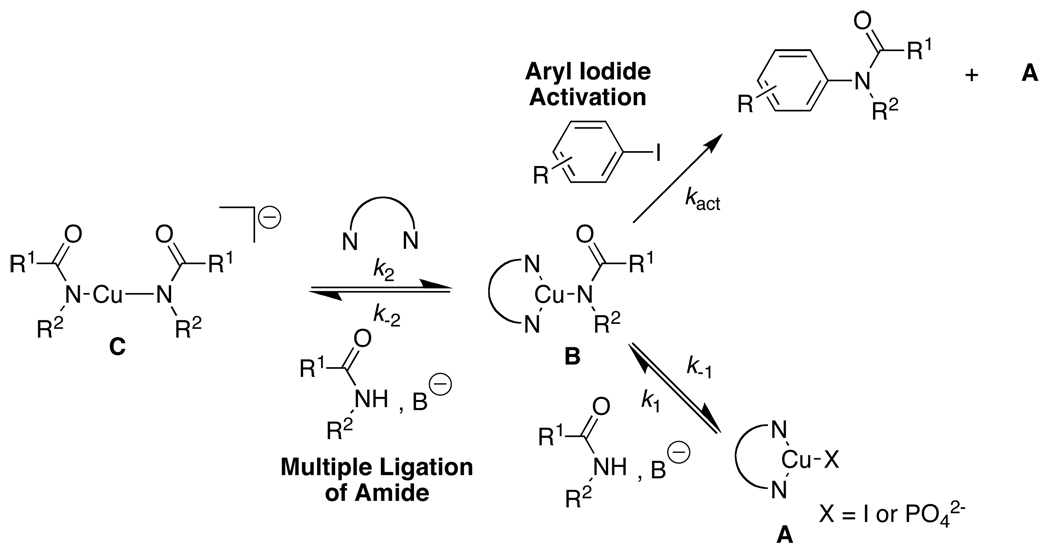
Equation (6a–6c) provide specific insights into the mechanism of the Cu(I)-catalyzed N-arylation of amides with aryl iodides. The nonlinear rate dependence on [1,2-diamine] (Figure 2), specifically, the inhibition of the reaction rate by the amide at low [3] and the acceleration of the reaction rate by the amide at high [3] suggest a complex process involving multiple equilibria. Since the increase in reaction rate with [3] cannot be explained by the increase in solubility of copper or prevention of catalyst decomposition, the other alternative resides in the prevention of multiple ligation of the amide to the copper at high [3], which would lead to inactive copper species. The mechanism shown in Scheme 4 proposes that the intermediate Cu(I) amidate (B) is formed either through amide coordination to A followed by deprotonation or through 1,2-diamine association and subsequent amide dissociation from C.49 Once formed, B reacts with the aryl iodide, affording the desired N-arylated amide.
Scheme 4.
Proposed Mechanism for the Cu(I)-Catalyzed N-Arylation of Amides.
The corresponding rate expression for the mechanism in Scheme 4 is given by eq 9, with the concentrations of base, K3PO4, and the liberated KI treated as constants (the reaction rate is independent of the concentration of each of these species, see Figure 7 and Supporting Information). Quasi-equilibria are assumed for K1 = k1/k−1 (= [B]/[A][amide]) and K2 = k2/k−2(= [B][amide]/[C][ 1,2-diamine]) on the basis that aryl iodide activation serves as the turnover-limiting step at both high and low [3]. It is important to point out that the proper description of rate laws requires due consideration of activity coefficients, thus, the concentration terms in our analysis refer to the real concentrations and the activity effects are implicitly contained in the rate constants. Equation 9 is consistent with the kinetic data as exemplified by the nonlinear least-squares fit to the experimental data in Figure 6, which provides the kinetic parameters: K1 = 0.85 ± 0.05, K2 = 2.0 + 0.2, kact = 12 ± 3 M−1·min−1.50
| (9) |
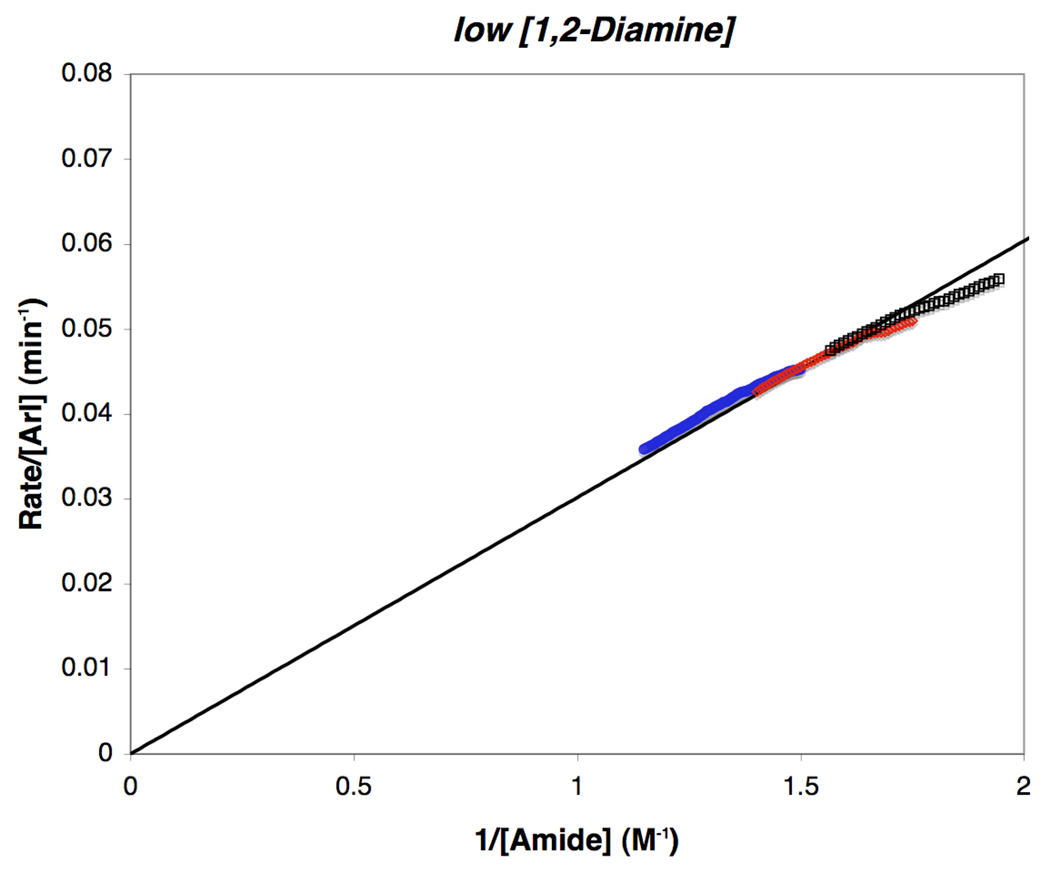
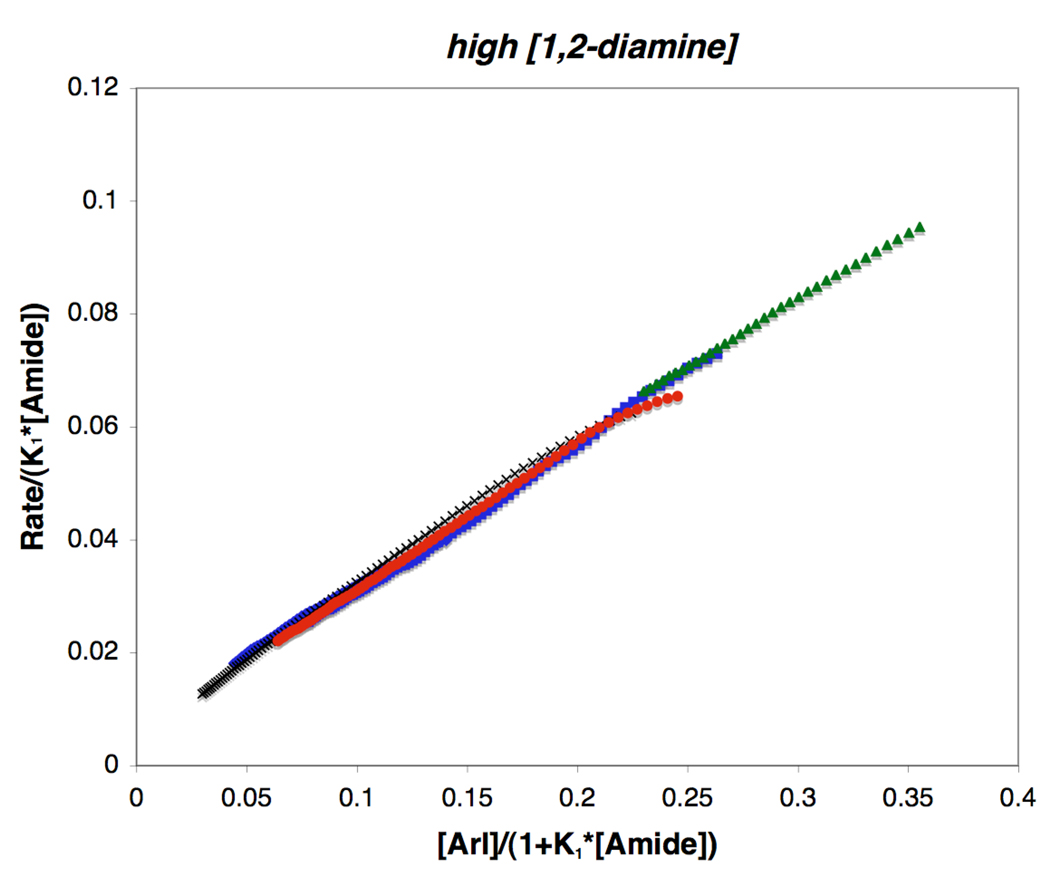
The first-order rate dependence on 1,2-diamine concentration at low [3] suggests that under these conditions the equilibrium between B and C dominates over that between B and A (Scheme 4). Increasing the concentrations of the 1,2-diamine 3 or 4 drives the reaction back to intermediate B in equilibrium with A. Thus, increasing concentrations of 1,2-diamine increases the reaction rate, while increasing amide concentrations should suppress it. This results in the limiting case of the rate expression of eq 9 shown in eq 10 and eq 11. The straight-line relationship between the function rate/[ArI] and l/[amide] provided by eq 11 is demonstrated in Figure 13, where three experiments performed at different [amide] converge into approximately the same straight-line relationship with slope equal to K′. These data confirm the inverse dependence on [amide] at low [3]. In contrast, under conditions of high [3], Figure 14 reveals that a straight-line relationship is observed between the function rate/K1[amide] versus [ArI]/(1 + K1[Amide]) when K1 is 0.85±0.05, congruent with the kinetic parameters obtained from eq 9 and the limiting form of eq 9 shown in eq 12 and eq 13. This implies that, under high [3], the situation holds for ca. 3-half lives of 1 the equilibrium between A and B governs the reaction network (Scheme 4), affording first-order kinetics in [ArI], saturation kinetics in [amide] and zero-order kinetics in added [3]. Also of significance, the value for kact can be obtained from the slope in Figure 14 (kact = 0.2 ± 0.02 M−1·s−1 based on eq 13), which allows for comparisons to be made between the stoichiometric and catalytic N-arylation reactions.
Figure 13.
Reaction rate dependence on [amide] at low [3]. The quasilinear relationship between rate/[ArI] and l/[Amide] is shown based on eq 11, with slope = 3.02 ± 0.06×l0−2. Conditions: low [3] (10 mol % 3, 5 mol % CuI) [1]o = 0.4 M, ( ) [2]o = 0.94 M, (
) [2]o = 0.94 M, ( ) [2]o = 0.78 M, (□) [2]o = 0.66 M.
) [2]o = 0.78 M, (□) [2]o = 0.66 M.
Figure 14.
The quasilinear relationship between rate/K1[Amide] and [ArI]/(1+K1 [Amide]), where K1 is 0.85 ± 0.05, is shown based on eq 13. The slope, which is equal to kact[Cu]t is 0.25 ± 0.02 min−1. Conditions: high [3] (70 mol % 3, 5 mol % CuI), ( ) [2]o = 0.8 M, [1]o = 0.8 M, (
) [2]o = 0.8 M, [1]o = 0.8 M, ( ) [2]o = 0.9 M, [1]o = 0.6 M, (
) [2]o = 0.9 M, [1]o = 0.6 M, ( ) [2]o = 0.8, [1]o = 0.6 M, (×) [2]o = 1.0 M, [1]o = 0.6 M.
) [2]o = 0.8, [1]o = 0.6 M, (×) [2]o = 1.0 M, [1]o = 0.6 M.
At Low [Diamine]
| (10) |
| (11) |
At High [Diamine]
| (12) |
| (13) |
Correlation Between the Stoichiometric N-Arylation of Cu(I) Amidates and the Cu(I)-Catalyzed N-Arylation of Amides
To establish a relationship between the catalytic reaction mechanism and the stoichiometric N-arylation of the Cu(I) amidate, the kinetic data from the stoichiometric process was extrapolated to 90 °C. Using the Eyring plot shown in Figure 11, a value for kapp at 90 °C is calculated to be 0.20 ± 0.01 M−1·s−1. This value is nearly identical to that obtained from the slope in Figure 14 (kact = 0.2 ± 0.02 M−1·s−1), which suggests that the 1,2-diamine ligated Cu(I) amidate is a kinetically competent intermediate in the catalytic N-arylation reaction.
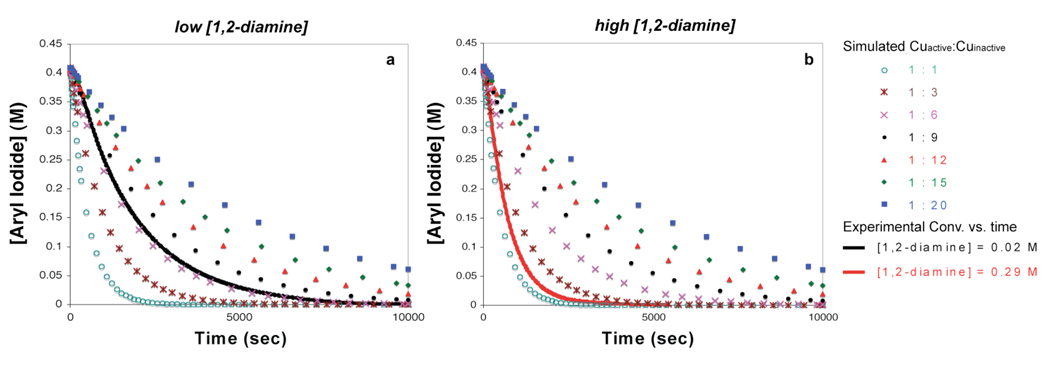
Using the kinetic data obtained from the stoichiometric N-arylation reaction, the relevancy of the 1,2-diamine ligated Cu(I) amidate to the catalytic reaction was further evaluated by simulating conversion versus time profiles. According to the proposed mechanism in Scheme 4, the Cu(I) amidate (B) exists in rapid equilibrium with the two catalytically inactive species A and C. Therefore, in addition to kapp and [ArI], the overall reaction rate also depends on the ratio of Cuactive(B):Cuinactive(A/C). The value for kapp was then applied to the simplified kinetic equation described in eq 14, which takes into account the equilibrium between Cuactive and Cuinactive. Upon numerical integration of eq 14 by keeping kapp fixed at 0.20 M−1·s−1 and varying the ratio of kf : kr (kf : kr = Cuactive:Cuinactive), simulated concentration-time profiles were obtained. For comparison, the simulated concentration-time profiles were plotted along with the experimental concentration-time profiles obtained from reactions conducted with both high and low [1,2-diamine]. As shown in Figure 15, the experimental conversion-time profiles for the Cu-catalyzed N-arylation with high [1,2-diamine] ([1,2-diamine] = 0.29 M) and low [1,2-diamine] ([1,2-diamine] = 0.02 M) are in good agreement the simulated conversion-time profiles within the Cuactive:Cuinactive range of 1:1 to 1:10, respectively. The significance of this correlation is that the extrapolated value for kapp, which was obtained from the stoichiometric Cu(I)-mediated N-arylation, provides simulated conversion-time profiles that are in good agreement with the conversion-time profiles obtained from the catalytic reaction, again suggesting that the stoichiometric N-arylation of Cu(I)-amidates is kinetically relevant to the catalytic Cu(I)-catalyzed N-arylation. Another important conclusion from the correlation between the experimental and simulated data is the effect of the 1,2-diamine concentration on the Cuactive:Cuinactive ratio; higher concentrations of Cuactive are present with higher [1,2-diamine], which is consistent with the mechanism proposed in Scheme 4.
| (14) |
Figure 15.
Comparison between experimental conversion vs. time data, and results obtained by numerically integrating equation 14 with kapp = 0.2 M−1•s−1 for different ratios of kf : kr (= Cuactive:Cuinactive). Conditions: [ArI]o = 0.4 M, [Cuinactive]o = 0.02 M, a) experimental [3] = 0.02 M, b) experimental [3] = 0.29 M.
The values obtained for the kinetic parameters K1 and K2 are used to determine how the Cuactive:Cuinactive ratio is affected by the amide and diamine concentrations. More specifically, given K1 and K2 obtained from the fit to eq 9 or from the limiting forms of eq 9 shown in eq 11 and eq 13, the ratio of Cuactive:Cuinactive species during the catalytic process can be estimated since K1 = [B]/[A][amide] and K2 = [B][amide]/[C][1,2-diamine]. For example, under the typical high [1,2-diamine] reaction conditions, [A]/[B] = 1/K1[amide] ≈ 1/(0.85×0.8) = 1.5, and under the typical low [1,2-diamine] conditions [C]/[B] = [amide]/K2[1,2-diamine] ≈ 0.8/(2×0.04) = 10. The above values of K1 and K2 indicate that there is generally more of the inactive species A and C than the active Cu(I) amidate B, consistent with the results of numerical integrations. Future work will focus of developing more effective ligands for Cu(I) so as to generate higher concentrations of active catalyst.
In summary, the Cu(I)/1,2-diamine catalyst system has been applied to a variety of N-arylation reactions as well as halogen-exchange reactions and this mechanistic study on the N-arylation of 2-pyrrolidinone with aryl iodides provides insights into the factors that control catalyst activity. We have, complemented the kinetic study of a Cu(I)-catalyzed Goldberg reaction with the direct N-arylation of a Cu(I) amidate. Such data facilitated the elucidation of the detailed mechanism of Cu(I)-nucleophile formation and also revealed the intricacies involved in multiple ligation of the N-based nucleophile to the Cu(I) catalyst. In particular, the nonlinear rate dependence on the [1,2-diamine] highlighted the role of the 1,2-diamine in establishing a high concentration of active catalyst throughout the course of the reaction. This was further verified by establishing the kinetic competency of a 1,2-diamine-ligated Cu(I) amidate. Initial insights into the mechanism of aryl iodide activation were obtained, albeit, the precise mechanism of the Cu(I)-mediated activation could not be established and warrants further study.
Supplementary Material
ACKNOWLEDGMENT
Support has been provided by the National Institutes of Health (GM 58160), the American Chemical Society (Organic Division Fellowship to E.R.S., sponsored by Albany Molecular Research), Merck, and Novartis. We thank Prof. Donna G. Blackmond (Imperial College, London) for insightful discussions and Dr. Timothy E. Barder for X-ray crystallographic analysis of 6. We also thank the reviewers of this manuscript for many helpful suggestions.
Footnotes
SUPPORTING INFORMATION. Experimental procedures, reaction rate derivation, and coordinates for the X-ray structure of 6 (PDF). This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.(a) Ullmann F. Chem. Ber. 1901;34:2174. [Google Scholar]; (b) Ullmann F. Chem. Ber. 1903;36:2382. [Google Scholar]; (c) Ullmann F, Sponagel P. Chem. Ber. 1905;38:2211. [Google Scholar]; (d) Goldberg I. Chem. Ber. 1906;39:1619. [Google Scholar]
- 2.For an older review highlighting the application of the Ullmann/Goldberg reaction in synthesis, see: Lindley J. Tetrahedron. 1984;40:1433.
- 3.For reviews on palladium-catalyzed C-N bond formation, see: Jiang L, Buchwald SL. In: Palladium-Catalyzed Aromatic Carbon-Nitrogen Bond Formation. In Metal-Catalyzed Cross-Coupling Reactions. 2nd Ed; de Meijere A, Diederich F, editors. Wiley-VCH; Weinheim: 2004. p. 699. ; (b) Muci AR, Buchwald SL. Top. Curr. Chem. 2002;219:131. [Google Scholar]; (c) Hartwig JF. In: Handbook of Organopalladium Chemistry for Organic Synthesis. Negishi E, editor. New York: Wiley-Interscience; 2002. p. 1051. [Google Scholar]
- 4.(a) Shen Q, Shekhar S, Stambuli JP, Hartwig JF. Angew. Chem. Int. Ed. 2005;44:1371. doi: 10.1002/anie.200462629. [DOI] [PubMed] [Google Scholar]; (b) Huang X, Anderson KW, Zim D, Jiang L, Klapars A, Buchwald SL. J. Am. Chem. Soc. 2003;125:6653. doi: 10.1021/ja035483w. [DOI] [PubMed] [Google Scholar]; (c) Harris MC, Huang X, Buchwald SL. Org. Lett. 2002;4:2885. doi: 10.1021/ol0262688. [DOI] [PubMed] [Google Scholar]; (d) Link JT, Sorensen B, Liu G, Pei Z, Reilly EB, Leitza S, Okasinski G. Bioorg. Med. Chem. Lett. 2001;11:973. doi: 10.1016/s0960-894x(01)00105-6. [DOI] [PubMed] [Google Scholar]; (e) Prashad M, Hu B, Lu Y, Draper R, Har D, Repic O, Blacklock TJ. J. Org. Chem. 2000;65:2612. doi: 10.1021/jo991949a. [DOI] [PubMed] [Google Scholar]; (f) Batch A, Dodd RH. J. Org. Chem. 1998;63:872. doi: 10.1021/jo971485l. [DOI] [PubMed] [Google Scholar]; (g) Willoughby CA, Chapman KT. Tetrahedron Lett. 1996;37:7181. [Google Scholar]; (h) Ward YD, Farina V. Tetrahedron Lett. 1996;37:6993. [Google Scholar]
- 5.(a) Yin J, Buchwald SL. J. Am. Chem. Soc. 2002;124:6043. doi: 10.1021/ja012610k. [DOI] [PubMed] [Google Scholar]; (b) Cacchi S, Fabrizi G, Goggiamani A, Zappia G. Org. Lett. 2001;3:2539. doi: 10.1021/ol016208m. [DOI] [PubMed] [Google Scholar]; (c) Artamkina GA, Sergeev AG, Beletskaya IP. Tetrahedron. Lett. 2001;42:4381. [Google Scholar]; (d) Yin J, Buchwald SL. Org. Lett. 2000;2:1101. doi: 10.1021/ol005654r. [DOI] [PubMed] [Google Scholar]; (e) Shakespeare WC. Tetrahedron. Lett. 1999;40:2035. [Google Scholar]
- 6.Kiyomori A, Marcoux J-F, Buchwald SL. Tetrahedron. Lett. 1999;40:2657. [Google Scholar]
- 7.Goodbrand HB, Hu N-X. J. Org. Chem. 1999;64:670. [Google Scholar]
- 8.Gujadhur RK, Bates CG, Venkataraman D. Org. Lett. 2001;3:4315. doi: 10.1021/ol0170105. [DOI] [PubMed] [Google Scholar]
- 9.Kwong FY, Klapars A, Buchwald SL. Org. Lett. 2002;4:581. doi: 10.1021/ol0171867. [DOI] [PubMed] [Google Scholar]
- 10.Ma D, Cai Q, Zhang H. Org. Lett. 2003;5:2453. doi: 10.1021/ol0346584. [DOI] [PubMed] [Google Scholar]
- 11.Kwong FY, Buchwald SL. Org. Lett. 2003;5:793. doi: 10.1021/ol0273396. [DOI] [PubMed] [Google Scholar]
- 12.(a) Antilla JC, Baskin JM, Barder TE, Buchwald SL. J. Org. Chem. 2004;69:5578. doi: 10.1021/jo049658b. [DOI] [PubMed] [Google Scholar]; (b) Zanon J, Klapars A, Buchwald SL. J. Am. Chem. Soc. 2003;125:2890. doi: 10.1021/ja0299708. [DOI] [PubMed] [Google Scholar]; (c) Jiang L, Job GE, Klapars A, Buchwald SL. Org. Lett. 2003;5:3667. doi: 10.1021/ol035355c. [DOI] [PubMed] [Google Scholar]; (d) Klapars A, Buchwald SL. J. Am. Chem. Soc. 2002;124:14844. doi: 10.1021/ja028865v. [DOI] [PubMed] [Google Scholar]; (e) Antilla JC, Klapars A, Buchwald SL. J. Am. Chem. Soc. 2002;124:11684. doi: 10.1021/ja027433h. [DOI] [PubMed] [Google Scholar]; (f) Klapars A, Huang X, Buchwald SL. J. Am. Chem. Soc. 2002;124:7421. doi: 10.1021/ja0260465. [DOI] [PubMed] [Google Scholar]; (g) Klapers A, Antilla JC, Huang X, Buchwald SL. J. Am. Chem. Soc. 2001;123:7727. doi: 10.1021/ja016226z. [DOI] [PubMed] [Google Scholar]
- 13.For a critical review concerning copper-catalyzed cross coupling reactions, see: Beletskaya IP, Cheprakov AV. Coord. Chem. Rev. 2004;248:2337. For other more recent reviews, see: Ley SV, Thomas AW. Angew. Chem. Int. Ed. 2003;42:5400. doi: 10.1002/anie.200300594. Kunz K, Scholz U, Ganzer D. Synlett. 2003;15:2428.
- 14.Weston PW, Adkins HJ. Am. Chem. Soc. 1928;50:859. [Google Scholar]
- 15.Weingarten H. J. Org. Chem. 1964;29:3624. [Google Scholar]
- 16.Kondratov SA, Shein SM. Zh. Org. Khim. 1979;15:2160. [Google Scholar]
- 17.Paine AJ. J. Am. Chem. Soc. 1987;109:1496. [Google Scholar]
- 18.(a) Aalten HL, van Koten G, Grove DM, Kuilman T, Piekstra OG, Hulshof LA, Sheldon RA. Tetrahedron. 1989;45:5565. [Google Scholar]; (b) Resnik R, Cohen T, Fernando Q. J. Am. Chem. Soc. 1961;83:3344. [Google Scholar]
- 19.Bacon RGR, Karim A. J. Chem. Soc, Perkin Trans. 1. 1973:272. [Google Scholar]
- 20.Whitesides GM, Sadowski JS, Lilburn J. J. Am. Chem. Soc. 1974;96:2829. [Google Scholar]
- 21.Yamamoto T, Ehara Y, Kubota M, Yamamoto A. Bull. Chem. Soc. Jpn. 1980;53:1299. [Google Scholar]
- 22.a) Strieter ER, Blackmond DG, Buchwald SL. J. Am. Chem. Soc. 2005;127:4120. doi: 10.1021/ja050120c. [DOI] [PubMed] [Google Scholar]; b) Strieter Eric R. Ph.D. thesis. Massachusetts Institute of Technology; 2005. [Google Scholar]
- 23.Tye JW, Weng Z, Johns AM, Incarvito CD, Hartwig JF. J. Am. Chem. Soc. 2008;130:9971. doi: 10.1021/ja076668w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.This time lapse manifests itself as a plateau in the concentration vs. time profiles, thus, in some of the figures, e.g., Figure 4–Figure 6, the data at the beginning of the reaction is not shown. Moreover, in some instances an induction period lasting until approximately 15 % conversion is observed. The length of the induction period, i.e., whether it last until 5% conversion or until 15% conversion, was not always reproducible. The method in which the inorganic base was dried and stored clearly had an effect on this induction period and reproducible results for the remainder of the reaction, once the induction period subsided, were only obtained with K3PO4 available from Fluka (catalog number 04347, Riedel-de Haën product; free-flowing, fine granule of uniform size). K3PO4 was dried under high vacuum at 150 °C for 3 days and stored in a nitrogen-filled glovebox. Based on these observations, we suspect that the induction period is not mechanistically relevant.
- 25.Due to the limited solubility of K3PO4 in toluene it is difficult to estimate the concentrations. Thus, the values for [K3PO4]o are reported in mmol of K3PO4 used in the reaction.
- 26.Figure 2 data at constant [Arl], [Cu]total, and [Amide] fit to an equation of the form: rate = C1[l,2-Diamine]/(C2 + [1,2-Diamine]), where C1 and C2 are adjustable parameters.
- 27.For previous characterization of related structures, see: Raubenheimer HG, Cronje S, Kruger GJ, Olivier PJ. Polyhedron. 1995;14:2389. ; (b) Davies G, El-Kady R, Onan KD, Shomaly W, El-Sayed MA, El-Toukhy A. Inorg. Chim. Acta. 1988;149:21. [Google Scholar]; (c) Davies G, El-Kady N, El-Sayed MA, El-Toukhy A, Schure MR. Inorg. Chim. Acta. 1988;149:31. [Google Scholar]; (d) Healy PC, Pakawatchai C, White AH. J. Chem. Soc, Dalton Trans. 1985:2531. [Google Scholar]; (e) Haitko DA. J. Coord. Chem. 1984;13:119. [Google Scholar]
- 28.Enantiomerically pure (R,R)-3 was used to obtain X-ray quality crystals.
- 29.Preliminary kinetic studies with the dimeric Cu(I) complex, 6, indicate that the reaction rate also exhibits a first-order dependence on [Cu]total. These results suggest that the dimeric complex is not a kinetically relevant species.
- 30.(a) Tsuda T, Yazawa T, Watanabe K, Fujii T, Saegusa T. J. Org. Chem. 1981;46:292. [Google Scholar]; (b) Gambarotta S, Floriani C, Chiesi-Villa A, Guastini C. J. Chem. Soc, Chem. Commun. 1983:1156. [Google Scholar]; (c) Meyer EM, Gambarotta S, Floriani C, Chiesi-Villa A, Guastini C. Organometallics. 1989;8:1067. [Google Scholar]; (d) Tsuda T. In: Encyclopedia of Reagents for Organic Synthesis. Paquette L, editor. New York: Wiley; 1995. p. 3271. [Google Scholar]; (e) Eriksson H, Håkansson M. Organometallics. 1997;16:4243. [Google Scholar]
- 31.For the synthesis of copper(I)-amides, see: Tsuda T, Watanabe K, Miyata K, Yamamoto H, Saegusa T. Inorg. Chem. 1981;20:2728. ; (b) Hope H, Power PP. Inorg. Chem. 1984;23:936. [Google Scholar]; (c) Gamboratta S, Bracci M, Floriani C, Chiesi-Villa A, Guastini C. J. Chem. Soc, Dalton Trans. 1987:1883. [Google Scholar]
- 32.A similar procedure was used to characterize Cu(I) alkoxides, see ref 20.
- 33.(a) Lopes C, Håkansson M, Jagner S. Inorg. Chim. Acta. 1997;254:361. doi: 10.1021/ic961287x. [DOI] [PubMed] [Google Scholar]; (b) Håkansson M, Lopes C, Jagner S. Inorg. Chim. Acta. 2000;304:178. [Google Scholar]; (c) Gustafsson B, Håkansson M, Westman G, Jagner S. J. Organomet. Chem. 2002;649:204. [Google Scholar]
- 34.Hibble SJ, Eversfield SG, Cowley AR, Chippindale AM. Angew. Chem. Int. Ed. 2004;43:628. doi: 10.1002/anie.200352844. [DOI] [PubMed] [Google Scholar]
- 35.(a) Clark EP. Ind. Eng. Chem., Anal. Ed. 1941;13:820. [Google Scholar]; (b) Burger BJ, Bercaw JE. In Experimental Organometallic Chemistry: A Practice in Synthesis and Characterization. In: Wayada AL, Darensbourg MY, editors. ACS Symposium Series 357; American Chemical Society; Washington, DC. 1987. pp. 94–96. Chapter 4. [Google Scholar]; (c) Finn MG, Sharpless KB. J. Am. Chem. Soc. 1991;113:113. [Google Scholar]
- 36.Arylation of Cu(I) amidate in the absence of 3 did not precede at temperatures between 0 °C and 90 °C.
- 37.As described in ref. 21, PPh3-ligated Cu(I) amidates also undergo N-arylations, however, these reactions were not kinetically characterized either stoichiometrically or in the context of a catalytic reaction.
- 38.Bunnett JF. Ace. Chem. Res. 1978;11:413. [Google Scholar]
- 39.(a) Kochi JK. J. Am. Chem. Soc. 1957;79:2942. [Google Scholar]; (b) Jenkins CL, Kochi JK. J. Am. Chem. Soc. 1972;94:843. [Google Scholar]; (c) Jenkins CL, Kochi JK. J. Am. Chem. Soc. 1972;94:856. [Google Scholar]
- 40.(a) Whitesides GM, Fischer WF, San Filippo J, Bashe RW, House HO. J. Am. Chem. Soc. 1969;91:4871. [Google Scholar]; (b) Whitesides GM, Kendall PE. J. Org. Chem. 1972;37:3718. [Google Scholar]
- 41.Johnson CR, Dutra GA. J. Am. Chem. Soc. 1973;95:7783. [Google Scholar]
- 42.(a) Cohen T, Wood J, Dietz AG. Tetrahedron Lett. 1974;40:3555. [Google Scholar]; (b) Cohen T, Lewarchik RJ, Tarino JZ. J. Am. Chem. Soc. 1974;96:7753. [Google Scholar]; (c) Cohen T, Christea I. J. Am. Chem. Soc. 1976;98:748. [Google Scholar]
- 43.Arai S, Hida M, Yamagishi T. Bull. Chem. Soc. Jpn. 1978;51:277. [Google Scholar]
- 44.Bethell D, Jenkins IL, Quan PM. J. Chem. Soc., Perkin Trans. II. 1985:1789. [Google Scholar]
- 45.Huffman LM, Stahl SS. J. Am. Chem. Soc. 2008;130:9196. doi: 10.1021/ja802123p. [DOI] [PubMed] [Google Scholar]
- 46.Amatore C, Pflüger F. Organometallics. 1990;9:2276. [Google Scholar]
- 47.For studies demonstrating the relative affinities of aromatic acids to Cu(I), see: Saphier M, Burg A, Sheps S, Cohen H, Meyerstein D. J. Chem. Soc, Dalton Trans. 1999:1845.
- 48.Zhang S-L, Liu L, Fu Y, Guo Q-X. Organometallics. 2007;26:4546. [Google Scholar]
- 49.While this manuscript was being prepared ref. 23 was published, which provides experimental evidence that an intermediate such as C in Scheme 4 is unreactive towards aryl iodides and aryl bromides.
- 50.Nonlinear least-squares fits to eq 9 were obtained by using the Solver function within Microsoft Excel.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.