FEEDBACK REGULATION IN MULTISTAGE CELL LINEAGES

Abstract

Studies of developing and self-renewing tissues have shown that differentiated cell types are typically specified through the actions of multistage cell lineages. Such lineages commonly include a stem cell and multiple progenitor (transit amplifying; TA) cell stages, which ultimately give rise to terminally differentiated (TD) cells. In several cases, self-renewal and differentiation of stem and progenitor cells within such lineages have been shown to be under feedback regulation. Together, the existence of multiple cell stages within a lineage and complex feedback regulation are thought to confer upon a tissue the ability to autoregulate development and regeneration, in terms of both cell number (total tissue volume) and cell identity (the proportions of different cell types, especially TD cells, within the tissue). In this paper, we model neurogenesis in the olfactory epithelium (OE) of the mouse, a system in which the lineage stages and mediators of feedback regulation that govern the generation of terminally differentiated olfactory receptor neurons (ORNs) have been the subject of much experimental work. Here we report on the existence and uniqueness of steady states in this system, as well as local and global stability of these steady states. In particular, we identify parameter conditions for the stability of the system when negative feedback loops are represented either as Hill functions, or in more general terms. Our results suggest that two factors – autoregulation of the proliferation of transit amplifying (TA) progenitor cells, and a low death rate of TD cells – enhance the stability of this system.

1. Introduction

Tissue development is charged with the difficult task of specifying correct types of terminally differentiated (TD) cells (whose function typically characterizes the tissue), at the same time it must specify correct numbers and proportions of the various TD and progenitor cell types that compose the tissue. Studies have shown that multistage cell lineages, which typically include a multi-potent stem cell that gives rise to successively more differentiated progenitor cell types (transit amplifying cells; TA cells), underlie the specification of TD cells in many tissues [22, 28, 37]. In some tissues, control and coordination of development is mediated by feedback signals, which regulate proliferation and differentiation at specific lineage stages [38]. Although often established during embryonic development, the continued presence of feedback controls in adult organisms is believed to enable tissues to respond robustly to injury, rapidly and accurately regenerating appropriate cell numbers and proportions [11, 18].

The olfactory epithelium (OE) of the mouse is a useful model system for understanding how feedback regulation controls tissue development and regeneration [26]. The OE is a neuroepithelium similar in structure to the early embryonic central nervous system, but simpler in that it possesses only one major type of neuron, the olfactory receptor neuron (ORN). ORNs, the TD cells of the OE, extend apical (dendritic) cytoplasmic processes to the surface of the OE; these dendrites are in direct contact with the external environment via the nasal cavity. ORNs also extend axonal cytoplasmic processes basally; these axons traverse the basal lamina of the OE, grow through the connective tissue stroma that underlies the OE, and then make contact with the olfactory bulb of the forebrain; olfactory sensory information is conducted from the periphery to the central nervous system via the axons of the ORNs [4, 10]. The OE is subject to constant environmental impact due to its exposed position in the body, and therefore must regenerate ORNs continually, throughout the lifetime of the organism [7].

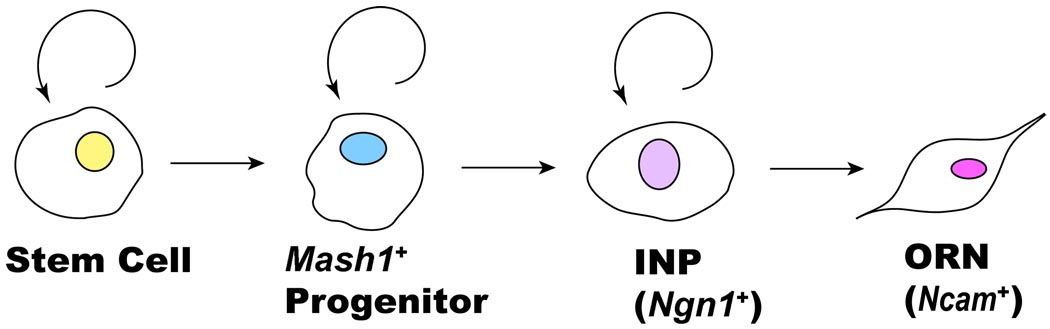
Studies of mouse OE have supported the view that ORNs derive from a multistage lineage with three proliferating cell types (reviewed in [5]): (1) self-renewing stem cells, which give rise to (2) TA progenitors that can be identified by their expression of the proneural gene Mash1. Mash1-expressing progenitors give rise to (3) immediate neuronal precursors (INPs), which comprise a second TA population, whose members expresses Ngn1, a proneural gene distinct from Mash1. INPs divide to give rise to daughter cells that undergo terminal differentiation into (4) ORNs. The four stages in the ORN lineage are depicted in Figure 1.

FIGURE 1.

A schematic diagram of the OE lineage. Adapted from [5, 6, 17].

It has long been known that cell proliferation in the OE is rapidly up-regulated when death of a large number of ORNs is induced (reviewed in [7]). More recently, in vitro observations showed that proliferation and generation of ORNs by cultured OE neuronal progenitors is inhibited by the presence of large numbers of ORNs [24]. These results suggest that ORNs produce signals that normally inhibit neurogenesis, such that the elimination of such signals upon ORN loss leads to an increase in ORN production. Subsequently, it has emerged that growth and differentiation factor 11 (GDF11), and ActivinβB, two members of transforming growth factor-β (TGFβ) superfamily, are strong candidates for such factors [13, 18, 31, 32, 38]. In particular, in vitro and in vivo experimental data indicate that GDF11, which is produced by INPs and ORNs, inhibits the proliferation of INPs, while ActivinβB, which appears to be produced by all cells in the lineage, inhibits proliferation of the stem cell [13]. There is evidence that both molecules slow the rates at which their target cells divide and increase the probability that the products of those divisions differentiate into cells at the next lineage stage [13, 18]. Other types of molecules, such as Follistatin (an inhibitor of GDF11 and ActivinβB), and bone morphogenetic proteins (BMPs), may also regulate the lineage [13, 18, 31, 32, 38]. It has been proposed that a multiplicity of feedback mechanisms and target lineage stages is required for tight control of cell population sizes and regeneration rates [18].

Evidence for feedback strategies analogous to those used in the OE has been found in many tissues and organs. For example, muscle cells produce myostatin/GDF8, a molecule closely related to GDF11, which exerts an inhibitory effect on myogenesis [19, 23]. In well-studied hematopoietic and epithelial lineages, other proliferative feedback mechanisms have been proposed or described [1, 29].

Various models have been proposed for different cell lineages. One of the influential works by Tomlinson and Bodmer [36] was a study of tumorigenesis based on discrete cell models, later followed by Johnston et al. [16] for cell population dynamics in the colonic crypt and colorectal cancer. Continuum models were also proposed for the same biological systems [15, 16]. Recently, using stochastic and discrete modeling, Mangel and Bonsall [21] studied variability and replacement in multistage cell lineages, and Glauche et al. [12] considered lineage specification of hematopoietic stem cells. Most of these works primarily used numerical simulations for model exploration. Other biological systems involving multiple cell types, such as hematopoiesis for myelogenous leukemia [8, 9] and T-cells in autoimmune diabetes [20], were studied using dynamic systems approach. On mathematical analysis, a linear stability analysis was performed in [3, 30] for a class of cyclic systems and a cellular control process with positive feedback; a global stability analysis was carried out for monotone cyclic systems [34] using the Poincaré-Bendixon Theorem in multi-dimension based on the discrete Lyapunov function method [33]. In particular, global stability may be studied using ω–limit set [2], Lyapunov function method [3] or standard Poincaré-Bendixon Theorem in two-dimension [14].

In this paper, we study the OE lineage (and analogous multistage cell lineages) using a continuum dynamic model. In the system, the feedbacks considered are negative feedbacks of the type supported by experiments [13, 38]. First, we study a system with a constant stem cell population, and two feedbacks on proliferation of TA cells. For this simplified system, the existence and uniqueness of the steady state, and local and global stability of the steady state are analyzed. It is found that a unique positive steady state exists, and both self-regulation of the proliferation of TA cells, and a low death rate of TD cells, enhances global stability of the steady state. Next, we consider more general lineages involving potentially dynamic stem, TA and TD cells, with a general form of negative feedback. For existence and stability of three possible steady states, conditions on the feedback are derived, with detailed analysis on parameter ranges when the feedbacks take the form of Hill functions. We find that self-regulation on the proliferation of stem cells and TA cells, as well as a large ratio of stem cell cycle length to TA cell cycle length, can enhance local stability. While the existing models typically used computational tools to explore the mechanisms of the cell population control, our work utilizes mathematical analysis to explain the functions of different feedback loops.

This paper is organized as follows. In Section 2, we introduce the mathematical model; in Section 3, we study the model with a lineage in which the size of the stem cell population is constant (not influenced by feedback); in Section 4, we consider the more general case in which the populations of all three cell types are dynamically regulated; in Section 5, we discuss and summarize.

2. A cell lineage model with endogenous negative feedback

The cell lineage system is assumed to have three types of cells: stem cells, transit amplifying (TA) cells and terminally differentiated (TD) cells, with the populations at time t denoted by χ₀(t), χ₁(t) and χ₂(t) respectively. In the model, the stem cells and TA cells proliferate with a probability p_i and differentiate with its complementary probability 1 − p_i, where 0 < p_i < 1, i = 0, 1. The TD cells undergo apoptosis (programmed death) with rate δ. ζ_i (i = 0, 1, 2) represents the cell cycle length divided by log 2 for each type of cell.

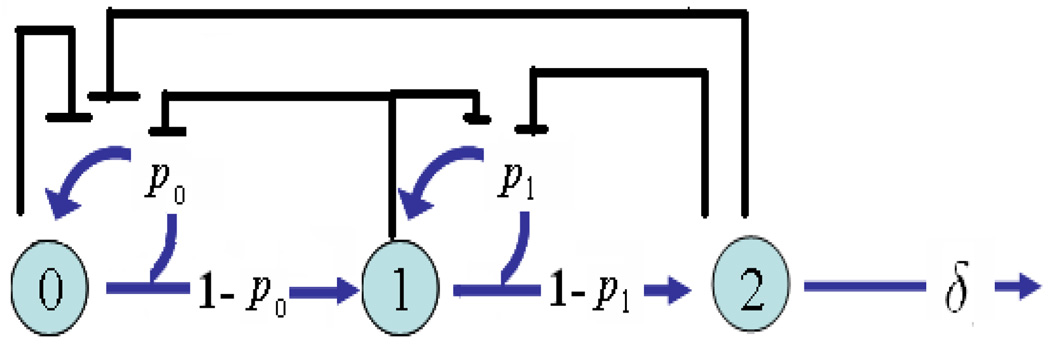
In many systems, such as the OE lineage, the proliferation of cells may be inhibited by substances produced by the cells at the same or later stages in their lineage. By assuming the amounts of substances are proportional to the sizes of the cell populations that produce the substances, the proliferative probabilities become functions of the cell populations, p₀ = p₀(χ₀, χ₁, χ₂) and p₁ = p₁(χ₁, χ₂). Figure 2 shows a schematic relationship and possible negative regulation among different types of cells in the cell lineage.

FIGURE 2.

Three-stage lineage of cells with negative feedback on cell proliferation.

A continuum model of Figure 2 takes the form:

$$\frac{d{\chi }_0}{\mathit{\text{dt}}}=\frac{{\chi }_0}{{\zeta }_0}(2_{p0}({\chi }_0,{\chi }_1,{\chi }_2)-1)$$ (1)

$$\frac{d{\chi }_1}{\mathit{\text{dt}}}=2\frac{{\chi }_0}{{\zeta }_0}(1-p_0({\chi }_0,{\chi }_1,{\chi }_2))+\frac{{\chi }_1}{{\zeta }_1}(-1+{2p}_1({\chi }_1,{\chi }_2))$$ (2)

$$\frac{d{\chi }_2}{\mathit{\text{dt}}}=-\delta {\chi }_2+\frac{2{\chi }_1}{{\zeta }_1}(1-p_1({\chi }_1,{\chi }_2))$$ (3)

with 0 < p₀(χ₀, χ₁, χ₂) < 1, 0 < p₁(χ₁, χ₂) < 1. Because proliferation is negatively regulated by different types of cells (as motivated data on the OE lineage), the functions p_i are assumed to be decreasing in all variables, with their partial derivatives satisfying p_iχj ≤ 0 (p_iχj = ∂p_i/∂χ_j). To non-dimensionalize the system, we scale time by the cell cycle length parameter ζ₁ through t̂ := t/ζ₀, ζ̂ := ζ₁/ζ₀, δ̂ := δζ₀. After discarding the hat on each variable, the non-dimensional form of system (1)–(3) becomes

$$\frac{d{\chi }_0}{\mathit{\text{dt}}}={\chi }_0({2p}_0({\chi }_0,{\chi }_1,{\chi }_2)-1)$$ (4)

$$\frac{d{\chi }_1}{\mathit{\text{dt}}}=2{\chi }_0(1-p_0({\chi }_0,{\chi }_1,{\chi }_2))+\frac{{\chi }_1}{\zeta }(-1+2p_1({\chi }_1,{\chi }_2))$$ (5)

$$\frac{d{\chi }_2}{\mathit{\text{dt}}}=-\delta {\chi }_2+\frac{2{\chi }_1}{\zeta }(1-p_1({\chi }_1,{\chi }_2)).$$ (6)

3. A model with a constant stem cell population

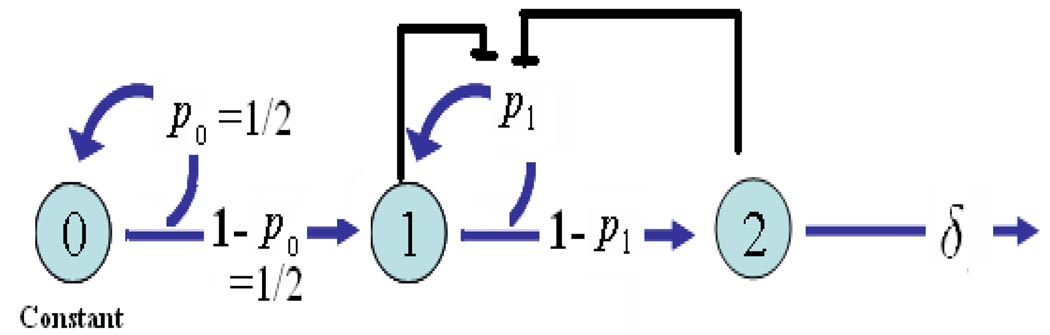
A special case of system (4)–(6) is that the stem cell population does not change in time and the proliferation of the stem cells is not regulated. This can be achieved if and only if, in equation (4), p₀(χ₀, χ₁, χ₂) = 0.5 with a positive χ₀ (see Figure 3). In this case, half of the stem cells progeny remain stem cells and the other half differentiate; as a result the stem cell population remains unchanged. The three-equation system (4)–(6) therefore becomes a two-equation system:

$$\frac{d{\chi }_1}{\mathit{\text{dt}}}={\chi }_0^{*}+\frac{{\chi }_1}{\zeta }(-1+2p_1({\chi }_1,{\chi }_2))$$ (7)

$$\frac{d{\chi }_2}{\mathit{\text{dt}}}=-\delta {\chi }_2+\frac{2{\chi }_1}{\zeta }(1-p_1({\chi }_1,{\chi }_2))$$ (8)

with ${\chi }_0^{*}$ a given positive constant. The reduced system (7)–(8) can be regarded as a two-cell lineage with a constant supply. In this model, only two negative feedbacks occur at the proliferation probability of the TA cells, and this simplicity allows a comprehensive analysis for the existence and uniqueness of the steady state, and their local and global stability of the system (7)–(8). As a result, roles of the two negative feedbacks are better understood.

FIGURE 3.

Lineage of cells with a fixed stem cell population.

3.1. Existence and uniqueness of the steady state

Because χ₁ and χ₂ represent the size of cell populations, only non-negative steady state solutions are considered in this paper.

The steady state equations of system (7)–(8) can be obtained by setting their left-hand side zero. Adding the two steady state equations yields

$${\chi }_2=\frac{1}{\delta }({\chi }_0^{*}+\frac{{\chi }_1}{\zeta });$$ (9)

and substituting equation (9) into the first steady state equation yields

$${\chi }_0^{*}+\frac{{\chi }_1}{\zeta }\left(-1+2p_1({\chi }_1,\frac{1}{\delta }({\chi }_0^{*}+\frac{{\chi }_1}{\zeta }))\right)=0.$$ (10)

The steady state $({\chi }_1^{*},{\chi }_2^{*})$ can be found by first solving equation (10) for χ₁ and then using (9) to derive χ₂. The number of the steady states of system (7)–(8) equals the number of roots in equation (10), and the function p₁ determines the number of steady states.

3.1.1. The steady state is unique if the minimal proliferation probability is smaller than its corresponding differentiation probability

As shown below, a necessary and sufficient condition for the existence and uniqueness of a positive steady state of system (7)–(8) is:

$$\underset{{\chi }_1,{\chi }_2\to \infty }{\text{lim}}{p}_1({\chi }_1,{\chi }_2)<1/2.$$ (11)

With the assumption that p₁ is non-increasing and using (11), one-half is an upper bound for the minimum of p₁ if and only if the unique postive steady state exists. Biologically, this condition means that the inhibition on the proliferation probability, from either the TA cells or the TD cells, must be strong enough such that at a certain time, more than half of the TA cells differentiate to the next stage per cell cycle.

To prove (11), consider the function

$$K({\chi }_1):={\chi }_0^{*}+\frac{{\chi }_1}{\zeta }\left(-1+2p_1({\chi }_1,\frac{1}{\delta }({\chi }_0^{*}+\frac{{\chi }_1}{\zeta }))\right).$$ (12)

With δ > 0 and ζ > 0, it is straightforward to show $K(0)={\chi }_0^{*}>0$, and lim_χ1→∞ K(χ₁) = −∞ if and only if (11) is satisfied. By continuity of K, there exists a positive ${\chi }_1^{*}$ such that $K({\chi }_1^{*})=0$, if and only if (11) is true; therefore, (11) is necessary and sufficient for the existence of a positive root for K. Next, we claim that ${\chi }_1^{*}$ is the only positive root of K = 0. Consider

$$\frac{K({\chi }_1)}{{\chi }_1}=\frac{{\chi }_0^{*}}{{\chi }_1}+\frac{1}{\zeta }\left(-1+2p_1({\chi }_1,\frac{1}{\delta }({\chi }_0^{*}+\frac{{\chi }_1}{\zeta }))\right),$$ (13)

the first term is strictly decreasing and the second term is monotonically decreasing in χ₁ so $\frac{K({\chi }_1)}{{\chi }_1}$ is strictly decreasing in χ₁. Therefore, $\frac{K({\chi }_1)}{{\chi }_1}$ has at most one root for χ₁ > 0. Since $\frac{K({\chi }_1)}{{\chi }_1}$ and K(χ₁) share same positive roots, K(χ₁) has at most one root. It implies that (11) is a necessary and sufficient condition for the existence of the steady states, and if a steady state exists, it must be positive and unique.

3.1.2. A system with negative feedback represented by Hill functions has a unique steady state

The feedback in biological models is often represented in terms of Hill functions [25]. Two possible Hill function forms of p₁ are

$$p_1({\chi }_1,{\chi }_2)=\frac{{\overline{p}}_1}{1+{(g_1{\chi }_1)}^m+{(g_2{\chi }_2)}^n},$$ (14)

and

$$p_1({\chi }_1,{\chi }_2)=\frac{{\overline{p}}_1}{[1+{(g_1{\chi }_1)}^m][1+{(g_2{\chi }_2)}^n]}$$ (15)

with the feedback coefficients g₁, g₂ ≥ 0 and at least one of them being positive, p̄₁ > 0 the maximal differentiation probability, and m, n denoting the Hill exponents. Hence, p₁(χ₁, χ₂) in (14) and (15) satisfies the conditions (11) and the system has a unique positive steady state. In the rest of this section, when the Hill function form of p₁ is referenced, only the first expression (14) is considered. However, the same results can be obtained for (15) through similar arguments.

3.2. Local stability analysis

Assume the system has a non-negative steady state ${\chi }^{*}=({\chi }_1^{*},{\chi }_2^{*})$, (i.e. p₁ satisfies (11)). Denoting $p_1^{*}=p_1({\chi }_1^{*},{\chi }_2^{*}),p_{1{\chi }_1}^{*}=\frac{\partial p_1}{\partial {\chi }_1}({\chi }_1^{*},{\chi }_2^{*})\text{and}{p}_{1{\chi }_2}^{*}=\frac{\partial p_1}{\partial {\chi }_2}({\chi }_1^{*},{\chi }_2^{*})$, the Jacobian matrix evaluated at the steady state is

$$J({\chi }^{*})=\left(\begin{array}{cc}\frac{2p_1^{*}-1}{\zeta }+\frac{2p_{1{\chi }_1}^{*}{\chi }_1^{*}}{\zeta }& \frac{2p_{1{\chi }_2}^{*}{\chi }_1^{*}}{\zeta }\\ \frac{2(1-p_1^{*})}{\zeta }-\frac{2p_{1{\chi }_1}^{*}{\chi }_1^{*}}{\zeta }& -\delta -\frac{2p_{1{\chi }_2}^{*}{\chi }_1^{*}}{\zeta }\end{array}\right).$$ (16)

The characteristic equation of the Jacobian matrix (16) is

$$\begin{array}{cc}\hfill {\lambda }^2-& \left(\frac{2p_1^{*}-1}{\zeta }+\frac{2p_{1{\chi }_1}^{*}{\chi }_1^{*}}{\zeta }-\delta -\frac{2p_{1{\chi }_2}^{*}{\chi }_1^{*}}{\zeta }\right)\lambda \hfill \\ & -\frac{2p_1^{*}-1}{\zeta }\delta -\frac{2p_{1{\chi }_1}^{*}{\chi }_1^{*}}{\zeta }\delta -\frac{2p_{1{\chi }_2}^{*}{\chi }_1^{*}}{{\zeta }^2}=0.\end{array}$$ (17)

Then, the steady state χ* is locally asymptotically stable if and only if both the roots of equation (17) have negative real parts, namely, if and only if

$$\frac{2p_1^{*}-1}{\zeta }+\frac{2p_{1{\chi }_1}^{*}{\chi }_1^{*}}{\zeta }-\delta -\frac{2p_{1{\chi }_2}^{*}{\chi }_1^{*}}{\zeta }<0$$ (18)

and

$$-\frac{2p_1^{*}-1}{\zeta }\delta -\frac{2p_{1{\chi }_1}^{*}{\chi }_1^{*}}{\zeta }\delta -\frac{2p_{1{\chi }_2}^{*}{\chi }_1^{*}}{{\zeta }^2}>0.$$ (19)

Because $({\chi }_1^{*},{\chi }_2^{*})$ is a steady state, by equation (10), $2p_1^{*}-1$ is negative. Also, by the fact that $p_{1{\chi }_1}^{*}\le 0$ and $p_{1{\chi }_2}^{*}\le 0$, inequality (19) is always satisfied. Therefore, equation (18) dictates the local stability.

3.2.1. The inhibition by TD cells determines stability

To find p₁ satisfying (18), here we consider p₁ in the Hill function form (14). The partial derivative of the function p₁(χ₁, χ₂) is

$$p_{1{\chi }_2}=-\frac{2n{\overline{p}}_1{g}_2^n{({\chi }_2)}^{n-1}{\chi }_1}{{(1+{(g_1{\chi }_1)}^m+{(g_2{\chi }_2)}^n)}^2}.$$ (20)

Because the first two terms are negative, the inequality (18) is proved if

$$-\delta -\frac{2p_{1{\chi }_2}^{*}{\chi }_1^{*}}{\zeta }<0.$$ (21)

By equation (9), we have ${\chi }_1^{*}\le \zeta \delta {\chi }_2^{*}$, so equation (21) is true if

$$-1-2p_{1{\chi }_2}^{*}{\chi }_2^{*}<0,$$

which is equivalent to

$$-1+\frac{2n{\overline{p}}_1{(g_2{\chi }_2^{*})}^n}{{(1+{(g_1{\chi }_1^{*})}^m+{(g_2{\chi }_2^{*})}^n)}^2}\le 0.$$

When the Hill exponent n = 1, by $p_1^{*}<\frac{1}{2}$ we obtain

$$-1+\frac{2{\overline{p}}_1(g_2{\chi }_2^{*})}{{(1+{(g_1{\chi }_1^{*})}^m+(g_2{\chi }_2^{*}))}^2}\le -1+\frac{g_2{\chi }_2^{*}}{1+(g_2{\chi }_2^{*})}<0.$$

When n = 2, by p̄₁ < 1 we obtain

$$-1+\frac{4{\overline{p}}_1{(g_2{\chi }_2^{*})}^2}{{(1+{(g_1{\chi }_1^{*})}^m+{(g_2{\chi }_2^{*})}^2)}^2}\le -1+\frac{4{(g_2{\chi }_2^{*})}^2}{{(1+{(g_2{\chi }_2^{*})}^2)}^2}<0.$$

Therefore, when n = 1, 2, condition (21) (and hence (18)) is satisfied, the steady state is unique and locally asymptotically stable.

3.2.2. Negative regulation from TA cells increases the range of parameters for local stability

For n ≥ 3, the above analysis cannot be carried out directly. In fact, unstable steady states for n ≥ 3 are observed through direct numerical simulations. Here, we study the linear stability for two cases: 1) n = 3 and g₁ = 0, a case with feedback only from the TD cells; and 2) n = 3, m = 1, a case with both feedbacks.

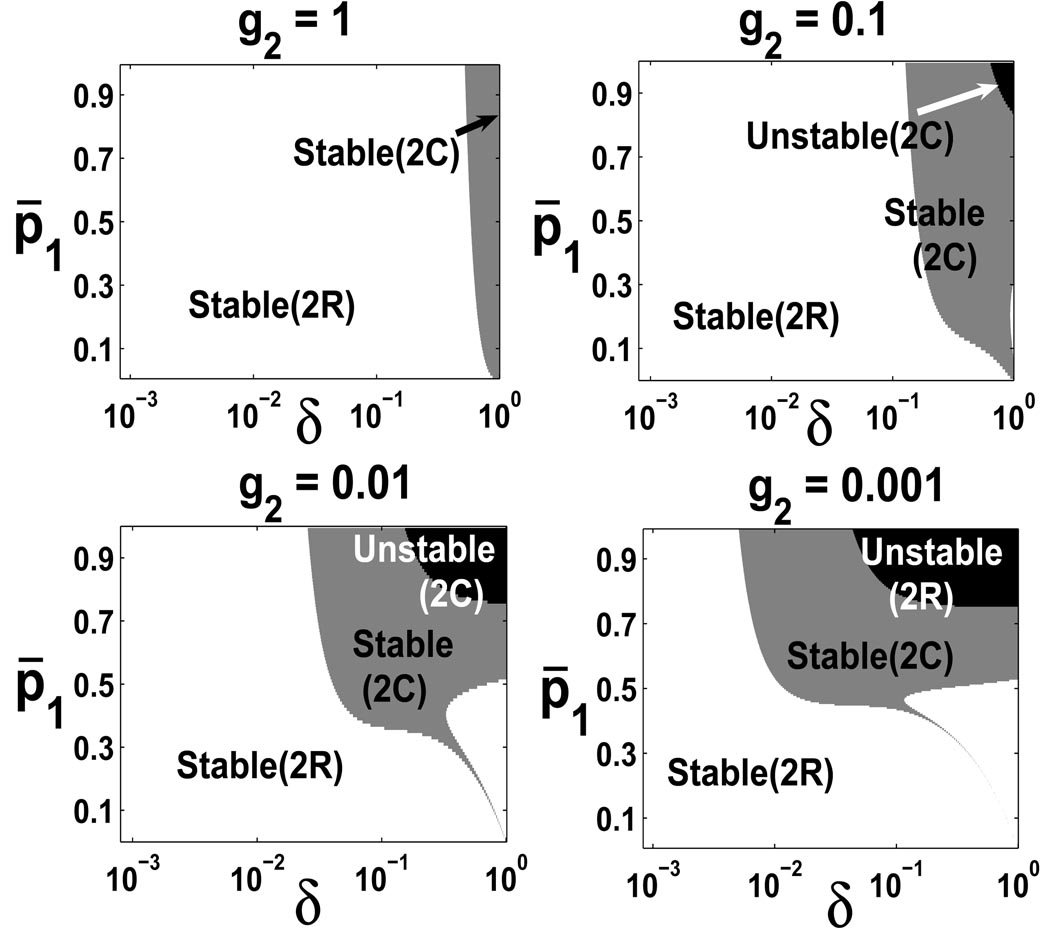
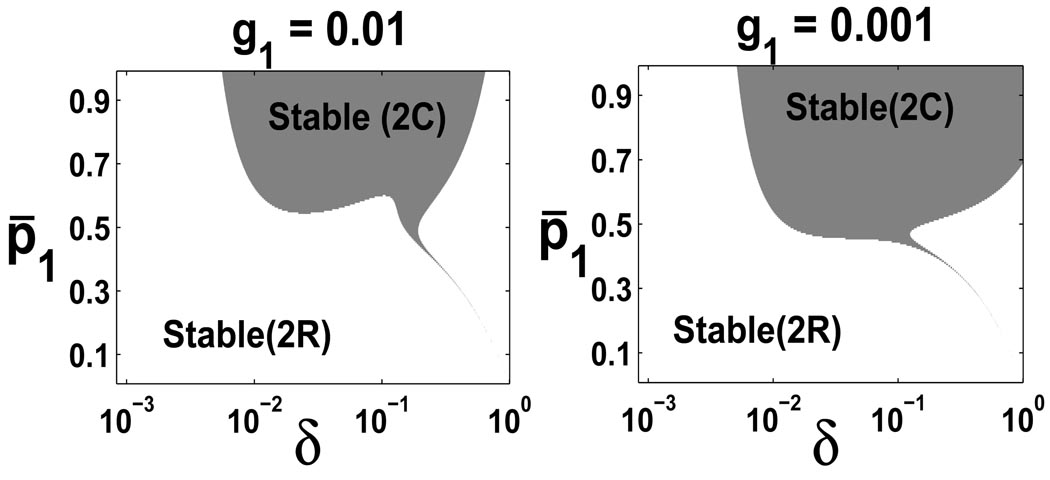
Figure 4 plots the stability regions for p̄₁ and δ at four different g₂, a parameter measuring the feedback coefficient of the TD cells and thus the gain of the feedback. The area of unstable region increases as g₂ decreases, as shown in Figure 4. A low death rate for the TD cells leads to stability of the steady state without any oscillations. A high death rate for the TD cells requires a low maximal proliferation probability p̄₁ to guarantee a stable steady state without oscillations (because the perturbed solutions away from the steady state converge to the steady state in the Stable (2C) region with oscillations). When both the death rate of TD cells and the proliferation probability of TA cells are high, the steady state becomes unstable. This instability can be removed when a negative feedback from TA cells to its own proliferation probability is included (see Figure 5). This suggests both negative feedbacks help improve the stability of the steady state.

FIGURE 4.

Stability regions at four different g₂ with ζ = 1, g₁ = 0, n = 3 and ${\chi }_0^{*}=1$. The Jocobian J(χ*) has two negative real eigenvalues in Stable(2R) region, two complex eigenvalues with negative real parts in Stable(2C), and two complex eigenvalues with positive real parts in Unstable(2C).

FIGURE 5.

Stability regions at different g₁ with ζ = 1, g₂ = 0.001, m = 1, n = 3 and ${\chi }_0^{*}=1$.

Finally, a limit cycle exists when the steady state is unstable for the systems in Figure 4 and Figure 5. This can be proved by Poincaré-Bendixson Theorem [27] using the fact that the real parts of the two eigenvalues of the Jacobian matrix at the unique steady state have the same sign. The detailed proof is not presented here.

3.3. Global stability analysis

Local stability analysis studies the behavior of a system when the solution is a small perturbation away from a steady state. For an arbitrary perturbation of the steady state solution, a global stability analysis [35] is needed. The following theorem gives a condition on p₁(χ₁, χ₂) for the global stability of a positive steady state of system (7)–(8).

Theorem 3.1

Suppose system (7)–(8) has a unique positive steady state. If p₁ satisfies

$$\begin{array}{c}[1-p_1({\chi }_1,{\chi }_2)]({\chi }_0^{*}+\delta {\chi }_1)-{\chi }_1{p}_{1{\chi }_1}({\chi }_1,{\chi }_2)({\chi }_0^{*}+\frac{{\chi }_1}{\zeta })\hfill \\ \hfill +\delta {\chi }_1{\chi }_2{p}_{1{\chi }_2}({\chi }_1,{\chi }_2)>0\end{array}$$ (22)

for all non-negative (χ₁, χ₂), the steady state is globally stable.

The proof of the theorem is a direct application of Poincaré-Bendixson Theorem [27] and it is sketched as follows with details presented in Appendix A.1.

1. If the system satisfies (22), there are no limit cycles in the non-negative region {(χ₁, χ₂)|χ₁ ≥ 0, χ₂ > 0}.

2. A solution starting in the non-negative region {(χ₁, χ₂)|χ₁ ≥ 0, χ₂ ≥ 0} stays non-negative and remains bounded at all time.

3. If the system satisfies (22), the steady state solution is locally stable.

4. Using the Poincaré-Bendixson Theorem and the above three statements, one can prove the global stability of the steady state.

Based on the theorem, a simpler condition for the global stability can be obtained:

Corollary 1

If p₁ satisfies

$$1-p_1+{\chi }_2{p}_{1{\chi }_2}>0,$$ (23)

then it satisfies the condition (22). By Theorem 3.1, the positive steady state is globally stable.

Because the stability analysis is on the long-time asymptotic behavior of the solution, Theorem 3.1 and Corollary 1 remain true if the two variables χ₁, χ₂ are replaced by lim inf_t→∞ χ₁(t) and lim inf_t→∞ χ₂(t).

3.3.1. Low death rate of TD cells leads to global stability

It can be shown that the steady state is globally stable if

$${\overline{p}}_1<\text{max}\left\{\frac{4n}{{(n+1)}^2},1-\frac{\sqrt[n]{n-1}\delta }{2g_2{\chi }_0^{*}}\right\}.$$ (24)

The proof is presented in the Appendix A.2.

One immediate result from (24) is that when n = 1 the steady state is always globally stable regardless of choice of other parameters.

When n > 1, one possibility of increasing the stability region for p̄₁ is decreasing the death rate δ. Another possibility is to increase the inhibition strength g₂, that is, to increase the level of the negative feedback from the TD cells to the proliferation probability of the TA cells. Both results are consistent with the linear stability analysis shown in Figure 4 and Figure 5. For the OE system, the δ is usually very small [26], and this fact is consistent with the mathematical strategy to enhance the stability region.

To better analyze (24), one may use a more strict yet simpler inequality to replace (24):

$${\overline{p}}_1<\frac{4n}{{(n+1)}^2},$$ (25)

which says p̄₁ is bounded by a decreasing function of the Hill exponent for the negative feedback from the TD cells on proliferation probability of TA cell. For example, n = 2 implies p̄₁ < 2/(1.5)² = 8/9 for existence of a globally stable steady state while n = 3 implies p̄₁ < 3/2² = 0.75, a more restricted condition than the case for n = 2.

4. Full model with stem, TA and TD cells

For the full system (4)–(6) with stem cells, TA cells and TD cells, there exist at most three types of steady state solutions for a fixed set of parameters:

$$\begin{array}{ccc}(0,0,0)(\mathrm{S}1),& (0,{\chi }_1^{*},{\chi }_2^{*})(\mathrm{S}2),& ({\chi }_0^{*},{\chi }_1^{*},{\chi }_2^{*})(\mathrm{S}3)\end{array}$$

where ${\chi }_i^{*}$ (i = 0, 1, 2) is positive. We use S1, S2 and S3 to represent each type of steady state, respectively. By direct examination of the the full system (4)–(6), it is easy to show that the five other types of solutions, such as $(0,{\chi }_1^{*},0)$, cannot be the steady state of (4)–(6).

In the rest of the section, we first discuss each type of steady state, without specifying any functional form for the negative feedback, and present the conditions for the existence and stability for that type of steady state. Then, by using Hill functions for the feedback with Hill exponent taken to be one, we are able to classify four different parameter regimes based on the maximal proliferation probabilities of the stem and TA cells to identify all steady states in each parameter regime, and provide stability properties for some of the steady states. Finally, we present a linear stability analysis for the steady state S3.

4.1. Three types of steady state

• S1 steady state

  It is easy to see from the system (4)–(6) that S1, a case with zero population for each cell type, is always a steady state for any parameters. The interesting question is on its stability. Because the eigenvalues of the Jacobian at S1 are

  $$-1+2p_0(0,0,0),\frac{-1+2p_1(0,0)}{\zeta },-\delta ,$$ (26)

  S1 is locally stable if and only if p₀(0, 0, 0) < 0.5 and p₁(0, 0) < 0.5. This shows that given small populations of each cell type, the populations will decrease and vanish eventually if the proliferation probabilities of stem cells and TA cells are both lower than their differentiating rates.

  Regarding global stability, S1 is a global attractor if p₀(χ₀, χ₁, χ₂), p₁(χ₁, χ₂) < 0.5 for all (χ₀, χ₁, χ₂), because the right-hand side of equation (4)–(6) will eventually become negative under this condition. Since we assume that p_i are decreasing functions, the condition of global stability is equivalent to that of local stability, namely, p₀(0, 0, 0) < 0.5 and p₁(0, 0) < 0.5. This suggests that in order to avoid the S1 steady state, the proliferation probability for either the stem cells or the TA cells must be larger than its corresponding differentiation probability at some time during the evolution.

• S2 steady state

  In the S2 steady state, there are no stem cells and the cell populations are maintained by the proliferation and differentiation of TA cells. At S2, the proliferation probability of TA cells has to be the same as the differentiation probability as seen from the equation (4)–(6). Mathematically, the existence of S2 thus depends on whether p₁ can achieve 0.5 at some nonzero TA and TD populations. Because p₁ is assumed as a non-increasing function, a necessary condition for existence of S2 is that the maximal proliferation probability

  $$p_1(0,0)\ge 0.5$$ (27)

  and the feedback is strong enough such that p₁(χ₁, χ₂) ≤ 0.5 at some (χ₁, χ₂). If p₁ is assumed to be a strictly decreasing function in either χ₁ or χ₂, then there exist a unique S2.
  The eigenvalues of the Jacobian matrix at S2 are $-1+2p_0(0,{\chi }_1^{*},{\chi }_2^{*})$ and the two roots of the quadratic equation

  $$\begin{array}{c}{\mathrm{\lambda }}^2-\left(\frac{2p_{1{\mathrm{\chi }}_1}^{*}{\mathrm{\chi }}_1^{*}}{\zeta }-\delta -\frac{2p_{1{\mathrm{\chi }}_2}^{*}{\mathrm{\chi }}_1^{*}}{\zeta }\right)\mathrm{\lambda }\\ +\frac{2p_{1{\mathrm{\chi }}_1}^{*}{\mathrm{\chi }}_1^{*}}{\zeta }\left(-\delta -\frac{2p_{1{\mathrm{\chi }}_2}^{*}{\mathrm{\chi }}_1^{*}}{\zeta }\right)-\frac{2p_{1{\mathrm{\chi }}_2}^{*}{\mathrm{\chi }}_1^{*}}{{\zeta }^2}(1-2p_{1{\mathrm{\chi }}_1}^{*}{\mathrm{\chi }}_1^{*})=0.\end{array}$$

  So S2 is locally stable if

  $$\begin{array}{ccc}{p}_0(0,{\mathrm{\chi }}_1^{*},{\mathrm{\chi }}_2^{*})<0.5& \text{and}\hfill & -\delta -\frac{2p_{1{\mathrm{\chi }}_2}^{*}{\mathrm{\chi }}_1^{*}}{\zeta }<0.\hfill \end{array}$$ (28)

  These conditions may be achieved by allowing a longer cell cycle for TA cells than stem cells along with a low stem cell proliferation probability.

• S3 steady state

  By first adding the steady state equations of system (4)–(6), one obtains

  $${\chi }_0=-\frac{{\chi }_1}{\zeta }+\delta {\chi }_2.$$ (29)

  Substituting (29) into the first two equations of (4)–(6), one obtains

  $$p_0(\delta {\chi }_2-\frac{{\chi }_1}{\zeta },{\chi }_1,{\chi }_2)=1/2,$$ (30)

  $$\frac{2{\chi }_1}{\zeta }(1-p_1({\chi }_1,{\chi }_2))=\delta {\chi }_2.$$ (31)

  The number of S3 steady states is determined by the number of roots of system (30)–(31). From the discussion of S1, S3 exists only if the proliferation probability of stem cells is larger than its differentiation probability at some time. One of the necessary condition for existence of S3 is

  $$p_0(0,0,0)\ge 0.5.$$ (32)

4.2. Parameter regimes for existence of the three types of steady states

In order to derive more specific conditions for existence and stability of the three steady states, we use the following Hill functions for the proliferative feedback:

$$p_0({\chi }_0,{\chi }_1,{\chi }_2)=\frac{{\overline{p}}_0}{1+k_0{\chi }_0+k_1{\chi }_1+k_2{\chi }_2},$$ (33)

$$p_1({\chi }_1,{\chi }_2)=\frac{{\overline{p}}_1}{1+g_1{\chi }_1+g_2{\chi }_2},$$ (34)

where k_i (i = 0, 1, 2) ≥ 0 and g_i (i = 1, 2) ≥ 0 with at least one of them being positive, and 0 < p̄₀, p̄₁ < 1 are constants. Based on the values of p̄₀ and p̄₁, we classify the system into four regimes with results summarized in Table 1.

• p̄₀ ≤ 0.5 and p̄₁ ≤ 0.5: S1 is globally stable and there is no other non-negative steady state.

  Because the sign of the right-hand side of equation (4)–(5) becomes negative as t → ∞ under this condition, χ₀, χ₁ tend to zero. Consequently, so is χ₂ by (6). Because of (27) and (32), both S2 and S3 cannot be the steady states. This implies that S1 is a unique and globally stable steady state of the system.

• p̄₀ ≤ 0.5 and p̄₁ > 0.5: S1 is unstable and there exists a unique globally stable S2 but no other non-negative steady state.

  S1 is locally unstable by using (26). There exists a unique S2 steady state given by

  $$\left(0,\frac{\delta \zeta (2{\overline{p}}_1-1)}{g_2+g_1\delta \zeta },\frac{2{\overline{p}}_1-1}{g_2+g_1\delta \zeta }\right).$$ (35)

  The eigenvalues of the Jacobian at this S2 steady state can be easily shown to be negative using a similar discussion as in Section 3.2. So S2 is locally stable. This steady state can further be proved globally stable for any initial conditions (χ₀, χ₁, χ₂) when χ₀ > 0 or χ₁ > 0, using a proof similar to that in Section 3.3. In addition, it can be shown that for an initial condition (0, 0, χ₂), the solution converges to S1, meaning that if there are only TD cells which cannot proliferate and only undergo death, the whole population will vanish eventually.

• p̄₀ > 0.5 and p̄₁ ≤ 0.5: S1 is unstable and there exists a unique S3 but no other non-negative steady state.

  S1 is locally unstable by linear stability analysis, but it is stable if the initial condition is of the form (0, 0, χ₂), as explained in the first case. With 2p̄₁ ≤ 1, there exists no non-negative S2. The existence of a unique steady state S3 is proved in Appendix A.4. The stability of S3 is discussed in subsection 4.3.

• p̄₀ > 0.5 and p̄₁ > 0.5: S1 is unstable and either there exist a unique stable S2 and no other non-negative steady state, or a unique unstable S2 and a unique S3 if

  $$\frac{2{\overline{p}}_0-1}{k_1\delta \zeta +k_2}>\frac{2{\overline{p}}_1-1}{g_1\delta \zeta +g_2}.$$ (36)
  Similar to the previous cases, S1 is locally unstable because p̄₀ > 0.5, but it is stable with initial conditions (0, 0, χ₂). If (36) holds, there is a unique, unstable S2 and a unique S3. On the other hand, if

  $$\frac{2{\overline{p}}_0-1}{k_1\delta \zeta +k_2}<\frac{2{\overline{p}}_1-1}{g_1\delta \zeta +g_2},$$ (37)

  then S2 is locally stable, and steady state S3 does not exist. The proof is given in Appendix A.4. When the left-hand side of (36) equals the right-hand side, S3 does not exist, and in our numerical simulations, S2 is found to be stable. On the $\delta -{\chi }_0^{*}$ plane, a bifurcation takes place when the inequality in (36) becomes equality, as shown in Figure 6 with two sets of parameters.

TABLE 1.

Existence and stability of S1, S2 and S3. The feedbacks are Hill functions with exponent one.

	S1	S2	S3
p̄0 ≤ 0.5,p̄1 ≤ 0.5	Globally stable	Does not exist	Does not exist
p̄0 ≤ 0.5,p̄1 > 0.5	Locally unstable If χ(0) = (0, 0, χ2), then χ(t) → (0, 0, 0) as t → ∞	Locally stable If χ(0) = (χ0, χ1, χ2) when χ0 ≠ 0 or χ1 ≠ 0, then $\chi (t)\to (0,{\chi }_1^{**},{\chi }_2^{**})$ as t → ∞	Does not exist
p̄0 > 0.5,p̄1 ≤ 0.5	Locally unstable If χ(0) = (0, 0, χ2), then χ(t) → (0, 0, 0) as t → ∞	Does not exist	Exists Stability – Section 4.3
p̄0 > 0.5,p̄1 > 0.5 if (36) is not true	Locally unstable If χ(0) = (0, 0, χ2), then χ(t) → (0, 0, 0) as t → ∞	Locally stable If χ(0) = (0, χ1, χ2) when χ1 ≠ 0, then $\chi (t)\to (0,{\chi }_1^{**},{\chi }_2^{**})$ as t → ∞	Does not exist
p̄0 > 0.5,p̄1 > 0.5 if (36) is true	Locally unstable If χ(0) = (0, 0, χ2), then χ(t) → (0, 0, 0) as t → ∞	Locally unstable If χ(0) = (0, χ1, χ2) when χ1 ≠ 0, then $\chi (t)\to (0,{\chi }_1^{**},{\chi }_2^{**})$ as t → ∞	Exists Stability – Section 4.3

FIGURE 6.

A bifurcation diagram for δ. (a) g₁ = 1.5, g₂ = 1, k₀ = 1, k₂ = 1.02; (b) g₁ = 1, g₂ = 1.02, k₀ = 1, k₁ = 1.5, k₂ = 1.

4.3. Stability conditions for the S3 steady state

When a unique S3 steady state ${\chi }^{*}=({\chi }_0^{*},{\chi }_1^{*},{\chi }_2^{*})$ exists, we consider the cubic characteristic polynomial of the Jacobian at S3,

$$\begin{array}{ll}\hfill & C(\mathrm{\lambda })\hfill \\ =\hfill & (2p_{0{\chi }_0}^{*}{\chi }_0^{*}-\mathrm{\lambda })\{-2p_{0{\chi }_1}^{*}{\chi }_0^{*}+\frac{2p_{1{\chi }_1}^{*}}{\zeta }{\chi }_1^{*}+\frac{2p_1^{*}-1}{\zeta }-\mathrm{\lambda }\}(-\delta -\frac{2}{\zeta }{p}_{1{\chi }_2}^{*}{\chi }_1^{*}-\mathrm{\lambda })\hfill \\ \hfill & +\mathrm{\lambda }\left\{(-2p_{0{\chi }_2}^{*}{\chi }_0^{*}+\frac{2p_{1{\chi }_2}^{*}}{\zeta }{\chi }_1^{*})(\frac{2}{\zeta }[(1-p_1^{*})-p_{1{\chi }_1}^{*}{\chi }_1^{*}])+2p_{0{\chi }_1}^{*}{\chi }_0^{*}(1-2p_{0{\chi }_0}^{*}{\chi }_0^{*})\right\}\hfill \\ \hfill & -\left(2p_{0{\chi }_0}^{*}{\chi }_0^{*}\frac{2p_{1{\chi }_2}^{*}}{\zeta }{\chi }_1^{*}-2p_{0{\chi }_2}^{*}{\chi }_0^{*}\right)\left(\frac{2}{\zeta }[(1-p_1^{*})-p_{1{\chi }_1}^{*}{\chi }_1^{*}]\right)\hfill \\ \hfill & -2p_{0{\chi }_1}^{*}{\chi }_0^{*}(1-2p_{0{\chi }_0}^{*}{\chi }_0^{*})(-\delta -\frac{2}{\zeta }{p}_{1{\chi }_2}^{*}{\chi }_1^{*}).\hfill \end{array}$$ (38)

where $p_{i{\chi }_j}^{*}=p_{i{\chi }_j}({\chi }^{*})$. Let λ₁, λ₂, λ₃ be the three roots of C(λ), the S3 steady state χ* is locally asymptotically stable if and only if

$$\begin{array}{ccc}{\mathrm{\lambda }}_1+{\mathrm{\lambda }}_2+{\mathrm{\lambda }}_3& <\hfill & 0,\hfill \end{array}$$ (39)

$$\begin{array}{ccc}{\mathrm{\lambda }}_1{\mathrm{\lambda }}_2{\mathrm{\lambda }}_3& <\hfill & 0,\hfill \end{array}$$ (40)

$$\begin{array}{ccc}C({\mathrm{\lambda }}_1+{\mathrm{\lambda }}_2+{\mathrm{\lambda }}_3)& >\hfill & 0.\hfill \end{array}$$ (41)

These conditions are equivalent to that λ₁, λ₂ and λ₃ are all negative, and its proof is shown in the appendix A.5. From the property of the cubic polynomial C(λ), one can easily obtain:

$$\begin{array}{ll}{\mathrm{\lambda }}_1+{\mathrm{\lambda }}_2+{\mathrm{\lambda }}_3=\hfill & 2p_{0{\chi }_0}^{*}{\chi }_0^{*}-2p_{0{\chi }_1}^{*}{\chi }_0^{*}+\frac{2p_{1{\chi }_1}^{*}}{\zeta }{\chi }_1^{*}-\frac{2p_{1{\chi }_2}^{*}}{\zeta }{\chi }_1^{*}+\frac{2p_1^{*}-1}{\zeta }-\delta \hfill \\ \hfill {\mathrm{\lambda }}_1{\mathrm{\lambda }}_2{\mathrm{\lambda }}_3=& 2p_{0{\chi }_1}^{*}{\chi }_0^{*}\left(\delta +\frac{2p_{1{\chi }_2}^{*}}{\zeta }{\chi }_1^{*}\right).+2p_{0{\chi }_2}^{*}{\chi }_0^{*}(\frac{2}{\zeta }(1-p_1^{*})-\frac{2p_{1{\chi }_1}^{*}}{\zeta }{\chi }_1^{*})\hfill \\ \hfill & +2p_{0{\chi }_0}^{*}{\chi }_0^{*}\left(\frac{1-2p_1^{*}}{\zeta }\delta -\delta \frac{2p_{1{\chi }_1}^{*}}{\zeta }{\chi }_1^{*}-\frac{1}{\zeta }(\frac{2p_{1{\chi }_2}^{*}}{\zeta }{\chi }_1^{*})\right).\hfill \end{array}$$

So (39)–(41) give a set of conditions on the parameters for the local stability of χ*. For more specific results, we consider several Hill feedback forms with the corresponding stability results described below and summarized in Table 2.

• p₀(χ₂) is a Hill function and p₁ is a constant less than 0.5

  The proliferation probability of stem cells is assumed in terms of Hill function:

  $$p_0({\chi }_2)=\frac{{\overline{p}}_0}{1+{(k_2{\chi }_2)}^n},$$ (42)

  with p̄₀ > 0.5 and k₂ > 0.
  This function and parameters satisfy the conditions (39) and (40), and the condition (41) is equivalent to

  $${\overline{p}}_0<\frac{1}{2}\left(\frac{1+\delta +\frac{1-2p_1}{\zeta }}{1+\left(1-\frac{1}{n}\right)\left(\delta +\frac{1-2p_1}{\zeta }\right)}\right).$$ (43)

  When n = 1, $\delta +\frac{1-2p_1}{\zeta }\ge 1$ implies that the steady state is locally stable for any p̄₀. In general, the range of p̄₀ which allows local stability increases as $\delta +\frac{1-2p_1}{\zeta }$ increases, that is, if the cell cycle of the TA cell is shorter than that of the stem cell, or the death rate of TD cells is larger, the S3 steady state is stable for a larger range of proliferation probabilities.

• p₀(χ₁, χ₂) is a Hill function with exponent one, and p₁ is a constant less than 0.5

  The proliferation probability of stem cells is assumed as

  $$p_0({\chi }_1,{\chi }_2):=\frac{{\overline{p}}_0}{1+k_1{\chi }_1+k_2{\chi }_2},$$ (44)

  with p̄₀ > 0.5 and k₁ > 0.
  The function and parameters satisfy the conditions (39) and (40), and by (41), we derive a sufficient condition for the local stability:

  $$\delta +\frac{1-2p_1}{\zeta }\ge 1,$$ (45)

  which is similar to the first example where p₀ only depends on χ₂. Also, if the condition (45) is not satisfied, S3 can be stable if

  $$\frac{k_2}{k_1}<\frac{\delta (1-2p_1+2\delta \zeta )}{4(1-\delta -\frac{1-2p_1}{\zeta })(1-p_1)}.$$ (46)

  Therefore, if ζ is small (the cell cycle of the TA cell is much shorter than that of the stem cell) or $\frac{k_2}{k_1}$ is small (the feedback strength from TA cells is much stronger than that from TD cells), S3 is locally stable.

• p₀(χ₀, χ₁) and p₁(χ₁, χ₂) are both Hill functions

  The two proliferation probabilities p₀ and p₁ are assumed to be

  $$p_0({\chi }_0,{\chi }_1):=\frac{{\overline{p}}_0}{1+{(k_0{\chi }_0)}^r+{(k_1{\chi }_1)}^s},p_1({\chi }_1,{\chi }_2):=\frac{{\overline{p}}_1}{1+{(g_1{\chi }_1)}^m+{(g_2{\chi }_2)}^n},$$

  with s = 1 or 2, n = 1 or 2, k_i (i = 0, 1) ≥ 0, g_j (j = 1, 2) ≥ 0 and one of them being positive.
  Assume a unique S3 exists, using a similar proof in Section 3.2, we obtain

  $$-\delta -\frac{2p_{1{\chi }_2}^{*}{\chi }_1^{*}}{\zeta }<0\text{\hspace{1em}and\hspace{1em}}\frac{-1+2p_1^{*}}{\zeta }-2p_{0{\chi }_1}^{*}{\chi }_0^{*}<0.$$ (47)

  Consequently, the conditions (39)–(41) hold for any parameters, and the unique S3 is locally stable unconditionally.

TABLE 2.

Local stability at S3 for three different feedbacks.

Examples	p0(χ0, χ1, χ2)	p1(χ1, χ2)	Stability of $({\chi }_0^{*},{\chi }_1^{*},{\chi }_2^{*},{\chi }_1^{*},{\chi }_2^{*})$
1.	$p_0({\chi }_2):=\frac{{\overline{p}}_0}{1+{(k_2{\chi }_2)}^n}$	p1 = p̄1 constant less than 0.5	(43) is true ⇔ Locally Stable
2.	$p_0({\chi }_1,{\chi }_2):=\frac{{\overline{p}}_0}{1+k_1{\chi }_1+k_2{\chi }_2}$	p1 = p̄1 constant less than 0.5	(45) or (46) is true ⇒ Locally Stable
3.	$p_0({\chi }_0,{\chi }_1):=\frac{{\overline{p}}_0}{1+{(k_0{\chi }_0)}^r+{(k_1{\chi }_1)}^s}$ with s = 1 or 2	$p_1({\chi }_1,{\chi }_2):=\frac{{\overline{p}}_1}{1+{(g_1{\chi }_1)}^m+{(g_2{\chi }_2)}^n}$ with n = 1 or 2	Locally Stable (unconditionally)

5. Conclusion and discussion

In this paper, mathematical models for the Olfactory Epithelium (OE) lineage were developed and analyzed. Three different types of cells – stem cell, transit amplifying (TA) cell, and terminally differentiated (TD) cell, were considered, and the dynamic modulation of proliferation by secreted signaling molecules (such as GDF11 or ActivinβB) was modeled as negative feedback between lineage stages. For a simplified system with a constant stem cell population size, the conditions for the existence, uniqueness, local and global stability of the steady state were derived for negative feedback represented in terms of both general decreasing functions and Hill functions. It was found that a unique positive steady state exists, and both self-regulation of the proliferation of TA cells, and a low death rate of TD cells, can enhance global stability of the steady state. This might explain in the OE system why GDF11, which is secreted by TA and TD cells, inhibits the proliferation of TA cells. For the full system in which all three cell populations can vary in time, conditions on existence and linear stability of three possible steady states were obtained for feedback represented by Hill functions. It was found that self-regulation of the proliferation of stem cells and TA cells can enhance local stability. In addition, having the cell cycle lengths of stem cells be larger than those of TA cells also makes the local stability region larger.

The model developed in this study can be used as a generic model of cell lineages in which three sequential lineage stages cells coupled through negative feedback. Our analysis of the steady states and their stability in such a system could improve understanding of interactions and regulation among different cell types, and the dynamics and stability of different cell populations, and lead to new experimental approaches.

In OE, as in other epithelial tissues such as the epidermis and the colonic mucosa, cells at different lineage stages are usually stratified along basal-apical axis, leading to the expectation that the distributions of feedback signaling molecules (e.g. GDF11) will also be non-uniform [18]. In the future, it will also be important to incorporate spatial inhomogeneity and spatial dynamics into models such as the ones described here. Although numerical simulation will likely be the most appropriate tool for exploring such models, the analytical results derived in this paper will provide insights into the choice of parameters, and can serve as a guide for systematic computational exploration.

APPENDIX

A.1. Proof of Theorem 3.1

Proof. The proof consists of three steps:

1. If the system satisfies (22), there is no limit cycle in the non-negative region {(χ₁, χ₂)|χ₁ ≥ 0, χ₂ ≥ 0}.

   Define a function

   $$N({\chi }_1,{\chi }_2):=\frac{1}{{\chi }_1(1-p_1({\chi }_1,{\chi }_2))}$$ (48)

   and f⃗(χ₁, χ₂) to be the right-hand side of the system (7)–(8), namely,

   $$\overrightarrow{f}({\chi }_1,{\chi }_2)=({\chi }_0^{*}+\frac{{\chi }_1}{\zeta }(-1+2p_1({\chi }_1,{\chi }_2)),-\delta {\chi }_2+\frac{2{\chi }_1}{\zeta }(1-p_1({\chi }_1,{\chi }_2))).$$
   One can verify that

   $$\nabla \cdot [N({\chi }_1,{\chi }_2)\overrightarrow{f}({\chi }_1,{\chi }_2)]<0\iff$$ (49)

   $$(1-p_1({\chi }_1,{\chi }_2))({\chi }_0^{*}+\delta {\chi }_1)-{\chi }_1{p}_{1{\chi }_1}({\chi }_1,{\chi }_2)({\chi }_0^{*}+\frac{{\chi }_1}{\zeta })+\delta {\chi }_1{\chi }_2{p}_{1{\chi }_2}({\chi }_1,{\chi }_2)>0.$$

   By Dulac’s Criteria [27], there is no limit cycle in {(χ₁, χ₂)|χ₁ ≥ 0, χ₂ ≥ 0} if (22) holds.

2. All the solutions which have non-negative initial conditions will he non-negative and bounded.

   Assuming non-negative initial conditions, we consider four cases to exhaust all the possible behaviors of the trajectories.

   1. If χ₁ (t) = 0 and χ₂(t) > 0 for some time t, then $\frac{d{\chi }_1(t)}{\mathit{\text{dt}}}>0$ and $\frac{d{\chi }_2(t)}{\mathit{\text{dt}}}<0$; if χ₁(t) = 0 and χ₂(t) = 0, then $\frac{d{\chi }_2(t)}{dt}=0$ and $\frac{d{\chi }_1(t)}{dt}>0$, so the trajectories do not cross the χ₂-axis.
   2. If χ₂(t) = 0 and χ₁(t) > 0 for some time t, then $\frac{d{\chi }_2(t)}{dt}>0$; if χ₂(t) = 0 and χ₁(t) = 0, then $\frac{d{\chi }_2(t)}{dt}=0$ and $\frac{d{\chi }_1(t)}{dt}>0$, so the trajectories do not cross the χ₁-axis.
   3. If χ₁ ≫ 0, then χ₂ ≫ 0. Since (−1 + 2p₁(χ₁, χ₂)) goes to some negative constant as χ₁ and χ₂ are very large, $\frac{d{\chi }_1}{dt}$ goes to some negative constant and χ₁ will decrease. Consequently, with (a), χ₁ is bounded in non-negative region.
   4. If χ₂ ≫ 0, then $\frac{d{\chi }_2}{dt}$ goes to some negative constant because in (c) we showed that χ₁ is bounded. So χ₂ will decrease when χ₂ ≫ 0. With (b), χ₂ is bounded in non-negative region.

   The above proved that all the solutions with non-negative initial conditions will remain bounded in the non-negative region {(χ₁, χ₂)|χ₁ ≥ 0, χ₂ ≥ 0}.

3. If the system satisfies (22), then the steady state solution is locally stable. Since $({\chi }_1^{*},{\chi }_2^{*})$ is the steady state, the right-hand side $\overrightarrow{f}({\chi }_1^{*},{\chi }_2^{*})=0$ and we get

   $$[\nabla \cdot (N\overrightarrow{f})]({\chi }_1^{*},{\chi }_2^{*})=-N({\chi }_1^{*},{\chi }_2^{*})\left(\frac{1-2p_1}{\zeta }+\delta -\frac{2p_{1{\chi }_1}{\chi }_1^{*}}{\zeta }+\frac{2p_{1{\chi }_2}{\chi }_1^{*}}{\zeta }\right).$$
   If (22) holds, then

   $$-N({\chi }_1^{*},{\chi }_2^{*})\left(\frac{1-2p_1}{\zeta }+\delta -\frac{2p_{1{\chi }_1}{\chi }_1^{*}}{\zeta }+\frac{2p_{1{\chi }_2}{\chi }_1^{*}}{\zeta }\right)<0.$$ (50)

   By $N({\chi }_1^{*}{\chi }_2^{*})>0$ and (18), the steady state is locally stable.

Combining these three results and using Poincaré-Bendixson Theorem, we proved that the steady state is globally stable in {(χ₁, χ₂)|χ₁ ≥ 0, χ₂ ≥ 0} if the system satisfies (22).

A.2. Prove that (24) implies global stability of system (7)–(8)

Proof. Substitute p₁ as given by (14) into the left-hand side of (23) and get

$$\begin{array}{ll}\hfill & 1-\frac{{\overline{p}}_1}{1+{(g_1{\chi }_1)}^m+{(g_2{\chi }_2)}^n}-\frac{{\overline{p}}_1{(g_2{\chi }_2)}^n}{{(1+{(g_1{\chi }_1)}^m+{(g_2{\chi }_2)}^n)}^2}\hfill \\ =\hfill & \frac{{(1+{(g_1{\chi }_1)}^m+{(g_2{\chi }_2)}^n)}^2-{\overline{p}}_1(1+{(g_1{\chi }_1)}^m+{(g_2{\chi }_2)}^n)-n{\overline{p}}_1{(g_2{\chi }_2)}^n}{{(1+{(g_1{\chi }_1)}^m+{(g_2{\chi }_2)}^n)}^2}\hfill \\ \ge \hfill & \frac{{(1+{(g_2{\chi }_2)}^n)}^2-{\overline{p}}_1(1+{(g_2{\chi }_2)}^n)-n{\overline{p}}_1{(g_2{\chi }_2)}^n}{{(1+{(g_1{\chi }_1)}^m+{(g_2{\chi }_2)}^n)}^2}\hfill \end{array}$$

Inequality (23) will be satisfied if

$${(1+{(g_2{\chi }_2)}^n)}^2-{\overline{p}}_1(1+{(g_2{\chi }_2)}^n)-n{\overline{p}}_1{(g_2{\chi }_2)}^n>0.$$ (51)

The aim here is to find conditions for p̄₁ such that (51) holds for χ₂ > lim inf_t→∞ χ₂(t).

First, we can prove that the unique steady state is globally stable if (25) holds:

$${\overline{p}}_1<\frac{4n}{{(n+1)}^2}.$$ (52)

The condition (51) can be simplified by taking y = (g₂χ₂)ⁿ and considering the function

$$h(y)=(1+y-{\overline{p}}_1)(1+y)-n{\overline{p}}_{1}y,\text{for}y\ge 0,$$ (53)

which assumes the minimal value ${\overline{p}}_1(n-{\left(\frac{n+1}{2}\right)}^2{\overline{p}}_1)$ at $y_{\mathit{\text{min}}}=\frac{(n+1){\overline{p}}_1}{2}-1$. Thus, if (52) is true, then h(y) ≥ h(y_min) > 0 for any y ≥ 0, equivalent to (51), then the steady state is globally stable.

The upper bound in (52) can be relaxed due to the fact that only the asymptotic behavior of the solution is relevant to global stability, so (51) has to be true only when t is very large. Hence, it is not necessary to require h(y) > 0 for all y ≥ 0 in (53); instead, we only need to find a lower bound ỹ, associated with the asymptotic behavior of χ₂, with h(y) positive only for y ≥ ỹ. The derivation of the upper bound in (24) uses the following lemma to be proved in A.3:

Lemma A.1

Suppose x(t), F(t) and G(x(t)) are functions satisfying

$$x\prime (t)\ge F(t)-G(x),$$

and the following properties:

1. There is a unique solution x̃ of the equation G(x) = lim inf_t→∞ F(t);

2. G(x) is continuous and strictly increasing in (−∞, ∞).

   Then,

   $$\underset{t\to \infty }{\text{lim inf}}x(t)\ge \tilde{x}.$$ (54)

With this lemma and p₁ in Hill function form (14), we get by equation (7) and (8),

$$\frac{d{\chi }_1}{dt}\ge {\chi }_0^{*}-\frac{{\chi }_1}{\zeta }$$ (55)

$$\frac{d{\chi }_2}{dt}\ge \frac{2{\chi }_1}{\zeta }(1-{\overline{p}}_1)-\delta {\chi }_2$$ (56)

Take x(t) := χ₁(t), $F(t):={\chi }_0^{*}$ and $G(x):=\frac{{\chi }_1}{\zeta }$, it is easy to verify that (55) and the two properties in the hypotheses are satisfied, and hence by Lemma A.1

$$\underset{t\to \infty }{\text{lim inf}}{\chi }_1(t)\ge \zeta {\chi }_0^{*}.$$ (57)

Similarly we take x(t) := χ₂(t), $F(t):=\frac{2_{{\chi }_1}(t)}{\zeta }(1-{\overline{p}}_1)$ and G(χ₁) := δχ₂, and apply Lemma A.1 can be applied with (57) to get

$$\underset{t\to \infty }{\text{lim inf}}{\chi }_2(t)\ge \frac{2(1-{\overline{p}}_1){\chi }_0^{*}}{\delta }.$$ (58)

In (53), h(y) > 0 if y > n − 1, and by (58), the unique steady state is globally stable if

$${\left(g_2\frac{2(1-{\overline{p}}_1){\chi }_0^{*}}{\delta }\right)}^n>n-1.$$ (59)

Combining (52) and (59), we proved that the unique steady state is globally stable if (24) is true.

A.3. Proof of Lemma A.1

Proof. Suppose (54) is not true, that is,

$$\underset{t\to \infty }{\text{lim inf}}x(t)<\tilde{x},$$ (60)

we would like to prove Lemma A.1 by contradiction.

By (60), there exists x₀ such that

$$\underset{t\to \infty }{\text{lim inf}}x(t)<x_0<\tilde{x},$$ (61)

and hence for all t₀ > 0, there exists t₁ > t₀ such that x(t₁) < x₀.

By property (2), G(x(t₁)) < G(x₀) < G(x̃) and by the definition of x̃, we get

$$G(x(t_1))<G(x_0)<\underset{t\to \infty }{\text{lim inf}}F(t).$$ (62)

Therefore, there exists t₁ > t₀ such that

$$G(x(t_1))<G(x_0)<F(t)\text{for all}t>t_0.$$ (63)

Here we discuss two possible cases:

1. If there exists t₂ > t₀ such that x(t₂) > x₀, then by the same argument as above, there exists t₃ > t₂ such that

   $$G(x(t_3))<G(x_0)<F(t)\text{for all}t>t_2.$$ (64)

   By (64), x(t₃) < x₀ < x(t₂), and by the continuity of x, there must exist t₄ such that t₃ > t₄ > t₂ such that x(t₄) = x₀ and x′(t₄) ≤ 0. Since x′(t₄) ≥ F(t₄) − G(x(t₄)) = F(t₄) − G(x₀) > 0, contradicting x′(t₄) ≤ 0. So there is no t > t₀ such that x(t) > x₀.
2. If x(t) < x₀ for all t > t₀, then

   $$G(x(t))<G(x_0)<\underset{t\to \infty }{\text{lim inf}}F(t).$$ (65)

   There exists a constant C such that

   $$G(x(t))<G(x_0)<C<\underset{t\to \infty }{\text{lim inf}}F(t).$$ (66)

   so for large enough t₀, we have

   $$G(x(t))<G(x_0)<C<F(t)\text{for all}t>t_0.$$ (67)

   Therefore x′(t) ≥ F(t) − G(x(t)) > C − G(x₀) > 0, and after integration,

   $$x(t)-x(t_0)>(C-G(x_0))(t-t_0).$$ (68)

   If t is large enough, by (C − G(x₀)) > 0, x(t) will be greater than x₀. This is a contradiction to the assumption that x(t) < x₀ for all t > t₀.

With above, we have proved (54).

A.4. Condition for the existence of unique S3

1. When p̄₀ > 0.5 and p̄₁ ≤ 0.5, there always exists a unique S3 steady state.

   Proof. Using p₀ and p₁ in Hill form (33)–(34) and substituting into (30) and (31), we get steady states $({\chi }_0^{*},{\chi }_1^{*},{\chi }_2^{*})$, where

   $${\chi }_2^{*}=b{\chi }_1^{*}+a,{\chi }_0^{*}=\delta a+(b\delta -\frac{1}{\zeta }){\chi }_1^{*}$$ (69)

   and

   $$(2-b\delta \zeta )(g_1+b{g}_2){({\chi }_1^{*})}^2$$ (70)

   $$+[(1-b\zeta \delta )+(1-2{\overline{p}}_1)+(2-b\delta \zeta )a{g}_2-a\delta \zeta (g_1+b{g}_2)]{\chi }_1^{*}-a\delta \zeta (1+a{g}_2)=0,$$

   with a and b defined as

   $$a=\frac{2{\overline{p}}_0-1}{k_0\delta +k_2}\text{\hspace{1em}and\hspace{1em}}b=\frac{\frac{k_0}{\zeta }-k_1}{k_0\delta +k_2}.$$

   It is easy to verify that a > 0 and 1 − bδζ > 0. To get positive steady states, we require that ${\chi }_0^{*}>0$, which is equivalent to

   $${\chi }_1^{*}<\frac{a\delta \zeta }{1-b\delta \zeta }.$$ (71)

   Therefore, the number of S3 depends on the number of ${\chi }_1^{*}$ as roots of (70) satisfying (71). Let $Q({\chi }_1^{*})$ be the left-hand side of (70) and we consider the following three cases:

   • If g₁ + bg₂ > 0, then $\frac{-a\delta \zeta (1+a{g}_2)}{(2-b\delta \zeta )(g_1+b{g}_2)}<0$ and $Q({\chi }_1^{*})=0$ has only one positive root. Since $Q\left(\frac{a\delta \zeta }{1-b\delta \zeta }\right)>0$, (70) has only one positive root which satisfies the inequality (71).
   • If g₁ + bg₂ < 0, then $\frac{-a\delta \zeta (1+a{g}_2)}{(2-b\delta \zeta )(g_1+b{g}_2)}>0$, so $Q({\chi }_1^{*})=0$ has two roots with the same sign. Because $Q\left(\frac{a\delta \zeta }{1-b\delta \zeta }\right)>0$, there must be a root larger than the positive number $\frac{a\delta \zeta }{1-b\delta \zeta }$. Therefore, $Q({\chi }_1^{*})=0$ has only one positive root that satisfies the inequality (71).
   • If g₁ + bg₂ = 0, then $Q({\chi }_1^{*})=0$ has one positive root. By $Q\left(\frac{a\delta \zeta }{1-b\delta \zeta }\right)>0,Q\left({\chi }_1^{*}\right)=0$ has only one positive solution satisfying the inequality (71).

   The above shows that in any case, (70) only has one positive root satisfying (71), so there is a unique S3 steady state when p̄₀ > 0.5 and p̄₁ < 0.5.

2. When p̄₀ > 0.5 and p̄₁ > 0.5, there exists a unique S3 if and only if (36) is true.

   Proof. Following the notations in the first part, where p̄₀ > 0.5 and p̄₁ ≤ 0.5, we know from the analysis that there exist a unique S3 if and only if

   $$Q\left(\frac{a\delta \zeta }{1-b\delta \zeta }\right)>0.$$ (72)

   When p̄₁ > 0.5, (72) is equivalent to condition (36). Therefore, there is a unique S3 if and only if (36) holds.

3. S2 is locally unstable if (36) is true.

   Proof. One can easily verify that if (36) is ture, $p_0(0,{\chi }_1^{*},{\chi }_2^{*})>0.5$, resulting in a positive eigenvalue of the Jacobian at the S2 steady state $(0,{\chi }_1^{*},{\chi }_2^{*})$, so it is locally unstable.

   Moreover, if

   $$\frac{2{\overline{p}}_0-1}{k_1\delta \zeta +k_2}<\frac{2{\overline{p}}_1-1}{g_1\delta \zeta +g_2},$$ (73)

   by checking (28), one can show that S2 is unstable.

A.5. Proof of the conditions for locally stability of S3

Proof. Suppose χ* is locally asymptotically stable, which means that the three eigenvalues have negative real parts, possibly three real negative roots or one real root with two conjugate complex roots, so λ₁ + λ₂ + λ₃ < 0 and λ₁λ₂λ₃ < 0. Note that the characteristic polynomial C(λ) has a negative leading coefficient, and therefore lim_λ→−∞ C(λ) > 0 and lim_λ→∞ C(λ) < 0. Without loss of generality, assume λ₁ is the most negative real root, and by the fact that λ₂ and λ₃ has negative real parts, we have λ₁ + λ₂ + λ₃ < λ₁. With lim_λ→−∞ C(λ) > 0 and the assumption that λ₁ is the most negative real root, C(λ₁ + λ₂ + λ₃) > C(λ₁) = 0 when λ₁ + λ₂ + λ₃ < λ₁.

Conversely, if (39)–(41) is true, we would like to prove that χ* is locally stable. Suppose χ* is not locally stable, then at least one of the three eigenvalues has positive real part. Because C(0) = λ₁λ₂λ₃ < 0 and lim_λ→−∞ C(λ) > 0, we know that there is one negative real eigenvalue, assuming to be λ₁. By the assumption, λ₂ or λ₃ has positive real parts, but since λ₁ < 0, λ₂, λ₃ are either conjugates or both positive. Hence, λ₁ < λ₁ + λ₂ + λ₃ < 0. Because lim_λ→−∞ C(λ) > 0 and C has a unique negative root λ₁ and two other roots with positive real parts, C(λ) < 0 if λ₁ < λ < 0. Consequently, C(λ₁ + λ₂ + λ₃) < C(λ₁) = 0, contradicting (41). We conclude that (39)–(41) is a sufficient condition.