Abstract
Intracardiac echocardiography has proven to be useful for online anatomical imaging during catheterization. Our objective was to develop a speckle tracking method for myocardial motion estimation from intracardiac echocardiographic image sequences in order to provide a mean for regional functional imaging. Our approach was to solve two problems in motion estimation from two-dimensional intracardiac echocardiographic image sequences: non-rigid myocardial deformation and speckle decorrelation. To achieve robust noise resistance, we employed maximum likelihood estimation while fully exploiting ultrasound speckle statistics, and treated the maximization of motion probability as the minimization of an energy function. Non-rigid myocardial deformation was estimated by optimizing this energy function within a framework of parametric elastic registration. Evaluation of the method was carried out using a computer model that synthesized echocardiographic image sequences, and subsequently an animal model that provided continuous intracardiac echocardiographic images as well as reference measurements using sonomicrometry crystals. In conclusion, accurate estimation of regional myocardial deformation from intracardiac echocardiography by novel speckle tracking is feasible. This approach may have important clinical implications for multimodal imaging during catheterization.
Index Terms: Cardiac imaging, myocardial strain, elastic registration, non-rigid deformation, sonomicrometry
I. INTRODUCTION
Intracardiac echocardiography (ICE) has provided considerable advantages in guiding clinical electro-physiology procedures such as imaging anatomical structures, confirming electrode-tissue contact, monitoring ablation lesions, and providing hemodynamic assessment [1]–[4]. These capabilities have made ICE an attractive imaging modality to better understand complex rhythm disorders in relation to underlying anatomy and physiological outcome [5], [6]. Clinically, ICE is predominantly implemented on the basis of a catheter carrying at its distal end a rotating transducer that operates at a frequency of 9 MHz and provides two-dimensional (2-D) tomographic images of the heart’s interior, or a catheter with a phased transducer array operating at a lower ultrasound frequency for deeper penetration (5.5–10 MHz) and provides a 2-D sector view of the heart (80° −90° opening angle). Intracardiac echocardiography potentially affords capabilities for dynamic functional analysis by employing motion estimation techniques for extracting structural information from image sequences.
Tracking ultrasound speckling in transthoracic echocardiographic image sequences has been shown to be useful in assessing regional myocardial deformation and function [7]–[11]. In developing a similar scheme for estimating myocardial motion from 2-D ICE images by speckle tracking, two factors have to be considered and appropriately managed: non-rigid myocardial deformation and ultrasound speckle decorrelation. Myocardial motion is complex and includes various motion patterns. During systole, the myocardial wall thickens and the endocardium moves inward to eject blood, whereas during diastole the wall thins and the endocardium moves outward. Additional deformations include circumferential and longitudinal shortening of the myocardial muscle fibers. The varieties of myocardial motion suggest that a non-rigid motion model (deformable model) is necessary. Ideally, speckle patterns of moving tissue are temporally stable under the condition of small motion, and tissue motion can be estimated by relying on the speckle temporal constancy. In ICE images, however, such temporal constancy usually is not valid due to non-uniform myocardial motion and speckle decorrelation, which originates from catheter motion with respect to the myocardium. Gaussian noise-based estimation techniques (e.g., least square estimation) often encounter false matching when subjected to texture varied ICE images. Intuitively, ultrasound motion estimation can be better solved if an ultrasound statistical model is incorporated into the estimation. To resolve speckle decorrelation, we assume that the myocardium in two motion-related ICE images has the same echogenicity. This assumption allows the motion estimation to tolerate texture variation due to speckle decorrelation.
In this paper, we presented and validated a deformable speckle tracking approach for motion estimation in ICE images. The method incorporated statistical features of ultrasound images into a maximum likelihood motion analysis, and treated maximization of the similarity measure as energy minimization. Thus, within the framework of deformable registration, tissue motion was estimated via optimization of a speckle-featured energy function. The robustness of our algorithm was evaluated by studying speckle decorrelation on a series of simulated ultrasound image sequences. The accuracy of speckle tracking in predicting regional myocardial displacement was validated in animal experiments.
II. METHODS
A. Observations from Myocardial Motion in ICE Images
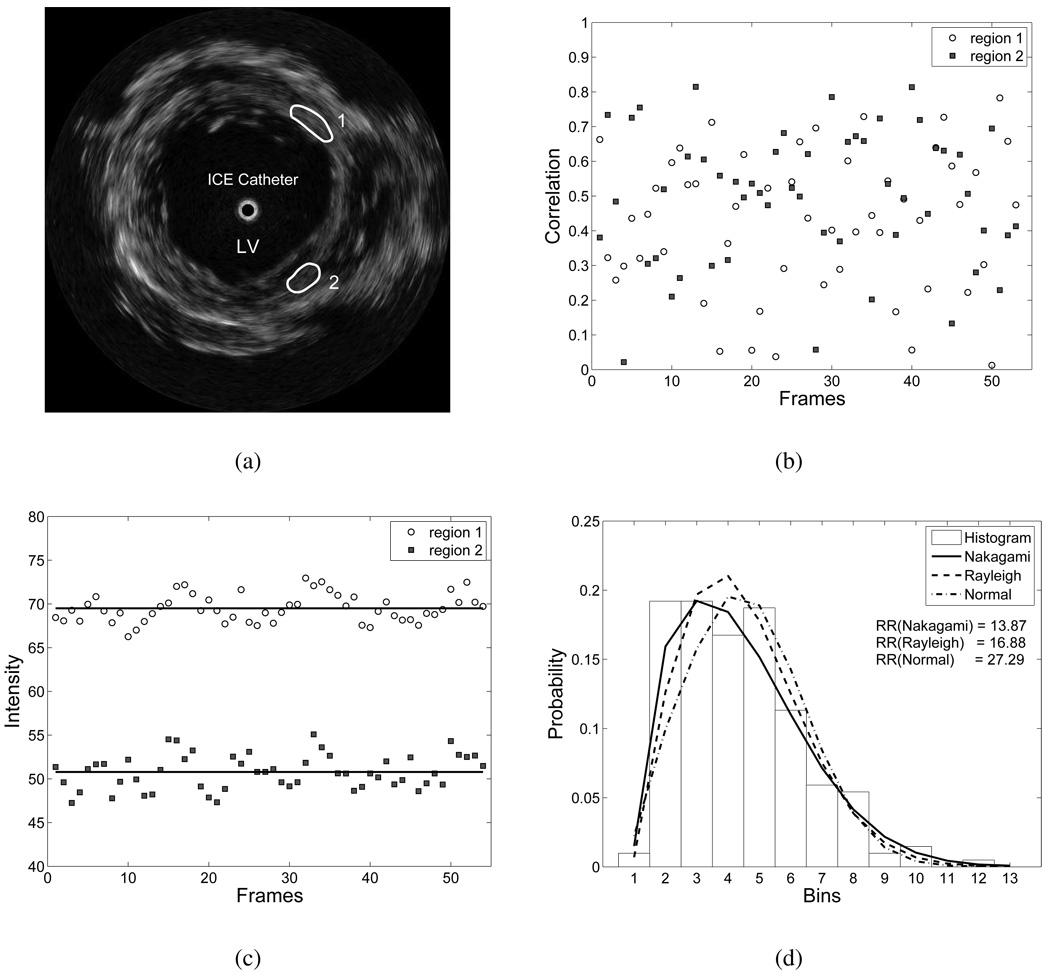
We initially performed analysis to investigate plausible solutions for myocardial motion estimation in ICE images. Two-dimensional ICE images, acquired by a catheter carrying a rotating transducer placed inside the left ventricle (LV) along its major axis, predominantly contain information on myocardial radial and circumferential motion (See Section III.B for more details). A sequence of ICE images (3 cardiac cycles, total of 54 frames) were acquired at a frame rate of 30 frames/s (single image size, 512 × 512 pixels). Fig. 1(a) shows a sample frame from the image sequence. We selected two homogenous regions in mid LV as regions of interest (ROIs). The two ROIs were manually tracked throughout the sequence such that a ROI in one frame had the same segment of myocardium as the one in the previous frame. We examined correlation, local mean intensity, and statistical properties of the ICE image sequence on the basis of ROIs. We found that ultrasound texture of the moving myocardium generally has the following features:
Fig. 1.
Analysis of ICE image sequence (3 cardiac cycles, total of 54 frames), acquired in mid LV. (a) A sample frame of a sequence, with two ROIs demarcated, (b) Correlation coefficients between ROIs among consecutive frames, (c) Intensities of ROIs, and (d) Rao-Rabson goodness-of-fit test on Nakagami, Rayleigh and Normal distributions for ROI 1 in (a).
1) Random texture variation
The speckle pattern (or texture) of ROIs varied randomly during the sequence, although the underlying myocardial segments in consecutive frames were closely motion related. This observation was verified by the results of correlation coefficients between the ROIs in consecutive frames. Fig. 1(b) shows that only 4% of correlation coefficients were larger than 0.8, while most of correlation coefficients (69%) were smaller than 0.6, and 22% of correlation coefficients were below 0.3. The variation in correlation coefficients was independent of cardiac motion. The low and random correlation might have been caused by system noise, tissue deformation, and speckle decorrelation [12]. Speckle decorrelation has the most profound effect on texture variation. All types of spatial motion can result in speckle decorrelation. Speckle decorrelation due to axial and lateral motion can be usually solved by relying on the similarity between speckle patterns [13], whereas speckle decorrelation due to elevational (cardiac longitudinal) motion is generally difficult to track, since tissue may move out of the scanning plane. For ICE images, the random variation in the correlation coefficients suggests that off-plane speckle decorrelation plays a major role in texture variation. Therefore, motion tracking based solely on the consistency of speckle pattern is error-prone and unreliable.
2) Stable local mean intensities
Although the texture of the homogenous ROIs varied largely, the mean intensities generally remained stable. Fig. 1(c) depicts mean intensities of the two ROIs through the sequence. The mean intensity of ROI 1 was 60.49±1.59, and 50.79±1.96 for ROI 2. This result suggests that the underlying echogenicity of the homogenous regions remains stable during cardiac motion. When the heart deforms, the scanning plane of the ICE catheter undergoes small longitudinal displacement. The displacement might be small (a few millimeters) such that myocardial echogenicity remains the same. However, since scatterers in the scanning plane change, the ultrasound texture varies largely. Therefore, the same myocardial segment in the ICE image sequence is usually featured with relatively stable mean local intensity, but randomly varied texture.
3) Typical speckle statistic
We further examined the statistical properties of speckle in ICE images. The B-mode images were first decompressed into envelope-detected images [14]. The ROIs were then selected for the statistical test. We chose three parametric distributions to model myocardial speckle statistics: Nakagami, Rayleigh, and Normal distributions. The Rayleigh distribution is a typical statistical model for the fully developed speckle [15], [16]. The Nakagami distribution has been verified in [17], [18], which can encompass Poisson, K, Rayleigh and Rician distribution. The histograms of B-mode ultrasound images generally have significant spike-empty-bin pattern [19], which appears as a high-count bin followed by a low-count bin. To suppress this artifact, the histograms were first reduced into 13 bins before feeding into the statistical tests, which was a good compromise between compensating for the effect of the spike artifact and preserving the overall shape of the histogram. We employed goodness-of-fit tests on three models, and chose the Rao-Rabson statistic instead of the chi-square test as suggested in [19]. Using the computed Rao-Rabson statistic, the significance value was obtained from the standard chi-square significance table. A large significance value means a better match with the model. For ROI 1 in Fig 1(a), the average significance value over the test sequence was 0.1565 for Nakagami distribution, 0.0629 for Rayleigh distribution, and 0.0021 for Normal distribution. The significance values of the results suggest that the Nakagami model is a better model for the homogenous myocardium in the ICE image. However, the Nakagami distribution is quite complex to implement in motion estimation. On the other hand, the Rayleigh distribution is superior to the Normal distribution, and is applicable for most of homogenous speckle regions in the ICE images. In addition, as shown in Fig. 1(d), the fits of the models to the data were quite close. We therefore chose the Rayleigh distribution as a speckle model for motion estimation.
From our preliminary analysis, speckle decorrelation (due to longitudinal heart motion) complicates any tracking algorithm that relies on texture constancy. To solve this problem, we assume that the myocardial regions in two motion-related ICE images have the same echogenicity. The recent application of maximum likelihood motion estimation to ultrasound image sequences [20], [21] suggests that a good tracking strategy would be one that incorporates statistics of the ultrasound image into the estimation process. We therefore proceeded with the assumptions of constancy of echogenicity and Rayleigh speckle model, and adapted this strategy into a non-rigid motion estimation model.
B. Maximum Likelihood Motion Estimation
Let a reference image (Ir) and test image (It) be two motion related frames in a given sequence, where I ⊂ℤ2. In the framework of image registration, a pixel x(xx, xy) ∈ Ir is displaced by u
| (1) |
, where , and is an approximation to It. Let fr = fr (x) represents the intensity value of image Ir at pixel x, and u = u(x) represents the displacement of pixel x. According to the maximum likelihood method for parameter estimation, the estimated displacement vector û is obtained by maximization of the conditional probability density function (pdf) [20]
| (2) |
.
Since Ir and It are directly related within the same image acquisition model, the conditional probability of fr given its homologue ft and displacement u is described by [22]
| (3) |
where is obtained by applying the spatial transform on ft, i.e.,
Speckle is considered as signal-dependent noise in ultrasound images [16]. The envelope-detected ultrasound image can also be modeled as the result of interaction between the ultrasound point spread function and a complex field T(x) = t(x) + j^t(x), such that f (x) = |h(x) * T(x)|. Assuming that the amplitude of the scattering function varies slowly within the resolution cell, the envelope-detected ultrasound image can be approximated [16] as:
where g(x) = |a(x)| is the amplitude of scattering function (representing tissue echogenicity), and n(x) is the noise term. For fully developed speckle, n(x) is identical independent Rayleigh distributed [15], [16].
To consider speckle decorrelation due to tissue motion, we assume that two motion-related ICE images have the same echogenicity. Here, we adapt the strategy proposed in [20], [21] by using the ratio between two ultrasound images:
| (4) |
where fr(x) = g(x)nr(x), ft(x) = g(x)nt(x), and η = nt/ nr represent the ratio of two Rayleigh random variables. In most medical applications, one deals directly with displayed ultrasonic images, which are logarithm-compressed versions of envelope-detected images. This kind of nonlinear compression changes the statistics of the envelope-detected signals, and different compression coefficients can lead to different statistical distributions of signals [14]. Consequently, direct use of displayed ultrasonic images is highly preferred. To this end, the log-transform is applied to both sides of (4) to obtain f̃t(x) = f̃r(x) + η̃ (x). The pdf of η̃ is derived as a function of random variable η [23] The conditional pdf for displayed ultrasound images is given by
| (5) |
Here, for convenience, we continue to use the symbol f to denote the input log-compressed image instead of f̃ The motion between frames is estimated by maximizing (5).
C. Speckle Tracking
To formulate the ultrasound motion estimation problem as an optimization process, we apply the normalized negative log likelihood function to (5) and define a maximum likelihood cost function for ultrasound speckle tracking (USST) as:
| (6) |
where N is the number of pixels in the image, and Maximization of the conditional pdf (5) is equivalent to
| (7) |
We refer to this algorithm as a USST-based maximum likelihood motion estimator to distinguish it from the more conventional sum of square differences (SSD) based maximum likelihood estimator.
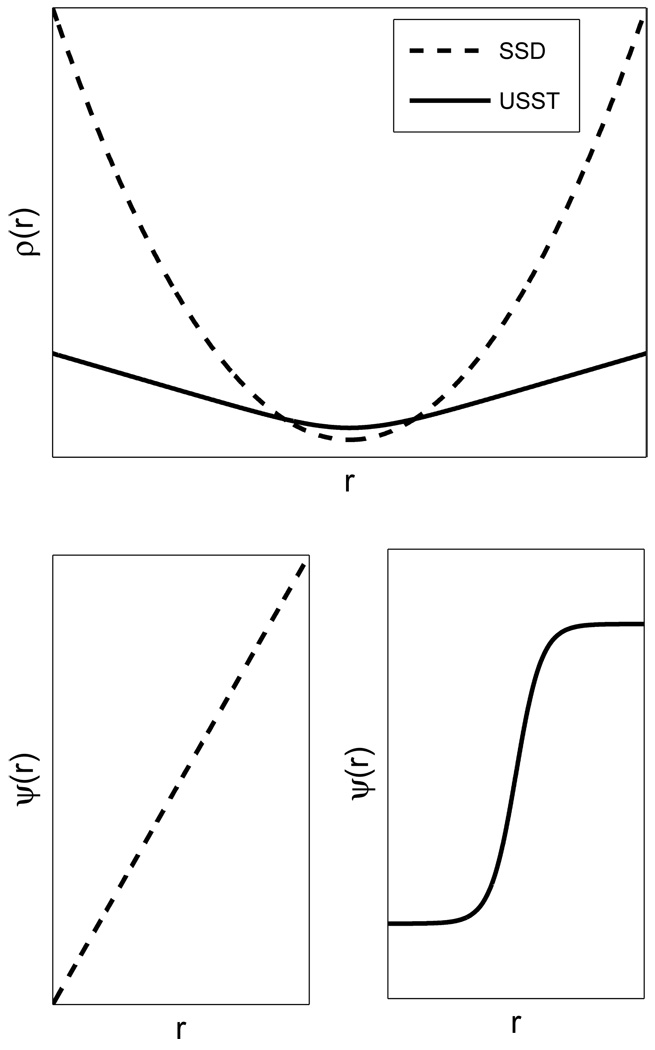
1) Robust Noise Resistance
Robust estimation is often used to achieve accurate estimation for the case of missing data or isolated points having high residual errors (outliers) [24]. One class of robust estimators, called M-estimators, is designed to minimize the sum of residuals. Let r be the residual of the difference between the ith fitted value and the observation. The objective function of the SSD method is a least-squares estimator, ρ (r) = r2 and the influence function is ψ (r) = 2r. The least-squares solution is highly sensitive to outliers as its influence function is unbounded to residual error. As a consequence, the accuracy of the SSD method is limited in the presence of speckle decorrelation in the ultrasound image sequence. This kind of speckle outlier is extremely difficult to exclude from the estimation due to its coherent nature. However, the USST estimator has the necessary features that lead to robust estimation [24], whereby the objective function is given by
and its influence function is
| (8) |
Figure 2 illustrates the difference between the SSD and USST estimators. For the SSD estimator, the influence of a datum on the estimation increases linearly with its error. On the other hand, the influence function of the USST estimator is bounded by ±1, which suggests that the USST estimator has a better outlier resistance than the SSD estimator. Moreover, the robustness of the USST estimator is fairly obvious in a linear system with limited parameters, (e.g., affine transform) where one may show that the objective function has a unique minimum in parameters and is convex in every transform variable. This explains why the speckle similarity measure is more accurate than the cross-correlation measure [20], [21].
Fig. 2.
Comparison of robustness between SSD and USST estimators. Top, object functions of SSD and USST estimators in relation to residual r. Bottom left, SSD influence function, Bottom right, USST influence function.
2) Deformable Registration
Myocardial motion is mostly non-rigid, hence tissue displacement u(x) in an ICE image can be described by a 2-D non-rigid transformation based on cubic B-splines [25]:
| (9) |
where is the deformation parameter, h = (h1 ,h2) is the space between nodes, and
is the tensor product of cubic B-splines.
During the warping process, computed u(x) may have a non-integer value. Thus, we interpolate the image using B-splines as:
| (10) |
where bi is a set of interpolation coefficients, and B3(x – i) = β3(x – i)β 3(y – j) is a tensor product of cubic B-splines.
The solution for the minimum of the cost function (6) is the displacement, u(x), which is obtained by using an optimization algorithm that acts upon the parameters First partial derivative of Λ is calculated explicitly as:
| (11) |
where
| (12) |
The cubic B-spline interpolation affords convenience by explicit differentiation of the cubic B-spline window, which reduces to the difference of two shifted quadratic B-splines [26].
3) Implementation Details
To minimize the cost function in (6), we use the limited memory optimization algorithm of Broyden-Fletcher-Goldfarb-Shanno with bound (L-BFGS-B) [27]. Applying L-BFGS-B is appropriate and efficient for our large scale problem. The optimization is stopped if ‖Λ'(ck)‖ ≤ ε , where ε is tolerance value. The deformation parameter is iteratively updated during optimization as ck+1 = ck + Δc [25].
The objective function of the USST method and its influence function (8) suggest that the USST estimator is a robust estimator for a rigid transform. To fit non-rigid B-spline registration framework, we further employ multiresolution and iterative refinement techniques to reduce the local minima, wherein the global difference between two images at a coarse scale is propagated to finer scales. This strategy has desirable features in that it speeds up the convergence process and increases the ability to capture deformations. Both reference and test images are resized so as to construct an image pyramid from coarse to fine resolution. When the solution converges at a given pyramid scale, the computed parameters are then used as initial estimates for the parameters at the next finer resolution. This process is repeated until the finest (original) scale is reached.
4) Motion field
To compute the motion field of an image sequence, we apply the registration algorithm to a whole image sequence (e.g., a cardiac cycle). An advantage of using multiresolution deformable registration is in its ability to capture large deformations, thus allowing the employment of a relatively simple update strategy. Specifically, the first image of an ICE sequence (usually at end diastole) is used as the reference image, and every subsequent image in the sequence is registered with respect to the first image. Such a method avoids temporal drift errors (normally quite significant) when using consecutive image pair registration. The motion field v(x) at time t is computed from the displacement of consecutive image pairs
| (13) |
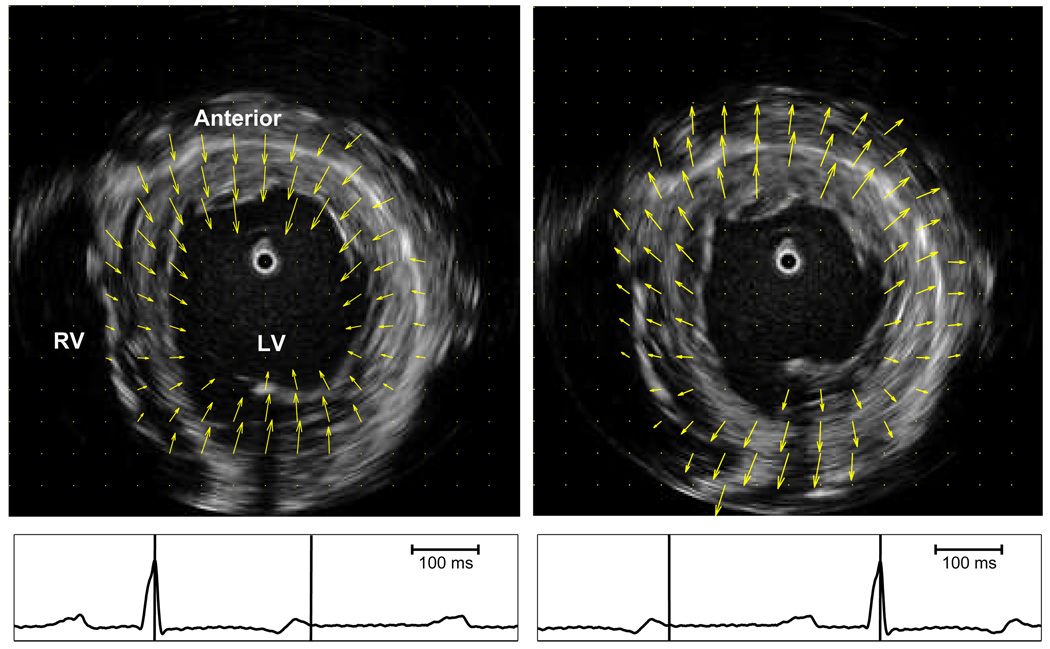
The motion field depicts regional myocardial deformation. Figure 7 illustrates myocardial motion fields at end systole and end distole for an heathy dog.
Fig. 7.
ICE images in mid LV at end diastole (left) and end systole (right). Arrows indicate motion field of the LV myocardium during systole (left) and diastole (right). Intervals for motion fields are indicated by vertical bars on corresponding ECG.
III. EXPERIMENTAL VALIDATION AND RESULTS
A. Validation by Computer Model
Motion tracking was initially tested on a computer model that simulated ultrasound image sequences. The USST method was validated by comparing its performance with that of the SSD-based deformable registration [7], [25]. Quality indices were used as quantitative measures of estimation performance. To obtain statistically meaningful results, extensive tests were performed on ultrasound image sequences corrupted by different noise levels.
1) Ultrasonic Image Phantom
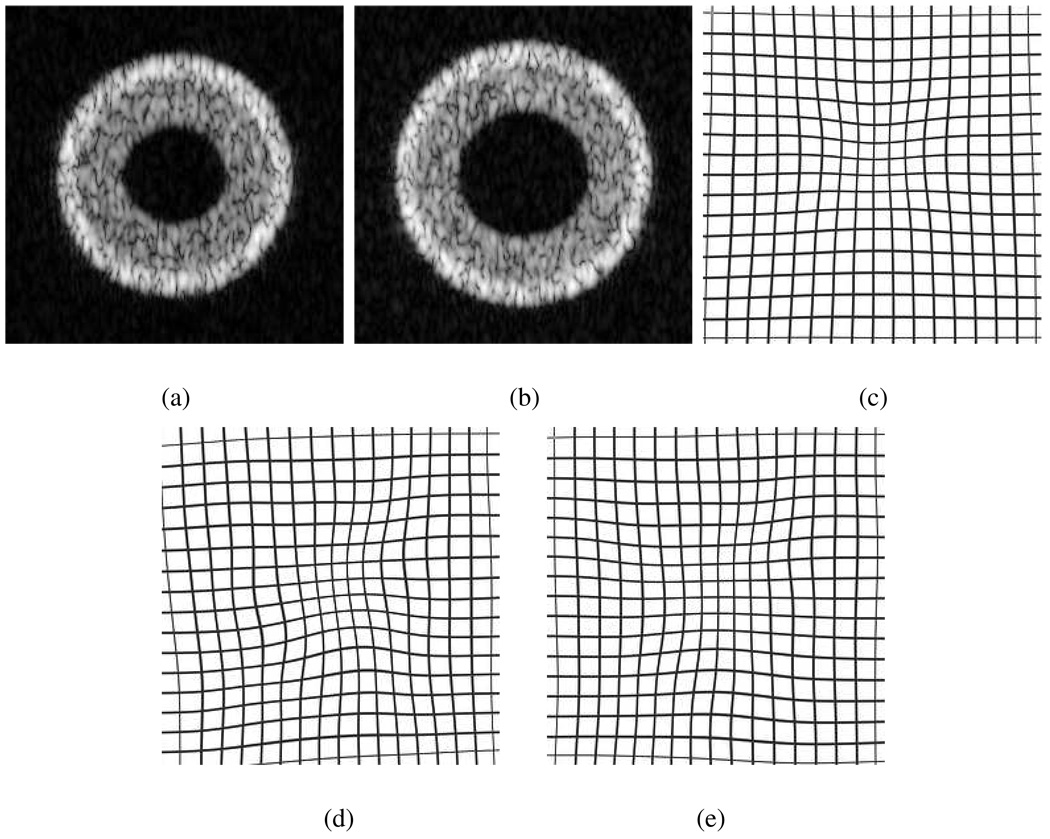
Envelope-detected 2-D ultrasound images were generated to mimic tissue structure in a typical ICE image of the LV. These images simulated a cavity, ventricular myocardium, epicardium and background tissues. Speckle in the homogenous regions was verified to be Rayleigh distributed. To simulate a commercial medical-grade ultrasonic image, the envelope-detected image was then log-compressed. An example of a phantom image is shown in Fig. 3(a).
Fig. 3.
Warped results of a pair of synthesized ultrasound images. (a) reference, and (b) test image. (c) true deformation field. (d) the result of the SSD method. (e) the result of the USST method.
A test image was synthesized by simulating the ultrasound imaging process [28], [29]. Specifically, a moving tissue scattering function was generated by transforming the reference tissue scattering function using a predefined displacement field. To mimic the real ICE image to an even greater extent, we also introduced speckle decorrelation into the test image. Most severe speckle decorrelation occurs in 2-D echocardiographic images when myocardial scatterers move out of the scanning plane. To reproduce this situation, some scatterers were randomly selected to have elevational motion. The vacancies thus created were randomly occupied by new scatterers. The decorrelation degree was indexed by λ, which relates the portion of scatterers in out-of-plane motion to the total number of scatterers in the tissue scattering function. Hence, λ = 0 represents the ideal 2-D motion that is free of elevational motion, whereas λ = 1 represents severe corruption by elevational speckle decorrelation.
2) Experiments on a Pair of Images
We first considered the registration of a pair of motion-related ultrasound images. The reference image is shown in Fig. 3(a) (image size: 256 × 256 pixels). The test image (Fig.3(b)) was generated by employing a non-rigid displacement field on the reference scattering function, and corrupting the image with heavy motion speckle.
The SSD and USST methods were applied to register the test image with the reference image using the same computational conditions for both algorithms. Cubic B-splines were used as basis functions for the image interpolation and deformation function. The knot spacing h in (9) was set as [32,32]. The optimization stop criteria were set to achieve global energy minimization for both methods: ε was set at 0.001, and the maximum iteration number being resolution dependent was 200 for the coarsest level (size 32×32) and 20 for the original image. The quality of motion estimation is demonstrated by comparing the true deformation field with recovered deformation fields (Fig. 3(d) and (e)). The results show that the USST method is more accurate than the SSD method in recovering the true displacement field.
To quantitatively evaluate registration performance, two different quality indices were used: an angular error measure,
| (14) |
and a relative magnitude displacement error
| (15) |
where u is estimated displacement, and uc is true deformation. Both θ and ϵ have been used as measures of error in optical flow techniques [28], [29].
3) Experiments on Image Sequences
We tested both USST and SSD algorithms on synthesized ultrasound image sequences that mimicked real echocardiographic images throughout a cardiac cycle. To model cardiac motion, we simulated a periodic displacement field that maintained a constant cross-sectional area of the myocardium. This was achieved by applying a radial displacement field with a magnitude decreasing with distance from the center. The displacement field was cosine modulated in time to simulate myocardial relaxation and contraction, and subsequent thinning and thickening of the ventricular wall during diastole and systole, respectively.
We generated 6 ultrasound image sequences corrupted with different levels of elevational speckle decorrelation. Each sequence consisted of 22 images representing a complete cardiac cycle. Elevational speckle decorrelation was controlled by the parameter λ. Specifically, for the first sequence, tissue motion was limited to the scanning plane with λ = 0. For the rest of the sequences, out-of-plane motion was gradually introduced with λ = 0.05 for the second, 0.1 for the third, 0.3 for the fourth, 0.6 for the fifth, and 1.0 for the last sequence. For the last case, the tissue scattering function was totally changed for every frame during motion, such that every scatterer in the scanning plane was moved out of plane at random.
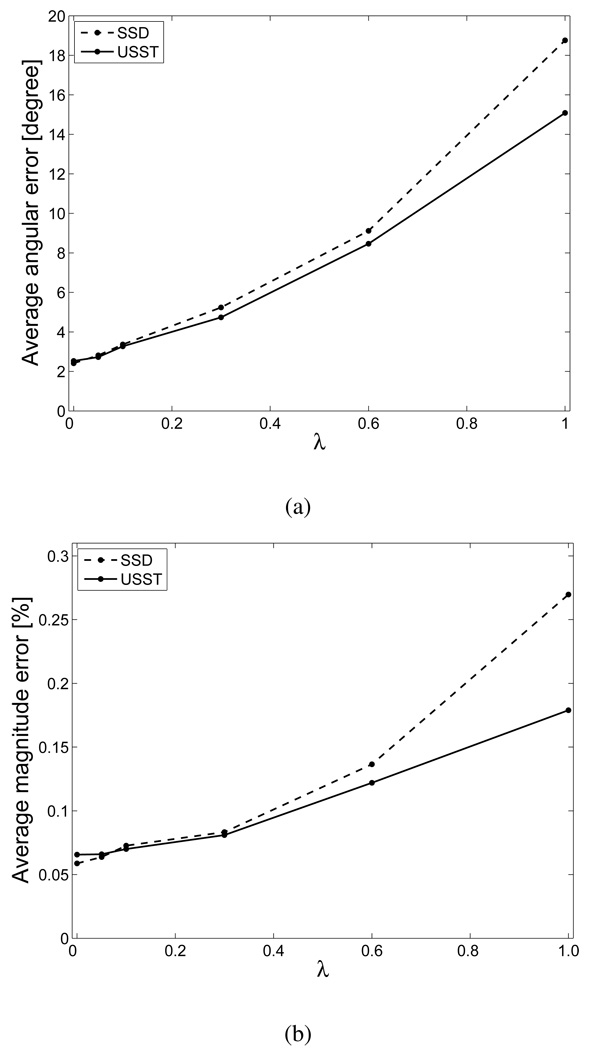
Image sequence registration was performed based on a non-temporal update strategy, i.e. every frame in a sequence was registered to the same reference frame in the sequence (the first frame in our experiments). Computational conditions were the same as those used above for single-pair image registration. The average angular error and magnitude error are depicted in Fig. 4 as functions of λ. The results indicate that estimation errors for both algorithms increase with increasing λ, and further illustrate that speckle tracking by the USST method is robust for ultrasound image sequences corrupted by a wide range of speckle decorrelation.
Fig. 4.
Average angular error (a) and average magnitude errors (b) associated with SSD and USST methods, displayed as functions of speckle decorrelation index λ.
B. Validation by Animal Model
1) Experiments
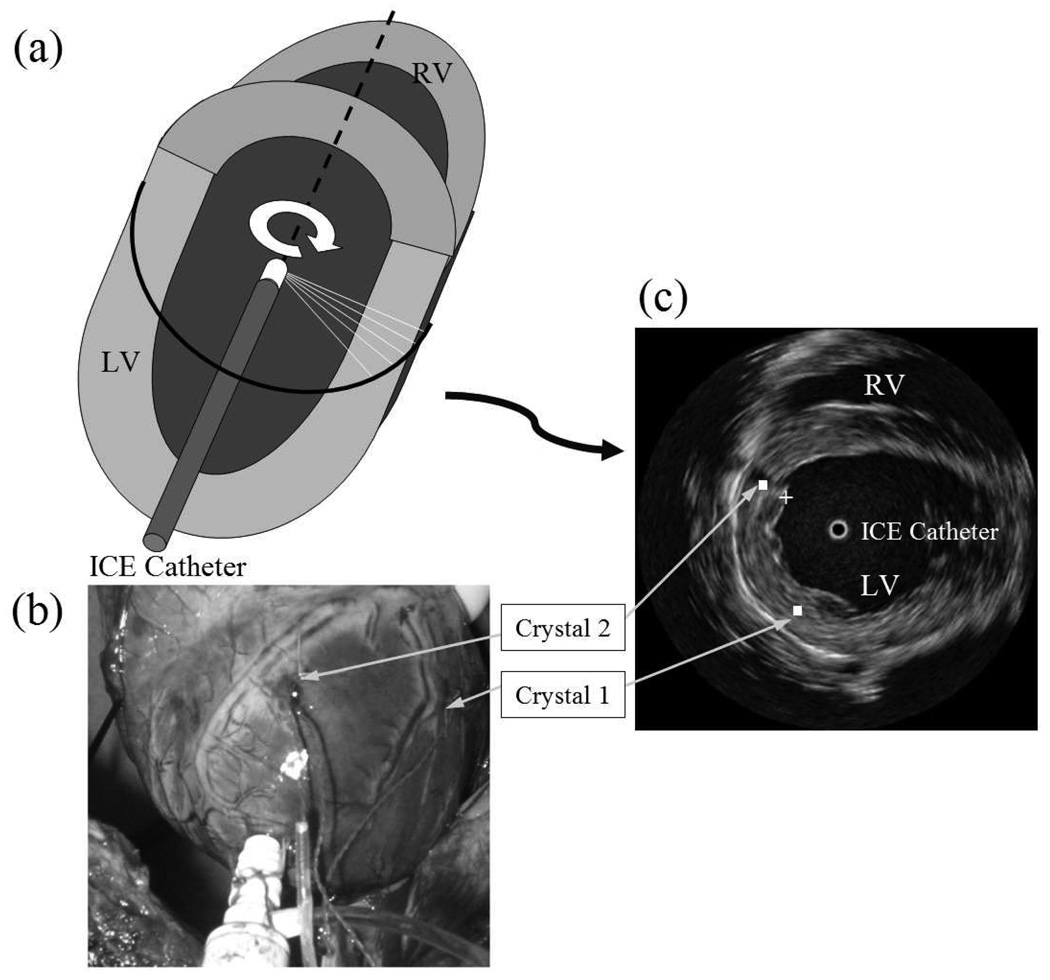
The feasibility and accuracy of depicting regional myocardial deformation were examined using ICE images acquired from an animal model. Four healthy mongrel dogs (weight, 30 – 35 kg) were included in the study, and the protocol adhered to the PHS guidelines for the care and use of laboratory animals. The dogs were preanesthetized with xylazine, atropin, and propofol, endotracheally intubated, and ventilated using an external respirator while anesthesia maintained by isoflurane inhalation. Electrodes were attached to the limbs to record ECG leads I, II, and III (model ECG100; Biopac Systems, Goleta, CA). Midline thoracotomy was performed and the heart was suspended in a pericardial cradle. A 9-F sheath (length, 10 mm) was inserted through a purse string suture in the LV apex. A standard 9-F 9-MHz ICE catheter (model Ultra ICE; Boston Scientific, Boston, MA) was inserted through the sheath and forwarded along the LV major axis, as illustrated in Fig. 5(a). Motion of the LV apex was not restricted. The ICE catheter had a distal transducer that emitted and received ultrasound pulses. Tomographic short-axis views of the cavity were derived by attaching the ICE catheter to a motor drive unit that enabled automatic and continuous rotation of the transducer at a fixed speed. The ICE catheter was connected to an imaging console (model iLab; Boston Scientific) to acquire continuous 2-D echocardiographic images (rate=30 frame/s). A calibrated high-fidelity pressure catheter (5F, model SPC-350; Millar Instruments, Houston, TX) was also inserted into the LV via the apex. The echocardiographic images were acquired continuously throughout the cardiac cycle, along with ECG and LV pressure signals (ICE sampling rate was 30 frame/s; ECG and pressure sampling rates were each 1000 sample/s). Myocardial regional displacement was measured by standard sonomicrometry (Sonometrics Corporation, London, Ontario, Canada). Two segment-length ultrasound crystals (diameter=2 mm) were fixed under the guidance of ICE in mid myocardium of anterior LV wall. As shown in Fig. 5(b) and (c), the first crystal was placed in mid lateral region of the LV. The second crystal was placed in mid anterior LV, about 2–3 cm from the first crystal. Circumferential displacement around the long axis was recorded continuously with a time resolution of 1.0 ms. To eliminate effects of breathing, the respirator was temporarily turned off for a brief period during each acquisition. Due to overlapping frequency bands of operation, sonomicrometry and ICE imaging were performed in sequence. Data were collected at baseline as well as at two levels of increased contractility induced by dobutamine (DOB) administration (1–2.5 µg/kg.min).
Fig. 5.
Validation experiments in animals. (a) Schematic of the ICE catheter operating inside the LV. (b) Photo of a dog heart during surgery depicting points of entry of sonomicrometry crystals. (c) Representative ICE image in mid LV.
2) Results
Each data set consisted of three consecutive cardiac cycles of ICE recording that were selected for computation of the deformation field, where a cardiac cycle was defined as the R-R interval on a synchronously recorded ECG. For a typical baseline recording, there were about 18–20 frames per cardiac cycle. With the increased heart rate during DOB infusion, there were about 12 frames at the high dose (DOB1), and 15 frames at the low dose (DOB2). Both the SSD-based and USST-based registration algorithms were employed to compute the deformation field. We used the same initial parameters and stop criteria as those employed in the previous phantom image experiments. In each cardiac cycle, the first frame taken at the peak R wave was used as the reference image, whereas the other frames in the same cycle were registered to the first frame.
Illustrated in Fig. 5(c), the distance between the two crystals measures the circumferential deformation of the myocardium. The crystal location was identified in the reference ICE image, then the locations in other frames were computed from the deformation field. To compute the regional deformation, a region of interest (ROI) of size 5×5 pixels was selected around each crystal location. An additional ROI was also selected in the subendocardium, and was radially positioned relative to the second crystal in mid anterior LV. The center of this ROI, marked by the symbol ‘+’ in Fig. 5(c), was used to compute the radial deformation of the myocardium with respect to the second crystal. The position of every pixel in the ROIs was updated as a function of time throughout the pre-computed deformation field. In every updated ROI, centers of gravity were used to calculate the positions of crystals. Finally, the circumferential distance (Euclidean distance between the crystals) and radial distance were computed, and updated as functions of the cardiac cycle.
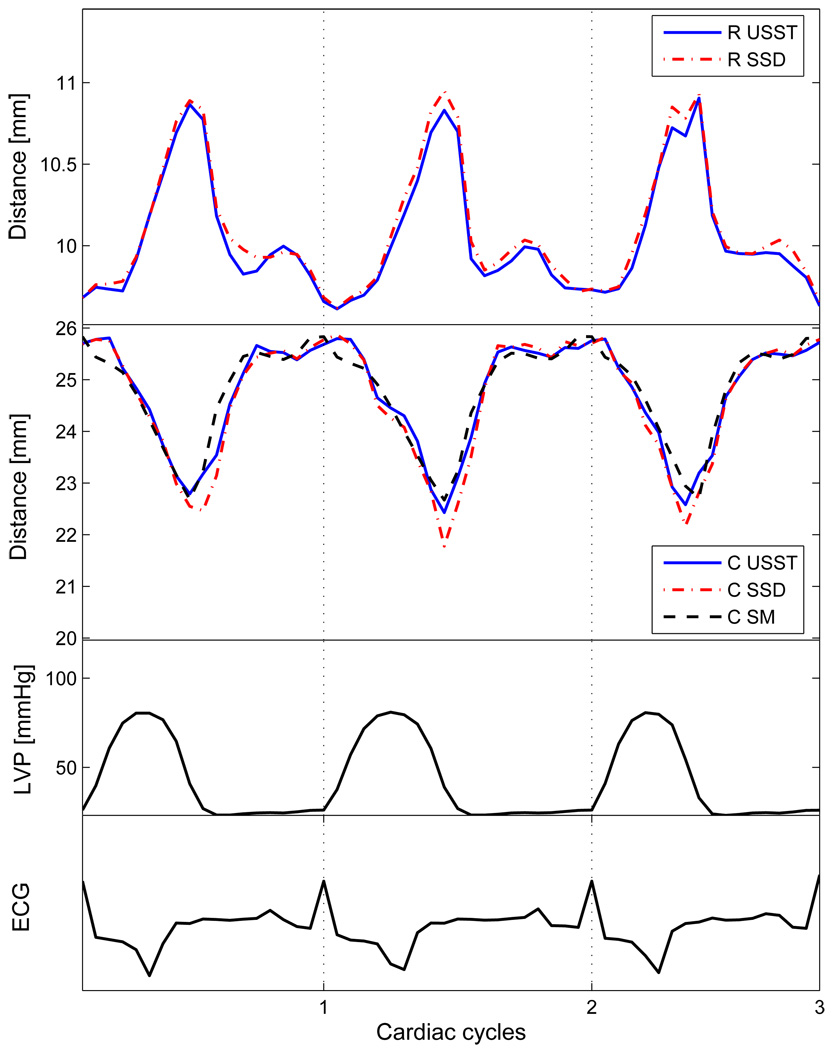
Examples of circumferential and radial displacements at baseline of an animal experiment are shown in Fig. 6. The results depict good agreement between motion displacements computed using the USST method and the reference motion displacements measured by sonomicrometry. The correlation coefficients were 0.94 for the SSD method, and 0.96 for the USST method. Figure 7(a) shows an ICE image at end diastole, and Fig. 7(b) shows an ICE image at end systole, both with their respective computed motion fields superimposed.
Fig. 6.
Displacement determined by computed deformation field and sonomicrometry, where ‘R’ represents radial displacement, ‘C’ represents circumferential displacement, and ‘SM’ represents sonomicrometry. Displacements are shown for both USST and SSD methods
We compared regional myocardial strains using the Lagrangian strain S, defined as the relative elongation with respect to the initial distance , i.e.,
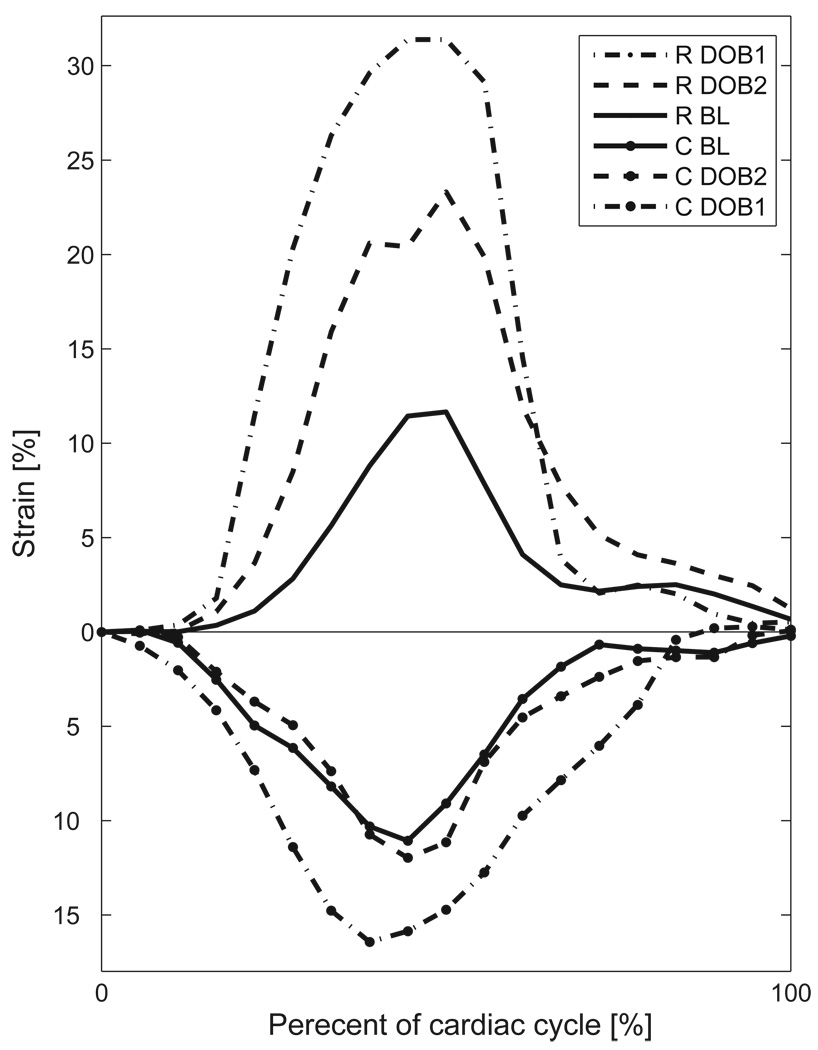
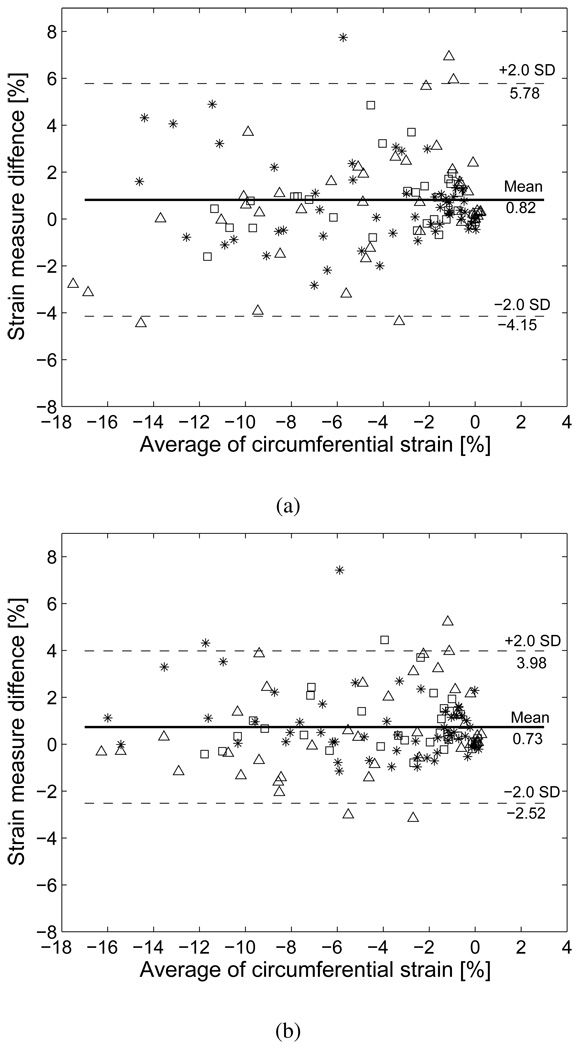
Figure 8 illustrates an example of myocardial strains at three different recording stages (baseline, DOB1 and DOB2). The strains were calculated on the basis of displacements averaged over three cardiac cycles. The results clearly show that myocardial strain increased relative to baseline with dobutamine infusion. Since dobutamine concentration was higher in DOB1 than DOB2, the strain was also larger with DOB1. We further validated the two registration methods at every time frame against sonomicrometric measurement by Bland-Altman analysis on circumferential strain. Figure 9(a) and 9(b) show that the SSD method yields larger mean error (0.82) and wider variation than the USST method (0.73), suggesting that the USST method achieved better agreement with sonomicrometry than the SSD method.
Fig. 8.
Radial and circumferential strains computed by the USST method at three recording stages: baseline (BL), DOB1 and DOB2. Dobutamine concentration in DOB1 was higher than DOB2. ‘R’ represents radial strain, and ‘C’ represents circumferential strain.
Fig. 9.
Bland-Altman plots comparing circumferential strains as determined by two methods: (a) SSD and sonomicrometry, and (b) USST and sonomicrometry. Baseline (*), DOB1(△) and DOB2 (□).
IV. DISCUSSION AND CONCLUSIONS
Several methods have been employed for the assessment of myocardial deformations from images acquired by ultrasound. Echocardiographic segmentation algorithms only provide the deformation of the endocardium, instead of the wall [30]–[32]. Tissue Doppler imaging [33], [34] can provide an operator-independent quantitative analysis of regional myocardial function through the analysis of myocardial velocities and determination of strain and strain rate [35], [36]. However, only deformations in the direction of the ultrasound beam are measured using tissue Doppler imaging, and comparative measurements at multiple sites depend on the angle of the ultrasound beam. Meanwhile, speckle tracking in echocardiography has proven to be a useful angle-independent method for assessing regional myocardial deformation [8].
Two dimensional ICE provides superior spatial resolution of cardiac structures in comparison with transthoracic echocardiography. To further advance the utility of ICE and provide capabilities for multimodal imaging during catheterization, we developed and validated a speckle tracking method for regional myocardial motion estimation from ICE image sequences. Our method exploits ultrasound statistics by utilizing maximum likelihood motion estimation, and treats the maximization of motion probability as the minimization of a derived energy function. Myocardial displacement was estimated by optimization of this energy function while relying on the framework of non-rigid registration. We have validated our speckle tracking method in both computer and animal models.
In our method, we first considered random texture variation in ultrasound images as the major factor hindering motion estimation. Instead of treating texture variation as system Gaussian noise, we recognized its speckle-like nature and considered it as the result of motion-related speckle decorrelation. Our analysis suggested that a tracking method based on the constancy of echogenicity was much more reliable than one utilizing only constancy of the speckle pattern. Employing this constant echogenicity assumption, our method provided an optimal solution for myocardial motion by integrating speckle tracking with non-rigid motion estimation. We further showed that our method was theoretically feasible in the sense of robust estimation.
We have provided a fundamental platform for motion estimation in ultrasound image sequences. A methodological improvement can be achieved by incorporating an invertibility constraint into the cost function [37]. The algorithm can be further improved by updating the maximum likelihood estimation using a Bayesian maximum a posteriori framework, wherein a priori information about the periodicity of myocardial motion would be taken into account.
Radial displacement computed from in vivo experiments by our USST method was not validated by sonomi-crometry in a manner similar to circumferential displacement. However, the similarity of USST results to those of the SSD method, and the consistency of computed radial displacement with previous studies in its relationship to circumferential displacement are supportive of the capability of our USST method in depicting regional radial myocardial deformation. Results from in vivo animal experiments indicate that our method has significant relevance to the analysis of regional myocardial function, such as automated detection of ischemia and infarction. Specifically, speckle tracking of catheter derived ICE images could evolve clinically as a useful method in diagnosing, monitoring, and guiding applications appropriate for the cardiac catheterization laboratory.
In conclusion, assessment of regional myocardial deformation by novel speckle tracking in intracardiac echocar-diographic image sequence is feasible. This method has important clinical implications for multimodal imaging during cardiac catheterization.
Acknowledgement
The authors thank Dr. Liyun Rao and Ms. April Gilbert for their assistance in conducting the animal studies and collecting the data, and Dr. Fathi Ghorbel and Dr. Richard Baraniuk for their guidance throughout the research.
This work was supported in part by grant R01-HL68768 (DSK) from the National Institutes of Health, Bethesda, MD.
Contributor Information
Yong Yue, Department of Electrical and Computer Engineering, Rice University, Houston, TX 77005 USA (e-mail: yyue@ieee.org).
John W. Clark, Jr., Department of Electrical and Computer Engineering, Rice University, Houston, TX 77005 USA (e-mail: jwc@rice.edu).
Dirar S. Khoury, Department of Cardiology, Methodist DeBakey Heart and Vascular Center, the Methodist Hospital Research Institute, Houston, TX 77030 USA (e-mail: dkhoury@tmhs.org).
REFERENCES
- 1.Ren J, Schwartzman D, Callans D, Brode S, Gottlieb C, Marchlinski F. Intracardiac echocardiography (9 mhz) in humans: methods, imaging views and clinical utility. Ultrosound Med. Biol. 1999;vol. 25:1077–1086. doi: 10.1016/s0301-5629(99)00064-2. [DOI] [PubMed] [Google Scholar]
- 2.Roithinger F, Steiner P, Goseki Y, Liese K, Scholtz D, Sippensgroenewegen A, Ursell P, Lesh M. Low-power radiofrequency application and intracardiac echocardiography for creation of continuous left atrial linear lesions. J. Cardiovasc. Electrophysiol. 1999;vol. 10:680–691. doi: 10.1111/j.1540-8167.1999.tb00245.x. [DOI] [PubMed] [Google Scholar]
- 3.Friedman P, Luria D, Fenton A, Munger T, Jahangir A, Shen W, Rea R, Stanton M, Hammill S, Packer DL. Global right atrial mapping of human atrial flutter: the presence of posteromedial (sinus venosa region) functional block and double potentials. a study in biplane fluoroscopy and intracardiac echocardiography. Circulation. 2000;vol. 101:1568–1577. doi: 10.1161/01.cir.101.13.1568. [DOI] [PubMed] [Google Scholar]
- 4.Marrouche N, Martin D, Wazni O, Gillinov A, Klein A, Bhargava M, Saad E, Bash D, Yamada H, Jaber W, Schweikert R, Tchou P, Abdul-Karim A, Saliba W, Natale A. Phased-array intracardiac echocardiography monitoring during pulmonary vein isolation in patients with atrial fibrillation: impact on outcome and complications. Circulation. 2003;vol. 107 doi: 10.1161/01.CIR.0000070541.83326.15. 2710-2706. [DOI] [PubMed] [Google Scholar]
- 5.Rao L, Ling Y, He R, Gilbert A, Frangogiannis N, Wang J, Nagueh S, Khoury D. Integrated multimodal-catheter imaging unveils principal relationships among ventricular electrical activity, anatomy, and function. Am J Physiol: Heart Circ Physiol. 2008;vol. 294:H1002–H1009. doi: 10.1152/ajpheart.01297.2006. [DOI] [PubMed] [Google Scholar]
- 6.Ding C, Rao L, Nagueh S, Khoury D. Dynamic three-dimensional visualization of the left ventricle by intracardiac echocardiography. Ultrasound Med. Biol. 2005;vol. 31:15–21. doi: 10.1016/j.ultrasmedbio.2004.09.016. [DOI] [PubMed] [Google Scholar]
- 7.Ledesma-Carbayo M, Kybic J, Desco M, Santos A, Suhling M, Hunziker P, Unser M. Spatio-temporal nonrigid registration for ultrasound cardiac motion estimation. IEEE Trans. Med. Imag. 2005;vol. 24:1113–1126. doi: 10.1109/TMI.2005.852050. [DOI] [PubMed] [Google Scholar]
- 8.Langeland S, D’hooge J, Wouters P, Leather H, Claus P, Bijnens B, Sutherland G. Experimental validation of a new ultrasound method for the simultaneous assessment of radial and longitudinal myocardial deformation independent of insonation angle. Circulation. 2005;vol. 112:2157–2162. doi: 10.1161/CIRCULATIONAHA.105.554006. [DOI] [PubMed] [Google Scholar]
- 9.Suffoletto M, Dohi K, Cannesson M, Saba S, Gorcsan J., 3rd Novel speckle-tracking radial strain from routine black-and-white echocardiographic images to quantify dyssynchrony and predict response to cardiac resynchronization therapy. Circulation. 2006;vol. 113:960–968. doi: 10.1161/CIRCULATIONAHA.105.571455. [DOI] [PubMed] [Google Scholar]
- 10.Wang J, Khoury D, Yue Y, Torre-Amione G, Nagueh S. Left ventricular untwisting rate by speckle tracking echocardiography. Circulation. 2007;vol. 116:2580–2586. doi: 10.1161/CIRCULATIONAHA.107.706770. [DOI] [PubMed] [Google Scholar]
- 11.Pirat B, Khoury D, Hartley C, Tiller L, Rao L, Schulz D, Nagueh S, Zoghbi W. A novel feature-tracking echocardiographic method for the quantitation of regional myocardial function. J Am Coll Cardiol. 2008;vol. 51:651–659. doi: 10.1016/j.jacc.2007.10.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Yeung F, Levinson S, Fu D, Parker K. Feature-adaptive motion tracking of ultrasound image sequences using a deformable mesh. IEEE Trans. Med. Imag. 1998;vol. 17:945–956. doi: 10.1109/42.746627. [DOI] [PubMed] [Google Scholar]
- 13.Li P, Li C, Yeh W. Tissue motion and elevational speckle decorrelation in freehand 3d ultrasound. Ultrason. Imaging. 2002;vol. 24:1–12. doi: 10.1177/016173460202400101. [DOI] [PubMed] [Google Scholar]
- 14.Dutt V, Greenleaf J. Adaptive speckle reduction filter for log-compressed b-scan images. IEEE Trans. Med. Imag. 1996;vol. 15:802–813. doi: 10.1109/42.544498. [DOI] [PubMed] [Google Scholar]
- 15.Tur M, Chin KC, Goodman JW. When is speckle noise multiplicative? Applied Optics. 1982 April;vol. 21:1157–1159. doi: 10.1364/AO.21.001157. [DOI] [PubMed] [Google Scholar]
- 16.Wagner R, Smith S, Sandrik J, Lopez H. Statistics of speckle in ltrasound b-scans. IEEE Trans. Son. Ultrason. 1983;vol. 30:156–163. [Google Scholar]
- 17.Shankar P. A general statistical model for ultrasonic backscattering from tissues. IEEE Trans. Ultrason., Ferroelect., Freq. Contr. 2000;vol. 47:727–736. doi: 10.1109/58.842062. [DOI] [PubMed] [Google Scholar]
- 18.Hao X, Bruce C, Pislaru C, Greenleaf J. Characterization of reperfused infarcted myocardium from high-frequency intracardiac ultrasound imaging using homodyned k distribution. IEEE Trans. Ultrason., Ferroelect., Freq. Contr. 2002;vol. 49:1530–1542. doi: 10.1109/tuffc.2002.1049735. [DOI] [PubMed] [Google Scholar]
- 19.Tao Z, Tagare H, Beaty J. Evaluation of four probability distribution models for speckle in clinical cardiac ultrasound images. IEEE Trans. on Medical Imaging. 2006;vol. 25:1483–1491. doi: 10.1109/TMI.2006.881376. [DOI] [PubMed] [Google Scholar]
- 20.Strintzis MG, Kokkinidis I. Maximum likelihood motion estimation in ultrasound image sequences. IEEE Signal Process. Lett. 1997;vol. 4:156–157. [Google Scholar]
- 21.Cohen B, Dinstein I. New maximum likelihood motion estimation schemes for noisy ultrasound images. Pattern Recogn. 2002;vol. 35:455–463. [Google Scholar]
- 22.Roche A, Malandain G, Ayache N. Unifying maximum likelihood approaches in medical image registration. Int. J. Imag. Syst. Technol.: Special Issue on 3D Imaging. 2000;vol. 11:71–80. [Google Scholar]
- 23.Boukerroui D, Noble A, Brady M. Velocity estimation in ultrasound images: a block matching approach. Ambleside, UK. Proc. 18th Int. Conf on Inf Process Med Imaging; 2003. pp. 586–598. [DOI] [PubMed] [Google Scholar]
- 24.Huber PJ. Robust Statistics. New York: Wiley; 1981. [Google Scholar]
- 25.Kybic J, Unser M. Fast parametric elastic image registration. IEEE Trans. Image Processing. 2003;vol. 12:1427–1442. doi: 10.1109/TIP.2003.813139. [DOI] [PubMed] [Google Scholar]
- 26.Mattes D, Haynor D, Vesselle H, Lewellen T, Eubank W. Pet-ct image registration in the chest using free-form deformations. IEEE Trans. Med. Imag. 2003;vol. 22:120–128. doi: 10.1109/TMI.2003.809072. [DOI] [PubMed] [Google Scholar]
- 27.Zhu C, Byrd R, Nocedal J. L-BFGS-B: Algorithm 778: L-BFGS-B, FORTRAN routines for large scale bound constrained optimization. ACM Trans. Math. Software. 1997;vol. 23:550–560. [Google Scholar]
- 28.Baraldi P, Sarti A, Lamberti C, Prandini A, Sgallari F. Evaluation of differential optical flow techniques on synthesized echo images. IEEE Trans. Biomed. Eng. 1996;vol. 43:259–272. doi: 10.1109/10.486283. [DOI] [PubMed] [Google Scholar]
- 29.Sühling M, Arigovindan M, Jansen C, Hunziker P, Unser M. Myocardial motion analysis from B-mode echocardiograms. IEEE Trans. Image Processing. 2005;vol. 14:525–536. doi: 10.1109/tip.2004.838709. [DOI] [PubMed] [Google Scholar]
- 30.Kapetanakis S, Kearney M, Siva A, Gall N, Cooklin M, Monaghan M. Real-time three-dimensional echocardiography: a novel technique to quantify global left ventricular mechanical dyssynchrony. Circulation. 2005;vol. 112:992–1000. doi: 10.1161/CIRCULATIONAHA.104.474445. [DOI] [PubMed] [Google Scholar]
- 31.Corsi C, Lang R, Veronesi F, Weinert L, Caiani E, MacEneaney P, Lamberti C, Mor-Avi V. Volumetric quantification of global and regional left ventricular function from real-time three-dimensional echocardiographic images. Circulation. 2005;vol. 112:1161–1170. doi: 10.1161/CIRCULATIONAHA.104.513689. [DOI] [PubMed] [Google Scholar]
- 32.Herz S, Ingrassia C, Homma S, Costa K, Holmes J. Parameterization of left ventricular wall motion for detection of regional ischemia. Ann. Biomed. Eng. 2005;vol. 33:912–919. doi: 10.1007/s10439-005-3312-7. [DOI] [PubMed] [Google Scholar]
- 33.Gorcsan J, 3rd, Strum D, Mandarino W, Gulati V, Pinsky M. Quantitative assessment of alterations in regional left ventricular contractility with color-coded tissue doppler echocardiography: comparison with sonomicrometry and pressure-volume relations. Circulation. 1997;vol. 95:2423–2433. doi: 10.1161/01.cir.95.10.2423. [DOI] [PubMed] [Google Scholar]
- 34.Isaaz K, del Romeral LM, Lee E, Schiller N. Quantification of the motion of the cardiac base in normal subjects by doppler echocardiography. J. Am. Soc. Echocardiogr. 1993;vol. 6:166–176. doi: 10.1016/s0894-7317(14)80487-2. [DOI] [PubMed] [Google Scholar]
- 35.Urheim S, Edvardsen T, Torp H, Angelsen B, Smiseth O. Myocardial strain by doppler echocardiography: validation of a new method to quantify regional myocardial function. Circulation. 2000;vol. 102:1158–1164. doi: 10.1161/01.cir.102.10.1158. [DOI] [PubMed] [Google Scholar]
- 36.Edvardsen T, Gerber B, Garot J, Bluemke D, Lima J, Smiseth O. Quantitative assessment of intrinsic regional myocardial deformation by doppler strain rate echocardiography in humans: validation against three-dimensional tagged magnetic resonance imaging. Circulation. 2002;vol. 106:50–56. doi: 10.1161/01.cir.0000019907.77526.75. [DOI] [PubMed] [Google Scholar]
- 37.Christensen G, Johnson H. Consistent image registration. IEEE Trans. Med. Imag. 2001;vol. 20:568–582. doi: 10.1109/42.932742. [DOI] [PubMed] [Google Scholar]