The vibrational energy flow transition in organic molecules: Theory meets experiment

Abstract

Most large dynamical systems are thought to have ergodic dynamics, whereas small systems may not have free interchange of energy between degrees of freedom. This assumption is made in many areas of chemistry and physics, ranging from nuclei to reacting molecules and on to quantum dots. We examine the transition to facile vibrational energy flow in a large set of organic molecules as molecular size is increased. Both analytical and computational results based on local random matrix models describe the transition to unrestricted vibrational energy flow in these molecules. In particular, the models connect the number of states participating in intramolecular energy flow to simple molecular properties such as the molecular size and the distribution of vibrational frequencies. The transition itself is governed by a local anharmonic coupling strength and a local state density. The theoretical results for the transition characteristics compare well with those implied by experimental measurements using IR fluorescence spectroscopy of dilution factors reported by Stewart and McDonald [Stewart, G. M. & McDonald, J. D. (1983) J. Chem. Phys. 78, 3907–3915].

The notion of treating the dynamics of molecules with a high density of quantum states as ergodic has a long history. This assumption is made in most chemical rate theories (1, 2). Yet molecular spectroscopy and computational studies show that at low energies, or for small enough systems, the idea that all parts of the energetically allowed phase space are accessible does not apply (3–8). This fact raises the question as to how the transition to facile energy flow occurs. This question, while vital to physical chemistry, also has been raised recently by work in nuclear physics (9) and in the study of quantum dots (10). Fifteen years ago, in pioneering work, McDonald and coworkers provided the experimental basis for answering this fundamental question by studying the final extent of intramolecular vibrational redistribution (IVR) in a large class of organic molecules (11). Here we show how the characteristics of the behavior seen by them can be understood by using recent theoretical ideas.

Is there an easily computable parameter that traces the energy flow transition with high fidelity? Generally, because molecular size is clearly relevant, the total density of states has been taken as the parameter that determines the extent of vibrational state mixing. For example, McDonald and coworkers tabulated the results of their experiments on the final extent of IVR as a function of the total density of states of the molecules studied (11). These experiments probe the transition to facile energy flow by using IR fluorescence spectroscopy to measure the dilution factor σ upon exciting a CH fundamental

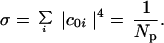1

|c_0i|² is the intensity borrowed by an eigenstate i from a bright state 0 assumed to carry all the oscillator strength. N_p is the effective number of states participating in IVR. When there is little state mixing, N_p lies near unity because only one or a few eigenstates (due to isolated anharmonic resonances) lie within the vibrational band contour. When molecular size and energy increase, N_p finally increases to a maximum value roughly equal to the product of the total symmetry-allowed density of states and the width Γ of the band contour:

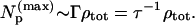2

The change in N_p is not gradual. Instead, McDonald and coworkers noted a drop of σ as the total density of states reached 10–100 cm⁻¹. When looked at in terms of ρ_tot, the transition, while noticeable, is still strikingly broad. We must question whether the total density of states is the controlling factor.

It has been suggested that the relevant parameter that determines the transition to ergodic state mixing is not the total density of states but rather is related to the local density of states coupled by anharmonic resonances (12–15). In 1990, Logan and Wolynes (12) mapped the mathematical description of vibrational energy flow in molecules caused by anharmonic coupling to that of single-particle quantum transport in disordered media, the problem of Anderson localization. Because of both the local nature of coupling in a vibrational Hamiltonian and the statistical nature of this theory, we refer to this work and more recent developments as Local Random Matrix Theory (LRMT). LRMT naturally leads to an understanding of how the ergodicity transition is approached in molecules. In this theory the dilution factor is shown to vary with the local density of anharmonically coupled states (16), not the total state density. According to LMRT the transition to ergodicity (minimal possible σ) depends not on ρ_tot, but on the local quantity

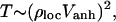3

where V_anh is the local anharmonic coupling strength and ρ_loc is the local density of coupled states.

Like ρ_tot, ρ_loc and therefore T increase with energy and molecular size, but more slowly (see below). When T = T_crit = 1, a transition to facile energy flow is predicted. In their development of LRMT Leitner and Wolynes provided a simple expression for the local parameter T in Eq. 3, calculable once the behavior of anharmonicities with order is known (15–17).

In complementary work, Bigwood and Gruebele have introduced a factorization method to treat the exponentially decreasing anharmonic coupling terms of the vibrational Hamiltonian (14, 17–22). The model was later incorporated into a computational local random matrix model [Bose Statistics Triangle Rule or BSTR (20)]. This model retains the most important features of empirical vibrational Hamiltonians by using known spectroscopic frequencies as input. For large molecules it is much easier to use these techniques than those based on ab-initio potential surfaces. The merit of BSTR is that a reasonable description of IVR in specific molecules results. Results computed using these models showed that when the states mediating IVR are off-resonant, “classic” Golden Rule-like behavior is often observed. However, when IVR becomes resonant, features predicted by the analytical results derived for the LRMT were observed, including a linear scaling of IVR rates with V_anh at large V_anh and a dependence of IVR thresholds on local quantities (20, 21). In fact, it was found that these features apply to the vast majority of states on the energy shell, named “interior states” because they occupy the interior of the vibrational state space.

In this paper, we recast the experimental IVR data obtained by McDonald and coworkers by using the local state counting parameters T (analytical theory) (15–17) and N_loc (numerical model) (14, 19). N_loc and T are defined in Eqs. 6 and 7, respectively. A much sharper transition is obtained when viewed in terms of these local parameters, which considerably improves upon a representation of the data in terms of ρ_tot. At the same time we find the transition near to the analytical transition value of T_crit = 1. Large fluctuations in σ are expected from theory and observed in the data near T_crit (16). Well above the transition, σ is simply given in terms of ρ_tot and the width of the band contour, as in Eq. 2. This analysis of the McDonald data suggests that local random matrix models provide a reasonably reliable indication of whether molecular energy redistribution will be ergodic or not.

MODELS

We briefly review the three principles we use to interpret experimentally observed dilution factors in organic molecules. The first is a factorization model for the Hamiltonian, which provides a simple description of vibrational couplings in the normal mode picture. The second is a numerical simulation of T that involves minimal averaging over molecular quantities. The third is an analytical model for T that involves some additional assumptions, but can provide deeper insight into the nature of the IVR transition.

Important quantities that enter the discussion are the harmonic vibrational frequencies ω_i, the energy gap ΔE_ii′, and the coupling matrix element V_ii′ between two normal mode basis states |i〉 and |i′〉.

Factorized Vibrational Hamiltonian.

It has been shown that the vibrational potential surface of a molecule can be exactly factorized as the number of vibrational degrees of freedom approaches infinity, as long as the normal modes are sufficiently random combinations of Cartesian coordinates (18). For finite-size but highly branched molecules, the factorization Hamiltonian is still a good asymptotic approximation (18), and

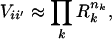4

where n_k = |v_k − v′_k| is the quantum number difference between two normal mode basis states |i〉 and |i′〉. The total distance between two states in state space is given by Q = Σ n_k. Eq. 4 is a particularly good approximation for highly branched or ring compounds (18, 22), such as those considered here. The factor R_i scales with mean occupation number and vibrational frequency as ω_i^1/2 (18, 23), and a least-squares fit to sample potential surfaces of organic molecules in ref. 18 yields good agreement if one chooses the specific numerical relation

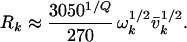5

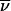_k is the geometric mean occupation number of mode k in the two states |i〉 and |i′〉, as defined in ref. 17.

Eq. 4 embodies a simplified version of the factorization model, which depends only on the molecular vibrational frequencies. The main assumption implicit in its prefactors is that bond dissociation energies must be several 10,000 cm⁻¹ (i.e., Eq. 4 could not be applied to weakly bound clusters). Of course, this model does not describe the molecular couplings with spectroscopic accuracy, but it is very useful when describing averaged quantities such as σ. The frequencies required in Eq. 5 were taken from the references listed in table 1 of ref. 11.

Simulations.

In ref. 14, a perturbation coupling criterion ℒ_ii′ was summed to yield the effective number N₁ of states |i′〉 that can directly mix with a state |i〉 in a normal mode basis (19, 22). N₁ has an energy window proportional to Q^1/2ω̄, where ω̄ is the average molecular frequency. It serves as a conservative selector for candidate states participating in IVR (18, 22). Here we introduce a related criterion

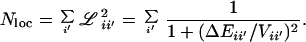6

N_loc is a local state count with a smaller energy window proportional to V_anh (22). Although N₁ and N_loc vary in parallel fashion, the latter is a more direct measure of local state density (22). In practice, Eq. 6 was computed by a direct state count of all levels of the correct symmetry in a 1000-cm⁻¹ window around the C—H stretching state of interest, using Eqs. 4 and 5 for the evaluation of the matrix element V_ii′. Some tests with a 3000-cm⁻¹ band showed deviations of less than 5%, which are negligible considering the approximate nature of Eq. 6. The resulting values of N_loc were used instead of ρ_tot to reanalyze the experimental values of the dilution factor σ.

Computed values of σ were also obtained for comparison with N_loc by using a local random matrix generated according to the prescription of the BSTR model (20). BSTR differs from the deterministic use of Eqs. 4 and 5 in that the distance Q between two states |i〉 and |i′〉 is drawn from an exponential distribution that simulates actual molecular distributions of Q, subject to a “triangle rule” constraint (20). BSTR matrices were varied in two ways: increasing N_loc (done by increasing ρ_tot, then computing N_loc by using Eq. 6) shows how σ decreases with increasing N_loc; sampling Q values from different nominally identical pseudorandom distributions shows how σ fluctuates because of accidental resonances at a given value of N_loc. The BSTR model was also used to calculate distributions of σ at a given local coupling strength. This was done simply by binning σ values from different randomly seeded calculations into constant intervals.

Analytical Model.

The analytical treatment of a model for the vibrational Hamiltonian of a molecule that embodies the local coupling described by Eq. 3 (15–17) begins by assuming that each element V_i,i′ is random with mean value 〈|V_Q|〉. The theory uses a self-consistent analysis of the most probable flow rate through its most probable value, k_IVR^mp. According to theory the transition depends on

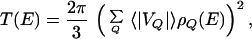7

where ρ_Q(E) is the local density of resonantly coupled states Q away. k_IVR^mp is finite only when T > 1, meaning that there is facile energy flow. On the other hand, for T < 1 energy flow is confined to a subset of the energetically allowed states. Thus T = T_crit is the transition criterion. While this criterion for molecules concerns interacting vibrational motions, a similar analysis was later made for fermions interacting with each other. Altshuler et al. (10) have used an approach analogous to the Logan–Wolynes theory to study quasiparticle lifetimes in finite size quantum dots, yielding such a criterion for this system also.

The self-consistent analysis suggests that when T(E) < 1, the dilution factor σ is distributed according to the distribution

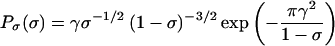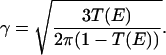8

Eq. 8 predicts a rather broad range of σ at a given T(E), which, as we shall see, is also apparent in the experimental data. Binning the experimental distribution of σ allows direct comparison with Eq. 8.

The empirical parameter N_loc described in the previous subsection is closely related to T, as both are proportional to (V_i,i′/ΔE_i,i′)² for two states in the perturbation limit, corresponding to a mixing intensity. Essentially, N₁, N_loc, and T represent different statistical moments of a quantum connectivity distribution. Unlike T, N_loc is sensitive to accidental resonances. At low density of states, one would therefore expect N_loc to fluctuate mostly on the high side of T in a correlation plot between the two quantities.

RESULTS AND DISCUSSION

Calculations were carried out for all C—H stretching fundamentals listed in table 1 of ref. 11 for which σ was determined experimentally. This process yielded a total of 39 separately determined dilution factors, or 99 data points if quasidegenerate bands in the experimental data are counted separately. The molecules, C—H fundamental T values, and range of N_loc values calculated for the experimentally observed fundamentals in each molecule are summarized in Table 1.

Table 1.

Molecules, dilution factors, T values, and N_loc values

Molecule	σ	T	Nloc	Molecule	σ	T	Nloc
Methane	1	—	0.005	Cyclopentene	0.003	0.89	5.7
Ethylene oxide	0.5	0.015	0.16		0.008	0.70	5.0–5.1
	0.7	0.018	0.12		0.01	0.35	3.1–4.5
	0.8	0.01	0.10		0.01	0.67	2.9
Cyclopropane	0.7	0.0035	2.4		0.02	0.4	2.3–3.9
	0.3	0.0174	1.3	2,3-Dihydrofuran	0.5	0.2	5.3
Ethane	1	0.01	1.1	Tetrahydrofuran	0.01	0.75	2.2–4.0
	0.8	0.02	2.9	Cyclopentanone	0.003	1.3	2.6–5.5
Oxetane	1	0.13	1.84	Norbornene	0.01	1.6	6.8–12
	1	0.18	0.22		0.1	2.6	10
	1	0.22	0.29	Cyclopentane	0.01	1.7	6.1–9.0
	1	0.22	0.14		0.02	1.4	6.2
Methyl formate	0.3	0.05	1.67		0.09	0.5	3.2–5.2
Propylene oxide	0.02	0.5	2.4	Cyclohexane	0.005	1.3	8.1–12
	0.02	0.6	1.8		0.01	2.2	9.4
Fluorobenzene	1	0.9	2.2–3.7		0.01	1.1	—
Cyclobutanone	0.4	0.24	1.3–3.2	Isobutane	0.05	0.2	3.8
	0.3	0.4	1.5	2-Methyltetrahydrofuran	0.003	1.2	11–13
Propane	0.2	0.08	3.5		0.004	1.5	13
	0.4	0.26	0.4–1.1

From the data of Stewart and McDonald (11), modes other than C—H stretches and results where σ had only an upper bound were excluded. The mean value of the N_loc is about an order of magnitude larger than T; the correlation between the two is shown in Fig. 1. Where Stewart and McDonald listed a group of bands under one frequency, ranges are given for N_loc indicating the minimum and maximum values obtained numerically for the bands near that frequency. 

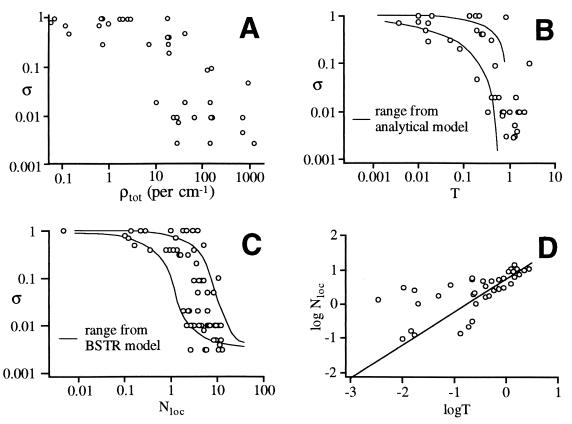
The main results are summarized in Fig. 1. Fig. 1A shows the original plot of experimental dilution factor vs. the total density of states, adopted from Stewart and McDonald (11). Although σ decreases for larger molecules, the transition is not very sharply defined. Fig. 1 B and C shows the same experimental results replotted against the analytical local coupling parameter T and the computed local parameter N_loc. The resulting points map out a clear transition, with midpoints at T ≈ 0.3 for the analytical LRMT, and N_loc ≈ 3 for the deterministic numerical model.

Figure 1.

Experimental dilution factors σ correlated with different molecular quantities. (A) Plotted vs. the total density of states. (B) plotted vs. T, an analytical local coupling strength. (C) plotted vs. N_loc, a computational local number of coupled states. (D) Correlation between N_loc and T. Because T and σ extend over several orders of magnitude, all plots are shown on log–log scales.

The transition to free energy flow is complete at T = 1 (ref. 16). For N_loc, the transition should occur slightly above 1: if N_loc = 1, each state is on average coupled to one other state. Apparently, this is not quite sufficient for free energy flow because it permits isolated pairs of coupled states in state space. As N_loc exceeds 1, the likelihood of isolated clusters of coupled levels rapidly decreases, and by N_loc = 10 every basis state is integrated into the quantum connectivity network.

This behavior of N_loc near the transition is exactly what is found. Fig. 1D plots the correlation between N_loc and T, indicating good correlation between the two types of calculations. N_loc is about one order of magnitude larger than T, reflecting the shift in the transition midpoint. The correlation is strongest for high local densities of states, where accidental resonances are unimportant. The scatter gets larger for small values of T, where the detailed nature of accidental resonances in Eq. 6 becomes important. As expected, N_loc tends to be larger than T at sparse densities of states because it involves no averaging over resonances.

A critical result of Fig. 1 is that even a fairly large molecule such as cyclohexane, with a total vibrational density of states exceeding 1,000 per cm⁻¹ at 3000 cm⁻¹, can have a relatively small local density of coupled states. None of the molecules investigated by McDonald and coworkers fall far beyond the onset of free IVR. One should therefore be very cautious in assuming that an organic molecule with even 20–30 atoms already supports unfettered vibrational energy flow (19, 24).

One would also expect that near T ≈ N_loc ≈ 1, IVR will be exquisitely sensitive to the details of the molecular coupling structure. This is so because at the transition, a single state or a few states coupled to the initial state of interest can make the difference between localization and free energy flow. Depending on the nature of accidentally small ΔE_ii′ and the distribution of matrix elements V_ii′, nominally similar states or molecules can therefore have very different dilution factors. This effect should be particularly pronounced for edge states (14) (the CH stretching fundamentals in the experiments), which have the sparsest coupling structure.

Such dispersion of σ is again borne out by the simulations for N_loc and for T derived analytically. The solid lines in Fig. 1 B and C indicate the range of dilution factors predicted by the analytical result and by the BSTR model, showing large fluctuations in the transition region (see below). Although the BSTR calculation in Fig. 1C is for interior states (those with many active vibrational modes), it matches the experimentally observed edge states (the CH fundamentals). Again, the analytical model explains this result: only the speed with which ergodicity is established (IVR rate) is affected by the sparser coupling structure of edge states, whereas the location of the ergodicity transition depends only on the parameter T in Fig. 1B, representative of couplings among the interior states.

Above the ergodicity transition, the measured dilution factors should be similar to the inverse of the number of states participating in IVR—i.e., the entire energetically and symmetry allowed state space should be filled. To check whether this is indeed the case, we estimated the participation number N_p^(max) using Eq. 2, where the linewidth was computed by LRMT and the total state density, by direct count. For nearly all cases where T > 1, N_p^(max) ≈ σ⁻¹ as expected. For some of the smallest dilution factors, which are the most difficult to measure (e.g., for 2-methyltetrahydofuran), we found a theoretical value about an order of magnitude smaller than observed.

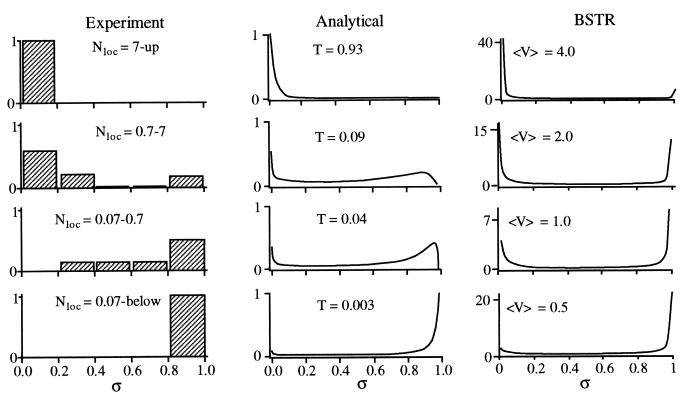
An exact prediction of any specific σ would of course require a quantum dynamical calculation on a nearly exact potential surface, as has been done for smaller systems (5). However, both the analytical model (16) (Eq. 8) and numerical simulations (19, 21) make specific predictions about the distribution of dilution factors as a function of T or N_loc. Fig. 2 shows the experimental σ values from Fig. 1C binned according to different ranges of N_loc. The most striking feature of the distribution is its bimodal behavior at values of N_loc near the transition: either states tend to be isolated or IVR results in efficient state mixing with σ < 0.2. The analytical result in Eq. 8 is plotted for comparison, and it shows the same bimodal behavior emerging from LRMT. Numerical simulations in Fig. 2 using the BSTR Hamiltonian matrices are also bimodal, corroborating Eq. 8.

Figure 2.

Distribution P(σ) of dilution factors for four different values of the locally coupled number of states. (Left) Experimental distribution obtained by binning the data in Fig. 1C into the N_loc ranges shown. (Center) Analytical P(t) (normalized to 1) from Eq. 8 for four values of T. (Right) Numerical BSTR P(t) (normalized so ∫dσP(σ) = 1) for different coupling strengths.

In conclusion, the transition from weak anharmonic resonances and restricted energy flow to free energy flow takes place over a narrow range of the effective locally coupled number of states. By comparing with experimental data, we find that within this range (0.8 < N_loc < 8 or 0.2 < T < 2), state-specific “accidental” resonances are important contributors to σ. In this transition region, the high sensitivity to “accidental” resonances results in a bimodal dilution factor distribution. Beyond the transition range, energy flow reaches all the accessible state space and σ becomes correlated with the total density of states. However, even surprisingly large molecules can show nonergodic behavior due to the local nature of IVR.

ABBREVIATIONS

IVR

intramolecular energy flow (intramolecular vibrational redistribution)

LRMT

local random matrix theory

BSTR

Bose statistics triangle rule