Intramolecular vibrational dephasing obeys a power law at intermediate times

Abstract

Experimental intramolecular vibrational dephasing transients for several large organic molecules are reanalyzed. Fits to the experimental data, as well as full numerical quantum calculations with a factorized potential surface for all active degrees of freedom of fluorene indicate that power law decays, not exponentials, occur at intermediate times. The results support a proposal that power law decays describe vibrational dephasing dynamics in large molecules at intermediate times because of the local nature of energy flow.

The standard description for the time evolution of pure vibrational dephasing in large isolated molecules (intramolecular vibrational relaxation or redistribution; IVR) is based on the Golden Rule formulae:

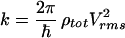1a

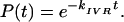1b

Eq. 1 was successfully applied to radiationless transitions by Jortner and coworkers (1) and to IVR by Freed (2). Some limitations of Eq. 1 as applied to pure dephasing were clear early on (3): it does not properly represent the t = 0 rolloff due to a finite (although large) number of participating eigenstates; it does not represent the quantum beats, which arise even in large molecules at low vibrational energy; and it does not describe the leveling-off of P(t) at a value greater than zero due to the finite size of molecular state space (4). However, it is generally thought that Eq. 1b adequately describes the dynamics of a sufficiently large and highly excited molecule (“statistical limit”) on all but the longest time scales.

For a general manifold of coupled states, Eq. 1 is a result of first order perturbation theory, where V_rms is an average over individual couplings V_0i from the bright state |0> to a prediagonalized manifold {|i>}. It can be systematically augmented by a perturbation expansion (2), but such a treatment is difficult to connect to standard molecular parameters. The prediagonalized manifold {|i>} offers no additional insights or practical time savings compared with full diagonalization because V_rms or its generalizations are not related to known spectroscopic parameters (e.g., cubic potential constants) in a simple fashion (5). Hence, there has been an ongoing discussion, both experimental (6) and theoretical (5, 7–10), that Eq. 1a should be represented in terms of local molecular parameters rather than the total density of states ρ_tot. There has been much less focus on the question of whether the IVR process can be globally described by an exponential rate law at all (11). This latter question will be considered in this paper.

In 1993, a landmark paper by Schofield and Wolynes (11) introduced a different description of IVR time evolution, which emphasizes the local nature of energy flow through state space. By introducing a size scaling law for quantum transport in the molecular state space, they concluded that vibrational dephasing is better represented by a power law

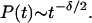2

The coefficient δ was proposed to vary from 2 near the IVR threshold, to 𝒩 − 1 for a molecule with 𝒩 vibrational modes well beyond the IVR threshold. Power law decays were observed subsequently at intermediate times in quantum dynamics simulations of IVR by Bigwood and Gruebele (12) and others (5, 13). Although Eq. 2 cannot apply at very short or very long times for reasons already discussed above, its predictions differ drastically from the Golden Rule at intermediate times. IVR appears as a multi-time scale process, increasingly slowed by localization effects as dephasing proceeds.

In the early to late 1980s, the Zewail (14, 15) and McDonald (16, 17) groups conducted a series of pioneering experiments that directly measured the survival probabilities P(t) associated with IVR in large organic molecules such as anthracene (14) or fluorene(16). The picosecond fluorescence depletion method described by Kauffman et al. achieved a time resolution as low as 2 ps (16), limited only by the probe laser duration. Such measurements allow the determination of IVR transients with a dynamic range of two orders of magnitude in time.

The present analysis shows that some of this data is not well described by exponential decay laws even in the absence of significant quantum beats. Instead, simple model fits and full quantum dynamics simulations using the factorized potential model of Madsen et al. (18) qualitatively validate the Schofield–Wolynes proposal, allowing the range of validity of exponential rate processes in IVR to be better defined.

Model and Computations

An important motivation for quantum dynamics simulations is that they can be carried out without rotational excitation or some of the other complications inherent in experiment. They can therefore reaffirm that carefully designed experiments are indeed not hampered by inhomogeneous rotational or other effects.

Full quantum calculations of the IVR dynamics of a large molecule require two ingredients: a potential energy surface (PES) and a means of propagating an initial state on it. For molecules such as anthracene and fluorene, with 𝒩 > 50 anharmonically coupled vibrational degrees of freedom, ab-initio approaches or standard propagators suitable for small systems are not applicable.

For the vibrational Hamiltonian, the factorized normal mode surface was therefore used (12, 18, 19). A related method also has been reported by Bullock et al. (20) Our approach provides a very compact representation of the PES in terms of ladder operators

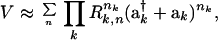3

where n = Σn_i = 3,4,^… is the overall order of the coupling terms and n_i the power to which individual unitless normal coordinates (a_k^† + a_k) are raised. The R_i approximately factor the potential constants. As discussed elsewhere (19), this representation is particularly good for highly connected molecules and ring compounds and can predict IVR spectra and transients semiquantitatively (5, 12, 21). Because a force field for fluorene is not available, a scaling law for the factors R_i was used to calculate the necessary high order potential constants:

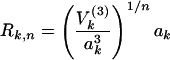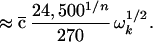4

The first line is the definition of R_k,n given in ref. 18: V⁽³⁾ is the diagonal cubic molecular anharmonicity, and a is a Born–Oppenheimer scaling parameter on the order of 0.05–0.2 depending on the vibrational mode (not to be confused with the ladder operators a). The second line is the result of fitting the first line to two prototype organic molecules from ref. 18, combined with the fact that V⁽³⁾ ∝ ω^3/2 and a ∝ ω^1/2. 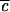lies between 1/2 and 1 to take into account bond locality effects (19).

Vibrational frequencies for fluorene were taken from ref. 22, except for the unobserved A₂ symmetry modes which were estimated using a PM3 semiempirical force field (Table 1) (23). Available S₁ vibrational frequencies for anthracene (24) were combined with S₀ frequencies scaled by 0.95 (25, 26).

Table 1.

A₂ symmetry harmonic frequencies of fluorene (H₄C₆CH₂C₆H₄) estimated from a PM3 semiempirical force field

ω23 = 125 cm−1	ω28 = 792 cm−1
ω24 = 259 cm−1	ω28 = 863 cm−1
ω25 = 416 cm−1	ω30 = 896 cm−1
ω26 = 509 cm−1	ω31 = 961 cm−1
ω27 = 747 cm−1	ω32 = 1,003 cm−1

All other frequencies and symmetry assignments were taken from ref. 22. 

Matrix elements of Eq. 3 were evaluated in a filtered normal mode representation. The perturbative “L filter” of ref. 12 was used to construct a tiered set of basis states and prune unconnected states successively in each tier. However, no tier structure was imposed on the off-diagonal matrix elements, and all matrix elements above a cutoff value for L were included. Convergence was monitored as a function of L, of the energy window δE around the bright state, and of the PES order. L ≈ 0.001, δE ≈ 400 cm⁻¹, and at least a fifth order surface in six tiers were required; the small energy window was possible because the C-H stretching vibrations are not strongly coupled to the ≈1,800-cm⁻¹ experimental bright state combination bands, eliminating the largest cubic terms and reducing the effective dimensionality. The filter algorithm was modified to take into account C_2v or D_2h vibrational symmetries and to limit the search radius in state space, resulting in a smaller Hamiltonian block of the correct bright state symmetry. Matrix element signs were assigned at random (5, 19).

An eigenstate-resolved spectrum was calculated using the matrix fluctuation-dissipation (MFD) algorithm (27, 28), which is a nonrecursive analog of the recursive residue generation method (RRGM) algorithm (29), to obtain spectral intensities without knowledge of the molecular eigenvectors. Matrices ranged in size from 8,000 to 25,000 active states. P(t) was calculated from the eigenvalues and intensities using the standard coherence sum expression (30). IVR wave packets also were calculated using the shifted update (SUR) propagator to analyze their localization (31).

The computational results were obtained for the rotationless case J = 0, which precludes exact agreement even with magic angle-detected molecular beam experiments. The most significant rotational contributions to dephasing are due to the vibrational dependence of the rotational constant and to Coriolis coupling (32). The vibrational dependence of the B_i would lead to additional averaging of quantum beat structure in experiments as compared with theory; it is an inhomogeneous effect due to phase-uncorrelated initial rotational populations of molecules. The Coriolis interaction scales as 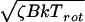, where ζB is the average Coriolis coupling and T_rot the rotational temperature. Under the experimental conditions, this corresponds to a time scale of >1 ns, and should not significantly affect the IVR behavior for molecules as large as fluorene at times <500 ps. It could be a factor in cyclohexylaniline due to internal rotation couplings.

Data Analysis

The calculated as well as the experimental IVR P(t) transients were fitted either to Eq. 1b, or to empirical threshold-power law expressions, which have proved useful in other model calculations (33). The two expressions used here are

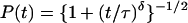5a

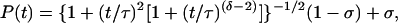5b

where −δ/2 is the asymptotic power law exponent. Both expressions approach 1 as t → 0. Both expressions decay to zero much more slowly than an exponential, indicative of a generic bottleneck in IVR. Eq. 5a has the advantage of simplicity. For δ ≥ 2 Eq. 5b has the correct cosine roll off at small t and the correct average asymptotic behavior. It could describe in principle an averaged P(t) over the entire time scale. In our fits to the data, the normalized experimental noise exceeded σ in all cases, precluding a determination from experiment.

The fluorene magic angle time resolved fluorescence depletion transients (TRFD) of McDonald and coworkers (16) reflect IVR from vibrational features in the excited ¹B₂ S₁ electronic state. The long fluorescent/radiationless decay lifetime (≈18 ns) (16), large quantum yield (34), and highly single exponential of the electronic band origin indicate little vibronic activity in this molecule. Similarly, the ¹A₁ S₁ state of cyclohexylaniline has a long decay lifetime (≈7.5 ns) near the band origin and high fluorescence yield (17). It represents a class of molecules even larger than fluorene, with internal rotation modes. The anthracene molecule studied via direct fluorescence by Felker and Zewail (14) also has a high quantum yield and long fluorescence/radiationless lifetime (6.5 ns). There is no evidence for chemical reaction below 2,000 cm⁻¹ in these molecules.

The uncorrected decays can be grouped into three general categories: (i) slow single exponential decays due to fluorescence/radiationless processes with or without large quantum beats (e.g., 0⁰ band); (ii) decaying irregular quantum beats superimposed on fluorescence/radiationless decays (e.g., 1,792-cm⁻¹ band of anthracene); and (iii) nearly smooth fast decays with at most small residual quantum beats superimposed on slow exponential fluorescence/radiationless decays (e.g., 1,886-cm⁻¹ band of fluorene). Here, we consider the latter two cases which lie near or in the “statistical limit.” It is clear, even on visual inspection (16), that the IVR part of these decays is not well described by exponential functions (Fig. 1).

Figure 1.

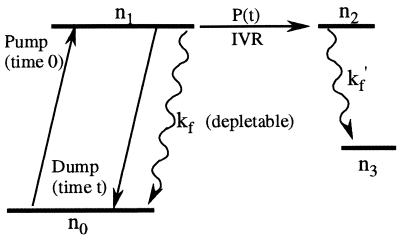
Simplified four-level scheme for IVR. The dephased manifold is represented by a population n₂(t) connected to n₁(t) by a general decay law P(t). In TRFD, the resonant dump pulse cannot access population in n₂ at long times, resulting in a transient linearly dependent on the IVR signal P(t) with an added slow dependence due to fluorescence k_f/k_f′ and radiationless transitions (35). In direct fluorescence detection, the signal decays both due to IVR and due to slower fluorescence/radiationless losses, depending on what fraction of the fluorescence from n₁ and n₂ is detected.

As in direct fluorescence, in TRFD the IVR is detected linearly because the resonant dump pulse cannot dump population transferred to “relaxed” states by dephasing (Fig. 1). In both TRFD (35) and direct fluorescence experiments (30), a decay due to fluorescence/radiationless processes is superimposed on the IVR P(t). This decay is of no interest here, and can be removed from the data as follows:

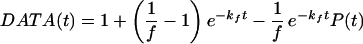6a

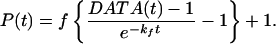6b

Eq. 6a is obtained by solving the coupled differential equations for population transfer in the four-level system of Fig. 1 with a generalized rate law P(t); the main assumption is that fluorescence/radiationless processes (e^−k_ft) and P(t) must be statistically independent. This approach is analogous to the well-known treatment for radiationless processes (36). The factor f depends on the relative amount of fluorescence collected from levels n₁ and n₂ in Fig. 1, on differences in fluorescence/nonradiative rate constants k_f and k_f′, and in TRFD on the degree of saturation. Because it is a population analysis, Eq. 6 neglects laser coherence effects. In the TRFD studies, the pulse width of 2 ps is much shorter than the IVR or fluorescence time scales. Therefore, overlapping pulse data needed not to be considered and a population analysis is sufficient.

The TRFD data must be scaled to go from 0 to 1 for use in Eq. 6b, whereas direct fluorescence data must be scaled to go from 1 to 0 as t → ∞. Use was made of the “two-lobed” feature of the raw TRFD data (16) to improve the signal-to-noise ratio by a factor of 1.4 by averaging.

Because the IVR time scales analyzed here are approximately a factor 50 faster than fluorescence/radiationless time scales in these molecules, it is very easy to remove the uninteresting exponential component from the data. Robustness of the resulting P(t) was checked in various ways. (i) Exponentials with lifetimes up to 30% shorter than measured lifetimes were used in Eq. 6; (ii) f was varied within the maximum bounds compatible with the IVR and fluorescence components in the data; and (iii) the baseline was shifted to as high a value as compatible with the noise in the data to favor more rapidly decaying exponential functions. None of these attempts affected the conclusions in the next section, although they contribute to the uncertainties in Table 2.

Table 2.

Power law coefficients determined by fit to experimental data and quantum dynamics simulation

Molecule	Band	τ, ps	δ	Equation	kexp, ps−1	σ
Fluorene	1,425 cm−1	19(3)	3.2(4)	5b	0.03
	1,707 cm−1	25(3)	2.3(4)	5b	0.02
	1,886 cm−1	5.0(5)	2.0(5)	5b	0.11
	1,953 cm−1	6.0(5)	2.2(5)	5b	0.13
	2,045 cm−1	7.0(1.0)	2.5(3)	5b	0.08
Cyclohexylaniline	1,276 cm−1	4.0(5)	1.1(2)	5a	0.05
	883 cm−1	5.0(5)	1.1(2)	5a	0.05
Fluorene calc.	1,886 cm−1	2.0	2.0	5b	0.16	0.008
	1,953 cm−1	0.4	2.9	5b	0.40	0.005

Results and Discussion

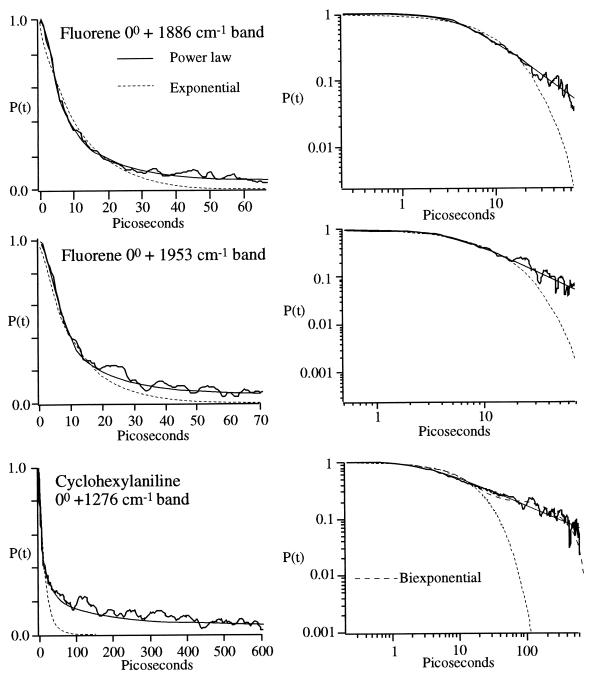
Fig. 2 shows three examples of experimental P(t), as well as fits to Eqs. 1 and 5, both on a linear and log–log scale. The exponentials are best fits at short times. Examination of seven smooth P(t) yielded not a single case that could be adequately described by a single exponential. Better descriptions were possible with a three-parameter double exponential function. All of the cases were best accounted for by the two-parameter models in Eq. 5 with χ² values at least a factor of 2.2 below the other fits. The relevant information is summarized in Table 2. The addition of Gaussian noise to an exponential function will appear to “raise” its long-time envelope on a log–log plot but also introduces undefined regions (P(t) < 0). The decays in Fig. 2 could not be simulated by such “noisy exponentials,” as the observed slowing of the decay at long times greatly exceeded the signal-to-noise limitations of the experiment. The observed nonexponential effect is very robust.

Figure 2.

Experimentally observed IVR decays obtained by McDonald and coworkers (16, 17), fitted to exponential and power law models given in the text. The log–log plots clearly become linear with small quantum beats at long times, before eventually settling to a constant average value. The exponential function provides a good fit only at short times where I(t) ≥ 1/e. The Bottom also shows a biexponential fit, which provided a reasonable representation of the cyclohexylaniline data due to the low coefficient of the power law. However, in all cases χ² of the fit was a least a factor of 1.8 better with the two-parameter power law model than with the three-parameter biexponential.

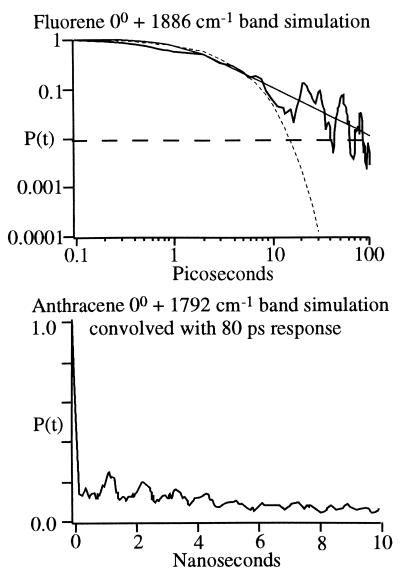
Fig. 3 (Top) shows a quantum dynamics simulation of the 1,886-cm⁻¹ band of fluorene, tentatively assigned to a v₅ + v₃₉ B₁ symmetry combination band. All but the 10 hydrogenic stretching modes were active in the calculation. Without any adjustable parameters, the calculation yields a 6-ps 1/e lifetime, which compares favorably with the 11-ps experimental value. The calculation displays power law behavior with an exponent δ = 2, identical to the experimental value of 2.0. A similar calculation for the 1,953-cm⁻¹ v₄ + v₉ A₁ combination band yields a 2.5-ps lifetime and δ = 2.9 (8 ps and 2.2 in experimental fits, respectively).

Figure 3.

(Top) Quantum dynamics calculation with 53 active vibrational modes for the 1,886-cm⁻¹ combination band of fluorene. The calculation shows the same characteristic power law behavior as experiment before settling into a constant value of σ. Because the power law behavior becomes evident only once P(t) drops below 0.1, its effect on the lineshape is subtle, resulting in a lineshape with slight additional intensity near the line center when compared with a Lorentzian. A power law decay or slightly non-Lorentzian line shape are a clear indication that the couplings V_0iare correlated with the bright state energy. Eq. 1a neglects such correlations. (Bottom) quantum dynamics calculation with 56 active modes for the 1,792-cm⁻¹ combination band of anthracene. The beat structure is similar to experiment, indicating a coupling regime on the threshold of power law behavior (see Fig. 4).

Fig. 3 (Bottom) shows a quantum dynamics simulation of the “dissipative quantum beat” IVR in the 1,792-cm⁻¹ mode of anthracene observed by Felker and Zewail, assigned as v_5̄+ v₁₂ (24). Although the envelope is not sufficiently smooth for a powerlaw fit, the result shows beat structure similar to experiment (Fig. 4) and represents an important transition to power law behavior, discussed in more detail below.

Figure 4.

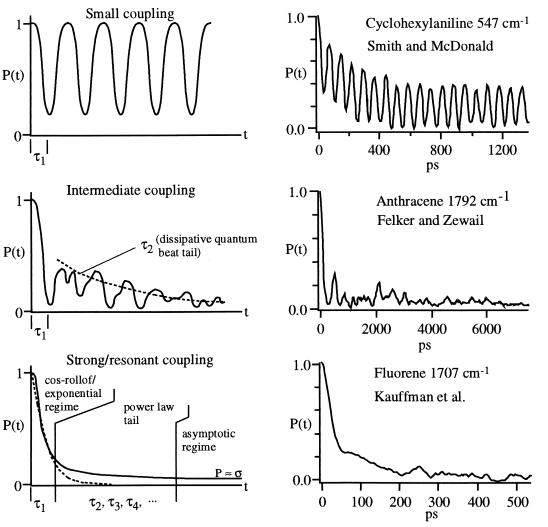
Schematic illustration of the behavior of P(t) as the relative anharmonic coupling strength is scaled from zero to one. Beyond isolated resonance (Top), at least two time scales arise even if the quantum beat periods are neglected (Middle), which eventually give rise to a multiplicity of timescales at intermediate times (Bottom); in the last case, the short time dynamics can still be described by a cosine rolloff and exponential decay, but the dynamics are power law at intermediate times before P(t) settles into a constant value σ. The right-hand figures illustrate these regimes with actual experimental data obtained by the Zewail (Middle) (14, 15) and McDonald groups (Top and Bottom) (16, 17).

These calculations demonstrate that the filtered factorization PES model of Eqs. 3 and 4 yields IVR decays, which compare favorably with experimental observations. The main difference is that the model tends to slightly underestimate lifetimes, whereas overestimating the size of the residual quantum beats. The first is most likely due to an overestimate of low order terms in Eq. 4 compared with high order terms. Presently, there is not enough data to make it worthwhile to adjust the coefficients in Eq. 4 empirically, but such fitting may be a useful refinement of the model in the future. The larger predicted quantum beats are most likely due to the lack of rotational averaging for J = 0. Different incoherently excited rotational manifolds in the experiment probably have slightly different level spacings, averaging out quantum beat structure.

By adjusting the parameter 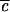between 0 and 1, the effective strength of the anharmonic coupling can be varied continuously in the computations. The result, illustrated schematically in Fig. 4, indicates that the long time tail of P(t) is due to the same localization phenomena that result in quantum beats. When 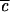→ 0, no lifetime can be defined, and oscillations of large amplitude with period 2τ₁ occur. As 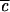increases, the quantum beats eventually begin to decay upon successive recurrence. There are now at least two time scales: τ₁ for the initial decay (former “half quantum beat”), and τ₂, which characterizes the decay envelope of the quantum beats. τ₁ is often referred to as the “IVR lifetime” corresponding to the initial 1/e decay. As 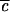increases further, the spectral line profile fills in and more quantum beats of different frequencies combine to yield a smooth envelope that persists well beyond the “exponential” scale τ₁ and has the characteristic power law dependence on time, before settling into a constant average value σ.

Examples of experimental data (with the fluorescence/radiationless exponential component removed) from the Zewail (14, 15) and McDonald (17) groups further illustrate these regimes in Fig. 4. It is worth noting that computational (5, 12) and analytical (5, 11, 12) predictions do not rule out exponential IVR decays at short times. Rather, they define beyond what time scale experiments cannot be modeled by the simple Golden Rule any more. Computations indicate that for X–H-stretching overtones (12), this time scale is rather long; for backbone combination bands (5, 12, 33) including the data presented here for fluorene and cyclohexylaniline, the time scale is rather short and no significant exponential phase exists.

The localization effects that slow down IVR at increasingly long times are due to both bond locality (18) and localization in state space (7, 9). The latter arises because the full vibrational Hamiltonian is only weakly resonant even at fairly high energies and retains memory of the uncoupled normal mode-like states in the form of spectral features (33). This fact is evident when the fluorene IVR wavepacket (calculated using SUR; ref. 31) corresponding to Fig. 3 (Top) is examined at 40 ps: only 15 of the total 13,200 basis states in the calculation account for 50% of its magnitude, indicating localization in a small fraction of normal mode state space at early times.

The exponents δ in Table 2 all lie close to 2. This result agrees well with the lower limit of the analytical prediction by Schofield and Wolynes (11), which posits δ = 2 at the localization threshold. However, the analysis of cyclohexylaniline shows two bands with δ ≈ 1.1. Because δ can be interpreted as the dimensionality of the IVR manifold in state space, this value is surprisingly low. There are two alternative explanations. First, the small exponent could be due to contributions other than pure IVR to P(t). Although fluorene transients were essentially independent of beam temperature (16), experiments indicate some dependence for cyclohexylaniline (17), which implicates Coriolis effects. Further experiments at the lowest possible beam temperatures are needed to resolve this issue. Second, a more specific bottleneck could be present in cyclohexylaniline than those suggested by analytical power law scaling (11), resulting in approximately biexponential behavior. Although it accounts extremely well for intermediate time IVR, it should be kept in mind that power law scaling is still a “zero order” model. Pronounced resonances in the Hamiltonian could result in time scale separations leading to distinguishable multiexponential components in some cases, particularly at lower energies.

At the other extreme, no values of δ much greater than three have been observed in the present work or in previous quantum dynamics simulations of SCCl₂ at 12,000 cm⁻¹ (δ ≈ 3) (5) and 1-propyne at 9,000 cm⁻¹ (δ ≈ 2.2) (12). There are two possible explanations. Either the experiments and simulations were not carried out at sufficiently high energies or localization effects “clamp” the value of δ above threshold. The latter possibility is particularly appealing in large molecules, in which bond locality limits the coherent interaction of different parts of the molecule even if σ indicates maximal access to the allowed state space at long times. The manifold on which the IVR wavepacket moves in state space could then have a low dimensionality δ. Finally, power laws with large exponents −δ/2 would appear more like exponentials. It thus may be difficult to observe large power law exponents experimentally.

These issues can be addressed in two ways: First, experiments and simulations at higher energies should be carried out to see how δ increases with vibrational energy; indications at present (e.g., SCCl₂ simulations) are that δ will increase very slowly with energy. Second, there is a need for extensions of the analytical theory, which directly connect δ to molecular properties such as vibrational frequencies, anharmonicities, directionality of energy flow (37), and total available vibrational energy.

In conclusion, there is strong experimental and computational evidence that the best “zero-order” picture of IVR at intermediate times (0.1 > P(t) > ρ) involves the power law decays proposed by Schofield and Wolynes (11). The simplest version of the Golden Rule and low order PES are useful only at short times, typically when P(t) > 0.1 for combination bands of backbone vibrations. The slowing of IVR at ever longer time scales results from the fundamentally local nature of the vibrational Hamiltonian. This property of dephasing could have important consequences for polyatomic molecular control (33).

ABBREVIATIONS

IVR

intramolecular vibrational relaxation or redistribution

TRFD

time-resolved fluorescence depletion

PES

potential energy surface