Anisotropic Mechanical Properties of Magnetically Aligned Fibrin Gels Measured by Magnetic Resonance Elastography

Abstract

The anisotropic mechanical properties of magnetically aligned fibrin gels were measured by magnetic resonance elastography (MRE) and by a standard mechanical test: unconfined compression. Soft anisotropic biomaterials are notoriously difficult to characterize, especially in vivo. MRE is well-suited for efficient, non-invasive, and nondestructive assessment of shear modulus. Direction-dependent differences in shear modulus were found to be statistically significant for gels polymerized at magnetic fields of 11.7T and 4.7T compared to control gels. Mechanical anisotropy was greater in the gels polymerized at the higher magnetic field. These observations were consistent with results from unconfined compression tests. Analysis of confocal microscopy images of gels showed measurable alignment of fibrils in gels polymerized at 11.7T. This study provides direct, quantitative measurements of the anisotropy in mechanical properties that accompanies fibril alignment in fibrin gels.

1. Introduction

Structural anisotropy of soft tissues varies from strongly anisotropic skeletal muscle to weakly anisotropic brain tissue (Fung, 1993). Anisotropy in fibrous tissues is primarily due to the alignment and organization of the extracellular matrix components: collagen, fibrin and elastin (Fratzl, 2008). Empirical measurements of structural anisotropy from optical and electron microscopy have been performed for two dimensional (2D) soft tissue in vitro at different length scales (Karlon et al, 1999; Sander and Barocas 2009). Structural anisotropy has been characterized in vivo in three dimensions (3D) by magnetic resonance based diffusion tensor imaging (DTI) (Pierpaoli and Basser, 1996). The dependence of nuclear magnetic resonance properties of anisotropic tissues on their orientation in the static magnetic field had also been used to characterize structural anisotropy (Xia, 1998; Haken and Blumich, 2000).

Mechanical anisotropy, on the other hand, describes the direction-dependent mechanical response of soft tissue to applied loads. The degree of mechanical anisotropy also varies among soft tissues. Ligaments and tendons, for example, are much stiffer in tension along fiber directions than perpendicular to fibers (Quapp and Weiss, 1998). Heart muscle tissue is similarly highly anisotropic (Holmes et al., 2005). Non-load-bearing organs like brain tissue have weaker mechanical anisotropy and less is known about its relation to structural anisotropy.

Structurally anisotropic extracellular matrices (ECMs) based on collagen and fibrin, are of interest for a wide range of potential tissue engineering applications. Anisotropic ECMs influence cell micromechanics by a phenomenon termed “cell contact guidance” (Dubey et al., 2001). Load transfer from the macro to the microscale is influenced by extracellular matrix (ECM) microstructure; the local tissue anisotropy in turn affects cellular behavior (Saez et al., 2007). Anisotropic soft substrates are assumed to provide direction-dependent mechanical properties for cellular mobility and viability.

Structurally anisotropic matrices can be made by magnetic alignment of collagen or fibrin molecules (Yamagishi et al., 1990). Anisotropic soft tissue constructs have been created from fibrin gels polymerized in a magnetic field (Dubey et al., 2001). Differences in mechanical properties were inferred based on structural differences (i.e. fiber direction), but quantitative differences in gel mechanical properties were not measured (Dubey et al., 2001). The challenges of characterizing soft gels include gripping, loading, and measuring deformation accurately. Typically, anisotropic mechanical properties of soft tissues have been estimated by biaxial testing in 2D (Billiar and Sacks, 1997; Thomopoulos et al., 2007) and by unconfined compression testing in 3D (Wang et al., 2003; Cheng and Bilston, 2007; Van Loocke et al., 2006). Indentation-based methods have also been proposed for anisotropic materials (Cox et al., 2006).

Magnetic resonance elastography (MRE) is a noninvasive technique to measure tissue mechanical properties from images of propagating shear waves (Muthupillai et al., 1995). Since shear wave propagation speed depends on shear modulus and density, at a given frequency the wavelength is a direct correlate of shear modulus. MRE has been used to estimate tissue properties in several recent studies (Sack et al., 2008; Sinkus et al., 2005; Venkatesh et al., 2008). Notably, different wave speeds are observed in different directions in anisotropic soft tissues (Bensamoun et al., 2008; Chen et al., 2007; Papazoglou et al., 2006).

The current study incorporates MRE to estimate anisotropic mechanical properties of aligned fibrin gels. Results are complemented by in vitro tissue mechanical testing. Finally, the anisotropy in mechanical properties is compared to the structural anisotropy measured by confocal microscopy.

2. Methods

2.1. Fibrin Gel Preparation

Human plasminogen-free fibrinogen (EMD Biosciences, La Jolla, CA, product no. 341578) was dissolved in tris-buffered saline (TBS) (33 mM Tris, 8 g/L NaCl, 0.2 g/L KCl, pH 7.4) and dialyzed in TBS overnight in polymer tubing (Thermo Scientific, Rockford, IL, product no. 68700, 8,000 MWCO). The fibrinogen solution was filtered with a 5 μm filter, and the concentration determined by measuring light absorbance at 280 nm with a spectrophotometer. Equal volumes of fibrinogen and thrombin (Sigma-Aldrich, St. Louis, MO, product no. T4648) solutions were mixed with CaCl₂ solution yielding the final concentrations: 10 mg/mL fibrinogen, 25 mM Ca⁺⁺, and 0.2 NIH units/mL thrombin. The solution was poured into a 20 mm × 20 mm × 20 mm hollow plastic cube.

Gels were polymerized for 2hrs at room temperature (24°C). In one set of samples (n=7) the cube with fibrin + thrombin solution was placed in the center of the bore of an 11.7T MRI scanner (Varian, Inc., Palo Alto, CA). For each sample, a control sample was polymerized in an adjacent room outside the 5 gauss perimeter. A second set of samples (n=4) was polymerized in the bore of an MRI magnet with field strength of 4.7T. The direction of the magnetic field during polymerization, denoted by the unit vector e_B was recorded and marked on each sample.

2.2. Magnetic Resonance Elastography

MRE was performed in a 4.7T magnet (Oxford Instruments, Oxfordshire, UK) with a Varian imaging system (Varian Inc., Palo Alto, CA). A piezoelectric actuator (Model APA100M-NM, CEDRAT Technologies, Meylan, France) was attached with the cube to a rigid plastic base. The actuator arm was coupled to the surface of the gel in order to excite shear motion at 400Hz in either of two directions parallel to the gel surface, depending on the orientation of the cube. The actuator and gel assembly was placed in the transmit/receive coil of the scanner, and a standard spin-echo sequence, modified to include motion encoding gradients (Muthupillai et al., 1995; Atay et al., 2008), was used to acquire images. First, the actuator was excited to provide surface displacements in the direction of e_B (i.e., parallel to the axis of the sample that was aligned with the magnetic field when the gel was polymerized). Second, the specimen was rotated by 90° so that actuator shear wave motion in the gel was normal to e_B. Baseline MR images were obtained without imposed shear motion for both configurations (Fig. 1a, c).

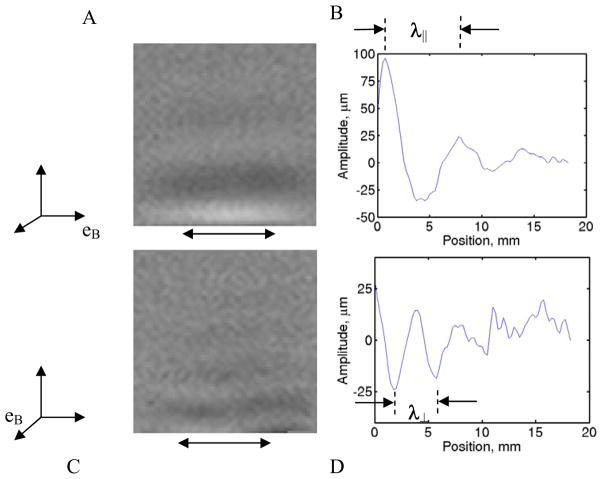
Figure 1.

Phase contrast plots from MRE show “snapshots” of propagating shear waves in a fibrin gel induced by horizontal displacement of the boundary. Boundary displacement is provided by a piezoceramic driver in each of two orthogonal directions with respect to the sample (A, C): parallel or perpendicular to the material-fixed direction (e_B) of the magnetic field (B₀=11.7T e_B) in which the gel was polymerized Line intensity plots (B, D) in the middle region of (A, C) show sinusoidal variation of displacement with position. The wavelength, λ is calculated from intensity peaks or valleys (C, D). The region of actuator contact with sample is avoided to eliminate boundary effects.

Standard MRE procedures were used to visualize wave motion. MRI data obtained during wave propagation were Fourier-transformed into the spatial (image) domain, normalized with respect to the baseline image, and phase-unwrapped (PhaseVisionTM, Loughborough, UK) to remove the 2π phase ambiguity, resulting in a phase-contrast image (Fig. 1a, 1c) with intensity proportional to displacement, u(x,y) (Atay et al., 2008). The wavelength λ of the shear wave pattern is related directly to wave propagation speed c and frequency f by c=λf. In a transversely isotropic material the propagation speed of a shear wave polarized either perpendicular or parallel to the normal of the plane of isotropy is $c_{\perp }=\sqrt{\frac{{\mu }_{\perp }}{\rho }}$ or $c_{\parallel }=\sqrt{\frac{{\mu }_{\parallel }}{\rho }}$. Here μ is the shear modulus, ρ is the gel density assumed equivalent to water density, and the subscript indicates whether displacements are parallel or perpendicular to the normal of the plane of isotropy (e_B, in this case). In this study, since the sample is approximately homogeneous, the wavelength was simply estimated from the average distance between successive peaks or valleys in the displacement images. The shear modulus governing the corresponding wave was calculated from the previous expressions as μ_⊥ = ρλ_⊥² f² or μ_|| = ρλ_||² f².

2.3. Unconfined compression tests

Fibrin gels were removed from their mold after MRE testing, placed in PBS and stored at 4°C. On the day of testing the gels were warmed to room temperature (~23°C) and placed in a Petri dish submerged in PBS. The submerged gel was positioned between two glass slides and tested in unconfined compression using a custom-built uniaxial testing machine: a DC motor driven actuator (NSC-1 series, Newmark Systems Inc, CA) with a load cell (Model 31, 9.8 N range, Sensotec Sensors, Columbus, OH) and LVDT (Model PRH-812-200, ± 5 mm displacement, Macro Sensors Inc, Pennsauken, NJ) attached to the tip. The actuator was driven until the glass slide made full contact with the surface of the gel and a preload of 0.2N was applied. From this position, the specimen was then compressed to a maximum strain of 10% at a rate of 100%/sec and held at maximum strain by allowing the gel to relax for ~360s. No preconditioning was applied. Force and displacement data were acquired at 60 samples/second using a PC-based data acquisition system (PCI-MIO-16E-1 I/O card, Labview 7.0 software, National Instruments, Austin, TX).

2.4. Confocal Microscopy

After MRE and unconfined compression testing, fibrin gels were fixed in 4% paraformaldehyde in PBS. Slices with dimensions ~5mm × 5mm × 0.1mm were cut from only the central region of the gel with a vibrating microtome (Vibratome 1000, Technical Products, St. Louis, MO) along planes parallel and perpendicular to the magnetic field. The slices were placed on a thin glass slide with PBS on the gel slice and imaged using confocal reflectance imaging (Zeiss LSM 510). Excitation light was from a 543nm HeNe laser, an 80/20 beamsplitter was in place of the main dichroic, and a 530–560nm bandpass filter was used as the emission filter (which passes the 543nm reflected light). Samples were imaged at 40x magnification with a water immersion objective and a HeNe laser at 543 nm. At least five images with resolution of 512 × 512 or 2048 × 2048 were acquired randomly from different positions on the aligned and control gel slices.

2.5. Fiber orientation calculation

Structural anisotropy of the fibrin gels was analyzed using Matlab R2007 (The Mathworks, Inc., Natick, MA). The confocal images were converted to grayscale and Fourier transformed to obtain the power spectrum as a function of spatial frequency, or wavenumber (Marquez, 2006). The spectrum was low-pass filtered and the spatial frequencies were transformed into polar co-ordinates (wavenumber magnitude and direction). Finally, the magnitudes of the power spectrum were averaged over angular increments in direction (Δθ=1°) to obtain a 2D “orientation tensor” (Marquez, 2006). The preferred orientation of the fibers was calculated from the major eigenvector of the orientation tensor. Strength of fiber alignment was given by the anisotropy index (AI), a function of the ratio of eigenvalues (Sander and Barocas, 2008): $AI=1-\frac{{\lambda }_2}{{\lambda }_1}$.

3. RESULTS

Polymerization of fibrinogen and thrombin mixture in the high field strength magnets with B₀=11.7T and B₀=4.7T resulted in cubic specimens approximately 20 mm × 20 mm × 20 mm. Although the samples were all left for 120 minutes, the time to polymerization observed in the control samples varied from batch to batch (~60–90 minutes).

3.1. Dynamic shear modulus estimated with MRE

Shear waves were clearly visible in MRE images as decaying sinusoidal patterns in space (Fig. 1b, 1d). In the fibrin gel, shear waves with displacement polarization normal to e_B had a wavelength (λ_⊥), which was lower than the wavelenth (λ_||) obtained from shear waves with displacement polarization parallel to e_B (Fig. 1a, 1c).

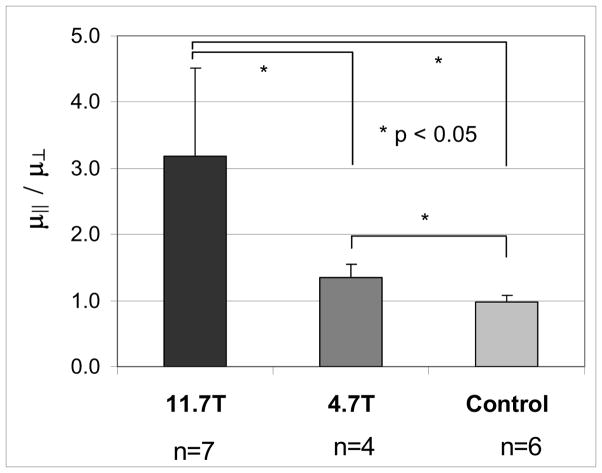
The ratio of dynamic shear moduli parallel vs. normal to e_B (μ_||/μ_⊥) empirically represents anisotropy in shear (Figure 2). Anisotropy ratios of shear moduli from MRE of gels polymerized in magnets and from control gels polymerized outside the magnet were μ_||/μ_⊥ =3.17 ± 1.34 (B₀ = 11.7T, n=7), μ_||/μ_⊥ =1.35 ± 0.20 (B₀ = 4.7T, n=4) and μ_||/μ_⊥ =0.97 ± 0.10 (control, n=6) respectively (Fig. 2). The differences in anisotropy between the control gels and gels made in the magnets were statistically different (p<0.05, Student’s t-test). The difference between ratio of anisotropic shear moduli in gels made at 11.7T and 4.7T was also statistically significant (p<0.05, Student’s t-test). The dynamic shear moduli in two orthogonal directions μ_||, μ_⊥ of gels at B₀ = 11.7T are μ_||=6.50 ± 1.69kPa, μ_⊥=2.48 ± 1.55kPa (n=7). For gels made at B₀=4.7T shear moduli were μ_||=8.86 ± 2.66kPa and μ_⊥=6.84 ± 2.54kPa (n=4). Shear moduli for control gels were 9.07 ± 2.63kPa (n=12). Differences between the absolute shear moduli of the gels were not statistically significant, probably because of the relatively large batch-to-batch variations in polymerization.

Figure 2.

The ratio of dynamic shear moduli μ_||/μ_⊥ in anisotropic fibrin gels. Dynamic shear moduli are calculated from measured wavelengths (B, D) of propagating shear waves in magnetic resonance elastography experiments. The modulus μ_|| is obtained from waves with polarization aligned with the direction of the magnetic field during polymerization (unit vector e_B). The modulus μ_⊥ measured from waves with polarization normal to e_B. Fibrin gels were polymerized at B₀ = 11.7T e_B and B₀ = 4.7T e_B while the control was left to polymerize outside the magnetic field. The ratio of dynamic moduli was statistically different (p<0.05) between all three cases (11.7T vs. 4.7T, and both vs. control).

3.2. Mechanical properties of gels under unconfined compression

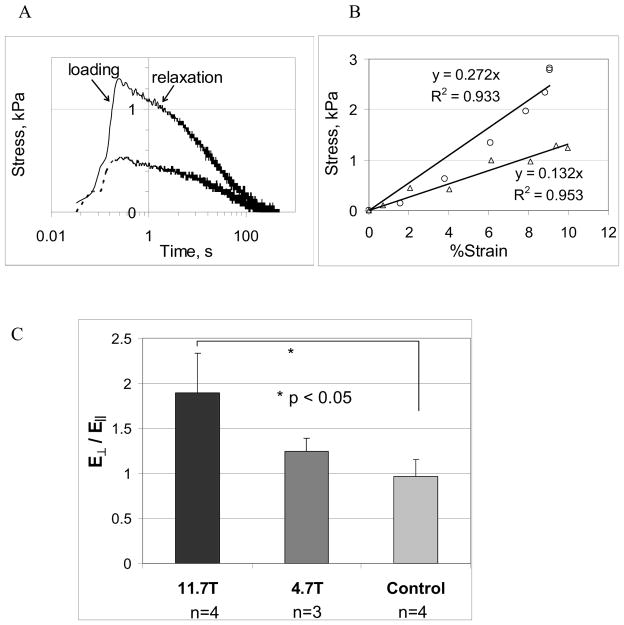
A fast loading ramp was applied at a strain rate of 100%/s to a maximum strain of 10%. Force was observed to decay after reaching a peak (Fig. 3a). Plots of stress vs. strain in the fast loading regime were qualitatively different in loading directions parallel and perpendicular to e_B (Fig. 3b). The slope of the linear fit to the stress-strain curve was denoted by E^C, the apparent Young’s modulus in compression.

Figure 3.

Fibrin gels were tested in unconfined compression by compressing the gels between glass platens to a maximum strain ε = 10% at a fast loading rate (loading ramp was approximately 0.1s). Solid and dashed lines in Fig. 3A are force-displacement curves obtained when applied compressive loading is perpendicular and parallel to e_B respectively. Fig. 3B shows linear fits to force-displacement curves in the loading phase; with circles and triangles representing compressive loading parallel and perpendicular to e_B. From the linear fits of the two loading curves (Fig. 3B), ratio of compressive moduli perpendicular to e_B (E_⊥) vs. parallel to e_B (E_||) were calculated and shown in Fig. 3C.

The compressive modulus $E_{\perp }^C$ due to a rapid step load, applied perpendicular to e_B, was found to be higher than compressive modulus parallel to e_B (Fig. 3b) on gels made at 11.7T. The ratio of anisotropic compressive moduli ( $E_{\perp }^C/E_{\parallel }^C$) for gels polymerized under three different conditions (Fig. 3c) was highest for gels made at 11.7T followed by gels made at 4.7T. Using ratios of compressive moduli in two orthogonal directions as an indicator of mechanical anisotropy, statistically-significant differences (established by Student’s t-test) were found between gels polymerized in the magnets and the control gel. The mean (± std. deviation) ratio of anisotropic moduli, $E_{\perp }^C/E_{\parallel }^C$ for gels polymerized at 11.7T was $E_{\perp }^C/E_{\parallel }^C=1.89\pm 0.44$ (n=4); for gels polymerized at 4.7T the mean ratio was $E_{\perp }^C/E_{\parallel }^C=1.24\pm 0.14$ (n=3); and for control gels $E_{\perp }^C/E_{\parallel }^C=0.96\pm 0.19$ (n=4). The average values of compressive moduli obtained from gels made at B₀=11.7T were $E_{\parallel }^C=10.20\pm 7.06\text{kPa}$ and $E_{\perp }^C=17.4\pm 9.22\text{kPa}$ (n=4); for 4.7T gels $E_{\parallel }^C=15.63\pm 1.50\text{kPa}$ and $E_{\perp }^C=19.33\pm 1.86\text{kPa}$ (n=3); and for control gels E^C=16.98 ± 7.68kPa (n=8). However, no statistically-significant differences in compressive moduli ( $E_{\parallel }^C$ and $E_{\perp }^C$) were found between the gels made under different magnetic field strengths and controls, again likely due to batch-batch differences.

3.3. Microstructural organization of fibrin gels with confocal microscopy

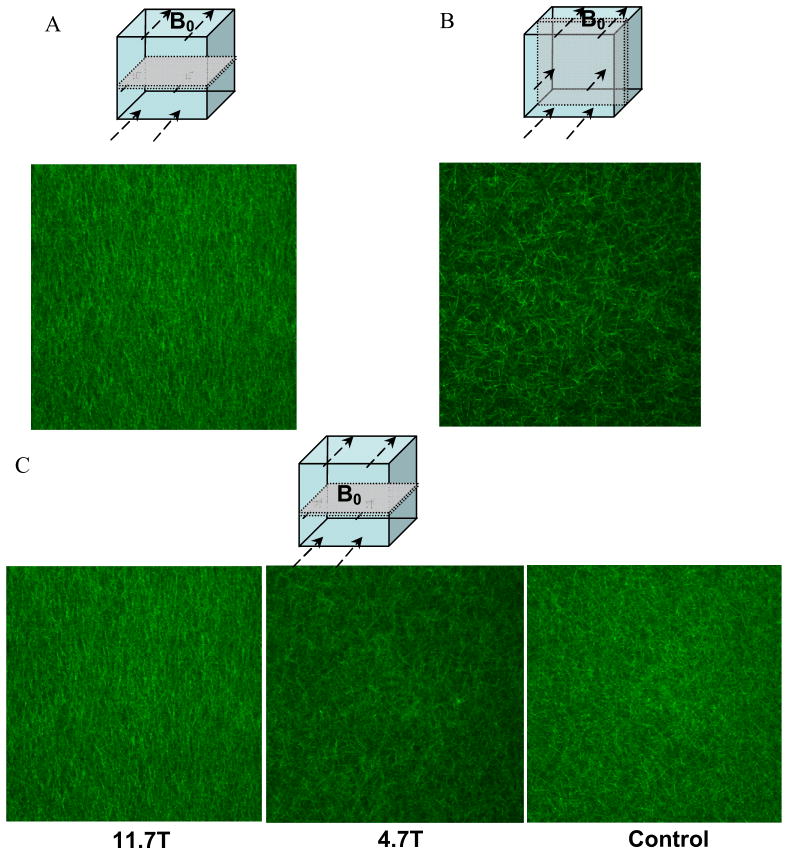
Confocal microscopy images of aligned fibrin gels were obtained in two cutting planes on samples polymerized at B₀ = 11.7T and at a magnification of 40X (Figure 4a, 4b). Highly aligned fibers were seen in a horizontal plane parallel to e_B (Fig. 4a) compared to a random appearance of fibers (Fig. 4b). The strength of this alignment is compared at two field strengths B₀ = 11.7T and 4.7T with the control (Fig. 4c). At the lower field strength B₀ = 4.7T fiber alignment was not discernible. No alignment of the fibers was discernible in the control sample.

Figure 4.

Confocal microscopy slices of aligned fibrin gels were obtained in two cutting planes on the same sample polymerized at B₀ = 11.7T (A, B) at a magnification of 20X. Highly aligned fibers were seen in a plane parallel to B₀ (A) whereas no visible alignment was found in a perpendicular plane (B). The strength of this alignment is compared at two field strengths B₀ = 11.7T & 4.7T with the control (C). At a lower field strength B₀=4.7T fiber alignment was not discernible. No alignment of the fibers was discernible in the control.

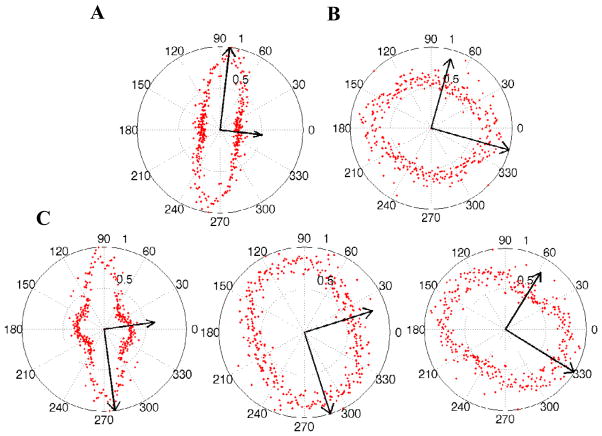
3.4. Fiber alignment direction of fibrin gels from confocal images

The preferred fiber orientation obtained from 2D confocal images corresponding to Figure 4, were shown as polar plots in Figure 5. The angular distribution of fiber orientation is narrower in the highly aligned fibrin fiber network in samples polymerized at B₀=11.7T. The distribution is close to circular in the control gel and slightly aligned in the sample polymerized at B₀= 4.7T. The orientation angle (θ) and anisotropy index (A.I.) calculated from the image processing algorithm were averaged from images obtained at randomly selected positions on the sample. The orientation angle θ = 90.3° ± 6.0° and A.I. = 0.5 ± 0.1 (n=3) for gels made in B₀ = 11.7T and θ = 136.4° ± 26.7° and A.I. = 0.25 ± 0.13 (n=3) for control gels.

Figure 5.

Confocal images corresponding to Figure 4 were converted to grayscale intensity images and Fourier transformed to obtain an amplitude power spectrum (Marquez, 2006). After removing high frequency noise with a low-pass filter from each image, the wavenumbers were transformed into polar co-ordinates (wavenumber magnitude and direction). The magnitudes of the transformed spectrum were averaged over each angular increment (Δθ=1⁰) and displayed as a function of θ in a polar plot. A 2D orientation tensor is calculated from the averaged intensity values and the major and minor eigenvectors are superimposed on the polar plot (Sander and Barocas, 2009).

4. Discussion

By polymerizing a cube of fibrinogen and thrombin in a strong magnetic field, structural anisotropy in the gel was obtained with preferred fiber alignment parallel to the magnetic field direction (Fig. 4). The strength of the preferred alignment was dependent on the magnetic field, B₀, confirming prior observations (Yamagishi et al., 1990). The ratio of thrombin to fibrinogen concentration was chosen to be low in order to increase the gelation time; this allowed the polymerizing fibers to align in the direction of the magnetic field. Due to longer gelation times, the aligned gels cannot be seeded with cells during polymerization in the magnet. However, it is conceivable that cells might be seeded in the polymerized gels and allowed to migrate into the anisotropic matrix.

In this study we show that anisotropy in mechanical properties is similarly dependent on B₀. The mechanical responses of magnetically aligned fibrin gels to dynamic shear and compression depended on the direction of the applied loads. Ratios of the dynamic shear and compressive moduli of anisotropic gels were directly related to the strength of the magnetic field at which the gels were polymerized.

Fibrin microstructure as revealed by confocal microscopy images revealed spatial organization of the fibrin fibers polymerized under two magnetic field strengths and a control sample (Fig. 4c). The microstructure in the control gel was less organized compared to the gels polymerized in the magnetic fields. The gels polymerized at B₀ = 11.7T showed highly aligned fibers (Fig. 4c). Anisotropy index (AI) and orientation angle obtained from the confocal images serve as quantitative measures of structural anisotropy in the gels. A higher anisotropy index in the gels polymerized at B₀=11.7T corresponded to higher ratios of dynamic shear moduli and compressive moduli.

When comparing the shear and compressive moduli to the direction of fiber alignment, several observations are noteworthy. Dynamic shear modulus was higher for wave motion with displacements in the plane containing e_B compared to wave motion involving displacements in the plane normal to e_B. This can be explained by the fact that shear deformation in the plane perpendicular to fibers (Fig. 1a) does not require any deformation of the fibers. On the other hand, the modulus of anisotropic gels in unconfined compression during a fast loading ramp was lower in the direction of e_B versus normal to e_B. During unconfined compression in the direction of fiber orientation, the fibers probably buckle and are unable to resist the load. However, when compressed in a direction perpendicular to the fibers, the applied loads cause stretching along the length of the fibers due to Poisson’s effect. Since the fibers are stiffest in tension the gels have a higher compressive modulus normal to e_B ( $E_{\perp }^C>E_{\parallel }^C$).

Thomopoulos et al., (2007) incorporate structural anisotropy in their study of fibroblast-populated collagen and show that mechanical anisotropy observed in tension is independent of fiber orientation. The current study suggests that in magentically-aligned fibrin gels, fibril direction is a major contributor to mechanical anisotropy in shear. The structural properties that govern shear deformation of native fibrin gel, have some overlap, but also distinct differences, with those of cell-populated collagen under tension.

The conclusions of the current study are limited to the experimental conditions used, and are subject to assumptions governing the analysis. Most importantly, the material is assumed to obey linear theory of elastic media undergoing small deformations. Since the maximum strain is 10%, the linear approximation is reasonable. Also, the material is viscoelastic, so that the apparent shear moduli and compressive moduli almost certainly depend on strain rate. Since the dynamic shear modulus is directly proportional to the square of the wavelength, any error in measurement of the wavelength will be amplified. Confocal microscopy was performed after mechanical testing, since preparation for imaging involved fixation and slicing. It is possible that mechanical testing may have slightly affected fiber orientation; Chandran and Barocas (2004) studied this effect in collagen gels. They note, however, that except near boundaries, samples subjected to confined compression of 10% regained their optical properties after complete load removal, suggesting minimal fiber reorientation in central “bulk” regions in response to moderate mechanical loading. Therefore, for the following reasons we believe that the testing most likely did not significantly alter the degree of fiber orientation: the applied compressive strain was only 10% (in the linear elastic range of the fibrin gel); the gel was compressed only twice, in two different directions with respect to fiber orientation; the gel was allowed to completely relax after each test and gel slices were obtained from the interior of the sample for confocal imaging.

Complete characterization of a transversely isotropic linear elastic material requires estimates of five independent material parameters (Chapman, 2004): E_||, E_⊥, μ_||, μ_⊥, and ν_⊥/||. For an incompressible material only three independent parameters (E_⊥, μ_||, μ_⊥) remain to be specified. Our studies provide estimates of these parameters, but under mixed conditions, so we have not completely characterized the material. In particular, we were not able to test the fibrin gel in tension along the fiber direction. Difficulty in gripping and maintaining a uniform sample thickness also prevented us from using standard rotational rheometry to characterize material anisotropy. The difficulty of rheometer testing underscores the utility of the MRE approach. Finally, the properties of this material under large deformation were not investigated. This was deemed outside the scope of the present study; the linear response is considered the primary and most important characteristic in determining the material’s effects on cell growth and behavior.