Backward Genotype-Trait Association (BGTA)-Based Dissection of Complex Traits in Case-Control Designs

Abstract

Background

The studies of complex traits project new challenges to current methods that evaluate association between genotypes and a specific trait. Consideration of possible interactions among loci leads to overwhelming dimensions that cannot be handled using current statistical methods.

Methods

In this article, we evaluate a multi-marker screening algorithm – the backward genotype-trait association (BGTA) algorithm for case-control designs, which uses unphased multi-locus genotypes. BGTA carries out a global investigation on a candidate marker set and automatically screens out markers carrying diminutive amounts of information regarding the trait in question. To address the ‘too many possible genotypes, too few informative chromosomes’ dilemma of a genomic-scale study that consists of hundreds to thousands of markers, we further investigate a BGTA-based marker selection procedure, in which the screening algorithm is repeated on a large number of random marker subsets. Results of these screenings are then aggregated into counts that the markers are retained by the BGTA algorithm. Markers with exceptional high counts of returns are selected for further analysis.

Results and Conclusion

Evaluated using simulations under several disease models, the proposed methods prove to be more powerful in dealing with epistatic traits. We also demonstrate the proposed methods through an application to a study on the inflammatory bowel disease.

Introduction

The mapping of complex traits is one of the central and challenging areas of human genetics today. This is a consequence of the ‘complex’ or multifactorial characteristic of a large number of common human disorders, in that they cannot be attributed to alleles of a single gene or risk factor [1–3]. Rather, these disorders find their sources within the combined action of a multitude of genes and environmental factors, each contributing modest effects. Encouragingly, the evolution of technologies on DNA polymorphisms has led to the identification of a large number of new markers, covering almost every region of the human genome. Facilitated by this dense marker map, studies involving a large number of markers (usually on a genomic scale) have recently become popular in the search for the susceptibility genes of complex human disorders. However, most current statistical methods, when applied in such studies, can only extract partial (marginal only) information out of the data. This is because these statistical methods, developed during the last two decades [e.g., 4–9], were primarily designed to deal with small numbers of markers and simpler disease model assumptions. It is easily realized then that these methods are less than readily applicable for comprehensive large-scale genome-wide searches of complex human disorders. Even for studies on the scale of hundreds to thousands of markers, the number of possible interactions among genetic loci becomes overwhelmingly large.

Current strategies, therefore, compromise either by ignoring higher dimensions of interaction (as seen in marginal association mapping); or by focusing on small numbers of regions at a time (as seen in candidate gene studies; see [10] and [11] for some considerations on this strategy for complex traits).

Although marginal association based searches are relatively easy to implement, we find that there are serious drawbacks to the method. In large-scale studies such as genome scans, marginal association-based searches typically involve a test statistic that examines association locally and repeatedly at each marker or at a combination of nearby markers. The problem becomes that the search ignores potential interaction information among markers of potential importance, especially those located on different chromosomes. Thus these methods are less likely to have adequate power in detecting disease loci for complex traits, where substantial amounts of information are reflected in the interactions among loci as well as other non-genetic risk factors. New methodologies capable of inspecting disjoint marker loci while running large-scale scans are in order.

Detailed analyses that focus on a small numbers of regions, such as candidate gene studies, are powerful tools when several important loci have been identified through a larger-scale preliminary selection. The success of such a study, however, relies on the informativeness of the loci selected, with respect to the trait in question. If the preliminary search fails to capture some of the major genomic regions for the trait under study, the subsequent detailed study will be much hampered, especially for complex traits where genes have shown substantial interdependence. Unfortunately, for most current candidate gene studies, the marker selection is done through a marginal association mapping. Methodologies that improves the informativeness of genome scans will lead to more efficient candidate gene studies.

This article presents a fundamentally different method to address the mapping problems of dichotomous traits in genome scans or large-scale studies with hundreds to thousands of markers, focusing on the analysis with consideration of gene-gene interaction using case-control data. Although such a density of genome scans is sparse in the light of current whole-genome association studies, we have chosen to work with such a scale since we are primarily interested in dealing with gene-gene interactions using markers at not-tightly-linked loci. Statistical interactions observed among these markers are more likely due to genetic interactions among different genes, rather than dependence between these two loci due to a common neighboring gene.

More specifically, we investigate a novel large-scale marker selection procedure that efficiently uses information and considers possible interactions among loci. This procedure has more power detecting genes in epistatic interactions than current strategies. We will also outline, in the discussion section, how the statistics and the proposed BGTA method can be applied to candidate gene studies and studies with a denser marker map (say, using a current 100 k or 500 k platform).

The main idea studied in this article represents an important extension to unphased genotyped data in case-control study of what we proposed and developed in [12], a global marker screening approach with a BHTA algorithm (the backward haplotype transmission association algorithm) that is suitable for case-parent trios. In [13], BHTA was successfully applied to an analysis of inflammatory bowel disease data. The novel findings in this case study illustrate and project the usefulness and potential values of this new approach to the analysis of common diseases more generally.

In this article, we first introduce a large-scale genotype-based marker screening algorithm that selects a set of influential markers exhibiting signs of association with disease genes and their interactions. At each iteration the algorithm deletes the marker that contributes least genotype association information, operating in a backward manner that thus leads to its name, ‘backward genotype-trait association (BGTA) algorithm’. Two statistics are used in the evaluation of markers’ contributions: genotype- trait distortion (GTD) and genotype-trait association (GTA). These two statistics are formulated using unphased multi-locus genotypes observed from cases and controls. Heuristically speaking, GTD measures the amount of disease information contained in the current marker set, whereas GTA determines the (relative) importance of each marker that remains in the current marker set under study. An advantage of the statistic GTA is that its expected value under the null hypothesis remains zero no matter the markers under evaluation. As a result, the screening algorithm can be carried out without using a reference probability distribution at each iteration. The algorithm continues to the next cycle once the least important marker is removed and stops if the deletion of any additional marker causes GTD to drop. Therefore, BGTA screening algorithm is a greedy algorithm searching for a marker set that displays a maximum of association with the disease trait, rather than a testing procedure that identifies the most statistical significant marker set.

Secondly, we propose a marker selection procedure using BGTA-based random subset screenings to counter the dilemma posed by moderate sample sizes of individuals and large numbers of genotypes. This procedure allows the BGTA screening algorithm to survey the genome-scale candidate marker set using the largest informative scope allowed by the sample size. Information extracted by the algorithm is then aggregated to rank the overall importance of the markers.

The BGTA method is evaluated using three simulated examples. The first is a simple genetic heterogeneity model, whereas the second and the third are from the class of epistatic models. Performance of BGTA under these models is then compared with marker-by-marker χ² tests and a thoroughly evaluated [14] current large-scale screening method – the set-association method proposed by Hoh et al. [15]. In all examples calculated, BGTA demonstrates high detection power and well-controlled false positive rates. Results from the second and the third example most clearly illustrate BGTA’s power in extraction of useful information on interaction among trait loci, which is then transformed into joint return patterns in BGTA-based screenings. We also illustrate the proposed method through an application to an inflammatory bowel disease data set originally studied by Rioux et al. [16]. Using 56 unrelated cases and 56 controls sampled from this set of pedigrees, we demonstrate the BGTA method using genotypes on 402 markers. Despite the small size of the data used, BGTA detects association signals on three previously identified IBD loci.

Based on our single-CPU computational experiments, the proposed BGTA method can analyze studies with the number of markers ranging from dozens to 5000+. Especially, BGTA was recently applied to a Rheumatoid Arthritis [MIM 180300] study, originally studied in Amos et al. [17], with more than 5000 SNPs genotyped on ~ 400 of selected RA patients and unaffected individuals (implemented in [18]). Given a cluster of 10 CPUs, the proposed BGTA method can realistically analyze within a reasonable amount of time a 10k genome scan or large-scale genomic studies of a similar size. The proposed BGTA method and related computer programs are readily applicable to current research on human disorders in a number of scenarios such as genome-wide scans involving several hundreds to 10k markers [e.g., 19–21], second-stage analyses of whole-genome association studies [e.g., 22], studies for a given large genomic region of interests [e.g., 23] and candidate gene studies with a few SNPs at each of many candidate loci [e.g., 24, 25]. The computer programs (including an MPI implementation for parallel computing [26]) for methods described in this article can be downloaded at http://statgene.stat.columbia.edu/

Methods

In light of the problems facing the field of mapping complex traits today, there is a great demand for new methods that are capable of capturing interactions among disease loci [27] by maximizing the use of information contained in data sets. Since the term ‘interaction’ does not have completely overlapping meanings in statistics and in genetics, for the convenience of discussion in this article, we define there is interaction between two genes if the disease penetrance given their two-gene genotypes depends on the allele values at both gene loci. In the sense of a two-locus disease penetrance table of these two genes, this is equivalent to require that this table cannot be reduced to a single-locus disease model. This represents a more generalized definition of ‘interactions’ than most mathematical models of epistasis (such as an additive or multiplicative penetrance model) [28–30] but a closer definition to that ‘the effect of one locus is altered or masked by effects at another locus’ as discussed in [31].

To capture such gene-gene interaction, it is then important to examine genetic variants across multiple loci at a time. Important interaction information is lost if the markers are tested independent of each other. For example, in the case-parent trio design, allelic transmissions on multiple unlinked loci (or transmitted haplotypes) contain valuable association information regarding interaction among the marker loci besides information on marginal effects. Haplotype transmission distortion is not a mere combination of association between individual markers and possible disease genes nearby.¹ It contains information that can reveal possible epistatic structures among the disease loci. For designs where haplotype data are not available, such as population-based case-control studies, unphased multi-locus genotypes should be used to extract interaction information across difference genomic loci. In the following, we define information-measuring statistics based on unphased multi-locus genotypes and propose a marker selection procedure through marker screenings based on the novel statistics. More details on algorithm statistics and theoretical issues are given in the Appendix.

Assumptions and Data Notation

In studies given patients of a certain disease and unrelated controls, genotypes are observed at each marker locus for every individual studied. Since the cases and controls are genetically unrelated, no information is available for the inference of haplotypes (phases) across different marker loci. Thus we directly use the unphased genotypes in such case-control designs.

Assume a case-control study for a dichotomous trait (diseased or disease-free), with n_d cases and n_u unrelated controls randomly sampled from the diseased and disease-free subpopulations respectively. Suppose that k diallelic markers M₁, M₂, …, M_k are being studied. The two alleles of marker M_i are denoted as a_i and b_i, i = 1, 2, …, k, with corresponding genotypes: a_i/a_i, a_i/b_i, and b_i/b_i. Consequently, these k diallelic markers generate a total of 3^k possible genotypes. Let the possible genotypes be $\{g_1^{(k)},g_2^{(k)},\dots ,g_{3^k}^{(k)}\}$. To evaluate the global disease information carried by these k markers, we define the following genotype counts, for each genotype $g_i^{(k)}:n_{d,i}^{(k)}$ is the number of cases that carry genotype $g_i^{(k)}$, and $n_{u,i}^{(k)}$ is the corresponding count in controls. In the following discussion on the method proposed, we also use the following notations on genotypes:

$$\begin{array}{c}P(g_i^{(k)}|D)\text{or}{p}_i^d:\hfill \\ \text{the frequencies (proportions) of}{g}_i^{(k)}\text{among cases};\hfill \\ P(g_i^{(k)}|U)\text{or}{p}_i^u:\hfill \\ \text{the frequencies (proportions) of}{g}_i^{(k)}\text{among controls}.\hfill \end{array}$$

Here, and in the following, D or d is short for ‘disease’ and U or u is short for ‘unaffected’ or ‘disease-free’.

Association between Unphased Multi-Locus Genotypes and a Dichotomous Trait

The primary goal of a genome scan or a large scale genetic study is to identify or to narrow down the locations of the disease-predisposing variants for the dichotomous trait under study. For convenience, assume that there are k_d unknown genes affecting the risk of the dichotomous trait (for complex traits, usually k_d > 1). The penetrance of the trait status – say, ‘diseased’ or ‘disease-free’ – varies among different disease-predisposing genotypes, say L different ones, spanned by these k_d trait loci. Denote these L disease-predisposing genotypes with $g_l^D,l=1,2,\dots ,L$, each with population frequency $\mathrm{P}(g_l^D)$ and disease penetrance $\mathrm{P}(D|g_l^D)$. The population disease prevalence P(D) simply equals ${\displaystyle {\sum }_{l=1}^L\mathrm{P}(D|g_l^D)\mathrm{P}(g_l^D)}$. The trait genotypes, $g_l^D’\mathrm{s}$, at the unknown trait loci and their corresponding trait penetrances can only be studied through marker loci close to and associated with these trait loci. Thus, for the set of k candidate markers under study, it is natural to consider the ‘penetrances’ (conditional probability of the given trait) given the k-marker genotypes and measure the trait information carried by them through their association with the trait genes. Define the ‘penetrance’ given the genotype $g_i^{(k)}\text{as}\mathrm{P}(D|g_i^{(k)})$.²

If none of the k markers are in association with the disease loci, i.e., $\mathrm{P}(g_l^D|g_i^{(k)})\equiv \mathrm{P}(g_l^D)$, for all $g_l^D’\mathrm{s}$ and all $g_i^{(k)}’\mathrm{s},\text{then P}(D|g_i^{(k)})=\mathrm{P}(D)$. On the other hand, if one or more markers are in association with the trait, such association must be reflected in the fact that, for some $g_i^{(k)},\mathrm{P}(D|g_i^{(k)})\ne \mathrm{P}(D)$. It can be shown using simple algebra that

$$P(D|g_i^{(k)})\ne \mathrm{P}(D)\iff \mathrm{P}(g_i^{(k)}|D)\ne \mathrm{P}(g_i^{(k)}|U),i=1,2,\dots ,3^k,$$

which indicates that multi-locus genotype-trait association can be studied through the comparison of the genotype distributions among the cases and the controls.

Screening Statistics

In the previous section, we have shown that a set of k markers’ association to the trait under study can be measured through comparison of multi-locus marker genotype distributions among the cases and the controls. If the genotype counts of the cases and the controls are organized into a two-column table, comparing these two genotype distributions (as two multinomial distributions) is related to tests of independence on this 3^k × 2 table. In current statistical literature, such a test is usually carried out using the Pearson χ² test [32] and the likelihood-ratio χ² test if n/3^k is close to or greater than 5, or the Fisher’s exact test for small n/3_k values [33, chapter 3]. The χ² tests rely heavily on the approximation of the χ² distribution to the sampling distribution of the test statistics which is poor when n is relatively small. The exact test is highly computationally intensive even when Monte Carlo strategies are employed. Additionally, these test statistics intend to measure the statistical significance but not the extent of the association. For more reliable evaluation of association information and faster screening, we introduce two important new statistics in the following.

Genotype-Trait Distortion (GTD) statistic is intended to measure the current markers’ association information regarding the trait through aggregated genotype counts (as genotype distributions) from the samples collected. Considering the natural empirical estimates of genotype frequencies, we have $\widehat{P}(g_i^{(k)}|D)-\widehat{P}(g_i^{(k)}|U)=n_{d,i}^{(k)}/n_d-n_{u,i}^{(k)}/n_u$, where genotype counts such as $n_{d,i}^{(k)}$ are defined as previously. Thus GTD is formulated straightforwardly as

$${\text{GTD}}^{(k)}={{\displaystyle \sum _{i=1}^{3^k}\left(\frac{n_{d,i}^{(k)}}{n_d}-\frac{n_{u,i}^{(k)}}{n_u}\right)}}^2.$$ (2)

The expectation of GTD is derived as

$$\mathrm{E}\left({\text{GTD}}^{(k)}\right)={\displaystyle \sum {(p_i^d-p_i^u)}^2}+\left[\frac{1}{n_d}{\displaystyle \sum p_i^d\left(1-p_i^d\right)+\frac{1}{n_u}{\displaystyle \sum p_i^u}\left(1-p_i^u\right)}\right],$$ (3)

where $p_i^d$ is short for $\mathrm{P}(g_i^{(k)}|D)$ and $p_i^u$ for $\mathrm{P}(g_i^{(k)}|U)$ to simplify the formulations. From the first term in (3), which is of a higher order and dominates over the second term, it is seen that the larger the difference between the genotypic distributions among the cases and among the controls, the larger the expected value of GTD^(k) is. This explains why we chose GTD^(k) to serve as a measure for genotype-trait association information.

From (3) we also note that GTD shows its smallest value when none of the markers are associated with the trait. If some of the current set of markers used in calculating GTD are associated with the trait, E(GTD^(k)) will increase as $p_i^d’\text{s and}{p}_i^u’\mathrm{s}$ diverge. The stronger the association signal, the greater the difference between $p_i^d’\text{s and}{p}_i^u’\mathrm{s}$, and the larger the value of the GTD score. However, for a given marker set, a large value of GTD ^(k) only indicates that some of the markers in the set are important or associated with the trait, while others may just simply contribute noise. If these unimportant markers are removed from the marker set, the association signals with respect to the trait under study should become stronger. Naturally, the importance of any marker M_r can then be evaluated through the difference between the GTDs before and after removing the given marker. Unlike other statistics that evaluate individual marker one at a time, GTD ^(k) is calculated based on the k-marker genotypes instead of genotypes at individual loci. Therefore, the use of the ‘information’ drop measured by ΔGTD to evaluate a single marker can take advantage of both signals from interactions among markers and that of this given marker.

We consider a current set of k markers, {M₁, M₂, …, M_k}, and the new set with the reduction of the marker M_r; that is, {M₁, M₂, …, M_r−1, M_r+1, …, M_k}. The statistic Genotype-Trait Association (GTA) is defined as

$$\text{GTA}(r)=\frac{1}{2}\mathrm{\Delta }\text{GTA}+\tilde{A}$$ (4)

where r indicates the underlying marker evaluated by this GTA score and ΔGTD is the difference between the GTD scores computed on the new marker set and the old marker set. Despite its seemingly complicated expressions (for details, see the Appendix), the adjusting term à has a symmetric form and is of a lower order. By adding this term, GTA(r) has expectation 0 when none of the markers are associated with the trait. While some of the current markers are associated with the trait, the value of GTA(r) reflects the importance of the given marker. More specifically, if marker M_r is not associated with the trait, while other markers in the current marker set are, the expected value of GTA(r) will be strictly positive; if M_r is associated with the trait, the expected value of GTA(r) will be negative, and the magnitude of the value will reflect M_r’s importance. Since GTA(r) measures directly the information score’s change due to the removal of M_r, the most attractive advantage of using GTA(r) is that the importance of a given marker can be evaluated without reference to a probability distribution. More computing details and theoretical properties of GTA can be found in the Appendix.

BGTA Screening Algorithm

Based on the properties of GTD and GTA, we propose in this section a multi-locus screening algorithm. Unlike conventional hypothesis testing, our algorithm is an inferential procedure in the sense that each marker is evaluated and ranked by statistics measuring its association with the trait. During each step of the screening, markers in the current set are assessed for their importance in terms of the relative association to the trait measured by the GTA statistic. Each marker with the least association (with the largest positive GTA score value) is deleted and the screening process then moves to the next cycle on the reduced marker set until all remaining markers show important associations with the trait.

More specifically, the screening process uses the properties of GTA such that a negative value of GTA indicates the importance of a marker under evaluation and a positive GTA suggests that the removal of the given marker would increase the association signal strength of the reduced set (measured by GTD). The backward genotype-trait association (BGTA) marker screening algorithm is developed as follows, based on such properties, which can be viewed as a greedy marker reduction process rather than a series of tests.

1. Start with all markers in the candidate set.

2. Given the current marker set with k markers, calculate the GTA(r) score for each marker, r = 1, 2, …, k. If there are non-negative scores, delete the marker with the maximum GTA(r) score; otherwise stop and return the remaining markers.

3. If there is no marker remains in the set, stop; otherwise set k = k - 1 and continue on to step 2.

Due to the backward fashion of BGTA, markers with strong interactions tend to return together. This is because removing any one of these markers would weaken the association strength dramatically. This property of BGTA is even more preferable when these markers only demonstrate weak or no marginal signals. It also renders BGTA more powerful in detecting genes in epistasis, an outcome less likely to be achieved by traditional marker-wise methods [27].

Marker Selection Based on Random Subset BGTA Screenings

The BGTA screening algorithm proposed in the previous section is a powerful procedure that efficiently uses multi-locus association information. However, the performance of the BGTA algorithm is limited by the dimension of the data. Since the number of genotypes generated by a moderately sized marker set is often much larger than the sizes of the cases and the controls, it is difficult for BGTA to screen informatively all the candidate markers during one iteration. For instance, in theory 30 markers generate 3³⁰ genotypes. Even if we consider the haplotype blocks [34–36], the actual number of possible genotypes is often much larger than the magnitude of regular sample size of individuals, usually in the hundreds. This becomes a problem of sparseness for BGTA where the genotype counts are mostly ‘0’ or ‘1’s at the beginning of the backward screening of all markers. When based on these counts GTA(r)’s are noninformative, and so markers are deleted randomly until the dimension of the genotypes reduces to a level that can be studied using the number of individuals in the data.

The ‘small n, large p’ dilemma as observed here for the analysis of current data from genetics has been one of the major challenges in genomic studies. A small number of observations, cases and controls in this article, allow one to only study informatively the interactions among a small number of dimensions. As such a scope of inspection is decided by the size of data, there is no statistical or mathematical tactic can overcome this limitation.

If the BGTA screening algorithm is applied to all the markers in a a large-scale study, it is possible that important markers may be missed due to the noninformative deletion at the beginning of the process. At the same time, these noninformative deletions can also pose unnecessary computational complexities. We therefore suggest in the following a marker selection procedure based on repeated BGTA screenings on random subsets of markers to address this issue of dimensionality:

1. Randomly select a subset of k out of all the markers in a large-scale study scan, where k is relatively small, say 10, so that the screening on these k markers is more informative. Repeat BGTA screening on a large number B, say 10,000, of random subsets and record the screening result of each repetition. (See section 2.6 for discussion on choice of B.)

2. Calculate the number of times (out of B screenings) a marker is returned by BGTA, or the return frequency for each marker, and then rank them by those frequencies. Important markers, those with significantly higher return frequencies, are selected based on their distribution. Joint returning patterns observed in such random subset screenings contain information on inter-locus interactions. More details on joint returning patterns are illustrated in the discussion of examples 2 and 3 (3.3).

Randomly subsetting the markers and carrying out a detailed screening allows one to take advantage of more of the information contained in the data because the algorithm explores the large candidate marker set using the largest scope of inspection allowed by the data. The study of each random subset is comprehensive because the screening algorithm takes into account all possible interactions among the loci by using multi-point genotypes. Using a large though not comprehensive number of random subsets, the algorithm navigates much of the interactions among the markers under study. This is different from other approaches that employ a dimension reduction based on marginal information strategy before detailed modeling.

After markers have been evaluated based on a large number of random subset BGTA screenings, the return frequency is calculated. We then further separate the markers into two groups based on the distribution of their return frequencies, one with significantly higher return frequencies, defined as the ‘important’ marker group, and one with the remaining markers with lower frequencies, defined as the ‘unimportant’ group. To do so, one needs to decide a selection threshold based on the observed set of return frequencies. In this article, we assume that of all markers examined only a small proportion are associated, which is usually true for a large-scale study. Therefore, for moderate number of markers (for example, several hundreds), we define a selection threshold that is 1.8 times IQR (inter-quartile range) above the 3rd quartile of the observed return frequencies. Markers with return frequencies greater than this threshold will be selected into the ‘important’ group. This IQR-based criterion is roughly equivalent to a 3.1 standard deviation above the mean.³ For larger numbers of markers, the selection may be achieved through the strategy based on local false discovery rate proposed in [37], as illustrated in [13]. The above strategies are based on the assumption that most markers under study are unassociated, which is usually true for a large-scale study with hundreds to thousands of markers.

Selection of B and k

The selection of B (number of repeated random subset screening) and k (size of initial subset) are important for the markers’ return frequencies to reflect gene-gene interaction information, which also depend on the total number of markers under study, denoted by K. Under the null hypothesis, markers are returned or deleted at random. Under the alternative, markers with association to the disease trait are returned with a higher probability than markers with no association to the disease. Assume that, in a study, an unassociated marker has probability p₁ to be selected and returned in a random subset BGTA screening (including situations where this marker is not included in the initial subset). Usually, p₁ can be written in the form of c/K, where c is a constant (usually, the average size of returned subsets). Assume there is a marker M₁ that has weak or no marginal signal but have strong detectable signal with another marker M₂, so that once they are both selected into an initial k-marker subset, they will be returned together as important. Thus the probability that M₁ is returned as important is as follows:

$$p_2=\frac{\left(\begin{array}{c}K-2\hfill \\ k-2\hfill \end{array}\right)}{\left(\begin{array}{c}K\hfill \\ k\end{array}\right)}+\left(1-\frac{\left(\begin{array}{c}K-2\hfill \\ k-2\hfill \end{array}\right)}{\left(\begin{array}{c}K\hfill \\ k\end{array}\right)}\right)p_1=p_1+\frac{k(k-1)}{K(K-1)}(1-p_1).$$

We have derived in [12] a general formula for B in terms of p₁, p₂ and K,

$$B>{\left(\frac{3.1+2.33\sqrt{p_2/p_1}}{p_2/p_1-1}\right)}^2\frac{1-p_2}{p_2}\approx {\left(\frac{3.1+2.33\sqrt{p_2/p_1}}{p_2/p_1-1}\right)}^2(K-1),$$

in order to have approximately 99% probability to separate an important marker from an unimportant marker. If k scales up with $\sqrt{K,}{p}_2/p_1$ is close to a constant, and thus B should increase linearly with K. If k is kept as a constant, B needs to be approximately proportional to K³ in order to detect M₁. It should be noted that what presented above is the most difficult situation for detecting M₁, in reality, M₁ may have some moderate marginal signal or interactions with multiple markers, which will increase the value of p₂ and lead to a much smaller value of B needed. Larger sample sizes will allow larger initial subset size k and improve screening efficiency (lower value for p₁) and consequently require smaller B values. For example, if K = 1000 and c = 2, if one uses k = 15, for the most extreme case outlined above, B should be approximately 3,000,000. Under current computational power, BGTA is applicable to studies with hundreds to several thousands of markers.

Simulations and Results

We have introduced a marker selection procedure based on random subset BGTA screenings. To best understand how the marker selection works, in this section, we evaluate the methods proposed in the previous section using simulated examples. It is instructive to compare the empirical power of BGTA method with some current approaches. The suitable method for comparison should use the genotype information under case-control study; more importantly, it should be designed to have joint analysis on multiple markers so that it also considers the interactions among disease genes. For these reasons, we consider the set-association method proposed by Hoh et al. [15], which has been thoroughly studied in [14]. For a more complete comparison, we also compare BGTA to marker-by-marker genotype Pearson χ² tests on 3 × 2 contingency table (one column is a marker’s genotype distribution among the cases and the other is that of the controls). Finally, we demonstrate the BGTA method using an application to a real data set on inflammatory bowel disease (IBD [MIM 266600]), originally studied in [16].

The Set-Association Method by Hoh et al. [15]

The set-association method [15] evaluates a set of possibly interacting trait-associated SNP markers at various positions on the genome. For the ith marker, its association to the disease is measured by the product of the allelic association (t_i) and the Hardy-Weinberg disequilibrium information (u_i), that is, a single-marker statistic s_i = t_i × u_i. For multiple markers, the association to the disease is measured by the sum of these single-marker statistics, defined as the set-association score S = Σ(t_i × u_i). The motivation of this sum statistic is that, conditioning on the disease trait, the test statistics of markers at loci that are in association with interacting disease predisposing genes would be dependent and hopefully positively correlated. Such a dependence does not exist for loci that are not linked or in association with the disease trait. Thus, by adding the marginal test statistics, the power of detecting multiple disease predisposing loci becomes greater.

To initialize, all N markers under study are ranked by their single-marker statistics, from the highest to the lowest, with corresponding ordered statistics s₍₁₎ ≥ s₍₂₎ … ≥ s_(N). Then, cumulative sums of top markers are calculated and evaluated: S(1) = s₍₁₎, S(2) = s₍₁₎ + s₍₂₎, and so on until $S(N)={\displaystyle {\sum }_{i=1}^N{s}_{(i)}}$. Each S(n) has an associated p value that indicates the strength of the association between the top n markers and the disease. As the number of n increases from 1, the p value may decrease, which means more informative markers are included. The process stops when a minimum p value (strongest association) is reached, where adding any further marker will introduce noise to current n top genes and increase the p value. The final p-value of these markers, adjusting for the optimizing selecting process, is then evaluated using permutation tests. If the p value is significant at a pre-decided level, the current n top markers are then selected as the important markers with marginal and potential joint effects on the disease. In our simulation study, we use the Sumstat package downloaded from http://linkage.rockefeller.edu/ott/sumstat.html.

Genetic Heterogeneity Model: Example 1

We first evaluate the utility of BGTA method on multiple disease loci under a genetic heterogeneity model. Without much biological interaction among the disease loci, genetic heterogeneity characterizes a disease where independent mutations at several susceptibility loci lead to a same disease outcome. As a result, individuals who have mutations at any of these loci will have a higher susceptibility to the disease. These loci may be unlinked or on different chromosomes, such as well-apart genes that are on a common biochemical pathway. Under the heterogeneity model, marginal effects of disease loci are strong and dominant.

Such a model is usually regarded as ‘lack of epistasis’ in biological sense. However, as illustrated in [31], even such a model can be interpreted as epistatic under some definitions. Especially, such models can be show to have a statistical interaction term under the additive model of penetrance. However, when the disease alleles have relatively low population frequency, it is rare to observe cases who are homozygous of the disease predisposing allele at both loci. Thus, with a moderate-sized sample, association information under such a model is mostly marginal.

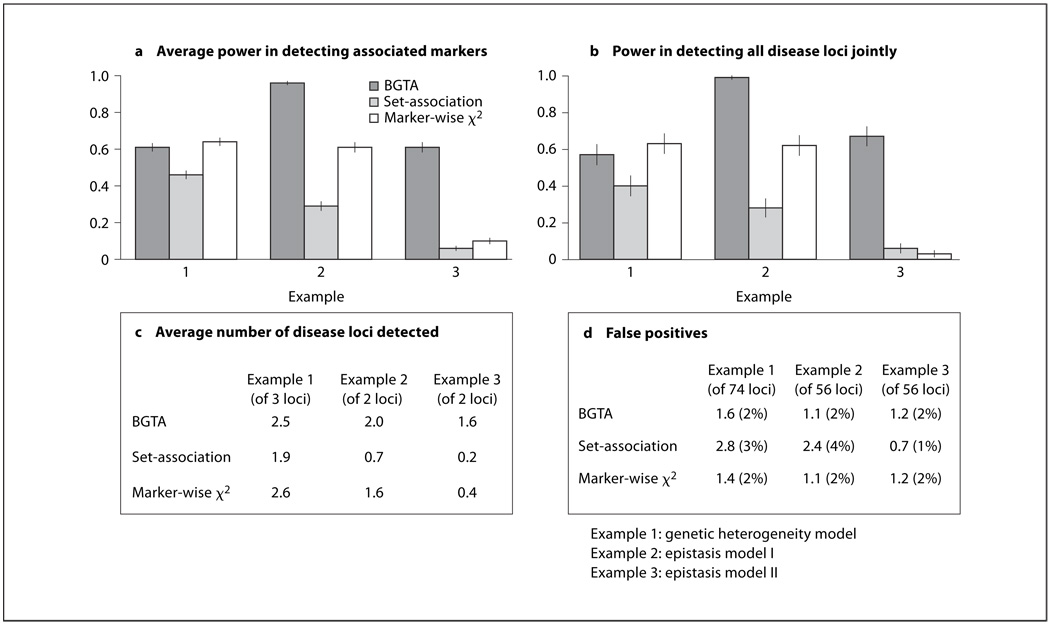
For this example we assume a disease with three susceptibility loci, which are not linked and have no interactions. Two copies of mutated allele at any of these three disease loci cause a higher penetrance of the disease. 80 diallelic markers are simulated. For each susceptibility locus, there are two markers in linkage/association with the disease genes, which makes a total of six associated markers. Figure 1 (example 1) displays the comparison of BGTA, set-association methods and marker-by-marker χ² tests using 300 simulated data sets of a moderate sample size, 150 cases and 150 controls.

Fig. 1.

Comparison between BGTA, set-association and markerwise χ² tests using simulations. BGTA, the set-association algorithm and marker-wise χ² tests are compared using simulations under three disease models (examples 1–3). a Average power in detecting associated markers with 95% confidence bars, which is the average probability for an associated marker to be selected (averaged over 4 or 6 associated markers: 2 markers per disease gene loci are simulated). b Power in (or the probability of) detecting all disease loci jointly with 95% confidence bars. c Average number of disease loci detected. d Average number of unassociated markers selected with corresponding estimated probability of false positives. The performance is evaluated using 300 simulated data sets of 150 diseased (cases) and 150 undiseased (controls) individuals. For example 1, 80 markers are simulated and for examples 2 and 3, 60 markers are simulated. Simulation specifications: (1) for example 1, disease gene predisposing allele is set to have population frequency 0.05; for examples 2 and 3, disease gene predisposing allele is set to have population frequency 0.5. (2) Marker allele population frequencies are set to 0.5. (3) Linkage/ LD between disease loci and associated markers: θ = 0.01 (recombination fraction) and Δ = 0.8 (standard LD). (4) Inter-markers linkage/LD are randomly generated from θ ~ U (0.05, 0.1) and Δ ~ U (0.1, 0.2). (5) For all examples, individuals without the disease predisposing genotypes have a 0.001 probability to be affected. BGTA specifications: random subset size used is k = 10; B = 5,000 random subset screenings were run for each simulation; marker selection is through IQR-based criterion on return frequencies. Set-association specifications: maximum number of top markers to sum is set to 20; the final selection significance level is set to 0.05.

As shown in figure 1 (example 1), under the genetic heterogeneity model where strong marginal effects of disease loci are present, BGTA method performed slightly better than the set-association method and comparable to the marker-wise χ² tests. All methods demonstrated satisfactory control of false positives. We will show in the next examples that the BGTA method becomes relatively more powerful when the interactions among susceptibility loci become substantial.

Disease Models with Epistasis: Examples 2 and 3

Recently, more attention has been devoted to the detection and investigation of the epistatic interactions [1, 27]. Cordell [31] provided a historical account of the study of epistasis, including different definitions and methods, where penetrance tables were used to demonstrate several examples with two interacting disease loci. Frankel and Schork [38] illustrated a model with pronounced epistatic interaction, where marginally association to either of the two disease loci is not readily detectable. Here, we study BGTA using simulations under two epistatic models with different extent of epistasis, in order to understand how BGTA detects epistatic interactions by using multi-locus genotypes. These two models are quite hypothetical. Actually, they represent the cases where information would be hard to extract completely at marginal. We use these difficult examples to illustrate the potential of the BGTA method.

In the first model, the genes have substantial interactions among themselves, while maintain readily detectable marginal effects. The second model has only joint detectable effects (complete epistasis), similar to the model discussed in [38], and is an extreme and hypothetical case. For either model, two interactive disease loci A and B are simulated. Locus A has two possible alleles, A (normal) or a (mutated), and locus B has alleles, B (normal) and b (mutated). 60 diallelic markers are simulated with two markers in association with each disease loci (a total of four markers are associated with the disease). The disease models are shown in the penetrance tables in table 1. For each model, we evaluate the methods using 300 data sets simulated with 150 cases and 150 controls.

Table 1.

Penetrance tables for two disease loci under epistatic models

a Epistatic model I
Genotype at locus A	Genotype at locus B			Marginal effect
	b/b (1/4)	b/B (1/2)	BB (1/4)
a/a (1/4)	0	0	1	0.25
a/A (1/2)	0	1	0	0.5
AA (1/4)	1	0	0	0.25
Marginal effect	0.25	0.5	0.25
b Epistatic model II
a/a (1/4)	0	0	1	0.25
a/A (1/2)	0	0.5	0	0.25
AA (1/4)	1	0	0	0.25
Marginal effect	0.25	0.25	0.25

Table 1a displays the disease model for example 2, which is set up so that an individual is affected if and only if two deleterious alleles and two normal alleles are present. Such a disease model might be possible when one mutation is not enough to intrigue the disease and having more than 2 mutations will lead to much different disease outcomes. The frequency of each single-locus genotype is given (in parentheses) next to the genotype. The marginal effect is shown as well, measured by the penetrance associated with single-locus genotypes at each locus individually. For example, the penetrance of genotype a/a in locus A is computed by multiplying each penetrance in the first row by the given frequency in the column: [(1/4) × 0 + (1/2) × 0 + (1/4) × 1] = 0.25.

Under the settings in table 1a, there are notable joint effects between loci A and B since the penetrance depends on the two-locus genotypes at both loci. On the other hand, since the marginal penetrances of three single- locus genotypes at each locus are not all equal, each gene can still be detected marginally.

Table 1b follows a similar setting as in table 1a. However, it defines a hypothetical situation where two genes A and B can not be detected marginally, and have only detectable joint effects. Note that the marginal penetrances given the three single-locus genotypes at each locus are all equal, which suggests that if one studied any disease locus independently of the other, no detectable effect at that locus would be observed.

The performances of BGTA method in comparison with the set-association method and the marker-wise χ² under epistatic models I and II are displayed in figure 1 as examples 2 and 3.

Figure 1 shows clearly that, compared with the set association method and the marker-wise χ² tests, BGTA method gains more advantage on power when the joint effects among disease loci become more substantial. Especially in the complete epistatic model (epistatic model II), BGTA method demonstrated an absolute advantage over the other two methods, which rely on marker-wise statistics and thus has no power in detecting any disease locus. For example 2, the high power of BGTA indicates the association signal between the markers and the disease is extremely strong. The performance of the markerwise genotype association χ² tests appears to be satisfactory but actually suffers a more than 30% efficiency drop. The performance of the set-association method suffers from its use of marginal statistics and also possibly its selection of test statistics (allelic association and HWD statistics may not be the most appropriate statistics for this disease model).

Moreover, in the random subset BGTA screening results, one could observe the joint returning patterns between markers that are associated with the interacting genes (details not shown). We call the smaller set of returned markers from one random subset BGTA screening a return cluster. For example 1, if we look at the B = 5000 returned marker clusters, the return clusters with more than one markers all have very low frequencies and are mostly unimportant marker pairs, meaning that these pairs do not point to two separate important disease susceptibility loci. This is due to the fact that, for example 1, the genes are not simulated to have strong interactions. For the epistatic models, examples 2 and 3, however, the most frequently returned pairs are those pointing to the two interacting disease loci, and their frequencies are significantly higher than the other returned clusters. This indicates that the BGTA method extracts important information on inter-locus interaction as it screens out unimportant markers. Another important indicator of gene-gene interaction is the GTD scores. Returned clusters with high GTD values are good candidates of interacting genes for further analysis. An easy strategy to fully explore interactions among selected marker loci is to calculate the GTD scores for pairs of these markers. The higher the score is, the stronger is the indication of gene-gene interaction. Higher-order interactions can be further identified by looking at the GTD scores on subsets with more than two markers.

Application to Inflammatory Bowel Disease Data: Example 4

For demonstration purposes, we apply BGTA to a data set of inflammatory bowel disease pedigrees analyzed in [16] and then re-analyzed by Lo and Zheng (2004) [13].

The inflammatory bowel disease (IBD [MIM 266600]) can be further diagnosed as ulcerative colitis (UC [MIM 191390]) or Crohn’s disease (CD) – two chronic idiopathic inflammatory diseases of the gastrointestinal tract. UC and CD are considered together because of their overlapping clinical, epidemiological, and pathogenetic features and their shared complications and therapies. For a comprehensive review of IBD and previous genome-wide screens, the readers are referred to Chapter 15 of [39]. Datasets used in this study are retrieved from the files (in LINKAGE format) provided by Whitehead Institute, MIT, on a study investigated by Rioux et al. [16]. The dataset contains 112 IBD pedigrees with more than two Crohn’s disease patients (89 with two patients, 20 with three patients and 3 with four patients), which is about 66% of the original dataset used in [16].

In order for BGTA to be applicable, we divide the 112 pedigrees in the data arbitrarily into two halves. From each pedigree in the first half, we sample one IBD patient; and we sample one non-patient from each pedigree in the second half. The haplotype phases, inferred from the pedigree data, are ignored. The resulting genotype data set is not exactly a population- based case-control data set but the 56 cases and 56 controls are independent. Thus, the BGTA method is still valid. We investigate the same set of 402 markers as in [13] and practice multiple imputations to address the issue of missing data. The readers are referred to [13] for details on data preparation.

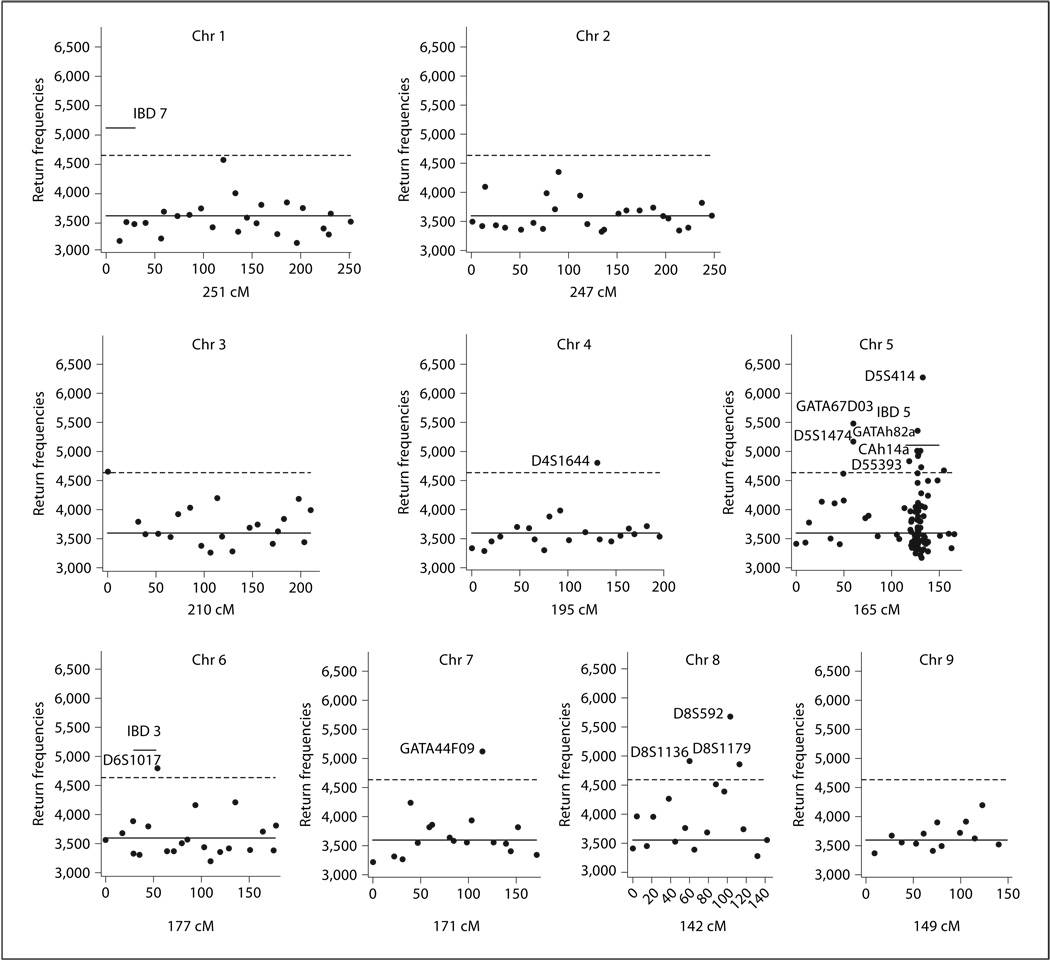
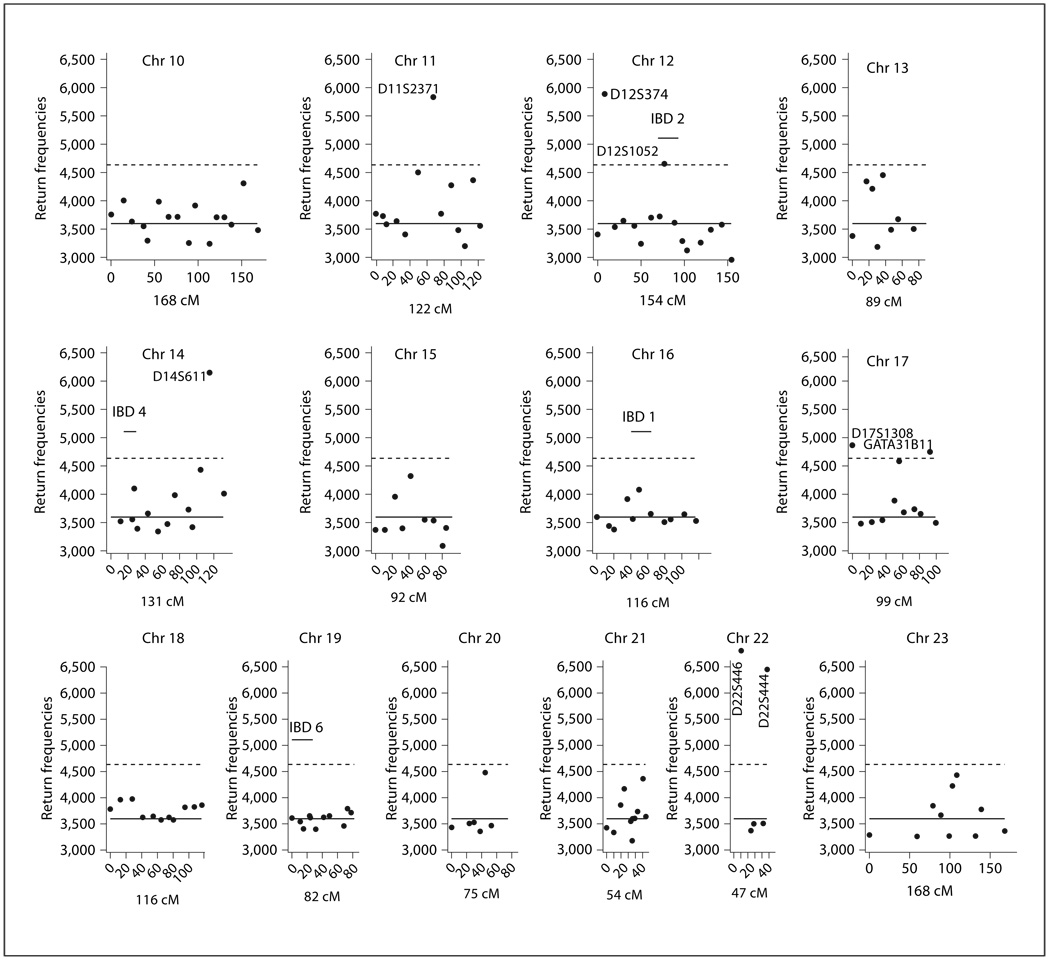
We run B = 50,000 random subset screenings on each of the 10 imputed data sets, which gives us a total of 500,000 BGTA screening result sets. The aggregated return frequencies for the markers studied are plotted in figure 2 and figure 3. BGTA identifies the same association signals at the loci of IBD2, IBD3 and IBD5, as detected by BHTA [12] in [13]. For IBD1 and IBD4, weaker signals result in somewhat higher return frequencies but not significantly higher. Considering the small size of the cases and controls used, the amount of information extracted by BGTA is rather impressive.

Fig. 2.

BGTA return frequencies for IBD data: chromosomes 1–9. Aggregated return frequencies from 500,000 BGTA random subset screenings (k = 8) are plotted versus marker location on the genome. Only markers included in the screening are shown. The median return is marker by a horizontal solid line, whereas the selection threshold is marked by a broken line. Selected important markers are labeled for readers’ reference. Seven horizontal bars indicate the previously reported IBD susceptibility loci, IBD1–IBD7. BGTA identified IBD2, IBD3 and IBD5 and showed weak signals on IBD1 and IBD4.

Fig. 3.

BGTA return frequencies for IBD data: chromosomes 10–23. Aggregated return frequencies from 500,000 BGTA random subset screenings (k = 8) are plotted versus marker location on the genome. See legend of figure 2.

Conclusion and Discussion

In this article, we have shown that BGTA-based marker selection provides a powerful approach to the association mapping of dichotomous complex traits under designs where only unphased genotypes are available. It utilizes the genotype-based statistics GTD and GTA, which can capture the marginal and joint effects of multiple susceptibility loci on the disease under study. Moreover, the random subset screening mechanism efficiently screens the largescale genomic data and explores the possible interactions, even clusters, among multiple markers. Different from conventional methods which examine markers locally and draw conclusions on one after another, BGTA marker selection procedure ranks the markers by their return frequencies and selects important ones for further detailed study. Additionally, the resulted marker set from each BGTA subset screening can be used to study the interaction among those markers who are returned together.

For simplicity, we only consider, in this article, diallelic markers, such as SNPs. This method can be applied to multiallelic markers straightforwardly. Recall the definition of key statistic GTD (page 11), it only uses the genotype information – the counts of multi-locus genotypes observed in cases and controls. Therefore, the ‘study unit’ in BGTA algorithm is the genotype instead of marker. For example, a triallelic marker has six possible genotypes; then the difference between GTDs before and after deleting a triallelic marker, equation (A.5), will have 15 cross product terms. The algorithm will be carried out similarly though the calculations are tedious. However, it is notable that the increased allele number deteriorates the sparseness problem given a certain sample size. Further investigation should be conducted to find a solution to this issue.

In all previous examples, our simulations are based on relatively small marker sets such as sets with 60 or 80 markers in total. Under these settings, B = 5000 repeated random subset screenings are enough to detect the disease- associated markers. However, as more and more markers become available with the development of biotechnology, the number of candidate markers in a genome scan study is now in the thousands or even hundreds of thousands. For studies with hundreds to several thousands of markers, one needs to increase B according to the discussion in section 2.6. For studies with hundreds of thousands of markers, we are currently considering possible multi-stage strategies. One possible way is to have exhaustive marginal scan (or scan of all pairs of markers as in [40]) in the first stage and then carry out full BGTA scan on selected markers. Another possible strategy is to start with an equally-spaced subset of markers (say, 2000 of them) and carry out a first stage of BGTA screening; after the first stage, increase density of markers at loci identified in the first stage for the second stage of BGTA screening. Due to the challenging dimensions of current whole-genome association studies, both strategies inevitably make some compromising choices: the first strategy might miss some important loci that have weak or no marginal signal; the second strategy might miss some important loci if the initially selected markers do not have strong linkage disequilibrium with the disease predisposing genes nearby.

In addition to genetic markers, information on some covariates can also be used in the BGTA-based methods, such as sex, age, environmental factors, etc. We can treat them as ‘pseudomarkers’ and discretize theirs value into several levels as the ‘pseudogenotypes’. Incorporating such covariates into the screening has the potential to reveal important gene-covariate interactions.

For candidate gene studies, the BGTA methods can help identify gene-gene interactions. One possible strategy is that one selects several markers from each candidate gene under evaluation to form a random subset for each BGTA screening. Since under a candidate gene study, a substantial percentage of the markers may show association with the disease trait, return frequencies from random subset screening may not be informative. GTD scores, as the association information measure, carry more detailed information about each gene-cluster identified. For a candidate gene study, one should record the gene-cluster returned from each random subset screening and rank these clusters by their GTD scores. Clusters with high GTD scores may represent important inter-region interactions.

Either in a whole-genome association study or a candidate gene study, the density of markers at a given loci is usually high. In other words, there might exist high linkage disequilibrium (LD) among the markers, especially for markers that are at a same gene locus. For markers that are associated with a disease gene, the GTD score of two markers that are in complete LD will have the same expectation as their individual GTD scores separately. One of these two markers will be removed randomly since either marker’s GTA score will be zero given the other marker. For two markers that are in high LD, the marker that has the weaker association with the disease will be removed since it adds noises to the information contained in the other marker. Screening on subsets that contain both markers discovers a similar amount of information as on subsets that contain only one of them. Therefore, to make the method more efficient, initial marker sets should have markers that are not highly associated among themselves. Such initial marker sets can be achieved via more structured sampling of markers. For example, one can randomly select k genetic regions, and within each region, randomly select one marker.

The proposed methods are not for multiple hypothesis testing, but rather should be viewed as part of an inferential process to select for further analysis, the markers and other risk factors that have demonstrated important association with the trait under study. As demonstrated in the examples we have evaluated using simulation studies, BGTA methods have shown great potential in dissecting the complex interactions simulated among the associated markers.

Appendix

The BGTA algorithm employs two important statistics, GTD and GTA, which carry both marginal and joint association information between the candidate markers and the disease loci. In this appendix, we demonstrate the mathematical justifications of these properties.

For convenience, we apply the commonly used genotype coding to the multi-locus unphased genotypes used in the algorithm, where each entry in such a vector represents a diallelic marker and its value is the number of a certain allele at that marker. For example, a four-marker genotype below can be represented by a four-dimension vector with each entry value as the number of allele b_i, i = 1, 2, 3, 4,

$$\begin{array}{ccc}\hfill \text{unphased genotype}\hfill & \hfill \Rightarrow \hfill & \hfill \text{coded genotype data}\hfill \\ \hfill \left(\begin{array}{c}\hfill \{a_1,a_1\}\hfill \\ \hfill \{a_2,b_2\}\hfill \\ \hfill \{a_3,b_3\}\hfill \\ \hfill \{b_4,b_4\}\hfill \end{array}\right)\hfill & \hfill \Rightarrow \hfill & \hfill \left(\begin{array}{c}\hfill 0\hfill \\ 1\\ \hfill 1\hfill \\ \hfill 2\hfill \end{array}\right).\hfill \end{array}$$

A Derivation and Expectation of the GTA Statistic

Same as in the METHODS section, let S_k be the current set with k markers, S_k = {M₁, M₂, …, M_k}, and $S_{k-1}^r$ denotes the new set less a certain marker M_r, that is,

$$S_k^r=S_k\backslash M_r=\{M_1,M_2,\dots ,M_{r-1},M_{r+1},\dots ,M_k\}.$$

For S_k and $S_k^r$, we define the genotype sets as $𝔾=\{g_1^{(k)},g_2^{(k)},\dots ,g_{3^k}^{(k)}\}\text{and}{𝔾}^r=\{g_1^{(k-1)},g_2^{(k-1)},\dots ,g_{3^{k-1}}^{(k)}\}$, respecitively. Then, 𝔾 can be rewritten as an extended set from G^r,

$$𝔾=\left\{\left(\begin{array}{c}\hfill g_i^{(k-1)}\hfill \\ \hfill 0\hfill \end{array}|,\begin{array}{c}\hfill g_i^{(k-1)}\hfill \\ \hfill 1\hfill \end{array}|,\begin{array}{c}\hfill g_i^{(k-1)}\hfill \\ \hfill 2\hfill \end{array}|\right):i=1,2,\dots 3^{k-1}\right\}$$ (A.1)

where 0, 1 and 2 represent the three possible genotypes at marker M_r. For convenience, we use $g_i^{(k-1)}$ (s) to represent the extended vector of genotypes

$$\begin{array}{c}\hfill g_i^{(k-1)}\hfill \\ \hfill s\hfill \end{array}|,s=0,1\text{or}2,$$

so that $g_i^{(k-1)}$ (s) ∈ 𝔾 and $g_i^{(k-1)}$ (s) ∈ 𝔾^r. Similar to $n_{d,i}^{(k)}’\text{s and}{n}_{u,i}^{(k)}’\mathrm{s}$ as in the METHODS section on page 8, we define $n_{d,i}^{(k-1)}\text{and}{n}_{u,i}^{(k-1)}$ as the numbers of times that genotype $g_i^{{(k-1)}^{d,i}}$ ∈ 𝔾_r is observed among the cases and controls, representatively. We further define $n_{d,i}^{(k-1)}$ (s) and $n_{u,i}^{(k-1)}$ (s) as the counts for the ex tended genotype $g_i^{(k-1)}$ (s) ∈ 𝔾, s = 0, 1 or 2.

These genotype counts satisfy that

$$n_{d,i}^{(k-1)}=n_{d,i}^{(k-1)}(0)+n_{d,i}^{(k-1)}(1)+n_{d,i}^{(k-1)}(2),$$ (A.2)

and

$$n_{u,i}^{(k-1)}=n_{u,i}^{(k-1)}(0)+n_{u,i}^{(k-1)}(1)+n_{u,i}^{(k-1)}(2),$$ (A.3)

Thus, using these counts, it is easier to examine explicitly the information loss due to the deletion of marker M_r, measured by the difference between GTD(k) and GTD^(k-1). More specifically, we rewrite these two scores as follows.

Before removing M_r,

$$\begin{array}{ll}{\text{GTD}}^{(k)}\hfill & ={\displaystyle \sum _{i=1}^{3^k}{\left(\frac{n_{d,i}^{(k)}}{n_d}-\frac{n_{u,i}^{(k)}}{n_u}\right)}^2}\hfill \\ \hfill & ={\displaystyle \sum _{i=1}^{3^{k-1}}\{{\left(\frac{n_{d,i}^{(k-1)}(0)}{n_d}-\frac{n_{u,i}^{(k-1)}(0)}{n_u}\right)}^2+{\left(\frac{n_{d,i}^{(k-1)}(1)}{n_d}-\frac{n_{u,i}^{(k-1)}(1)}{n_u}\right)}^2}\hfill \\ \hfill & +{\left(\frac{n_{d,i}^{(k-1)}(2)}{n_d}-\frac{n_{u,i}^{(k-1)}(2)}{n_u}\right)}^2\}.\hfill \end{array}$$ (A.4)

After Mr is removed,

$$\begin{array}{ll}{\text{GTD}}^{(k-1)}\hfill & ={\displaystyle \sum _{i=1}^{3^{k-1}}{\left(\frac{n_{d,i}^{(k-1)}}{n_d}-\frac{n_{u,i}^{(k-1)}}{n_u}\right)}^2}\hfill \\ \hfill & ={\displaystyle \sum _{i=1}^{3^{k-1}}\{\left(\frac{n_{d,i}^{(k-1)}(0)}{n_d}+\frac{n_{d,i}^{(k-1)}(1)}{n_d}+\frac{n_{d,i}^{(k-1)}(2)}{n_d}\right)}\hfill \\ \hfill & -\left(\frac{n_{u,i}^{(k-1)}(0)}{n_d}+\frac{n_{u,i}^{(k-1)}(1)}{n_d}+\frac{n_{u,i}^{(k-1)}(2)}{n_d}\right){\}}^2\hfill \\ \hfill & ={\text{GTD}}^{(k)}+2·{\displaystyle \sum _{i=1}^{3^{k-1}}\{R_i(0,1)+R_i(0,2)+R_i(1,2)\}}\hfill \end{array}$$ (A.5)

where

$$R_i(s,t)=\left(\frac{n_{d,i}^{(k-1)}(s)}{n_d}-\frac{n_{u,i}^{(k-1)}(s)}{n_u}\right)\left(\frac{n_{d,i}^{(k-1)}(t)}{n_d}-\frac{n_{u,i}^{(k-1)}(t)}{n_u}\right)$$ (A.6)

and s, t = 0, 1, 2. From the above equations, one can write explicitly the difference between GTD^(k) and GTD^(k-1) as

$$\mathrm{\Delta }\text{GTD}=\left({\text{GTD}}^{(k-1)}-{\text{GTD}}^{(k)}\right)=2{\displaystyle \sum _{i=1}^{3^{k-1}}\{R_i(0,1)+R_i(0,2)+R_i(1,2)\}.}$$

The statistic GTA(r) is then defined as:

$$\text{GTA}(r)=\frac{1}{2}\mathrm{\Delta }\text{GTA}+\tilde{A}={\displaystyle \sum _{i=1}^{3^{k-1}}\{R_i(0,1)+R_i(0,2)+R_i(1,2)\}+\tilde{A}}$$ (A.7)

where

$$\{\begin{array}{c}{R}_i(s,t)=\left(\frac{n_{d,i}^{(k-1)}(s)}{n_d}-\frac{n_{u,i}^{(k-1)}(s)}{n_u}\right).\left(\frac{n_{d,i}^{(k-1)}(t)}{n_d}-\frac{n_{u,i}^{(k-1)}(t)}{n_u}\right)\hfill \\ \tilde{A}=\left(\widehat{N}(0,1)+\widehat{N}(0,2)+\widehat{N}(1,2)\right)\hfill \end{array}$$

and

$$\widehat{N}(s,t)={\displaystyle \sum _{i=1}^{3^{k-1}}\left(\frac{1}{n_d}·\frac{n_{d,i}^{(k-1)}(s)·n_{d,i}^{(k-1)}(t)}{n_d(n_d-1)}+\frac{1}{n_u}·\frac{n_{u,i}^{(k-1)}(s)·n_{u,i}^{(k-1)}(t)}{n_u(n_u-1)}\right)},$$

s, t = 0, 1, 2.

To clearly show the expectation of GTA(r), notations for the parameters and statistics for the genotypes before and after deleting M_r are to be defined systematically. Generally, for genotypes $g_i^{(k-1)}$ (s) (before deleting M_r) and $g_i^{(k-1)}$ (after deleting M_r), where s ∈ {0,1,2}, ∈ {1,2, …,3^k-1}, the systematic notations are described as follows:

	before deleting Mr	after deleting Mr
genotype	$g_i^{(k-1)}$(s)	$g_i^{(k-1)}$
risk ratio	ri(s)	ri
population probability	pi(s)	pi
counts in cases	$n_{d,i}^{(k-1)}$	$n_{d,i}^{(k-1)}$
counts in controls	$n_{u,i}^{(k-1)}$(s)	$n_{u,i}^{(k-1)}$

where s indicates the genotype at the M_r locus. Here risk ration, r_i, is the ratio of the disease penetrance given genotype g_i and the population disease prevalence.

They satisfy the equations:

$$\{\begin{array}{l}{r}_i{p}_i=r_i(0)·p_i(0)+r_i(1)·p_i(1)+r_i(2)·p_i(2),\hfill \\ (1-r_i{p}_d)p_i=(1-r_i(0)p_d)·p_i(0)+(1-r_i(1)p_d)·p_i(1)+\hfill \\ (1-r_i(2)p_d)·p_i(2),\hfill \\ n_{d,i}^{(k-1)}=n_{d,i}^{(k-1)}(0)+n_{d,i}^{(k-1)}(1)+n_{d,i}^{(k-1)}(2),\hfill \\ n_{u,i}^{(k-1)}=n_{u,i}^{(k-1)}(0)+n_{u,i}^{(k-1)}(1)+n_{u,i}^{(k-1)}(2).\hfill \end{array}$$ (A.8)

In the case or control group, the count of each genotype can be considered as a random variable. For example, the counts $(n_{d,i}^{(k-1)}(0),n_{d,i}^{(k-1)}(1),n_{d,i}^{(k-1)}(2))$, given their sum $n_{d,i}^{(k-1)}$, will follow a multinomial distribution with the probability function

$$\begin{array}{c}P(n_{d,i}^{(k-1)}(0),n_{d,i}^{(k-1)}(1),n_{d,i}^{(k-1)}(2)|n_{d,i}^{(k-1)})\hfill \\ =\frac{n_{d,i}^{(k-1)}!}{{\displaystyle {\prod }_{s=0}^2{n}_{d,i}^{(k-1)}(S)!}}{\displaystyle \prod _{s=0}^2({\frac{r_i(s)p_i(s)}{r_i{p}_i})}^{n_{d,i}^{(k-1)}(s)}.}\hfill \end{array}$$ (A.9)

In other words, the probability of observing the extended genotype $g_i^{(k-1)}$(s) given $g_i^{(k-1)}$ is

$$\frac{r_i(s)p_i(s)}{r_i{p}_i},$$

s = 0,1,2. Therefore, one can derive the following conditional expectations:

$$\mathrm{E}(n_{d,i}^{(k-1)}(s)|n_{d,i}^{(k-1)})=n_{d,i}^{(k-1)}·\frac{r_i(s)p_i(s)}{r_i{p}_i}$$ (A.10)

$$\mathrm{E}\left(n_{d,i}^{(k-1)}(s)·n_{d,i}^{(k-1)}(t)|n_{d,i}^{(k-1)}\right)=n_{d,i}^{(k-1)}\left(n_{d,i}^{(k-1)}-1\right)·\frac{r_i(s)p_i(s)}{r_i{p}_i}·\frac{r_i(t)p_i(t)}{r_i{p}_i}$$ (A.11)

and then

$$\begin{array}{ll}\mathrm{E}(n_{d,i}^{(k-1)}(s)·n_{d,i}^{(k-1)}(t))\hfill & =\mathrm{E}(\mathrm{E}(n_{d,i}^{(k-1)}(s)·n_{d,i}^{(k-1)}(t)|n_{d,i}^{(k-1)}))\hfill \\ \hfill & =\mathrm{E}(n_{d,i}^{(k-1)}(n_{d,i}^{(k-1)}-1))·\frac{r_i(s)p_i(s)}{r_i{p}_i}·\frac{r_i(t)p_i(t)}{r_i{p}_i}\hfill \\ \hfill & =n_d(n_d-1){(r_i{p}_i)}^2·\frac{r_i(s)p_i(s)}{r_i{p}_i}·\frac{r_i(t)p_i(t)}{r_i{p}_i}\hfill \\ \hfill & =n_d(n_d-1)p_i(s)p_i(t)r_i(s)r_i(t).\hfill \end{array}$$ (A.12)

Similarly, in the control group, the probability of observing genotype $g_i^{(k-1)}$(s) given $g_i^{(k-1)}$ is

$$\frac{(1-r_i(s)p_d)p_i(s)}{(1-r_i{p}_d)p_i}$$

and

$$\begin{array}{c}\mathrm{E}(n_{u,i}^{(k-1)}(s)·n_{u,i}^{(k-1)}(t))=\mathrm{E}(\mathrm{E}(n_{u,i}^{(k-1)}(s)·n_{u,i}^{(k-1)}(t)|n_{u,i}^{(k-1)}))\hfill \\ =\mathrm{E}(n_{u,i}^{(k-1)}(n_{u,i}^{(k-1)}-1))·\frac{(1-r_i(s)p_d)p_i(s)}{(1-r_i{p}_d)p_i}·\frac{(1-r_i(t)p_d)p_i(t)}{(1-r_i{p}_d)p_i}\hfill \\ =n_u(n_u-1){\left(\frac{(1-r_i{p}_d)p_i}{1-p_d}\right)}^2·\frac{(1-r_i(s)p_d)p_i(s)}{(1-r_i{p}_d)p_i}·\frac{(1-r_i(t)p_d)p_i(t)}{(1-r_i{p}_d)p_i}\hfill \\ =n_u(n_u-1)p_i(s)p_i(t)·\frac{1-r_i(s)p_d}{1-p_d}·\frac{1-r_i(t)p_d}{1-p_d}.\hfill \end{array}$$ (A.13)

Recall the fact that the case and control groups are sampled independently, so the expectation of cross product of counts between case and control groups is

$$\begin{array}{ll}\mathrm{E}(n_{d,i}^{(k-1)}(s)·n_{u,i}^{(k-1)}(t))\hfill & =\mathrm{E}\left(n_{d,i}^{(k-1)}(s))·\mathrm{E}(n_{u,i}^{(k-1)}(t)\right)\hfill \\ \hfill & =n_d·r_i(s)p_i(s)·n_u·\frac{(1-r_i(t)p_d)p_i(t)}{1-p_d}\hfill \\ \hfill & =n_d{n}_u{p}_i(s)p_i(t)r_i(s)\frac{1-r_i(t)p_d}{1-p_d}.\hfill \end{array}$$ (A.14)

To calculate the expectation of GTA(r), that is, E(GTA(r)) = E(1/2 Δ GTD) + E(Ã), we first calculate E (1/2 ΔGTD) based on (A.12), (A.13) and (A.14),

$$\begin{array}{ll}\mathrm{E}(\frac{1}{2}\mathrm{\Delta }\text{GTD})\hfill & =\mathrm{E}({\displaystyle \sum _{i=1}^{3^{k-1}}\{R_i(0,1)+R_i(0,2)+R_i(1,2)\}})\hfill \\ \hfill & ={\displaystyle \sum _{i=1}^{3^{k-1}}\{\mathrm{E}\left(R_i(0,1)\right)+\mathrm{E}\left(R_i(0,2)\right)+\mathrm{E}\left(R_i(1,2)\right)\}}\hfill \\ \hfill & =C·\{{\displaystyle \sum _{i=1}^{3^{k-1}}(p_i(0)p_i(1)(r_i(0)-1)(r_i(1)-1)}\hfill \\ \hfill & +p_i(0)p_i(2)(r_i(0)-1)(r_i(2)-1)\hfill \\ \hfill & +p_i(1)p_i(2)(r_i(1)-1)(r_i(2)-1))\}\hfill \\ \hfill & -\left\{N\left(0,1\right)+N\left(0,2\right)+N(1,2)\right\}.\hfill \end{array}$$ (A.15)

In the above equation,

$$\{\begin{array}{c}C=\frac{1}{{(1-p_d)}^2}\hfill \\ N(s,t)={\displaystyle \sum _{i=1}^{3^{k-1}}{p}_i(s)p_i(t)\left(\frac{1}{n_d}{r}_i(s)r_i(t)+\frac{1}{n_u}\frac{1-r_i(s)p_d}{1-p_d}·\frac{1-r_i(t)p_d}{1-p_d}\right).}\hfill \end{array}$$ (A.16)

N(s,t) can be estimated unbiasedly by

$$\widehat{N}(s,t)={\displaystyle \sum _{i=1}^{3^{k-1}}\left(\frac{1}{n_d}\frac{n_{d,i}^{(k-1)}(s)n_{d,i}^{(k-1)}(t)}{n_d(n_d-1)}+\frac{1}{n_u}\frac{n_{u,i}^{(k-1)}(s)n_{u,i}^{(k-1)}(t)}{n_u(n_u-1)}\right)}$$ (A.17)

which is an item in the adjusting term à as defined in (A.7). Finally, the expectation of GTA can be derived by combining (A.15) and (A.17)

$$\begin{array}{ll}\mathrm{E}(\text{GTA}(r))\hfill & =C·\{{\displaystyle \sum _{i=1}^{3^{k-1}}(p_i(0)p_i(1)(r_i(0)-1(r_i(1)-1)}\hfill \\ \hfill & +p_i(0)p_i(2)(r_i(0)-1(r_i(2)-1)\hfill \\ \hfill & +p_i(1)p_i(2)(r_i(1)-1(r_i(2)-1))\}.\hfill \end{array}$$ (A.18)

From (A.18), one can easily conclude that E(GTA(r)) = 0 under the null hypothesis of no association, that is, r_i(s) = 1, i ∈ {1,2, …,3^k-1}, s ∈ {0,1,2}.

B Properties of the GTA Statistic

In the previous section, we computed the expectation of GTA(r) in terms of population probabilities p_i(s) and risk ratios r_i(s) for genotype g_i^(k-1)(s), s ∈ {0,1,2}, i ∈ {1,2, …, 3^k-1}. In this section, we discuss the relation between the importance of a marker M_r and the values of E(GTA).

Under the null hypothesis of no association, that is, r_i (0) = r_i (1) = r_i (2) = 1, i = 1,2, …,3^k-1, then it is easy to obtain that E(GTA(r)) = 0 from (A.18).

Under the alternative hypothesis, that is, there is one or more markers in association with the disease trait, then we can find some i ∈ {1,2, …, 3^k-1} and some s ∈ {0,1,2} such that r_i(s) ≠ 1. However, the mechanism of the associations among k markers is complicated. In the following, we will discuss three scenarios under the alternative hypothesis.

Scenario One: M_r is not in association with the disease while some other current markers are. Thus, the conditional probabilities satisfy the equation P(D|g_i) = P(D|g_i(0)) = P(D|g_i(1)) = P(D|g_i(2)), and consequently, we have r_i = r_i(0) = r_i(1) = r_i(2). In this case,

$$\mathrm{E}\left(\text{GTA}(r)\right)=C·\{{\displaystyle \sum _{i=1}^{3^{k-1}}(p_i(0)p_i(1)+p_i(0)p_i(2)+p_i(1)p_i(2))}{\left(r_i-1\right)}^2\}$$ (B.1)

Since one or more of the remaining markers other than M_r have association with the disease, then r_i ≠ 1 for some i ∈ {1,2, …,3^k-1}. Thus, E(GTA(r)) is strictly positive under this scenario.

Scenario Two: M_r is in association with the disease while none of the other current markers are. More specifically, we have P(g_i | D) = P(g_i), i = 1,2, …,3^k-1, and r_i(s) ≠ 1 for some s ∈ {0,1,2}. Define A_i = p_i (0) p_i(1)(r_i(0) - 1)(r_i(1) - 1) + p_i (0) p_i(2)(r_i(0) - 1) (r_i(2) - 1) + p_i(1) p_i(2)(r_i(1) - 1)(r_i(2) - 1), where i = 1,2, …,3^k-1. Then

$$\begin{array}{ll}2A_i\hfill & =\{p_i(0)p_i(1)(r_i(0)-1)(r_i(1)-1)+p_i(0)p_i(2)(r_i(0)-1)(r_i(2)-1)\}\hfill \\ \hfill & +\{p_i(0)p_i(1)(r_i(0)-1)(r_i(1)-1)+p_i(1)p_i(2)(r_i(1)-1)(r_i(2)-1)\}\hfill \\ \hfill & +p_i(0)p_i(2)(r_i(0)-1)(r_i(2)-1)+p_i(1)p_i(2)(r_i(1)-1)(r_i(2)-1)\hfill \\ \hfill & =\{p_i{(0)}^2(r_i(0)-1)(1-r_i(0))\}+\dots \hfill \\ \hfill & =-p_i{(0)}^2{(1-r_i(0))}^2-p_i{(1)}^2{(1-r_i(1))}^2-p_i{(2)}^2{(1-r_i(2))}^2<0\hfill \end{array}$$ (B.2)

Therefore, under this scenario,

$$\mathrm{E}(\text{GTA}(r))=C·{\displaystyle \sum _{i=1}^{3^{k-1}}{A}_i<0.}$$

Scenario Three: M_r is in association with the disease, and also has interactions with some other markers. Without losing generality, assume that only one of the other marker M_q has interaction with M_r, and all the other markers are independent of the disease. Therefore, the disease status is determined by the marginal and joint effects of M_r and M_q. To distinguish from marker M_r, let {0_q, 1_q, 2_q} denote the genotypes at the locus of M_q. In addition, let $g_i^{(k-2)}’\mathrm{s}$ denote the genotypes on the remaining k - 2 markers. The corresponding population probability and risk ratio are $p_i^{(k-2)}\text{and}{r}_i^{(k-2)}$ respectively. Based on these notations, the extended k-marker genotype can be written as $g_i^{(k-2)}$ (s, t_q), i = 1,2, …,3^k-2, where s and t_q are genotypes for M_r and M_q respectively, and similarly we define p_i(s, t_q) and r_i(s, t_q). It is worth to mention that the set

$$\{g_i^{(k-1)}(s):i=1,2,\dots ,3^{k-1},s=0,1,2\}$$

can also be re-written as

$$\{g_j^{(k-2)}(s,0_q),g_j^{(k-2)}(s,1_q),g_j^{(k-2)}(s,2_q):j=1,2,\dots ,3^{k-2},3^{k-2},s=0,1,2\}.$$

To shorten the formulations, we define Δ_i(s) = p_i(s)(r_i(s) - 1).

Following the above notations, we have

$$\begin{array}{l}\mathrm{E}(\text{GTA}(r))=\hfill \\ =C·{\displaystyle \sum _{i=1}^{3^{k-1}}\{{\mathrm{\Delta }}_i(0){\mathrm{\Delta }}_i(1)+{\mathrm{\Delta }}_i(0){\mathrm{\Delta }}_i(2)+{\mathrm{\Delta }}_i(1){\mathrm{\Delta }}_i(2)\}}\hfill \\ =C·{\displaystyle \sum _{l=1}^{3^{k-2}}[{\mathrm{\Delta }}_l(0,0_q){\mathrm{\Delta }}_l(1,0_q)+{\mathrm{\Delta }}_l(0,0_q){\mathrm{\Delta }}_l(2,0_q)+{\mathrm{\Delta }}_l(1,0_q){\mathrm{\Delta }}_l(2,0_q)}\hfill \\ +{\mathrm{\Delta }}_l(0,1_q){\mathrm{\Delta }}_l(1,1_q)+{\mathrm{\Delta }}_l(0,1_q){\mathrm{\Delta }}_l(2,1_q)+{\mathrm{\Delta }}_l(1,1_q){\mathrm{\Delta }}_l(2,1_q)\hfill \\ +{\mathrm{\Delta }}_l(0,2_q){\mathrm{\Delta }}_l(1,2_q)+{\mathrm{\Delta }}_l(0,2_q){\mathrm{\Delta }}_l(2,2_q)+{\mathrm{\Delta }}_l(1,2_q){\mathrm{\Delta }}_l(2,2_q)]\hfill \end{array}$$ (B.3)

where Δ_l(s, t_q) is defined as p_l(s, t_q)(r_l(s, t_q) - 1). From the assumption that the other k - 2 markers (excluding M_r and M_q) are independent of the disease, their risk ratios satisfy r^(k-2)_l = 1, l = 1, 2, …, 3^k-2. Then Δ_l (•, •), l = 1, 2, …, 3^{k -2} will satisfy

$${\displaystyle \sum _{s=0}^2\left\{{\mathrm{\Delta }}_l\left(0,s_q\right)+{\mathrm{\Delta }}_l\left(1,s_q\right)+{\mathrm{\Delta }}_l\left(2,s_q\right)\right\}=p_l^{(k-2)}(r_l^{(k-2)}-1)=0.}$$ (B.4)

This leads to a constraint on the nine terms, Δ_l (s, t_q), (s, t = 0, 1, 2), that they add up to zero. This implies that some of them are positive and some negative. In order to see the interactions between marker M_r and M_q, the signs of each value will be analyzed within three sets Ω₀ = {Δ_l (0,0_q), Δ_l (1, 0_q), Δ_l (2, 0_q)}, Ω₁ = {Δ_l(0, 1_q), Δ_l (1, 1_q), Δ_l (2, 1_q)}, and Ω₂ = {Δ_l (0, 2_q), Δ_l (1, 2_q), Δ_l (2, 2_q)}. For example, if the signs in Ω₀ are all ‘+’ (or all ‘−’), we use ‘same’ to characterize the signs in Ω₀; otherwise, we say ‘change’. It is easy to observe that the within-set changes are due to M_r whereas M_qcontributes to between-set differences. As shown in table 2, the last two columns indicate the signs of E(GTA(r)) and the importance of M_r under different levels, which shows strong agreement with our marker selection criteria. Due to the symmetry, Ω₀, Ω₁ and Ω₂ can be discussed exchangeably and table 2 only lists all unique-by-symmetry scenarios of possible interactions between markers M_r and M_q and the corresponding signs of E(GTA).

Table 2.

E(GTA) reflects a marker’s importance in the presence of gene-gene interactions

Within-class changes of penetrance due to Mr	Classes defined by Mq			E(GTA(r))	Importance of Mr
	Ω0	Ω1	Ω2
1 No class w. change	same	same	same	positive	low
2 One class w. change	change	same (+ or −)	same (− or +)	positive	low
3 One class w. change	change	same (+ or −)	same (+ or −)	negative	high
4 Two classes w. change	change	change	same	negative	high
5 Three classes w. change	change	change	change	negative	high

The computation is based on a simplifying assumption that all high risk genotypes share a same penetrance and all low risk genotypes also share a same penetrance. The difference between case 2 and 3 is that in case 2, M_q is dominantly more important than M_r, much so that including M_r will only add noises to the signals due to M_q. For case 3, M_q does not have such major effects and relatively M_r is important. Future investigation is needed to allow GTA pick up signals from M_r even when a dominating major gene such as M_q is present.