Determinants of change of prostate-specific antigen over time and its association with recurrence following external beam radiation therapy of prostate cancer in 5 large cohorts

Abstract

Purpose

To assess the relationship between prognostic factors, post-radiation prostate-specific antigen (PSA) dynamics, and clinical failure following prostate cancer radiation therapy using contemporary statistical models.

Methods and materials

Data from 4,247 patients with 40,324 PSA measurements treated with external beam radiation monotherapy in five cohorts were analyzed. Temporal change of PSA following treatment completion was described by a specially developed linear mixed model (LMM), including standard prognostic factors. These factors, along with predicted PSA evolution, were incorporated into a Cox model to establish their predictive value for the risk of clinical recurrence over time.

Results

Consistent relationships were found across cohorts. The initial PSA decline after radiation therapy was associated with baseline PSA and T-stage (p<0.001). The long-term PSA rise was associated with baseline PSA, T-stage and Gleason score (p<0.001). The risk of clinical recurrence increased with current level (p<0.001) and current slope of PSA (p<0.001). In a pooled analysis, higher doses of radiation were associated with a lower long-term PSA rise (p<0.001) but not with the risk of recurrence after adjusting for PSA trajectory (p=0.63). Conversely, after adjusting for other factors, increased age at diagnosis was not associated with long-term PSA rise (p=0.85) but directly associated with increased risk of recurrence (p<0.001).

Conclusions

LMM can be reliably used to construct typical patient PSA profiles following prostate cancer radiation therapy. Pre-treatment factors along with PSA evolution and the associated risk of recurrence provide an efficient and quantitative way to assess impact of risk factors on disease progression.

INTRODUCTION

The serum marker prostate-specific antigen (PSA) is widely used in making clinical decisions related to prostate cancer treated with external beam radiation therapy (EBRT). It stands alongside Gleason score and clinical T-stage as a well-characterized pre-treatment predictor of clinical outcome for clinically localized prostate cancer (1–3). Subsequent to EBRT, PSA levels follow a broadly predictable path which may also have clinical prognostic significance. In cases where EBRT has been successful, PSA levels typically fall to a nadir level over the first post-treatment year and henceforth remaining stable at these low levels (4,5). In cases of subsequent therapeutic failure however, a superimposed rising PSA pattern is usually the initial evidence of recurrence. These asymptomatic but rising PSA levels almost universally precede the development of clinically apparent prostate cancer recurrence (6–8).

During the phase described by asymptomatic and rising PSA levels, kinetic indices such as PSA doubling time and velocity have been associated with a worsened clinical outcome (9–11). As such, PSA kinetics are often incorporated into the clinical decision-making process of when to initiate salvage therapy; a decision which is typically made prior to the development of symptomatic disease in contemporary practice (12). However, exactly which features of the post-treatment profile of PSA should be used in decision-making is not settled presently. A simple approach is to reduce the PSA rise to a binary variable. The well known concept of biochemical failure (bF) is one such variable, which in the radiation therapy literature has been defined as three consecutive rises (13) or more recently as a PSA rise of 2 ng/mL or more above the PSA nadir (14). This latter definition has been shown to be associated with clinical failure (8). However, as PSA is a continuous variable this dichotomous reduction may not provide optimal prognostic information (15).

More accurate prediction of clinical recurrence can be obtained by a unification of the relationships between pre-treatment prognostic factors, post-therapy PSA kinetics and clinical recurrence. Based on our previously published concept for such a model (16), we now aim to refine and further investigate the relationship between post-therapy PSA kinetics and risk of recurrence in multiple large datasets. This risk model quantifies the average post-radiation PSA trajectory which could be expected across heterogeneous patient populations. It includes pre-treatment prognostic factors that influence the PSA profile, and assesses the predictive value of the pattern of PSA for risk of clinical failure, providing unique insights into the role that post-therapy PSA monitoring plays in mediating the effect of prognostic factors.

METHODS and MATERIALS

Patient cohort

All eligible cases had clinically localized prostate cancer of clinical stage T1-4, were node- and metastasis-negative, and treated with EBRT. Loco-regional and systemic disease was assessed at the discretion of the treating physician, and typically included computed tomography of the abdomen and pelvis, along with whole body bone scanning. Surgical staging of lymph nodes was done in <1% of cases. Those having planned neoadjuvant or adjuvant androgen deprivation therapy (ADT) were ineligible. Cases were drawn from five cohorts, four of which are previously described: University of Michigan, Michigan, USA (UM) (16); Radiation Therapy Oncology Group, USA (RTOG 9406) (17,18); William Beaumont Hospital, Detroit, Michigan, USA (WBH) (5); Peter MacCallum Cancer Centre, Melbourne, Australia (PMCC); Royal Brisbane Hospital, Brisbane, Australia (RBH) (19,20). All data were acquired under Institutional Review Board approval at the respective institutions and at UM, where the data were aggregated and analysed.

In summary, EBRT (either 2D or 3D conformal) was targeted to the prostate or prostate plus seminal vesicles depending on clinical risk. Whole pelvic radiotherapy was not routinely performed. All cases were required to have at least one year follow-up without clinical recurrence or salvage ADT and at least two PSA measurements before end of follow-up. All PSA measures collected after EBRT until the end of follow-up (minimum time to clinical recurrence or lost to follow-up) or initiation of salvage ADT were analysed. Complete PSA, clinical failure and salvage therapy histories were individually assessed for data consistency. All PSA measures were logarithmically transformed using ln(PSA+0.1 ng/mL) to satisfy normality assumptions for inclusion in the statistical models.

Prognostic factors evaluated were Gleason score category (2–6, 7, 8–10), T-stage category (1, 2, 3 or 4), pre-treatment (initial) level of PSA (iPSA; transformed on continuous scale to iPSA = ln(iPSA+0.1 ng/mL)), age at onset of EBRT and radiation dose. Two measures of dose were considered, the crude total dose (D) defined as the sum of all fractional doses given during therapy, and a corrected total dose (D^C). The D^C accounts for the differing dose per fraction (d_j) across the J total fractions using a linear-quadratic relationship (the α/β ratio): D^C=(α/β Σ_j=1,J d_j +Σ_j=1,J d_j²/(α/)β + 2), which is the equivalent total dose as if all fractions were 2Gy. A recent analysis suggested an α/β ratio in the range of 2 to 5Gy (20), hence α/β=4 was used in the analysis.

Due to the multicenter nature of the dataset, clinical recurrence assessment was not uniform for frequency or indication across the cohorts, and for the RBH cohort clinical recurrence data was unavailable. In order to reduce biases due to follow-up variations between cohorts, a common clinical failure criterion was applied as any of the following: distant metastases, nodal recurrence, any palpable or biopsy-detected local recurrence three years or later after radiation; any local recurrence within 3 years of EBRT if the most previous PSA was >2 ng/mL; death from prostate cancer. This definition was to allow for the possibility of residual local disease. In patients with more than one clinical recurrence, only the first was used.

Statistical analysis

Distributions of prognostic factors over cohorts were compared using a Kruskall Wallis test for continuous variables and a χ²-test for categorical variables.

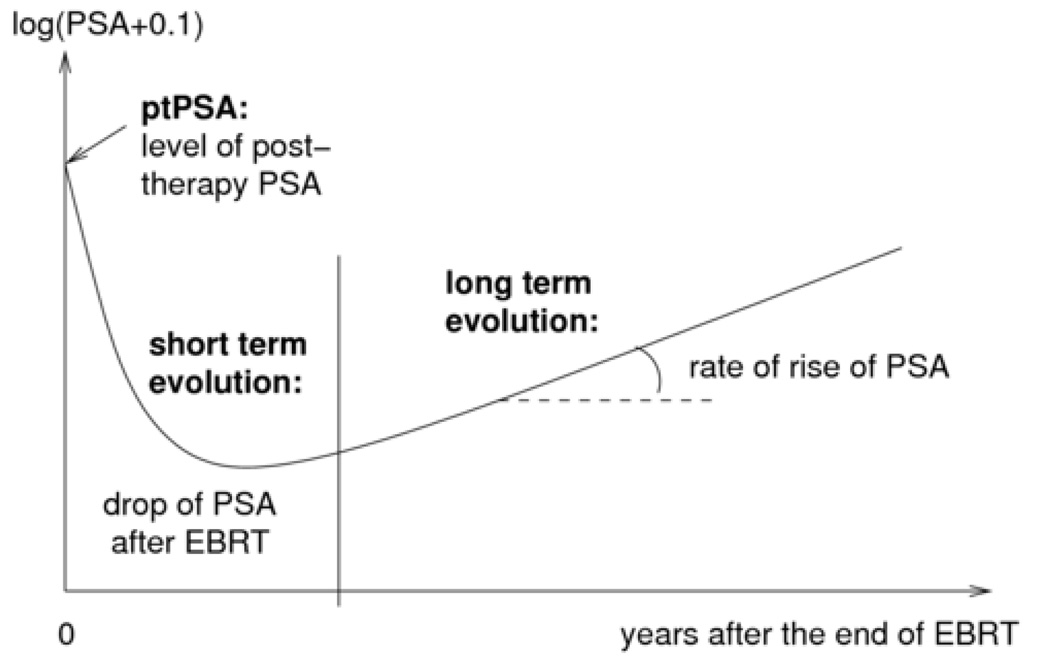
PSA evolution following EBRT was analysed by a linear mixed model (LMM) (21) with 3 components: the post-therapy level at end of EBRT (denoted as post-therapy PSA [ptPSA]), the short-term evolution in the first year after RT (denoted f₁(t)) and the long-term evolution (denoted f₂(t)) as described in Figure 1. The function of time t which gave a good description of the short-term evolution of ln(PSA(t)+0.1) was f₁(t)=((1+t)^−1.5 −1). The long-term evolution was best described using a linear function f₂(t)=t, corresponding to an exponential PSA rise. The model also included a Gaussian random-effect for each individual for each phase to account for between-person differences in the pattern of PSA. Details are provided in Appendix 1. Association of prognostic covariates iPSA, T-stage and Gleason score with the ptPSA level, short-term PSA fall and long-term trend were tested with the Wald test and the statistically significant associations were retained in the final model. To develop the LMM, the three phase PSA model was first fit independently to each cohort. In a second step, cohorts were pooled and the same LMM fit with the addition of cohort-specific fixed effects on the three phases of PSA evolution to account for heterogeneity.

Figure 1.

Three phases of PSA evolution after the end of EBRT: post-therapy level, short-term decline and long-term evolution.

Once the LMM was defined, a Cox proportional hazards regression with time-varying covariates was used to evaluate the association of pre-treatment prognostic factors and post-treatment pattern of PSA with the time to recurrence of prostate cancer after EBRT (Appendix 1). Two time-varying measures of PSA were considered as predictors: transformations of the absolute level and of the slope of PSA. Using a “twostage” analysis (22), both quantities were firstly estimated at current time t from the LMM for PSA, using respectively the individual predicted means and derivatives of the mean function. In a second-stage, we inserted into the Cox model chosen transformations of these individual predictions. Salvage ADT was included as a binary time-varying predictor set to 0 before ADT and 1 after initiation of ADT. Cox regression was first applied independently to each cohort. Next the cohorts were pooled in order to evaluate the common effect of the prognostic factors on the risk of recurrence. When pooling the cohorts, a stratification of baseline risk functions over the cohorts was done to account for the heterogeneity of the risk of recurrence over cohorts. Regression parameters significance was tested using the Wald test. All analyses were performed by the SAS statistical software system Version 9.1, and statistical tests performed at the two-sided α=0.05 level of significance.

RESULTS

Description of the cohorts

A total of 4247 patients were eligible for analysis (Table 1). Of these 339 (12.2%) clinical recurrences were observed, the proportion varying from 5.6% for PMCC to 16.9% for UM cases. The median time until first clinical recurrence was 4.1 years while the median time until last contact for those who did not have any recurrence was 5.4 years. In total 40,324 PSA measurements were analyzed over the 5 cohorts and the median number of PSA measures per patient was 9. As can be seen from Table 1, each cohort contained a broad range of patients and there were some statistically significant differences between the cohorts. For example, subjects from WBH were a little older (p<0.001), subjects from RTOG9406 had very few T-stage 3 and 4 patients (p<0.001) and the pre-treatment PSA values tended to be higher in the RBH cohort (p<0.001). Total dose of EBRT also differed between cohorts and was lowest in RBH (median =63.2 Gy) and highest in RTOG9406 (median=78.0 Gy).

Table 1.

Description of the 5 cohorts. Continuous data depicted as median (5^th,95th percentiles), with categorical data shown as number and percentage.

Cohort		UM	RTOG9406	PMCC	WBH	RBH	Pooled
Location		Ann Arbor, USA	Multicenter, USA	Melbourne, Australia	Detroit, USA	Brisbane, Australia
Period of recruitment		1988–2004	1994–2001	1997–2003	1987–2003	1990–1998
Number of patients		503	615	395	1268	1466	4247
Number of PSA measures		4607	6416	3285	11380	14636	40324
Age (years)		69.8 (56.2,78.7)	69.0 (54.0,77.0)	69.8 (58.5,76.7)	73.0 (61.0,83.0)	68.9 (57.7,77.3)	70.2 (57.7,79.4)
Pre-therapy PSA (ng/mL)		8.2 (2.3,43.7)	7.4 (2.6,19.2)	10.5 (4.0,27.0)	7.7 (2.3,38.2)	15.0 (3.5,54.0)	9.6 (2.6,43.7)
Clinical T-stage	1	163 (32.4%)	348 (56.6%)	74 (18.7%)	431 (34.0%)	298 (20.3%)	1314 (30.9)
	2	290 (57.7%)	253 (41.1%)	236 (59.8%)	792 (62.5%)	1047 (71.4%)	2618 (61.7%)
	3,4	50 (9.9%)	14 (2.3%)	85 (21.5%)	45 (3.5%)	121 (8.3%)	315 (7.4%)
Gleason Score	2–6	276 (54.9%)	421 (68.4%)	247 (62.5%)	902 (71.1%)	1116 (76.1%)	2962 (69.7%)
	7	188 (37.4%)	156 (25.4%)	129 (32.7%)	252 (19.9%)	262 (17.9%)	987 (23.3%)
	8–10	39 (7.7%)	38 (6.2%)	19 (4.8%)	114 (9.0%)	88 (6.0%)	298 (7.0%)
Crude Total Dose (Gy)		70.4 (66.0,77.8)	78.0 (70.3,82.4)	70.0 (66.0,74.0)	66.6 (66.0,77.4)	63.2 (52.5,66.0)	66.6 (52.6,79.8)
Corrected Total Dose* (Gy)		69.5 (64.4,75.9)	78.4 (68.5,83.7)	70.0 (66.0,74.0)	66.0 (64.1,74.8)	64.3 (58.0,66.0)	66.0 (58.2,80.0)
Number of PSA measures per patient		8 (3,19)	11 (4,17)	8 (3,14)	8 (3,19)	9 (3,18)	9 (3,18)
Clinical recurrence		85 (16.9%)	42 (6.8%)	22 (5.6%)	190 (15.0%)	NA	339 (12.2%)†
Salvage Androgen Deprivation Therapy		44 (8.8%)	47 (7.6%)	42 (10.6%)	170 (13.4%)	563 (38.4%)	866 (20.4%)
Time to clinical recurrence (years)		3.0 (1.3,8.3)	4.2 (2.0,8.0)	4.3 (1.3,6.0)	4.4 (1.4,10.0)	NA	4.1 (1.4,9.2)†
Time-to-last contact (years)		5.9 (1.3,12.2)	5.6 (2.6,9.8)	4.8 (2.1,7.6)	5.6 (1.5,11.5)	NA	5.4 (1.7,10.9)†

^*obtained using α/β=4

^†excluding RBH

NA=not available

PSA pattern and its determinants

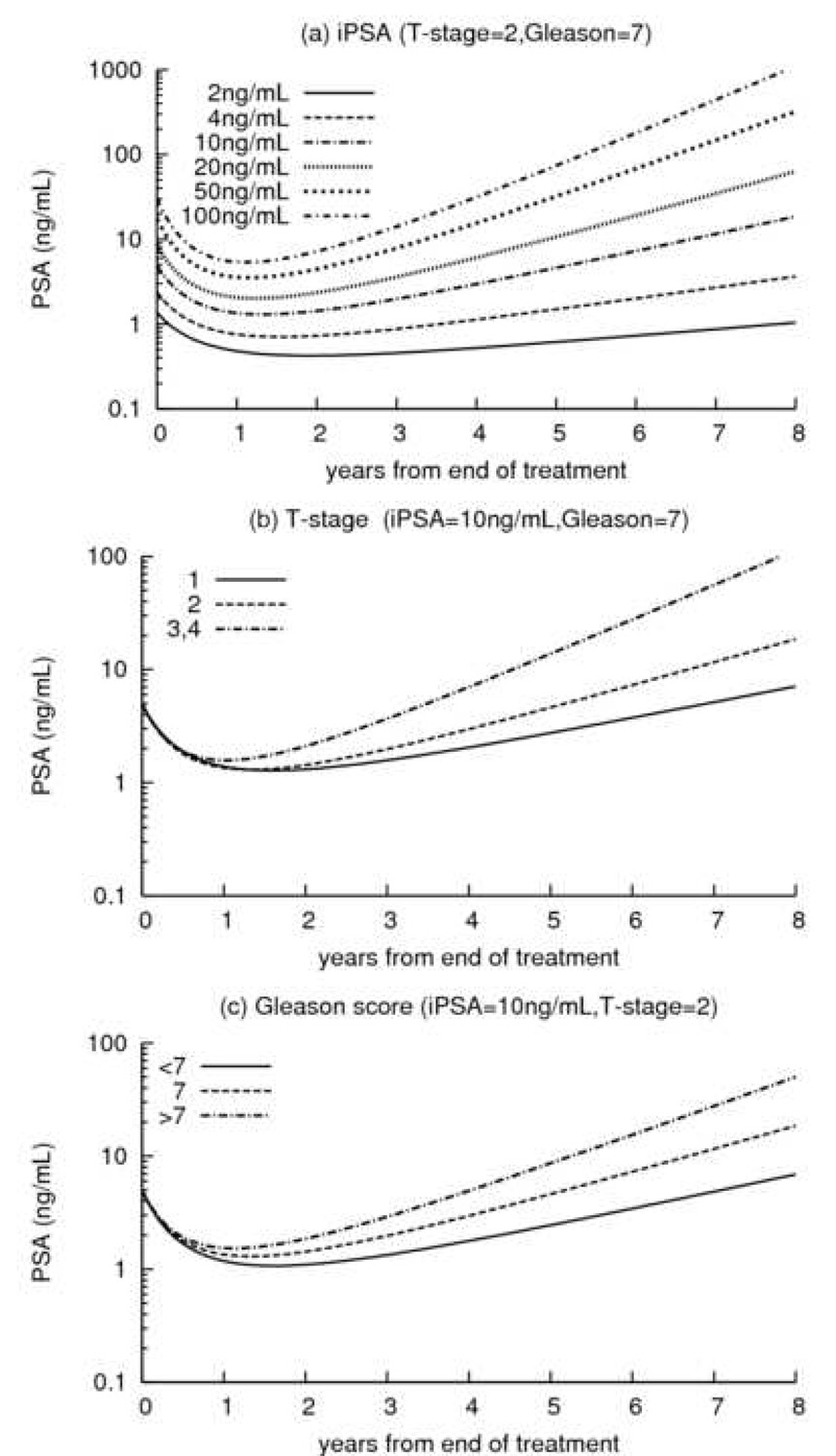
Influences of pre-treatment PSA (iPSA), T-stage and Gleason score on the three phases of post-radiation PSA time course (Figure 1) are shown in Table 2 and interpretation of the parameters is given in appendix 1. For all five cohorts there was general consistency about which factors influenced the three phases, and the direction and magnitude of influence. For ptPSA, all five cohorts showed only iPSA to be of statistical significance (all p<0.001), with higher pre-treatment PSA levels corresponding to higher posttreatment PSA levels (Figure 2a). Pre-treatment PSA (iPSA) and T-stage were significantly associated with the short-term PSA decline after radiation, with higher values associated with a larger fall of PSA (Figure 2a,b) (nearly all p<0.001 for iPSA). iPSA, T-stage and Gleason score were all significantly associated with the long-term PSA time course, with higher values corresponding to higher rates of rise (Figure 2a,b,c). Goodness-of-fit of the model was evaluated, including a residual analysis for the assumption of normality (not shown). It indicated that the model fit the observed data well across each of the five cohorts.

Table 2.

Regression parameters and degree of significance for post-therapy PSA level and short- and long-term PSA evolution. Positive (negative) entries represent increase (decrease) in post-therapy PSA measure for a unit-increase in the predictor.

Prognostic factor		UM	RTOG9406	PMCC	WBH	RBH	POOLED
Effect on Post-treatment PSA level
Intercept		−0.01	−0.29	−0.02	−0.34	−0.03	−0.20
Initial PSA		0.76	0.83	0.65	0.85	0.71	0.78
Effect on PSA drop in the first year after EBRT
Intercept		0.98	0.63	1.38	0.63	1.43	0.97
Initial PSA		0.70	0.76	0.32	0.74	0.48	0.62
T-stage*	2	0.37	0.38	0.47	0.37	0.06	0.27
	3–4	0.39	−0.08	0.83	0.02	0.42	0.43
Effect on long term PSA rise
Intercept		−0.10	−0.05	−0.24	−0.30	−0.18	−0.25
Initial PSA		0.15	0.08	0.15	0.21	0.24	0.20
T-stage*	2	0.10	0.16	0.19	0.22	0.08	0.15
	3–4	0.53	0.11	0.40	0.46	0.33	0.40
Gleason Score†	7	0.12	−0.01	0.18	0.02	0.26	0.12
	8–10	0.27	0.09	0.29	0.14	0.39	0.25

Bold underlined highly significant p<0.001; bold significant p in [0.001,0.05]; : not significant p>0.05.

^*Reference level T-stage 1

^†Reference level Gleason score 2--6

Figure 2.

Predicted evolution of PSA after EBRT according to: (a) initial PSA for a subject with a Tstage= 2 and Gleason=7 (PSA range from 0.1 to 1000ng/mL); (b) T-stage for a subject with an initial PSA=10ng/mL and Gleason=7; (c) Gleason score for a subject with an initial PSA=10ng/mL and Tstage= 2.

Risk of recurrence and its determinants

Relative risks for the prognostic factors obtained for the four suitable cohorts (excluding RBH) and for the overall pooled cohort are given in Table 3; separated by whether or not post-radiation PSA dynamics (absolute level and rate of change) were adjusted for in the analysis. Across all four cohorts current PSA level contributed statistically significant prognostic information independent to all pre-radiation prognostic factors (nearly all p<0.001). Similarly, the rate of PSA change was highly significant in all cohorts (p<0.001) except RTOG 9406 (p=0.28). In the pooled analysis both factors were highly significant in predicting clinical failure (both p<0.001). Therefore, for the same iPSA, T-stage level and Gleason score, the higher the current level of PSA, the higher the risk of recurrence and likewise, for identical current PSA levels, the risk of recurrence was higher in those with a higher current rate of PSA rise. Statistical significance of all the pre-treatment prognostic factors was reduced when the post-radiation PSA profile (which included both the current level of PSA and current rate of rise of PSA) was adjusted for in the analysis. With adjustment for PSA kinetics, subjects with T-stage 3 or 4 had a 39% higher risk of clinical recurrence than subjects with T-stage 1 or 2 (RR=1.39, 95%CI=1.03,1.89). Subjects with a Gleason score of 7 had a 62% higher risk of recurrence than subjects with a Gleason score below 7 (RR=1.62, 95%CI=1.03,1.89) while no difference in the risk of recurrence was found for subjects with a Gleason score of 8, 9 or 10 (RR=1.16, 95%CI=0.84,1.61). For each unit-increase of log(iPSA+0.1), the risk of clinical recurrence decreased by 21% (RR=0.79, 95%CI=0.69,0.90). With adjustment of the risk of recurrence for the PSA dynamics, the impact of a salvage ADT received during the follow-up was consistent over cohorts, the risk of recurrence being reduced by 67% after a salvage ADT (RR=0.33, 95%CI=0.24,0.46), whereas when neglecting the influence of PSA dynamics on the risk of recurrence, the impact of a salvage ADT was typically larger than one and was heterogeneous over the cohorts with a relative risk varying from 0.72 for WBH to 4.11 for RTOG9406.

Table 3.

Relative risks of clinical recurrence without and with adjustment for post-therapy PSA dynamics.

		Without adjustment for post-radiation PSA					With adjustment for post-radiation PSA
		UM	RTOG9 406	PMCC	WBH	Pooled	UM	RTOG9 406	PMCC	WBH	Pooled
Initial PSA		1.38	1.28	0.89	1.68	1.47	0.76	0.74	0.38	0.83	0.79
T-stage*	3 or 4	3.24	1.21	3.30	1.05	1.94	1.78	1.18	1.98	0.95	1.39
Gleason Score†	7	2.92	1.98	3.30	1.72	2.11	2.07	2.23	1.54	1.40	1.62
	8–10	2.78	1.79	1.76	1.45	1.66	2.01	1.09	1.84	0.97	1.16
Salvage ADT		1.42	4.11	4.03	0.72	1.09	0.35	0.55	0.37	0.29	0.33
PSA(t)††							1.64	1.58	1.85	1.56	1.58
Rate of PSA (t) change§							2.32	1.73	3.99	3.34	2.93

Bold underlined highly significant p<0.001; bold significant p in [0.001,0.05]; : not significant p>0.05.

^*Reference level T-stage 1--2

^†Reference level Gleason score 2--6

^††PSA(t) gives the relative risk (RR) of recurrence associated with an increase of 0.1 in the rescaled logistic link function of log(PSA+0.1) at current time

^§Rate of PSA(t) change gives the RR of recurrence associated with an unit-increase of rate of change of log(PSA+0.1) at current time

Evaluation of other factors on disease progression

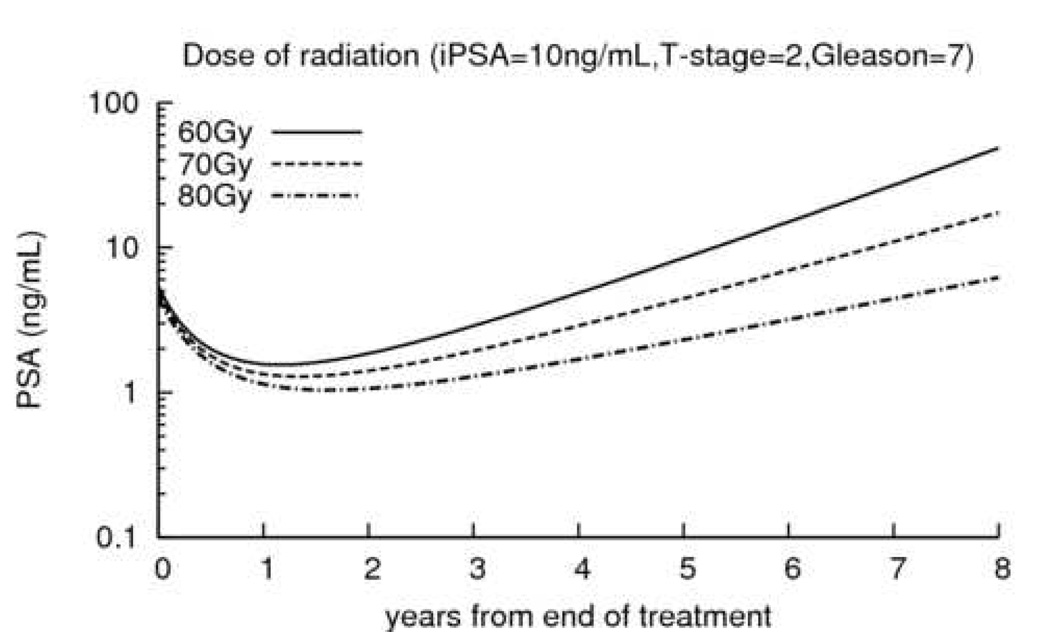
This model provided a framework to assess the impact of other factors. As an illustration, we evaluated the impact of the EBRT dose and patient age on clinical outcome. Table 4 displays the results of the effects of dose when using either the crude EBRT dose or D^c. Results for crude dose and dose corrected for α/β ratio were similar. Higher levels of total RT dose were statistically significantly associated with lower ptPSA levels (p=0.022 for D and p=0.029 for D^c) and lower rates of long-term PSA growth (p<0.001 for both). Total dose was of statistical significance in relation to risk of recurrence (p=0.022, RR=0.88 95%CI=0.81,0.96 for D and p=0.012, RR=0.91, 95%CI=0.84,0.98 for D^c), but lost statistical significance when the post-radiation PSA profile, and particularly the rate of PSA change, was adjusted for (p=0.33, RR=0.96, 95%CI=0.89,1.04 for D and p=0.63, RR=0.98, 95%CI=0.91,1.06 for D^c). Figure 3 shows the impact of dose on post-radiation PSA trajectories.

Table 4.

Effect estimates for dose of radiation (crude or α/β-adjusted measure) and age for PSA evolution and clinical recurrence without and with adjustment for post-therapy PSA dynamics. For effects on PSA evolution, positive (negative) values denote an increase (decrease) in evolution summary for a unitincrease in dose or age.

	DOSE (for 2Gy difference)				Age
	Crude measure		α/β-adjusted measure*		(for 10 years difference)
Evolution of PSA:†	estimate [95% CI]	p-value††	estimate [95% CI]	p-value††	estimate [95% CI]	p-value††
initial level	−0.017 [−0.031,−0.002]	0.022	−0.018 [−0.034,−0.002]	0.029	−0.115 [−0.147,−0.083]	<0.001
short term	−0.010 [−0.039,0.019]	0.502	−0.022 [−0.054,0.011]	0.190	0.0003 [−0.0004,−0.0011]	0.347
long term	−0.018 [−0.027,−0.009]	<0.001	−0.026 [−0.036,−0.016]	<0.001	0.00003 [−0.0003,0.0003]	0.850
Risk of recurrence:†	HR [95% CI]	p-value††	HR [95% CI]	p-value††	HR [95% CI]	p-value††
without adjustment for PSA evolution	0.880 [0.811,0.955]	0.022	0.906 [0.838,0.979]	0.012	0.776 [0.656,0.918]	0.003
with adjustment for PSA evolution	0.961 [0.886,1.042]	0.332	0.981 [0.907,1.060]	0.626	0.736 [0.627,0.864]	<0.001

^*obtained using α/β=4

^†Pooled data include UM, RTOG9406, PMCC, WBH and RBH for the PSA evolution and UM, RTOG9406, PMCC and WBH for the risk of recurrence

^††p-value from the Wald test

Figure 3.

Predicted evolution of PSA after EBRT according to dose of radiation for a subject with an initial PSA=10ng/mL, a Gleason=7 and a T-stage=2.

The effect of age on post-treatment PSA and risk of recurrence are displayed in Table 4. Age was statistically significantly associated with ptPSA (p<0.001), but not with the subsequent pattern of PSA (p=0.35 and p=0.85). It was also associated with the risk of clinical recurrence whether or not the PSA pattern and other prognostic factors were adjusted for (respectively p=0.003 and p<0.001). For two patients, one 10 years younger than the other, having the same prognostic factors and the same evolution of PSA, the younger patient had a 36% higher risk of clinical recurrence (RR=1.36, 95%CI=1.16,1.60).

DISCUSSION

A great deal is known about PSA and the risk of therapeutic failure when prostate cancer is treated with radiation therapy. It is of well described prognostic significance when measured prior to therapy (3,23), and there appears to be post-therapy prognostic implications attached to the failure of PSA to reach a low nadir (4,24) or to a rising PSA pattern (9,19,25–27). However, the measurement error in PSA, high variability between patients, multiple aspects of the post-radiation PSA profile, and the need to integrate with pre-treatment prognostic factors pose challenges for construction of a coherent model of clinical prognosis. Using advanced statistical modelling, this report has constructed such a prognostic tool by partitioning the post-radiation PSA profile into three phases, accounting for the impact of pre-treatment prognostic factors on each phase, and incorporating this information into a predictor for risk of clinical recurrence which simultaneously accounts for pre-treatment standard risk factors and post-treatment PSA dynamics. Effects of factors on the post-therapy PSA profile and risk of recurrence were similar across 5 large heterogeneous cohorts, justifying a pooled model based on a total of 4274 EBRT patients and 40,324 PSA measures, one of the largest ensembles for this population to date. Using these data, we were able to provide a precise form for the statistical model and an accurate description of the significance of various pre- and post-therapy factors to enable clinical failure prognostication.

Traditional prognostic factors of iPSA, Gleason score and stage have been both validated and further understood by these data. In terms of the phases of PSA evolution after EBRT, the post-therapy level of PSA, the rate of fall, and the subsequent rate of rise have different influences. The estimated PSA at the end of EBRT was, somewhat expectedly, associated with the higher pre-treatment PSA levels. The initial PSA fall was associated with the iPSA and the stage of disease, with higher levels of either having larger falls. Regardless of the fall however, both of these factors also predict for a faster rate of PSA rise, as does higher Gleason scores. The late rising phase of PSA evolution can be seen as a continuous nonlinear descriptor of biochemical failure - a term familiar to most radiation oncologists treating prostate cancer. By not enforcing binary reduction of the PSA rise to define biochemical failure (as is typical in the literature (14)), maximal statistical power is retained in the model and correlations to prognostic markers can be optimised. These results are consistent with studies involving the same factors and a binary biochemical failure endpoint (1,3).

The subsequent use of longitudinal PSA data provides valuable insights when incorporated into an actuarial model of clinical failure. The conventional prognostic factors iPSA, Gleason score, stage and, to a lesser degree, EBRT dose have been independently associated with clinical failure in many conventional analyses (3,28,29). These are soundly reiterated in the present data when used without consideration of the post-therapy PSA dynamics. However, their prognostic influence is largely abrogated by inclusion of the temporal absolute and relative PSA levels into the prognostic model, suggesting that the pattern of PSA following EBRT is of major prognostic significance for clinical recurrence. This is not a new concept, with investigators previously suggesting that indices such as PSA doubling time (dT) be factored into patient follow-up assessment (9,11,24). Our model strengthens that call, with consistent findings to suggest that both the dT and the absolute PSA be taken into account, rather than only traditional pre-treatment variables, when estimating the risk of clinical failure in a patient who is being considered for salvage therapy.

Although the data cannot directly offer rules for the optimal timing of salvage ADT, it does provide increased appreciation into the true therapeutic effect it has. Using conventional analysis, including salvage ADT as a time-dependent covariate showed no consistent effect with the relative risk of failure related to its use varying from a benefit to a strong detrimental outcome across cohorts while a consistent benefit to salvage ADT use was seen when accounting for the PSA dynamics. This suggests in the simplified analysis the therapeutic effect is overwhelmed by the PSA dynamic factors, given that these same factors are likely to be strongly aligned with those used in the decision to implement salvage ADT. Conversely, the impact of stage and high grade cancers of clinical failure becomes less pronounced once PSA follow-up data is included, suggesting that their effect is largely spelled out through PSA dynamics. Thus, the approach we use provides an appropriate framework to evaluate how factors are involved in the progression of prostate cancer, and especially whether their effect on clinical recurrence is mediated by their effect on PSA post-treatment evolution. This statistical model can be used as a framework for consideration of the impact of other factors. We illustrated this with age at diagnosis and dose of radiation, but it could also be used for factors such as field size, pre-treatment PSA doubling time, fraction size or pre-treatment biomarkers. We found dose associated with clinical recurrence as has been observed by others (28,29) but interestingly, we found that the association between higher dose of radiation and lower risk of recurrence was completely mediated by the association between dose of radiation and the post-radiation-therapy PSA pattern and particularly the long-term rate of PSA rise. Over the five cohorts, age at diagnosis was independently associated with the risk of recurrence adjusting or not for the PSA dynamics with younger subjects having a higher risk of recurrence. This suggests that age is associated with clinical recurrence but not with the long-term pattern of PSA kinetics after adjusting for other factors. However, this finding would need to be substantiated in other studies before it can be clinically implemented, as the significance of age as an outcome predictor is still unclear (30).

One strength of the findings in this paper was the high degree of replication of the important prognostic factors across five large independent cohorts, suggesting a high degree of validity and generalizability. There is a degree of subjectivity in the assessment of both Gleason score and T-stage, thus despite potential differences in these between cohorts, it is noteworthy that they show consistent effects. The high levels of statistical significance seen, particularly in the combined analyses, naturally relates to the analytic power afforded by the large and diverse cohorts. The generalizability we have seen across cohorts does in no way, however, diminish the need for well designed prospective validation studies. One restriction is that the data is limited to those treated with EBRT alone, and as such is not able to be extrapolated to those treated with combined neoadjuvant or adjuvant ADT, or brachytherapy which are known to have quite different PSA evolution (31).

The complexity of the statistical modelling we have used to account precisely both for PSA pattern and risk of recurrence goes well beyond models of binary biochemical failure. Despite the complexity, pre-treatment factors and time since treatment can be relatively easily combined in this model to arrive at an estimated PSA pattern as described in Appendix 2 and provided on the website http://psacalc.sph.umich.edu/. As this pattern is shown to have a strong relationship to clinical failure, we plan in the future to develop an on-line electronic calculator to provide relevant estimates of clinical failure over time associated with observed patterns of post-treatment PSA. We suggest that individualised clinical monitoring based on detailed understanding of PSA dynamics will be forthcoming.

APPENDIX1: ‘Two-stage’ model

PSA Evolution

For subject i (i=1,...,N) and occasion j (j=1,...,n_i), PSA(t_ij) is the PSA level measured at time t_ij after the end of EBRT and PSA^*(t_ij)=log(PSA(t_ij)+0.1) the PSA level in the logarithm scale. Evolution of PSA^* was described using the following linear mixed model (21):

$${\mathrm{\text{PSA}}}^{*}({\mathrm{t}}_{\mathrm{i}\mathrm{j}})=({\mathrm{\mu }}_0+{\mathrm{u}}_{0\mathrm{i}}+{\mathrm{X}}_{0\mathrm{i}}{\mathrm{\beta }}_0)+({\mathrm{\mu }}_1+{\mathrm{u}}_{1\mathrm{i}}+{\mathrm{X}}_{1\mathrm{i}}{\mathrm{\beta }}_1)\times {\mathrm{f}}_1({\mathrm{t}}_{\mathrm{i}\mathrm{j}})+({\mathrm{\mu }}_2+{\mathrm{u}}_{2\mathrm{i}}+{\mathrm{X}}_{2\mathrm{i}}{\mathrm{\beta }}_2)\times {\mathrm{f}}_2({\mathrm{t}}_{\mathrm{i}\mathrm{j}})+{\mathrm{\epsilon }}_{\mathrm{i}\mathrm{j}},$$

The pattern of PSA^* after EBRT was divided into three phases (Figure 1): post-therapy level, short-term evolution in the first year after EBRT (f₁(t)), and long-term evolution (f₂(t)). The functions f₁ and f₂ relating time to PSA levels in short- and long-term phases were determined using a profile likelihood method yielding f₁=(1+t)^λ −1 with λ=−1.5, and f₂(t)=(t)^1+α/(1+t)^α with α=0; (µ₀, µ₁, µ₂), (X_0i, X_1i ,X_2i ), and (β₀, β₁,β₂) are phase-specific intercepts, covariates and regression parameters; u_i=(u_0i,u_1i,u_2i)^T are phase-specific random-effects Normally distributed with mean 0 and variance-covariance matrix B; ε_ij are residual error terms Normally distributed with mean 0 and variance σ². When pooling the cohorts, different phase-specific intercepts were considered for each cohort.

Interpretation of the LMM parameters

Post-treatment PSA (ptPSA) is defined as the PSA value immediately following the end of EBRT. For parameters associated with ptPSA, intercept denotes the average ln(PSA+0.1) value at the beginning of post-treatment period for an initial pre-treatment PSA (iPSA) of .9. The parameter for iPSA denotes the change in the transformed ptPSA (ln(ptPSA+0.1)) corresponding to a unit-increase in transformed iPSA (ln(iPSA+0.1)).

Short-term PSA dynamics is the change in ln(PSA+0.1) for a unit-increase of the time transformation variable f₁(t)=((t+1)^−1.5−1) at t years post-radiation. Higher (respectively lower) short-term PSA dynamics correspond to higher declines in PSA (respectively less declines and potential increases). For parameters associated with short-term evolution, intercept denotes average short-term PSA decline for an individual with iPSA=.9 and T-stage=1; the parameter associated with iPSA denotes the change in short-term PSA for a unit-increase in transformed iPSA (positive values correspond to higher short-term PSA declines during the first year post-radiation; negative values to lower declines), and the parameter associated with T-stage denotes the difference in short-term PSA dynamics for T-stages 2 and (3 or 4) compared to Tstage 1 (a positive value means T-stage 2 and (3 or 4) have a greater PSA decline compared to T-stage 1, respectively).

Long-term PSA dynamics denotes the change in log (PSA + 0.1) for a unit-increase in year post-radiation. Higher long-term PSA velocities correspond to larger rises in PSA. For parameters associated with long-term PSA dynamics, intercept denotes average long-term PSA dynamics for iPSA=.9, T-stage=1 and Gleason score 2–6, the parameter corresponding to iPSA denotes the change in long-term PSA dynamics for a unit-increase in transformed iPSA (positive values denote larger increase), the parameter associated with T-stage denotes the difference in long-term PSA dynamics for T-stages 2 or (3–4) compared to T-stage 1 (same interpretation as for short-term) while parameters associated with Gleason score categories 7 and >7 have similar meanings referenced to scores 2--6.

Prediction of PSA^* kinetics

Predictions of PSA^* (PŜA_i^*(t)) and rate of PSA^* change (slope) (slPŜA_i^*(t)) over time for individual i were formed from the maximum likelihood estimates:

$$\{\begin{array}{c}\mathrm{P}\widehat{\mathrm{S}}{\mathrm{A}}_{\mathrm{i}}^{*}(\mathrm{t})=({\widehat{\mu }}_0+{\widehat{\mathrm{u}}}_{\mathrm{0}\mathrm{i}}+{\mathrm{X}}_{\mathrm{0}\mathrm{i}}{\widehat{\beta }}_{\mathrm{0}})+({\widehat{\mu }}_1+{\widehat{\mathrm{u}}}_{1\mathrm{i}}+{\mathrm{X}}_{1\mathrm{i}}{\widehat{\beta }}_{\mathrm{1}})\times {\mathrm{f}}_1(\mathrm{t})+({\widehat{\mu }}_2+{\widehat{\mathrm{u}}}_{2\mathrm{i}}+{\mathrm{X}}_{2\mathrm{i}}{\widehat{\beta }}_2)\times \mathrm{t}\hfill \\ \mathrm{s}\mathrm{l}\mathrm{P}\widehat{\mathrm{S}}{{\mathrm{A}}_{\mathrm{i}}}^{*}(\mathrm{t})=({\widehat{\mu }}_1+{\widehat{\mathrm{u}}}_{1\mathrm{i}}+{\mathrm{X}}_{1\mathrm{i}}{\widehat{\beta }}_1)\times {{\mathrm{f}}_1}^{\text{'}}(\mathrm{t})+({\widehat{\mu }}_2+{\widehat{\mathrm{u}}}_{2\mathrm{i}}+{\mathrm{X}}_{2\mathrm{i}}{\widehat{\beta }}_2)\hfill \end{array}$$

û_i = (û_0i, û_li, û_2i)_Tare the empirical Bayes estimates of the individual random-effects, µ̂₀ = (µ̂₁, µ̂₂)^T and (β̂₀,β̂₁,β̂₂)^T are respectively the maximum likelihood estimates of phase-specific intercepts and regression parameters, and f_1'(t)=−(1+t) ^−2.5/1.5 is the first derivative of f₁(t). When using pooled data, µ̂₀ = (µ̂₁, µ̂₂)^T were replaced by cohort-specific intercepts µ̂_0k = (µ̂_1k, µ̂_2k)^T_k=1,5.

Risk of clinical recurrence

A time-dependent Cox proportional hazard model described the risk of recurrence over time as a function of the covariates X_i, the current PSA level deduced from the LMM PŜA_i^* (t), the current rate of PSA change slPŜA_i^* (t) and a time-dependent indicator of salvage ADT 1{t>t_ADTi} (1{t>t_ADTi}=1 if ADT before time t and 0 otherwise):

$$\lambda (\mathrm{t})={\lambda }_0(\mathrm{t})\exp (\mathrm{\gamma }{\mathrm{X}}_{\mathrm{i}}+\delta \mathbf{1}\left\{\mathrm{t}>{\mathrm{t}}_{\text{ADTi}}\right\}+\mathrm{\eta }{\mathrm{h}}_1(\mathrm{P}\widehat{\mathrm{S}}{{\mathrm{A}}_{\mathrm{i}}}^{*}(\mathrm{t}))+\mathrm{\phi }\mathrm{s}\mathrm{l}\mathrm{P}\widehat{\mathrm{S}}{{\mathrm{A}}_{\mathrm{i}}}^{*}(\mathrm{t}))$$

Transformations of the current prediction of PSA^* and the rate of PSA^* change were investigated to assess whether they improved goodness-of-fit. A preliminary analysis revealed that the effect of current PSA^* on the risk of recurrence was nonlinear, correctly approximated by h₁(PSA_i^*(t))=exp((PSA_i^*(t)-0.71)/0.44)/(1+exp((PSA_i^*(t)−0.71)/0.44)), while the effect of slPSA^* was linear. The h₁ transformation implies that the effect of a unit-increase of PSA^* on the risk of recurrence is maximal in the 1.0–4.0 ng/mL range of PSA. For the pooled analysis the baseline hazard (λ₀(t)) was stratified across cohorts.

APPENDIX2: Prediction of PSA evolution using pre-treatment covariates

From the statistical model in Appendix1 applied to the 5 cohorts, the expected PSA evolution for a subject given his pre-treatment factors iPSA, T-stage and Gleason is obtained by substituting maximum likelihood estimates into the LMM (using the mean value over the 5 cohorts for the phase-specific intercepts). Defining iPSA=ln(iPSA+0.1); Tst2=1 if T-stage=2 and 0 otherwise; Tst34=1 if T-stage>=3 and 0 otherwise; GS7=1 if Gleason=7 and 0 otherwise and GS8h=1 if Gleason>=8 and 0 otherwise, the mean PSA^* at time t is

$$\begin{array}{c}\mathrm{P}\widehat{\mathrm{S}}{\mathrm{A}}^{*}(\mathrm{t})=-0.1959+0.7821\times \mathrm{i}\mathit{\text{PSA}}\hfill \\ +\left({(1+\mathrm{t})}^{-1.5}-1\right)\times \left[0.9739+0.6173\times \mathrm{i}\mathit{\text{PSA}}+0.2745\times Tst2+0.4316\times Tst34\right]\hfill \\ +\mathrm{t}\times \left[-0.2480+0.1988\times \text{iPSA}+0.1520\times Tst2+0.3973\times Tst34+0.1226\times GS7+0.2465\times GS8h\right]\hfill \end{array}$$

For example if iPSA=10, T-stage=2 and Gleason=7

$$\begin{array}{ccc}\mathrm{P}\widehat{\mathrm{S}}{\mathrm{A}}^{*}(\mathrm{t})\hfill & =\hfill & -0.1959+0.7821\times 1\mathit{n}(10.1)+\left({(1+\mathrm{t})}^{-1.5}-1\right)\times \left[0.9739+0.6173\times 1\mathit{n}(10.1)+0.2745\right]\hfill \\ \hfill & \hfill & +\mathrm{t}\times \left[-0.2480+0.1988\times 1\mathit{n}(10.1)+0.1520+1.226\right]\hfill \\ \hfill & =& 1.6127+2.6759\times \left({(1+\mathrm{t})}^{-1.5}-1\right)+0.4864\times \mathit{t}\hfill \end{array}$$

At 2, 4 and 6 years after EBRT, the mean predicted PSA^* are 0.42, 1.12 and 2.00. The corresponding predicted PSA values are 1.43, 2.97 and 7.29 ng/mL respectively, as shown in Figure 2. A calculator that automatically performs this prediction is available online at http://psacalc.sph.umich.edu/. The online predictor includes also the EBRT dose.