Role of endplates in contributing to compression behaviors of motion segments and intervertebral discs

Abstract

The purpose of this study was to gain an improved understanding of the mechanical behavior of the intervertebral disc in the presence and absence of the vertebral endplates. Mechanical behaviors of rat caudal motion segments, vertebrae and isolated disc explants under two different permeability conditions were investigated and viscoelastic behaviors were evaluated using a stretched-exponential function to describe creep and recovery behaviors. The results demonstrated that both vertebrae and discs underwent significant deformations in the motion segment even under relatively low-loading conditions. Secondly, disruption of the collagenous network had minimal impact on equilibrium deformations of disc explants as compared to disc deformations occurring in the motion segments provided that vertebral deformations were accounted for; however, differences in endplate permeability conditions had a significant effect on viscoelastic behaviors. Creep occurred more quickly than recovery for motion segment and explant specimens. In addition, disc explants and motion segments both exhibited non-recoverable deformations under axial compression under low- and high-loading conditions. Results have important implications for interpreting the role of vertebral endplates in contributing to disc mechanical behaviors and direct application to mechanobiology studies involving external loading to rodent tail intervertebral discs.

1. Introduction

Intervertebral discs play essential biomechanical roles allowing load support and mobility of the spine. Overloading and immobilization both contribute to accelerated disc degeneration which compromises this function and involves mechanical damage, diminished nutrient transport, loss of cell viability and altered biosynthesis (Stokes and Iatridis, 2004). Mechanical behaviors of motion segments are related to combined and interactive responses of discs and vertebrae. Discs and vertebrae both exhibit time-dependent behaviors associated with flow-dependent and flow-independent viscoelasticity mechanisms. Some biomechanical studies of the disc assumed vertebral endplates are rigid and impermeable (Spilker et al., 1984; Zimmerman et al., 1992; Shirazi-Adl and Parnianpour, 1993), an assumption often considered reasonable because the material properties of the disc tissues are substantially lower than that of bone. However, vertebral endplates bulge under axial deformations (Brinckmann et al., 1983) and undergo fracture at higher loads (Brinckmann and Horst, 1985; Adams et al., 2000). This apparent contrast demonstrates a lack of complete understanding of the role of endplates in contributing to disc mechanical behaviors under compression. Furthermore, improved knowledge of interactions between vertebrae and discs in biomechanical testing will clarify the appropriate in vitro test configuration for studying disc degeneration, damage, remodeling, gene therapy and tissue engineering.

Evaluating discs in the motion segment complex most closely mimics in vivo conditions but creates difficulty separating disc and vertebral mechanical behaviors, and leaves minimal control over post-mortem boundary condition changes such as decreased permeability due to clotting in the endplate (Lee et al., 2006). Isolating discs as explants allow for direct assessments of disc mechanical properties and improved control over boundary conditions; however the consequences of cutting the annulus fibers that anchor the disc to the vertebrae must be accounted for. In preparing explants in this study, we cut through the annular fibers anchoring the disc to the vertebrae yet used porous platens as endplates to insure frictional, rigid and highly permeable boundary conditions. Investigating how endplate deformation and permeability conditions affect intervertebral disc bio-mechanics is also a priority since endplate permeability plays a role in the degeneration process (Roberts et al., 1996; Bibby et al., 2001; Benneker et al., 2005).

The use of animal models in spine research is commonplace and important in its ability to test specific hypothesis despite obvious differences in geometry of motion segments and vertebrae (e.g. Lotz, 2004; Ledet et al., 2005). Use of rodent models for in vitro mechanical testing is limited because the small size presents differences in geometry with the human and makes sample preparation difficult. Caudal discs were also used as a representative structural and compositional model for discs research (Ohshima et al., 1993;Demers et al., 2004), and remain an attractive model because of the geometric simplicity and lack of sagittal curvature. Rat caudal discs are used in this study because of the substantial and growing body of in vivo and ex vivo mechanobiology research using small animals (e.g. rabbits, rats, and mice) (Iatridis et al., 1999; Gruber et al., 2002; Ching et al., 2003; Hsieh and Lotz, 2003; Norcross et al., 2003; Risbud et al., 2003;Maclean et al., 2004; An et al., 2005; Kim et al., 2005;Sobajima et al., 2005). It was recently reported that mouse lumbar discs matched the previously reported nonlinear response of human lumbar discs while mouse caudal discs only matched the linear response provided differences in cross-sectional areas were accounted for (Sarver and Elliott, 2005).

This study addresses the role of endplate conditions on mechanical behaviors of intervertebral discs by investigating mechanical behaviors of rat caudal motion segments, caudal disc explants, and vertebrae. This study tested the hypotheses that: (1) deformations of both the vertebrae and intervertebral discs account for observed deformation behaviors of the intact motion segment; (2) mechanical behaviors of the intervertebral disc tested as explants are similar to those in the motion segments provided that endplate boundary conditions are similar; and (3) axial compression loading on motion segments will lead to non-recoverable deformations in both the vertebrae and intervertebral disc.

2. Methods

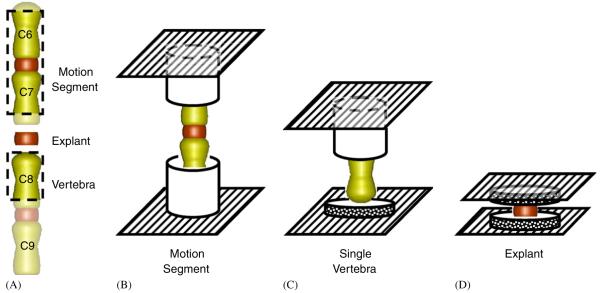
Four experimental groups consisting of motion segments (Group 1, vertebra-disc-vertebra), disc explants (Group 2—using permeable platens & Group 3—using impermeable platens), and single vertebrae (Group 4) were isolated from adjacent caudal levels of Sprague-Dawley rats (n = 44, 11 per group). Rats were obtained within 2 h of their death, skin and soft tissues were removed from the tail which was flash frozen in liquid nitrogen. A motion segment, disc explant and vertebra were harvested from c6-c8 levels of each tail, and 11 additional c7-8 discs were harvested for the second explant group (Fig. 1).

Fig. 1.

Schematic of rat tail demonstrating where specimens were harvested (A), and the testing setup for motion segments (B), single vertebrae (C), and disc explants (D).

For ‘motion segment’ specimens, approximately ⅓ of the proximal c6 and distal c7 vertebrae were removed in order to promote fluid flow while leaving enough bone to grip the specimens, which were potted in aluminum tubes using cyanoacrylate. Care was taken to insure axial alignment of the specimens within the pots, and that no adhesive covered either end of the vertebrae. Custom grips were used to load potted specimens in an environmental bath.

Disc ‘explant’ specimens (c7-8 with no endplates) were harvested using a scalpel by making transverse cuts through each endplate. A 5-mm biopsy punch and scalpel were then used to isolate the disc from the surrounding tissue. Care was taken to insure the disc remained completely frozen during dissection in order to preserve nucleus material. Disc height and diameter were measured using a dissecting microscope prior to mechanical testing. Explant specimens were placed in the test chamber between sintered steel platens with a permeability of 3.2×10^-10 m⁴/N s and pore size of 20 μm (Mott Metallurgical Corp., Farmington, CT) which is several orders of magnitude greater than that reported for native endplates (Setton et al., 1993; Ayotte et al., 2001). The second set of explants was tested using sintered steel porous platens that were modified to reduce the permeability without affecting surface roughness, by applying silicone sealant over the entire surface except for the area where the disc made contact. A permeability test demonstrated no fluid was transported through the modified platens indicating average platen permeability was reduced to zero.

‘Single vertebra’ specimens from c8 were harvested and, as with motion segments, approximately ⅓ of the proximal end was removed and the remaining vertebrae was potted in an aluminum tube. The disc was dissected off of the distal end of the vertebrae with a scalpel, which was loaded against the same porous platen used for explant testing. The sharp dissection removed all soft disc tissue and cartilage endplate so that all deformations measured represented vertebral deformation only.

All specimens in Groups 1-3 underwent a force-controlled test protocol at room temperature using our axial testing machine (Enduratec ELF-3200, Bose Corporation, Minnetonka, MN) while equilibrated in PBS with protease-inhibitors (1 mM Iodoacetamide, 1 mM Benzamidine, 2 mM EDTA, Sigma—Aldrich St. Louis, MO). Load (±0.001 N), displacement (±1.0 μm) and time data were record continuously during the following five-stage loading procedure (Fig. 2): (1) equilibration at 0.04MPa (~0.5 N) compression for 4 h, (2) 0.2MPa (~2.5 N) creep for 4 h, (3) recovery-1 at 0.04MPa for 6 h, (4) 1.0MPa (~12.6 N) creep for 4 h, and (5) recovery-2 at 0.04MPa for 6 h, where the ‘apparent’ stresses applied were based on disc cylindrical cross-sectional area at dissection. Specimens in Group 4 underwent only stages 1 and 4 of the loading procedure, but were otherwise treated identically.

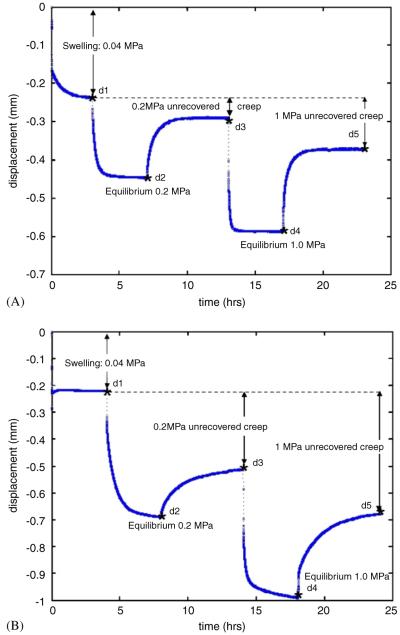
Fig. 2.

Displacement data with time obtained for the full mechanical testing protocol for a typical (A) explant and (B) motion segment. Displacement point’s d1, d2, d3, d4, and d5 refer to the displacement after 4 h at 0.04 MPa, after 4 h at 0.2 MPa, after 6 h of recovery following the 0.2MPa load, after 4 h at 1.0MPa and after 6 h of recovery following the 1.0MPa load, respectively. These markers are slightly offset from data for increased visibility.

The elastic properties were determined from load, displacement and time data, while viscoelastic parameters were determined by curve fitting to a stretched-exponential model describing the time-dependent displacement (Berry and Plazek, 1997; Lakes, 1999) as used previously for motion segments (Sarver and Elliott, 2005)

$$d\left(t\right)=d_0+(d_{\infty }-d_0){\mathrm{e}}^{-{(t∕\tau )}^{\beta }},$$

where d(t) is the time-dependent displacement, t the time, d₀ the instantaneous displacement, d_∞ the equilibrium displacement, τ the time constant, β the stretch parameter (0<β<1). The stretched exponential model has 2 parameters describing the transient nature of the mechanical response. The value of τ may be considered an average time constant for creep (or recovery) process while the parameter β was related to the ‘slope’ of the creep (or recovery) curve on a semi-log plot. The time constant β was <1 for all samples indicating a single time constant was insufficient to describe viscoelastic behaviors and suggesting creep behaviors involved multiple deformation mechanisms (e.g. disc bulge, vertebral deformations, fluid transport, flow-independent deformations). The curve fit was performed using code written in MATLAB and a Gauss-Newton search algorithm (Mathworks, Natick, MA). Robust testing was done on the curve-fitting procedure with a very wide range of initial guesses and we are confident that a unique set of solutions (within physiological ranges for parameters) was obtained for each specimen. All 4 parameters were determined for each of the 2 creep and recovery tests on each specimen.

Relative disc deformations in the motion segment were determined by subtracting twice the deformation measured in the isolated c8 vertebrae (Group 4) from the deformation measured in the tail matched c6-7 motion segment (Group 1) and were compared to explant deformations measured in the c7-8 disc (Group 3) using a paired t-test. Parameters obtained for transient data using the stretched exponential function were evaluated using a 2-factor ANOVA with factors test type (i.e. motion segment, explant—impermeable boundary, explant—permeable boundary) and load level (i.e. repeated measures with values 0.2 and 1MPa) and Fisher’s PLSD post hoc analysis. All statistical analyses were performed with Statview software (SAS Institute, Cary, NC) and significance level p<0.05. Viscoelastic parameters compiled were used for the following 3 comparisons: first, comparison between test types (i.e. motion segment, explant—impermeable endplate, explant—permeable endplate) allowed characterization of the influence of endplate conditions on viscoelastic response; second, comparison between load magnitudes (i.e. 0.2 and 1MPa) allowed characterization of the amount of amplitude-dependent nonlinear behaviors present; third, comparison of creep and recovery response allowed characterization of the differences between these loading modes on the viscoelastic response.

3. Results

Explant specimens were at equilibrium after the initial dwell period and at the end of all creep and recovery stages. Motion segment specimens were at equilibrium at the end of each creep stage, yet small transient recovery behaviors continued in a few specimens past the 6 h recovery periods for several specimens (e.g. Fig. 2B), however pilot tests that extended the recovery to 24 h demonstrated only a very small amount of additional recovery occurred (≤0.02 mm). Equilibrium behaviors demonstrated that motion segments underwent substantially larger deformations under 1.0MPa loading than disc explants (Fig. 3). However, after accounting for vertebral deformations, the disc deformations in the motion segments were not significantly different from explants (p = 0.4).

Fig. 3.

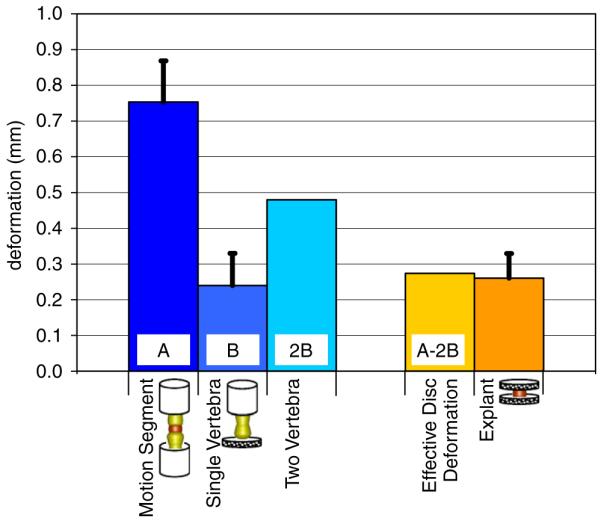
Equilibrium displacement data for motion segment, vertebrae and explants loaded to 1MPa apparent stress. Comparison demonstrates the equilibrium disc deformation is similar in the disc explant and motion segment. However motion segment undergoes large total deformations due to contributions from vertebrae and discs.

Permanent deformations were recorded in motion segments and explants and are referred to as “unrecovered creep” after 0.2 or 1MPa (Table 1). The unrecovered creep displacements were greater for motion segments than for explants and also demonstrated amplitude-dependent nonlinearities since increasing applied load by 5-fold (from 0.2 to 1 MPa) resulted in an increase in unrecovered creep less than 2-fold.

Table 1.

Non-recoverable displacement for 0.2 and 1MPa loading experiments

Loading (MPa)	Permanent deformation
	Motion segment	Explant
0.2	0.20±0.09	0.03±0.02
1.0	0.32±0.12	0.06±0.03

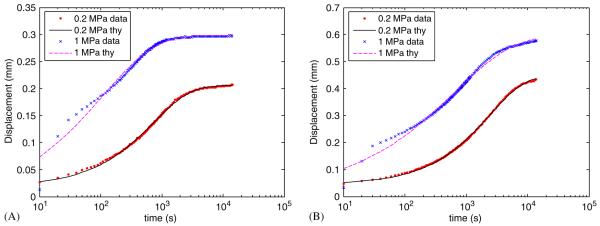
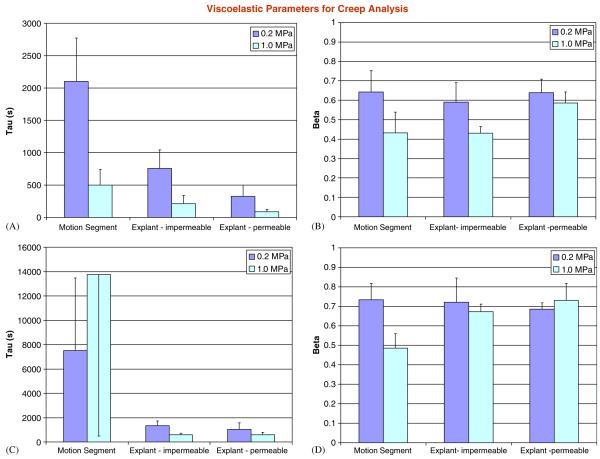
All specimens underwent creep and recovery that was well described by the stretched-exponential function (Fig. 4 and Table 2). For both creep and recovery data, there were highly significant effects of test type on all model parameters (d₀, d_∞, d_∞ - d₀, τ, and β). Significant effects of loading magnitude (0.2 vs. 1 MPa) were also detected for all parameters for the creep analysis and for all parameters from the recovery analysis except for the time constant τ (p = 0.08). Significant interactions were also detected for d₀, τ, and β for the creep analysis andfor all parameters for the recovery analysis. Of particular relevance for the creep analysis was the fact that time constants, τ, were significantly different between all test types with the motion segment having the largest values followed by the explants with impermeable and then permeable platens (Fig. 5). For the parameter β significant differences were detected between motion segments and explants with permeable platens (p = 0.03), and for explants with impermeable vs. permeable platens (p = 0.005), but not for explants with impermeable platens vs. motion segments (p = 0.46). Also of interest was the fact that the time constants for the recovery analysis were substantially longer than for the creep analysis (Table 2). Average coefficients of determination for nonlinear regression analyses for all creep and recovery analyses were 0.993±0.004 indicating the curve fits were excellent.

Fig. 4.

Creep data for (A) disc explant and (B) motion segment samples subjected to effective stresses of 0.2 and 1MPa. Experimental data and stretched exponential model are both shown with creep deformations given as positive in compression, with time-axis adjusted so that both 0.2 and 1MPa experiments begin at t = 0⁺ and with different y-axis scales.

Table 2.

Viscoelastic model parameters for the 0.2 and 1MPa creep and recovery tests for motion segments (MS), explants with impermeable platen (exp-imp) and explants with permeable platen (exp-perm) boundary conditions

Parameter	Creep analysis			Recovery analysis
	MS	Exp-imp	Exp-perm	MS	Exp-imp	Exp-perm
0.2MPa
d0 (mm)	0.062±0.024	0.024±0.016	0.008±0.006	0.014±0.012	0.009±0.004	-0.001±0.002
d∞ (mm)	0.49±0.12	0.24±0.03	0.15±0.06	0.29±0.22	0.16±0.03	0.11±0.03
d∞-d0 (mm)	0.43±0.11	0.21±0.03	0.14±0.05	0.28±0.21	0.15±0.03	0.11±0.03
τ (s)	2102±671	757±285	325±173	7508±5967	1343±394	1032±535
β	0.64±0.11	0.59±0.10	0.64±0.07	0.73±0.08	0.72±0.12	0.68±0.03
r2	0.994±0.006	0.994±0.004	0.996±0.002	0.997±0.003	0.995±0.003	0.999±0.001
1.0MPa
d0 (mm)	0.024±0.020	0.006±0.013	-0.003±0.008	-0.025±0.015	-0.034±0.008	-0.02±0.004
d∞ (mm)	0.57±0.16	0.36±0.05	0.22±0.06	0.64±0.39	0.26±0.04	0.17±0.04
d∞-d0 (mm)	0.55±0.14	0.35±0.04	0.22±0.06	0.66±0.39	0.29±0.04	0.19±0.04
τ (s)	498±245	212±129	87±42	13750±13259	604±117	599±212
β	0.43±0.11	0.43±0.03	0.59±0.06	0.49±0.07	0.67±0.04	0.73±0.09
r2	0.991±0.004	0.990±0.002	0.989±0.004	0.993±0.003	0.990±0.003	0.993±0.004

Fig. 5.

Average values for the time constants from the stretched exponential fits for 0.2 and 1MPa experiments for creep (A,B) and recovery (C,D) experiments. The time constant, τ, was significantly affected by endplate permeability conditions for both creep and recovery experiments while the time constant β was insensitive to endplate permeability conditions. Note that scales are different in each sub-figure.

4. Discussion

This study evaluated the influence of endplate conditions on equilibrium and viscoelastic mechanical behaviors of intervertebral discs by testing rat caudal motion segments, isolated vertebrae, and intervertebral disc explants with two platen permeability conditions. There were four major findings. First, we demonstrated motion segment testing involved significant deformations of vertebrae and intervertebral discs, even under relatively low-compression loading conditions, in support of our first hypothesis. Second, we found that cutting the annular fibers that anchor into the vertebrae to create explant specimens had minimal impact on equilibrium deformations of disc explants as compared to disc deformations occurring in the motion segments provided that vertebral deformations were accounted for, consistent with our second hypothesis. Third, decreasing the permeability of the porous platen had significant effects on transient behaviors of explants prolonging both creep and recovery time, also consistent with our second hypothesis. Fourth, we found both disc explants and motion segments had non-recoverable deformations under axial compression under low and high loading conditions consistent with our third hypothesis.

This study highlights potentials and limitations of testing motion segments vs. explants when studying the disc. Motion segment testing preserves in situ conditions most closely; however our results underscore the importance of considering vertebral deformations when interpreting spine biomechanics and mechanobiology studies. Of particular relevance is the understanding that large deformations reported in mechanobiology studies applying compression loading to rodent tail motion segments using external fixators result in strains in both the discs and in the vertebral endplates (Lotz et al., 1998; Iatridis et al., 1999; Ching et al., 2003; MacLean et al., 2003; Maclean et al., 2004; Walsh and Lotz, 2004) as has been observed in the vertebral endplates of human lumbar motion segments (Brinckmann et al., 1983). On the other hand, disc explant testing allows more precise control over boundary conditions and our results suggest that cutting the annulus fibers that anchor the disc to vertebrae had minimal impact on disc equilibrium deformations compared to motion segments provided that the vertebral deformations were accounted for and also provided that the surface roughness of the platens created an adequate frictional condition to allow the severed annulus fibers to support the radial bulge of the nucleus. In explant testing, the presence of the stiff-sintered steel platens prevents the nucleus from bulging in the axial direction, as is reported to occur in the motion segment, implying that the nucleus would impart greater than normal radial pressure to the annulus. Therefore, despite the fact that the one-dimensional steady-state creep behavior of isolated explants was similar to the discs within the motion segments, it is likely that the mechanism for load support and three-dimensional strain fields were some-what different. While one-dimensional measurements of motion segment or disc deformation are commonly used in the literature it is well established that disc deformations occur in three-dimensions particularly for human spinal motion segments due to their ‘kidney-bean’ shape and substantial sagittal curvature (Brinckmann et al., 1983; Seroussi et al., 1989; Meakin and Hukins, 2000; Tsantrizos et al., 2004).

Significant differences in the transient behavior of explants and motion segments were observed in this study and are most likely related to differences in boundary conditions (platen stiffness, permeability, and surface roughness); however, structural differences in the explants resulting from annulus fibers being severed may also contribute to the observed changes. A larger time constant for the impermeable case and the motion segments is entirely expected and suggests a different path for fluid flow. Our technique of applying silicone sealant to the platens effectively reduced the permeability; however, it is possible that fluid transport may have occurred adjacent to the disc explants explaining some of the differences in time constants between the motion segment and explant with impermeable boundary condition. Differences in boundary conditions affecting flow-independent viscoelastic responses may also contribute to differences in time constants.

For creep studies, the value for β was lower for 1MPa loading and also lower for motion segments and explants with impermeable platens than for explants with permeable platens suggesting there were more complex deformation mechanisms under higher loading conditions and when endplates were not fully permeable.

Time constants were greater for recovery than for creep under all experimental conditions suggesting the mechanisms for viscoelastic recovery did not occur as rapidly as for creep. This is in contrast to the concept of disc permeability as a bi-directional valve where disc recovery occurs more quickly during the diurnal cycle than does creep compression (Ayotte et al., 2001). This apparent difference may be due to the fact that in the Ayotte et al. study only a very thin section of vertebral bone remained, great care was taken to remove coagulated marrow, and there was forced convection in the perfusion study while in our study a much larger section of vertebral body was included and convective transport occurred only due to passive recovery via the disc’s swelling propensity. However, this contrast may also be indicative of differences between compression creep and recovery occurring in vivo compared to in vitro. For example, creep in vivo involves spinal deformations in the upright posture that includes decreased disc height and increased spinal curvature (Kimura et al., 2001; Jorgensen et al., 2005) upon resting in the supine posture, resulting changes in curvature involve bending moments that may add tensile stresses providing an ‘active’ loading component to recovery in vivo. Dynamic loads resulting from respiration may further contribute to active loading states in vivo during recovery (Keller et al., 1990). Finally, understanding differences between osmotic pressure and hydrostatic pressures while under loading and recovery (Gu and Yao, 2003; Iatridis et al., 2003; Ekstrom et al., 2004; Huyghe and Drost, 2004; Natarajan et al., 2004) are necessary to further understand how load carriage mechanisms and transport phenomena in discs occur in vivo as well as to understand how to interpret in vitro results.

We reported non-recoverable deformations of the motion segment and intervertebral discs under load levels as low as 0.2MPa and increasing in a nonlinear manner with applied load magnitude. These non-recoverable deformations may be compared to initial heights of disc explants (~0.8 mm) and motion segment specimens (~8 mm) indicating these permanent deformations represent less than 7.5% and 4% height loss, respectively. Disc stiffness and relaxation levels were previously reported to return to pre-loaded levels after 18 h of recovery yet disc height before and after loading was not measured (Johannessen et al., 2004). Non-recoverable deformations were previously reported in a porcine model under cyclic loading (Ekstrom et al., 1996), and non-recoverable deformations in cartilage were also reported under strains as low as 2% (Langelier and Buschmann, 2003) consistent with our findings. Non-recoverable deformations in motion segments are consistent with the hypothesis that minor damage to vertebral bodies can lead to progressive disruption of the adjacent discs (Adams et al., 2000). Our results indicate minor losses in height of both vertebrae and discs occur simultaneously in vitro. Additional recovery of motion segments in vivo is likely where active processes and permeable vertebral endplates are present, yet we suggest that some small amount of disc and vertebral height loss may also occur in vivo under fairly modest loading as part of a natural turnover/repair process. As loading becomes more extreme damage accumulates and height loss becomes permanent. In this study, testing of the vertebrae only group was performed for the purpose of evaluating deformation under loading and did not include a recovery phase. As a result, we are unable to evaluate the relative amounts of permanent deformation in the motion segment that can be accounted for by the vertebrae alone.

Some limitations in this study include the linear model which was used in a piece-wise manner to obtain amplitude-dependent nonlinear responses and may, in the future, warrant refinements that include both material and geometric nonlinearities when describing disc and motion segment behaviors. In addition, previous studies have reported that cyclic preconditioning can effectively equilibrate material and model parameters (Dhillon et al., 2001), yet a swelling equilibration was used in our study. This protocol was chosen so as to avoid large cyclic deformations that may affect measurements of non-recoverable deformations but may exaggerate the magnitude of un-recovered creep which we reported.

In conclusion, motion segment testing involved significant deformations of vertebrae and intervertebral discs even under relatively low compression loading conditions. Accurate testing and interpretation of biomechanical studies on intervertebral discs and motion segments must consider both of these deformation mechanisms. During explant testing, surface roughness was sufficient to maintain elastic behaviors of the disc but additional modifications to boundary conditions are necessary to more closely simulate viscoelastic behaviors of motion segments. Testing of motion segments is appropriate provided that consideration is given to the influence of vertebral deformations and endplate permeability conditions. On the other hand, testing explants is appropriate when the most precise control over mechanical and permeability boundary condition is desired. These findings have important implications for interpreting the role of vertebral endplates in contributing to disc mechanical behaviors and direct application to mechanobiology studies involving external loading to rodent tail intervertebral discs.